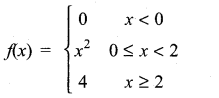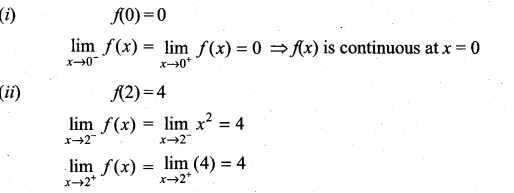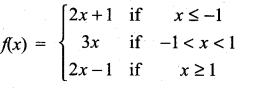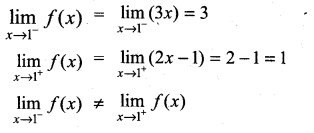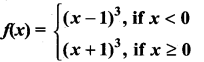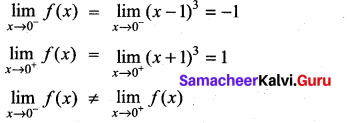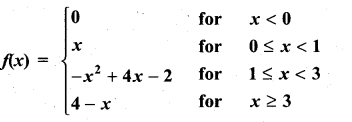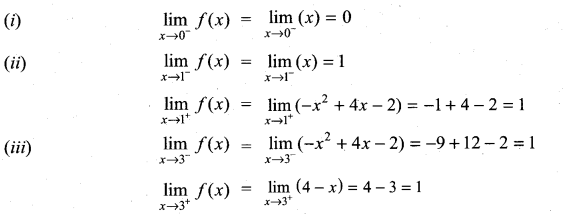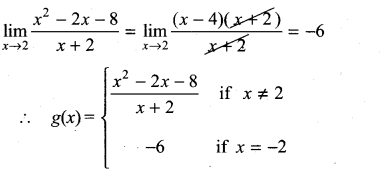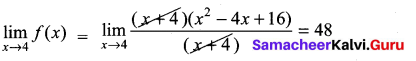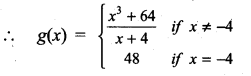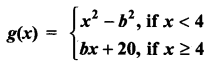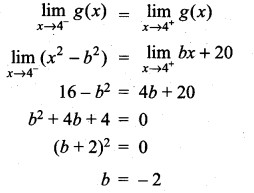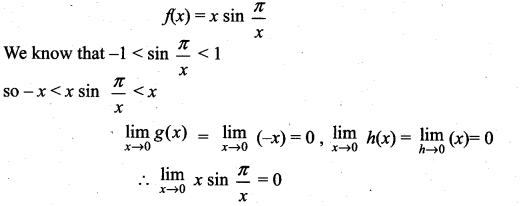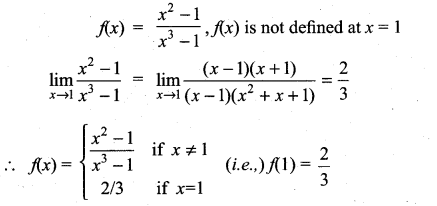You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.5
Question 1.
Solve 2x2 + x – 15 ≤ 0.
Solution:
To find the solution of the inequality
ax2 + bx + c ≥ 0 or ax2 + bx +c ≤ 0 (for a > 0)
First we have to solve the quadratic equation ax2 + bx + c = 0
Let the roots be a and P (where a < P)
So for the inequality ax2 + bx + c ≥ 0 the roots lie outside α and β
(i.e.,) x ≤ α and x ≥ β
So for the inequality ax2 + bx + c ≤ 0. The roots lie between α and β
(i.e.,) x > α and x < β (i.e.) a ≤ x ≤ β

![]()
Question 2.
Solve -x2 + 3x – 2 ≥ 0
Solution:
-x2 + 3x – 2 ≥ 0 ⇒ x2 – 3x + 2 ≤ 0
(x – 1) (x – 2) ≤ 0
[(x – 1) (x – 2) = 0 ⇒ x = 1 or 2. Here α = 1 and β = 2. Note that α < β]
So for the inequality (x – 1) (x – 2) ≤ 2
x lies between 1 and 2
(i.e.) x ≥ 1 and x ≤ 2 or x ∈ [1, 2] or 1 ≤ x ≤ 2
Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.5 Additional Questions
Question 1.
Solve for x.
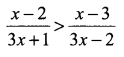
Solution:
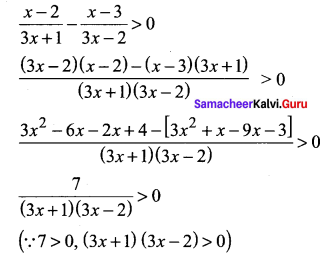
Select the intervals in which (3x +1) (3x – 2) is positive
(3x + 1) > 0 and (3x – 2) > 0 or
3x +1 < 0 and 3x – 2 < 0
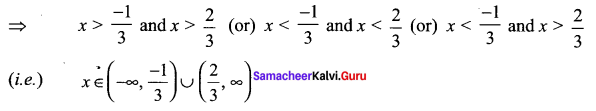
![]()
Question 2.
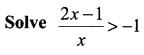
Solution:

![]()
Question 3.
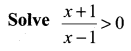
Solution:

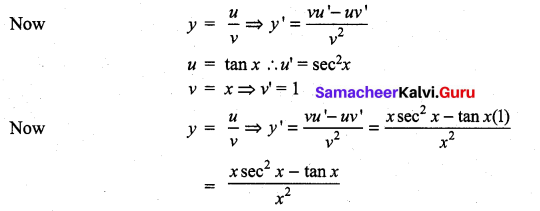
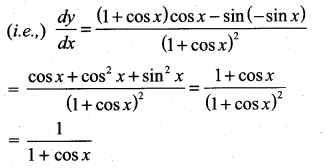
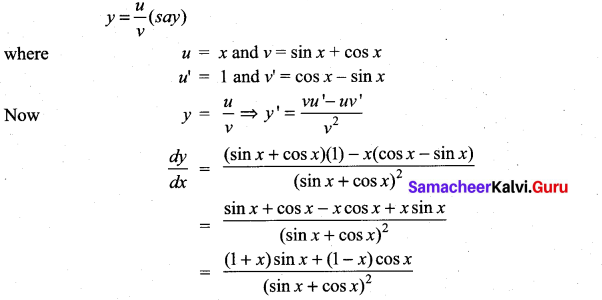

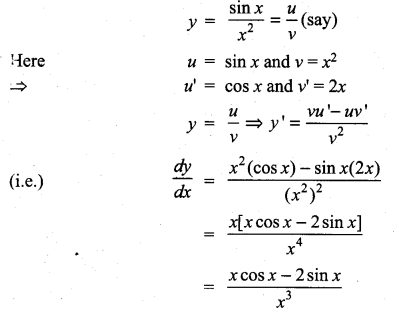

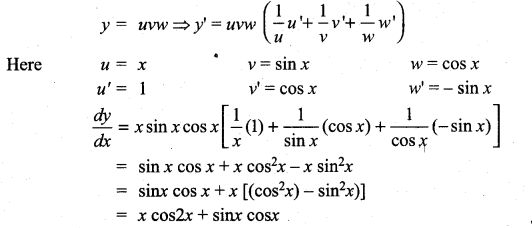
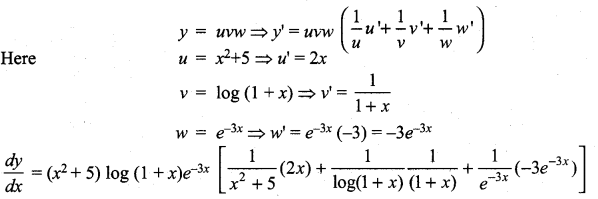
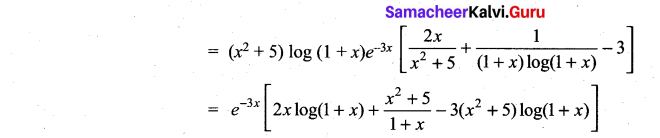
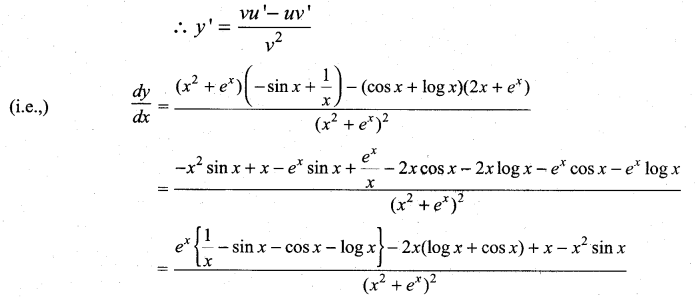

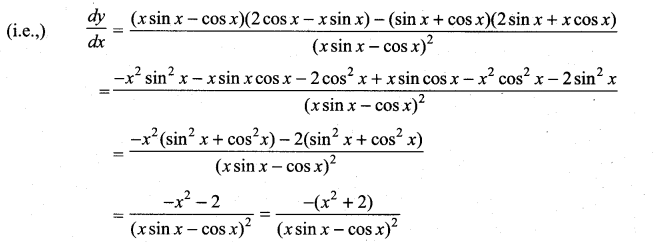

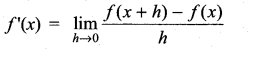

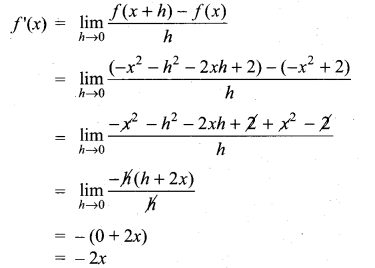
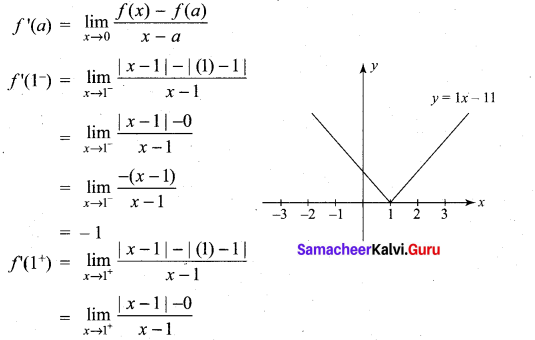
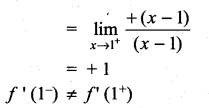
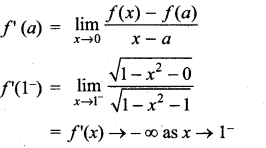
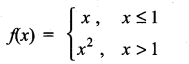
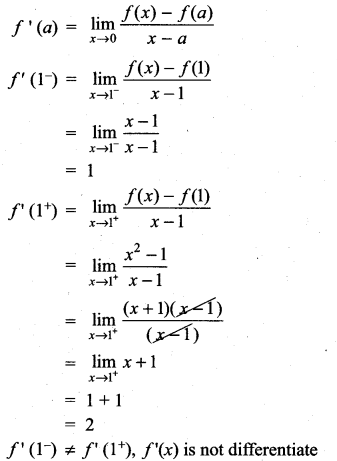
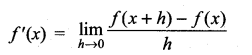
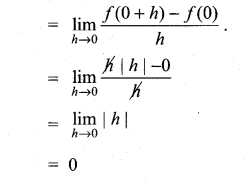

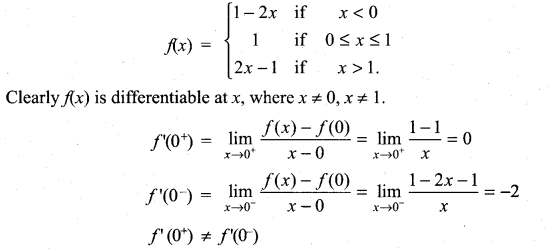
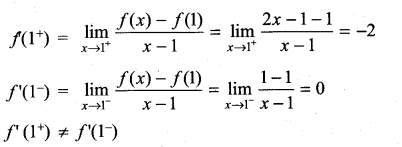
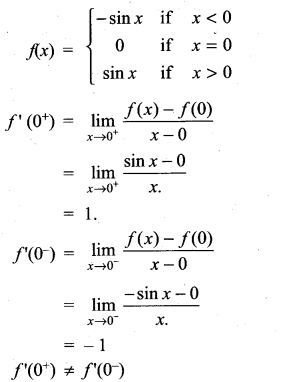
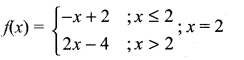

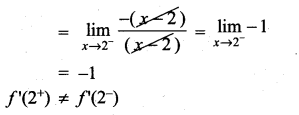
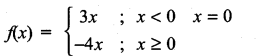
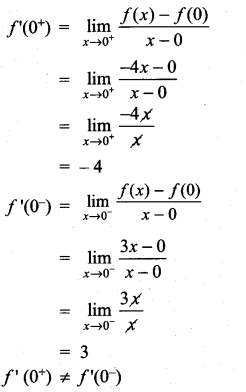

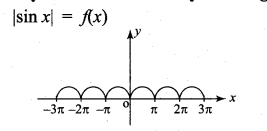
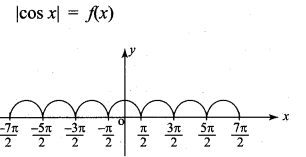

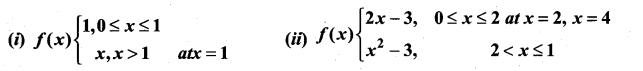

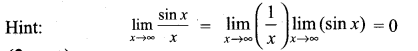
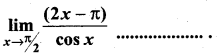

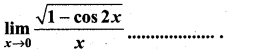
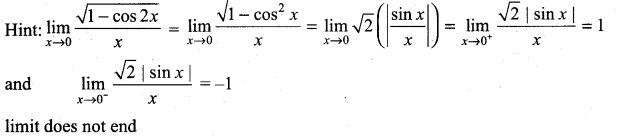

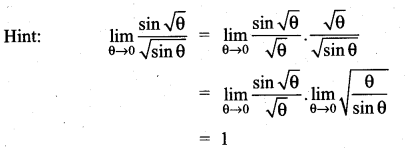
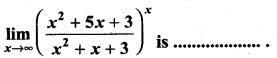

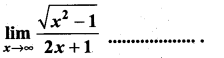
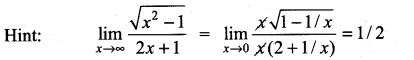
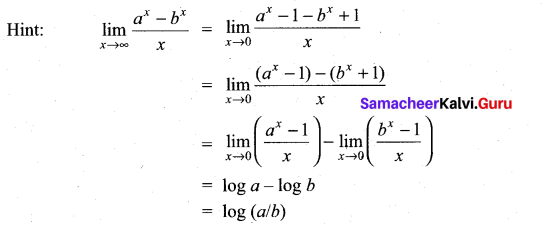
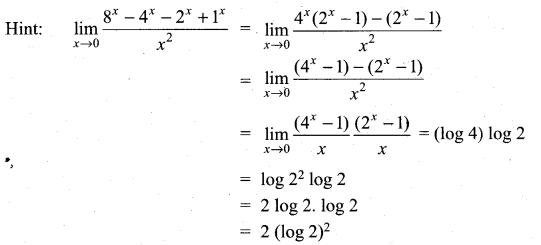
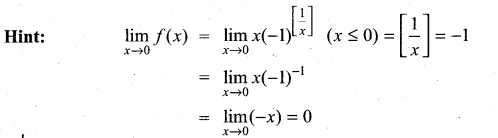
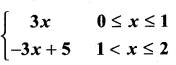 then ……………
then ……………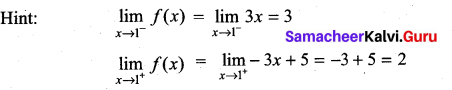
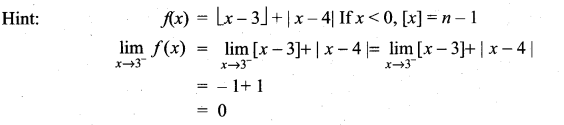
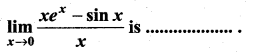
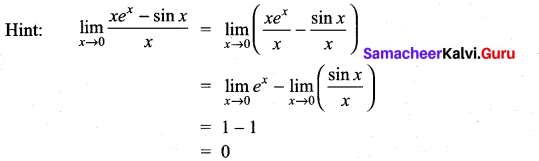
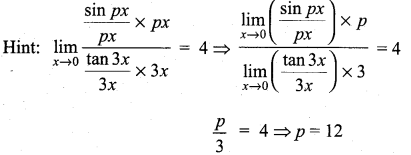
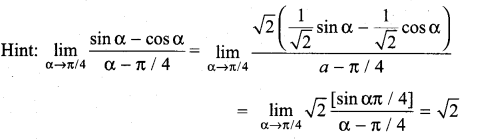
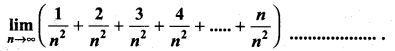
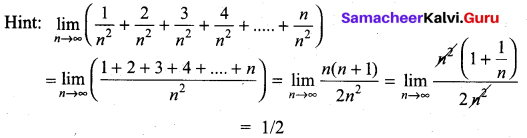
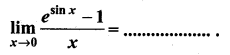
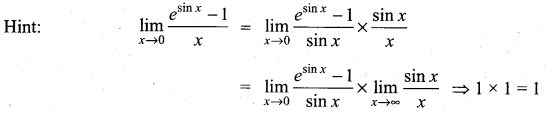
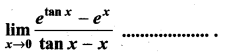

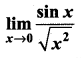 is ……………
is ……………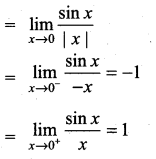
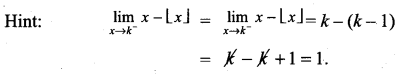
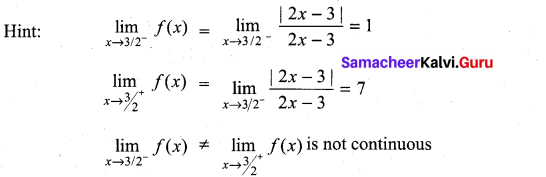
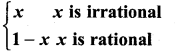 then f is ……………
then f is ……………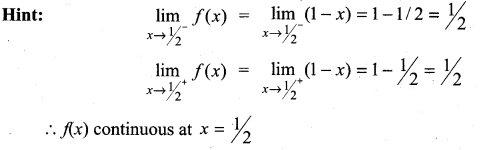
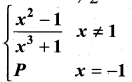 is not defined for x = -1. The value of f(-1) so that the function extended by this value is continuous is …………..
is not defined for x = -1. The value of f(-1) so that the function extended by this value is continuous is …………..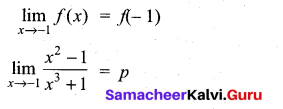
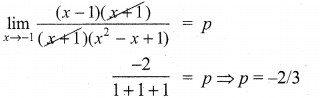
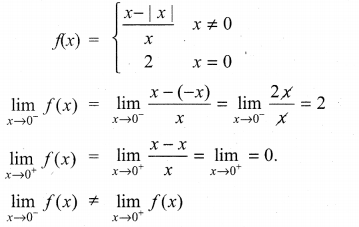
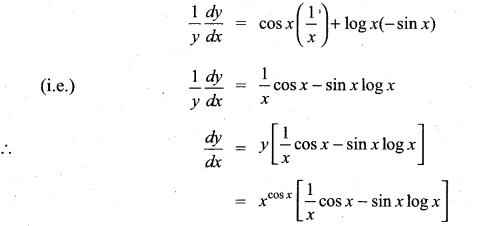


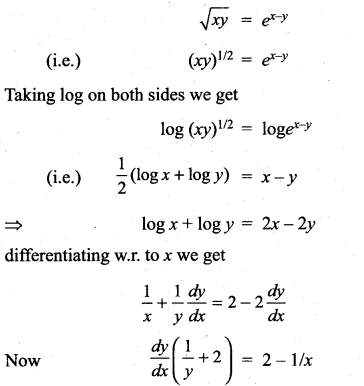
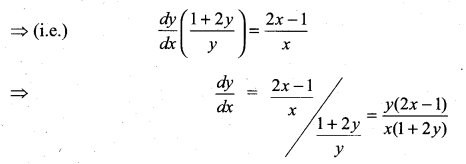
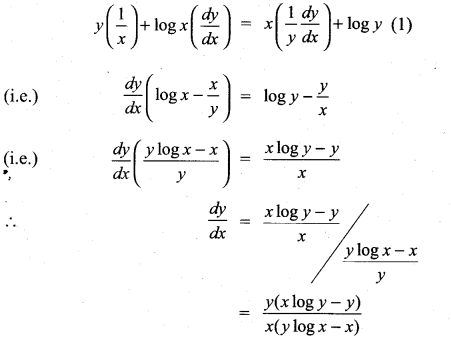
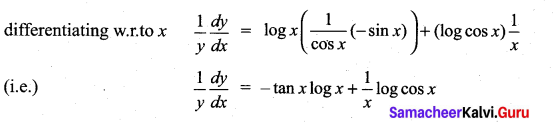
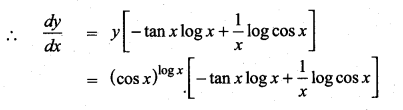

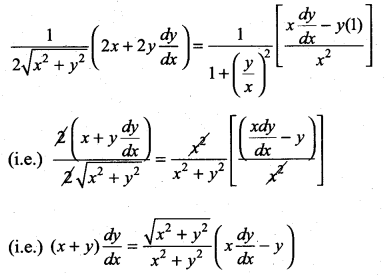
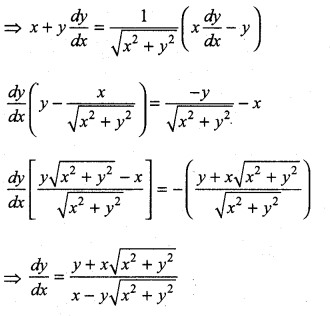
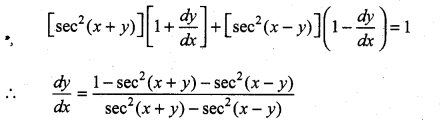

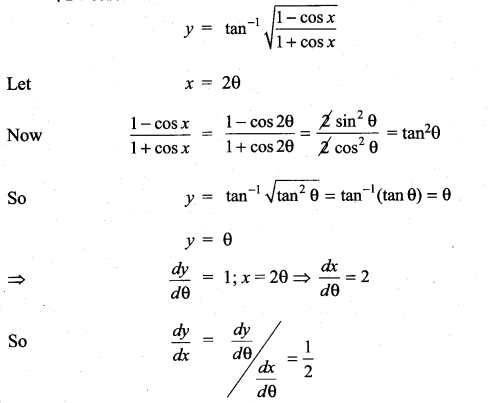
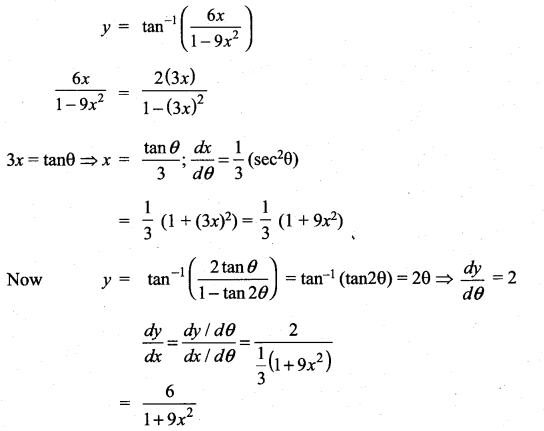
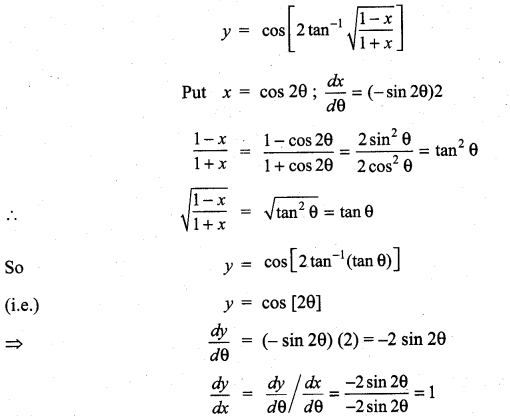
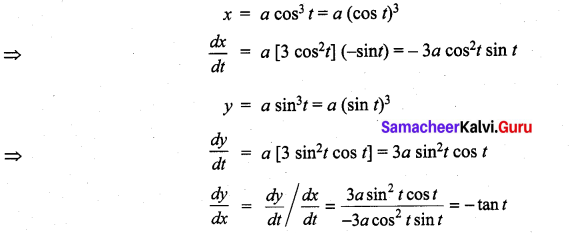
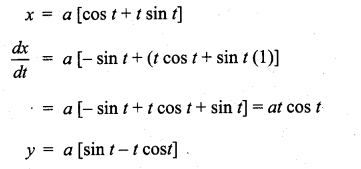
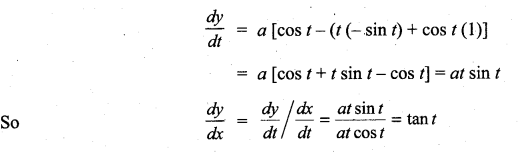

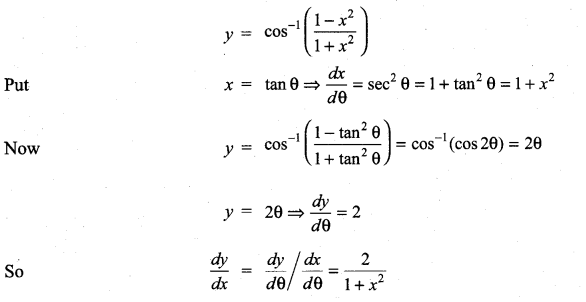
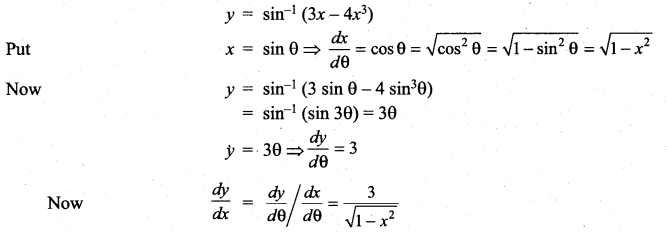
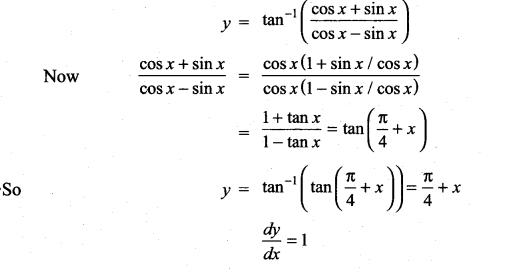

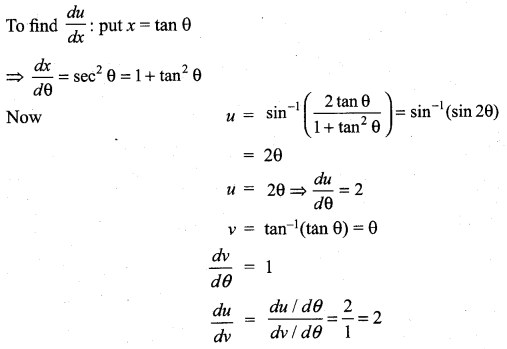
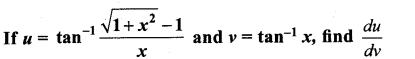

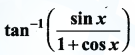 with respect to
with respect to 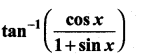
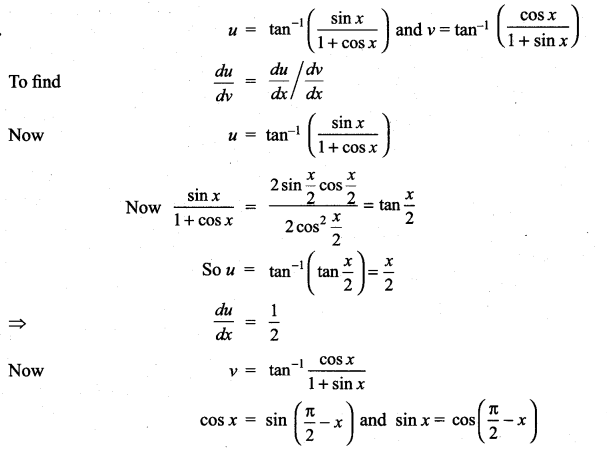
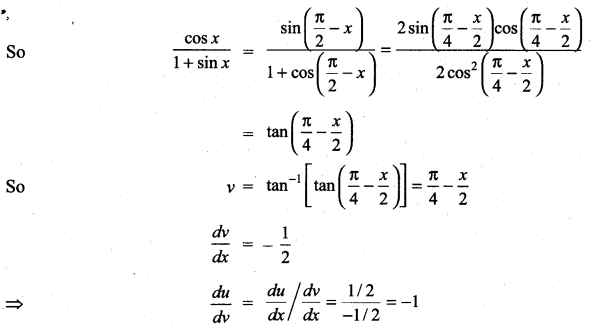
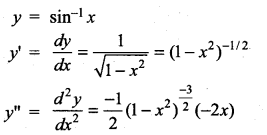
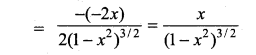

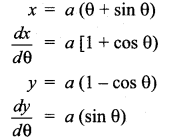

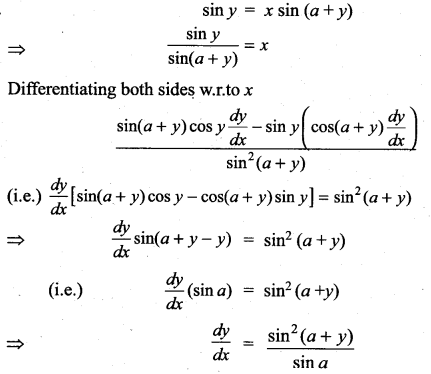

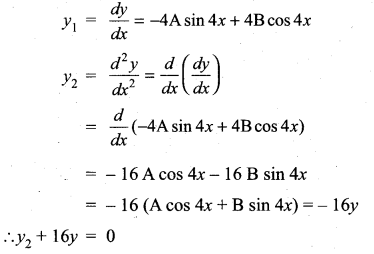



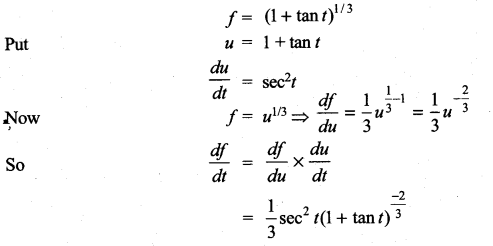
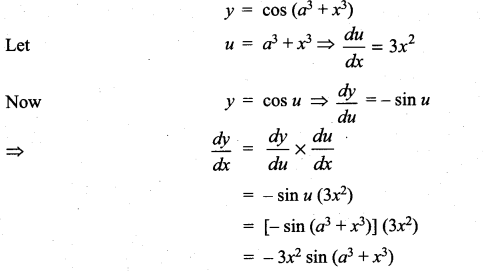
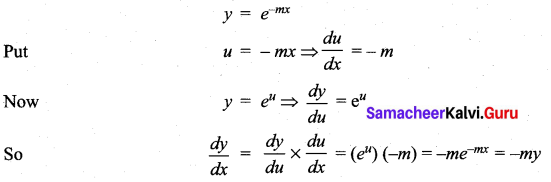
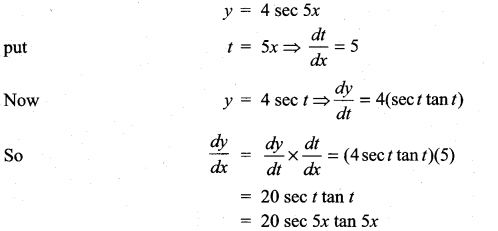

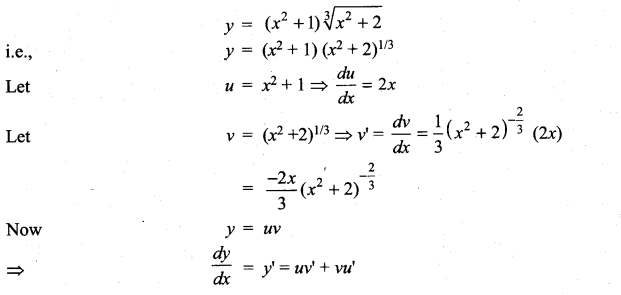
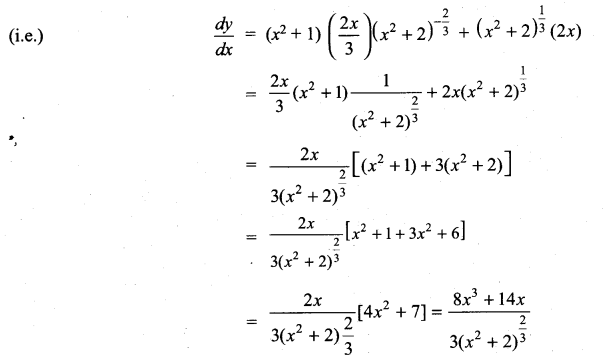
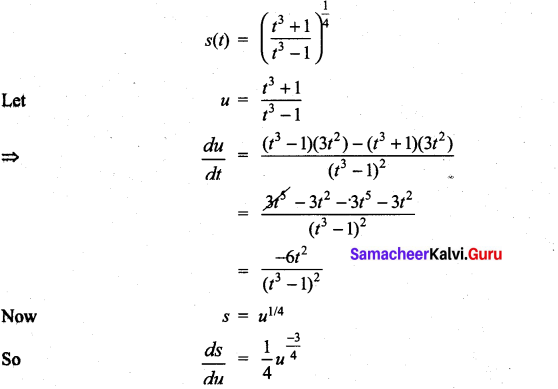
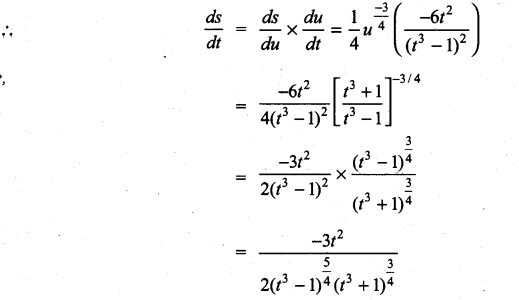
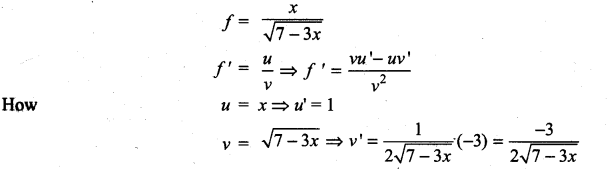
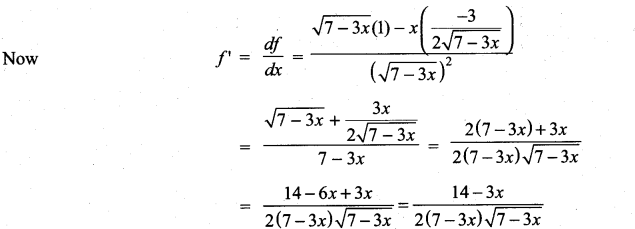
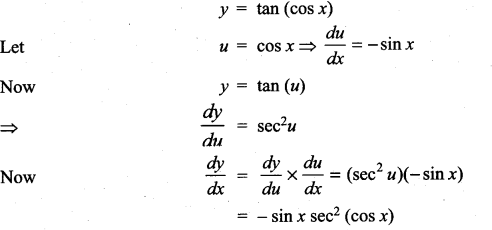


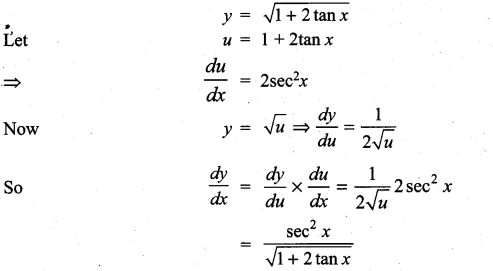
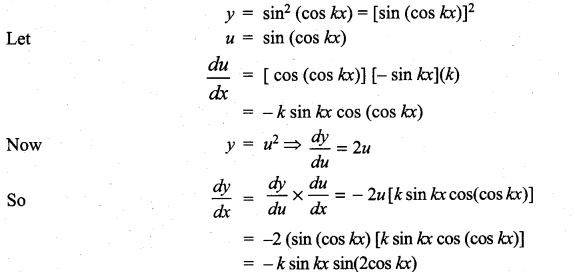
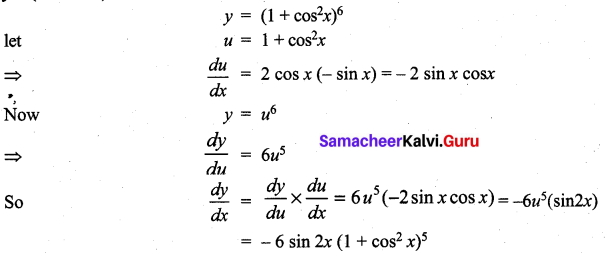
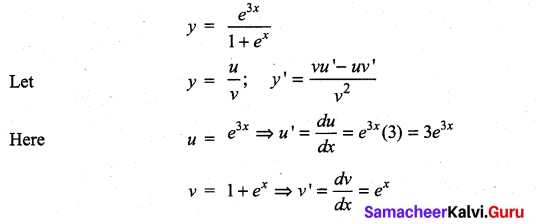
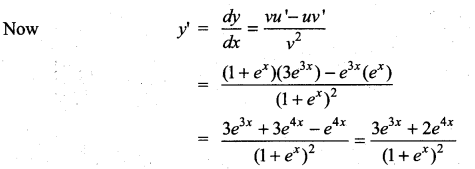
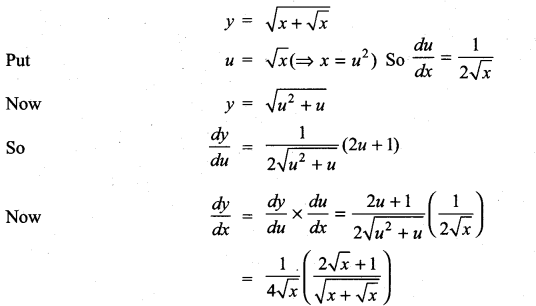
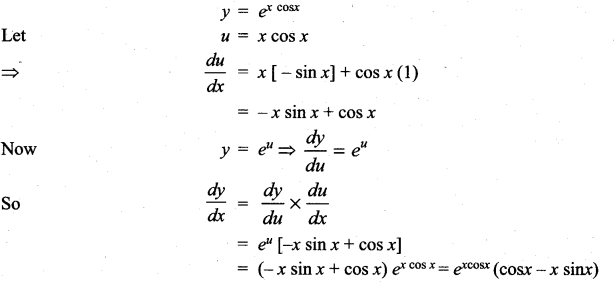
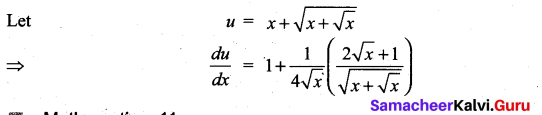
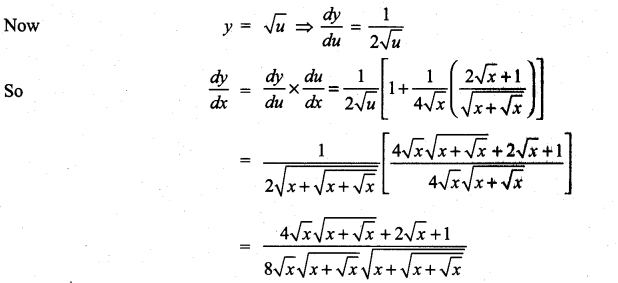
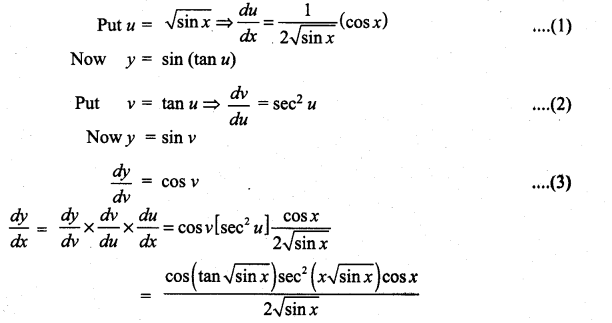

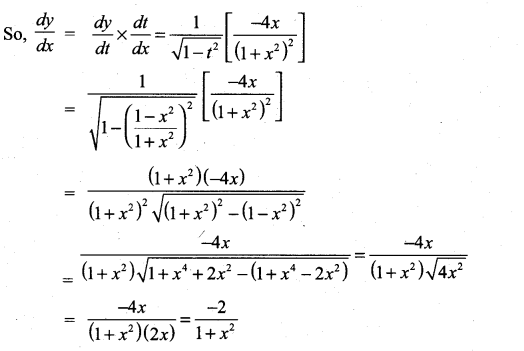
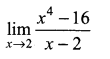
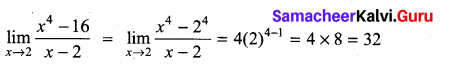
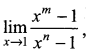 m and n are integers.
m and n are integers.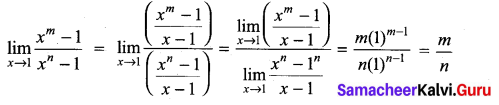
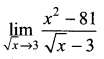
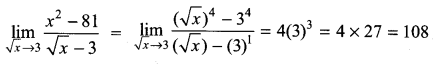
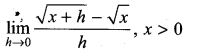
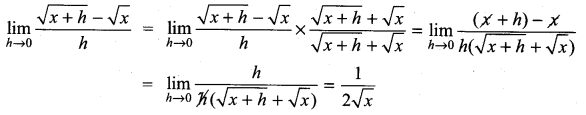
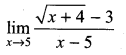
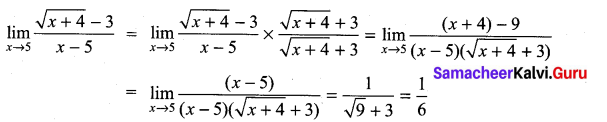
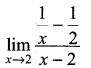
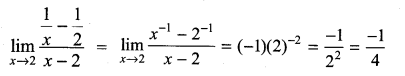
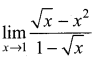
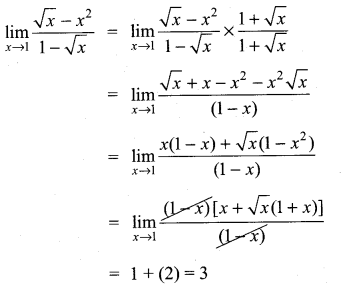
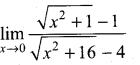
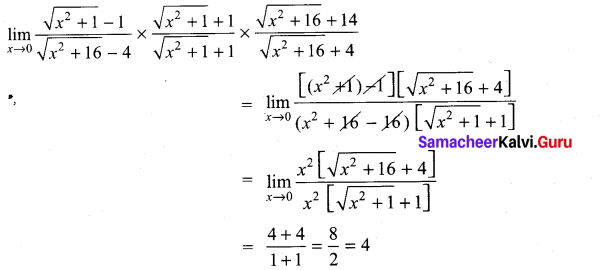
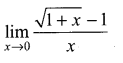
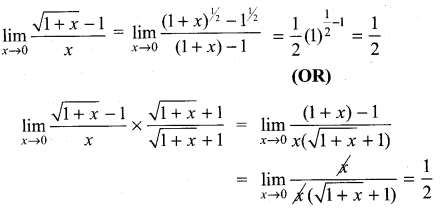
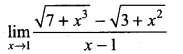
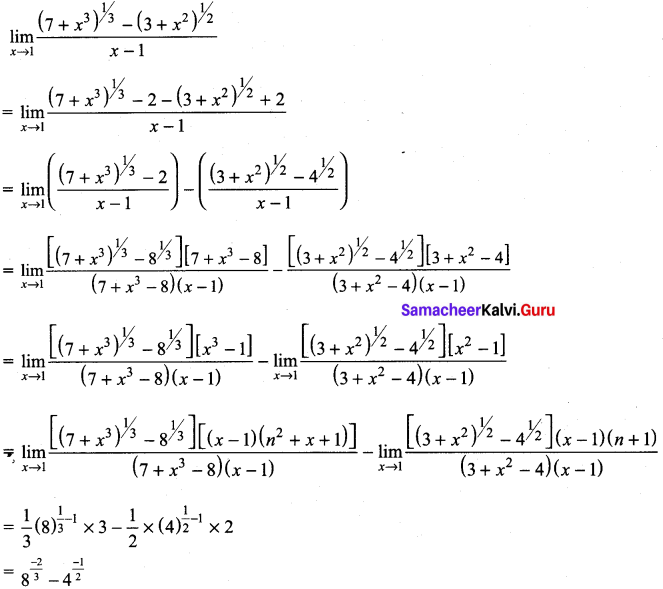
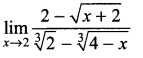
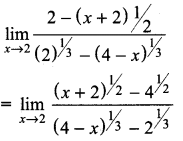
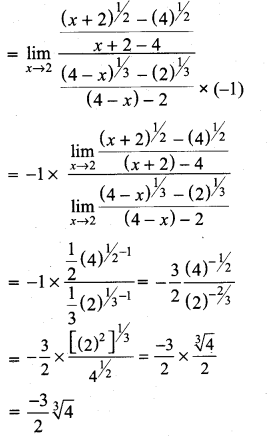
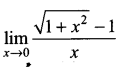
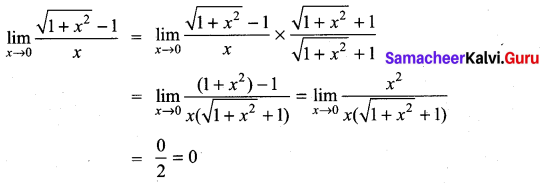
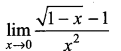
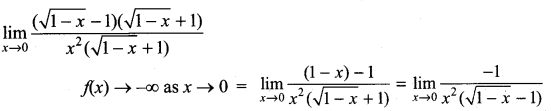
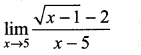
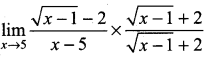

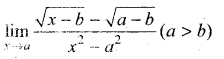

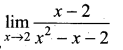

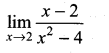

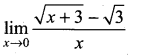

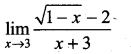




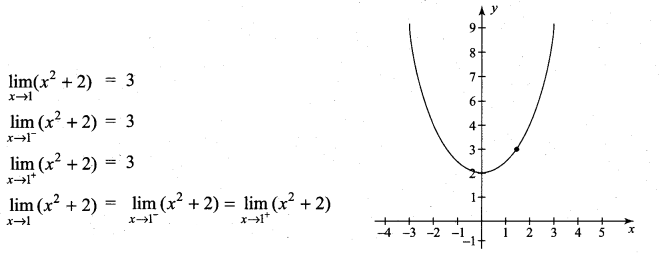
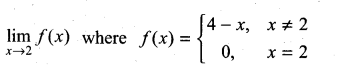
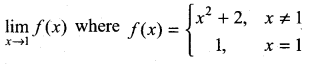
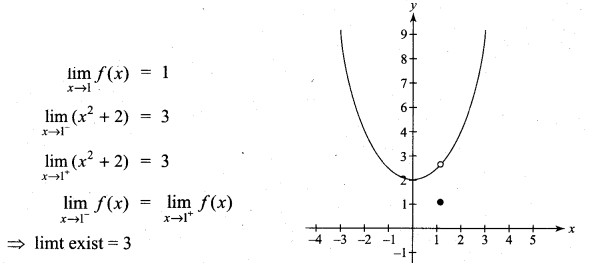
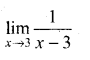
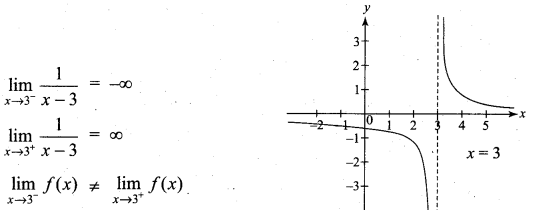
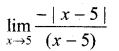
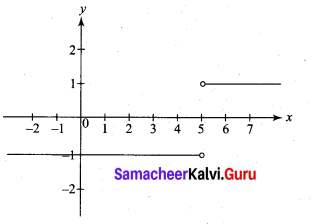
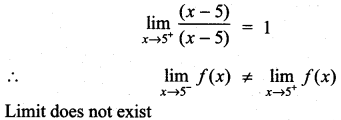
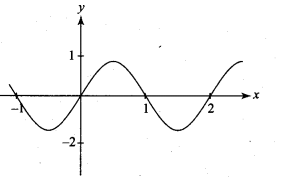
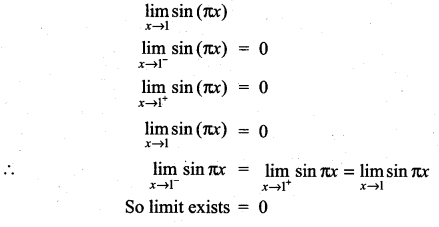
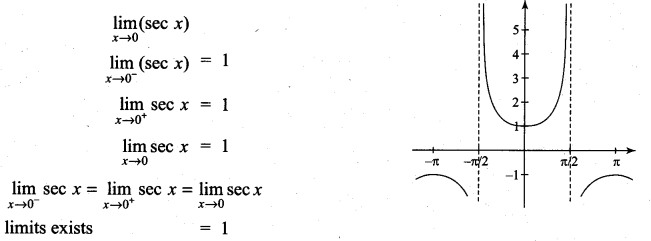
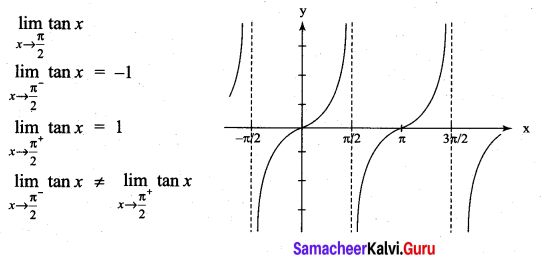
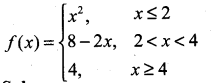
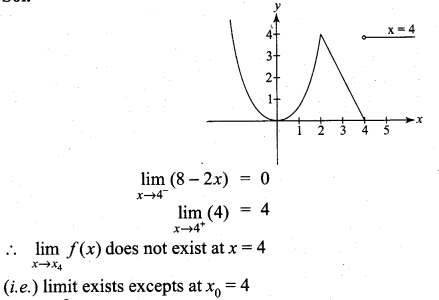
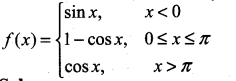
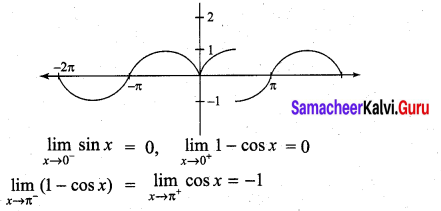

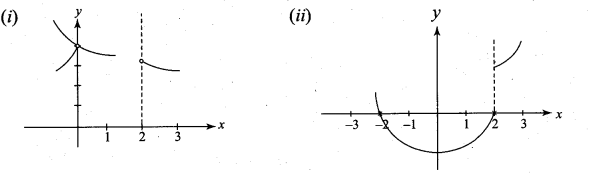
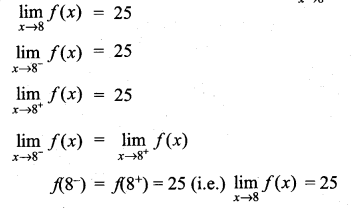
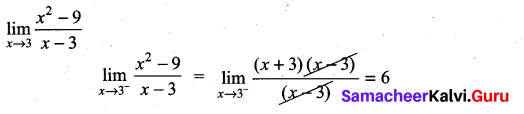
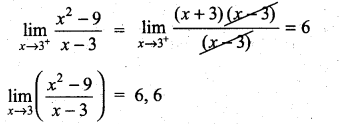
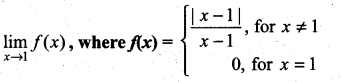
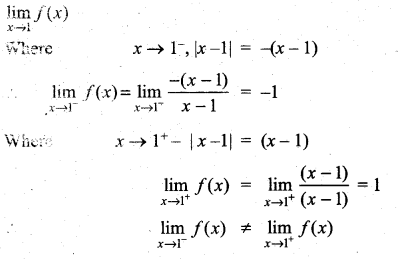
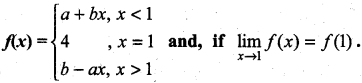 . What are possible values of a and b?
. What are possible values of a and b?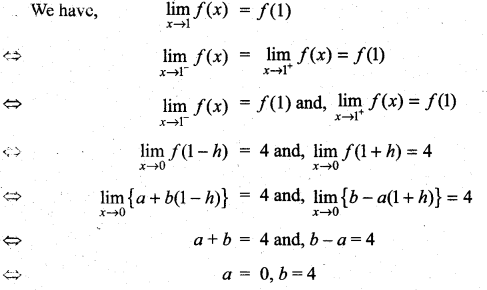
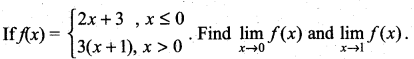

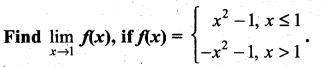
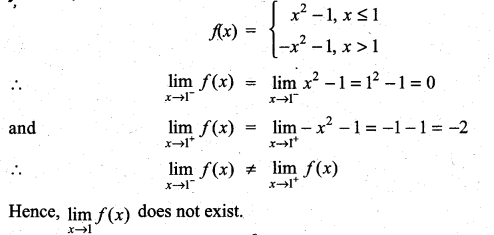
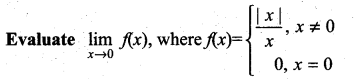
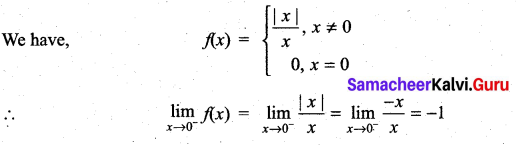
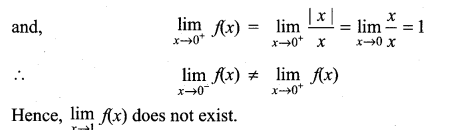
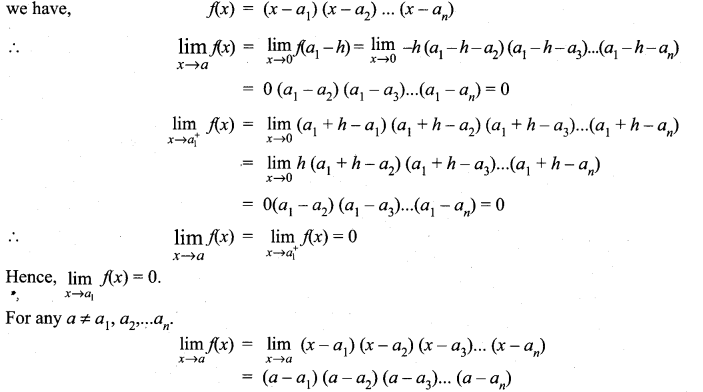
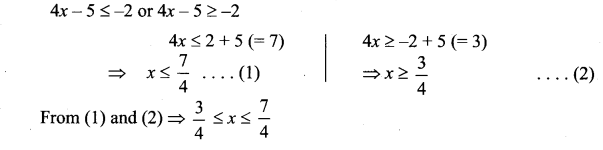
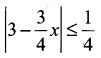
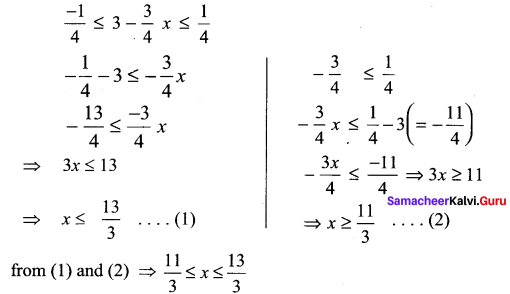

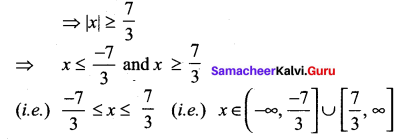

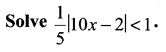
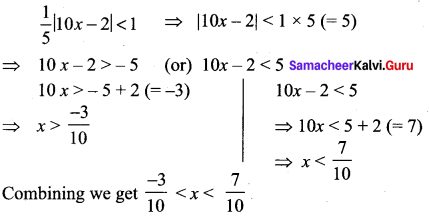

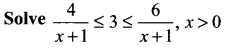

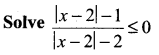
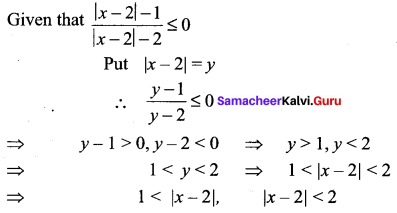
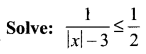

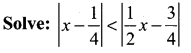

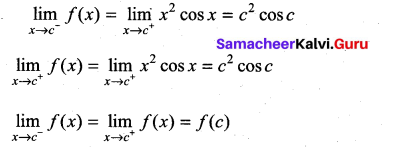
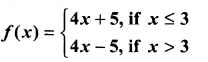

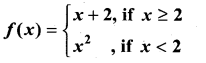
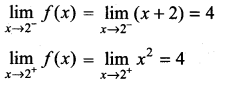
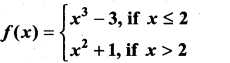

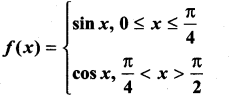
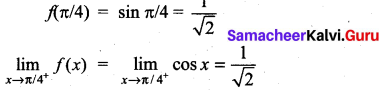
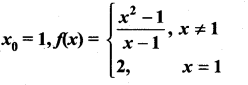
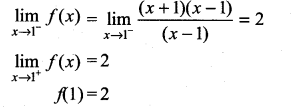
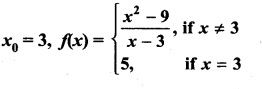
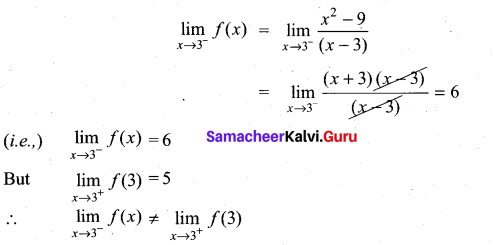
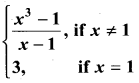 is continuous on (-∞, ∞)
is continuous on (-∞, ∞)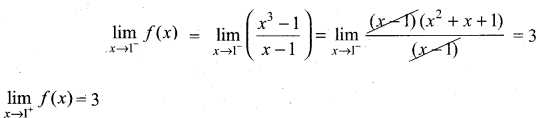
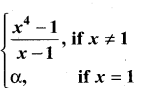 continuous at x = 1?
continuous at x = 1?
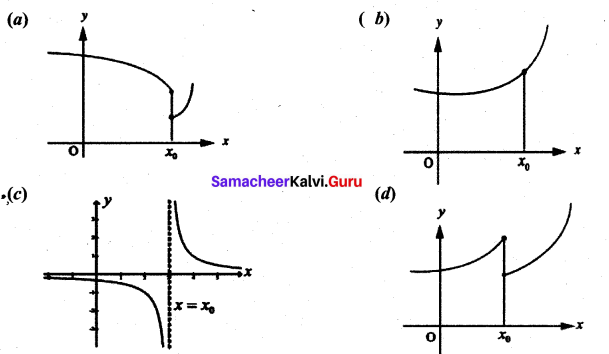
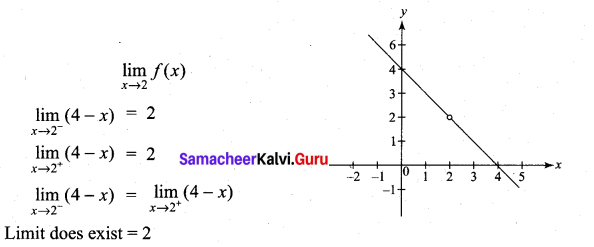
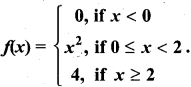 Graph the function. Show that f(x) continuous on (-∞, ∞)
Graph the function. Show that f(x) continuous on (-∞, ∞)