Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.1

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.1

Question 1.
Find the derivatives of the following functions using first principle.
(i) f(x) = 6
Solution:
Given f(x) = 6
f(x + h) = 6

[h → 0 means h is very nears to zero from left to right but not zero]

(ii) f(x) = -4x + 7
Solution:
Given f(x) = -4x + 7
f(x + h) = -4(x + h) + 7
= -4x – 4h + 7

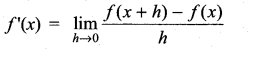
(iii) f(x) = -x² + 2
Given f(x) = -x² + 2
f(x + h) = -(x + h)² + 2
= -x² – h² – 2xh + 2

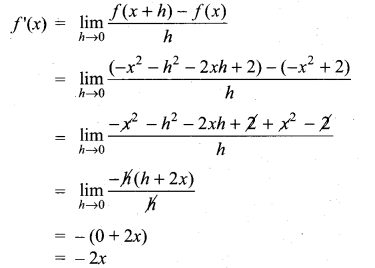
Question 2.
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
(i) f(x) = |x – 1|
Solution:


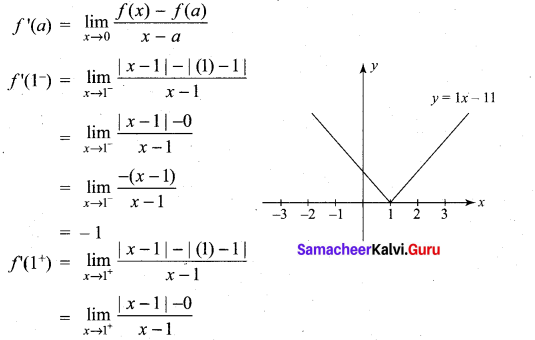
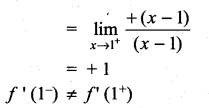
f'(1) does not exist
∴ ‘f’ is not differentiable at x = 1.

(ii) f(x) = \(\sqrt{1-x^{2}}\)
Solution:

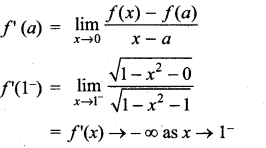
∴ ‘f’ is not differentiable at x = 1.

(iii)

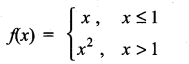
Solution:

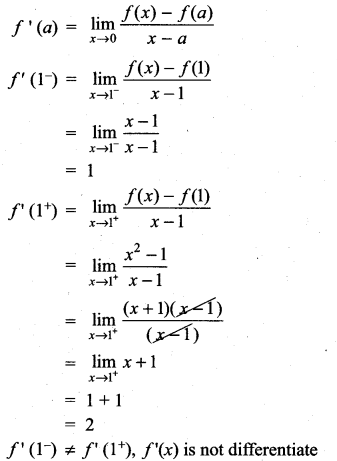
‘f’ is not differentiable at x = 1

Question 3.
Determine whether the following functions is differentiable at the indicated values.
(i) f(x) = x |x| at x = 0
Solution:


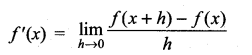
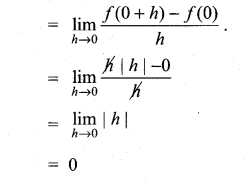
Limits exists
Hence ‘f’ is differentiable at x = 0.

(ii) f(x) = |x² – 1| at x = 1
Solution:

f(x) is not differentiable at x = 1.

(iii) f(x) = |x| + |x – 1| at x = 0, 1
Solution:

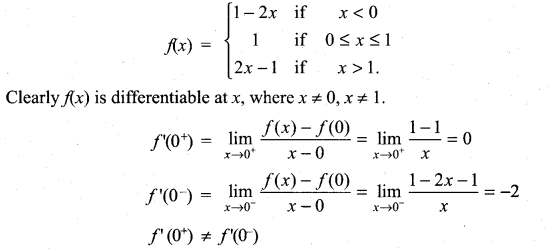
∴ f(x) is not differentiable at x = 0.

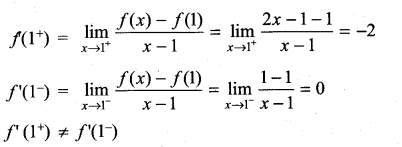
∴ f(x) is not differentiable at x = 1.

(iv) f(x) = sin |x| at x = 0
Solution:

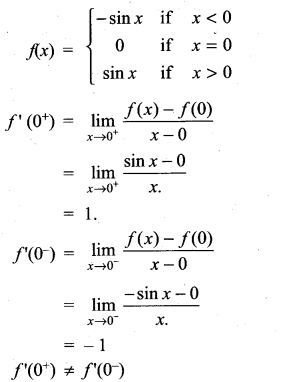
∴ f(x) is not differentiable at x = 0.

Question 4.
Show that the following functions are not differentiable at the indicated value of x.
(i)

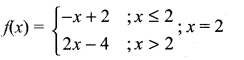
Solution:


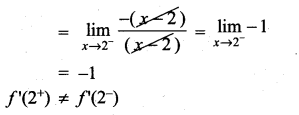
f(x) is not differentiable at x = 2.

(ii)

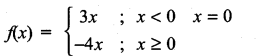
Solution:

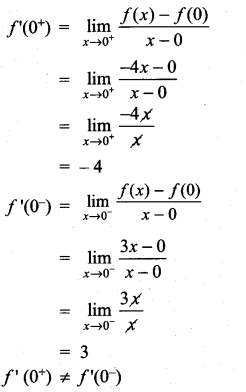
f(x) is not differentiable at x = 0.

Question 5.
The graph off is shown below. State with reasons that x values (the numbers), at which f is not differentiable.
Solution:

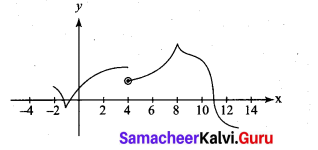
(i) at x = – 1 and x = 8. The graph ‘ is not differentiable since ‘ has vertical tangent at x = -1 and x = 8(also At x = -1. The graph has shape edge v] and at x = 8;The graph has shape peak ^]
(ii) At x = 4: The graph f is not differentiable, since at x =4. The graph f’ is not continuous.
(iii) At x = 11; The graph f’ is not differentiable, since at x = 11. The tangent line of the graph is perpendicular.

Question 6.
If f(x) = |x + 100| + x², test whether f’ (-100) exists.
Solution:
f(x) = |x + 100| + x²

Question 7.
Examine the differentiability of functions in R by drawing the diagrams.
(i) |sin x|
Solution:

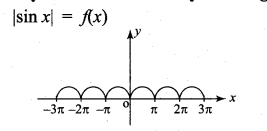
Limit exist and continuous for all x ∈ R clearly, differentiable at R — {nπ n ∈ z) Not differentiable at x = nπ , n ∈ z.

(ii) |cos x|
Solution:

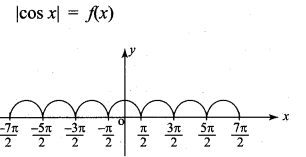
Limit exist and continuous for all x ∈ R clearly, differentiable at R {(2n + 1)π/2/n ∈ z} Not differentiable at x = (2n + 1) \(\frac{\pi}{2}\), n ∈ Z.

Samacheer Kalvi 11th Maths Solutions Chapter 10 Differentiability and Methods of Differentiation Ex 10.1 Additional Questions

Question 1.
Is the function f(x) = |x| differentiable at the origin. Justify your answer.
Solution:

Question 2.
Discuss the differentiability of the functions:

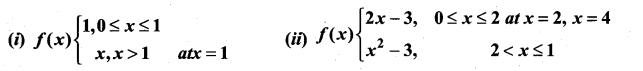
Solution:

∴ f(2) is not differentiable at x = 2. Similarly, it can be proved for x = 4.