Prasanna

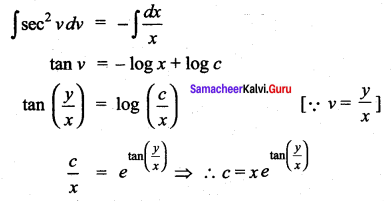
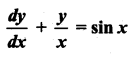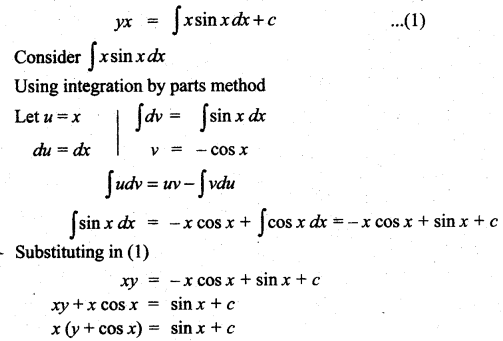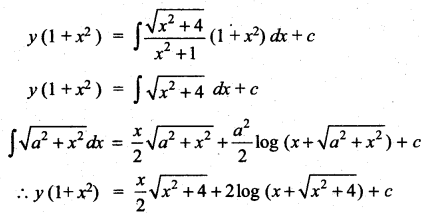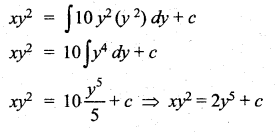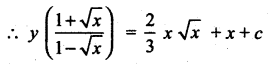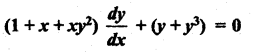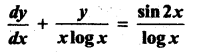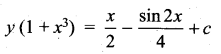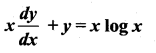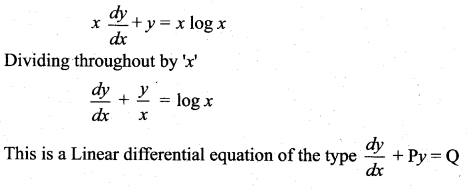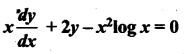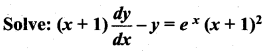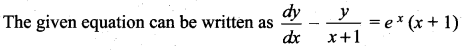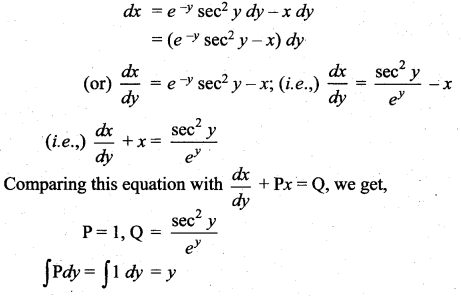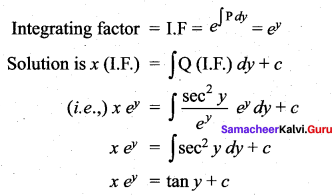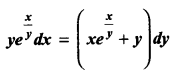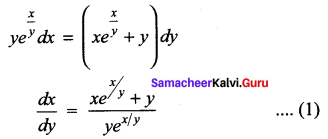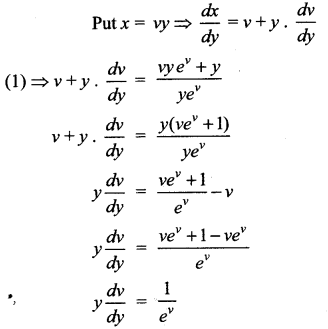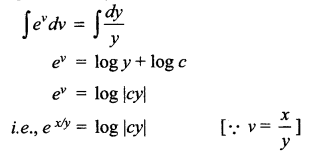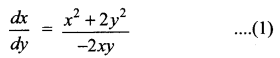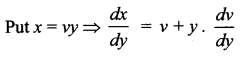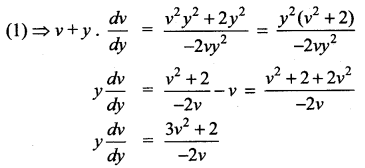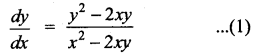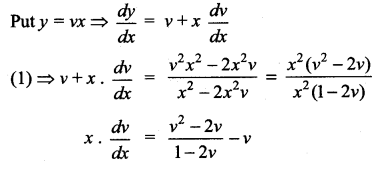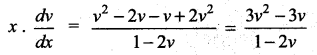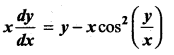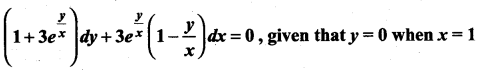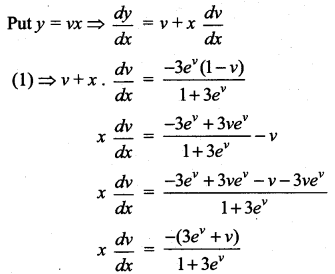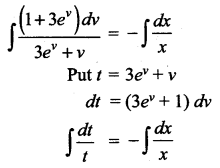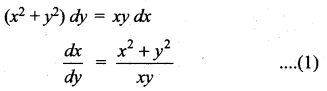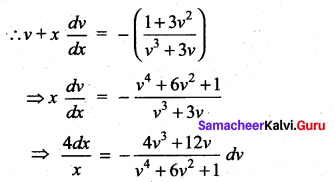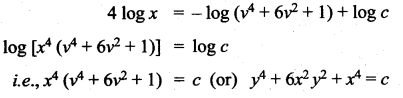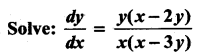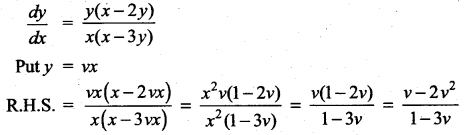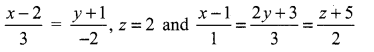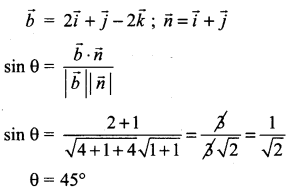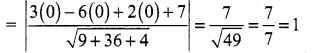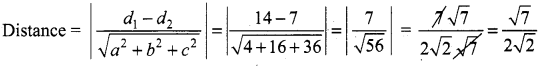Students can Download Computer Science Chapter 5 Python -Variables and Operators Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Computer Science Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 5 Python – Variables and Operators

Samacheer Kalvi 12th Computer Science Python – Variables and Operators Text Book Back Questions and Answers

PART – 1
I. Choose The Best Answer

12th Computer Science Book Back Answers Question 1.
Who developed Python?
(a) Ritche
(b) Guido Van Rossum
(c) Bill Gates
(d) Sunder Pitchai
Answer:
(b) Guido Van Rossum

12th Computer Science Samacheer Kalvi Question 2.
The Python prompt indicates that Interpreter is ready to accept instruction?
(a) >>>
(b) <<<
(c) #
(d) <<
Answer:
(a) >>>

Samacheer Kalvi Guru 12th Computer Science Question 3.
Which of the following shortcut is used to create new Python Program?
(a) Ctrl + C
(b) Ctrl + F
(c) Ctrl + B
(d) Ctrl + N
Answer:
(d) Ctrl + N

12th Computer Science Book Back Answers Pdf Question 4.
Which of the following character is used to give comments in Python Program?
(a) #
(b) &
(c) @
(d) $
Answer:
(a) #

Samacheer Kalvi 12th Computer Science Book Back Answers Question 5.
This symbol is used to print more than one item on a single line?
(a) Semicolon
(b) Dollor($)
(c) Comma(,)
(d) Colon(;)
Answer:
(c) Comma(,)

Samacheer Kalvi 12th Computer Science Question 6.
Which of the following is not a token?
(a) Interpreter
(b) Identifiers
(c) Keyword
(d) Operators
Answer:
(a) Interpreter

Samacheer Kalvi 12th Computer Science Book Question 7.
Which of the following is not a Keyword in Python?
(a) Break
(b) While
(c) Continue
(d) Operators
Answer:
(d) Operators

Class 12 Computer Science Book Back Answers Question 8.
Which operator is also called as Comparative operator?
(a) Arithmetic
(b) Relational
(c) Logical
(d) Assignment
Answer:
(b) Relational

12th Computer Science Solution Book Question 9.
Which of the following is not Logical operator?
(a) And
(b) Or
(c) Not
(d) Assignment
Answer:
(d) Assignment

12th Computer Book Back Answers Question 10.
Which operator is also called as Conditional operator?
(a) Ternary
(b) Relational
(c) Logical
(d) Assignment
Answer:
(a) Ternary

PART – II
II. Answer The Following Questions

Samacheer Kalvi Class 12 Computer Science Question 1.
What are the different modes that can be used to test Python Program?
Answer:
In Python, programs can be written in two ways namely Interactive mode and Script mode. The Interactive mode allows us to write codes in Python command prompt (>>>) whereas in script mode programs can be written and stored as separate file with the extension .py and executed. Script mode is used to create and edit python source file.

12th Computer Science Book Answers Question 2.
Write short notes on Tokens?
Answer:
Python breaks each logical line into a sequence of elementary lexical components known as Tokens. The normal token types are;

1. Identifiers
2. Keywords
3. Operators
4. Delimiters
5. Literals

Whitespace separation is necessary between tokens, identifiers or keywords.

12 Computer Science Book Back Answers Question 3.
What are the different operators that can be used in Python?
Answer:
In computer programming languages operators are special symbols which represent computations, conditional matching etc. The value of an operator used is called operands. Operators are categorized as Arithmetic, Relational, Logical, Assignment etc.

Samacheer Kalvi Computer Science Book Question 4.
What is a literal? Explain the types of literals?
Answer:
Literal is a raw data given in a variable or constant. In Python, there are various types of literals.

1. Numeric
2. String
3. Boolean

12th Computer Science Deleted Book Back Questions Question 5.
Write short notes on Exponent data?
Answer:
An Exponent data contains decimal digit part, decimal point, exponent part followed by one or more digits.
12.E04, 24.e04 # Exponent data

PART – III
III. Answer The Following Questions

12 Computer Science Samacheer Kalvi Question 1.
Write short notes on Arithmetic operator with examples?
Answer:
Arithmetic operators:
An arithmetic operator is a mathematical operator that takes two operands and performs a calculation on them. They are used for simple arithmetic. Most computer languages contain a set of such operators that can be used within equations to perform different types of sequential calculations.
Python supports the following Arithmetic operators.

Book Back Answers For 12th Computer Science Question 2.
What are the assignment operators that can be used in Python?
Answer:
Assignment operators:
In Python, = is a simple assignment operator to assign values to variable. Let a = 5 and b = 10 assigns the value 5 to a and 10 to b these two assignment statement can also be given as a, b = 5, 10 that assigns the value 5 and 10 on the right to the variables a and b respectively. There are various compound operators in Python like + =, – =,* =, / = % =,** = and //= are also available.

12th Std Computer Science Book Back Answers Question 3.
Explain Ternary operator with examples?
Answer:
Conditional operator:
Ternary operator is also known as conditional operator that evaluate something based on a condition being true or false. It simply allows testing a condition in a single line replacing the multiline if – else making the code compact.
The Syntax conditional operator is,
Variable Name = [on – true] if [Test expression] else [on – false]
Example:
min = 50 if 49 < 50 else 70 # min = 50 min = 50 if 49 > 50 else 70 # min = 70

Question 4.
Write short notes on Escape sequences with examples?
Answer:
Escape Sequences:
In Python strings, the backslash “\” is a special character, also called the “escape” character. It is used in representing certain whitespace characters: “\t” is a tab, “\n” is a newline, and “\r” is a carriage return. For example to print the message “It’s raining”, the Python command is >>> print (“It\’s rainning”)
It’s rainning
Python supports the following escape sequence characters.

Question 5.
What are string literals? Explain?
Answer:
String Literals:
In Python a string literal is a sequence of characters surrounded by quotes. Python supports single, double and triple quotes for a string. A character literal is a single character surrounded by single or double quotes. The value with triple – quote is used to give multi – line string literal.
Strings = “This is Python”
char = “C”
multiline _ str = “This is a multiline string with more than one line code”.

PART – IV
IV. Answer The Following Questions

Question 1.
Describe in detail the procedure Script mode programming?
Answer:
Script mode Programming:
Basically, a script is a text file containing the Python statements. Python Scripts are reusable code. Once the script is created, it can be executed again and again without retyping. The Scripts are editable.
Creating Scripts in Python:
(I) Choose File → New File or press Ctrl + N in Python shell window.

(II) An untitled blank script text editor will be displayed on screen

(III) Type the following code in Script editor
a = 100
b = 350
c = a + b
print (“The Sum = “, c)

Saving Python Script
(I) Choose File → Save or Press Ctrl + S

(II) Now, Save As dialog box appears on the screen

(III) In the Save As dialog box, select the location where you want to save your Python code, and type the file name in File Name box. Python files are by default saved with extension .py. Thus, while creating Python scripts using Python Script editor, no need to specify the file extension.

(IV) Finally, click Save button to save your Python script.
Executing Python Script

(I) Choose Run → Run Module or Press F5

(II) If your code has any error, it will be shown in red color in the IDLE window, and Python describes the type of error occurred. To correct the errors, go back to Script editor, make corrections, save the file using Ctrl + S or File → Save and execute it again.

(III) For all error free code, the output will appear in the IDLE window of Python:

Question 2.
Explain input ( ) and print ( ) functions with examples?
Answer:
Input and Output Functions:
A program needs to interact with the user to accomplish the desired task; this can be achieved using Input – Output functions. The input ( ) function helps to enter data at run time by the user and the output function print ( ) is used to display the result of the program on the screen after execution.
The print ( ) function
In Python, the print Q function is used to display result on the screen. The syntax for print Q is as follows:
Example
print (“string to be displayed as output ”)
print (variable)
print (“String to be displayed as output ”, variable)
print (“String1 ”, variable, “String 2”, variable, “String 3”)
Example
>>> print (“Welcome to Python Programming”)
Welcome to Python Programming
>>> x = 5
>>> y = 6
>>> z = x + y
>>> print (z)
11
>>> print (“The sum = ”, z)
The sum = 11
>>> print (“The sum of”, x, “and”, y, “is”, z)
The sum of 5 and 6 is 11
Th print ( ) evaluates the expression before printing it on the monitor. The print ( ) displays an entire statement which is specified within print ( ). Comma ( , ) is used as a separator in print ( ) to print more than one item.
input ( ) function
In Python, input ( ) function is used to accept data as input at run time. The syntax for input ( ) function is,
Variable = input (“prompt string”)
Where, prompt string in the syntax is a statement or message to the user, to know what input can be given.
If a prompt string is used, it is displayed on the monitor; the user can provide expected data from the input device. The input ( ) takes whatever is typed from the keyboard and stores the entered data in the given variable. If prompt string is not given in input ( ) no message is displayed on the screen, thus, the user will not know what is to be typed as input.

Example 1:
input ( ) with prompt string
>>> city = input (“Enter Your City: ”)
Enter Your City: Madurai
>>> print (“I am from “, city)
I am from Madurai

Example 2:
input ( ) without prompt string
>>> city = input ( )
Rajarajan
>>> print (I am from”, city)
I am from Rajarajan
Note that in example – 2, the input ( ) is not having any prompt string, thus the user will not know what is to be typed as input. If the user inputs irrelevant data as given in the above example, then the output will be unexpected. So, to make your program more interactive, provide prompt string with input ( ).
The input ( ) accepts all data as string or characters but not as numbers. If a numerical value is entered, the input values should be explicitly converted into numeric data type. The int ( ) function is used to convert string data as integer data explicitly. We will leam about more such functions in later chapters.

Example 3:
x = int (input(“Enter Number 1: ”))
y = int (input(“Enter Number 2: ”))
print (“The sum =”, x + y)
Output:
Enter Number 1:34
Enter Number 2:56
The sum = 90

Example 4:
Alternate method for the above program
x, y = int (input(“Enter Number 1 :”)), int(input(“Enter Number 2:”))
print (”X = “,x,”Y = “,y)
Output:
Enter Number 1:30
Enter Number 2:50
X = 30 Y= 50

Question 3.
Discuss in detail about Tokens in Python?
Answer:
Tokens:
Python breaks each logical line into a sequence of elementary lexical components known as Tokens. The normal token types are

1. Identifiers
2. Keywords
3. Operators
4. Delimiters
5. Literals.

Whitespace separation is necessary between tokens, identifiers or keywords.

(I) Identifiers:
An Identifier is a name used to identify a variable, function, class, module or object.

1. An identifier must start with an alphabet (A..Z or a..z) or underscore ( _ ).
2. Identifiers may contain digits (0 .. 9)
3. Python identifiers are case sensitive i.e. uppercase and lowercase letters are distinct.
4. Identifiers must not be a python keyword.
5. Python does not allow punctuation character such as %, $, @ etc., within identifiers.

Example of valid identifiers
Sum, total _ marks, regno, num 1

Example of invalid identifiers
12 Name, name$, total – mark, continue

(II) Keywords
Keywords are special words used by Python interpreter to recognize the structure of program. As these words have specific meaning for interpreter, they cannot be used for any other purpose.

(III) Operators
In computer programming languages operators are special symbols which represent computations, conditional matching etc. The value of an operator used is called operands. Operators are categorized as Arithmetic, Relational, Logical, Assignment etc. Value and variables when used with operator are known as operands.

Arithmetic operators:
An arithmetic operator is a mathematical operator that takes two operands and performs a calculation on them. They are used for simple arithmetic. Most computer languages contain a set of such operators that can be used within equations to perform different types of sequential calculations.
Python supports the following Arithmetic operators.

Relational or Comparative operators:
A Relational operator is also called as Comparative operator which checks the relationship between two operands. If the relation is true, it returns True; otherwise it returns False.

Logical operators:
In python, Logical operators are used to perform logical operations on the given relational expressions. There are three logical operators they are and, or and not.

Assignment operators:
In Python, = is a simple assignment operator to assign values to variable. Let a = 5 and b = 10 assigns the value 5 to a and 10 to b these two assignment statement can also be given as a, b = 5, 10 that assigns the value 5 and 10 on the right to the variables a and b respectively. There are various compound operators in Python like + =, – =, * =, / =, % =, ** = and //= are also available.

Conditional operator:
Ternary operator is also known as conditional operator that evaluate something based on a condition being true or false. It simply allows testing a condition in a single line replacing the multiline if – else making the code compact.
The Syntax conditional operator is,
Variable Name = [on _ true] if [Test expression] else [on _ false]
Example:
min = 50 if 49 < 50 else 70 # min = 50 min = 50 if 49 > 50 else 70 # min = 70

(IV) Delimiters
Python uses the symbols and symbol combinations as delimiters in expressions, lists, dictionaries and strings. Following are the delimiters.

(V) Literals
Literal is a raw data given in a variable or constant. In Python, there are various types of literals.

1. Numeric
2. String
3. Boolean

1. Numeric Literals:
Numeric Literals consists of digits and are immutable (unchangeable). Numeric literals can belong to 3 different numerical types Integer, Float and Complex.

2. String Literals:
In Python a string literal is a sequence of characters surrounded by quotes. Python supports single, double and triple quotes for a string. A character literal is a single character surrounded by single or double quotes. The value with triple-quote is used to give multi-line string literal.

3. Boolean Literals:
A Boolean literal can have any of the two values: True or False.

Escape Sequences:
In Python strings, the backslash “\” is a special character, also called the “escape” character. It is used in representing certain whitespace characters: “\t” is a tab, “\n” is a newline, and “\r” is a carriage return. For example to print the message “It’s raining”, the Python command is
>>>print (“It\’s rainning”)
It’s rainning
Python supports the following escape sequence characters.

Samacheer kalvi 12th Computer Science Python – Variables and Operators Additional Questions and Answers

PART – 1
I. Choose The Best Answer:

Question 1.
Python language was released in the year …………………………….
(a) 1991
(b) 1993
(c) 1995
(d) 1997
Answer:
(a) 1991

Question 2.
CWI means ……………………………
Answer:
Centrum Wiskunde & Information

Question 3.
Python got its name from ……………………………
Answer:
Monthly Python’s Flying Circus

Question 4.
Find the wrong statement from the following.
(a) Python supports procedural approaches
(b) Python supports object oriented approaches
(c) Python is DBMS tool
Answer:
(c) Python is DBMS tool

Question 5.
IDLE means ……………………………
Answer:
Integrated Development Learning Environment

Question 6.
How many modes of programming are there in python?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(a) 2

Question 7.
The extension for python file is ……………………………
(a) .pyt
(b) .pt
(c) .py
(d) .pyth
Answer:
(c) .py

Question 8.
…………………………… mode is used to create and edit python source file.
(a) Line
(b) Script
(c) Interactive
(d) Interface
Answer:
(b) Script

Question 9.
Which mode can be used as a simple calculator?
(a) Line
(b) Script
(c) Interactive
(d) Interface
Answer:
(c) Interactive

Question 10.
What does prompt (>>>) indicator?
(a) Compiler is ready to debug
(b) Results are ready
(c) Waiting for the Input data
(d) Interpreter is ready to accept Instructions
Answer:
(d) Interpreter is ready to accept Instructions

Question 11.
Which command is used to get output ……………………………
(a) Cout
(b) Print
(c) Print f
(d) Write
Answer:
(b) Print

Question 12.
Find the correct one from the following.
(a) Scripts are reusable and not editable
(b) Scripts are not reusable and they are editable
(c) Scripts are not reusuable, not editable
(d) Scripts are both reusable and editable
Answer:
(d) Scripts are both reusable and editable

Question 13.
Which command is selected from file menu create new script text editor?
(a) New
(b) New file
(c) New editor
(d) New Script file
Answer:
(b) New file

Question 14.
What is the default name for blank script text editor?
(a) Untitled
(b) Untitled 1
(c) Document 1
(d) Editor 1
Answer:
(b) Untitled 1

Question 15.
What is the keyboard shortcut to Run?
(a) F5
(b) Alt + F5
(c) Shift + F5
(d) Ctrl + F5
Answer:
(a) F5

Question 16.
…………………………… command is used to execute python script?
(a) Run
(b) Compile
(c) Run → Run Module
(d) Compile → Compile Run
Answer:
(c) Run → Run Module

Question 17.
Errors in the python script appears in …………………………… color.
(a) Yellow
(b) Red
(c) Blue
(d) Black
Answer:
(b) Red

Question 18.
…………………………… function helps to enter data at run time by the user.
Answer:
input ( )

Question 19.
If …………………………… is not given in input ( ), no message is displayed on the screen.
Answer:
Prompt sting

Question 20.
Identify the wrong statement from the following. The input ( ) accepts all data as
(a) Strings
(b) Characters
(c) Numbers
(d) All the above
Answer:
(c) Numbers

Question 21.
The …………………………… function is used to convert string data as integer data explicitly.
Answer:
int ( )

Question 22.
…………………………… are ignored by the python interpreter.
(a) Keywords
(b) Tokens
(c) Delimiters
(d) Comments
Answer:
(d) Comments

Question 23.
Comments are of …………………………… or …………………………… lines.
Answer:
Single, multi

Question 24.
…………………………… are used to indicate blocks of codes in python.
(a) Whitespaces
(b) { }
(c) [ ]
(d) < >
Answer:
(a) Whitespaces

Question 25.
Python breaks each logical line into a sequence of elementary lexical components called ……………………………
Answer:
Tokens

Question 26.
How many types of tokens are there?
(a) 1
(b) 2
(c) 5
(d) 10
Answer:
(c) 5

Question 27.
Pick the odd one out.
Identifiers, Keywords, Delimiters, Comments, Literals
Answer:
Comments

Question 28.
An identifier is a name used to identify a ……………………………
(a) Variable
(b) Function
(c) Class
(d) All of these
Answer:
(d) All of these

Question 29.
Pick the odd one out.
(a) Sum, regno, numl, 12Name, – Marks
(b) False, class, is, as, if, end
(c) Relational, while, logical, Assignment,
(d) + * % ** = =
Answer:
(a) 12 Name, (b) end, (c) while, (d) =

Question 30.
Find the correct statement from the following
(a) Continue is an identifier
(b) Sum is a keyword
(c) ** = is a delimiter
(d) = = is an assignment operator
Answer:
(c) ** = is a delimiter

Question 31.
How many types of operators are there?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(d) 5

Question 32.
Match the following
1. // – (i) Modulus
2. # – (ii) Floor division
3. % – (iii) Strings
4. ||| ||| – (iv) Comments
(a) 1 – (ii), 2 – (iv), 3 – (i), 4 – (iii)
(b) 1 – (i), 2 – (ii), 3 – (iii), 4 – (iv)
(c) 1 – (iv), 2 – (ii), 3 – (i), 4 – (iii)
(d) 1 – (iv), 2 – (i), 3 – (iii), 4 – (ii)
Answer:
(a) 1 – (ii), 2 – (iv), 3 – (i), 4 – (iii)

Question 33.
…………………………… are special words used by Python Interpreter
Answer:
Keywords

Question 34.
The value of an operator used is ……………………………
(a) 0
(b) 1
(c) Operands
(d) NULL
Answer:
(c) Operands

Question 37.
Match the following expressions with their equivalent output a = 100, b = 10
(1) >>> a % 30 – (i) 100
(2) >>> a // 30 – (ii) 10.0
(3) >>> a/b – (iii) 3
(4) >>> a * b – (iv) 10
(a) 1 – (iv), 2 – (iii), 3 – (ii), 4 – (i)
(b) 1 – (i), 2 – (ii), 3 – (iii), 4 – (iv)
(c) 1 – (i), 2 – (ii), 3 – (iv), 4 – (iii)
(d) 1 – (iv), 2 – (ii), 3 – (iii), 4 – (i)
Answer:
(a) 1 – (iv), 2 – (iii), 3 – (ii), 4 – (i)

Question 38.
Which operator checks the relationship between two operands.
(a) Relational
(b) Comparative
(c) Both
(d) None of the these
Answer:
(c) Both

Question 39.
Assume a = 100 and b = 35. Find the true statements.
(i) >>> a > b
(ii) >>> a = = b
(iii) >>> a ! = b
(a) (i), (iii) are true
(b) (ii), (iii) are true
(c) (i), (ii) are true
Answer:
(a) (i), (iii) are true

Question 40.
Identify Not equal to operator in python?
(a) < >
(b) ==
(c) NOT EQUAL
(d) ! =
Answer:
(d) ! =

Question 41.
How many logical operators are there?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(b) 3

Question 42.
How many comparative operators are there?
(a) 4
(b) 5
(c) 6
(d) 7
Answer:
(c) 6

Question 43.
…………………………… is the simple assignment operator.
(a) ! =
(b) >
(c) >>
(d) =
Answer:
(d) =

Question 44.
Compound operators comes under the category of …………………………… operators.
Answer:
Assingnment

Question 45.
Find the wrongly matched pair.
(a) ! = – relational operator
(b) not a > b – Comparative Operator
(c) **= – delimitors operator
(d) Assingnment Operator
Answer:
(b) not a > b – Comparative Operator

Question 46.
Identify which is not a delimiter
(a) & =
(b) :
(c) ;
(d) ::
Answer:
(d) ::

Question 47.
How many types of literals are there?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(b) 3

Question 48.
Numeric literals are ……………………………
(a) Integer, Float, Complex
(b) Int, Float, Void
(c) Int, Float, Char
(d) Int, Float, Boolean
Answer:
(a) Integer, Float, Complex

Question 49.
Strings in python are represented using
(a) ”
(b) “”
(c) “‘ “‘
(d) All of these
Answer:
(d) All of these

Question 50.
Multiline string literal is given by ……………………………
Answer:
“‘ “‘ triple quotes

Question 51.
The two values accepted by Boolean literals are …………………………… or ……………………………
Answer:
True, False

Question 52.
…………………………… is the escape character.
(a) +
(b) t
(c) \
(d) %
Answer:
(c) \

Question 53.
Which one of the following is the newline character?
(a) \t
(b) \v
(c) \r
(d) \n
Answer:
(d) \n

Question 54.
…………………………… is the escape character for carriage return.
Answer:
\r

Question 55.
Pick the odd one out.
(a) Tuples, for, list, dictionaries, Number
(b) \n, \”, V, \r, \k
(c) and, or, not, true
(d) >, > =, <, < =, < >
Answer:
(a) for, (b) \k, (c) true, (d) <>

Question 56.
How many Interger data are there?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(b) 3

Question 57.
OX represents …………………………… integer.
Answer:
Hexadecimal

Question 58.
Octal integer uses …………………………… to denote octal digits
(a) OX
(b) O
(c) OC
(d) Od
Answer:
(b) O

Question 59.
Find the hexadecimal Integer.
(a) 0102
(b) 0876
(c) 0432
(d) 0X102
Answer:
(d) 0X102

Question 60.
How many floating point values are there in a complex number?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2

Question 61.
What is the another name for fundamental data type?
(a) Class
(b) Built – in
(c) Typedef
(d) User defined
Answer:
(b) Built – in

Question 62.
Which one of the following statement is wrong?
(a) Octal Integer uses upper and lower case O
(b) Hexadecimal Integer uses upper and lower case OX
(c) Long integer uses upper and lower case 1.
Answer:
(c) Long integer uses upper and lower case 1.

PART – II
II. Answer The Following Questions.

Question 1.
How will you create scripts in python?
Answer:
(I) Choose File → New File or press Ctrl + N in Python shell window.

(II) An untitled blank script text editor will be displayed on screen.

Question 2.
Write note on keywords. Give examples?
Answer:
Keywords are special words used by Python interpreter to recognize the structure of program. As these words have specific meaning for interpreter, they cannot be used for any other purpose. Eg, While, if.

PART – III
III. Answer The Following Questions.

Question 1.
What are the key features of python?
Answer:
Key features of Python:
It is a general purpose programming language which can be used for both scientific and non – scientific programming
It is a platform independent programming language.
The programs written in Python are easily readable and understandable

Question 2.
How will you execute python script?
Executing Python Script
(I) Choose Run → Run Module or Press F5

(II) If your code has any error, it will be shown in red color in the IDLE window, and Python describes the type of error occurred. To correct the errors, go back to Script editor, make corrections, save the file using Ctrl + S or File → Save and execute it again.

(III) For all error free code, the output will appear in the IDLE window of Python.

Question 3.
Give the syntax for print ( ) function?
Answer:
The syntax for print ( ) is as follows:
Example:
print (“string to be displayed as output ” )
print (variable)
print (“String to be displayed as output ”, variable)
print (“String 1 ”, variable, “String 2”, variable, “String 3”)

Question 4.
Explain the Syntax of input ( ) function?
Answer:
The syntax for inputQ function is,
Variable = input (“prompt string”)
Where, prompt string in the syntax is a statement or message to the user, to know what input can be given.

If a prompt string is used, it is displayed on the monitor; the user can provide expected data from the input device. The input) ) takes whatever is typed from the keyboard and stores the entered data in the given variable. If prompt string is not given in input() no message is displayed on the screen

Question 5.
Give an example for input with and without prompt string?
Example 1: input ( ) with prompt string
>>> city = input (“Enter Your City: ”)
Enter Your City: Madurai

Example 2: input ( ) without prompt string
>>> city = input ( )
Rajarajan

Question 6.
Write a short note on comments?
Answer:
Comments in Python
In Python, comments begin with hash symbol (#). The lines that begins with # are considered as comments and ignored by the Python interpreter. Comments may be single line or no multi – lines. The multiline comments should be enclosed within a set of # as given below.
# It is Single line Comment
# It is multiline comment
which contains more than one line #

Question 7.
Mention some rules for Identifiers?
Answer:

1. An identifier must start with an alphabet (A..Z or a..z) or underscore (_).
2. Identifiers may contain digits (0 .. 9)
3. Python identifiers are case sensitive i.e. uppercase and lowercase letters are distinct.
4. Identifiers must not be a python keyword.
5. Python does not allow punctuation character such as %,$, @ etc., within identifiers.

Question 8.
Give any 6 keywords in Python?
Answer:
false, class, none, continue, finally, return, is

Question 9.
Give an example program for Ternary operator?
To test Conditional (Ternary) Operator:
# Program to demonstrate conditional operator
a, b = 30, 20
# Copy value of a in min if a < b else copy b
min = a if a < b else b print (“The Minimum of A and B is “,min) # End of the Program Output: The Minimum of A and B is 20.

Question 10.
Write any 6 delimiters in python?
Answer:

PART – IV
IV. Answer The Following Questions

Question 1.
Explain operators in detail?
Answer:
Operators: In computer programming languages operators are special symbols which represent computations, conditional matching etc. The value of an operator used is called operands. Operators are categorized as Arithmetic, Relational, Logical, Assignment etc. Value and variables when used with operator are known as operands.

(I) Arithematic operators An arithmetic operator is a mathematical operator that takes two operands and performs a calculation on them. They are used for simple arithmetic. Most computer languages contain a set of such operators that can be used within equations to perform different types of sequential calculations.

Python supports the following Arithmetic operators.

To test Arithmetic Operators: #Demo Program to test Arithmetic Operators a = 100 b = 10 print (“The Sum = “,a + b) print (“The Difference = “,a – b) print (“The Product = “,a * b) print (“The Quotient = “,a / b) print (“The Remainder = “,a % 30) print (“The Exponent = “, a ** 2) print (“The Floor Division =”, a // 30) #Program End Output: The Sum = 110 The Difference = 90 The Product = 1000 The Quotient = 10.0 The Remainder = 10 The Exponent = 10000 The Floor Division = 3

(II) Relational or Comparative operators A Relational operator is also called as Comparative operator which checks the relationship between two operands. If the relation is true, it returns True; otherwise it returns False.

To test Relational Operators: #Demo Program to test Relational Operators a = int (input(“Enter a Value for A:”)) b = int (input(“Enter a Value for B:”)) print (“A = “,a,” and B = “,b) print (“The a = = b = “,a = = b) print (“The a > b = “,a > b)
print (“The a < b = “,a < b) print (“The a > = b = “, a > = b)
print (“The a! = b = “,a! = 0)
print (“The a! = b = “,a! = b)
#Program End

Output:
Enter a Value for A: 35
Enter a Value for B: 56
A = 35 and B = 56
The a = =b = False
The a > b = False
The a < b = True The a > = b = False
The a < = b = False
The a ! = b = True

(III) Logical operators
In python, Logical operators are used to perform logical operations on the given relational expressions. There are three logical operators they are and, or and not.

To test Logical Operators:

(IV) Assignment operators
In Python, = is a simple assignment operator to assign values to variable. Let a = 5 and b = 10 assigns the value 5 to a and 10 to b these two assignment statement can also be given as a, b = 5, 10 that assigns the value 5 and 10 on the right to the variables a and b respectively. There are various compound operators in Python like + =, – =, * =, /=, % =, ** = and //= are also available.

To test Assingnment Operators:

(V) Conditional operator
Ternary operator is also known as conditional operator that evaluate something based on a condition being true or false. It simply allows testing a condition in a single line replacing the multiline if – else making the code compact.
The Syntax conditional operator is,
Variable Name = [on _ true] if [Test expression] else [on _ false]
Example:
min = 50 if 49 < 50 else 70 # min = 50 min = 50 if 49 > 50 else 70 # min = 70
To test Conditional (Ternary) Operator:
# Program to demonstrate conditional operator
a, b = 30, 20
# Copy value of a in min if a < b else copy b
min = a if a < b else b print (“The Minimum of A and B is “,min) # End of the Program Output: The Minimum of A and B is 20.

Question 2.
Write the Output for the given program?
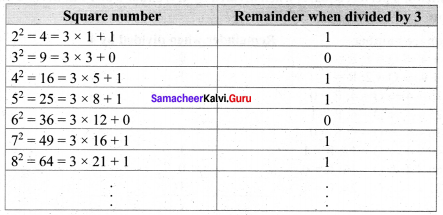
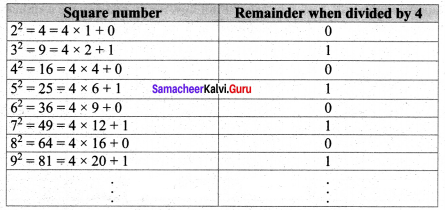
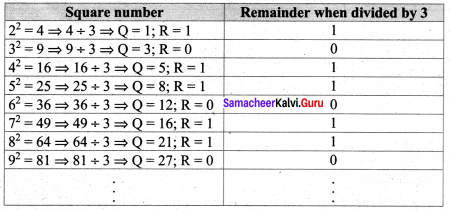
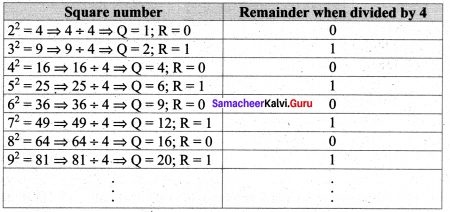
Answer:

Question 3.
Explain literals and its types?
Answer: Literal is a raw data given in a variable or constant. In Python, there are various types of literals.

(I) Numeric Literals Numeric Literals consists of digits and are immutable (unchangeable). Numeric literals can belong to 3 different numerical types Integer, Float and Complex. To demonstrate Numeric literals # Program to demonstrate Numeric Literals a = Ob 1010 #Binary Literals b = 100 #Decimal Literal c = 0o310 #Octal Literal d = Ox 12c #Hexadecimal Literal print (“Integer Literals :”,a, b, c, d) #Float Literal float_1 = 10.5 float_2 = 1.5e2 print (“Float Literals :”,float_1, float_2) #Complex Literal x = 1 + 3.14 j print (“Complex Literals:”, x) Print (“x = “, x , “Imaginary part of x = “, x.imag, “Real part of x = “, x.real) #End of the Program Output: Integer Literals: 10 100 200 300 Float Literals: 10.5 150.0 Complex Literals: x = (1.3.14) Imaginary part of x = 3.14 Real part of 9 x = 1.0

(II) String Literals: In Python a string literal is a sequence of characters surrounded by quotes. Python supports single, double and triple quotes for a string. A character literal is a single character surrounded by single or double quotes. The value with triple-quote is used to give multi – line string literal. To test String Literals # Demo Program to test String Literals strings = “This is Python” char = “C” multiline_str = ‘”This is a multiline string with more than one line code.'” print (strings) print (char) print (multiline_str) # End of the Program Output: This is Python C C This is a multiline string with more than one line code.

(III) Boolean Literals A Boolean literal can have any of the two values: True or False. # Demo Program to test String Literals boolean _ 1 = True boolean _ 2 = False print (“Demo Program for Boolean Literals”) print (“Boolean Value 1 :”,boolean_1) print (“Boolean Value2 :”,boolean_2) # End of the Program Output: Demo Program for Boolean Literals Boolean Value 1: True Boolean Value2: False (iv) Escape Sequences In Python strings, the backslash “\” is a special character, also called the “escape” character. It is used in representing certain whitespace characters: “\t” is a tab, “\n” is a newline, and “\r” is a carriage return. For example to print the message “It’s raining”, the Python command is >>> print (“ItVs rainning”)
It’s rainning
Python supports the following escape sequence characters.

Question 4.
Explain data types in python?
Answer:
Python Data types:
All data values in Python are objects and each object or value has type. Python has Built-in or Fundamental data types such as Number, String, Boolean, tuples, lists and dictionaries.

Number Data type:
The built – in number objects in Python supports integers, floating point numbers and complex numbers.
Integer Data can be decimal, octal or hexadecimal. Octal integer use O (both upper and lower case) to denote octal digits and hexadecimal integer use OX (both upper and lower case) and L (only upper case) to denote long integer.
Example:
102, 4567, 567 # Decimal integers
0102, o876, 0432 # Octal integers
0X102, oX876, 0X432 # Hexadecimal integers
34L, 523L # Long decimal integers
A floating point data is represented by a sequence of decimal digits that includes a decimal point. An Exponent data contains decimal digit part, decimal point, exponent part followed by one or more digits.
Example :
123.34, 456.23, 156.23 # Floating point data
12.E04, 24.e04 # Exponent data
Complex number is made up of two floating point values, one each for the real and imaginary parts.

Boolean Data type:
A Boolean data can have any of the two values: True or False.

Example:
Bool_varl = True
Bool_var2 = False

String Data type:
String data can be enclosed with single quote or double quote or triple quote.

Example:
Char_data = ‘A’
String_data = “Computer Science”
Multiline_data= “““String data can be enclosed with single quote or double quote or triple quote.”””

Must refer:

BHARATFORG Pivot Calculator

Students can Download Maths Chapter 1 Numbers Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Intext Questions

Exercise 1.1
Think (Text book page No. 3)

Question 1.
Is the square of a prime number, prime?
Solution:
No, the square of a prime number ‘P’ has at least 3 divisors 1, P and P². But a prime number is a number which has only two divisors, 1 and the number itself. So square of a prime number is not prime.

Question 2.
Solution:
The sum of two perfect squares, need not be always a perfect square. Also the difference of two perfect squares need not be always a perfect square. Bu the product of two perfect square is a perfect square.

Try These (Text book Page No. 3)

Consider the following square numbers:
(i) 441
(ii) 225
(iii) 289
(iv) 1089.
Express each of them as the sum of two consecutive positive integers.
Solution:
(i) 441 = 220 + 221
(ii) 225 = 112 + 113
(iii) 289 = 144 + 145
(iv) 1089 = 544 + 545

Think (Text book Page No. 4)

Question 1.
Take an even natural number, say, 46 (or any other even number of your choice). Try to express it as a sum of consecutive odd numbers starting with 1. Do you succeed?
Solution:
1 + 3 + 5 + 7 + 9 + 11 = 36
1 + 3 + 5 + 7 + 9 + 11 + 13 = 49
So 46 cannot be expressed as a sum of consecutive odd numbers starting with 1. But 36 also an even natural number. It can be expressed as the sum of consecutive odd numbers as 36 = 1 +3 + 5 + 7 + 9 + 11.

Question 2.
The square of an odd number can always be written as the sum of two consecutive natural numbers. Can the reverse statement be true? Is the sum of any two consecutive natural numbers a perfect square of a number?
Solution:
No, the reverse is not true. The sum of any two consecutive natural numbers need not be a perfect square of a number. Example: 35 + 36 = 71, not a perfect square.

Try These (Text book Page No. 4)

(i) Which among 256, 576, 960, 1025, 4096 are perfect square numbers?
(Hint: Try to extend the table of squares already seen).
Solution:
256 = 16²
576 = 24²
4096 = 64²
∴ 256, 576 and 4096 are perfect squares

(ii) One can judge just by look, that the each of the following numbers (82, 113, 2057, 24353, 8888,1972) is not a perfect square. Explain why?
Solution:
Because the unit digit of a perfect square will be 0, 1, 4, 5, 6, 9. But the given numbers have unit digits 2, 3, 7, 8. So they are not perfect squares.

(iii) Find the squares by diagonal method and also the ones digit in the squares of the following numbers: 11, 27, 42, 79, 146, 324, 520.
Solution:
Ones digit is the squares of

Think (Text book Page No. 5)

Consider the claim: “Between the squares of the consecutive numbers n and (n+1), there are 2n non-square numbers”. Can it be true? Find how many non-square numbers are there
(i) between 4 and 9?
(ii) between 49 and 64?
and verify the claim.
Solution:

Therefore we conclude that there are 2n non-square numbers between two consecutive square numbers.

Activity 1. (Text book Page No. 5)

Verify the following statements:
(i) The square of a natural number, other than 1, is either a multiple of 3 or exceeds a multiple of 3 by 1.
Verification

Hence verified that the square of a natural number other than 1, is either a multiple of 3 or exceeds a multiple of 3 by 1.

(ii) The square of a natural number, other than 1, is either a multiple of 4 or exceeds a multiple of 4 by 1.
Verification

So a perfect square leaves remainder 0 or 1 on division by 4.

(iii) The remainder of a perfect square when divided by 3, is either 0 or 1 but never 2.
Verification

So in all the cases the remainder is either 0 or 1, but not 2. Hence verified.

(iv) The remainder of a perfect square, when divided by 4, is either 0 or 1 but never 2 and 3.
Verification

From the table it is verified that the remainder of a perfect square when divided by 4 is either 0 or 1 but never 2 and 3.

(v) When a perfect square number is divided by 8, the remainder is either 0 or 1 or 4, but never be equal to 2, 3, 5, 6 or 7.
Verification

From the table it is verified when a perfect square number is divided by 8, the remainder is 0 or 1 or 4. but never be equal to 2, 3, 5, 6 or 7

Activity 2. (Text book Page No. 6)

Consider any natural number m > 1.We find that (2m, m² – 1, m² + 1) will form a Pythagorean triplet. (A little algebra can help you to verify this!). With this formula, generate a few Pythagorean triplets.
Solution:
For any natural number m, we have 2m, m² – 1, m² + 1 is a Pythagorean triplet.
(i) Consider 2m = 16 ⇒ m = 8
m² – 1 = 64 – 1 = 63
m² + 1 = 64 + 1 = 65
So Pythagorean triplet is 16, 63, 65.

(ii) Consider 2m = 18 ⇒ m = 9
m² – 1 = 81 – 1 = 80
m² + 1 = 81 + 1 = 82
So Pythagorean triplet is 18, 80, 82.

Try These (Text book Page No. 7)

Use the method of successive subtraction of odd numbers (starting from 1) to examine the following numbers and find if they are perfect squares or not. For perfect square numbers that you find, identify the square root.
(i) 144
(ii) 256
(iii) 360
Solution:
(i) 144
Step 1: 144 – 1 = 143
Step 2: 143 – 3 = 140
Step 3: 140 – 5 = 135
Step 4: 135 – 7 = 128
Step 5: 128 – 9 = 119
Step 6: 119 – 11 = 108
Step 7: 108 – 13 = 95
Step 8: 95 – 15 = 80
Step 9: 80 – 17 = 63
Step 10: 63 – 19 = 44
Step 11: 44 – 21 = 23
Step 12: 23 – 23 = 0.
We get 0 in the 12th step. ∴ 144 is a perfect square and ∴ \(\sqrt{144} \) = 12.

(ii) 256
Step 1: 256 – 1 = 255
Step 2: 255 – 3 = 252
Step 3: 252 – 5 = 247
Step 4: 247 – 7 = 240
Step 5: 240 – 9 = 231
Step 6: 231 – 11 = 220
Step 7: 220 – 13 = 207
Step 8: 207 – 15 = 192
Step 9: 192 – 17 = 175
Step 10: 175 – 19 = 156
Step 11: 156 – 21 = 135
Step 12: 135 – 23 = 112
Step 13: 112 – 25 = 87
Step 14: 87 – 27 = 60
Step 15: 60 – 29 = 31
Step 16: 31 – 31 = 0
We have subtracted odd numbers starting from 1 repeatedly from 256. We get 0 in the 1 step.
∴ 256 is a perfect square and \(\sqrt{256} \) = 16.

(iii) 360
Step 1: 360 – 1 = 359
Step 2: 359 – 3 = 356
Step 3: 356 – 5 = 351
Step 4: 351 – 7 = 344
Step 5: 344 – 9 = 335
Step 6: 335 – 11 = 324
Step 7: 324 – 13 = 311
Step 8: 311 – 15 = 296
Step 9: 296 – 17 = 279
Step 10: 279 – 19 = 260
Step 11: 260 – 21 = 239
Step 12: 239 – 23 = 216
Step 13: 216 – 25 = 191
Step 14: 191 – 27 = 164
Step 15: 164 – 29 = 135
Step 16: 135 – 31 = 104
Step 17: 104 – 33 = 71
Step 18: 71 – 35 = 36
Step 19: 36 – 37 = -1
We have subtracted successive odd numbers starting from 1, repeatedly from 360, we didn’t get zero.
∴ The given number is not perfect square.

Think (Text book Page No. 8)

In this case, if we want to find the smallest factor with which we can multiply or divide 108 to get a square number, what should we do?
Solution:
108 = 2 × 2 × 3 × 3 × 3 = 2² × 3² × 3
If we multiply the factors by 3, then we get
2² × 3² × 3 × 3 ⇒ 2² × 3² × 3² = (2 × 3 × 3)²
Which is a perfect square.
∴ Again if we divide by 3 then we get 2² × 3² ⇒ (2 × 3 )², a perfect square.
∴ We have to multiply or divide 108 by 3 to get a perfect square.

Exercise 1.2
Try These (Text book Page No. 11)

Find the square root by long division method.
(i) 400
(ii) 1764
(iii) 4356
Solution:

Try These (Text book Page No. 12)

Question 1.
Without calculating the square root, guess the number of digits in the square root of the following numbers:
(i) 14400
(ii) 100000000
(iii) 390625
Solution:
(i) \(\sqrt{14400}=\sqrt{144 \times 100}=\sqrt{144} \times \sqrt{100}\) = 12 x 10 = 120.
(ii) \(\sqrt{100000000}=\sqrt{10000 \times 10000}=\sqrt{10000} \times \sqrt{10000}\) = 100 × 100 = 10,000
(iii) \(\sqrt{390625}=\sqrt{25 \times 25 \times 25 \times 25}=\sqrt{25 \times 25} \times \sqrt{25 \times 25}\) = 25 x 25 = 625

Question 2.
Find the square root of
(i) 19.36
(ii) 1.2321
(iii) 116.64
Solution:

Think (Text book Page No. 13)

Fill up the table:

Solution:

Activity 3. (Text book Page No. 13)

Attempt to prepare a table of square root problems as in the above case to show that if a and b are two perfect square numbers, then \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\) (b ≠ 0) We can use this idea to compute easily certain square-root problems.
Solution:

Try These (Text book Page No. 13)

Using the above method, find the square root of 1.2321 and 11.9025.
Solution:
(i) \(\sqrt{1.2321}=\sqrt{\frac{12321}{10000}}=\frac{111}{100}\) = 1.11
(ii) \(\sqrt{11.9025}=\frac{\sqrt{119025}}{\sqrt{10000}}=\frac{345}{100}\) = 3.45

Try These (Text book Page No. 14)

Put the numbers
(i) 4, \(\sqrt{14} \), 5 and
(ii) 7, \(\sqrt{65} \), 8 in ascending order.
Solution:
(i) 4, \(\sqrt{14} \), 5
Squaring all the numbers we get 4², \((\sqrt{14})^2 \) , 5² ⇒ 16, 14, 25
∴Ascending order: 14, 16, 25
Ascending order: \(\sqrt{14} \), 4, 5

(ii) 7, \(\sqrt{65} \), 8
Squaring 7, \(\sqrt{65} \) and 8 we get 7², \((\sqrt{65})^2 \), 8² ⇒ 49, 65, 64
Ascending order: 49, 64, 65
Ascending order: 7, 8, \(\sqrt{65} \)

Exercise 1.3
Try These (Text book Page No. 17)

Find the ones digit in the cubes of each of the following numbers,
(i) 17
(ii) 12
(iii) 38
(iv) 53
(v) 71
(vi) 84
Solution:
(i) 17
17 ends with 7, so its cube ends with 3. i.e, ones digit in 17³ is 3.
(ii) 12
12 ends with 2, so its cube ends with 8. i.e, ones digit in 12³ is 8.
(iii) 38
38 ends with 8, so its cube ends with 2. i.e, ones digit in 38³ is 2.
(iv) 53
53 ends with 3, so its cube ends with 7. i.e, ones digit in 53³ is 7.
(v) 71
71 ends with 1, so its cube ends with 1. i.e, ones digit in 71³ is 1
(vi) 84
84 ends with 4, so its cube ends with 4. i.e, ones digit in 84³ is 4.

Think (Text book Page No. 17)

Find the smallest number by which 675 must be divided to obtain a perfect cube.
Solution:

We find that 675 = 3 x 3 x 3 x 5 x 5
= 3 x 3 x 3 x 5 x 5
Here we have an ungrouped 5 x 5.
So if we divide 675 by 5 x 5 then the new number will be a perfect cube.
ie. 675 ÷ 25 = 27
The new number is 27
\(\sqrt[3]{27}=\sqrt[3]{3 \times 3 \times 3}\) = 3

Exercise 1.4
Try These (Text book Page No. 21)

Expand the following numbers using exponents:
(i) 8120
(ii) 20305
(iii) 3652.01
(iv) 9426.521
Solution:
(i) 8120 = (8 x 1000) + (1 x 100) + (2 x 10) + 0 x 1
= (8 x 10³) + (1 x 10²) + (2 x 10¹)

(ii) 20305 = (2 x 10000) + (0 x 1000) + (3 x 100) + (0 x 10) + (5 x 1)
= (2 x 10⁴) + (3 x 10²) + 5

(iii) 3652.01 = 3000 + 600 + 50 + 2 + \(\frac{0}{10}+\frac{1}{100}\)
= (3 x 1000) +(6 x 100) + (5 x 10) + (2 x 1) + (1 x \(\frac{1}{100}\))
= (3 x 10³) + (6 x 10²) + (5 x 10¹) + 2 + (1 x 10^-2)

(iv) 9426.521 = (9 x 1000) + (4 x 100) + (2 x 10) + (6 x 1) + \(\left(\frac{5}{10}\right)+\left(\frac{2}{100}\right)+\left(\frac{1}{1000}\right)\)
= (9 x 10³) + (4 x 10²) + (2 x 10¹) + 6 + (5 x 10^-1) + (2 x 10^-2) + (1 x 10^-3)

Try These (Text book Page No. 23)

Verify the following laws (as we did above). Here, a, b are non-zero integers and m, n are any integers.
1. Zero exponent rule: a⁰ = 1.
2. Product of same powers to power of product rule: a^m x b^m = (ab)^m
3. Quotient of same powers to power of quotient rule: \(\frac{a^{m}}{b^{m}}=\left(\frac{a}{b}\right)^{m}\)
Verification:
Let a = 2; b = 3; m = 2
1. a⁰ = 2⁰ = 1.
2. a^m x b^m = 2² x 3² = 4 x 9 = 36 = (2 x 3)²
3. \(\frac{a^{m}}{b^{m}}=\frac{2^{2}}{3^{2}}=\frac{4}{9}=\left(\frac{2}{3}\right)^{2}\)

Try These (Text book Page No. 26)

Question 1.
Write in standard form: Mass of planet Uranus = 8.68 x 10²⁵ kg.
Solution:
Mass of Planet Uranus = 86800000000000000000000000 kg
[23 zeros after 868]

Question 2.
Write in scientific form:
(i) 0.000012005
(ii) 4312.345
(iii) 0.10524
(iv) The distance between the Sun and the planet Saturn 1.4335 x 10¹² miles.
Solution:

(iv) The distance between Sun and the planet Saturn is 1.4335 x 10¹² miles

Activity 4. (Text book Page No. 29)

Observe that
2³ – 1³ = 1 + 2 x 1 x 3
3³ – 2³ = 1 + 3 x 2 x 3
4³ – 3³ = 1 + 4 x 3 x 3
Find the value of 15³ – 14³ in the above pattern.
Solution:
15³ – 14³ = 1 + 15 x 14 x 3

Think (Text book Page No. 29)

1³ = 1 = 1
2³ = 8 = 3 + 5
3³ = 27 = 7 + 9 + 11
Observe and continue this pattern to find the value of 73 as the sum of consecutive odd numbers.
1³ = 1 = 1
2³ = 8 = 3 + 5
3³ = 27 = 7 + 9 + 11
4³ = 64 = 13 + 15 + 17 + 19
5³ = 125 = 21 + 23 + 25 + 27 + 29
6³ = 216 = 31 + 33 + 35 + 37 + 39 + 41
7³ = 343 = 43 + 45 + 47 + 49 + 51 + 53 + 55

Students those who are preparing for the 12th Physics exam can download this Samacheer Kalvi 12th Physics Book Solutions Questions and Answers for Chapter 10 Semiconductor Electronics from here free of cost. These Tamilnadu State Board Solutions for Class 12th Physics PDF cover all Chapter 10 Semiconductor Electronics Questions and Answers. All these concepts of Samacheer Kalvi 12th Physics Book Solutions Questions and Answers are explained very conceptually as per the board prescribed Syllabus & guidelines.

Tamilnadu Samacheer Kalvi 12th Physics Solutions Chapter 10 Communication Systems

Samacheer Kalvi 12th Physics Communication Systems Textual Evaluation Solved

Samacheer Kalvi 12th Physics Communication Systems Multiple Choice Questions

Question 1.
The output transducer of the communication system converts the radio signal into …………. .
(a) Sound
(b) Mechanical energy
(c) Kinetic energy
(d) None of the above
Answer:
(a) Sound.

Question 2.
The signal is affected by noise in a communication system …………. .
(a) At the transmitter
(b) At the modulator
(c) In the channel
(d) At the receiver
Answer:
(c) In the channel.

Question 3.
The variation of frequency of carrier wave with respect to the amplitude of the modulating signal is called …………. .
(a) Amplitude modulation
(b) Frequency modulation
(c) Phase modulation
(d) Pulse width modulation
Answer:
(b) Frequency modulation.

Question 4.
The internationally accepted frequency deviation for the purpose of FM broadcasts …………. .
(a) 75 kHz
(h) 68 kHz
(c) 80 kHz
(d) 70 kHz
Answer:
(a) 75 kHz.

Question 5.
The frequency range of 3 MHz to 30 MHz is used for …………. .
(a) Ground wave propagation
(b) Space wave propagation
(c) Sky wave propagation
(d) Satellite communication
Answer:
(c) Sky wave propagation.

Samacheer Kalvi 12th Physics Communication Systems Short Answer Questions

Question 1.
Give the factors that are responsible for transmission impairments.
Answer:

•  Attenuation
• Distortion (Harmonic)
• Noise

Question 2.
Distinguish between wireline and wireless communication? Specify the range of electromagnetic waves in which it is used.
Answer:

Question 3.
Explain centre frequency or resting frequency in frequency modulation.
Answer:
When the frequency of the baseband signal is zero (no input signal), there is no change in the frequency of the carrier wave. It is at its normal frequency and is called as centre frequency or resting frequency.

Question 4.
What does RADAR stand for?
Answer:
Radar basically stands for Radio Detection and Ranging System.

Question 5.
What do you mean by Internet of Things?
Answer:
Internet of Things (IoT), it is made possible to control various devices from a single device. Example: home automation using a mobile phone.

Samacheer Kalvi 12th Physics Communication Systems Long Answer Questions

Question 1.
What is modulation? Explain the types of modulation with necessary diagrams.
Answer:
Modulation:
For long distance transmission, the low frequency baseband signal (input signal) is superimposed onto a high frequency radio signal by a process called modulation. There are 3 types of modulation based on which parameter is modified. They are (i) Amplitude modulation, (ii) Frequency modulation, and (iii) Phase modulation.

(i) Amplitude Modulation (AM):
If the amplitude of the carrier signal is modified according to the instantaneous amplitude of the baseband signal, then it is called amplitude modulation. Here the frequency and the phase of the carrier signal remain constant. Amplitude modulation is used in radio and TV broadcasting.

The signal shown in figure (a) is the message signal or baseband signal that carries information, figure (b) shows the high frequency carrier signal and figure (c) gives the amplitude modulated signal. We can see clearly that the carrier wave is modified in proportion to the amplitude of the baseband signal

(ii) Frequency Modulation (FM):
The frequency of the carrier signal is modified according to the instantaneous amplitude of the baseband signal in frequency modulation. Here the amplitude and the phase of the carrier signal remain constant. Increase in the amplitude of the baseband signal increases the frequency of the carrier signal and vice versa. This leads to compressions and rarefactions in the frequency spectrum of the modulated wave. Louder signal leads to compressions and relatively weaker signals to rarefactions.

When the amplitude of the baseband signal is zero in Figure (a), the frequency of the modulated signal is the same as the carrier signal. The frequency of the modulated wave increases when the amplitude of the baseband signal increases in the positive direction (A,C). The increase in amplitude in the negative half cycle (B,D) reduces the frequency of the modulated wave (Figure (c)).

(iii) Phase Modulation (PM)
The instantaneous amplitude of the baseband signal modifies the phase of the carrier signal keeping the amplitude and frequency constant is called phase modulation. This modulation is used to generate frequency modulated signals. It is similar to frequency modulation except that the phase of the carrier is varied instead of varying frequency.

The carrier phase changes according to increase or decrease in the amplitude of the baseband signal. When the modulating signal goes positive, the amount of phase lead increases with the amplitude of the modulating signal. Due to this, the carrier signal is compressed or its frequency is increased.

On the other hand, the negative half cycle of the baseband signal produces a phase lag in the carrier signal. This appears to have stretched the frequency of the carrier wave. Hence similar to frequency modulated wave, phase modulated wave also comprises of compressions and rarefactions. When the signal voltage is zero (A, C and E) the carrier frequency is unchanged.

Question 2.
Elaborate on the basic elements of communication system with the necessary block diagram.
Elements of an electronic communication system:
1. Information (Baseband or input signal):
Information can be in the form of a sound signal like speech, music, pictures, or computer data Information can be in the form of a sound signal like speech, music, pictures, or computer data which is given as input to the input transducer.

2. Input transducer:
A transducer is a device that converts variations in a physical quantity (pressure, temperature, sound) into an equivalent electrical signal or vice versa. In communication system, the transducer converts the information which is in the form of sound, music, pictures or computer data into corresponding electrical signals. The electrical equivalent of the original information is called the baseband signal. The best example for the transducer is the microphone that converts sound energy into electrical energy.

3. Transmitter:
It feeds the electrical signal from the transducer to the communication channel. It consists of circuits such as amplifier, oscillator, modulator, and power amplifier. The transmitter is located at the broadcasting station.

4. Amplifier:
The transducer output is very weak and is amplified by the amplifier.

5. Oscillator:
It generates high-frequency carrier wave (a sinusoidal wave) for long distance transmission into space. As the energy of a wave is proportional to its frequency, the carrier wave has very high energy.

6. Modulator:
It superimposes the baseband signal onto the carrier signal and generates the modulated signal.

7. Power amplifier:
It increases the power level of the electrical signal in order to cover a large distance.

8. Transmitting antenna:
It radiates the radio signal into space in all directions. It travels in the form of electromagnetic waves with the velocity of light (3 x 10⁸ ms^-1).

9. Communication channel:
Communication channel is used to carry the electrical signal from transmitter to receiver with less noise or distortion. The communication medium is basically of two types: wireline communication and wireless communication.

10. Noise:
It is the undesirable electrical signal that interfaces with the transmitted signal. Noise attenuates or reduces the quality of the transmitted signal. It may be man-made (automobiles, welding machines, electric motors etc .) or natural (lightening, radiation from sun and stars and environmental effects). Noise cannot be completely eliminated. However, it can be reduced using various techniques.

11. Receiver:
The signals that are transmitted through the communication medium are received with the help of a receiving antenna and are fed into the receiver. The receiver consists of electronic circuits like demodulator, amplifier, detector etc. The demodulator extracts the baseband signal from the carrier signal. Then the baseband signal is detected and amplified using amplifiers. Finally, it is fed to the output transducer.

12. Repeaters:
Repeaters are used to increase the range or distance through which the signals are sent. It is a combination of transmitter and receiver. The signals are received, amplified, and retransmitted with a carrier signal of different frequency to the destination. The best example is the communication satellite in space.

13. Output transducer:
It converts the electrical signal back to its original form such as sound, music, pictures or data. Examples of output transducers are loudspeakers, picture tubes, computer monitor, etc.

14. Attenuation:
The loss of strength of a signal while propagating through a medium is known as attenuation. Range It is the maximum distance between the source and the destination up to which the signal is received with sufficient strength.

Question 3.
Explain the three modes of propagation of electromagnetic waves through space. Propagation of electromagnetic waves:
Answer:
The electromagnetic wave transmitted by the transmitter travels in three different modes to reach the receiver according to its frequency range:

1. Ground wave propagation (or) surface wave propagation (nearly 2 kHz to 2 MHz)
2. Sky wave propagation (or) ionospheric propagation (nearly 3 MHz to 30 MHz)
3. Space wave propagation (nearly 30 MHz to 400 GHz)

1. Ground wave propagation:
If the electromagnetic waves transmitted by the transmitter glide over the surface of the earth to reach the receiver, then the propagation is called ground wave propagation. The corresponding waves are called ground waves or surface waves.

Both transmitting and receiving antennas must be close to the earth. The size of the antenna plays a major role in deciding the efficiency of the radiation of signals. During transmission, the electrical signals are attenuated over a distance. Some reasons for attenuation are as follows:

1. Increasing distance:
The attenuation of the signal depends on (i) power of the transmitter (ii) frequency of the transmitter, and (iii) condition of the earth surface.

2. Absorption of energy by the Earth:
When the transmitted signal in the form of EM wave is in contact with the Earth, it induces charges in the Earth and constitutes a current. Due to this, the earth behaves like a leaky capacitor which leads to the attenuation of the wave.

3. Tilting of the wave:
As the wave progresses, the wavefront starts gradually tilting according to the Skywave curvature of the Earth. This increase in the tilt decreases the electric field strength of the wave. Finally, at some distance, the surface wave dies out due to energy loss.

The frequency of the ground waves is mostly less than 2 MHz as high frequency waves undergo more absorption of energy at the earth’s atmosphere. The medium wave signals received during the day time use surface wave propagation. It is mainly used in local broadcasting, radio navigation, for ship-to-ship, ship-to-shore communication and mobile communication.

2. Sky Wave Propagation:
The mode of propagation in which the electromagnetic waves radiated from an antenna, directed upwards at large angles gets reflected by the ionosphere back to earth is called sky wave propagation or ionospheric propagation. The corresponding waves are called sky waves.

The frequency range of EM waves in this mode of propagation is 3 to 30 MHz. EM waves of frequency more than 30 MHz can easily penetrate through the ionosphere and does not undergo reflection. It is used for short wave broadcast services. Medium and high frequencies are for long-distance radio communication.

Extremely long distance communication is also possible as the radio waves can undergo multiple reflections between the earth and the ionosphere. A single reflection helps the radio waves to travel a distance of approximately 4000 km.

Ionosphere acts as a reflecting surface. It is at a distance of approximately 50 km and spreads up to 400 km above the Earth surface. Due to the absorption of ultraviolet rays, cosmic ray, and other high energy radiations like a, p rays from sun, the air molecules in the ionosphere get ionized.

This produces charged ions and these ions provide a reflecting medium for the reflection of radio waves or communication waves back to earth within the permitted frequency range. The phenomenon of bending the radio waves back to earth is nothing but the total internal reflection.

3. Space wave propagation:
The process of sending and receiving information signal through space is called space wave communication. The electromagnetic waves of very high frequencies above 30 MHz are called as space waves. These waves travel in a straight line from the transmitter to the receiver. Hence, it is used for a line of sight communication (LOS).

For high frequencies, the transmission towers must be high enough so that the transmitted and received signals (direct waves) will not encounter the curvature of the earth and hence travel with less attenuation and loss of signal strength. Certain waves reach the receiver after getting reflected from the ground.

Question 4.
What do you know about GPS? Write a few applications of GPS.
Answer:
GPS stands for Global Positioning System. It is a global navigation satellite system that offers geolocation and time information to a GPS receiver anywhere on or near the Earth. GPS system works with the assistance of a satellite network. Each of these satellites broadcasts a precise signal like an ordinary radio signal.

These signals that convey the location data are received by a low-cost aerial which is then translated by the GPS software. The software is able to recognize the satellite, its location, and the time taken by the signals to travel from each satellite. The software then processes the data it accepts from each satellite to estimate the location of the receiver.

Applications:
Global positioning system is highly useful many fields such as fleet vehicle management (for tracking cars, trucks and buses), wildlife management (for counting of wild animals) and engineering (for making tunnels, bridges etc).

Question 5.
Give the applications of ICT in mining and agriculture sectors.
Answer:
(i) Agriculture:
The implementation of information and communication technology (ICT) in agriculture sector enhances the productivity, improves the living standards of farmers and overcomes the challenges and risk factors.
(a) ICT is widely used in increasing food productivity and farm management.
(b) It helps to optimize the use of water, seeds and fertilizers etc.
(c) Sophisticated technologies that include robots, temperature and moisture sensors, aerial images, and GPS technology can be used.
(d) Geographic information systems are extensively used in farming to decide the suitable place for the species to be planted.

(ii) Mining:
(a) ICT in mining improves operational efficiency, remote monitoring and disaster locating system.
(b) Information and communication technology provides audio-visual warning to the trapped underground miners.
(c) It helps to connect remote sites.

Question 6.
Modulation helps to reduce the antenna size in wireless communication – Explain. Antenna size:
Answer:
Antenna is used at both transmitter and receiver end. Antenna height is an important parameter to be discussed. The height of
the antenna must be a multiple of \(\frac { λ }{ 4 }\),
h = \(\frac { λ }{ 4 }\) ….. (1)
where λ is wavelength ( λ = \(\frac { c}{ v }\)), c is the velocity of light and v is the frequency of the signal to be transmitted.

An example:
Let us consider two baseband signals. One signal is modulated and the other is not modulated. The frequency of the original baseband signal is taken as v = 10 kHz while the modulated signal is v = 1 MHz. The height of the antenna required to transmit the original baseband signal of frequency v = 10 kHz is
h₁ = \(\frac { λ }{ 4 }\) = \(\frac { c }{ 4v }\) = \(\frac { 3\times { 10 }^{ 8 } }{ 4\times 10\times { 10 }^{ 3 } } \) = 7.5 km …. (2)
The height of the antenna required to transmit the modulated signal of frequency v = 10 kHz is
h₁ = \(\frac { λ }{ 4 }\) = \(\frac { c }{ 4v }\) = \(\frac { 3\times { 10 }^{ 8 } }{ 4\times 10\times { 10 }^{ 6 } } \) = 75 m …. (3)
Comparing equations (2) and (3), we can infer that it is practically feasible to construct an antenna of height 75 m while the one with 7.5 km is not possible. It clearly manifests that modulated signals reduce the antenna height and are required for long distance transmission.

Question 7.
Fiber optic communication is gaining popularity among the various transmission media -justify.
Answer:
The method of transmitting information from one place to another in terms of light pulses through an optical fiber is called fiber optic communication. It is in the process of replacing wire transmission in communication systems. Light has very high frequency (400 THz – 790 THz) than microwave radio systems.  The fibers are made up of silica glass or silicon dioxide which is highly abundant on Earth.

Now it has been replaced with materials such as chalcogenide glasses, fluoroaluminate crystalline materials because they provide larger infrared wavelength and better transmission capability. As fibers are not electrically conductive, it is preferred in places where multiple channels are to be laid and isolation is required from electrical and electromagnetic interference.

Applications:
Optical fiber system has a number of applications namely, international communication, inter-city communication, data links, plant and traffic control and defense applications.

Merits:

1. Fiber cables are very thin and weight lesser than copper cables.
2. This system has much larger bandwidth. This means that its information canying capacity is larger.
3. Fiber optic system is immune to electrical interferences.
4. Fiber optic cables are cheaper than copper cables.

Demerits:

1. Fiber optic cables are more fragile when compared to copper wires.
2. It is an expensive technology.

Samacheer Kalvi 12th Physics Communication Systems Additional Questions

Samacheer Kalvi 12th Physics Communication Systems Multiple Choice Questions

Question 1.
Which of the following frequencies will be suitable for beyond the horizon communication using sky waves?
(a) 10 kHz
(b) 10 MHz
(c) 1 GHz
(d) 1000 GHz
Answer:
(b) 10 MHz
Hint:
Frequency of 10 KHz will require very large radiating antenna while frequencies 1GHz and 1000 GHz will penetrate the ionosphere and cannot be reflected by it.

Question 2.
Frequency in the UHF range normally propagate by means of:
(a) Ground waves
(b) sky waves
(c) surface waves
(d) space waves
Answer:
(d) space waves.
Hint:
Frequency in the UHF (0.3 to 3 GHz) range normally propagate by means of space waves. Their sky wave reflection from ionosphere is not possible.

Question 3.
Antenna is
(a) inductive
(b) capacitive
(c) resistive above its resonant frequency
(d) resistive at resonant frequency
Answer:
(d) resistive at resonant frequency.
Hint:
An antenna is tuned circuit consisting of an inductance and a capacitance. At resonant frequency, it is resistive.

Question 4.
In frequency modulated wave
(a) frequency varies with time
(b) amplitude varies with time
(c) both frequency and amplitude vary with time
(d) both frequency and amplitude are constant
Answer:
(a) frequency varies with time.
Hint:
In frequency modulated wave, frequency of the carrier wave varies in accordance with the modulating signal.

Question 5.
Laser light is considered to be coherent because it consist of
(a) many wavelengths
(b) uncoordinated wavelengths
(c) coordinated waves of exactly the same wavelength
(d) divergent beam
Answer:
(c) coordinated waves of exactly the same wavelength
Hint:
Laser light consists of waves of save wavelength exactly in same phase. So it is highly coherent.

Question 6.
The waves used by artificial satellites for communication purposes are
(a) microwaves
(b) AM radiowaves
(c) FM radiowaves
(d) X-rays
Answer:
(a) microwaves
Hint:
Microwaves are used in artificial satellites for communication purposes.

Question 7.
An oscillator is producing FM waves of frequency 2 kHz with a variation of 10 kHz. What is the modulation index?
(a) 0.67
(b) 5.00
(c) 0.20
(d) 1.5
Answer:
(b) 5.00
Hint:
m_f = \(\frac { ∆f }{ f }\) = \(\frac { 10kHz }{ 2kHz }\) = 5

Question 8.
A laser beam is used for locating distant object because it
(a) has small angular spread
(b) is not absorbed
(c) is coherent
(d) is monochromatic
Answer:
(a) has small angular spread
Hint:
Laser beam has very small angular spread.

Question 9.
In short wave communication, waves of which of the following frequencies will be reflected back by the ionospheric layer having electron density 10¹¹ m^-3?
(a) 2 MHz
(b) 10 MHz
(c) 12 MHz
(d) 18 MHz
Answer:
(a) 2 MHz
Hint:
Critical frequency, f_c = 9 (N_max)^1/2
= 9(10¹¹)^1/2 = 2.8 x 10⁶ Hz = 2.8 MHz
∴ The wave of frequency 2 MHz will be reflected by the ionosphere.

Question 10.
The maximum distance upto which TV transmission from a TV tower of height h can be received is proportional to
(a) h^1/2
(b) h
(c) ^3/2
(d) h²
Answer:
(a) h^1/2
Hint:
d = \(\sqrt { 2Rh } \) ; d ∝ h^1/2

Question 11.
If the highest modulating frequency of the wave is 5 kHz, the number of stations that can be accommodated in a 150 kHz band width is
(a) 15
(b) 10
(c) 5
(d) none of these
Answer:
(a) 15
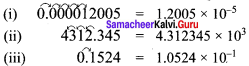
= \(\frac { 150khz }{ 2×5kHz }\) = 15

Question 12.
In communication with help of antenna if height is doubled, then the range covered with which was initially r would become
(a) \(\sqrt { 2r } \)
(b) 3r
(c) 4r
(d) 5r
Answer:
(a) \(\sqrt { 2r } \)
Hint:
Initial range, r – \(\sqrt { 2Rh } \)
When height of antenna is doubled, r’ = \(\sqrt { 2R\times 2h } \) – \(\sqrt { 2r } \)

Question 13.
A laser beam is used for carrying out surgery, because it
(a) is highly monochromatic
(b) is highly coherent
(e) is highly directional
(d) can be sharply focused
Answer:
(d) can be sharply focused
Hint:
A laser beam is highly monochromatic, directional and coherent and hence it can be sharply focused for carrying out surgery.

Question 14.
Ozone layer is present in
(a) troposphere
(b) stratosphere
(c) ionosphere
(d) mesosphere
Answer:
(b) stratosphere

Question 15.
Ozone layer blocks the radiation of wavelength
(a) less than 3 x 10^-7 m
(b) equal to 3 x 10^-7 m
(c) more than 3 x 10^-7 m
(d) none of these
Answer:
(a) less than 3 x 10^-7 m
Hint:
Ozone layer blocks ultraviolet radiation from the sun for this radiation λ < 3 x 10^-7 m.

Question 16.
What is the cause of Green house effect?
(a) Infrared rays
(b) ultraviolet rays
(c) X-rays
(d) radiowaves
Answer:
(a) Infrared rays

Question 17.
Ozone layer in atmosphere is useful, because it
(a) stops ultraviolet radiation
(b) stops green house effect
(c) stops increase in temperature of atmosphere
(d) absorbs pollutent gases
Answer:
(a) stops ultraviolet radiation

Question 18.
Biological importance of ozone layer is
(a) ozone layer controls O₂ / H₂ ratio in atmosphere
(b) it stops ultraviolet rays
(c ) ozone layer reduces green house
(d) ozone layer reflects radio waves
Answer:
(b) it stops ultraviolet rays
Hint:
Ozone layer stops ultraviolet radiation.

Question 19.
The principle used in the transmission of signals through an optical fibre is
(a) total internal reflection
(b) refraction
(c) dispersion
(d) interference
Answer:
(a) total internal reflection
Hint:
Signals propagate through an optical fibre by suffering repeated total internal reflections.

Question 20.
LANDSAT series of satellites move in near polar orbits at an altitude of
(a) 3600 km
(b) 3000 km
(c) 918 km
(d) 512 km
Answer:
(c) 918 km
Hint:
LANDSAT satellites are polar satellites which move in polar orbit at a height of 918 km above the surface of the earth.

Question 21.
Which of the following is not a transducer?
(a) loudspeaker
(b) amplifier
(c) microphone
(d) all of these
Answer:
(b) amplifier
Hint:
Any device which converts energy from one form to another is called a transducer. Loudspeaker and microphone are transducers but not an amplifier.

Question 22.
If a radio receiver amplifies all the signal frequencies equally well, it is said to have high
(a) fidelity
(b) distortion
(c) sensitivity
(d) selectivity
Answer:
(a) fidelity
Hint:
If a radio receiver amplifies all the signal frequencies equally well, it is said to have high fidelity.

Question 23.
The sky wave propagation is suitable for radio waves of frequency
(a) from 2 MHz to 50
(b) upto 2MHz
(c) from 2 MHz to 30 MHz
(d) from 2MHz to 20 MHz
Answer:
(c) from 2 MHz to 30 MHz

Question 24.
Refractive index of ionosphere is
(a) zero
(b) more than one
(c) less than one
(d) one
Answer:
(c) less than one
Hint:
Ionosphere is the upper most layer of earth’s atmosphere having veiy low density. Its refractive index is less than one.

Question 25.
When radiowaves pass through ionosphere phase difference between space current and capacitive displacement current is
(a) 0 rad
(b) 3π/2 rad
(c) π/2 rad
(d) π rad
Answer:
(a) 0 rad
Hint:
The phase difference between space current and capacitive displacement current is zero.

Question 26.
Advantages of optical fibres are
(a) high bandwidth and EM interference
(b) low bandwidth and EM interference
(c) high bandwidth, low transmission capacity and no EM interference
(d) high bandwidth, high data transmission capacity and no EM interference
Answer:
(d) high bandwidth, high data transmission capacity and no EM interference
Hint:
Optical fibres have high bandwidth, high data transmission capacity and are free from electromagnetic interference.

Question 27.
A TV tower has a height of 100 m. What is the maximum distance upto which the TV transmission can be received? R = 8 x 10⁶ m
(a) 34.77 km
(b) 32.70 km
(c) 40 km
(d) 40.70 km
Answer:
(c) 40 km
Hint:
d = \(\sqrt { 2hr } \) = \(\sqrt { 2\times 100\times 8\times { 10 }^{ 6 } } \) = 40,000 m = 40 km

Question 28.
Modem is a device which performs
(a) modulation
(b) demodulation
(c) rectification
(d) modulation and demodulation
Answer:
(d) modulation and demodulation

Question 29.
Which of the following device is full duplex?
(a) Mobile phone
(b) walky-talky
(c) loud-speaker
(d) radio
Answer:
(a) Mobile phone
Hint:
A mobile phone is a full duplex device by which two persons can talk and hear each other at the same time.

Question 30.
For a radio signal to travel 150 km from the transmitter to a receiving antenna, it takes
(a) 5 x 10^-4 second
(b) 4.5 x 10^-3 second
(c) 5 x 10^-8 second
(d) 4.5 x 10^-6 second
Answer:
(a) 5 x 10^-4 second
Hint:
t = \(\frac { s }{ v }\) = \(\frac { 150\times { 10 }^{ 3 }m }{ 3\times { 10 }^{ 8 }{ ms }^{ -1 } } \) = 5 x 10^-4 s.

Samacheer Kalvi 12th Physics Communication Systems Short Answer Questions

Question 1.
What is a communication system?
Answer:
The set up used to transmit information from one point to another is called a communication system.

Question 2.
Write down the advantages and limitations of amplitude modulation (AM)?
Answer:
Advantages of AM:

1. Easy transmission and reception
2. Lesser bandwidth requirements
3. Low cost

Limitations of AM:

1. Noise level is high
2. Low efficiency
3. Small operating range

Question 3.
Write down the advantages and limitations of frequency modulation (FM)?
Answer:
Advantages of FM:

1. Large decrease in noise. This leads to an increase in signal-noise ratio.
2. The operating range is quite large.
3. The transmission efficiency is very high as all the transmitted power is useful.
4. FM bandwidth covers the entire frequency range which humans can hear. Due to this, FM radio has better quality compared to AM radio.

Limitations of FM:

1. FM requires a much wider channel.
2. FM transmitters and receivers are more complex and costly.
3. In FM reception, less area is covered compared to AM.

Question 4.
Write down the advantages of phase modulation (PM)?
Answer:
Advantages of PM:

1. FM signal produced from PM signal is very stable.
2. The centre frequency called resting frequency is extremely stable.

Question 5.
Define bandwidth?
Answer:
The frequency range over which the baseband signals or the information signals such as voice, music, picture, etc. is transmitted is known as bandwidth.

Question 6.
Define bandwidth of transmission system?
Answer:
The range of frequencies required to transmit a piece of specified information in a particular channel is called channel bandwidth or the bandwidth of the transmission system.

Question 7.
Define skip distance.
Answer:
The shortest distance between the transmitter and the point of reception of the sky wave along the surface is called as the skip distance.

Question 8.
What is skip zone or skip area.
Answer:
There is a zone in between where there is no reception of electromagnetic waves neither ground nor sky, called as skip zone or skip area.

Question 9.
What is mean by fibre optic communication?
Answer:
The method of transmitting information from one place to another in terms of light pulses through an optical fiber is called fiber optic communication.

Question 10.
Write down the application of ICT in Fisheries?
Answer:
Fisheries:
(a) Satellite vessel monitoring system helps to identify fishing zones.
(b) Use of barcodes helps to identify time and date of catch, species name, quality of fish.

Samacheer Kalvi 12th Physics Communication Systems Long Answer Questions

Question 1.
Explain the concept of satellite communication? Write its applications.
Answer:
The satellite communication is a mode of communication of signal between transmitter and receiver via satellite. The message signal from the Earth station is transmitted to the satellite on board via an uplink (frequency band 6 GHz), amplified by a transponder and then retransmitted to another earth station via a downlink (frequency band 4 GHz).

The high-frequency radio wave signals travel in a straight line (line of sight) may come across tall buildings or mountains or even encounter the curvature of the earth. A communication satellite relays and amplifies such radio signals via transponder to reach distant and far off places using uplinks and downlinks. It is also called as a radio repeater in sky. The applications are found to be in all fields and are discussed below.

Applications:
Satellites are classified into different types based on their applications. Some satellites are discussed below.

1. Weather Satellites:
   They are used to monitor the weather and climate of Earth. By measuring cloud mass, these satellites enable us to predict rain and dangerous storms like hurricanes, cyclones etc.
2. Communication satellites:
   They are used to transmit television, radio, internet signals etc. Multiple satellitesare used for long distances.
3. Navigation satellites:
   These are employed to determine the geographic location of ships, aircrafts or any other object.

Question 2.
Explain the mobile communication? Write its applications.
Answer:
Mobile communication is used to communicate with others in different locations without the use of any physical connection like wires or cables. It allows the transmission over a wide range of area without the use of the physical link. It enables the people to communicate with each other regardless of a particular location like office, house, etc. It also provides communication access to remote areas.

It provides the facility of roaming:
that is. the user may move from one place to another without the need of compromising on the communication. The maintenance and cost of installation of this communication network are also cheap.

Applications:

1. It is used for personal communication and cellular phones offer voice and data connectivity with high speed.
2. Transmission of news across the globe is done within a few seconds.
3. Using Internet of Things (IoT), it is made possible to control various devices from a single device.
   Example: home automation using a mobile phone.
4. It enables smart classrooms, online availability of notes, monitoring student activities etc. in the field of education.

Question 3.
What do you know about INTERNET? Write its few applications?
Answer:
Internet is a fast growing technology in the field of communication system with multifaceted tools. It provides new ways and means to interact and connect with people. Internet is the largest computer network recognized globally that connects millions of people through computers. It finds extensive applications in all walks of life.

Applications:

1. Search engine:
   The search engine is basically a web-based service tool used to search for information on World Wide Web.
2. Communication:
   It helps millions of people to connect with the use of social networking: emails, instant messaging services and social networking tools.
3. E-Commerce:
   Buying and selling of goods and services, transfer of funds are done over an electronic network.

Samacheer Kalvi 12th Physics Communication Systems Additional problems

Question 1.
A radio can tune to any station in 7.5 MHz to 12 MHz band. What is the corresponding wavelength band?
Solution:
Frequency of 7.5 MHz belongs to SW band. The corresponding wavelength is
λ = \(\frac { c }{ υ }\) = \(\frac { 3\times { 10 }^{ 8 } }{ 7.5\times { 10 }^{ 6 } } \) = 40m
Frequency of 12 MHz belongs to HF band, the corresponding wavelength is
λ = \(\frac { c }{ υ }\) = \(\frac { 3\times { 10 }^{ 8 } }{ 12\times { 10 }^{ 6 } } \) = 25m
Corresponding to the given frequency band, the wavelength band is 25 m – 40 m band.

Question 2.
A TV transmitting antenna is 125 m tall. How much service area can this transmitting antenna cover, if the receiving antenna is at the ground level? Radius of earth = 6400 km.
Solution:
h_T = 125 m and R = 6400 x 10³ m
d = \(\sqrt { 2{ h }_{ T }R } \) = \(\sqrt { 2{ h }_{ T }R } \) = 40 x 10³m = 40 km
Area covered A = πd² = 3.14 x (40)² = 5024 km²

Question 3.
A transmitting antenna at the top of a tower has a height 32 m and that of the receiving antenna is 100 m. What is the maximum distance between them for satisfactory communication in LOS mode? Given radius of earth 6.4 x 10⁶ m.
Solution:
h_T = 32 m, h_R = 100 m
R = 6.4 x 10⁶ m
d_m = \(\sqrt { 2R{ h }_{ T } } \) = \(\sqrt { 2R{ h }_{ R } } \)
= \(\sqrt { 2\times 604\times { 10 }^{ 6 }\times 32 } \) + \(\sqrt { 2\times 604\times { 10 }^{ 6 }\times 100 } \)
= (64 x 10²√10) + 98 x 10³√10) = 144 x 10²√10 machines
d_m = 45. 5 km

We believe that the shared knowledge about Tamilnadu State Board Solutions for 12th Physics Chapter 10 Semiconductor Electronics Questions and Answers learning resource will definitely guide you at the time of preparation. For more details visit Tamilnadu State Board Solutions for 12th Physics Solutions and for more information ask us in the below comments and we’ll revert back to you asap.

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.4

Question 1.
Find the combined equation of the straight lines whose separate equations are x – 2y – 3 = 0 and x + y + 5 = 0.
Solution:
Separate equations are x – 2y – 3 = 0; x + y + 5 = 0
So the combined equation is (x – 2y – 3) (x + y + 5) = 0
x² + xy + 5x – 2y² – 2xy – 10y – 3x – 3y – 15 = 0
(i.e) x² – 2y² – xy + 2x – 13y – 15 = 0

Question 2.
Show that 4x² + 4xy + y² – 6x – 3y – 4 = 0 represents a pair of parallel lines.
Solution:
Comparing this equation with ax² + 2hxy + by² + 2gx + 2fy + c = 0
we get a = 4, h = \(\frac{4}{2}\) = 2 , b = 1, g = – 3, f = – 3/2, c = – 4
The condition for the lines to be parallel is h² – ab = 0
Now h² – ab = 2² – (4) (1) = 4 – 4 = 0
h² – ab = 0 ⇒ The given equation represents a pair of parallel lines.

Question 3.
Show that 2x² + 3xy – 2y² + 3x + y + 1 = 0 represents a pair of perpendicular lines.
Solution:
Comparing the given equation with the general form a = 2,h = 3/2, b = -2,g= 3/2, f = 1/2 and c = 1
Condition for two lines to be perpendicular is a + b = 0. Here a + b = 2 – 2 = 0
⇒ The given equation represents a pair of perpendicular lines.

Question 4.
Show that the equation 2x² – xy – 3y² – 6x + 19y – 20 = 0 represents a pair of intersecting lines. Show further that the angle between them is tan^-1(5).
Solution:

The given equation represents a pair of straight lines.

Question 5.
Prove that the equation to the straight lines through the origin, each of which makes an angle α with the straight line y = x is x² – 2xy sec 2α + y² = 0
Solution:
Slope of y = x is m = tan θ = 1
⇒ θ = 45°
The new lines slopes will be
m = tan(45 + α) and m = tan (45 – α)
∴ The equations of the lines passing through the origin is given by
y = tan(45 + α)x and y = tan(45 – α)x
(i.e) y = tan(45 + α)x = 0 and y = tan(45 – α)x = 0
The combined equation is [y – tan (45 + α)x] [y – tan (45 – α)x] = 0
y² + tan(45 + α)tan(45 – α)x² – xy[tan(45 – α) + tan(45 + α)] = 0


Let the equation of lines passes through the origin
So the equations are y = m₁x = 0 and y = m₂x = 0
So the combined equations is (y – m₁x) (y – m₂x) = 0
(i.e)y² – xy(m₁ + m₂) + m₁m₂x = 0
(i.e) y² – xy(2sec α) + x²(1) = 0
(i.e) y² – 2xy sec 2α + x² = 0

Question 6.
Find the equation of the pair of straight lines passing through the point (1, 3) and perpendicular to the lines 2x – 3y + 1 = 0 and 5x + y – 3 = 0
Solution:
Equation of a line perpendicular to 2x – 3y + 1 = 0 is of the form 3x + 2y + k = 0.
It passes through (1, 3) ⇒ 3 + 6 + k = 0 ⇒ k = – 9
So the line is 3x + 2y – 9 = 0
The equation of a line perpendicular to 5x + y – 3 = 0 will be of the form x – 5y + k = 0.
It passes through (1, 3) ⇒ 1 – 15 + k = 0 ⇒ k = 14
So the line is x – 5y + 14 = 0.
The equation of the lines is 3x + 2y – 9 = 0 and x – 5y + 14 = 0
Their combined equation is (3x + 2y – 9)(x – 5y + 14) = 0
(i.e) 3x² – 15xy + 42x + 2xy – 10y² + 28y – 9x + 45y – 126 = 0
(i.e) 3x² – 13xy – 10y² + 33x + 73y – 126 = 0

Question 7.
Find the separate equation of the following pair of straight lines
(i) 3x² + 2xy – y² = 0
(ii) 6 (x – 1)² + 5(x – 1)(y – 2) – 4(y – 2)² = 0
(iii) 2x² – xy – 3y² – 6x + 19y – 20 = 0
Solution:
(i) Factorising 3x² + 2xy – y² we get
3x² + 3xy – xy – y² = 3x (x + y) – y (x + y)
= (3 x – y)(x + y)
So 3x² + 2xy – y² = 0 ⇒ (3x – y) (x + y) = 0
⇒ 3x – y = 0 and x + y = 0

(ii) 6 (x – 1)² + 5 (x – 1)(y – 2) – 4(y – 2)² = 0
⇒ 6(x² – 2x +1) + 5(xy – 2x – y + 2) – 4( y² – 4y + 4) = 0
(i.e) 6x² – 12x + 6 + 5xy – 10x – 5y + 10 – 4y² + 16y – 16 = 0
(i.e) 6x² + 5xy – 4y² – 22x + 11y = 0
Factorising 6x² + 5xy – 4y² we get
6x² – 3xy + 8xy – 4y² = 3x (2x – y) + 4y (2x – y)
= (3x + 4y)(2x – y)
So, 6x² + 5xy – 4y² – 22x + 11y = (3x + 4y + l )(2x – y + m)
Equating coefficient of x ⇒ 3m + 21 = -22 …….. (1)
Equating coefficient of y ⇒ 4m – l = 11 ……. (2)
Solving (1) and (2) we get l = -11, m = 0
So the separate equations are 3x + 4y – 11 = 0 and 2x – y = 0

(iii) 2x² – xy – 3y² – 6x + 19y – 20 = 0
Factorising 2x² – xy – 3y² we get
2x² – xy – 3y² = 2x² + 2xy – 3xy – 3y²
= 2x(x + y) – 3y(x + y) = (2x – 3y) (x + y)
∴ 2x² – xy – 3y² – 6x + 19y – 20 = (2x – 3y + l)(x + y + m)
Equating coefficient of x 2m + l = -6 ……. (1)
Equating coefficient of y -3m + l = 19 …….. (2)
Constant term -20 = lm
Solving (1) and (2) we get l = 4 and m = – 5 where lm = – 20.
So the separate equations are 2x – 3y + 4 = 0 and x + y – 5 = 0

Question 8.
The slope of one of the straight lines ax² + 2hxy + by² = 0 is twice that of the other, show that 8h² = 9ab.
Solution:
ax² + 2 hxy + by² = 0
We are given that one slope is twice that of the other.
So let the slopes be m and 2m.
Now sum of the slopes = m + 2m

Question 9.
The slope of one of the straight lines ax² + 2hxy + by² = 0 is three times the other, show that 3h² = 4ab.
Solution:
Let the slopes be m and 3m.

Question 10.
A ∆OPQ is formed by the pair of straight lines x² – 4xy + y² = 0 and the line PQ. The equation of PQ is x + y – 2 = 0. Find the equation of the median of the triangle ∆OPQ drawn from the origin O.
Solution:
Equation of pair of straight lines is x² – 4xy + y² = 0 ….. (1)
Equation of the given line is x + y – 2 = 0 ⇒ y = 2 – x ……… (2)
On solving (1) and (2) we get x² – 4x (2 – x) + (2 – x)² = 0
(i.e) x² – 8x + 4x² + 4 + x² – 4x = 0
(i.e) 6x² – 12x + 4 = 0
(÷ by 2) 3x² – 6x + 2 = 0

Mid point of PQ is

Question 11.
Find p and q, ¡f the following equation represents a pair of perpendicular lines 6x² + 5xy – py² + 7x + qy – 50
Solution:
6x² + 5xy – py² + 7x + qy – 50
The given equation represents a pair of perpendicular lines
⇒ coefficient of x² + coefficient of y² = 0
(i.e) 6 – p = 0 ⇒ p = 6
Now comparing the given equation with the general form
ax² + 2hxy + by² + 2gx + 2fy + c = 0
we get a = 6, b = -6 and c = -5, f = q/2, g = 7/2 and h = 5/2
The condition for the general form to represent a pair of straight lines is abc + 2fgh – af² – bg² – ch² = 0

Question 12.
Find the value of k, if the following equation represents a pair of straight lines. Further, find whether these lines are parallel or intersecting, 12x² + 7xy – 12y² – x + 7y + k = 0.
Solution:
Comparing the given equation with the general form ax² + 2hxy + by² + 2gx + 2fy + c = 0
we get a = 12, b = -12, c = k, f = 7/2, g = – 1/2, h = 7/2
Here a + b = 0 ⇒ the given equation represents a pair of perpendicular lines
To find k: The condition for the given equation to represent a pair of straight lines is abc + 2fgh – af² – bg² – ch² = 0

Question 13.
For what value of k does the equation 12x² + 2kxy + 2y², + 11x – 5y + 2 = 0 represent two straight lines.
Solution:
12x² + 2 kxy + 2y² + 11x – 5y + 2 = 0
Comparing this equation with the general form we get

4k² + 55k + 175 = 0
4k² + 20k + 35k + 175 = 0
4k(k + 5) + 35(k + 5) = 0
(4k + 35) (k + 5) = 0
k = -5 or -35/4

Question 14.
Show that the equation 9x² – 24xy + 16y² – 12x + 16y – 12 = 0 represents a pair of parallel lines. Find the distance between them.
Solution:
Comparing the given equation with ax² + 2kxy + by² = 0 we get a = 9, h = -12, b = 16.
Now h² = (-12)² = 144, ab = (9) (16) = 144
h² = ab ⇒ The given equation represents a pair of parallel lines.
To find their separate equations:
9x² – 24xy + 16y² = (3x – 4y)²
So, 9x² – 24xy +16y² – 12x + 16y – 12 = (3x – 4y + l )(3x – 4y + m)
Here coefficient of x ⇒ 3m + 3l = -12 ⇒ m + l = -4
coefficient of y ⇒ -4m – 4l = 16 ⇒ m + l = -4
Constant term l m = -12
Now l + m = -4 and lm = -12 ⇒ l = -6 and m = 2
So the separate equations are 3x – 4y – 6 = 0 and 3x – 4y + 2 = 0

Question 15.
Show that the equation 4x² + 4xy + y² – 6x – 3y – 4 = 0 represents a pair of parallel lines. Find the distance between them.
Solution:
4x² + 4xy + y² – 6x – 3y – 4 = 0
a = 4,
b = 1,
h = 4/2 = 2
h² – ab = 2² – (4) (1) = 4 – 4 = 0
⇒ The given equation represents a pair of parallel lines.
To find the separate equations 4x² + 4xy + y² = (2x + y)²
So, 4x² + 4xy + y² – 6x – 3y – 4 = (2x + y + l )(2x + y + m)
Coefficient of x ⇒ 2m + 2l = -6 ⇒ l + m = – 3 ……. (1)
Coefficient of y ⇒ l + m = – 3 ……… (2)
Constant term ⇒ l m = – 4 ……… (3)
Now l + m = -3 and lm = -4 ⇒ l = -4, m = 1
So the separate equations are 2x + y + 1 = 0 and 2x + y – 4 = 0

Question 16.
Prove that one of the straight lines given by ax² + 2hxy + by² = 0 will bisect the angle between the co-ordinate axes if (a + b)² = 4h².
Solution:
Let the slopes be l and m
∵ One line bisects the angle between the coordinate axes ⇒ θ = 45°
So tan θ = 1
The slopes are l and m

Question 17.
If the pair of straight lines x² – 2kxy – y² = 0 bisect the angle between the pair of straight lines x² – 2lxy – y² = 0, show that the later pair also bisects the angle between the former.
Solution:
Given that x² – 2kxy – y² = 0 …….. (1)
Bisect the angle between the lines x² – 11xy – y² = 0 …… (2)

x² – 2kxy – y² = 0

Question 18.
Prove that the straight lines joining the origin to the points of intersection of 3x² + 5xy – 3y² + 2x + 3y = 0 and 3x – 2y – 1 = 0 are at right angles.
Solution:
Homogenizing the given equations 3x² + 5xy – 3y² + 2x + 3y = 0 and 3x – 2y – 1 = 0
(i.e) 3x – 2y = 1.
We get (3x² + 5xy – 3y²) + (2x + 3y)( 1) = 0
(i.e) (3x² + 5xy – 3y²) + (2x + 3y)(3x – 2y) = 0
3x² + 5xy – 3y² + bx² – 4xy + 9xy – 6y² = 0
9x² + 10xy – 9y² = 0
Coefficient of x² + coefficient of y² = 9 – 9 = 0
⇒ The pair of straight lines are at right angles.

Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.4 Additional Questions Solved

Question 1.
Find the angle between the pair of straight lines given by
(a² – 3b² )x² + 8ab xy + (b² – 3a²)y² =0 .
Solution:

Question 2.
Show that 9x² + 24xy + 16y² + 21x + 28y + 6 = 0 represents a pair of parallel straight lines and find the distance between them.
Solution:
9x² + 24xy + 16y² + 21x + 28y + 6 = 0
Here a = 9.6,
b = 16,
g = \(\frac{21}{2}\),
f = 14,
c = 6,
h = 12
h² – ab = (12)² – 9(16) = 144 – 144 = 0
∴ The lines are parallel.
9x² + 24xy + 16y² = (3x + 4y)(3x + 4y)
Let 9x² + 24xy + 16y² + 21x + 28y + 6 = (3x + 4y + l)(3x + 4y + m)
Equating the coefficients of x and constant term
3l + 3m = 21
lm = 6
Solving we get, l = 1 or 6
m = 6 or 1
∴ The separate equations are 3x + 4y + 1 = 0 and 3x + 4y + 6 = 0

Question 3.
If the equation 12x² – 10xy + 2y² + 14x – 5y + c = 0 represents a pair of straight lines, find the value of c. Find the separate equations of the straight lines and also the angle
between them.
Solution:
12x² – 10xy – 2y² + 14x – 5y + c = 0
ax² + 2hxy + by² +2gx + 2fy – c = 0
Here a = 12,
b = 2,
g = 7,
f = 5/2,
c = c,
h = -5
af² + bg² + ch² – 2fgh – abc = 0 is the condition

The equation is 12x² – 10y + 2y² + 14x – 5y + 2 = 0
12x² – 10xy + 2y = (3x – y)(4x – 2y)
Let 12x² – 10y + 2y² + 14x – 5y + 2(3x – y + l)(4x – 2y + m)
So that 4l + 3m = 14 , -2l – m = -5

Question 4.
For what value of k does 12x² + 7xy + ky² + 13x – y + 3 = 0 represents a pair of straight lines? Also write the separate equations.
Solution:
12x² + 7xy + ky² + 13x – y + 3 = 0
a = 12,
h = \(\frac{7}{2}\),
f = \(-\frac{1}{2}\) ,
c = 3
af² + bg² + ch² – abc – 2fgh = 0

⇒ 12 + 169k + 147 – 144k + 91 = 0
25k = – 250 ⇒ k = -10
The equation is 12x² + 7xy – 10y² + 13x – y + 3 = 0
To find separate equations: 12x² + 7xy – 10y² = (3x – 2y)(4x + 5y)
Let 12x² + 7xy – 10y² + 13x – y + 3 = 0(3x – 2y + l)(4x + 5y + m)
Equating the coefficient of x ⇒ 4l + 3m = 13 …… (1)
Equating the coefficient of y ⇒ 5l – 2m = -1 …… (2)
(1) × 2 ⇒ 8l + 6m = 26
(2) × 3 ⇒ 15l – 6m = -3
23l = 23 ⇒ l = 1
4 + 3 m = 13
3 m = 9 ⇒ m = 3
The separate equations are 3x – 2y + 1 = 0 and 4x + 5y + 3 = 0

Question 5.
Show that 3x² + 10xy + 8y² + 14x + 22y + 15 = 0 represents a pair of straight lines and the angle between them is tan^-1\(\left(\frac{2}{11}\right)\)
Solution:
3x² + 10xy + 8y² + 14x + 22y + 15 = 0
a = 3,
A = 5,
b = 8,
g = 7,
f = 11,
c = 15
The condition is af² + bg² + ch² – abc – 2fgh = 0
3(11)² + 8(7)² + 15 (5)² – (3)(8)(15) – 2(11)(7)(5) = 363 + 392 + 375 – 360 – 770 = 0
The angle between the pair of straight line is given by

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.7

Solve the following Linear differential equations:

Question 1.

Solution:

Dividing throughout by ‘cos x’

This is a linear differential equation of the type \(\frac{d y}{d x}\) + Py = Q
Where P = tan x,
Q = sec x

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.
(2x – 10y³)dy + ydx = 0
Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:


2y = (x + a)⁴ + 2c(x + a)²

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

2x³y = x² + 3

Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.7 Additional Problems

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.
Solve: (1 + y²)dx = (tan^-1y – x)dy
Solution:

Question 5.
Solve: dx + x dy = e^-y sec² y dy
Solution:

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.2

Question 1.
Find all the values of x such that
(i) -6π ≤ x ≤ 6π and cos x = 0
(ii) -5π ≤ x ≤ 5π and cos x = 1
Solution:
(i) cos x = 0
⇒ x = (2n + 1) ± \(\frac{\pi}{2}\)
n = 0, ±1, ±2, ±3, ±4, ±5
(ii) cos x = 1 = cos 0
⇒ x = 2nπ ± 0
n = 0, ±1, ±2

Question 2.
State the reason for \(\cos ^{-1}\left[\cos \left(-\frac{\pi}{6}\right)\right] \neq-\frac{\pi}{6}\)
Solution:
We know cos(-π) = cos π
so

Question 3.
Is cos^-1 (-x) = π – cos^-1 x true? Justify your answer.
Solution:
Let π = cos^-1(-x)
⇒ cos π = -x
⇒ -cos π = x
⇒ cos(π – π) = x
⇒ π – π = cos^-1 x
⇒ π – cos^-1 x = π
⇒ π – cos^-1 x = cos^-1(-x)

Question 4.
Find the principal value of \(\cos ^{-1}\left(\frac{1}{2}\right)\)
Solution:
Let \(\cos ^{-1}\left(\frac{1}{2}\right)\) = π
⇒ cos π = \(\frac { 1 }{ 2 }\) = cos \(\frac{\pi}{3}\)
⇒ π = \(\frac{\pi}{3}\)
⇒ \(\cos ^{-1}\left(\frac{1}{2}\right)\) = \(\frac{\pi}{3}\)

Question 5.
Find the value of
(i) \(2 \cos ^{-1}\left(\frac{1}{2}\right)+\sin ^{-1}\left(\frac{1}{2}\right)\)
(ii) \(\cos ^{-1}\left(\frac{1}{2}\right)+\sin ^{-1}(-1)\)
(iii) \(\cos ^{-1}\left(\cos \frac{\pi}{7} \cos \frac{\pi}{17}-\sin \frac{\pi}{7} \sin \frac{\pi}{17}\right)\)
Solution:

Question 6.
Find the domain of
(i) \(f(x)=\sin ^{-1}\left(\frac{|x|-2}{3}\right)+\cos ^{-1}\left(\frac{1-|x|}{4}\right)\)
(ii) g(x) = sin^-1 x + cos^-1 x
Solution:
(i) \(f(x)=\sin ^{-1}\left(\frac{|x|-2}{3}\right)+\cos ^{-1}\left(\frac{1-|x|}{4}\right)\) = U(x) + V(x) say
U(x):
\(-1<\frac{|x|-2}{3}<1\)
-3 < |x| – 2 < 3
-1 < |x| ≤ 5
V(x):
\(-1 \leq \frac{1-|x|}{4} \leq 1\)
-4 ≤ 1 – |x| ≤ 4
-5 ≤ -|x| ≤ 3
-3 ≤ |x| ≤ 5
from U(x) and V(x)
⇒ |x| ≤ 5
⇒ -5 ≤ |x| ≤ 5
(ii) g(x) = sin^-1 x + cos^-1 x
-1 ≤ x ≤ 1

Question 7.
For what value of x, the inequality \(\frac{\pi}{2}\) < cos^-1 (3x -1) < π holds?
Solution:
\(\frac{\pi}{2}\) < cos^-1 (3x -1) < π
⇒ cos\(\frac{\pi}{2}\) < 3x – 1 < cos π
⇒ 0 < 3x – 1 < -1
⇒ 1 < 3x < 0
⇒ \(\frac{1}{3}\) < x < 0
This inequality holds only if x < 0 or x > \(\frac{1}{3}\)

Question 8.
Find the value of
(i) \(\cos \left(\cos ^{-1}\left(\frac{4}{5}\right)+\sin ^{-1}\left(\frac{4}{5}\right)\right)\)
(ii) \(\cos ^{-1}\left(\cos \left(\frac{4 \pi}{3}\right)\right)+\cos ^{-1}\left(\cos \left(\frac{5 \pi}{4}\right)\right)\)
Solution:

Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.2 Additional Problems

Question 1.
Find the principal value of:
Solution:

Question 2.

Solution:

Question 3.

Solution:

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1

Question 1.
Find all the values of x such that
(i) -10π ≤ x ≤ 10π and sin x = 0
(ii) -8π ≤ x ≤ 8π and sin x = -1
Solution:
(i) sin x = 0
⇒ x = nπ
where n = 0, ±1, ±2, ±3, ……., ±10
(ii) sin x = -1
⇒ x = (4n – 1) \(\frac{\pi}{2}\), n = 0, ±1, ±2, ±3, 4

Question 2.
Find the period and amplitude of
(i) y = sin 7x
(ii) y = -sin(\(\frac{1}{3}\)x)
(iii) y = 4 sin(-2x)
Solution:
(i) y = sin 7x
Period of the function sin x is 2π
Period of the function sin 7x is \(\frac{2 \pi}{7}\)
The amplitude of sin 7x is 1.

(ii) y = -sin\(\frac{1}{3}\)x
Period of sin x is 2π
So, period of sin\(\frac{1}{3}\)x is 6π and the amplitude is 1.

(iii) y = 4 sin(-2x) = -4 sin 2x
Period of sin x is 2π
π Period of sin 2x is π and the amplitude is 4.

Question 3.
Sketch the graph of y = sin(\(\frac{1}{3}\)x) for 0 ≤ x < 6π.
Solution:
The period of sin(\(\frac{1}{3}\)x) is 6π and the amplitude is 1.

The graph is

Question 4.
Find the value of
(i) \(\sin ^{-1}\left(\sin \left(\frac{2 \pi}{3}\right)\right)\)
(ii) \(\sin ^{-1}\left(\sin \left(\frac{5 \pi}{4}\right)\right)\)
Solution:

Question 5.
For that value of x does sin x = sin^-1 x?
Solution:
sin x = sin^-1 x is possible only when x = 0 (∵ x ∈ R)

Question 6.
Find the domain of the following
(i) \(f(x)=\sin ^{-1}\left(\frac{x^{2}+1}{2 x}\right)\)
(ii) \(g(x)=2 \sin ^{-1}(2 x-1)-\frac{\pi}{4}\)
Solution:
(i) \(f(x)=\sin ^{-1}\left(\frac{x^{2}+1}{2 x}\right)\)
The range of sin-1 x is -1 to 1
\(-1 \leq \frac{x^{2}+1}{2 x} \leq 1\)
⇒ \(\frac{x^{2}+1}{2 x} \geq-1\) or \(\frac{x^{2}+1}{2 x} \leq 1\)
⇒ x² + 1 ≥ -2x or x² + 1 ≤ 2x
⇒ x² + 1 + 2x ≥ 0 or x² + 1 – 2x ≤ 0
⇒ (x+ 1)² ≥ 0 or (x – 1)² ≤ 0 which is not possible
⇒ -1 ≤ x ≤ 1 or
(ii) \(g(x)=2 \sin ^{-1}(2 x-1)-\frac{\pi}{4}\)
-1 ≤ (2x – 1) ≤ 1
0 ≤ 2x ≤ 2
0 ≤ x ≤ 1
x ∈ [0, 1]

Question 7.
Find the value of \(\sin ^{-1}\left(\sin \frac{5 \pi}{9} \cos \frac{\pi}{9}+\cos \frac{5 \pi}{9} \sin \frac{\pi}{9}\right)\)
Solution:

Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1 Additional Problems

Question 1.

Solution:

Question 2.

Solution:

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.6

Solve the following differential equations:

Question 1.

Solution:

This is a Homogeneous differential equation

Seperating the variables

Question 2.
(x³ + y³) dy – x²y dx = 0
Solution:
(x³ + y³) dy – x²y dx = 0
(x³ + y³) dy = x³y dx

This is a Homogeneous differential equation.

Separating the variables

Question 3.

Solution:

This is a Homogeneous differential equation

Seperating the variables

Question 4.
2xydx + (x² + 2y²) dy = 0
Solution:
2xy dx + (x² + 2y²) dy = 0
(x² + 2y²) dy = – 2xy dx

This is a Homogeneous differential equation


Separating the variables

Question 5.
(y² – 2xy)dx = (x² – 2xy)dy
Solution:
(y² – 2xy) dx = (x² – 2xy) dy

This is a Homogeneous differential equation


Seperating the variables

Question 6.

Solution:

Seperating the variables

Question 7.

Solution:

This is a Homogeneous differential equation

Separating the variables

Question 8.
(x² + y²) dy = xy dx. It is given that y(1) = 1 and y(x₀) = e. Find the value of x₀.
Solution:

This is a Homogeneous differential equation

Seperating the variables

Samacheer Kalvi 12th Maths Solutions Chapter 10 Ordinary Differential Equations Ex 10.6 Additional problems

Question 1.
Solve: (2\(\sqrt{x y}\))dy + y dx = 0
Solution:

Question 2.
Solve: (x³ + 3xy²)dx + (y³ + 3x²y)dy = 0
Solution:


Integrating, we have

Question 3.

Solution:

Which is in terms of v alone.
⇒ the given problem comes under homogeneous type.

Question 4.
Solve: (x² + y²)dy = xy dx
Solution:

Which is a function in v alone.
⇒ the given problem comes under homogeneous type.

Question 5.
Find the equation of the curve passing through (1, 0) and which has slope \(1+\frac{y}{x}\) at (x, y).
Solution:


Given the curve passes through (1, 0) ⇒ at x = 1, y = 0
0 = log 1 +c ⇒ c = 0

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.10

Choose the correct or the most suitable answer from the given four alternatives:
Question 1.
If \(\vec{a}\) and \(\vec{b}\) are parallel vector, then \([\vec{a}, \vec{c}, \vec{b}]\) is equal to ………………..
(a) 2
(b) -1
(c) 1
(d) 0
Solution:
(d) 0
Hint:
\(\vec{a}\) and \(\vec{b}\) are parallel vectors, so \(\vec{a} \times \vec{b}\) = 0
then \([\vec{a} \vec{c} \vec{b}]=-[\vec{a} \vec{b} \vec{c}]=-(\vec{a} \times \vec{b}) \cdot \vec{c}\) = 0

Question 2.
If a vector \(\vec{\alpha}\) lies in the plane of \(\vec{\beta}\) and \(\vec{\gamma}\), then …………

Solution:
(c) \([\vec{\alpha}, \vec{\beta}, \vec{\gamma}]\) = 0
Hint:
Since \([\vec{\alpha}, \vec{\beta}, \vec{\gamma}]\) are lie in the same plane
so \([\vec{\alpha}, \vec{\beta}, \vec{\gamma}]\) = 0

Question 3.
If \(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{c}=\vec{c} \cdot \vec{a}\)= 0, then the value of \(|[\vec{a}, \vec{b}, \vec{c}]|\) is ……………….
(a) \(|\vec{a}||\vec{b}||\vec{c}|\)
(b) \(\frac{1}{3}|\vec{a}||\vec{b}||\vec{c}|\)
(c) 1
(d) -1
Solution:
(a) \(|\vec{a}||\vec{b}||\vec{c}|\)
Hint:

Question 4.
If \(\vec{a}, \vec{b}, \vec{c}\) are three unit vectors such that \(\vec{a}\) is perpendicular to \(\vec{b}\), and is parallel to \(\vec{c}\) then \(\vec{a} \times(\vec{b} \times \vec{c})\)is equal to ………………….
(a) \(\vec{a}\)
(b) \(\vec{b}\)
(c) \(\vec{c}\)
(d) \(\vec{0}\)
Solution:
(b) \(\vec{b}\)
Hint:

Question 5.

(a) 1
(b) -1
(c) 2
(d) 3
Solution:
(a) 1
Hint:

Question 6.
The volume of the parallelepiped with its edges represented by the vectors \(\hat{i}+\hat{j}, i+2 \hat{j}\), \(\hat{i}+\hat{j}+\pi \hat{k}\) is ……………

Solution:
(c) π
Hint:
Volume = \([\vec{a} \vec{b} \vec{c}]=\left|\begin{array}{ccc}{1} & {1} & {0} \\ {1} & {2} & {0} \\ {1} & {1} & {\pi}\end{array}\right|\)
= π(2 – 1) = π cubic units

Question 7.
If \(\vec{a}\) and \(\vec{b}\) are unit vectors such that \([\vec{a}, \vec{b}, \vec{a} \times \vec{b}]=\frac{\pi}{4}\) then the angle between \(\vec{a}\) and \(\vec{b}\) is …………

Solution:
(a) \(\frac{\pi}{6}\)
Hint:

Question 8.

(a) 0
(b) 1
(c) 6
(d) 3
Solution:
(a) 0
Hint:

Equate corresponding coefficients on both sides
λ + µ = 0 and λ = -1 this gives µ = 1
∴ Then the value of λ + µ = 0.

Question 9.
If \(\vec{a}, \vec{b}, \vec{c}\) are three non-coplanar vectors such that \(\vec{a} \times(\vec{b} \times \vec{c})=\frac{\vec{b}+\vec{c}}{\sqrt{2}}\), then the angle between \(\vec{a}\) and \(\vec{b}\) is …………
(a) 81
(b) 9
(c) 27
(d) 18
Solution:
(a) 81
Hint:

Question 10.

Solution:
(b) \(\frac{3 \pi}{4}\)
Hint:

Question 11.
If the volume of the parallelepiped with \(\vec{a} \times \vec{b}, \vec{b} \times \vec{c}, \vec{c} \times \vec{a}\) as coterminous edges is 8 cubic units, then the volume of the parallelepiped with \((\vec{a} \times \vec{b}) \times(\vec{b} \times \vec{c}),(\vec{b} \times \vec{c}) \times(\vec{c} \times \vec{a})\) and \((\vec{c} \times \vec{a}) \times(\vec{a} \times \vec{b})\) as coterminous edges is ………………
(a) 8 cubic units
(b) 512 cubic units
(c) 64 cubic units
(d) 24 cubic units
Solution:
(c) 64 cubic units
Hint:

Question 12.
Consider the vectors \(\vec{a}, \vec{b}, \vec{c}, \vec{d}\) such that \((\vec{a} \times \vec{b}) \times(\vec{c} \times \vec{d})=\overrightarrow{0}\). Let P₁ and P₂ be the planes determined by the pairs of vectors \(\vec{a}, \vec{b}\) and \(\vec{c}, \vec{d}\) respectively. Then the angle between P₁ and P₂ is ……………..
(a) 0°
(b) 45°
(c) 60°
(d) 90°
Solution:
(a) 0°
Hint:

Question 13.

(a) perpendicular
(b) parallel
(c) inclined at an angle \(\frac{\pi}{3}\)
(d) inclined at an angle \(\frac{\pi}{6}\)
Solution:
(b) parallel
Hint:

Question 14.
If , then a vector perpendicular to \(\vec{a}\) and lies in the plane containing \(\vec{b}\) and \(\vec{c}\) is

Solution:
(d) \(-17 \hat{i}-21 \hat{j}-97 \hat{k}\)
Hint:

Question 15.
The angle between the lines is ………..

Solution:
(d) \(\frac{\pi}{2}\)
Hint:

Question 16.
If the line lies in the plane x + 3 + αz + β = 0, then (α, β) is …………..
(a) (-5, 5)
(b) (-6, 7)
(c) (5, -5)
(d) (6, -7)
Solution:
(d) (-6, 7)
Hint:
d.c.s of the first line = (3, -5, 2)
d.c.s of the line perpendicular to plane = (1, 3, -α)
a₁a₂ + b₁b₂ + c₁c₂ = 0
3 – 15 – 2α = 0 => -12 – 2α = 0
-2α =12 => α = -6
Plane passes through the point (2, 1, -2) so
2 + 3 + 6(-2) + β = 0 => β = 7
(α, β) = (-6, 7)

Question 17.
The angle between the line \(\vec{r}=(\hat{i}+2 \hat{j}-3 \hat{k})+t(2 \hat{i}+\hat{j}-2 \hat{k})\) and the plane \(\vec{r} \cdot(\hat{i}+\hat{j})+4\) = 0 is ……………
(a) 0°
(b) 30°
(c) 45°
(d) 90°
Solution:
(c) 45°
Hint:

Question 18.
The coordinates of the point where the line \(\vec{r}=(6 \hat{i}-\hat{j}-3 \hat{k})+t(-\hat{i}+4 \hat{k})\) meets the plane \(\vec{r} \cdot(\hat{i}+\hat{j}-\hat{k})\) are
(a) (2, 1, 0)
(b) (7, -1, -7)
(c) (1, 2, -6)
(c) (5, -1, 1)
Solution:
(d) (5, -1, 1)
Hint:
Cartesian equation of the line
\(\frac{x-6}{-1}=\frac{y+1}{0}+\frac{z+3}{4}\) = λ
(-λ + 6, -1, 4λ – 3)
This meets the plane x + y – z = 3
-λ + 6 – 1 – 41 + 3 = 3 ⇒ -5λ = -5
λ = 1
The required point (5, -1, 1).

Question 19.
Distance from the origin to the plane 3x – 6y + 2z + 7 = 0 is ………………
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 1
Hint:
Distance from the origin (0, 0, 0) to the plane

Question 20.
The distance between the planes x + 2y + 3z + 7 = 0 and 2x + 4y + 6z + 7 = 0 is ……………

Solution:
(a) \(\frac{\sqrt{7}}{2 \sqrt{2}}\)
Hint:
x + 2y + 3z + 1 = 0; 2x + 4y + 6z + 7 = 0
Multiplying 2 on both sides
2x + 4y + 6z + 14 = 0 .
a = 2, b = 4, c = 6, d₁ = 14, d₂ = ?

Question 21.
If the direction cosines of a line are \(\frac{1}{c}, \frac{1}{c}, \frac{1}{c}\), then ……………….
(a) c = ±3
(b) c = ± \(\sqrt{3}\)
(c) c > 0
(d) 0 < c < 1
Solution:
(b) c = ± \(\sqrt{3}\)
Hint:
We know that sum of the squares of direction cosines = 1

Question 22.
The vector equation \(\vec{r}=(\hat{i}-2 \hat{j}-\hat{k})+t(6 \vec{j}-\hat{k})\) represents a straight line passing through the points ……………. (a) (0, 6, -1) and (1, -2, -1) (b) (0, 6, -1) and (-1, -4, -2) (c) (1, -2, -1) and (1, 4, -2) (d) (1, -2, -1) and (0, -6, 1)
Solution:
(c) (1, -2, -1) and (1, 4, -2)
Hint:
The required vector equation is \(\vec{r}=\vec{a}+t(\vec{b}-\vec{a})\)

From (1) and (2) The points are (1, -2, -1) and (1, 4, -2)

Question 23.
If the distance of the point (1, 1, 1) from the origin is half of its distance from the plane x + y + z + k= 0, then the values of k are ………….. (a) ±3 (b) ±6 (c) -3, 9 (d) 3, -9
Solution:
(d) 3, -9
Hint:

Question 24.
If the planes \(\vec{r} \cdot(2 \hat{i}-\lambda \hat{j}+\hat{k})=3 \text { and } \vec{r} \cdot(4 \hat{i}+\hat{j}-\mu \hat{k})\) = 5 are parallel, then the value of λ and µ are ……………
Solution:
(c) \(-\frac{1}{2}\), -2
Hint:

Question 25.
If the length of the perpendicular from the origin to the plane 2x + 3y + λz = 1, λ > 0 is \(-\frac{1}{5}\), then the value of λ is …………..
(a) \(2 \sqrt{3}\)
(b) \(3 \sqrt{2}\)
(c) 0
(d) 1
Solution:
(a) \(2 \sqrt{3}\)
Hint:
Given length of perpendicular from origin to the plane = \(-\frac{1}{5}\)

Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.10 Additional Problems

Question 1.

(a) 6
(b) 10
(c) 12
(d) 24
Solution:
(c) 12
Hint:

Question 2.

(a) only x
(b) only y
(c) Neither x nor y
(d) Both x and y
Solution:
(c) Neither x nor y
Hint:

Question 3.

(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(b) 3
Hint:

Question 4.
The value of = ………………
(a) 1
(b) 3
(c) -3
(d) 0
Solution:
(b) 3
Hint:

Question 5.
Let a, b, c be distinct non-negative numbers. If the vectors lie in a plane, then c is ……………..
(a) the A.M. of a and b
(b) the G.M. of a and b
(c) the H.M. of a and b
(d) equal to zero.
Solution:
(b) the G.M. of a and b
Hint:

Question 6.
The value of \(\hat{i} \cdot(\hat{j} \times \hat{k})+(\hat{i} \times \hat{k}) \cdot \hat{j}\) ………….
(a) 1
(b) -1
(c) 0
(d) \(\hat{j}\)
Solution:
(c) 0
Hint:

Question 7.
The value of \((\hat{i}-\hat{j}, \hat{j}-\hat{k}, \hat{k}-\hat{i})\) is …………..
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(a) 0
Hint:

Question 8.

Solution:
(c) \(\vec{u}=\overrightarrow{0}\)
Hint:

Question 9.
The area of the parallelogram having a diagonal \(3 \vec{i}+\vec{j}-\vec{k}\) and a side \(\vec{i}-3 \vec{j}+4 \vec{k}\) is ………………

Solution:
(d) \(3 \sqrt{30}\)
Solution:

Question 10.
If , then ……………….

Solution:
(d) \(\vec{x}=\overrightarrow{0} \text { or } \vec{y}=\overrightarrow{0} \text { or } \vec{x} \text { and } \vec{y}\) are parallel
Hint:

Question 11.
If \(\overrightarrow{\mathrm{PR}}=2 \vec{i}+\vec{j}+\vec{k}, \overrightarrow{\mathrm{Question}}=-\vec{i}+3 \vec{j}+2 \vec{k}\), then the area of the quadrilateral PQRS is ………………..

Solution:
(c) \(\frac{5 \sqrt{3}}{2}\)
Hint:

Question 12.

Solution:
(c) \(\vec{c}\) parallel to \(\vec{a}\)
Hint:

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.7

Question 1.
Find intervals of concavity and points of inflexion for the following functions:
(i) f(x) = x (x – 4)³
(ii) f(x) = sin x + cos x, 0 < x < 2π

Solution:
(i) f(x) = x(x – 4)³
f(x) = x[x³ – 12x² + 48x – 64]
(i.e.,) f(x) = x⁴ – 12x³ + 48x² – 64x
f'(x) = 4x³ – 36x² + 96x – 64
f”(x) = 12x² – 72x + 96
f”(x) = 0 ⇒ 12(x² – 6x + 8) = 0
⇒ 12 (x – 2) (x – 4) = 0 ⇒ x = 2 or 4
Marking the points in the number line

in the interval (-∞, 2) the curve concave upwards
when x ∈ (2, 4), f”(x) = (3 – 2) (3 – 4)
[say x = 3] = -ve
⇒ The curve concave upwards in (2,4)
when x ∈ (4, ∞), f”(x) = (5 – 2) (5 – 4)
[say x = 5] = (+) (+) = +ve ⇒ The curve concave downwards is (4, ∞) in (-∞, 2) concave upwards and in (2, 4) the concave downwards
⇒ x = 2 is a point of inflection at x = 2, f(2) = -16
So (2, -16) is a point of inflection
Again in (2, 4) the curve concave downwards and in (4, ∞) the curve concave upwards ⇒ x = 4 is a point of inflection f(4) = 0
∴ (4, 0) is a point of inflection
So points of inflection are (2, -16) and (4, 0)

(ii) f(x) = sin x + cos x
f'(x) = cos x – sin x
f”(x) = – sin x – cos x
f”(x) = 0 ⇒ – sin x = cos x



So the intervals are (-∞, 0), (0, ∞) when x ∈ (-∞, 0) f”(x) is negative
⇒ the curve concave downwards and when x ∈ (0, ∞) f”(x) is positive
⇒ the curve concave upwards
⇒x = 0 is a point of inflection f(0) = \(\frac{1}{2}\)(1 – 1) = 0
So (0, 0) is the point of inflection and the curve concave upwards in (0, ∞) and curve concave downwards in (-∞, 0) and (0, 0) is the point of inflection.

Question 2.
Find the local extrema for the following functions using second derivative test:
(i) f(x) = – 3x⁵ + 5x³
(ii) f(x) = x log x
(iii) f(x) = x² e^-2x
Solution:
(i) f(x) = – 3x⁵ + 5x³
f'(x) = 0, f”(x) = -ve at x = a
⇒ x = a is a maximum point
f'(x) = 0, f”(x) = +ve at x = 6
⇒ x = b is a minimum point
f(x) = – 3x⁵ + 5x³
f’ (x) = -15x⁴ + 15x²
f”(x) = -60x³ + 30x
f'(x) = 0 ⇒ – 15x² (x² – 1) = 0
⇒ x = 0, +1, -1
at x = 0, f”(x) = 0
at x = 1, f”(x) = -60 + 30 = – ve
at x = -1, f”(x) = 60 – 30 = + ve
So at x = 1, f'(x) = 0 and f”(x) = -ve
⇒ x = 1 is a local maximum point.
and f(1) = 2
So the local maximum is (1, 2)
at x = -1, f'(x) = 0 and f”(x) = +ve
⇒ x = -1 is a local maximum point and f(-1) = -2.
So the local minimum point is (-1, -2)
∴ local minimum is -2 and local maximum is 2.

(ii) f(x) = x log x

(iii) f(x) = x² e^-2x
f'(x) = x²[-2e^-2x] + e^-2x (2x)
= 2e^-2x (x – x²)
f”(x) = 2e^-2x(1 – 2x) + (x – ²) (-4e^-2x)
= 2e^-2x [(1 – 2x) + (x – x²) (- 2)]
= 2e^-2x [2x² – 4x + 1]
f'(x) = 0 ⇒ 2e^-2x(x – x²) = 0
⇒ x (1 – x) = 0
⇒ x = 0 or x = 1
at x = 0, f”(x) = 2 × 1 [0 – 0 + 1] = +ve
⇒ x = 0 is a local minimum point and the minimum value is f(0) = 0 at x = 1,
f”(x) = 2e^-2 [2 – 4 + 1] = -ve
⇒ x = 1 is a local maximum point and the maximum value is f(1) = \(\frac{1}{e^{2}}\)
Local maxima \(\frac{1}{e^{2}}\) and local minima = 0

Question 3.
For the function f(x) = 4x³ + 3x² – 6x + 1 find the intervals of monotonicity, local extrema, intervals of concavity and points of inflection.
Solution:
4x³ + 3x² – 6x + 1
f'(x) = 12x² + 6x – 6
f”(x) = 24x + 6
f'(x) = 0 ⇒ 6(2x² + x – 1) = 0
6(x + 1)(2x – 1) = 0

From (1) and (2)
x = -1 is a maximum point,
and f(-1)= -4 + 3 + 6 + 1 = 6
So local maximum is 6

Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.7 Additional Problems

Question 1.
Discuss the curves y = x⁴ – 4x³ with respect to concavity and points of inflection.
Solution:
f(x) = x⁴ – 4x³ ⇒ f'(x) = 4x³ – 12x²
f”(x) = 12x² – 24x = 12x (x – 2)
Since f”(x) = 0 when x = 0 or 2, we divide the real line into three intervals.
(-∞, 0) , (0, 2), (2, ∞) and complete the following chart.

The point (0, f(0) i.e., (0, 0) is an inflection point since the curve changes from concave upward to concave downward there. Also (2, f(2)) i.e., (2, -16) is an inflection point since the curve changes from concave downward to concave upward there.

Question 2.
Find the intervals of concavity and the points of inflection of the following functions.
f(x) = 2x³ + 5x² – 4x
Solution:
y = f (x) = 2x³ + 5x² – 4x
f'(x) = 6x² + 10x – 4
f”(x) = 12x + 10; f'” (x) = 12
f”(x) = 0 ⇒ 12x + 10 = 0

Consider x in (-∞, -5/6) say x = -1
f”(x)= -12 + 10 = -2 < 0 ⇒ the curve convex upward in the interval (-∞, -5/6) Consider x in (-5/6, ∞) say x = 0 f”(x) = 0 + 10 = 10 > 0
⇒ the curve is concave upward in (-5/6, -∞)
Thus, the curve is concave upward in (-5/6, ∞) and convex upward in (-∞, – 5/6)

Question 3.
f(x) = x⁴ – 6x²
Solution:

So, the points of inflection are at x = ± 1.
f”(x) = 0 ⇒ x² = 1 ⇒ x = ± 1
So, the intervals are (-∞, -1), (-1, 1), (1, ∞)
When x ∈ (-∞, -1), say x = -2
f”(x) = 12(-2)² – 12 = 48 – 12 = 36 > 0
⇒ f(x) is concave upward in (-∞, -1) when x ∈ (-1, 1) say x = 0.
f”(x) = 0 – 12 = -12 < 0
⇒ f(x) convex upward.
⇒ x = -1 is a point of inflection. Again when x ∈ (-1, 1), the curve is convex upward and when x ∈ (1, ∞) say x = 2.
f”(x) = (1, ∞) say x = 2.
f”(x) = 12 (4) – 12 > 0
⇒ the curve is concave upward.
⇒ x = 1 is a point of inflection.
Thus x = ± 1 are the points of inflection.
At x = 1, f(x) = 1 – 6 = -5
At x = -1, f(x) = (-1)⁴ – 6(-1)² = 1 – 6 = -5
The curve concave upward in (-∞, -1) u (1, ∞) and convex upward in (-1, 1) and the points of inflection are (1, -5) and (-1, -5).

Question 4.
f(θ) = sin 2θ in (θ, π)
Solution:
f'(θ) = sin 2θ
f’ (θ) = (cos 2θ) (2) = 2 cos 2θ
f”(θ)= 2[-sin 2θ] (2) = – 4 sin 2θ
f”(θ) = 0 ⇒ – 4 sin 2θ = 0

Question 5.
y = 12x² – 2x³ – x⁴
Solution:

So the intervals are (-∞, -2), (-2, 1)(1, ∞)
When x ∈ (-∞, -2) say x = -3

The curve is concave upward.
When x ∈ (-2, 1) say x = 0.

⇒ The curve is concave upward.

⇒ The curve is convex upward. So, x = 1 is a point of inflection.
At x = – 2, y = 12(4) – 2(-8) – (16) = 48 + 16 – 16 = 48
At x = 1, y = 12(1) – 2(1) – 1 = 12 – 2 – 1 = 9
So, the points of inflection are (1, 9) and (-2, 48)