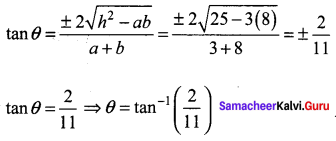You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.4
Question 1.
Find the combined equation of the straight lines whose separate equations are x – 2y – 3 = 0 and x + y + 5 = 0.
Solution:
Separate equations are x – 2y – 3 = 0; x + y + 5 = 0
So the combined equation is (x – 2y – 3) (x + y + 5) = 0
x2 + xy + 5x – 2y2 – 2xy – 10y – 3x – 3y – 15 = 0
(i.e) x2 – 2y2 – xy + 2x – 13y – 15 = 0
Question 2.
Show that 4x2 + 4xy + y2 – 6x – 3y – 4 = 0 represents a pair of parallel lines.
Solution:
Comparing this equation with ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
we get a = 4, h = \(\frac{4}{2}\) = 2 , b = 1, g = – 3, f = – 3/2, c = – 4
The condition for the lines to be parallel is h2 – ab = 0
Now h2 – ab = 22 – (4) (1) = 4 – 4 = 0
h2 – ab = 0 ⇒ The given equation represents a pair of parallel lines.
![]()
Question 3.
Show that 2x2 + 3xy – 2y2 + 3x + y + 1 = 0 represents a pair of perpendicular lines.
Solution:
Comparing the given equation with the general form a = 2,h = 3/2, b = -2,g= 3/2, f = 1/2 and c = 1
Condition for two lines to be perpendicular is a + b = 0. Here a + b = 2 – 2 = 0
⇒ The given equation represents a pair of perpendicular lines.
Question 4.
Show that the equation 2x2 – xy – 3y2 – 6x + 19y – 20 = 0 represents a pair of intersecting lines. Show further that the angle between them is tan-1(5).
Solution:
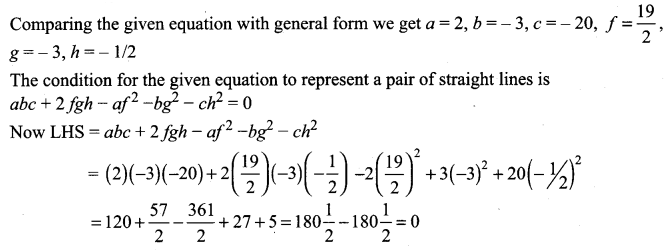
The given equation represents a pair of straight lines.
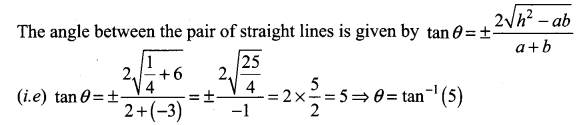
Question 5.
Prove that the equation to the straight lines through the origin, each of which makes an angle α with the straight line y = x is x2 – 2xy sec 2α + y2 = 0
Solution:
Slope of y = x is m = tan θ = 1
⇒ θ = 45°
The new lines slopes will be
m = tan(45 + α) and m = tan (45 – α)
∴ The equations of the lines passing through the origin is given by
y = tan(45 + α)x and y = tan(45 – α)x
(i.e) y = tan(45 + α)x = 0 and y = tan(45 – α)x = 0
The combined equation is [y – tan (45 + α)x] [y – tan (45 – α)x] = 0
y2 + tan(45 + α)tan(45 – α)x2 – xy[tan(45 – α) + tan(45 + α)] = 0

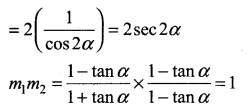
Let the equation of lines passes through the origin
So the equations are y = m1x = 0 and y = m2x = 0
So the combined equations is (y – m1x) (y – m2x) = 0
(i.e)y2 – xy(m1 + m2) + m1m2x = 0
(i.e) y2 – xy(2sec α) + x2(1) = 0
(i.e) y2 – 2xy sec 2α + x2 = 0
Question 6.
Find the equation of the pair of straight lines passing through the point (1, 3) and perpendicular to the lines 2x – 3y + 1 = 0 and 5x + y – 3 = 0
Solution:
Equation of a line perpendicular to 2x – 3y + 1 = 0 is of the form 3x + 2y + k = 0.
It passes through (1, 3) ⇒ 3 + 6 + k = 0 ⇒ k = – 9
So the line is 3x + 2y – 9 = 0
The equation of a line perpendicular to 5x + y – 3 = 0 will be of the form x – 5y + k = 0.
It passes through (1, 3) ⇒ 1 – 15 + k = 0 ⇒ k = 14
So the line is x – 5y + 14 = 0.
The equation of the lines is 3x + 2y – 9 = 0 and x – 5y + 14 = 0
Their combined equation is (3x + 2y – 9)(x – 5y + 14) = 0
(i.e) 3x2 – 15xy + 42x + 2xy – 10y2 + 28y – 9x + 45y – 126 = 0
(i.e) 3x2 – 13xy – 10y2 + 33x + 73y – 126 = 0
Question 7.
Find the separate equation of the following pair of straight lines
(i) 3x2 + 2xy – y2 = 0
(ii) 6 (x – 1)2 + 5(x – 1)(y – 2) – 4(y – 2)2 = 0
(iii) 2x2 – xy – 3y2 – 6x + 19y – 20 = 0
Solution:
(i) Factorising 3x2 + 2xy – y2 we get
3x2 + 3xy – xy – y2 = 3x (x + y) – y (x + y)
= (3 x – y)(x + y)
So 3x2 + 2xy – y2 = 0 ⇒ (3x – y) (x + y) = 0
⇒ 3x – y = 0 and x + y = 0
![]()
(ii) 6 (x – 1)2 + 5 (x – 1)(y – 2) – 4(y – 2)2 = 0
⇒ 6(x2 – 2x +1) + 5(xy – 2x – y + 2) – 4( y2 – 4y + 4) = 0
(i.e) 6x2 – 12x + 6 + 5xy – 10x – 5y + 10 – 4y2 + 16y – 16 = 0
(i.e) 6x2 + 5xy – 4y2 – 22x + 11y = 0
Factorising 6x2 + 5xy – 4y2 we get
6x2 – 3xy + 8xy – 4y2 = 3x (2x – y) + 4y (2x – y)
= (3x + 4y)(2x – y)
So, 6x2 + 5xy – 4y2 – 22x + 11y = (3x + 4y + l )(2x – y + m)
Equating coefficient of x ⇒ 3m + 21 = -22 …….. (1)
Equating coefficient of y ⇒ 4m – l = 11 ……. (2)
Solving (1) and (2) we get l = -11, m = 0
So the separate equations are 3x + 4y – 11 = 0 and 2x – y = 0
(iii) 2x2 – xy – 3y2 – 6x + 19y – 20 = 0
Factorising 2x2 – xy – 3y2 we get
2x2 – xy – 3y2 = 2x2 + 2xy – 3xy – 3y2
= 2x(x + y) – 3y(x + y) = (2x – 3y) (x + y)
∴ 2x2 – xy – 3y2 – 6x + 19y – 20 = (2x – 3y + l)(x + y + m)
Equating coefficient of x 2m + l = -6 ……. (1)
Equating coefficient of y -3m + l = 19 …….. (2)
Constant term -20 = lm
Solving (1) and (2) we get l = 4 and m = – 5 where lm = – 20.
So the separate equations are 2x – 3y + 4 = 0 and x + y – 5 = 0
Question 8.
The slope of one of the straight lines ax2 + 2hxy + by2 = 0 is twice that of the other, show that 8h2 = 9ab.
Solution:
ax2 + 2 hxy + by2 = 0
We are given that one slope is twice that of the other.
So let the slopes be m and 2m.
Now sum of the slopes = m + 2m

Question 9.
The slope of one of the straight lines ax2 + 2hxy + by2 = 0 is three times the other, show that 3h2 = 4ab.
Solution:
Let the slopes be m and 3m.

Question 10.
A ∆OPQ is formed by the pair of straight lines x2 – 4xy + y2 = 0 and the line PQ. The equation of PQ is x + y – 2 = 0. Find the equation of the median of the triangle ∆OPQ drawn from the origin O.
Solution:
Equation of pair of straight lines is x2 – 4xy + y2 = 0 ….. (1)
Equation of the given line is x + y – 2 = 0 ⇒ y = 2 – x ……… (2)
On solving (1) and (2) we get x2 – 4x (2 – x) + (2 – x)2 = 0
(i.e) x2 – 8x + 4x2 + 4 + x2 – 4x = 0
(i.e) 6x2 – 12x + 4 = 0
(÷ by 2) 3x2 – 6x + 2 = 0
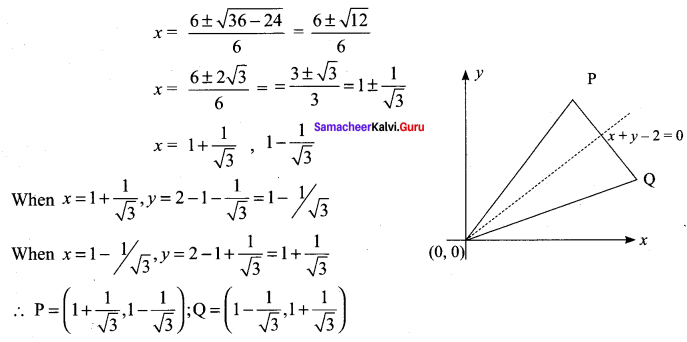
Mid point of PQ is

Question 11.
Find p and q, ¡f the following equation represents a pair of perpendicular lines 6x2 + 5xy – py2 + 7x + qy – 50
Solution:
6x2 + 5xy – py2 + 7x + qy – 50
The given equation represents a pair of perpendicular lines
⇒ coefficient of x2 + coefficient of y2 = 0
(i.e) 6 – p = 0 ⇒ p = 6
Now comparing the given equation with the general form
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
we get a = 6, b = -6 and c = -5, f = q/2, g = 7/2 and h = 5/2
The condition for the general form to represent a pair of straight lines is abc + 2fgh – af2 – bg2 – ch2 = 0

Question 12.
Find the value of k, if the following equation represents a pair of straight lines. Further, find whether these lines are parallel or intersecting, 12x2 + 7xy – 12y2 – x + 7y + k = 0.
Solution:
Comparing the given equation with the general form ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
we get a = 12, b = -12, c = k, f = 7/2, g = – 1/2, h = 7/2
Here a + b = 0 ⇒ the given equation represents a pair of perpendicular lines
To find k: The condition for the given equation to represent a pair of straight lines is abc + 2fgh – af2 – bg2 – ch2 = 0
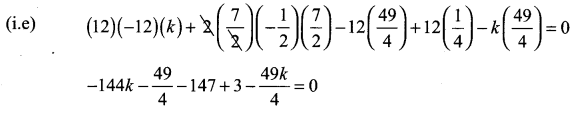
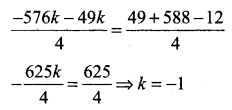
![]()
Question 13.
For what value of k does the equation 12x2 + 2kxy + 2y2, + 11x – 5y + 2 = 0 represent two straight lines.
Solution:
12x2 + 2 kxy + 2y2 + 11x – 5y + 2 = 0
Comparing this equation with the general form we get
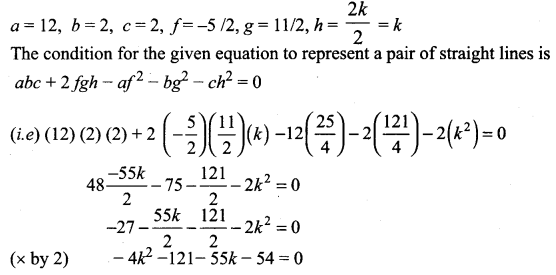
4k2 + 55k + 175 = 0
4k2 + 20k + 35k + 175 = 0
4k(k + 5) + 35(k + 5) = 0
(4k + 35) (k + 5) = 0
k = -5 or -35/4
Question 14.
Show that the equation 9x2 – 24xy + 16y2 – 12x + 16y – 12 = 0 represents a pair of parallel lines. Find the distance between them.
Solution:
Comparing the given equation with ax2 + 2kxy + by2 = 0 we get a = 9, h = -12, b = 16.
Now h2 = (-12)2 = 144, ab = (9) (16) = 144
h2 = ab ⇒ The given equation represents a pair of parallel lines.
To find their separate equations:
9x2 – 24xy + 16y2 = (3x – 4y)2
So, 9x2 – 24xy +16y2 – 12x + 16y – 12 = (3x – 4y + l )(3x – 4y + m)
Here coefficient of x ⇒ 3m + 3l = -12 ⇒ m + l = -4
coefficient of y ⇒ -4m – 4l = 16 ⇒ m + l = -4
Constant term l m = -12
Now l + m = -4 and lm = -12 ⇒ l = -6 and m = 2
So the separate equations are 3x – 4y – 6 = 0 and 3x – 4y + 2 = 0

Question 15.
Show that the equation 4x2 + 4xy + y2 – 6x – 3y – 4 = 0 represents a pair of parallel lines. Find the distance between them.
Solution:
4x2 + 4xy + y2 – 6x – 3y – 4 = 0
a = 4,
b = 1,
h = 4/2 = 2
h2 – ab = 22 – (4) (1) = 4 – 4 = 0
⇒ The given equation represents a pair of parallel lines.
To find the separate equations 4x2 + 4xy + y2 = (2x + y)2
So, 4x2 + 4xy + y2 – 6x – 3y – 4 = (2x + y + l )(2x + y + m)
Coefficient of x ⇒ 2m + 2l = -6 ⇒ l + m = – 3 ……. (1)
Coefficient of y ⇒ l + m = – 3 ……… (2)
Constant term ⇒ l m = – 4 ……… (3)
Now l + m = -3 and lm = -4 ⇒ l = -4, m = 1
So the separate equations are 2x + y + 1 = 0 and 2x + y – 4 = 0

Question 16.
Prove that one of the straight lines given by ax2 + 2hxy + by2 = 0 will bisect the angle between the co-ordinate axes if (a + b)2 = 4h2.
Solution:
Let the slopes be l and m
∵ One line bisects the angle between the coordinate axes ⇒ θ = 45°
So tan θ = 1
The slopes are l and m
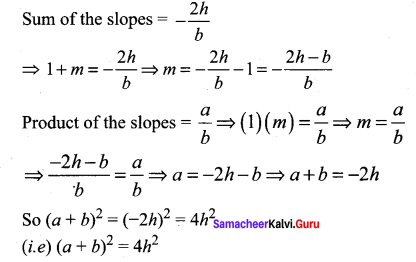
Question 17.
If the pair of straight lines x2 – 2kxy – y2 = 0 bisect the angle between the pair of straight lines x2 – 2lxy – y2 = 0, show that the later pair also bisects the angle between the former.
Solution:
Given that x2 – 2kxy – y2 = 0 …….. (1)
Bisect the angle between the lines x2 – 11xy – y2 = 0 …… (2)

x2 – 2kxy – y2 = 0
Question 18.
Prove that the straight lines joining the origin to the points of intersection of 3x2 + 5xy – 3y2 + 2x + 3y = 0 and 3x – 2y – 1 = 0 are at right angles.
Solution:
Homogenizing the given equations 3x2 + 5xy – 3y2 + 2x + 3y = 0 and 3x – 2y – 1 = 0
(i.e) 3x – 2y = 1.
We get (3x2 + 5xy – 3y2) + (2x + 3y)( 1) = 0
(i.e) (3x2 + 5xy – 3y2) + (2x + 3y)(3x – 2y) = 0
3x2 + 5xy – 3y2 + bx2 – 4xy + 9xy – 6y2 = 0
9x2 + 10xy – 9y2 = 0
Coefficient of x2 + coefficient of y2 = 9 – 9 = 0
⇒ The pair of straight lines are at right angles.
Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.4 Additional Questions Solved
Question 1.
Find the angle between the pair of straight lines given by
(a2 – 3b2 )x2 + 8ab xy + (b2 – 3a2)y2 =0 .
Solution:

![]()
Question 2.
Show that 9x2 + 24xy + 16y2 + 21x + 28y + 6 = 0 represents a pair of parallel straight lines and find the distance between them.
Solution:
9x2 + 24xy + 16y2 + 21x + 28y + 6 = 0
Here a = 9.6,
b = 16,
g = \(\frac{21}{2}\),
f = 14,
c = 6,
h = 12
h2 – ab = (12)2 – 9(16) = 144 – 144 = 0
∴ The lines are parallel.
9x2 + 24xy + 16y2 = (3x + 4y)(3x + 4y)
Let 9x2 + 24xy + 16y2 + 21x + 28y + 6 = (3x + 4y + l)(3x + 4y + m)
Equating the coefficients of x and constant term
3l + 3m = 21
lm = 6
Solving we get, l = 1 or 6
m = 6 or 1
∴ The separate equations are 3x + 4y + 1 = 0 and 3x + 4y + 6 = 0
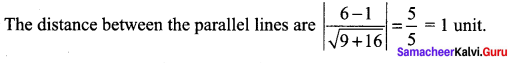
Question 3.
If the equation 12x2 – 10xy + 2y2 + 14x – 5y + c = 0 represents a pair of straight lines, find the value of c. Find the separate equations of the straight lines and also the angle
between them.
Solution:
12x2 – 10xy – 2y2 + 14x – 5y + c = 0
ax2 + 2hxy + by2 +2gx + 2fy – c = 0
Here a = 12,
b = 2,
g = 7,
f = 5/2,
c = c,
h = -5
af2 + bg2 + ch2 – 2fgh – abc = 0 is the condition
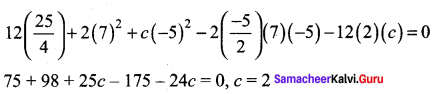
The equation is 12x2 – 10y + 2y2 + 14x – 5y + 2 = 0
12x2 – 10xy + 2y = (3x – y)(4x – 2y)
Let 12x2 – 10y + 2y2 + 14x – 5y + 2(3x – y + l)(4x – 2y + m)
So that 4l + 3m = 14 , -2l – m = -5

Question 4.
For what value of k does 12x2 + 7xy + ky2 + 13x – y + 3 = 0 represents a pair of straight lines? Also write the separate equations.
Solution:
12x2 + 7xy + ky2 + 13x – y + 3 = 0
a = 12,
h = \(\frac{7}{2}\),
f = \(-\frac{1}{2}\) ,
c = 3
af2 + bg2 + ch2 – abc – 2fgh = 0
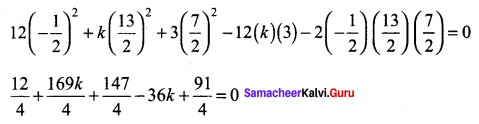
⇒ 12 + 169k + 147 – 144k + 91 = 0
25k = – 250 ⇒ k = -10
The equation is 12x2 + 7xy – 10y2 + 13x – y + 3 = 0
To find separate equations: 12x2 + 7xy – 10y2 = (3x – 2y)(4x + 5y)
Let 12x2 + 7xy – 10y2 + 13x – y + 3 = 0(3x – 2y + l)(4x + 5y + m)
Equating the coefficient of x ⇒ 4l + 3m = 13 …… (1)
Equating the coefficient of y ⇒ 5l – 2m = -1 …… (2)
(1) × 2 ⇒ 8l + 6m = 26
(2) × 3 ⇒ 15l – 6m = -3
23l = 23 ⇒ l = 1
4 + 3 m = 13
3 m = 9 ⇒ m = 3
The separate equations are 3x – 2y + 1 = 0 and 4x + 5y + 3 = 0
![]()
Question 5.
Show that 3x2 + 10xy + 8y2 + 14x + 22y + 15 = 0 represents a pair of straight lines and the angle between them is tan-1\(\left(\frac{2}{11}\right)\)
Solution:
3x2 + 10xy + 8y2 + 14x + 22y + 15 = 0
a = 3,
A = 5,
b = 8,
g = 7,
f = 11,
c = 15
The condition is af2 + bg2 + ch2 – abc – 2fgh = 0
3(11)2 + 8(7)2 + 15 (5)2 – (3)(8)(15) – 2(11)(7)(5) = 363 + 392 + 375 – 360 – 770 = 0
The angle between the pair of straight line is given by