You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.7
Question 1.
Find intervals of concavity and points of inflexion for the following functions:
(i) f(x) = x (x – 4)3
(ii) f(x) = sin x + cos x, 0 < x < 2π
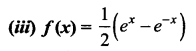
Solution:
(i) f(x) = x(x – 4)3
f(x) = x[x3 – 12x2 + 48x – 64]
(i.e.,) f(x) = x4 – 12x3 + 48x2 – 64x
f'(x) = 4x3 – 36x2 + 96x – 64
f”(x) = 12x2 – 72x + 96
f”(x) = 0 ⇒ 12(x2 – 6x + 8) = 0
⇒ 12 (x – 2) (x – 4) = 0 ⇒ x = 2 or 4
Marking the points in the number line
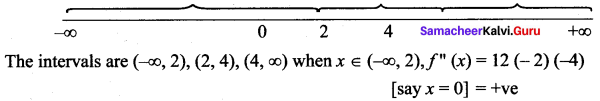
in the interval (-∞, 2) the curve concave upwards
when x ∈ (2, 4), f”(x) = (3 – 2) (3 – 4)
[say x = 3] = -ve
⇒ The curve concave upwards in (2,4)
when x ∈ (4, ∞), f”(x) = (5 – 2) (5 – 4)
[say x = 5] = (+) (+) = +ve ⇒ The curve concave downwards is (4, ∞) in (-∞, 2) concave upwards and in (2, 4) the concave downwards
⇒ x = 2 is a point of inflection at x = 2, f(2) = -16
So (2, -16) is a point of inflection
Again in (2, 4) the curve concave downwards and in (4, ∞) the curve concave upwards ⇒ x = 4 is a point of inflection f(4) = 0
∴ (4, 0) is a point of inflection
So points of inflection are (2, -16) and (4, 0)
![]()
(ii) f(x) = sin x + cos x
f'(x) = cos x – sin x
f”(x) = – sin x – cos x
f”(x) = 0 ⇒ – sin x = cos x


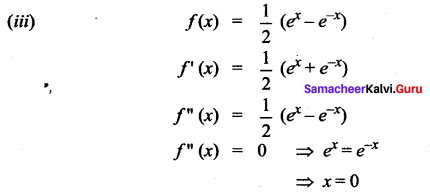
So the intervals are (-∞, 0), (0, ∞) when x ∈ (-∞, 0) f”(x) is negative
⇒ the curve concave downwards and when x ∈ (0, ∞) f”(x) is positive
⇒ the curve concave upwards
⇒x = 0 is a point of inflection f(0) = \(\frac{1}{2}\)(1 – 1) = 0
So (0, 0) is the point of inflection and the curve concave upwards in (0, ∞) and curve concave downwards in (-∞, 0) and (0, 0) is the point of inflection.
Question 2.
Find the local extrema for the following functions using second derivative test:
(i) f(x) = – 3x5 + 5x3
(ii) f(x) = x log x
(iii) f(x) = x2 e-2x
Solution:
(i) f(x) = – 3x5 + 5x3
f'(x) = 0, f”(x) = -ve at x = a
⇒ x = a is a maximum point
f'(x) = 0, f”(x) = +ve at x = 6
⇒ x = b is a minimum point
f(x) = – 3x5 + 5x3
f’ (x) = -15x4 + 15x2
f”(x) = -60x3 + 30x
f'(x) = 0 ⇒ – 15x2 (x2 – 1) = 0
⇒ x = 0, +1, -1
at x = 0, f”(x) = 0
at x = 1, f”(x) = -60 + 30 = – ve
at x = -1, f”(x) = 60 – 30 = + ve
So at x = 1, f'(x) = 0 and f”(x) = -ve
⇒ x = 1 is a local maximum point.
and f(1) = 2
So the local maximum is (1, 2)
at x = -1, f'(x) = 0 and f”(x) = +ve
⇒ x = -1 is a local maximum point and f(-1) = -2.
So the local minimum point is (-1, -2)
∴ local minimum is -2 and local maximum is 2.
(ii) f(x) = x log x

(iii) f(x) = x2 e-2x
f'(x) = x2[-2e-2x] + e-2x (2x)
= 2e-2x (x – x2)
f”(x) = 2e-2x(1 – 2x) + (x – 2) (-4e-2x)
= 2e-2x [(1 – 2x) + (x – x2) (- 2)]
= 2e-2x [2x2 – 4x + 1]
f'(x) = 0 ⇒ 2e-2x(x – x2) = 0
⇒ x (1 – x) = 0
⇒ x = 0 or x = 1
at x = 0, f”(x) = 2 × 1 [0 – 0 + 1] = +ve
⇒ x = 0 is a local minimum point and the minimum value is f(0) = 0 at x = 1,
f”(x) = 2e-2 [2 – 4 + 1] = -ve
⇒ x = 1 is a local maximum point and the maximum value is f(1) = \(\frac{1}{e^{2}}\)
Local maxima \(\frac{1}{e^{2}}\) and local minima = 0
![]()
Question 3.
For the function f(x) = 4x3 + 3x2 – 6x + 1 find the intervals of monotonicity, local extrema, intervals of concavity and points of inflection.
Solution:
4x3 + 3x2 – 6x + 1
f'(x) = 12x2 + 6x – 6
f”(x) = 24x + 6
f'(x) = 0 ⇒ 6(2x2 + x – 1) = 0
6(x + 1)(2x – 1) = 0
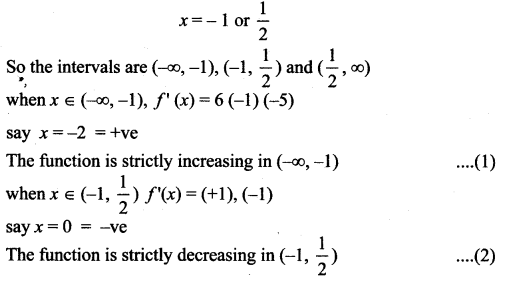
From (1) and (2)
x = -1 is a maximum point,
and f(-1)= -4 + 3 + 6 + 1 = 6
So local maximum is 6
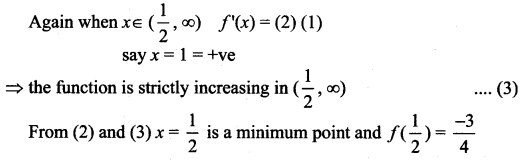


Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.7 Additional Problems
Question 1.
Discuss the curves y = x4 – 4x3 with respect to concavity and points of inflection.
Solution:
f(x) = x4 – 4x3 ⇒ f'(x) = 4x3 – 12x2
f”(x) = 12x2 – 24x = 12x (x – 2)
Since f”(x) = 0 when x = 0 or 2, we divide the real line into three intervals.
(-∞, 0) , (0, 2), (2, ∞) and complete the following chart.

The point (0, f(0) i.e., (0, 0) is an inflection point since the curve changes from concave upward to concave downward there. Also (2, f(2)) i.e., (2, -16) is an inflection point since the curve changes from concave downward to concave upward there.
Question 2.
Find the intervals of concavity and the points of inflection of the following functions.
f(x) = 2x3 + 5x2 – 4x
Solution:
y = f (x) = 2x3 + 5x2 – 4x
f'(x) = 6x2 + 10x – 4
f”(x) = 12x + 10; f'” (x) = 12
f”(x) = 0 ⇒ 12x + 10 = 0

Consider x in (-∞, -5/6) say x = -1
f”(x)= -12 + 10 = -2 < 0 ⇒ the curve convex upward in the interval (-∞, -5/6) Consider x in (-5/6, ∞) say x = 0 f”(x) = 0 + 10 = 10 > 0
⇒ the curve is concave upward in (-5/6, -∞)
Thus, the curve is concave upward in (-5/6, ∞) and convex upward in (-∞, – 5/6)
![]()
![]()
Question 3.
f(x) = x4 – 6x2
Solution:

So, the points of inflection are at x = ± 1.
f”(x) = 0 ⇒ x2 = 1 ⇒ x = ± 1
So, the intervals are (-∞, -1), (-1, 1), (1, ∞)
When x ∈ (-∞, -1), say x = -2
f”(x) = 12(-2)2 – 12 = 48 – 12 = 36 > 0
⇒ f(x) is concave upward in (-∞, -1) when x ∈ (-1, 1) say x = 0.
f”(x) = 0 – 12 = -12 < 0
⇒ f(x) convex upward.
⇒ x = -1 is a point of inflection. Again when x ∈ (-1, 1), the curve is convex upward and when x ∈ (1, ∞) say x = 2.
f”(x) = (1, ∞) say x = 2.
f”(x) = 12 (4) – 12 > 0
⇒ the curve is concave upward.
⇒ x = 1 is a point of inflection.
Thus x = ± 1 are the points of inflection.
At x = 1, f(x) = 1 – 6 = -5
At x = -1, f(x) = (-1)4 – 6(-1)2 = 1 – 6 = -5
The curve concave upward in (-∞, -1) u (1, ∞) and convex upward in (-1, 1) and the points of inflection are (1, -5) and (-1, -5).
Question 4.
f(θ) = sin 2θ in (θ, π)
Solution:
f'(θ) = sin 2θ
f’ (θ) = (cos 2θ) (2) = 2 cos 2θ
f”(θ)= 2[-sin 2θ] (2) = – 4 sin 2θ
f”(θ) = 0 ⇒ – 4 sin 2θ = 0

![]()
Question 5.
y = 12x2 – 2x3 – x4
Solution:
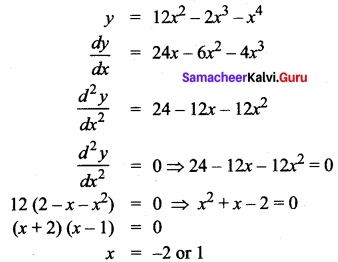
So the intervals are (-∞, -2), (-2, 1)(1, ∞)
When x ∈ (-∞, -2) say x = -3
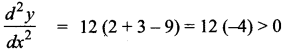
The curve is concave upward.
When x ∈ (-2, 1) say x = 0.
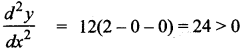
⇒ The curve is concave upward.
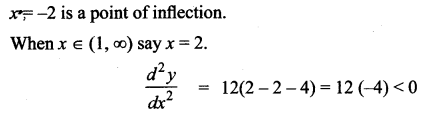
⇒ The curve is convex upward. So, x = 1 is a point of inflection.
At x = – 2, y = 12(4) – 2(-8) – (16) = 48 + 16 – 16 = 48
At x = 1, y = 12(1) – 2(1) – 1 = 12 – 2 – 1 = 9
So, the points of inflection are (1, 9) and (-2, 48)