Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1

Question 1.
Find all the values of x such that
(i) -10π ≤ x ≤ 10π and sin x = 0
(ii) -8π ≤ x ≤ 8π and sin x = -1
Solution:
(i) sin x = 0
⇒ x = nπ
where n = 0, ±1, ±2, ±3, ……., ±10
(ii) sin x = -1
⇒ x = (4n – 1) \(\frac{\pi}{2}\), n = 0, ±1, ±2, ±3, 4

Question 2.
Find the period and amplitude of
(i) y = sin 7x
(ii) y = -sin(\(\frac{1}{3}\)x)
(iii) y = 4 sin(-2x)
Solution:
(i) y = sin 7x
Period of the function sin x is 2π
Period of the function sin 7x is \(\frac{2 \pi}{7}\)
The amplitude of sin 7x is 1.

(ii) y = -sin\(\frac{1}{3}\)x
Period of sin x is 2π
So, period of sin\(\frac{1}{3}\)x is 6π and the amplitude is 1.

(iii) y = 4 sin(-2x) = -4 sin 2x
Period of sin x is 2π
π Period of sin 2x is π and the amplitude is 4.

Question 3.
Sketch the graph of y = sin(\(\frac{1}{3}\)x) for 0 ≤ x < 6π.
Solution:
The period of sin(\(\frac{1}{3}\)x) is 6π and the amplitude is 1.

The graph is

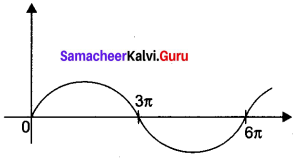
Question 4.
Find the value of
(i) \(\sin ^{-1}\left(\sin \left(\frac{2 \pi}{3}\right)\right)\)
(ii) \(\sin ^{-1}\left(\sin \left(\frac{5 \pi}{4}\right)\right)\)
Solution:

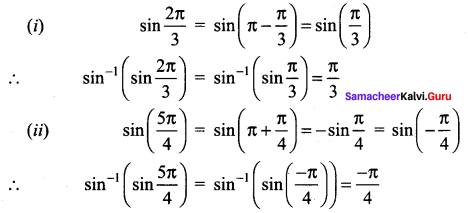
Question 5.
For that value of x does sin x = sin^-1 x?
Solution:
sin x = sin^-1 x is possible only when x = 0 (∵ x ∈ R)

Question 6.
Find the domain of the following
(i) \(f(x)=\sin ^{-1}\left(\frac{x^{2}+1}{2 x}\right)\)
(ii) \(g(x)=2 \sin ^{-1}(2 x-1)-\frac{\pi}{4}\)
Solution:
(i) \(f(x)=\sin ^{-1}\left(\frac{x^{2}+1}{2 x}\right)\)
The range of sin-1 x is -1 to 1
\(-1 \leq \frac{x^{2}+1}{2 x} \leq 1\)
⇒ \(\frac{x^{2}+1}{2 x} \geq-1\) or \(\frac{x^{2}+1}{2 x} \leq 1\)
⇒ x² + 1 ≥ -2x or x² + 1 ≤ 2x
⇒ x² + 1 + 2x ≥ 0 or x² + 1 – 2x ≤ 0
⇒ (x+ 1)² ≥ 0 or (x – 1)² ≤ 0 which is not possible
⇒ -1 ≤ x ≤ 1 or
(ii) \(g(x)=2 \sin ^{-1}(2 x-1)-\frac{\pi}{4}\)
-1 ≤ (2x – 1) ≤ 1
0 ≤ 2x ≤ 2
0 ≤ x ≤ 1
x ∈ [0, 1]

Question 7.
Find the value of \(\sin ^{-1}\left(\sin \frac{5 \pi}{9} \cos \frac{\pi}{9}+\cos \frac{5 \pi}{9} \sin \frac{\pi}{9}\right)\)
Solution:

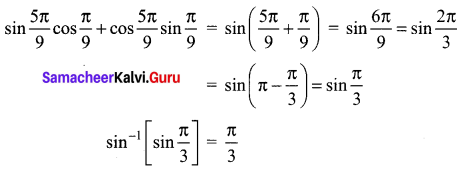
Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.1 Additional Problems

Question 1.

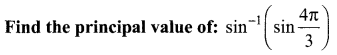
Solution:

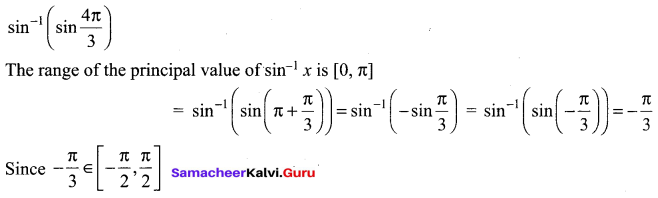
Question 2.

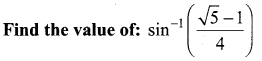
Solution: