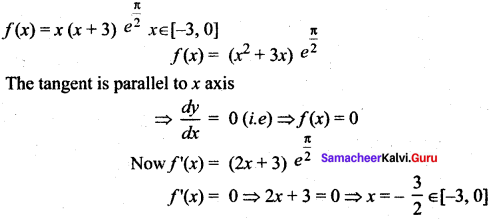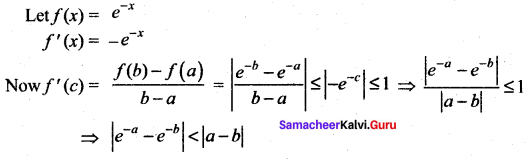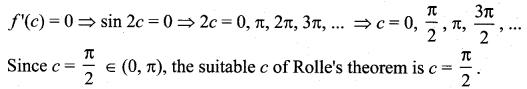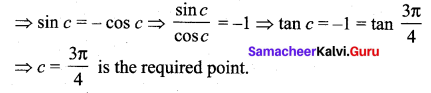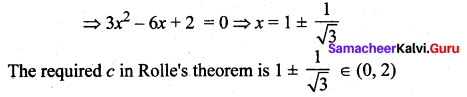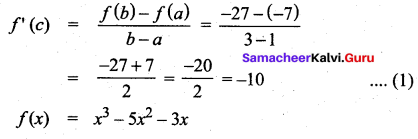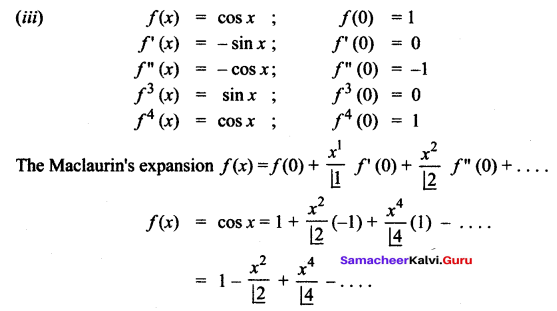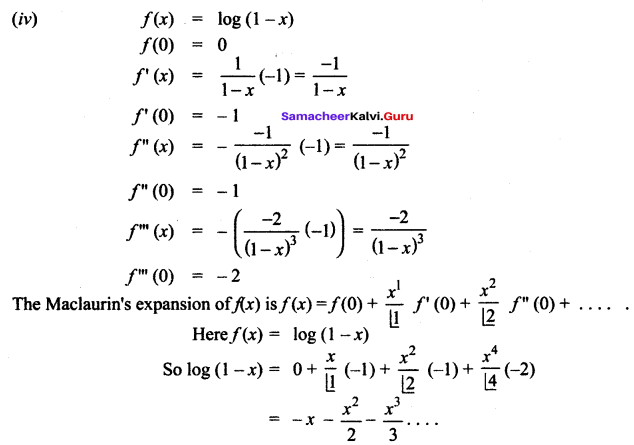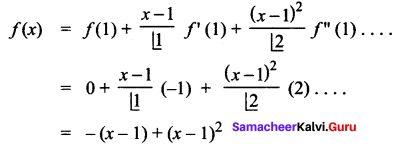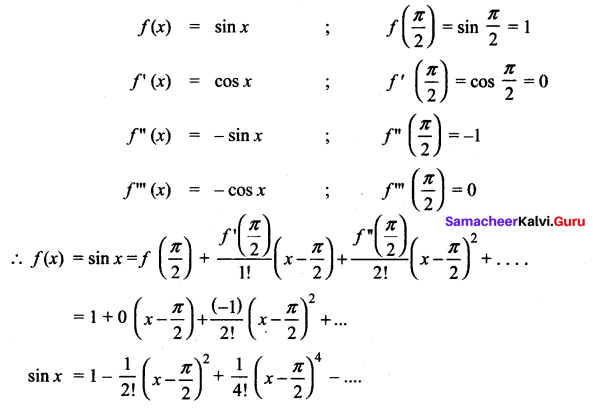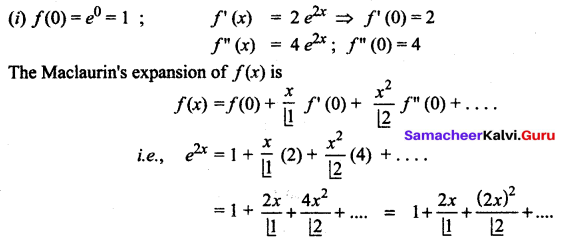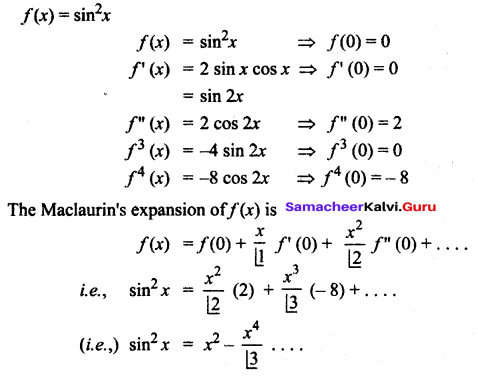Prasanna

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 1 Numbers Ex 1.1

Question 1.
Fill in the blanks.
(i) The number of prime numbers between 11 and 60 is _______
(ii) The numbers 29 and _______ are twin primes.
(iii) 3753 is divisible by 9 and hence divisible by _______
(iv) The number of distinct prime factors of the smallest 4 digit number is______
(v) The sum of distinct prime factors of 30 is ________
Solution:
(i) 12
(ii) 31
(iii) 3
(iv) 2
(v) 10

Question 2.
Say True or False
(i) The sum of any number of odd numbers is always even.
(ii) Every natural number is either prime or composite.
(iii) If a number is divisible by 6, then it must be divisible by 3.
(iv) 16254 is divisible by each of 2, 3, 6 and 9.
(v) The number of distinct prime factors of 105 is 3.
Solution:
(i) False
(ii) False
(iii) True
(iv) True
(v) True

Question 3.
Write the smallest and the biggest two digit prime number.
Solution:
Smallest is 11
Biggest is 97

Question 4.
Write the smallest and the biggest three-digit composite number.
Solution:
Smallest three-digit composite number – 100
Biggest three-digit composite number – 999

Question 5.
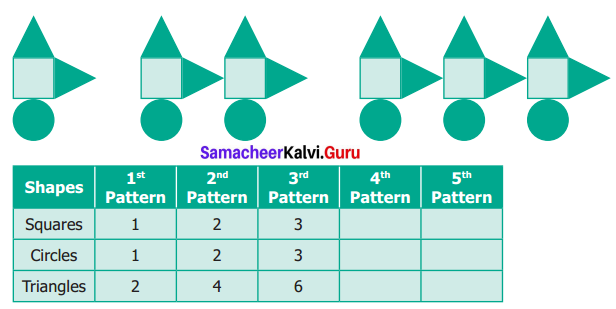
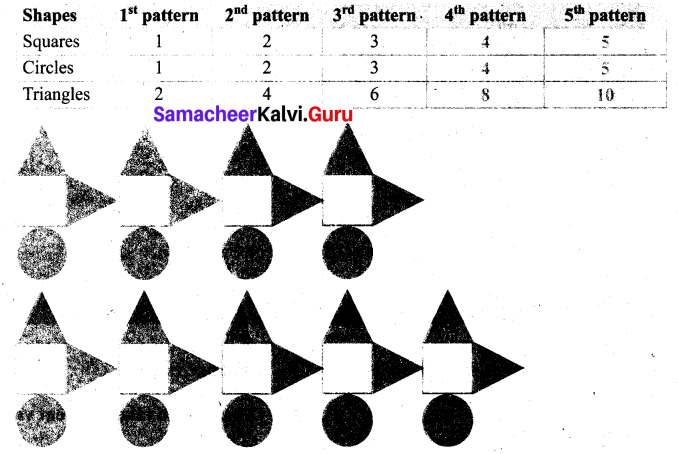
The sum of any three odd natural numbers is odd. Justify this statement with an example.
Solution:
True, as we know, that,“the sum of any three odd numbers is always an odd number”.
Example: 3 + 7 + 9 = 19 is odd.

Question 6.
The digits of the prime number 13 can be reversed to get another prime number 31. Find if any such pairs exist up to 100.
Solution:
(17, 71), (37, 73) and (79, 97)

Question 7.
Your friend says that every odd number is prime. Give an example to prove him/her wrong.
Solution:
15 is an odd number not prime.

Question 8.
Each of the composite numbers has at least three factors. Justify this statement with an example.
Solution:
True. The composite number 4 has 3 factors namely 1, 2 and 4.

Question 9.
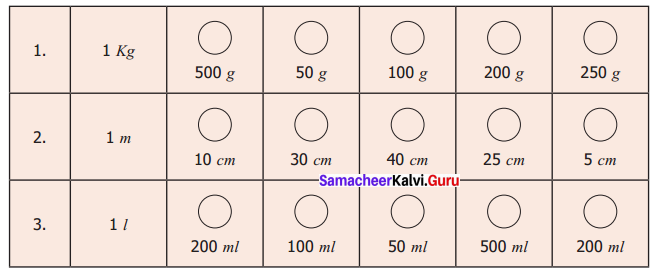
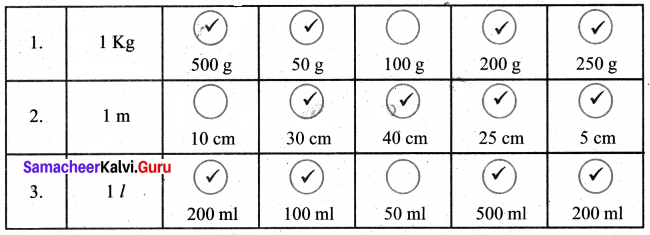
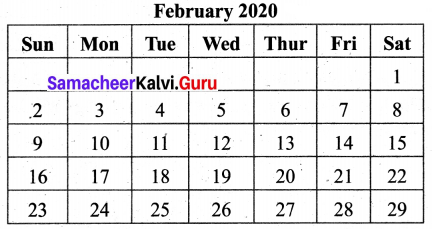
Find the dates of any month of a calendar which are divisible by both 2 and 3.
Solution:
Every month the dates 6, 12, 18, 24 and 30 (excluding February) are divisible by both 2 and 3.

Question 10.
I am a two-digit prime number and the sum of my digits is 10.1 am also one of the factors of 57. Who am I?
Solution:
19

Question 11.
Find the prime factorisation of each number by factor tree method and division method.
(a) 60
(b) 128
(c) 144
(d) 198
(e) 420
(f) 999
Solution:
(a) 60

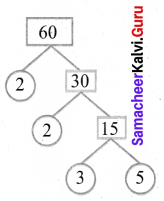
∴ 60 = 2 × 2 × 3 × 5
Also

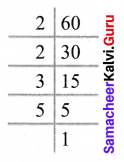
∴ 60 = 2 × 2 × 3 × 5
(b) 128

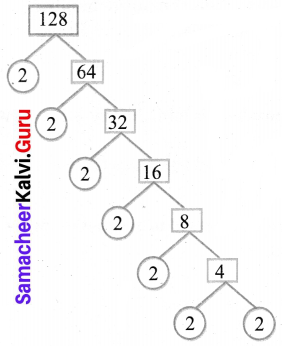
∴ 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Also

∴ 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
(c) 144

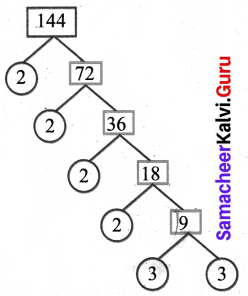
∴ 144 = 2 × 2 × 2 × 2 × 3 × 3
Also

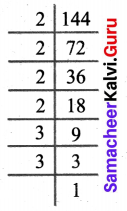
∴ 144 = 2 × 2 × 2 × 2 × 3 × 3
(d) 198

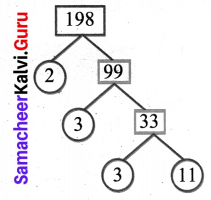
∴ 198 = 2 × 3 × 3 × 11
Also

∴ 198 = 2 × 3 × 3 × 11
(e) 420

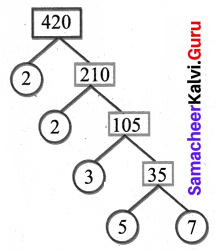
∴ 420 = 2 × 2 × 3 × 5 × 7
Also

∴ 420 = 2 × 2 × 3 × 5 × 7
(f) 999

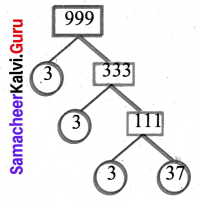
∴ 999 = 3 × 3 × 3 × 37
Also

∴ 999 = 3 × 3 × 3 × 37

Question 12.
If there are 143 math books to be arranged in equal numbers in all the stacks, then find the number of books in each stack and also the number of stacks.
Solution:
Total number of books = 143
Factorizing 143 = 11 × 13

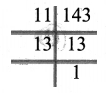
A number of stacks and number of books in each stack may be (11, 13) or (13, 11).

Objective Type Questions

Question 13.
The difference between two successive odd number is
(a) 1
(b) 2
(c) 3
(d) 0
Solution:
(b) 2

Question 14.
The only even prime number is
(a) 4
(b) 6
(c) 2
(d)
Solution:
(c) 2

Question 15.
Which of the following numbers is not prime?
(a) 53
(b) 92
(c) 97
(d) 71
Solution:
(b) 92

Question 16.
The sum of the factors of 27 is
(a) 28
(b) 37
(c) 40
(d) 31
Solution:
(c) 40

Question 17.
The factors of a number are 1, 2, 4, 5, 8, 10, 16, 20, 40 and 80. What is the number?
(a) 80
(b) 100
(c) 128
(d) 160
Solution:
(a) 80

Question 18.
The prime factorisation of 60 is 2 × 2 × 3 × 5. Any other number which has the same prime factorisation as 60 is
(a) 30
(b) 120
(c) 90
(d) impossible
Solution:
(d) impossible

Question 19.
If the number 6354*97 is divisible by 9, then the value * is
(a) 2
(b) 4
(c) 6
(d) 7

Solution:
(a) 2

Question 20.
The number 87846 is divisible by
(a) 2 only
(b) 3 only
(c) 11 only
(d) all of these
Solution:
(d) all of these

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 4 Geometry Ex 4.2

Miscellaneous Practice problems

Question 1.
Draw and answer the following.
i) A triangle which has no line of symmetry
ii) A triangle which has only one line of symmetry
iii) A triangle which has three lines of symmetry
Solution:
(i) A Scalene triangle has no line of symmetry

(ii) An isosceles triangle has only one

(iii) An equilateral triangle has three lines of symmetry.

Question 2.
Find the alphabets in the box which have
i) No Line of symmetry
ii) Rotational symmetry
iii) Reflection symmetry
iv) Reflection and rotational symmetry

Solution:
i) The alphabets which have no line of symmetry are P, N, S, Z
ii) The alphabets which have Rotational symmetry are I, O, N, X, S, H, Z
iii) The alphabets which have reflection symmetry are A, M, E, D, I, K, O, X, H, U, V, W.
iv) The alphabets which has reflection and rotational symmetry are I, O, X, H.

Question 3.
For the following pictures, find the number of lines of symmetry and also find the order of rotation.

Solution:
Number of lines of symmetry is 0; order of rotation is 2

ii)
Number of lines of symmetry is 1.
Order of rotation is 0, because it is an isosceles triangle

iii) Number of lines of symmetry are 2
Order of rotation is 2

iv) Number of lines of symmetry 8 and order of rotation 8

v)

Number of line of symmetry is 1 and order of rotation 0

Question 4.
The three digit number 101 has rotational and reflection symmetry. Give five more examples of three digit number which have both rotational and reflection symmetry.
Solution:
181, 111, 808, 818, 888

Question 5.
Translate the given pattern and com ilete the design in rectangular strip?

Solution:

Challenge Problems

Question 6.
Shade one square so that it possesses
i) One line of symmetry
ii) Rotational symmetry of order 2

Solution:

Question 7.
Join six identical squares so that atleast one side of a square fits exactly with any other side of the square and have reflection symmetry (any three ways).
Solution:
The required combination of squares are given below.

Question 8.
Draw the following:
Solution:
i) A figure which has reflection symmetry but no rotational symmetry.

ii) A figure which has rotational symmetry but no reflection symmetry.

iii) A figure which has both reflection and rotational symmetry.

Question 9.
Find the line of symmetry and the order of rotational symmetry of the given regular polygons and complete the following table and answer the questions given below.

i) A regular polygon of 10 sides will have ____ lines of symmetry.
ii) If a regular polygon has 10 lines of symmetry, then its order of rotational symmetry is _____
iii) A regular polygon of ‘n’ sides ______ has lines of symmetry and the order of rational symmery is _____.

Question 10.
Color the boxes in such a way that it possess translation symmetry.

Solution:
The following figures coloured to posses translation symmetry.

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.5

Miscellaneous Practice Problems

Question 1.
The maximum speed of some of the animals are given below:
the Elephant = 20 km/h, the Lion = 80 km/hr; the Cheetah = 100 km/h.
Find the following ratios of their speeds in simplified form and find which ratio is the least?
(i) the Elephant and the Lion
(ii) the Lion and the Cheetah
(iii) the Elephant and the Cheetah.
Solution:

∴ The ratio of Elephant to Cheetah is the least.

Question 2.
A particular high school has 1500 students, 50 teachers and 5 administrators. If the school grow s to 1800 students and the ratios are mentioned, then find the number of teachers and administrators.
Solution:
The ratio of Students : teachers : administrators = 1500 : 50 : 5.
The new ratio of Students : teachers : administrators = 1800 : new teachers : new administrators.
Given the ratios are maintained. i.e., they are proportional.

∴ For 1800 students 60 teachers and 6 administrators are needed.

Question 3.
I have a box which has 3 green, 9 blue, 4 yellow, 8 orange coloured cubes in it.
(a) What is the ratio of orange to yellow cubes?
(b) What is the ratio of green to blue cubes?
(c) How many different ratios can be formed, when you compare each colour to any one of the other colours?

Solution:
Number of green cubes = 3
Number of blue cubes = 9
Number of yellow cubes = 4
Number of orange cubes = 8
(a) Ratio of orange to yellow cubes \(\frac{\text { Number of orange cubes }}{\text { Number of yellow cubes }}=\frac{8}{4}=\frac{2}{1}=2: 1\)
Ratio of orange to yellow cubes = 2 : 1
(b) \(\frac{\text { Number of green cubes }}{\text { Number of blue cubes }}=\frac{3}{9}=\frac{1}{3}\)
Ratio of green to blue cubes = 1 : 3
(c) The ratios can be Orange : Yellow, Orange: blue, Orange : green, Yellow : Orange, yellow : blue, yellow : green, blue : green, blue : orange, blue : yellow, green : orange, green : yellow, green : blue. Thus 12 ratios can be formed.

Question 4.
A gets double of what B gets and B gets double of what C gets. Find A : B and B : C and verify whether the result is in proportion or not.
Solution:
A : B = 2 : 1
B : C = 2 : 1
They are in proportion

Question 5.
The ingredients required for the preparation of Ragi Kali, a healthy dish of Tamilnadu is given below.

(a) If one cup of ragi flour is used then, what would be the amount of raw rice required?
(b) If 16 cups of water are used, then how much of ragi flour should be used?
(c) Which of these ingredients cannot be expressed as a ratio? Why?
Solution:
(a) Given Ragi flour: raw rice = 4 : 1
If one cup of ragi flour used then the ratio of ragi flour : raw rice = \(\frac{4}{4}: \frac{1}{4}=1: \frac{1}{4}\)
Raw rice required = \(\frac{1}{4}\) cup
(b) Ratio of water : ragi flour = 8 : 4
If 16 cups of water used then ratio of water : ragi flour = 8 × 2 : 4 × 2 = 16 : 8
8 cups of ragi flour are used.
(c) We know that the quantities of the same units can be compared. Here Ragi flour, Raw rice and water are in one unit, Sesame oil and salt are in different units, these different units cannot be compared and cannot be expressed as a ratio.

Challenging Problem (Textbook Page No. 74)

Question 6.
Antony brushes his teeth in the morning and night on all days in a week. Shabeen brushes her teeth only in the morning. What is the ratio of the number of times they brush their teeth in a week?
Solution:
Number of times = 14 : 7 = 2 : 1

Question 7.
Thirumagal’s mother wears a bracelet made of 35 red beads and 30 blue beads. Thirumagal wants to make smaller bracelets using the same two coloured beads in the same ratio. In how many different ways can she make the bracelets?

Solution:
Ratio of red beads : blue beads = 35 : 30 = 7 : 6
Also given that the bracelet made is smaller in size
∴ The possible ways are red beads : blue beads = 7 : 6 (or) 14 : 12 (or) 21 : 18 (or) 28 : 24
In 4 different way can she made.

Question 8.
Team A wins 26 matches out of 52 matches. Team B wins three-fourth of 52 matches played. Which team has a better winning record?
Solution:
Team A = \(\frac{26}{52}\) = \(\frac{1}{2}\)
Team B = \(\frac{3}{4}\) × 52 = 39
Team B has a better winning record.

Question 9.
In a school excursion, 6 teachers and 12 students from 6th standard and 9 teachers and 27 students from 7th standard, 4 teachers and 16 students from 8th standard took part. Which class has the least teacher to student ratio?
Solution:
Teacher to Student Ratio of 6th Std = 6 : 12 = 1 : 2
Teacher to Student Ratio of 7th Std = 9 : 27 = 1 : 3
Teacher to Student Ratio of 8th Std = 4 : 16 = 1 : 4
In standard 8th the ratio of teacher to student is 1 : 4 and which is the least.

Question 10.
Fill the blanks using any set of suitable numbers 6 : …… :: ……. : 15
Solution:
6 : ……. = …….. : 15
Product of the extremes = 6 × 15 = 90
Set of suitable numbers
1 and 90, 2 and 45, 3 and 30, 5 and 18, 6 and 15

Question 11.
From your school diary, write the ratio of the number of holidays to the number of working days in the current academic year.
Solution:
Number of working days in an academic year = 220
Number of holidays = 365 – 220 = 145
\(\frac{\text { Number of holidays }}{\text { Number of working days }}=\frac{145}{220}=\frac{29}{44}\)
Number of holidays : No of working days = 29 : 44

Question 12.
If the ratio of Green, Yellow and Black balls in a bag is 4 : 3 : 5, then
(a) Which is the most likely ball that you can choose from the bag?
(b) How many balls in total are there in the bag if you have 40 black balls in it?
(c) Find the number of green and yellow balls in the bag.
Solution:
Green : Yellow : Black = 4 : 3 : 5
(i) Blackballs;
(ii) 96 balls (32 + 24 + 40);
(iii) green balls = 32
yellow balls = 24

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 2 Introduction to Algebra Ex 2.1

Question 1.
Fill in the blanks:
(i) The letters a, b, c, .., x, y, z are used to represent _____
(ii) A quantity that takes _____ values is called a variable.
(iii) If there are 5 students on a bench, then the number of students in ‘n’ benches is ‘5 × n’. Here _____ is a variable.
Solution:
(i) Variables
(ii) Different
(iii) n

Question 2.
Say True or False:
(i) The length of part B in the pencil shown is ‘a – 6’.

(ii) If the cost of an apple is ‘x’ and cost of banana is ₹ 5, then the total cost of fruits is ₹ ‘x + 5′
(iii) If there are 11 players in a team, then there will be ’11 + q’ players in ‘q’ teams.
Solution:
(i) False
Length of B is 6 – a
(ii) True
(iii) False
There will be 11q players.

Question 3.
Draw the next two patterns and complete the table.

Solution:

Question 4.
Use a variable to write the rule, which gives the number of ice candy sticks required to make the following patterns.
(a) a pattern of letter C as

(b) the pattern of letter M as

Solution:
(a) A number of sticks used for 1  is 3.

If the number of  formed is ‘n’ then
the number of ice candy sticks required = 3 × n = 3n.
(b) A number of sticks used for one’ is 4.

The number of ice candy sticks required = 4n.

Question 5.
The teacher forms a group of five students in a class. How many students will be there in ‘p’ groups?
Solution:

5p students will be there in groups.

Question 6.
Arivazhagan is 30 years younger to his father. Write Arivazhagan’s age in terms of his father’s age.
Solution:
Let Arivazhagan’s father’s age be x years
According to the problem,
Arivazhagan’s age = (x – 30) years

Question 7.
If ‘u’ is an even number, how would you represent?
(i) the next even number?
(ii) the previous even number?
Solution:
(i) Difference between two even numbers = 2
Given that ‘u’ is an even number.
Next, even number is u + 2.
(ii) Previous even number is u – 2.

Objective Type Questions

Question 8.
Variable means that it
(a) can take only a few values
(b) has a fixed value
(c) can take different values
(d) can take only 8 values
Solution:
(c) can take different values

Question 9.
‘6y’ means.
(a) 6 + y
(b) 6 – y
(c) 6 × y
(d) \(\frac{6}{y}\)
Solution:
(c) 6 × y

Question 10.
Radha is ‘x’ years of age now 4 years ago, her age was
(a) x – 4
(b) 4 – x
(c) 4 + x
(d) 4x
Solution:
(a) x – 4

Question 11.
The number of days in ‘w’ weeks is
(a) 30 + w
(b) 30w
(c) 7 + w
(d) 7w
Solution:
(d) 7w

Question 12.
The value of ‘x’ in the circle is

(a) 6
(b) 8
(c) 21
(d) 22
Solution:
(d) 22
2 + 2 = 4, 4 + 3 = 7, 7 + 4 = 11, 11 + 5 = 16, 16 + 6 = 22

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.3

Miscellaneous Practice Problems

Question 1.
Two pipes whose lengths are 7 m 25 cm and 8 m 13 cm joined by welding and then a small piece 60 cm is cut from the whole. What is the remaining length of the pipe?
Solution:

Question 2.
The saplings are planted at a distance of 2 m 50 cm in the road of length 5 km by saravanan. If he has 2560 saplings, how many saplings will be planted by him? how many saplings are left?
Solution:
Distance between two saplings = 2 m 50 cm = 250 cm
Total length of the road = 5000 m = 500000 cm

Question 3.
Put ✓ a mark in the circles which adds up to the given measure.

Solution:

Question 4.
Make a calendar for the month of February 2020 (Hint: January 1st 2020 is Wednesday)
Solution:
Given Jan 1st 2020 is Wednesday.
1st + 7 = 8th Wednesday
8th + 7 = 15th Wednesday
15th + 7 = 22nd Wednesday
22nd + 7 = 29th Wednesday
Jan = 30th Thursday
Jan 31st Friday
Feb 1st Saturday
February has 29 days as 2020 is a leap year.

Question 5.
Observe and Collect the data for a minute:

Solution:

Challenge Problems

Question 6.
A squirrel wants to eat the grains quickly. Help the squirrel to find the shortest way to reach the grains. (Use your scale to measure the length of the line segments)

Solution:
The squirrel is in A and the grains are at E
The ways are (i) A → B → C → D → E
(ii) A → G → F → K → E
(iii) A → H → I → J → E
Distance
(i) AB + BC + CD + DE = 2 cm + 2.5 cm + 2.5 cm + 2 cm = 9 cm
(ii) AG + GF + FK + KE = (2.6 + 1.7 + 1.8 + 3) cm = 9.1 cm
(iii) AH + HI + IJ + JE = 3 cm + 2.3 cm + 1 cm + 3.2 cm = 9.5 cm.
1st way ABCDE is the shortest one.

Question 7.
A room has a door whose measures are 1 m wide and 2 m 50 cm high.
(i) Can we make a bed of 2 m and 20 cm length and 90 cm wide into the room?
Solution:
Measures of the door length 2 m 50 cm width and lm (100 cm)
(i) Measures of the bed 2 m 20 cm width and 90 cm
Measures of the bed < measures of the door
∴ Yes, we can take the bed into the room.

Question 8.
A post office functions from 10 a.m to 5.45 pm with a lunch break of 1 hour. If the post office works for 6 days a week. Find the total duration of working hours in a week.
Solution:
Working hours in a day = 6 hrs 45 min
= (6 × 60 min) + 45 min
= (360 + 45) min
= 405 min
Total duration of working hours in a week
= 6 × 405 min
= 2430 min
= \(\frac{2430}{60}\)
= \(\frac{810}{20}\)
= 40 \(\frac{1}{2}\)
= 40 hours 30 minutes

Question 9.
Seetha wakes up at 5.20 a.m. She spends 35 minutes to get ready and travels 15 minutes to reach the railway station. If the train departs exactly at 6 : 00 a.m, will Seetha catch the train?
Solution:
Time of wake up = 5.20 a.m = 5 hour 20 minutes
Time spends = 35 minutes
Then the time = 5 hour 55 minutes
Travelling time to reach railway station = 15 minutes
Now the time will be = 5 hours 70 minutes
= 5 hours (60 + 10) minutes
= 5 hours + (1 hour 10 minutes)
= 6 hours 10 minutes
= 6.10 a.m.
The departure time of the train to get ready = 6.0 a.m.
∴ She will not be able to catch the train.

Question 10.
A doctor advised Vairavan to take one tablet every 6 hours once in the 1st day and once every 8 hours on the 2nd and 3rd day. If he starts to take 9.30 a.m first dose. Prepare a time chart to take the tablet in railway time.
Solution:
The first dose is taken at 9.30 a.m. = 09:30 hours
Duration of every dose in 1st day = 6 hours
Duration of every dose in 2nd and 3rd day = 8 hours
Time Chart.

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.4

Miscellaneous Practice Problems

Question 1.
Find the type of lines marked in thick lines (Parallel, intersecting or perpendicular)

Solution:
(i) Parallel lines
(ii) Parallel lines
(iii) Parallel lines and Perpendicular lines
(iv) Intersecting lines

Question 2.
Find the parallel and intersecting line segments in the picture given below.

Solution:
(a) Parallel line segments

• \(\overline{\mathrm{YZ}} \text { and } \overline{\mathrm{DE}}\)
• \(\overline{\mathrm{EA}} \text { and } \overline{\mathrm{ZV}}\)
• \(\overline{\mathrm{VW}} \text { and } \overline{\mathrm{AB}}\)
• \(\overline{\mathrm{WX}} \text { and } \overline{\mathrm{BC}}\)
• \(\overline{\mathrm{YX}} \text { and } \overline{\mathrm{DC}}\)
• \(\overline{\mathrm{YD}} \text { and } \overline{\mathrm{XC}}\)
• \(\overline{\mathrm{XC}} \text { and } \overline{\mathrm{WB}}\)
• \(\overline{\mathrm{WB}} \text { and } \overline{\mathrm{VA}}\)
• \(\overline{\mathrm{VA}} \text { and } \overline{\mathrm{ZE}}\)
• \(\overline{\mathrm{ZE}} \text { and } \overline{\mathrm{YD}}\)

(b) Intersecting line segments

• DE and ZV
• WX and DC

Question 3.
Name the following angles as shown in the figure.

Solution:
(i) ∠1 = ∠DBC or ∠CBD
(ii) ∠2 = ∠DBE or ∠EBD
(iii) ∠3 = ∠ABE or ∠EBA
(iv) ∠1 + ∠2 = ∠EBC or ∠CBE
(v) ∠2 + ∠3 = ∠ABD or ∠DHA
(vi) ∠1 + ∠2 + ∠3 = ∠ABC or ∠B or ∠CBA

Question 4.
Measure the angles of the given figures using a protractor and identify the type of angle as acute, obtuse, right or straight.

Solution:
(i) 90° – Right Angle
(ii) 45° – Acute Angle
(iii) 180° – Straight Angle
(iv) 105° – Obtuse Angle

Question 5.
Draw the following angles using the protractor.
(i) 45°
(ii) 120°
(iii) 65°
(iv) 135°
(v) 0°
(vi) 180°
(vii) 38°
(viii) 90°
Solution:
(i) 45°

Construction:
1. Drawn the base ray PQ.
2. Placed the centre of the protractor at the vertex P. Lined up the ray \(\overrightarrow{\mathrm{PQ}}\) with the 0° line. Then drawn and labelled a pointed (R) at the 45° mark on the inner scale (a) anticlockwise and (b) outer scale (clockwise)
3. Removed the protractor and drawn at \(\overrightarrow{\mathrm{PR}}\) to complete the angle
Now ∠P = ∠QPR – ∠RPQ = 45°.

(ii) 120°

Construction:
1. Placed the centre of the protractor at the vertex X. Lined up the ray \(\overline{\mathrm{XY}}\) with the 0° Line. Then draw and label a point Z at 120° mark on the (a) inner scale (anti-clockwise) and (b) outer scale (clockwise).
2. Removed the protractor and draw \(\overline{\mathrm{XZ}}\) to complete the angle.
Now, ∠X = ∠ZXY = ∠YXZ = 120°.

(iii) 65°

Construction:
1. Placed the centre of the protractor at the vertex A. Line up the ray \(\overrightarrow{\mathrm{AB}}\) with the 0° line. Then draw and label a point C at the 65° mark on the (a) inner scale (anti-clockwise) (b) outer scale (clockwise).
2. Removed the protractor and draw \(\overrightarrow{\mathrm{AB}}\) to complete the angle.
Now ∠A = ∠BAC = ∠CAB = 65°.

(iv) 135°

Construction:
1. Placed the centre of the protractor at the Vertex A. Lined up the ray \(\overrightarrow{\mathrm{EG}}\) with the 0° line. Then draw and label a point F at the 135° mark on the (a) inner scale (anti-clockwise) and (b) outer scale (clockwise)
2. Removed the protractor and draw \(\overrightarrow{\mathrm{EF}}\) to complete the angle.
Now ∠E = ∠FEG = ∠GEF = 135°.

(v) 0°

Construction:
1. Placed the centre of the protractor at the vertex G. Lined up the ray \(\overrightarrow{\mathrm{GH}}\) with the 0° line. Then draw and label a point I at the 0° mark on the
(a) inner scale (anti-clockwise)
(b) outer scale (clockwise)
2. Removed the protractor and seen \(\overrightarrow{\mathrm{GI}}\) lies exactly on \(\overrightarrow{\mathrm{GH}}\)
Now ∠G = ∠HGI = ∠IGH = 0°, which is a zero angle.

(vi) 180°

Construction:
1. Placed the centre of the protractor at the vertex I. Lined up the ray \(\overrightarrow{\mathrm{IJ}}\) with the 0° line. Then draw and labelled a point K at the 180° mark on the (a) inner scale (anticlockwise) (b) outer scale (clockwise)
2. Removed the protractor and draw \(\overrightarrow{\mathrm{IK}}\) to complete the angle.
Now ∠I = ∠JHK = ∠KIJ = 180°, which is a straight Angle.

(vii) 38°

Construction:
1. Placed the centre of the protractor at the vertex L. Lined up the ray \(\overrightarrow{\mathrm{LM}}\) with the 0° line. Then draw and label a point N at 38° mark on the (a) inner scale (anticlockwise) and (b)*huter scale (clockwise).
2. Removed the protractor and draw \(\overrightarrow{\mathrm{LN}}\) to complete the angle.
Now ∠L = ∠MLN = ∠NLM = 38°.

(viii) 90°

Construction:
1. Placed the centre of the protractor at the vertex ‘O’. Lined up the ray \(\overrightarrow{\mathrm{OP}}\) with the 0° line. Then draw and label a point Q at 90° mark on the (a) inner scale (anticlockwise) and (b) outer scale (clockwise)
2. Removed the protractor and draw \(\overrightarrow{\mathrm{OQ}}\) to complete the angle.
Now ∠O = ∠POQ = ∠QOP = 90°.

Question 6.
From the figures given below, classify the following pairs of angles into complementary and non-complementary.

Solution:
We know that the two angles are complementary if they add up to 90°.
Therefore (a) (i) is complementary.
In (v) ∠ABC and ∠CBD are complementary
(b) (ii), (iii), (iv) and (v) are non-complementary

Question 7.
From the figures given below, classify the following pairs of angles into supplementary and non-supplementary.

Solution:
If two angles add up to 180°, then they are supplementary angles.
(a) In (ii) ∠AOB and ∠BOD are supplementary. In (iv) the pair is supplementary
(b) (i) and (iii) are not supplementary.

Question 8.
From the figure.
(i) name a pair of complementary angles
(ii) name a pair of supplementary angles

Solution:
(i) ∠FAE and ∠DAE are complementary
(ii) ∠FAD and ∠DAC are supplementary

Question 9.
Find the complementary angle of
(i) 30°
(ii) 26°
(iii) 85°
(iv) 0°
Solution:
When we have an angle, how far we need to go to reach the right angle is called the complementary angle.
(i) Complementary angle of 30° is 90° – 30° = 60°
(ii) Complementary angle of 26° is 90° – 26° = 64°
(iii) Complementary angle of 85° is 90° – 85° = 5°
(iv) Complementary angle of 0° is 90° – 0° = 90°
(v) Complementary angle of 90° is 90° – 90° = 0°

Question 10.
Find the supplementary angle of
(i) 70°
(ii) 35°
(iii) 165°
(iv) 90°
(v) 0°
(vi) 180°
(vii) 95°
Solution:
How far we should go in the same direction to reach the straight angle (180°) is called supplementary angle.
(i) Supplementary angle of 70° = 180° – 70° = 110°
(ii) Supplementary angle of 35° is 180° – 35° = 145°
(iii) Supplementary angle of 165° is 180° – 165° = 15°
(iv) Supplementary angle of 90° is 180° – 90° = 90°
(v) Supplementary angle of 0° is 180° – 0° = 180°
(vi) Supplementary angle of 180° is 180° – 180° = 0°
(vii) Supplementary angle of 95° is 180° – 95° = 85°

Challenging Problems

Question 11.
Think and write and object having.
(i) Parallel Lines
1. _____________
2. _____________
3. _____________
(ii) Perpendicular lines
1. _____________
2. _____________
3. _____________
(iii) Intersecting lines
1. _____________
2. _____________
3. _____________
Solution:
(i) 1. Opposite edges of a Table.
2. Path traced by the wheels of a car on a straight road
3. Opposite edges of a black board
(ii) 1. Adjacent edges of a Table.
2. Hands of the block when it shows 3.30
3. Strokes of the letter ‘L’
(iii) 1. Sides of a triangle
2. Strokes of letter ‘V’
3. Hands of a scissors

Question 12.
Which angle is equal to twice of its complement?
Solution:
We know that the sum of complementary angles 90°
Given Angle = 2 × Complementary angle

By trial and error, we find that Angle = 2 × Complement for 60°
The required angle = 60°
Another method:
Let the angle be x given
x = 2 (90 – x)
⇒ x = 180 – 2x
⇒ x + 2x = 180
⇒ 3x = 180
⇒ x = 60°

Question 13.
Which angle is equal to two-thirds of its supplement.
Solution:
Supplementary angles sum upto 180°
Given Angle = \(\frac{2}{3}\) × Supplement.
Forming the Table.

By trial and error, we find that angle = \(\frac{2}{3}\) × supplement for 72°.
The required angle 72°.

Question 14.
Given two angles are supplementary and one angle is 20° more than other. Find the two angles.
Solution:
Given two angles are supplementary i.e. their sum = 180°.
Let the angle be x
Then another angle = x + 20 (given)

The two angles are 80° and 100°.

Question 15.
Two complementary angles are in the ratio 7 : 2. Find the angles.
Solution:
Let the angles be 7x, 2x
According to the problem,
7x + 2x = 90
9x = 90
x = \(\frac{90}{9}\)
x = 10
7x = 7 × 10
= 70
2x = 2 × 10
= 20
∴ Two angles are 70° and 20°

Question 16.
Two supplementary angles are in ratio 5 : 4. Find the angles.
Solution:
Total of two supplementary angles = 180°
Given they are in the ratio 5 : 4
Dividing total angles to 5 + 4 = 9 equal parts.
One angle \(=\frac{5}{9} \times 180=100^{\circ}\)
Another angle \(=\frac{4}{9} \times 180=80^{\circ}\)
Two angles are 100° and 80°.

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Ex 1.3

Question 1.
Fill in the blanks.

1. If Arulmozhi saves ₹ 12 per day then she saves ₹ ____ in 30 days.
2. If a person ‘A’ earns ₹ 1800 in 12 days, then he earns ₹ ____ in a day.
3. 45 ÷ (7 + 8) – 2 = _____

Solution:

1. 12 × 30 = ₹ 360
2. \(\frac{1800}{12}=150\)
3. 45 ÷ 15 – 2 = 3 – 2 = 1

Question 2.
Say True or False.

1. 3 + 9 × 8 = 96
2. 7 × 20 – 4 = 136
3. 40 + (56 – 6) ÷ 2 = 45

Solution:

1. False
2. True
3. False

Question 3.
The number of people who visited the Public Library for the past 5 months was 1200, 2000, 2450, 3060 and 3200 respectively. How many people visited the library in the last 5 months.
Solution:
People visited the library for past 5 months = 1200 + 2000 + 2450 + 3060 + 3200 = 11910
Total people visited = 11910

Question 4.
Cheran had a bank savings of Rs 7,50,250. He withdrew Rs 5,34,500 for educational purpose. Find the balance amount in his account.
Solution:
Savings = Rs 7,50,250 Cash withdrawn = Rs 5,34,500
Balance amount = Rs 7,50,250 – Rs 5,34,500 = Rs 2,15,750

Question 5.
In a cycle factory, 1560 bicycles were manufactured every day. Find the number of bicycles manufactured in 25 days.
Solution:
Number of bicycles manufactured in one day = 1560
Number of bicycles manufactured in 25 days = 1560 × 25 = 39000

Question 6.
Rs 62500 was equally distributed as a New Year bonus for 25 employees of a company. How much did each receive?
Ans:
Total amount = Rs 62500
Total number of employees = 25
Bonus amount received by each employee = Rs 62500 ÷ 25
= RS \(\frac{62500}{25}\)
= Rs 2500

Question 7.
Simplify the following numerical expression:
(i) (10 + 17) ÷ 3
(ii) 12 – [3 – {6 – (5 – 1)}]
(iii) 100 + 8 ÷ 2 + {(3 × 2) – 6 ÷ 2}
Solution:
(i) (10 + 17) ÷ 3 (Given)
= 27 ÷ 3 (Bracket completed first)
= 9 (÷ completed)
∴ (10 + 17) ÷ 3 = 9

(ii) 12 – [3 – {6 – (5 – 1)}] (Given)
= 12 – [3 – {6 – 4}] (Innermost bracket completed first)
= 12 – [3 – 2] (Again Inner bracket completed second)
= 12 – 1 (Bracket completed third)
= 11 (- completed)
∴ 12 – [3 – {6 – (5 – 1)}] = 11

(iii) 100 + 8 ÷ 2 + {(3 × 2) – 6 ÷ 2} (Given)
= 100 + 8 ÷ 2 + {6 – 6 ÷ 2} (Innermost bracket completed first)
= 100 + 8 ÷ 2 + {6 – 3} (To remove the next bracket ÷ within the bar completed second)
= 100 + 8 ÷ 2 + 3 (bar completed third)
= 100 + 4 + 3 (÷ completed fourth)
= 107 (+ completed)
∴ 100 + 8 ÷ 2 + {(3 × 2) – 6 ÷ 2} = 107

Objective Type Questions

Question 8.
The value of 3 + 5 – 7 × 1 is …….
(a) 5
(b) 7
(c) 8
(d) 1
Solution:
(d) 1

Question 9.
The value of 24 ÷ {8 – (3 × 2)} is ______
(a) 0
(b) 12
(c) 3
(d) 4
Answer:
(b) 12
24 ÷ {8 – 3 × 2} = 24 ÷ {8 – 6} = 24 ÷ 2 = 12

Question 10.
Use BIDMAS and put the correct operator in the box.
2₹6 – 12 ÷ (4 + 2) = 10
(a) +
(b) –
(c) ×
(d) ÷
Solution:
(c) ×

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.4

Question 1.
Fill in the blanks.
(i) If the cost of 3 pens is ₹ 18, then the cost of 5 pens is ____
(ii) If Karkuzhali earns ₹ 1800 in 15 days, then she earns ₹ 3000 in ___ days
Solution:
(i) ₹ 30
Hint: \(5 \times \frac{18}{3}\) = 5 × 6 = ₹ 30
(ii) 25 Days
Hint:
\(\frac{1800}{3000}=\frac{15}{x}\)
⇒ x = \(\frac{15 \times 3000}{1800}\) = 25 days

Question 2.
Say True or False.
(i) If the weight of 40 books is 8 kg, then the weight of 15 books is 3 kg.
(ii) A car travels 90 km in 3 hours with constant speed, It will travel 140 km in 5 hours at the same speed.
Solution:
(i) True
(ii) False

Question 3.
If a person reads 20 pages of a book in 2 hours, how many pages will he read in 8 hours at the same speed.
Solution:
Pages read in 2 hours = 20
Then pages read in 1 hour = \(\frac{20}{2}\) = 10 pages.
Pages will be read in 8 hours = 8 × 10 = 80 pages.
Number of pages will be read in 8 hrs = 80 pages

Question 4.
The cost of 15 chairs is Rs 7500. Find the number of such chairs that can be purchased for Rs 12000?
Solution:
Cost of 15 chairs = Rs 7500
Cost of 1 chair = Rs \(\frac{7500}{15}\) = Rs 500
Number of chairs that can be purchased for Rs 12000 = \(\frac{12000}{500}\)
= 24 chairs

Question 5.
A car covers a distance of 125 km in 5 kg of LP Gas. How much distance will it cover in 3 kg of LP Gas?
Solution:
With 5kg LP Gas distance covered = 125 km
With 1 kg LP Gas distance covered = \(\frac{125}{5}\) = 25 km
With 3 kg LP Gas distance covered = 25 × 3 = 75 km.
75 km can be covered with 3 kg LP Gas.

Question 6.
Cholan walks 6 km in 1 hour at constant speed. Find the distance covered by him in 20 minutes at the same speed.
Solution:
In 1 hour (60 minutes), distance covered = 6 km
In 1 minute, distance covered = \(\frac{6 km}{60 min}\) = \(\frac{6000 m}{60}\)
= 100 m
In 20 minutes, distance covered = 20 × 100 m = 2000 m = 2 km

Question 7.
The number of correct answers given by Kaarmugilan and Kavitha in a quiz competition is in the ratio 10 : 11. If they had scored a total of 84 points in the competition, then how many points did Kavitha get?
Solution:
Correct answers given by Kaarmugilan and Kavitha are in the ratio 10 : 11
Total of 84 points will be divided into 10 + 11 = 21 equal parts
Points scored by Kavitha = \(\frac{11}{21} \times 84\) = 44 points
Kavitha scored 44 points in the quiz.

Question 8.
Karmegam made 54 runs in 9 overs and Asif made 77 runs in 11 overs. Whose run rate is better? (run rate = ratio of runs to overs)
Solution:
Karmegam Runs made in 9 overs = 54
Runs made in 1 over = \(\frac{54}{9}\) = 6 runs
Asif
Runs made in 11 overs = 77
Runs made in 1 over = \(\frac{77}{11}\) = 7 runs
∴ Asif’s run rate is better than Karmegam.

Question 9.
You purchase 6 apples for ₹ 90 and your Mend purchases 5 apples for ₹ 70. Whose purchase is better?
Solution:
In my purchase cost of 6 apples = ₹ 90
Cost of 1 apple = \(\frac{90}{6}\) = ₹ 15
In my friend’s purchase cost of 5 apples = ₹ 70
Cost of 1 apple = \(\frac{70}{5}\) = ₹ 14
My friend buy for lower prize.
My friend’s purchase is a better buy.

Objective Type Questions

Question 10.
If a Barbie doll costs Rs 90, then the cost of 3 such dolls is Rs …….
(a) 260
(b) 270
(c) 30
(d) 93
Solution:
(b) 270

Question 11.
If 8 oranges cost ₹ 56, then the cost of 5 oranges is ₹ _____
(a) 42
(b) 48
(c) 35
(d) 24
Solution:
(c) 35
Hint:
Cost of 1 Orange = \(\frac{56}{8}\) = ₹ 7
Cost of 5 Orange = 7 × 5 = ₹ 35

Question 12.
If a man walks 2 km in 15 minutes, then he will walk ………. km in 45 minutes.
(a) 10
(b) 8
(c) 6
(d) 12
Solution:
(c) 6

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.3

Queston 1.
Explain why Rolle’s theorem is not applicable to the following functions in the respective intervals.

Solution:

f(x) is not continuous at x = 0. So Rolle’s Theorem is not applicable.

(ii) f (x) = tan x
f(x) is not continuous at x = \(\frac{\pi}{2}\). So Rolle’s Theorem is not applicable..

(iii) f(x) = x – 2 log x
f(x) = x – 2 log x
f(2) = 2 – 2 log 2 = 2 – log 4
f(7) = 7 – 2 log 7 = 7 – log 49
f(2) ≠ f(7)
So Rolle’s theorem is not applicable.

Question 2.
Using the Rolle’s theorem, determine the values of x at which the tangent is parallel to the x-axis for the following functions:

Solution:

Question 3.
Explain why Lagrange’s mean value theorem is not applicable to the following functions in the respective intervals :

Solution:

The function is not continuous at x = 0. So Lagrange’s mean value theorem is not applicable in the given interval.

(ii) f(x) =|3x + 1|, x ∈ [-1, 3]
The function is not differentiable at x = \(\frac{-1}{3}\). So Lagrange’s mean value theorem is not applicable in the given interval.

Question 4.
Using the Lagrange’s mean value theorem determine the values of x at which the tangent is parallel to the secant line at the end points of the given interval:
(i) f(x) = x³ – 3x + 2, x ∈ [-2, 2]
(ii) f(x) = (x – 2)(x – 7), x ∈ [3, 11]
Solution:
(i) f(x) = x³ – 3x + 2
Here a = -2, b = 2

Question 5.
Show that the value in the conclusion of the mean value theorem for

Solution:
(i)

Question 6.
A race car driver is racing at 20th km. If his speed never exceeds 150 km/hr, what is the maximum distance he can cover in the next two hours.
Solution:

Here the interval is [0, 2] and f(0) = 20, f(2) = ?
f(b) – f(a) ≤ (b – a)f’c)
here f (a) = 20
⇒ f(b) – 20 ≤ 150(2 – 0)
⇒ f(b) ≤ 320
(i.e) f(2) = 320 km.

Question 7.
Suppose that for a function f(x), f'(x) ≤ 1 for all 1 ≤ x ≤ 4. Show that f(4) – f(1) ≤ 3.
Solution:

Question 8.
Does there exist a differentiable function f(x) such that f(0) = -1, f(2) = 4 and f'(x) ≤ 2 for all x. Justify your answer.
Solution:
f(0) = -1, f(2) = 4, f(x) ≤ 2

Here a = 0, b = 2

So this is not possible

Question 9.
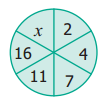
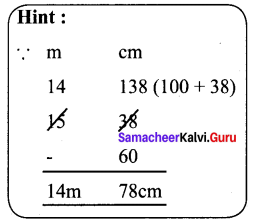
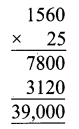
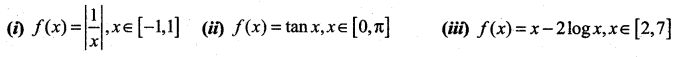
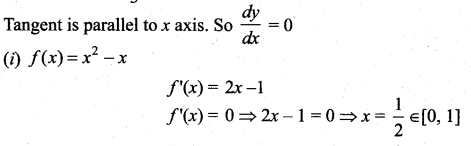
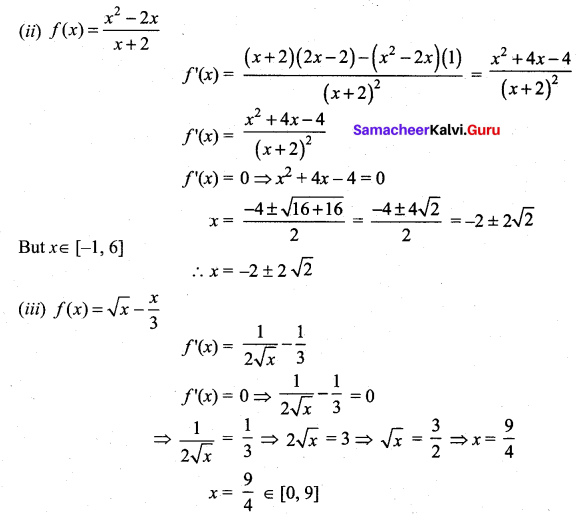
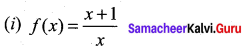
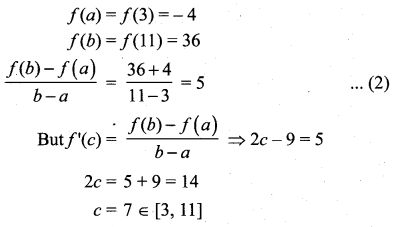
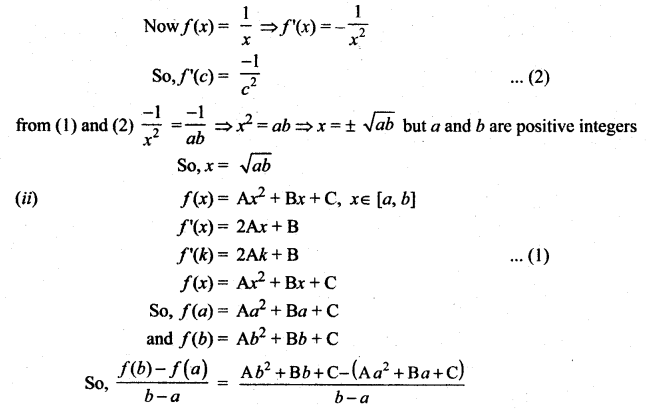
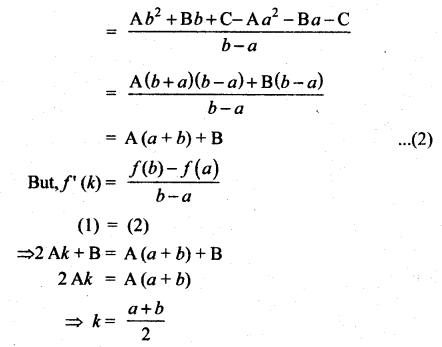
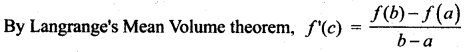
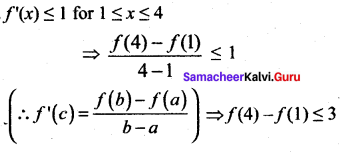
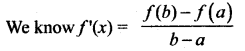
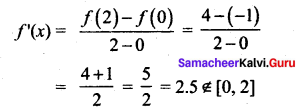
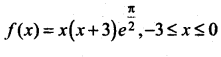Show that there lies a point on the curve where tangent drawn is parallel to the x – axis.
Solution:

⇒ There lies a point in [-3,0], where tangent is parallel to x axis.

Question 10.
Using mean value theorem prove that for, a > 0, b > 0, |e^-a – e^-b| < |a – b|
Solution:

Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.3 Additional Questions Solved

Question 1.
Verify Rolle’s theorem for the following:
(i) f(x) = x³ – 3x + 3, 0 ≤ x ≤ 1
(ii) f(x) = tan x, 0 ≤ x ≤ π
(iii) f(x) = | x |, – 1 ≤ x ≤ 1
(iv) f (x) = sin² x, 0 ≤ x ≤ π
(v) f(x) = e^x sin x, 0 ≤ x ≤ π
(vi) f(x) = x(x – 1) (x – 2), 0 ≤ x ≤ 2
Solution:
(i) f(x) = x³ – 3x + 3, 0 ≤ x ≤ 1. f is continuous on [0, 1] and differentiable in (0, 1)
f(0) = 3 and f(1) = 1 ∴ f(a) ≠ f(b)
∴ Rolle’s theorem, does not hold, since f(a) = f(b) is not satisfied.
Also note that f’ (x) = 3x² – 3 = 0 ⇒ x² = 1 ⇒ x = ±1
There exists no point c ∈ (0, 1) satisfying f’ (c) = 0.

(ii) f(x) = tan x, 0 ≤ x ≤ π.
f ‘(x) is not continuous in [0, π] as tan x tends to + ∞ at x = \(\frac{\pi}{2}\),
∴ Rolle’s theorem is not applicable.

(iii) f (x) = | x |, -1 ≤ x ≤ 1
f is continuous in [-1, 1] but not differentiable in (-1, 1) since f'(0) does not exist.
∴ Rolle’s theorem is not applicable.

(iv) f (x) = sin²x, 0 ≤ x ≤ π
f is continuous in [0, π] and differentiable in (0, π). f(0) = f(π) = 0
(i.e.,) f satisfies hypothesis of Rolle’s theorem.
f’ (x) = 2 sin x cos x = sin 2x

(v) f(x) = e^x, sin x, 0 ≤ x ≤ π
e^x and sin x are continuous for all x, therefore the product e^x sin x is continuous in 0 ≤ x ≤ π.
f’ (x) = e^x sin x + e^x cos x = e^x (sin x + cos x) exist in 0 < x < π ⇒ f'(x) is differentiable in (0, π)
f (0) = e° sin 0 = 0
f (π) = e^π sin π = 0
∴ f satisfies hypothesis of Rolle’s theorem.
Thus there exists c ∈ (0, π) satisfying f'(c) = 0 ⇒ e^c (sin c + cos c) = 0
⇒ e^c = 0 or sin c + cos c = 0
⇒ e^c = 0 ⇒ c = -∞ which is not meaningful here.

(vi) f(x) = x (x – 1) (x – 2), 0 ≤ x ≤ 2
f is not continuous in [0, 2] and differentiable in (0, 2)
f(0) = 0 = f(2), satisfying hypothesis of Rolle’s theorem.
Now f'(x) = (x – 1) (x – 2) + x(x – 2) + x(x – 1) = 0

Note: There could exist more than one such ‘c’ appearing in the statement of Rolle’s theorem.

Question 2.
Suppose that f(0) = -3 and f'(x) ≤ 5 for all values of x, how large can f(2) possibly be?
Solution:
Since by hypothesis f is differentiable, f is continuous everywhere. We can apply Lagrange’s Law of the mean on the interval [0, 2], There exist atleast one ‘c’ ∈ (0, 2) such that
f(2) – f(0) = f'(c)(2 – 0)
f(2) = f(0) + 2f'(c) = -3 + 2f'(c)
Given that f'(x) ≤ 5 for all x.
In particular we know that f'(c) ≤ 5. Multiplying both sides of the inequality by 2, we have
2f'(c) ≤ 10
f(2) = -3 + 2f'(c) < -3 + 10 = 7
i.e., the largest possible value of f(2) is 7.

Question 3.
Using Rolle’s theorem find the points on the curves = x² +1, -2 ≤ x ≤ 2 where the tangent is parallel to X-axis
Solution:

a = -2,
b = 2
f(x) = x² + 1
f(a) = f(-2) = 4 + 1 = 5
f(b) = f(2) = 4 + 1 = 5
So, f(a) = f(b)
f'(x) = 2x
f'(x) = 0 ⇒ 2x = 0
x = 0 where 0 ∈ (-2, 2)
at x = 0, y = 0 + 1 = 1
So, the point is (0, 1) at (0, 1) the tangent drawn is parallel to X-axis

Question 4.
Find ‘C’ of Lagrange’s mean value theorem for the function f(x) = 2x³ + x² – x – 1, [0, 2]
Solution:
f(x) = 2x³ + x² – x – 1
a = 0,
b = 2
f(a) = f(0) = -1
f(b) = f(2) = 2(8) = 4 – 2 – 1 = 16 + 4 – 2 – 1 = 17
By Lagrange’s mean value theorem, we get a constant c ∈ (a, b) such that

Question 5.
Find ‘C’ of Lagrange’s mean value theorem for the function f(x) = x³ + x² – 3x in [1, 3]
Solution:
f(x) = x³ + x² – 3x
a = 1,
b=3
f(a) = f(1) = 1 – 5 – 3 = -7
f(b) = f(3) = 27 – 5(9) – 3(3)
= 27 – 45 – 9 = -27

f'(x) = 3x² – 10x – 3
f'(x) = 3c² – 10c – 3
From (1) and (2),
3c² – 10c – 3 = -10
3c² – 10c – 3 + 10 = 0
3c² – 10c + 7 = 0
3c² – 3c – 7c + 7 = 0

So, Lagrange’s mean value theorem is true with c = \(\frac{7}{3}\)

Must Read:

INDUSINDBK Pivot Point Calculator

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.4

Question 1.
Write the Maclaurin series expansion of the following functions:
(i) e^x
(ii) sin x
(iii) cos x
(iv) log (1 – x); -1 ≤ x < 1
(v) tan^-1 (x) ; -1 ≤ x ≤ 1
(vi) cos² x
Solution:

(vi) f(x) = cos² x
f(0) = 1
f'(x) = 2 cos x (- sin x) = – sin 2x
f'(0) = 0
f”(x) = (-cos 2x)(2)
f”(0) = -2
f”'(x) = -2[- sin 2x](2) = 4 sin 2x
f”'(0) = 0
f⁴ (x) = 4(cos 2x)(2) = 8 cos 2x
f⁴ (0) = 8

Question 2.
Write down the Taylor series expansion, of the function log x about x = 1 upto three non-zero terms for x > 0.
Solution:

Question 3.
Expand sin x in ascending powers x – \(\frac{\pi}{4}\) upto three non-zero terms.
Solution:
f (x) = sin x

Question 4.
Expand the polynomial f(x) = x² – 3x + 2 in powers of x – 1
Solution:
f(x) = x² – 3x + 2 = (x – 1) (x – 2)
f(1) = 0
f'(x) = 2x – 3 ; f'(1) = -1
f”(x) = 2 ; f”(1) = 2

Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.4 Additional Problems

Question 1.
The Taylor’s series expansion of f(x) = sin x about x = \(\frac{\pi}{2}\) is obtained by the following way.
Solution:

Question 2.
Obtain the Maclaurin’s series expansion for the following functions.
(i) e^x
(ii) sin² x
(iii) \(\frac{1}{1+x}\)
Solution:
(i)

(ii)

(iii)

Read More:

ICICIBANK Pivot Point Calculator