Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.4

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.4

Question 1.
Write the Maclaurin series expansion of the following functions:
(i) e^x
(ii) sin x
(iii) cos x
(iv) log (1 – x); -1 ≤ x < 1
(v) tan^-1 (x) ; -1 ≤ x ≤ 1
(vi) cos² x
Solution:

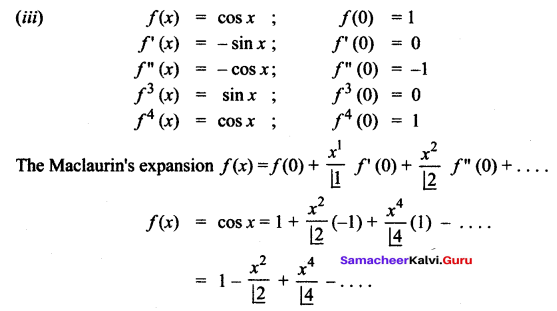
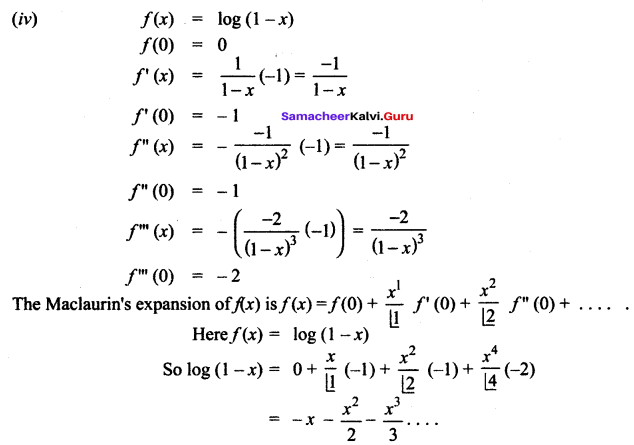
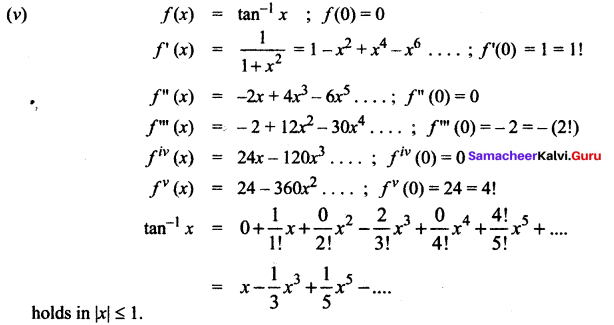
(vi) f(x) = cos² x
f(0) = 1
f'(x) = 2 cos x (- sin x) = – sin 2x
f'(0) = 0
f”(x) = (-cos 2x)(2)
f”(0) = -2
f”'(x) = -2[- sin 2x](2) = 4 sin 2x
f”'(0) = 0
f⁴ (x) = 4(cos 2x)(2) = 8 cos 2x
f⁴ (0) = 8

Question 2.
Write down the Taylor series expansion, of the function log x about x = 1 upto three non-zero terms for x > 0.
Solution:

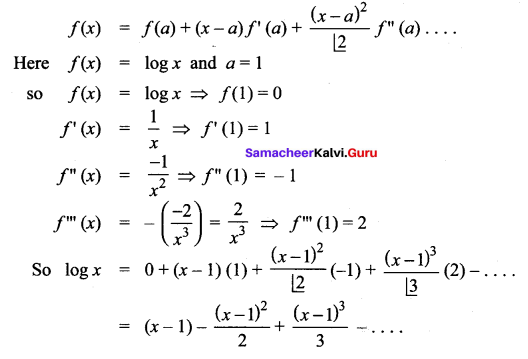
Question 3.
Expand sin x in ascending powers x – \(\frac{\pi}{4}\) upto three non-zero terms.
Solution:
f (x) = sin x

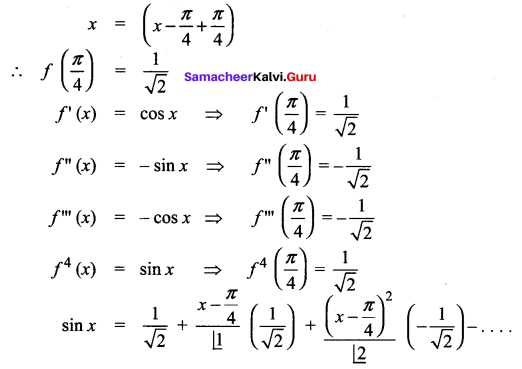
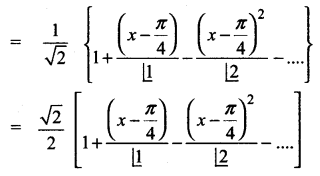
Question 4.
Expand the polynomial f(x) = x² – 3x + 2 in powers of x – 1
Solution:
f(x) = x² – 3x + 2 = (x – 1) (x – 2)
f(1) = 0
f'(x) = 2x – 3 ; f'(1) = -1
f”(x) = 2 ; f”(1) = 2

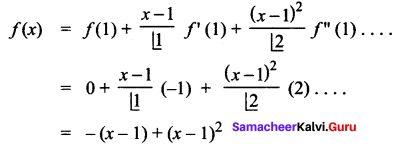
Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.4 Additional Problems

Question 1.
The Taylor’s series expansion of f(x) = sin x about x = \(\frac{\pi}{2}\) is obtained by the following way.
Solution:

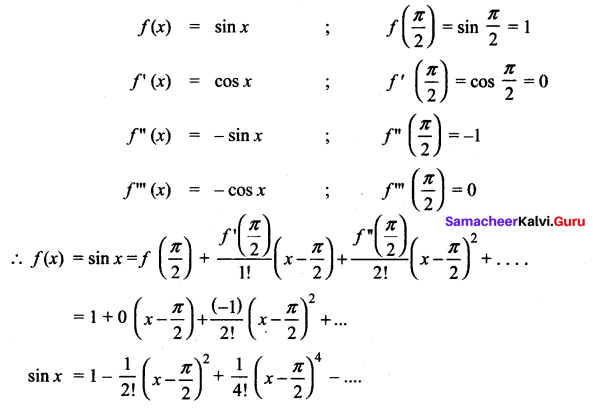
Question 2.
Obtain the Maclaurin’s series expansion for the following functions.
(i) e^x
(ii) sin² x
(iii) \(\frac{1}{1+x}\)
Solution:
(i)

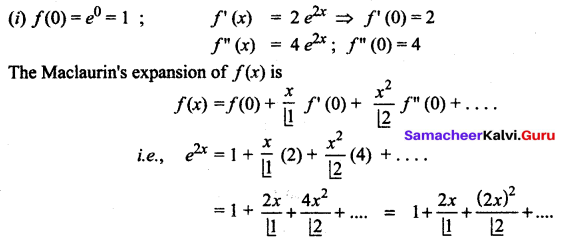
(ii)

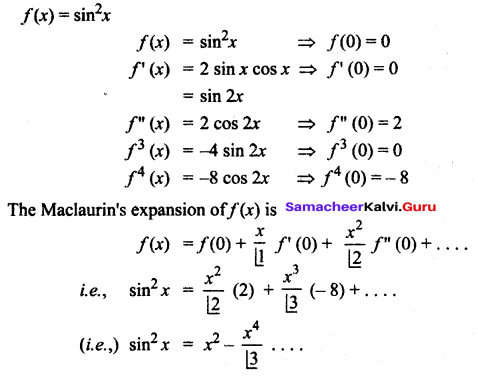
(iii)

Read More:

ICICIBANK Pivot Point Calculator