Prasanna

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.4 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.4

கேள்வி 1.
கீழ்க்காணும் சார்புகளுக்கு மெக்லாரனின் விரிவைக் காண்க :
(i) e^x
(ii) sin x
(iii) cos x
(iv) log (1 – x); -1 ≤ x ≤ 1
(v) tan^-1 (x) ; -1 ≤ x ≤ 1
(vi) cos² x
தீர்வு:
(i) e^x

(ii) sinx
f(x) = sin x என்க ⇒ f(0) = sin 0 = 0
f^I(x) = cos x ⇒ f^I(0) = cos 0 = 1
f^II(x) = – sinx ⇒ f^II(0) = -sin 0 = 0
f^III(x) = -cos x ⇒ f^III(0) = -cos 0 = 0
f^IV(x) = + sin x ⇒ f^IV(0) = sin 0 = 0
f^V(x) = cos x ⇒ f^V(0) = cos 0 = -1
f^VI(x) = -sin x ⇒ f^VI(0) = -sin 0 = 0
f^VII(x) = -cos x ⇒ f^VII(0) = -cos 0 = -1
∴ மெக்லாரனின் தொடர் விரிவாக்கம்

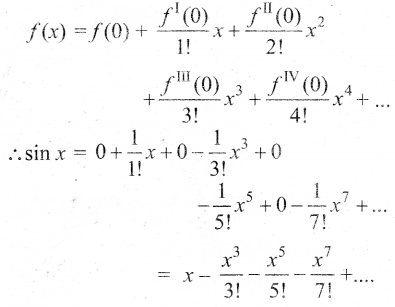
(iii) cos x

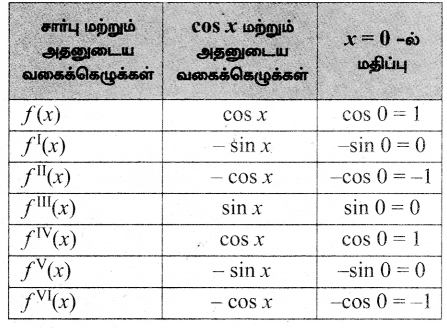
மெக்லாரனின் தொடர் விரிவாக்கம்

(iv) log (1 – x); -1 ≤ x ≤ 1

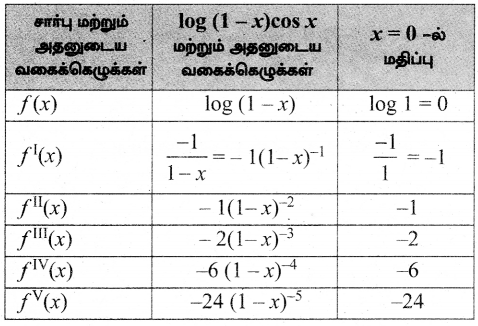
மெக்லாரனின் தொடர் விரிவாக்கம்

(v) tan^-1 (x) ; -1 ≤ x ≤ 1
f(x) = tan^-1 (x) என்க
⇒ f(0) = tan^-1 (0) = 0
f'(x) = \(\frac{1}{1+x^{2}}\) = (1 + x²)^-1
⇒ f^I(0) = 1
f^II(x) = -1(1 + x)^-2 (2x)
= -2x (1 + x^2-2
⇒ f^II(0) = 0
= -2[-4x² (1 + x²)^-3 + (1 + x²)^-2]
f^III(x) = – 2 [x(-2) (1 + x²)^-3 (2x) + (1 + x²)^-2]
⇒ f^III(0) = 2

⇒ f^IV(x) = -2 [ 4x² (-3) (1 + x²)^-4 (2x) + (1 + x²)^-3 (-8x) + (1 + x²)^-3 (-2) (2x)]
= -2 [24x³ (1 + x²)^-4 – 8x (1 + x²)^-3 – 4x (1 + x²)^-3]
= – 2 [24x³ (1 + x²)^-4 – 12x (1 + x²)^-3]

f^IV(x) = – 24 [2x³ (1 + x²)^-4 – x (1 + x²)^-3]
⇒ f^II(0) = 0
f^V(x) = – 24 [2x³ (-4)(1 + x²)^-5 (2x) + (1 + x²)^-4 + 6x² – x (- 3)(1 + x²) + (2x) – (1 + x²)^-3]
= – 24 [16x⁴ (1 + x²)^-5 + 6x² (1 + x²)^-4 – (1 + x²)^-3]
= – 24 [16x⁴ + (1 + x²)^-5 + 12x² (1 + x²)^-4 – (1 + x²)^-3]
⇒ f^V(0) = 24
⇒ f(0) = tan^-1 (0) = 0
⇒ f^-1(0) = 1
⇒ f^II(0) = ()
⇒ f^III(0) = -2
⇒ f^IV(0) = 0
⇒ f^V(0) = 24
மெக்லாரனின் விரிவு
f(x) = f(0) + \(\frac{f^{\mathrm{I}}(0)}{1 !} x+\frac{f^{\mathrm{II}}(0)}{2 !} x^{2}+\frac{f^{\mathrm{III}}(0)}{3 !} x^{3}+\frac{f^{\mathrm{IV}}(0)}{4 !} x^{4}+\ldots\)
= 0 + \(\frac{1}{1 !} x+0 \frac{2}{3 !} x^{3}+0+\frac{24}{5 !} x^{5}+\ldots\)
= x – \(\frac{x^{3}}{3}+\frac{x^{5}}{5}+\ldots\)

(vi) cos² x
f(x) = cos² x என்க
f(x) = 2cos x (- sinx)
= -sin 2x ⇒ f^I(0) = 0
f^II(x) = – 2 cos 2x ⇒ f^II(0) = -2
f^III(x) = +4 sin 2x ⇒ f^III(0) = 0
f^IV(x) = 8 cos 2x ⇒ f^IV(0) = 8
f^V(x) = -16 sin2x ⇒ f^V(0) = 0
f^VI(x) = -32cos 2x ⇒ f^VI(0) = -32
மெக்லாரனின் விரிவு

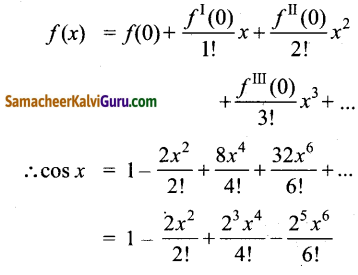
கேள்வி 2.
log x, x > 0 என்ற சார்பின் டெய்லர் தொடரின் விரிவை x = 1 -ஐ பொருத்து முதல் மூன்று பூச்சியமற்ற உறுப்புகள் வரை காண்க.
தீர்வு:
f(x) = log x என்க
f^I(x) = \(\frac{1}{x}\) = x^-1
f^II(x) = -1x^-2
f^III(x) = 2 x^-3
f^IV(x) = -6 x^-4
⇒ f(1) = log 1 = 0
f^I(1) = \(\frac{1}{1}\) =1
f^II(1) = -1
f^III(1) = 2
f^IV(1) = -6
x= 1ல் f (x) க்கான டெய்லரின் தொடர்

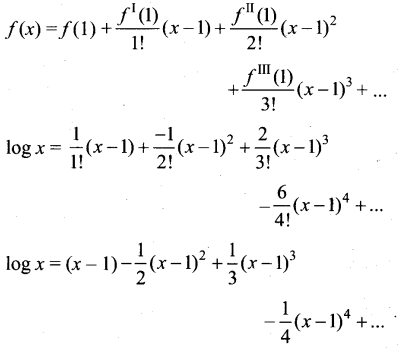
கேள்வி 3.
sin x -ன் விரிவை x – \(\frac{\pi}{4}\) -ன் அடுக்குகளாக முதல் மூன்று பூச்சியமற்ற உறுப்புகள் வரை காண்க.
தீர்வு:
f(x) = sin x என்க
f^I(x) = cos x
f^II(x) = – sin x
f^III(x) = – cos x|
⇒ f\(\left(\frac{\pi}{4}\right)\) = sin \(\frac{\pi}{4}\) = \(\frac{1}{\sqrt{2}}\)
f^I\(\left(\frac{\pi}{4}\right)\) = cos \(\frac{\pi}{4}\) = \(\frac{1}{\sqrt{2}}\)
f^II\(\left(\frac{\pi}{4}\right)\) = -sin \(\frac{\pi}{4}\) = –\(\frac{1}{\sqrt{2}}\)
f^III\(\left(\frac{\pi}{4}\right)\) = -cos \(\frac{\pi}{4}\) = –\(\frac{1}{\sqrt{2}}\)
x = \(\frac{\pi}{4}\) ல் f(x) க்கான டெய்லரின் தொடர்

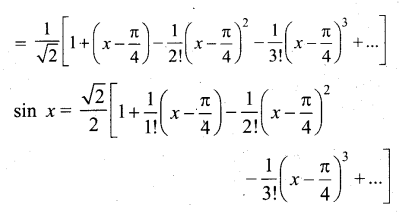
கேள்வி 4.
f (x) = x² – 3x + 2 என்ற பல்லுறுப்புக் கோவையின் வரிசை x – 1 -ன் அடுக்குகளாக காண்க.
தீர்வு:
f(x) = x² – 3x + 2
f^I(x) = 2x – 3
f^II(x) = 2
⇒ f(1) = 0)
f^I(1) = 2 – 3 = -1
f^II(1) = 2
x = 1ல் f (x) க்கான டெய்லரின் தொடர்
f(x) = f(1) + \(\frac{f^{\mathrm{l}}(1)}{1 !}(x-1)+\frac{f^{\mathrm{Il}}(1)}{2 !}(x-1)^{2}\)
= 0 + \(\frac{1}{1 !}(x-1)+\frac{2}{2 !}(x-1)^{2}\)
f(x) = – (x – 1) + (x – 1)²

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 9 நிகழ்தகவு Ex 9.1 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 9 நிகழ்தகவு Ex 9.1

கேள்வி 1.
நீங்கள் ஒரு தெருவில் நடந்து செல்கிறீர்கள். நீவிர் சந்தித்தவர்களில் ஒரு புதிய மனிதரைத் தேர்ந்தெடுக்கவும். அந்த மனிதரின் பிறந்த நாள் ஞாயிற்றுக்கிழமையாக இருக்க நிகழ்தகவு என்ன?
விடை:
S = {ஞாயிறு, திங்கள், செவ்வாய், புதன், வியாழன், வெள்ளி, சனி}
n(S) = 7
A என்பது அந்த மனிதரின் பிறந்தநாள் ஞாயிற்றுக்கிழமையாக இருக்கும் நிகழ்ச்சி என்க.
n(A) = 1
P(A) = 7 = \(\frac{n(A)}{n(S)}=\frac{1}{7}\)

கேள்வி 2.
52 சீட்டுகள் கொண்ட ஒரு சீட்டுக்கட்டிலிருந்து ஒரு படச்சீட்டு (அதாவது இராசா, இராணி அல்லது மந்திரி (Jack)?) தேர்ந்தெடுப்பதற்கான நிகழ்தகவு என்ன?
விடை:
n(S) = 52
A, B மற்றும் C என்பன ஒரு சீட்டுக்கட்டிலிருந்து
இராசா, இராணி அல்லது மந்திரியைத் தேர்ந்தெடுப்பதற்கான நிகழ்ச்சி என்க.
P(A) = \(\frac{4}{52}\)
P(B) = \(\frac{4}{52}\)
P(C) = \(\frac{4}{52}\)
ஒன்றையொன்று சாராத நிகழ்ச்சியாக இருப்பதால்
P(AUBUC) = P(A) + P(B) + P(C)
= \(\frac{4}{52}\) + \(\frac{4}{52}\) + \(\frac{4}{52}\)
= \(\frac{4+4+4}{52}\) = \(\frac{12}{52}\)
= \(\frac{3}{52}\)

கேள்வி 3.
ஒரு சீரான பகடையை உருட்டும் போது ஓர் இரட்டை எண் கிடைப்பதற்கான நிகழ்தகவு என்ன ?
விடை:
S = {1, 2, 3, 4, 5, 6}
n(S) = 6 A
என்பது ஓர் இரட்டை எண் கிடைப்பதற்கான நிகழ்ச்சி என்க.
n(A) = {2, 4, 6}
P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

கேள்வி 4.
ஒரு பானையில் 24 பந்துகள் உள்ளன. அவற்றில் 3 சிவப்பு, 5 நீலம் மற்றும் மீதி இருப்பவை பச்சை நிறமுடையதாகும். அவற்றில் ஒன்றைத் தேர்ந்தெடுக்கும் போது அது
(i) ஒரு நீல நிறப் பந்து
(ii) ஒரு சிவப்பு நிறப்பந்து
(iii) ஒரு பச்சை நிறப் பந்தாக இருக்க நிகழ்தகவு என்ன?
விடை :
n(S) = 24
சிவப்பு = 3, நீலம் = 5,
பச்சை = 24 – (3 + 5) = 16
A என்பது நீலநிறப் பந்தைத் தேர்ந்தெடுப்பதற்கான நிகழ்ச்சி என்க.
P(A) = \(\frac{5}{24}\)

B என்பது சிவப்பு நிறப் பந்தைத் தேர்ந்தெடுப்பதற்கான நிகழ்ச்சி என்க
P(B) = \(\frac{3}{24}\) = \(\frac{1}{8}\)

C என்பது பச்சை நிற நிறப் பந்தைத் தேர்ந்தெடுப்பதற்கான நிகழ்ச்சி என்க. மா 16 2|
P(C) = \(\frac{16}{24}\) = \(\frac{2}{3}\)

கேள்வி 5.
இரண்டு சீரான நாணயங்களை ஒரே நேரத்தில் சுண்டும் போது, இரு தலைகள் கிடைப்பதற்கான நிகழ்தகவு யாது?
விடை:
S = {HH, HT, TH, TT}
n(S) = 4
A என்பது இரு தலைகள் கிடைப்பதற்கான நிகழ்ச்சி என்க.
n(A) = 1
P(A) = \(\frac{n(A)}{n(S)}\)
= \(\frac{1}{4}\)

கேள்வி 6.
இரு பகடைகள் உருட்டப்படும் போது கிடைக்கும் எண்க ளின் கூடுதல்
(i) 1 இக்குச் சமமாக
(ii) இக்குச் சமமாக
(iii) 13-ஐ விடச் சிறியதாக
விடை:
S = {(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) …………. (6, 6)}
n(S) = 36
(i) எண்களின் கூடுதல் 1 இக்குச் சமமாக கிடைக்கும் நிகழ்தகவு. இது ஒரு இயலா நிகழ்ச்சி ஆகும்.
P(A) = 0

(ii) B என்பது எண்களின் கூடுதல் 4 இக்குச் சமமாகக் கிடைக்கும் நிகழ்ச்சி என்க.
B= {(1, 3) (2, 2) (3, 1)}
n(B) = 3
P(B) = \(\frac{n(B)}{n(S)}=\frac{3}{36}=\frac{1}{12}\)

(iii) C என்பது எண்க ளின் கூடுதல் 13 ஐ விடச் சிறியதாக கிடைக்கும் நிகழ்ச்சி என்க.
n(C) = 36
P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{36}{36}\) = 1

கேள்வி 7.
ஒர் உற்பத்தியாளர் 7000 ஒளி உமிழ் இருமுனைய (LED Lights) விளக்குகளை சோதனை செய்ததில் அவற்றில் 25 விளக்குகள் குறைபாடுடையதாகக் கண்டறியப்பட்டன. சமவாய்ப்பு முறையில் ஒரு விளக்கைத் தேர்ந்தெடுக்கும் போது அது குறைபாடுடையதாக இருக்க நிகழ்தகவு என்ன ?
விடை:
ஒளி உமிழ் இருமுனைய விளக்குகளின் எண்ணிக்கை n(S) = 7000
குறைபாடு உள்ளவை n(A) = 25
குறைபாடற்றவை = 6975
E என்பது குறைபாடுடையதாக இருக்கும் நிகழ்ச்சி என்க.
PE = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{25}{7000}=\frac{1}{280}\)

கேள்வி 8.
ஒரு கால்பந்தாட்டத்தில் ஓர் இலக்குக் காப்பாளரால் (Goal – Keeper) 40 இல் 32 முயற்சிகளைத் தடுக்க இயலும் எனில், எதிரணியானது ஒரு முயற்சியை இலக்காக மாற்றுவதற்கான நிகழ்தகவு காண்க.
விடை:
n(S) = 40
A என்பது எதிரணியானது ஒரு முயற்சியை இலக்காக மாற்றுவதற்கான நிகழ்ச்சி என்க.
n(A) = 8
n(S) = 40
P(E) = \(\frac{8}{40}=\frac{1}{5}\)

கேள்வி 9.
கொடுக்கப்பட்ட சுழலட்டையின் (Spinner) முள் 3 இன் மடங்குகளில் நிலை கொள்ளாமல் இருப்பதற்கான நிகழ்தகவு என்ன?
விடை:
n(S) = 8
A என்பது 3 இன் மடங்குகளில் நிலைகொள்ளும் நிகழ்ச்சி என்க.

A = {(3, 6)}
n(A) = 2
P(A) = \(\frac{2}{8}=\frac{1}{4}\)
\(\overline{\mathrm{A}}\) என்பது 3 இன் மடங்குகளில் நிலைகொள்ளாமல் இருப்பதற்கான நிகழ்ச்சி என்க.
\(\mathrm{P}(\overline{\mathrm{A}})\) = 1 – P(A)
= 1 – \(\frac{1}{4}=\frac{4-1}{4}\)
= \(\frac{3}{4}\)

கேள்வி 10.
கொடுக்கப்பட்ட சுழலட்டையை அடிப்படையாகக் கொண்டு நிகழ்தகவைக் கணக்கிடுமாறு எவையேனும் இரு வினாக்களை உருவாக்குக.
விடை:
n(S) = 8
A என்பது 2 இன் மடங்குகளில் நிலைகொள்ளும் நிகழ்ச்சி என்க.
A = {2, 4, 6, 8}
n(A) = 4
P(A) = \(\frac{4}{8}=\frac{1}{2}\)
\(\overline{\mathrm{A}}\) என்பது 2 இன் மடங்குகளில் நிலைகொள்ளாமல் இருப்பதற்கான நிகழ்ச்சி என்க.
\(\mathrm{P}(\overline{\mathrm{A}})\) = 1 – P(A)
= 1 – \(\frac{1}{2}=\frac{2-1}{2}\)
= \(\frac{1}{2}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 7 அளவியல் Ex 7.4 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 7 அளவியல் Ex 7.4

பலவுள் தெரிவு வினாக்கள்.

கேள்வி 1.
15செ.மீ., 20 செ.மீ. மற்றும் 25 செ.மீ. பக்க அளவுகள் கொண்ட ஒரு முக்கோணத்தின் அரைச்சுற்றளவு
(1) 60செ.மீ.
(2) 45செ.மீ.
(3) 30செ.மீ.
(4) 15 செ.மீ.
விடை:
(3) 30செ.மீ.

கேள்வி 2.
ஒரு முக்கோணத்தின் பக்க அளவுகள் 3 செ.மீ. 4செ.மீ. மற்றும் 5 செ.மீ. எனில் அதன் பரப்பளவு
(1) 3செ.மீ.²
(2) 6செ.மீ.²
(3) 9செ.மீ.²
(4) 12செ. மீ.²
விடை:
(2) 6செ.மீ.²

கேள்வி 3.
ஒரு சமபக்க முக்கோணத்தின் சுற்றளவு 30 செ.மீ. எனில், அதன் பரப்பளவு
(1) 10\(\sqrt{3}\) செ.மீ.²
(2) 12\(\sqrt{3}\) செ.மீ.²
(3) 15\(\sqrt{3}\) செ.மீ.²
(4) 25\(\sqrt{3}\) செ.மீ.²
விடை:
(4) 25\(\sqrt{3}\) செ.மீ.²

கேள்வி 4.
12 செ.மீ. பக்க அளவுள்ள ஒரு கனச்சதுரத்தின் பக்கப்பரப்பு
(1) 144செ.மீ.²
(2) 196செ.மீ.²
(3) 576செ.மீ.²
(4) 664செ.மீ.²
விடை:
(3) 576செ.மீ.²

கேள்வி 5.
ஒரு கனச்சதுரத்தின் பக்கப்பரப்பு 600செ.மீ.- எனில், அதன் மொத்தப்பரப்பு
(1) 150செ.மீ.²
(2) 400செ.மீ.²
(3) 900செ.மீ.²
(4) 1350செ.மீ.²
விடை:
(3) 900செ.மீ.²

கேள்வி 6.
10செ.மீ. × 6செ.மீ. × 5 செ.மீ. அளவுள்ள ஒரு கனச்செவ்வகப் பெட்டியின் மொத்தப்பரப்பு
(1) 280செ.மீ.²
(2) 300செ.மீ.²
(3) 360செ.மீ.²
(4) 600செ.மீ.²
விடை:
(1) 280செ.மீ.²

கேள்வி 7.
இரு கனச்சதுரங்களின் பக்கங்களின் விகிதமானது 2:3 எனில் அதன் புறப்பரப்புகளின் விகிதங்கள்
(1) 4 : 6
(2) 4 : 9
(3) 6 : 9
(4) 16 : 36
விடை:
(2) 4 : 9

கேள்வி 8.
ஒரு கனச்செவ்வகத்தின் கனஅளவு 660 செ.மீ.³ மற்றும் அதன் அடிப்பரப்பு 33செ.மீ.² எனில் அதன் உயரம்
(1) 10செ.மீ.
(2) 12செ.மீ.
(3) 20செ.மீ.
(4) 22செ.மீ.
விடை:
(3) 20செ.மீ.

கேள்வி 9.
10மீ. × 55மீ. × 1.5மீ. அளவுள்ள ஒரு நீர்த்தொட்டியின் கொள்ளளவு
(1) 75 லிட்டர்
(2) 750 லிட்டர்
(3) 7500 லிட்டர்
(4) 75000 லிட்டர்
விடை:
(4) 75000 லிட்டர்

கேள்வி 10.
5மீ × 3மீ × 2மீ. அளவுள்ள ஒரு சுவர் எழுப்ப, 50செ.மீ. × 30செ.மீ. × 20செ.மீ. அளவு கொண்ட செங்கற்கள் எத்தனை தேவை?
(1) 1000
(2) 2000
(3) 3000
(4) 5000
விடை:
(1) 1000

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 1 கண மொழி Ex 1.5 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 1 கண மொழி Ex 1.5

கேள்வி 1.
அருகில் உள்ள வென்படத்திலிருந்து கீழ்க்காணும் கணங்களைக் காண்க.
i) A – B
ii) B – C
iii) A|∪B|
iv) A|∪B|
v) (B∪C)
vi) A – (B∪C)
vii) A – (B∩C)

தீர்வு:
i) A – B = {3, 4, 6}
ii) B – C = {-1, 5, 7}
iii) A = U – A
= {1, 2, 4, 6, 3, -1, -2, 5, 7, 8, 0,-3} – {4, 6, 3,-1, -2} = {1, 2, 5, 7, 8, 0, -3}
= {-3, 0, 1, 2, 5, 7, 8}
B| = U – B
= U – {-1, -2, 5, 7, 8}
= {1, 2, 4, 6, 3, 0, -3}
iv) A|∪B| = {-3, 0, 1, 2, 3, 4, 5, 6, 7, 8}
v) A|∪B| = {-3, 0, 1, 2}
vi) B∪C = {-1, -2, 3, 0, -3, 5, 7, 8}
(B∪C) = ∪ – (B∪C)
= {1, 2, 4, 6}
vi) B∪C = {-1,- 2, 5, 7, 8, 3, -3, 0}
A-(B∪C) = {-1, -2,3,6,4} – {-1, -2, 5, 7, 8, 3, 0, -3)
A-(B∪C) = {6, 4}
vii) B∩C = {-2, -8}
A-(B∩C) = {-1, -2, 3, 6,4} – {-2, -8}
= {-1, 3, 6, 4}

கேள்வி 2.
K = {a, b, d, e, f}; L = {b,c,d, g} மற்றும் M = {a, b, c,d, h} என்ற கணங்க ளுக்குப் பங்கீடு விதிகளைக் சரிபார்க்க :
i) K∪(L∩M)
ii) K∩(L∪M)
iii) (K∪L)∩(K∪M)
iv) (K∩L)∪(K∩M)
விடை:
L∩M = {b, c, d}
i) K∪(L∩M) = {a, b, c, d, e, f }
L∪M = {a, b, c, d, g, h}
ii) K∩(L∪M) = {a, b, d}
K∪L = {a, b, c, d, e, f, g}
K∪M = {a, b, c, d, e, f, h}
iii) (K∪L) ∩(K∪M) = {a, b, c, d, e, f}
K∩L = {b, d}
K∩M = {a, b, d}
iv) (K∩L) ∪(K∩M) = {a, b, d}

கேள்வி 3.
A = {x : x ∈ Z, – 2 < x ≤ 4}, B = {x 😡 ∈ W, x ≤ 5}, மற்றும் C = {-4,-1, 0, 2, 3, 4} என்ற கணங்க ளுக்கு A∪(B∩C) = (A∪B)
∩(A∪C) என்பதைச் சரிபார்க்க.
விடை:
A = {-1, 0, 1, 2, 3, 4}, B = {0, 1, 2, 3, 4, 5}, C = {-4, -1, 0, 2, 3,4}
B∩C = {0, 2, 3, 4}
A∩(B∩C) = {-1, 0, 1, 2, 3, 4} …….. 1
A∪B = {-1, 0, 1, 2, 3, 4, 5}
A∪C = {-4, -1, 0, 1, 2, 3, 4}
(A∪B) (A∪C) = {-1, 0, 1, 2, 3, 4} ….. 2
1 மற்றும் 2 லிருந்து
A∪ (B∪C) = (A∪B)∩(A∪C)

கேள்வி 4.
வென் படங்களைப் பயன்படுத்தி A∪(B∪C) = (A∪B)) (A∪C) என்பதைச் சரிபார்க்க.
விடை:

கேள்வி 5.
A = {b, c, e, g, h} B = {a, c, d, g, i} மற்றும் C = {a, d, e, g, h} எனில், A – (B∩C ) = (A – B)∪(A – C) எனக்காட்டுக.
விடை:
B∩C = {a, d, g}
A – (B∩C) = {b, c, e, g, h} – {a, d, g}
= {b, c, e, h} … 1
A – B = {b,e, h}
A – C = {b, c}
(A – B)∪(A – C) = {b, c, e, h} … 2
சரிபார்க்கப்பட்டது
A – (B∩C) = (A – B)∪(A – C)

கேள்வி 6.
A = {x : x = 6n, n ∈ W மற்றும் n < 6}, B = {x : x = 2n, n ∈ N மற்றும் 2 < n ≤ 9}, மற்றும் C = {x : x = 3n, n ∈N மற்றும் 4 ≤ n < 10} எனில், A – (B∩C) = (A – B)∪(A – C) எனக் காட்டுக.
விடை:
A = {0, 6, 12, 18, 24, 30}
B = {6, 8, 10, 12, 14, 16, 18}
C = {12, 15, 18, 21, 24, 27}
B∩C = {12, 18}
A – (B∩C) = {0, 6, 24, 30} … 1
A – B = {0, 24, 30}
A – C = {0, 6, 30}
(A – B) ∪(A – C) = {0, 6, 24, 30} ….. 2
1 மற்றும் 2 லிருந்து
A – (B∪C) = (A – B)∩(A – C)

கேள்வி 7.
A = {-2, 0, 1, 3, 5}, B = {-1, 0, 2, 5, 6}, மற்றும் C = {-1, 2, 5, 6, 7} எனில், A – (B∪C) = (A – B)∩(A – C) எனக் காட்டுக.
விடை:
B∪C = {-1, 0, 2, 5, 6,7}
A – (B)∪C) = {-2, 0, 1, 3, 5} – {-1, 0, 2, 5, 6, 7}
= {-2, 1, 3} … 1
A – B = {-2, 1, 3}
A – C = {-2, 0, 1, 3}
(A – B) ∩ (A – C) = {-2, 1, 3} …….. 2
1 மற்றும் 2 லிருந்து
A – (B∪C) = (A – B) ∩ (A – C)

கேள்வி 8.

விடை:

1 மற்றும் 2 லிருந்து
A – (B) ∪ C) = (A – B) ∩ (A – C)

கேள்வி 9.
வென்படங்களைப் பயன்படுத்தி A – (B∩C) = (A – B) ∩ (A – C) என்பதைச் சரிபார்க்க.
விடை:

கேள்வி 10.
∪ = {4, 7, 8, 10, 11, 12, 15, 16}, A = {7, 8, 11, 12} மற்றும் B = {4, 8, 12, 15} எனில், கணநிரப்பிக்கான விதிகளைச் சரிபார்க்க. விடை:
A∪B = {4, 7, 8, 11, 12, 15}
A∩B = {8, 12}
(A∪B)^| = U – (A∪B)
= {10, 16}
(A∩B)^| = U – (A∩B)
= {4, 7, 10, 11, 15, 16}
A^| = U – A
= {4, 10, 15, 16}
B^| = {7, 10, 11, 16}
A^|∩B^| = {10, 16}
(A∪B)^| = A^|∩B^|
(A∩B)^| = {4, 7, 10, 11, 15, 16}
A^|∪B^| = {4, 7, 10, 11, 15, 16}
(A∩B)^| = A^|∪B^|

கேள்வி 11.
வென்படங்களைப் பயன்படுத்தி

விடை:

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 1 கண மொழி Ex 1.4 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 1 கண மொழி Ex 1.4

கேள்வி 1.
P = {1, 2, 5, 7, 9}, Q = {2, 3, 5, 9, 11}, R = {3, 4, 5, 7, 9} மற்றும் S = {2, 3, 4, 5, 8} எனில்,
i) (P∪Q)∪R
ii) (P∪Q)∪S
iii) (Q∩S)∩Rஆகியவற்றைக் காண்க.
விடை :
P = {1, 2, 5, 7, 9},
Q = {2, 3, 5, 9, 11},
R = {3, 4, 5, 7, 9},
S = {2, 3, 4, 5, 8}
P∪Q = {1, 2, 3, 5, 7, 9, 11}
(P∪Q) R = {1, 2, 3, 5, 7, 9, 11}∪{3, 4, 5, 7, 9}
= {1, 2, 3, 4, 5, 7, 9, 11}
P∩Q = {2, 5, 9}
(P∩Q)∩s = {2, 5, 9,} ∩ {2, 3, 4, 5, 8}
= {2, 5}
Q∩S = {2, 3, 5}
(Q∩S) ∩R = {2, 3, 5,}∩{3, 4, 5, 7, 9}
= {3, 5}

கேள்வி 2.
பின்வரும் கணங்களுக்குப் பரிமாற்றுப் பண்புகளைச் சோதிக்க. P = { x : x ஆனது 2 மற்றும் 7-க்கு இடையே உள்ள மெய்யெண்கள்} மற்றும் Q = {x : x ஆனது 2 மற்றும் 7 – க்கு இடையே உள்ள விகிதமுறா எண்கள்}
விடை :
P மற்றும் முடிவிலி கணங்கள் ஆகும். முடிவிலி கணங்களுக்கு சேர்ப்பு மற்றும் வெட்டுக்கான பரிமாற்றுப் பண்பு உண்டு.

கேள்வி 3.
A = {p, q, r, s}, B = {m, n, q, s, t}, மற்றும் C = {m, n, p, q, s} எனில், கணங்க ளின் சேர்ப்புக்கான சேர்ப்புப் பண்புகளைச்
சரிபார்க்க.
விடை:
A= {p, q, r, s}, B = {m, n, q, s, t},
C = {m, n, p, q, s}
B∪C = {m, n, q, p, s, t}
A∪(B∪C) = {r, p, q, s, }∪{m, n, q, p, s,t}
= {m, n, p, q, r, s, t} ……… 1
A∪B = {m, n, p, q, r, s, t}
(A∪B)∪C = {m, n, p, q, r, s, t}∪{m, n, p, q, s} …….. 2
= {m, n, p, q, r, s, t}
1 மற்றும் 2 லிருந்து.
(A∪B)∪C = A∪(B∪C)

கேள்வி 4.
A = {-11, \(\sqrt{2}\), \(\sqrt{5}\), \(\sqrt{7}\)}, B = {\(\sqrt{3}\), \(\sqrt{5}\), 6,13}, மற்றும் C = {\(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{5}\),9} ஆகியவற்றிற்குக் கணங்களின் வெட்டுக்கான சேர்ப்புப் பண்பினைச் சரிபார்க்க.
விடை:
B∩C = {\(\sqrt{3}\), \(\sqrt{5}\)}
A∩(B∩C) = {\(\sqrt{5}\)} …. 1
A∩B= {\(\sqrt{5}\)}
(A∩B)∩C = {\(\sqrt{5}\)} …. 2
1 மற்றும் 2 லிருந்து
A∩(B∩C) = (A∩B)∩C

கேள்வி 5.
A = {x : x = 2ⁿ, n ∈ W மற்றும் n < 4}, B = {x 😡 = 2n, n ∈ N மற்றும் n ≤ 4} மற்றும் C = {0, 1, 2, 5, 6} எனில், கணங்க ளின் வெட்டுக்கான சேர்ப்புப் பண்பினைச் சரிபார்க்க.
விடை:
A= {1, 2, 4, 8}, B = {2, 4, 6, 8},
C = {0, 1, 2, 5, 6}
B∩C = {2, 6}
A∩(B∩C) = {2} ……. 1
A∩B = {2, 4, 8}
(A∩B)∩C = 2} ……. 2
1 மற்றும் 2 லிருந்து
A∩(B∩C) = (A∩B)∩C

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 7 அளவியல் Ex 7.3 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 7 அளவியல் Ex 7.3

கேள்வி 1.
கீழ்க்கண்ட அளவுகளைக் கொண்ட கனச்செவ்வகத்தின் கனஅளவைக் காண்க.
(i) நீளம் = 12செ.மீ., அகலம் = 8செ.மீ., உயரம் = 6செ.மீ.
(ii) நீளம் = 60மீ., அகலம் = 25மீ., உயரம் = 1.5மீ.
விடை:
i) நீளம் = 12செ.மீ., அகலம் = 8செ.மீ., உயரம் = செ.மீ.
விடை:
l = 12செ.மீ., b = 8செ.மீ., h = 6செ.மீ.
கனச்செவ்வகத்தின் கனஅளவு = lbh க. அ.
= 12 × 8 × 6 செ.மீ.³
= 576 செ.மீ.³

ii) நீளம் = 60மீ., அகலம் = 25மீ., உயரம் = 1.5மீ.
விடை:
l = 60மீ., b = 25மீ., h = 1.5மீ.
கனச்செவ்வகத்தின் கனஅளவு = lbh க. அ.
= 60 × 25 × 1.5 மீ³
= 2250 மீ³

கேள்வி 2.
ஒரு தீப்பெட்டியின் அளவுகள் 6செ.மீ. × 3.5செ.மீ. × 2.5செ.மீ. என உள்ளது. இதே அளவுகளை உடைய 12 தீப்பெட்டிகள் கொண்ட ஒரு கட்டின் கனஅளவைக் காண்க.
விடை:
l = 6செ.மீ., b = 3.5செ.மீ., h = 2.5செ.மீ.
1 தீப்பெட்டியின் கனஅளவு = lbh க. அலகுகள்
= 6 × 2.5 × 3.5 செ.மீ.³
= 52.5 செ.மீ.³
12 தீப்பெட்டிகளின் கனஅளவு
= 52.5 செ.மீ.³ × 12
= 630 செ.மீ.³

கேள்வி 3.
ஒரு சாக்லேட் பெட்டியின் நீளம், அகலம் மற்றும் உயரம் முறையே 5:4:3 என்ற விகிதத்தில் உள்ளது. அதன் கனஅளவு 7500 செ.மீ.’ எனில், அதன் பக்க அளவுகளைக் காண்க.
விடை:
விகிதம் = 5 : 4 : 3
பெட்டியின் நீளம், அகலம் மற்றும் உயரம் முறையே 5x, 4x, 3x என்க.
பெட்டியின் கனஅளவு = lbh க. அலகுகள்
7500 = 5x × 4x × 3x
7500 = 60x³
60x³ = 7500
x³ = \(\frac{7500}{60}\)
x³ = \(\frac{750}{6}\)
x³ = 125
x = \(\sqrt [ 3 ]{ 125 }\)
x = 5
நீளம் = 5x = 5 × 5 = 25 செ.மீ.
அகலம் = 4x = 4 × 5 = 20 செ.மீ.
உயரம் = 3x = 3 × 5 = 15 செ.மீ.

கேள்வி 4.
ஒரு குளத்தின் நீளம், அகலம் மற்றும் ஆழம் முறையே 20.5மீ , 16மீ மற்றும் 8மீ எனில், அந்தக் குளத்தின் கொள்ளளவை லிட்டரில் காண்க.
விடை:
l = 20.5மீ., b = 16மீ., h = 8மீ.
குளத்தின் கொள்ளளவு = lbh க. அலகுகள்
= 20.5 × 16 × 8மீ.³
= 2624மீ.³
1மீ³ = 1000 லி.
= 2624000 லி.

கேள்வி 5.
ஒரு செங்கல்லின் அளவுகள் 24செ.மீ × 12செ.மீ x8செ.மீ ஆகும். 20 மீ நீளம், 48செ.மீ. அகலம் மற்றும் 6மீ உயரமுள்ள ஒரு சுவர் எழுப்புவதற்கு இது போன்ற எத்தனை செங்கற்கள் தேவை?
விடை:
l = 24செ.மீ, b = 12செ.மீ, h = 8செ.மீ
செங்கல்லின் கனஅளவு = lbh க. அலகுகள்
= 24 × 12 × 8 செ.மீ³
= 2304 செ.மீ³
கனச்செவ்வக சுவரின் கனஅளவு = lbh க. அ.
= 2000 × 48 × 600 செ.மீ³
= 57600000 செ.மீ³
தேவையான செங்கற்கள் = \(\frac{57600000}{2304}\)
= \(\frac{6400000}{2}\)
= \(\frac{800000}{2}\)
= \(\frac{100000}{2}\)
= 25000

கேள்வி 6.
ஒரு கொள்கலனின் (Container) கனஅளவு 1440மீ’ அதன் நீளம் மற்றும் அகலம் முறையே 15மீ மற்றும் 8மீ எனில் அதன் உயரத்தைக் காண்க.
விடை:
கனஅளவு = 1440மீ’, l = 15மீ³, b = 8மீ, h = ?
கொள்கலனின் கனஅளவு = lbh க. அலகுகள்
1440 = 15 × 8 × h
h = \(\frac{1440}{15 \times 8}\)
h = \(\frac{1440}{120}\)
h = 12
உயரம் = 12மீ

கேள்வி 7.
பின்வரும் பக்க அளவைக் கொண்ட கனச்சதுரத்தின் கனஅளவைக் காண்க.
(i) 5செ .மீ.
(ii) 3.5மீ.
(iii) 21 செ.மீ.
விடை:
i) a = 5செ.மீ.
கனச்சதுரத்தின் கனஅளவு = a³க. அலகுகள்
= 5 × 5 × 5 செ.மீ³
= 125 செ.மீ³

ii) a = 3.5 மீ.
கனச்சதுரத்தின் கனஅளவு = a³க. அலகுகள்
= 3.5 × 3.5 × 3.5 மீ³
= 42.875 மீ³

iii) a = 21செ .மீ.
கனச்சதுரத்தின் கனஅளவு = a³க. அலகுகள்
= 21 × 21 × 21 செ.மீ³
= 9261 செ.மீ³

கேள்வி 8.
ஒரு கனச்சதுர வடிவிலான பால் தொட்டியானது 1,25,000 லிட்டர் கொள்ளளவைக் கொண்டுள்ளது. அத்தொட்டியின் பக்கநீளத்தை மீட்டரில் காண்க.
விடை:
கனச்சதுர வடிவ தொட்டியின் நீளம் a என்க.
தொட்டியின் கொள்ளளவு = 125000 லிட்டர்
a³ = 125000
a³ = \(\frac{125000}{1000}\) (10000லி = 1மீ³)
a³ = 125மீ³
a =\(\sqrt[3]{125}\)
a = 5மீ
கனச்சதுர தொட்டியின் பக்கநீளம் = 5மீ

கேள்வி 9.
15 செ.மீ. பக்க அளவுள்ள ஒர் உலோகத்தால் ஆன கனச்சதுரமானது உருக்கப்பட்டு ஒரு கனச்செவ்வகமாக உருவாக்கப்படுகிறது. கனச்செவ்வகத்தின் நீளம் மற்றும் உயரம் முறையே 25செ.மீ. மற்றும் 9 செ.மீ. எனில் அதன் அகலத்தைக் காண்க.
விடை:
a = 15செ.மீ., l = 25செ.மீ., h = 9செ.மீ.
கனச்செவ்வகத்தின் கனஅளவு = கனச்சதுரத்தின் கனஅளவு
lbh = a³
25 × b × 9 = 15 × 15 × 15
b = \(\frac{15\times 15 \times 15}{25 \times 9}\)
b = 15செ.மீ.
கனச்செவ்வகத்தின் அகலம் = 15செ.மீ.

Tamilnadu State Board New Syllabus Samacheer Kalvi 4th Maths Guide Pdf Term 3 Chapter 2 எண்கள் Ex 2.6 Textbook Questions and Answers, Notes.

TN Board 4th Maths Solutions Term 3 Chapter 2 எண்கள் Ex 2.6

பின்வரும் கணக்குகளை 10, 100 இன் மடங்குகளைப் பயன்படுத்திக் கூட்டுக மற்றும் கழிக்க (மனதால்)

கேள்வி 1.
745 + 40 = ________
தீர்வு:
785

கேள்வி 2.
328 + 30 = ________
தீர்வு:
358

கேள்வி 3.
566 + 20 = ________
தீர்வு:
586

கேள்வி 4.
475 + 100 = ________
தீர்வு:
575

கேள்வி 5.
686 + 300 = ________
தீர்வு:
986

கேள்வி 6.
345 + 600 = _______
தீர்வு:
945

கேள்வி 7.
6348 – 10 = ______
தீர்வு:
6338

கேள்வி 8.
541 – 40 = _________
தீர்வு:
501

கேள்வி 9.
495 – 300 = ________
தீர்வு:
195

கேள்வி 10.
657 – 500 = ________
தீர்வு:
157

கேள்வி 11.
895 – 500 = ______
தீர்வு:
395

கேள்வி 12.
365 – 300 = ________
தீர்வு:
65

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 7 அளவியல் Ex 7.2 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 7 அளவியல் Ex 7.2

கேள்வி 1.
பின்வரும் அளவுகளைக் கொண்ட கனச் செவ்வகத்தின் மொத்தப்பரப்பு மற்றும் பக்கப் பரப்பைக் காண்க.
i) நீளம் = 20செ.மீ. அகலம் = 15செ.மீ. உயரம் = 8செ.மீ.
ii) நீளம் = 20 செ.மீ. அகலம் = 15 செ.மீ. உயரம் = 8 செ.மீ.
விடை:
l = 20செ.மீ., b = 15செ.மீ., h = 8செ.மீ.
மொத்தப்பரப்பு = 2 (lb + bh + lh) ச. அ.
= 2 (20 × 15 + 15 × 8 + 8 × 20) செ.மீ.²
= 2 (300 + 120 + 160) செ.மீ..
= 2 (580) செ.மீ.²
= 1160 செ.மீ.²
பக்கப்பரப்பு = 2 (l + b) × h ச. அலகுகள்
= 2 (20 + 15) × 8 செ.மீ.²
= 2 (35) × 8 செ.மீ.²
= 70 × 8 செ.மீ.²
= 560 செ.மீ.²

கேள்வி 2.
ஒரு கனச் செவ்வக வடிவப் பெட்டியின் அளவுகளானது 6மீ x 400செ.மீ. x 1.5மீ ஆகும். அப்பெட்டியின் வெளிப்புறம் முழுவதும் வண்ண ம் பூசுவதற்கு 1 சதுர மீட்டருக்கு ₹22 வீதம் ஆகும் எனில், மொத்தச் செலவைக் காண்க.
விடை:
l = 6மீ, b = 4மீ, h = 1.5மீ.
கனச் செவ்வகப் பெட்டியின் மொத்தப் பரப்பு
= 2 (lb + bh + lh) ச. அலகுகள்
= 2 (6 × 4 + 4 × 1.5 + 1.5 × 6) மீ²
= 2 (24 + 6 + 9) மீ²
= 2 (39) மீ²
= 78 மீ²
1மீ² வண்ண ம் பூச ஆகும் செலவு = ரூ. 22
78 ச.மீ. வண்ண ம் பூச ஆகும் செலவு
= ரூ.22 × 78
= ரூ. 1716.

கேள்வி 3.
ஒரு கூடத்தின் அளவு 10மீ x 9மீ x 8e என்றவாறு உள்ளது. அக்கூடத்தின் சுவர்கள் மற்றும் மேற்கூரைக்கு வெள்ளையடிக்க ஒரு சதுர மீட்டருக்கு 78.50 வீதம் ஆகும் மொத்தச் செலவைக் காண்க.
விடை:
l = 10மீ, b = 9மீ, h = 8மீ
நான்கு சுவர்களின் பரப்பளவு =
கனச்செவ்வகத்தின் பக்கப் பரப்பு
= 2 (l + b) × h ச. அலகுகள்
= 2 (10 + 9) × 8 மீ²
= 2 (19) × 8 மீ²
= 38 × 8 மீ²
= 304 மீ²
மேற்கூரையின் பரப்பளவு = l × b ச. அ.
= 10 × 9 மீ.²
= 90 மீ²
வெள்ளை அடிக்க வேண்டிய மொத்தப் பரப்பளவு
= நான்கு சுவர்களின் பரப்பளவு + மேற்கூரையின் பரப்பளவு
= (304 + 90) மீ²
= 394 மீ²
1 ச.மீ. வெள்ளை அடிக்க ஆகும் செலவு= ரூ.8.50
394 ச.மீ. வெள்ளை அடிக்க ஆகும் செலவு
= ரூ. 8.50 × 394
= ரூ.3349

கேள்வி 4.
கீழ்க்காணும் பக்க அளவைக் கொண்ட கனச் சதுரங்களின் மொத்தப்பரப்பு மற்றும் பக்கப் பரப்பைக் காண்க.
(i) 8மீ
(ii) 21செ. மீ.
(iii) 7.5 செ.மீ.
விடை:
a = 8மீ
மொத்தப் பரப்பு = 6a² ச. அலகுகள்
= 6 × (8) மீ²
= 6 × 64 மீ²
= 384 மீ²
பக்கப்பரப்பு = 4a² ச. அலகுகள்
= 4 × (8)² மீ²
= 4 × 64 மீ²
= 256 மீ²

ii) a = 21செ.மீ.
மொத்தப் பரப்பு = 6a ச. அலகுகள்
= 6 × (21) செ.மீ.²
= 6 × 441 செ.மீ.²
= 2646 செ.மீ.²
பக்கப் பரப்பு = 4a² ச. அலகுகள்
= 4 × (21) செ.மீ.²
= 4 × 441 செ.மீ.²
= 1764 செ.மீ.²

iii) a = 7.5செ.மீ.
மொத்தப் பரப்பு = 6a² ச. அலகுகள்
= 6 × (7.5) செ.மீ.²
= 6 × 56.25 செ.மீ.²
= 337.5 செ.மீ.²
பக்கப் பரப்பு = 4a ச. அலகுகள்
= 4 × (7.5) செ.மீ.²
= 4 × 56.25 செ.மீ.²
= 225.00 செ.மீ.²
= 225 செ.மீ.²

கேள்வி 5.
ஒரு கனச்சதுரத்தின் மொத்தப்பரப்பு 2400செ.மீ.² எனில் அதன் பக்கப் பரப்பைக் காண்க.
விடை:
கனச்சதுரத்தின் மொத்தப் பரப்பு = 2400 செ.மீ.²
6a² = 2400
a² = \(\frac{2400}{6}\)
a² = 400 செ.மீ.²
= 20 செ.மீ.
பக்கப்பரப்பு = 4a² ச. அலகுகள்
= 4 × (20)² செ.மீ.²
= 4 × 400 செ.மீ.²
= 1600 செ.மீ.²

கேள்வி 6.
5மீ. பக்க அளவுள்ள ஒரு கனச்சதுரக் கொள்கலனின் மேற்புரம் முழுவதும் வண்ணம் பூசப்படுகிறது. இதற்கு வண்ணம் பூச வேண்டிய பரப்பு மற்றும் 1 சதுர மீட்டருக்கு ₹24 வீதம் வண்ண ம் பூச ஆகும் மொத்தச் செலவு ஆகியவற்றைக் காண்க.
விடை:
a = 6.5 மீ கனச்சதுரக் கொள்கலனின் மொத்தப் பரப்பு
= 6a² ச. அலகுகள்
= 6 × (6.5) மீ²
= 6 × 42.25 மீ²
= 253.5 மீ²
1சமீ வண்ண ம் பூச ஆகும் செலவு = ரூ. 24
253.5 ச.மீ. வண்ண ம் பூச ஆகும் செலவு
= ரூ. 24 × 253.5
= ரூ. 6084

கேள்வி 7.
4 செ.மீ. பக்க அளவு உடைய ஒரே மாதிரியான மூன்று கனச்சதுரங்கள் ஒன்றோடு ஒன்று பக்கவாட்டில் இணைக்கப்படும் போது கிடைக்கும் புதிய கனச்செவ்வகத்தின் மொத்தப் பரப்பு மற்றும் பக்கப் பரப்பு ஆகியவற்றைக் காண்க.
விடை:
a = 4 செ.மீ.
புதிய கனச்செவ்வகத்தின் நீளம் = 4 + 4 + 4 செ.மீ.
= 12 செ.மீ.
l = 12 செ.மீ., b = 4 செ.மீ., h = 4 செ.மீ.
மொத்தப் பரப்பு = 2 (lb + bh + Ih) ச. அ.
= 2 (12 × 4 + 4 × 4 + 4 × 12) செ.மீ.²
= 2 (48 + 16 + 48) செ.மீ.²
= 2 (112) செ.மீ.²
= 224 செ.மீ.²
பக்கப் பரப்பு = 2 (l + b) × h ச. அலகுகள்
= 2 (12 +4) × 4 செ.மீ.²
= 2 (16) × 4 செ.மீ.²
= 32 × 4 செ.மீ.²
= 128 செ.மீ.²

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 1 கண மொழி Ex 1.3 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 1 கண மொழி Ex 1.3

கேள்வி 1.
கொடுக்கப்பட்ட வெண்படத்தில் இருந்து கீழேயுள்ள கணங்களின் உறுப்புகளை எழுதுக.

(i) A
விடை:
(i) A ={ 2, 4, 7, 8, 10}

(ii) B.
விடை:
B = {3, 4, 6, 7, 9, 11}

(iii) A∪B
விடை:
A∪B={2, 3, 4, 6, 7, 8, 9, 10, 11}

(iv) A∩B
விடை:
A∩B = {4, 7}

(v) A – B
விடை:
A – B = {2, 8, 10}

(vi) B – A
விடை:
B – A = {3, 6, 9, 11}

(vii) A’
விடை:
A’ = U – A
A’ = {1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12} – {2, 4, 7, 8, 10}
= {1, 3, 6, 9, 11, 12}

(viii) B’
விடை:
B’ = U – B
= {1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12} – {3, 4, 6, 7, 9, 11}
= {1, 2, 8, 10, 12}

(ix) U
விடை:
U = {1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12}

கேள்வி 2.
பின்வரும் கணங்களுக்கு A∪B, A∩B, A – B, மற்றும் B – A காண்க
(i) A = {2, 6, 10, 14} மற்றும் B = {2, 5, 14, 16}
விடை:
A = {2, 6, 10, 14}
B = {2, 5, 14, 16}
A∪B = {2, 5, 6, 10, 14, 16}
A∩B = {2, 14}
A – B = {6, 10}
B – A = {5, 16}

(ii) A = {a, b, c, e, u} மற்றும் B = {a, e, i, o, u}
விடை:
A = {a, b, c, e, u} B = {a, e, i, o, u}
A∪B = {a, b, c, e, i, o, u}
A∩B ={a, e, u}
A – B = {b, c}
B – A = {i, o}

(iii) A ={x : x ∈ N, x ≤ 10} மற்றும் B = {x : x ∈ W, x < 6}
விடை:
A ={x : x ∈ N, x ≤ 10} A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B = {x : x ∈ W, x < 6}
B = {0, 1, 2, 3, 4, 5)
A∪B = {0, 1, 2, …,10
A∩B = {1, 2, 3, 4, 5)
A – B = {6, 7, 8, 9, 10}
B – A= {0}

(iv) A = ‘mathematics’ என்ற சொல்லில் உள்ள எழுத்துகளின் கணம் B = ‘geometry’ என்ற சொல்லில் உள்ள எழுத்துகளின் கணம் விடை:
A = {m, a, t, h, e, i, c, s}
B = {g, e, 0, m, t, r, y}
A∪B = {m, a, t, h, e, i, c, s, g, 0, r, y}
A∩B = {t, m, e}
A – B = {a, h, i, c, s}
B – A = {g, 0, r, y}

கேள்வி 3.

(i) A’
விடை:
A’ = U – A
= {a, c, e, g}

(ii) B’
விடை:
B’ = U – B
= {b, c, f, g}

(iii) A’∪B’
விடை:
A’ ∪B’ = {a, b, c, e, f, g}

(iv) A’∩B’
விடை:
A’∩B’ = {c, g}
A∩B = {a, b, d, e, f, h}
A∪B = {a, b, d, e, f, h}
(A∪B)’ = U – (A∪B)
= {c, g}
A∩B = {d, h}
(A∩B)’ = U – (A∩B)
(A∩B)’ = {a, b, c, e, f, g}

(v) (A∪B)’
விடை:
A∪B = {0, 1, 2, 3, 5, 7}
(A∪B)’ = U – (A∪B)
= {4, 6}
A∩B = {3, 5, 7}

(vi) (A∩B)’
விடை:
(A∩B)’ = U – (A∩B)
= {0, 1, 2, 4, 6}

(vii) (A’)’
விடை:
(A’)’ = A = U – (A’)
= {1, 3, 5, 7}

(viii) (B’)’
விடை:
(B’)’ = U = (B’) = B = {0, 2, 3, 5, 7}

கேள்வி 4.

விடை:
(i) A’ = U – A = {0, 2, 4, 6}

(ii) B’ = {1, 4, 6}

(iii) A’UB’={0, 1, 2, 4, 6}

(iv) A’∩B’ = {4, 6}

(v) (AUB)’ = {U – (AUB)}
AUB = {0, 1, 2, 3,5,7}
(AUB)’ = U – (AUB)
= {4, 6}
A∩B = {3, 5, 7}

(vi) (A∩B)’= U – (A ∩ B)
= {0, 1, 2, 4, 6} 

(vii) (A’)’ = A = U – (A’)
= {1, 3, 5, 7}  

(viii) (B’) = U – (B’) = B = {0, 2, 3, 5, 7}

கேள்வி 5.
கொடுக்கப்பட்ட கணங்களின் சமச்சீர் வித்தியாசம் காண்க.
(i) P = {2, 3, 5, 7, 11} மற்றும் Q ={1, 3, 5, 11}
விடை:
P = {2, 3, 5, 7, 11}
Q = {1, 3, 5, 11}
P – Q = {2, 7}
Q – P = {1}
P∆Q = (p – Q) ∪(Q – P)
= {1, 2, 7}

(ii) R = {l, m, n, o, p} மற்றும் S = {j, l, n, q}
விடை:
R = {l, m, n, 0, p}
S = {j, l, n, q}
R – S = {m, 0, p}
S – R = {j, q}
R∆S = (R – S) ∪ (S – R)= {m, 0, p, j,q}

(iii) X = {5, 6, 7} மற்றும் Y ={5, 7, 9, 10}
விடை:
X = {5, 6, 7}
Y = {5, 7, 9, 10}
X – Y = {6}
Y – X = {9, 10}
X∆Y =(6, 9, 10)

கேள்வி 6.
கணக் குறியீடுகளைக் கொண்டு பின்வரும் நிழலிட்ட பகுதியினைக் குறிப்பிடவும்.

விடை:
(i) B – A
(ii) (A∪B)’
(iii) (A – B) ∪(B – A)

கேள்வி 7.
A, B என்பன வெட்டுக்கணங்கள் மற்றும் U என்பது அனைத்துக் கணம் எனில், பின்வருவனவற்றை வெண்படத்தில் குறிக்கவும்.
(i) A∪B
(ii) A∩B
(iii) (A∩B)’
(iv) (B – A)’
(V) A’∪B’
(vi) A’∩B’
(vii) வென்படம் (iii) மற்றும் (v) ஐ உற்றுநோக்கி உன்னுடைய கருத்தை எழுதுக.
விடை:

(vii) (A∩ B)’ = A’∪B’
நினைவு கூர்வதற்கான கருத்துகள்
A மற்றும் B எனும் எவையேனும் இரு முடிவுறு கணங்களில்
(i) n(A∪B) = n(A) + n(B) – n(A∩B)
(ii) n(A∩B) = n(A) + n(B) – n(A∪B)
(iii) n(A – B) = n(A) – (A∩B)
(iv) n(B – A) = n(B) – n(A∩B)
(v) n(U) = n(A) + n(A’)
(vi) n(A’) = n(∪) – n(A)
(vii) A மற்றும் B என்பன வெட்டாக்கணங்கள் எனில் n(A∪B) = n(A) + n(B)

Tamilnadu State Board New Syllabus Samacheer Kalvi 4th Maths Guide Pdf Term 3 Chapter 2 எண்கள் Ex 2.5 Textbook Questions and Answers, Notes.

TN Board 4th Maths Solutions Term 3 Chapter 2 எண்கள் Ex 2.5

மதிப்பிட்டுக் கணக்கிடுக.:

தீர்வு: