Prasanna

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 7 Mensuration Ex 7.4

Multiple Choice Questions:

Question 1.
The semi-perimeter of a triangle having sides 15 cm, 20 cm and 25 cm is
(1) 60 cm
(2) 45 cm
(3) 30 cm
(4) 15 cm
Solution:
(3) 30 cm


Question 2.
If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
(1) 3 cm²
(2) 6 cm²
(3) 9 cm²
(4) 12 cm²

Solution:
(2) 6 cm²

Question 3.
The perimeter of an equilateral triangle is 30 cm. The area is
(1) \(10 \sqrt{3}\) cm²
(2) \(12 \sqrt{3}\) cm²
(3) \(15 \sqrt{3}\) cm²
(4) \(25 \sqrt{3}\) cm²
Solution:
3a = 30
a = 10 cm

Solution:
(4) \(25 \sqrt{3}\) cm²

Question 4.
The lateral surface area of a cube of side 12 cm is
(1) 144 cm²
(2) 196 cm²
(3) 576 cm²
(4) 664 cm²
Hint: 4a² = 4 × 12 × 12 = 4 × 144 = 576 cm²
Solution:
(3) 576 cm²

Question 5.
If the lateral surface area of a cube is 600 cm², then the total surface area is
(1) 150 cm²
(2) 400 cm²
(3) 900 cm²
(4) 1350 cm²
Hint:
4a² = 600 cm²

Solution:
(3) 900 cm²

Question 6.
The total surface area of a cuboid with dimension 10 cm × 6 cm × 5 cm is
(1) 280 cm²
(2) 300 cm²
(3) 360 cm²
(4) 600 cm²
Hint:
TSA = 2 (lb + bh + hl)
= 2 (10 × 6 + 6 × 5 + 5 × 10) = 2 (60 + 30 + 50) = 2 (140) = 280 cm²
Solution:
(1) 280 cm²

Question 7.
If the ratio of the sides of two cubes are 2 : 3, then ratio of their surface areas will be
(1) 4 : 6
(2) 4 : 9
(3) 6 : 9
(4) 16 : 36
Hint:
a : b = 2 : 3
4a² : 4b² = 4 × 2² : 4 : 3²
⇒ 16 : 36
⇒ 4 : 9
Solution:
(2) 4 : 9

Question 8.
The volume of a cuboid is 660 cm3 and the area of the base is 33 cm². Its height is
(1) 10 cm
(2) 12 cm
(3) 20 cm
(4) 22 cm
Hint:
V = 660 cm³
lb = 33 cm²
h = ?
lbh = 660

Solution:
(3) 20 cm

Question 9.
The capacity of a water tank of dimensions 10 m × 5 m × 1.5 m is
(1) 75 litres
(2) 750 litres
(3) 7500 litres
(4) 75000 litres
Hint: Volume of cuboid = l × b × h
Solution:
(4) 75000 litres

Question 10.
The number of bricks each measuring 50 cm × 30 cm × 20 cm that will be required to build a wall whose dimensions are 5m × 3m × 2m is
(1) 1000
(2) 2000
(3) 3000
(4) 5000
Hint:

Solution:
(1) 1000

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.3

Question 1.
Represent the following irrational numbers on the number line.
(i) \(\sqrt { 3}\)
(ii) \(\sqrt { 4.7 }\)
(iii) \(\sqrt { 6.5 }\)
Solution:
(i) \(\sqrt { 3}\)

(i) Draw a line and mark a point A on it.
(ii) Mark a point B such that AB = 3 cm.
(iii) Mark a point C on this line such that BC = 1 unit.
(iv) Find the midpoint of AC by drawing perpendicular bisector of AC and let it be O.
(v) With O as center and OC = OA as radius, draw a semicircle.
(vi) Draw a line BD, which is perpendicular to AB at B.
(vii) Now BD = \(\sqrt { 3}\), which can be marked in the number line as the value of BE = BD = \(\sqrt { 3}\)

(ii) \(\sqrt { 4.7 }\)

(i) Draw a line and mark a point A on it.
(ii) Mark a point B such that AB = 4.7 cm.
(iii) Mark a point C on this line such that BC = 1 unit.
(iv) Find the midpoint of AC by drawing perpendicular bisector of AC and let it be O.
(v) With O as center and OC = OA as radius, draw a semicircle.
(vi) Draw a line BD, which is perpendicular to AB at B.
(vii) Now BD = \(\sqrt { 4.7 }\), which can be marked in the number line as the value of BE = BD = \(\sqrt { 4.7 }\)

(iii) \(\sqrt { 6.5 }\)

(i) Draw a line and mark a point A on it.
(ii) Mark a point B such that AB = 6.5 cm.
(iii) Mark a point C on this line such that BC = 1 unit.
(iv) Find the midpoint of AC by drawing perpendicular bisector of AC and let it be O.
(v) With O as center and OC = OA as radius, draw a semicircle.
(vi) Draw a line BD, which is perpendicular to AB at B.
(vii) Now BD = \(\sqrt { 6.5 }\), which can be marked in the number line as the value of BE = BD = \(\sqrt { 6.5 }\).

Question 2.
Find any two irrational numbers between
(i) 0.3010011000111…. and 0.3020020002….
(ii) \(\frac { 6 }{ 7 }\) and \(\frac { 12 }{ 13 }\)
(iii) \(\sqrt { 2}\) and \(\sqrt { 3}\)
Solution:
(i) 0.3010011000111…. and 0.3020020002….
Two irrational numbers 0.301202200222 …., 0.301303300333…..

(ii) \(\frac { 6 }{ 7 }\) and \(\frac { 12 }{ 13 }\)
\(\frac { 6 }{ 7 }\) = 0.857142…
\(\frac { 12 }{ 13 }\) = 0.923076
Two irrational numbers between 0.8616611666111……, 0.8717711777111…..

(iii) \(\sqrt { 2}\) and \(\sqrt { 3}\)

\(\sqrt { 2 }\)= 1.414……

\(\sqrt { 3}\) = 1.732….
∴ Two irrational numbers between 1.5155…., 1.6166…….

Question 3.
Find any two rational numbers between 2.2360679….. and 2.236505500….
Solution:
Any two rational numbers are 2.2362, 2.2363

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.4

Multiple Choice Questions

Question 1.
Let m be the mid point and b be the upper limit of a class in a continuous frequency distribution. The lower limit of the class is
(1) 2 m – b
(2) 2m + b
(3) m – b
(4) m – 2b
Solution:
(1) 2m – b

Question 2.
The mean of a set of seven numbers is 81. If one of the numbers is discarded, the mean of the remaining numbers is 78 . The value of discarded number is
(1) 101
(2) 100
(3) 99
(4) 98
Solution:
Hint:

∴ The discarded number = 567 – 41 = 99
Solution:
(3) 99

Question 3.
A particular observation which occurs maximum number of times in a given data is called its

(1) Frequency
(2) range
(3) mode
(4) Median
Solution:
(3) mode

Question 4.
For which set of numbers do the mean, median and mode all have the same values?
(1) 2, 2, 2, 4
(2) 1, 3, 3, 3, 5
(3) 1, 1, 2, 5, 6
(4) 1, 1, 2, 1, 5
Hint:

Median = 3
Mode = 3
Solution:
(2) 1, 3, 3, 3, 5

Question 5.
The algebraic sum of the deviations of a set of n values from their mean is
(1) 0
(2) n – 1
(3) n
(4) n + 1
Solution:
(1) 0

Question 6.
The mean of a, b, c, d and e is 28 . If the mean of a, c and e is 24, then mean of b and d is
(1) 24
(2) 36
(3) 26
(4) 34
Hint:

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Additional Questions

Text Book Activities

Question 1.
Discuss and give as many examples of collections from your daily life situations, which are sets and which are not sets.
Solution:
Which are sets

1. Collection of pen
2. Collection of dolls
3. Collection of books
4. Collection of red flower etc.

Which are not sets

1. Collection of good students in a class.
2. Collection of beautiful flowers in a garden etc.

Question 2.
Write the following sets in respective forms.
Solution:

Question 3.
Fill in the blanks with appropriate cardinal numbers.
Solution:

Additional Questions and Answers

Exercise 1.1

Question 1.
Let A = {0, 1, 2, 3, 4, 5}. Insert the appropriate symbol G or g in the blank spaces,
(i) 0 ___ A
(ii) 6 ___ A
(iii) 3 ___ A
(iv) 4 ____ A
(v) 7 ____ A
Solution:
(i) 0 ∈ A
(ii) 6 ∉ A
(iii) 3 ∈ A
(iv) 4 ∈ A
(v) 7 ∉ A

Question 2.
Write the following in Set-Builder form.
(i) The set of all positive even numbers.
(ii) The set of all whole numbers less than 20.
(iii) The set of all positive integers which are multiple of 3.
(iv) The set of all odd natural numbers less than 15.
(v) The set of all letters in the word ‘computer’.
Solution:
(i) A = {x : x is a positive even number}
(ii) B = {x : x is a whole number and x < 20}
(iii) C = {x : x is a positive integer and multiple of 3}
(iv) D = {x : x is an odd natural number and x < 15}
(v) E = {x : x is a letter in the word “Computer”}

Question 3.
Write the following sets in Roster form.
(i) A = {x : x ∈ N, 2< x < 10 }
(ii) B = {x : x ∈ Z, –\(\frac { 1 }{ 2 }\) < x < \(\frac { 11 }{ 2 }\) }
(iii) C = {x : x is a prime number and a divisor of 6 }
(iv) x = {x : x = 2ⁿ, it n ∈ N and n ≤ 5}
(v) M = {x : x = 2y – 1, y ≤ 5, j ∈ W}
Solution:
(i) A = {3,4, 5, 6, 7, 8, 9}
(ii) B = {0, 1, 2, 3, 4, 5}
(iii) C = {2, 3}
(iv) Given, x = 2ⁿ, n ∈ N and n ≤ 5.
Here n = 1, 2, 3, 4, 5
n = 1 ⇒ 21 = 2
n = 2 ⇒ 22 = 4
n = 3 ⇒ 23 = 8
n = 4 ⇒ 24 = 16
n = 5 ⇒ 25 = 32
X = {2, 4, 8, 16, 32}

(v) Given, x = 2y – 1, y ≤ 5 and y ∈ W Here j = 0, 1,2, 3, 4, 5
y = 0 ⇒ x = 2 (0) – 1 = -1
y = 1 ⇒ x = 2 (1) – 1 = 2 – 1 = 1
y = 2 ⇒ x = 2 (2) – 1 = 4 – 1 = 3
y = 3 ⇒ x = 2 (3) – 1 = 6 – 1 = 5
y = 4 ⇒ x = 2 (4) – 1 = 8 – 1 = 7
y = 5 ⇒ x = 2 (5) – 1 = 10 – 1= 9
M = {-1, 1, 3, 5, 7, 9}

Exercise 1.2

Question 1.
Find the number of subsets and number of proper subsets of a set X = {a, b, c, x, y, z}.
Solution:
Given X = {a, b, c, x, y, z}.
Then, n(X) = 6
The number of subsets = n[P(X)] = 2⁶ = 64
The number of proper subsets = n[P(X)] – 1 = 2⁶ – 1 = 64 – 1 = 63

Question 2.
Find the cardinal number of the following sets.
(i) A = {x : x is a prime factor of 12}.
(ii) B = {x : x ∈ W, x ≤ 5}.
(iii) X = {x : x is an even prime number}
Solution:
(i) Factors of 12 are 1, 2, 3, 4, 6, 12. So, the prime factors of 12 are 2,3.
We write the set A in roster form as A = {2, 3} and hence n(A) = 2.
(ii) In Tabular form B = {0, 1, 2, 3, 4, 5}
The set B has six elements and hence n(B) = 6
(iii) X = {2} [2 is the only even prime number]
∴ n (X) = 1

Question 3.
State whether the following sets are finite or infinite.
(i) A = {x : x is a multiple of 5, x ∈ N}.
(ii) B = {0,1, 2, 3, 4, 75}.
(iii) The set of all positive integers greater than 50.
Solution:
(i) A = {5, 10, 15, 20, …… } ∴A is an infinite set
(ii) Finite
(iii) Let X be the set of all positive integers greater than 50
Then X= (51, 52, 53, ….. }
∴ X is an infinite set.

Question 4.
Which of the following sets are equal?
(i) A = (1, 2, 3, 4}, B = {4, 3, 2, 1}
(ii) A = (4, 8, 12, 16}, B = (8, 4, 16, 18}
(iii) X ={2, 4, 6, 8}
Y = {x : x is a positive even integer and 0 < x < 10}
Solution:
(i) Since A and B contain exactly the same elements, A and B are equal sets.
(ii) A and B has different elements.
∴ A and B are not equal sets.
(iii) X = {2, 4, 6, 8}, Y = {2, 4, 6, 8}
∴ X and Y are equal sets.

Question 5.
Write ⊆ or ⊈ in each blank to make a true statement.
(i) {4, 5, 6, 7} ____ {4, 5, 6, 7, 8}
(ii) {a, b, c} ____ {b, e, f, g}
Solution:
(i) {4, 5, 6, 7} ⊈ {4, 5, 6, 7, 8}
(ii) {a, b, c} ⊈ {b, e, f, g}

Question 6.
Write down the power set of A= {3, {4, 5}}.
Solution:
The subsets of A are {Ø, {3}, {4, 5}, {3,{4, 5}}
P(A) = {Ø, {3}, {4,5}, {3{4,5}}

Exercise 1.3

Question 1.
Find the union of the following sets.
(i) A = {1, 2, 3, 5, 6} and B = {4, 5, 6, 7, 8}
(ii) X = {3, 4, 5} and Y = Ø
Solution:
(i) A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8}
(ii) X ∪ Y = {3, 4, 5}

Question 2.
Find A ∩ B if (i) A = {10, 11, 12, 13}, B = {12, 13, 14, 15}, (ii) A = {5, 9, 11}, B = Ø.
Solution:
(i) A ∩ B = {12, 13}
(ii) A ∩ B = Ø

Question 3.
Given the sets A = {4, 5, 6, 7} and B = {1, 3, 8, 9}, find A ∩ B.
Solution:
A ∩ B = Ø

Question 4.
If A= {-2, -1, 0, 3, 4}, B = {-1, 3, 5}, find (i) A – B, (ii) B – A.
Solution:
(i) A – B = {-2, 0, 4}
(ii) B – A = {5}

Question 5.
If A = {2, 3, 5, 7,11} and B = {5, 7, 9, 11, 13}, find A ∆ B.
Solution:
A ∆ B= {2, 3, 9, 13}

Question 6.
Draw a venn diagram similar to one at the side and shade the regions representing the following sets (i) A’, (ii) B’, (iii) A’ ∪ B’, (iv) (A ∪ B)’, (v) A’ ∩ B’
Solution:
(i) A’

(ii) B’

(iii) A’ ∪ B’

(iv) (A ∪ B)’

(v) A’ ∩ B’

Question 7.
State which of the following sets are disjoint.
(i) A = {2, 4, 6, 8}, B = {x : x is an even number < 10, x ∈ N}
(ii) X = {1, 3, 5, 7, 9}, Y = {0, 2, 4, 6, 8, 10}
(iii) R = {a, b, c, d, e}, S = {d, e, b, c, a}
Solution:
(i) A = {2, 4, 6, 8}, B = {2, 4, 6, 8}
A ∩ B = {2, 4, 6, 8} ≠ Ø
∴ A and B are not disjoint sets.
(ii) X ∩ Y = { } = Φ, X and Y are disjoint sets.
(iii) R ∩ S = {a, b, c, d, e} ≠ Ø
∴ R and S are not disjoint sets.

Question 8.
If A = {a, b, c, d, e}and B = {a, e, i, o, u} find AB.
Solution:
A ∩ B = {a, b, c, d, e} ∩ {a, e, i, o, u} = {a, e}

Exercise 1.4

Question 1.
If A and B are two sets containing 13 and 16 elements respectively, then find the minimum and maximum number of elements in A ∪B?
Solution:

n(A) = 13 ; n(B) = 16
Minimum n(A ∪ B) = 16
Maximum n(A ∪ B) = 13 + 16 = 29

Question 2.
If n(U) = 38, n(A) = 16, n(A ∩ B) = 12, n(B’) = 20, find n(A ∪ B).
Solution:

n(U) = 38
n(A) = 16
N(A ∩ B) = 12
n(B’) = 20
n(A ∪ B) = ?
Hint: n(B) = n(U) – n(B)’
n(B) = 38 – 20
n(B) = 18
n(A ∪ B) = n(A) + n(B) – n (A ∩ B)
n(A ∪ B) = 16 – 12 + 18
n(A ∪ B) = 4 + 18 = 22.

Question 3.
Let A = {b, d, e, g, h} and B = {a, e, c, h} verify that n(A – B) = n(A) – n(A ∩ B)
Solution:
A = {b, d, e, g, h),
B = {a, e, c, h}
A ∩ B = {b, d, g}
n(A ∩ B) = 3 ………….. (1)
A ∩ B = {e, h}
n(A ∩ B) = 2, n(A) = 5
n(A) – n(A ∩ B) = 5 – 2 = 3 ……………… (2)
Form (1) and (2) we get
n(A – B) = n(A) – n(A ∩ B)

Question 4.
If A = {2, 5, 6, 7} and B = {3, 5, 7, 8}, then verify the commutative property of
(i) union of sets
(ii) intersection of sets
Solution:
Given, A = {2, 5, 6, 7} and B = {3, 5, 7, 8}
(i) A ∪ B = {2, 3, 5, 6, 7, 8} ……………. (1)
B ∪ A = {2, 3, 5, 6, 7, 8} …………… (2)
From (1) and (2) we have A ∪ B = B ∪ A
It is verified that union of sets is commutative.

(ii) A n B = {5, 7} …………… (3)
B n A = {5, 7} ……………. (4)
From (3) and (4) we get, A ∩ B = B ∩ A
It is verified that intersection of sets is commutative.

Question 5.
If A = {b, c, d, e} and B = {b, c, e, g} and C = {a, c, e}, then verify A ∪ (B ∪ C) = (A ∪ B) ∪ C.
Solution:
Given, A = {b, c, d, e} and B = {b, c, e, g} and C = {a, c, e}
Now B ∪ C = {a, b, c, e, g}
Au(B ∪C) = {a, b, c, d, e, g} ……………. (1)
Then, A ∪ B = {b, c, d, e, g}
(A ∪ B) ∪ C = {a, b, c, d, e, g} ……………… (2)
From (1) and (2) it is verified that
A ∪ (B ∪ C) = (A ∪ B) ∪ C

Exercise 1.5

Question 1.
If A = {1, 3, 5, 7, 9}, B = {x : x is a composite number and x < 12} and C = {x : x ∈ N and 6 < x < 10} then verify A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
Solution:
Given, A = {1, 3, 5, 7, 9} and B = {4, 6, 8, 9, 10}and C = {6, 7, 8, 9}
B ∩ C = {4, 6, 8, 9, 10} n {6, 7, 8, 9} = {6, 8, 9}
A ∪ (B ∩ C) = {1, 3, 5, 6, 7, 8, 9} ……………. (1)
Then (A ∪ B) = {1, 3, 5, 7, 9} ∪ {4, 6, 8, 9, 10} = {1, 3, 4, 5, 6, 7, 8, 9, 10}
(A ∪ C) = {1, 3, 5, 7, 9} ∪ {6, 7, 8, 9} = {1,3, 5, 6, 7, 8, 9}
(A ∪ B) ∩ (A ∪ C) = {1, 3, 4, 5, 6, 7, 8, 9, 10} ∩ {1, 3, 5, 6, 7, 8, 9}
= {1, 3, 5, 6, 7, 8, 9} …………….. (2)
From (1) and (2), it is verified that
A ∪ (B ∩C) = (A ∪ B) ∩ (A ∪ C)

Question 2.
If A, B and C are overlapping sets, draw venn diagram for : A ∩ B
Solution:

Question 3.
Draw Venn diagram for A ∩ B ∩ C
Solution:

Question 4.
If P = {x : x ∈ N and 1 < x < 11}, Q = {x : x = 2n, n ∈ N and it < 6} and R = {4, 6, 8, 9, 10, 12}, then verify P – (Q ∩ R) = (P – Q) ∪ (P – R).
Solution:
The roster form of sets P, Q and R are P = {2, 3, 4, 5, 6, 7, 8, 9, 10}, Q = {2, 4, 6, 8, 10} and R = {4, 6, 8, 9, 10, 12}
First, we find Q ∩ R = {4, 6, 8, 10}
Then, P – (Q ∩ R) = {2, 3, 5, 7, 9} ………….. (1)
Next, P – Q = {3, 5, 7, 9}
and P – R = {2, 3, 5, 7}
and so, (P – Q) ∪ (P – Q) = {2, 3, 5, 7, 9} ……………. (2)
Hence from (1) and (2), it verified that P – (Q ∩ R) = (P – Q) ∪ (P – R)
Finding the elements of set Q
Given, x = 2 n
n = 1 → x = 2 (1) = 2
n = 2 → x = 2(2) = 4
n = 3 → x = 2 (3) = 6
n = 4 → x = 2(4) = 8
n = 5 → x = 2(5) = 10
Therefore, x takes values such as 2, 4, 6, 8, 10

Question 5.
If U = {x : x ∈ Z, -3 < x ≤ 9}, A = {x : x = 2P + 1, P ∈ Z , -2 ≤ P ≤ 3}, B = {x : x = q + l, q ∈ Z, 0 ≤ q ≤ 3}, verify De Morgan’s laws for complementation.
Solution:
Given, U = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {-3, -1, 1, 3, 5, 7} and B = {1, 2, 3, 4}
Law (i) (A ∪ B)’ = A’ ∩ B’
Now, A ∪ B = {-3, -1, 1, 2, 3, 4, 5, 7}
(A ∪ B)’ = {-2, 0, 6, 8, 9} ………….. (1)
Then, A’ = {-2, 0, 2, 4, 6, 8, 9) and
B’ = {-3, -2, -1, 0, 5, 6, 7, 8, 9}
A’ ∩ B’ = {-2, 0, 6, 8, 9} ……………… (2)
From (1) and (2) it is verified that
(A ∪ B)’ = A’ ∩ B’
Law (ii) (A ∩ B)’ = A’ ∪ B’
Now, A ∩ B = {1, 3}
(A ∩ B)’ = {-3, -2, -1, 0, 2, 4, 5, 6, 7, 8, 9} ………….. (3)
Then, A’ ∪ B’ = {-3, -2, -1, 0, 2, 4, 5, 6, 7, 8, 9} ………………. (4)
From (3) and (4) it is verified that
(A ∩ B)’ = A’ ∪ B’

Exercise 1.6

Question 1.
From the given venn diagram. Find (i) A, (ii) B, (iii) A ∪ B (iv) A ∩ B also verify that n(A ∪B) = n(A) + n(B) – n(A ∩ B).

Solution:
A = {a, b, d, e, g, h}
B = {b, c, e, f, h, i, j}
A ∪ B = {a, b, c, d, e, f, g, h, i, j}
A ∩ B = {b, e, h}
So, n(A) = 6, n(B) = 7, n(A ∪B) = 10, n(A ∩ B) = 3
Now, n(A) + n(B) – n(A ∩ B) = 6 + 7 – 3 = 10
Hence, n(A) + n(B) – n(A ∩ B) = n(A ∪ B)

Question 2.
If n(A) = 12, n(B) = 17 and n(A ∪ B) = 21, find n(A ∩B).
Solution:
Given that n(A) = 12, n(B) = 17 and n(A ∪ B) =21
By using the formula n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
n(A ∩ B) = 12 + 17 – 21 = 8

Question 3.
In a school, 80 students like Maths, 90 students like Science, 82 students like History, 21 like both Maths and Science, 19 like both Science and History 20 like both Maths and History and 8 liked all the three subjects. If each student like atleast one subject, then find (i) the number of students in the school (ii) the number of students who like only one subject.
Solution:
Let M, S and H represent sets of students who like Maths, Science and History respectively.
Then, n(M) = 80, n(S) = 90, n(H) = 82, n(M ∩ S) = 21, n(S ∩ H) = 19, n(M ∩ H) = 20, n(M ∩ S ∩ H) = 8
Let us represents the given data in a venn diagram.

(i) The number of student in the school = 52 + 59 + 55 + 12 + 11 + 8 + 8 = 205
(ii) The number of students who like only one subject = 52 + 59 + 55 = 166

Question 4.
State the formula to find n(A ∪ B ∪ C).
Solution:
n( A ∪ B ∪ C) = n(A) + n(B) +n(C) – n(A ∩ B) – (B ∩ C) – n(A ∩ C) + (A ∩ B ∩ B)

Question 5.
Verify n (A ∪ B ∪ C) = n (A) + n(B) + n (C) – n(A ∩ B) – (B ∩ C) – n(A ∩ C) + (A ∩ B ∩ C) for the following sets A = {1, 3, 5, 6, 8}, B = {3, 4, 5, 6} and C = {1, 2, 3, 6}
Solution:
(A ∪ B ∪ C) = {1,2, 3, 4, 5, 6, 8}
n (A ∪ B ∪ C) = 7
Also, n (A) = 5, n (B) = 4, n (C) = 4,
Further, A ∩ B = {3, 5, 6} ⇒ n(A ∩ B) = 3
B ∩ C = {3, 6} ⇒ n(B ∩ C) = 2
A ∩ C = {3, 5, 6} ⇒ n(A ∩ C) = 3
Also, A ∩ B ∩ C = {3, 6} ⇒ n(A ∩ B ∩ C) = 2
Now n (A ∪ B ∪ C) = n (A) + n (B) + n (C) – n(A ∩ B) – n( B ∩ C) – n (A ∩ C) + n(A ∩ B ∩ C)
7 = 5 + 4 + 4 – 3 – 2 – 3 + 2
7 = 13 – 8 + 2
7 = 5 + 2
7 = 7
Thus verified

Exercise 1.7

Multiple Choice Questions
Question 1.
If A = {5, {5, 6}, 7} which of the following is correct?
(1) {5, 6} ∈ A
(2) {5} ∈ A
(3) {7} ∈ A
(4) {6} ∈ A
Solution:
(1) {5, 6} ∈ A
Hint: {5, 6} is an element of A.

Question 2.
If x = {a, {b, c}, d}, which of the following is a subset of X?
(1) {a, b}
(2) {b, c}
(3) {c, d}
(4) {a, d}
Solution:
(4) {a, d}
Hint: b is not an element of X. Similarly c.

Question 3.
If a finite set A has m elements, then the number of non-empty proper subset of A is
(1) 2^m
(2) 2^m – 1
(3) 2^m-1
(4) 2(2^m-1 – 1)
Solution:
(4) 2(2^m-1 – 1)
Hint: P(A) = 2m Proper non empty subset = 2m – 2 = 2 (2^m-1 – 1)

Question 4.
For any three A, B and C, A – (B ∪ C) is
(1) (A – B) ∪ (A – C)
(2) (A – B) ∩ (A ∪ C)
(3) (A – B) ∪C
(4) A ∪ (B – C)
Solution:
(2) (A – B) ∩ (A ∪ C)

Question 5.
Which of the following is true?
(1) (A ∪ B) = B ∪ A
(2) (A ∪ B)’ = A’ – B’
(3) (A ∩ B)’ = A’ ∩ B’
(4) A – (B ∩ C) = (A – B) ∩ (A – C)
Solution:
(1) (A ∪ B) = B ∪ A

Question 6.
The shaded region in the venn diagram is
(1) A ∪ B
(2) A ∩ B
(3) (A ∩ B)’
(4) (A – B) ∪ (B – A)
Solution:
(4) (A – B) ∪ (B – A)
Hint:

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.2

Question 1.
Find the median of the given values : 47, 53, 62, 71, 83, 21, 43, 47, 41.
Solution:
47, 53, 62, 71, 83, 21, 43, 47, 41
Ascending order = 21, 41, 43, 47, 47, 53, 62, 71, 83
The number of values 9, which is odd

Question 2.
Find the Median of the given data: 36, 44, 86, 31, 37, 44, 86, 35, 60, 51.
Solution:
36, 44, 86, 31, 37, 44, 86, 35, 60, 51
Ascending order 31, 35, 36, 37, 44, 44, 51, 60, 86, 86
The number of values = 10, which is an even number


Question 3.
The median of observation 11, 12,14, 18, x + 2, x + 4, 30, 32, 35, 41 arranged in ascending order is 24. Find the values of x.
Solution:
11, 12, 14, 18, x + 2, , x + 4, 30, 32, 35, 41
The number of values = 10, which is an even number

Question 4.
A researcher studying the behaviour of mice has recorded the time (in seconds) taken by each mouse to locate its food by considering 13 different mice as 31, 33, 63, 33, 28, 29, 33, 27, 27, 34, 35, 28, 32. Find the median time that mice spent in searching its food.
Solution:
31, 33, 63, 33, 28, 29, 33, 27, 27, 34, 35, 28, 32 Writing in ascending order we get 27, 27, 28, 28, 29, 31, 32, 33, 33, 33, 34, 35, 63
Number of values = 13 which is an odd number

Question 5.
The following are the marks scored by the students in the Summative Assessment exam

Calculate the median.
Solution:


Question 6.
The mean of five positive integers is twice their median. If four of the integers are 3, 4, 6, 9 and median is 6, then find the fifth integer.
Solution:
The five integers are 3, 4, 6, 9, x

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.7

Multiple Choice Questions
Question 1.
Which of the following is correct?
(1) {7} ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(2) 7 ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(3) 7 ∉ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(4) {7} ⊈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Solution:
(2) 7 ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Question 2.
The set P = {x | x ∈ Z, -1 < X < 1} is a
(1) Singleton set
(2) Power set
(3) Null set
(4) Subset
Solution:
(1) Singleton set
Hint: P = {0}

Question 3.
If U = {x | x ∈ N, x < 10} and A = {x | x ∈ N, 2 ≤ x < 6} then (A’)’ is
(1) {1, 6, 7, 8, 9}
(2) {1, 2, 3, 4}
(3) {2, 3, 4, 5}
(4) { }
Solution:
(3) {2, 3, 4, 5}
Hint: (A’) = A= {2, 3, 4, 5}

Question 4.
If B ⊆ A then n(A ∩ B) is
(1) n(A – B)
(2) n(B)
(3) n(B – A)
(4) n(A)
Solution:
(2) n(B)
Hint: B ⊆ A ⇒ A ∩ B = B

Question 5.
If A= {x, y, z} then the number of non-empty subsets of A is
(1) 8
(2) 5
(3) 6
(4) 7
Solution:
(4) 7
Hint: Number of non-empty subsets = 2 – 1 = 8 – 1 = 7

Question 6.
Which of the following is correct ?
(1) Ø ⊆ {a,b}
(2) Ø ∈ {a, b}
(3) {a} ∈ {a, b}
(4) a ⊆ {a, b}
Solution:
(1) Ø ⊆ {a,b}
Hint: Empty set is an improper subset

Question 7.
If A ∪ B = A ∩ B, then
(1) A ≠ B
(2) A = B
(3) A ⊂ B
(4) B ⊂ A
Solution:
(2) A = B

Question 8.
If B – A is B, then A ∩ B is
(1) A
(2) B
(3) U
(4) Ø
Solution:
(4) Ø
Hint: B – A = B ⇒ A and B are disjoint sets.

Question 9.
From the adjacent diagram n[P(A ∆ B) is
(1) 8
(2) 16
(3) 32
(4) 64

Solution:
(3) 32
Hint: A ∆ B = { 60, 85, 75, 90, 70}
⇒ n(A ∆ B) = 5
⇒ n(P(A ∆ B)) = 2⁵ = 32

Question 10.
If n(A) = 10 and n(B) = 15 then the minimum and maximum number of elements in A ∩ B is
(1) (10, 15)
(2) (15, 10)
(3) (10, 0)
(4) (0, 10)
Solution:
(4) (0, 10)

Question 11.
Let A = {Ø} and B = P(A) then A ∩ B is
(1) {Ø, {Ø} }
(2) {Ø}
(3) Ø
(4) {0}
Solution:
(2) {Ø}
Hint: P(A) = {Ø {Ø}}

Question 12.
In a class of 50 boys, 35 boys play carom and 20 boys play chess then the number of boys play both games is
(1) 5
(2) 30
(3) 15
(4) 10
Solution:
(1) 5
Hint: n(A ∪ B) = n(A) + n(B) – n(A n B) ⇒ 50 = 35 + 20 – n(A ∩ B) ⇒ n(A ∩ B) = 5

Question 13.
If U = {x : x ∈ N and x < 10}, A = {1, 2, 3, 5, 8} and B = {2, 5, 6, 7, 9}, then n[(A ∪ B)’] is
(1) 1
(2) 2
(3) 4
(4) 8
Solution:
(1) 1
Hint: U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 5, 8}
B = {2, 5, 6, 7, 9}
A ∪ B = {1, 2, 3, 5, 6, 7, 8, 9}
(A ∪ B)’ = {4},
n(A ∪ B)’ = 1

Question 14.
For any three sets P, Q and R, P – (Q ∩ R) is
(1), P – (Q ∪ R)
(2) (P ∩ Q) – R
(3) (P – Q) ∪ (P – R)
(4) (P – Q) ∩ (P – R)
Solution:
(3) (P – Q) ∪ (P – R)
Hint: P – (Q ∩ R) = (P – Q) ∪ (P – R)

Question 15.
Which of the following is true?
(1) A – B = A ∩ B
(2) A – B = B – A
(3) (A ∪ B)’ = A’ ∪ B’
(4) (A ∩ B)’ = A’ ∪ B’
Solution:
(4) (A ∩ B)’ = A’ ∪ B’

Hint: (1) (A – B) = A ∩ B ✘
(2) A – B = B – A ✘
(3) (A ∪ B) = A’ ∪ B’ ✘
(4) (A ∩ B)’ = A’ ∪ B’ ✓

Question 16.
If n(A ∪ B ∪ C) = 100, n(A) = 4x, n(B) = 6x, n(C) = 5x, n(A ∩ B) = 20, n(B ∩ C) = 15, n(A ∩ C) = 25 and n(A ∩ B ∩ C)= 10 , then the value of x is
(A) 10
(B) 15
(C) 25
(D) 30
Solution:
(A) 10
Hint:
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)
100 = 4x + 6x + 5x – 20 – 15 – 25 + 10
100 = 15x -60 + 10
100 = 15x – 50
∴ 15x = 100 + 50 = 150
x = 10

Question 17.
For any three sets A, B and C, (A – B) ∩ (B – C) is equal to
(1) A only
(2) B only
(3) C only
(4) ϕ
Solution:
(4) ϕ
Hint: (A – B) ∩ (B – C) is equal to Φ

Question 18.
If J = Set of three sided shapes, K = Set of shapes with two equal sides and L = Set of shapes with right angle, then J ∩ K ∩ L is
(1) Set of isoceles triangles
(2) Set of equilateral triangles
(3) Set of isoceles right triangles
(4) Set of right angled triangles
Solution:
(3) Set of isoceles right triangles
Hint:

Question 19.
The shaded region in the Venn diagram is
(1) Z – (X ∪ Y)
(2) (X ∪ Y) ∩ Z
(3) Z – (X ∩ Y)
(4) Z ∪ (X ∩ Y)
Answer:
(3) Z – (X ∩ Y)
Hint:

Z – (X ∩ Y)

Question 20.
In a city, 40% people like only one fruit, 35% people like only two fruits, 20% people like all the three fruits. How many percentage of people do not like any one of the above three fruits?
(1) 5
(2) 8
(3) 10
(4) 15
Answer:
(1) 5
Hint:

40 + 35 + 20 + x = 100%
95% + x = 100%
x = 5%

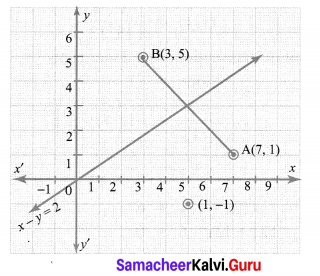
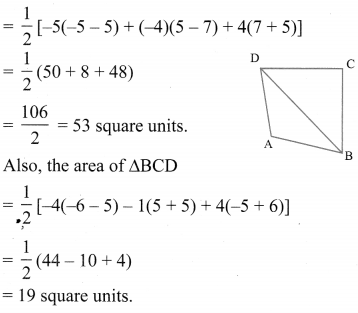
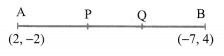
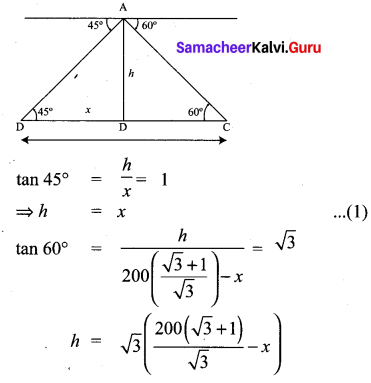
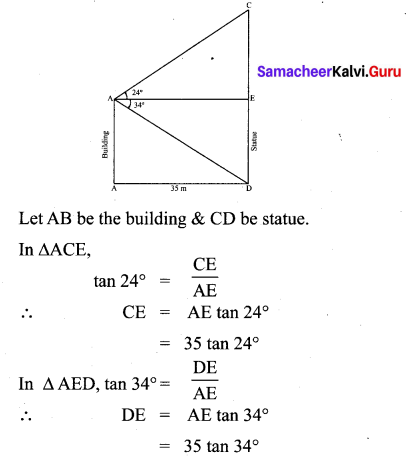
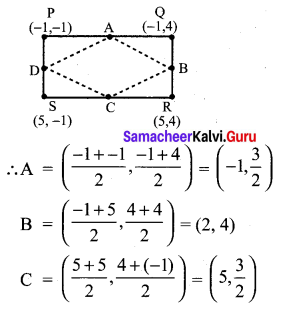
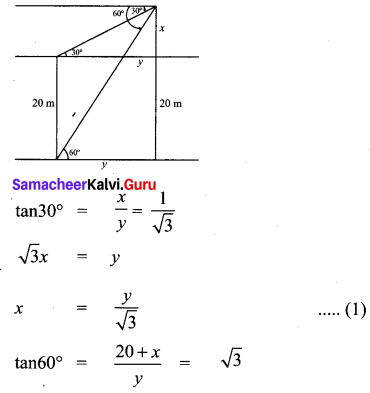
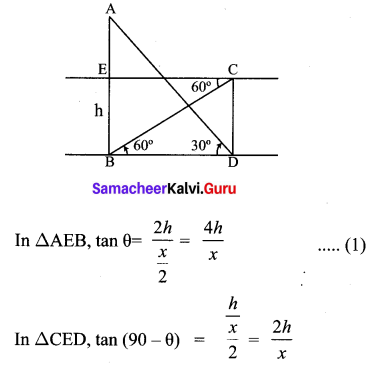
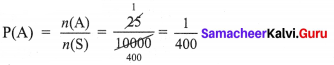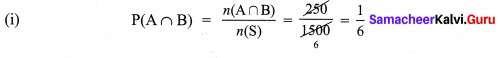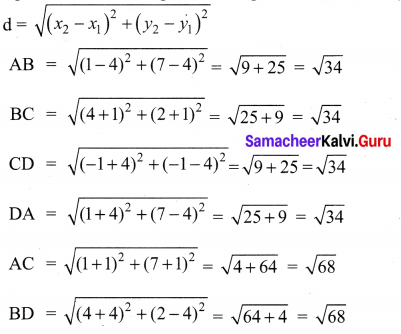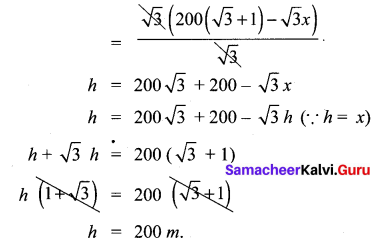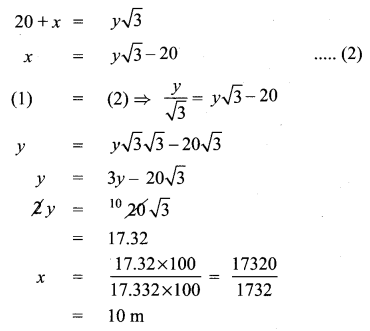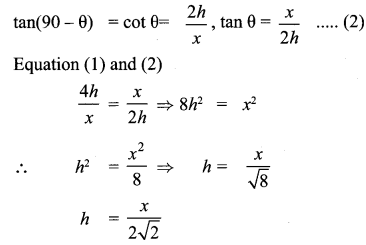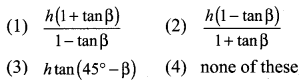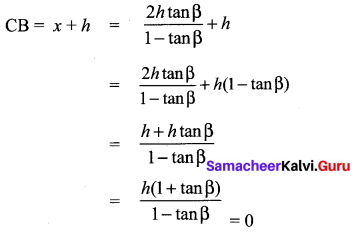You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Additional Questions

EXERCISE 9.1

Question 1.
An unbiased die is thrown. What is the probability of getting
(i) an even number or a multiple of 3.
(ii) a number between 3 and 6.
Solution:
(i) Probability of getting an even number \(\frac{3}{6}=\frac{1}{2}\)
Probability of getting a multiple of 3 = \(\frac{2}{6}\)
Probability of getting an even multiple of 3 = \(\frac{1}{6}\)
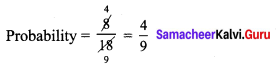
Probability of getting an even number or


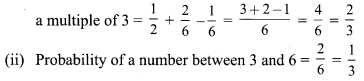
Question 2.
Two unbiased coins are tossed simultaneously find the probability of getting
(i) two heads
(ii) one head
(iii) at least one head
(iv) at most one head.
Solution:
S = {HH, HT, TH, TT}
(i) probability of two heads = \(\frac{1}{4}\)
(ii) probability of one head = \(\frac{1}{2}\)
(iii) probability of at least one head = \(\frac{3}{4}\)
(iv) probability of at most one head = \(\frac{3}{4}\)

Question 3.
Find the probability that a leap year selected at random will contain 53 Sundays.
Solution:
S = {Sunday Monday, Monday Tuesday, Tuesday Wednesday, Wednesday Thursday, Thursday Friday, Friday Saturday, Saturday Sunday}
n (S) = 7; n (A) = 2; P(A) = \(\frac{2}{7}\)

Question 4.
What is the probability that a number selected from the numbers 1, 2, 3, 25 is a prime number when each of the given numbers is equally likely to be selected?
Solution:
A = {2, 3, 5, 7, 11, 13, 17, 19,23}
P(A) = \(\frac{9}{25}\)

EXERCISE 9.2

Question 1.
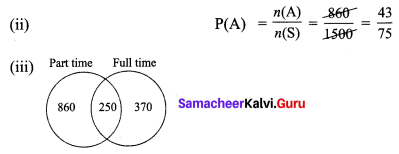
Tickets numbered from 1 to 20 are mixed up together and then a ticket is drawn at random. What is the probability that the ticket has a number which is a multiple of 3 or 7?
Solution:
A = {3, 6, 9, 12, 15, 18, 7, 14}

Question 2.
One card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that the card drawn is
(i) an ace,
(ii) either red card or king.
Solution:

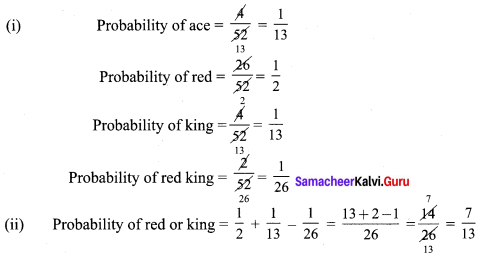
Question 3.
A bag contains 3 red and 2 blue marbles. A marble is drawn at random. What is the probability of drawing a blue marble?
Solution:

Question 4.
Two dice are thrown simultaneously. Find the probability of getting
(i) an even number as the sum.
(ii) a total of at least 10
(iii) a doublet of even number.
Solution:

n(S) = 36


Question 5.
An urn contains 10 red and 8 white balls. One ball is drawn at random. Find the probability that the ball drawn is white.
Solution:

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Ex 9.3

Question 1.
A number between 0 and 1 that is used to measure uncertainty is called
(1) Random variable
(2) Trial
(3) Simple event
(4) Probability
Solution:
(4) Probability

Question 2.
Probability lies between
(1) -1 and +1
(2) 0 and 1
(3) 0 and n
(4) 0 and ∞
Solution:
(2) 0 and 1

Question 3.
The probability based on the concept of relative frequency theory is called
(1) Empirical Probability
(2) Classical Probability
(3) Both (1) and (2)
(4) Neither (1) or (2)
Solution:
(1) Empirical Probability

Question 4.
The probability of an event cannot be
(1) Equal to zero
(2) Greater than zero
(3) Equal to one
(4) Less than zero
Solution:
(4) Less than zero

Question 5.
The probability of all possible outcomes of a random experiment is always equal to
(1) one
(2) Zero
(3) Infinity
(4) Less than one
Solution:
(1) one

Question 6.
If A is any event in S then its complement is A’ then, P(A’) is equal to
(1) 1
(2) 0
(3) 1 – A
(4) 1 – P(A)
Solution:
(4) 1 – P(A)

Question 7.
Which of the following cannot be taken as probability of an event?
(1) 0
(2) 0.5
(3) 1
(4) -1
Solution:
(4) -1

Question 8.
A particular result of an experiment is called
(1) Trial
(2) Simple event
(3) Compound event
(4) Outcome
Solution:
(4) Outcome

Question 9.
A collection of one or more outcomes of an experiment is called
(1) Event
(2) Outcome
(3) Sample point
(4) None of above
Solution:
(1) Event

Question 10.
The six faces of the dice are called equally likely if the dice is
(1) Small
(2) Fair
(3) Six-faced
(4) Round
Hint: Fair means all outcomes are equally likely.
Solution:
(2) Fair

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Ex 9.2

Question 1.
A company manufactures 10000 Laptops in 6 months. Out of which 25 of them are found to be defective. When you choose one Laptop from the manufactured, what is the probability that selected Laptop is a good one.
Solution:
Total n(S) = 10,000
Defective n( A) = 25

No. of good laptops = 1000 – 25
n(B) = 9975


Question 2.
In a survey of 400 youngsters aged 16-20 years, it was found that 191 have their voter ID card. If a youngster is selected at random, find the probability that the youngster does not have their voter ID card.
Solution:
No. of youngsters n(S) = 400
No. of youngsters having voter id n(A) = 191
No. of youngsters do not have their voter id n(B) = 400 – 191 = 209

Question 3.
The probability of guessing the correct answer to a certain question is \(\frac{x}{3}\). If the probability of not guessing the correct answer is \(\frac{x}{5}\), then find the value of x.
Solution:

Question 4.
If a probability of a player winning a particular tennis match is 0.72. What is the probability of the player loosing the match?
Solution:
P(A) = 0.72
P(A’) = 1 – 0.72 = 0.28

Question 5.
1500 families were surveyed and following data was recorded about their maids at homes

A family is selected at random. Find the probability that the family selected has
(i) Both types of maids
(ii) Part time maids
(iii) No maids
Solution:
n(S) = 1500 (Total families)
n(A) = 860 (Part time maids)
n(B) = 370 (Only full time)
n(A∩B) = 250 (Both)


Total families n(S) = 1500
No. of families have maids = 860 + 250 + 370 = 1480
No. of families do not have maids = 1500 – 1480
n( A) = 20