You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions
Question 1.
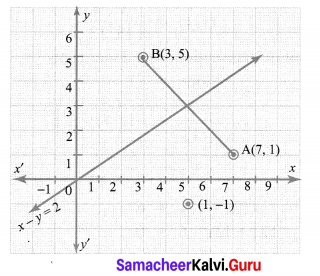
Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Solution:
Let P(x, y) be equidistant from the points A(7, 1) and B(3, 5).
We are given that AP = BP. So, AP2 = BP2
(x – 7)2 + (y – 1)2 =(x – 3)2 + (y – 5)2
x2 – 14x + 49 + y2 – 2y + 1 = x2 – 6x + 9 + y2 – 10y + 25
x – y = 2
Which is the required relation
Question 2.
Show that the points (1, 7), (4, 2), (-1, -1) and (-4, 4) are the vertices of a square.
Solution:
Let A(1, 7), B(4, 2), C(-1, -1) and D(-4, 4) be the given points. To prove that ABCD is a square, we have to prove that all its sides are equal and both its diagonals are equal.
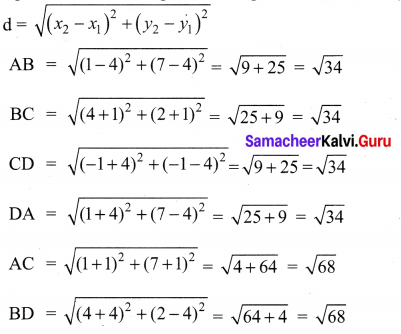
Since, AB = BC = CD = DA and AC = BD, all the four sides of the quadrilateral ABCD are equal and its diagonals AC and BD are also equal. Therefore, ABCD is a square.
![]()
Question 3.
If A (-5, 7), B (-4, -5), C (-1, -6) and D (4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.
Solution:
By joining B to D, you will get two triangles ABD and BCD.
Now, the area of ∆ABD
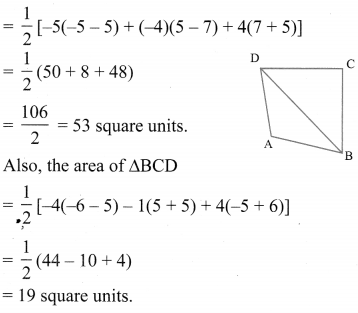
So, the area of quadrilateral ABCD = 53 + 19 = 72 square units.
Question 4.
Find the coordinates of the points of trisection (i.e. points dividing in three equal parts) of the line segment joining the points A(2, -2) and B(-7, 4).
Solution:
Let P and Q be the points of trisection at AB. i.e., AP = PQ = QB
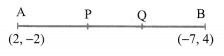
Therefore, P divides AB internally in the ratio 1 : 2. Therefore, the coordinates at P, by applying the section formula, are
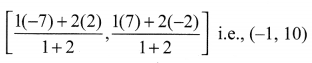
Now, Q also divides AB internally in the ratio 2 : 1, so, the coordinates at Q are
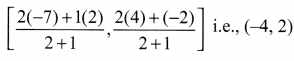
Therefore, the coordinates of the points at trisection of the line segment joining A and B are (-1, 0) and (-4, 2).
![]()
Question 5.
If the points A(6, 1), B(8, 2), C(9, 4) and D(P, 3) are the vertices of a parallelogram, taken in order. Find the value of P.
Solution:
We know that diagonals of a parallelogram bisect each other.
So, the coordinates at the mid-point of AC = coordinates of the mid-point of BD.
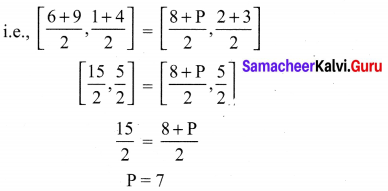
Question 6.
Find the area of a triangle whose vertices are (1,-1), (-4, 6) and (-3, -5).
Solution:
The area of the triangle formed by the vertices A(1, -1), B(-4, 6) and C(-3, -5), by using the formula
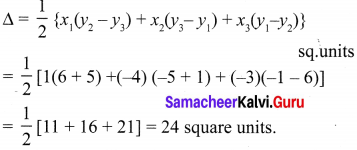
So, the area of the triangle is 24 square units.
Question 7.
If A(-2, -1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram, find the values of a and b.
Solution:
We know that the diagonals of a parallelogram bisect each other. Therefore the co-ordinates of the midpoint of AC are same as the co-ordinates of the mid-point of BD. i.e.
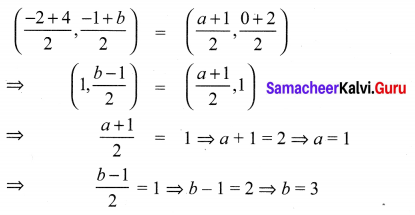
![]()
Question 8.
Find the area of the quadrilateral whose vertices, taken in order, are (-3, 2), (5, 4), (7, -6) and (-5, -4).
Solution:
We have Area of the quadrilateral

Question 9.
Find the area of the triangle formed by the points P(-1.5, 3), Q(6, -2) and R(-3, 4).
Solution:
The area of the triangle formed by the given points is equal to
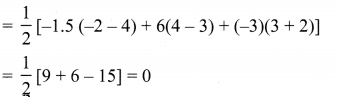
Can we have a triangle of area 0 square units? What does this mean?
If the area of a triangle is 0 square units, then its vertices will be collinear.
Question 10.
Find the value of k if the pointsA(2, 3), B(4, k) and (6, -3) are collinear.
Since the given points are collinear, the area a the triangle formed by them must be 0, i.e.
