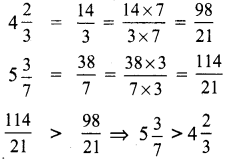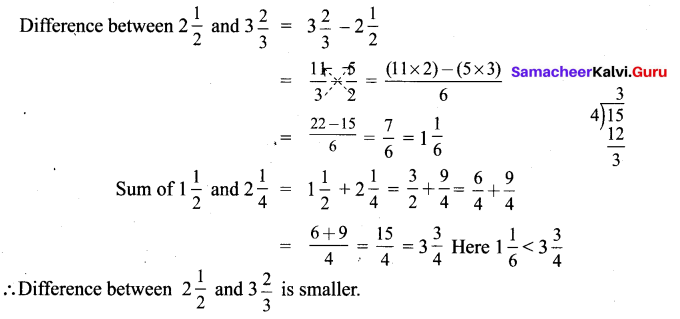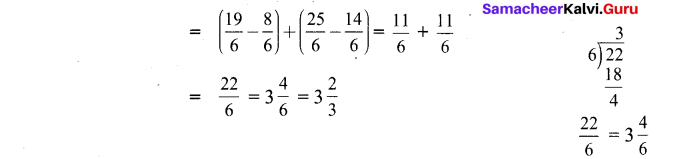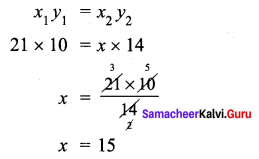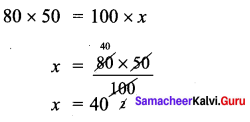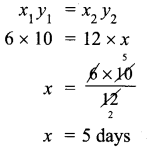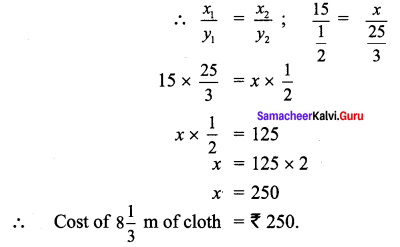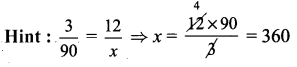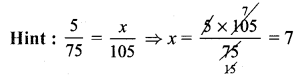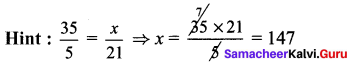Prasanna

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 2 Integers Ex 2.1

Question 1.
Fill in the blanks.
(i) The potable water available at 100m below the ground level is denoted as ______ m.
Hint: Below ground level – negative; ground level – 0; above ground level – positive.
(ii) A swimmer dives to a depth of 7 feet from the ground into the swimming pool. The integer that represents this, is ______ feet.
Hint: Below ground level – negative numbers.
(iii) -46 is to the _____ of -35 on the number line.
Hint: -46 <-35
(iv) There are _____ integers from -5 to +5 (both inclusive).

(v) ______ is an integer which is neither positive nor negative.

Solutions:
(i) -100
(ii) -7
(iii) Left
(iv) 11
(v) 0

Question 2.
Say True or False.
(i) Each of the integers -18, 6, -12, 0 is greater than -20.
(ii) -1 is to the right of 0.
(iii) -10 and 10 are at equal distance from 1.
(iv) All negative integers are greater than zero.
(v) All whole numbers are integers.
Solution:
(i) True
(ii) False
(iii) False
(iv) False
(v) True

Question 3.
Mark the numbers 4, -3, 6, -1 and -5 on the number line.
Solution:

Question 4.
On the number line, which number is
i) 4 units to the right of-7?
ii) 5 units to the left of 3?
Solution:

(i) – 3 is 4 units to the right of -7
(ii) – 2 is 5 units to the left of 3

Question 5.
Find the opposite of the following numbers.
(i) 44
(ii) -19
(iii) 0
(iv) -312
(v) 789
Solution:
(i) Opposite of 44 is – 44
(ii) Opposite of-19 is + 19 or 19
(iii) Opposite of 0 is 0
(iv) Opposite of-312 is + 312 or 312
(v) Opposite of 789 is – 789.

Question 6.
If 15 km east of a place is denoted as + 15 km, what is the integer that represents 15 km west of it?
Solution:
Opposite of east is west.
∴ If 15 km east is + 15 km, then 15 km west is – 15 km.

Question 7.
From the following number lines, identify the correct and the wrong representations with reason?

Solution:
(i) This representation is wrong. Because the numbers are not continuously marked as -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6,
(ii) This is the correct representation of Integers
(iii) The representation is wrong. – 2 is misplaced in the number line.
(iv) This representation is correct as the numbers are marked at equal intervals in the correct order.
(v) Here negative integers are marked wrongly to the left of 0

Question 8.
Write all the integers between the given numbers.
(a) 7 and 10
(b) -5 and 4
(c) -3 and 3
(d) -5 and 0
Solution:

Question 9.
Put the appropriate signs as <, > or = in the box?

Solution:
(i) We know that -7 is to the left of 8.
(ii) -8 is to the left of -7,
(iii) -1000 is to the left of -999,
(iv) -111 and-111 coincides in the number line.
(v) 0 is to the right of -200,

Question 10.
Arrange the following integers in ascending order.
i) -11, 12, -13, 14, -15, 16, -17, 18, -19, -20
ii) -28, 6, -5, -40, 8, 0, 12, -1, 4, 22
iii) -100, 10, -1000, 100,0, -1, 1000, 1, -10
Solution:
(i) -11, 12, -13, 14, -15, 16, -17, 18, -19, -20

• First separating the positive integers 12, 14, 16, 18 and the negative integers -11,-13,-15,-17,-19,-20.
• Then arranging the positive integers in ascending order we get 12, 14, 16, 18 and negative integers in ascending order as -20, -19, -17, -15, -13, -11 4
• Now the ascending order : -20, -19, -17, -15, -13, -11, 12, 14, 16, 18.

(ii) -28, 6, -5, -40, 8, 0, 12, -1, 4, 22

• Positive integers are 6, 8, 12, 4, 22 Negative integers are -28, -5, -40, -1
• Arranging the positive integers in ascending order we get 4, 6, 8, 12, 22 and the negative integers in ascending order -40, -28, -5, -1
• The number 0 is neither positive nor negative and stand in the middle.
• In ascending order : -40, -28, -5, -1, 0, 4, 6, 8,12, 22

(iii) -100, 10, -1000, 100, 0, -1, 1000, 1, -10

• Separating positive integers 10, 100, 1000, 1 and negative integers -100, -1000, -1, -10.
• Now the positive integers in ascending order 1,10,100,1000 and the negative integers in ascending order. -1000, -100, -10, -1
• Also ‘0’ stand in the middle as its is neither positive nor negative.
• ∴ The numbers in ascending order: -1000, -100, -10, -1, 0, 1, 10, 100, 1000.

Question 11.
Arrange the following integers in descending order.
i) 14, 27, 15, -14, -9, 0, 11, -17
ii) -99, -120, 65, -46, 78, 400, -600
iii) 111, -222, 333, -444, 555, -666, 7777, -888
Solution:
(i) 14, 27, 15, -14, -9, 0,11, -17

• Separating the positive integers 14, 27, 15, 11 and negative integers -14, -9, -17
• Arranging in descending order we get the positive integers 27,15,14,11 and the negative integers -9, -14, -17.
• ‘0’ is neither positive nor negative and so it stand in middle.
• ∴ The numbers in descending order : 27, 15, 14, 11, 0, -9, -14, -17

(ii) -99, -120, 65, -46, 78, 400, -600

• Separating the positive integers 65, 78, 400 and negative integers -99, -120, -46, -600
• Arranging the positive integers in descending order as 400, 78, 65 and the negative integers in descending order -46, -99, -120, -600.
• The numbers in descending order : 400, 78, 65, -46, -99, -120, -600.

(iii) 111, -222, 333, -444, 555, -666, 7777, -888

• Separating the positive integers 111, 333, 555, 7777 and negative integers -222, -444, -666, -888
• Arranging the positive integers in descending order as 7777, 555, 333, 111 and negative integers in descending order as -222, -444, -666, -888
• The numbers in descending order : 7777, 555, 333, 111, -222, -444, -666, -888

Objective Type Questions

Question 12.
There are _______ positive integers from – 5 to 6.
(a) 5
(b) 6
(c) 7
(d) 11
Solution:
(b) 6
Hint:

Question 13.
The opposite of 20 units to the left of 0 is
(a) 20
(b) 0
(c) -20
(d) 40
Solution:
(a) 20
Hint:

Question 14.
One unit to the right of -7 is
(a) +1
(b) -8
(c) -7
(d) -6
Solution:
(d) -6
Hint:

Question 15.
3 units to the left of 1 is
(a) -4
(b) -3
(c) -2
(d) 3
Solution:
(c) -2
Hint:

Question 16.
The number which determines marking the position of any number to its opposite on a number line is?
(a) -1
(b) 0
(c) 1
(d) 10
Solution:
(b) 0
Hint:

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 1 Fractions Intext Questions

(Try These Textbook Page No. 2)

Question 1.
If all the three cakes are divided among the total participants of the function what would be each one’s share? Discuss.
Solution:
Total participants of the function = 9
Total number of cakes = 3
∴ Each cake should be divided into 3 equal parts.
∴ Total number of equal parts of cake = 9
∴ Each one’s share may be \(\frac{1}{9}\) of total cakes or \(\frac{1}{3}\) of a cake.

Question 2.
Observe the following and represent the shaded parts as fraction.

Solution:
(i) Total number of equal parts = 8
Shaded Parts = 3
Fraction representing the shaded parts = \(\frac{3}{8}\)

(ii) Total number of equal parts = 15
Shaded parts = 5
∴ Fraction representing the shaded parts = \(\frac{5}{15}\)

(iii) Total number of equal parts = 9
Shaded parts = 3
∴ Fraction representing the shaded parts = \(\frac{3}{9}\)

(iv) Total number of equal parts = 9
Shaded parts = 5
Fraction representing the shaded parts = \(\frac{5}{9}\)

Question 3.
Look at the following beakers, express the quantity of water as fraction and arrange them in ascending order:

Solution:
Quantity of water in the first beaker = 1 full
Quantity of water in the second beaker = \(\frac{1}{4}\)
Quantity of water in the third beaker = \(\frac{3}{4}\)
Quantity of water in the fourth beaker = \(\frac{1}{2}\)
Ascending order \(\frac{1}{4}\) < \(\frac{1}{2}\) < \(\frac{3}{4}\) < 1

Question 4.
Write the fraction of shaded part in the following.

Solution:
(i) Total number of equal parts = 3
Shaded parts = 2
Fraction representing the shaded portion = \(\frac{2}{3}\)

(ii) Total number of equal parts = 4
Shaded parts = 3
Fraction representing the shaded parts = \(\frac{3}{4}\)

(iii) Total number of equal parts = 5
Shaded parts = 4
Fraction representing the shaded parts = \(\frac{4}{5}\)

Question 5.
Write the fraction that represents the dots In the triangle.

Solution:
Total number of dots = 24
Number of dots in the triangle = 6
∴ Fraction represents the dots in the triangle = \(\frac{6}{24}\)

Question 6.
Find the fractions of the shaded and unshaded portions in the following.

Solution:
(a) Total number of equal parts = 8
Shaded parts = 2
∴ Fraction representing shaded parts = \(\frac{2}{8}\)

(b) Total number of equal parts = 8
Unshaded parts = 6
∴ Fraction of unshaded portion = \(\frac{6}{8}\)

(Activity Textbook Page No. 3)

Take a rectangular paper. Fold it into two equal parts. Shade one part, write the fraction. Again fold it into two halves. Write the fraction for the shaded part. Continue this process 5 times and write the fraction of the shaded part. Establish the equivalent fractions of \(\frac{1}{2}\) in the folded paper to your friends.

Solution:
First time = \(\frac{1}{2}\)
Second time = \(\frac{2}{4}\)
Third time = \(\frac{4}{8}\)
Fourth time = \(\frac{8}{16}\)
Fifth time = \(\frac{16}{32}\)

(Try These Textbook Page No. 4)

Question 1.
Find the unknown in the following equivalent fractions.

Solution:

(Try These Textbook Page No. 7)

Question 1.
Shade the rectangle for the given pair of fractions and say which is greater among them.

Solution:

Question 2.
Which is greater \(\frac{3}{8}\) or \(\frac{3}{5}\) ?
Solution:
LCM of the denominators 8 and 5 is 40.
Finding the equivalent fractions.

Question 3.
Arrange the fractions in ascending order : \(\frac{3}{5}, \frac{9}{10}, \frac{11}{15}\)
Solution:

Question 4.
Arrange the fractions in descending order : \(\frac{9}{20}, \frac{3}{4}, \frac{7}{12}\)
Solution:

(Try These Textbook Page No. 9)

(i) \(\frac{2}{3}+\frac{5}{7}\)
Solution:
By cross multiplication technique

(ii) \(\frac{3}{5}-\frac{3}{8}\)
Solution:
By cross multiplication technique

(Activity Textbook Page No. 10)

Question 1.
Using the given fractions \(\frac{1}{5}, \frac{1}{6}, \frac{1}{10}, \frac{1}{15}, \frac{2}{15}, \frac{4}{15}, \frac{1}{30}, \frac{7}{30} \text { and } \frac{9}{30}\) fill in the missing ones in the given 3 × 3 square in such a way that the addition of fractions through rows, columns and diagonals give the same total \(\frac{1}{2}\)

Solution:

(Try These Textbook Page No. 10)

Question 1.
Complete the following table. The first one is done for you.

(Try These Textbook Page No. 11)

Question 1.
(i) Are 5\(\frac{2}{3}\) and 5\(\frac{4}{6}\) equal?
Solution:

(ii) \(\frac{3}{2} \neq 3 \frac{1}{2}\) why?
Solution:

Question 2.
Convert 3\(\frac{1}{3}\) into improper fraction.
Solution:

Question 3.
Convert \(\frac{45}{7}\) into mixed fraction.
Solution:

(Try These Textbook Page No. 13)

Question 1.
Find the sum of 5\(\frac{4}{9}\) and 3\(\frac{1}{6}\).
Solution:

Question 2.
Subtract 7\(\frac{1}{6}\) and 12\(\frac{3}{8}\)
Solution:

Question 3.
Subtract the sum of 6\(\frac{1}{6}\) and 3\(\frac{1}{5}\) from the sum of 9\(\frac{2}{3}\) and 2\(\frac{1}{2}\).
Solution:

(Try These Textbook Page No. 15)

Question 1.
2\(\frac{1}{4}\) × 3 is not equal to 6\(\frac{1}{4}\). Why?
Solution:

Question 2.
Simplify : 35 × \(\frac{3}{7}\).
Solution:

Question 3.
Find the value of \(\frac{1}{5}\) of 15.
Solution:
\(\frac{1}{5}\) of 15 = \(\frac{1}{5}\) × 15 = \(\frac{15}{5}\) = 3

Question 4.
Find the value of \(\frac{1}{3}\) of \(\frac{3}{4}\)
Solution:

Question 5.
Multiply 7\(\frac{3}{4}\) by 5\(\frac{1}{2}\).
Solution:

(Activity Textbook Page No. 15)

Take a paper. Fold it into 4 parts vertically of equal width. Shade one part of it with red. Then, fold it into 3 parts horizontally of equal width. Shade two parts of it with blue. Now, you count the number of shaded grids which have both the colours. (Hint: The total number of grids is the product of \(\frac{2}{3}\) and \(\frac{1}{4}\))
Solution:
Activity to be done by the students themselves

(Try These Textbook Page No. 17)

Question 1.
(i) How many 6s are there in 18?
Solution:
Number of 6s in 18 are \(\frac{18}{6}\) = 3

(ii) How many \(\frac{1}{4}\)s are there in 5?
Solution:
Number of \(\frac{1}{4}\) s in 5 are 5 ÷ \(\frac{1}{4}\) = 5 × \(\frac{4}{1}\) = 20

(iii) \(\frac{1}{3}\) ÷ 5 = ?
Solution:
\(\frac{1}{3}\) ÷ 5 = \(\frac{1}{3} \times \frac{1}{5}\) = \(\frac{1}{15}\)

(Try These Textbook Page No. 18)

Question (i)
Find the value of 5 ÷ 2\(\frac{1}{2}\).
Solution:

Question (ii)
Simplify: \(1 \frac{1}{2} \div \frac{1}{2}\)
Solution:

Question (iii)
Divide 8 \(\frac{1}{2}\) by 4\(\frac{1}{4}\).
Solution:

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 5 Information Processing Intext Questions

Exercise 5.1

Try These (Text book Page No. 74)

Question 1.
Find the 10th term of the Fibonacci sequence
Solution:
We have the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,….
The 10th term is 55.

Question 2.
If the 11^th term of the Fibonacci sequence is 89 and 13^th term is 233 then, what is the 12^th term?
Solution:
Given 11^th term of the Fibonacci sequence is 89 and 13^th term of is 233
We know that a number in Fibonacci sequence is got by adding the previous two consecutive numbers.
11^th term + 12^th term = 13^th term
89 +12^th term =233
∴ 12^th term = 233 – 89 = 144
∴ 12^th term in Fibonacci sequence = 144.

Try this (Text book Page No.75)

Question 1.
Are two consecutive Fibonacci numbers relatively prime?
Solution:
GCD of two consecutive numbers in Fibonacci sequence is 1.
∴ They are relatively prime.

Try These (Text book Page No. 78)

Question 1.
The teacher should give oral instructions to the students to draw the geometrical figure already drawn by him / her.
i) Draw a square. In the middle of the square, draw a circle in such a way that the circle does not touch any side of the square. Divide the circle into four equal parts. Shade the bottom right part of the circle. Ask the students to show that figure drawn by them.
ii) Draw a triangle on a piece of paper. Make it crazy looking by adding some features. Give instructions to your friend to draw it exactly the same.

Solution:
i) The figure will be as drawn below.
ii) The instructions may be:

1. Draw a square of side 3 cm.
2. Draw an equilateral triangle of side 2 cm inside the square without touching the sides of the square.
3. Draw a small circle at the middle of the triangle.
4. Draw two eyes above the circle.
5. Draw a mouth below the circle.
6. Draw two legs at the base of the triangle.
7. Draw hands to the other to sides of the triangle stretching inside the square. Draw two ears above the hands.

Question 2.
Suppose your friend wants to come to your house from his/her house. Give clear instructions in order, to reach your house.
Solution:
Activity to be done by the students themselves

Students can Download Maths Chapter 3 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Additional Questions

Additional Questions and Answers

Exercise 3.1

Question 1.
Write any three expressions each having 4 terms:
Solution:
(i) 2x³ – 3x² + 3xy + 8
(ii) 7x³ + 9y² – 2xy² – 6
(iii) 9x² – 2x + 3xy – 1

Question 2.
Identify the co-efficients of the terms of the following expressions
(i) 2x – 2y
(ii) x + y +3
Solution:
(i) 2x – 2y
The co-efficient of x in 2x is 2
The co-efficient of y in – 2y is – 2

(ii) x + y + 3
The co-efficient of x is 1
The co-efficient ofy is 1
The constant term is 3

Question 3.
Group the like terms together from the following: 6x, 6, -5x, – 5, 1, x, 6y, y, 7y, 16x, 3
Solution:
We have 6x, -5x, x, 16x are like terms
6y, y, 7y, are like terms
6, – 5, 1, 3 are like terms

Question 4.
Give the algebraic expressions for the following cases:
(i) One half of the sum of a and b.
(ii) Numbers p and q both squared and added
Solution:
(i) \(\frac{1}{2}\) (a + b)
(ii) p² + q²

Exercise 3.2

Question 1.
If A = 2a² – 4b – 1 ; B = 5a² + 3b – 8 and C = 2a² – 9b + 3 then find the value of A – B + C.
Solution:
Given A = 2a² – 4b – 1 ; B = 5a² + 3b – 8 ; C = 2a² – 9b + 3
A – B + C = (2a² – 4b – 1) – (5a² + 3b – 8) + (2a² – 9b + 3)
= 2a² – 4b – 1 + (-5a² – 3b + 8) + 2a² – 9b + 3
= 2a² – 4b – 1 – 5a² – 3b + 8 + 2a² – 9b + 3
= 2a² – 5a² + 2a² – 4b – 3b – 9b – 1 + 8 + 3
= (2 – 5 + 2) a² + (-4 – 3 – 9) 6 + (-1 + 8 + 3)
= -a² – 16b + 10

Question 2.
How much 2x³ – 2x² + 3x + 5 is greater than 2x³ + 7x² – 2x + 7?
Solution:
The required expression can be obtained as follows.
= 2x³ – 2x² + 3x + 5 – (2x³ + 7x² – 2x + 7)
= 2x³ – 2x² + 3x + 5 + (-2x³ – 7x² + 2x – 7)
= 2x³– 2x² + 3x + 5 – 2x³ – 7x² + 2x – 7
= (2 – 2) x³ + (-2 – 7) x² + (3 + 2) x + (5 – 7)
= 0x³ + (-9x²) + 5x – 2 = -9x² + 5x – 2
∴ 2x³ – 2x² + 3x + 5 is greater than 2x³ + 7x² – 2x + 7 by -9x² + 5x – 2

Question 3.
What should be added to 2b² – a² to get b² – 2a²
Solution:
The required expression is obtained by subtracting 2b² – a² from b² – 2a²
b² – 2a² – (2b² – a²) = b² – 2a² + (-2b² + a²)
= b² – 2a² – 2b² + a²
= (1 – 2) b² + (-2 + 1) a² = -b² – a²
So -b² – a² must be added

Exercise 3.3

Question 1.
Length of one side of an equilateral triangle is 3x – 4 units. Find the perimeter.
Solution:
Equilateral triangle has three sides equal.
Perimeter = Sum of three sides
= (3x – 4) + (3x – 4) + (3x – 4) = 3x – 4 + 3x – 4 + 3x – 4
= (3 + 3 + 3)x + [(-4) + (-4) + (-4)] = 9x + (-12) = 9x – 12
∴ Perimeter = 9x – 12 units.

Question 2.
Find the perimeter of a square whose side is y – 2 units.
Solution:
Perimeter = (y – 2) + (y – 2) + (y – 2) + (y – 2)
= y – 2 + y – 2 + y – 2 + y – 2 = 4y – 8
Perimeter of the square = 4y – 8 units.

Question 3.
Simplify 3x – 5 – x + 9 if x = 3
Solution:
3x – 5 – x + 9 = 3(3) – 5 – 3 + 9
= 9 – 5 – 3 + 9 = 18 – 8 = 10

Students can Download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.4

Miscellaneous Practice Problems

Question 1.
Subtract – 3ab – 8 from 3ab – 8. Also subtract 3ab + 8 from -3ab – 8.
Solution:
Subtracting -3ab – 8 from 3ab + 8
= 3ab + 8 – (-3ab – 8) = 3ab + 8 + (3ab + 8)
= 3ab + 8 + 3ab + 8 = (3 + 3) ab + (8 + 8)
= 6ab + 16
Also subtracting 3 ab + 8 from – 3ab – 8
= – 3ab – 8 – (3ab + 8) = – 3ab – 8 + (-3ab – 8) = – 3ab – 8 – 3 ab – 8
= [(-3) + (- 3)] ab + [(-8) + (-8)] = – 6ab + (- 16)
= -6ab – 16

Question 2.
Find the perimeter of a triangle whose sides are x + 3y, 2x + y, x – y.
Solution:
Perimeter of a triangle = Sum of three sides
= (x + 3y) + (2x + y) + (x – y)
= x + 3y + 2x + y + x – y
= (1 + 2 + 1)x + (3 + 1 + (-1))y = 4x + 3y
∴ Perimeter of the triangle = 4x + 3y

Question 3.
Thrice a number when increased by 5 gives 44. Find the number.
Solution:
Let the required number be x.
Thrice the number = 3x.
Thrice the number increased by 4 = 3x + 5
Given 3x + 5 = 44
3x + 5 – 5 = 44 – 5
3x = 39
\(\frac{3 x}{3}=\frac{39}{3}\)
x = 13
∴ The required number = 13

Question 4.
How much smaller is 2ab + 4b – c than 5ab – 3b + 2c.
Solution:
To find the answer we have to find the difference.
Here greater number 5ab – 3ab + 2c.
∴ Difference = 5ab – 3b + 2c – (2ab + 4b – c) = 5ab – 3b + 2c + (- 2ab -4b + c)
= 5ab – 3b + 2c – 2ab – 4b + c
= (5 – 2) ab + (-3 – 4) b + (2 + 1) c = 3ab + (-7)b + 3c
= 3ab – 7b + 3c
It is 3ab – 7b + 3c smaller.

Question 5.
Six times a number subtracted from 40 gives – 8. Find the number.
Solution:
Let the required number be x. Six times the number = 6x.
Given 40 – 6x = – 8
-6x + 40 – 40 = -8 – 40
– 6x = – 48
\(\frac{-6 x}{-6}=\frac{-48}{-6}\)
x = 8
∴ The required number is 8.

Challenge Problems

Question 6.
From the sum of 5x + 7y -12 and 3x – 5y + 2, subtract the sum of 2x – 7y – 1 and – 6x + 3y + 9.
Solution:
Sum of 5x + 7y – 12 and 3x – 5y + 2 .
= 5x + 7y- 12 + 3x – 5y + 2 = (5 + 3) x + (7 – 5) y + ((- 12) + 2)
= 8x + 2y – 10.
Again Sum of 2x – 7y – 1 and – 6x + 3y + 9
= 2x – 7y – 1 + (- 6x + 3y + 9) = 2x – 7y – 1 – 6x + 3y + 9
= (2 – 6) x + (- 7 + 3) y + (- 1 + 9)
= – 4x – 4y + 8
Now 8x + 2y – 10 – (-4x – 4y + 8)
= 8x + 2y – 10 + (4x + 4y – 8)
= 8x + 2y – 10 + 4x + 4y – 8
= (8 + 4) x + (2 + 4) y + ((- 10) + (- 8))
= 12x + 6y – 18

Question 7.
Find the expression to be added with 5a – 3b – 2c to get a – 4b – 2c?
Solution:
To get the required expression we must subtract 5a – 3b + 2c from a – 4b – 2c.
∴ a – 4b – 2c – (5a – 3b + 2c) = a – 4b – 2c + (- 5a + 3b – 2c)
= a – 4b – 2c – 5a + 3b -2c
= (1 – 5) a + (- 4 + 3) b + (- 2 – 2) c
= – 4a – b – 4c.
∴ -4a – b – 4c must be added.

Question 8.
What should be subtracted from 2m + 8n + 10 to get – 3m + 7n + 16?
Solution:
To get the expression we have to subtract – 3m + 7n + 16 from 2m + 8n + 10.
(2m + 8n + 10) – (-3m + 7n + 16) = 2m + 8n + 10 + 3m – 7n – 16
= (2 + 3) m + (8 – 7) n + (10 – 16)
= 5m + n – 6

Question 9.
Give an algebraic equation for the following statement:
“The difference between the area and perimeter of a rectangle is 20”.
Solution:
Let the length of a rectangle = l and breadth = b then Area = lb; Perimeter = 2(1 + b)
Area – Perimeter = 20
∴ lb – 2(l + b)

Question 10.
Add : 2a + b + 3c and a + \(\frac{1}{3}\)b + \(\frac{2}{5}\)c
Solution:

Students can Download Maths Chapter 3 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Intext Questions

Exercise 3.1

Try These (Text Book Page No. 51)

Question 1.
Identify the variable and constants among the following terms.
a, 11 – 3x, xy, -89, -m, -n, 5, 5ab, -5 3y, 8pqr, 18, -9t, -1, -8
Solution:
Variable : a, -3x, xy, -m, -n, 5ab, 3y, -9t, 8pqr
Constants : 11, -89, 5, -5, 18, -1, -8

Question 2.
Complete the following table.

Solution:

Try this (Text book Page No. 53)

Question 1.
Can we use the operations multiplication and division to combine terms?
Solution:
No, We can use addition and subtraction to combine terms.
If we use multiplication or division to combine then it become a single term.
Eg : xy, \(\frac{x}{y}\) are monomials.

Try This (Text book Page No. 54)

Question 1.
Complete the following table by forming expressions using the terms given. One is done for you.

Solution:

Try this (Text book Page No. 56)

Question 1.
Identify the like terms among the following and group them.
7xy, 19x, 1, 5y, x, 3yx, 15, -13y, 6x, 12xy, -5, 16y, -9x, 15xy, 23, 45y, -8y, 23x, -y, 11
Solution:
7xy, 3yx, 12xy, 15xy, are like terms
19x, x, 6x,-9x, 23x, are like terms
5y, -13y, 16y, 45y, -8y, -y, are like terms
1, 15, -5, 23, 11, are like terms.

Try This (Text book Page No. 57)

Question 1.
Try to find the value of the following expressions if p = 5 and q = 6.
(i) p + q
(ii) q – p
(iii) 2p + 2 > q
(iv) pq – p – q
(v) 5pq – 1
Solution:
(i) Given p = 5; q = 6
p + q = 5 + 6 = 11
(ii) q – p = 6 – 5 = 1
(iii) 2p + 2 > q = 2(5) + 3(6) = 10 + 18 = 28
(iv) pq – p – q = (5) (6) – 5 – 6 = 30 – 5 – 6 = 25 – 6 = 19

Exercise 3.2

Try These (Text book Page No. 59)

Question 1.
Add the terms
(i) 3p, 14p
(ii) m, 12m, 21m
(iii) 11abc, 5abc
(iv) 12y, -y
(v) 4x, 2x, -7x.
Solution:
(i) 3p + 14p = 17p
(ii) m + 12m + 21m = (1 + 12 + 21 )m
= 34 m
(iii) 11abc + 5abc = (11 + 5) abc
= 16 abc
(iv) 12y + (-y) = (12 + (-1))y
= (12 – 1 )y
= 11y
(v) 4x + 2x + (-7x) = (4 + 2+(-7))x
= (6 + (-7))x
= -1x

Ty this (Text Book Page No. 60)

Question 1.
3x; + (y – x) = 3x + y – x, but 3x – (y – x) ≠ 3x – y – x. why ?
Solution:
In the first case
LHS = 3x + (y – x) = 3x + y – x = 3x – x + y = (3 – 1)x + y
= 2x + y
RHS = 3x + y – x = 2x + y
LHS = RHS ⇒ 3x + (y – x) = 3x + y – x
But in the second case
LHS = 3x – (y – x) = 3x – y + x
= (3 + 1)x – y = 4x – y
RHS = 3x – y – x = 3x – x – y
LHS ≠ RHS
∴ 3x – (y – x) ≠ 3x – y – x

Try this (Page No. 1)

Question 1.
What will you get if twice a number is subtracted from thrice the same number?
Solution:
Let the unknown number be x.
Twice the number = 2x.
Thrice the number = 3x.
Twice the number is subtracted from thrice the number = 3x – 2x = (3 – 2)x = x

Exercise 3.3

Try These (Text book Page No. 65)

Question 1.
Try to construct algebraic equations for the following verbal statements.

Question 1.
One third of a number plus 6 to 10.
Solution:
\(\frac{1}{3}\) + 6 = 10

Question 2.
The sum of five times of x and 3 is 28
Solution:
5 (x + 3) = 28

Question 3.
Taking away 8 from y gives 11
Solution:
y – 8 = 11

Question 4.
Perimeter of a square with side a is 16 cm.
Solution:
4 × a = 16

Question 5.
Venkat’s mother’s age is 7 years more than 3 times venkat’s age. His mother’s age is 43 years.
Solution:
3x + 7 = 43, where x is venkat’s age.

Try this (Text book Page No. 65)

Question 1.
Why should we subtract 5 and not some other number ? why don’t we add 5 on both sides? Discuss.
Solution:
Given x + 5 = 12
(i) Our aim is to find the value of x. Which means we have to eliminate the other values from LHS. Since 5 is given with x it should be subtracted.
(ii) If we add 5 on both sides we cannot eliminate the numbers from LHS and we get x + 10.

Try this (Text book Page No. 66)

Question 1.
If the dogs, cats and parrots represents unknown find them. Substitute each of the values so obtained in the equations and verify the answers.
Solution:
(i) 1 dog + 1 dog + 1 dog = 24
3 dog = 24

(ii) 1 dog + 1 cat + 1 cat = 14
1 dog + 2cat = 14
8 + 2cat = 14
2cat = 14 – 8
2 cat = 6
ditional Questions 63″ width=”107″ height=”87″ />

(iii) 1 dog + 1 cat – 1 parrot = 9
8 + 3 – 1 parrot = 9
8 + 3 – 9 = 1 parrot
11 – 9 = 1 parrot
2 = 1 parrot
1 parrot = 2

(iv) 1 dog + 1 cat + 1 parrot = ?
8 + 3 + 2 = 13
Verification:
(i) 8 + 8 + 8 = 24
(ii) 8 + 3 + 3 = 14
(iii) 8+ 3 – 2 = 9
(iv) 8 + 3 + 2 = 13

Try These (Text book Page No. 68)

Question 1.
Kandhan and kaviya are friends. Both of them are having some pen. Kandhan: If you give me one pen then, we will have equal number of pens. Will you? Kaviya: But, if you give me one of your pens, then mine will become twice as yours. Will you?
Construct algebraic equations for this situation, can you guess and find the actual number of pens, they have?
Solution:
Let the number of pens initially Kandhan and Kaviya had be x and y respectively.

Students can Download Maths Chapter 3 Algebra Ex 3.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.3

Question 1.
Fill in the blanks.
(i) An expressions equated to another expression is called _______.
(ii) If a = 5, the value of 2a + 5 is _______.
(iii) The sum of twice and four times of the variable x is ______.
Solution:
(i) an equation
(ii) 15
(iii) 6x

Question 2:
Say True or False
(i) Every algebraic expression is an equation.
(ii) The expression 7x + 1 cannot be reduced without knowing the value of x.
(iii) To add two like terms, its coefficients can be added.
Solution:
(i) False
(ii) True
(iii) True

Question 3.
Solve (i) x + 5 = 8
(ii) p – 3 = 1
(iii) 2x = 30
(iv) \(\frac{m}{6}\) = 5
(v) 7x + 10 = 80
Solution:
(i) Given x + 5 = 8 ; Subtracting 5 on both the sides
x + 5 – 5 = 8 – 5
x = 3

(ii) Given p – 3 = 7 ; Adding 3 on both the sides,
p – 3 + 3 = 7 + 3
p = 10

(iii) Given 2x = 30 ; Dividing both the sides by 2,
\(\frac{2 x}{2}=\frac{30}{2}\)
x = 15

(iv) Given \(\frac{m}{6}\) = 5 ; Multiplying both the sides by 6,
\(\frac{m}{6}\) × 6 = 5 × 6
m = 30

(v) Given 7x + 10 = 80 ; Subtracting 10 from both the sides,
7x + 10 – 10 = 80 – 10
7x = 70
Dividing both sides by 7,
\(\frac{7 x}{7}=\frac{70}{7}\)
x = 10

Question 4.
What should be added to 3x + 6y to get 5x + 8y?
Solution:
To get the expression we should subtract 3x + 6y from 5x + 8y
5x + 8y – (3x + 6y) = 5x + 8y + (-3x – 6y)
= 5x + 8y – 3x – 6y = (5 – 3) x + (8 – 6) y
= 2x + 2y
So 2x + 2y should be added.

Question 5.
Nine added to thrice a whole number gives 45. Find the number
Solution:
Let the whole number required be x.
Thrice the whole number = 3x
Nine added to it = 3x + 9
Given 3x + 9 = 45
3x + 9 – 9 = 45 – 9 [Subtracting 9 on both sides]
3x = 36
\(\frac{3 x}{3}=\frac{36}{3}\)
x = 12
∴ The required whole number is 12

Question 6.
Find the two consecutive odd numbers whose sum is 200
Solution:
Let the two consecutive odd numbers be x and x + 2
∴ Their sum = 200
x + (x + 2) = 200
x + x + 2 = 200
2x + 2 = 200
2x + 2 – 2 = 200 – 2 [∵ Subtracting 2 from both sides]
2x = 198
\(\frac{2 x}{2}=\frac{198}{2}\) [Dividing both sides by 2]
x = 99
The numbers will be 99 and 99 + 2.
∴ The numbers will be 99 and 101.

Question 7.
The taxi charges in a city comprise of a fixed charge of ₹ 100 for 5 kms and ₹ 16 per km for ever additional km. If the amount paid at the end of the trip was ₹ 740, find the distance traveled.
Solution:
Let the distance travelled by taxi be ‘x’ km
For the first 5 km the charge = ₹ 100
For additional kms the charge = ₹ 16(x – 5)
∴ For x kms the charge = 100 + 16(x – 5)
Amount paid = ₹ 740
∴ 100 + 16 (x – 5) = 740
100 + 16 (x – 5) – 100 = 740- 100
16 (x – 5) = 640
\(\frac{16(x-5)}{16}=\frac{640}{16}\)
x – 5 = 40
x – 5 + 5 = 45 + 5
x = 45
x = 45 km
∴ Total distance travelled = 45 km

Objective Type Questions

Question 8.
The generalization of the number pattern 3, 6, 9, 12, …………. is
(i) n
(ii) 2n
(iii) 3n
(iv) 4n
Solution:
(iii) 3n

Question 9.
The solution of 3x + 5 = x + 9 is t
(i) 2
(ii) 3
(iii) 5
(iv)4
Solution:
(i) 2
Hint: 3x + 5 = x + 9 ⇒ 3x – x = 9 – 5 ⇒ 2x = 4 ⇒ x = 2

Question 10.
The equation y + 1 = 0 is true only when y is
(i) 0
(ii) -1
(iii) 1
(iv) – 2
Solution:
(ii) -1

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 1 Fractions Additional Questions

Question 1.
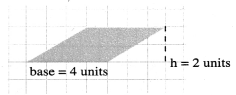
Color the part according to the given fraction.

Solution:
(i) Here \(\frac{3}{4}\) shows out of 4 parts 3 parts are shaded

(ii) Here \(\frac{2}{4}\) shows out of 4 parts 2 parts are shaded

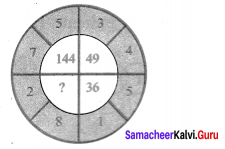
Question 2.
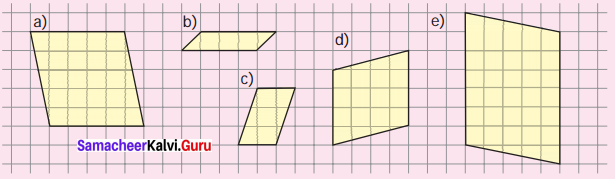
Identify the error if any

Solution:
In the given figure, shaded portion is not equal to unshaded portion. So the fraction is not equal to \(\frac{1}{2}\).

Question 3.
What fraction of an hour is 20 minutes?
Solution:
We know that total minutes in an hour = 60 min
∴ Required fraction = \(\frac{20 \min }{60 \min }=\frac{20}{60}=\frac{1}{3}\)

Question 4.
Write a fraction equivalent to \(\frac{3}{5}\) with numerator 15.
Solution:
Given, numerator of an equivalent fraction = 15
Equivalent fraction of \(\frac{3}{5}=\frac{3 \times 5}{5 \times 5}=\frac{15}{25}\)

Question 5.
Which is the larger fraction \(\frac{6}{10}\) or \(\frac{7}{10}\)?
Solution:
Here the denominators, of both fractions are same.
Also 7 > 6 So \(\frac{7}{10}>\frac{6}{10}\)

Question 6.
Sona got one-fifth of the total marks and Mala got one-third of the total marks. Who got more?
Solution:
We know that if the numerators are same in two fractions, the fraction with smaller denominator is greater.
∴ \(\frac{1}{3}>\frac{1}{5}\)
∴ Mala got more marks.

Question 7.
A piece of rope \(\frac{7}{8}\) metre long is cut into two pieces. One piece was \(\frac{1}{4}\) m long. How long is the other?
Solution:

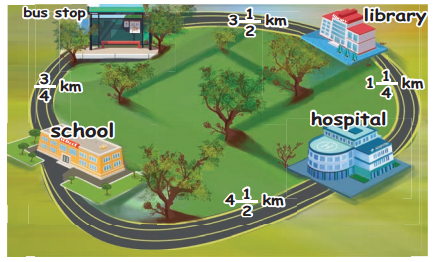
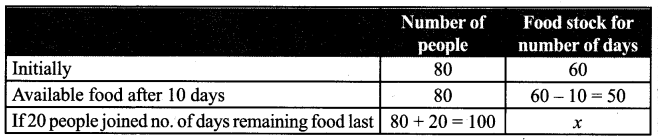
Question 8.
Meena travelled 3\(\frac{1}{2}\) km by bus, then she walked 1\(\frac{1}{8}\) km to reach a town. How much she travelled to reach-the town?
Solution:

She travelled 4\(\frac{5}{8}\) km

Question 9.
What should be subtracted from the sum of 2\(\frac{1}{4}\) and 3\(\frac{1}{7}\) to get 2\(\frac{3}{28}\) ?
Solution:

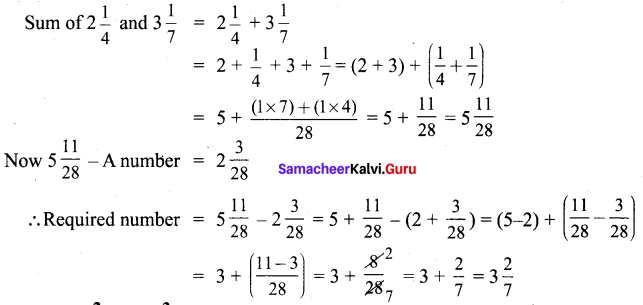
Question 10.
Compare 4\(\frac{2}{3}\) and 5\(\frac{3}{7}\)?
Solution:

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 5 Information Processing Additional Questions

Question 1.
Find the figure which is different from others.

Hint:
D is different from other figures.
All other figures has 5 lines and D has 6 lines in it.
Solution:
(d)

Question 2.
If GARIMA is coded as 725432 and TINA as 6482, how will MARTINA be coded?
(a) 3256482
(b) 3265842
(c) 3645862
(d) 3658426
Hint: GARIMA and TINA both have the lettersT and A and they are coded as 4 and 2 repectively.
∴ In MARTINA, I coded as 4 and A coded as 2 in (A) 3256482
Solution:
(a) 3256482

Question 3.
If ‘+’ is ‘×’, is ‘+% ‘×’ is ‘÷’ and ‘÷’ is then answer the following 21 ÷ 8 8 + 2 – 12 × 3 = ?
(a) 14
(b) 9
(c) 13
(d) 11

Solution:
(a) 14

Question 4.
Which number will replace the question mark?

(a) 7
(b) 14
(c) 48
(d) 49
Hint: [∴ Left side numbers are square numbers] .
Solution:
(d) 49.

Question 5.
Find the correct figure which replaces the ‘?

Hint: Upside down
Solution:

Question 6.
Which comes next ?

Hint : Here the figures rotate clockwise and anticlockwise alternatively making an angle 90° and one arrow deleted in every successive block.
Solution:

Question 7.
Find the number which replaces the question mark in the following series.

(a) 25
(b) 49
(c) 97
(d) 193

Solution:
(d) 193

Question 8.
Identify the number which replaces the question mark?

(a) 82
(b) 124
(c) 100
(d) 64
Hint: (2 + 8)² = 10² = 100
Solution:
(c) 100

Question 9.

Hint: In each step each one of the existing elements moves to the clockwise adjacent
comer. Also in one step, the element that reaches the upper-right comer gets replaced by a new element and in the next step, the element that reaches the lower left comer gets replaced by a new element.
Solution:
(d) 5

Question 10.
1, 6, 15, ?, 45, 66, 91. Find the missing term.
(a) 25
(b) 28
(c) 33
(d) 38
Hint: 1 + 5 = 6, 6 + 9 = 15, so missing term = 15 + 13 = 28
Solution:
(b) 28

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 1 Fractions Ex 1.2

Miscellaneous Practice Problems

Question 1.
Sankari purchased 2\(\frac{1}{2}\) m cloth to stitch a long skirt and 1\(\frac{3}{4}\) m cloth to stitch blouse. If the cost is ₹ 120 per metre then find the cost of cloth purchased by her
Solution:
Cloth to stitch a long skirt = 2\(\frac{1}{2}\) m
Cloth to stitch a blouse = 1\(\frac{3}{4}\) m
Total length of the cloth = \(2 \frac{1}{2}+1 \frac{3}{4} m=2+\frac{1}{2}+1+\frac{3}{4}\) m

Cost of cloth purchased by Sankari = ₹ 510

Question 2.
From his office, a person wants to reach his house on foot which is at a distance of 5\(\frac{3}{4}\) km. If he had walked 2\(\frac{1}{2}\) km, how much distance still he has to walk to reach his house?
Solution:

Distance still he has to be walked = 3\(\frac{1}{4}\) km

Question 3.
Which is smaller? The difference between \(\frac{1}{2}\) and 3\(\frac{2}{3}\) or the sum of 1\(\frac{1}{2}\) and 2\(\frac{1}{4}\)
Solution:

Question 4.
Mangai bought 6\(\frac{3}{4}\) kg of apples. If Kalai bought 1\(\frac{1}{2}\) times as Mangai bought, then how many kilograms of apples did Kalai buy?
Solution:
Weight of apples Mangai bought = 6\(\frac{3}{4}\) kg

Weight of apples Kalai bought = 10\(\frac{1}{8}\) kg

Question 5.
The length of the staircase is 5 \(\frac{1}{2}\) m. If one step is set at \(\frac{1}{4}\) m, then how many steps will be there in the staircase?
Solution:
Length of the staircase = 5\(\frac{1}{2}\) m
Distance between each step = \(\frac{1}{4}\) m
∴ Number of steps in the staircase = \(5 \frac{1}{2} \div \frac{1}{4}=\frac{11}{2} \div \frac{1}{4}=\frac{11}{2} \times \frac{4}{1}\) = 22
There will be 22 steps in the staircase

Challenge Problems

Question 6.
By using the following clues, find who am I?
(i) Each of my numerator and denominator is a single digit number.
(ii) The sum of my numerator and denominator is a multiple of 3.
(iii) The product of my numerator and denominator is a multiple of 4
Solution:
The numerator may be any one of!, 2, 3,4, 5, 6, 7, 8, 9 and the denominator may be any one of 1, 2,3,4, 5,6, 7,8,9. Sum of numerator and denominator is a multiple of 3.
∴ Possible proper fractions are \(\frac{1}{2}, \frac{1}{5}, \frac{1}{8}, \frac{2}{4}, \frac{2}{7}, \frac{3}{6}, \frac{3}{9}, \frac{4}{5}, \frac{4}{8}, \frac{5}{7}, \frac{6}{9}\)
Also given the product of numerator and denominator is a multiple of 4.
∴ Possible fractions are \(\frac{1}{8}, \frac{2}{4}, \frac{4}{5}, \frac{4}{8}\)

Question 7.
Add the difference between 1\(\frac{1}{3}\) and 3\(\frac{1}{6}\) and the difference between 4\(\frac{1}{6}\) and 2\(\frac{1}{3}\)
Solution:

Question 8.
What fraction is to be subtracted from 9\(\frac{3}{7}\) to get 3\(\frac{1}{5}\) ?
Solution:

Question 9.
The sum of two fractions is 5\(\frac{3}{9}\). If one of the fractions is 2\(\frac{3}{4}\), find the other fraction.
Solution:

The other number is 2\(\frac{7}{12}\)

Question 10.
By what number should 3\(\frac{1}{16}\) be multiplied to get 9\(\frac{3}{16}\) ?
Solution:

The number to be multiplied is 3.

Question 11.
Complete the fifth row in the Leibnitz triangle which is based on subtraction.

Solution:

Question 12.
A painted \(\frac{3}{8}\) of the wall of which one third is painted in yellow colour. What fraction is the yellow colour of the entire wall.

Solution:

\(\frac{1}{8}\) of the wall is painted yellow.

Question 13.
A rabbit has to cover 26\(\frac{1}{4}\) m to fetch its food. If it covers 1\(\frac{3}{4}\) m in one jump, thenhow many jumps will it take to fetch its food?

Solution:
Total distance to be covered by the rabbit = 26\(\frac{1}{4}\)m
Distance covered in one jump = 1\(\frac{3}{4}\) m

∴ The rabbit jumps 15 times to fetch its food.

Question 14.
Look at the picture and answer the following questions :
(i) What is the distance from School to library via bus stop?
(ii) What is the distance between school and library via Hospital?
(iii) Which is the shortest distance between (i) and (ii)?
(iv) The distance between School and Hospital is ____ times the distance between school and Bus stop.

Solution:


The distance between school and Hospital is 6 times the distance between school and bus stop.