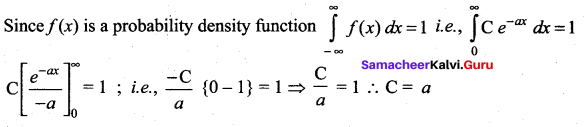You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.3
Question 1.

Solution:

Question 2.
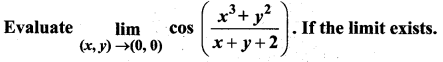
Solution:
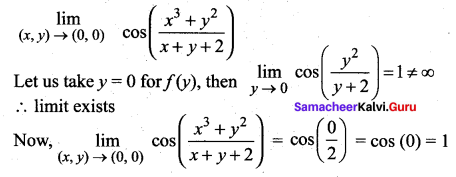
![]()
Question 3.
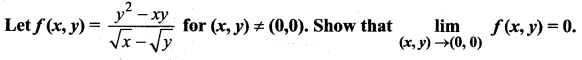
Solution:
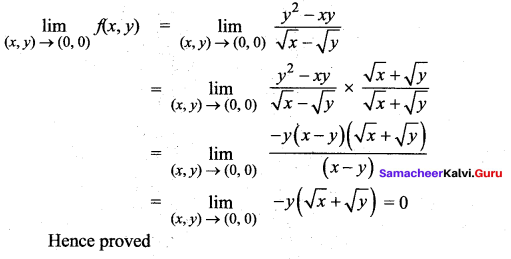
Question 4.
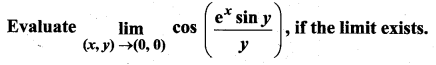
Solution:

Question 5.
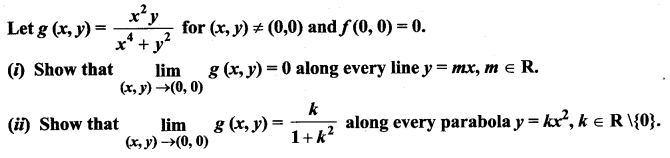
Solution:

![]()
Question 6.

Solution:

Here, f satisfies all the three conditions of continuity at (a, b). Hence, f’ is continuous at every point of R2 as (a, b) ∈ R2.
Question 7.
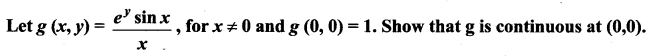
Solution:

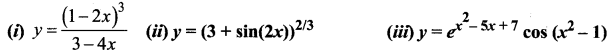

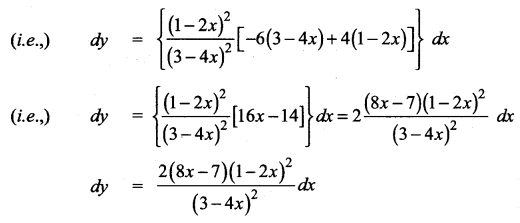

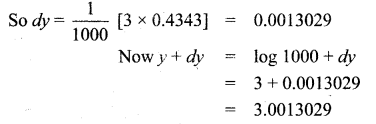

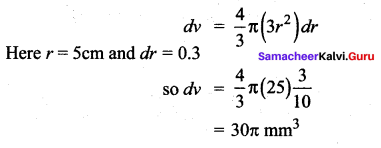
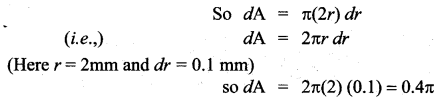

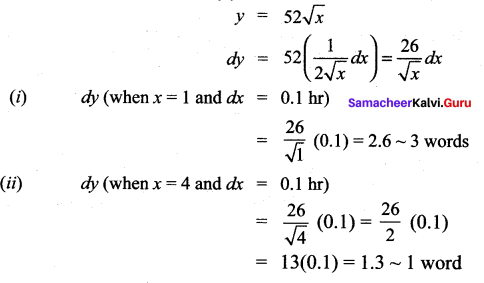

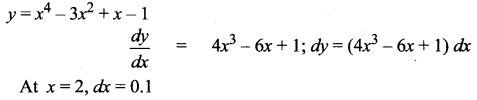


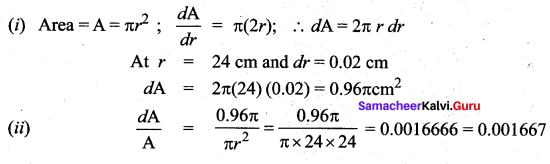
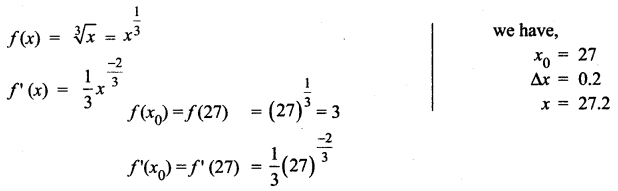


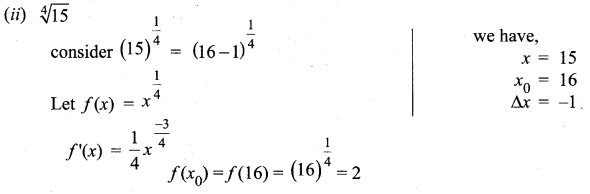

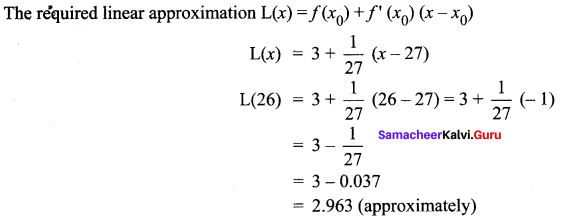





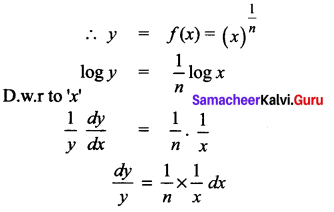



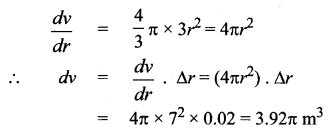
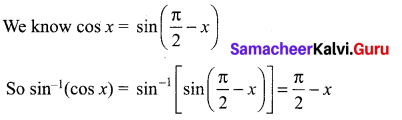

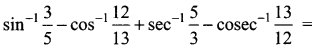 ……………
……………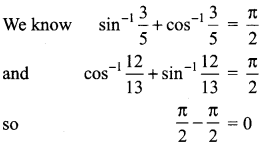

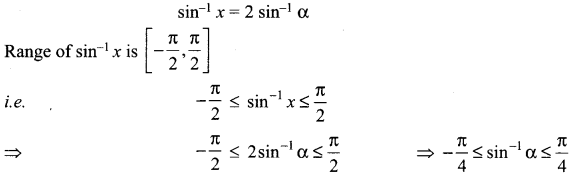
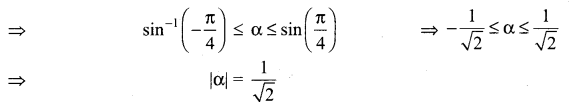


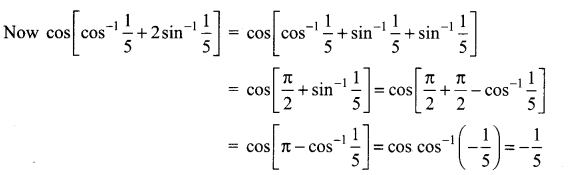
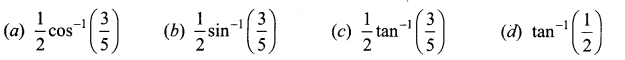
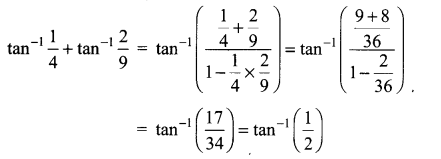


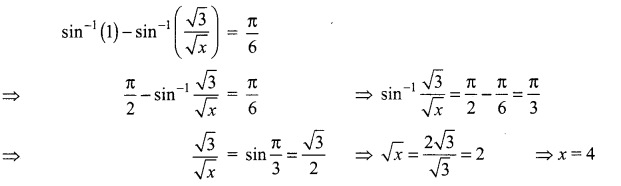


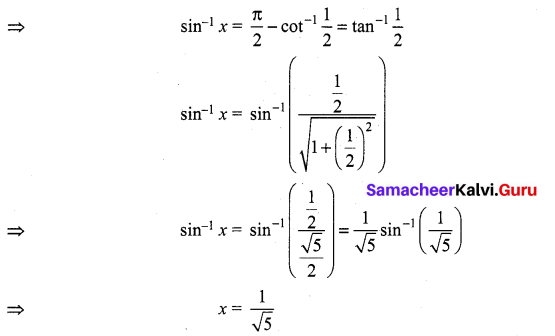


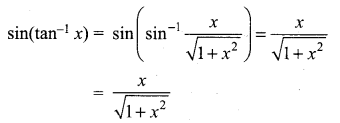
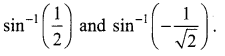
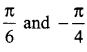
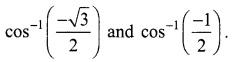
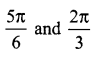
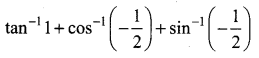
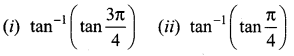
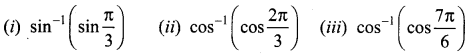
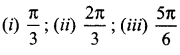
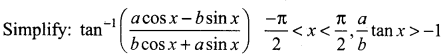

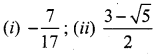
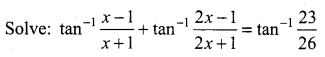
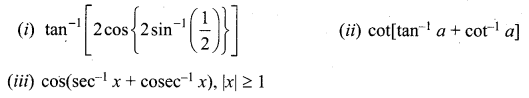
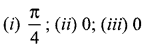
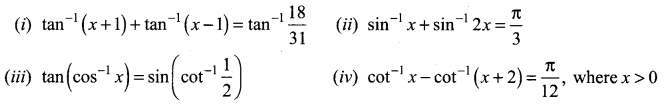
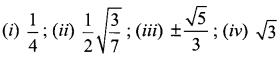

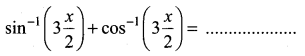

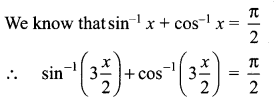

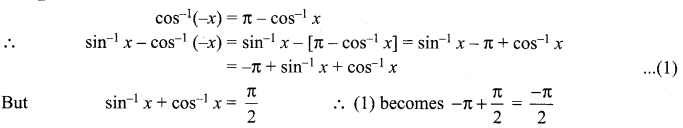
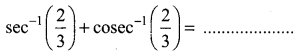
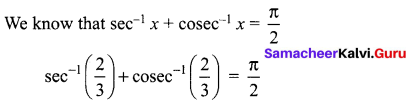
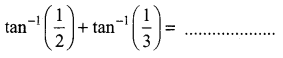
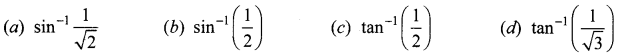
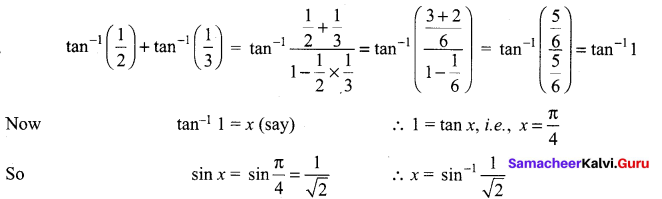
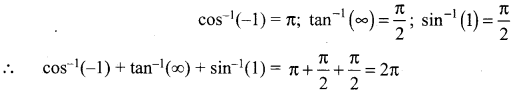
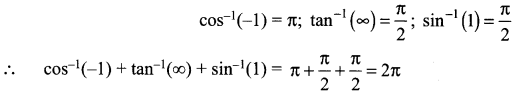
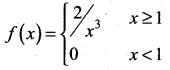

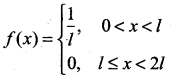 The mean and variance of the shorter of the two pieces are respectively ……..
The mean and variance of the shorter of the two pieces are respectively ……..
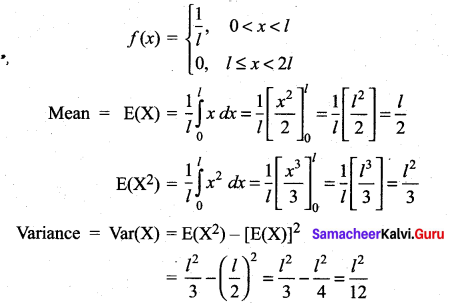

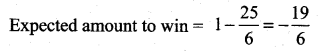
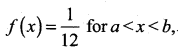 represents a probability density function of a continuous random variable X, then which of the following cannot be the value of a and b?
represents a probability density function of a continuous random variable X, then which of the following cannot be the value of a and b?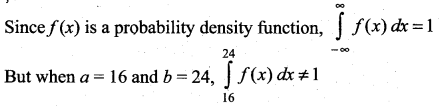
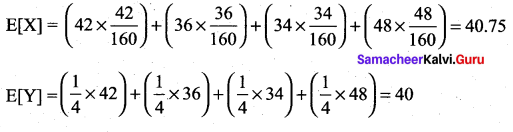

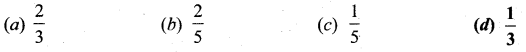
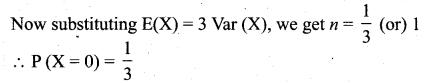
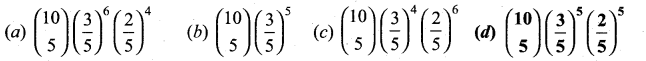
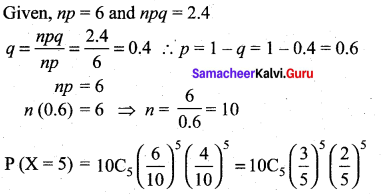


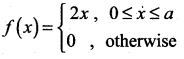 is a probability density function of a random variable, then the value of a is ……..
is a probability density function of a random variable, then the value of a is ……..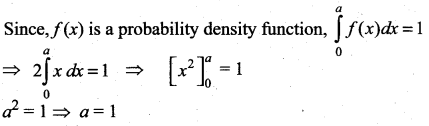


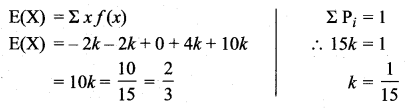
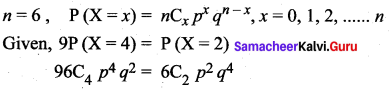
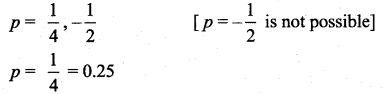

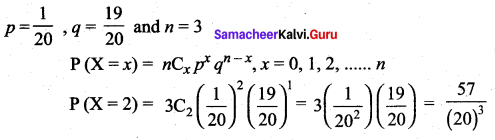
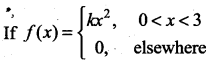 is a probability density function then the value of k is ……..
is a probability density function then the value of k is ……..
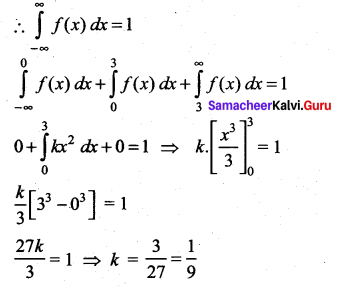
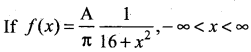 is a probability density function of a continuous random variable X, then the value of A is …………
is a probability density function of a continuous random variable X, then the value of A is …………
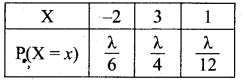
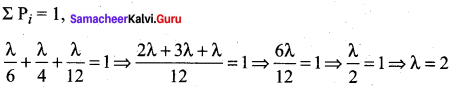
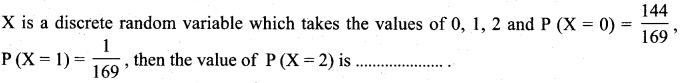

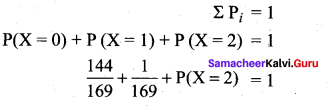
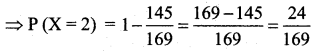


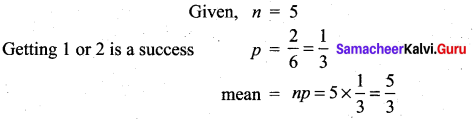
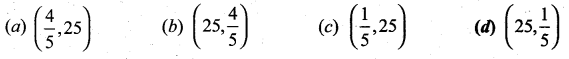


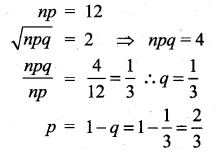


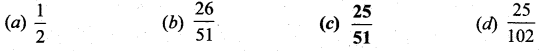






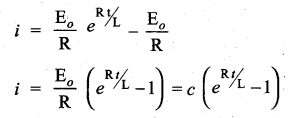
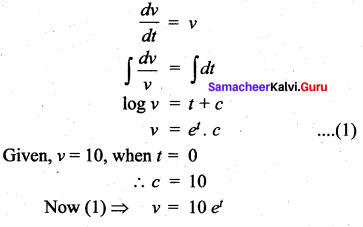

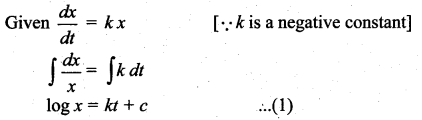

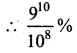 of radioactive element will remain after 1000 years.
of radioactive element will remain after 1000 years.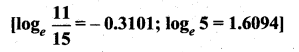

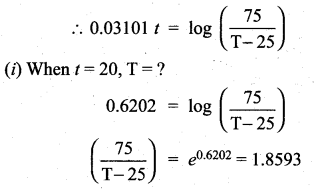


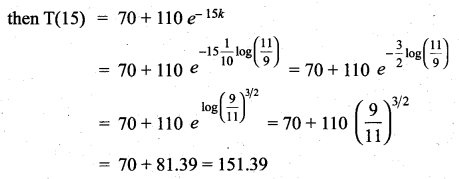

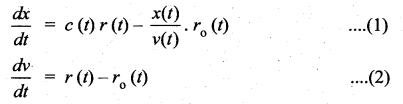
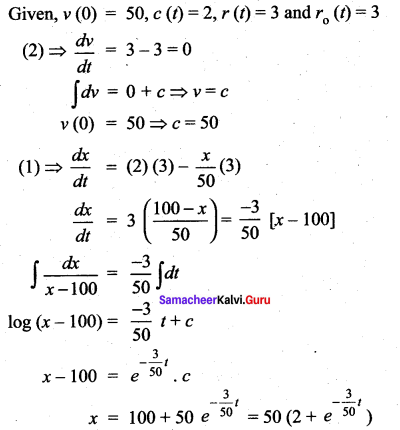
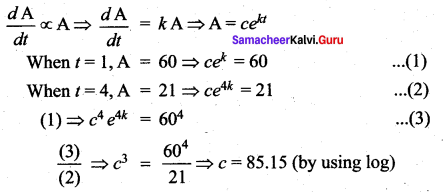
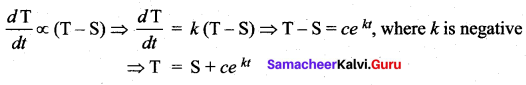
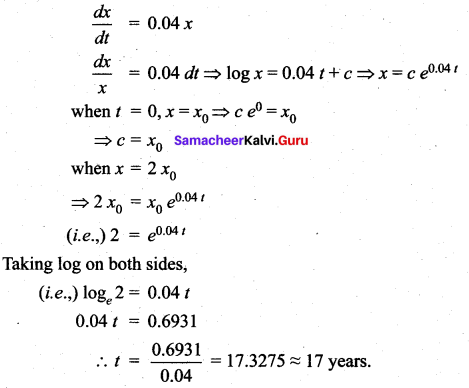
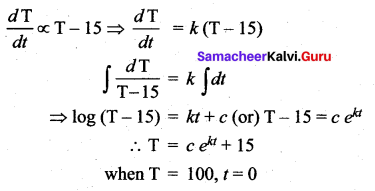
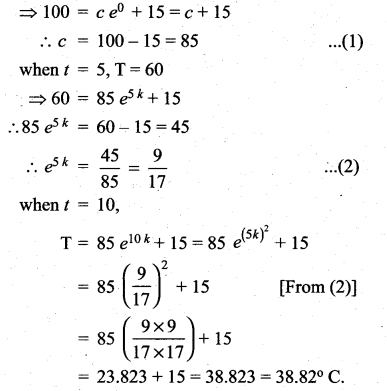



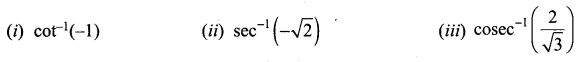


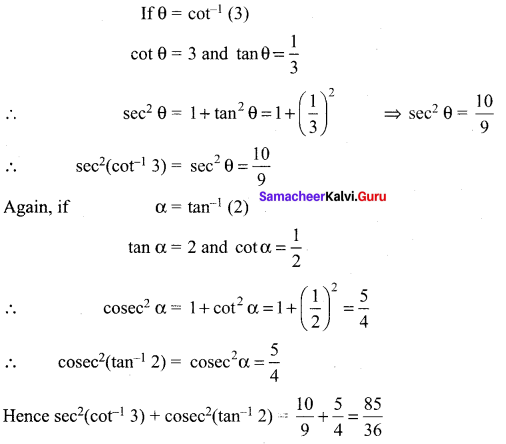
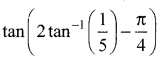
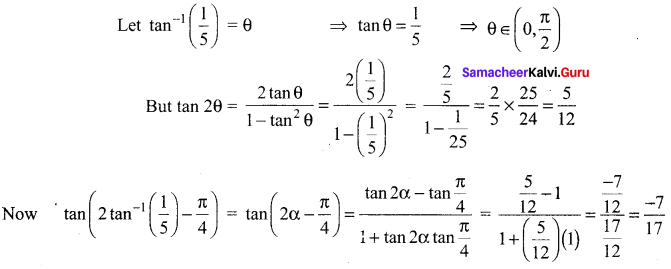



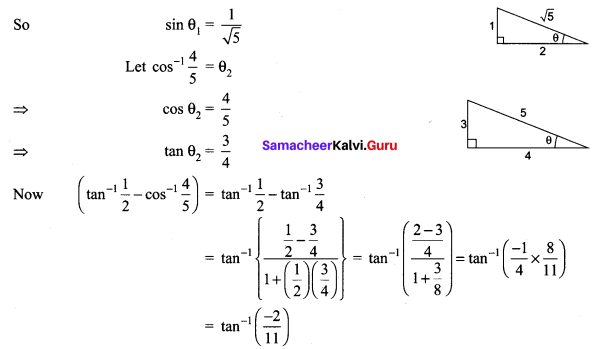


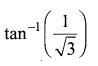

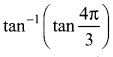

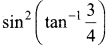





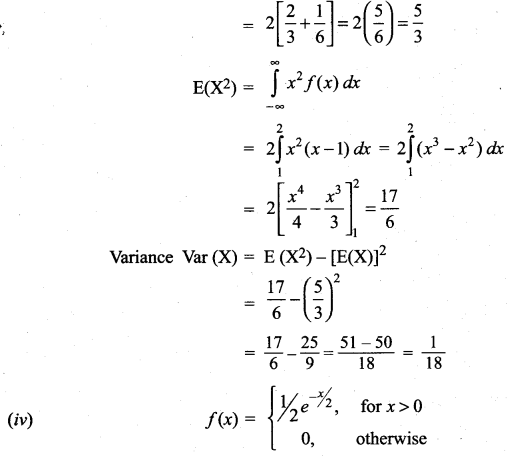

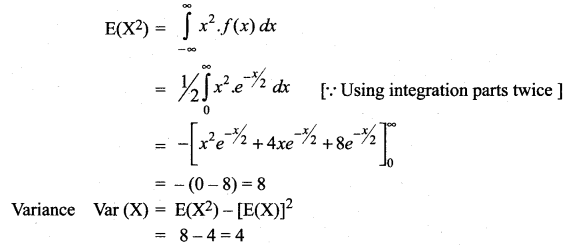

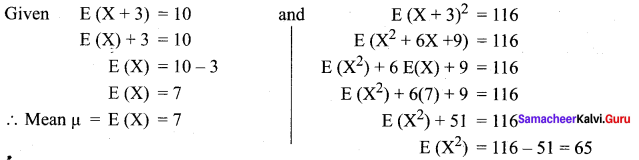

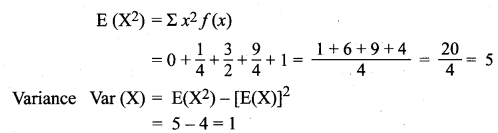
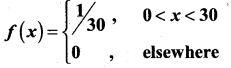
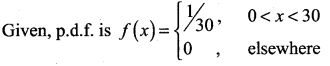
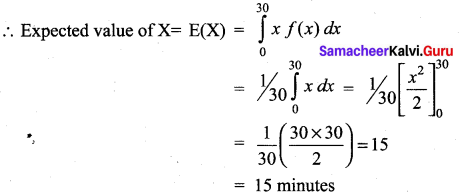
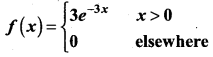 Find the expected life of this electronic equipment.
Find the expected life of this electronic equipment.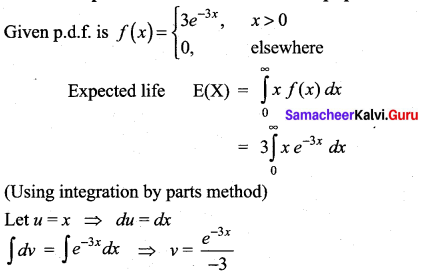

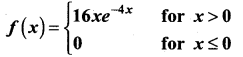 Find the mean and variance of X.
Find the mean and variance of X.

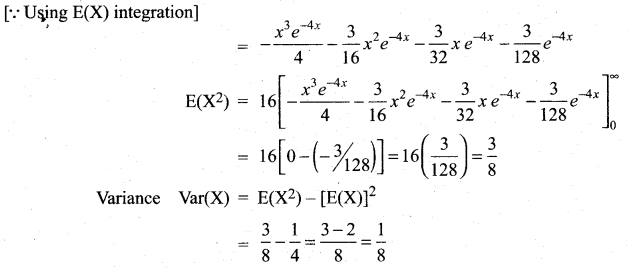

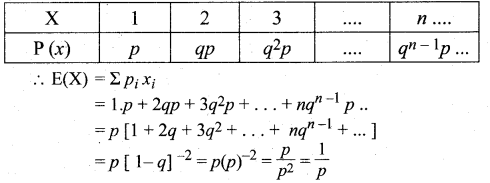

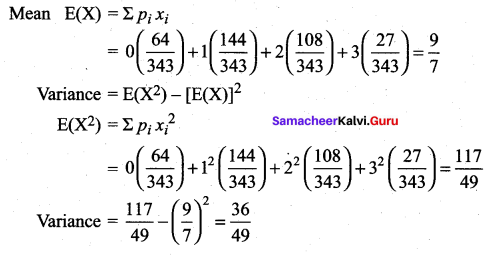
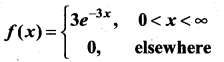


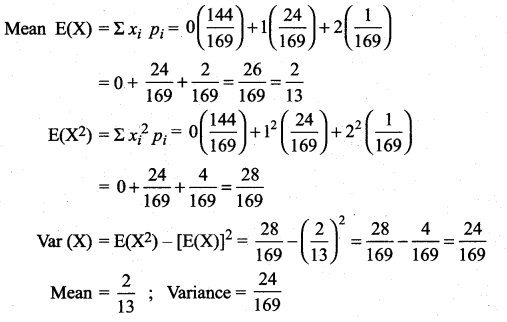
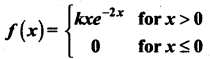 Find the value of k.
Find the value of k.
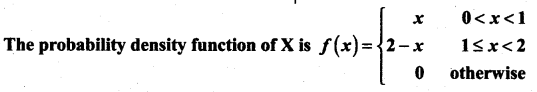


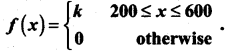

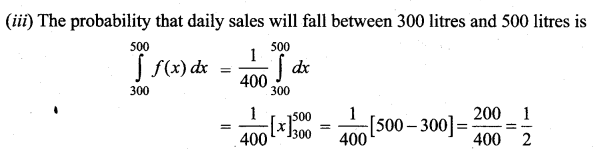




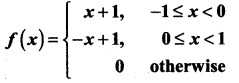

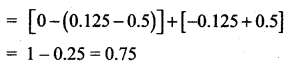
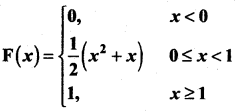 then find (i) the distribution function f(x)
then find (i) the distribution function f(x)
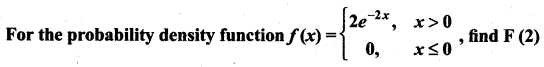

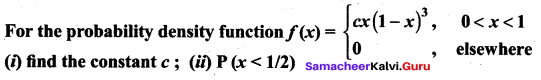
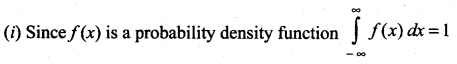
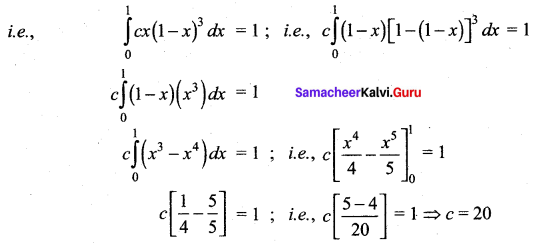

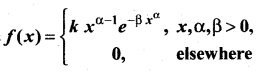 Find
Find
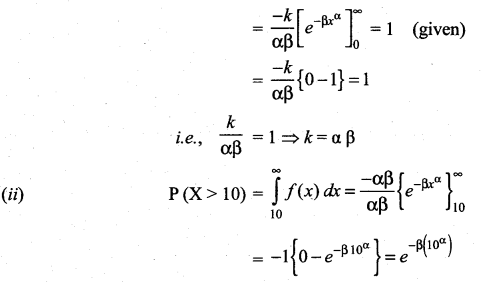
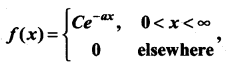 find the value of C if a > 0.
find the value of C if a > 0.