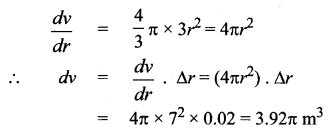You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.1
Question 1.
Let f(x) = \(\sqrt[3]{x}\). Find the linear approximation at x = 27. Use the linear approximation to \(\sqrt[3]{27.2}\).
Solution:
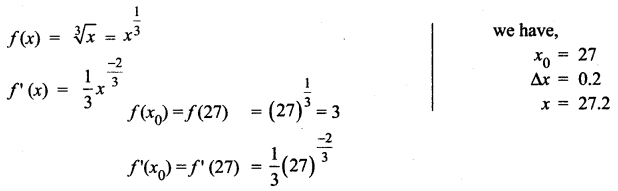

Question 2.
Use the linear approximation to find approximate values of
![]()
Solution:

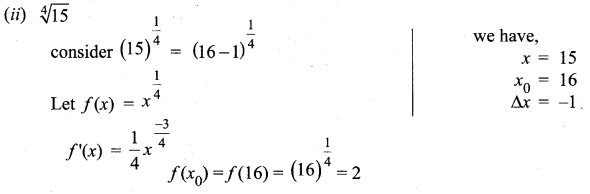

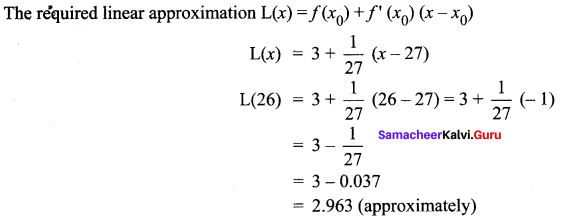
![]()
Question 3.
Find a linear approximation for the following functions at the indicated points.
(i) f(x) = x3 – 5x + 12, x0 = 2
(ii) g(x) = \(\sqrt{x^{2}+9}\) + x0 = -4
(iii) h(x) = \(\frac{x}{x+1}\), x0 = 1
Solution:
f(x) = x3 – 5x + 12
f'(x) = 3x2 – 5
f(x0) = f(2) = (2)3 – 5(2) + 12 = 8 – 10 + 12 = 10
f'(x0) = f'(2) = 3(2)2 – 5 = 12 – 5 = 7
The required linear approximation L(x) = f(x0) + f'(x0) (x – x0)
= 10 + 7 (x – 2)
= 10 + 7x – 14
= 7x – 4


Question 4.
The radius of a circular plate is measured as 12.65 cm instead of the actual length 12.5 cm. find the following in calculating the area of the circular plate:
(i) Absolute error
(ii) Relative error
(iii) Percentage error
Solution:
We know that Area of the circular plate A(r) = πr2, A'(r) = 2πr
Change in Area = A’ (12.5) (0.15) = 3.75 π cm2
Exact calculation of the change in Area = A (12.65) – A (12.5)
= 160.0225π – 156.25π
= 3.7725π cm2
(i) Absolute error = Actual value – Approximate value
= 3.7725 π – 3.75 π
= 0.0225 π cm2

![]()
Question 5.
A sphere is made of ice having radius 10 cm. Its radius decreases from 10 cm to 9.8 cm. Find approximations for the following:
(i) change in the volume
(ii) change in the surface area
Solution:
(i) We know that Volume of sphere

∴ Volume decreases by 80π cm3
(ii) Surface area of the sphere
S(r) = 4π r2
S'(r) = 8πr
Change in surface area at r = 10 is
= S'(r) [10 – 9.8]
= 8π (10) (0.2) = 16π cm2
∴ Surface Area decreases by 16π cm2
Question 6.
The time T, taken for a complete oscillation of a single pendulum with length l, is given
by the equation T = \(2 \pi \sqrt{\frac{l}{g}}\), where g is a constant. Find the approximate percentage error in the calculated value of T corresponding to an error of 2 percent in the value of 1.
Solution:

Question 7.
Show that the percentage error in the nth root of a number is approximately \(\frac{1}{n}\) times the percentage error in the number.
Solution:
Let x be the number
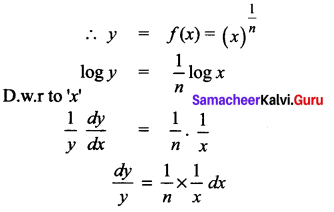
Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.1 Additional Questions Solved
Question 1.
Using differentials, find the approximate value of each of the following upto 3 places of decimal. \((255)^{\frac{1}{4}}\)
Solution:

![]()
Question 2.
Using differentials, find the approximate value of each of the following upto 3 places of decimal. \((401)^{\frac{1}{2}}\)
Solution:


Question 3.
Find approximate value of f(5.001) where f(x) = x3 – 7x2 + 15.
Solution:
Here f(x) = x3 – 7x2 + 15
f'(x) = 3x2 – 14x
Let x = 5 and x + ∆x = 5.001
∴ ∆x (x + ∆x) – x = 5.001 – 5
= 0.001
f(5.001) = f(x + ∆x)
Now ∆y = f(x + ∆x) – f(x)
f(x + ∆x) = f(x) + ∆y
= f(x) + f'(x).∆x [∴ ∆y = f'(x).∆x ]
= (x3 – 7x2 + 15) + (3x2 – 14x)(0.001)
= (53 – 7 × 52 + 15) + (3 × 52 – 14 × 5) [0.001]
= [125 – 175 + 15] + [75 – 70][0.001]
= -35 + 0.005 = – 34.995
Thus approximate value of f(5.001) is – 34.995
![]()
Question 4.
If the radius of a sphere is measured as 7m with an error of 0.02 m then find the approximate error in calculating its volume.
Solution:
Le r be the radius of the sphere and ∆r be the error in measuring the radius.
Then r = 7 m and ∆r = 0.02 m
Now volume of a sphere is given by
![]()