Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.3

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.3

Question 1.
Find the domain of the following functions:
(i) \(\tan ^{-1}(\sqrt{9-x^{2}})\)
(ii) \(\frac{1}{2} \tan ^{-1}\left(1-x^{2}\right)-\frac{\pi}{4}\)
Solution:
(i) f(x) = \(\tan ^{-1}(\sqrt{9-x^{2}})\)
We know the domain of tan^-1 x is (-∞, ∞) and range is \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
So, the domain of f(x) = \(\tan ^{-1}(\sqrt{9-x^{2}})\) is the set of values of x satisfying the inequality
\(-\infty \leq \sqrt{9-x^{2}} \leq \infty\)
⇒ 9 – x² ≥ 0
⇒ x² ≤ 9
⇒ |x| ≤ 3
Since tan x is an odd function and symmetric about the origin, tan^-1 x should be an increasing function in its domain.
∴ Domain is (2n + 1)\(\frac{\pi}{2}\)

The domain of y is (-∞, ∞) {x | x ∈ -1} and range is [-1, ∞) {y | y ≥ -1}
The domain for tan^-1(x² – 1) is (2n + 1)π. Since tan x is an odd function.

Question 2.
Find the value of
(i) \(\tan ^{-1}\left(\tan \frac{5 \pi}{4}\right)\)
(ii) \(\tan ^{-1}\left(\tan \left(-\frac{\pi}{6}\right)\right)\)
Solution:

Question 3.
Find the value of
(i) \(\tan \left(\tan ^{-1} \frac{7 \pi}{4}\right)\)
(ii) tan(tan^-1(1947))
(iii) tan(tan^-1(-0.2021))
Solution:
We know that tan(tan^-1 x) = x
(i) \(\tan \left(\tan ^{-1} \frac{7 \pi}{4}\right)=\frac{7 \pi}{4}\)
(ii) tan(tan^-1(1947))= 1947
(iii) tan(tan^-1 (-0.2021)) = -0.2021

Question 4.
Find the value of
(i) \(\tan \left(\cos ^{-1}\left(\frac{1}{2}\right)-\sin ^{-1}\left(-\frac{1}{2}\right)\right)\)
(ii) \(\sin \left(\tan ^{-1}\left(\frac{1}{2}\right)-\cos ^{-1}\left(\frac{4}{5}\right)\right)\)
(iii) \(\cos \left(\sin ^{-1}\left(\frac{4}{5}\right)-\tan ^{-1}\left(\frac{3}{4}\right)\right)\)
Solution:

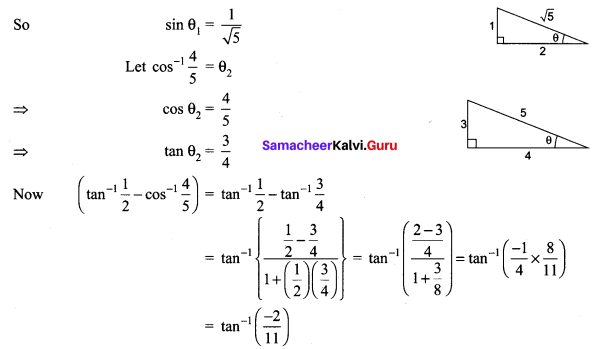
Samacheer Kalvi 12th Maths Solutions Chapter 4 Inverse Trigonometric Functions Ex 4.3 Additional Problems

Question 1.
Find the principle value of: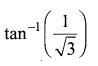
Solution:

Question 2.
Find the value of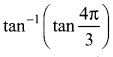
Solution:

Question 3.
Find the value of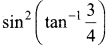
Solution: