Category: Class 7

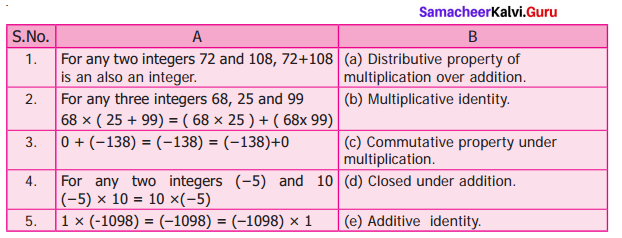
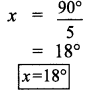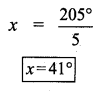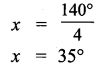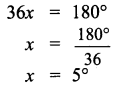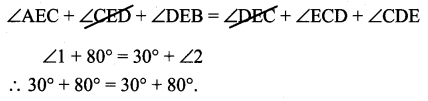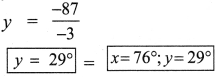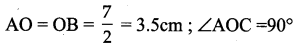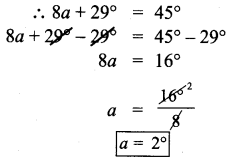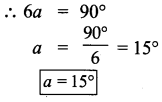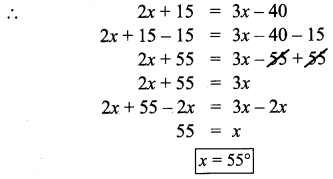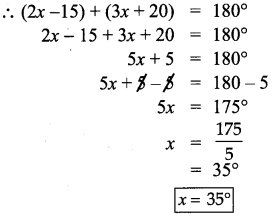Students can Download Maths Chapter 5 Geometry Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Additional Questions

Exercise 5.1

Question 1.
Can two adjacent angles be supplementary?
Solution:
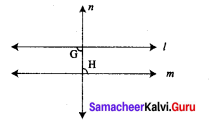
Yes, In the figure

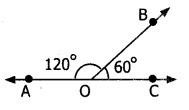
∠AOB and ∠BOC are adjacent angles.
Also ∠AOB + ∠BOC = 180°
∴ ∠AOB and ∠BOC are supplementary

Question 2.
Can two obtuse angles form a linear pair?
Solution:
No, the sum of the measures of two obtuse angles is more than 180°.

Question 3.
Can two right angles form a linear pair?
Solution:
Yes, because the sum of two right angles is 180° and form a linear pair.

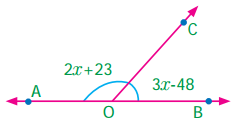
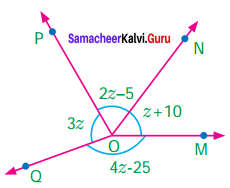
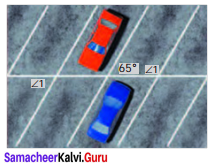
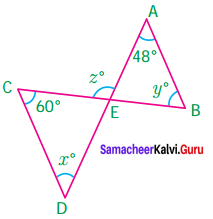
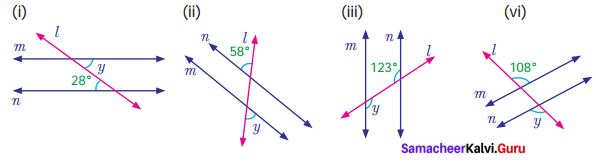
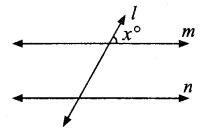
Question 4.
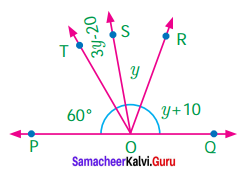
Find x, y and z from the figure.

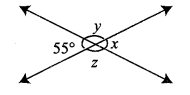
Solution:
x = 55° vertically opposite angles
y + 55° = 180°
y = 180°- 55°
y = 125°

Execise 5.2

Question 1.
Can two lines intersect in more than one point ?
Solution:
No, two lines cannot intersect in more than one point.

Question 2.
In the figure EF parallel to GH
Solution:
∠EAB = 60° and ∠ACD = 105°
Determine (i) ∠CAF and
(ii) ∠BAC

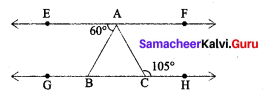
Solution:
(i) Since EF || GH and AC is a transversal
⇒ ∠CAF + ∠ACH = 180°
⇒ ∠CAF + 105° = 180° .
= 75°
(ii) ∴ EF || GH and AC is transversal.
∴ ∠EAC = ∠ACH [ ∵ Alternate interior angles]
⇒ ∠BAC = 105°
⇒ ∠BAC + ∠BAB = 105°
⇒ ∠BAC + 60° = 105°
⇒ ∠BAC = 105° – 60°
= 45°
∴ ∠CAF = 75° and ∠BAC = 45°.

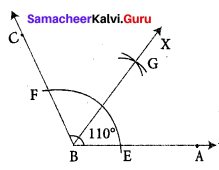
Question 3.
In the given figure, the arms of two angles are parallel. If ∠ABC = 70°, then find
(i) ∠DGC
(ii) ∠DEF

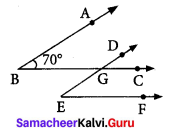
Solution:
We have AB||ED and BC || EF
(i) BC is transversal
∠DGC = ∠ABC [corresponding angles]
But ∠ABC = 70°
∠DGC = 70°

(ii) ED is a transversal to BC||EF
∴ ∠DEF = ∠DGC [corresponding]
∠DGC = 70°
∠DEF = 70°

Exercise 5.6

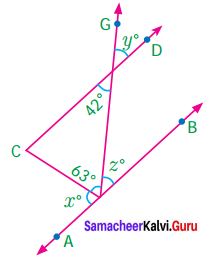
Question 1.
In the following figure, show that CD || EF
Solution:

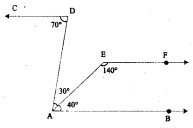
∠BAD = ∠BAE + ∠EAD
= 40°+ 30° = 70°.
and ∠CDA = 70°
∠BAD = ∠CDA
But they form a pair of alternate angles
⇒ AB || CD
Also ∠BAE + ∠AEF = 40° + 140° = 180°
But they form a pair of interior opposite angles.
⇒ AB || EF
From (1) and (2), we get
AB || CD || EF
⇒ CD || EF

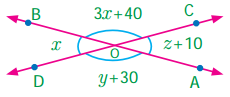
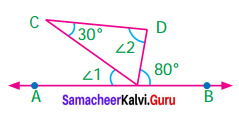
Question 2.
In the adjoining figure, the lines \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { CD } \) intersect at ‘O’. If ∠COB = 50°, find the measures of the other three angles.
Solution:
∠COB = 50°
∠AOD = 50° (vertically opposite angles)
Now ∠AOC and ∠COB form a linear pair,
Thus ∠AOC + ∠COB = 180°
⇒ ∠AOC + 50° = 180°.
∠AOC = 180° – 50° = 130°
Also ∠AOC and ∠BOD are vertically opposite angles.
∴ ∠BOD = ∠AOC = 130°
Thus the three angles are
∠AOD = 50°
∠AOC =130°
∠BOD = 130°

Students can Download Maths Chapter 5 Geometry Ex 5.6 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.6

Miscellaneous Practice Problems

Question 1.
Find the value of x if ∠AOB is a right angle.
Solution:
Given that ∠AOB = 90°

∠AOB = ∠AOC + ∠COB = 90° (Adjacent angles)
3x + 2x = 90°
5x = 90°

Question 2.
In the given figure, find the value of x.
Solution:
Since ∠BOC and ∠AOC are linear pair, their sum = 180°
2x + 23 + 3x – 48 = 180°
5x – 25 = 180°
5x – 25 + 25 = 180° + 25

Question 3.
Find the value of x, y and z.
Solution:

∠DOB and ∠BOC are linear pair
∴ ∠DOB + ∠BOC = 180°
x + 3x + 40 = 180°
4x + 40 = 180°
4x + 40 – 40 = 180° – 40°
4x = 140°

Also ∠BOD and ∠AOC are vertically opposite angles.
∴ ∠BOD = ∠AOC
x = z + 10
35° = z + 10
z + 10 – 10 = 35 – 10
z = 25°
Again ∠AOD and ∠AOC are linear pair.
∴ ∠AOD + ∠AOC = 180°
y + 30 + z + 10 = 180°
y + 30 + 25 + 10 = 180°
y + 65 = 180°
y + 65 – 65 = 180° – 65
y = 115°
∴ x = 35°,
y = 115°,
z = 25°

Question 4.
Two angles are in the ratio 11 : 25. If they are linear pair, find the angles.
Solution:
Given two angles are in the ratio 11 : 25.
Let the angles be 11x and 25x.
They are also linear pair
∴ 11x + 25x = 180°.

∴ The angles 11x = 11 × 5° = 55° and 25x = 25 × 5 = 125°.
∴ The angles are 55° and 125°.

Question 5.
Using the figure, answer the following questions and justify your answer.
(i) Is ∠1 adjacent to ∠2?
(ii) Is ∠AOB adjacent to ∠BOE?
(iii) Does ∠BOC and ∠BOD form a linear pair?
(iv) Are the angles ∠COD and ∠BOD supplementary.
(v) Is ∠3 vertically opposite to ∠1 ?

Solution:
(i) Yes, ∠1 is adjacent to ∠2.
Because they both have the common vertex ‘O’ and the common arm OA . Also their interiors do not overlap.
(ii) No, ∠AOB and ∠BOB are not adjacent angles because they have overlapping interiors.
(iii) No, ∠BOC and ∠BOD does not form a linear pair.
Because ∠BOC itself a straight angle, so the sum of ∠BOC and ∠BOD exceed 180°.
(iv) Yes, the angles ∠COD and ∠BOD are supplementary ∠COD + ∠BOD = 180°, [∵ linear pair of angles]
∴ ∠COD and ∠BOD are supplementary.
(v) No. ∠3 and ∠1 are not formed by intersecting lines. So they are not vertically opposite angles.

Question 6.
In the figure POQ, ROS and TOU are straight lines. Find the x°.

Solution:
Given TOU is a straight line.
∴ The sum of all angles formed at a point on a straight line is 180°
∠TOR + ∠ROP + ∠POV + ∠VOU = 180°.
36° + 47°+ 45° + x° = 180°.
128° + x° = 180°
128° + x° – 128° = 180° – 128°
x = 52°

Question 7.
In the figure AB is parallel to DC. Find the value of ∠1 and ∠2. Justify your answer.

Solution:
Given AB || DC
AB and CD are parallel lines Taking CE as transversal we have.
∠1 = 30°, [∵ alternate interior angles]
Taking DE as transversal
∠2 = 80°.[∵ alternate interior angles]
∠1 = 30° and ∠2 = 80°
Justification:
CDE is a triangle

Question 8.
In the figure AB is parallel to CD. Find x, y and z.

Solution:
Given AB || CD
∴ Z = 42 (∵ Alternate interior angles)
Also y = 42° [vertically opposite angles]
Also x° + 63° + z° = 180°
x° + 63° + 42° = 180°
x° + 105° = 180°
x°+ 105° – 105° = 180° – 105°
x° = 75°
∴ x = 75°;
y = 42°;
z = 42°

Question 9.
Draw two parallel lines and a transversal. Mark two alternate interior angles G and H. If they are supplementary, what is the measure of each angle?
Solution:
l and m are parallel lines and n is the transversal.
∠G and ∠H are alternate interior angles.
∠G = ∠H …… (1)
Given ∠G and ∠G are Suplementary

Question 10.
A plumber must install pipe 2 parallel to pipe 1. He knows that ∠1 is 53. What is the measure of ∠2?

Solution:
Given ∠1 = 53°

Clearly ∠1 and ∠2 are interior angles on the same side of the transversal and so they are supplementary.
∠1 + ∠2 = 180°
53° + ∠2 = 180°
53° + ∠2 – 53° = 180° – 53°
∠2 = 127°

Challenge Problems

Question 11.
Find the value of y.

Solution:
Cleary POQ is a straight line”
Sum of all angles formed at a point on a straight line is 180°
∴ ∠POT + ∠TOS + ∠SOR + ∠ROQ = 180°
60° + (3y – 20°) + y° + (y + 10°) = 180°
60° + 3y – 20° + y° + y° + 10° = 180°
5y + 50° = 180°
5y + 50° – 50° = 180° – 50
5y = 130°
\(y=\frac{130^{\circ}}{5}\)
y = 26°

Question 12.
Find the value of z.

Solution:
The sum of angles at a point is 360°.
∴ ∠QOP + ∠PON + ∠NOM + ∠MOQ = 360°
3z + (2z – 5) + (z + 10) + (4z – 25) = 360°
3z + 2z + z + 4z — 5 +10 — 25 = 360°
10z – 20° = 360°
10z – 20° + 20 = 360°+ 2
10z = 380°
\(z=\frac{380^{\circ}}{10}\)
z = 38°

Question 13.
Find the value of x and y if RS is parallel to PQ.

Solution:
Given RS || PQ
Considering the transversal RU, we have y = 25° (corresponding angles)
Considering ST as transversal

Question 14.
Two parallel lines are cut by a transversal. For each pair of interior angles on the same side of the transversal, if one angle exceeds the twice of the other angle by 48°. Find the angles.
Solution:
Let the two parallel lines be m and n and l be the transversal
Let one of the interior angles on the same side of the transversal be x°
Then the other will be 2x + 48.
We know that they are supplementary.

Question 15.
In the figure, the lines GH and IJ are parallel. If ∠1 = 108° and ∠2 = 123°, find the value of x, y and z.
Solution:
Given GH || IZ
∠1 = 108°
∠2 = 123°
∠1 + ∠KGH = 180 [linear pair]
108° + ∠KGH = 180°

108° + ∠KGH – 108° = 180° – 108°
∠KGH = 72°
∠KGH = x° (corresponding angles if KG is a transversal)
∴ x° = 72°
Similarly
∠2 + ∠GHK = 180° (∵ linear pair)
123° + ∠GHK = 180°
123° + ∠GHK – 123° = 180° – 123°
∠GHK = 57°
Again ∠GHK = y° (corresponding angles if KH is a transversal)
y = 57°
x° +y° + z° = 180° (sum of three angles of a triangle is 180°)
72° + 57° + z° = 180°
129° + z° = 180°
129° + z° – 129° = 180° – 129°
z = 51°
x = 72°,
y = 57°,
z = 51°

Question 16.
In the parking lot shown, the lines that mark the width of each space are parallel. If
∠1 = (2x – 3y)°; ∠2 = (x + 39)° find x° and y°.

Solution:
From the picture
∠2 + 65° = 180° [Sum of interior angles on the same side of a transversal]
x + 39° + 65° = 180°
x + 104° = 180°
x + 104° – 104° = 180° – 104°
x = 76°
Also from the picture
∠1 = 65° [alternate exterior angles]
2x – 3y = 65°
2 (76) – 3y = 65°
152° – 3y = 65°
152° – 3y – 152° = 65 – 152°
-3y = -87

Question 17.
Draw two parallel lines and a transversal. Mark two corresponding angles A and B. If ∠A = 4x, and ∠B = 3x + 7, find the value of x. Explain.
Solution:
Let m and n are two parallel lines and l is the transversal.
A and B are corresponding angles.
We know that corresponding angles are equals,

Question 18.
In the figure AB in parallel to CD. Find x°, y° and z°.
Solution:

Given AB||CD
Then AD and BC are transversals.
x = 48°, alternate interior angles; AD is transversal y = 60°, alternate interior angles; BC is transversal
∠AEB + 48° + y° = 180°, (sum of angles of a triangle is 180°)

Question 19.
Two parallel lines are cut by transversal. If one angle of a pair of corresponding angles can be represented by 42° less than three times the other. Find the corresponding angles.
Solution:
We know that the corresponding angles are equal.
Let one of the corresponding angles be x.
Then the other will be 3x – 42°.

Question 20.
In the given figure, ∠8 = 107°, what is these sum of the angles ∠2 and ∠4.
Solution:
Given ∠8 = 107°
∠2 = 107°
[∵ ∠8 and ∠2 are alternate exterior angles, ∵ ∠8 = ∠2]

Students can Download Maths Chapter 5 Geometry Ex 5.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.5

Question 1.
Construct the following angles using ruler and compass only.
(i) 60°
(ii) 120°
(iii) 30°
(iv) 90°
(v) 45°
(vi) 150°
(vii) 135°
Solution:
(i) 60°
Construction :
Step 1: Drawn a line and marked a point ‘A’ on it.
Step 2: With A as center drawn an arc of convenient radius to meet the line at a point B.

Step 3: With the same radius and B as center drawn an arc to cut the previous arc at C.
Step 4: Joined AC. The ∠ABC is the required angle with the measure 60°.

(ii) 120°
Construction :

We know that there are two 60° angles in 120°.
∴ We can construct two 60° angles consecutively construct 120°
Step 1: Drawn a line and marked a point ‘A’ on it.
Step 2: With ‘A’ as center, drawn an arc of convenient radius to the line at a point B.
Step 3: With the same radius and B as center, drawn an arc to cut the previous arc at C.
Step 4: With the same radius and C as center, drawn an arc to cut the arc drawn in step 2 at D.
Step 5: Joined AD. Then ∠BAD is the required angle with measure 120°.

(iii) 30°
Constructions :

Since 30° is half of 60°, we can construct 30° by bisecting the angle 60°.
Step 1: Drawn a line and marked a point A on it.
Step 2: With A as center drawn an arc of convenient radius to the line to meet at a point B.
Step 3: With the same radius and B as center drawn an arc to cut the previous arc at C.
Step 4: Joined AC to get ∠BAC = 60°
Step 5: With B as center drawn an arc of convenient radius in the interior of ∠BAC
Step 6: With the same radius and C as center drawn an arc to cut the previous arc at D.
Step 7: Joined AD.
∴ ∠BAD is the required angle of measure 30°.

(iv) 90°
Construction :

Step 1: Drawn a line and marked a point ‘A’ on it.
Step 2: With ‘A’ as center, drawn an arc of convenient radius to the line at a point B.
Step 3: With the same radius and B as center drawn an arc to cut the previous arc at ‘C’.
Step 4: With the same radius and C as center, drawn an arc to cut the arc drawn in step 2 at D.
Step 5: Joined AD. ∠BAD = 120°.
Step 6: With C as center, drawn an arc of convenient radius in the interior of ∠CAD.
Step 7: With the same radius and D as center, drawn an arc to cut the arc at E.
Step 8: Joined AF ∠BAE = 90°.

(v) 45°
Construction :
Step 1: Drawn a line and marked a point A on it

Step 2: With A as center, drawn an arc of convenient radius to the line at a point B.
Step 3: With the same radius and B as center drawn an arc to cut the previous arc at C.
Step 4: With the same radius and C as center, drawn an arc to cut the arc drawn in step 2 at D.
Step 5: Joined AD. ∠BAD = 120°.
Step 6: With G as center and any convenient radius drawn an arc in the interior of ∠GAB
Step 7: With the same radius and B as center drawn an arc to cut the arc at F.
Step 8: Joined AF. ∠BAF = 45°

(vi) 150°
Construction :

Since 150° = 60° + 60° + 30°; we construct as follows
Step 1: Drawn a line and marked a point A on it.
Step 2: With ‘A’ as center, drawn a full arc of convenient radius to the line at a point B and at E the other end.
Step 3: With the same radius and B as center, drawn an arc to cut the previous arc at C.
Step 4: With the same radius and C as center drawn an arc to cut the already drawn arc at D.
Step 5: With D as center, drawn an arc of convenient radius in the interior of ∠DAE
Step 6: With E as center and with the same radius drawn an arc to cut the previous arc at F.
Step 7: Joined AF, ∠FAB = 150°.

(vii) 135°
Construction :

Step 1: Drawn a line and marked a point A on it.
Step 2: With ‘A’ as center, drawn an arc of convenient radius to the line at a point B.
Step 3: With the same radius and B as center drawn an arc to cut the previous arc at C.
Step 4: With the same radius and C as center, drawn an arc to cut the arc at D.
Step 5: With C and D as centers drawn arcs of convenient (same) radius in the interior of ∠CAD. Marked the point of intersection as E.
Step 6: Joined AE, through G. ∠BAE = 90°.
Step 7: Drawn angle bisector to ∠GAH through F.
Now ∠BAF = 135°.

Students can Download Maths Chapter 2 Measurements Ex 2.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.3

Question 1.
Find the missing values.

Solution:
(i) Given Height h = 10 m ; Parallel sides a = 12 m ; b = 20 m
Area of the Trapezium = \(\frac{1}{2}\)h(a + b) sq. units = \(\frac{1}{2}\) × 10 × (12 + 20)m²
= (5 × 32)m² = 160 m²

(ii) Given the parallel sides a = 13 cm ; 6 = 28 cm
Area of the trapezium = 492 sq. cm
\(\frac{1}{2}\)h(a + b) = 492
\(\frac{1}{2}\) × h × (13 + 28) = 492
h × 41 = 492 × 2
h = \(\frac { 492\times 2 }{ 41 } \)
h = 24 cm

(iii) Given height ‘h’ = 19 m; Parallel sides b = 16 m
Area of the trapezium = 323 sq. m
\(\frac{1}{2}\)h(a + b) = 323
\(\frac{1}{2}\) × h × (a + 16) = 323
a + 16 = \(\frac { 323\times 2 }{ 19 } \) = 34
a = 34 – 16 = 18 m
a = 18 m

(iv) Given the height h- 16 cm ; Parallel sides a = 15 cm
Area of the trapezium = 360 sq. cm
\(\frac{1}{2}\) × h × (a + b) = 360
\(\frac{1}{2}\) × 16 × (15 + 6) = 360
15 + b = \(\frac{360}{8}\) =45
b = 45 – 15 = 30
b = 30 cm
Tabulating the results we get

Question 2.
Find the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm.
Solution:
Given the parallel sides a = 24 cm; b = 20 cm

Distance between a and b is ‘h’ = 15 cm
Area of the trapezium = \(\frac{1}{2}\) × h × (a + b) sq. units
= \(\frac{1}{2}\) × 15 × (24 + 20) cm²
= \(\frac{1}{2}\) × 15 × 44 = 330 cm²
Area of the trapezium = 330 cm²

Question 3.
The area of a trapezium is 1586 sq. cm. The distance between its parallel sides is 26 cm. If one of the parallel sides is 84 cm then find the other side.
Solution:
Given one parallel side = 84 cm. Let the other parallel side be ‘b’ cm.
Distance between a and b is h = 26 cm.
Area of the trapezium = 1586 sq. cm

∴ The other parallel side = 38 cm.

Question 4.
The area of a trapezium is 1080 sq. cm. If the lengths of its parallel sides are 55.6 cm and 34.4 cm. Find the distance between them.
Solution:
Length of the parallel sides a = 55.6 cm ; b = 34.4 cm
Area of the trapezium = 1080 sq. cm

Distance between parallel sides = 24 cm.

Question 5.
The area of a trapezium is 180 sq. cm and its height is 9 cm. If one of the parallel sides is longer than the other by 6 cm. Find the length of the parallel sides.
Solution:
Let one of the parallel side be ‘a’ cm. Given one parallel sides is longer than the other by 6 cm.
i.e. b = a + 6 cm Also given height ‘h’ = 9 cm
Area of trapezium = 180 sq. cm

2a + 6 = 40
2a = 40 – 6 = 34
a = \(\frac{34}{2}\) = 17 cm
b = a + 6= 17 + 6 = 23 cm
∴ The parallel sides are a = 17 cm and b = 23 cm

Question 6.
The sunshade of a window is in the form of isoceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq. cm.
Solution:
Given the parallel sides a = 81 cm ; b = 64 cm
Distance between ‘a’ and ‘b’ is height h = 6 cm
Area of the trapezium = \(\frac{1}{2}\) × h(a + b) sq. units
= \(\frac{1}{2}\) × 6³ × (81 + 64) = 3 × 145 cm² = 435 cm²
Cost of painting 1 cm² = ₹ 2
Cost of painting 435 cm² = ₹ 435 × 2 = ₹ 870
Cost of painting = ₹ 870 .

Question 7.
A window is in the form of trapezium whose parallel sides are 105 cm and 50 cm respectively and the distance between the parallel sides is 60 cm. Find the cost of the glass used to cover the window at the rate of ₹ 15 per 100 sq. cm.
Solution:
Given the parallel sides a = 105 cm ; b = 50 cm ; Height = 60 cm
Area of the trapezium = \(\frac{1}{2}\) × h × (a + b)sq. units = \(\frac{1}{2}\) × 60 × (105 + 50) cm²
= 30 × 155 cm² = 4650 cm²
For 100 cm² cost of glass used = ₹15
∴ For 4650 cm² cost of glass = ₹ \(\frac{4650}{100}\) × 15 = ₹ 697.50
Cost of the glass used = ₹ 697.50

Objective Type Questions

Question 8.
The area of the trapezium, if the parallel sides are measuring 8 cm and 10 cm and the height 5 cm is
(i) 45 sq. cm
(ii) 40 sq. cm
(iii) 18 sq. cm
(iv) 50 sq. cm
Solution:
(i) 45 sq. cm
Hint: \(\frac{1}{2}\) × h × (a + b) = \(\frac{1}{2}\) × 5 × (10 + 8) = 45

Question 9.
In a trapezium if the sum of the parallel sides is 10 m and the area is 140 sq.m, then the height is
(i) 7 cm
(ii) 40 cm
(iii) 14 cm
(iv) 28 cm
Solution:
(iv) 28 cm
Hint: Area = \(\frac{1}{2}\) × h × (a + b) = 140 = \(\frac{1}{2}\) × h × 10 ⇒ h = 28

Question 10.
When the non-parallel sides of a trapezium are equal then it is known as
(i) a square
(ii) a rectangle
(iii) an isoceles trapezium
(iv) a parallelogram
Solution:
(iii) an isoceles trapezium

Students can Download Maths Chapter 5 Geometry Ex 5.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.4

Question 1.
Construct the following angles using protractor and draw a bisector to each of the angle using ruler and compass.
(a) 60°
(b) 100°
(c) 90°
(d) 48°
(e) 110°.
Solution:
(a) 60°
Construction:

Step 1: Drawn the given angle ∠ABC with the measure 60° using protractor.
Step 2: With B as centre and convenient radius, drawn an arc to cut BA and BC. Marked the points of intersection as E on BA and F on BC.
Step 3: With the same radius and E as centre drawn an arc in the interior of ∠ABC and another arc of same measure with centre at F to cut the previous arc.
Step 4: Marked the point of intersection as G. Drawn a ray BX through G. BG is the required bisector of the given ∠ABC

(b) 100°

Construction :
Step 1: Drawn the given angle ∠ABC with the measure 100° c using protractor.
Step 2: With B as centre and convenient radius, drawn an arc to cut BA and BC. Marked the points of intersection as E on BA and F on BC.
Step 3: With the same radius and E as centre drawn an arc in the interior of ∠ABC and another arc of the same measure with centre at F to cut the previous arc.
Step 4: Marked the point of intersection at G. Drawn a ray BX through G.
BG is the required bisector of angle ∠ABC
∠ABG = ∠GBC = 50°

(c) 90°
Construction :

Step 1: Drawn the given angle ∠ABC with the measure 90° using protractor.
Step 2: With B as center and convenient radius, drawn an arc to cut BA and BC. Marked the points of intersection as E on BA and F on BC.
Step 3: With the same radius and E as center drawn an arc in the interior of ∠ABC and another arc of same measure with center at F to cut the previous arc.
Step 4: Mark the point of interaction as G. Drawn a ray BX through G. BG is the required bisector of the given angle ∠ABC
∠ABG = ∠GBC = 45°

(d) 48°

Construction :
Step 1: Drawn the given angle ∠ABC with the measure 48° using protractor.
Step 2: With B as center and convenient radius, drawn an arc to cut BA and to cut BA and BC. Marked the points of intersection as E on BA and F on BC.
Step 3: With the same radius and E as center drawn an arc in the interior of ∠ABC and another arc of the same measure with center at F to cut the previous arc.
Step 4: Marked the point of intersection as G. Drawn a ray BX through G. BG is the required bisector of the given angle ∠ABC
Now ∠ABC = ∠GBC = 24°

(e) 110°
Construction:

Step 1: Drawn the given angle ∠ABC with the measure 110° using protractor.
Step 2: With B as center and convenient radius, drawn an arc to cut BA and BC. Marked points of intersection as E on BA and F BC.
Step 3: With the same radius and E as center, drawn an arc in the interior of ∠ABC and another arc of same measure with center at F to cut the previous arc.
Step 4: Mark the point of intersection as G. Drawn a ray BX through G. BG is the
required bisector of the given angle ∠ABC
∠ABG = ∠GBC = 55°

Students can Download Maths Chapter 5 Geometry Ex 5.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.3

Question 1.
Draw a line segment of given length and construct a perpendicular bisector to each line segment using scale and compass
(a) 8 cm
(b) 7 cm
(c) 5.6 cm
(d) 10.4 cm
(e) 58 cm
Solution:
(a) 8 cm
Construction :

Step 1: Drawn a line. Marked two points A and B on it so that AB = 8 cm
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of the same length one above AB and one below AB
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs drawn in step 2. Marked the points of intersection of the arcs as C and D.
step 4: Joined C and D, CD intersect AB. Marked the point of intersection as ‘O’.
CD is the required perpendicular bisector of AB.

(b) 7 cm
Construction :

step 1: Drawn a line and marked points A and B on it so that AB = 7 cm.
step 2: Using compass with A as centre and radius more than half of the length of AB drawn two arcs of same length one above AB and one below AB.
step 3: With the same radius and B as centre drawn two arcs to cut the already drawn arcs in step 2. Marked the intersection of the arcs as C and D
step 4: Joined C and D, CD is the required perpendicular bisector of AB.

(c) 5.6 cm.
Construction :

Step 1: Drawn a line and marked two points A and B on it so that AB = 5.6cm
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of the same length, one above AB and one below AB
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs drawn in step 2 and marked the points of intersection of the arcs as C and D
Step 4: Joined C and D. CD intersects AB. Marked the point of intersection as ‘O’CD is the required perpendicular bisector of AB.
Now ∠AOC = 90° AO = BO = 2.8 cm

(d) 10.4 cm
Construction :

Step 1: Drawn a line and marked two points A and B on it so that AB = 10.4 cm.
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of same length one above AB and one below AB.
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs drawn in step 2 and marked the points of intersection of the arcs as C and D.
Step 4: Joined C and D. CD intersects AB. Marked the points of intersection as O. CD is the required perpendicular bisector.
Now ∠AOC = 90° ; AO = BO = 5.2 cm

(e) 58 mm

Construction :

Step 1: Drawn a line. Marked two points A and B on it so that
AB = 5.8 cm = 58 mm.
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of the same length one above AB and one below AB.
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs of drawn in step 2. Marked the points of intersection of the arcs as C and D.
Step 4: Joined C and D. CD intersects AB. Marked the point of intersection as O. CD is the required perpendicular bisector. ∠AOC = 90°
AO = BO = 2.9 cm

Students can Download Maths Chapter 1 Number System Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 1 Number System Additional Questions

Additional Questions and Answers

Exercise 1.1

Question 1.
When Malar woke up her temperature was 102°F. Two hours later it was 3° lower, what was her temperature then?
Solution:
Initially Malar’s temperature = 102°F
After two hours it lowered 3° ⇒ -3°F
Here present temperature = 102° + (-3°) = 99°F

Question 2.
An elevator is on the twentieth floor. It goes down 11 floors and then up 5 floors.
What floor is the elevator on now?
Solution:
Present location of the elevator = 20th floor
If it goes down 11 floor ⇒ (-11)
= 20 +(-11) = 9th floor
If it goes up 5 floor ⇒ 9 + 5
= 14th floor

Question 3.
16 + ___ = 16. The property expressed here is ____
Solution:
16 + 0 = 16.
0 is the additive identity on integers.

Exercise 1.2

Question 1.
Roman civilization began in 509 BC and ended in 476 AD. How long did Romans civilization last.
Solution:
From the start of common era no. of years upto 476
AD = 476
From 509 BC to start of common era years = 509
Total years Roman civilization last = 476 + 509 = 985 years.

Question 2.
A submarine was situated 450 feet below sea level. If it descends 300 feet. What is its new position?
Solution:
Position of submarine = -450 ft.
Again it descends 300 feet ⇒ -300 feet
∴ New position = —450 + (-300) = -750 ft.
∴ It was 750 feet below sea level.

Question 3.
In January the high temperature recorded was 90°F and the low temperature was -2°F. Find the difference between the high and the low temperatures?
Solution:
The high temperature recorded = 90°F
The low temperature recorded = -2°F
Difference = 90°F – (-2°F)
= 90°F + (Additive inverse of -2°F)
= 90°F + (+2°F) = 92°F

Exercise 1.3

Question 1.
Ani is scuba diving. She descends 5 feet below sea level. She descends the same distance 4 more times. What is Anis final elevation?
Solution:
Ani descends 5 feet below sea level once she descends 4 more times
∴ She descends (5 × 4) + 5 feet in total = 20 + 5 = 25 feet below sea level

Question 2.
The price of a plant reduced ₹ 6 per week for 7 weeks. By how much did the price of the plant change over the 7 weeks?
Solution:
The price of plant reduced in a week = ₹ 6
∴ The price reduced in 7 weeks = 7 × 6 = 42

Question 3.
The product of three integers is -3. Determine all of the possible values for the three factors?
Solution:
Product of three integers = -3
Possible factors are (1 × -1 × 3), (-1 × -1 × -3), (1 × 1 × -3)

Exercise 1.6

Question 1.
Simplify the following using suitable properties.
(a) (-1650) × (-2) + (-1650) × (-98)
(b) (9150 × 405) – (8150 × 405)
Solution:
(a) (-1650) × (-2) + (-1650) × (-98)
= 1650 [(-1) × (-2) + (-1) × -98] = 1650 (2 + 98) [Distributive property]
= 1650 × 100= 1,65,000

(b) (9150 × 405) – (8150 × 405)
= 405 (9150 – 8150) = 405 × 1000
= 4,05,000

Question 2.
Which is greater: (9 + 7) × 1000 or 9 + 7 × 1000?
Solution:
(9 + 7) × 1000 = 16 × 1000 = 16,000
9 + 7 × 1000 = 9 + 7000 = 7,009
16,000 > 7009
∴ (9 + 7) × 1000 > [9 + 7 × 1000]

Question 3.
Simiplify: 80 ÷ [240 ÷ (-24)] + 7
Solution:
We have
80 ÷ [240 ÷ (-24)] + 7
= 80 ÷ \(\left[\frac{240}{-24}\right]\) + 7
= 80 ÷ (-10) + 7 = \(-\left[\frac{80}{10}\right]\) + 7 = (-8) + 7 = -1

Students can Download Maths Chapter 1 Number System Ex 1.6 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 1 Number System Ex 1.6

Miscellaneous Practice Problems

Question 1.
What should be added to -1 to get 10?
Solution:
(-1) + a number = 10
∴ The number = 10 + 1 = 11

Question 2.

Solution:

Question 3.
Substract 94860 from (-86945)
Solution:
-86945 – (94860) = -86945 + (Additive inverse of 94860)
= -86945 + (-94860) = -1,81,805

Question 4.
Find the value of (-25) + 60 + (-95) + (-385)
Solution:
(-25) + 60 + (-95) + (-385) = 35 + (-95) + (-385) = -60 + (-385) = -445

Question 5.
Find the sum of (-9999) (-2001) and (-5999).
Solution:
(-9999) + (-2001) + (-5999) = -12,000 + (-5999) = -17,999

Question 6.
Find the product of (-30) × (-70) × 15.
(-30) × (-70) × 15 = (+2100) × 15 = 31,500

Question 7.
Divide-72 by 8.
Solution:
\(\frac{-72}{8}\) = -9

Question 8.
Find two pairs of integers whose product is +15.
Solution:
(i) (+3) × (+5)
(ii) (-3) × (-5)

Question 9.
Check the following for equality.
(i) (11 + 7) + 10 and 11 + (7 + 10)
(ii) (8 – 13) × 7 and 8 – (13 × 7)
(iii) [(-6) – (+8)] × (-4) and (-6) – [8 × (-4)]
(iv) 3 × [(-4) + (-10)] and [3 × (-4) + 3 × (-10)]
Solution:
(i) LHS = (11 + 7) + 10 = 18 + 10 = 28
RHS = 11 + (7 + 10)
= 11 + (17) = 28
LHS = RHS
∴ (11 + 7) + 10 = 11 + (7 + 10)

(ii) LHS = (8 – 13) × 7 = -5 × 7 = -35
RHS = 8 – (13 × 7) = 8 – 91 = -83
LHS ≠ RHS
∴ (8 – 13) × 7 ≠ 8 – (13 × 7)

(iii) LHS = [(-6) – (+8)] × (-4) = [(-6) + (-8)] × (-4) = (-14) × (-4) = +56
RHS = (-6) – [8 × (-4)] = -6 – (-32)
= -6 + (+32) = +26
LHS ≠ RHS
∴ [(-6) – (+8)] × (-4) ≠ (-6) – [8 × (-4)]

(iv) LHS = 3 × [(-4) + (-10)] = 3 × (-14) = -42
RHS = [3 × (-4) + 3 × (-10)] = (-12) + (-30) = -42
LHS = RHS
3 × [(-4) + (-10)] = [3 × (-4) + 3 × (-10)]

Question 10.
Kalaivani had ₹ 5000 in her bank account on 01.01.2018. She deposited ₹ 2000 in January and withdrew ₹ 700 in February. What was Kalaivani’s bank balance on 01.04.2018, if she deposited ₹ 1000 and withdraw ₹ 500 in March.
Solution:
Initial bank balance = ₹ 5000 ; Total deposits: January : ₹ 2000 ; March : ₹ 1000
Total deposits upto March = ₹ 5000 + ₹ 2000 + ₹ 1000 = ₹ 8000
Amount withdrawn: February : ₹ 700 (-)
March : ₹ 500 (-)
∴ Total amount withdrawn = (-700) + (-500) ₹ -1200
Net bank balance = ₹ 8000 – ₹ 1200 = ₹ 6800

Question 11.
The price of an item x increases by ₹ 10 every year and an item y decreases by ₹ 15 every year. If in 2018, the price of x is ₹ 50 andy is ₹ 90, then which item will be costlier in the year 2020?
Solution:
Amount increases for x every year = ₹ 10.
Price ofx in 2018 = ₹ 50 ; Price of x in 2019 = ₹ 50 + ₹ 10 = ₹ 60
Price of x in 2020 = ₹ 60 + ₹ 10 = ₹ 70 Amount decreases for y per year = ₹ 15
Price of y in 2018 = ₹ 90
Price of y in 2019 = ₹ 90 – ₹ 15 = ₹ 75
Price of y in 2020 = ₹ 75 – ₹ 15 = ₹ 60
Here 70 > 60. Item x will costlier in year 2020.

Question 12.
Match the statements in Column A and Column B.

Solution:
1. – d
2. – a
3. – e
4. – c
5. – b

Challenge Problems

Question 13.
Say True or False.
(i) The sum of a positive integer and a negative integer is always a positive integer.
(ii) The sum of two integers can never be zero
(iii) The product of two negative integers is a positive integer.
(iv) The quotient of two integers having opposite sign is a negative integer.
(v) The smallest negative integer is -1.
Solution:
(i) False
(ii) False
(iii) True
(iv) True
(v) False

Question 14.
An integer divided by 7 gives a result -3. What is that integer?
Solution:
According to the problem \(\frac{\text { An integer }}{7}\) = -3
∴ The integer = -3 × 7
The required integer = -21.

Question 15.
Replace the question mark with suitable integer in the equation.

Solution:

Question 16.
Can you give 10 pairs of single digit integers whose sum is zero?
Solution:
1 + (-1) + 2 + (-2) + 3 + (-3) + 4 + (-4) + 5 + (-5) = 0

Question 17.
If P = -15 and Q = 5 find (P – Q) – (P + Q).
Solution:
Given P = 15 ; Q = 5

Question 18.
If the letters in the English alphabets A to M represent the number from 1 to 13 respectively and N represents 0 and the letters O to Z correspond from -1 to -12, find the sum of integers for the names given below. For example,
MATH → Sum → 13 + 1 – 6 + 8 = 16
(i) YOUR NAME
(ii) SUCCESS
Solution:
Given

(i) My name LEENA → 12 + 5 + 5 + 0 + 1 = 23
(ii) SUCCESS → (-5) + (-7) + 3 + 3 + 5 + (-5) + (-5)
= -12 + 6 + 5 + (-10) = -6 + 5 + (-10) = (-1) + (-10)
= -11

Question 19.
From a water tank 100 litres of water is used every day. After 10 days there is 2000 litres of water in the tank. How much water was there in the tank before 10 days?
Solution:
Water used for one day = 100 litres.
Water used for 10 days = 100 × 10 = 1000 litres.
After 10 days water left in the tank = 2000 litres
Initially amount of water will be = 2000 + 1000 = 3000 litres

Question 20.
A dog is climbing down into a well to drink water. In each jump it goes down 4 steps. The water level is in 20th step. How many jumps does the dog take to reach the water level?
Solution:
The water in the well is at 20th step.
For each jump the dog goes low 4 steps. 5
∴ Number of jumps the dog to reach the water = \(\frac{20}{4}\) = 5 jumps

Question 21.
Kannan has a fruit shop. He sells 1 dozen banana at a loss of ? 2 each because it may get rotten next day. What is his loss?
Solution:
1 dozen = 12 bananas
For 1 banana loss = ₹ 2
For 12 bananas loss = ₹ 2 × 12 = ₹ 24

Question 22.
A submarine was situated at 650 feet below the sea level. If it descends 200 feet, what is its new position?
Solution:
Position of submarine = 650 feet below sea level = -650 feet
Again the depth it descends = 200 feet below = – 200 feet
∴ Position of submarine = (-650) + (-200) = -850 feet
The submarine will be 850 feet below the sea level.

Question 23.
In a magic square given below each row, column and diagonal should have the same sum. Find the values of x, y, and z.

Solution:
Column total = Row total = diagonal total
∴ 1 + y + (-6) = (-10) + (-3) + 4
y + (- 5) = -13 + 4
y = -9 + 5
y = -4
So 1 + (-10) + x = y + (-3) + (-2)
-9 + x = (-4) + (-3) + (-2)
-9 + x = -9
x = -9 + 9
x = 0
Now x + (-2) + z = (-10) + (-3) + 4
0 + (-2) + z = (-13) + 4
-2 + z = -9
z = -9 + 2 = -7
z = -7
∴ x = 0, y = -4, z = -7

Students can Download Maths Chapter 5 Geometry Ex 5.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.2

Question 1.
From the figures name pair of angles.

Solution:
(i) m and n are parallel lines and l is the transversal.
∴ ∠1 and ∠2 are exterior angles on the same side of the transversal.

(ii) m and n are parallel lines and l is the transversal
∠1 and ∠2 are alternate exterior angles.

(iii) m and n are parallel lines l is the transversal
∠1 and ∠2 are corresponding angles.

(iv) m and n are parallel lines l is the transversal.
∠1 and ∠2 are interior angles on the same side of the transversal.

(v) m and n are parallel lines and l is the transversal.
∠1 and ∠2 are alternate interior angles.

(vi) o and q are parallel lines and n is the transversal.
∠1 and ∠2 are corresponding angles.

Question 2.
Find the measure of angle x in each of the following figures.

Solution:
(i) m and n are parallel lines and l is the transversal.
x° and 35° are corresponding angles and so they are equal.
∴ x = 35°

(ii) m and n are parallel lines and l is the transversal.
∴ x = 65°
[∴ corresponding angles are equal].

(iii) n and m are parallel lines and l is the transversal.
Corresponding angles are equal
∴ x = 145°

(iv) m and n are parallel lines and l is the transversal.
Corresponding angles are equal
∴ x = 135°

(v) m and n are parallel lines, l is the transversal perpendicular to both the lines
∴ x = 90°

Question 3.
Find the measure of angles in each of the following figures.

Solution:
(i) m and n are parallel lines. l is the transversal. Then alternate interior angles are equal
∴ y = 28°

(ii) m and n are parallel lines. l is the transversal. Alternate exterior angles are equal
∴ y = 58°

(iii) m and n are parallel lines. l is the transversal.
Alternate interior angles are equal
∴ y = 123°

(iv) m and n are parallel lines . l is the transversal
alternate exterior angles are equal.
∴ y = 108°

Question 4.
Find the measure of angle z in each of the following figures.

Solution:
(i) m and n are parallel lines l is the transversal
Then interior angles that lie on the same side of the transversal are supplementary
∴ z + 31° = 180°
z + 31° – 31° = 180° – 31°
z = 149°

(ii) m and n are parallel lines, l is the transversal
Interior angles that lie on the same side of the transversal are supplementary
∴ z + 135° = 180°
z + 135° – 135° = 180° – 135°
z = 45°

(iii) m and n are parallel lines l is the transversal exterior angles that lie on the same side of the transversal are supplementary.
∴ z + 79° = 80°
z + 79° – 79° = 180° – 79°
z = 101°

(iv) m and n are parallel lines and l is the transversal. Corresponding angles are equal
z + 22° = 180°
z + 22° – 22° = 180° – 22°
z = 158°

Question 5.
Find the value of angle ‘a’ in each of the following figures

Solution:
(i) m and n are parallel lines. l is the transversal
∴ Corresponding angles are equal

(ii) m and n are parallel lines l is the transversal
Exterior angles that lie on the same side of the transversal are supplementary
∴ (4a + 13) + 135° = 180°
4a + 13 + 135° = 180°
4a +148° = 180°
4a + 148° – 148° = 180° – 148°
4a = 32°

(iii) m and n are parallel lines l is the transversal
∴ Alternate interior angles are equal

(iv) m and n are parallel lines l is the transversal which is perpendicular to m and n

Question 6.
Find the value of the angle x in both the figures

Solution:
(i) m and n are parallel lines. l is the transversal
∴ Alternate interior angles are equal

(ii) m and n are parallel lines. l is the transversal
Exterior angles on the same side of the transversal are supplementary

Question 7.
Anbu has marked the angles as shown below in (i) and (ii). Check whether both of them are correct. Give reasons

Solution:
(i) m and n are parallel lines. l is the transversal.
Interior angles on the same side of the transversal are supplementary. But here it is 75 + 75 ≠ 180°
105 + 105 ≠ 180°
∴ Angles marked are not correct

(ii) m and n are parallel lines. l is the transversal.
Corresponding angles must be equal. So here the marking is wrong.

Question 8.
Mention two real life situations where we use parallel lines.
Solution:
Two angles of a wall in a building Cross rods in a window.

Question 9.
Two parallel lines are intersected by a transversal. What is the minimum number of angles you need to know to find the remaining angles. Give reasons.
Solution:

When two parallel lines are intersected by a transversal, we need a minimum of a single angle to find the remaining angle.
Using the concept of linear pair of angles, we can final one more angle.
By the concepts of corresponding angles, alternate interior angles and alternate , exterior angles we could find all other angles.

Objective Type Questions

Question 10.
A line which intersects two or more lines in different points is known as
(i) parallel lines
(ii) transversal
(iii) non-parallel lines
(iv) Intersecting lines
Solution:
(ii) Transversal

Question 11.
In the given figure angles a and b are
(i) alternate exterior angles
(ii) corresponding angles
(iii) Alternate interior angles
(iv) Vertically opposite angles
Solution:
(i) alternate exterior angles

Question 12.
Which of the following statement is ALWAYS TRUE when parallel lines are cut by a transversal
(i) corresponding angles supplementary
(ii) alternate interior angles supplementary
(iii) alternate exterior angles supplementary
(iv) interior angles on the same side of the transversal are supplementary
Solution:
(iv) Interior angles on the same side of the transversal are
supplementary.

Question 13.
In the diagram what is the value of angle x?
(i) 43°
(ii) 44°
(iii) 132°
(iv) 134°
Hint:

Students can Download Maths Chapter 1 Number System Ex 1.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 1 Number System Ex 1.5

Question 1.
One night in Kashmir, the temperature is -5°C. Next day the temperature is 9°C. What is the increase in temperature?
Solution:
Temperature in the first day = -5°C
Temperature in the next day = 9°C
∴ Increase in temperature = 9°C – (-5°C)
= 9°C + (+5°C) = 14°C

Question 2.
An atom can contain protons which have a positive charge (+) and electrons which have a negative charge (-). When an electron and a proton pair up, they become neutral (0) and cancel the charge at. Now determine the net charge:
(i) 5 electrons and 3 protons → -5 + 3 = -2 that is 2 electrons \(\ominus\ominus\)
(ii) 6 protons and 6 electrons →
(iii) 9 protons and 12 electrons →
(iv) 4 protons and 8 electrons →
(v) 7 protons and 6 electrons →
Solution:
(ii) 6 protons and 6 electrons → (+6) + (-6) = 0
(iii) 9 protons and 12 electrons → (+9) + (-12) = 9-12 = -3 ⇒ 3 electrons \(\ominus\ominus\ominus\)
(iv) 4 protons and 8 electrons → (+4) + (-8) = +4 – 8 = -4 ⇒ 4 electrons \(\ominus\ominus \ominus\ominus\)
(v) 7 protons and 6 electrons → (+7) + (-6) = +1 = 1 proton \(\oplus\)

Question 3.
Scientists use the Kelvin scale (K) as an alternative temperature scale to degrees Celsius (°C) by the relation T°C = (T + 273)K. Convert the following to Kelvin:
(i) -275°C
(ii) 45°C
(iii) -400°C
(iv) -273°C
Solution:
(i) -275°C = (-275 + 273)K = -2K
(ii) 45°C = (45 + 273)K = 318 K
(iii) -400°C = (-400 + 273)K = -127 K
(iv) -273°C = (-273 + 273) K = 0K

Question 4.
Find the amount that is left in the student’s bank account, if he has made the following transaction in a month. His initial balance is ₹ 690.
(i) Deposit (+) of ₹ 485
(ii) Withdrawal (-) of ₹ 500
(iii) Withdrawal (-) of ₹ 350
(iv) Deposit (+) of ₹ 89
(v) If another ₹ 300 was withdrawn, what would the balance be?
Solution:
(i) Initial balance of student’s account = ₹ 690
Deposited amount = ₹ 485 (+)
∴ Amount left in the account = ₹ 690 + ₹ 485 = ₹ 1175

(ii) Balance in the account = ₹ 1175
Amount withdrawn = ₹ 500 (-)
Amount left = ₹ 1175 – ₹ 500 = ₹ 675

(iii) Balance in the account = ₹ 675
Amount withdrawn = ₹ 350 (-)
Amount left = ₹ 675 – ₹ 350 = ₹ 325

(iv) Balance in the account = ₹ 325
Amount deposited = ₹ 89(+)
Amount left = ₹ 325 + ₹ 89 = ₹ 414

(v) Balance in the account = ₹ 414
Amount withdrawn = ₹ 300 (-)
Amount left = ₹ 414 – ₹ 300 = ₹ 114

Question 5.
A poet Tamizh Nambi lost 35 pages of his ‘lyrics’ when his file had got wet in the rain. Use integers, to determine the following.
(i) If Tamil Nambi wrote 5 pages per day, how many day’s work did he lose?
(ii) If four pages contained 1800 characters, (letters) how many characters were lost?
(iii) If Tamil Nambi is paid ₹ 250 for each page produced, how much money did he lose?
(iv) If Kavimaan helps Tamizh Nambi and they are able to produce 7 pages per day, how many days will it take to recreate the work lost?
(v) Tamizh Nambi pays Kavimann ₹ 100 per page for his help. How much money does Kavimaan receive?
Solution:
Total pages lost – 35
One day work = 5 page 35
35 pages = \(\frac{35}{5}\) = 7 days work
∴ 7 day’s work he lost.

(ii) Number of characters in four pages = 1800
Number of characters in one page = \(\frac{1800}{4}\) = 450
∴ Number of characters in 35 pages = 450 × 35 = 15,750 characters

(iii) Payment for one page = ₹ 250
∴ Payment for 35 pages = ₹ 250 × ₹ 35 = ₹ 8,750

(iv) Number of pages recreated a day = 7
∴ To recreate 35 pages day’s needed = \(\frac{35}{7}\) = 5 days

(v) Payment of Kavimaan = ₹ 100 per page
∴ for 35 pages payment = ₹ 100 × 35 = ₹ 3,500

Question 6.
Add 2 to me. Then multiply by 5 and subtract 10 and divide new by 4 and I will give you 15! Who am I?
Solution:
According to the problem {[(I + 2) × 5] – 10} ÷ 4 = 15
{[(I + 2) × 5] – 10} = 15 × 4 = 60
I + 2 = \(\frac{70}{5}\) = 14
(I + 2) × 5 = 60 + 10 = 70
I = 14 – 2 ; I = 12

Question 7.
Kamatchi, a fruit vendor sells 30 apples and 50 pomegranates. If she makes a profit of ? 8 per apple and loss ? 5 per pomegranate. What will be her overall profit or loss?
Solution:
Number of apples Kamatchi sold = 30
Profit per apple = ₹ 8(+)
∴ Profit for 30 apples = 30 × 8 = ₹ 240
Number of pomegranates sold 50
Loss per pomegranate = ₹ 5(-)
Loss on selling 50 pomegranates = 50 × (-5) = ₹ -250
Overall loss = -250 + 240 = ₹ -10
i.e. loss ₹ 10.

Question 8.
During a drought, the water level in a dam fell 3 inches per week for 6 consecutive weeks. What was the change in the water level in the dam at the end of this period?
Solution:
Water level fall per week = -3 inches
∴ Water level decrease for 6 weeks = 6 ₹ (-3) = 18 inches
∴ decrease of 18 inches of water level.

Question 9.
Buddha was born in 563 BC (BCE) and died in 483 BC (BCE). Was he alive in 500 BC (BCE)? and find his life time. (Source: Compton’s Encyclopedia)
Solution:
Years in BCC (BCE) are taken as negative integers.

Buddha was bom in -563
and died in -483
So he was alive in 500 BC (BCE)
Life time = -483 – (-563) = -483 + 563 = +80
Buddha’s life time = 80 years.