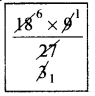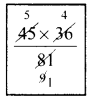Prasanna

Students can Download Maths Chapter 3 Geometry Ex 3.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 3 Geometry Ex 3.3

Question 1.
Construct the following rhombuses with the given measurements and also find their area.
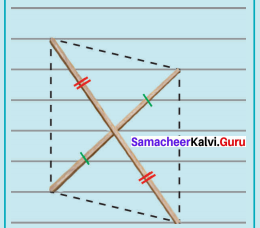
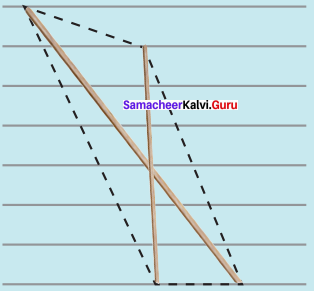
(i) FACE, FA = 6 cm and FC = 8 cm
Solution:
Given FA = 6 cm and FC = 8cm

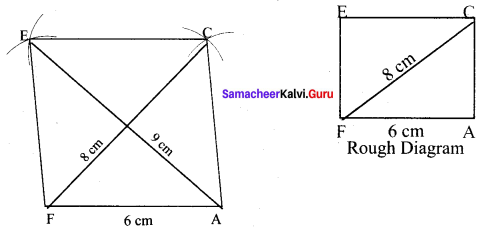
Steps :
(i) Drawn a line segment FA = 6 cm.
(ii) With F and A as centres, drawn arcs of radii 8 cm and 6 cm respectively and let them cut at C.
(iii) Joined FC and AC.
(iv) With F and C as centres, drawn arcs of radius 6 cm each and let them cut at E. Joined FE and EC.
(v) FACE is the required rhombus.

Calculation of Area :
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq.units = \(\frac{1}{2}\) × 8 × 9 sq.units = 36 cm²

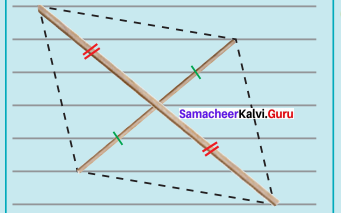
(ii) RACE, RA = 5.5 cm and AE = 7 cm
Solution:
Given RA = 5.5 cm and AE = 7 cm

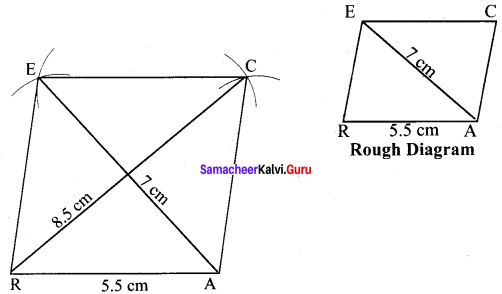
Steps :
(i) Drawn a line segment RA = 5.5 cm.
(ii) With R and A as centres, drawn arcs of radii 5.5 cm and 7 cm respectively and let them cut at E.
(iii) Joined RE and AE.
(iv) With E and A as centres, drawn arcs of radius 5.5 cm each and let them cut at C.
(v) Joined AC and EC.
(vi) RACE is the required rhombus.

Calculation of Area :
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq.units = \(\frac{1}{2}\) × 7 × 8.5 cm² = 29.75 cm²

(iii) CAKE, CA = 5 cm and ∠A = 65°
Solution:
Given CA = 5 cm and ∠A = 65°

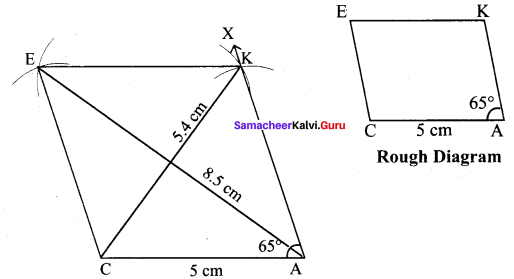
(i) Drawn a line segment CA = 5 cm.
(ii) At A on AC, made ∠CAX = 65°
(iii) With A as centre, drawn arc of radius 5 cm. Let it cut AX at K.
(iv) With K and C as centres, drawn arcs of radius 5 cm each and let them cut at E. Joined KE and CE.
(v) CAKE is the required rhombus.

Calculation of Area :
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq.units = \(\frac{1}{2}\) × 5.4 × 8.5 cm² = 22.95 cm²

(iv) MAKE, MA= 6.4 cm and ∠M = 80°
Solution:
Given MA = 6.4 cm and ∠M = 80°

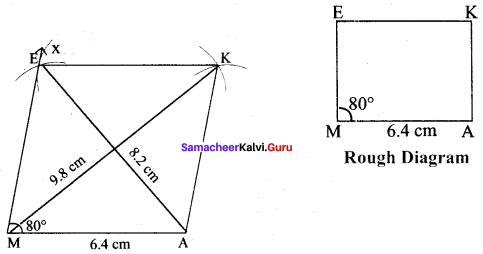
Steps :
(i) Drawn a line segment MA = 6.4 cm.
(ii) At M on MA, made ∠AMX = 80°
(iii) With M as centres, drawn arc of radius 6.4 cm. Let it cut MX at E.
(iv) With E and A as centres, drawn arcs of radius 6.4 cm each and let them cut at K.
(v) Joined EK and AK.
(vi) MAKE is the required rhombus.

Calculation of Area :
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq.units = \(\frac{1}{2}\) × 8.2 × 9.8 cm² = 40.18 cm²

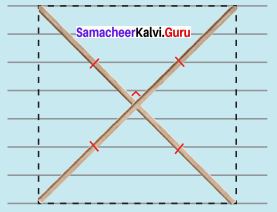
(v) LUCK, LC = 7.8 cm and UK = 6 cm
Solution:
Given LC = 7.8 cm and UK = 6 cm

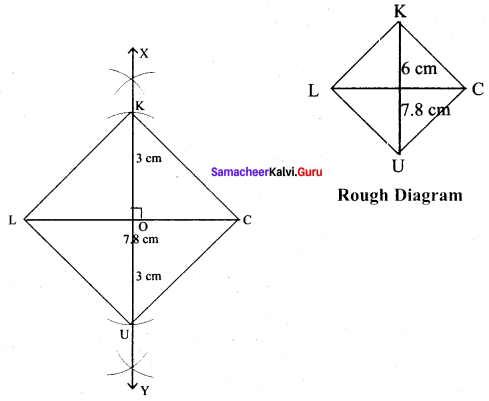
Steps :
(i) Drawn a line segment LC = 7.8 cm.
(ii) Drawn the perpendicular bisector XY to LC. Let it cut LC at ‘O’
(iii) With O as centres, drawn arc of radius 3 cm on either side of O which cut OX at K and OY at U.
(iv) Joined LU, UC, CK and LK.
(v) LUCK is the required rhombus.

Calculation of Area :
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq.units = \(\frac{1}{2}\) × 7.8 × 6 cm² = 23.4 cm²

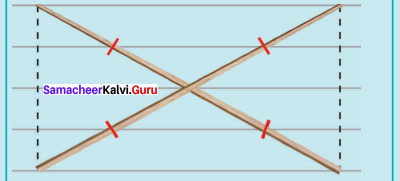
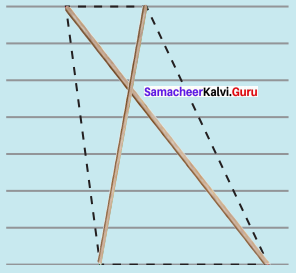
(vi) DUCK, DC = 8 cm and UK = 6 cm
Solution:
Given DC = 8 cm and UK = 6 cm

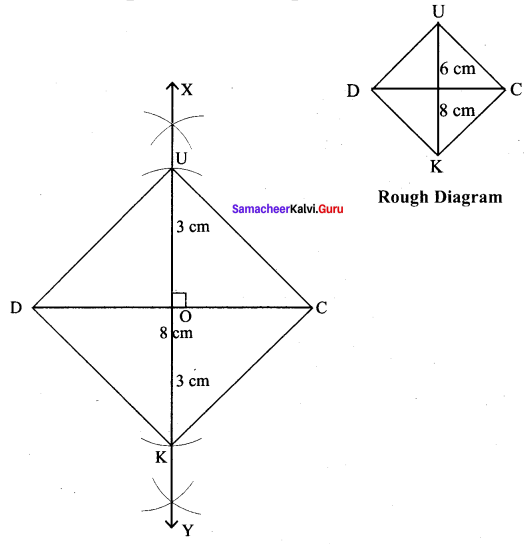
Steps :
(i) Drawn a line segment DC = 8 cm.
(ii) Drawn the perpendicular bisector XY to DC. Let it cut DC at ‘O’
(iii) With O as centres, drawn arc of radius 3 cm on either side of O which cut OX at U and OYat K.
(iv) Joined DK, KC, CU and DU.
(v) DUCK is the required rhombus.

Calculation of Area :
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq.units = \(\frac{1}{2}\) × 8 × 6 cm² = 24 cm²

(vii) PARK, PR = 9 cm and ∠P = 70°
Solution:
Given PR = 9 cm and ∠P = 70°

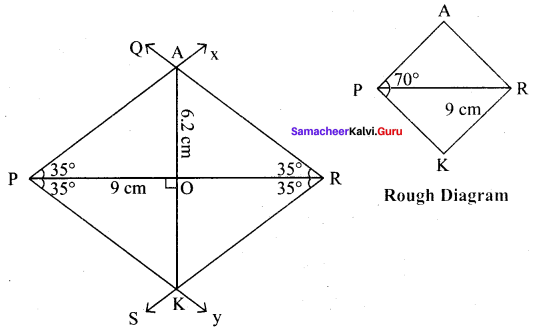
Steps :
(i) Drawn a line segment PR = 9 cm.
(ii) At P, made ∠RPX = ∠RPY = 35° on either side of PR.
(iii) At R, made ∠PRQ = ∠PRS = 35° on either side of PR
(iv) Let PX and RQ cut at A and PY and RS at K.
(v) PARK is the required rhombus

Calculation of Area :
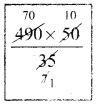
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq.units = \(\frac{1}{2}\) × 9 × 6.2 cm² = 27.9 cm²

(viii) MARK, AK =7.5 cm and ∠A = 80°
Solution:
Given AK = 7.5 cm and ∠A = 80°

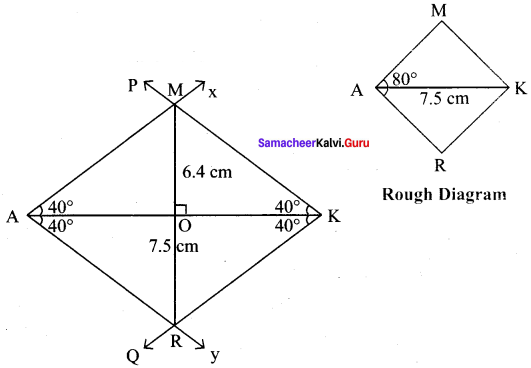
(i) Drawn a line segment AK = 7.5 cm.
(ii) At A, made ∠KAX = ∠KAY = 40° on either side of AK.
(iii) At K, made ∠AKP = ∠AKQ = 40° on either side of AK
(iv) Let AX and KP cut at M and AY and KQ at R.
(v) MARK is the required rhombus

Calculation of Area :
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq.units = \(\frac{1}{2}\) × 7.5 × 6.4 cm² = 24 cm²

Question 2.
(i) Construct the following rectangles with the given measurements and also find their area.
(i) HAND, HA = 7 cm and AN = 4 cm
Solution:
Given HA = 7 cm and AN = 4 cm

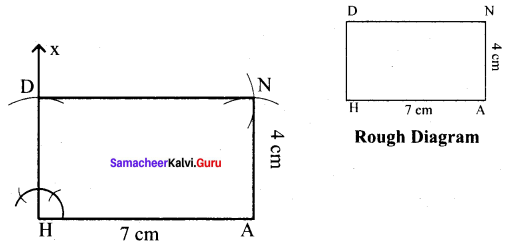
Steps :
(i) Drawn a line segment HA = 7 cm.
(ii) At H, constructed HX ⊥ HA.
(iii) With H as centre, drawn an arc of radius 4 cm and let it cut at HX at D.
(iv) With A and D as centres, drawn arcs of radii 4 cm and 7 cm respectively and let them cut at N.
(v) Joined AN and DN.
(vi) HAND is the required rectangle.

Calculation of Area :
Area of the rectangle HAND = l × b sq.units = 7 × 4 cm² = 28 cm²

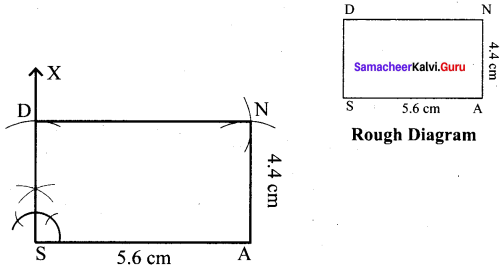
(ii) SAND, SA = 5.6 cm and SN = 4.4 cm
Solution:
Given SA = 5.6 cm and SN = 4.4 cm

Steps :
(i) Drawn a line segment SA = 5.6 cm.
(ii) At S, constructed SX ⊥ SA.
(iii) With S as centre, drawn an arc of radius 4.4 cm and let it cut at SX at D.
(iv) With A and D as centres, drawn arcs of radii 4.4 cm and 5.6 cm respectively and let them cut at N.
(v) Joined DN and AN.
(vi) SAND is the required rectangle.

Calculation of Area :
Area of the rectangle SAND = l × b sq.units = 5.6 × 4.4 cm² = 26.64 cm²

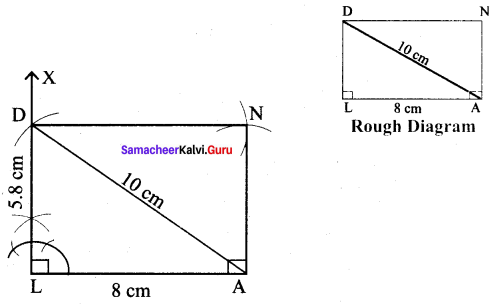
(iii) LAND, LA = 8 cm and AD = 10 cm
Solution:
Given LA = 8 cm and AD = 10 cm

Steps :
(i) Drawn a line segment LA = 8 cm.
(ii) At L, constructed LX ⊥ LA.
(iii) With A as centre, drawn an arc of radius 10 cm and let it cut at LX at D.
(iv) With A as centre and LD as radius drawn an arc. Also with D as centre and LA as radius drawn another arc. Let then cut at N.
(v) Joined DN and AN.
(vi) LAND is the required rectangle.

Calculation of Area :
Area of the rectangle LAND = l × b sq.units = 8 × 5.8 cm² = 46.4 cm²

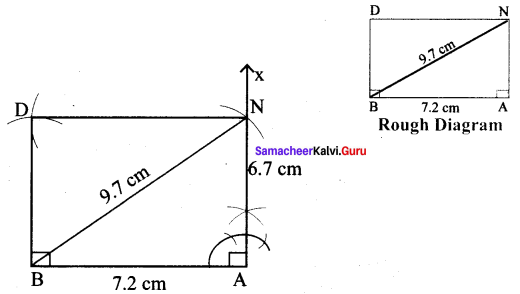
(iv) BAND, BA = 7.2 cm and BN = 9.7 cm
Solution:
Given = 7.2 cm and BN = 9.7 cm

Steps :
(i) Drawn a line segment BA = 7.2 cm.
(ii) At A, constructed NA ⊥ AB.
(iii) With B as centre, drawn an arc of radius 9.7 cm and let it cut at AX at N.
(iv) With B as centre and AN as radius drawn an arc. Also with N as centre and BA as radius drawn another arc. Let then cut at D.
(v) Joined ND and BD.
(vi) BAND is the required rectangle.

Calculation of Area :
Area of the rectangle BAND = l × b sq.units = 7.2 × 6.7 cm² = 48.24 cm²

Question 3.
Construct the following squares with the given measurements and also find their area.
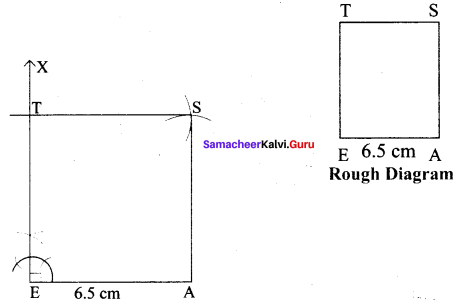
(i) EAST, EA = 6.5 cm
Solution:
Given side = 6.5 cm

Steps :
(i) Drawn a line segment EA = 6.5 cm.
(ii) At E, constructed EX ⊥ EA.
(iii) With E as centre, drawn an arc of radius 6.5 cm and let it cut EX at T.
(iv) With A and T as centre drawn an arc of radius 6.5 cm each and let them cut at S.
(v) Joined TS and AS.
(vi) EAST is the required square.

Calculation of Area :
Area of the square EAST = a² sq.units = 6.5 × 6.5 cm² = 42.25 cm²

(ii) WEST, ST = 6 cm
Solution:
Given side of the square = 6 cm

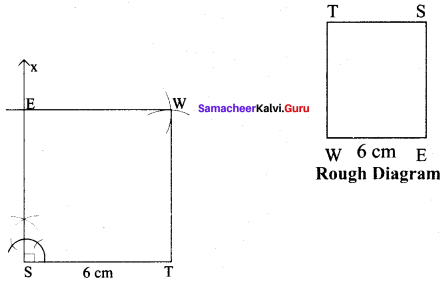
Steps :
(i) Drawn a line segment ST = 6 cm.
(ii) At S, constructed SX ⊥ ST.
(iii) With S as centre, drawn an arc of radius 6 cm and let it cut SX at E.
(iv) With E and T as centre drawn an arc of radius 6 cm each and let them cut at W.
(v) Joined TW and EW.
(vi) WEST is the required square.

Calculation of Area :
Area of the square WEST = a² sq.units = 6 × 6 cm² = 36 cm²

(iii) BEST, BS = 7.5 cm
Solution:
Given diagonal = 7.5 cm

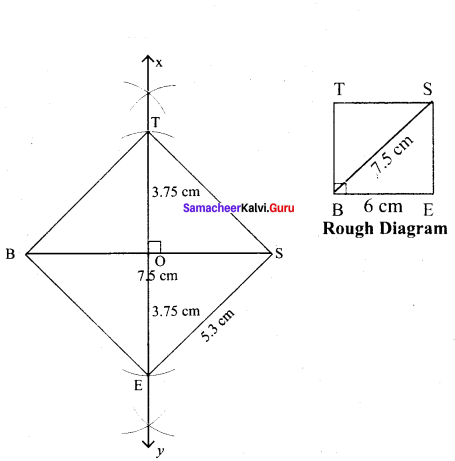
Steps :
(i) Drawn a line segment BS = 7.5 cm.
(ii) Drawn the perpendicular bisector XY to BS. Let it bisect BS at O.
(iii) With O as centre, drawn an arc of radius 3.7 cm on either side of O which cut OX at T and OY at E
(iv) Joined BE, ES, ST and BT.
(v) BEST is the required square.

Calculation of Area :
Area of the square BEST = a² sq.units = 5.3 × 5.3 cm² = 28.09 cm²

(iv) REST, ET = 8 cm
Solution:
Given diagonal = 8 cm

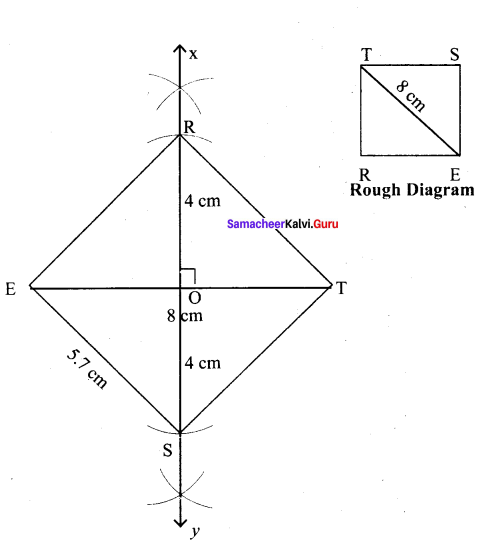
Steps:
(i) Drawn a line segment ET = 8 cm.
(ii) Drawn the perpendicular bisector XY to ET. Let it bisect ET at O.
(iii) With O as centre, drawn an arc of radius 4 cm on either side of O which cut OX at R and OY at S
(iv) Joined ES, ST, TR and ER.
(v) REST is the required square.

Calculation of Area :
Area of the square REST = a² sq.units = 5.7 × 5.7 cm² = 32.49 cm²

Students can Download Maths Chapter 3 Geometry Ex 3.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 3 Geometry Ex 3.2

Miscellaneous and Practice Problems

Question 1.
Identify the centroid of ΔPQR.

Solution:
In ΔPQR, PT = TR ⇒ QT is a median from vertex Q.
QS = SR ⇒ PS is a median from vertex P.
QT and PS meet at W and therefore W is the centroid of ΔPQR.

Question 2.
Name the orthocentre of ΔPQR.

Solution:
∠P = 90°
This is a right triangle
∴ orthocentre = P [∴ In right triangle orthocentre is the vertex containing 90°]

Question 3.
In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA.

Solution:
Given A is the midpoint of YZ.
∴ ZA = AY
G is the centroid of ΔXYZ centroid divides each median in a ratio 2 : 1 ⇒ XG : GA = 2 : 1
\(\frac{XG}{GA}\) = \(\frac{2}{1}\)
\(\frac{XG}{3}\) = \(\frac{2}{1}\)
XG = 2 × 3
XG = 6 cm
XA = XG + GA
= 6 + 3 ⇒ XA = 9 cm

Challenging Problems

Question 4.
Find the length of an altitude on the hypotenuse of a right angled triangle of legs of length 15 feet and 20 feet.
Solution:

Since ∠B = 90°
Using pythagoras theorem
AC² = AB² + BC² = 20² + 15²
= 400 + 225
AC² = 62⁵
AC² = 25⁵
AC = 25
Area of a triangle ΔABC = \(\frac{1}{2}\) × 15 × 20 = 150 feet²
Again Area of ΔABC = \(\frac{1}{2}\) × AC × BD
150 = \(\frac{1}{2}\) × 25 × BD
BD = \(\frac{2 × 150}{25}\) = \(\frac{300}{25}\)
BD = 12 feet
∴ Length of the altitude on the hypotenuse of the right angled triangle is 12 feet.

Question 5.
If I is the incentre of ΔXYZ, ∠IYZ = 30° and ∠IZY = 40°, find ∠YXZ.

Solution:
Since I is the incentre of ΔXYZ
∠IYZ = 30° ⇒ ∠IYX = 30°
∠IZY = 40° ⇒ ∠IZX = 40°
∴ ∠XYZ = ∠XYI + ∠IYZ = 30° + 30°
∠XYZ = 60°
lll ly ∠XYZ = ∠XZI + ∠IZY = 40° + 40°
∠XYZ = 80°
By angle sum property of a triangle
∠XZY + ∠XYZ + ∠YXZ = 180°
80° + 60° + ∠YXZ = 180°
140° + ∠YXZ = 180°
∠YXZ = 180° – 140°
∠YXZ = 40°

Question 6.
In ΔDEF, DN, EO, FM are medians and point P is the centroid. Find the following.
(i) If DE = 44, then DM = ?
(ii) If PD = 12, then PN = ?
(iii) If DO = 8, then FD = ?
(iv) If OE = 36, then EP = ?

Solution:
Given DN, EO, FM are medians.
∴ FN = EN
DO = FO
EM = DM
(i) If DE = 44, then
DM = \(\frac{44}{2}\) = 22
DM = 22

(ii) If PD = 12, PN = ?
\(\frac{PD}{PN}\) = \(\frac{2}{1}\)
\(\frac{12 }{PN}\) = \(\frac{2}{1}\) ⇒ PN = \(\frac{12}{2}\) = 6
PN = 6

(iii) If DO = 8, then
FD = DO + OF = 8 + 8
FD = 16

(iv) If OE = 36,
then \(\frac{EP}{PO}\) = \(\frac{2}{1}\)
\(\frac{EP}{2}\) = PO
OE = OP + PE
36 = \(\frac{PE}{2}\) + PE
36 = \(\frac{PE}{2}\) + \(\frac{2PE}{2}\)
36 = \(\frac{3PE}{2}\)
PE = \(\frac{36 × 2}{3}\)
PE = 24

Students can Download Maths Chapter 3 Geometry Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 3 Geometry Intext Questions

Exercise 3.1
Think (Text book Page no. 53)

Question 1.
In any acute angled triangle, all three altitudes are inside the triangle. Where will be the orthocentre? In the interior of the triangle or in its exterior?

Solution:
Interior of the triangle.

Question 2.
In any right angled triangle, the altitude perpendicular to the hypotenuse is inside the triangle; the other two altitudes are the legs of the triangle. Can you identify the orthocentre in this case?

Solution:
Vertex containing 90°

Question 3.
In any obtuse angled triangle, the altitude connected to the obtuse vertex is inside the triangle, and the two altitudes connected to the acute vertices are outside the triangle. Can you identify the orthocentre in this case?

Solution:
Exterior of the triangle.

Try These (Text book Page no. 56)

Identify the type of segment required in each triangle:
(median, altitude, perpendicular bisector, angle bisector)

(i) AD = ……….
(ii) l1 = ………..
(iii) BD = …………
(iv) CD = …………
Solution:
(i) AD = Altitude
(ii) l₁ = Perpendicular bisector
(iii) BD = Median
(iv) CD = Angular bisector

Exercise 3.3
Activity 1. (Text book Page no. 60)

Question 1.
A pair of identical 30°-60°-90° set-squares are needed for this activity. Place them as shown in the figure.

1. What is the shape we get? It is a parallelogram.
2. Are the opposite sides parallel?
3. Are the opposite sides equal?
4. Are the diagonals equal?
5. Can you get this shape by using any other pair of identical set-squares?

Solution:

1. It is a parallelogram.
2. Yes
3. Yes
4. no
5. yes

Question 2.
We need a pair of 30°-60°-90° set- squares for this activity. Place them as shown in the figure.

(i) What is the shape we get?
(ii) Is it a parallelogram?
It is a quadrilateral; infact it is a rectangle. (How?)
(iii) What can We say about its lengths of sides, angles and diagonals? Discuss and list them out.
Solution:
(i) Rectangle
(ii) Yes, Opposite sides are equal. All angles = 90°
(iii) Opposite sides are equal.
All angles are equal and are = 90°.
Diagonals are equal

Question 3.
Repeat the above activity, this time with a pair of 45°-450-90° set-squares.

(i) How does the figure change now? Is it a parallelogram? It becomes a square! (How did it happen?)
(ii) What can we say about its lengths of sides, angles and diagonals? Discuss and list them out.
(iii) How does it differ from the list we prepared for the rectangle?
Solution:
(i) All sides are equal
(ii) All sides are equal
All angles = 90°
Diagonals equal
(iii) All sides are equal.
Diagonals bisects each other.

Question 4.
We again use four identical 30°-60°-90° set- squares for this activity.
Note carefully how they are placed touching one another.

(i) Do we get a parallelogram now?
(ii) What can we say about its lengths of sides, angles and diagonals?
(iii) What is special about their diagonals?
Solution:
(i) Yes
(ii) All sides equal.
(iii) Diagonals bisects perpendicularly.

Try These (Text book Page no. 62)

Question 1.
Say True or False:
(a) A square is a special rectangle.
(b) A square is a parallelogram.
(c) A square is a special rhombus.
(d) A rectangle is a parallelogram
Solution:
(a) True
(b) True
(c) True
(d) True

Question 2.
Name the quadrilaterals
(a) Which have diagonals bisecting each other.
(b) In which the diagonals are perpendicular bisectors of each other.
(c) Which have diagonals of different lengths.
(d) Which have equal diagonals.
(e) Which have parallel opposite sides.
(f) In which opposite angles are equal.
Solution:
(a) Square, rectangle, parallelogram, rhombus.
(b) Rhombus and square.
(c) Parallelogram and Rhombus
(d) Rectangle, square.
(e) Square, Rectangle, Rhombus, parallelogram.
(f) Square, rectangle, rhombus, parallelogram

Question 3.
Two sticks are placed on a ruled sheet as shown. What figure is formed if the four corners of the sticks are joined?
(a)
Two unequal sticks. Placed such that their midpoints coincide.
Solution:
Parallelogram

(b)
Two equal sticks. Placed such that their midpoints coincide.
Solution:
Rectangle

(c)
Two unequal sticks. Placed intersecting at mid points perpendicularly.
Solution:
Rhombus

(d)
Two equal sticks. Placed intersecting at mid points perpendicularly.
Solution:
Square

(e)
Two unequal sticks. Tops are not on the same ruling. Bottoms on the same ruling. Not cutting at the mid point of either.
Solution:
Quadrilateral

(f)
Two unequal sticks. Tops on the same ruling. Bottoms on the same ruling. Not necessarily cutting at the mid point of either.
Solution:
Trapezium

Students can Download Maths Chapter 3 Geometry Ex 3.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 3 Geometry Ex 3.1

Question 1.
Fill in the blanks:

1. The altitudes of a triangle intersect at………..
2. The medians of a triangle cross each other at………..
3. The meeting point of the angle bisectors of a triangle is………..
4. The perpendicular bisectors of the sides a triangle meet at………..
5. The centroid of a triangle divides each medians in the ratio………..

Solution:

1. Orthocentre
2. Centroid
3. Incentre
4. Circumcentre
5. 2 : 1

Question 2.
Say True or False:
(i) In any triangle the Centroid and the Incentre are located inside the triangle.
(ii) The centroid, orthocentre, and incentre of a triangle are collinear.
(iii) The incentre is equidistant from all the vertices of a triangle.
Solution:
(i) True
(ii) True
(iii) False

Question 3.
(a) Where does the circumcentre lie in the case of
(i) An acute angled triangle.
Solution:
Inside the triangle.

(ii) An obtuse-angled triangle.
Solution:
Exterior of the triangle.

(iii) A right angled triangle.
Solution:
On the hypotenuse.

(b) Where does the orthocentre lie in the case of
(i) An acute-angled triangle.
Solution:
Interior of the triangle.

(ii) An obtuse-angled triangle.
Solution:
Exterior of the triangle.

(iii) A right angled triangle.
Solution:
On the vertex containing 90°.

Question 4.
Fill in the blanks:
In the triangle ABC,

(i) The angle bisector is……….
(ii) The altitude is………..
(iii) The median is…………
Solution:
(i) BE
(ii) AD
(iii) CF

Question 5.
In right triangle ABC, what is the length of altitude drawn from the vertex A to BC?

Solution:
In this right angled triangle ΔABC, length of the altitude drawn from vertex A is the leg AB itself. By Pythagoras theorem.
AC² = AB² + BC²
13² = AB² + 12²
169 = AB² + 144
AB² = 169 – 144 = 25
AB² = 52
AB = 5cm

Question 6.
In triangle XYZ, YM is the angle bisector of ∠Y and ∠Y is 100°. Find ∠XYM and ∠ZYM.

Solution:
Given YM is the angle bisector of ∠Y.
also ∠Y = 100°
Angle -bisector divides the angle into two congruent angles.
∠XYM = ∠ZYM
∠Y = ∠XYM + ∠ZYM
100° = ∠XYM + ∠ZYM [∴ ∠XYM = ∠ZYM]
2 ∠XYM = 100°
∠XYM = \(\frac{1}{2}\) (100°)
∠XYM = 50°
∴ ∠ZYM = 50°

Question 7.
In triangle PQR, PS is a median and QS = 3.5 cm, then find QR?

Solution:
Given PS is the median and QS = 3.5 cm
Median is the line drawn from a vertex to the midpoint of the opposite side.
∴ QS = RS
so QS = RS = 3.5 cm
∴ QR = QS +SR = 3.5 + 3.5 = 7 cm
QR = 7 cm

Question 8.
In triangle ABC, line is a perpendicular bisector of BC. If BC = 12 cm, SM = 8 cm, find CS.

Solution:
Given l₁ is the perpendicular bisector of BC.
∴ ∠SMC = 90° and BM = MC
BC = 12 cm
⇒ BM + MC = 12 cm
MC + MC = 12 cm [∴ BM = MC]
2MC = 12
MC = \(\frac{12}{2}\)
MC = 6 cm
Given SM = 8 cm
By Pythagoras theorem SC² = SM² + MC²
SC² = 8² + 6²
SC² = 64 + 36
CS² = 100
CS² = 10²
CS = 10 cm

Students can Download Maths Chapter 2 Life Mathematics Ex 2.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 2 Life Mathematics Ex 2.2

Miscellaneous and Practice Problems

Question 1.
5 boys or 3 girls can do a science project in 40 days. How long will it take for 15 boys and 6 girls to do the same project?
Solution:
Let B and G denote Boys and Girls respectively.
Given 5B = 3G ⇒ 1B = \(\frac{3}{5}\)G
now 15B + 6G = 15 × \(\frac{3}{5}\) G + 6G = 9G + 6G = 15G
If 3 girls can do the project in 40 days then 15 girls can do it in
3G × 40 ÷ 15G = 3G × 40 × \(\frac{1}{15G}\) = \(\frac{40}{5}\)
= 8 days.
∴ 15 boys and 6 girls can complete the project in 8 days.

Question 2.
If 32 men working 12 hours a day can do a work in 15 days, how many men working 10 hours a day can do double that work in 24 days?
Solution:
Let the required number of men be x.

Let P₁= 32, H₁ = 12, D₁ = 12, W₁ = 1
P₂ = x, H₂ = 10, D₂ = 24, W₂ = 1

x = 24 persons
To complete the same work 24 men needed.
To complete double the work 24 × 2 = 48 men are required.

Question 3.
Amutha can weave a saree in 18 days. Anjali is twice as good a weaver as Amutha. If both of them weave together, in how many days can they complete weaving the saree?
Solution:
Amutha can weave a saree in 18 days. Anjali is twice as good as Amutha.
ie. If Amutha weave for 2 days, Anjali do the same work in 1 day.
If Anjali weave the saree she will take
\(\frac{18}{2}\) = 9 days
Hence time taken by them together = \(\frac{ab}{a + b}\) days = \(\frac{18 × 9}{18 + 9}\) = \(\frac{18 × 9}{27}\) = 6 days

In 6 days they complete weaving the saree.

Question 4.
A, B and C can complete a work in 5 days. If A and C can complete the same work in 7½ days and A alone in 15 days then, in how many days can B and G finish the work?
Solution:
A + B + C complete the work in 5 days.
∴ (A + B + C)’s 1 day work = \(\frac{1}{5}\)
(A + C) complete the work in 7 \(\frac{1}{2}\) days = \(\frac{15}{2}\) days
∴ (A + C)’s 1 day work = \(\frac{1}{\frac{15}{2}}\) = \(\frac{2}{15}\)
∴ B’s 1 day work = (A + B + C)’s 1 day work – (A + C)’s 1 day work.
\(\frac{1}{5}\) – \(\frac{2}{15}\) = \(\frac{3}{15}\) – \(\frac{2}{15}\)
C’s 1 day work = (A + C)’s 1 day work – A’s 1 day work
= \(\frac{2}{5}\) – \(\frac{1}{15}\) = \(\frac{1}{15}\)
Now (A + C)’s 1 day work = B’s 1 day work + C’s 1 day work
= \(\frac{1}{15}\) + \(\frac{1}{15}\) = \(\frac{2}{15}\)
∴ (B + C) can complete the work in \(\frac{1}{\frac{2}{15}}\) days. = \(\frac{15}{2}\) days = 7\(\frac{1}{2}\) days
∴B and C finish the work in 7\(\frac{1}{2}\) days.

Question 5.
P and Q can do a piece of work in 12 days and 15 days respectively. P started the work alone and then, after 3 days Q joined him till the work was completed. How long did the work last?
Solution:
p can do a piece of work in 12 days.
∴ p’s 1 day work = \(\frac{1}{12}\)
p’s 1 day work = 3 × \(\frac{1}{12}\) = \(\frac{3}{12}\)
Q can do a piece of work in 15 days.
∴ Q’s 1 day work = \(\frac{1}{15}\)
Remaining work after 3 days = 1 – \(\frac{3}{12}\) = \(\frac{9}{12}\)
(P + Q)’s 1 day work = \(\frac{1}{12}\) + \(\frac{1}{15}\) = \(\frac{5}{60}\) + \(\frac{4}{60}\) = \(\frac{9}{60}\)
Number of days required to finish the remaining work
= \(\frac{Remaining work}{(P + Q)’s 1 day work}\) = \(\frac{\frac{9}{12}}{\frac{9}{60}}\) = \(\frac{9}{12}\) × \(\frac{60}{9}\) = 5
Remaining work lasts for 5 days. Total work lasts for 3 + 5 = 8 days.

Challenging Problems

Question 6.
A camp had provisions for 490 soldiers for 65 days. After 15 days, more soldiers arrived and the remaining provisions lasted for 35 days. How many soldiers joined the camp?
Solution:

Now as the soldiers increases food last for less days.
∴ It is inverse proportion.
The proportion is (490 + x): 490 : : 50 : 35
Product of the extremes = Product of the means
(490 + x) × 35 = 490 × 50
(490 + x) = \(\frac{490 × 50}{35}\)

x = 700 – 490
x = 210
∴ 210 soldiers joined the camp.

Question 7.
A small – scale company undertakes an agreement to produce 540 motor pumps in 150 days and employs 40 men for the work. After 75 days, the company could make only 180 motor pumps. How many more men should the company employ so that the work is completed on time as per the agreement?
Solution:
Let the number of men to be appointed more be x.

To produce more pumps more men required
∴ It is direct variation.
∴ The multiplying factor is \(\frac{360}{180}\)
More days means less employees needed.
∴ It is Indirect proportion.
∴ The multiplying factor is \(\frac{75}{75}\)
Now 40 + x = 40 × \(\frac{360}{180}\) × \(\frac{75}{75}\)
40 + x = 80
x = 80 – 40
x = 40
40 more man should be employed to complete the work on time as per the agreement.

Question 8.
A can do a work in 45 days. He works at it for 15 days and then, B alone finishes the remaining work in 24 days. Find the time taken to complete 80% of the work if they work together.
Solution:
A can do a work in 45 days.
A’s 1 day work = \(\frac{1}{45}\)
∴ A’s 15 days work = 15 × \(\frac{1}{45}\) = \(\frac{1}{3}\)
Remaining work = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
B alone completes the remaining \(\frac{2}{3}\) work in 24 days
∴ B completes the whole work in \(\frac{24}{\frac{2}{3}}\) days = 24 × \(\frac{3}{2}\) = 36 days.
∴ B’s 1 day’s work = \(\frac{1}{36}\)
∴ (A + B)’s together complete the work in \(\frac{ab}{a + b}\) days = \(\frac{45 × 36}{45 + 36}\) = \(\frac{45 × 36}{81}\)

Whole wok will be completed by (A + B) in = 20 days.
∴ 80% of the work will be completed in \(\frac{80 × 20}{100}\) = 16 days.

Question 9.
P alone can do \(\frac{1}{2}\) of a work in 6 days and Q alone can do \(\frac{2}{3}\) of the same work in 4 days. In how many days working together, will they finish \(\frac{3}{4}\) of the work?
Solution:
\(\frac{1}{2}\) of the work is done by P in 6 days
∴ Full work is done by P in \(\frac{6}{\frac{1}{2}}\) = 6 × 2 = 12 days
\(\frac{2}{3}\) of work done by Q in 4 days.
∴ Full work done by Q in \(\frac{4}{\frac{2}{3}}\) = 4 × \(\frac{3}{2}\) = 6 days
(P + Q) will finish the whole work in \(\frac{ab}{a + b}\) days = \(\frac{12 × 6}{12 + 6}\) = \(\frac{12 × 6}{18}\) = 4 days
(P + Q) will finish \(\frac{3}{4}\) of the work in 4 × \(\frac{3}{4}\) = 3 days.

Question 10.
X alone can do a piece of work in 6 days and Y alone in 8 days. X and Y undertook the work for Rs 4800. With the help of Z, they completed the work in 3 days. How much is Z’s share?
Solution:
X can do the work in 6 days.
X’s 1 day work = \(\frac{1}{6}\)
X’s share for 1 day = \(\frac{1}{6}\) × 48000 = Rs 800
X’s share for 3 days = 3 × 800 = 2400
Y can complete the work in 8 days.
Y’s 1 day work = \(\frac{1}{8}\)
Y’s 1 day share = \(\frac{1}{8}\) × 4800 = 600
Y’s 3 days share = 600 × 3 = 1800
(X + Y)’s 3 days share = 2400 + 1800 = 4200
Remaining money is Z’s share
∴ Z’s share = 4800 – 4200 = 600

Students can Download Maths Chapter 1 Numbers Ex 1.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Ex 1.5

Miscellaneous and Practice Problems

Question 1.
A square carpet covers an area of 1024 m² of a big hall. It is placed in the middle of the hall. What is the length of a side of the carpet?
Solution:
Area of the carpet = 1024 m²
side × side = 1024 m²
(side)² = 1024 m²

(side)² = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2² × 2² × 2² × 2² × 2²
= (2 × 2 × 2 × 2 × 2)²
(side)² = 32²
side = 32
Length of a side of the carpet = 32 m

Question 2.
There is a large square portrait of a leader that covers an area of 4489 cm². If each side has a 2 cm liner, what would be its area?
Solution:
Area of the square = 4489 cm²
(side)² = 4489 cm²

(side)² = 67 x 67
side² = 67²
Length of a side = 67

Length of a side Length of a side with liner = 67 + 2 + 2 cm = 71 cm
Area of the larger square = 71 x 71 cm²
= 5041 cm²
Area of the liner = Area of big square-Area of small square
= (5041 – 4489) cm² = 552 cm²

Question 3.
2401 plants are planted in a garden such that each contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution:
Given number of plants in a row = Number of rows.
Number of rows × number of plants in a row = Total plants
Total plants = 2401

= 7 × 7 × 7 × 7 = 7² × 7²
= 49 × 49
∴ number of rows = 49
number of plants in a row = 49

Question 4.
If \(\sqrt[3]{1906624} \times \sqrt{x}\) = 3100, find x.
Solution:

\(\sqrt{x}\) = 25
Squaring on both sides \((\sqrt{x})^{2}\) = 25²
x = 625

Question 5.
If (625)^x = 15625, find x² and x³
Solution:
(625)^x = 15625

(5 x 5 x 5 x 5)^x = 5 x 5 x 5 x 5 x 5 x 5
(5⁴)^x = 5⁶
5^4x = 5⁶
5^4x = 5⁶
Comparing the powers of 5 both sides
4x = 6
x = \(\frac{6}{4}\)
x = \(\frac{3}{2}\)

Question 6.
If 2^m-1 + 2^m+1 = 640, then find ‘m’
Solution:
Given 2^m-1 + 2^m+1 = 640
2^m-1 + 2^m+1 = 128 + 512 [consecutive powers of 2]
2^m-1 + 2^m+1 = 2⁷+ 2⁹ [powers of 2: 2, 4, 8, 16, 32, 64, 128, 256, 512, …..]
m – 1 = 7
m = 7 + 1
m = 8

Question 7.
Simplify \(\frac{16 \times 10^{2} \times 64}{4^{2} \times 2^{4}}\)
Solution:

\(\frac{16 \times 10^{2} \times 64}{4^{2} \times 2^{4}}\) = \(\frac{2^{4} \times 10^{2} \times 2^{6}}{\left(2^{2}\right)^{2} \times 2^{4}}=\frac{2^{4+6} \times 10^{2}}{2^{4} \times 2^{4}}=\frac{2^{10} \times 100}{2^{8}}\)
= 2^10-8 × 100= 2² × 100 = 400

Question 8.
Give the answer in scientific notation:
A human heart beats at an average of 80 beats per minute. How many times does it beat in
(i) an hour?
(ii) a day?
(iii) a year?
(iv) 100 years?
Solution:
Heart beat per minute = 80 beats
(i) an hour One hour = 60 minutes
Heart beat in an hour = 60 x 80 = 4800 = 4.8 x 10³

(ii) In a day
One day = 24 hours = 24 x 60 minutes
∴ Heart beat in one day = 24 x 60 x 80 = 24 x 4800 = 115200 = 1.152 x 10⁵

(iii) a year
One year = 365 days = 365 x 24 hours = 365 x 24 x 60 minutes
∴ Heart beats in a year = 365 x 24 x 60 x 80 = 42048000 = 4.2048 x 10⁷

(iv) 100 years
Heart beats in one year = 4.2048 x 10⁷
Heart beats in 100 years = 4.2048 x 10⁷ x 100 = 4.2048 x 10⁷ x 10²
= 4.2048 x 10⁹

Challenging Problems

Question 9.
A greeting card has an area 90 cm². Between what two whole numbers is the length of its side?
Solution:
Area of the greeting card = 90 cm²
(side)² = 90 cm²

(side)² = 2 x 5 x 3 x 3 = 2 x 5 x 3²
\(\sqrt{({side})^{2}}=\sqrt{2 \times 5 \times 3^{2}}\)

side = 3 \(\sqrt{2 × 5}\)
side = \(\sqrt{10}\) cm
side = 3 × 3.2 cm
side = 9.6 cm
∴ Side lies between the whole numbers 9 and 10.

Question 10.
225 square shaped mosaic tiles, each of area 1 square decimetre exactly cover a square shaped verandah. How long is each side of the square shaped verandah?
Solution:
Area of one tile = 1 sq. decimeter
Area of 225 tiles = 225 sq.decimeter
225 square tiles exactly covers the square shaped verandah.
∴ Area of 225 tiles = Area of the verandah
Area of the verandah = 225 sq.decimeter
side x side = 15 x 15 sq.decimeter
side = 15 decimeters
Length of each side of verandah = 15 decimeters.

Question 11.
A group of 1536 cadets wanted to have a parade forming a square design. Is it possible? If it is not possible how many more cadets would be required?
Solution:
Number of cadets to form square design

1536 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3
The numbers 2 and 3 are unpaired
It is impossible to have the parade forming square design with 1536 cadets.

39 x 39 = 1521
Also 40 x 40 = 1600
∴ We have to add (1600 – 1536) = 64 to make 1536 a perfect square.
∴ 64 more cadets would be required to form the square design.

Question 12.
Find the decimal fraction which when multiplied by itself gives 176.252176.
Solution:
We will find the square root of 176.252176

176.252176 = 13.276 x 13.276
∴ The required number is 13.276

Question 13.
Evaluate \(\sqrt{286225}\) and use it to compute \(\sqrt{2862.25}\) + \(\sqrt{28.6225}\)
Solution:

Question 14.
The speed of light in glass is about 2 x 10⁸ m/sec. Use the formula, time = \(\frac{distence}{speed}\) to find the time (in hours) for a pulse of light to travel 7200 km in glass.
Solution:

Required time = 10^-5 hours

Question 15.
Simplify : (3.769 x 10⁵) + (4.21 x 10⁵)
Solution:

(3.769 x 10⁵) + (4.21 x 10⁵) = 3,76,900 + 4,21,00
= 7,97,900 = 7.979 x 10⁵

Question 16.
Order the following from the least to the greatest: 1625, 8100, 3500, 4400, 2600
Solution:
16²⁵ = (2⁴)²⁵ = 2¹⁰⁰
8¹⁰⁰ = (2³)¹⁰⁰ = 2³⁰⁰
4⁴⁰⁰ = (2²)⁴⁰⁰ = 2⁸⁰⁰
2⁶⁰⁰ = 2⁶⁰⁰
Comparing the powers we have, 2¹⁰⁰ < 2³⁰⁰ < 2⁶⁰⁰< 2⁸⁰⁰
∴ The required order : 16²⁵, 8¹⁰⁰, 2⁶⁰⁰, 3⁵⁰⁰, 4⁴⁰⁰

Students can Download Maths Chapter 1 Numbers Ex 1.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Ex 1.3

Question 1.
Fill in the blanks:
(i) The ones digits in the cube of 73 is……….
(ii) The maximum number of digits in the cube of a two digit number is……….
(iii) The cube root of 540 × 50 is………..
(iv) The cube root of 0.000004913 is………..
(v) The number to be added to 3333 to make it a perfect cube is………….
Solution:
(i) 7
(ii) 6
(iii) 30
(iv) 0.017
(v) 42

Question 2.
Say True or False:
(i) The cube of 0.0012 is 0.000001728.
(ii) The cube root of 250047 is 63.
(iii) 79570 is not a perfect cube.
Solution:
(i) false
(ii) true
(iii) true

Question 3.
Show that 1944 is not a perfect cube.
Solution:

1994 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3
= 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3
= 2³ × 3³ × 3 × 3
There are two triplets to make further triplets we need one more 3.
∴ 1944 is not a perfect cube.

Question 4.
Find the cube root of 24 × 36 × 80 × 25.
Solution:

Question 5.
Find the smallest number by which 10985 should be divided so that the quotient is a perfect cube.
Solution:

We have 10985 = 5 × 13 × 13 × 13
= 5 × 13 × 13 × 13
Here we have a triplet of 13 and we are left over with 5.
If we divide 10985 by 5, the new number will be a perfect cube.
∴ The required number is 5.

Question 6.
Find two smallest perfect square numbers which when multiplied together gives a perfect cube number.
Solution:
Consider the numbers 22 and 42
The numbers are 4 and 16.
Their product 4 × 16 = 64
64 = 4 × 4 × 4
∴ The required square numbers are 4 and 16

Question 7.
If the cube of a squared number is 729, find the square root of that number.
Solution:
729 = 3 × 3 × 3 × 3 × 3 × 3
(729)^1/3 = 3 × 3 = 9
∴ The cube of 9 is 729.
9 = 3 × 3 [ie 3 is squared to get 9]

we have to find out √3, √3 = 1.732

Question 8.
What is the square root of cube root of 46656?
Solution:
We have to find out \(\sqrt{(\sqrt[3]{46656})}\)
First we will find \(\sqrt[3]{46656}\)

\(\sqrt[3]{46656}\) = (2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3)^1/3
\(\sqrt[3]{46656}\) = 2 × 2 × 3 × 3
\(\sqrt[3]{46656}\) = 2² × 3² = 36
Now \(\sqrt{(\sqrt[3]{46656})}\) = \(\sqrt{36}\) = \(\sqrt{2^2×3^2 }\) = 2 × 3 = 6
∴ The required is 6.

Question 9.
Find the cube root of 729 and 6859 by prime factorisation.
Solution:

(i) \(\sqrt[3]{729}\) = \(\sqrt[3]{3 × 3 × 3 × 3 × 3 × 3}\)
= 3 × 3
\(\sqrt[3]{729}\) = 9

(ii) \(\sqrt[3]{6859}\) = \(\sqrt[3]{19 × 19 × 19 }\)
\(\sqrt[3]{6859}\) = 19

Question 10.
Find the smallest number by which 200 should be multiplied to make it a perfect cube.
Solution:
We find 200 = 2 × 2 × 2 × 5 × 5
Grouping the prime factors of 200 as triplets, we are left with 5 × 5
We need one more 5 to make it a perfect cube.
So to make 200 a perfect cube multiply both sides by 5.

200 × 5 = (2 × 2 × 2 × 5 × 5) × 5
1000 = 2 × 2 × 2 × 5 × 5 × 5
Now 1000 is a perfect cube.
∴ The required number is 5.

Students can Download Maths Chapter 2 Life Mathematics Ex 2.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 2 Life Mathematics Ex 2.1

Question 1.
Fill in the blanks:
(i) A can finish a job in 3 days whereas B finishes it in 6 days. The time taken to complete the job together is………..days.
(ii) If 5 persons can do 5 jobs in 5 days, then 50 persons can do 50 jobs in………..days.
(iii) A can do a work in 24 days. A and B together can finish the work in 6 days. Then B alone can finish the work in…………days.
(iv) A alone can do a piece of work in 35 days. If B is 40% more efficient than A, then B will finish the work in………..days.
(v) A alone can do a work in 10 days and B alone in 15 days. They undertook the work for Rs 200000. The amount that A will get is………
Solution:
(i) 2 days
(ii) 5
(iii) 8
(iv) 25
(v) Rs 1,20,000

Question 2.
210 men working 12 hours a day can finish a job in 18 days. How many men are required to finish the job in 20 days working 14 hours a day?
Solution:
Let the required number of men be x.

More working hours ⇒ less men required.
∴ It is inverse proportion.
∴ Multiplying factor is \(\frac{12}{14}\)
Also more number of days ⇒ less men
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{18}{20}\)
∴ x = 210 × \(\frac{12}{14}\) × \(\frac{18}{20}\)= 162 men

162 men are required.

Question 3.
A cement factory makes 7000 cement bags in 12 days with the help of 36 machines. How many bags can be made in 18 days using 24 machines?
Solution:
Let the required number of cement bags be x.

Number of days more ⇒ More cement bags.
∴ It is direct variation.
∴ The multiplying factor = \(\frac{18}{12}\)
Number of machines more ⇒ More cement bags.
∴ It is direct variation.
∴ The multiplying factor = \(\frac{24}{36}\)
∴ x = 7000 × \(\frac{18}{12}\) × \(\frac{24}{36}\)

x = 7000 cement bags
7000 cement bags can be made.

Question 4.
A soap factory produces 9600 soaps in 6 days working 15 hours a day. In how many days will it produce 14400 soaps working 3 hours more a day?
Solution:
Let the required number of days be x.

To produce more soaps more days required.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{14400}{9600}\)
If more hours spend, less days required.
∴ It is indirect proportion.
∴ Multiplying factor = \(\frac{15}{18}\)
∴ x = 6 × \(\frac{14400}{9600}\) × \(\frac{15}{18}\)

x = \(\frac{15}{2}\)
\(\frac{15}{2}\) days will be needed.

Question 5.
If 6 container lorries transport 135 tonnes of goods in 5 days, how many more lorries are required to transport 180 tonnes of goods in 4 days?
Solution:
Let the number of lorries required more = x.

As the goods are more ⇒ More lorries are needed to transport.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{180}{135}\)
Again if more days ⇒ less number of lorries enough.
∴ It is direct proportion.
∴ Multiplying factor = \(\frac{5}{4}\)
∴ 6 + x = 6 × \(\frac{180}{135}\) × \(\frac{5}{4}\)

6 + x = 10
x = 10 – 6
x = 4
∴ 4 more lorries are required.

Question 6.
A can do a piece of work in 12 hours, B and C can do it 3 hours whereas A and C can do it in 6 hours. How long will B alone take to do the same work?
Solution:
Time taken by A to complete the work =12 hrs.
∴ A’s 1 hr work = \(\frac{1}{12}\)…………(1)
(B + C) complete the work in 3 hrs.
∴ (B + C)’s 1 hour work = \(\frac{1}{3}\)…………(2)
(1) + (2) ⇒
∴ (A + B + C)’s 1 hour work = \(\frac{1}{12}\) + \(\frac{1}{3}\) = \(\frac{1+4}{12}\) = \(\frac{5}{12}\)
Now (A + C) complete the work in 6 hrs.
∴(A + C)’s 1 hour work = \(\frac{1}{6}\)
∴ B’s 1 hour work = (A + B + C)’s 1 hour work – (A + C)’s 1 hour work
= \(\frac{5}{12}\) – \(\frac{1}{6}\) = \(\frac{5-2}{12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
∴ B alone take 4 days to complete the work.

Question 7.
A and B can do a piece of work in 12 days, while B and C can do it in 15 days whereas A and C can do it in 20 days. How long would each take to do the same work?
Solution:
(A + B) complete the work in 12 days.
∴ (A + B)’s 1 day work = \(\frac{1}{12}\)……….(1)
(B + C) complete the work in 15 days
∴ (B + C)’s 1 day work = \(\frac{1}{15}\)……….(2)
(A + C) complete the work in 20 days
∴ (A + C)’s 1 day work = \(\frac{1}{20}\)……….(3)
Now (1) + (2) + (3) ⇒
[(A + B) + (B + C) + (A + C)]’s 1 day work = \(\frac{1}{12}\) + \(\frac{1}{15}\) + \(\frac{1}{20}\)

(2A + 2B + 2C)’s 1 day work = \(\frac{5}{60}\) + \(\frac{4}{60}\) + \(\frac{3}{60}\)
2(A + B + C)’s 1 day work = \(\frac{5+4+3}{60}\)
(A + B + C)’s 1 day work = \(\frac{12}{60×2}\)
(A + B + C)’s 1 day work = \(\frac{1}{10}\)
Now A’s 1 day’s work = (A + B + C)’s 1 day work – (B + C)’s 1 day work
\(\frac{1}{10}\) – \(\frac{1}{15}\) = \(\frac{3}{30}\) – \(\frac{2}{30}\) = \(\frac{1}{30}\)
∴ A takes 30 days to complete the work.
B’s 1 day work = (A + B + C)’s 1 day’s work – (A + C)’s 1 day’s work
= \(\frac{1}{10}\) – \(\frac{1}{20}\) = \(\frac{6}{60}\) – \(\frac{3}{60}\)
\(\frac{6-3}{60}\) = \(\frac{3}{60}\) = \(\frac{1}{20}\)
B takes 20 days to complete the work.
C’s 1 day work = (A + B + C)’s 1 day work – (A + B)’s 1 day work
\(\frac{1}{10}\) – \(\frac{1}{12}\) = \(\frac{6}{60}\) – \(\frac{5}{60}\) = \(\frac{6-5}{60}\) = \(\frac{1}{60}\)
∴ C takes 60 days to complete the work.

Question 8.
Carpenter A takes 15 minutes to fit the parts of a chair while Carpenter B takes 3 more minutes than A to do the same work. Working together, how long will it take for them to fit the parts for 22 chairs?
Solution:
Time taken by A to fit a chair = 15 minutes
Time taken by B = 3 minutes more than A
= 15 + 3 = 18 minutes
∴ A’s 1 minute work = \(\frac{1}{15}\)
B’s 1 minute work = \(\frac{1}{18}\)
(A + B)’s 1 minutes work = \(\frac{1}{15}\) + \(\frac{1}{18}\)

\(\frac{12}{180}\) + \(\frac{22}{180}\) = \(\frac{22}{180}\) = \(\frac{11}{90}\)
∴ Time taken by (A + B) to fit a chair
= \(\frac{1}{\frac{11}{90}}\) = \(\frac{90}{11}\) minutes
∴ Time taken by (A + B) to fit 22 chairs
= \(\frac{90}{11}\) × 22 = 180 minutes
= \(\frac{180}{60}\) = 3 hours

Question 9.
A man takes 10 days to finish a job where as a woman takes 6 days to finish the same job. Together they worked for 3 days and then the woman left. In how many days will the man complete the remaining job?
Solution:
Man can finish the work in 10 days and women can finish the same work in 6 days.
∴ Man’s 1 day work = \(\frac{1}{10}\)
Woman’s 1 day work = \(\frac{1}{6}\)
(Man + Woman)s 1 day work = \(\frac{1}{10}\) + \(\frac{1}{6}\) = \(\frac{6}{60}\) + \(\frac{10}{60}\) = \(\frac{16}{60}\)
(Man + Woman)s 3 days work

In 3 days \(\frac{4}{5}\) th of the whole work is completed.
Remaining work = 1 – \(\frac{4}{5}\) = \(\frac{5}{5}\) – \(\frac{4}{5}\) = \(\frac{1}{5}\)
Complete work is done by the man by 10 days
∴ \(\frac{1}{5}\) of the work is done by man in \(\frac{1}{5}\) × 10 = 2 days.

Question 10.
A is thrice as fast as B. If B can do a piece of work in 24 days then, find the number of days they will take to complete the work together.
Solution:
If B does the work in 3 days, A will do it in 1 day.
B complete the work in 24 days.
∴ A complete the same work in \(\frac{24}{3}\) = 8 days.
∴ (A + B) complete the work in \(\frac{ab}{a+b}\) days = \(\frac{24×8}{24+8}\) days = \(\frac{24×8}{32}\)days = 6 days

They together complete the work in 6 days.

Students can Download Maths Chapter 1 Numbers Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Additional Questions

Question 1.
Find the least number by which 1100 must be multiplied so that the product becomes a perfect square. Also, in each case find the square root of the perfect square so obtained.
Solution:
We find 1100 = 2 × 2 × 5 × 5 × 11 =2² × 5² × 11
∴ The prime factor 11 has no pair.
∴ If we multiply 1100 by 11, then the product becomes a perfect square.
∴ New number = 1100 × 11 = 12100

12100 = 2² × 5² × 11²
\(\sqrt{12100}\) = 2 × 5 × 11 = 110
Square root of the new number = 110

Question 2.
Find the square of 509 using (a + b)² = a² + 2ab + b²
Solution:
509² = (500 + 9)² = 500² + 2 x 500 x 9 + 9²
= 250000 + 9000 + 81
509² = 259081

Question 3.
Find the sum without adding
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
Solution:
Given sum is the sum of first 12 odd natural numbers.
Sum of first n odd natural numbers is n².
∴ 1 +3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = 12² = 144

Question 4.
Write a Pythagorean triplet whose one number is 110
Solution:
Here let 2m = 110
m = 55

m² – 1 = 55² – 1 = 3025 – 1 = 3024
m² + 1 = 55² + 1 = 3025 + 1 = 3026
∴ Pythagorean triplet is 110, 3024, 3026.

Question 5.
Find the square root of 10 \(\frac{2}{3}\) correct to three places of decimal.
Solution:
10 \(\frac{2}{3}\) = 10.6666…….

\(\sqrt{10 \frac{2}{3}}=3.2659 \Rightarrow \sqrt{10 \frac{2}{3}}\) = 3.266 correct to three places of decimal.

Question 6.
Find the square root of 0.053361
Solution:

\(\sqrt{0.053361}\) = 0.231

Question 7.
Three numbers are in the ratio 2:3:4. The sum of their cubes is 33957. Find the numbers.
Solution:
Let the numbers be 2x, 3x and 4x
(2x)³ + (3x)³ + (4x)³ = 33957
8x³ + 27x³ + 64x³ = 33957
99x³ = 33957
x³ = \(\frac{33957}{99}\)
x³ = 343
x³ = 7 × 7 × 7
x³ = 7³
x = 7
∴ The numbers are 2x = 2 × 7 = 14
3x = 3 × 7 = 21
4x = 4 × 7 = 28

Question 8.
The volume of a cube is 9261000 m³. Find the side of the cube?
Solution:
Volume of the cube = side x side x side
side x side x side = 9261000
side = \(\sqrt[3]{9261×1000}\) = \(\sqrt[3]{9261}\) × \(\sqrt[3]{1000}\)
= \(\sqrt[3]{3^{3}×7^{3}}\) × \(\sqrt[3]{10×10×10}\) = 3 × 7 × 10 = 210
∴ Side of the cube = 210 m

Question 9.
If the diameters of the sun and Earth are 1.4 × 109 m and 1.275 × 107 m respectively. compare these two.
Solution:

So the diameter of the Sun is about 100 times the diameter of the Earth.

Question 10.
The size of a red blood cell is 0.000007 m and that of a plant, cell is 0.00001275 m. Compare these two.
Solution:

∴ RBC size if half the size of a plant cell.

Students can Download Maths Chapter 2 Life Mathematics Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 2 Life Mathematics Intext Questions

Exercise 2.1
Try These (Text book Page No. 33)

Classify the given examples as direct or inverse proportion:
(i) Weight of pulses to their cost.
Solution:
As weight increases cost also increases.
∴ Weight and cost are direct proportion.

(ii) Distance travelled by bus to the price of ticket.
Solution:
As the distance increases price to travel also increases.
∴ Distance and price are direct proportion.

(iii) Speed of the athelete to cover a certain distance.
Solution:
As the speed increases, the time to cover the distance become less.
So speed and time are in indirect proportion.

(iv) Number of workers employed to complete a construction in a specified time.
Solution:
As the number of workers increases, the amount of work become less, so they are in indirect proportion.

(v) Volume of water flown through a pipe to its pressure.
Solution:
As the pressure increases, volume also increases.
∴ They are direct proportions.

(vi) Area of a circle to its radius.
Solution:
If the radius of the circle increases its area also increases.
∴ Area and radius of circles are direct proportion.

Use the concept of direct and inverse proportions and try to answer the following questions:
Question 1.
A student can type 21 pages in 15 minutes. At the same rate, how long will it take the student to type 84 pages?
Solution:
Direct proportion
No. of minutes = x
k = \(\frac{21}{15}\)
\(\frac{21}{15}\) = \(\frac{84}{x}\)

Question 2.
The weight of an iron pipe varies directly with its length. If 8 feet of an iron pipe weighs 3.2 kg, find the proportionality constant k and determine the weight of a 36 feet iron pipe.
Solution:

Weight of 36 feet iron pipe = x
\(\frac{36}{x}\) = 2.5

Question 3.
A car covers a distance of 765 km in 51 litres of petrol. How much distance would it cover in 30 litres of petrol?
Solution:
Direct proportion
k = \(\frac{51}{765}\)
Distance cover = x km
\(\frac{30}{x}\) = \(\frac{51}{765}\)

Question 4.
If x and y vary inversely and x = 24 when y = 8, find x when y = 12.
Solution:
k = xy = 24 × 8 = 192
∴ 12 × x = 192

Question 5.
If 35 women can do a piece of work in 16 days, in how many days will 28 women do the same work?
Solution:
Inverse proportion
No. of days = x
k = 35 × 16
∴ 28 × x = 35 × 16

Question 6.
A farmer has food for 14 cows which can last for 39 days. How long would the food last, if 7 more cows join his cattle?
Solution:
Inverse variation
k = xy = 14 × 39
No. of cow = 14 + 7 = 21
No. of days = x
21 × x = 14 × 39

Question 7.
Identify the type of proportion and fill in the blank boxes:

Solution:
Direct proportion
\(\frac{x}{y}\) = k = \(\frac{1}{20}\)
(i) x = 2; y = ?
\(\frac{2}{y}\) = \(\frac{1}{20}\) ⇒ y = 2 × 20 = 40

(ii) x = ?; y = 60
\(\frac{x}{60}\) = \(\frac{1}{20}\) ⇒ x = \(\frac{60}{20}\) = 3

(iii) x = 4; y = ?
\(\frac{4}{y}\) = \(\frac{1}{20}\) ⇒ y = 80

(iv) x = 4; y = ?
\(\frac{8}{y}\) = \(\frac{1}{20}\) ⇒ y = 20 × 8 = 160

(v) x = ?; y = 180
\(\frac{x}{180}\) = \(\frac{1}{20}\)
x = \(\frac{180}{20}\) = 9

(vi) x = 12; y = ?
\(\frac{12}{y}\) = \(\frac{1}{20}\)
y = 12 × 20 = 240

(vii) x = ?; y = 360
\(\frac{x}{360}\) = \(\frac{1}{20}\) ⇒ x = \(\frac{360}{20}\) = 18

(viii) x = 24; y = ?
\(\frac{24}{y}\) = \(\frac{1}{20}\) ⇒ y = 24 × 20 = 480

Question 8.
Identify the type of proportion and fill in the blank boxes:

Solution:
Inverse proportion
k = xy = 1 × 144 = 144
(i) x = 2; y = ?
2y = 144
y = 72

(ii) X = ?; y = 48
48x = 144
x = \(\frac{144}{48}\) = 3

(iii) x = 4; y = ?
4y = 144
y = \(\frac{144}{4}\) = 36

(iv) x = 8; y = ?
8 y = 144
y = \(\frac{144}{8}\) = 18

(v) x = ?; y = 16
16x = 144
y = \(\frac{144}{16}\) = 9

(vi) x = 12; y = ?
12y = 144
y = \(\frac{144}{12}\) = 12

(vii) x = ?; y = 9
9x = 144
x = \(\frac{144}{9}\) = 16

(viii) x = 24; y = ?
24y = 144
y = \(\frac{144}{24}\) = 6

Try These (Text book Page No. 38)

Question 1.
When x = 5 and y = 5 find k, if x and y vary directly.
Solution:
If x and y vary directly then \(\frac{x}{y}\) = k
Here x = 5; y = 5
∴ k = \(\frac{5}{5}\)
k = 1

Question 2.
When x and y vary inversely, find the constant of variation when x = 64 and y = 0.75
Solution:
Given
x =64, y = 0.75
and also given x and y vary inversely.
∴ xy = k. the constant of variation.
∴ Constant = 64 × 0.75
Constant of variation = 48

Think (Text book Page No. 38)

(i) When x and y are in direct proportion and if y is doubled, then what happens to x?
Solution:
If x and y are in direct proportion \(\frac{x}{y}\) = k, constant.
if y is doubled, then \(\frac{x}{2}\) must be equal to k. So x also to be doubled.

(ii) if \(\frac{x}{y-x}\) = \(\frac{6}{7}\) What is \(\frac{x}{y}\)?
Solution:
if \(\frac{x}{y-x}\) = \(\frac{6}{7}\)
\(\frac{y-x}{x}\) = \(\frac{7}{6}\)
\(\frac{y}{x}\) – \(\frac{x}{x}\) = \(\frac{7}{6}\)
\(\frac{y}{x}\) = \(\frac{7}{6}\) + \(\frac{x}{x}\)
\(\frac{y}{x}\) = \(\frac{7}{6}\) + 1
\(\frac{y}{x}\) = \(\frac{7+6}{6}\)
\(\frac{y}{x}\) = \(\frac{13}{6}\)
\(\frac{x}{y}\) = \(\frac{6}{13}\)

Try These (Text book Page No. 40)

Identify the different variations present in the following questions:
Question 1.
24 men can make 48 articles in 12 days. Then, 6 men can make …………. articles in 6 days.
Solution:
Let the required no. of articles be x

(i) Mens and days are Indirect variables.
(ii) Men and Articles are direct variables
(iii) Days and articles are also direct variables using formula.
Let P₁ = 24, D₁ = 12, W₁ = 48
P₂ = 6, D₂ = 6, W₂ = x

Question 2.
15 workers can lay a road of length 4 km In 4 hours. Then, …………. workers can lay a road of length 8 km in 8 hours.
Solution:
Let the required number of workers be x

Length and workers are direct variable as more length need more workers.
The proportion is 4 : 8 : : 15 : x ……….(1)
Hours and workers are indirect variables as more working hours need less men.
∴ The proportion is 8 : 4 : : 15 : x ………..(2)
Combining (1) and (2)

Product of the extremes = product of the means
4 × 8 × x = 8 × 4 × 15
x = \(\frac{8×4×15}{4×8}\)
x = 15 workers

Question 3.
25 women working 12 hours a day can complete a work in 36 days. Then, 20 women must ……….. work hours to complete the same work in 30 days.
Solution:
Let the required hours be x

As women increases hours to work decreases
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{25}{20}\)
As days increases hours needed become less
∴ It is also an indirect variation.
∴ Multiplying factor is \(\frac{36}{30}\)
∴ x = 12 × \(\frac{25}{20}\) × \(\frac{36}{30}\)
x = 18 hours

Question 4.
In a camp, there are 420 kg of rice sufficient for 98 persons for 45 days. The number of days that 60 kg of rice will last for 42 persons is…………
Solution:
Let the required number of days be x.

If amount of rice is more it will last for more days.
∴ It is Direct Proportion.
∴ Multiplying factor is \(\frac{60}{420}\)
If men increases number of days the rice lasts decreases
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{98}{42}\)
x = 45 × \(\frac{60}{420}\) × \(\frac{98}{42}\)

x = 15 days

Try These (Text book Page No. 44)

Question 1.
Vikram can do one-third of work in p days. He can do \(\frac{3}{4}\)th of work in ………… days.
Solution:
\(\frac{1}{3}\) of the work will be done in p days
∴ Full work will be completed in 3p days
\(\frac{3}{4}\)th of the work will be done in = 3p × \(\frac{3}{4}\) = \(\frac{9}{4}\)p = 2\(\frac{1}{4}\)p days

Question 2.
If m persons can complete a work in n days, then 4m persons can complete the same work in ……….. days and \(\frac{m}{4}\) persons can complete the same work in…….. days
Solution:
Given m persons complete a work in n days
(i) Then work measured in terms of Man days = mn
4 m men do the work it will be completed in \(\frac{mn}{4m}\) days = \(\frac{n}{4}\) days.
(ii) \(\frac{m}{4}\) persons can complete the same work in \(\frac{mn}{\frac{m}{4}}\) days = \(\frac{4mn}{m}\) = 4n days