Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Ex 1.5

Students can Download Maths Chapter 1 Numbers Ex 1.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Ex 1.5

Miscellaneous and Practice Problems

Question 1.
A square carpet covers an area of 1024 m² of a big hall. It is placed in the middle of the hall. What is the length of a side of the carpet?
Solution:
Area of the carpet = 1024 m²
side × side = 1024 m²
(side)² = 1024 m²

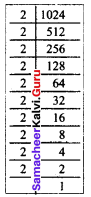
(side)² = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2² × 2² × 2² × 2² × 2²
= (2 × 2 × 2 × 2 × 2)²
(side)² = 32²
side = 32
Length of a side of the carpet = 32 m

Question 2.
There is a large square portrait of a leader that covers an area of 4489 cm². If each side has a 2 cm liner, what would be its area?
Solution:
Area of the square = 4489 cm²
(side)² = 4489 cm²

(side)² = 67 x 67
side² = 67²
Length of a side = 67

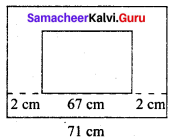
Length of a side Length of a side with liner = 67 + 2 + 2 cm = 71 cm
Area of the larger square = 71 x 71 cm²
= 5041 cm²
Area of the liner = Area of big square-Area of small square
= (5041 – 4489) cm² = 552 cm²

Question 3.
2401 plants are planted in a garden such that each contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution:
Given number of plants in a row = Number of rows.
Number of rows × number of plants in a row = Total plants
Total plants = 2401

= 7 × 7 × 7 × 7 = 7² × 7²
= 49 × 49
∴ number of rows = 49
number of plants in a row = 49

Question 4.
If \(\sqrt[3]{1906624} \times \sqrt{x}\) = 3100, find x.
Solution:

\(\sqrt{x}\) = 25
Squaring on both sides \((\sqrt{x})^{2}\) = 25²
x = 625

Question 5.
If (625)^x = 15625, find x² and x³
Solution:
(625)^x = 15625

(5 x 5 x 5 x 5)^x = 5 x 5 x 5 x 5 x 5 x 5
(5⁴)^x = 5⁶
5^4x = 5⁶
5^4x = 5⁶
Comparing the powers of 5 both sides
4x = 6
x = \(\frac{6}{4}\)
x = \(\frac{3}{2}\)

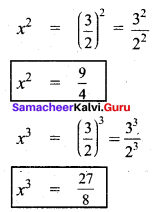
Question 6.
If 2^m-1 + 2^m+1 = 640, then find ‘m’
Solution:
Given 2^m-1 + 2^m+1 = 640
2^m-1 + 2^m+1 = 128 + 512 [consecutive powers of 2]
2^m-1 + 2^m+1 = 2⁷+ 2⁹ [powers of 2: 2, 4, 8, 16, 32, 64, 128, 256, 512, …..]
m – 1 = 7
m = 7 + 1
m = 8

Question 7.
Simplify \(\frac{16 \times 10^{2} \times 64}{4^{2} \times 2^{4}}\)
Solution:

\(\frac{16 \times 10^{2} \times 64}{4^{2} \times 2^{4}}\) = \(\frac{2^{4} \times 10^{2} \times 2^{6}}{\left(2^{2}\right)^{2} \times 2^{4}}=\frac{2^{4+6} \times 10^{2}}{2^{4} \times 2^{4}}=\frac{2^{10} \times 100}{2^{8}}\)
= 2^10-8 × 100= 2² × 100 = 400

Question 8.
Give the answer in scientific notation:
A human heart beats at an average of 80 beats per minute. How many times does it beat in
(i) an hour?
(ii) a day?
(iii) a year?
(iv) 100 years?
Solution:
Heart beat per minute = 80 beats
(i) an hour One hour = 60 minutes
Heart beat in an hour = 60 x 80 = 4800 = 4.8 x 10³

(ii) In a day
One day = 24 hours = 24 x 60 minutes
∴ Heart beat in one day = 24 x 60 x 80 = 24 x 4800 = 115200 = 1.152 x 10⁵

(iii) a year
One year = 365 days = 365 x 24 hours = 365 x 24 x 60 minutes
∴ Heart beats in a year = 365 x 24 x 60 x 80 = 42048000 = 4.2048 x 10⁷

(iv) 100 years
Heart beats in one year = 4.2048 x 10⁷
Heart beats in 100 years = 4.2048 x 10⁷ x 100 = 4.2048 x 10⁷ x 10²
= 4.2048 x 10⁹

Challenging Problems

Question 9.
A greeting card has an area 90 cm². Between what two whole numbers is the length of its side?
Solution:
Area of the greeting card = 90 cm²
(side)² = 90 cm²

(side)² = 2 x 5 x 3 x 3 = 2 x 5 x 3²
\(\sqrt{({side})^{2}}=\sqrt{2 \times 5 \times 3^{2}}\)

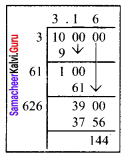
side = 3 \(\sqrt{2 × 5}\)
side = \(\sqrt{10}\) cm
side = 3 × 3.2 cm
side = 9.6 cm
∴ Side lies between the whole numbers 9 and 10.

Question 10.
225 square shaped mosaic tiles, each of area 1 square decimetre exactly cover a square shaped verandah. How long is each side of the square shaped verandah?
Solution:
Area of one tile = 1 sq. decimeter
Area of 225 tiles = 225 sq.decimeter
225 square tiles exactly covers the square shaped verandah.
∴ Area of 225 tiles = Area of the verandah
Area of the verandah = 225 sq.decimeter
side x side = 15 x 15 sq.decimeter
side = 15 decimeters
Length of each side of verandah = 15 decimeters.

Question 11.
A group of 1536 cadets wanted to have a parade forming a square design. Is it possible? If it is not possible how many more cadets would be required?
Solution:
Number of cadets to form square design

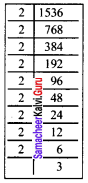
1536 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3
The numbers 2 and 3 are unpaired
It is impossible to have the parade forming square design with 1536 cadets.

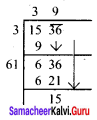
39 x 39 = 1521
Also 40 x 40 = 1600
∴ We have to add (1600 – 1536) = 64 to make 1536 a perfect square.
∴ 64 more cadets would be required to form the square design.

Question 12.
Find the decimal fraction which when multiplied by itself gives 176.252176.
Solution:
We will find the square root of 176.252176

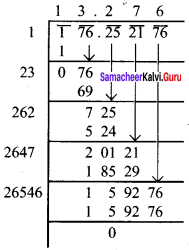
176.252176 = 13.276 x 13.276
∴ The required number is 13.276

Question 13.
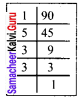
Evaluate \(\sqrt{286225}\) and use it to compute \(\sqrt{2862.25}\) + \(\sqrt{28.6225}\)
Solution:

Question 14.
The speed of light in glass is about 2 x 10⁸ m/sec. Use the formula, time = \(\frac{distence}{speed}\) to find the time (in hours) for a pulse of light to travel 7200 km in glass.
Solution:

Required time = 10^-5 hours

Question 15.
Simplify : (3.769 x 10⁵) + (4.21 x 10⁵)
Solution:

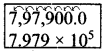
(3.769 x 10⁵) + (4.21 x 10⁵) = 3,76,900 + 4,21,00
= 7,97,900 = 7.979 x 10⁵

Question 16.
Order the following from the least to the greatest: 1625, 8100, 3500, 4400, 2600
Solution:
16²⁵ = (2⁴)²⁵ = 2¹⁰⁰
8¹⁰⁰ = (2³)¹⁰⁰ = 2³⁰⁰
4⁴⁰⁰ = (2²)⁴⁰⁰ = 2⁸⁰⁰
2⁶⁰⁰ = 2⁶⁰⁰
Comparing the powers we have, 2¹⁰⁰ < 2³⁰⁰ < 2⁶⁰⁰< 2⁸⁰⁰
∴ The required order : 16²⁵, 8¹⁰⁰, 2⁶⁰⁰, 3⁵⁰⁰, 4⁴⁰⁰