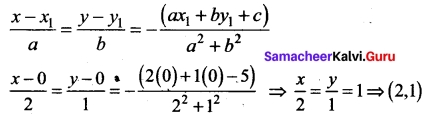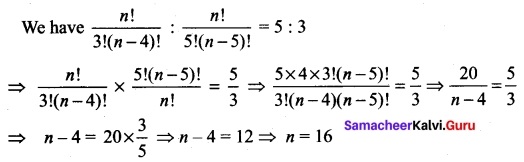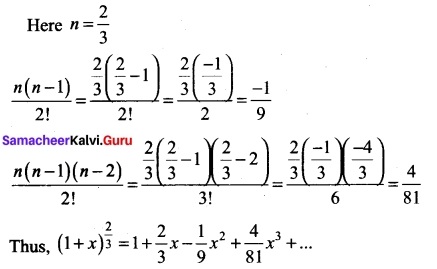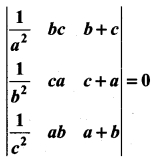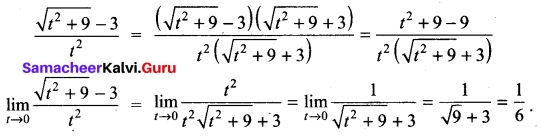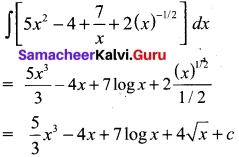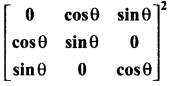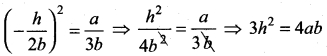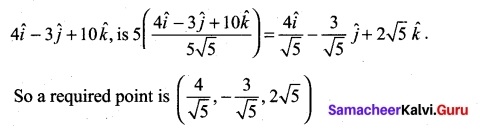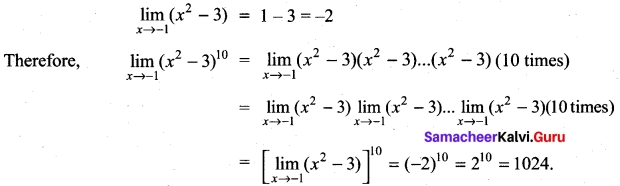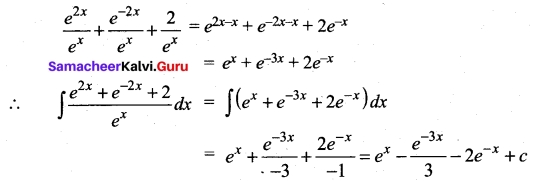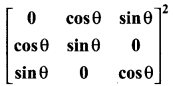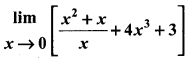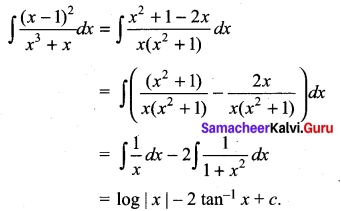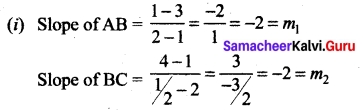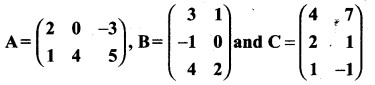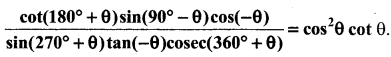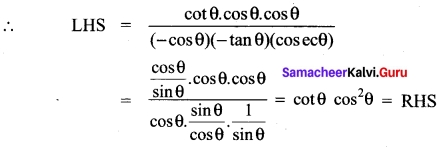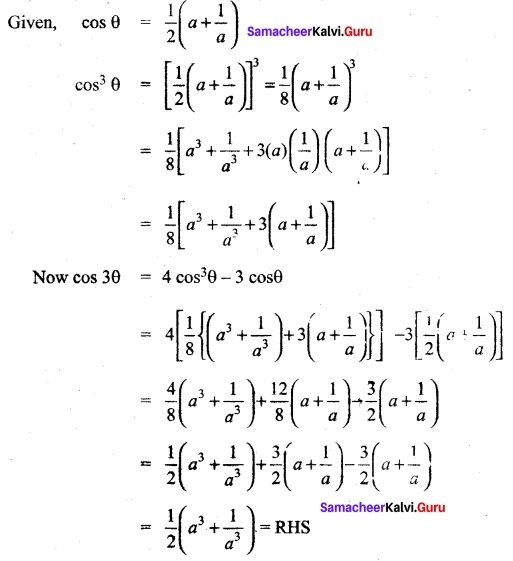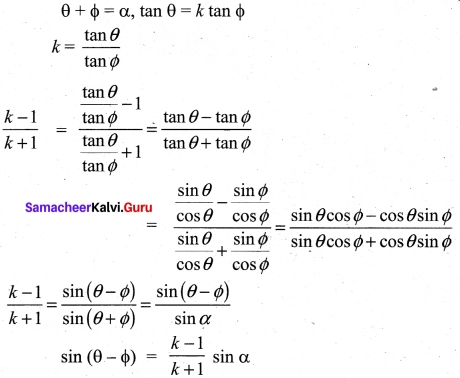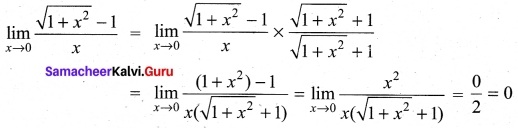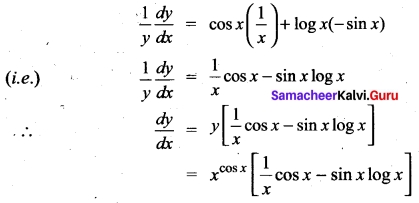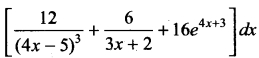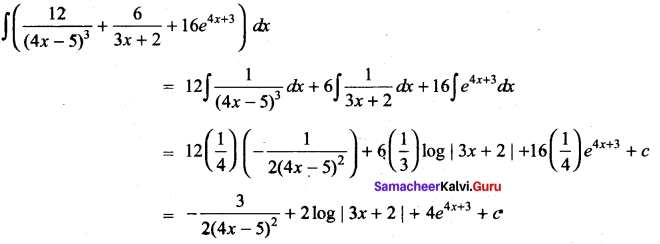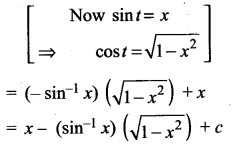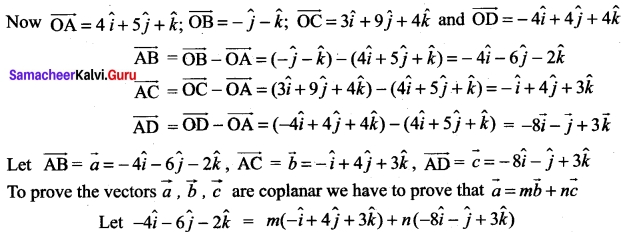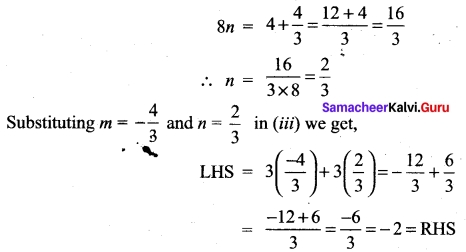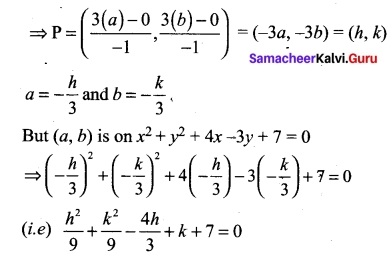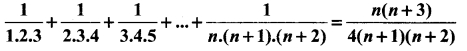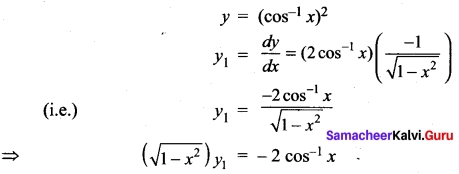Prasanna

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.1

Question 1.
Fill in the blanks.
(a) Every triangle has at least _____ acute angles.
(b) A triangle in which none of the sides equal is called a _____.
(c) In an isosceles triangle ______ angles are equal.
(d) The sum of three angles of a triangle is ______.
(e) A right-angled triangle with two equal sides is called ______.
Solution:
(a) Two
(b) Scalene Triangle
(c) Two
(d) 180°
(e) Isosceles right-angled triangle

Question 2.
Match the following:

Solution:

Question 3.
In ∆ABC, name the

(a) Three sides: ____, _____, _____
(b) Three Angles: _____, _____, _____
(c) Three Vertices: _____, _____, _____
Solution:
(a) \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CA}}\)
(b) ∠ABC, ∠BCA, ∠CAB or ∠A, ∠B, ∠C
(c) A, B, C

Question 4.
Classify the given triangles based on its sides as scalene, isosceles or equilateral.

Solution:
(i) Equilateral Triangle
(ii) Scalene Triangle
(iii) Isosceles Triangle
(iv) Scalene Triangle

Question 5.
Classify the given triangles based on its angles as acute-angled, right-angled or obtuse-angled.

Solution:
(i) Acute angled triangle
(ii) Right angled triangle
(iii) Obtuse angled triangle
(iv) Acute angled triangle

Question 6.
Classify the following triangles based on its sides and angles.

Solution:
(i) Isosceles Acute angled triangle
(ii) Scalene Right angled triangle
(iii) Isosceles Obtuse angled triangle
(iv) Isosceles Right angled triangle
(v) Equilateral Acute angled triangle
(vi) Scalene Obtuse angled triangle

Question 7.
Can a triangle be formed with the following sides? If yes, name the type of triangle.
(i) 8 cm, 6 cm, 4 cm
(ii) 10 cm, 8 cm, 5 cm
(iii) 6.2 cm, 1.3 cm, 3.5 cm
(iv) 6 cm, 6 cm, 4 cm
(v) 3.5 cm, 3.5 cm, 3.5 cm
(vi) 9 cm, 4 cm, 5 cm
Solution:
(i) Sum of two smaller sides of the triangle
= 6 + 4 = 10 cm > 8 cm
It is greater than the third side. So, a triangle can be formed scalene triangle.

(ii) Sum of two smaller sides of the triangle
= 8 + 5 = 13 cm > 10 cm
It is greater than the third side. So, a triangle can be formed scalene triangle.

(iii) Sum of two smaller sides of the triangle
= 1.3 + 3.5 = 4.8 cm < 6.2 cm
It is not greater than the third side. So, a triangle cannot be formed.

(iv) Two sides are equal.
So, a triangle can be formed. Isosceles triangle.

(v) Three sides are equal.
So, a triangle can be formed equilateral triangle.

(vi) Sum of two smaller sides of the triangle
= 4 + 5 = 9 cm = 9 cm
It is equal to the third side. No, a triangle cannot be formed.

Question 8.
Can a triangle be formed with the following angles? if yes, name the type of triangle.
(i) 60°, 60°, 60°
(ii) 90°, 55°, 35°
(iii) 60°, 40°, 42°
(iv) 60°, 90°, 90°
(v) 70°, 60°, 50°
(vi) 100°, 50°, 30°
Solution:
(i) 60°, 60°, 60°
Sum of three angles = 60° + 60° + 60° = 180°
Yes, a triangle can be formed.
∴ It is Acute angled triangle. [∵ all the angles < 90°]

(ii) 90°, 55°, 35°.
Sum of three angles = 90° + 55° + 55° = 180°
Yes, a triangle can be formed.
∴ It is a right-angled triangle, [∵ one angle is 90°]

(iii) 60°, 40°, 42°.
Sum of three angles = 60° + 40° + 42° = 142° ≠ 180°
No, The triangle cannot be formed.

(iv) 60°, 90°, 90°.
Sum of three angles = 60° + 90° + 90° = 240° ≠ 180°
∴ No, The triangle cannot be formed. [∵ one angle is > 90°]

(v) 70°, 60°, 50°.
Sum of three angles = 70° + 60° + 50° = 180°
Yes, A triangle can be formed.
∴ It is an acute-angled triangle.

(vi) 100°, 50°, 30°.
Sum of three angles = 100° + 50° + 30° = 180°
Yes, A triangle can be formed.
∴ It is an obtuse-angled triangle.

Question 9.
Two angles of the triangles are given. Find the third angle.
(i) 80°, 60°
(ii) 52°, 68°
(iii) 75°, 35°
(iv) 50°, 90°
(v) 120°, 30°
(vi) 55°, 85°
Solution:
(i) 80°, 60°
Let the third angle be x.
Sum of the angles = 180°
80° + 60° + x = 180°
140 + x = 180°
x = 180°- 140°
x = 40°
Third angle = 40°

(ii) 52°, 68°
Let the third angle be x.
Sum of the angles = 180°
52° + 68° + x = 180°
120 + x = 180°
180° – 120°
x = 60°
Third angle = 60°

(iii) 75°, 35°
Let the third angle be x.
Sum of the angles 180°
75° + 35° + x = 180°
110 + x = 180°
x = 180° – 110°
x = 70°
Third angle = 70°

(iv) 50°, 90°
Let the third angle be x. Sum of the angles = 180°
50° + 90° + x = 180°
140 + x = 180°
x = 180° – 140°
x = 40°
Third angle = 40°

(v) 120°, 30°
Let the third angle be x.
Sum of the angles = 180°
120° + 30° + x = 180°
150 + x = 180°
x = 180° – 150°
x = 30°
Third angle = 30°

(vi) 55°, 85°
Let the third angle be x.
Sum of the angles = 180°
55° + 85° + x = 180°
140 + x = 180°
x = 180° – 140°
x = 40°
Third angle = 40°

Question 10.
I am a closed figure with each of my three angles is 60°. Who am I?
Solution:
Equilateral Triangle.

Question 11.
Using the given information, write the type of triangle in the table given below.

Solution:

Objective Type Questions

Question 12.
The given triangle is _____.

(a) a right angled triangle
(b) an equilateral triangle
(c) a scalene triangle
(d) an obtuse angled triangle
Solution:
(b) an equilateral triangle

Question 13.
If all angles of a triangle are less than a right angle, then it is called ……….
(a) an obtuse angled triangle
(b) a right angled triangle
(c) an isosceles right angled triangle
(d) an acute angled triangle
Solution:
(d) an acute angled triangle

Question 14.
If two sides of a triangle are 5 cm and 9 cm then the third side is _____.
(a) 5 cm
(b) 3 cm
(c) 4 cm
(d) 14 cm
Solution:
(a) 5 cm

Question 15.
The angles of a right angled triangle are
(a) acute, acute, obtuse
(b) acute, right, right
(c) right, obtuse, acute
(d) acute, acute, right
Solution:
(d) acute, acute, right

Question 16.
An equilateral triangle is
(a) an obtuse-angled triangle
(b) a right-angled triangle
(c) an acute-angled triangle
(d) scalene triangle
Solution:
(c) an acute-angled triangle

Read More:

HDFCAMC Pivot Point Calculator

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.3

Miscellaneous Practice Problems

Question 1.
What are the angles of an isosceles right-angled triangle?
Solution:
Since it is a right-angled triangle
One of the angles is 90°
Other two angles are equal because it is an isosceles triangle.
Other two angles must be 45° and 45°
Angles are 90°, 45°, 45°.

Question 2.
Which of the following correctly describes the given triangle.

(a) It is a right isosceles triangle.
(b) It is an acute isosceles triangle.
(c) It is an obtuse isosceles triangle.
(d) it is an obtuse scalene triangle.
Solution:
(c) It is an obtuse isosceles triangle.

Question 3.
Which of the following is not possible?
(a) An obtuse isosceles triangle
(b) An acute isosceles triangle
(c) An obtuse equilateral triangle
(d) An acute equilateral triangle
Solution:
(c) an obtuse equilateral triangle

Question 4.
If one angle of an isosceles triangle is 124°, then find the other angles.
Solution:
In an isosceles triangle, any two sides are equal. Also, two angles are equal.
Sum of three angles of a triangle = 180°
Given one angle = 124°
Sum of other two angles = 180° – 124° = 56°
Other angles are = \(\frac{56}{2}\) = 28°
28° and 28°.

Question 5.
The diagram shows a square ABCD. If the line segment joints A and C, then mention the type of triangles so formed.

Solution:
For a square all sides are equal and each angle is 90°.
∆ABC and ∆ADC are isosceles right-angled triangles.

Question 6.
Draw a line segment AB of length 6 cm. At each end of this line segment AB, draw a line perpendicular to the line AB. Are these lines parallel?
Solution:
Here CA and DB are perpendicular to AB.
Yes CA and DB are parallel.

Construction:
(i) Drawn a line segment AB of length 6 cm.
(ii) Place the set square on the line in such a way that the vertex of its right angle coincides with B first and A next and one arm of the right angle coincides with the line AB.
(iii) Drawn lines DB and CA through B and A, the other arm of the right angle of the set square.
(iv) The line CA and DB are perpendicular to AB at A and B.

Challenge Problems

Question 7.
Is a triangle possible with the angles 90°, 90° and 0°? Why?
Solution:
No, a triangle cannot have more than one right angle

Question 8.
Which of the following statements is true. Why?
(a) Every equilateral triangle is an isosceles triangle.
(b) Every isosceles triangle is an equilateral triangle.
Solution:
(a) It is true
In an equilateral triangle, all three sides are equal.
It can be an isosceles triangle also, which has two sides equal.
(b) But every isosceles triangle need not be an equilateral triangle.

Question 9.
If one angle of an isosceles triangle is 70°, then find the possibilities for the other two angles.
Solution:
70°, 40° (or) 55°, 55°

Question 10.
Which of the following can be the sides of an isosceles triangle?
(a) 6 cm, 3 cm, 3 cm
(b) 5 cm, 2 cm, 2 cm
(c) 6 cm, 6 cm, 7 cm
(d) 4 cm, 4 cm, 8 cm
Solution:
In a triangle sum of any two sides greater than the third side
(a), (b) and (d) cannot form a triangle.
(c) can be the sides of an isosceles triangle.

Question 11.
Study the given figure and identify the following triangles.

(a) equilateral triangle
(b) isosceles triangles
(c) scalene triangles
(d) acute triangles
(e) obtuse triangles
(f) right triangles
Solution:
(a) BC = 1 + 1 + 1 + 1 = 4 cm
AB = AC = 4 cm
∆ABC is an equilateral triangle.
(b) ∆ABC and ∆AEF are isosceles triangles.
Since AB = AC = 4 cm Also AE = AF.
(c) In a scalene triangle, no two sides are equal.
∆AEB, ∆AED, ∆ADF, ∆AFC, ∆ABD, ∆ADC, ∆ABF and ∆AEC are scalene triangles.
(d) In an acute-angled triangle all the three angles are less than 90°.
∆ABC, ∆AEF, ∆ABF and ∆AEC are acute-angled triangles.
(e) In an obtuse-angled triangle any one of the angles is greater than 90°.
∆AEB and ∆AFC are obtuse angled triangles.
(f) In a right triangle, one of the angles is 90°.
∆ADB, ∆ADC, ∆ADE and ∆ADF are right-angled triangles.

Question 12.
Two sides of the triangle are given in the table. Find the third side of the triangle?

Solution:

Question 13..
Complete the following table.

Solution:

(i) Always acute angles
(ii) Acute angle
(iii) Obtuse angle

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.2

Question 1.
Fill in the blanks of the given equivalent ratios.
(i) 3 : 5 = 9 : ___
(ii) 4 : 5 = ___ : 10
(iii) 6 : ____ = 1 : 2
Solution:
(i) 15
Hint: \(\frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15}\)
(ii) 8
Hint: \(\frac{4}{5}=\frac{4 \times 2}{5 \times 2}=\frac{8}{10}\)
(iii) 12
Hint: \(\frac{1}{2}=\frac{1 \times 6}{2 \times 6}=\frac{6}{12}\)

Question 2.
Complete the Table:

Solution:

Question 3.
Say True or False.
(i) 5 : 7 is equivalent to 21 : 15.
(ii) If 40 is divided in the ratio 3 : 2, then the larger part is 24.
Solution:
(i) False
(ii) True

Question 4.
Give two equivalent ratios for each of the following.
(i) 3 : 2
(ii) 1 : 6
(iii) 5 : 4
Solution:

Question 5.
Which of the two ratios is larger?
(i) 4 : 5 or 8 : 15
(ii) 3 : 4 or 7 : 8
(iii) 1 : 2 or 2 : 1
Solution:

Question 6.
Divide the numbers given below in the required ratio.
(i) 20 in the ratio 3 : 2
(ii) 27 in the ratio 4 : 5
(iii) 40 in the ratio 6 : 14
Solution:
(i) Ratio = 3 : 2
Sum of the ratio = 3 + 2 = 5
5 parts = 20
1 part = \(\frac{20}{5}\)
= 4
3 parts = 3 × 4 = 12
2 parts = 2 × 4 = 8
20 can be divided in the form as 12, 8.

(ii) Ratio = 4 : 5
Sum of the ratio = 4 + 5 = 9
9 parts = 27
1 part = \(\frac{27}{9}\) = 3
4 parts = 4 × 3 = 12
5 parts = 5 × 3 =15
27 can be divided in the form as 12, 15.

(iii) 40 in the ratio 6 : 14
Ratio = 6 : 14
Sum of the ratio = 6 + 14 = 20
20 parts = 40
1 part = \(\frac{40}{20}\) = 2
6 parts = 2 × 6 = 12
14 parts = 2 × 14 = 28
40 can be divided in the form as 12, 28.

Question 7.
In a family, the amount spent in a month for buying Provisions and Vegetables are in the ratio 3 : 2. If the allotted amount is ₹ 4000, then what will be the amount spent for
(i) Provisions and
(ii) Vegetables?
Solution:
Dividing the total amount ₹ 4000 into 3 + 2 = 5 equal parts then
(i) For Provisions:
3 out of 5 parts are spent for provisions and 2 out of 5 parts for vegetables.
\(4000 \times \frac{3}{5}=2400\) for provisions
(ii) For vegetables:
\(4000 \times \frac{2}{5}=1600\) for Vegetables.
₹ 2400 spend on provisions and ₹ 1600 spend on Vegetables.

Question 8.
A line segment 63 cm long is to be divided into two parts in the ratio 3 : 4. Find the length of each part.
Solution:
Total length = 63 cm Ratio = 3 : 4
Sum of the ratio = 3 + 4 = 7
7 parts = 63 cm
1 part = \(\frac{63}{7}\) = 9 cm
3 parts = 3 × 9 cm = 27 cm
4 parts = 4 × 9 cm = 36 cm
∴ 63 cm can be divided into the parts as 27 cm and 36 cm.

Objective Type Questions

Question 9.
If 2 : 3 and 4 : ___ or equivalent ratios, then the missing term is ____
(a) 6
(b) 2
(c) 4
(d) 3
Solution:
(a) 6
Hint: \(\frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{4}{6}\)

Question 10.
An equivalent ratio of 4 : 7 is
(a) 1 : 3
(b) 8 : 15
(c) 14 : 8
(d) 12 : 21
Solution:
(d) 12 : 21

Question 11.
Which is not an equivalent ratio of \(\frac{16}{24}\) ?
(a) \(\frac{6}{9}\)
(b) \(\frac{12}{18}\)
(c) \(\frac{10}{15}\)
(d) \(\frac{20}{28}\)
Solution:
(d) \(\frac{20}{28}\)
Hint: \(\frac{16}{24}=\frac{8 \times 2}{8 \times 3}=\frac{2}{3}\)

Question 12.
If Rs 1600 is divided
(a) Rs 480
(b) Rs 800
(c) Rs 1000
(d) Rs 200
Solution:
(c) Rs 1000

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.3

Question 1.
Observe the diagram and fill the blanks.

(i) ‘A’, ‘O’ and ‘B’ are ______ points
(ii) ‘A’, ‘O’ and ‘C’ are ______ points
(iii) ‘A’ ‘B’ and ‘C’ are _____ points
(iv) ______ is the point of concurrency
Solution:
(i) collinear points
Hint: Points on a line.
(ii) non collinear points
Hint: Points not on a line
(iii) end points/non collinear points
(iv) O is the point of concurrency.
Hint: A points where lines meet

Question 2.
Draw any line and mark any 3 points that are collinear.
Solution:

L, M, N are collinear points

Question 3.
Draw any line and mark any 4 points that are not collinear.
Solution:

X, Y, Z and A are non-collinear points.

Question 4.
Draw any 3 lines to have a point of concurrency.
Solution:

l₁, l₂ and l₃ are the concurrent lines.
‘O’ is the point of concurrency.

Question 5.
Draw any 3 lines that are not concurrent. Find the number of points of intersection.
Solution:

l₁, l₂ and l₃ are non concurrent lines.
A, B and C are the 3 points of intersection.
There are two points of intersection X and Y

Objective Type Questions

Question 6.
A set of collinear points in the figure are ……….
(a) A. B, C
(b) A, F, C
(c) B, C, D
(d)A,C,D
Solution:
(b) A, F, C

Question 7.
A set of non-collinear points in the figure are _____
(a) A, F, C
(b) B, F, D
(c) E, F, G
(d) A, D, C
Solution:
(d) A, D, C
Hint: Non-collinear points are points which are not on a line.

Question 8.
A point of concurrency in the figure is ……..
(a) E
(b) F
(c) G
(d) H
Solution:
(b) F

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Ex 1.1

Question 1.
Fill in the blanks.

1. The smallest 7 digit number is _______
2. The largest 8 digit number is _______
3. The place value of 5 in 7005380 is ________
4. The expanded form of the number 76,70,905 is _______

Solution:

1. 10,00,000
2. 9,99,99,999
3. 5 × 1000 = 5000
4. 7 × 10,00,000 + 6 × 1,00,000 + 7 × 10,000 + 0 + 9 × 100 + 0 + 5 × 1
   (or)
   70,00,000 + 6,00,000 + 70,000 + 900 + 5

Question 2.
Say True or False.

1. In the Indian System of Numeration, the number 67999037 is written as 67999037
2. The successor of a one-digit number is always a one-digit number.
3. The predecessor of a 3-digit number is always a 3 or 4-digit number.
4. 88888 = 8 × 10000 + 8 × 100 + 8 × 10 + 8 × 1

Solution:

1. True
2. False
3. False
4. False

Question 3.
Complete the given order.
Ten crore, crore, ten lakh, ____, ____, _____ , _____, _____.
Solution:
Ten crores, Crore, Ten lakh, Lakh, Ten Thousand, Thousand, Hundred, Ten, One

Question 4.
How many ten thousands are there in the smallest 6 digit number?
Solution:
Smallest six-digit number is 1,00,000
1 lakh = Ten Thousand
Another Method:
Lakh is only one place to the left of Ten thousand
1 lakh is 10 times ten thousand

1 lakh = Ten-Ten Thousand

Question 5.
Using the digits 5, 2, 0, 7, 3 forms the largest 5 digit number and the smallest 5 digit number.
Solution:
Given digits = 5, 2, 0, 7, 3
Largest 5 digit number – 75320
Smallest 5 digit number – 20357

Question 6.
Observe the commas and write down the place value of 7.

1. 56,74,56,345
2. 567,456,345

Solution:

1. 56,74,56,345
   Place value of 7 is 7 × 10,00,000 = 70,00,000 = Seventy Lakhs.
2. 567,456,345
   Place value of 7 is 7 × 1,000,000 = 7,000,000 = Seven Million.

Question 7.
Write the following numbers in the International system by using commas.
(i) 347056
(ii) 7345671
(iii) 634567105
(iv) 1234567890
Solution:

Question 8.
Write the largest six-digit number and put commas in the Indian and the International Systems.
Solution:
The largest six-digit number is 999999

Question 9.
Write the number names of the following numerals in the Indian System.
(i) 75,32,105
(ii) 9,75,63,453
Solution:
(i) 75,32,105

Seventy-Five Lakhs Thirty-Two Thousand One Hundred and Five
(ii) 9,75,63,453

Nine crores Seventy Five Lakhs Sixty Three Thousand Four Hundred and Fifty-Three.

Question 10.
Write the number names in words using the International System
(i) 345,678
(ii) 8,343,710
(iii) 103,456,789
Solution:
(i) 345,678

Three Hundred and Forty-Five Thousand Six Hundred and Seventy-Eight
(ii) 8,343,710

Eight Million Three Hundred and Forty-Three Thousand Seven Hundred and Ten.
(iii) 103,456,789

One Hundred Three Million Four Hundred Fifty-Six Thousand Seven Hundred and Eighty’ Nine.

Question 11.
Write the number name in numerals.

1. Two crores thirty lakhs fifty-one thousand nine hundred eighty.
2. Sixty-six million three hundred forty-five thousand twenty-seven.
3. Seven hundred eighty-nine million, two hundred thirteen thousand four hundred fifty six.

Solution:

1. 2,30,51,980
2. 66,345,027
3. 789,213,456

Question 12.
Tamil Nadu has about twenty-six thousand three hundred forty-five square kilometre of Forest land. Write the number mentioned in the statement in the Indian System.
Solution:
26,345 sq km.

Question 13.
The number of employees in the Indian Railways is about 10 lakhs. Write this in the International System of numeration.
Solution:
1.000,000 (one million)

Objective Type Questions

Question 14.
1 billion is equal to
(a) 100 crore
(b) 100 million
(c) 100 lakh
(d) 10000 lakh
Solution:
(a) 100 crore

Question 15.
The successor of 10 million is
(a) 1000001
(b) 10000001
(c) 9999999
(d) 100001
Solution:
(b) 10000001

Question 16.
The difference between successor and predecessor of 99999 is
(a) 90000
(b) 1
(c) 2
(d) 99001
Solution:
(c) 2

Question 17.
The expanded form of the number 6,70,905 is
(a) 6 × 10000 + 7 × 1000 + 9 × 100 + 5 × 1
(b) 6 × 10000 + 7 × 1000 + 0 × 100 + 9 × 100 + 0 × 10 + 5 × 1
(c) 6 × 1000000 + 7 × 10000 + 0 × 1000 + 9 × 100 + 0 × 10 + 5 × 1
(d) 6 × 100000 + 7 × 10000 + 0 × 1000 + 9 × 100 + 0 × 10 + 5 × 1
Solution:
(d) 6 × 100000 + 7 × 10000 + 0 × 1000 + 9 × 100 + 0 × 10 + 5 × 1

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.1

Question 1.
Fill in the blanks.
(i) 250 ml + \(\frac{1}{2}\) ml = _____ l.
(ii) 150 kg 200 g + 55 kg 750 g = ____ kg ____ g.
(iii) 20 l – 1 l 500 ml = ____ l ___ ml
(iv) 450 ml × 5 = ____ l ____ ml.
(v) 50 Kg ÷ 100 g = ______
Solution:
(i) \(\frac{3}{4}\) l
(ii) 205 kg 950 g
(iii) 18 l 500 ml
(iv) 2l 250 ml
(v) 500

Question 2.
True or False
(i) Pugazhenthi ate 100 g of nuts which is equal to 0.1 kg.
(ii) Meena bow it 250 ml of butter milk which is equal to 2.5 l.
(iii) Karkuzhali’s bag 1 kg 250 g and poong- kodi’s bag 2 kg 750 g. The total weight of their bags 4 kg.
(iv) Vanmathi bought 4 books each weighing 500 g. Total weight of 4 books is 2 kg.
(v) Gayathiri bought 1 kg of birthday cake. She shared 450 g with her friends.
The weight of cake remaining is 650 g
Solution:
(i) True
(ii) False
(iii) True
(iv) True
(v) False

Question 3.
Convert into indicated units:
(i) 10 l and 5 ml into ml
(ii) 4 km and 300 m into m
(iii) 300 mg into g
Solution:
(i) 10 l and 5 ml
= 10 × 1000 ml + 5 ml
= 10,000 ml + 5 ml [∴ 1l = 1000 ml]
= 10,005 ml.
∴ 10 l and 5 ml = 10,005 ml.
(ii) 4 km and 300 m into m.
4 km and 300 m
= 4 × 1000 m + 300 m
= 4000 m + 300 m [∴ 1 km = 1000 m]
= 4300 m
∴ 4 km and 300 m = 4300 m
(iii) 300 mg into g.

Question 4.
Convert into higher units:
(i) 13000 mm (km, m, cm)
(ii) 8257 ml (kl, l)
Solution:
(i) 13000 mm (km, m, cm)
(ii) 8257 ml (kl, l)

Question 5.
Convert into lower units:
(i) 15 km (m, cm, mm)
Solution:
15 km = 15 × 1000 m = 15000 m
15 km = 15 × 100000 cm
= 1500000 cm
15 km = 15 × 1000000 mm
= 15000000 mm

(ii) 12 kg (g, mg)
Solution:
12 kg = 12 × 1000 g
= 12000 g
12 kg = 12 × 1000000 mg
= 12000000 mg

Question 6.
Compare and put > or < or = in the following:
(i) 800 g + 150 g ____ 1 kg
(ii) 600 ml + 400 ml ____ 1 l
(iii) 6 m 25 cm ____ 600 cm + 25 cm
(iv) 88 cm ____ 8 m 8 cm
(v) 55 g ____ 550 mg
Solution:
(i) 800 g + 150g < 3kg
(ii) 600 ml + 400 ml = 1 l
(iii) 6 m 25 cm = 600 cm + 25 cm
(iv) 88 cm < 8 m 8 cm
(v) 55 g > 550 mg

Question 7.
Geetha brought 2 l and 250 ml of water in a bottle. Her friend drank 300 ml from it. How much of water is remaining in the bottle?
Solution:
Total Capacity of water = 2 l 250 ml
= (2 x 1000 + 250) l
= 2000 + 250 ml
= 2250 ml
Water Consumed = 300 ml
Water remaining in the bottle = (2250 – 300) ml
= 1950 ml
= 1 litre 950 ml

Question 8.
Thenmozhi’s height is 1.25 m now. She grows for 5 cm every year. What would be her height after 6 years?
Solution:
Thenmozhi’s present height = 1.25 m
Rate of growth per year = 5 cm
Her growth in 6 years = 5 cm × 6 = 30 cm.
After 6 years her height = 1.25 m + 30 cm
= 1.25 × 100 + 30 cm
= 125 + 30 cm
= 155 cm.
∴ After 6 years Thenmozhi’s height will be 155 cm.

Question 9.
Priya bought 22 \(\frac{1}{2}\) kg of onion/ Krishna bought 18 \(\frac{3}{4}\) kg of onion and sethu bought 9 kg 250 g of onion, what is the total weight of onion did they buy?
Solution:
Total weight of onion bought
= 22 \(\frac{1}{2}\) + 18 \(\frac{3}{4}\) + 9 \(\frac{1}{4}\) kg
= 22 kg 500 g + 18 kg 750 g + 9 kg 250 g
= 49 kg 1500 g
= 50 kg 500 g

Question 10.
Maran walks 1.5 km every day to reach the school while Mahizhan walks 1400 m. Who walks more distance and by how much?
Solution:
Distance which Maran walks = 1.5 km = 1.5 × 1000 m = 1500 m
The distance which Mahizhan walks = 1400 m.
Here 1500 > 1400
∴ Difference = 1500 – 1400 = 100 m.
∴ Maran walks more distance = 100 m.

Question 11.
In a JRC one day camp, 150 gm of rice and 15 ml oil are needed for a student. If there are 40 students to attend the camp how much of rice and oil are needed?
Solution:
Rice needed for a student = 150 gm
Rice needed for 40 students = 40 × 150 gm = 6000 gm = 6 kg
Oil needed for a student = 15 ml
Oil needed for 40 students = 40 × 15 ml = 600 ml

Question 12.
In a school, 200 litres of lemon juice is prepared. If 250 ml lemon juice is given to each student, how many students get the juice?
Solution:
Total lemon juice prepared = 200 l = 200 × 1000 ml = 2,00,000 ml.
∴ Quantity of Lemon juice given to one student = 250 ml.
∴ Number of students can get = \(\frac{2,00,000}{250}\) = 800
∴ 800 students can get the lemon juice.

Question 13.
How many glasses of the given capacity will fill a 2 litre jug?
(i) 100 ml ……….
(ii) 50 ml ……….
(iii) 500 ml ………
(iv) 1 l ………
(v) 250 ml ………
Solution:
(i) 20
(ii) 40
(iii) 4
(iv) 2
(v) 8

Objective Type Questions

Question 14.
9 m 4 cm is equal to _____
(a) 94 cm
(b) 904 cm
(c) 9.4 cm
(d) 0.94 cm
Solution:
(b) 904 cm

Question 15.
1006 g is equal to ………
(i) 1 kg 6 g
(ii) 10 kg 6 g
(iii) 100 kg 6 g
(iv) 1 kg 600 g
Solution:
(i) 1 kg 6 g

Question 16.
Every day 150 l of water is sprayed in the garden. Water sprayed in a week is ____
(a) 700 l
(b) 1000 l
(c) 950 l
(d) 1050 l
Solution:
(d) 1050 l

Question 17.
Which is the greatest? 0.007 g, 70 mg, 0.07 cg ……….
(i) 0.07 cg
(ii) 0.007 g
(iii) 70 mg
(iv) all are equal
Solution:
(iii) 70 mg

Question 18.
7 km – 4200 m is equal to
(a) 3 km 800 m
(b) 2 km 800 m
(c) 3 km 200 rn
(d) 2 km 200 m
Solution:
(b) 2 km 800 m

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.2

Question 1.
Use any number of the given dots to make different angles.

Solution:

Question 2.
Name the vertex and sides that form each angle.

Solution:

Question 3.
Pick out the Right angles from the given figures.

Solution:
(i), (iii) and (v) are Right Angles.

Question 4.
Pick out the Acute angles from the given figures.

Solution:
(i), (iii) and (iv) are the Acute Angles.

Question 5.
Pick out the Obtuse Angles from the given figures.

Solution:
(i) and (ii) are the Obtuse Angles.

Question 6.
Name the angle in each figure given below in all the possible ways.

Solution:
(i) ∠M or ∠LMN or ∠NML
(ii) ∠Q or ∠PQR or ∠RQP
(iii) ∠N or ∠MNO or ∠ONM
(iv) ∠A or ∠TAS or ∠SAT
(v) ∠Y or ∠XYZ or ∠ZYX
(vi) There are 3 angles in (vi)

• ∠ADC or ∠CDA
• ∠ CDB or ∠BDC
• ∠D or ∠ADB or ∠BDA

Question 7.
Say True or False.

1. 20° and 70° are complementary.
2. 88° and 12° are complementary.
3. 80° and 180° are supplementary.
4. 0° and 180° are supplementary.

Solution:

1. True
2. False
3. False
4. True

Question 8.
Draw and label each of the angles
(i) ∠NAS = 90°
(ii) ∠BLG = 35°
(iii) ∠SMC = 145°
Solution:

Question 9.
Identify the types of angles shown by the hands of the given clock.

Solution:
(i) Obtuse Angle.
(ii) Zero Angle.
(iii) Straight Angle.
(iv) Acute Angle.
(v) Right Angle.

Question 10.
Find the supplementary ‘l’ complementary angles in each case.

Solution:
(i) If two angles add up to 180°, they are supplementary.
We know that the straight angle ∠CBC = 180°
Given ∠CBD = 25°
∴ ∠DBA = 180° – 25° = 155°
∴ Supplementary ∠DBA = 155°

(ii) If two angles add upto 90°, they are complementary
Given ∠ABC = 25°
∠CBD = 30°
∴ ∠DBA = 90° – 30° = 60°
∴ Complementary angle ∠DBA = 60°

(iii) Given ∠CBA = 90°
∠CBD = 46°
∴ ∠DBA = 90° – 46° = 44°
We know that the sum of two angles is 90°, then they are complementary
∴ Complementary angle ∠DBA = 44°

(iv) Given ∠DBE = 180°
∠DBC = 67°
∴ ∠CBE = 180° – 67° = 113°
Here ∠DBC + ∠DBE = 180°
∴ Supplementary angle ∠CBE = 113°

Objective Type Questions

Question 11.
In this Figure, which is not the correct way of naming an angle?

(a) ∠Y
(b) ∠ZXY
(c) ∠ZYX
(d) ∠XYZ
Solution:
(b) ∠ZXY

Question 12.
In this Figure, ∠AYZ = 45°. If the point ‘A’ is shifted to point ‘B’ along the ray, then the measure of ∠BYZ is ____

(a) more than 45°
(b) 45°
(c) less than 45°
(d) 90°
Solution:
(b) 45°
Hint: ∠XYZ = ∠BYZ = ∠AYZ

Students can Download Tamil Nadu 11th Maths Model Question Paper 2 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Maths Model Question Paper 2 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 2.30 Hours
Maximum Marks: 90

PART – I

Choose the correct answer. Answer all the questions. [20 × 1 = 20]

Question 1.
The range of the function \(\frac{1}{1-2sin x}\) is………..
(a) (-∞, -1) ∪(\(\frac{1}{3}\), ∞)
(b) (-1, -1)
(c) (-1, \(\frac{1}{3}\))
(d) (-∞, -1] ∪[\(\frac{1}{3}\), ∞)
Solution:
(d) (-∞, -1] ∪[\(\frac{1}{3}\), ∞)

Question 2.
The value of log_√2 512 is……….
(a) 16
(b) 18
(c) 9
(d) 12
Solution:
(b) 18

Question 3.
If a and b are the roots of the equation x² – kx + 16 = 0 and satisfy a² + b² = 32 then the value of k is………..
(a) 10
(b) -8
(c) -8, 8
(d) 6
Solution:
(c) -8, 8

Question 4.
The value of log₉ 27 is …………
(a) \(\frac{2}{3}\)
(b) \(\frac{3}{2}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{4}{3}\)
Solution:
(b) \(\frac{3}{2}\)

Question 5.
The value of \(\frac{\sin 3 \theta+\sin 5 \theta+\sin 7 \theta+\sin 9 \theta}{\cos 3 \theta+\cos 5 \theta+\cos 7 \theta+\cos 9 \theta}\) = ………….
(a) tan 3θ
(b) tan 6θ
(c) cot 3θ
(d) cot 6θ
Solution:
(b) tan 6θ

Question 6.
In 3 fingers the number of ways 4 rings can be worn in ways.
(a) 4³ – 1
(b) 3⁴
(c) 68
(d) 64
Solution:
(d) 64

Question 7.
Everybody in a room shakes hands with everybody else. The total number of shake hands is 66. The number of persons in the room is……….
(a) 11
(b) 12
(c) 10
(d) 6
Solution:
(b) 12

Question 8.
The H.M of two positive number whose AM and G.M. are 16, 8 respectively is
(a) 10
(b) 6
(c) 5
(d) 4
Solution:
(d) 4

Question 9.
The co-efficient of the term independent of x in the expansion of (2x + \(\frac{1}{3x}\))⁶ is……….
(a) \(\frac{160}{27}\)
(b) \(\frac{160}{37}\)
(c) \(\frac{80}{3}\)
(d) \(\frac{80}{9}\)
Solution:
(a) \(\frac{160}{27}\)

Question 10.
The value of \(\left|\begin{array}{lll} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end{array}\right|^{2}\) is……….
(a) abc
(b) -abc
(c) 0
(d) a²b²c²
Solution:
(d) a²b²c²

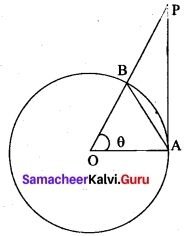
Question 11.

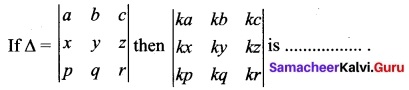
(a) Δ
(b) kΔ
(c) 3kΔ
(d) k³Δ
Solution:
(d) k³Δ

Question 12.
A vector makes equal angle with the positive direction of the co-ordinate axes then each angle is equal to………..
(a) cos^-1 (\(\frac{1}{3}\))
(b) cos^-1 (\(\frac{2}{3}\))
(c) cos^-1 (\(\frac{1}{√3}\))
(d) cos^-1 (\(\frac{2}{√3}\))
Solution:
(c) cos^-1 (\(\frac{1}{√3}\))

Question 13.
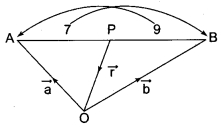
If the centroids of AABC and A’B’C’ are respectively G and G’ then \(\bar{AA’}\) + \(\bar{BB’}\) + \(\bar{CC’}\)…………
(a) \(\bar{GG’}\)
(b) 3\(\bar{GG’}\)
(c) 2\(\bar{GG’}\)
(d) 0
Solution:
(b) 3\(\bar{GG’}\)

Question 14.
If f(x) = \(\left\{\begin{aligned} k x^{2} & \text { for } \quad x \leq 2 \\ 3 & \text { for } \quad x>2 \end{aligned}\right.\) is continuous at x = 2 then the value of k is ………..
(a) \(\frac{3}{4}\)
(b) 0
(c) 1
(d) \(\frac{4}{3}\)
Solution:
(d) \(\frac{4}{3}\)

Question 15.
If x = \(\frac{1-t²}{1+t²}\) and y = \(\frac{2t}{1+t²}\) then \(\frac{dx}{dy}\) = ……….
(a) \(\frac{y}{x}\)
(b) \(\frac{-y}{x}\)
(c) –\(\frac{x}{y}\)
(d) \(\frac{x}{y}\)
Solution:
(c) –\(\frac{x}{y}\)

Question 16.
\(\lim _{x \rightarrow \infty}\left(\frac{x^{2}+5 x+3}{x^{2}+x+3}\right)^{x}\) is ……….
(a) e⁴
(b) e²
(c) e³
(d) 1
Solution:
(a) e⁴

Question 17.
\(\int \frac{e^{x}\left(x^{2} \tan ^{-1} x+\tan ^{-1} x+1\right)}{x^{2}+1}\) dx is ……….
(a) e^xtan^-1(x + 1) + c
(b) tan^-1(e^x) + c
(c) e^x \(\frac{tan^{-1}x}{2}\) + c
(d) e^xtan^-1x + c
Solution:
(d) e^xtan^-1x + c

Question 18.
\(\int \frac{\sec x}{\sqrt{\cos 2 x}}\) dx = ………
(a) tan^-1(sin x) + c
(b) 2 sin^-1(tan x) + c
(c) tan^-1(cos x) + c
(d) sin^-1(tan x) + c
Solution:
(d) sin^-1(tan x) + c

Question 19.
\(\int \frac{e^{6 \log x}-e^{5 \log x}}{e^{4 \log x}-e^{3 \log x}}\)
(a) x + c
(b) \(\frac{x³}{3}\) + c
(c) \(\frac{3}{x³}\) + c
(d) \(\frac{1}{x²}\) + c
Solution:
(b) \(\frac{x³}{3}\) + c

Question 20.
It is given that the events A and B are such that P(A) = \(\frac{1}{4}\), P(A/B) = \(\frac{1}{2}\) and P(B/A) = \(\frac{2}{3}\) then P(B) = …………
(a) \(\frac{1}{6}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{2}{3}\)
(d) \(\frac{1}{2}\)
Solution:
(b) \(\frac{1}{3}\)

PART- II

II. Answer any seven questions. Question No. 30 is compulsory.

Question 21.
Find x such that -π ≤ x ≤ π and cos 2x = sin x
Solution:
We have cos 2x = sin x which gives
2sin² x + sin x – 1 = 0
The roots of the equation are sin x = \(\frac{-1±3}{4}\) = -1 (or) \(\frac{1}{2}\)
Now, sin x = \(\frac{1}{2}\) ⇒ x = \(\frac{π}{6}\), \(\frac{5π}{6}\)
Also sin x = -1 ⇒ x = \(\frac{π}{2}\)
Thus x = \(\frac{π}{2}\), \(\frac{π}{6}\), \(\frac{5π}{6}\)

Question 22.
If ^(n-1)P₃ : ⁿP₄ = 1 : 10 find n.
Solution:

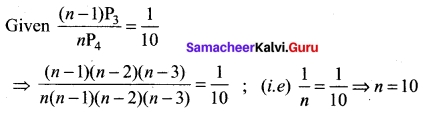
Question 23.
Find the 18^th and 25^th terms of the sequence defined by

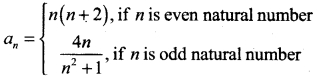
Solution:
When n = 18 (even)
a_n = n(n + 2) = 18(18 + 2) = 18 (20) = 360
When n = 25 (odd)

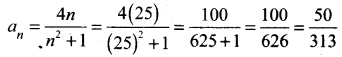
Question 24.
Show that the lines are 3x + 2y + 9 = 0 and 12x + 8y – 15 = 0 are parallel lines.
Solution:

Here m₁ = m₂ ⇒ the two lines are parallel.

Question 25.
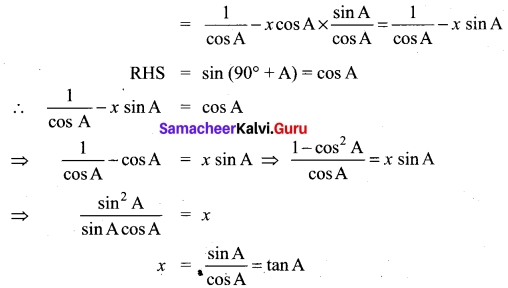
Prove that

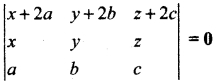
Solution:

= 0 + 2(0) (∴ R₁ = R₃)
= 0 = RHS

Question 26.
Find the value of λ for which the vectors \(\vec{a}\) = 2\(\vec{i}\) + λ\(\vec{j}\) + \(\vec{k}\) and \(\vec{b}\) = \(\vec{i}\) – 2\(\vec{j}\) + 3\(\vec{k}\) are perpendicular.
Solution:
When \(\vec{a}\) and \(\vec{b}\) are ⊥^r If then \(\vec{a}\).\(\vec{b}\) = 0
\(\vec{a}\) ⊥^r \(\vec{b}\) ⇒ \(\vec{a}\).\(\vec{b}\) = 0
(2) (1) + (λ) (-2) + (1) (3) = 0 ⇒ λ = 5/2

Question 27.
If y = \(\frac{tan x}{x}\) and \(\frac{dx}{dy}\)
Solution:
now y = \(\frac{u}{v}\) ⇒ y’ =\(\frac{vu’-uv’}{v²}\)
u = tan x ⇒ u’ = sec²x
v = x ⇒ v’ = 1

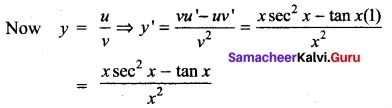
Question 28.
Evaluate \(\int \sqrt{25 x^{2}-9}\) dx
Solution:

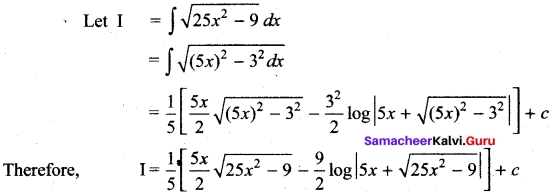
Question 29.
If A and B are two independent events such that
P(A) = 0.4 and P(A ∪ B) = 0.9. Find P(B).
Solution:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∪ B) = P(A) + P(B) – P(A).P(B)(since A and B are independent)
That is, 0.9 = 0.4 + P(B) – (0.4) P(B)
0.9 – 0.4 = (1 – 0.4) P(B)
Therefore, P(B) = \(\frac{5}{6}\)

Question 30.
A rope of length 12 m is given. Find the largest area of the triangle formed by this rope and find the dimensions of the triangle so formed.
Solution:
The largest triangle will be an equilateral triangle
∴ side of the triangle = \(\frac{12}{3}\) = 4 m = a
Area of the triangle = \(\frac{a²√3}{4}\) = \(\frac{4²√3}{4}\) = 4√3 sq.m

PART – III

III. Answer any seven questions. Question No. 40 is compulsory. [7 × 3 = 21]

Question 31.
Let A = {a, b, c} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it

1. reflexive
2. symmetric
3. transitive
4. equivalence

Solution:

1. (c, c)
2. (c, a)
3. nothing
4. (c, c) and (c, a)

Question 32.
Solve 2|x + 1| – 6 ≤ 7 and graph the solution set in a number line.
Solution:
2|x + 1| – 6 ≤ 7
⇒ 2|x + 1| ≤ 7 + 6 (= 13)
⇒ |x + 1| ≤ \(\frac{13}{2}\)
⇒ x + 1 > \(\frac{-13}{2}\)
x + 1 > \(\frac{-13}{2}\)
⇒ x > \(\frac{-13}{2}\) -1 (= \(\frac{-15}{2}\)) ……….(1)
(or) x + 1 > \(\frac{13}{2}\)
x + 1 < \(\frac{-13}{2}\)
⇒ x < \(\frac{13}{2}\) -1 (= \(\frac{11}{2}\)) ……….(2)
From (1) and (2) \(\frac{-15}{2}\) ≤ x ≤ \(\frac{11}{2}\)

Question 33.
If the different permutations of all letters of the word BHASKARA are listed as in a dictionary, how many strings are there in this list before the first word starting with B?
Solution:
The required number of strings is the total number of strings starting with A and using the letters A, A, B, H, K, R, S = \(\frac{7!}{2}\) = 2520

Question 34.
Find the sum up to n terms of the series: 1 + \(\frac{6}{7}\) + \(\frac{11}{49}\) + \(\frac{16}{343}\) + ….
Solution:
Here a = 1, d = 5 and r = \(\frac{1}{7}\)

Question 35.
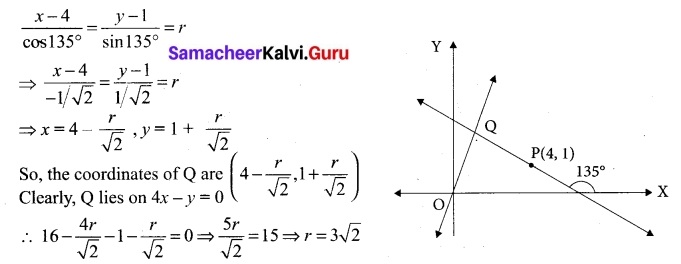
Area of the triangle formed by a line with the coordinate axes, is 36 square units. Find the equation of the line if the perpendicular drawn from the origin to the line makes an angle of 45° with positive the x-axis.
Solution:
Let p be the length of the perpendicular drawn from the origin to the required line.
The perpendicular makes 45° with the x-axis.
The equation of the required line is of the form,
x cos α + y sin α = p
⇒ x cos 45° + y sin 45° = p
⇒ x + y= √2 P
This equation cuts the coordinate axes at A(√2p, 0) and B (o, √2p).
Area of the ΔOAB is \(\frac{1}{2}\) × √2p × √2p = 36 ⇒ p = 6 (∵ p is positive)
Therefore the equation of the required line is x + y = 6 √2

Question 36.
If A^T = \(\left(\begin{array}{cc} 4 & 5 \\ -1 & 0 \\ 2 & 3 \end{array}\right)\) and B = \(\left(\begin{array}{ccc} 2 & -1 & 1 \\ 7 & 5 & -2 \end{array}\right)\) verify that (A – B)^T = A^T – B^T
Solution:
(A – B)^T = A^T – B^T

Here (1) and (2) ⇒ (A – B)^T = A^T – B^T

Question 37.
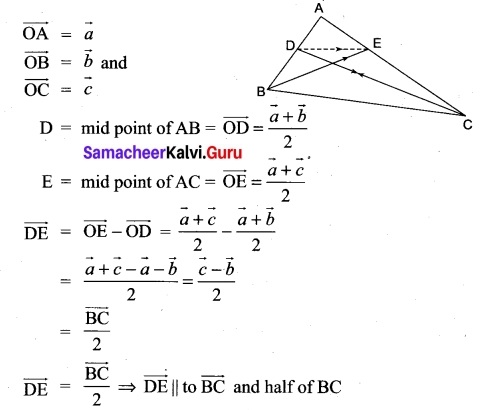
For any vector \(\vec{a}\) prove that \(|\vec{a} \times \hat{i}|^{2}+|\vec{a} \times \hat{j}|^{2}+|\vec{a} \times \hat{k}|^{2}=2|\vec{a}|^{2}\)
Solution:
Let = \(\vec{a}\) = a₁\(\hat{i}\) + a₂\(\hat{j}\) + a₃\(\hat{k}\)

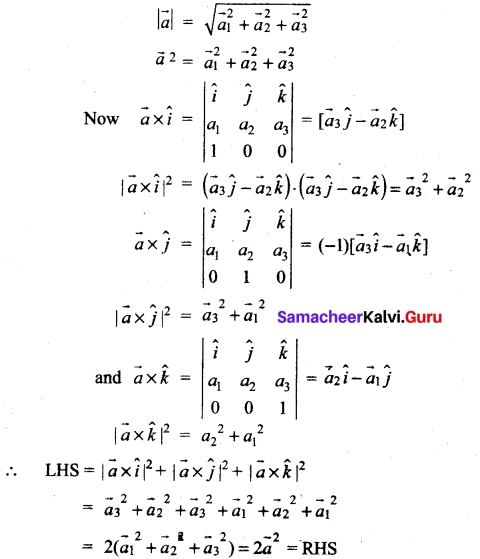
Question 38.
Given y = cos^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\) find \(\frac{dx}{dy}\)
Solution:
put x = tan θ
so \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\) = \(\left(\frac{1-tan^{2}θ}{1+tan{2}θ}\right)\) = 2 cos θ
y = cos^-1 (cos 2θ) = 2θ
⇒ \(\frac{dy}{dθ}\)
Now x = tan θ
⇒ \(\frac{dx}{dθ}\) = sec²θ
= 1 + tan² θ
= 1 + x²
so \(\frac{dx}{dy}\) = \(\frac{dy}{dθ}\)/\(\frac{dx}{dθ}\) = \(\frac{2}{1+x²}\)

Question 39.
A wound is healing in such a way that t days since Sunday the area of the wound has been decreasing at a rate of –\(\frac{3}{(t+2)²}\) cm² per day. If on Monday the area of the wound was 2 cm²
(i) What was the area of the wound on Sunday?
(ii) What is the anticipated area of the wound on Thursday if it continues to heal at the same rate ?
Solution:
Let A be the area of wound at time ‘ t ‘

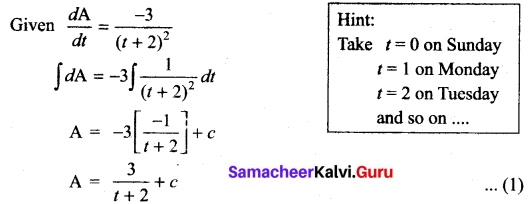
By the given, condition area of the wound on monday is 2 cm²
⇒ A = 2, t = 1
⇒ 2 = \(\frac{3}{1+2}\) + c
c = 1
∴ Area of wound at any day.
⇒ 1 ⇒ A = \(\frac{3}{1+2}\) + 1
(i) The area of the wound on Sunday
t = 0 ⇒ A = \(\frac{3}{2}\) + 1 = \(\frac{5}{2}\) = 2.5 cm²
(ii) The area of the wound on Thursday
t = 4 ⇒ A = \(\frac{3}{6}\) + 1 = \(\frac{1}{2}\) + 1 = 1.5 cm²

Question 40.
An integer is chosen at random from the first fifty positive integers. What is probability that the integer chosen is a prime or multiple of 4?
Solution:
S = {1, 2, 3, ……. ,50} ∴ n(S) = 50
Let A be the event of getting prime number.
∴ A = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47}
n(A) = 15, so P(A) = 15/50
Let B be the event of getting number multiple of 4
∴B = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48}
n(B) = 12, so P(B) = 12/50
Here A and B are mutually exclusive. (i.e.,) A ∩ B = Φ
∴ P(A ∪ B) = P(A) + P(B) = 15/50+ 12/50 = 27/50

PART – IV

IV. Answer all the questions. [7 × 5 = 35]

Question 41 (a).
The formula for converting from Fahrenheit to Celsius temperatures is y = \(\frac{5x}{9}\) – \(\frac{160}{9}\) Find the inverse of this function and determine whether the inverse is also a function.
Solution:

[OR]

(b) If f : R → R is defined by f(x) = 2x – 3 prove that f is a injection and find its inverse.
Solution:
Method 1:
One-to-one: Let f(x) = f(y). Then 2x – 3 = 2y – 3; this implies that x = y. That is, f(x) = f(y) implies that x = y. Thus f is one-to-one.

Onto: Let y ∈ R. Let x =\(\frac{y+3}{2}\) Then f(x) = 2(\(\frac{y+3}{2}\)) -3 = y. Thus f is onto. This also can be proved by saying the following statement. The range of f is R (how?) which is equal to the co-domain and hence f is onto.

Inverse: Inverse: Let y = 2x – 3. Then y + 3 = 2x and hence x = \(\frac{y+3}{2}\) Thus f^-1 (y) = \(\frac{y+3}{2}\). By replacing y as x, we get f^-1 (x) = \(\frac{y+3}{2}\)

Method 2:
Let y = 2x – 3 then x = \(\frac{y+3}{2}\). Let, g(y) = \(\frac{y+3}{2}\)
Now (g o f) (x) = g(f(x)) = g(2x – 3) = \(\frac{(2x-3)+3}{2}\) = x
(f o g)(y) = f(g(y)) = f(\(\frac{y+3}{2}\)) = 2(\(\frac{y+3}{2}\)) -3 = y
This implies that f and g are bijections and inverses to each other. Hence f is a bijection and f^-1(y) = \(\frac{y+3}{2}\). Replacing y by x we get, f^-1(x) = \(\frac{x+3}{2}\)

Question 42 (a).
If the equations x² – ax + b = 0 and x² – ex + f = 0 have one root in common and if the second equation has equal roots then prove that ae = 2(b + f).
Solution:
Let a be the common root
then a² – aα + b = 0 . . . .(1)
we are given that
x² – ex + f = 0 has equal roots.
So the roots will be α, β
Now sum of roots = 2α
= -(-e) ⇒ a = e/2
product of the roots
α × α = α²f
substituting a and α², values in (1) we get
f – a (\(\frac{e}{2}\)) + b = 0
f – \(\frac{ae}{2}\) + b = 0
\(\frac{ae}{2}\) = b + f ⇒ ae = 2(b + f)

[OR]

(b) Prove that
cos θ + cos(\(\frac{2π}{2}\)– θ) + (cos\(\frac{2π}{3}\) + θ) = 0
Solution:
we have

cos θ – cos θ = 0 = RHS

Question 43 (a).
Find the number of strings that can be made using all letters of the word THING. If these words are written as in a dictionary, what will be the 85th string?
Solution:
(i) Number of words formed = 5! = 120
(ii) The given word is THING
Taking the letters in alphabetical order G H I N T
To find the 85th word
The No. of words starting with G = 4! = 24
The No. of words starting with H = 4! = 24
The No. of words starting with 1 = 4! = 24
The No. of words starting with NG = 3! = 6
The No. of words starting with NH = 3! = 6
The No. of words starting with NIGH = 1! = 1
Total = 85
So the 85th word is NIGHT

[OR]

(b) A straight line passes through a fixed point (6, 8). Find the locus of the foot of the perpendicular drawn to it from the origin O.
Solution:
Let the point (x₁, y₁) be (6, 8). and P (h, k) be a point on thr lequired locus.
Family of equations of the straight lines passing through the fixed point (x₁, y₁) is y – y₁ = m (x – x₁) ⇒ y – 8 = m(x – 6)
Since OP is perpendicular to the line (6.25)
m × (\(\frac{k-0}{h-0}\)) = -1 ⇒ m = –\(\frac{h}{k}\)
Also P(h, k) lies on (6.25)
⇒ k – 8 = – \(\frac{h}{k}\)(h – 6) ⇒ k (k – 8) = -h(h – 6) ⇒ h² + k² – 6h – 8k = 0
Locus of P (h, k) is x² + y² – 6x – 8y = 0

Question 44 (a).
If p is a real number and if the middle term in the expansion of (\(\frac{π}{2}\) + 2)⁸ is 1120, find p.
Solution:
In the equation of (\(\frac{π}{2}\) + 2)⁸, number of terms = 8 + 1 = 9 (odd)
∴ There is only one middle term i.e. (\(\frac{9+1}{2}\))^th or 5^th term

[OR]

(b) Express the matrix A = \(\left[\begin{array}{rrr} 1 & 3 & 5 \\ -6 & 8 & 3 \\ -4 & 6 & 5 \end{array}\right]\) the sum Of skew-symmetric matrices.
Solution:

Thus A is expressed as the sum of symmetric and skew-symmetric matrices.

Question 45 (a).
For any vector a prove that \(|\vec{a} \times \hat{i}|^{2}+|\vec{a} \times \hat{j}|^{2}+|\vec{a} \times \hat{k}|^{2}=2|\vec{a}|^{2}\)
Solution:

[OR]

(b) If y = e^tan-1x show that (1 + x²) y” + (2x – 1) y’ = 0
Solution:
y = e^tan-1x
y’ = e^tan-1x (\(\frac{1}{1+x²}\))
y’ = \(\frac{y}{1+x²}\) ⇒ y’ (1 + x²) = y
differentiating w.r.to x
y’ (2x) + (1 + x²)(y”) = y’
(i.e.) (1 + x²) y” + y’(2x) – y’ = 0
(i.e.) (1 + x²)y” + (2x – 1) y’ = 0

Question 46 (a).
Evaluate \(\lim _{x \rightarrow \infty} \frac{(x+1)^{10}+(x+2)^{10}+\ldots+(x+100)^{10}}{x^{10}+10^{10}}\)
Solution:

[OR]

(b) Evaluate

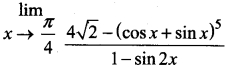
Solution:

Question 47 (a).
Evaluate \(\int \sin ^{-1}\)x dx
Solution:
Let 1 = sin^-1x dx
u = sin^-1x dv = dx

[OR]

(b) A factory has two machines I and II. Machine I produces 40% of items of the output and Machine II produces 60% of the items. Further 4% of items produced by Machine I are defective and 5% produced by Machine II are defective. An item is drawn at random. If the drawn item is defective, find the probability that it was produced by Machine II.
Solution:
Let A₁ be the event that the items are produced by Machine-I, A₂ be the event that items are produced by Machine-II, Let B be the event of drawing a defective item. Now we are asked to find the conditional probability P(A₂/B). Since A₁, A₂ are mutually exclusive and exhaustive events, by Bayes theorem,

Students can Download Tamil Nadu 11th Maths Model Question Paper 3 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Maths Model Question Paper 3 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 2.30 Hours
Maximum Marks: 90

PART – I

I. Choose the correct answer. Answer all the questions. [20 × 1 = 20]

Question 1.
Let A and B be subsets of the universal set N, the set of natural numbers. Then A’∪[(A ∩ B) ∪B’] is
(a) A
(b) A’
(c) B
(d) N
Solution:
(d) N

Question 2.
For any two sets A and B if (A – B) ∪ (B – A) = ………..
(a) (A – B) ∪ A
(b) (B – A) ∪ B
(c) (A ∪ B) – (A ∩ B)
(d) (A ∪ B) ∩ (A ∩ B)
Solution:
(c) (A ∪ B) – (A ∩ B)

Question 3.
The equations whose roots are numerically equal but opposite in sign to the roots of 3x² – 5x – 7 = 0 is ……….
(a) 3x² – 5x – 7 = 0
(b) 3x² + 5x – 7 = 0
(c) 3x² – 5x + 7 = 0
(d) 3x² + x – 7 = 0
Solution:
(b) 3x² + 5x – 7 = 0

Question 4.
The value of sin(45° + θ) – cos (45° – θ) is
(a) 2 cos θ
(b) 1
(c) 0
(d) 2 sin θ
Solution:
(c) 0

Question 5.
If tan α sin β = 840, are the roots of x² + ax + b = 0 then \(\frac{\sin (\alpha+\beta)}{\sin \alpha \sin \beta}\) is equal to ……..
(a) \(\frac{b}{a}\)
(b) \(\frac{a}{b}\)
(c) –\(\frac{a}{b}\)
(d) –\(\frac{b}{a}\)
Solution:
(c) –\(\frac{a}{b}\)

Question 6.
If a² – aC₂ = a² – aC₄ then the a value of a is ………
(a) 2
(b) 3
(c) 4
(d) 5
Solution:
(b) 3

Question 7.
If ⁿP_r = 840, ⁿC_r = 35 then n = …………
(a) 7
(b) 6
(c) 5
(d) 4
Solution:
(a) 7

Question 8.
If 2x² + 3xy – cy² = 0 represents a pair of perpendicular lines then c = ……….
(a) -2
(b) \(\frac{1}{2}\)
(c) –\(\frac{1}{2}\)
(d) 2
Solution:
(d) 2

Question 9.
If the nth term of an A.P is 2n – 1 then sum to n terms of that A.P. is……….
(a) n²
(b) n² + 1
(c) 2n – 1
(d) n² – 1
Solution:
(a) n²

Question 10.
If A = \(\left(\begin{array}{ll} 1 & -1 \\ 2 & -1 \end{array}\right)\), B = \(\left(\begin{array}{cc} a & 1 \\ b & -1 \end{array}\right)\)
(a) a = 4, b = 1
(b) a = 1, b = 4
(c) a = 0, 6 = 4
(d) a = 2, 6 = 4
Solution:
(b) a = 1, b = 4

Question 11.
If the points (x – 2), (5, 2), (8, 8) are collinear then x is equal to………..
(a) -3
(b) \(\frac{1}{3}\)
(c) 1
(d) 3
Solution:
(d) 3

Question 12.
In a regular hexagon ABCDEF if \(\vec { AB }\) and \(\vec { BC }\) are represented by \(\vec { a}\) and \(\vec { b }\) respectively then \(\vec { EF }\) =
(a) \(\vec { a }\) – \(\vec { b }\)
(b) \(\vec { a}\)
(c) –\(\vec { b }\)
(d) \(\vec { a }\) + \(\vec { b }\)
Solution:
(c) –\(\vec { b }\)

Question 13.
If |\(\vec { a }\) + \(\vec { b }\)| = 60, |\(\vec { a }\) – \(\vec { b }\)| = 40 and |\(\vec { b }\)| = 46, then |\(\vec { a }\)| is………….
(a) 42
(b) 12
(c) 22
(d) 32
Solution:
(c) 22

Question 14.
For \(\vec { a }\) = \(\vec { i }\) + \(\vec { j }\) – 2\(\vec { k }\), \(\vec { b }\) = –\(\vec { i }\) + 2\(\vec { j }\) + \(\vec { k }\) and \(\vec { c }\) = \(\vec { i }\) – 2\(\vec { j }\) + 2\(\vec { k }\), the unit vector parallal to \(\vec { a }\) + \(\vec { b }\) + \(\vec { c }\) is ………….
(a) \(\frac{\vec{i}+\vec{j}-\vec{k}}{\sqrt{3}}\)
(b) \(\frac{\vec{i}+\vec{j}+\vec{k}}{\sqrt{3}}\)
(c) \(\frac{\vec{i}+\vec{j}+\vec{k}}{3}\)
(d) \(\frac{\vec{i}+\vec{j}+\vec{k}}{\sqrt{6}}\)
Solution:
(b) \(\frac{\vec{i}+\vec{j}+\vec{k}}{\sqrt{3}}\)

Question 15.
The differential co-efficient of log₁₀x with respect to log₁₀ x is……….
(a) 1
(b) -(log₁₀x)²
(c) (log_x10)²
(d) \(\frac{x²}{100}\)
Solution:
(b) -(log₁₀x)²

Question 16.
\(\frac{d}{dx}\)(e_x+5logx) is………
(a) e₁₀x₁₀(x + 5)
(b) e_xx(x + 5)
(c) e_x + \(\frac{5}{x}\)
(d) e_x – \(\frac{5}{x}\)
Solution:
(a) e₁₀x₁₀(x + 5)

Question 17.
If f(x) = x tan_-1x then f'(1) = ……………
(a) 1 + \(\frac{π}{4}\)
(b) \(\frac{1}{2}\) + \(\frac{π}{4}\)
(c) \(\frac{1}{2}\) – \(\frac{π}{4}\)
(d) 2
Solution:
(b) \(\frac{1}{2}\) + \(\frac{π}{4}\)

Question 18.
∫ cosec x dx = ………..
(a) log tan \(\frac{π}{2}\) + c
(b) -log (cosec x + cot x) + c
(c) -log (cosec x + cot x) + c
(d) All of them
Solution:
(d) All of them

Question 19.
If A and B are two events such that A⊂B and P(B) ≠ 0, then which of the following is correct?
(a) P(A / B) = \(\frac{p(A)}{p(B)}\)
(b) P(A/B) < P(A)
(c) P(A/B ≥ P(A))
(d) P(A/B) > P(B)
Solution:
(c) P(A/B ≥ P(A))

Question 20.
A number x is chosen at random from the first 100 natural numbers. Let A be the event of numbers which satisfies \(\frac{(x-10)(x-50)}{x-30}\) ≥ 0, then P(A) is ………..
(a) 0.20
(b) 0.51
(c) 0.71
(d) 0.70
Solution:
(c) 0.71

PART – II

II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]

Question 21.
Write the values of f at -4, 1, -2, 7, 0 if

Solution:
f (- 4) = 4 + 4 = 8
f(1) = 1 – 1² = 0
f(-2) = 4 + 2 = 6
f(7) = 0
f(0) = 0

Question 22.
Solve 23x < 100 when
(i) x is a natural number
(ii) x is an integer
Solution:
23x < 100
⇒ \(\frac{23x}{23}\) < \(\frac{100}{23}\) (i.e.,) x > 23
(i) x = 1, 2, 3, 4 (x ∈ N)
(ii) x = -3, -2, -1, 0, 1, 2, 3, 4 (x ∈ Z)

Question 23.
Expand \(\frac{1}{5+x}\) in ascending powers of x.
Solution:

Question 24.
Find the nearest point on the line 2x +.y = 5 from the origin.
Solution:
The required point is the foot of the perpendicular from the origin on the line 2x + y = 5.
The line perpendicular to the given line, through the origin is x – 2y = 0.
Solving the equations 2x + y = 5 and x – 2y = 0, we get x = 2, y = 1.
Hence the nearest point on the line from the origin is (2, 1).
Alternate method: Using the formula

Question 25.
Determine 3B + 4C – D if B, C and D are given by

Solution:

Question 26.
Find the constant b that makes g continuous on (-∞, ∞) g(x) = \(\left\{\begin{array}{l} x^{2}-b^{2}, \text { if } x<4 \\ b x+20, \text { if } x \geq 4 \end{array}\right.\)
Solution: Since g(x) is continuous,
\(lim _{x \rightarrow 4^{-}}\) g(x) =\(lim _{x \rightarrow 4^{+}}\) g(x)
\(lim _{x \rightarrow 4^{-}}\)(x² – b²) = \(lim _{x \rightarrow 4^{+}}\) bx + 20
16 – b² = 4b + 20
b² + 4b + 4 = 0
(b + 2)² = 0
b = -2

Question 27.
Find \(\frac{dx}{dy}\) if x² + y² = 1
Solution:
We differentiate both sides of the equation.

Solving for the derivative yields
\(\frac{dx}{dy}\) = –\(\frac{x}{y}\)

Question 28.
Evaluate ∫ \(\frac{1}{sin²x cos²x}\) dx
Solution:

Question 29.
If P(A) = 0.5, P(B) = 0.8 and P(B/A) = 0.8 find P(A/B) and P(A ∪ B)
Solution:
Given P(A) = 0.5, P(B) = 0.8 and P(B/A) = 0.8
p(B/A) = \(\frac{p(A ∩ B)}{p(A)}\) = 0.8 (given)
⇒ \(\frac{p(A ∩ B)}{0.5}\) = 0.8
⇒ p(A ∩ B) = 0.8 × 0.5 = 0.4
(i.e.,) p(A ∩ B) = 0.4
(i) P(A/B) = \(\frac{p(A ∩ B)}{p(B)}\) = \(\frac{0.4}{0.8}\) = \(\frac{4}{8}\) = 0.5
(ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.5 + 0.8 – 0.4 = 0.9
So, P(A/B) = 0.5 and P(A ∩ B) = 0.9.

Question 30.
Find the angle between the vectors 2\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\) and \(\hat{i}\) + 2 \(\hat{j}\) + \(\hat{i}\) using vector product.
Solution:
The angle between \(\vec{b}\) and \(\vec{b}\) using vector product is given by

PART – III

Answer any seven questions. Question No. 40 is compulsory.

Question 31.
If (x^1/2 + x^-1/2)² = \(\frac{9}{2}\) find the value of (x^1/2 – x ^-1/2) for x > 1
Solution:

Question 32.
If \(\frac{n!}{3!(n-4)!}\) and \(\frac{n!}{5!(n-5)!}\) are in the ratio 5 : 3 find the value of n.
Solution:

Question 33.
Expand (1 + x)^{\(\frac{2}{3}\)} up to four terms for |x| < 1.
Solution:

Question 34.
Find the equation of the line if the perpendicular drawn from the origin makes an angle 30° with x axis and its length is 12.
Solution:
The equation of the line is x cos a + y sin a = p
here a = 30°, cos a = cos 30° = \(\frac{√3}{2}\) ; sin a = sin 30° = 1/2; p = 12.
So equation of the line is x\(\frac{√3}{2}\)+ v\(\frac{1}{2}\) = 12
(i.e) √3x + y = 12 × 2 = 24 ⇒ √3x + y – 24 = 0

Question 35.
Prove that

Solution:

Question 36.
Find \(\lim _{t \rightarrow 0} \frac{\sqrt{t^{2}+9}-3}{t^{2}}\)
Solution:
We can’t apply the quotient theorem immediately. Use the algebra technique of rationalising the numerator.

Question 37.
Find \(\frac{dy}{dx}\) where x = \(\frac{1-t²}{1+t²}\), y = \(\frac{2t}{1+t²}\)
Solution:

Question 38.
Evaluate ∫(5x² – 4 + \(\frac{7}{x}\) + \(\frac{2}{√x}\))dx
Solution:

Question 39.
What is the chance that leap year should have fifty three Sundays?
Solution:
Leap Year: In 52 weeks we have 52 Sundays. We have to find the probability of getting one Sunday form the remaining 2 days the remaining 2 days can be a combination of the following S = {Saturday and Sunday, Sunday and Monday, Monday and Tuesday, Tuesday and Wednesday, Wednesday and Thursday, Thursday and Friday, Friday and Saturday}.
(i.e) n(s) = 7
In this n(A) = {Saturday and Sunday, Sunday and Monday}
(i.e) n(A) = 2
So, P(A) = \(\frac{2}{7}\)

Question 40.
Find x from the equation cosec (90° + A) + x cos A cot (90° + A) = sin (90° + A).
Solution:
cosec (90° + A) = sec A, cot (90° + A) = – tan A
LHS = sec A + x cos A (-tan A)

PART – IV

IV. Answer all the questions. [7 × 5 = 35]

Question 41 (a).
From the curve y = x, draw
(i) y = -x
(ii) y = 2x
(iii) y = x + 1
(iv) y= \(\frac{1}{2}\)x + 1
(v) 2x + y + 3 = 0
Solution:

[OR]

(b) Solve √3 sin θ – cos θ = √2
Solution:
√3 sin θ – cos θ = √2
Here a = -1; b = √3 ; c = √2 ; r = \(\sqrt{a²+b²}\) = 2
Thus, the given equation can be rewritten as

Question 42 (a).
Solve \(\frac{x^{2}-4}{x^{2}-2x-15}\) ≤ 0
Solution:
\(\frac{x^{2}-4}{x^{2}-2x-15}\) ≤ 0 ⇒ \(\frac{(x-2)(x+2)}{(x+3)(x-5)}\) ≤ 0
x – 2 ⇒ x = 2; x + 2 = 0 ⇒ x = -2
x + 3 = 0 ⇒ x = -3; x – 5 = 0 ⇒ x = 5
plotting the points -3, -2, 2, 5 in the number line and taking the intervals

So the solution for the inequality \(\frac{x^{2}-4}{x^{2}-2x-15}\) ≤ 0 are (-3, -2) ∪ (2, 5)

[OR]

(b) Solve \(\frac{x+1}{x-1}\) > 0
Solution:
\(\frac{x+1}{x-1}\) > 0 ⇒ \(\frac{(x+1)(x-1)}{(x-1)²}\) > 0
(x + 1)(x – 1) > 0 (∵(x – 1)² >0 for all x ≠ l)

(x + 1) (x – 1) > 0
⇒ x ∈ (-∞, -1) ∪ (1, ∞)

Question 43 (a).
Use the principle of mathematical induction to prove that for every natural number n.

Solution:
Let P(n) be the given statement

For n = 1, LHS = 1 + \(\frac{3}{1}\) = 4
RHS = (1 + 1)² = 2² = 4
LHS = RHS
∴ ⇒ P(1) is true.
We note than P(n) is true for n = 1.
Assume that P(k) is true.

= k² +2k+ 1 + 2k + 3 = k² + 4k + 4 = (k + 2)²
= (k + 1 + 1)²
∴ p(k + 1)is also true whenever P(k) is true Hence, by the principle of mathematical induction, P(n) is also true for all n ∈ N.

[OR]

(b) If cos 2θ = 0 determine
Solution:
Given cos 2θ = 0
⇒ 2θ = π/2 ⇒ θ = π/4
∴ cos θ = cos π/4 = 1/√2
and
sin θ = sin π/4 = 1/√2

Question 44 (a).
Find the distance of the line 4x – y = 0 from the point P(4,1) measured along the line making an angle 135° with the positive x axis.
Solution:
The equation in distance form of the line passing through P (4, 1) and making an angle of 135° with the positive x – axis is
\(\frac{x-4}{cos135°}\) = \(\frac{y-1}{sin135°}\)
Suppose it cuts 4x – y – 0 at Q such that PQ = r then the coordinates of Q are given by

Hence, required distance is 3√2 units.

[OR]

(b) Evaluate \(\lim _{x \rightarrow \infty} x\left[3^{\frac{1}{x}}+1-\cos \left(\frac{1}{x}\right)-e^{\frac{1}{x}}\right]\)
Solution:

Question 45 (a).
Prove that \(\sqrt[3]{x^{3}+7}-\sqrt[3]{x^{3}+4}\) is approximately equal to \(\frac{1}{x²}\) when x is large.
Solution:

Since x is large, \(\frac{1}{x}\) is very small and hence higher powers of \(\frac{1}{x}\) are negligible. Thus

[OR]

(b) Evaluate sec³ 2x
I = ∫sec³ 2x dx = ∫sec 2x sec² 2x dx
Let u = sec 2x; du = 2 sec 2x tan 2x dx
sec²2x dx = dv

Question 46 (a).
Evaluate y = sin(tan(\(\sqrt{sin x}\)))
Solution:

[OR]

(b) Evaluate y = \(\sqrt{x+\sqrt{x+\sqrt{x}}}\)
Solution:

Question 47 (a).
Prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side whose length is half of the length of the third side.
Solution:
In ΔABC,

[OR]

(b) Given P(A) = 0.4 and P(A ∪ B) = 0.7 Find P(B) if
(i) A and B are mutually exclusive
(ii) A and B are independent events
(iii) P(A / B) = 0.4
(iv) P(B / A) = 0.5
Solution:
P(A) = 0.4, P(A ∪ B) = 0.7
(i) When A and B are mutually exclusive
P(A ∪ B) = P(A) + P(B)
(i.e.,) 0.7 = 0.4 + P(B)
0.7 – 0.4 = P(B)
(i.e.,) P(B) = 0.3

(ii) Given A and B are independent
⇒ P(A ∩ B) = P(A). P(B)
Now, P(A ∪ B) = P(A) + P(B) – P (A ∩ B)
(i.e.,) 0.7 = 0.4 + P(B) – (0.4) (P(B)
(i.e.,) 0.7 – 0.4 = P(B)(1 – 0.4)
0.3 = P (B) 0.6
⇒ P(B) = \(\frac{0.3}{0.6}\) = \(\frac{3}{6}\) = 0.5

(iii) P(A/B) = 0.4
(i.e.,) \(\frac{P(A ∩ B)}{P(B)}\) = 0.4
⇒ P(A ∩ B) = 0.4 P(B) …..(i)
But We know P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
⇒ P(A ∩ B) = 0.4 + P(B) – 0.7
= P(B) – 0.3
from (i) and (it) (equating RHS) we get
0-4 [P(B)] = P(B) – 0.3
0.3 = P(B)(1 – 0.4)
0.6 (P(B)) = 0.3 ⇒ P(B) = \(\frac{0.3}{0.6}\) = \(\frac{3}{6}\) = 0.5

(iv) P(B/A) = 0.5
(i.e.,) \(\frac{P(A ∩ B)}{P(A)}\) = 0.5
(i.e.,) P(A ∩ B) = 0.5 × P(A)
= 0.5 × 0.4 = 0.2
Now P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ 0.7 = 0.4 + P(B) – 0.2
⇒ 0.7 = P(B) + 0.2
⇒ P(B) =0.7 – 0.2 = 0.5

Students can Download Tamil Nadu 11th Maths Model Question Paper 1 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Maths Model Question Paper 1 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 2.30 Hours
Maximum Marks: 90

Part – I

Choose the correct answer. Answer all the questions. [20 × 1 = 20]

Question 1.
The number of students who take both the subjects Mathematics and Chemistry is 70. This represents 10% of the enrollment in Mathematics and 14% of the enrollment in Chemistry. The number of students take at least one of these two subjects, is
(a) 1120
(b)1130
(c) 1100
(d) insufficient data
Answer:
(b)1130

Question 2.
If 8 and 2 are the roots of x² + ax + c = 0 and 3, 3 are the roots of x² + dx + b = 0, then the roots of the equation x² + ax + b = 0 are
(a) 1, 2
(b) -1, 1
(c) 9, 1
(d) -1, 2
Answer:
(c) 9, 1

Question 3.
If tan 40° = λ then \(\frac{tan 140° – tan 130°}{1+tan 140° tan 130°}\) = ………….
(a) \(\frac{1-λ²}{λ}\)
(b) \(\frac{1+λ²}{λ}\)
(c) \(\frac{1+λ²}{2λ}\)
(d) \(\frac{1-λ²}{2λ}\)
Answer:
(d) \(\frac{1-λ²}{2λ}\)

Question 4.
The value of 2 sin A cos³ A – 2 cos A sin³ A is………..
(a) sin 4A
(b) cos 4A
(c) \(\frac{1}{2}\) sin 4A
(d) \(\frac{1}{2}\) cos 4A
Answer:
(c) \(\frac{1}{2}\) sin 4A

Question 5.
In a triangle ABC, sin²A + sin²B + sin²C = 2 then the triangle is ………. triangle.
(a) equilateral
(b) isosceles
(c) right
(d) scalene
Answer:
(c) right

Question 6.
The number of ways in which a host lady invite 8 people for a party of 8 out of 12 people of whom two do not want to attend the party together is ………….
(a) 2 × 11C₇ + 10C₈
(b) 11C₇+ 10C₈
(c) 12C₈ – 10C₆
(d) 10C₆ + 2!
Answer:
(c) 12C₈ – 10C₆

Question 7.
If a is the arithmetic mean and g is the geometric mean of two numbers then…………
(a) a ≤ g
(b) a ≥ g
(c) a = g
(d) a > g
Answer:
(b) a ≥ g

Question 8.
The number of rectangles that a chessboard has…………
(a) 81
(b) 9⁹
(c) 1296
(d) 6561
Answer:
(c) 1296

Question 9.
The intercepts of the perpendicular bisector of the line segment joining (1,2) and (3,4) with coordinate axes are………….
(a) 5, -5
(b) 5, 5
(c) 5, 3
(d) 5, -4
Answer:
(b) 5, 5

Question 10.
The coordinates of the four vertices of a quadrilateral are (-2, 4), (-1, 2), (1, 2) and (2, 4) taken in order.The equation of the line passing through the vertex (-1, 2) and dividing the quadrilateral in the equal areas is…………
(a) x + 1 = 0
(b) x + y= 1
(c) x + y + 3 = 0
(d) x – y + 3 = 0
Answer:
(c) x + y + 3 = 0

Question 11.
The vectors \(\vec{a}\) – \(\vec{b}\), \(\vec{b}\) – \(\vec{c}\), \(\vec{c}\) – \(\vec{a}\) are …………. vectors.
(a) parallel
(b) unit
(c) mutually perpendicular
(d) coplanar
Answer:
(d) coplanar

Question 12.
If |\(\vec{a}\) + \(\vec{b}\)| = 60, |\(\vec{a}\) – \(\vec{b}\)| = 40, |\(\vec{b}\)| = 46 then |\(\vec{a}\)| is ……………
(a) 42
(b) 12
(c) 22
(d) 32
Answer:
(c) 22

Question 13.
Given \(\vec{a}\) = 2\(\vec{i}\) + \(\vec{j}\) – 8\(\vec{k}\) and \(\vec{b}\) = \(\vec{i}\) + 3\(\vec{j}\) – 4\(\vec{k}\) then |\(\vec{a}\) + \(\vec{b}\)|= …………..
(a) 13
(b) \(\frac{13}{3}\)
(c) \(\frac{4}{13}\)
(d) \(\frac{3}{13}\)
Answer:
(a) 13

Question 14.
If \(\vec{r}\) = \(\frac{9\vec{a}+7\vec{b}}{16}\) then the point P whose position vector \(\vec{r}\) divides the line joining the points with position vectors \(\vec{a}\) and \(\vec{b}\) in the ratio……….

(a) 7 : 9 internally
(b) 9 : 7 internally
(c) 9 : 7 externally
(d) 7 : 9 externally
Answer:
(a) 7 : 9 internally

Question 15.
If f(x) = x + 2 then f’ (f(x)) at x = 4 is…………
(a) 8
(b) 1
(c) 4
(d) 5
Answer:
(b) 1

Question 16.
The derivative of (x + \(\frac{1}{x}\))² w.r.to. x is ……….
(a) 2x – \(\frac{2}{x³}\)
(b) 2x + \(\frac{2}{x³}\)
(c) 2(x + \(\frac{1}{x}\) )
(d) 0
Answer:
(a) 2x – \(\frac{2}{x³}\)

Question 17.
If y = \(\frac{1}{a-z}\) then \(\frac{dz}{dy}\) is………..
(a) (a – z)²
(b) – (z – a)²
(c) (z + a)²
(d) -(z + a)²
Answer:
(a) (a – z)²

Question 18.
∫sin7x cos5x dx = ……….

Answer:
(b) –\(\frac{1}{2}\) [\(\frac{cos 12x}{2}\) + \(\frac{cos 2x}{2}\)] + c

Question 19.
∫\(\frac{1}{e^x}\) dx = …………..
(a) log e^x + c
(b) x + c
(c) \(\frac{1}{e^x}\) + c
(d) \(\frac{-1}{e^x}\) + c
Answer:
(d) \(\frac{-1}{e^x}\) + c

Question 20.
A letter is taken at random from the letters of the word ‘ASSISTANT’ and another letter is taken at random from the letters of the word ‘ STATISTICS ’. The probability that the selected letters are the same………..
(a) \(\frac{7}{45}\)
(b) \(\frac{17}{90}\)
(c) \(\frac{29}{90}\)
(d) \(\frac{19}{90}\)
Answer:
(d) \(\frac{19}{90}\)

PART- II

II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]

Question 21.
For a set A, A × A contains 16 elements and two of its elements are (1,3) and (0,2). Find the elements of A.
Answer:
A × A = 16 elements = 4 × 4
⇒ A has 4 elements
∴ A = {0, 1, 2, 3}

Question 22.
Find the area of the triangle whose sides are 13 cm, 14 cm and 15 cm.
Answer:

Question 23.
If \(\frac{1}{7!}\) + \(\frac{1}{9!}\) = \(\frac{x}{10!}\) find x.
Answer:
Here \(\frac{1}{7!}\) + \(\frac{1}{9!}\) = \(\frac{x}{10!}\)

Question 24.
Find \(\sqrt[3]{1001}\) approximately (two decimal places)
Answer:

Question 25.
The slope of one of the straight lines ax² + 2hxy + by² = 0 is three times the other, show that 3h² = 4 ab.
Answer:
Let the slopes be m and 3m.
Now m + 3m = 4m = –\(\frac{2h}{b}\)
⇒ m = –\(\frac{2h}{4b}\) = –\(\frac{h}{2b}\) …….. (1)
m × 3m = \(\frac{a}{b}\) ⇒ 3m² = \(\frac{a}{b}\) ⇒ m² = \(\frac{a}{3b}\) ………. (2)
Eliminating m from (1) and (2)
we get

Question 26.
Simplify

Answer:
If we denote the given expression by A, then using the scalar multiplication rule, we get

Question 27.
Find a point whose position vector has magnitude 5 and parallel to the vector 4\(\hat{i}\) – 3\(\hat{j}\) + 10\(\hat{k}\).
Answer:
Let \(\vec{a}\) be the vector 4\(\hat{i}\) – 3\(\hat{j}\) + 10\(\hat{k}\)
The unit vector \(\hat{a}\) along the direction of \(\hat{a}\) is \(\frac{\vec{a}}{|\vec{a}|}\) which is equal to \(\frac{4 \hat{i}-3 \hat{j}+10 \hat{k}}{5 \sqrt{5}}\). the vector whose magnitude is 5 and parallel to

Question 28.
Evaluate \(\lim _{x \rightarrow-1}\left(x^{2}-3\right)^{10}\)
Answer:

Question 29.
Evaluate \(\int \frac{e^{2 x}+e^{-2 x}+2}{e^{x}}\)
Answer:

Question 30.
If A and B are mutually exclusive events P(A) = 3/8 and P(B) = 1/8 then find
(i) P(\(\bar{A}\) ∩ B)
(ii) p(\(\bar{A}\) ∪ \(\bar{B}\))
Answer:
(i) P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= 3/8 + 1/8 – 1/2
P(A ∩ B) = \(\frac{4-4}{8}\) = 0
P(\(\bar{A}\) ∩ B) = P(B) – P (A ∩ B) = 1/8 – 0 = 1/8

(ii) p(\(\bar{A}\) ∪ \(\bar{B}\)) = P[(A ∩B)’] = 1 – P(A ∩ B)
= 1 – 0 = 1

PART- III

III. Answer any seven questions. Question No. 40 is compulsory. [7 × 3 = 21]

Question 31.
Find the range of the function f(x) = \(\frac{1}{1-3cos x}\)
Answer:
Clearly, -1 ≤ cos x ≤ 1
⇒ 3 ≥ -3 cos x ≥ -3
⇒ -3 ≤ -3 cos x ≤ 3
⇒ 1 – 3 ≤ 1 – 3 cos x ≤ 1 + 3
Thus we get -2 ≤ 1 – 3 cos x and 1 – 3 cos x ≤ 4.
By taking reciprocals, we get \(\frac{1}{1-3 cos x}\) ≤ –\(\frac{1}{2}\) and \(\frac{1}{1-3 cos x}\) ≥ \(\frac{1}{4}\).
Hence the range of f is (-∞, –\(\frac{1}{2}\) ] ∪ [\(\frac{1}{4}\), ∞)

Question 32.
Solve for x, -x² + 3x – 2 ≥ 0
Answer:
-x² + 3x – 2 ≥ 0 ⇒ x² – 3x + 2 ≤ 0
(x – 1)(x – 2) ≤ 0
[(x – 1) (x – 2) = 0 ⇒ x = 1 or 2. Here α = 1 and β = 2. Note that α < β]
So for the inequality (x – 1) (x – 2) ≤ 2
x lies between 1 and 2
(i.e.) x ≥ 1 and x ≤ 2 or x ∈ [1, 2] or 1 ≤ x ≤ 2

Question 33.
Solve the following equation for which solutions lies in the interval 0° ≤ θ ≤ 360°. sin⁴x = sin²x
Answer:
sin²x – sin⁴x = 0
sin² x (1 – sin² x) = 0
sin²x (cos² x) = 0
[\(\frac{1}{2}\) (2 sinx cos x)]² = 0
⇒ (sin2 x)² = 0
⇒ sin 2x = 0 = 0, π, 2π, 3π, 4π
x = 0, \(\frac{π}{2}\), π, \(\frac{π}{2}\), 2π

Question 34.
Find n if n – 1 P₃: nP₄ = 1 : 9
Answer:
Here ^{n – 1}P₃ : ⁿP₄ = 1 : 9

Question 35.
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5 kg includes the empty cylinders tare weight of 15.3 kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced (i) Find the equation relating the quantity of gas in the cylinder to the days. (ii) Draw the graph for first 96 days.
Answer:
Since the usage is in constant rate and it is the slope m = \(\frac{14.2}{24}\)

which is the equation relating the quantity.
y – f(x) is a periodic function with period 24. (i.e.) f(x) = f(x + 24)

Question 36.
If cos 2θ = 0, determine
Answer:
Given cos 2θ = 0
⇒ 2θ = π/2 ⇒ θ = π/4

Question 37.
Show that the points (4, -3, 1), (2, -4, 5) and (1, -1, 0) form a right angled triangle.
Answer:
Trivially they form a triangle. It is enough to prove one angle is \(\frac{π}{2}\) . So find the sides of the triangle.
Let O be the point of reference and A, B, C be (4, -3, 1), (2, -4, 5) and (1, -1, 0) respectively.
\(\vec{OA}\) = 4\(\hat{i}\) -3\(\hat{j}\) + \(\hat{k}\), \(\vec{OB}\) = 2\(\hat{i}\) – 4\(\hat{j}\) + 5\(\hat{k}\), \(\vec{OC}\) = \(\hat{i}\) – \(\hat{j}\)
Now, \(\vec{AB}\) = \(\vec{OB}\) – \(\vec{OA}\) = -2\(\hat{i}\) – \(\hat{j}\) + 4\(\hat{k}\)
Similarly, \(\vec{BC}\) = –\(\hat{i}\) + 3\(\hat{j}\) – 5\(\hat{k}\); \(\vec{CA}\) = 3\(\hat{i}\) – 2\(\hat{j}\) + \(\hat{k}\)
Clearly \(\vec{AB}\) . \(\vec{CA}\) = 0
Thus one angle is \(\frac{π}{2}\). Hence they form a right angled triangle.

Question 38.
Compute

Answer:

= (0 + 1) + (0 + 3)
= 4

Question 39.
If for two events A and B, P(A) = \(\frac{3}{4}\), P(B) = \(\frac{2}{5}\) and A∪B conditional probability P(A/B).
Answer:
Given P(A) = \(\frac{3}{4}\), P(B) = \(\frac{2}{5}\) and P(A ∪ B) = l
Now P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
1 = \(\frac{3}{4}\) + \(\frac{2}{5}\) – P(A ∩ B)
P(A ∩ B) = \(\frac{3}{4}\) + \(\frac{2}{5}\) – 1 = \(\frac{15+8-20}{20}\)
P(A ∩ B) = 3/20
so P(A/B) = \(\frac{P(A ∪ B)}{P(B)}\) = \(\frac{3/20}{2/5}\) = \(\frac{3}{20}\) × \(\frac{5}{2}\) = \(\frac{3}{8}\)

Question 40.
Evaluate \(\int \frac{(x-1)^{2}}{x^{3}+x}\) dx
Answer:

PART – IV

IV. Answer all the questions. [7 × 5 = 35]

Question 41 (a).
Find the range of the function
Answer:
The range of cos x is – 1 to 1
– 1 < cos x < 1
(x by 2) – 2 < 2 cos x < 2
adding -1 throughout
-2 – 1 < 2 cos x – 1 < 2 – 1
(i.e.,) -3 < 2 cos x -1 < 1
so 1 < \(\frac{1}{2cosx – 1}\) < \(\frac{-1}{3}\)
The range is outside \(\frac{-1}{3}\) and 1
i.e., range is (-∞, \(\frac{-1}{3}\)]∪[1, ∞)

[OR]

(b) In any triangle ABC prove that a² = (b + c)² sin² \(\frac{A}{2}\) + (b – c)² cos² \(\frac{A}{2}\) Answer:
RHS = (b + c)² sin² \(\frac{A}{2}\) + (b – c)² cos² \(\frac{A}{2}\)
= (b² + c² + 2bc) sin² \(\frac{A}{2}\) + (b² + c² – 2bc) cos² \(\frac{A}{2}\)
= (b² + c²) [sin² \(\frac{A}{2}\) + cos² \(\frac{A}{2}\)] + 2bc [sin² \(\frac{A}{2}\) – cos² \(\frac{A}{2}\)]
= b² + c² – 2bc cos A = a² = LHS

Question 42 (a).
Find all values of x for which \(\frac{x³(x-1)}{x-2}\) > 0
Answer:
\(\frac{x³(x-1)}{x-2}\) > 0
Now we have to find the signs of
x³, x – 1 and x – 2 as follows
x³ = 0 ⇒ x = 0; x – 1 = 0 ⇒ x = 1; x – 2 = 0 ⇒ x = 2.
Plotting the points in a number line and finding intervals

So the solution set = (0, 1) ∪ (2, ∞)

[OR]

(b) resolve \(\frac{x}{(x²+1)(x-1)(x+2)}\) Into partial fractions.
Answer:

Equating numerator on both sides
x = A (x + 2) (x² + 1) + B (x – 1) (x² + 1) + (Cx + D) (x – 1) (x + 2)
This equations is true for any value of x to find A, B, C and D.
put x = 1
1 = A (3) (2) + B (0) + (0)
6A = 1 ⇒ A= 1/6
put x = -2
-2 = + 0 + B (-3) (5) + 0
⇒ -15B = -2 ⇒ B = 2/15
put x = 0
⇒ 2A – B – 2D = 0
(i.e.,) \(\frac{2}{6}\) – \(\frac{2}{15}\) – 2D = 0

Question 43 (a).
7 relatives of a man comprises 4 ladies and 3 gentlemen, his wife has also 7 relatives; 3 of them are ladies and 4 gentlemen. In how many ways can they invite a dinner party of 3 ladies and 3 gentlemen so that there are 3 of mens relative and 3 of the wifes relatives?
Answer:

We need 3 ladies and 3 gentlemen for the party which consist of 3 Husbands relative and 3 wifes relative.
This can be done as follows

⁴C₀ = ⁴C₄ = 1; ³C₀ = ³C₃ = 1
⁴C₁ = ⁴C₃ = 4; ³C₁ = ³C₂ = 3
⁴C₂ = \(\frac{4×3}{2×1}\) = 6
(4) (1) (1) (4) + (6) (3) (3) (6) + (4) (3) (3) (4) + (1) (1) (1) (1)
= 16 + 324 + 144 + 1 = 485 ways.

[OR]

(b) Show that the points (1, 3), (2, 1) and (\(\frac{1}{2}\), 4) are collinear, by using
(i) Concept of slope
(ii) Using a straight line and
(iii) Any other method.
Answer:
Let the given points be A (1, 3), B (2, 1), and C(\(\frac{1}{2}\), 4)

Slope of AB = Slope of BC ⇒ AB parallel to BC but B is a common point.
⇒ The points A, B, C are collinear.

(ii) Equation of the line passing through A and B is \(\frac{y-1}{3-1}\) = \(\frac{x-2}{1-2}\) ⇒ \(\frac{y-1}{2}\) = \(\frac{x-2}{-1}\)
1 – y = 2x – 4
2x +y = 5 ……….(1)
Substituting C\(\frac{1}{2}\), 4 in (1),
We get LHS = 2(\(\frac{1}{2}\)) + 4 = 1 + 4 = 5 = RHS
C is a point on AB
⇒ The points A, B, C lie on a line.
⇒ The points A, B, C are collinear.

(iii) Area of ΔABC = \(\frac{1}{2}\)(x₁) (y₂ y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)
= \(\frac{1}{2}\) {1(1, -4) + 2(4 – 3) +\(\frac{1}{2}\)(3 – 1)} = \(\frac{1}{2}\)(-3 + 2 + 1) = 0
⇒ The points A, B, C are collinear.

Question 44 (a).
Prove by vector Method’s that the Medians of a triangle are concurrent.
Answer:
Theorem: The medians of a triangle are concurrent.
Proof: Let ABC be a triangle and let D, E, F be the mid points of its sides BC, CA and AB respectively. We have to prove that the medians AD, BE, CF are concurrent.
Let O be the origin and \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) be the position vectors of A, B, and C respectively.
The position vectors of D, E and F are respectively.
\(\frac{\vec{b}}{\vec{c}}\), \(\frac{\vec{c}}{\vec{a}}\), \(\frac{\vec{a}}{\vec{b}}\)
Let G₁, be the point on AD dividing it internally in the ratio 2 : 1.

From (1), (2) and (3) we find that the position vectors of the three points G₁, G₂, G₃ are one and the same. Hence they are not different points. Let the common point be G.
Therefore the three medians are concurrent and the point of concurrence is G.

[OR]

(b) If y = Ae^6x + Be^-x prove that \(\frac{d²y}{dx²}\) – 5\(\frac{dy}{dx}\) – 6y = 0
Answer:

Question 45 (a).
If a and b are distinct integers, prove that a – b is a factor of aⁿ – bⁿ, whenever n is a positive integer. [Hint: write aⁿ = (a-b + b)ⁿ and expand]
Answer:
a = a – b + b
So, aⁿ = [a – b + b]ⁿ =[(a – b) + b]ⁿ
= ⁿC₀ (a – b)ⁿ + ⁿC₁ (a -b)^n-1b¹ + ⁿC₂ (a – b)^n-2b² + ……… + ⁿC_n-1(a – b) b^n-1
+ ⁿC_n(bⁿ)
⇒ aⁿ – bⁿ = (a – b)ⁿ + ⁿC₁ (a – b)^n-1b + _nC₂ (a – b)^n-2b² + ……. + ⁿC_n-1 (a – b) b^n-1
= (a – b) [(a – b)^n-1 + ⁿC₁(a – b)^n-2b + ⁿC₂ (a – b)^n-3b² + ……… + ⁿC_n-1, b^n-1]
= (a – b) [an integer]
⇒ aⁿ – 6ⁿ is divisible by (a – b)

[OR]

(b) Verify the property A (B + C) = AB + AC when the matrices A, B and C are given by

Answer:

Question 46 (a).
Evaluate \(\lim _{x \rightarrow \infty} \sqrt{x^{2}+x+1}-\sqrt{x^{2}+1}\)
Answer:
Here the expression assumes the form ∞ to – ∞ as x → ∞. SO, we first reduce it to the rational form \(\frac{f(x)}{g(x)}\)

[OR]

(b) Evaluate \(\lim _{x \rightarrow \infty} x\left[3^{\frac{1}{x}}+1-\cos \left(\frac{1}{x}\right)-e^{1 / x}\right]\)
Answer:
Let y = \(\frac{1}{x}\) as x → ∞, y → 0

Question 47 (a).
Evaluate \(\int \tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)\) dx.
Answer:

[OR]

(b) Suppose the chances of hitting a target by a person X is 3 times in 4 shots, by Y is 4 times in 5 shots, and by Z is 2 times in 3 shots. They fire simultaneously exactly one time. What is the probability that the target is damaged by exactly 2 hits?
Answer:
Given P(X) = 3/4, P(X’) = 1 – 3/4 = 1/4
P(Y) = 4/5, P(Y’) = 1 – 4/5 = 1/5
P(Z) = \(\frac{2}{3}\) P(Z’) = 1 – \(\frac{2}{3}\) = \(\frac{1}{3}\)