Tamil Nadu 11th Maths Model Question Paper 3 English Medium

Students can Download Tamil Nadu 11th Maths Model Question Paper 3 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Maths Model Question Paper 3 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 2.30 Hours
Maximum Marks: 90

PART – I

I. Choose the correct answer. Answer all the questions. [20 × 1 = 20]

Question 1.
Let A and B be subsets of the universal set N, the set of natural numbers. Then A’∪[(A ∩ B) ∪B’] is
(a) A
(b) A’
(c) B
(d) N
Solution:
(d) N

Question 2.
For any two sets A and B if (A – B) ∪ (B – A) = ………..
(a) (A – B) ∪ A
(b) (B – A) ∪ B
(c) (A ∪ B) – (A ∩ B)
(d) (A ∪ B) ∩ (A ∩ B)
Solution:
(c) (A ∪ B) – (A ∩ B)

Question 3.
The equations whose roots are numerically equal but opposite in sign to the roots of 3x² – 5x – 7 = 0 is ……….
(a) 3x² – 5x – 7 = 0
(b) 3x² + 5x – 7 = 0
(c) 3x² – 5x + 7 = 0
(d) 3x² + x – 7 = 0
Solution:
(b) 3x² + 5x – 7 = 0

Question 4.
The value of sin(45° + θ) – cos (45° – θ) is
(a) 2 cos θ
(b) 1
(c) 0
(d) 2 sin θ
Solution:
(c) 0

Question 5.
If tan α sin β = 840, are the roots of x² + ax + b = 0 then \(\frac{\sin (\alpha+\beta)}{\sin \alpha \sin \beta}\) is equal to ……..
(a) \(\frac{b}{a}\)
(b) \(\frac{a}{b}\)
(c) –\(\frac{a}{b}\)
(d) –\(\frac{b}{a}\)
Solution:
(c) –\(\frac{a}{b}\)

Question 6.
If a² – aC₂ = a² – aC₄ then the a value of a is ………
(a) 2
(b) 3
(c) 4
(d) 5
Solution:
(b) 3

Question 7.
If ⁿP_r = 840, ⁿC_r = 35 then n = …………
(a) 7
(b) 6
(c) 5
(d) 4
Solution:
(a) 7

Question 8.
If 2x² + 3xy – cy² = 0 represents a pair of perpendicular lines then c = ……….
(a) -2
(b) \(\frac{1}{2}\)
(c) –\(\frac{1}{2}\)
(d) 2
Solution:
(d) 2

Question 9.
If the nth term of an A.P is 2n – 1 then sum to n terms of that A.P. is……….
(a) n²
(b) n² + 1
(c) 2n – 1
(d) n² – 1
Solution:
(a) n²

Question 10.
If A = \(\left(\begin{array}{ll} 1 & -1 \\ 2 & -1 \end{array}\right)\), B = \(\left(\begin{array}{cc} a & 1 \\ b & -1 \end{array}\right)\)
(a) a = 4, b = 1
(b) a = 1, b = 4
(c) a = 0, 6 = 4
(d) a = 2, 6 = 4
Solution:
(b) a = 1, b = 4

Question 11.
If the points (x – 2), (5, 2), (8, 8) are collinear then x is equal to………..
(a) -3
(b) \(\frac{1}{3}\)
(c) 1
(d) 3
Solution:
(d) 3

Question 12.
In a regular hexagon ABCDEF if \(\vec { AB }\) and \(\vec { BC }\) are represented by \(\vec { a}\) and \(\vec { b }\) respectively then \(\vec { EF }\) =
(a) \(\vec { a }\) – \(\vec { b }\)
(b) \(\vec { a}\)
(c) –\(\vec { b }\)
(d) \(\vec { a }\) + \(\vec { b }\)
Solution:
(c) –\(\vec { b }\)

Question 13.
If |\(\vec { a }\) + \(\vec { b }\)| = 60, |\(\vec { a }\) – \(\vec { b }\)| = 40 and |\(\vec { b }\)| = 46, then |\(\vec { a }\)| is………….
(a) 42
(b) 12
(c) 22
(d) 32
Solution:
(c) 22

Question 14.
For \(\vec { a }\) = \(\vec { i }\) + \(\vec { j }\) – 2\(\vec { k }\), \(\vec { b }\) = –\(\vec { i }\) + 2\(\vec { j }\) + \(\vec { k }\) and \(\vec { c }\) = \(\vec { i }\) – 2\(\vec { j }\) + 2\(\vec { k }\), the unit vector parallal to \(\vec { a }\) + \(\vec { b }\) + \(\vec { c }\) is ………….
(a) \(\frac{\vec{i}+\vec{j}-\vec{k}}{\sqrt{3}}\)
(b) \(\frac{\vec{i}+\vec{j}+\vec{k}}{\sqrt{3}}\)
(c) \(\frac{\vec{i}+\vec{j}+\vec{k}}{3}\)
(d) \(\frac{\vec{i}+\vec{j}+\vec{k}}{\sqrt{6}}\)
Solution:
(b) \(\frac{\vec{i}+\vec{j}+\vec{k}}{\sqrt{3}}\)

Question 15.
The differential co-efficient of log₁₀x with respect to log₁₀ x is……….
(a) 1
(b) -(log₁₀x)²
(c) (log_x10)²
(d) \(\frac{x²}{100}\)
Solution:
(b) -(log₁₀x)²

Question 16.
\(\frac{d}{dx}\)(e_x+5logx) is………
(a) e₁₀x₁₀(x + 5)
(b) e_xx(x + 5)
(c) e_x + \(\frac{5}{x}\)
(d) e_x – \(\frac{5}{x}\)
Solution:
(a) e₁₀x₁₀(x + 5)

Question 17.
If f(x) = x tan_-1x then f'(1) = ……………
(a) 1 + \(\frac{π}{4}\)
(b) \(\frac{1}{2}\) + \(\frac{π}{4}\)
(c) \(\frac{1}{2}\) – \(\frac{π}{4}\)
(d) 2
Solution:
(b) \(\frac{1}{2}\) + \(\frac{π}{4}\)

Question 18.
∫ cosec x dx = ………..
(a) log tan \(\frac{π}{2}\) + c
(b) -log (cosec x + cot x) + c
(c) -log (cosec x + cot x) + c
(d) All of them
Solution:
(d) All of them

Question 19.
If A and B are two events such that A⊂B and P(B) ≠ 0, then which of the following is correct?
(a) P(A / B) = \(\frac{p(A)}{p(B)}\)
(b) P(A/B) < P(A)
(c) P(A/B ≥ P(A))
(d) P(A/B) > P(B)
Solution:
(c) P(A/B ≥ P(A))

Question 20.
A number x is chosen at random from the first 100 natural numbers. Let A be the event of numbers which satisfies \(\frac{(x-10)(x-50)}{x-30}\) ≥ 0, then P(A) is ………..
(a) 0.20
(b) 0.51
(c) 0.71
(d) 0.70
Solution:
(c) 0.71

PART – II

II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]

Question 21.
Write the values of f at -4, 1, -2, 7, 0 if

Solution:
f (- 4) = 4 + 4 = 8
f(1) = 1 – 1² = 0
f(-2) = 4 + 2 = 6
f(7) = 0
f(0) = 0

Question 22.
Solve 23x < 100 when
(i) x is a natural number
(ii) x is an integer
Solution:
23x < 100
⇒ \(\frac{23x}{23}\) < \(\frac{100}{23}\) (i.e.,) x > 23
(i) x = 1, 2, 3, 4 (x ∈ N)
(ii) x = -3, -2, -1, 0, 1, 2, 3, 4 (x ∈ Z)

Question 23.
Expand \(\frac{1}{5+x}\) in ascending powers of x.
Solution:

Question 24.
Find the nearest point on the line 2x +.y = 5 from the origin.
Solution:
The required point is the foot of the perpendicular from the origin on the line 2x + y = 5.
The line perpendicular to the given line, through the origin is x – 2y = 0.
Solving the equations 2x + y = 5 and x – 2y = 0, we get x = 2, y = 1.
Hence the nearest point on the line from the origin is (2, 1).
Alternate method: Using the formula

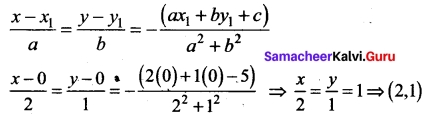
Question 25.
Determine 3B + 4C – D if B, C and D are given by

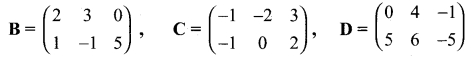
Solution:

Question 26.
Find the constant b that makes g continuous on (-∞, ∞) g(x) = \(\left\{\begin{array}{l} x^{2}-b^{2}, \text { if } x<4 \\ b x+20, \text { if } x \geq 4 \end{array}\right.\)
Solution: Since g(x) is continuous,
\(lim _{x \rightarrow 4^{-}}\) g(x) =\(lim _{x \rightarrow 4^{+}}\) g(x)
\(lim _{x \rightarrow 4^{-}}\)(x² – b²) = \(lim _{x \rightarrow 4^{+}}\) bx + 20
16 – b² = 4b + 20
b² + 4b + 4 = 0
(b + 2)² = 0
b = -2

Question 27.
Find \(\frac{dx}{dy}\) if x² + y² = 1
Solution:
We differentiate both sides of the equation.

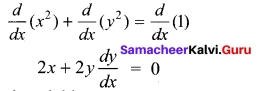
Solving for the derivative yields
\(\frac{dx}{dy}\) = –\(\frac{x}{y}\)

Question 28.
Evaluate ∫ \(\frac{1}{sin²x cos²x}\) dx
Solution:

Question 29.
If P(A) = 0.5, P(B) = 0.8 and P(B/A) = 0.8 find P(A/B) and P(A ∪ B)
Solution:
Given P(A) = 0.5, P(B) = 0.8 and P(B/A) = 0.8
p(B/A) = \(\frac{p(A ∩ B)}{p(A)}\) = 0.8 (given)
⇒ \(\frac{p(A ∩ B)}{0.5}\) = 0.8
⇒ p(A ∩ B) = 0.8 × 0.5 = 0.4
(i.e.,) p(A ∩ B) = 0.4
(i) P(A/B) = \(\frac{p(A ∩ B)}{p(B)}\) = \(\frac{0.4}{0.8}\) = \(\frac{4}{8}\) = 0.5
(ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.5 + 0.8 – 0.4 = 0.9
So, P(A/B) = 0.5 and P(A ∩ B) = 0.9.

Question 30.
Find the angle between the vectors 2\(\hat{i}\) + \(\hat{j}\) – \(\hat{k}\) and \(\hat{i}\) + 2 \(\hat{j}\) + \(\hat{i}\) using vector product.
Solution:
The angle between \(\vec{b}\) and \(\vec{b}\) using vector product is given by

PART – III

Answer any seven questions. Question No. 40 is compulsory.

Question 31.
If (x^1/2 + x^-1/2)² = \(\frac{9}{2}\) find the value of (x^1/2 – x ^-1/2) for x > 1
Solution:

Question 32.
If \(\frac{n!}{3!(n-4)!}\) and \(\frac{n!}{5!(n-5)!}\) are in the ratio 5 : 3 find the value of n.
Solution:

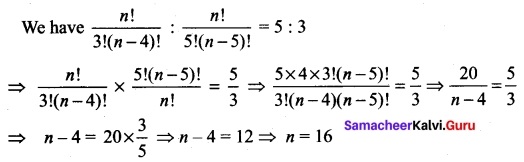
Question 33.
Expand (1 + x)^{\(\frac{2}{3}\)} up to four terms for |x| < 1.
Solution:

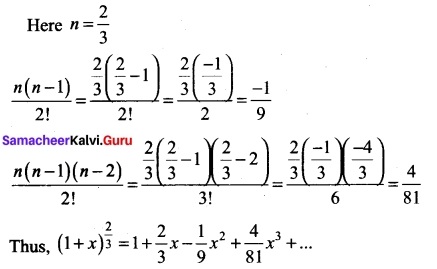
Question 34.
Find the equation of the line if the perpendicular drawn from the origin makes an angle 30° with x axis and its length is 12.
Solution:
The equation of the line is x cos a + y sin a = p
here a = 30°, cos a = cos 30° = \(\frac{√3}{2}\) ; sin a = sin 30° = 1/2; p = 12.
So equation of the line is x\(\frac{√3}{2}\)+ v\(\frac{1}{2}\) = 12
(i.e) √3x + y = 12 × 2 = 24 ⇒ √3x + y – 24 = 0

Question 35.
Prove that

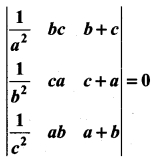
Solution:

Question 36.
Find \(\lim _{t \rightarrow 0} \frac{\sqrt{t^{2}+9}-3}{t^{2}}\)
Solution:
We can’t apply the quotient theorem immediately. Use the algebra technique of rationalising the numerator.

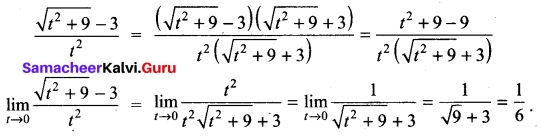
Question 37.
Find \(\frac{dy}{dx}\) where x = \(\frac{1-t²}{1+t²}\), y = \(\frac{2t}{1+t²}\)
Solution:

Question 38.
Evaluate ∫(5x² – 4 + \(\frac{7}{x}\) + \(\frac{2}{√x}\))dx
Solution:

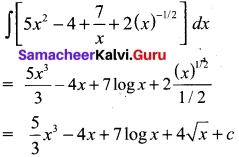
Question 39.
What is the chance that leap year should have fifty three Sundays?
Solution:
Leap Year: In 52 weeks we have 52 Sundays. We have to find the probability of getting one Sunday form the remaining 2 days the remaining 2 days can be a combination of the following S = {Saturday and Sunday, Sunday and Monday, Monday and Tuesday, Tuesday and Wednesday, Wednesday and Thursday, Thursday and Friday, Friday and Saturday}.
(i.e) n(s) = 7
In this n(A) = {Saturday and Sunday, Sunday and Monday}
(i.e) n(A) = 2
So, P(A) = \(\frac{2}{7}\)

Question 40.
Find x from the equation cosec (90° + A) + x cos A cot (90° + A) = sin (90° + A).
Solution:
cosec (90° + A) = sec A, cot (90° + A) = – tan A
LHS = sec A + x cos A (-tan A)

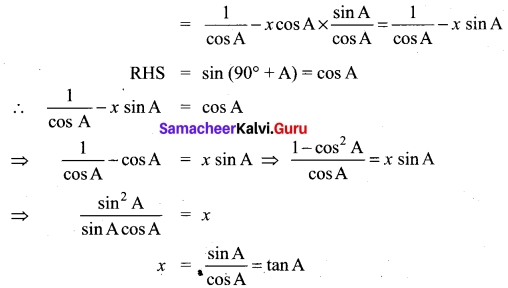
PART – IV

IV. Answer all the questions. [7 × 5 = 35]

Question 41 (a).
From the curve y = x, draw
(i) y = -x
(ii) y = 2x
(iii) y = x + 1
(iv) y= \(\frac{1}{2}\)x + 1
(v) 2x + y + 3 = 0
Solution:

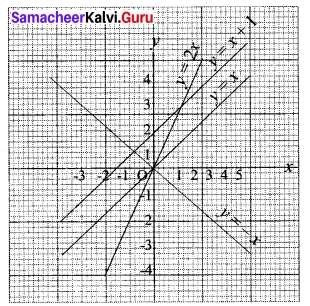
[OR]

(b) Solve √3 sin θ – cos θ = √2
Solution:
√3 sin θ – cos θ = √2
Here a = -1; b = √3 ; c = √2 ; r = \(\sqrt{a²+b²}\) = 2
Thus, the given equation can be rewritten as

Question 42 (a).
Solve \(\frac{x^{2}-4}{x^{2}-2x-15}\) ≤ 0
Solution:
\(\frac{x^{2}-4}{x^{2}-2x-15}\) ≤ 0 ⇒ \(\frac{(x-2)(x+2)}{(x+3)(x-5)}\) ≤ 0
x – 2 ⇒ x = 2; x + 2 = 0 ⇒ x = -2
x + 3 = 0 ⇒ x = -3; x – 5 = 0 ⇒ x = 5
plotting the points -3, -2, 2, 5 in the number line and taking the intervals

So the solution for the inequality \(\frac{x^{2}-4}{x^{2}-2x-15}\) ≤ 0 are (-3, -2) ∪ (2, 5)

[OR]

(b) Solve \(\frac{x+1}{x-1}\) > 0
Solution:
\(\frac{x+1}{x-1}\) > 0 ⇒ \(\frac{(x+1)(x-1)}{(x-1)²}\) > 0
(x + 1)(x – 1) > 0 (∵(x – 1)² >0 for all x ≠ l)

(x + 1) (x – 1) > 0
⇒ x ∈ (-∞, -1) ∪ (1, ∞)

Question 43 (a).
Use the principle of mathematical induction to prove that for every natural number n.

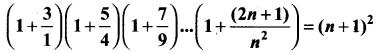
Solution:
Let P(n) be the given statement

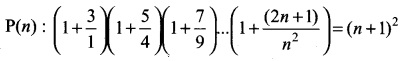
For n = 1, LHS = 1 + \(\frac{3}{1}\) = 4
RHS = (1 + 1)² = 2² = 4
LHS = RHS
∴ ⇒ P(1) is true.
We note than P(n) is true for n = 1.
Assume that P(k) is true.

= k² +2k+ 1 + 2k + 3 = k² + 4k + 4 = (k + 2)²
= (k + 1 + 1)²
∴ p(k + 1)is also true whenever P(k) is true Hence, by the principle of mathematical induction, P(n) is also true for all n ∈ N.

[OR]

(b) If cos 2θ = 0 determine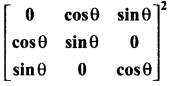
Solution:
Given cos 2θ = 0
⇒ 2θ = π/2 ⇒ θ = π/4
∴ cos θ = cos π/4 = 1/√2
and
sin θ = sin π/4 = 1/√2

Question 44 (a).
Find the distance of the line 4x – y = 0 from the point P(4,1) measured along the line making an angle 135° with the positive x axis.
Solution:
The equation in distance form of the line passing through P (4, 1) and making an angle of 135° with the positive x – axis is
\(\frac{x-4}{cos135°}\) = \(\frac{y-1}{sin135°}\)
Suppose it cuts 4x – y – 0 at Q such that PQ = r then the coordinates of Q are given by

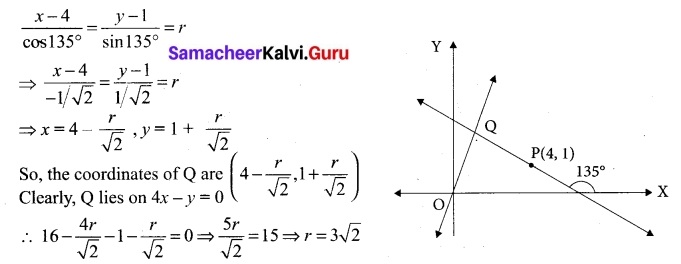
Hence, required distance is 3√2 units.

[OR]

(b) Evaluate \(\lim _{x \rightarrow \infty} x\left[3^{\frac{1}{x}}+1-\cos \left(\frac{1}{x}\right)-e^{\frac{1}{x}}\right]\)
Solution:

Question 45 (a).
Prove that \(\sqrt[3]{x^{3}+7}-\sqrt[3]{x^{3}+4}\) is approximately equal to \(\frac{1}{x²}\) when x is large.
Solution:

Since x is large, \(\frac{1}{x}\) is very small and hence higher powers of \(\frac{1}{x}\) are negligible. Thus

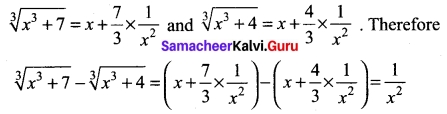
[OR]

(b) Evaluate sec³ 2x
I = ∫sec³ 2x dx = ∫sec 2x sec² 2x dx
Let u = sec 2x; du = 2 sec 2x tan 2x dx
sec²2x dx = dv

Question 46 (a).
Evaluate y = sin(tan(\(\sqrt{sin x}\)))
Solution:

[OR]

(b) Evaluate y = \(\sqrt{x+\sqrt{x+\sqrt{x}}}\)
Solution:

Question 47 (a).
Prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side whose length is half of the length of the third side.
Solution:
In ΔABC,

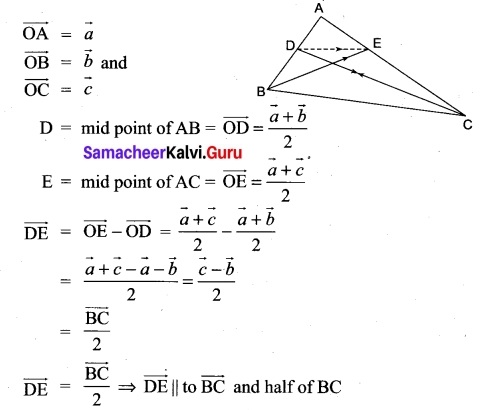
[OR]

(b) Given P(A) = 0.4 and P(A ∪ B) = 0.7 Find P(B) if
(i) A and B are mutually exclusive
(ii) A and B are independent events
(iii) P(A / B) = 0.4
(iv) P(B / A) = 0.5
Solution:
P(A) = 0.4, P(A ∪ B) = 0.7
(i) When A and B are mutually exclusive
P(A ∪ B) = P(A) + P(B)
(i.e.,) 0.7 = 0.4 + P(B)
0.7 – 0.4 = P(B)
(i.e.,) P(B) = 0.3

(ii) Given A and B are independent
⇒ P(A ∩ B) = P(A). P(B)
Now, P(A ∪ B) = P(A) + P(B) – P (A ∩ B)
(i.e.,) 0.7 = 0.4 + P(B) – (0.4) (P(B)
(i.e.,) 0.7 – 0.4 = P(B)(1 – 0.4)
0.3 = P (B) 0.6
⇒ P(B) = \(\frac{0.3}{0.6}\) = \(\frac{3}{6}\) = 0.5

(iii) P(A/B) = 0.4
(i.e.,) \(\frac{P(A ∩ B)}{P(B)}\) = 0.4
⇒ P(A ∩ B) = 0.4 P(B) …..(i)
But We know P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
⇒ P(A ∩ B) = 0.4 + P(B) – 0.7
= P(B) – 0.3
from (i) and (it) (equating RHS) we get
0-4 [P(B)] = P(B) – 0.3
0.3 = P(B)(1 – 0.4)
0.6 (P(B)) = 0.3 ⇒ P(B) = \(\frac{0.3}{0.6}\) = \(\frac{3}{6}\) = 0.5

(iv) P(B/A) = 0.5
(i.e.,) \(\frac{P(A ∩ B)}{P(A)}\) = 0.5
(i.e.,) P(A ∩ B) = 0.5 × P(A)
= 0.5 × 0.4 = 0.2
Now P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
⇒ 0.7 = 0.4 + P(B) – 0.2
⇒ 0.7 = P(B) + 0.2
⇒ P(B) =0.7 – 0.2 = 0.5