Prasanna

Students can download 12th Business Maths Chapter 8 Sampling Techniques and Statistical Inference Ex 8.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 8 Sampling Techniques and Statistical Inference Ex 8.2

Question 1.
Mention two branches of statistical inference?
Solution:
The two branches of statistical inference are estimation and testing of hypothesis.

Question 2.
What is an estimator?
Answer:
An estimator is a statistic that is used to infer the value of an unknown population parameter in a statistical model. The estimator is a function of the data arid so it is also a random variable.

Question 3.
What is an estimate?
Solution:
Any specific numerical value of the estimator is called an estimate. For example, sample means are used to estimate population means.

Question 4.
What is point estimation?
Solution:
Point estimation involves the use of sample data to calculate a single value which is to serve as a best estimate of an unknown population parameter. For example the mean height of 145 cm from a sample of 15 students is‘a point estimate for the mean height of the class of 100 students.

Question 5.
What is interval estimation?
Solution:
Interval estimation is the use of sample data to calculate an interval of possible values of an unknown population parameter. For example the interval estimate for the population mean is (101.01, 102.63).This gives a range within which the population mean is most likely to be located.

Question 6.
What is confidence interval?
Solution:
A confidence interval L a type of interval estimate, computed from the statistics of the observed data, that might contain the true value of an unknown population parameter. The numbers at the upper and lower end of a confidence interval are called confidence limits. For example, if mean is 7.4 with confidence interval (5.4, 9.4), then the numbers 5.4 and 9.4 are the confidence limits.

Question 7.
What is null hypothesis? Give an example.
Solution:
A null hypothesis is a type of hypothesis, that proposes that no statistical significance exists in a set of given observations. For example, let the average time to cook a specific dish is 15 minutes. The null hypothesis would be stated as “The population mean is equal to 15 minutes”, (i.e) H₀ : µ = 15

Question 8.
Define the alternative hypothesis.
Solution:
The alternative hypothesis is the hypothesis that is contrary to the null hypothesis and it is denoted by H₁.
For example if H₁ : µ = 15, then the alternative hypothesis will be : H₁ : µ ≠ 15, (or) H₁ : µ < 15 (or) H₁ : µ > 15.

Question 9.
Define the critical region.
Solution:
The critical region is the region of values that corresponds to the rejection of the null hypothesis at some chosen probability level. For the two-tailed test, the critical region is given below.

where α is the level of significance.

Question 10.
Define critical value.
Solution:
A critical value is a point on the test distribution that is compared to the test statistic to determine whether to reject the null hypothesis. It depends on the level of significance. For example, if the confidence level is 90% then the critical value is 1.645.

Question 11.
Define the level of significance
Solution:
The level of significance is defined as the probability of rejecting a null hypothesis by the test when it is really true, which is denoted as α. That is P(Type 1 error) = α. For example, the level of significance 0.1 is related to the 90% confidence level.

Question 12.
What is a type I error?
Solution:
In statistical hypothesis testing, a Type f error is the rejection of a true null hypothesis. Example of Type I errors includes a test that shows a patient to have a disease when he does not have the disease, a fire alarm going on indicating a fire when there is no fire (or) an experiment indicating that medical treatment should cure a disease when in fact it does not.

Question 13.
What is the single-tailed test?
Solution:
A single-tailed test or a one-tailed test is a statistical test in which the critical area of a distribution is one-sided so that it is either greater than or less than a certain value, but not both. For the null hypothesis H₀ : µ = 16.91, the alternative hypothesis H₁ : µ > 16.91 or H₁ : µ < 16.91 are one-tailed tests.

Question 14.
A sample of 100 items, draw from a universe with mean value 4 and S.D 3, has a mean value 3.5. Is the difference in the mean significant?
Solution:
Given Sample size n = 100
Sample mean \(\bar{x}\) = 3.5
Population mean µ = 4
Population SD σ = 3
Now, null hypothesis H₀ : µ = 4
Alternative hypothesis H₁ : µ ≠ 4 (Two tail)
We take level of significance α = 5% = 0.05
The table value \(\mathrm{Z}_{\alpha / 2}\) = 1.96
Test statistic

Since the alternative hypothesis is of the two-tailed test we can take |Z| = 1.667. We observe that 1.667 < 1.96 (i.e) |Z| < \(\mathrm{Z}_{\alpha / 2}\). So at 5% level of significance, the null hypothesis H0 is accepted. Therefore, we conclude that there is no significant difference between the sample mean and the population mean.

Question 15.
A sample of 400 individuals is found to have a mean height of 67.47 inches. Can it be reasonably regarded as a sample from a large population with a mean height of 67.39 inches and standard deviation of 1.30 inches?
Solution:
Given Sample size n = 400
Sample mean \(\bar{x}\) = 67.47
Population mean µ = 67.39
Population SD σ = 1.3
Null hypothesis H₀ : µ = 67.39 inches
(the sample has been drawn from the population with mean heights 67.39 inches)
Alternative hypothesis H₁ : µ ≠ 67.39 inches
(the sample has not been drawn from the population with mean height 67.39 inches)
The level of significance α = 5% = 0.05
Test statistic

The significant value or table value \(\mathrm{Z}_{\alpha / 2}\) = 1.96. We see that 1.2308 < 1.96 (i.e) Z < \(\mathrm{Z}_{\alpha / 2}\). Since the calculated value is less than the table value at 5% level of significance, the null hypothesis is accepted. Hence we conclude that the data does not provide us with any evidence against the null hypothesis. Thus, the sample has been drawn from a large population with a mean height of 67.39 inches and S.D 1.3 inches.

Question 16.
The average score on a nationally administered aptitude test was 76 and the corresponding standard deviation was 8. In order to evaluate a state’s education system, the scores of 100 of the state’s students were randomly selected. These students had an average score of 72. Test at a significance level of 0.05 if there is a significant difference between the state scores and the national scores.
Solution:
Given Population mean µ = 76
Population SD σ = 8
Sample size n = 100
Sample mean \(\bar{x}\) = 72
Significance level α = 0.05
Null hypothesis H0 : µ = 76
(i.e) there is no difference between the state scores and the national scores.
Alternative hypothesis H₁ : µ ≠ 76
(i.e) there is a significant difference between the state scores and the nationals scores of the aptitude test.
Test statistic

The significant value or table value \(\mathrm{Z}_{\alpha / 2}\) = 1.96. Comparing the calculated value and table value, we find that |Z| > \(\mathrm{Z}_{\alpha / 2}\) (i.e) 5 > 1.96. So the null hypothesis is rejected and we accept the alternative hypothesis. So we conclude that at the significance level of 5%, there is a difference between the state scores and the national scores of the nationally administered amplitude test.

Question 17.
The mean breaking strength of cables supplied by a manufacturer is 1,800 with a standard deviation of 100. By a new technique in the manufacturing process it is claimed that the breaking strength of the cables has increased. In order to test this claim a sample of 50 cables is tested. It is found that the mean breaking strength is 1,850. Can you support the claim at 0.01 level of significance?
Solution:
Given Population mean µ = 1800
Population SD σ = 100
Sample size n = 50
Sample mean \(\bar{x}\) = 1850
Significance level α = 0.01
Null hypothesis H₀ : µ = 1800
(i.e) the breaking strength of the cables has not increased, after the new technique in the manufacturing process.
Alternative hypothesis H₁ : µ > 1800 (i.e) the new technique was successful.
Test statistic

The table value for the one-tailed test is Zα = 2.33.
Comparing the calculated value and table value, we find that Z > Zα (i.e.) 3.536 > 2.33.

Inference: Since the calculated value is greater than the table value at 1 % level of significance, the null hypothesis is rejected and we accept the alternative hypothesis. We conclude that by the new technique in the manufacturing process the breaking strength of the cables is increased. So the claim is supported at 0.01 level of significance.

Students can download 12th Business Maths Chapter 7 Probability Distributions Ex 7.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Ex 7.2

Question 1.
Define Poisson distribution.
Solution:
Poisson distribution is a discrete frequency distribution which gives the probability of a number of independent events occurring in a fixed time. It is useful for characterizing events with very low probabilities of occurrence within some definite time or space.

Question 2.
Write any 2 examples for Poisson distribution.
Solution:
Examples of Poisson distribution are given by

• The number of printing mistakes per page in a textbook.
• A number of lightning per second.
• The number of bacteria in one cubic centimetre.

Question 3.
Write the conditions for which the Poisson distribution is a limiting case of the binomial distribution.
Solution:
Poisson distribution is a limiting case of binomial distribution under the following conditions:

• the number of trials ‘n’ is indefinitely large i.e, → ∞
• the probability of success ‘p’ in each trial is very small, i.e, p → 0
• np = λ is finite. Thus p = \(\frac{\lambda}{n}\) and q = 1 – \(\frac{\lambda}{n}\), λ > 0

Question 4.
Derive the mean and variance of the Poisson distribution.
Solution:
Let X be a Poisson random variable with parameter λ. The p.m.f is given by



Thus the mean and variance of Poisson distribution are both equal to λ.

Question 5.
Mention the properties of Poisson distribution.
Solution:

1. Poisson distribution is the only distribution in which the mean and variance are equal.
2. The probability that an event occurs in a given time, distance, area or volume is the same.

Question 6.
The mortality rate for a certain disease is 7 in 1000. What is the probability for just 2 deaths on account of this disease in a group of 400? [Given e^-2.8 = 0.06]
Solution:
Let X denote the number of deaths due to the disease
P(death) = \(\frac{7}{1000}\) = 0.007 ⇒ p = 0.007 and n = 400
The value of mean λ = np = (0.007) (400) = 2.8
Hence X follows a Poisson distribution with

So the probability of just 2 deaths on account of this disease in a group of 400 is 0.2352.

Question 7.
It is given that 5% of the electric bulbs manufactured by a company are defective. Using Poisson distribution find the probability that a sample of 120 bulbs will contain no defective bulb.
Solution:
Given p = \(\frac{5}{100}\) = 0.05 and n = 120
⇒ λ = np = (0.05) (120) = 6
Thus X is a Poisson random variable with P (X = x) = \(\frac{e^{-6} 6^{x}}{x !}\)
We want P (no defective bulb) = P (X = 0)
= \(\frac{e^{-6} 6^{0}}{0 !}\)
= e^-6
= 0.0025 (Using exponent table)
Thus the probability that a sample of 120 bulbs will not contain any defective bulb is 0.0025.

Question 8.
A car hiring firm has two cars. The demand for cars on each day is distributed as a Poisson variate, with mean 1.5. Calculate the proportion of days on which
(i) Neither car is used
(ii) Some demand is refused.
Solution:
Let X be the Poisson variable denoting the demand for the cars.
It is given that mean is 1.5 ⇒ λ = 1.5
(i) P (Neither car is used) = P (X = 0) = \(\frac{e^{-1.5}(1.5)^{0}}{0 !}=e^{-1.5}=0.2231\)
(ii) Some demand is refused when demand is more than 2 since the firm has only 2 cars. So we want P (X > 2)
Now P (X > 2) = 1 – P (X ≤ 2)
= 1 – [P(X = 2) + P(X = 1) + P(X = 0)]

Question 9.
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be
(i) no phone at all
(ii) exactly 3 calls
(iii) at least 5 calls.
Solution:
Let X be the Poisson variable denoting the number of phone calls per minute.

P (X = 1) = \(\frac{e^{-2.5}(2.5)}{1 !}\) = (0.08208) (2.5) = 0.2052
Using the above values and P (X = 0) and P (X = 3) from the previous subdivisions in (A) we get,
P(X ≥ 5) = 1 – [0.1336 + 0.2138 + 0.2565 + 0.2052 + 0.08208]
= 1 – 0.89118
= 0.10882

Question 10.
The distribution of the number of road accidents per day in a city is Poisson with mean 4. Find the number of days out of 100 days when there will be
(i) no accident
(ii) at least 2 accidents and
(iii) at most 3 accidents.
Solution:
Let X be the Poisson variable denoting the number of accidents per day.
Given that mean is 4 (i.e,) λ = 4. The p.m.f is given by P(X = x) = \(\frac{e^{-4} 4^{x}}{x !}\)
(i) P (no accident) = P(X = 0) = e^-4 = 0.0183
For 100 days we have 100 × 0.0183 = 1.83 ~ 2
Hence out of 100 days there will be no accident for 2 days.

(ii) P (atleast 2 accidents) = P (X ≥ 2)
= 1 – P (X < 2)
= 1 – [P(X = 1) + P(X = 0)]
= 1 – [e^-4 (4) + e^-4]
= 1 – (0.0183) (5)
= 1 – 0.0915
= 0.9085
For 100 days we have 100 × 0.9085 ~ 91
Hence out of 100 days there will be at least 2 accidents for 91 days.

(iii) P (atmost 3 accidents) = P (X ≤ 3)
= P (X = 0 ) + P (X = 1 ) + P (X = 2) + P (X = 3)
= \(e^{-4}\left[1+\frac{4}{1}+\frac{16}{2}+\frac{64}{6}\right]\)
= (0.0183) [23.6667]
= 0.4331
For 100 days we have 100 × 0.4331 ~ 43
Hence out of 100 days, there will be atmost 3 accidents for 43 days.

Question 11.
Assuming that a fatal accident in a factory during the year is 1/1200, calculate the probability that in a factory employing 300 workers there will be at least two fatal accidents in a year, (given e^-0.25 = 0.7788).
Solution:
Let X denote the number of accidents.
Given that probability of accidents ‘p’ is 1/1200 and n = 300

= 1 – [e^-0.25 + e^-0.25 (0.25)]
= 1 – e^-0.25 (1.25)
= 1 – (0.7788) (1.25)
= 0.0265
Thus the probability that there will be atleast two fatal accidents in a year is 0.0265.

Question 12.
The average number of customers, who appear in a counter of a certain bank per minute is two. Find the probability that during a given minute
(i) No customer appears
(ii) three or more customers appear.
Solution:
Let X denote the number of customers.
Given λ = 2
(i) P (no customer) = P (X = 0)
= \(\frac{e^{-2}(2)^{0}}{0 !}\)
= e^-2
= 0.1353
(ii) P (3 or more customers) = P (X ≥ 3)

Thus during a given minute, the probability that three or more customers appear is 0.3235.

Students can download 12th Business Maths Chapter 8 Sampling Techniques and Statistical Inference Ex 8.1 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 8 Sampling Techniques and Statistical Inference Ex 8.1

Question 1.
What is the population?
Solution:
A population is a set of similar items or events which is of interest for some question or experiment. A population can be specific or vague. Examples of population defined vaguely include the number of newborn babies in Tamil Nadu, a total number of tech startups in India, the average height of all exam candidates, mean weight of taxpayers in Chennai etc. Examples of population defined specifically include a number of fans produced in a particular factory, the number of students in a class, the number of boys and girls in a tuition centre etc.

Question 2.
What is the sample?
Solution:
A sample is a set of data collected from a statistical population by a defined procedure. The elements of a sample are called sample size or sample points. Samples are collected and statistics are calculated from the samples, so that one can make inferences from the sample to the population.

Question 3.
What is statistic?
Solution:
A statistic is used to estimate the value of a population parameter. For instance, we selected a random sample of 100 students from a school with 1000 students. The average height of the sampled students would be an example of a statistic. Examples, sample variance, sample quartiles, sample percentiles, sample moments etc.

Question 4.
Define parameter.
Solution:
A parameter is any numerical quantity that characterizes a given population or some aspect of it. This means the parameter tells us something about the whole population. For example, the population mean µ, variance σ2, population proportion P, population correlation ρ.

Question 5.
What is the sampling distribution of a statistic?
Solution:
Sampling distribution of a statistic is the probability distribution of a given random sample based statistic. It may be considered as the distribution of the statistic for all possible samples from the same population of a given sample size.
Example, the sampling distribution of the mean for n = 2 is given below:

Question 6.
What is the standard error?
Solution:
The standard error (S.E) of a statistic is the standard deviation of its sampling distribution. If the parameter or the statistic is the mean, it is called the standard error of the mean (SEM). The standard error provides a rough estimate of the interval in which the population parameters is likely to fall.

Question 7.
Explain in detail about simple random sampling with a suitable example.
Solution:
(i) Simple random sampling:
In this technique, the samples are selected in such a way that each and every unit in the population has an equal and independent chance of being selected as a sample. Simple random sampling may be done, with or without replacement of the samples selected. In a simple random sampling with replacement, there is a possibility of selecting the same sample any number of times. So, simple random sampling without replacement is followed.
Thus in simple random sampling from a population of N units, the probability of drawing any unit at the first draw is \(\frac{1}{N}\), the probability of drawing any unit in the second draw from among the available (N – 1) units is \(\frac{1}{(N-1)}\), and so on. Several methods have been adopted for random selection of the samples from the population. Of those, the following two methods are generally used and which are described below.

1. Lottery method
This is the most popular and simplest method when the population is finite. In this method, all the items of the population are numbered on separate slips of paper of the same size, shape and colour. They are folded and placed in a container and shuffled thoroughly. Then the required numbers of slips are selected for the desired sample size. The selection of items thus depends on chance.

For example, if we want to select 10 students, out of 100 students, then we must write the names/roll number of all the 100 students on slips of the same size and mix them, then we make a blindfold selection of 10 students. This method is called unrestricted random sampling because units are selected from the population without any restriction. This method is mostly used in lottery draws. If the population or universe is infinite, this method is inapplicable.

2. Table of Random number
When the population size is large, it is difficult to number all the items on separate slips of paper of same size, shape and colour. The alternative method is that of using the table of random numbers. The most practical, easy and inexpensive method of selecting a random sample can be done through “Random Number Table”. The random number table has been so constructed that each of the digits 0, 1, 2,…, 9 will appear approximately with the same frequency and independently of each other.

The various random number tables available are

• L.H.C. Tippett random number series
• Fisher and Yates random number series
• Kendall and Smith random number series
• Rand Corporation random number series.

Tippett’s table of random numbers is most popularly used in practice.

An example to illustrate how Tippett’s table of random numbers may be used is given below. Suppose we have to select 20 items out of 6,000. The procedure is to number all the 6,000 items from 1 to 6,000. A page from Tippett’s table may be selected and the first twenty numbers ranging from 1 to 6,000 are noted down. If the numbers are above 6000, choose the next number ranging from 1 to 6000. Items bearing those numbers will be selected as samples from the population. Making use of the portion of the random number table given, the required random samples are shaded. Here, we consider row-wise selection of random numbers.

Question 8.
Explain the stratified random sampling with a suitable example.
Solution:
Stratified Random Sampling
In stratified random sampling, first divide the population into subpopulations, which are called strata. Then, the samples are selected from each of the strata through random techniques. The collection of all the samples from all strata gives the stratified random samples.

When the population is heterogeneous or different segments or groups with respect to the variable or characteristic under study, then the Stratified Random Sampling method is studied.. First, the population is divided into the homogeneous number of sub-groups or strata before the sample is drawn. A sample is drawn from each stratum at random. Following steps are involved in selecting a random sample in a stratified random sampling method.

(a) The population is divided into different classes so that each stratum will consist of more or less homogeneous elements. The strata are so designed that they do not overlap each other.
(b) After the population is stratified, a sample of a specified size is drawn at random from each stratum using Lottery Method or Table of Random Number Method.

Stratified random sampling is applied in the field of the different legislative areas as strata in election polling, division of districts (strata) in a state etc…

Ex: From the following data, select 68 random samples from the population of the heterogeneous group with a size of 500 through stratified random sampling, considering the following categories as strata.

• Category 1: Lower income class – 39%
• Category 2: Middle income class – 38%
• Category 3: Upper income class – 23%

Solution:

Question 9.
Explain in detail about systematic random sampling with example.
Solution:
Systematic sampling:
In systematic sampling, randomly select the first sample from the first k units. Then every kth member, starting with the first selected sample, is included in the sample.

Systematic sampling is a commonly used technique if the complete and up-to-date list of the sampling units is available. We can arrange the items in numerical, alphabetical, geographical or in any other order. The procedure of selecting the samples starts with selecting the first sample at random, the rest being automatically selected according to some pre-determined ( pattern. A systematic sample is formed by selecting every item from the population, where k refers to the sample interval. The sampling interval can be determined by dividing the size of the population by the size of the sample to be chosen.
That is k = \(\frac{\mathrm{N}}{n}\), where k is an integer.
k = Sampling interval, N = Size of the population, n = Sample size.

Procedure for selection of samples by systematic sampling method
(i) If we want to select a sample of 10 students from a class of 100 students, the sampling interval is calculated as \(k=\frac{N}{n}=\frac{100}{10}=10\)
Thus sampling interval = 10 denotes that for every 10 samples one sample has to be selected.
(ii) The first sample is selected from the first 10 (sampling interval) samples through random selection procedures.
(iii) If the selected first random sample is 5, then the rest of the samples are automatically selected by incrementing the value of the sampling interval (k = 10) i.e., 5, 15, 25, 35, 45, 55, 65, 75, 85, 95.

Ex: Suppose we have to select 20 items out of 6,000. The procedure is to number all the 6,000 items from 1 to 6,000. The sampling interval is calculated as k = \(\frac{N}{n}=\frac{6000}{20}\) = 300. Thus sampling interval = 300 denotes that for every 300 samples one sample has to be selected. The first sample is selected from the first 300 (sampling interval) samples through random selection procedures. If the selected first random sample is 50, then the rest of the samples are automatically selected by incrementing the value of the sampling interval (k = 300) ie,50, 350, 650, 950, 1250, 1550, 1850, 2150, 2450, 2750, 3050, 3350, 3650, 3950, 4250, 4550, 4850, 5150, 5450, 5750. Items bearing those numbers will be selected as samples from the population.

Question 10.
Explain in detail about sampling error.
Solution:
Sampling Errors: Errors, which arise in the normal course of investigation or enumeration on account of chance, are called sampling errors. Sampling errors are inherent in the method of sampling. They may arise accidentally without any bias or prejudice.

Sampling Errors arise primarily due to the following reasons:

• Faulty selection of the sample instead of the correct sample by defective sampling technique.
• The investigator substitutes a convenient sample if the original sample is not available while investigation.
• In area surveys, while dealing with borderlines it depends upon the investigator whether to include them in the sample or not. This is known as Faulty demarcation of sampling units.

Question 11.
Explain in detail about the non-sampling error.
Solution:
Non-Sampling Errors:
The errors that arise due to human factors which always vary from one investigator to another in selecting, estimating or using measuring instruments( tape, scale) are called Non-Sampling errors.
It may arise in the following ways:

• Due to negligence and carelessness of the part of either investigator or respondents.
• Due to the lack of trained and qualified investigators.
• Due to the framing of a wrong questionnaire.
• Due to applying the wrong statistical measure
• Due to incomplete investigation and sample survey.

Question 12.
State any two merits of simple random sampling.
Solution:

• In simple random sampling personal bias is completely eliminated.
• This method is economical as it saves time, money and labour.

Question 13.
State any three merits of stratified random sampling.
Solution:

• A random stratified sample is superior to a simple random sample because it ensures representation of all groups and thus it is more representative of the population which is being sampled.
• A stratified random sample can be kept small in size without losing its accuracy.
• It is easy to administer if the population under study is sub-divided.

Question 14.
State any two demerits of systematic random sampling.
Solution:

• Systematic samples are not random samples.
• If N is not a multiple of n, then the sampling interval (k) cannot be an integer, thus sample selection becomes difficult.

Question 15.
State any two merits for systematic random sampling.
Solution:
Merits of systematic sampling are given below:

• This method distributes the sample more evenly over the entire listed population.
• The time and work are reduced much.

Question 16.
Using the following Tippet’s random number table.

Draw a sample of 10 three-digit numbers which are even numbers.
Solution:
There are many ways to select a sample of 10 3-digit even numbers. From the table, start from the first number and move along the column. Select the first three digits as the number. If it is an odd number, move to the next number. The selected sample is 416, 664, 952, 748, 524, 914, 154, 340, 140, 276.

Question 17.
A wholesaler in apples claims that only 4 % of the apples supplied by him are defective. A random sample of 600 apples contained 36 defective apples. Calculate the standard error concerning good apples.
Solution:
Sample size = 600
No. of defective apples = 36
Sample proportion p = \(\frac{36}{600}\) = 0.06
Population proportion P = probability of defective apples = 4% = 0.04
Q = 1 – P = 1 – 0.04 = 0.96
The S.E for sample proportion is given by S.E

Question 18.
A sample of 1000 students whose mean weight is 119 lbs (pounds) from a school in Tamil Nadu State was taken and their average weight was found to be 120 lbs with a standard deviation of 30 lbs. Calculate the standard error of the mean.
Solution:
Given n = 1000, \(\bar{X}\) = 119, σ = 30

Question 19.
A random sample of 60 observations was drawn from a large population and its standard deviation was found to be 2.5. Calculate the suitable standard error that this sample is taken from a population with standard deviation 3?
Solution:
Given sample size n = 60
Sample standard deviation = 2.5
Population standard deviation σ = 3
The S.E is given by

Question 20.
In a sample of 400 population from a village 230 are found to be eaters of vegetarian items and the rest non-vegetarian items. Compute the standard error assuming that both vegetarian and non-vegetarian foods are equally popular in that village?
Solution:
Given sample size 400 and 230 are vegetarian eaters.
So sample proportionp = \(\frac{230}{400}\) = 0.575
Population proportion P = Prob (vegetarian eaters from the village) = \(\frac{1}{2}\)
(Since vegetarian and non-vegetarian foods are equally popular)
Q = 1 – P = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)

Students can download 12th Business Maths Chapter 7 Probability Distributions Ex 7.1 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Ex 7.1

Question 1.
Define Binomial distribution.
Solution:
A random variable X is said to follow a binomial distribution with parameter ‘n’ and ‘p’ if it assumes only non-negative value and its probability mass function is given by

Question 2.
Define Bernoulli trials.
Solution:
A random experiment whose outcomes are of two types namely success S and failure F, occurring with probabilities p and q, is called a Bernoulli trial.
Example 1, Tossing of a coin (Head or Tail)
Example 2, Writing an exam (Pass or Fail)

Question 3.
Derive the mean and variance of binomial distribution.
Solution:
Let X be a random variable with the Binomial distribution.
The probability function of X is

Question 4.
Write down the conditions for which the binomial distribution can be used.
Solution:
The binomial distribution can be used under the following conditions:

• The number of trials (or) observations ‘n’ is fixed (finite).
• Each observation is independent of each other.
• In every trial, there are only two possible outcomes – success or failure.
• The probability of success ‘p’ is the same for each outcome.

Question 5.
Mention the properties of the binomial distribution.
Solution:
Property 1:
The binomial distribution is symmetrical when the probability of success ‘p’ is 0.5 (or) when a number of trials ‘n’ is very large. In other words, if p = q = 1/2, the distribution is symmetric about the median. If p ≠ q, then it is skewed distribution, (p < 0.5 → positively skewed, p > 0.5 → negatively skewed)

Property 2:
The variance is less than mean (i,e,) npq < np

Question 6.
If 5% of the items produced turn out to be defective, then find out the probability that out of 10 items selected at random there are
(i) exactly three defectives
(ii) at least two defectives
(iii) exactly 4 defectives
(iv) find the mean and variance
Solution:
Let p be the probability of a defective item.
Given that, p = 5% = \(\frac{5}{100}\) = 0.05
So q = 1 – p = 1 – 0.05 = 0.95. Also n = 10.
Let X be the random variable which follows the binomial distribution. Then X ~ B (10, 0.05)
(i) P(exactly three defectives) = P(X = 3)

(ii) P(atleast two defectives) = P (X ≥ 2) = 1 – P (X < 2)
= 1 – [P(X = 1) + P(X = 0)]

(iii) P(exactly 4 defectives) = P(X = 4)

(iv) We know that mean = np = (10) (0.05) = 0.5
Variance = npq = (10) (0.05) (0.95) = 0.475

Question 7.
In a particular university, 40% of the students are having newspaper reading habit. Nine university students are selected to find their views on reading habit. Find the probability that
(i) none of those selected has newspaper reading habit
(ii) all those selected have newspaper reading habit
(iii) at least two-third have newspaper reading habit.
Solution:
Let X be the binomial random variable which denotes the number of students having newspaper reading habit.
It is given that 40% of students have reading habit.
p = \(\frac{40}{100}\) = 0.4 and q = 1 – 0.4 = 0.6
(i) P(none of selected have newspaper reading habit) = P(X = 0)
Now X ~ B (9, 0.4)
The p.m.f is given by P (X = x) = p (x) = \(^{9} \mathrm{C}_{x}(0.4)^{x}(0.6)^{9-x}\)
P(X = 0) = \(^{9} \mathrm{C}_{0}(0.4)^{0}(0.6)^{9}\) = (0.6)⁹ = 0.01008 (using calculator)
(ii) P (all selected have newspaper reading habit)
= P (X = 9)
= \(^{9} \mathrm{C}_{9}(0.4)^{9}(0.6)^{0}\)
= (0.4)⁹
= 0.000262 (using calculator)
(iii) P (at least two third have newspaper reading habit) = P (X ≥ 6)
{9 students are selected. Two third of them means \(\frac{2}{3}\) (9) = 6}
Now P (X ≥ 6) = P (X = 6) + P (X = 7) + P (X = 8) + P (X = 9)

= (84) (0.004096) (0.216) + 36 (0.0016384) (0.36) + 9 (0.00065536) (0.6) + 0.000262
= 0.074318 + 0.021234 + 0.003539 + 0.000262
= 0.099353

Question 8.
In a family of 3 children, what is the probability that there will be exactly 2 girls?
Solution:
Let X denote the binomial variable which denotes the number of girls.
Given that n = 3 and p = q = \(\frac {1}{2}\)

Hence the probability that there will be exactly 2 girls is. 0.375.

Question 9.
Defects in yarn manufactured by a local mill can be approximated by a distribution with a mean of 1.2 defects for every 6 metres of length. If lengths of 6 metres are to be inspected, find the probability of fewer than 2 defects.
Solution:
Given mean np = 1.2 and n = 6
p = \(\frac{1.2}{6}\) = 0.2, q = 1 – 0.2 = 0.8
Let X be a binomial variable denoting the number of defects, (i.e,) X ~ B (6, 0.2)
p.m.f is given by P (X = x) = \(^{6} \mathrm{C}_{x}(0.2)^{x}(0.8)^{6-x}\)
We want P(X < 2) = P(X = 0) + P (X = 1)
= \(^{6} \mathrm{C}_{0}(0.2)^{0}(0.8)^{6}+^{6} \mathrm{C}_{1}(0.2)^{1}(0.8)^{5}\)
= (0.8)⁶ + 6 (0.2) (0.8)⁵
= 0.262144 + 0.393216
= 0.65536
Thus if lengths of 6 metres are to be inspected, the probability of less than 2 defects is 0.65536.

Question 10.
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random
(i) exactly one will be defective
(ii) none will be defective
(iii) at most 2 will be defective
Solution:
Let X be the random variable denoting the number of defective bolts.
The probability of defective bolts p = \(\frac{18}{100}\) = 0.18 ⇒ q = 0.82.
Also n = 4
The p.m.f is P (X = x ) = \(^{4} \mathrm{C}_{x}(0.18)^{x}(0.82)^{4-x}\)
(i) P (exactly one defective) = P(X = 1)
= \(^{4} \mathrm{C}_{1}(0.18)^{1}(0.82)^{3}\)
= 4 (0.18) (0.82)³
= 0.3969
(ii) P (no defective) = P(X = 0)
= \(^{4} \mathrm{C}_{0}(0.18)^{0}(0.82)^{4}\)
= (0.82)⁴
= 0.45212
(iii) P (atmost 2 defective) = P(X ≤ 2)
= P(X = 2) + P(X = 1) + P(X = 0)
= \(^{4} \mathrm{C}_{2}\) (0.18)² (0.82)² + 0.3969 + 0.45212
= 0.1307 + 0.3969 + 0.45212
= 0.97972

Question 11.
If the probability of success is 0.09, how many trials are needed to have a probability of at least one success as 1/3 or more?
Solution:
Given p = 0.09 (success)
q = 0.91 (failure)
We have to find number of trials ‘n.’
According to the problem,
P(X ≥ 1 ) > \(\frac{1}{3}\)
(We must have atleast one success)
1 – P(X < 1) > \(\frac{1}{3}\)
1 – P(X = 0) > \(\frac{1}{3}\)
(or) P(X = 0) < \(\frac{2}{3}\)
Using p.m.f, we have,
\(^{n} \mathrm{C}_{0}(0.09)^{0}(0.91)^{n}<\frac{2}{3}\)
(0.91)n < \(\frac{2}{3}\)
we can use log tables to calculate (or) by trial method try for n = 1, 2,…… using calculator.
We observe that (0.91)5 < \(\frac{2}{3}\). Thus we need minimum 5 trial or more.

Question 12.
Among 28 professors of a certain department, 18 drive foreign cars and 10 drive locally made cars. If 5 of these professors are selected at random, what is the probability that at least 3 of them drive foreign cars?
Solution:
Here n = 5, p = \(\frac{18}{28}=\frac{9}{14}\), q = \(\frac{10}{28}=\frac{5}{14}\)
(i.e.) the probability of professors driving foreign cars p = \(\frac{9}{14}\), and those who drive local cars q = \(\frac{5}{14}\).
Let X be the Binomial random variable denoting persons who drive foreign cars.
Then the p.m.f of X is given by P (X = x) = \(^{5} \mathrm{C}_{x}\left(\frac{9}{14}\right)^{x}\left(\frac{5}{14}\right)^{5-x}\)
We want P (X ≥ 3) = P (X = 3) + P (X = 4) + P (X = 5)

Question 13.
Out of 750 families with 4 children each, how many families would be expected to have
(i) at least one boy
(ii) at most 2 girls
(iii) and children of both sexes?
Assume equal probabilities for boys and girls.
Solution:
Given that 750 families are considered each with 4 children. We will find the probabilities for one particular family and then multiply by 750.
In other words, n = 4, p = q = \(\frac{1}{2}\) (since boy and girl child have equal probability).
Let X denote the binomial random variable which denotes the number of boys in the family.

So out of 750 families the number of families would be expected to have atleast one boy is \(\frac{15}{16}\) × 750 = 703
(ii) P(atmost 2 girls) = P(2G, 2B) + P(1G, 3B) + P(0G, 4B)
= P(X = 2) + P(X = 3) + P(X = 4)

Thus out of 750 families, 516 families would be expected to have atmost 2 girls.
(iii) P(children of both sexes) = P(both boys and girls)
Out of 4 children the sample space is given by {BGGG, BBGG, BBBG}and each case in any order.
So we require P(1B, 3G) + P(2B, 2G) + P(3B, 1G)
(i.e,) P(X = 1) + P(X = 2) + P(X = 3)

Thus out of 750 families, 656 families would be expected to have children of both sexes.

Question 14.
Forty percent of business travellers carry a laptop. In a sample of 15 business travelers
(i) what is the probability that 3 will have a laptop?
(ii) what is the probability that 12 of the travelers will not have a laptop?
(iii) what is the probability that atleast three of the travelers have a laptop?
Solution:
Let X be the binomial variables which denotes the number of business travellers having a laptop.
Given that n = 15 and P = 40% = 0.4. So q = 1 – 0.4 = 0.6. Thus X ~ B (15, 0.4).
The p.m.f of X is given by P (X = x) = \(^{15} \mathrm{C}_{x}(0.4)^{x}(0.6)^{15-x}\)
(i) P(3 travellers will have a laptop) = P (X = 3)

Note: The calculation can be done by method of logarithms also.
P(X = 3) = 455 (0.064) (0.002177) = 0.0634
(ii) P(12 of the travellers will not have a laptop)
= P(15 – 12 = 3 will have a laptop)
= P(X = 3) = 0.0634 (from the previous subdivision)
(iii) P(atleast three of the travellers have a laptop)

Using (0.6)¹² = 0.002177 from the previous subdivision, we have
= 1 – (0.002177) [10.08 + 2.16 + 0.216]
= 1 – (0.002177) (12.456)
= 1 – 0.02712
= 0.9729

Question 15.
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of 2 successes.
Solution:
Let p be the probability of getting a doublet, (i.e,) probability of success. When we throw a pair of dice there are 36 possibilities. The number of doublets is 6 [(1, 1) (2, 2), (3, 3) (4, 4) (5, 5) (6, 6)].
So p = \(\frac{6}{36}=\frac{1}{6}\)
q = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
Let X be the random variable denoting the number of doublet in 4 throws.
Then X ~ B (4, \(\frac{1}{6}[/latex)]

Hence the probability of 2 successes is [latex]\frac{25}{216}\)

Question 16.
The mean of a binomial distribution is 5 and the standard deviation is 2. Determine the distribution.
Solution:
Given mean = 5 and standard deviation = 2
(i.e,) np = 5 and √npq = 2 ⇒ npq = 4
5q = 4 ⇒ q = \(\frac{4}{5}\), p = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
Again np = 5 gives \(\frac{n}{5}\) = 5 ⇒ n = 25
So the p.m.f of the distribution is given by P (X = x) = \(\left(\begin{array}{c}
25 \\
x
\end{array}\right)\left(\frac{1}{5}\right)^{x}\left(\frac{4}{5}\right)^{25-x}\)

Question 17.
Determine the binomial distribution for which the mean is 4 and variance 3. Also find P(X = 15)
Solution:
Given mean = 4 and variance is 3.
(i.e,) np = 4 and npq = 3

Question 18.
Assume that a drug causes a serious side effect at a rate of three patients per one hundred. What is the probability that at least one person will have side effects in a random sample of ten patients taking the drug?
Solution:
According to the problem, n = 10, p = \(\frac{3}{100}\) = 0.03 where p is the probability that a drug causes side effect. Now X ~ B (10, 0.03). The p.m.f is given by

Thus the probability that at least one person will have side effects is 0.2626.

Question 19.
Consider five mice from the same litter, all suffering from Vitamin A deficiency. They are fed a certain dose of carrots. The positive reaction means recovery from the disease. Assume that the probability of recovery is 0.73. What is the probability that at least 3 of the 5 mice recover?
Solution:
Given n = 5 and the probability of recovery p = 0.73.
So q = 1 – 0.73 = 0.27. X ~ B (5, 0.73).
The p.m.f of X is given by

Thus the probability that at least 3 of the 5 mice recover is 0.8743.

Question 20.
An experiment succeeds twice as often as it fails, what is the probability that in the next five trials there will be
(i) three successes and
(ii) at least three successes.
Solution:
Given a number of trials n = 5.
Let P be the probability of success and q be the probability of failure. It is given that p = 2q.

Students can download 12th Business Maths Chapter 7 Probability Distributions Additional Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Additional Problems

Choose the correct answer:

Question 1.
If X is a poisson variate with P (X = 1) = P (X = 2), the mean of the poisson variate is equal to _____
(a) 1
(b) 2
(c) -2
(d) 3
Answer:
(b) 2
Hint:
P(X = 1) = P(X = 2)

Question 2.
If ‘λ’ is the mean of the Poisson distributions, then P (X = 0) is given by ________
(a) \(e^{-\lambda}\)
(b) \(e^{\lambda}\)
(c) e
(d) \(\lambda^{-e}\)
Answer:
(a) \(e^{-\lambda}\)
Hint:

Question 3.
A larger standard deviation for a normal distribution with an unchanged mean indicates that the curve becomes, ____
(a) narrower and more peaked
(b) flatter and wider
(c) more skewed to the right
(d) more skewed to the left
Answer:
(b) flatter and wider

Question 4.
If X ~ N (0, 4), the value of P(|X| ≥ 2.2) is ______
(a) 0.2321
(b) 0.8438
(c) 0.2527
(d) 0.2714
Answer:
(d) 0.2714
Hint:
P (|X| ≥ 2.2)
= P (X > 2.2) + P (X < -2.2)
= P(Z > \(\frac{2.2-0}{2}\)) + P(Z < \(\frac{-2.2-0}{2}\))
= P(Z > 1.1) + P(Z < -1.1)
= 2 P(Z > 1.1) (by symmetry)
= 2[0.5 – P(0 < Z < 1.1)]
= 2 [0.5 – 0.3643]
= 0.2714

Question 5.
For a binomial distribution.

1. If n = 1, then E(X) is ________
2. The variance is always ________
3. Successive trials are ______
4. Negatively skewed when _______
5. Number of parameters is _______
6. n = 10, p = 0.3, variance is _______
7. Is symmetrical when ______
8. n = 6, p = 0.9, P (X = 7) is _______
9. Mean, median and mode will be equal when ______

Answer:

1. p
2. less than mean
3. independent
4. p > \(\frac {1}{2}\)
5. two
6. 2.1
7. p = q
8. zero
9. p = 0.5

Question 6.
For a Normal distribution

1. The parameters which controls the flatness of the curve is _____ & ______
2. If Y = 5X + 10 and X ~ N (10, 25), then mean of Y is _______
3. Normal curve is asymptotic to the ________
4. The median corresponds to the value of Z = _______
5. The area under the normal curve on either side of mean is _______

Answer:

1. µ, σ
2. 60
3. X-axis
4. µ
5. 0.5

Question 7.
Heights of college girls follows a normal distribution with mean 65 inches and a standard deviation of 3 inches. About what proportion of girls are between 65 and 67 inches tall?
(a) 0.75
(b) 0.5
(c) 0.25
(d) 0.17
Answer:
(c) 0.25
Hint:
P (65 < X < 67)
= P(\(\frac{65-65}{3}\) < Z < \(\frac{67-65}{3}\))
= P(0 < Z < 67)
= 0.2486 ~ 0.25

Question 8.
Which one of these is a binomial random variable?
(a) time is taken by a randomly chosen student to complete an exam
(b) number of books bought by a randomly chosen student
(c) number of women taller than 150 cm in a random sample of 10 women
(d) number of CD’s a randomly selected person owns
Answer:
(c) number of women taller than 150 cm in a random sample of 10 women

Question 9.
Pulse rates of adult men follows a normal distribution with a mean of 70 and a standard deviation of 8. Which choice tells how to find the proportion of men that have a pulse rate greater than 78?

(a) find the area to the left of Z = 1 under the normal curve
(b) find the area between Z = -1 and Z = 1 under the standard normal curve
(c) find the area to the right of Z = 1 under the standard normal curve
(d) find the area to the right of Z = -1 under the standard normal curve
Answer:
(c) find the area to the right of Z = 1 under the standard normal curve
Hint:
P(X > 78) = P(Z > \(\frac{78-70}{8}\)) = P(Z > 1)

2 Mark Questions

Question 1.
The probability that a radio manufactured by a company will be defective is \(\frac{1}{10}\). If 15 such radios are inspected, find the probability that exactly 3 will be defective.
Solution:
Given n = 15, p = \(\frac{1}{10}\) = 0.1, q = 0.9 10
Let X be the binomial variable, denoting the number of radios.
We want probability of exactly 3 defectives, (i.e) P (X = 3)
Now P (X = 3) = \(^{15} \mathrm{C}_{3}(0.1)^{3}(0.9)^{12}\)
= 455 (0.001) [(0.9)⁴]³
= (455) (0.001) (0.6561)³
= 0.1285

Question 2.
The probability that a bulb produced in a factory will fuse after 10 days is 0.05. Find the probability that out of 5 such bulbs, not more than 1 will fuse after 400 days of use.
Solution:
Given that X ~ B (5, 0.05)
(i.e.) n = 5, p = 0.05, q = 0.95
P(X ≤ 1) = P(X = 0) + P(X = 1)
= \(^{5} \mathrm{C}_{0}(0.05)^{0}(0.95)^{5}+^{5} \mathrm{C}_{1}(0.05)^{1}(0.95)^{4}\)
= (0.95)⁵ + 5 (0.05) (0.95)⁴
= (0.95)⁴ + [0.95 + 0.25]
= 0.9774

Question 3.
The number of traffic accidents that occur in a particular road follows a Poisson distribution with a mean of 9.4. Find the probability that less than two accidents will occur on this road during a randomly selected month.
Solution:
Let X be the Poisson variate with mean λ = 9.4.
Now P(X < 2) = P (X = 0) + P (X = 1)
= \(e^{-9.4}\) [1 + 9.4]
= \(e^{-9.4}\) (10.4)
= 0.00086

Question 4.
What is the probability of getting 2 Sundays out of 15 days selected at random?
Solution:

Question 5.
Find the mean and standard deviation of a Poisson variate X which satisfies the condition P(X = 2 ) = P(X = 3)
Solution:
P(X = 2 ) = P(X = 3)
\(\frac{e^{-\lambda} \lambda^{2}}{2 !}=\frac{e^{-\lambda} \lambda^{3}}{3 !}\)
1 = \(\frac{\lambda}{3}\) (or) λ = 3
Variance for Poisson distribution is λ = 3. Hence s.d = √3

Question 6.
Between 5 to 6 p.m., the average number of phone calls per minute is 4. What is the probability that there is no phone call during a minute?
Solution:
Let X be the Poisson variate denoting the number of phone calls per minute.
Given that mean λ = 4. We want P(X = 0)
Now P(X = 0) = \(\frac{e^{-4} \lambda^{0}}{0 !}\) = e^-4 = 0.0183

Question 7.
2% cars are defective. What is the probability that one of 150 cars, there is exactly one defective car?
Solution:
Let X be the Poisson variate denoting the number of defective cars. The mean λ is given by
λ = \(\frac {2}{100}\) × 150 = 3
So P(X = 1) = \(\frac{e^{-3}(3)^{1}}{1 !}\) = 3e^-3 = 0.1494

Question 8.
What is the standard deviation of the number of recoveries among 48 patients, the probability of recovering is 0.75.
Solution:
Given n = 48, p = 0.75, q = 0.25
This is a binomial distribution.
The variance is given by Var (X) = npq
= (48) (0.75) (0.25)
= 9 .
So the standard deviation is √9 = 3

3 and 5 Mark Questions

Question 1.
What is the probability of success of the binomial distribution satisfying the following condition: 4P(X = 4) = P(X = 2) and having other parameter as 6?
Solution:
Given n = 6, 4P(X = 4) = P(X = 2).
We have to find p.

Question 2.
Wool fibre breaking strengths are normally distributed with mean µ = 23.56 and S.D σ = 4.55. What proportion of fibres would have a breaking strength of 14.45 or less?
Solution:

Let X be the normal variable denoting the breaking strengths.
We want to find
P(X ≤ 14.45) = P(Z ≤ \(\frac{14.45-23.56}{4.55}\)) = P(Z ≤ -2.00)
By Symmetry,
P(Z ≤ -2) = P(Z ≥ 2)
= 0.5 – P(0 ≤ Z ≤ 2)
= 0.5 – 0.4772
= 0.0228
Hence the proportion of fibres with a breaking strength of 14.45 or less is 2.28%

Question 3.
The finish times for marathon runners during a race are normally distributed with a mean of 195 minutes and a standard deviation of 25 minutes.
(a) What is the probability that a runner will complete the marathon within 3 hours?
(b) Calculate to the nearest minute, the time by which the first 8% runners have completed the marathon?
(c) What proportion of the runners will complete the marathon between 3 hours and 4 hours?
Solution:
Let X be the normal variate denoting the finish time of the marathon runners.
Given the mean µ = 195 and s.d σ = 25
(a) P(X ≤ 3 hours)
= P(X ≤ 180 minutes)
= P(Z ≤ \(\frac{180-195}{25}\))
= P(Z ≤ -0.6)
By symmetry
P(Z ≤ -0.6)
= P(Z ≤ 0.6)
= 0.5 – P(0 ≤ Z ≤ 0.6)
= 0.5 – 0.2258
= 0.2742
(i.e) Probability of a runner taking less than 3 hours is 0.2742

(b) Given the probability is 8% = 0.08
P (Z ≥ z) = 0.08
0.5 – P(0 ≤ Z ≤ z) = 0.08
P(0 ≤ Z ≤ z) = 0.42
z = 1.41 (from normal tables)
Hence \(\frac{X-195}{25}\) = -1.41
X = 25 (-1.41) + 195 = 159.75 = 160 minutes

(c) P(3 hours < X < 4 hours)
= P (180 min < X < 240 min)
= P(\(\frac{180-195}{25}\) < Z < \(\frac{240-195}{25}\))
= P(-0.6 < Z < 1.8)
= P (-0.6 < Z < 0) + P (0 < Z < 1.8)
= P(0 < Z < 0.6) + P(0 < Z < 1.8)
= 0.2258 + 0.4641
= 0.6899
Hence the proportion of runners taking between 3 hours and 4 hours is 68.99%

Question 4.
The probability that a driver must stop at any one traffic light is 0.2. There are 15 sets of traffic lights on the journey.
(а) What is the probability that a student must stop at exactly 2 of the 15 sets of traffic lights?
(b) What is the probability that a student will be stopped at 1 or more of the 15 sets of traffic lights?
Solution:
Let X be the binomial random variable denoting the number of traffic lights.
Given n = 15, p =0.2, q = 0.8

Question 5.
A radioactive source emits 4 particles on average during a five-second period.
(а) Calculate the probability that it emits 3 particles during a five-second period.
(b) Find the probability that it emits at least one particle during a 5 second period.
(c) During a 10 second period, what is the probability that 6 particles are emitted?
Solution:
Let X be the Poisson variable denoting the number of particles emitted.
Given the mean λ = 4

Question 6.
Given that X ~ B (n, p) and E(X) = 24, Var(X) = 8, find the values of n and p.
Solution:
We know E(X) = np = 24 and Var(X) = npq = 8

Question 7.
Given that X ~ N (6, 4), find the values of ‘a’ and ‘b’ such that P (X ≤ a) = 0.6500 and P(X ≤ b) = 0.8200
Solution:

Students can download 12th Business Maths Chapter 6 Random Variable and Mathematical Expectation Miscellaneous Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Miscellaneous Problems

Question 1.
The probability function of a random variable X is given by

Evaluate the following probabilities.
(i) P(X ≤ 0)
(ii) P(X < 0)
(iii) P(|X| ≤ 2)
(iv) P(0 ≤ X ≤ 10)
Solution:
(i) P(X ≤ 0) = P (X = 0) + P (X = -2)
\(=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\)
(ii) P(X < 0) = P (X = – 2) = \(\frac{1}{4}\)
(iii) P(|X| ≤ 2) = P(-2 ≤ X ≤ 2)
= P(X = -2) + P(X = -1) + P(X = 0) + P(X = 1) + P(X = 2)
= \(\frac{1}{4}\) + 0 + \(\frac{1}{4}\) + 0 + 0
= \(\frac{1}{2}\)
(iv) P(0 ≤ X ≤ 10) = P(X = 0) + P(X = 10) + 0
\(=\frac{1}{4}+\frac{1}{2}=\frac{3}{4}\)

Question 2.
Let X be a random variable with cumulative distribution function.

(a) Compute: (i) P(1 ≤ X ≤ 2) and (ii) P(X = 3).
(b) Is X a discrete random variable? Justify your answer.
Solution:
(a) (i) P(1 ≤ X ≤ 2) = F(2) – F(1)

(a) (ii) P(X = 3) = 0. The given random variable is continuous r.v.
Hence the probability for a particular value of X is zero.
(b) X is not discrete since the cumulative distribution function is a continuous function. It is not a step function.

Question 3.
The p.d.f. of X is defined as

Find the value of k and also find P(2 ≤ X ≤ 4).
Solution:

Question 4.
The probability distribution function of a discrete random variable X is

where k is some constant.
Find (a) k and (b) P(X > 2).
Solution:
(a) Given X is a discrete random variable.
The probability distribution can be written as

We know that Σp(x) = 1
⇒ 2k + 3k + 4k = 1
⇒ 9k = 1
⇒ k = 1/9
(b) P(X > 2) = P(X = 3) + P(X = 5)
= 3k + 4k
= 7k
= \(\frac{7}{9}\)

Question 5.
The probability density function of a continuous random variable X is

where a and b are some constants.
Find (i) a and b if E(X) = \(\frac{3}{5}\)
(ii) Var(X)
Solution:
Given that X is a continuous random variable and f(x) is density function.

Question 6.
Prove that if E(X) = 0, then V(X) = E(X²).
Solution:
Given E(X) = 0. To show V(X) = E (X²)
We know that Var (X) = E(X²) – [E(X)]²
So if E(X) = 0, Var (X) = E(X²)
From the definition of the variance of X also we can see the result.
Var(X) = Σ[x – E(x)]² p(x)
If E (X) = 0, then V(X) = Σ x² p(x) = E(X²)

Question 7.
What is the expected value of a game that works as follows: I flip a coin and if tails pay you ₹ 2; if heads pay you ₹ 1. In either case, I also pay you ₹ 50.
Solution:
Let X be the expected value of the game.
The probability distribution is given by,

Question 8.
Prove that
(i) V(aX) = a² V(X)
(ii) V(X + b) = V(X)
Solution:
(i) To show V(aX) = a² V(X)
We know V(X) = E(X²) – [E(X)]²
So V(aX) = [E(a² X²)] – [E(aX)]²
= a² E(X²) – [aE(X)]²
= a² E(X²) – a² [E(X)]²
= a² {{E(X²) – [E(X)]²}
= a² V(X)

(ii) V(X + b) = V(X)
LHS = V(X + b) = E[(X + b)²] – {E(X + b)}²
= E [X² + 2bX + b²] – [E(X) + b]²
= E(X²) + 2bE(X) + b² – [(E(X))² + b² + 2bE(X)]
= E(X²) + 2bE(X) + b² – [E(X)]² – b² – 2bE(X)
= E(X²) – [E(X)]²
= V(X)
= RHS

Question 9.
Consider a random variable X with p.d.f

Find E(X) and V(3X – 2).
Solution:

Question 10.
The time to failure in thousands of hours of an important piece of electronic equipment used in a manufactured DVD player has the density function.

Find the expected life of this piece of equipment.
Solution:
Let X be the random variable denoting the life of the piece of equipment.

Thus the expected life of the piece of equipment is \(\frac{1}{2}\) hrs (in thousands).

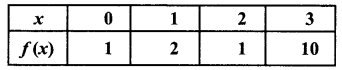
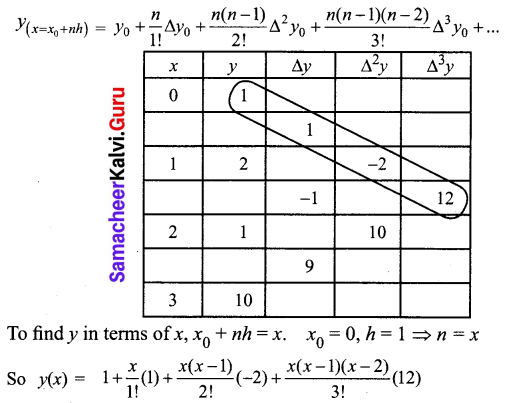
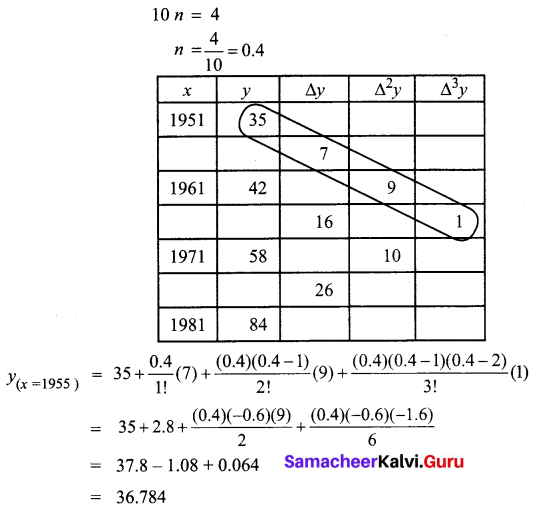
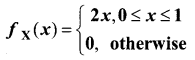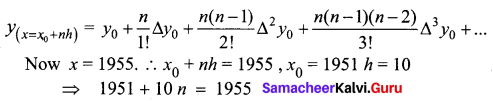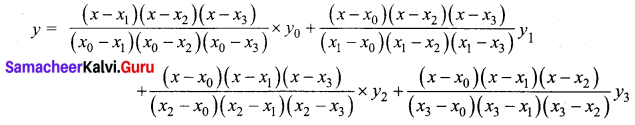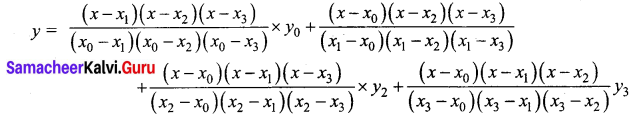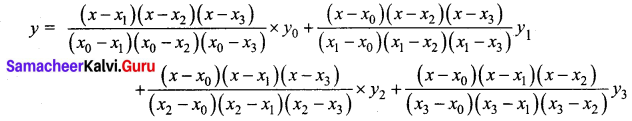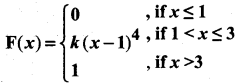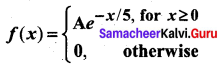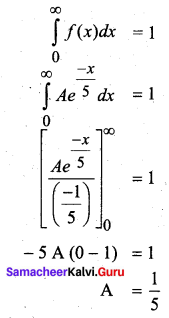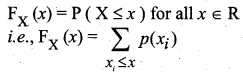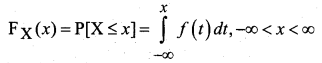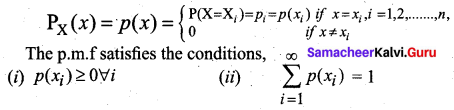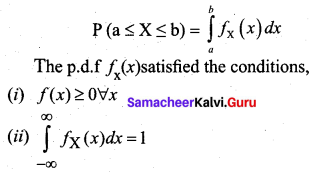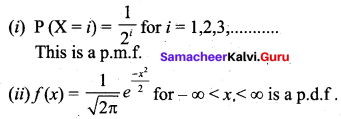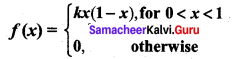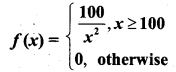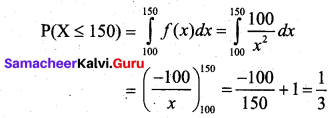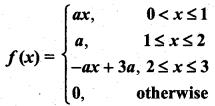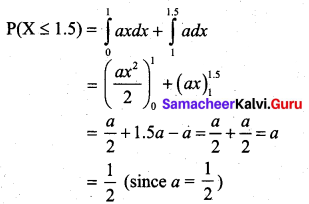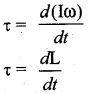Students can download 12th Business Maths Chapter 6 Random Variable and Mathematical Expectation Ex 6.3 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Ex 6.3

Choose the correct answer:

Question 1.
The value which is obtained by multiplying possible values of a random variable with a probability of occurrence and is equal to the weighted average is called ______
(a) Discrete value
(b) Weighted value
(c) Expected value
(d) Cumulative value
Answer:
(c) Expected value

Question 2.
Demand of products per day for three days are 21, 19, 22 units and their respective probabilities are 0.29, 0.40, 0.35. Profit per unit is 0.50 paisa then expected profits for three days are _______
(a) 21, 19, 22
(b) 21.5, 19.5, 22.5
(c) 0.29, 0.40, 0.35
(d) 3.045, 3.8, 3.85
Answer:
(d) 3.045, 3.8, 3.85
Hint:
The expected profit for three days are as follows:
For day 1 ⇒ 21 × 0.29 × 0.5 = 3.045
For day 2 ⇒ 19 × 0.4 × 0.5 = 3.8
For day 3 ⇒ 22 × 0.35 × 0.5 = 3.85

Question 3.
Probability which explains x is equal to or less than particular value is classified as _______
(a) discrete probability
(b) cumulative probability
(c) marginal probability
(d) continuous probability
Answer:
(b) cumulative probability

Question 4.
Given E(X) = 5 and E(Y) = -2, then E(X – Y) is _______
(a) 3
(b) 5
(c) 7
(d) -2
Answer:
(c) 7
Hint:
E(X – Y) = E(X) – E (Y) = 5 – (-2) = 7 .

Question 5.
A variable that can assume any possible value between two points is called _______
(a) discrete random variable
(b) continuous random variable
(c) discrete sample space
(d) random variable
Answer:
(b) continuous random variable

Question 6.
A formula or equation used to represent the probability distribution of a continuous random variable is called ______
(a) probability distribution
(b) distribution function
(c) probability density function
(d) mathematical expectation
Answer:
(c) probability density function

Question 7.
If X is a discrete random variable and p(x) is the probability of X, then the expected value of this random variable is equal to ________
(a) Σ f(x)
(b) Σ[x + f(x)]
(c) Σ f(x) + x
(d) ΣxP(x)
Answer:
(d) ΣxP(x)

Question 8.
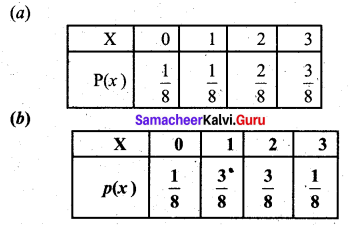
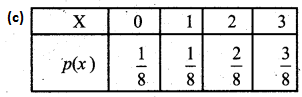
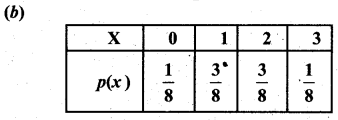
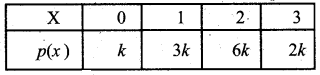
Which of the following is not possible in probability distribution?
(a) Σ p(x) ≥ 0
(b) Σ p(x) = 1
(c) Σ xp(x) = 2
(d) p(x) = -0.5
Answer:
(d) p(x) = -0.5
Hint:
p(x) = -0.5 is not possible since the probability cannot be negative.

Question 9.
If c is a constant, then E(c) is ________
(a) 0
(b) 1
(c) c f(c)
(d) c
Answer:
(d) c

Question 10.
A discrete probability distribution may be represented by ______
(a) table
(b) graph
(c) mathematical equation
(d) all of these
Answer:
(d) all of these

Question 11.
A probability density function may be represented by ________
(a) table
(b) graph
(c) mathematical equation
(d) both (b) and (c)
Answer:
(d) both (b) and (c)

Question 12.
If c is a constant in a continuous probability distribution, then p(x = c) is always equal to ______
(a) zero
(b) one
(c) negative
(d) does not exist
Answer:
(a) zero

Question 13.
E[X – E(X)] is equal to ______
(a) E(X)
(b) V[X]
(c) 0
(d) E(X) – X
Answer:
(c) 0
Hint:
E[X – E(X)] = E(X) – E [E(X)] = E(X) – E(X) = 0

Question 14.
E[X – E(X)]² is ______
(a) E(X)
(b) E(X²)
(c) V(X)
(d) S.D (X)
Answer:
(c) V(X)
Hint:
E[X – E(X)]² = E[X² – 2XE(X) + E(X)²]
= E[X²] – 2[E(X)]² + [E(X)]²
= E[X²] – [E(X)]²
= Var (X)

Question 15.
If the random variable takes negative values, then the negative values will have ________
(a) positive probabilities
(b) negative probabilities
(c) constant probabilities
(d) difficult to tell
Answer:
(a) positive probabilities

Question 16.
If we have f(x) = 2x, 0 ≤ x ≤ 1, then f(x) is a ________
(a) probability distribution
(b) probability density function
(c) distribution function
(d) continuous random variable
Answer:
(b) probability density function

Question 17.
A discrete probability function p(x) is always ________
(a) non-negative
(b) negative
(c) one
(d) zero
Answer:
(a) non-negative

Question 18.
In a discrete probability distribution, the sum of all the probabilities is always equal to ______
(a) zero
(b) one
(c) minimum
(d) maximum
Answer:
(b) one

Question 19.
The expected value of a random variable is equal to its _______
(a) variance
(b) standard deviation
(c) mean
(d) covariance
Answer:
(c) mean

Question 20.
A discrete probability function p(x) is always non-negative and always lies between ________
(a) 0 and ∞
(b) 0 and 1
(c) -1 and +1
(d) -∞ and +∞
Answer:
(b) 0 and 1

Question 21.
The probability density function p(x) cannot exceed _______
(a) zero
(b) one
(c) mean
(d) infinity
Answer:
(b) one

Question 22.
The height of persons in a country is a random variable of the type ________
(a) discrete random variable
(b) continuous random variable
(c) both (a) and (b)
(d) neither (a) nor (b)
Answer:
(b) continuous random variable

Question 23.
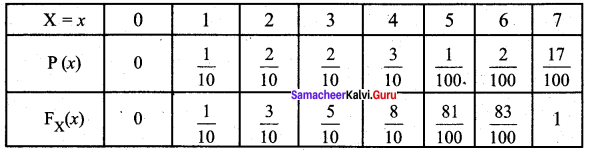
The distribution function F(x) is equal to ______
(a) P(X = x)
(b) P(X ≤ x)
(c) P(X ≥ x)
(d) all of these
Answer:
(b) P(X ≤ x)

Students can download 12th Business Maths Chapter 5 Numerical Methods Ex 5.3 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Ex 5.3

Choose the correct answer.

Question 1.
∆² y₀ = ______
(a) y₂ – 2y₁ + y₀
(b) y₂ + 2y₁ – y₀
(c) y₂ + 2y₁ + y₀
(d) y₂ – y₁ + 2y₀
Answer:
(a) y₂ – 2y₁ + y₀
Hint:
∆² y₀ = ∆(∆y₀) = ∆(y₁ – y₀) = ∆y₁ – ∆y₀
= (y₂ – y₁) – (y₁ – y₀)
= y₂ – 2y₁ + y₀

Question 2.
∆f(x) = _______
(a) f(x + h)
(b) f(x) – f(x + h)
(c) f(x + h) – f(x)
(d) f(x) – f(x – h)
Answer:
(c) f(x + h) – f(x)
Hint:
∆f(x) = f(x + h) – f(x)

Question 3.
E = ______
(a) 1 + ∆
(b) 1 – ∆
(c) 1 + ∇
(d) 1 – ∇
Answer:
(a) 1 + ∆
Hint:
E = 1 + ∆

Question 4.
If h = 1, then ∆(x²) = ________
(a) 2x
(b) 2x – 1
(c) 2x + 1
(d) 1
Answer:
(c) 2x + 1
Hint:
∆(x²) = (x + h)² – x² = (x + 1)² – x² = 2x + 1

Question 5.
If c is a constant then ∆c = ______
(a) c
(b) ∆
(c) ∆²
(d) 0
Answer:
(d) 0

Question 6.
If m and n are positive integers then ∆^m ∆ⁿ f(x) = _______
(a) ∆^m+n f(x)
(b) ∆^m f(x)
(c) ∆ⁿ f(x)
(d) ∆^m-n f(x)
Answer:
(a) ∆^m+n f(x)

Question 7.
If ‘n’ is a positive integer ∆ⁿ [∆^-n f(x)] _______
(a) f(2x)
(b) f(x + h)
(c) f(x)
(d) ∆ f(2x)
Answer:
(c) f(x)

Question 8.
E f(x) = _______
(a) f(x – h)
(b) f(x)
(c) f(x + h)
(d) f(x + 2h)
Answer:
(c) f(x + h)

Question 9.
∇ = _______
(a) 1 + E
(b) 1 – E
(c) 1 – E^-1
(d) 1 + E^-1
Answer:
(c) 1 – E^-1

Question 10.
∇ f(a) = ______
(a) f(a) + f(a – h)
(b) f(a) – f(a + h)
(c) f(a) – f(a – h)
(d) f(a)
Answer:
(c) f(a) – f(a – h)

Question 11.
For the given points (x₀ , y₀) and (x₁, y₁) the Lagrange’s formula is ______

Answer:

Question 12.
Lagrange’s interpolation formula can be used for ________
(a) equal intervals only
(b) unequal intervals only
(c) both equal and unequal intervals
(d) none of these
Answer:
(c) both equal and unequal intervals

Question 13.
If f(x) = x² + 2x + 2 and the interval of differencing is unity then ∆ f(x) _______
(a) 2x – 3
(b) 2x + 3
(c) x + 3
(d) x – 3
Answer:
(b) 2x + 3
Hint:
f(x) = 2x² + 2x + 2
h = 1
∆f(x) = (x + 1)² + 2(x + 1) + 2 – x² – 2x – 2
= x² + 2x + 1 +2x + 2 + 2 – x² – 2x – 2
= 2x + 3

Question 14.
For the given data find the value of ∆³ y₀ is _________

(a) 1
(b) 0
(c) 2
(d) -1
Answer:
(b) 0
Hint:

Students can download 12th Business Maths Chapter 6 Random Variable and Mathematical Expectation Ex 6.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 6 Random Variable and Mathematical Expectation Ex 6.2

Question 1.
Find the expected value for the random variable of an unbiased die.
Solution:
Let X denote the number on the top side of the unbiased die.
The probability mass function is given by the following table.

The expected value for the random variable X is E(X) = \(\sum_{x} x P_{x}(x)\)

Question 2.
Let X be a random variable defining number of students getting A grade. Find the expected value of X from the given table.

Solution:
Expected value of X, E(X) = \(\sum_{x} x P_{x}(x)\)
E(X) = (0 × 0.2) + (1 × 0.1) + (2 × 0.4) + (3 × 0.3)
= 0 + 0. 1 + 0.8 + 0.9
= 1.8

Question 3.
The following table is describing the probability mass function of the random variable X.

Find the standard deviation of x.
Solution:
The standard deviation of X, σ_x is given by σ_x = √Var[X]
Now Var(X) = E(X²) – [E(X)]²
From the given table,

Hence the standard deviation of X is 2.15

Question 4.
Let X be a continuous random variable with probability density function.

Find the expected value of X.
Solution:
The expected value of the random variable is given by E(X) = \(\int_{-\infty}^{\infty} x f(x) d x\)
According to the problem we have,

Question 5.
Let X be a continuous random variable with probability density function

Find the mean and variance of X.
Solution:
Given that X is a continuous random variable.
The mean of X is the expected value of X.

Question 6.
In investment, a man can make a profit of ₹ 5,000 with a probability of 0.62 or a loss of ₹ 8,000 with a probability of 0.38. Find the expected gain.
Solution:
Let X be the random variable which denotes the gain in the investment. It is given that X takes the value 5000 with probability 0.62 and -8000 with a probability 0.38.
(Note that we take -8000 since it is a loss)
The probability distribution is given by

E(X) = (0.38) (-8000) + (0.62) (5000)
= -3040 + 3100
= 60
Hence the expected gain is ₹ 60

Question 7.
What are the properties of Mathematical expectation?
Solution:
The properties of Mathematical expectation are as follows:
(i) E(a) = a, where ‘a’ is a constant
(ii) Addition theorem: For two r.v’s X and Y, E(X + Y) = E(X) + E(Y)
(iii) Multiplication theorem: E(XY) = E(X) E(Y)
(iv) E(aX) = aE(X), where ‘a’ is a constant
(v) For constants a and b, E(aX + b) = a E(X) + b

Question 8.
What do you understand by Mathematical expectation?
Solution:
The expected value of a random variable gives a measure of the center of the distribution of the variable. In other words, E(X) is the long-term average value of the variable. The expected value is calculated as a weighted average of the values of a random variable in a particular experiment. The weights are the probabilities. The mean of the random variable X is µ_X = E(X).

Question 9.
How do you define variance in terms of Mathematical expectation?
Solution:
Let X be a random variable. Let E(X) denote the expectation of X.
Then the variance is defined in terms of the mathematical expectation as follows.
(a) X is discrete r.v with p.m.f p(x). Then Var(X) = \(\sum[x-\mathrm{E}(\mathrm{X})]^{2} p(x)\)
(b) X is continuous r.v with p.d.f f_x(x). Then Var(X) = \(\int_{-\infty}^{\infty}[X-E(X)]^{2} f_{X}(x) d x\)

Question 10.
Define Mathematical expectation in terms of a discrete random variable.
Solution:
Let X be a discrete random variable with probability mass function (p.m.f) P(x). Then, its expected value is defined by E(X) = \(\sum_{x} x p(x)\)
In other words, if x₁, x₂, x₃,…… x_n are the different values of X, and p(x₁), p(x₂) …..p(x_n) are the corresponding probabilities, then E(X) = x₁ p(x₁) + x₂ p(x₂) + x₃ p(x₃) +… x_n p(x_n)

Question 11.
State the definition of Mathematical expectation using a continuous random variable.
Solution:
Let X be a continuous random variable with probability density function f(x). Then the expected value of X is
\(\mathrm{E}(\mathrm{X})=\int_{-\infty}^{\infty} x f(x) d x\)
If the integral exists, E(X) is the mean of the values, otherwise, we say that the mean does not exist.

Question 12.
In a business venture, a man can make a profit of ₹ 2,000 with a probability of 0.4 or have a loss of ₹ 1,000 with a probability of 0.6. What are his expected, variance and standard deviation of profit?
Solution:
Let X be the random variable denoting the profit of the business venture.
The probability distribution of X is given as follows

E(X) = (-1000) (0.6) + (2000) (0.4)
= – 600 + 800
= 200
E(X²) = (-1000)² (0.6) + (2000)² (0.4)
= 6,00,000 + 16,00,000
= 22,00,000
V(X) = E(X²) – [E(X)]²
= 22,00,000 – 40000
= 21,60,000
Standard deviation = √Var[X]
= \(\sqrt{2160000}\)
= 1469.69
Thus the expected value of profit is ₹ 200. The variance of profit is ₹ 21,60,000 and the standard deviation of profit is ₹ 1469.69.

Question 13.
The number of miles an automobile tyre lasts before it reaches a critical point in tread wear can be represented by a p.d.f.

Find the expected number of miles (in thousands) a tyre would last until it reaches the critical tread wear point.
Solution:
Let the continuous random variable X denote the number of miles (in thousands) till an automobile tyre lasts.
The expected value is E(X) = \(\int_{-\infty}^{\infty} x f(x) d x\)
From the problem we have,
\(E(X)=\int_{0}^{\infty}(x) \frac{1}{30} e^{\frac{-x}{30}} d x\)
We use integration by parts to evaluate the integral

Hence the expected number of miles is 30,000.

Question 14.
A person tosses a coin and is to receive ₹ 4 for a head and is to pay ₹ 2 for a tail. Find the expectation and variance of his gains.
Solution:
Let X be the discrete random variable which denotes the gain of the person.
The probability distribution of X is given by

(Here, since a coin is tossed the probability is equal for the outcomes head or tail)

Thus the expectation of his gains is 1 and the variance of his gains is 9.

Question 15.
Let X be a random variable and Y = 2X + 1. What is the variance of Y if the variance of X is 5?
Solution:
Given X is a random variable and Y = 2X + 1 and Var(X ) = 5
Var (Y) = Var (2X + 1) = (2)² = 4
Var X = 4(5) = 20