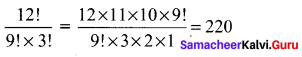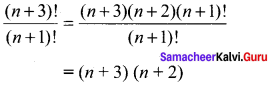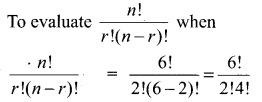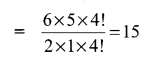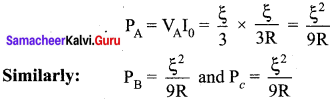Prasanna

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.2

9th Maths Algebra Exercise 3.2 Question 1.
Find the value of the polynomial f(y) = 6y – 3y² + 3 at (i) y = 1 (ii) y = -1 (iii) y = 0
Solution:
(i) At y = 1,
f(1) = 6(1) – 3(1)² + 3 = 6 – 3 + 3 = 6
(ii) At y = -1,
f(-1) = 6(-1) – 3(-1)² + 3 = -6 – 3 + 3 = -6
(iii) At y = 0,
f(0) = 6(0) – 3(0)² + 3 = 0 – 0 + 3 = 3

9th Maths Exercise 3.2 Question 2.
If f(x) = x² – \(2 \sqrt{2} x\) + 1, find p (\(2 \sqrt{2}\))
Solution:
p(\(2 \sqrt{2}\)) = (\(2 \sqrt{2}\))² – \(2 \sqrt{2}\)(\(2 \sqrt{2}\)) + 1
= 4 × 2 – 4 × 2 + 1
= 8 – 8 + 1 = 1

Ex 3.2 Class 9 Algebra Question 3.
Find the zeros of the polynomial in each of the following :
(i) p(x) = x – 3
(ii) p(x) = 2x + 5
(iii) q(y) = 2y – 3,
(iv) f(z) = 8z
(v) p(x) = ax where a ≠ 0,
(vi) h(x) = ax + b, a ≠ 0, a, b ∈ R
Solution:
(i) x = 3.
p( 3) = 3 – 3 = 0
∴ The zero of the polynomial is x = 3.

(iv) f(z) = 8z,
If 8z = 0
z = \(\frac{0}{8}\) = 0
f(0) = 8(0) = 0
∴ z = 0 is the zero of the given polynomial.

9th Maths 3.2 Question 4.
Find the roots of the polynomial equations.
(i) 5x – 6 = 0
(ii) x + 3 = 0
(iii) 10x + 9 = 0
(iv) 9x – 4 = 0
Solution:
(i) 5x – 6 = 0
5x = 6
∴ x = \(\frac{6}{5}\)

(ii) x + 3 = 0
∴ x = -3

(iii) 10x + 9 = 0
10x = -9
∴ x = \(\frac{-9}{10}\)

(iv) 9x – 4 = 0
9x = 4
∴ x = \(\frac{4}{9}\)

9th Standard Maths Exercise 3.2 Question 5.
Verify whether the following are zeros of the polynomial indicated against them, or not.
(i) p(x) = 2x – 1, x = \(\frac{1}{2}\)
(ii) p(x) = x³ – 1, x = 1,
(iii) p(x) = ax + b, x = \(\frac{-b}{a}\)
(iv) p(x) = (x + 3) (x – 4), x = 4, x = -3
Solution:
(i) p(x) = 2x – 1, x = \(\frac{1}{2}\)
p(\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\)) – 1 = 1 – 1 = 0
∴ x = \(\frac{1}{2}\) is the zero of the given polynomial.

(ii) p(x) = x³ – 1, x = 1
p(1) = 1³ – 1 = 1 – 1 = 0
∴ x = 1 is the zero of the given polynomial

(iii) p(x) = ax + b, x = \(\frac{-b}{a}\)
p(\(\frac{-b}{a}\)) = a(\(\frac{-b}{a}\)) + b
= -b + b = 0
∴ x = \(\frac{-b}{a}\) is the zero of the given polynomial.

(iv) p(x) = (x + 3) (x – 4), x = 4, x = -3
p(-3) = (-3 + 3) (-3 – 4) = 0(-7) = 0
p(4) = (4 + 3) (4 – 4) = 7(0) = 0
∴ x = -3, x = 4 are the zeros of the given polynomial.

Class 9 Maths Exercise 3.2 Solutions Question 6.
Find the number of zeros of the following polynomial represented by their graphs.

Solution:
(i) The curve cuts the x-axis at two points. ∴ The equation has 2 zeros.
(ii) Since the curve cuts the x-axis at 3 different points. The number of zeros of the given curve is three.
(iii) Since the curve doesn’t cut the x axis. The number of zeros of the given curve is zero.
(iv) The curve cut the x-axis at one point. ∴ The equation has one zero.
(v) The curve cut the x axis at one point. ∴ The equation has one zero.

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Tamil Book Solutions Guide Pdf Chapter 2.5 வினைமுற்று Text Book Back Questions and Answers, Summary, Notes.

Tamilnadu Samacheer Kalvi 8th Tamil Solutions Chapter 2.5 வினைமுற்று

கற்பவை கற்றபின்

Question 1.
‘வாழ்க’ என்னும் சொல்லை ஐந்து பால்களிலும், மூன்று இடங்களிலும் இடம் பெறுமாறு தொடர்களை எழுதுக.
எ.கா: அவன் வாழ்க. (ஆண்பால்) நாம் வாழ்க. (தன்மை )
Answer:
பால்கள்

• அவள் வாழ்க (பெண்பால்)
• அவர்கள் வாழ்க (பலர்பால்)
• அது வாழ்க (ஒன்றன் பால்)
• அவைகள் வாழ்க (பலவின்பால்)

இடங்கள்

• நீ வாழ்க (முன்னிலை)
• அவர்கள் வாழ்க (படர்க்கை)

பாடநூல் வினாக்கள்

சரியான விடையைத் தேர்ந்தெடுத்து எழுதுக.

Question 1.
மாடு வயலில் புல்லை மேய்ந்தது – இத்தொடரிலுள்ள வினைமுற்று …………………….
அ) மாடு
ஆ) வயல்
இ) புல்
ஈ) மேய்ந்தது
Answer:
ஈ) மேய்ந்தது

Question 2.
பின்வருவனவற்றுள் இறந்தகால வினைமுற்று …………………..
அ) படித்தான்
ஆ) நடக்கிறான்
இ) உண்பான்
ஈ) ஓடாது
Answer:
அ) படித்தான்

Question 3.
பின்வருவனவற்றுள் ஏவல் வினைமுற்றுச் சொல் ……………….
அ) செல்க
ஆ) ஓடு
இ) வாழ்க
ஈ) வாழிய
Answer:
ஆ) ஓடு

சிறுவினா

Question 1.
வினைமுற்று என்றால் என்ன?
Answer:
ஒரு வினை, எச்சப் பொருளில் அமையாமல், முழுமை பெற்று விளங்குவது. இவ்வாறு பொருள் முற்றுப் பெற்ற வினைச் சொற்களை முற்றுவினை அல்லது வினைமுற்று என்பர்.

Question 2.
தெரிநிலை வினைமுற்று எவற்றைக் காட்டும்?
Answer:
தெரிநிலை வினைமுற்று செய்பவர், கருவி, நிலம், செயல், காலம், செய்பொருள் ஆகியவற்றைக் காட்டும்.

Question 3.
வியங்கோள் வினைமுற்று விகுதிகள் யாவை?
Answer:
க, இய, இயர், அல் என்பன வியங்கோள் வினைமுற்று விகுதிகள் ஆகும்.

Question 4.
ஏவல் வினைமுற்றுக்கும் வியங்கோள் வினைமுற்றுக்கும் இடையேயுள்ள வேறுபாடுகள் யாவை?
Answer:

மொழியை ஆள்வோம்

கீழ்க்காணும் தலைப்பில் இரண்டு நிமிடம் பேசுக.

இயற்கையைப் பாதுகாப்போம்.
(i) வணக்கம்.

(ii) உயிர்கள் படைக்கப்பட்டபோதே, அவற்றின் வாழ்வுக்காக இயற்கை வளங்களும் சேர்த்தே படைக்கப்பட்டுள்ளன. இயற்கை வளங்களோடு அத்தனை உயிரினங்களின் வாழ்க்கையும் சிறப்பாக நடைபெற்று வந்தது.

(iii) அறிவியலின் ஆதிக்கம் பெருகியது. விளைவு, மனிதருக்கு மட்டுமே பூமி என்ற நிலை உருவானது. அதுவும் மாறி அறிவியல் வளர்ச்சியடைந்த நாடுகளுக்கு மட்டுமே இயற்கை வளம் யாவும் சொந்தம் என்ற நிலை உருவாகியுள்ளது.

(iv) மனிதர்களின் பேராசையால் இயற்கை வளங்கள் அழிக்கப்பட்டு, பிற உயிரினங்கள் யாவும் பாதிப்படைந்து வருகின்றன. நீர், நிலம், ஆகாயம், வாயு என நான்கு பூதங்களும் மாசடைந்து விட்டன. சீக்கிரமே, வாழ முடியாத இடமாகப் பூமி ஆகிவிடுமோ என்ற நிலை உருவாகி வருகிறது.

(v) உயிர்களின் வளர்ச்சிக்குத் தேவையான எல்லாவற்றையும் இயற்கை தருகிறது. காடுகள், நுண்ணுயிரிகள், ஆறுகள், ஏரிகள், கடற்பகுதிகள், மலைகள், மண்வளம், மேகங்கள், ஏன் ஒவ்வொரு மழைத்துளியும் கூட இயற்கையின் கொடைதான். இதில் ஒன்றை இழந்து கூட மனிதர்கள் வாழவே முடியாது.

(vi) உங்கள் தலைமுறைக்குச் சொத்து சேர்ப்பதைப்போல, இயற்கையையும் பாதுகாத்து சேர்த்து வையுங்கள்.

(vii) இயற்கை வளங்களின் இன்றியமையாமை குறித்து மக்களிடையே விழிப்புணர்வை உண்டாக்க, ஒவ்வோர் ஆண்டும் ஜூலை 28ம் நாள் உலக இயற்கை வளப்பாதுகாப்பு நாள் கடைபிடிக்கப்படுகிறது.

(viii) இந்த நாளில், இயற்கையைப் பாதுகாக்க நம்மால் ஆனதைச் செய்வோம். அதுவே, அந்த நாளுக்கான நமது மரியாதை என்று சொல்லலாம்.
(ix) என்ன செய்யப்போகிறோம் என்பதை நாம் தான் சிந்தித்து செயல்பட வேண்டும் என்று சொல்லி என்னுரையை நிறைவு செய்கின்றேன். நன்றி.

சொல்லக்கேட்டு எழுதுக.

இயற்கையை விரும்புவது மட்டுமன்றி, அதைப் பாதுகாப்பதும் இன்றியமையாதது. அது நமது கடமை மட்டுமன்று பொறுப்பும் ஆகும். நாம் விரும்பிக் கண்டுகளித்த இயற்கைச் செல்வங்களை, வரும் தலைமுறையினருக்காகச் சேர்த்தும் பாதுகாத்தும் வைக்கவேண்டும். இயற்கை வளங்களின் இன்றியமையாமை குறித்து விழிப்புணர்வு உண்டாக்க ஒவ்வோர் ஆண்டும் சூலை 28 ஆம் நாள் உலக இயற்கைவளப் பாதுகாப்பு நாளாகக் கடைப்பிடிக்கப்படுகிறது.

தமிழ் எண்கள் அறிவோம்.

விடுபட்ட கட்டங்களை நிரப்புக.

வண்ணமிடப்பட்டுள்ள எண்களுக்குரிய தமிழ் எண்களை எழுதுக.

1. உலக ஈர நில நாள் பிப்ரவரி 2.
2. உலக ஓசோன் நாள் செப்டம்பர் 16.
3. உலக இயற்கை நாள் அக்டோபர்
4. உலக வனவிலங்கு நாள் அக்டோபர் 6.
5. உலக இயற்கைச் சீரழிவுத் தடுப்பு நாள் அக்டோபர் 5.
Answer:
1. உ
2. கச
3. ங
4. க
5. ரு

கொடுக்கப்பட்டுள்ள தொடர்களின் வகையைக் கண்டறிந்து எழுதுக.

1. முக்காலமும் உணர்ந்தவர்கள் நம் முன்னோர்கள்.
2. கடமையைச் செய்.
3. பாரதியார் பாடல்களின் இனிமைதான் என்னே!
4. நீ எத்தனை புத்தகங்களைப் படித்திருக்கிறாய்?
Answer:
1. செய்தித்தொடர்
2. விழைவுத்தொடர்
3. உணர்ச்சித் தொடர்
4. வினாத்தொடர்

தொடர்களை மாற்றுக.

எ.கா: நேற்று நம் ஊரில் மழை பெய்தது. (வினாத் தொடராக மாற்றுக)
நேற்று நம் ஊரில் மழை பெய்ததா?

Question 1.
காடு மிகவும் அழகானது. (உணர்ச்சித் தொடராக மாற்றுக)
Answer:
என்னே , காட்டின் அழகு!

Question 2.
ஆ! பூனையின் காலில் அடிபட்டுவிட்டதே! (செய்தித் தொடராக மாற்றுக)
Answer:
பூனையின் காலில் அடிபட்டுவிட்டது.

Question 3.
அதிகாலையில் துயில் எழுவது நல்லது. (விழைவுத் தொடராக மாற்றுக)
Answer:
அதிகாலையில் துயில் எழு.

Question 4.
முகில்கள் திரண்டால் மழை பெய்யும் அல்லவா? (செய்தித்தொடராக மாற்றுக)
Answer:
முகில்கள் திரண்டால் மழை பெய்யும்.

Question 5.
காட்டில் புலி நடமாட்டம் உள்ளது. (வினாத் தொடராக மாற்றுக)
Answer:
காட்டில் புலி நடமாட்டம் உள்ளதா?

கடிதம் எழுதுக

விளையாட்டுப் போட்டியில் வெற்றி பெற்ற உங்கள் நண்பனுக்குப் பாராட்டுக் கடிதம் எழுதுக.

30, சாந்திநகர்,
திருப்பூர் – 2.
நாள்: 01.07.2020.

இனிய நண்பா ,
வணக்கம். நலம். நலம் அறிய ஆவலாய் உள்ளேன்.
இவ்வாண்டு உன் பள்ளியின் 50ஆம் ஆண்டு விளையாட்டு விழா 25.06.2020 அன்று நடைபெற்றதாய் மடல் எழுதியிருக்கின்றாய். இளைஞர்களுக்கான ஓட்டப்பந்தயத்தில் நீயும் கலந்து கொண்டதாகவும், முதலிடம் பெற்றுள்ளதாகவும் அதில் குறிப்பிட்டுள்ளாய். வெற்றி பெற்ற செய்தி அறிந்து அளவற்ற மகிழ்ச்சி அடைகின்றேன்.

என் அன்பு நிறைந்த பாராட்டினை உனக்குத் தெரிவித்துக் கொள்கின்றேன். உன்னை நண்பனாய் அடைந்தமையை எண்ணிப் பெருமைப்படுகின்றேன்.

படிப்பில் நீ காட்டி வருகின்ற ஆர்வமும், விடாமுயற்சியும், கடும் உழைப்பும் ஒவ்வொரு வகுப்பிலும் முதல் மாணவனாய் வர உதவுகின்றன. அதேபோல் விளையாட்டிலும் வெற்றி பெற்றுள்ளமை நீ படிப்பு, விளையாட்டு ஆகிய இரண்டிலும் கெட்டிக்காரன் என்பதைப் பறைசாற்றுகின்றன. மாநில, தேசியப் போட்டிகளிலும் தடகளத்தில் முத்திரை பதித்து பெருமை சேர்த்திடவும் வாழ்த்துகிறேன்.

உன் அன்பிற்குரிய நண்பன்,
அ. ராசா.

உறைமேல் முகவரி:
பெறுநர்
செல்வன். ந. கண்ண ன்,
16, பாரதியார் தெரு,
காந்தி நகர்,
மதுரை – 16.

மொழியோடு விளையாடு

உரிய வினைமுற்றுகளைக் கொண்டு கட்டங்களை நிரப்புக.

வினைமுற்றுக்கு உரிய வேர்ச்சொல்லை எழுதுக.

1. நடக்கிறது – நட
2. போனான் – போ
3. சென்றனர் – செல்
4. உறங்கினாள் – உறங்கு
5. வாழிய – வாழ்
6. பேசினாள் – பேசு
7. வருக – வா
8. தருகின்றனர் – தா
9. பயின்றாள் – பயில்
10. கேட்டார் – கேள்

நிற்க அதற்குத் தக.

என் பொறுப்புகள்:
1. நீர்நிலைகளைத் தூய்மையாக வைக்க உதவுவேன்.
2. மரம் நட வாய்ப்புள்ள இடங்களில் மரக்கன்றுகளை நட்டு வளர்ப்பேன்.

கலைச்சொல் அறிவோம்

1. பழங்குடியினர் – Tribes
2. சமவெளி – Plain
3. பள்ளத்தாக்கு – Valley
4. புதர் – Thicker
5. மலைமுகடு – Ridge
6. வெட்டுக்கிளி – Locust
7. சிறுத்தை – Leopard
8. மொட்டு – Bud

இணையத்தில் காண்க

Question 1.
பழங்குடி மக்களின் வாழ்க்கை முறைகளை இணையத்தில் கண்டு அறிக.
Answer:
பழங்குடிகள் என்போர் தொன்றுதொட்டு பன்னெடுங்காலமாகவோ (10,000 ஆண்டுகளுக்கும் மேலாக) ஒரு நிலப்பகுதியில் வாழ்ந்து வருபவர்கள். இவர்கள் தங்களுக்கென தனி பழக்க வழக்கங்களும், மொழியும், நிலமும் கொண்டு அதனைச் சார்ந்த செடி, கொடி, மரம், விலங்குகளைக் கொண்டு தங்கள் வாழ்க்கையைத் தன்னிறைவோடு வாழ்பவர்கள்.

இவர்கள் தங்களுக்கென தனி கலைகளும் கடவுள், சமயம் மற்றும் உலகம் பற்றிய கொள்கைகளும் கொண்டிருப்பர். தனிமனித வாழ்க்கையிலும் உறவு முறைகளிலும், சமூகமாக வாழ்வதிலும் தங்களுக்கென தனியான முறைகள் கொண்டவர்கள். தற்கால மக்களிடம் அதிகம் பழகாமலும், பணத்தை அடிப்படையாகக் கொண்ட பொருளாதாரம் இல்லாமலும், தற்கால தொழில் வளர்ச்சி வழி பெற்ற புதிய பொருட்கள், வசதிகள் எதையும் பெரிதாக ஏற்றுக் கொள்ளாதவர்களுமாக இருக்கிறார்கள்.

ஆஸ்திரேலியா, வட அமெரிக்கா, தென் அமெரிக்கா, இந்தியா, ஜப்பான், பசிபிக் தீவுகள் என்று உலகின் பல்வேறு பகுதிகளில் பல்வேறு பழங்குடி இனங்கள் வாழ்ந்து வருகின்றனர். பல பழங்குடியின மக்கள் பல இடங்களில் கடலிலேயே வாழ்கிறார்கள். மலேசியா, பிலிப்பைன்ஸ், இந்தோனேசியாபோன்ற நாடுகளுக்கு அருகில் அமைந்துள்ள பப்புவா நியூ கினியா தீவை அடுத்த கடல் பகுதியில் பஜாவு என்ற பழங்குடி மக்கள் நாடோடிகளாக வாழ்ந்து வருகிறார்கள்.

கூடுதல் வினாக்கள்

சரியான விடையைத் தேர்ந்தெடுத்து எழுதுக.

Question 1.
…………………… ஒன்றன் செயலைக் குறிக்கும் சொல் எனப்படும்.
அ) பெயர்ச்சொல்
ஆ) வினைச்சொல்
இ) உரிச்சொல்
ஈ) இடைச்சொல்
Answer:
ஆ) வினைச்சொல்

Question 2.
செயலை ………………………… என்றும் குறிப்பர்.
அ) பனை
ஆ) தினை
இ) வினை
ஈ) சுனை
Answer:
இ) வினை

Question 3.
பொருள் முற்றுப்பெற்ற வினைச் சொற்களை …………………… என்பர்.
அ) பெயர்முற்று
ஆ) இடைமுற்று
இ) வினைமுற்று
ஈ) வினையெச்சம்
Answer:
இ) வினைமுற்று

Question 4.
ஒரு செயல் நடைபெறுவதற்கான ……………………. வெளிப்படுமாறு அமைவது தெரிநிலை வினைமுற்று எனப்படும்.
அ) ஆறும்
ஆ) ஏழும்
இ) நான்கும்
ஈ) ஐந்தும்
Answer:
அ) ஆறும்

Question 5.
ஐம்பால், முக்காலம், மூவிடம் ஆகிய அனைத்திலும் ……………….. வரும்.
அ) பெயர்முற்றுகள்
ஆ) முற்றுகள்
இ) எழுவாய்
ஈ) வினைமுற்றுகள்
Answer:
ஈ) வினைமுற்றுகள்

Question 6.
………………… ல் செய்பவர், செயல், காலம் ஆகியவற்றை வெளிப்படையாக அறியலாம்.
அ) குறிப்பு வினைமுற்று
ஆ) முற்றெச்சம்
இ) தெரிநிலை வினைமுற்று
ஈ) ஏவல் வினைமுற்று
Answer:
இ) தெரிநிலை வினைமுற்று

Question 7.
காலத்தை வெளிப்படையாகக் காட்டாது செய்பவரை மட்டும் வெளிப்படையாகக் காட்டும் வினைமுற்று ………………………… எனப்படும்.
அ) குறிப்பு வினைமுற்று
ஆ) தெரிநிலை வினைமுற்று
இ) ஏவல் வினைமுற்று
ஈ) வியங்கோள் வினைமுற்று
Answer:
அ) குறிப்பு வினைமுற்று

Question 8.
ஒரு செயலைச் செய்யுமாறு கட்டளையிடும் வினைமுற்று ………………………….. வினைமுற்று.
அ) குறிப்பு
ஆ) தெரிநிலை
இ) ஏவல்
ஈ) வியங்கோள்
Answer:
இ) ஏவல்

Question 9.
க, இய, இயர், அல் என விகுதிகள் பெற்றுவரும் வினைமுற்று ……………………
அ) ஏவல் வினைமுற்று
ஆ) வியங்கோள் வினைமுற்று
இ) தெரிநிலை வினைமுற்று
ஈ) குறிப்பு வினைமுற்று
Answer:
ஆ) வியங்கோள் வினைமுற்று

Question 10.
வினைமுற்று …………………….. வகைப்படும்.
அ) இரண்டு
ஆ) மூன்று
இ) நான்கு
ஈ) ஆறு
Answer:
அ) இரண்டு

சிறுவினா

Question 1.
வினைச்சொல் என்றால் என்ன?
Answer:
ஒரு செயலைக் குறிக்கும் சொல் வினைச்சொல் எனப்படும். ஒன்றன் தொழிலை உணர்த்தி காலத்தைக் காட்டி நிற்கும் சொல் வினைச்சொல் எனப்படும். இது முற்றுவினை, எச்சவினை என்று இரு வகைப்படும்.

Question 2.
வினைமுற்றுகள் எத்தனை வகைப்படும்?
Answer:
தெரிநிலை வினைமுற்று, குறிப்பு வினைமுற்று என வினைமுற்று இருவகைப்படும்.

Question 3.
தெரிநிலை வினைமுற்று என்றால் என்ன?
Answer:
ஒரு செயல் நடைபெறுவதற்குச் செய்பவர், கருவி, நிலம், செயல், காலம், செய்பொருள் ஆகிய ஆறும் முதன்மையானவை ஆகும். இவை ஆறும் வெளிப்படுமாறு அமைவது தெரிநிலை வினைமுற்று எனப்படும். எ.கா: உழுதான்.

Question 4.
குறிப்பு வினைமுற்று என்றால் என்ன?
Answer:
பொருள், இடம், காலம், சினை, குணம், தொழில் ஆகியவற்றுள் ஒன்றனை அடிப்படையாகக் கொண்டு காலத்தை வெளிப்படையாகக் காட்டாது செய்பவரை மட்டும் வெளிப்படையாகக் காட்டும் வினைமுற்று, குறிப்பு வினைமுற்று எனப்படும். எ.கா: ஆதிரையான்.

Question 5.
ஏவல் வினைமுற்று என்றால் என்ன?
Answer:
தன்முன் உள்ள ஒருவரை ஒரு செயலைச் செய்யுமாறு ஏவும் வினைமுற்று, ஏவல் வினைமுற்று எனப்படும். ஏவல் வினைமுற்று ஒருமை, பன்மை ஆகிய இருவகைகளில் வரும்.

Question 6.
வியங்கோள் வினைமுற்று என்றால் என்ன?
Answer:

• வாழ்த்துதல், வைதல், விதித்தல், வேண்டல் ஆகிய பொருள்களில் வரும் வினைமுற்று வியங்கோள் வினைமுற்று எனப்படும்.
• இவ்வினைமுற்று இரு திணைகளையும், ஐந்து பால்களையும், மூன்று இடங்களையும் காட்டும்.
• இதன் விகுதிகள் க, இய, இயர், அல் என வரும். எ.கா: வாழ்க.

Question 7.
பால் எத்தனை வகைப்படும்? அவை யாவை?
Answer:

• பால் ஐந்து வகைப்படும்.
• அவை, ஆண்பால், பெண்பால், பலர்பால், ஒன்றன்பால், பலவின் பால் ஆகும்.

Students those who are preparing for the 12th Physics exam can download this Samacheer Kalvi 12th Physics Book Solutions Questions and Answers for Chapter 5 Electromagnetic Waves from here free of cost. These Tamilnadu State Board Solutions for Class 12th Physics PDF cover all Chapter 5 Electromagnetic Waves Questions and Answers. All these concepts of Samacheer Kalvi 12th Physics Book Solutions Questions and Answers are explained very conceptually as per the board prescribed Syllabus & guidelines.

Tamilnadu Samacheer Kalvi 12th Physics Solutions Chapter 5 Electromagnetic Waves

Kickstart your preparation by using this Tamilnadu State Board Solutions for 12th Physics Chapter 5 Electromagnetic Waves Questions and Answers and get the max score in the exams. You can cover all the topics of Chapter 5 Electromagnetic Waves Questions and Answers pdf. Download the Tamilnadu State Board Solutions by accessing the links provided here and ace up your preparation.

Samacheer Kalvi 12th Physics Electromagnetic Waves Textual Evaluation Solved

Samacheer Kalvi 12th Physics Electromagnetic Waves Multiple Choice Questions

12th Physics Chapter 5 Book Back Answers Question 1.
The dimension of \(\frac { 1 }{ { \mu }_{ 0 }{ \varepsilon }_{ 0 } } \) is ……….
(a) [LT^-1]
(b) [L² T^-2]
(c) [L^-1 T]
(d) [L^-2 T²]
Answer:
(b) [L² T^-2].

12th Physics Lesson 5 Book Back Answers Question 2.
If the amplitude of the magnetic field is 3 x 10^-6 T, then amplitude of the electric field for a electromagnetic waves is ……….
(a) 100 V m^-1
(b) 300 V m^-1
(c) 600 V m^-1
(d) 900 V m^-1
Answer:
(d) 900 V m^-1.

12th Physics 5th Lesson Book Back Answers Question 3.
Which of the following electromagnetic radiation is used for viewing objects through fog ……….
(a) microwave
(b) gamma rays
(c) X- rays
(d) infrared
Answer:
(d) infrared.

Samacheer Kalvi Guru 12th Physics Question 4.
Which of the following are false for electromagnetic waves ……….
(a) transverse
(b) mechanical waves
(c) longitudinal
(d) produced by accelerating charges
Answer:
(c) longitudinal.

12th Physics Samacheer Kalvi Question 5.
Consider an oscillator which has a charged particle and oscillates about its mean position with a frequency of 300 MHz. The wavelength of electromagnetic waves produced by this oscillator is ……….
(a) 1 m
(b) 10 m
(c) 100 m
(d) 1000 m
Answer:
(a) 1 m.

Physics Chapter 5 Class 12 Question 6.
The electric and the magnetic field, associated with an electromagnetic wave, propagating along X axis can be represented by ……….
(a) \(\vec { E } \) = E₀ \(\hat{j}\) and \(\vec { B } \) = B₀ \(\hat{k}\)
(b) \(\vec { E } \) = E₀ \(\hat{k}\) and \(\vec { B } \) = B₀ \(\hat{j}\)
(c) \(\vec { E } \) = E₀ \(\hat{i}\) and \(\vec { B } \) = B₀ \(\hat{j}\)
(d) \(\vec { E } \) = E₀ \(\hat{j}\) and \(\vec { B } \) = B₀ \(\hat{j}\)
Answer:
(b) \(\vec { E } \) = E₀ \(\hat{k}\) and \(\vec { B } \) = B₀ \(\hat{j}\).

Samacheer Kalvi Physics Question 7.
In an electromagnetic wave in free space the rms value of the electric field is 3 V m^-1. The peak value of the magnetic field is ……….
(a) 1.414 x 10^-8 T
(b) 1.0 x 10^-8 T
(c) 2.828 x 10^-8 T
(d) 2.0 x 10^-8 T
Answer:
(a) 1.414 x 10^-8 T.

Samacheer Kalvi 12th Physics Question 8.
A During the propagation of electromagnetic waves in a medium ……….
(a) electric energy density is double of the magnetic energy density
(b) electric energy density is half of the magnetic energy density
(c) electric energy density is equal to the magnetic energy density
(d) both electric and magnetic energy densities are zero
Answer:
(c) electric energy density is equal to the magnetic energy density.

Physics Class 12 Samacheer Kalvi Question 9.
If the magnetic monopole exists, then which of the Maxwell’s equation to be modified ……….

Answer:
(b) \(\oint { \vec { E } } \).d\(\vec { A } \) = 0

Samacheerkalvi.Guru 12th Physics Question 10.
A radiation of energy E falls normally on a perfectly reflecting surface. The momentum transferred to the surface is ……….
(a) \(\frac { E }{ c }\)
(b) 2\(\frac { E }{ c }\)
(c) Ec
(d) \(\frac { E }{{ c }^{2}}\)
Answer:
(b) 2\(\frac { E }{ c }\).

12 Physics Samacheer Kalvi Question 11.
Which of the following is an electromagnetic wave ……….
(a) α – rays
(b) β – rays
(c) γ – rays
(d) all of them
Answer:
(c) γ – rays.

Samacheer Kalvi Guru Physics Question 12.
Which one of them is used to produce a propagating electromagnetic wave ……….
(a) an accelerating charge
(b) a charge moving at constant velocity
(c) a stationary charge
(d) an uncharged particle
Answer:
(a) an accelerating charge.

Samacheer Kalvi.Guru 12th Physics Question 13.
Let E = E₀ sin[10⁶ x -ωt] be the electric field of plane electromagnetic wave, the value of to is ……….
(a) 0.3 x 10^-14 rad s^-1
(b) 3 x 10^-14 rad s^-1
(c) 0.3 x 10¹⁴ rad s^-1
(d) 3 x 10¹⁴ rad s^-1
Answer:
(d) 3 x 10¹⁴ rad s^-1.

Physics Samacheer Kalvi Question 14.
Which of the following is NOT true for electromagnetic waves ……….
(a) it transport energy
(b) it transport momentum
(c) it transport angular momentum
(d) in vacuum, it travels with different speeds which depend on their frequency
Answer:
(d) in vacuum, it travels with different speeds which depend on their frequency.

Samacheer Kalvi 12th Physics Solutions Question 15.
The electric and magnetic fields of an electromagnetic wave are ……….
(a) in phase and perpendicular to each other
(b) out of phase and not perpendicular to each other
(c) in phase and not perpendicular to each other
(d) out of phase and perpendicular to each other
Answer:
(a) in phase and perpendicular to each other.

Samacheer Kalvi 12th Physics Electromagnetic Waves Short Answer Questions

Class 12 Physics Samacheer Kalvi Question 1.
What is displacement current?
Answer:
The displacement current can be defined as the current which comes into play in the region in which the electric field and the electric flux are changing with time.

Physics Class 12 Samacheer Kalvi Solutions Question 2.
What are electromagnetic waves?
Answer:
Electromagnetic waves are non-mechanical waves which move with speed equals to the speed of light (in vacuum).

12th Samacheer Kalvi Physics Question 3.
Write down the integral form of modified Ampere’s circuital law.
Answer:
This law relates the magnetic field around any closed path to the conduction current and displacement current through that path.

Physics Solution Class 12 Samacheer Kalvi Question 4.
Explain the concept of intensity of electromagnetic waves.
Answer:
The energy crossing per unit area per unit time and perpendicular to the direction of propagation of electromagnetic wave is called the intensity.
Intensity, I = \(\left< u \right> \)c

Tn 12th Physics Solution Question 5.
What is meant by Fraunhofer lines?
Answer:
When the spectrum obtained from the Sun is examined, it consists of large number of dark lines (line absorption spectrum). These dark lines in the solar spectrum are known as Fraunhofer lines.

Samacheer Kalvi 12th Physics Electromagnetic Waves Long Answer Questions

12th Physics Solutions Samacheer Kalvi Question 1.
Write down Maxwell equations in integral form.
Answer:
Maxwell’s equations in integral form:
Electrodynamics can be summarized into four basic equations, known as Maxwell’s equations. These equations are analogous to Newton’s equations in mechanics. Maxwell’s equations completely explain the behaviour of charges, currents and properties of electric and magnetic fields. So we focus here only in integral form of Maxwell’s equations:
(i) First equation is nothing but the Gauss’s law. It relates the net electric flux to net electric charge enclosed in a surface. Mathematically, it is expressed as

Where \(\vec { E } \) is the electric field and Qenclosed is the charge enclosed. This equation is true for both discrete or continuous distribution of charges. It also indicates that the electric field lines start from positive charge and terminate at negative charge. This implies that the electric field lines do not form a continuous closed path. In other words, it means that isolated positive charge or negative charge can exist.

(ii) Second equation has no name. But this law is similar to Gauss’s law in electrostatics. So this law can also be called as Gauss’s law in magnetism. The surface integral of magnetic field over a closed surface is zero. Mathematically,
\(\oint { \vec { B } } \).d\(\vec { A } \) = 0
where \(\vec { B } \) is the magnetic field. This equation implies that the magnetic lines of force form a continuous closed path. In other words, it means that no isolated magnetic monopole exists.

(iii) Third equation is Faraday’s law of electromagnetic induction. This law relates electric field with the changing magnetic flux which is mathematically written as
\(\oint { \vec { E } } \).d\(\vec { l } \) = \(\frac { d }{ dt }\) Φ_B
where \(\vec { E } \) is the electric field. This equation implies that the line integral of the electric field around any closed path is equal to the rate of change of magnetic flux through the closed path bounded by the surface.

(iv) Fourth equation is modified Ampere’s circuital law. This is also known as ampere- Maxwell’s law. This law relates the magnetic field around any closed path to the conduction current and displacement current through that path.

Where \(\vec { B } \) is the magnetic field. This equation shows that both conduction and also displacement current produces magnetic field. These four equations are known as Maxwell’s equations in electrodynamics.

Physics Practical Class 12 Samacheer Kalvi Question 2.
Write short notes on (a) microwave (b) X-ray (c) radio waves (d) visible spectrum.
Answer:
Microwaves:
It is produced by electromagnetic oscillators in electric circuits. The wavelength range is 1 x 10^-3 m to 3 x 10^-1 m and frequency range is 3 x 10¹¹ Hz to 1 x 10⁹ Hz. It obeys reflection and polarization. It is used in radar system for aircraft navigation, speed of the vehicle, microwave oven for cooking and very long distance wireless communication through satellites.

X-rays:
It is produced when there is a sudden deceleration of high speed electrons at high- atomic number target, and also by electronic transitions among the innermost orbits of atoms. The wavelength range 10^-13 m to 10^-8 m and frequency range are 3 x 10²¹ Hz to 1 x 10¹⁶ Hz. X-rays have more penetrating power than ultraviolet radiation.

X-rays are used extensively in studying structures of inner atomic electron shells and crystal structures. It is used in detecting fractures, diseased organs, formation of bones and stones, observing the progress of healing bones. Further, in a finished metal product, it is used to detect faults, cracks, flaws and holes.

Radio waves:
It is produced by oscillators in electric circuits. The wavelength range is 1 x 10^-1 m to 1 x 10⁴ m and frequency range is 3 x 10⁹ Hz to 3 x 10⁴ Hz. It obeys reflection and diffraction. It is used in radio and television communication systems and also in cellular phones to transmit voice communication in the ultra high frequency band.

Visible light:
It is produced by incandescent bodies and also it is radiated by excited atoms in gases. The wavelength range is 4 x 10^-7 m to 7 x 10^-7 m and frequency range are 7 x 10¹⁴ Hz to 4 x 10¹⁴Hz. It obeys the laws of reflection, refraction, interference, diffraction, polarization, photo-electric effect and photographic action. It can be used to study the structure of molecules, arrangement of electrons in external shells of atoms and sensation of our eyes.

Question 3.
Discuss briefly the experiment conducted by Hertz to produce and detect electromagnetic spectrum.
Answer:
Production of electromagnetic waves-Hertz experiment: Maxwell’s prediction was experimentally confirmed by Heinrich Rudolf Hertz in 1888. The experimental set up used is shown in figure.

It consists of two metal electrodes which are made of small spherical metals. These are connected to larger spheres and the ends of them are connected to induction coil with very large number of turns. This is to produce very high electromotive force (emf). Since the coil is maintained at very high potential, air between the electrodes gets ionized and spark (spark means discharge of electricity) is produced. The gap between electrode (ring type – not completely closed and has a small gap in between) kept at a distance also gets spark.

This implies that the energy is transmitted from electrode to the receiver (ring electrode) as a wave, known as electromagnetic waves. If the receiver is rotated by 90° – then no spark is observed by the receiver. This confirms that electromagnetic waves are transverse waves as predicted by Maxwell. Hertz detected radio waves and also computed the speed of radio waves which is equal to the speed of light (3 x 10⁸ m s^-1).

Question 4.
Explain the Maxwell’s modification of Ampere’s circuital law.
Answer:
Maxwell argued that a changing electric field between the capacitor plates must induce a magnetic field. As currents are the usual sources of magnetic fields, a changing electric field must be associated with a current. Maxwell called this current as the displacement current.

If ‘A’ be the area of the capacitor plates and ‘q’ be the charge on the plates at any instant ‘t’ during the charging process, then the electric field in the gap will be

But \(\frac { dq }{ dt }\) is the rate of change of charge on the capacitor plates. It is called displacement current and is given by I_d = \(\frac { dq }{ dt }\) = ε₀ \(\frac {{ dΦ }_{E}}{ dt }\)
This is the missing term in Ampere’s Circuital Law. The total current must be the sum of the conduction current Ic and the displacement current ld. Thus, I = I_c + I_d = I_c + ε₀ \(\frac {{ dΦ }_{E}}{ dt }\).
Hence, the modified form of the Ampere’s Law is

Question 5.
Write down the properties of electromagnetic waves.
Answer:
Properties of electromagnetic waves:
(i) Electromagnetic waves are produced by any accelerated charge.

(ii) Electromagnetic waves do not require any medium for propagation. So electromagnetic wave is a non-mechanical wave.

(iii) Electromagnetic waves are transverse in nature. This means that the oscillating electric field vector, oscillating magnetic field vector and propagation vector (gives direction of propagation) are mutually perpendicular to each other.

(iv) Electromagnetic waves travel with speed which is equal to the speed of light in vacuum or free space, c = \(\frac { 1 }{ \sqrt { { \varepsilon }_{ 0 }{ \mu }_{ 0 } } } \) 3 x 10⁸ ms^-1

(v) The speed of electromagnetic wave is less than speed in free space or vacuum, that is, v < c. In a medium of refractive index,

(vi) Electromagnetic waves are not deflected by electric field or magnetic field.

(vii) Electromagnetic waves can show interference, diffraction and can also be polarized.

(viii) The energy density (energy per unit volume) associated with an electromagnetic wave propagating in vacuum or free space is
u = \(\frac { 1 }{ 2 }\) ε₀ E² + \(\frac { 1 }{{ 2µ }_{0}}\) Bε²
Where, \(\frac { 1 }{ 2 }\) ε₀ E² = u_E is the energy density in an electric field and \(\frac { 1 }{{ 2µ }_{0}}\) Bε² = u_B is the energy density in a managnetic field.
Since, E = Bc ⇒ u_B = u_E.
The energy density of the electromagnetic wave is = ε E² = -B²

(ix) The average energy density for electromagnetic wave, \(\left< u \right> \) = \(\frac { 1 }{ 2 }\) ε₀ E² = \(\frac { 1 }{ 2 }\) \(\frac { 1 }{{ µ }_{0}}\) Bε²

(x) The energy crossing per unit area per unit time and perpendicular to the direction of propagation of electromagnetic wave is called the intensity.
Intensity, I = \(\left< u \right> \)c

(xi) Like other waves, electromagnetic waves also carry energy and momentum. For the electromagnetic wave of energy U propagating with speed c has linear momentum which is given by = \(\frac { Energy }{ speed }\) = \(\frac { U }{ c }\). The force exerted by an electromagnetic wave on unit area speed of a surface is called radiation pressure.

(xii) If the electromagnetic wave incident on a material surface is completely absorbed, then the energy delivered is U and momentum imparted on the surface is p = \(\frac { U }{ c }\).

(xiii) If the incident electromagnetic wave of energy U is totally reflected from the surface, then the momentum delivered to the surface is ∆p = \(\frac { U }{ c }\) – \(\left( -\frac { U }{ c } \right) \) = 2\(\frac { U }{ c }\).

(xiv) The rate of flow of energy crossing a unit area is known as pointing vector for electromagnetic waves, which is \(\vec { S } \) = \(\frac { 1 }{{ µ }_{0}}\) (\(\vec { E } \)×\(\vec { B } \)) = c²ε₀ (\(\vec { E } \)×\(\vec { B } \)).The unit for pointing vector is W m^-2. The pointing vector at any point gives the direction of energy transport from that point.

(xv) Electromagnetic waves carries not only energy and momentum but also angular momentum.

Question 6.
Discuss the source of electromagnetic waves.
Answer:
Sources of electromagnetic waves:
Any stationary source charge produces only electric field. When the charge moves with uniform velocity, it produces steady current which gives rise to magnetic field (not time dependent, only space dependent) around the conductor in which charge flows.

If the charged particle accelerates, in addition to electric field it also produces magnetic field. Both electric and magnetic fields are time varying fields. Since the electromagnetic waves are transverse waves, the direction of propagation of electromagnetic waves is perpendicular to the plane containing electric and magnetic field vectors.

Any oscillatory motion is also an accelerating motion, so, when the charge oscillates (oscillating molecular dipole) about their mean position, it produces electromagnetic waves.

Suppose the electromagnetic field in free space propagates along z direction, and if the electric field vector points along y axis then the magnetic field vector will be mutually perpendicular to both electric field and the propagation vector direction,
which means
E_y = E₀ sin (kz – ωt)
B_x = B₀ sin (kz – ωt)
Where, E₀ and B₀ are amplitude of oscillating electric and magnetic field, k is a wave number, ω is the angular frequency of the wave and \(\hat{k}\) (unit vector, here it is called propagation vector) denotes the direction of propagation of electromagnetic wave.

Note that both electric field and magnetic field oscillate with a frequency (frequency of electromagnetic wave) which is equal to the frequency of the source (here, oscillating charge is the source for the production of electromagnetic waves). In free space or in vacuum, the ratio between E₀ and B₀ is equal to the speed of electromagnetic wave, which is equal to speed of light c.
c = \(\frac {{ E }_{0}}{ { B }_{0} }\)
In any medium, the ratio of E₀ and B₀ is equal to the speed of electromagnetic wave in that medium, mathematically, it can be written as
v = \(\frac {{ E }_{0}}{ { B }_{0} }\) < c
Further, the energy of electromagnetic waves comes from the energy of the oscillating charge.

Question 7.
What is emission spectra? Give their types.
Answer:
Emission spectra: When the spectrum of self luminous source is taken, we get emission spectrum. Each source has its own characteristic emission spectrum. The emission spectrum can be divided into three types:

(i) Continuous emission spectra (or continuous spectra):
If the light from incandescent lamp (filament bulb) is allowed to pass through prism (simplest spectroscope), it splits into seven colours. Thus, it consists of wavelengths containing all the visible colours ranging from violet to red. Examples: spectrum obtained from carbon arc, incandescent solids, liquids gives continuous spectra.

(ii) Line emission spectrum (or line spectrum):
Suppose light from hot gas is allowed to pass through prism, line spectrum is observed. Line spectra are also known as discontinuous spectra. The line spectra are sharp lines of definite wavelengths or frequencies.

Such spectra arise due to excited atoms of elements. These lines are the characteristics of the element which means it is different for different elements. Examples: spectra of atomic hydrogen, helium, etc.

(iii) Band emission spectrum (or band spectrum):
Band spectrum consists of several number of very closely spaced spectral lines which overlapped together forming specific bands which are separated by dark spaces, known as band spectra. This spectrum has a sharp edge at one end and fades out at the other end.

Such spectra arise when the molecules are excited. Band spectrum is the characteristic of the molecule hence, the structure of the molecules can be studied using their band spectra. Examples, spectra of hydrogen gas, ammonia gas in the discharge tube etc.

Question 8.
What is absorption spectra? Give their types.
Answer:
Absorption spectra: When light is allowed to pass through a medium or an absorbing substance then the spectrum obtained is known as absorption spectrum. It is the characteristic of absorbing substance. Absorption spectrum is classified into three types:
(i) Continuous absorption spectrum:
When the light is passed through a medium, it is dispersed by the prism, we get continuous absorption spectrum. For instance, when we pass white light through a blue glass plate, it absorbs everything except blue. This is an example of continuous absorption spectrum.

(ii) Continuous absorption spectrum:
When light from the incandescent lamp is passed through cold gas (medium), the spectrum obtained through the dispersion due to prism is line absorption spectrum. Similarly, if the light from the carbon arc is made to pass through sodium vapour,-a continuous spectrum of carbon arc with two dark lines in the yellow region of sodium vapour is obtained.

(iii) Band absorption spectrum:
When the white light is passed through the iodine vapour, dark bands on continuous bright background is obtained. This type of band is also obtained when white light is passed through diluted solution of blood or chlorophyll or through certain solutions of organic and inorganic compounds.

Samacheer Kalvi 12th Physics Electromagnetic Waves Numerical problems

Question 1.
Consider a parallel plate capacitor whose plates are closely spaced. Let R be the radius of the plates and the current in the wire connected to the plates is 5 A, calculate the displacement current through the surface passing between the plates by directly calculating the rate of change of flux of electric field through the surface.
Solution:
The conduction current I_c = 5A
According to Gauss’s Law,
Electric flux, θ_E = \(\frac { q }{{ ε }{0}}\)

Question 2.
A transmitter consists of LC circuit with an inductance of 1 μH and a capacitance of 1 μF. What is the wavelength of the electromagnetic waves it emits?
Solution:
Inductance of LC circuit, L = 1 μH = 1 × 10^-6 H
Capacitance of LC circuit, C = 1 μF = 1 × 10^-6 F
Wave length of the electromagnetic wave X = λ = \(\frac { C }{ f }\)
Velocity of light C = 3 x 10⁸ ms^-1
Frequency of electromagnetic wave, f = \(\frac { 1 }{ 2\pi \sqrt { LC } } \)

= 0.1884 × 10⁴
λ = 18.84 × 10² m

Question 3.
A pulse of light of duration 10^-6 s is absorbed completely by a small object initially at rest. If the power of the pulse is 60 x 10^-3 W, calculate the final momentum of the object.
Solution:
Duration of the absorption of light pulse, t = 10^-6 s
Power of the pulse P = 60 x 10^-3 W
Final momentum of the object, P = \(\frac { U }{ c }\)
Velocity of light, C = 3 x 10⁸
Energy U = power x time
Momentum, P = \(\frac{60 \times 10^{-3} \times 10^{-6}}{3 \times 10^{8}}\)
P = 20 × 10^-17 kg m s^-1

Question 4.
Let an electromagnetic wave propagate along the x direction, the magnetic field oscillates at a frequency of 10¹⁰ Hz and has an amplitude of 10^-5 T, acting along the y – direction. Then, compute the wavelength of the wave. Also write down the expression for electric field in this case.
Solution:
Frequency of electromagnetic wave, v = 10¹⁰ Hz
Amplitude of Oscillating magnetic field, B₀ = 10^-5 T
Wave length of the wave, λ = \(\frac { C }{ f }\) = \(\frac{3 \times 10^{8}}{10^{10}}\) = 3x 10^-2 m
Amplitude of oscillating electric field, E₀ = B₀ C
C = \(\frac {{ E }_{0}}{ { B }_{0} }\)
E₀ = 10^-5 × 3 × 10⁸
E₀ = 3 × 10³ = NC^-1
Experession for electric field in Oscillataing wave
E = E₀ sin (kx -wt)
K = \(\frac { 2π }{ λ }\) = \(\frac{2 \times 3.14}{3 \times 10^{-2}}\) = 209 x 10²
W = 2πƒ = 2 × 3.14 x 10¹⁰ = 6.28 × 10¹⁰
\(\vec { E } \) = 3 x 10³ sin (2.09 × 10² x – 6.28 × 10¹⁰ t) \(\hat{i}\) NC^-1.

Question 5.
If the relative permeability and relative permittivity of the medium is 1.0 and 2.25, respectively. Find the speed of the electromagnetic wave in this medium.
Solution:
Relative permeability of the medium, μ_r = 1
Relative permitivity of the medium, ε_r = 2.25

Speed of electromagnetic wave, v = \(\frac { 1 }{ \sqrt { \mu \varepsilon } } \)

Samacheer Kalvi 12th Physics Electromagnetic Waves Additional Questions Solved

I Choose the Correct Answer from the Following

Question 1.
The speed of electromagnetic waves in vacuum is given by
(a) μ₀ε₀
(b) \(\sqrt { { \mu }_{ 0 }{ \varepsilon }_{ 0 } } \)
(c) \(\frac { 1 }{ { \mu }_{ 0 }{ \varepsilon }_{ 0 } } \)
(d) \(\frac { 1 }{ \sqrt { { \mu }_{ 0 }{ \varepsilon }_{ 0 } } } \)
Answer:
(d) \(\frac { 1 }{ \sqrt { { \mu }_{ 0 }{ \varepsilon }_{ 0 } } } \).

Question 2.
In an electromagnetic wave the electric field vector E and magnetic field vector B are
(a) Perpendicular to each other
(b) Parallel to each other
(c) at 45° to each other
(d) can have any angle between them
Answer:
(a) Perpendicular to each other.

Question 3.
If E and B be the electric and magnetic field vectors of an electromagnetic wave, then the propagation of the wave is along the direction of
(a) E
(b) B
(c) E x B
(d) Bx E
Answer:
(c) E x B.

Question 4.
In which of the following sequences are the electro magnetic radiations in decreasing order of wavelength
(a) Infrared, radio, X-rays, visible
(b) Radio, infrared, visible, X-rays
(c) Radio, visible, infrared, X-rays
(d) X-rays, visible, infrared, radio
Answer:
(b) Radio, infrared, visible, X-rays .

Question 5.
Ozone layer absorbs
(a) Infrared radiation
(b) Microwaves
(c) Radio waves
(d) UV radiation
Answer:
(d) UV radiation.

Question 6.
A RADAR beam consists of
(a) X-rays
(b) IR rays
(c) UV rays
(d) Microwaves
Answer:
(d) Microwaves.

Question 7.
Which of the following radiations has the longest wavelength?
(a) Radio waves
(b) IR radiation
(c) X-ray
(d) Visible light
Answer:
(a) Radio waves.

Question 8.
TV waves have a wavelength range of 1 – 10 metre. Their frequency range in MHz is
(a) 300 – 3000
(b) 3 – 3000
(c) 30 – 300
(d) 3 – 30
Answer:
(c) 30 – 300.

Question 9.
The electromagnetic radiation most prevalent in the atmosphere is
(a) Visible light
(b) Infrared
(c) UV
(d) Radio waves
Answer:
(b) Infrared.

Question 10.
Consider an electric charge oscillating with frequency of 10MHz. The radiation emitted will have a wavelength eqal to
(a) 20m
(b) 30m
(c) 40m
(d) 10m
Answer:
(b) 30m
Hint:
Wave length, λ = \(\frac { C }{ v }\) = \(\frac{3 \times 10^{8}}{10 \times 10^{6}}\)
= 0.3x 10² = 30m.

Question 11.
The frequencies of X-rays, v-rays and UV rays are respectively a, b and c. Then
(a) a < b, b < c
(b) a < b, b > c
(c) a > b, b > c
(d) a > b, b < c
Answer:
(b) a < b, b > c .

Question 12.
Greenhouse effect is caused by
(a) UV rays
(b) X-rays
(c) Gamma rays
(d) IR rays
Answer:
(d) IRrays.

Question 13.
If a capacitance C is connected across an inductance L, then the angular frequency is
(a) \( \sqrt{LC} \)
(b) LC
(c) \(\sqrt { \frac { L }{ C } } \)
(d) \(\sqrt { \frac { 1 }{ LC } } \)
Answer:
(d) \(\sqrt { \frac { 1 }{ LC } } \).

Question 14.
If ε₀ and μ₀ are the electric permitivity and permeability of free space, ε and μ are the corresponding quantities in a medium, then the index of refraction of the medium is

Answer:
(d) \(\sqrt { \frac { \varepsilon \mu }{ { \varepsilon }_{ 0 }{ \mu }_{ 0 } } } \)
Hint:
Index of refraction

Question 15.
Dimensions of \(\frac { 1 }{ { \mu }_{ 0 }{ \varepsilon }_{ 0 } } \) where symbols have their usual meaning, are
(a) [L^-2 T²]
(b) [L² T^-2]
(c) [LT^-1]
(d) [L^-1 T]
Answer:
(b) [L² T^-2]
Hint:

Question 16.
If λ_v, λ_x, λ_m, represent the wavelength of visible light, X-rays and microwaves, respectively, then
(a) λ_m >λ_v > λ_x
(b) λ_m > λ_x > λ_v
(c) λ_v > λ_m > λ_x
(d) λ_v > λ_x > λ_m
Answer:
(a) λ_m >λ_v > λ_x.

Question 17.
The ratio of amplitude of magnetic field to the amplitude of electric field for an electromagnetic wave propagating in vacuum is equal to
(a) the speed of light in vacuum
(b) reciprocal of the speed of light in vacuum
(c) the ratio of magnetic permeability to electric susceptibility in vacuum
(d) unity
Answer:
(b) reciprocal of the speed of light in vacuum.

Question 18.
Which of the following radiations forms part of the electromagnetic spectrum?
(a) alpha rays
(b) Beta rays
(c) Gamma rays
(d) Cathode rays
Answer:
(c) Gamma rays.

Question 19.
The ozone layer absorbs radiation of wavelegnths
(a) Less than 3 x 10^-7 m
(b) More than 3 x 10^-7 m
(c) Less than 3 x 10^-5 m
(d) More than 3 x 10^-5 m
Answer:
(a) Less than 3 x 10^-7 m.

Question 20.
It is possible to take pictures of those objects which are not fully visible to the eye using camera films sensitive to
(a) UV rays
(b) IR rays
(c) Microwaves
(d) Radio waves
Answer:
(b) IRrays.

Question 21.
An electromagnetic wave has wavelength 10cm. It is in the
(a) Visible region
(b) Radio region
(c) UV region
(d) X-ray region
Answer:
(b) Radio region.

Question 22.
Electromagnetic radiation of frequency 3 x 10⁵ MHz lies in the
(a) Radio wave region
(b) Visible region
(c) IR region
(d) Microwave region
Answer:
(d) Microwave region.

Question 23.
Radio waves and visible light in vacuum have
(a) Same wavelength but different velocities
(b) Same velocity but different wavelength
(c) Different velocities and different wavelengths
(d) Same velocity and same wavelength
Answer:
(b) Same velocity but different wavelength.

Question 24.
Which of the following has maximum frequency?
(a) X-rays
(b) IR rays
(c) UV rays
(d) Radio waves
Answer:
(a) X-rays.

Question 25.
Electromagnetic radiation of frequency 1 GHz lies in
(a) UV region
(b) IR region
(c) Visible region
(d) Microwave region
Answer:
(d) Microwave region.

Question 26.
An electromagnetic wave of frequency v = 3.0MHz passes from vacuum into a dielectric medium with permitivity s = 4.0 ε₀. Then
(a) Wavelength is doubled and frequency becomes half
(b) Wavelength is doubled and the frequency remains unchanged.
(c) Wavelength and frequency both remain unchanged
(d) Wavelength is halved and frequency remains unchanged.
Answer:
(d) Wavelength is halved and frequency remain unchanged.
Hint:
When a wave goes from one medium to another, its frequency remains unchanged.
According to equation C = \(\frac { 1 }{ \sqrt { \mu \varepsilon } } \), the speed is halved. Therefore, the wavelength is also halved.

Question 27.
Frequency of a wave is 6 x 10¹⁵ Hz. The wave is
(a) Radio wave
(b) Microwave
(c) X-ray
(d) UV rays
Answer:
(d) UV rays.

Question 28.
In an electromagnetic wave the phase difference between electric field \(\vec { E } \) and magnetic field \(\vec { B } \) is
(a) \(\frac { π }{ 4 }\)
(b) \(\frac { π }{ 2 }\)
(c) π
(d) zero
Answer:
(d) Zero.

Question 29.
The energy in an electromagnetic wave is
(a) Wholly shared only by electric field vector
(b) Wholly shared only by magnetic field vector
(c) Equally divided between electric and magnetic field
(d) Zero
Answer:
(c) Equally divided between electric and magnetic field.

Question 30.
Electromagnetic waves are produced by
(a) Atoms and molecules in an electrical discharge
(b) Electric device
(c) Accelerated charges
(d) Molecules of hot bodies
Answer:
(c) Accelerated charges.

II Fill in The Blanks

Question 1.
Electromagnetic waves are ……………
Answer:
Transverse in nature

Question 2.
Accelerated charge is a source of ……………
Answer:
Electromagnetic radiation

Question 3.
In electromagnetic waves, angle between electric and magnetic field vectors is ……………
Answer:
90°

Question 4.
The electromagnetic waves travel in vacuum or free space with a velocity of ……………
Answer:
3 x 10⁸ ms^-1

Question 5.
The existance of electromagnetic waves was confirmed experimentally by ……………
Answer:
Hertz.

Question 6.
Radio frequency wave have wavelength ranging from ……………to ……………
Answer:
10 m to 10⁴ m

Question 7.
The waves that are used in radio and television communication system is ……………
Answer:
Radio waves

Question 8.
The frequency range of X-rays is from ……………
Answer:
3 x 10¹⁸ Hz to 10¹⁶ Hz

Question 9.
Higher frequencies upto 54 mHz are used for ……………
Answer:
Short wave brands

Question 10.
The wave that is used in radar communication system is ……………
Answer:
Microwaves.

Question 11
…………… rays are used to detect forged documents.
Answer:
UV-rays.

Question 12
…………… is used for treatment of cancer.
Answer:
γ – rays (gamma rays).

Question 13.
Structure of atoms can be studied with ……………
Answer:
X-rays

Question 14.
When the light emitted directly from a source is examined with a spectrometer, the spectrum obtained is …………… spectrum.
Answer:
Emission

Question 15.
When the light emitted from a source is made to pass through an absorbing material, the spectrum obtained is called …………… spectrum.
Answer:
Absorption.

Question 16.
Electromagnetic disturbance can be propagated through space ……………
Answer:
without the help of material medium.

Question 17.
The velocity of electromagnetic wave is given by the relation ……………
Answer:
C = \(\frac { 1 }{ \sqrt { { { \mu }_{ 0 } }{ { \varepsilon }_{ 0 } } } } \)

III Match the following

Question 1.
(i) Light – (a) Medical surgery
(ii) Laser – (b) Law of induction
(iii) Radar – (c) Electromagnetic waves
(iv) Maxwell – (d) Defence (detection system)
Answer:
(i) → (c)
(ii) → (a)
(iii) → (d)
(iv) → (b)

Question 2.
(i) Gauss Law – (a) Electromagnetic induction
(ii) Faraday’s Law – (b) φ =\(\frac { q }{{ ε }_{0}}\)
(iii) Speed of light – (c) Electromagnetic oscillators
(iv) Microwaves – (d) 3 x 10⁸ ms^-1
Answer:
(i) → (b)
(ii) → (a)
(iii) → (d)
(iv) → (c)

Question 3.
(i) Gamma ray – (a) Structure of molecules
(ii) Visible light – (b) Treatment of cancer
(iii) UV radiation – (c) Detecting fractures
(iv) X-rays – (d) Destroy bacteria
Answer:
(i) → (b)
(ii) → (a)
(iii) → (d)
(iv) → (c)

Question 4.
(i) Continuous emission spectra – (a) Atomic hydrogen
(ii) Line emission spectra – (b) Ammonia gas
(iii) Band emission spectra – (c) Incandescent solids
(iv) Band absorption spectra – (d) Blood (or) chlorophyl
Answer:
(i) → (c)
(ii) → (a)
(iii) → (b)
(iv) → (d)

IV Assertion and Reason Questions

(a) If both assertion and reason are true and the reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but the reason is not the correct explanation of the assertion.
(c) If assertion is true but-reason is false.
(d) If the assertion and reason both are false.
(e) If the assertion is false but reason is true.

Question 1.
Assertion: In Hertz experiment, the electric vector of radiation produced by the source gap is parallel to the gap.
Reason: Production of sparks between the detector gap is maximum when it is placed perpendicular to the source gap.
Answer:
(c) If assertion is true but reason is false.
Explanation:
Hertz experimentally observed that the production of spark between the detection gap is maximum when it is placed parallel to source gap. This means that the electric vector of radiation produced by the source gap is parallel to the two gaps.

Question 2.
Assertion: Ultraviolet radiation are of higher frequency waves are dangerous to human being.
Reason: Ultraviolet radiation are absorbed by the atmosphere.
Answer:
(b) If assertion and reason both are true but reason is not the correct explanation of the assertion.
Explanation:
The wavelength of these waves ranges between 6 x 10^-10m to 4 x 10^-7 m that is smaller wavelength and higher frequency. They are absorbed by atmosphere and convert oxygen into ozone. They cause skin diseases and they are harmful to eye and cause permanent blindness.

Question 3.
Assertion: Only microwaves are used in RADAR.
Reason: Because microwaves have very small wavelength.
Answer:
(a) If assertion and reason both are true and reason is the correct explanation of the assertion.
Explanation:
In a RADAR, a beam signal is needed in particular direction which is possible if wavelength of wave is very small. Since the wavelength of microwaves is a few millimeter, hence they are used in RADAR.

Question 4.
Assertion: Radio waves bend in a magnetic field.
Reason: Radio waves are electromagnetic in nature.
Answer:
(a) If assertion and reason both are true and reason is the correct explanation of the assertion.

Question 5.
Assertion:
In the visible spectrum of light, red light is more energetic than green light.
Reason:
The wavelength of red light is more than that of green light.
Answer:
(a) If assertion and reason both are true and reason is the correct explanation of the assertion.

Samacheer Kalvi 12th Physics Electromagnetic Waves Short Answer Questions

Question 1.
Name the scientist who first predicted the existence of electromagnetic waves.
Answer:
James Clerk Maxwell was first predicted the existence of EM waves.

Question 2.
Distinguish between conduction current and displacement current.
Answer:
Conduction Current:

1. It is due to the flow of electrons in a circuit.
2. It exists even if electrons flow at a uniform rate.

Displacement Current:

1. It is due to time-varying electric field.
2. It does not exist under steady conditions.

Question 3.
What oscillates in electromagnetic waves?
Answer;
In EM waves, electric and magnetic fields oscillate in mutually perpendicular directions. These waves are transverse in nature.

Question 4.
Name the basic source of electromagnetic waves.
Answer:
An electric dipole is a basic source of electro magnetic waves.

Question 5.
State Maxwell’s equations.
Answer:
The whole study of electricity and magnetism can be described mathematically with the help of four fundamental equations, called Maxwell’s equations. These are stated as follows:

1. Gauss law of electrostatics : \(\oint { \vec { E } } \).\(\vec { d } \)s = 0 \(\frac { q }{{ ε }{0}}\)
2. Gauss law of magnetism: \(\oint { \vec { E } } \).\(\vec { d } \)s = 0
3. Faraday’s Law of electromagnetic induction: \(\oint { \vec { E } } \).\(\vec { d } \)l = – \(\frac{d \phi_{\mathrm{B}}}{d t}\) = –\(\frac { d }{ dt }\) \(\left[ \oint { \vec { B. } \vec { d } s } \right] \)
4. Modified ampere’s circuital Law: \(\oint { \vec { E } } \).\(\vec { d } \)l = μ₀ \(\left[\mathrm{I}_{\mathrm{C}}+\varepsilon_{0} \frac{d \phi_{\mathrm{E}}}{d t}\right]\)

Question 6.
What is electromagnetic spectrum.
Answer:
The orderly distribution of electromagnetic radiations of all types according to their wavelength or frequency into distinct groups having widely differing properties is called electromagnetic spectrum.

Question 7.
Define spectrum.
Answer:
The definite pattern of colours obtained on the screen after dispersion is called as spectrum.

Question 8.
Write down the concept of black body spectrum.
Answer:
When an object bums, it emits colours. That is, it emits electromagnetic radiation which depends on temperature. If the object becomes hot then it glows in red colour. If the temperature of the object is further increased then it glows in reddish-orange colour and becomes white when it is hottest. The spectrum usually called as black body spectrum.

Question 9.
How are radio waves produced?
Answer:
Radiowaves are produced due to accelerated motion of electrons in conducting wires or oscillating circuits.

Question 10.
How are X-rays produced?
Answer:
X-rays are produced due to sudden deceleration of fast moving electrons by a metal target.

Question 11.
How are microwaves produced?
Answer:
Microwaves are produced due to oscillating currents in special vacuum tubes like Klystroms.

Question 12.
What is ‘Greenhouse effect’?
Answer:
Greenhouse effect is the phenomenon which keeps the earth’s surface warm at night. The earth reflects back infra red part of solar radiation. Infra-red rays are reflected back by low lying clouds and lower atmosphere and keep the earth’s surface warm at night.

Question 13.
Why are microwaves used in RADAR?
Answer:
Microwaves have wavelength of the order of a few millimetres. Due to their short wavelengths, these are not diffracted (bent) much by objects of normal dimensions. So they can be transmitted as a beam in a particular direction.

Question 14.
Write down the uses of radiowaves?
Answer:
It is used in radio and television communication systems and also in cellular phones to transmit voice communication in the ultra high frequency band.

Question 15.
Write down the uses of radiowaves?
Answer:
It is used in radar system for aircraft navigation, speed of the vehicle, microwave oven for cooking and very long distance wireless communication through satellites.

Question 16.
Write uses of IR rays (or) infra-red radiations.
Answer:
It is used to produce dehydrated fruits; in green houses to keep the plants warm, heat therapy for muscular pain or sprain, TV remote as a signal carrier, to look through haze fog or mist and used in night vision or infrared photography.

Question 17.
Write down the uses of UV rays (or) Ultraviolet radiations.
Answer:
It is used to destroy bacteria, sterilizing the surgical instruments, burglar alarm, detect the invisible writing, finger prints and also in the study of molecular structure.

Question 18.
What are the uses of X-rays?
Answer:
X-rays are used extensively in studying structures of inner atomic electron shells and crystal structures. It is used in detecting’fractures, diseased organs, formation of bones and stones, observing the progress of healing bones. Further, in a finished metal product, it is used to detect faults, cracks, flaws and holes.

Question 19.
What are emission spectrum? Write its types.
Answer:
When the spectrum of self luminous source is taken, we get emission spectrum. Each source has its own characteristic emission spectrum. The emission spectrum can be divided into
three types:

1. Continuous emission spectra.
2. Line emission spectrum (or line spectrum).
3. Band emission spectrum (or band spectrum).

Question 20.
What are absorption spectrum? Write its types
Answer:
When light is allowed to pass through a medium or an absorbing substance then the spectrum .obtained is known as absorption spectrum. It is the characteristic of absorbing substance.
Absorption spectrum is classified into three types:

1. Continuous absorption spectrum.
2. Line absorption spectrum.
3. Band absorption spectrum.

Samacheer Kalvi 12th Physics Electromagnetic Waves Long Answer Questions

Question 1.
Write short notes on (a) Infrared radiation (b) Ultraviolet radiation (c) Gamma radiation).
Answer:
(a) Infrared radiation:
It is produced from hot bodies (also known as heat waves) and also when the molecules undergo rotational and vibrational transitions. The wavelength range is 8 x 10^-7 m to 5 x 10³ m and frequency range are 4 x 10¹⁴ Hz to 6 x 10¹⁰ Hz. It provides electrical energy to satellites by means of solar cells. It is used to produce dehydrated fruits, in green houses to keep the plants warm, heat therapy for muscular pain or sprain, TV remote as a signal carrier, to look through haze fog or mist and used in night vision or infrared photography.

(b) Ultraviolet radiation:
It is produced by Sun, arc and ionized gases. The wavelength range is 6 x 10^-10 m to 4 x 10^-7 m and frequency range are 5 x 10¹⁷Hz to 7 x 10¹⁴ Hz. It has less penetrating power. It can be absorbed by atmospheric ozone and harmful to human body. It is used to destroy bacteria, sterilizing the surgical instruments, burglar alarm, detect the invisible writing, finger prints and also in the study of molecular structure.

(c) Gamma rays:
It is produced by transitions of atomic nuclei and decay of certain elementary particles. They produce chemical reactions on photographic plates, fluorescence, ionisation, diffraction. The wavelength range is 1 x 10^-14 m to 1 x 10^-10 m and frequency range are 3 x 10²² Hz to 3 x 10¹⁸ Hz. Gamma rays have high penetrating power than X-rays and ultraviolet radiations; it has no charge but harmful to human body. Gamma rays provide information about the structure of atomic nuclei. It is used in radio therapy for the treatment of cancer and tumour, in food industry to kill pathogenic microorganism.

Samacheer Kalvi 12th Physics Electromagnetic Waves Numerical Problems

Question 1.
A parallel plate capacitor has circular plates, each of radius 5.0 cm. It is being charged so that electric field in the gap between its plates rises steadily at the rate of 10¹² V m^-1 s^-1.What is the displacement current?
Solution:
Radius, r = 5cm = 5 x 10^-2 m
The rate okf electric frield, \(\frac { dE }{ dt }\) = 10¹² V m^-1 s^-1
Displacement current, I_d = ε₀ \(\frac {{ dφ }_{E}}{ dt }\) =ε₀ \(\frac { d }{ dt }\) (EA) = ε₀ (πr²) \(\frac { dE }{ dt }\)
= 8.85 x 10^-12 x 3.14 x (5 x 10^-2)² x 10¹²
I_d= 0.069
I_d = 0.07 (or) 70 mA

Question 2.
The voltage between the plates of a parallel – plate capacitor of capacitance 1 µF is changing at the rate of 5Vs^-1. What is the displacement current in the capacitor?
Solution:
Capacitance of parallel plate capacitor, C = 1 µF
C= 1 x 10^-6 F
The rate of voltage b/n the plate, \(\frac { dv }{ dt }\) = 5 Vs^-1
Displacement current,
I_d = ε₀ \(\frac {{ dφ }_{E}}{ dt }\) =ε₀ \(\frac { d }{ dt }\) (EA)
ε₀ = A \(\frac { d }{ dt }\) \(\left( \frac { V }{ d } \right) \) E = \(\frac { V }{ d }\)
= \(\frac{\varepsilon_{\mathrm{o}} \mathrm{A}}{d}\) \(\frac { dV }{ dt }\) = C. \(\frac { dV }{ dt }\)
I_d = 1 x 10^-6 × 5
Id = 5µA.

Question 3.
Electromagnetic waves travels in a medium at a speed of 2 x 10⁸ ms^-1. The relative permeability of the medium is 1. Find the relative permitivity.
Solution:
Speed of an em wave in a medium is given by

Relative permitivity,

Question 4.
A radiation of energy E falls normally on a perfectly reflecting surface. Find the momentum transferred to the surface.
Solution:
Momentum of radiation of energy E is P = \(\frac { E }{ C }\)
Since the radiation is completely reflected, its momentum changes by \(\frac { 2E }{ C }\)
Therefore, by the law of conservation of momentum the momentum transferred to the surface is \(\frac { 2E }{ C }\).

Question 5.
The energy of the EM wave is of the order of 15KeV. To which part of the spectrum does it belong?
Solution:
E =hv = \(\frac { hc }{ λ }\) ⇒ λ = \(\frac { hc }{ E }\)
h = 6.626 x 10^-34 Js; c = 3 x 10⁸ ms^-1
E= 15 x 10³ eV = 15 x 10³ x 1.6 x 10^-19 V

λ = 0.8282 x Å
Hence X-rays

Question 6.
Light With an energy flux of 25 x 10⁴ Wm^-2 falls on a perfectly reflecting surface at normal incidence. If surface area is 15cm², to calculate the average force exerted on the surface.
Solution:
Average force = momentum transferred per second
F_av = \(\frac { P }{ T }\) = \(\frac { 2u }{ C }\)
Where U is the energy falling on th surface per second.
F_av = \(\frac{2 \times 25 \times 10^{4} \times 15 \times 10^{-4}}{3 \times 10^{8}}\) = 250 x 10^-8
F_av = 2.5 x 10^-6 N.

Common Errors And Its Rectifications
Common Errors :
1. Students do the mistakes most of times in unit of frequency. They write the units in improper ways. Eg. Hertz (or) H. This is the wrong way.
2. They may confuse the frequency range of radiations and wavelength range of radiation.

Rectifications:
1. The correct way of unit is hertz (or) Hz. The unit of frequency is hertz (or) Hz (or) s^-1.
2. The easy way to understand frequency and wavelength range of radiations are, Frequency increases the order of gamma, X-ray, UV, visible, IR, microwave, radiowave. Wavelength increases the order of the reverse of frequency order.

We believe that the shared knowledge about Tamilnadu State Board Solutions for 12th Physics Chapter 5 Electromagnetic Waves Questions and Answers learning resource will definitely guide you at the time of preparation. For more details visit Tamilnadu State Board Solutions for 12th Physics Solutions and for more information ask us in the below comments and we’ll revert back to you asap.

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.2

11th Maths Exercise 8.2 Question 1.
Verify whether the following ratios are direction cosines of some vector or not.

Solution:

11th Maths Vector Algebra Solutions Question 2.
Find the direction cosines of a vectors whose direction ratios are
(i) 1, 2, 3
(ii) 3, -1, 3
(iii) 0, 0, 7
Solution:

11th Maths Exercise 8.2 Answers Question 3.
Find the direction cosines and direction ratios for the following vectors

Solution:

11th Maths Vector Algebra Exercise 8.2 Question 4.
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians.
Solution:

11th Maths 8.2 Question 5.
If \(\frac{1}{2}, \frac{1}{\sqrt{2}}\), a are the direction cosines of some vector, then find a.
Solution:

Class 11th Maths Exercise 8.2 Solution Question 6.
If (a, a + b, a + b + c) is one set of direction ratios of the line joining (1, 0, 0) and (0, 1, 0), then find a set of values of a, b, c.
Solution:
Let A be the point (1, 0, 0) and B be the point (0, 1, 0) (i.e.,) \(\overrightarrow{\mathrm{OA}}=\hat{i}\) and \(\overrightarrow{\mathrm{OB}}=\hat{j}\)
Then \(\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}=\hat{j}-\hat{i}=-\hat{i}+\hat{j}\)
= (-1, 1, 0)
= (a, a + b, a + b + c)
⇒ a = -1, a + b = 1 and a + b + c = 0
Now a = -1 ⇒ -1 + b = 1 ;a + b + c = 0
⇒ b = 2; -1 + 2 + c = 0 ⇒ c + 1 = 0
⇒ c = -1
∴ a = -1; b = 2; c = -1.
Note: If we taken \(\overrightarrow{\mathrm{BA}}\) then we get a = 1, b = -2 and c = 1.

Class 11 Maths Chapter 8 Exercise 8.2 Solutions Question 7.
Show that the vectors \(2 \hat{i}-\hat{j}+\hat{k}, 3 \hat{i}-4 \hat{j}-4 \hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}\) form a right angled triangle.
Sol:

⇒ The given vectors form the sides of a right angled triangle.

11th Maths Guide Question 8.
Find the value of k for which the vectors \(\vec{a}=3 \hat{i}+2 \hat{j}+9 \hat{k}\) and \(\vec{b}=\hat{i}+\lambda \hat{j}+3 \hat{k}\) are parallel.
Solution:

Samacheer Guru 11th Maths Question 9.
Show that the following vectors are coplanar.

Solution:
Let the given three vectors be \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\). When we are able to write one vector as a linear combination of the other two vectors, then the given vectors are called coplanar vectors.




We are able to write \(\vec{a}\) as a linear combination of \(\vec{b}\) and \(\vec{c}\)
∴ The vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) are coplanar

11th Samacheer Maths Solutions Question 10.
Show that the points whose position vectors and are coplanar
Solution:
Let the given points be A, B, C and D. To prove that the points A, B, C, D are coplanar, we have to prove that the vectors \(\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AC}}\) and \(\overrightarrow{\mathrm{AC}}\) are coplanar



∴ we are able to write one vector as a linear combination of the other two vectors ⇒ the given vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) are coplanar.
(i.e.,) the given points A, B, C, D are coplanar.

Samacheer Kalvi 11th Guide Maths Question 11.
If \(\vec{a}=2 \hat{i}+3 \hat{j}-4 \hat{k}\), \(\vec{b}=3 \hat{i}-4 \hat{j}-5 \hat{k}\) and \(\vec{c}=-3 \hat{i}+2 \hat{j}+3 \hat{k}\), find the magnitude and direction cosines of
(i) \(\vec{a}+\vec{b}+\vec{c}\)
(ii) \(3 \vec{a}-2 \vec{b}+5 \vec{c}\)
Solution:

>

Samacheer Kalvi 11th Maths Question 12.
The position vectors of the vertices of a triangle are and . Find the perimeter of the triangle
Solution:
Let A, B, C be the vertices of the triangle ABC,

11 Samacheer Maths Solutions Question 13.
Find the unit vector parallel to and
Solution:

12th Maths Exercise 8.2 Samacheer Kalvi Question 14.
The position vector \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) three points satisfy the relation \(2 \vec{a}-7 \vec{b}+5 \vec{c}=\overrightarrow{0}\). Are these points collinear?
Solution:

10th Maths Exercise 8.2 Samacheer Kalvi Question 15.
The position vectors of the point P, Q, R, S are and respectively. Prove that the line PQ and RS are parallel.
Solution:

Ex 8.2 Class 11 Question 16.
Find the value or values of m for which \(m(\hat{i}+\hat{j}+\hat{k})\) is a unit vector
Solution:

11th Maths 8th Chapter Question 17.
Show that the points A(1, 1, 1), B(1, 2, 3) and C(2, -1, 1) are vertices of an isosceles triangle.
Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.2 Additional Problems

Samacheer Kalvi Maths Guide 11th Question 1.
Show that the points whose position vectors given by


Solution:

Samacheer Kalvi.Guru 11th Maths Question 2.
Find the unit vectors parallel to the sum of \(3 \hat{i}-5 \hat{j}+8 \hat{k}\) and \(-2 \hat{j}-2 \hat{k}\)
Solution:

Maths Guide 11th Question 3.
The vertices of a triangle have position vectors Prove that the triangle is equilateral.
Solution:

Maths Solutions Class 11 Samacheer Kalvi Question 4.
Prove that the points form an equilateral triangle.
Solution:

Samacheer Kalvi 11th Maths Solution Book Question 5.
Examine whether the vectors are coplanar
Solution:


⇒ We are not able to write one vector as a linear combination of the other two vectors
⇒ the given vectors are not coplanar.

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 9 Probability Ex 9.1

9th Maths Exercise 9.1 Question 1.
You are walking along a street. If you just choose a stranger crossing you, what is the probability that his next birthday will fall on a Sunday?
Solution:
Days in a week (S) = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
n( S) = 7
∴ No. of days in week = 7
Event of selecting Sunday (A) = {Sunday}
n(A) = 1
∴ Probability of selecting Sunday = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{1}{7}\)

9th Class Maths Exercise 9.1 Solution Question 2.
What is the probability of drawing a King or a Queen or a Jack from a deck of cards?
Solution:
Number of cards n(S) = 52
No. of King cards n(A) = 4
No. of Queen cards n(B) = 4
No. of Jack cards n(C) = 4
Probability of drawing a King card
\(=\quad \frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{4}{52}\)
Probability of drawing a Queen card
\(=\frac{n(\mathrm{B})}{n(\mathrm{S})}=\frac{4}{52}\)
Probability of drawing a Jack card
\(=\frac{n(\mathrm{C})}{n(\mathrm{S})}=\frac{4}{52}\)
The Probability of drawing a King or a Queen or a Jack from a deck of cards
\(=\mathrm{P}(\mathrm{A})+\mathrm{P}(\mathrm{B})+\mathrm{P}(\mathrm{C})=\frac{4}{52}+\frac{4}{52}+\frac{4}{52}=\frac{4+4+4}{52}=\frac{12}{52}=\frac{3}{13}\)

9th Class Math 9.1 Exercise Solution Question 3.
What is the probability of throwing an even number with a single standard dice of six faces?
Solution:
Faces of a dice (S) = {1, 2, 3, 4, 5, 6}
n(S) = 6
Event of throwing an even number
A = {2, 4, 6}, n(A) = 3

Samacheer Kalvi 9th Maths Guide Question 4.
There are 24 balls in a pot. If 3 of them are Red, 5 of them are Blue and the remaining are Green then, what is the probability of picking out
(i) a Blue ball,
(ii) a Red ball and
(iii) a Green ball?
Solution:
n(S) = 24
Red – n(R) = 3
Blue – n(B) = 5
Green – n(G) = 16

9th Maths 9.1 Question 5.
When two coins are tossed, what is the probability that two heads are obtained?
Solution:
Sample space when two coins are tossed (S) = {HH, TT, HT, TH}
n(S) = 4
Event of getting two heads (A) = {HH}
n(A) = 1
Probability of getting two heads P(A) = \(\frac{n(\mathrm{A})}{n(\mathrm{S})}=\frac{1}{4}\)

Class 9 Maths Ex 9.1 Solutions Question 6.
Two dice are rolled, find the probability that the sum is
(i) equal to 1
(ii) equal to 4
(iii) less than 13
Solution:
When two dice are rolled Sample space

9th Maths Exercise 9.1 Samacheer Kalvi Question 7.
A manufacturer tested 7000 LED lights at random and found that 25 of them were defective. If a LED light is selected at random, what is the probability that the selected LED light is a defective one.
Solution:
n(S) = 7000 S – Total no. of lights.
n(A) = 25 A – Defective ones.

Samacheer Kalvi 9th Maths Question 8.
In a football match, a goalkeeper of a team can stop the goal, 32 times out of 40 attempts tried by a team. Find the probability that the opponent team can convert the attempt into a goal.
Solution:
Total no. of attempts n(S) = 40
Total no. of attempts by A team n(A) = 32
Total no. of attempts by the opponent team B = n(B) = 40 – 32 = 8

9 Maths Samacheer Kalvi Question 9.
What is the probability that the spinner will not land on a multiple of 3?
Solution:
Total no. of choices n(S) = 8
Total no. of multiples of 3 A = {3, 6}
n(A) = 2
Event of non-multiples of 3B = {1, 2, 4, 5, 7, 8}
n(B) = 6

Class 9th Maths Chapter 9 Exercise 9.1 Question 10.
Frame two problems in calculating probability, based on the spinner shown here.

Solution:
(i) What is the probability that the spinner will land on an even number?
(ii) What is the probability that the spinner will not land on a prime number.

Guys who are planning to learn and understand the topics of 10th Social ScienceEconomics can grab this Tamilnadu State board solutions for Chapter 3 Food Security and Nutrition Questions and Answers from this page for free of cost. Make sure you use them as reference material at the time of preparation & score good grades in the final exams.

Students who feel tough to learn concepts can take help from this Samacheer Kalvi 10th Social Science Book Solutions Guide Pdf, all the Questions and Answers can easily refer in the exams. Go to the below sections and get 10th Social ScienceEconomics Chapter 3 Food Security and Nutrition Tamilnadu State Board Solutions PDF.

Tamilnadu Samacheer Kalvi 10th Social Science Economics Solutions Chapter 3 Food Security and Nutrition

Do you feel scoring more marks in the 10th Social ScienceEconomics Grammar sections and passage sections are so difficult? Then, you have the simplest way to understand the question from each concept & answer it in the examination. This can be only possible by reading the passages and topics involved in the 10th Social ScienceEconomics Board solutions for Chapter 3 Food Security and Nutrition Questions and Answers. All the Solutions are covered as per the latest syllabus guidelines. Check out the links available here and download 10th Social ScienceEconomics Chapter 3 textbook solutions for Tamilnadu State Board.

Food Security and Nutrition Textual Exercise

I. Choose the correct answer.

Economics Class 10 Chapter 3 Question 1.
………….. of food is physical availability of food stocks in desired quantities, which is a function of domestic production, changes in stocks and imports.
(a) Availability of food
(b) Access to food
(c) Absorption of food
(d) none
Answer:
(a) Availability of food

Question 2.
Buffer stock is the stock of food grains, namely wheat and rice, procured by the government through the:
(a) FCI
(b) Consumer Cooperatives
(c) ICICI
(d) IFCI
Answer:
(a) FCI

Question 3.
Which is correct?
(i) HYV-High Yielding Varieties
(ii) MSP-Minimum Support Price
(iii) PDS-Public Distribution System
(iv) FCI-Food Corporation of India
(a) (i) and (ii) are correct
(b) (iii) and (iv) are correct
(c) (ii) and (iii) are correct
(d) all are correct
Answer:
(d) all are correct

Question 4.
……………….. extended assistance through its Public Law 480.
(a) United States of America
(b) India
(c) Singapore
(d) UK
Answer:
(a) United States of America

Question 5.
………….. revolution was bom in India paving way for self sufficiency in food grain production.
(a) Blue Revolution
(b) White Revolution
(c) Green Revolution
(d) Grey Revolution
Answer:
(c) Green Revolution

Question 6.
……………….. is the only state in India to adopt universal PDS.
(a) Kerala
(b) Andhra Pradesh
(c) Tamil Nadu
(d) Karnataka
Answer:
(c) Tamil Nadu

Question 7.
…………. is the process of providing or obtaining the food necessary for health and growth.
(a) Health
(b) Nutrition
(c) Sanitation
(d) Security
Answer:
(b) Nutrition

Question 8.
Tamil Nadu Integrated Nutrition Programme was started in:
(a) 1980
(b) 1975
(c) 1955
(d) 1985
Answer:
(a) 1980

Question 9.
………….. status is one of the indicators of the overall well-being of population and human resources development.
(a) Health
(b) Nutritional
(c) Economic
(d) Wealth

Question 10.
Tamil Nadu Health System Projects has launched ……………….. service at free of cost.
(a) 106 Ambulance
(b) 108 Ambulance
(c) 107 Ambulance
(d) 105 Ambulance
Answer:
(b) 108 Ambulance

II. Fill in the blanks.

1. ………….. foundation from USA introduced HYV in India.
2. ………… is an important indicator of nutrition deficiency.
3. In the year …………… National Food Security Act was passed by the Indian Parliament.
4. ………….. play an important role in the supply of quality goods at responsible rates to common people.
5. …………. is the value of currency expressed in terms of the amount of goods and services that one unit of money can buy.
Answers:
1. FORD
2. Underweight
3. 2013
4. Consumer co-operatives
5. Purchasing power

III. Match the following.

Answers:
1. (d)
2. (a)
3. (e)
4. (b)
5. (c)

IV. Assertion and Reason.

Question 1.
Assertion (A): Purchasing power increases, price decreases and vice versa.
Reason (R): The production of goods decline, the price of goods increases and then the purchasing power is affected.
(a) A is correct, R is false
(b) Both A and R are false statements
(c) A is correct but R is not a correct explanation
(d) A is correct, R is the correct explanation of A
Answer:
A is not correct and R is correct

V. Answer in Short.

Question 1.
Define food security according to FAO.
Answer:
“Food security exists when all people, at all times, have physical, social and economic access of sufficient, safe and nutritious food which meets their dietary needs and food preferences for an active and healthy life” FAO – 2009.

Question 2.
What are the basic components of food and nutrition security?
Answer:

• Availability of food
• Access to food
• Absorption of food

Question 3.
Explain ‘ship to mouth’ phenomenon.
Answer:
After India’s Independence, during early 1960’s India experienced severe drought that forced her to plead for food grains from richer countries at concessional rates. USA extended help through its Public Law 480 (PL480). This situation was popularly known as ship to mouth phenomenon.

Question 4.
What is the role of FCI in Green Revolution?
Answer:
Minimum support price (MSP) for the crops were announced at the beginning of the season and the state procured the harvested grains through the Food Corporation of India (FCI). The FCI had built huge storage godowns and built buffer stocks of food grain during the harvest season to be distributed all through the year.

Question 5.
What are the effects of Green Revolution?
Answer:

1. Country became self-sufficient in food production.
2. Increase in the yield of major cereal crops and area under cultivation.
3. Cheaper farm credit was given to farmers through co-operative banks.

Question 6.
Write a note on Differential Universal PDS and Targeted PDS.
Answer:
While Tamil Nadu has adopted an ‘Universal’ PDS, the rest of the states in India had a ‘Targeted’ PDS. Under universal PDS all the family ration card holders are entitled to the supplies from PDS. In the targeted PDS, the beneficiaries are identified based on certain criteria and given their entitlements, leaving out the rest. Both the Union and the State governments subsidised the supplies distributed through PDS. The level and quantum of subsidy also varied across states.

Question 7.
Write a short note on purchasing power.
Answer:
The financial power to purchase goods is called purchasing power. It is Indirectly related to price. It is the value of a currency expressed interms of the amount of goods and services that one unit of money can buy.

Question 8.
What are the main reasons for the New Agricultural Policy?
Answer:
The main reason is to give an assurance that organic or processed agricultural products will not be under any export restrictions such as export duty, export bans and quota restriction. Agricultural policy of a country is mostly designed by the Government for raising agricultural production and productivity and also for raising the level of income and standard of living of farmers within a definite time frame. This policy is formulated for all round and comprehensive development of the agricultural sector.

Question 9.
Write short note on multi-dimensional nature of poverty.
Answer:

1. Multi-dimensional Poverty Index (MPI) was launched by the United Nations Development Programme (UNDP) and the oxford poverty Human Development Initiative in 2010.
2. It constitute factors like health, education, living standards, Income, dis-empowerment, quality of work, non-violence etc.
3. India has reduced poverty drastically from 55% to 28% in 10 years from 2005 -06 to 2015 – 16.

Question 10.
Write some name of the nutrition programmes in Tamil Nadu.
Answer:

• Purachi Thalaivar M.G.R. Nutrition Meal Programme
• National Programme of Nutritional Support to Primary Education
• General ICDS Projects and World Bank Assisted Integrated Child Development Services
• Pradhan Manthri Gramodaya Yojana Scheme (PMGYS)
• Tamil Nadu Integrated Nutrition Programme
• Mid-Day Meal Programme

VI. Answer in detail.

Question 1.
Elucidate why the Green Revolution was born.
Answer:
The Green Revolution was bom in the country paving way for self-sufficiency in food grain production. Increased food grain production was made possible by an increase area cultivated with HYV of rice and wheat as also an increase in the yield of these major cereal crops. Area under food grains was a little more than 98 million hectares during early 1950s. The country was producing just 54 million tonnes of food grains then with an average yield of food grains of 547 kg per hectare.

The food situation has steadily improved over a period of 65 years. Area under food grain cultivation has grown to 122 million hectares, with an increase of five-fold increase in food grain production. Yield of food grains has increased four-fold between the time of independence and at present.

Question 2.
Explain Minimum Support Price.
Answer:

1. Minimum support price is the price announced by the Government to support the farmers with a better price for particular crops.
2. The MSP is much helpful for the farmer’s because they are certain / sure about the price they would get at the crop season.
3. After announcing the MSP, the state will open procurement centres in places where these crops are widely grown.
4. Farmers get an assured price by selling their produce to Food Corporation of India (FCI) after the harvest.
5. But, if the farmers find open market price is lower than the minimum support price, then they are free to sell in the open market.
6. Thus, the farmers gain a kind of protection against any price crash during the harvest season.

Question 3.
Elaborate the Public Distribution System.
Answer:
The increase in food grain production need not result in increase in access to food for all. Given the unequal distribution of income and the level of poverty that persists in Indian economy, the government took steps to distribute food grains at subsidised rates through the Public Distribution System (PDS). The nature, scope and functioning of PDS varies from state to state. While Tamil Nadu has adopted an ‘Universal’ PDS, the rest of the states in India had a ‘Targeted’ PDS.

Under universal PDS all the family ration card holders are entitled to the supplies from PDS. In the targeted PDS, the beneficiaries are identified based on certain criteria and given their entitlements, leaving out the rest. Both the Union and the State governments subsidised the supplies distributed through PDS. The level and quantum of subsidy also varied across states.

Question 4.
What are the factors affecting the purchasing power and explain them.
Answer:
Purchasing power is the value of a currency expressed interms of the amount of goods and services that one unit of money can buy.

The factors affecting purchasing power are:

1. Over Population: Large population leads to increasing demand. But supply was not equal to the demand. So, the normal price level will go higher.
2. Increasing price of essential goods: The continuous rise in the prices of essential goods erodes the purchasing power and adversely affect the poor people.
3. Demand for goods: When demand for goods increases, the prices of goods increases, then the purchasing power is affected.
4. Price of goods affect the value of currency: When prices increases, the purchasing power decreases and finally the value of the currency decreases and vice versa.
5. Production and supply of goods: When the production and the supply of goods decreases, the price of the goods increases, then the purchasing power is affected.
6. Poverty and Inequality: In general, purchasing power is affected by poverty and unequal distribution of Income and wealth.

Question 5.
Write briefly some of the important objectives of India’s agricultural policy.
Answer:
• Raising the productivity of inputs: One of the important objectives of India’s agricultural policy is to improve the productivity of inputs so purchased like, HYV seeds, fertilisers, pesticides, irrigation projects etc.

• Raising value-added per hectare: Agricultural policy is to increase per hectare value-added rather than raising physical output by raising the productivity of agriculture in general and productivity of small and marginal holding in particular.

• Protecting the interests of poor farmers: Agricultural policy is proposed to protect the interests of poor and marginal farmers by abolishing intermediaries through land reforms, expanding institutional credit support to poor farmers etc.

• Modernizing agricultural sector: Here the policy support includes the introduction of modem technology in agricultural operations and application of improved agricultural inputs like HYV seeds, fertilizers etc.

• Environmental degradation: Agricultural policy of India has set another objective to check environmental degradation of natural base of Indian agriculture.

• Removing bureaucratic obstacles: The policy has set another objective to remove bureaucratic obstacles on the farmer’s co-operative societies and self-help institutions so that they can work independently.

Question 6.
Discuss the Multi-Dimensional Poverty Index India and Tamil Nadu.
Answer:
A multi-Dimensional poverty index is a measure to reveal who is poor, how they are poor and the ranges of disadvantages they experience.

Multi-Dimensional Poverty Index of India:

1. Poverty rate reduced from 55% in 2005 – 06 to 28% in 2015 – 16.
2. The number of poor people reduced from 635 million people 2005 – 06 to 364 million poor people in 2015 – 16.
3. Of these 364 million poor people, 156 million were children which was (292 million in 2005-06).
4. From the people belonging to ST category 80% were poor in 2005 – 06 which reduced to 50% in 2015 -16.
5. In 2015 – 16, Bihar is stated as the poorest state with more than half of its population in poor condition.
6. Multi-Dimensional poverty index is reduced to the maximum in Kerala by around 92% claiming to be the least poor region in 2006.
7. The four poorest states of India are Bihar, Jharkhand, Uttarpradesh and Madhyapradesh where 196 million MPI poor people live which is half of MPI of India.

Multi – Dimensional Poverty Index of Tamil Nadu:

1. The state of Tamil Nadu has a smaller share of India’s poor relative to its population.
2. Tamil Nadu leads in the poverty alleviation programmes during 2014-17.
3. The districts in Tamil Nadu are classified into three categories namely high – poverty districts (> 40%) moderately poor districts (30% to 40%) low – level poverty districts (< 30%).
4. Government of India is implementing many polices and programmes to eradicated poverty.
5. In future, Tamil Nadu can become a model Of development in India.

Question 7.
Briefly explain the nutritional and health status of Tamil Nadu.
Answer:
Status of Nutrition:
We noted earlier that food security includes nutrition security too. Though our country has reached self-sufficiency in food production, the nutrition status of the population has not seen corresponding levels of improvement. In 2015-16, 27% of the rural women and 16% of the urban women (in the age group of 15-49 years) were counted as undernourished or chronically energy deficient by the National Family Health Survey.

More than half of the women in the reproductive age group (15 – 49 years) in both rural and urban India were anaemic in 2015-16. As regards children, about 60% of the rural and 56% of the urban children (in the age group of 6-59 months) are counted to be anemic, in 2015-16. About 41% of the rural and 31% of urban children are stunted, that is, they are not ‘ of the required height in correspondence to their age. Another indicator of nutrition deficiency among children is “underweight”, which is weight in relation to age. In India, in 2015-16, about 20% of children(in the age group of 6-59 months) in rural and urban India are estimated to be underweight.

VII. Project and activity

Question 1.
Visit nearby “Uzhavar Sandhai” and collect the information about the functions of market.
Answer:
Do it yourself.

Question 2.
Collect information about health centre functioning nearby your location.
Answer:
Do it yourself.

Food Security and Nutrition Additional Questions

I. Choose the correct answer.

Question 1.
………….. in the ability to biologically utilise the food consumed.
(a) Absorption of food
(b) Access to food
(c) Availability of food
Answer:
(a) Absorption of food

Question 2.
The rapid increase in food grain production was accompanied by the ……………… sector also.
(a) Dairy
(b) Poultry
(c) Fisheries
(d) All the above
Answer:
(d) All the above

Question 3.
………… plays a crucial role in human health and well-being.
(a) Health
(b) Security
(c) Nutrition
Answer:
(c) Nutrition

Question 4.
There are ……………… structure of consumer co-operative societies in India.
(a) Two-tier
(b) Three-tier
(c) Five-tier
(d) Seven-tier
Answer:
(b) Three-tier

II. Fill in the blanks :

1. ………… scheme is playing an important role in food security in India.
2. ……….. is the stock of food grains, namely wheat and rice, procured by the government through the FCI.
3. Tamil Nadu Integrated Nutrition Programme was started in ……………
4. Govt, of India is implementing many policies and programmes to eradicate ……………..
5. The NFSA covers …………. of urban household.
Answers:
1. Consumer Cooperations
2. Buffer Stock
3. 1980
4. poverty
5. 50%

III. Match the following.

Answers:
1. (e)
2. (d)
3. (a)
4. (c)
5. (b)

IV. Short Answer:

Question 1.
Define Food.
Answer:
Food is defined as any substance that people eat and drink to maintain life.

Question 2.
Write the role of Consumer Cooperatives in Food Security.
Answer:
• Consumer Cooperatives play an important role in-the supply of quality goods of at responsible rates to common people.

• There is a three-tier structure of Consumer Cooperative Societies in India. They are primary consumer cooperative societies. Central consumer cooperative stores and state level consumer federations. There are many benefits to consumer cooperatives such as health care, insurance, housing etc.

• This scheme is playing an important role in food security in India. For ex. out of all fair price shops running in Tamil Nadu around 94% are being run by cooperatives.

Question 3.
What is meant by Absorption of food?
Answer:
Absorption of food is the ability to biologically utilise the food consumed.

Question 4.
Describe HYV:
Answer:
HYV means High Yielding Variety. It refers to hybrid or cultivars which are purposefully developed for high yielding. This motto of developing HYV started in the 1965 famine which also leads to the green revolution to feed the population of India.

Question 5.
Write a note on SMART family cards.
Answer:
The Government of Tamil Nadu has declared that Bio-metric SMART family cards will be issued in the place of family cards. The advantage is that since it is based on unique identity, the data duplication of members and bogus cards can be eliminated.

VIII. Answer the following in detail.

Question 1.
Write about the basic components of food and nutrition security.
Answer:
The term was broadened to include the three basic components of food and nutrition security. They are availability, access and absorption.
(i) Availability of food:
Availability of food is physical availability of food stocks in desired quantities, which is a function of domestic production, changes in stocks and imports.

(ii) Access to food:
Access to food is primarily a matter, of purchasing power and is therefore closely linked with the capabilities and employment opportunities to earn. Capabilities and opportunities in turn are related to one’s access to assets and education.

(iii) Absorption of food:
Absorption of food is the ability to biologically at line the food consumed. Several factors such as nutrition, knowledge and practices, safe and hygienic, environmental conditions allow for effective biological absorption of food and health status.

Question 2.
Explain Buffer stock scheme.
Answer:

1. Buffer stock is the stock of food grains namely wheat and rice, which are stored in granaries.
2. It is procured by the Government through the FCI food corporation of India from the States of surplus production.
3. The farmers are paid a pre-announced price for their crops which is called as Minimum Support Price.
4. The minimum support price is announced by the Government every year before the sowing season.
5. This is to provide incentives to farmers for raising the production of these crops.
6. The Buffer stock is done to distribute food grains in the deficit areas among the poor people in the society.
7. Since the price is lower than the market price, it is also called as the Issue Price.
8. The stored food helps to resolve the problem of shortage of food during adverse weather conditions or during the periods of calamity.

We think the data given here clarify all your queries of Chapter 3 and make you feel confident to attempt all questions in the examination. So, practice more & more from Tamilnadu State Board solutions for 10th Social ScienceEconomics Chapter 3 Food Security and Nutrition Questions and Answers & score well. Need any information regarding this then ask us through comments & we’ll give the best possible answers very soon.

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.19

Multiple choice questions.
10th Maths Exercise 3.19 Answers Question 1.
A system of three linear equations in three variables is inconsistent if their planes
(1) intersect only at a point
(2) intersect in a line
(3) coincides with each other
(4) do not intersect.
Solution:
(4) do not intersect

10th Maths Exercise 3.19 Question 2.
The solution of the system x + y – 3z = – 6, -7y + 7z = 7, 3z = 9 is …………
(1) x = 1, y = 2, z = 3
(2) x = -1, y = 2, z = 3
(3) x = -1, y = -2, z = 3
(4) x = 1, y = 2, z = 3
Answer:
(1) x = 1, y = 2, z = 3
Hint.
x + y – 3x = – 6 ….(1)
– 7y + 7z = 7 ….(2)
3z = 9 ….(3)
From (3) we get
z = \(\frac { 9 }{ 3 } \) = 3
Substitute the value of z in (2)
-7y + 7(3) = 7
-7y = -14
Substitute the value of y = 2 and z = 3 in (1)
x + 2 – 3(3) = -6
x + 2 – 9 = -6
x = -6 + 7
x = 1
The value of x = 1, y = 2 and z = 3

Exercise 3.19 Class 10 Question 3.
If (x – 6) is the HCF of x² – 2x – 24 and x² – kx – 6 then the value of k is
(1) 3
(2) 5
(3) 6
(4) 8
Solution:
(2) 5

10th Maths 3.19 Question 4.

Solution:
(1) \(\frac{9 y}{7}\)

Samacheer Kalvi Guru 10th Maths Question 5.
\(\mathbf{y}^{2}+\frac{\mathbf{1}}{y^{2}}\) is not equal to

Solution:
(2) \(\left(y+\frac{1}{y}\right)^{2}\)
Hint:
\(y^{2}+\frac{1}{y^{2}} \neq\left[y+\frac{1}{y}\right]^{2}\)

Samacheer Kalvi 10th Maths Book Solutions Question 6.

Solution:
(3) \(\frac{x^{2}-7 x+40}{(x+5)(x-5)(x+1)}\)
Hint:

Samacheer Kalvi 10th Maths Question 7.

Solution:
(4) \(\frac{16}{5}\left|\frac{x z^{2}}{y}\right|\)
Hint:

10th Maths Solution Samacheer Kalvi Question 8.
Which of the following should be added to make x⁴ + 64 a perfect square ……….
(1) 4x²
(2) 16x²
(3) 8x²
(4) -8x²
Answer:
(2) 16x²
Hint.
x² + 64 = (x²)² + 8² – 2 × x² × 8
= (x² – 8)²
2 × x² × 8 must be added
i.e, 16x² must be added

Samacheer Kalvi 10th Maths Answers Question 9.
The solution of (2x – 1)² = 9 is equal to
(1) -1
(2) 2
(3) -1, 2
(4) None of these
Solution:
(3) -1, 2
Hint:
(2x – 1)² = (±3)²
⇒ 2x – 1 = +3
2x – 1 = 3, 2x – 1 = – 3
2x = 4, 2x = – 2
x = 2,-1

Samacheer Kalvi.Guru 10th Maths Question 10.
The values of a and b if 4x⁴ – 24x³ + 76x² + ax + b is a perfect square are
(1) 100, 120
(2) 10, 12
(3) -120, 100
(4) 12, 10
Solution:
(3) -120, 100
Hint:

Samacheer Kalvi 10th Maths Book Graph Solution Question 11.
If the roots of the equation q²x² + p²x + r² = 0 are the squares of the roots of the equation qx² +px + r = 0, then q,p, r are in ______.
(1) A.P
(2) G.P
(3) Both A.P and G.P
(4) none of these
Solution:
(2) G.P
Hint: q²x² + p²x + r² = 0
(2) G.P.

Samacheer Kalvi 10th Maths Graph Question 12.
Graph of a linear polynomial is a …………..
(1) straight line
(2) circle
(3) parabola
(4) hyperbola
Answer:
(1) straight line

Samacheer Kalvi 10th Maths Solution Question 13.
The number of points of intersection of the T quadratic polynomial x² + 4x + 4 with the X axis.
(1) 0
(2) 1
(3) 0 or 1
(4) 2
Solution:
(2) 1
(x + 2)² = (x + 2)(x + 2)
= x = -2, -2 = 1

10th Samacheer Kalvi Maths Guide Question 14.
For the given matrix A = \(\left[\begin{array}{cccc}{1} & {3} & {5} & {7} \\ {2} & {4} & {6} & {8} \\ {9} & {11} & {13} & {15}\end{array}\right]\) the order of the matrix A^T is
(1) 2 × 3
(2) 3 × 2
(3) 3 × 4
(4) 4 × 3
Solution:
(3) 3 × 4
Hint:

Samacheer Kalvi 10th Maths Solutions Question 15.
If A is a 2 × 3 matrix and B is a 3 × 4 matrix, how many columns does AB have
(1) 3
(2) 4
(3) 2
(4) 5
Solution:
(2) 4
Hint:

Samacheer Kalvi 10th Maths Book Graph Solutions Question 16.
If a number of columns and rows are not equal in a matrix then it is said to be a …………..
(1) diagonal matrix
(2) rectangular matrix
(3) square matrix
(4) identity matrix
Answer:
(2) rectangular matrix

Samacheer Kalvi Maths 10th Question 17.
Transpose of a column matrix is
(1) unit matrix
(2) diagonal matrix
(3) column matrix
(4) row matrix
Solution:
(4) row matrix

Samacheer Kalvi 10th Maths Guide Question 18.

Solution:
(2) \(\left(\begin{array}{cc}{2} & {2} \\ {2} & {-1}\end{array}\right)\)
Hint:

Question 19.
Which of the following can be calculated from the given matrices
A = \(\left[\begin{array}{ll}{1} & {2} \\ {3} & {4} \\ {5} & {6}\end{array}\right]\), B = \(\left[\begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right]\)
(i) A²
(ii) B²
(iii) AB
(iv) BA
(1) (i) and (ii) only
(2) (ii) and (iiii) only
(3) (ii) and (iv) only
(4) all of these
Solution:
(3) (ii) and (iv) only
Hint:

Question 20.

(1) (i) and (ii) only
(2) (ii) and (iii) only
(3) (ii) and (iv) only
(4) all of these
Solution:
(1) (i) and (ii) only
Hint:

Students those who are preparing for the 12th Physics exam can download this Samacheer Kalvi 12th Physics Book Solutions Questions and Answers for Chapter 4 Electromagnetic Induction and Alternating Current from here free of cost. These Tamilnadu State Board Solutions for Class 12th Physics PDF cover all Chapter 4 Electromagnetic Induction and Alternating Current Questions and Answers. All these concepts of Samacheer Kalvi 12th Physics Book Solutions Questions and Answers are explained very conceptually as per the board prescribed Syllabus & guidelines.

Tamilnadu Samacheer Kalvi 12th Physics Solutions Chapter 4 Electromagnetic Induction and Alternating Current

Kickstart your preparation by using this Tamilnadu State Board Solutions for 12th Physics Chapter 4 Electromagnetic Induction and Alternating Current Questions and Answers and get the max score in the exams. You can cover all the topics of Chapter 4 Electromagnetic Induction and Alternating Current Questions and Answers pdf. Download the Tamilnadu State Board Solutions by accessing the links provided here and ace up your preparation.

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Textual Evaluation Solved

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Multiple Choice Questions

12th Physics Chapter 4 Book Back Answers Question 1.
An electron moves on a straight, line path XY as shown in the figure. The coil abed is adjacent to the path of the electron. What will be the direction of current, if any, induced in the coil? (NEET – 2015)

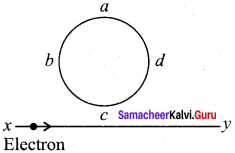
(а) The current will reverse its direction as the electron goes past the coil
(b) No current will be induced Electron
(c) abcd
(d) adcb
Answer:
(a) The current will reverse its direction as the electron goes past the coil

12th Physics Lesson 4 Book Back Answers Question 2.
A thin semi-circular conducting ring (PQR) of radius r is falling with its plane vertical in a horizontal magnetic field B, as shown in the figure. The potential difference developed across the ring when its speed v, is- (NEET 2014)

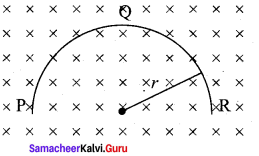
(a) Zero
(b) \(\frac {{ Bvπr }^{2}}{ 2 }\)
(c) πrBv and R is at higher potential
(d) 2rBv and R is at higher potential
Answer:
(d) 2rBv and R is at higher potential

Samacheerkalvi.Guru 12th Physics Question 3.
The flux linked with a coil at any instant t is given by Φ_B = 10t² – 50t + 250. The induced emf at t = 3s is-
(a) -190 V
(b) -10 V
(c) 10 V
(d) 190 V
Answer:
(b) -10 V

Samacheer Kalvi 12th Physics Solutions Question 4.
When the current changes from +2A to -2A in 0.05 s, an emf of 8 V is induced in a coil. The co-efficient of self-induction of the coil is-
(a) 0.2 H
(b) 0.4 H
(c) 0.8 H
(d) 0.1 H
Answer:
(d) 0.1 H

Samacheer Kalvi 12th Physics Solution Book Question 5.
The current i flowing in a coil varies with time as shown in the figure. The variation of induced emf with time would be- (NEET-2011)


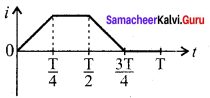
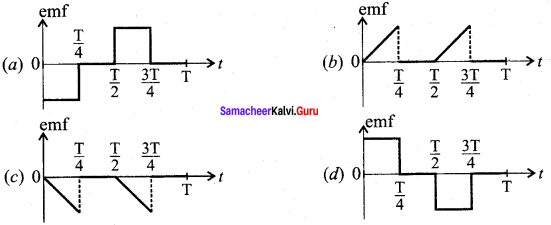
Answer:

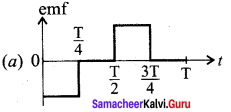
Tn 12th Physics Solution Question 6.
A circular coil with a cross-sectional area of 4 cm² has 10 turns. It is placed at the centre of a long solenoid that has 15 turns/cm and a cross-sectional area of 10 cm². The axis of the coil coincides with the axis of the solenoid. What is their mutual inductance?
(a) 7.54 μH
(b) 8.54 μH
(c) 9.54 μH
(d) 10.54 μH
Answer:
(a) 7.54 μH

Samacheer Kalvi Guru 12th Physics Question 7.
In a transformer, the number of turns in the primary and the secondary are 410 and 1230, respectively. If the current in primary is 6A, then that in the secondary coil is-
(a) 2 A
(b) 18 A
(c) 12 A
(d) 1 A
Answer:
(a) 2 A

Physics Class 12 Chapter 4 Notes Question 8.
A step-down transformer reduces the supply voltage from 220 V to 11 V and increase the current from 6 A to 100 A. Then its efficiency is-
(a) 1.2
(b) 0.83
(c) 0.12
(d) 0.9
Answer:
(b) 0.83

Alternating Current Class 12 Notes Pdf Download Question 9.
In an electrical circuit, R, L, C and AC voltage source are all connected in series. When L is removed from the circuit, the phase difference between the voltage and current in the circuit is \(\frac { 1 }{ 2 }\). Instead, if C is removed from the circuit, the phase difference is again \(\frac { π }{ 3 }\). The power factor of the circuit is- (NEET 2012)
(a) \(\frac { 1 }{ 2 }\)
(b) \(\frac { 1 }{ √ 2 }\)
(c) 1
(d) \(\frac { √ 3 }{ 2 }\)
Answer:
(c) 1

Physics Solution Class 12 Samacheer Kalvi Question 10.
In a series RL circuit, the resistance and inductive reactance are the same. Then the phase difference between the voltage and current in the circuit is-
(a) \(\frac { π }{ 4 }\)
(b) \(\frac { π }{ 2 }\)
(c) \(\frac { π }{ 6 }\)
(d) zero
Answer:
(a) \(\frac { π }{ 4 }\)

Samacheer 12th Physics Solutions Question 11.
In a series resonant RLC circuit, the voltage across 100 Ω resistor is 40 V. The resonant frequency co is 250 rad/s. If the value of C is 4 μF, then the voltage across L is-
(a) 600 V
(b) 4000 V
(c) 400 V
(d) 1 V
Answer:
(c) 400 V

Question 12.
An inductor 20 mH, a capacitor 50 μF and a resistor 40 Ω are connected in series across a source of emf v = 10 sin 340 t. The power loss in AC circuit is-
(a) 0.76 W
(b) 0.89 W
(c) 0.46 W
(d) 0.67 W
Answer:
(c) 0.46 W

Questions 13.
The instantaneous values of alternating current and voltage in a circuit are i = \(\frac { 1 }{ √ 2 }\) = sin(100πt) A and v = \(\frac { 1 }{ √ 2 }\) sin \(\left(100 \pi t+\frac{\pi}{3}\right)\) V. The average power in watts consumed in the circuit is-
(IIT Main 2012)
(a) \(\frac { 1 }{ 4 }\)
(b) \(\frac { √3 }{ 4 }\)
(c) \(\frac { 1 }{ 2 }\)
(d) \(\frac { 1 }{ 8 }\)
Answer:
(d) \(\frac { 1 }{ 8 }\)

Question 14.
In an oscillating LC circuit, the maximum charge on the capacitor is Q. The charge on the capacitor when the energy is stored equally between the electric and magnetic fields is-
(a) \(\frac { Q }{ 2 }\)
(b) \(\frac { Q }{ √3 }\)
(c) \(\frac { Q }{ √2 }\)
(d) \(\frac { Q }{ 2 }\)
Answer:
(c) \(\frac { Q }{ √2 }\)

Question 15.
\(\frac { 20 }{{ π }^{2}}\) H inductor is connected to a capacitor of capacitance C. The value of C in order to impart maximum power at 50 Hz is-
(a) 50 μF
(b) 0.5 μF
(c) 500 μF
(d) 5 μF
Answer:
(d) 5 μF

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Short Answer Questions

Question 1.
What is meant by electromagnetic induction?
Answer:
Whenever the magnetic flux linked with a closed coil changes, an emf (electromotive force) is induced and hence an electric current flows in the circuit.

Question 2.
State Faraday’s laws of electromagnetic induction.
Answer:
First law:
Whenever magnetic flux linked with a closed circuit changes, an emf is induced in the circuit.

Second law:
The magnitude of induced emf in a closed circuit is equal to the time rate of change of magnetic flux linked with the circuit.

Question 3.
State Lenz’s law.
Answer:
State Lenz’s law:
Lenz’s law states that the direction of the induced current is such that it always opposes the cause responsible for its production.

Question 4.
State Fleming’s right hand rule.
Answer:
The thumb, index finger and middle finger of right hand are stretched out in mutually perpendicular directions. If the index finger points the direction of the magnetic field and the Electromagnetic Induction and Alternating Current thumb indicates the direction of motion of the conductor, then the middle finger will indicate the direction of the induced current.

Question 5.
How is Eddy current produced? How do they flow in a conductor?
Answer:
Even for a conductor in the form of a sheet or plate, an emf is induced when magnetic flux linked with it changes. But the difference is that there is no definite loop or path for induced current to flow away. As a result, the induced currents flow in concentric circular paths. As these electric currents resemble eddies of water, these are known as Eddy currents. They are also called Foucault currents.

Question 6.
Mention the ways of producing induced emf.
Answer:
Induced emf can be produced by changing magnetic flux in any of the following ways:

1. By changing the magnetic field B
2. By changing the area A of the coil and
3. By changing the relative orientation 0 of the coil with magnetic field

Question 7.
What for an inductor is used? Give some examples.
Answer:
Inductor is a device used to store energy in a magnetic field when an electric current flows through it. The typical examples are coils, solenoids and toroids.

Question 8.
What do you mean by self-induction?
Answer:
If the magnetic flux is changed by changing the current, an emf is induced in that same coil. This phenomenon is known as self-induction.

Question 9.
What is meant by mutual induction?
Answer:
When an electric current passing through a coil changes with time, an emf is induced in the neighbouring coil. This phenomenon is known as mutual induction.

Question 10.
Give the principle of AC generator.
Answer:
Alternators work on the principle of electromagnetic induction. The relative motion between a conductor and a magnetic field changes the magnetic flux linked with the conductor which in turn, induces an emf. The magnitude of the induced emf is given by Faraday’s law of electromagnetic induction and its direction by Fleming’s right hand rule.

Question 11.
List out the advantages of stationary armature-rotating field system of AC generator.
Answer:

1. The current is drawn directly from fixed terminals on the stator without the use of brush contacts.
2. The insulation of stationary armature winding is easier.
3. The number of sliding contacts (slip rings) is reduced. Moreover, the sliding contacts are used for low-voltage DC Source.
4. Armature windings can be constructed more rigidly to prevent deformation due to any mechanical stress.

Question 12.
What are step-up and step-down transformers?
Answer:
If the transformer converts an alternating current with low voltage into an alternating current with high voltage, it is called step-up transformer. On the contrary, if the transformer converts alternating current with high voltage into an alternating current with low voltage, then it is called step-down transformer.

Question 13.
Define average value of an alternating current.
Answer:
The average value of alternating current is defined as the average of all values of current over a positive half-cycle or negative half-cycle.

Question 14.
How will you define RMS value of an alternating current?
Answer:
RMS value of alternating current is defined as that value of the steady current which when flowing through a given circuit for a given time produces the same amount of heat as produced by the alternating current when flowing through the same circuit for the same time.

Question 15.
What are phasors?
Answer:
A sinusoidal alternating voltage (or current) can be represented by a vector which rotates about the origin in anti-clockwise direction at a constant angular velocity ω. Such a rotating vector is called a phasor.

Question 16.
Define electric resonance.
Answer:
When the frequency of the applied alternating source is equal to the natural frequency of the RLC circuit, the current in the circuit reaches its maximum value. Then the circuit is said to be in electrical resonance.

Question 17.
What do you mean by resonant frequency?
Answer:
When the frequency of the applied alternating source (ω_r) is equal to the natural frequency \(\left[\frac{1}{\sqrt{L C}}\right]\) of the RLC circuit, the current in the circuit reaches its maximum value. Then the circuit is said to be in electrical resonance. The frequency at which resonance takes place is called resonant frequency. Resonant angular frequency, ω_r = \(\frac { 1 }{ \sqrt { LC } } \)

Question 18.
How will you define Q-factor?
Answer:
It is defined as the ratio of voltage across L or C to the applied voltage.

Question 19.
What is meant by wattles current?
Answer:
The component of current (I_RMS sin φ), which has a phase angle of \(\frac { π }{ 2 }\) with the voltage is called reactive component. The power consumed is zero. So that it is also known as ‘Wattless’ current.

Question 20.
Give any one definition of power factor.
Answer:
The power factor is defined as the ratio of true power to the apparent power of an a.c. circuit. It is equal to the cosine of the phase angle between current and voltage in the a.c. circuit.

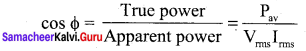
Question 21.
What are LC oscillations?
Answer:
Whenever energy is given to a LC circuit, the electrical oscillations of definite frequency are generated. These oscillations are called LC oscillations. During LC oscillations, the total energy remains constant. It means that LC oscillations take place in accordance with the law of conservation of energy.

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Long Answer Questions

Question 1.
Establish the fact that the relative motion between the coil and the magnet induces an emf in the coil of a closed circuit.
Answer:
Whenever the magnetic flux linked with a closed coil changes, an emf (electromotive force) is induced and hence an electric current flows in the circuit.
The relative motion between the coil and the magnet induces:
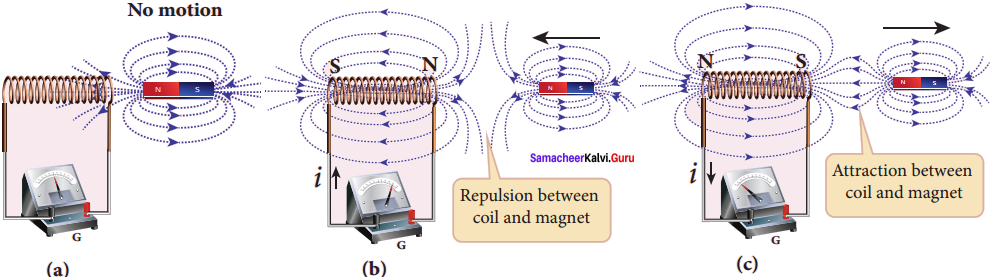
In the first experiment, when a bar magnet is placed close to a coil, some of the magnetic field lines of the bar magnet pass through the coil i.e., the magnetic flux is linked with the coil. When the bar magnet and the coil approach each other, the magnetic flux linked with the coil increases. So this increase in magnetic flux induces an emf and hence a transient electric current flows in the circuit in one direction (Figure(a)).

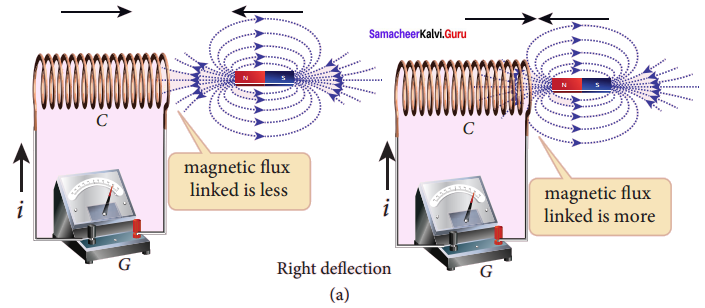
At the same time, when they recede away from one another, the magnetic flux linked with the coil decreases. The decrease in magnetic flux again induces an emf in opposite direction and hence an electric current flows in opposite direction (Figure (b)). So there is deflection in the galvanometer when there is a relative motion between the coil and the magnet.

In the second experiment, when the primary coil P carries an electric current, a magnetic field is established around it. The magnetic lines of this field pass through itself and the neighbouring secondary coil S.

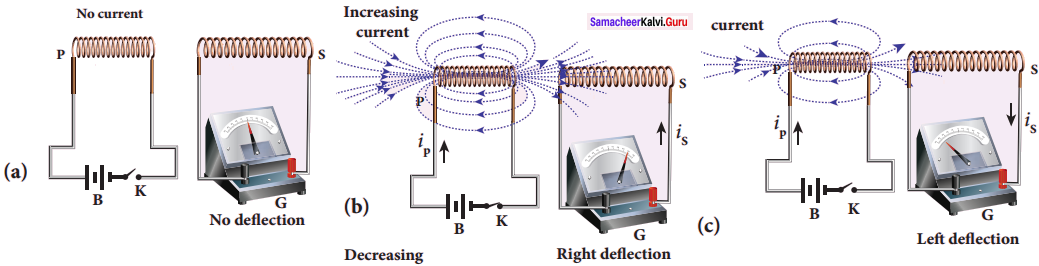
When the primary circuit is open, no electric current flows in it and hence the magnetic flux linked with the secondary coil is zero (Figure(a)).
However, when the primary circuit is closed, the increasing current builds up a magnetic field around the primary coil. Therefore, the magnetic flux linked with the secondary coil increases. This increasing flux linked induces a transient electric current in the secondary coil (Figure(b)).

When the electric current in the primary coil reaches a steady value, the magnetic flux linked with the secondary coil does not change and the electric current in the secondary coil will disappear. Similarly, when the primary circuit is broken, the decreasing primary current induces an electric current in the secondary coil, but in the opposite direction (Figure (c)). So there is deflection in the galvanometer whenever there is a change in the primary current

Question 2.
Give an illustration of determining direction of induced current by using Lenz’s law.
Answer:
Illustration 1:
Consider a uniform magnetic field, with its field lines perpendicular to the plane of the paper and pointing inwards. These field lines are represented by crosses (x) as shown in figure (a). A rectangular metallic frame ABCD is placed in this magnetic field, with its plane perpendicular to the field. The arm AB is movable so that it can slide towards right or left.

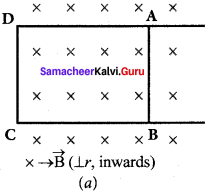
If the arm AB slides to our right side, the number of field lines (magnetic flux) passing through the frame ABCD increases and a current is induced. As suggested by Lenz’s law, the induced current opposes this flux increase and it tries to reduce it by producing another magnetic field pointing outwards i.e., opposite to the existing magnetic field.

The magnetic lines of this induced field are represented by circles in the figure (b). From the direction of the magnetic field thus produced, the direction of the induced current is found to be anti-clockwise by using right-hand thumb rule.

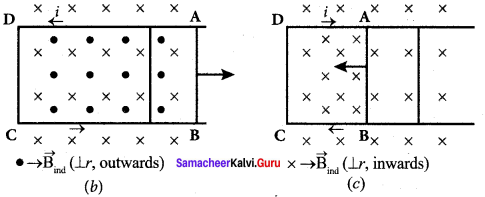
The leftward motion of arm AB decreases magnetic flux. The induced current, this time, produces a magnetic field in the inward direction i.e., in the direction of the existing magnetic field (figure (c)). Therefore, the flux decrease is opposed by the flow of induced current. From this, it is found that induced current flows in clockwise direction.

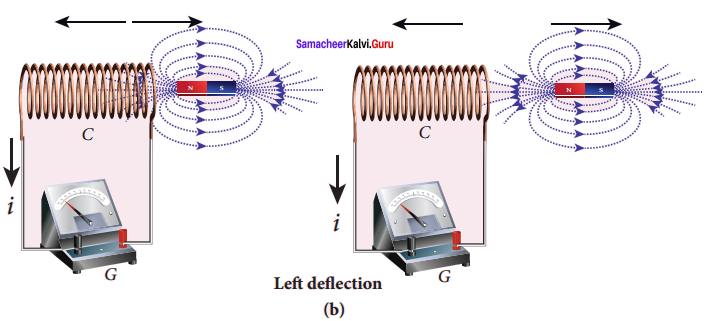
Illustration 2:
Let us move a bar magnet towards the solenoid, with its north pole pointing the solenoid as shown in figure (b). This motion increases the magnetic flux of the coil which in turn, induces an electric current. Due to the flow of induced current, the coil becomes a magnetic dipole whose two magnetic poles are on either end of the coil.

In this case, the cause producing the induced current is the movement of the magnet. According to Lenz’s law, the induced current should flow in such a way that it opposes the movement of the north pole towards coil. It is possible if the end nearer to the magnet becomes north pole (figure (b)).

Then it repels the north pole of the bar magnet and opposes the movement of the magnet. Once pole ends are known, the direction of the induced current could be found by using right hand thumb rule. When the bar magnet is withdrawn, the nearer end becomes south pole which attracts north pole of the bar magnet, opposing the receding motion of the magnet (figure (c)). Thus the direction of the induced current can be found from Lenz’s law.

Question 3.
Show that Lenz’s law is in accordance with the law of conservation of energy.
Answer:
Conservation of energy:
The truth of Lenz’s law can be established on the basis of the law of conservation of energy. According to Lenz’s law, when a magnet is moved either towards or away from a coil, the induced current produced opposes its motion. As a result, there will always be a resisting force on the moving magnet.

Work has to be done by some external agency to move the magnet against this resisting force. Here the mechanical energy of the moving magnet is converted into the electrical energy which in turn, gets converted into Joule heat in the coil i.e., energy is converted from one form to another.

Question 4.
Obtain an expression for motional emf from Lorentz force.
Answer:
Motional emf from Lorentz force:
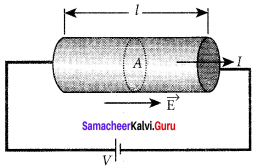
Consider a straight conducting rod AB of length l in a uniform magnetic field \(\vec { B } \) which is directed perpendicularly into the plane of the paper. The length of the rod is normal to the magnetic field. Let the rod move with a constant velocity \(\vec { v } \) towards right side.
When the rod moves, the free electrons present in it also move with same velocity \(\vec { v } \) in \(\vec { B } \). As a result, the Lorentz force acts on free electrons in the direction from B to A and is given by the relation
\(\vec { F } \)_B = -e(\(\vec { v } \) x \(\vec { B } \) ) ……. (1)
The action of this Lorentz force is to accumulate the free electrons at the end A. This accumulation of free electrons produces a potential difference across the rod which in turn establishes an electric field E directed along BA. Due to the electric field E, the coulomb force starts acting on the free electrons along AB and is given by
\(\vec { F } \)_E = -e\(\vec { E } \) ……. (2)
The magnitude of the electric field \(\vec { E } \) keeps on increasing as long as accumulation of electrons at the end A continues. The force \(\vec { F } \)_E also increases until equilibrium is reached. At equilibrium, the magnetic Lorentz force \(\vec { F } \)_B and the coulomb force \(\vec { F } \)_E balance each other and no further accumulation of free electrons at the end A takes place, i.e.,
\(\left| \vec { { F }_{ B } } \right| \) = \(\left| \vec { { F }_{ E } } \right| \)

vB sin 90° = E
vB = E ……. (3)
The potential difference between two ends of the rod is

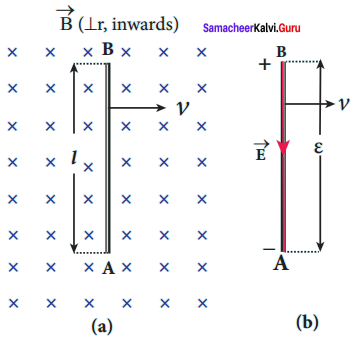
Figure: Motional emf from Lorentz force
V = El
V = vBl
Thus the Lorentz force on the free electrons is responsible to maintain this . potential difference and hence produces an emf
ε = Blv ….. (4)
As this emf is produced due to the movement of the rod, it is often called as motional emf.

Question 5.
Using Faraday’s law of electromagnetic induction, derive an equation for motional emf.
Answer:
Motional emf from Faraday’s law:
Let us consider a rectangular conducting loop of width l in a uniform magnetic field \(\vec { B } \) which is perpendicular to the plane of the loop and is directed inwards. A part of the loop is in the magnetic field while the remaining part is outside the field.

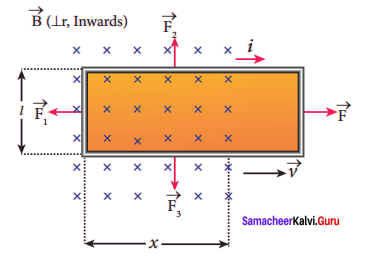
Figure: Motional emf from Faraday’s law

When the loop is pulled with a constant velocity \(\vec { v } \) to the right, the area of the portion of the loop within the magnetic field will decrease. Thus, the flux linked with the loop will also decrease. According to Faraday’s law, an electric current is induced in the loop which flow’s in a direction so as to oppose the pull of the loop.
Let x be the length of the loop which is still within the magnetic field, then its area is lx. The magnetic flux linked with the loop is

As this magnetic flux decreases due to the movement of the loop, the magnitude of the induced emf is given by
ε = \(\frac {{ dΦ }_{B}}{ dt }\) = \(\frac { d }{ dt }\) (Blx)
Here, both B and l are constants. Therefore,
ε = Bl \(\frac { dx}{ dl }\) = Blv …… (2)
where v = \(\frac { dx}{ dt }\) is the velocity of the loop. This emf is known as motional emf since it is produced due to the movement of the loop in the magnetic field.

Question 6.
Give the uses of Foucault current.
Answer:
Though the production of eddy current is undesirable in some cases, it is useful in some other cases. A few of them are

1. Induction stove
2. Eddy current brake
3. Eddy current testing
4. Electromagnetic damping

1. Induction stove:
Induction stove is used to cook the food quickly and safely with less energy consumption. Below the cooking zone, there is a tightly wound coil of insulated wire. The cooking pan made of suitable material, is placed over the cooking zone.

When the stove is switched on, an alternating current flowing in the coil produces high frequency alternating magnetic field which induces very strong eddy currents in the cooking pan. The eddy currents in the pan produce so much of heat due to Joule heating which is used to cook the food.

2. Eddy current brake:
This eddy current braking system is generally used in high speed trains and roller coasters. Strong electromagnets are fixed just above the rails. To stop the train, electromagnets are switched on. The magnetic field of these magnets induces eddy currents in the rails which oppose or resist the movement of the train. This is Eddy current linear brake.

In some cases, the circular disc, connected to the wheel of the train through a common shaft, is made to rotate in between the poles of an electromagnet. When there is a relative motion between the disc and the magnet, eddy currents are induced in the disc which stop the train. This is Eddy current circular brake.

3. Eddy current testing:
It is one of the simple non-destructive testing methods to find defects like surface cracks and air bubbles present in a specimen. A coil of insulated wire is given an alternating electric current so that it produces an alternating magnetic field.

When this coil is brought near the test surface, eddy current is induced in the test surface. The presence of defects causes the change in phase and amplitude of the eddy current that can be detected by some other means. In this way, the defects present in the specimen are identified.

4. Electro magnetic damping:
The armature of the galvanometer coil is wound on a soft iron cylinder. Once the armature is deflected, the relative motion between the soft iron cylinder and the radial magnetic field induces eddy current in the cylinder. The damping force due to the flow of eddy current brings the armature to rest immediately and then galvanometer shows a steady deflection. This is called electromagnetic damping.

Question 7.
Define self-inductance of a coil interns of (i) magnetic flux and (ii) induced emf.
Answer:
Self-inductance or simply inductance of a coil is defined as the flux linkage of the coil when 1A current flows through it.
When the current i changes with time, an emf is induced in it. From Faraday’s law of electromagnetic induction, this self-induced emf is given by
ε = –\(\frac{d\left(\mathrm{N} \Phi_{\mathrm{B}}\right)}{d t}\) = –\(\frac { d(Li)}{ dt }\)
∴ ε = -L\(\frac { di}{ dt }\) or L = \(\frac { -ε}{ di/dt }\)
The negative sign in the above equation means that the self-induced emf always opposes the change in current with respect to time. If \(\frac { di}{ dt }\) = 1 As^-1, then L= -ε. Inductance of a coil is also defined as the opposing emf induced in the coil when the rate of change of current through the coil is 1 A s^-1.

Question 8.
How will you define the unit of inductance?
Answer:
Unit of inductance: Inductance is a scalar and its unit is Wb A^-1 or V s A^-1. It is also measured in henry (H).
1 H = 1 Wb A^-1 = 1 V s A^-1
The dimensional formula of inductance is M L² T^-2A^-2.
If i = 1 A and NΦ_B = 1 Wb turns, then L = 1 H.
Therefore, the inductance of the coil is said to be one henry if a current of 1 A produces unit flux linkage in the coil.
If \(\frac { di}{ dt }\) = 1 As^-1 and ε = -1 V, then L = 1 H.
Therefore, the inductance of the coil is one henry if a current changing at the rate of 1 A s^-1 induces an opposing emf of 1 V in it.

Question 9.
What do you understand by self-inductance of a coil? Give its physical significance.
Answer:
Self-inductance or simply inductance of a coil is defined as the flux linkage of the coil when 1A current flows through it.
When the current i changes with time, an emf is induced in it. From Faraday’s law of electromagnetic induction, this self-induced emf is given by

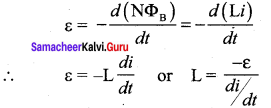
Physical significance of inductance:
When a circuit is switched on, the increasing current induces an emf which opposes the growth of current in a circuit. Likewise, when circuit is broken, the decreasing current induces an emf in the reverse direction. This emf now opposes the decay of current.

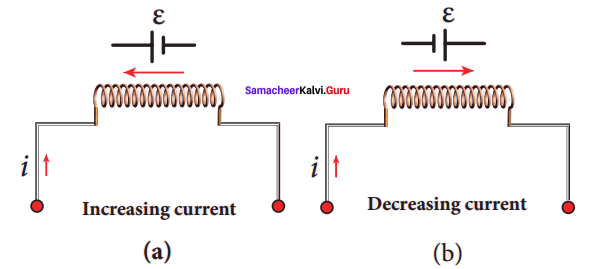
Figure: Induced emf ε opposes the changing current i

Thus, inductance of the coil opposes any change in current and tries to maintain the original state.

Question 10.
Assuming that the length of the solenoid is large when compared to its diameter, find the equation for its inductance.
Answer:
Self-inductance of a long solenoid:
Consider a long solenoid of length l and cross-sectional area A. Let n be the number of turns per unit length (or turn density) of the solenoid. When an electric current i is passed through the solenoid, a magnetic field is produced by it which is almost uniform and is directed along the axis of the solenoid. The magnetic field at any point inside the solenoid is given by
B = μ₀ni
As this magnetic field passes through the solenoid, the windings of the solenoid are linked by the field lines. The magnetic flux passing through each turn is

The total magnetic flux linked or flux linkage of the solenoid with N turns (the total number of turns N is given by N = nl) is

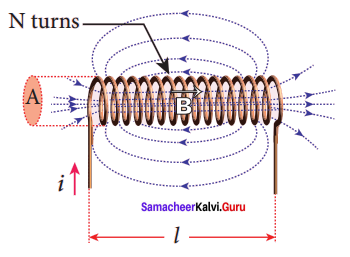
NΦ_B = n (nl) (μ₀ni)A
NΦ_B = (μ₀n²Al)i ….. (1)
From the self induction
NΦ_B = LI ….. (2)
Comparing equations (1) and (2), we have L = μ₀n²Al
From the above equation, it is clear that inductance depends on the geometry of the solenoid (turn density n, cross-sectional area A, length l) and the medium present inside the solenoid. If the solenoid is filled with a dielectric medium of relative permeability μ_r, then
L = μ₀
L = μn₀μ_rn²Al

Question 11.
An inductor of inductance L carries an electric current i. How much energy is stored while establishing the current in it?
Answer:
Energy stored in an inductor:
Whenever a current is established in the circuit, the inductance opposes the growth of the current. In order to establish a current in the circuit, work is done against this opposition by some external agency. This work done is stored as magnetic potential energy.

Let us assume that electrical resistance of the inductor is negligible and inductor effect alone is considered. The induced emf e at any instant t is
ε = -L\(\frac { di}{ dt }\) …… (1)
Let dW be work done in moving a charge dq in a time dt against the opposition, then
dW = -εdq = -εidi = εidi           [∵dq = idt]
Substituting for s value from equation (1)
= – \(\left(-\mathrm{L} \frac{d i}{d t}\right)\) idt
dW = Lid …… (2)
Total work done in establishing the current i is

This work done is stored as magnetic potential energy.
U_B = \(\frac { 1 }{ 2 }\) Li² …….. (4)

Question 12.
Show that the mutual inductance between a pair of coils is same (M₁₂ = M₂₁).
Answer:
Mutual induction:
When an electric current passing through a coil changes with time, an emf is induced in the neighbouring coil. This phenomenon is known as mutual induction and the emf is called mutually induced emf.

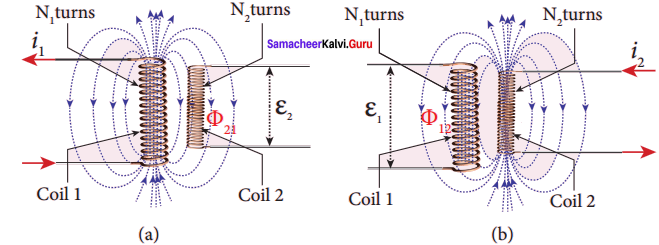
Consider two coils which are placed close to each other. If an electric current i₁ is sent through coil 1, the magnetic field produced by it is also linked with coil 2. Let Φ₂₁ be the magnetic flux linked with each turn of the coil 2 of N₂ turns due to coil 1, then the total flux linked with coil 2 (N₂Φ₂₁) is proportional to the current i₁ in the coil 1.

The constant of proportionality M₂₁ is the mutual inductance of the coil 2 with respect to coil 1. It is also called as coefficient of mutual induction. If i₁ = 1A, then M₂₁ = N₂Φ₂₁.
Therefore, the mutual inductance M₂₁ is defined as the flux linkage of the coil 2 when 1A current flows through coil 1. When the current changes with time, an emf ε₂ is induced in coil 2. From Faraday’s law of electromagnetic induction, this mutually induced emf ε₂ is given by

The negative sign in the above equation shows that the mutually induced emf always opposes the change in current i, with respect to time. If \(\frac { di }{ dt }\) = 1 As^-1, then M₂₁ = -ε₂. Mutual inductance M₂₁, is also defined as the opposing emf induced in the coil 2 when the rate of change of current through the coil 1 is 1 As^-1. Similarly, if an electric current i₂ through coil 2 changes with time, then emf ε₁ is induced in coil 1. Therefore,

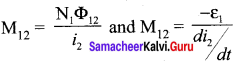
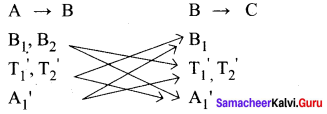
where M₁₂ is the mutual inductance of the coil 1 with respect to coil 2. It can be shown that for a given pair of coils, the mutual inductance is same, i.e., M₂₁ = M₁₂ = M.
In general, the mutual induction between two coils depends on size, shape, the number of turns of the coils, their relative orientation and permeability of the medium.

Question 13.
How will you induce an emf by changing the area enclosed by the coil?
Answer:
Induction of emf by changing the area of the coil:
Consider a conducting rod of length 1 moving with a velocity v towards left on a rectangular metallic framework. The whole arrangement is placed in a uniform magnetic field \(\vec { B } \) whose magnetic lines are perpendicularly directed into the plane of the paper. As the rod moves from AB to DC in a time dt, the area enclosed by the loop and hence the magnetic flux through the loop decreases.

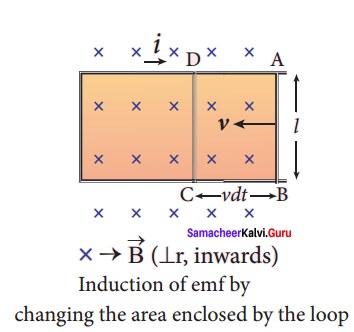
The change in magnetic flux in time dt is
dΦ_B = B x change in area
B x Area ABCD
= Blvdt since Area ABCD = l(vdt)
or \(\frac {{ dΦ }_{B}}{ dt }\) = Blv
As a result of change in flux, an emf is generated in the loop. The magnitude of the induced emf is
ε = \(\frac {{ dΦ }_{B}}{ dt }\) = Blv
This emf is called motional emf. The direction of induced current is found to be clockwise from Fleming’s right hand rule.

Question 14.
Show mathematically that the rotation of a coil in a magnetic field over one rotation induces an alternating emf of one cycle.
Answer:
Induction of emf by changing relative orientation of the coil with the magnetic field:
Consider a rectangular coil of N turns kept in a uniform magnetic field \(\vec { B } \) figure (a). The coil rotates in anti-clockwise direction with an angular velocity ω about an axis, perpendicular to the field. At time = 0, the plane of the coil is perpendicular to the field and the flux linked with the coil has its maximum value Φ_m = BA (where A is the area of the coil).

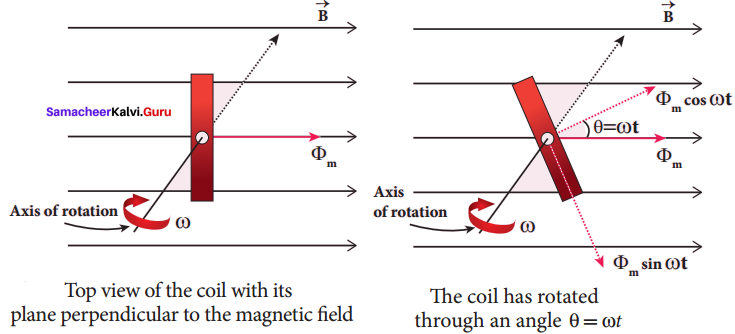
In a time t seconds, the coil is rotated through an angle θ (= ωt) in anti-clockwise direction. In this position, the flux linked is Φ_m cos ωt, a component of Φ_m normal to the plane of the coil (figure (b)). The component parallel to the plane (Φ_m sin ωt) has no role in electromagnetic induction. Therefore, the flux linkage at this deflected position is NΦ_B = NΦ_m cos ωt. According to Faraday’s law, the emf induced at that instant is

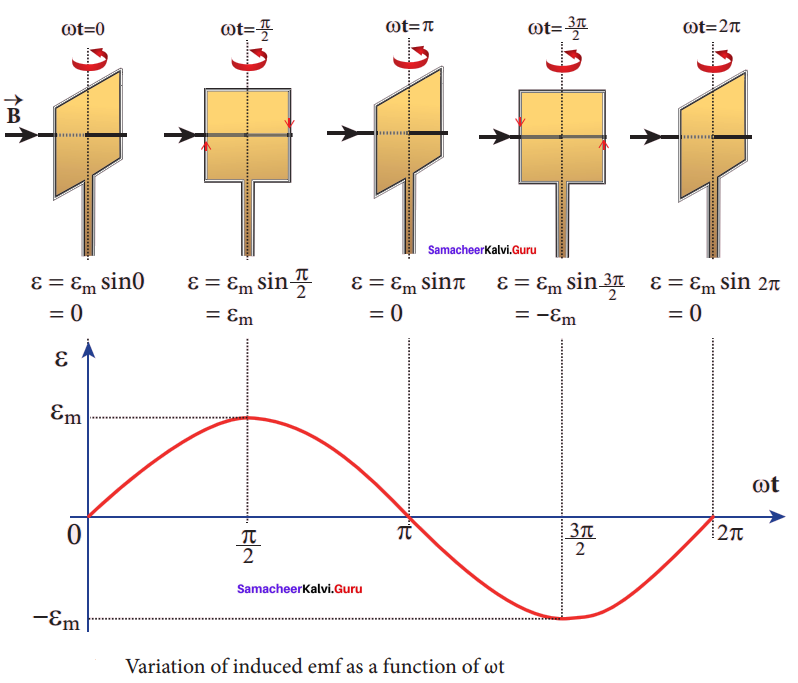
ε= \(\frac { d }{ dt }\) (NΦ_B ) = \(\frac { d }{ dt }\) (NΦ_m cos ωt)
= -NΦ_m (-sin ωt)ω = NΦ_m ω sin ωt
When the coil is rotated through 90° from initial position, sin ωt = 1, Then the maximum value of induced emf is
ε_m = NΦ_mω = NBAω since Φ_m = BA
Therefore, the value of induced emf at that instant is then given by
ε = ε_m sin ωt
It is seen that the induced emf varies as sine function of the time angle ωt. The graph between – induced emf and time angle for one rotation of coil will be a sine curve and the emf varying in this manner is called sinusoidal emf or alternating emf.

Question 15.
Elaborate the standard construction details of AC generator.
Answer:
Construction:
lternator consists of two major parts, namely stator and rotor. As their names suggest, stator is stationary while rotor rotates inside the stator. In any standard construction of commercial alternators, the armature winding is mounted on stator and the field magnet on rotor. The construction details of stator, rotor and various other components involved in them are given below.

(i) Stator:
The stationary part which has armature windings mounted in it is called stator. It has three components, namely stator frame, stator core and armature winding.

Stator frame:
This is the outer frame used for holding stator core and armature windings in proper position. Stator frame provides best ventilation with the help of holes provided in the frame itself.

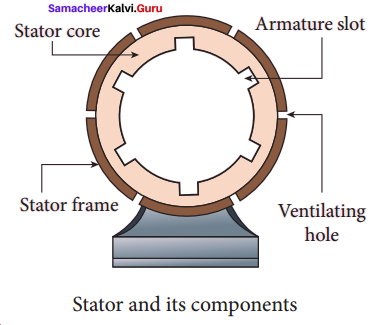
Stator core:
Stator core or armature core is made up of iron or steel alloy. It is a hollow cylinder and is laminated to minimize eddy current loss. The slots are cut on inner surface of the core to accommodate armature windings.

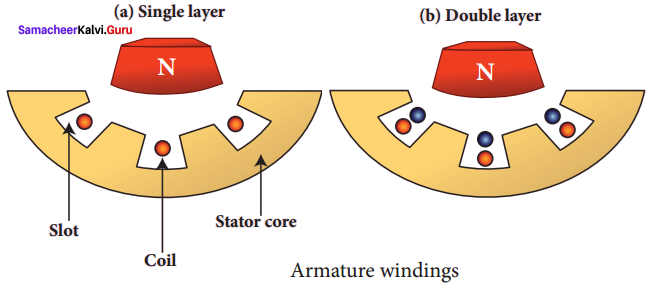
Armature winding:
Armature winding is the coil, wound on slots provided in the armature core. One or more than one coil may be employed, depending on the type of alternator. Two types of windings are commonly used. They are (i) single-layer winding and (ii) double-layer winding. In single-layer winding, a slot is occupied by a coil as a single layer. But in double-layer winding, the coils are split into two layers such as top and bottom layers.

(ii) Rotor:
Rotor contains magnetic field windings. The magnetic poles are magnetized by DC source. The ends of field windings are connected to a pair of slip rings, attached to a common shaft about which rotor rotates. Slip rings rotate along with rotor. To maintain connection between the DC source and field windings, two brushes are used which . continuously slide over the slip rings.

There are 2 types of rotors used in alternators:

1. salient pole rotor
2. cylindrical pole rotor.

1. Salient pole rotor:
The word salient means projecting. This rotor has a number of projecting poles having their bases riveted to the rotor. It is mainly used in low-speed alternators.

2. Cylindrical pole rotor:
This rotor consists of a smooth solid cylinder. The slots are cut on the outer surface of the cylinder along its length. It is suitable for very high speed alternators.

The frequency of alternating emf induced is directly proportional to the rotor speed. In order to maintain the frequency constant, the rotor must run at a constant speed. These are standard construction details of alternators.

Question 16.
Explain the working of a single-phase AC generator with necessary diagram.
Answer:
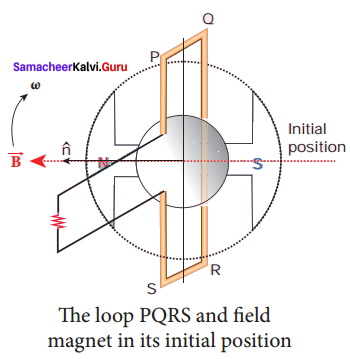
Single phase AC generator: In a single phase AC generator, the armature conductors are connected in series so as to form a single circuit which generates a single-phase alternating emf and hence it is called single-phase alternator.

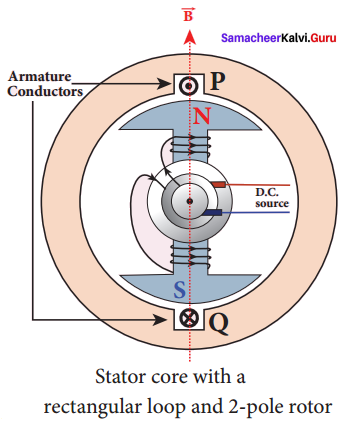
The simplified version of a AC generator is discussed here. Consider a stator core consisting of 2 slots in which 2 armature conductors PQ and RS are mounted to form single-turn rectangular loop PQRS. Rotor has 2 salient poles with field windings which can be magnetized by means of DC source.

Working:
The loop PQRS is stationary and is perpendicular to the plane of the paper. When field windings are excited, magnetic field is produced around it. The direction of magnetic field passing through the armature core. Let the field magnet be rotated in clockwise direction by the prime mover. The axis of rotation is perpendicular to the plane of the paper.

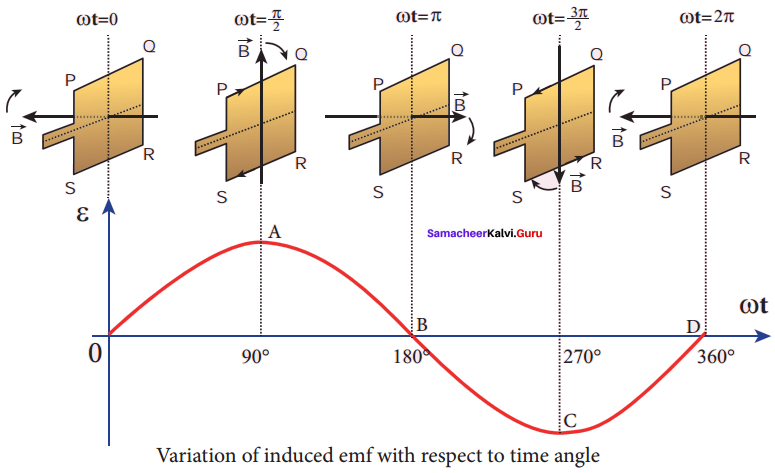
Assume that initial position of the field magnet is horizontal. At that instant, the direction of magnetic field is perpendicular to the plane of the loop PQRS. The induced emf is zero. This is represented by origin O in the graph between induced emf and time angle.

When field magnet rotates through 90°, magnetic field becomes parallel to PQRS. The induced cmfs across PQ and RS would become maximum. Since they are connected in series, emfs are added up and the direction of total induced emf is given by Fleming’s right hand rule. Care has to be taken while applying this rule; the thumb indicates the direction of the motion of the conductor with respect to field.

For clockwise rotating poles, the conductor appears to be rotating anti-clockwise. Hence, thumb should point to the left. The direction of the induced emf is at right angles to the plane of the paper. For PQ, it is downwards B and for RS upwards. Therefore, the current flows along PQRS. The point A in the graph represents this maximum emf.

For the rotation of 180° from the initial position, the field is again perpendicular to PQRS and the induced emf becomes zero. This is represented by point B. The field magnet becomes again parallel to PQRS for 270° rotation of field magnet. The induced emf is maximum but the direction is reversed. Thus the current flows along SRQP This is represented by point C.

On completion of 360°, the induced emf becomes zero and is represented by the point D. From the graph, it is clear that emf induced in PQRS is alternating in nature. Therefore, when field magnet completes one rotation, induced emf in PQRS finishes one cycle. For this construction, the frequency of the induced emf depends on the speed at which the field magnet rotates.

Question 17.
How are the three different emfs generated in a three-phase AC generator? Show the graphical representation of these three emfs.
Answer:
Three-phase AC generator:
Some AC generators may have more than one coil in the armature core and each coil produces an alternating emf. In these generators, more than one emf is produced. Thus they are called poly-phase generators. If there are two alternating emfs produced in a generator, it is called two-phase generator. In some AC generators, there are three separate coils, which would give three separate emfs. Hence they are called three-phase AC generators.

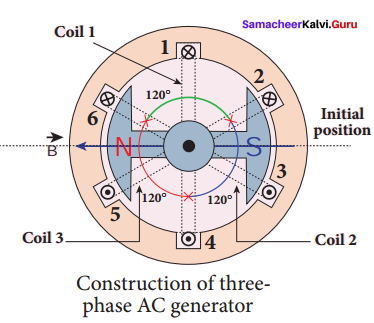
In the simplified construction of three-phase AC generator, the armature core has 6 slots, cut on its inner rim. Each slot is 60° away from one another. Six armature conductors are mounted in these slots. The conductors 1 and 4 are joined in series to form coil 1. The conductors 3 and 6 form coil 2 while the conductors 5 and 2 form coil 3. So, these coils are rectangular in shape and are 120° apart from one another.

The initial position of the field magnet is horizontal and field direction is perpendicular to the plane of the coil 1. As it is seen in single phase AC generator, when field magnet is rotated from that position in clockwise direction, alternating emf ε₁ in coil 1 begins a cycle from origin O.

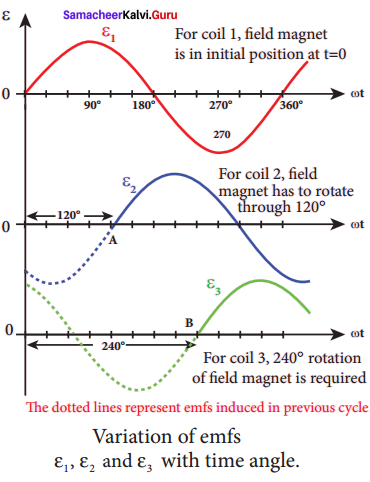
The corresponding cycle for alternating emf ε₂ in coil 2 starts at point A after field magnet has rotated through 120°. Therefore, the phase difference between ε₁ and ε₂ is 120°. Similarly, emf ε₃ in coil 3 would begin its cycle at point B after 240° rotation of field magnet from initial position. Thus these emfs produced in the three phase AC generator have 120° phase difference between one another.

Question 18.
Explain the construction and working of transformer.
Answer:
Construction and working of transformer:
Principle:
The principle of transformer is the mutual induction between two coils. That is, when an electric current passing through a coil changes with time, an emf is induced in the neighbouring coil.

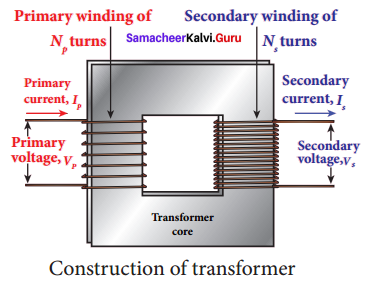
Construction:
In the simple construction of transformers, there are two coils of high mutual inductance wound over the same transformer core. The core is generally laminated and is made up of a good magnetic material like silicon steel. Coils are electrically insulated but magnetically linked via transformer core.

The coil across which alternating voltage is applied is called primary coil P and the coil from which output power is drawn out is called secondary coil S. The assembled core and coils are kept in a container which is filled with suitable medium for better insulation and cooling purpose.

Working:
If the primary’ coil is connected to a source of alternating voltage, an alternating magnetic flux is set up in the laminated core. If there is no magnetic flux leakage, then whole of magnetic flux linked with primary coil is also linked with secondary coif This means that rate at which magnetic flux changes through each turn is same for both primary and secondary coils. As a result of flux change, emf is induced in both primary and secondary coils. The emf induced in the primary coil ε_p is almost equal and opposite to the applied voltage υ_p and is given by
υ_p = ε_p = -N_p \(\frac {{ dΦ }_{B}}{ dt }\) …….. (1)
The frequency of alternating magnetic flux in the core is same as the frequency of the applied voltage. Therefore, induced emf in secondary will also have same frequency as that of applied voltage. The emf induced in the secondary coil eg is given by
ε_s = -N_s \(\frac {{ dΦ }_{B}}{ dt }\)
where N_p and N_s are the number of turns in the primary and secondary coil, respectively. If the secondary circuit is open, then ε_s = υ_s where υ_s is the voltage across secondary coil.
υ_s ε_s = -N_s \(\frac {{ dΦ }_{B}}{ dt }\) ……… (2)
From equation (1) and (2),
\(\frac {{ υ }_{s}}{{ ε }{s}}\) = \(\frac {{ N }_{s}}{{ N }{p}}\) = K …….. (3)
This constant K is known as voltage transformation ratio. For an ideal transformer,
Input power υ_p i_p = Output power υ_si_s
where iυ_p and i_s are the currents in the primary and secondary coil respectively. Therefore,
\(\frac {{ υ }_{s}}{{ υ }{p}}\) = \(\frac {{ N }_{s}}{{ N }{p}}\) = \(\frac {{ i }_{p}}{{ i }{s}}\)
Equation (4) is written in terms of amplitude of corresponding quantities,
\(\frac {{ V }_{s}}{{ V }{p}}\) = \(\frac {{ N }_{s}}{{ N }{p}}\) = \(\frac {{ I }_{p}}{{ I }{s}}\) = K ……. (4)

(i) If N_s > N_p ( or K > 1)
∴ V_s > V_p and I_s < I_p.
This is sthe case of step-up transformer in which voltage is decreased and the corresponding current is decreased.

(ii) If N_s < N_p (or K < 1)
∴ V_s < V_p and I_s > I_p
This is step-down transformer where voltage is decreased and the current is increased.

Question 19.
Mention the various energy losses in a transformer.
Answer:
Energy losses in a transformer: Transformers do not have any moving parts so that its efficiency is much higher than that of rotating machines like generators and motors. But there are many factors which lead to energy loss in a transformer.

(i) Core loss or Iron loss:
This loss takes place in transformer core. Hysteresis loss and eddy current loss are known as core loss or Iron loss. When transformer core is magnetized and demagnetized repeatedly by the alternating voltage applied across primary coil, hysteresis takes place due to which some energy is lost in the form of heat.

Hysteresis loss is minimized by using steel of high silicon content in making transformer core. Alternating magnetic flux in the core induces eddy currents in it. Therefore there is energy loss due to the flow of eddy current, called eddy current loss which is minimized by using very thin laminations of transformer core.

(ii) Copper loss:
Transformer windings have electrical resistance. When an electric current flows through them, some amount of energy is dissipated due to Joule heating. This energy loss is called copper loss which is minimized by using wires of larger diameter.

(iii) Flux leakage:
Flux leakage happens when the magnetic lines of primary coil arc not completely linked with secondary coil. Energy loss due to this flux leakage is minimized by winding coils one over the other.

Question 20.
Give the advantage of AC in long distance power transmission with an example.
Answer:
Advantages of AC in long distance power transmission:
Electric power is produced in a t large scale at electric power stations with the help of AC generators. These power stations are classified based on the type of fuel used as thermal, hydro electric and nuclear power stations. Most of these stations are located at remote places.

Hence the electric power generated is transmitted over long distances through transmission lines to reach towns or cities where it is actually consumed. This process is called power transmission. But there is a difficulty during power transmission. A sizable fraction of electric power is lost due to Joule heating (i²R) in the transmission lines which are hundreds of kilometer long.

This power loss can be tackled either by reducing current i or by reducing resistance R of the transmission lines. The resistance R can be reduced with thick wires of copper or aluminium. But this increases the cost of production of transmission lines and other related expenses. So this way of reducing power loss is not economically viable.

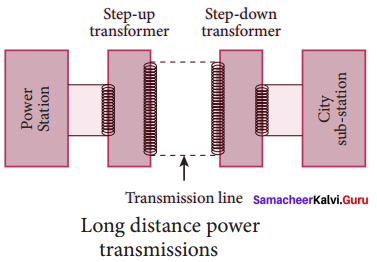
Since power produced is alternating in nature, there is a way out. The most important property of alternating voltage is that it can be stepped up and stepped down by using transformers could be exploited in reducing current and thereby reducing power losses to a greater extent.

At the transmitting point, the voltage is increased and the corresponding current is decreased by using step-up transformer. Then it is transmitted through transmission lines. This reduced current at high voltage reaches the destination without any appreciable loss.

At the receiving point, the voltage is decreased and the current is increased to appropriate values by using step-down transformer and then it is given to consumers. Thus power transmission is done efficiently and economically.

Illustration:
An electric power of 2 MW is transmitted to a place through transmission lines of total resistance, say R = 40 Ω, at two different voltages. One is lower voltage (10 kV) and the other is higher (100 kV). Let us now calculate and compare power losses in these two cases.

Case I:
P = 2 MW; R == 40 Ω; V = 10 kV Power,
Power, P = VI
∴ Current, I = \(\frac { P }{ V }\) = \(\frac {{ 2 × 10 }^{6}}{{ 10 × 10 }^{3}}\) 200 A
Power loss = Heat produced = I²R = (200)² × 40 = 1.6 × 10⁶ W
% of power loss =\(\frac {{ 1.6 × 10 }^{6}}{{ 2 × 10 }^{6}}\) × 100% = 0.8 × 100% = 80%

Case II:
P = 2 MW; R == 40 Ω; V = 100 kV
∴ Current, I = \(\frac { P }{ V }\) = \(\frac {{ 2 × 10 }^{6}}{{ 100 × 10 }^{3}}\) 20 A
Power loss = Heat produced = I²R = (20)² × 40 = 0.016 × 10⁶ W
% of power loss =\(\frac {{ 0.6 × 10 }^{6}}{{ 2 × 10 }^{6}}\) × 100% = 0.008 × 100% = 0.8%

Question 21.
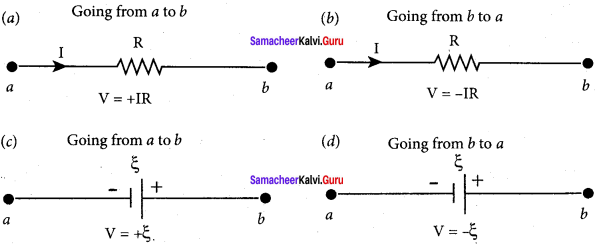
Find out the phase relationship between voltage and current in a pure inductive circuit.
Answer:
AC circuit containing only an inductor:
Consider a circuit containing a pure inductor of inductance L connected across an alternating voltage source. The alternating voltage is given by the equation.
υ = V_m sin ωt …(1)
The alternating current flowing through the inductor induces a self-induced emf or back emf in the circuit. The back emf is given by
Back emf, ε -L\(\frac { di }{ dt }\)
By applying Kirchoff’s loop rule to the purely inductive circuit, we get

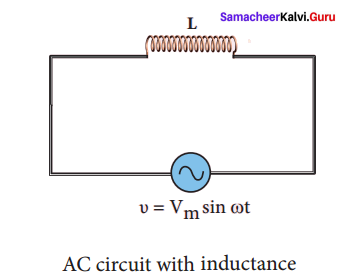
υ + ε = 0
V_m sin ωt = L\(\frac { di }{ dt }\)
di = L\(\frac {{ V }_{m}}{ L }\) sin ωt dt
i = \(\frac {{ V }_{m}}{ L }\) \(\int { sin } \) ωt dt = \(\frac{{ V }_{m}}{ Lω }\) (-cos ωt) + constant
The integration constant in the above equation is independent of time. Since the voltage in the circuit has only time dependent part, we can set the time independent part in the current (integration constant) into zero.

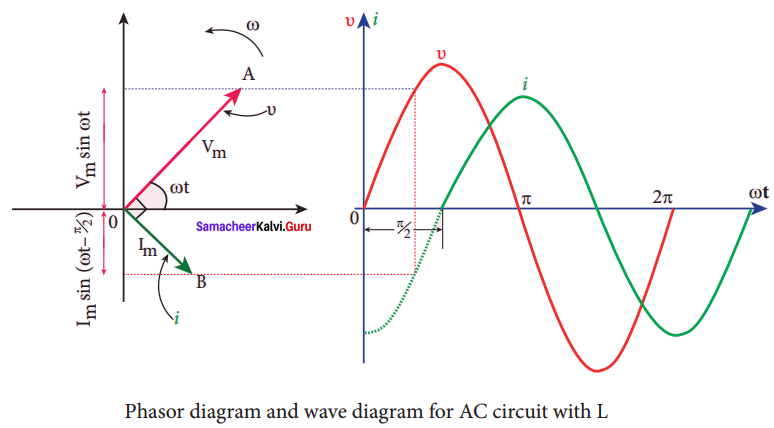
where \(\frac{{ V }_{m}}{ Lω }\) = I_m, the peak value of the alternating current in the circuit. From equation (1) and (2), it is evident that current lags behind the applied voltage by \(\frac{π}{ 2 }\) in an inductive circuit.
This fact is depicted in the phasor diagram. In the wave diagram also, it is seen that current lags the voltage by 90°.

Inductive reactance X_L:
The peak value of current I_m is given by I_m = \(\frac{{ V }_{m}}{ Lω }\) . Let us compare this equation with I_m = \(\frac{{ V }_{m}}{ R }\) from resistive circuit. The equantity ω_L Plays the same role as the resistance in resistive circuit. This is the resistance offered by the inductor, called inductive reactance (X_L). It is measured in ohm.
X_L = ω_L
The inductive reactance (X_L) varies directly as the frequency.
X_L = 2πfL …….. (3)
where ƒ is the frequency of the alternating current. For a steady current, ƒ= 0. Therefore, X_L = 0. Thus an ideal inductor offers no resistance to steady DC current.

Question 22.
Derive an expression for phase angle between the applied voltage and current in a series RLC circuit.
Answer:
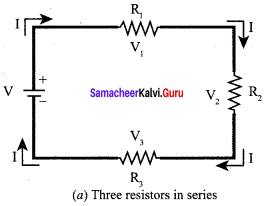
AC circuit containing a resistor, an inductor and a capacitor in series – Series RLC
circuit:
Consider a circuit containing a resistor of resistance R, a inductor of inductance L and a capacitor of capacitance C connected across an alternating voltage source. The applied alternating voltage is given by the equation.
υ = V_m sin ωt …… (1)

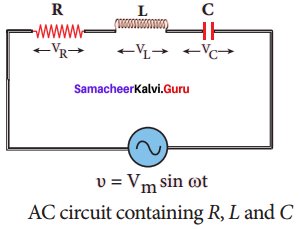
Let i be the resulting circuit current in the circuit at that instant. As a result, the voltage is developed across R, L and C.
We know that voltage across R (V_R) is in phase with i, voltage across L (V_L) leads i by π/2 and voltage across C (V_C) lags i by π/2.
The phasor diagram is drawn with current as the reference phasor. The current is represented by the phasor
\(\vec { OI } \), V_R by \(\vec { OA } \) ; V_L by \(\vec { OB } \) and V_C by \(\vec { OC } \).
The length of these phasors are
OI = I_m, OA = I_mR, OB = I_m,X_L; OC = I_mX_c
The circuit is cither effectively inductive or capacitive or resistive that depends on the value of V₁ or V_c Let us assume that V_L > V_C. so that net voltage drop across L – C combination is V_L < V_C which is represented by a phasor \(\vec { AD } \).
By parallelogram law, the diagonal \(\vec { OE } \) gives the resultant voltage u of VR and (V_L – V_C ) and its length OE is equal to V_m. Therefore,

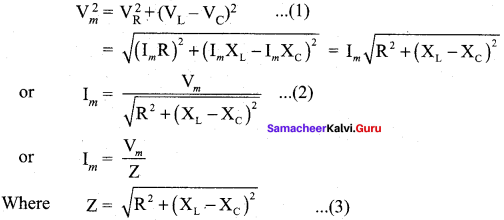
Z is called impedance of the circuit which refers to the effective opposition to the circuit current by the series RLC circuit. The voltage triangle and impedance triangle are given in the graphical figure.

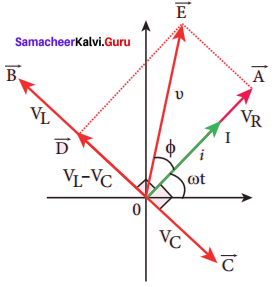
From phasor diagram, the phase angle between n and i is found out from the following relation

Special cases Figure: Phasor diagram for a series
(i) If X_L > X_C, (X_L – X_C) is positive and phase angle φ
is also positive. It means that the applied voltage leads the current by φ (or current lags behind voltage by φ). The circuit is inductive.
∴ υ = V_m sin ωt; i = I_m sin(ωt + φ)

(ii) If X_L < X_C, (X_L – X_C) is negative and φ is also negative. Therefore current leads voltage by φ and the circuit is capacitive.
∴ υ = Vm sin ωt; i = Im sin(ωt + φ)

(iii) If X_L = X_C, φ is zero. Therefore current and voltage are in the same phase and the circuit is resistive.
∴ υ = V_m sin ωt; i = I_m sin ωt

Question 23.
Define inductive and capacitive reactance. Give their units.
Answer:
Inductive reactance X_L:
The peak value of current I_m is given by I_m = \(\frac{{ V }_{m}}{ Lω }\). Let us compare
this equation with I_m \(\frac{{ V }_{m}}{ R }\) from resistive circuit. The quantity ωL plays the same role as the resistance R in resistive circuit. This is the resistance offered by the capacitor, called capacitive reactance (X_L). It measured in ohm.
X_L = ωL

Capacitive reactance X_C:
The peak value of current I is given by I_m = \(\frac{\mathrm{v}_{\mathrm{m}}}{1 / \mathrm{c} \omega}\). Let us compare this equation with I_m = \(\frac{{ V }_{m}}{ R }\) from resistive circuit. The quantity \(\frac { 1 }{ ωC }\) plays the same role as the resistance R in resistive circuit. This is the resistance offered by the capacitor, called capacitive reactance (X_C). It measured in ohm.
X_C = \(\frac{ 1 }{ ωC }\).

Question 24.
Obtain an expression for average power of AC over a cycle. Discuss its special cases. Power of a circuit is defined as the rate of consumption of electric energy in that circuit.
Answer:
It is given by the product of the voltage and current. In an AC circuit, the voltage and current vary continuously with time. Let us first calculate the power at an instant and then it is averaged over a complete cycle.
The alternating voltage and alternating current in the series RLC circuit at an instant are given by
υ = V_m sin ωt and i = I_m sin (ωt + 4>)
where φ is the phase angle between υ and i. The instantaneous power is then written as
P = υi = V_m I_m sin ωt sin(ωt + φ)
= V_m I_m sin ωt (sin ωt cos φ – cos ωt sin φ)
P = V_m I_m (cos φ sin² ωt – sin ωt cos ωt sin φ) …… (1)
Here the average of sin² ωt over a cycle is \(\frac { 1 }{ 2 }\) and that of sin ωt cos ωt is zero. Substituting these values, we obtain average power over a cycle.
P_av = V_m I_m cos φ x \(\frac { 1 }{ 2 }\) = \(\frac {{ V }_{m}}{ √2 }\) \(\frac {{ I }_{m}}{ √2 }\) cos φ
P_av = V_RMS I_RMS cos φ …… (2)
where V_RMS I_RMS is called apparent power and cos φ is power factor. The average power of an AC circuit is also known as the true power of the circuit.
Special Cases:
(i) For a purely resistive circuit, the phase angle between voltage and current is zero and cos
φ = 1.
∴ P_av = V_RMS I_RMS
(ii) For a purely inductive or capacitive circuit, the phase angle is ± \(\frac { π }{ 2 }\) and cos \(\left(\pm \frac{\pi}{2}\right)\) = 0
∴ P_av = 0
(iii) For series RLC circuit, the phase angle φ = tan^-1 \(\left(\frac{\mathrm{x}_{\mathrm{L}}-\mathrm{x}_{\mathrm{c}}}{\mathrm{R}}\right)\)
∴ P_av = V_RMS I_RMS cos φ
(iv) For series RLC circuit at resonance, the phase angle is zero and cos φ = 1.
∴ P_av = V_RMS I_RMS

Question 25.
Show that the total energy is conserved during LC oscillations.
Answer:
Conservation of energy in LC oscillations: During LC oscillations in LC circuits, the energy of the system oscillates between the electric field of the capacitor and the magnetic field of the inductor. Although, these two forms of energy vary with time, the total energy remains constant. It means that LC oscillations take place in accordance with the law of conservation of energy.
Total energy,

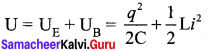
Let us consider 3 different stages of LC oscillations and calculate the total energy of the system.

Case I:
When the charge in the capacitor, q = Q_m and the current through the inductor, i = 0, the total energy is given by

The total energy is wholly electrical.

Case II:
When charge = 0; current = I_m, the total energy is

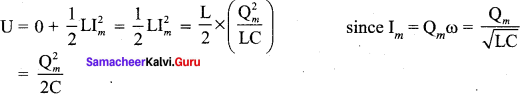
The total energy is wholly electrical.

Case III:
When charge = q; current = i, the total energy is

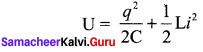
Since q = Q_m cos ωt, i = \(\frac { bq }{ dt }\) = Q_mω sin ωt. The negative sign in current indicates that the charge in the capacitor in the capacitor decreases with time.

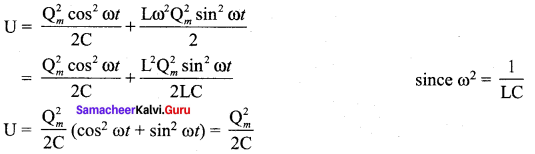
From above three cases, it is clear that the total energy of the system remains constant.

Question 26.
Prove that energy is conserved during electromagnetic induction.
Answer:
The mechanical energy of the spring-mass system is given by

The energy E remains constant for varying values of x and v. Differentiating E with respect to time, we get

This is the differential equation of the oscillations of the spring-mass system. The general solution of equation (2) is of the form
x(t) = X_m cos (ωt + φ) …… (3)
where X_m is the maximum value of x(t), ω, the angular frequency and φ, the phase constant. Similarly, the electromagnetic energy of the LC system is given by

Differentiating U with respect to time, we get

Equation (2) and (5) are proved the energy of electromagnetic induction is conserved.

Question 27.
Compare the electromagnetic oscillations of LC circuit with the mechanical oscillations of block spring system to find the expression for angular frequency of LC oscillators mathematically.
Answer:
The mechanical energy of the spring-mass system is given by

The energy E remains constant for varying values of x and v. Differentiating E with respect to time, we get

This is the differential equation of the oscillations of the spring-mass system. The general solution of equation (2) is of the form
x(t) = X_m cos (ωt + φ) …… (3)
where X_m is the maximum value of x(t), ω, the angular frequency and φ, the phase constant. Similarly, the electromagnetic energy of the LC system is given by

Differentiating U with respect to time, we get

Equation (2) and (5) are proved the energy of electromagnetic induction is conserved.
q(t) = Q_m cos (ωt + φ) …… (6)
where Q_m is the maximum value of q(t), ω, the angular frequency and φ, the phase constant.

Current in the LC circuit:
The current flowing in the LC circuit is obtained by differentiating q(t) with respect to time.
i(t) = \(\frac { dq }{ dt }\) = \(\frac { d }{ dt }\) [Q_m cos (ωt + φ)] = Q_m ω sin (ωt + φ) since I_m = Q_mω
(or)
i(t) -I_m sin (ωt + φ) ……. (7)
The equation (7) clearly shows that current varies as a function of time t. In fact, it is a sinusoidally varying alternating current with angular frequency ω.

Angular frequency of LC oscillations:
By differentiating equation (6) twice, we get
\(\frac { { d }^{ 2 }q }{ dt } \) = -Q_mω² cos (ωt + φ) …….. (8)
Substituting equations (6) and (8) in equation (5),
we obtain L[-Q_mω² cos (ωt + φ)] + \(\frac { 1 }{ C }\) Q_m cos (ωt + φ) = 0
Rearranging the terms, the angular frequency of LC oscillations is given by
ω = \(\frac { 1 }{ \sqrt { LC } } \) …… (9)
This equation is the same as that obtained from qualitative analogy.

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Numerical Problems

Question 1.
A square coil of side 30 cm with 500 turns is kept in a uniform magnetic field of 0.4 T. The plane of the coil is inclined at an angle of 30° to the field. Calculate the magnetic flux through the coil.
Solution:
Square coil of side (a) = 30 cm = 30 × 10^-2m
Area of square coil (A) = a² = (30 × 10^-2)2 = 9 × 10^-2 m²
Number of turns (N) = 500
Magnetic field (B) = 0.4 T
Angular between the field and coil (θ) = 90 – 30 = 60°
Magnetic flux (Φ) = NBA cos 0 = 500 × 0.4 × 9 × 10^-2 × cos 60° = 18 × \(\frac { 1 }{ 2 }\)
Φ = 9 W b

Question 2.
A straight metal wire crosses a magnetic field of flux 4 mWb in a time 0.4 s. Find the magnitude of the emf induced in the wire.
Solution:
Magnetic flux (Φ) = 4 m Wb = 4 × 10^-3 Wb
time (t) = 0.4 s
The magnitude of induced emf (e) = \(\frac { dΦ }{ dt }\) = \(\frac {{ 4 × 10 }^{-3}}{ 0.4 }\) 10^-2
e = 10 mV

Question 3.
The magnetic flux passing through a coil perpendicular to its plane is a function of time and is given by OB = (2t³ + 4t² + 8t + 8) Wb. If the resistance of the coil is 5 Ω, determine the induced current through the coil at a time t = 3 second.
Solution:
Magnetic flux (Φ_B) = (2t³ + 8t² + 8t + 8)Wb
Resistance of the coil (R) = 5 Ω
time (t) = 3 second
Induced current through the coil, I = \(\frac { e }{ R }\)
Induced emf, e = \(\frac {{ dΦ }_{B}}{ dt }\) = \(\frac { d }{ dt }\) ((2t³ + 4t² + 8t + 8) = 6t² + 8t + 8
Here time (t) = 3 second
e = 6(3)² + 8 × 3 + 8 = 54 + 24 + 8 = 86 V
∴ Induced current through the coil, I = \(\frac { e }{ R }\) = \(\frac { 86 }{ 5 }\) = 17.2 A

Question 4.
A closely wound coil of radius 0.02 m is placed perpendicular to the magnetic field. When the magnetic field is changed from 8000 T to 2000 T in 6 s, an emf of 44 V is induced. Calculate the number of turns in the coil.
Solution:
Radius of the coil (r) = 0.02 m
Area of the coil (A) = πr² = 3.14 × (0.02)²= 1.256 × 10^-3 m²
Change in magnetic field, dB = 8000 – 2000 = 6000 T
Time, dt = 6 second
Induced emf, e = 44 V
θ = 0°
Induced emf in the coil, e = NA \(\frac { d }{ dt }\) cos θ . dt
44 = N × 1.256 × 10^-3 × \(\frac { 600 }{ 6 }\) × Cos 0°

Number of turns N = 35 turns

Question 5.
A rectangular coil of area 6 cm² having 3500 turns is kept in a uniform magnetic field of 0.4 T, Initially, the plane of the coil is perpendicular to the field and is then rotated through an angle of 180°. If the resistance of the coil is 35 Ω, find the amount of charge flowing through the coil.
Solution:
Rectangular coil of their area, A = 6 cm² = 6 x 10^-4 m²
Number of turns N = 3500 turns
Magnetic field, B = 0.4 T
Resistance of the coil, R= 35 Ω
Induced emf (e) = change in flux per second = Φ₂ – Φ₁
e = NAB cos 180° – NBA cos 0° = -NBA – NBA = – 2 NBA
= – 2 x 3500 x 0.4 x 6 x 10^-4 – 16800 x 10^-4 = – 1.68 V
Current flowing the coil, I = \(\frac { e }{ R }\) = \(\frac { -1.68 }{ 35 }\) = 0.048
Magnitude of the current, I = 48 x 10^-3 A
Amount of charge flowing through the coil, q = It = 48 x 10^-3 x 1 = 48 x 10^-3 C

Question 6.
An induced current of 2.5 mA flows through a single conductor of resistance 100 Ω. Find out the rate at which the magnetic flux is cut by the conductor.
Solution:
Induced current, I = 2.5 mA
Resistance of conductor, R = 100 Ω
∴ The rate of change of flux, \(\frac {{ dΦ }_{B}}{ dt }\) = e
\(\frac {{ dΦ }_{B}}{ dt }\) = e = IR = 2.5 x 10-3 x 100 = 250 x 10^-3 dt
\(\frac {{ dΦ }_{B}}{ dt }\) = 250 mWb s^-1

Question 7.
A fan of metal blades of length 0.4 m rotates normal to a magnetic field of 4 x 10^-3 T. If the induced emf between the centre and edge of the blade is 0.02 V, determine the rate of rotation of the blade.
Solution:
Length of the metal blade, l = 0.4 m
Magnetic field, B = 4 x 10^-3 T
Induced emf, e = 0.02 V
Rotational area of the blade, A = πr² = 3.14 x (0.4)² = 0.5024 m²
Induced emf in rotational of the coil, e = NBA ω sin θ

= 9.95222 x 10^-3 x 10³
= 9.95 revolutions/second
Rate of rotational of the blade, ω = 9.95 revolutions/second

Question 8.
A bicycle wheel with metal spokes of 1 m long rotates in Earth’s magnetic field. The plane of the wheel is perpendicular to the horizontal component of Earth’s field of 4 x 10^-5 T. If the emf induced across the spokes is 31.4 mV, calculate the rate of revolution of the wheel.
Solution:
Length of the metal spokes, l = 1 m
Rotational area of the spokes, A = π² = 3.14 x (1)² = 3.14 m²
Horizontal component of Earth’s field, B = 4 x 10^-5 T
Induced emf, e = 31.4 mV
The rate of revolution of wheel,

ω = 250 revolutions / second

Question 9.
Determine the self-inductance of 4000 turn air-core solenoid of length 2m and diameter 0. 04 m.
Solution:
Length of the air core solenoid, l = 2 m
Diameter, d = 0.04 m
Radius, r = \(\frac { d }{ 2 }\) = 0.02 m
Area of the air core solenoid, A = π² = 3.14 x (0.02)² = 1.256 x 10^-3 m²
Number of Turns, N = 4000 turns
Self inductance, L = µ₀n² Al

Question 10.
A coil of 200 turns carries a current of 4 A. If the magnetic flux through the coil is 6 x 10^-5 Wb, find the magnetic energy stored in the medium surrounding the coil.
Solution:
Number of turns of the coil, N = 200
Current, I = 4 A
Magnetic flux through the coil, Φ = 6 x 10^-5 Wb
Energy stored in the coil, U = \(\frac { 1 }{ 2 }\) LI² = \(\frac { 1 }{ I2}\)
Self inductance of the coil, L = \(\frac { NΦ }{ I }\)
U =\(\frac { 1 }{ 2 }\) \(\frac { NΦ }{ I }\) x I² = \(\frac { 1 }{ 2}\) NΦI = \(\frac { 1 }{ 2}\) x 200 x 6 x 10^-5 x 4
U = 2400 x 10^-5 = 0.024 J (or) joules.

Question 11.
A 50 cm long solenoid has 400 turns per cm. The diameter of the solenoid is 0.04 m. Find the magnetic flux of a turn when it carries a current of 1 A.
Solution:
Length of the solenoid, l = 50 cm = 50 x 10^-2 m
Number of turns per cm, N = 400
Number of turns in 50 cm, N = 400 x 50 = 20000
Diameter of the solenoid, d = 0.04 m
Radius of the solenoid, r = \(\frac { d }{ 2}\) = 0.02 m
Area of the solenoid, A = π² = 3.14 x (0.02)² = 1.256 x 10^-3 m²
Current passing through the solenoid, I = 1 A
Magnetic fluex,

Question 12.
A coil of 200 turns carries a current of 0.4 A. If the magnetic flux of 4 mWb is linked with the coil, find the inductance of the coil.
Solution:
Number of turns, N = 200; Current, I = 0.4 A
Magnetic flux linked with coil, Φ = 4 mWb = 4 x 10^-3 Wb
Induction of the coil, L = \(\frac { NΦ }{ I }\) = \(\frac {{ 200 × 4 × 10 }^{-3}}{ 0.4 }\) = \(\frac {{ 800 × 10 }^{-3}}{ 0.4 }\) 2 H

Question 13.
Two air core solenoids have the same length of 80 cm and same cross-sectional area 5 cm². Find the mutual inductance between them if the number of turns in the first coil is 1200 turns and that in the second coil is 400 turns.
Solution:
Length of the solenoids, l = 80 cm = 8 x 10^-2 m
Cross sectional area of the solenoid, A = 5 cm² = 5 x 10^-4 m²
Number of turns in the I^st coil, N₁ = 1200
Number of turns in the IInd coil, N₂ = 400
Mutual inductance between the two coils,

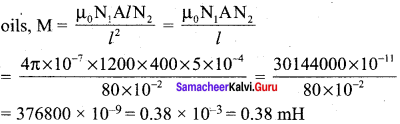
Question 14.
A long solenoid having 400 turns per cm carries a current 2A. A 100 turn coil of cross sectional area 4 cm² is placed co-axially inside the solenoid so that the coil is in the field produced by the solenoid. Find the emf induced in the coil if the current through the solenoid reverses its direction in 0.04 sec.
Solution:
Number of turns of long solenoid per cm =\(\frac { 400 }{{10}^{ -2 }}\); N₂ = 400 x 10²
Number of turns inside the solenoid, N₂ = 100
Cross-sectional area of the coil, A = 4 cm² = 4 x 10^-4 m²
Current through the solenoid, I = 2A; time, t = 0.04 s
Induced emf of the coil, e = -M \(\frac { dI }{ dt }\)
Mutual inductance of the coil,

Induced emf of the coil,

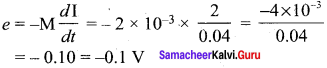
The current through the solenoid reverse its direction if the induced emf, e = -0.2 V

Question 15.
A 200 turn coil of radius 2 cm is placed co-axially within a long solenoid of 3 cm radius. If the turn density of the solenoid is 90 turns per cm, then calculate mutual inductance of the coil.
Solution:
Number of turns of the solenoid, N₂ = 200
Radius of the solenoid, r = 2cm = 2 x 10² m
Area of the solenoid, A = πr²= 3.14 x (2 x 10^-2)² = 1.256 x 10^-3 m²
Turn density of long solenoid per cm, N₁ = 90 x 10²
Mutual inductance of the coil,

= 283956.48 x 10^-8 ⇒ M = 2.84 mH

Question 16.
The solenoids S₁ and S₂ are wound on an iron-core of relative permeability 900. The area of their cross-section and their length are the same and are 4 cm² and 0.04 m, respectively. If the number of turns in S₁ is 200 and that in S₂ is 800, calculate the mutual inductance between the coils. The current in solenoid 1 is increased from 2A to 8A in 0.04 second. Calculate the induced emf in solenoid 2.
Solution:
Relative permeability of iron core, μ_r = 900
Number of turns of solenoid S₁, N₁ = 200
Number of turns of solenoid S₂, N₂ = ‘800
Area of cross section, A = 4 cm² = 4 x 10^-4 m²
Length of the solenoid S₁, l₁ = 0.04 m
current, I =I₂ – I₁ = 8 – 2 = 6A
time taken, t = 0.04 second
emf induced in solenoid S₂ e = -M \(\frac { dI }{ dt }\)
Mutual inductance between the two coils, M = \(\frac{\mu_{0} \mu_{r} N_{1} N_{2} A}{l}\)

M = 180864 x 10^-5 = 1.81 H
Emf induced in solenoid S₂, e = -M\(\frac { dI }{ dt }\) = -1.81 x \(\frac { 6 }{ 0.04 }\)
Magnitude of emf, e = 271.5 V

Question 17.
A step-down transformer connected to main supply of 220 V is made to operate 11 V, 88 W lamp. Calculate (i) Transformation ratio and (ii) Current in the primary.
Solution:
Voltage in primary coil, V_p = 220 V
Voltage in secondary coil, V_s = 11 V
Output power = 88 W
(i) To find transformation ratio, k = \(\frac {{ V }_{ s }}{{ V }_{ p }}\) = \(\frac { 11 }{ 220 }\) = \(\frac { 1 }{ 20 }\)
(ii) Current in primary, I_p = \(\frac {{ V }_{ s }}{{ V }_{ p }}\) x I_s
So, I_s = ?
Outputpower = V_s I_s
⇒ 88 = 11 x I_s
I_s = \(\frac { 88 }{ 11 }\) = 8A
Therefore, I_p = \(\frac {{ V }_{ s }}{{ V }_{ p }}\) x I_s = \(\frac { 11 }{ 220 }\) x 8 = 0.4 A

Question 18.
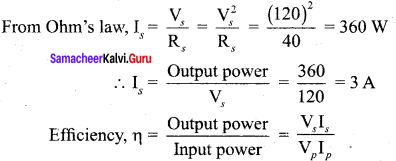
A 200V/120V step-down transformer of 90% efficiency is connected to an induction stove of resistance 40 Ω. Find the current drawn by the primary of the transformer.
Solution:
Primary voltage, V_p = 200 V
Secondary voltage, V_s = 120 V
Efficiency, η = 90%
Secondary resistance, R_s = 40 Ω
Current drawn by the primary of the transformc, I_p = \(\frac {{ V }_{ s }}{{ R }_{ s }}\) x I_s
Output power = V_s I_s

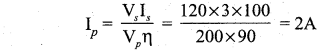
Question 19.
The 300 turn primary of a transformer has resistance 0.82 Ω and the resistance of its secondary of 1200 turns is 6.2 Ω. Find the voltage across the primary if the power output from the secondary at 1600V is 32 kW. Calculate the power losses in both coils when the transformer efficiency is 80%.
Solution:
Efficiency, η = 80% = \(\frac { 80 }{ 100 }\)
Number of turns in primary, N_p = 300
Number of turns in secondary, N_s = 1200
Resistance in primary, R_p = 0.82 Ω
Resistance in secondary, R_s = 6.2 Ω
Secondary voltage, V_s = 1600 V
Output power = 32 kW
Output power = V_s I_s

Power loss in primary = \({ { I }_{ p }^{ 2 }{ R }_{ p } }\) = (100)² x 0.82 = 8200 = 8.2 kW
Power loss in secondary = \({ { I }_{ s }^{ 2 }{ R }_{ s } }\) = (20)² x 6.2 = 2480 = 2.48 kW

Question 20.
Calculate the instantaneous value at 60°, average value and RMS value of an alternating current whose peak value is 20 A.
Solution:
Peak value of current, I_m = 20 A
Angle, θ = 60° [θ = ωt]
(i) Instantaneous value of current,
i = I_m sin ωt = I_m sin θ
= 20 sin 60° = 20 x \(\frac { √3 }{ 2 }\) = 10√3 = 10 x 1.732
i = 17.32 A

(ii) Average value of current,
I_av = \(\frac {{ 2I }_{m}}{ π }\) = \(\frac { 2 × 20 }{ 3.14 }\)
I_av = 12.74 A

(iii) RMS value of current,
I_RMS = 0.707 I_m
or \(\frac{\mathrm{I}_{\mathrm{m}}}{\sqrt{2}}\) = 0.707 x 20
I_RMS = 14. 14 A

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Conceptual Questions

Question 1.
A graph between the magnitude of the magnetic flux linked with a closed loop and time is given in the figure. Arrange the regions of the graph in ascending order of the magnitude of induced emf in the loop.
Answer:
According to electromagnetic induction, induced emf,

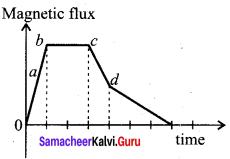
e = \(\frac { dΦ }{ dt }\)
Ascending order of induced emf from the graphical representation is b < c < d < a.

Question 2.
Using Lenz’s law, predict the direction of induced current in conducting rings 1 and 2 when current in the wire is steadily decreasing.
Answer:

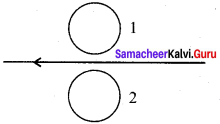
According to Lenz’s law, a current will be induced in the coil which will produce a flux in the opposite direction.

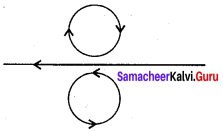
If the current decreases in the wire, the induced current flows in ring 1 in clockwise direction, the induced current flows in ring 2 in anti-clockwise direction.

Question 3.
A flexible metallic loop abed in the shape of a square is kept in a magnetic field with its plane perpendicular to the field. The magnetic field is directed into the paper normally. Find the direction of the induced current when the square loop is crushed into an irregular shape as shown in the figure.
Answer:

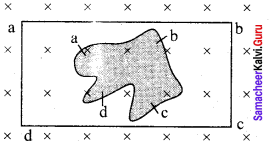
The magnetic flux linked with the wire decreases due to decrease in area of the loop. The induced emf will cause current to flow in the direction. So that the wire is pulled out ward direction from all sides. According to Fleming’s left hand rule, force on wire will act outward i direction from all sides.

Question 4.
Predict the polarity of the capacitor in a closed circular loop when two bar magnets are moved as shown in the figure.
Answer:

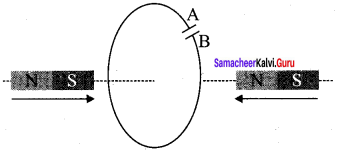
When magnet 1 is moved with its South pole towards to the coil, emf is induced in the coil as the magnetic flux through the coil changes. When seeing from the left hand side the direction of induced current appears to be clockwise. When seeing from the right hand side the direction of induced current appears to be anti-clockwise. In capacitor, plate A has positive polarity and plate B has negative polarity.

Question 5.
In series LC circuit, the voltages across L and C are 180° out of phase. Is it correct? Explain.
Answer:
In series LC circuit, the voltage across the capacitance lag the current by 90° while the voltage across the inductance lead the current by 90°. This makes the inductance and capacitance voltages 180° out of phase.

Question 6.
When does power factor of a series RLC circuit become maximum?
Answer:
For a series LCR circuit, power factor is

For purely resistive, Φ = 0°, cos 0° = 1
Thus the power factor assumes the maximum value for a purely resistive circuit.

Question 7.
Draw graphs showing the distribution of charge in a capacitor and current through an inductor during LC oscillations with respect to time. Assume that the charge in the capacitor is maximum initially.
Answer:
For a capacitor, the graph between charge and time.

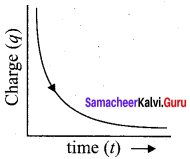
The charge decays exponentially decreases with time.

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Additional Questions solved

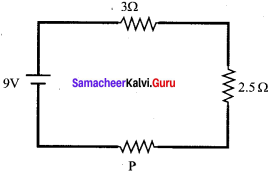
I Choose The Correct Answer

Question 1.
A coil of area of cross section 0.5 m² with 10 turns is in a plane which is perpendicular to an uniform magnetic field of 0.2 Wb/m². The flux through the coil is –
(a) 100 Wb
(b) 10 Wb
(c) 1 Wb
(d) zero
Answer:
(c) 1 Wb
Hint:
Φ = NBA cos θ
= 10 x 0.2 x 0.5 x cos 0° = 1 Wb

Question 2.
A rectangular coil of 100 turns and size 0.1 m x 0.05 m is placed perpendicular to a magnetic field of 0.1 T. If the field drops to 0.05 T in 0.05 s, the magnitude of the emf induced in the coil is-
(a) 0.5 V
(b) 0.75 V
(c) 1.0 V
(d) 1.5 V
Answer:
(a) 0.5 V
Hint:

ε = 0.5 V

Question 3.
A wire of length 1 m moves with a speed of 10 ms^-1 perpendicular to a magnetic field. If the emf induced in the wire is 1 V, the magnitude of the field is-
(a) 0.01 T
(b) 0.1 T
(c) 0.2 T
(d) 0.02 T
Answer:
(b) 0.1 T
Hint:
ε = Blv
⇒ B = \(\frac { ε }{ lv }\) = \(\frac { 1 }{ 1 × 10 }\) = 0.02 T

Question 4.
A coil of area 10 cm², 10 ms^-1 turns and resistance 20 Ω is placed in a magnetic field directed perpendicular to the plane of the coil and changing at the rate of 10⁸ gauss/second. The induced current in the coil will be-
(a) 5 A
(b) 0.5 A
(c) 0.05 A
(d) 50 A
Answer:
(a) 5 A
Hint:

Question 5.
A coil of cross sectional area 400 cm² having 30 turns is making 1800 rev/min in a magnetic field of IT. The peak value of the induced emf is-
(a) 113 V
(b) 226 V
(c) 339 V
(d) 452 V
Answer:
(b) 226 V
Hint:
ε_m = NBA ω = 30 x 1 x 400 x 10^-4 x 30 x 2π
= 226 V

Question 6.
Eddy currents are produced in a material when it is-
(a) heated
(b) placed in a time varying magnetic field
(c) placed in an electric field
(d) placed a uniform magnetic field
Answer:
(b) placed in a time varying magnetic field

Question 7.
An emf of 5 V is induced in an inductance when the current in it changes at a steady rate from 3 A to 2 A in 1 millisecond. The value of inductance is-
(a) 5 mH
(b) 5 H
(c) 5000 H
(d) zero
Answer:
(a) 5 mH

Question 8.
Faraday’s law of electromagnetic induction is related to the-
(a) Law of conservation of charge
(b) Law of conservation of energy
(c) Third law of motion
(d) Law of conservation of angular momentum
Answer:
(b) Law of conservation of energy

Question 9.
The inductance of a coil is proportional to-
(a) its length
(b) the number of turns
(c) the resistance of the coil
(d) square of the number of turns
Answer:
(d) square of the number of turns

Question 10.
When a direct current ‘i’ is passed through an inductance L, the energy stored is-
(a) Zero
(b) Li
(c) \(\frac { 1 }{ 2 }\) Li²
(d) \(\frac {{ L }^{ 2 }}{2i}\)
Answer:
(c) \(\frac { 1 }{ 2 }\) Li²

Question 11.
A coil of area 80 cm² and 50 turns is rotating with 2000 revolutions per minute about an axis perpendicular to a magnetic field of 0.05 T. The maximum value of the emf developed in it is-
(a) 2000 πV
(b) \(\frac { 10π }{ 3 }\) V
(c) \(\frac { 4π }{ 3 }\)V
(d) \(\frac { 2 }{ 3 }\) V
Answer:
(c) \(\frac { 4π }{ 3 }\)V
Hint:
ε = NBA ω = 50 x 0.05 x 80 x 10^-4 x \(\frac { 2π × 2000 }{ 60 }\) = \(\frac { 4π }{ 3 }\)V

Question 12.
The direction of induced current during electro magnetic induction is given by-
(a) Faraday’s law
(b) Lenz’s law
(c) Maxwell’s law
(d) Ampere’s law
Answer:
(b) Lenz’s law

Question 13.
AC power is transmitted from a power house at a high voltage as-
(a) the rate of transmission is faster at high voltages
(b) it is more economical due to less power loss
(c) power cannot be transmitted at low voltages
(d) a precaution against theft of transmission lines
Answer:
(b) it is more economical due to less power loss

Question 14.
In a step-down transformer the input voltage is 22 kV and the output voltage is 550 V. The ratio of the number of turns in the secondary to that in the primary is-
(a) 1 : 20
(b) 20 : 1
(c) 1 : 40
(d) 40 : 1
Answer:
(c) 1 : 40
Hint:
\(\frac {{ N }_{ s }}{{ N }_{ p }}\) = \(\frac {{ V }_{ s }}{{ V }_{ p }}\) = \(\frac { 550 }{ 22000 }\) = \(\frac { 1 }{ 40 }\)

Question 15.
The self-inductance of a coil is 5 H. A current of 1 A changes to 2 A within 5 s through the coil. The value of induced emf will be-
(a) 10 V
(b) 0.1 V
(c) 1.0 V
(d) 100 V
Answer:
(c) 1.0 V
Hint:

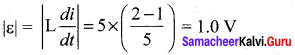
Question 16.
The low-loss transformer has 230 V applied to the primary and gives 4.6 V in the secondary. The secondary is connected to a load which draws 5 amperes of current. The current (in amperes) in the primary is-
(a) 0.1 A
(b) 1.0 A
(c) 10 A
(d) 250 A
Answer:
(a) 0.1 A
Hint:
I_p = \(\frac {{ V }_{ s }{ I }_{ s }}{{ V }_{ p }}\) = \(\frac { 4.6 × 5 }{ 230 }\) = 0.1A

Question 17.
A coil is wound on a frame of rectangular cross-section. If all the linear dimensions of the frame are increased by a factor 2 and the number of turns per unit length of the coil remains the same. Self-inductance of the coil increases by a factor of-
(a) 4
(b) 8
(c) 12
(d) 16
Answer:
(b) 8
Hint:
If all the linear dimensions are doubled, the cross-sectional are a becomes eight times. Therefore, the flux produced by a given current will become eight times. Hence, the selfinductance increases by a factor of 8.

Question 18.
If N is the number of turns in a coil, the value of self-inductance varies as-
(a) N°
(b) N
(c) N²
(d) N^-2
Answer:
(c) N²
Hint:
According to self inductance of long solenoid
L = \(\frac{\mu_{0} \mathrm{N}^{2} \mathrm{A}}{l}\)
⇒ L ∝ N²

Question 19.
A magnetic field 2 x 10^-2 T acts at right angles to a coil of area 100 cm² with 50 turns. The average emf induced in the coil will be 0.1 V if it is removed from the field in time.
(a) 0.01 s
(b) 0.1 s
(c) 1 s
(d) 10 s
Answer:
(b) 0.1 s
Hint:

Question 20.
Number of turns in a coil is increased from 10 to 100. Its inductance becomes-
(a) 10 times
(b) 100 times
(c) 1/10 times
(d) 25 times
Answer:
(a) 10 times

Question 21.
The north pole of a magnet is brought near a metallic ring as shown in the figure. The direction of induced current in the ring, as seen by the magnet is-

(a) anti-clockwise
(b) first anti-clockwise and then clockwise
(c) clockwise
(d) first clockwise and then anti-clockwise
Answer:
(a) anti-clockwise

Question 22.
Quantity that remains unchanged in a transformer is-
(a) voltage
(b) current
(c) frequency
(d) none of these
Answer:
(c) frequency

Question 23.
The core of a transformer is laminated to reduce.
(a) Copper loss
(b) Magnetic loss
(c) Eddy current loss
(d) Hysteresis loss
Answer:
(c) Eddy current loss

Question 24.
Which of the following has the dimension of time?
(a) LC
(b) \(\frac { R }{ L }\)
(c) \(\frac { L }{ R }\)
(d) \(\frac { C }{ L }\)
Answer:
(c) \(\frac { L }{ R }\)

Question 25.
A coil has a self-inductance of 0.04 H. The energy required to establish a steady-state current of 5 A in it is-
(a) 0.5 J
(b) 1.0 J
(c) 0.8 J
(d) 0.2 J
Answer:
(a) 0.5 J

Question 26.
Alternating current can be measured by
(a) moving coil galvanometer
(b) hot wire ammeter
(c) tangent galvanometer
(d) none of the above
Answer:
(b) hot wire ammeter

Question 27.
In an LCR circuit, the energy is dissipated in-
(a) R only
(b) R and L only
(c) R and C only
(d) R, L and C
Answer:
(a) R only

Question 28.
A 40 Ω electric heater is connected to 200 V, 50 Hz main supply. The peak value of the electric current flowing in the circuit is approximately-
(a) 2.5 A
(b) 5 A
(c) 7 A
(d) 10 A
Answer:
(c) 7 A
Hint:
I₀ = \(\frac {{ V }_{0}}{ R }\) = \(\frac{200 \sqrt{2}}{40}\) 5 √2 ≈ 7A

Question 29.
The rms value of an alternating current, which when passed through a resistor produces heat three times of that produced by a direct current of 2 A in the same resistor, is-
(a) 6 A
(b) 3 A
(c) 2 A
(d) 2√3 A
Answer:
(d) 2√3 A
Hint:
\({ I }_{ rms }^{ 2 }\)R = 3(2²R) (or) I_rms = 2√3 A

Question 30.
An inductance, a capacitance and a resistance are connected in series across a source of alternating voltages. At resonance, the applied voltage and the current flowing through the circuit will have a phase difference of-
(a) \(\frac { π }{ 4 }\)
(b) zero
(c) π
(d) \(\frac { π }{ 2 }\)
Answer:
(b) zero

Question 31.
In an AC circuit, the rms value of the current I_rms, is related to the peak current I₀ as-
(a) I_rms = \(\frac {{I}_{0}}{ π }\)
(b) I_rms = \(\frac {{I}_{0}}{ √2 }\)
(c) I_rms = √2 I₀
(d) I_rms = πI₀
Answer:
(b) I_rms = \(\frac {{I}_{0}}{ √2 }\)

Question 32.
The impedance of a circuit consists of 3 Ω resistance and 4 Ω resistance. The power factor of the circuit is
(a) 0.4
(b) 0.6
(c) 0.8
(d) 1.0
Answer:
(b) 0.6
Hint:
tan Φ = \(\frac { 4 }{ 3 }\).
Power factor = cos Φ = \(\frac { 3 }{ 5 }\) = 0.06

Question 33.
The reactance of a capacitance at 50 Hz is 5 Ω. Its reactance at 100 Hz will be-
(a) 5 Ω
(b) 10 Ω
(c) 20 Ω
(d) 2.5 Ω
Answer:
(d) 2.5 Ω.

Question 34.
In a LCR AC circuit off resonance, the current-
(a) is always in phase with the voltage
(b) always lags behind the voltage
(c) always leads the voltage
(d) may lead or lag behind the voltage
Answer:
(d) may lead or lag behind the voltage

Question 35.
The average power dissipation in a pure inductance L, through which a current I₀ sin ωt is flowing is-
(a) \(\frac { 1 }{ 2 }\) L\({ I }_{ 0 }^{ 2 }\)
(b) L\({ I }_{ 0 }^{ 2 }\)
(c) 2 L\({ I }_{ 0 }^{ 2 }\)
(d) zero
Answer:
(d) zero

Question 36.
The power in an AC circuit is given by P = V_rms I_rms cos Φ. The value of the power factor cos Φ in series LCR circuit at resonance is-
(a) zero
(b) 1
(c) \(\frac { 1 }{ 2 }\)
(d) \(\frac { 1 }{ √2 }\)
Answer:
(b) 1
Hint:

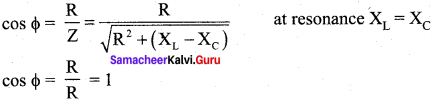
Question 37.
In an AC circuit with voltage V and current I, the power dissipated is-
(a) VI
(b) \(\frac { 1 }{ 2 }\) VI
(c) \(\frac { 1 }{ √2 }\) VI
(d) depends on the phase difference between I and V
Answer:
(d) depends on the phase difference between I and V

Question 38.
In an AC circuit containing only capacitance, the current-
(a) leads the voltage by 180°
(b) remains in phase with the voltage
(c) leads the voltage by 90°
(d) lags the voltage by 90°
Answer:
(c) leads the voltage by 90°

Question 39.
In a series LCR circuit R = 10 Ω and the impedance Z = 20 Ω. Then the phase difference between the current and the voltage is-
(a) 60°
(b) 30°
(c) 45°
(d) 90°
Answer:
(c) 60°
Hint:
cos Φ = \(\frac { R }{ Z }\) = \(\frac { 10 }{ 20 }\) = \(\frac { 1 }{ 2 }\)
⇒ Φ = 60°

Question 40.
What is the value of inductance L for which the current is maximum in a series LCR circuit with C = 10 μF and ω = 1000 s^-1?
(a) 1 mH
(b) 10 mH
(c) 100 mH
(d) Cannot be calculated unless R is known
Answer:
(c) 100 mH
Hint:
L = \(\frac { 1 }{ { \omega }^{ 2 }C } \) = \(\frac{1}{(1000)^{2} \times 10 \times 10^{-6}}\) = 0.1 H = 100 mH

II Fill in the Blanks

Question 1.
Electromagnetic induction is used in …………….
Answer:
transformer and AC generator

Question 2.
Lenz’s Law is in accordance with the law of …………….
Answer:
conservation of energy.

Question 3.
The self-inductance of a straight conductor is …………….
Answer:
zero

Question 4.
Transformer works on …………….
Answer:
AC only

Question 5.
The power loss is less in transmission lines when …………….
Answer:
voltage is more but current is less

Question 6.
The law that gives the direction of the induced current produced in a circuit is …………….
Answer:
Lenz’s law

Question 7.
Fleming’s right hand rule is otherwise called …………….
Answer:
generator rule

Question 8.
Unit of self-inductance is …………….
Answer:
Henry

Question 9.
The mutual induction is very large, if the two coils are wound on …………….
Answer:
soft iron core

Question 10.
When the coil is in vertical position, the angle between the normal to the plane of the coil and magnetic field is …………….
Answer:
zero

Question 11.
The emf induced by changing the orientation of the coil is ……………. in nature.
Answer:
sinusoidal

Question 12.
In a three phase AC generator, the three coils are inclined at an angle of …………….
Answer:
120°

Question 13.
The emf induced in each of the coils differ in phase by …………….
Answer:
120°

Question 14.
A device which converts high alternating voltage into low alternating voltage and vice versa is …………….
Answer:
transformer

Question 15.
For an ideal transformer efficiency η is …………….
Answer:
1

Question 16.
The alternating emf induced in the coil varies …………….
Answer:
periodically in both magnitude and direction

Question 17.
For direct current, inductive reactance is …………….
Answer:
zero

Question 18.
In an inductive circuit the average power of sinusoidal quantity of double the frequency over a complete cycle is …………….
zero

Question 19.
For direct current, the resistance offered by a capacitor is …………….
Answer:
infinity

Question 20.
In a capacitive circuit, power over a complete cycle is …………….
Answer:
zero

Question 21.
Q-factor measures the …………….in resonant circuit
Answer:
selectivity

Question 22.
Voltage drop across inductor and capacitor differ in phase by …………….
Answer:
180°

Question 23.
Angular resonant frequency (co) is …………….
Answer:
\(\frac { 1 }{ \sqrt { LC } } \)

Question 24.
A circuit will have flat resonance if its Q-value is …………….
Answer:
low

Question 25.
The average power consumed by the choke coil over a complete cycle is …………….
Answer:
zero

III Match the following

Question 1.

Answer:
(i) → (c)
(ii) → (a)
(iii) → (d)
(iv) → (b)

Question 2.

Answer:
(i) → (c)
(ii) → (a)
(iii) → (d)
(iv) → (b)

Question 3.

Answer:
(i) → (c)
(ii) → (d)
(iii) → (b)
(iv) → (a)

Question 4.
Type of impedance Phase between voltage and current

Answer:
(i) → (c)
(ii) → (d)
(iii) → (a)
(iv) → (b)

Question 5.
Energy in two oscillatory systems: (LC oscillator and spring mass system)

Answer:
(i) → (c)
(ii) → (d)
(iii) → (a)
(iv) → (b)

IV Assertion and reason

(a) If both assertion and reason are true and the reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If the assertion and reason both are false.
(e) If assertion is false but reason is true.

Question 1.
Assertion: Eddy currents is produced in any metallic conductor when flux is changed around it.
Reason: Electric potential determines the flow of charge.
Answer:
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
Solution:
When a metallic conductor is moved in a magnetic field, magnetic flux is “varied. It disturbs the free electrons of the metal and set up an induced emf in it. As there are no free ends of the metal i.e., it will be closed in itself so there will be induced current.

Question 2.
Assertion: Faraday’s laws are consequences of conservation of energy.
Reason: In a purely resistive AC circuit, the current lags behind the emf in phase.
Answer:
(c) If assertion is true but reason is false.
Solution:
According to Faraday’s law, the conversion of mechanical energy into electrical energy is in accordance with the law of conservation of energy. It is also clearly known that in pure resistance, the emf is in phase with the current.

Question 3.
Assertion: Inductance coil are made of copper.
Reason: Induced current is more in wire having less resistance.
Answer:
(a) If both assertion and reason are true and the reason in the correct explanation of the assertion.
Solution:
Inductance coils made of copper will have very small ohmic resistance.

Question 4.
Assertion: An aircraft flies along the meridian, the potential at the ends of its wings will be the same.
Reason: Whenever there is a change in the magnetic flux, and emf is induced.
Answer:
(e) If assertion is false but reason is true.
Solution:
As the aircraft flies magnetic flux change through its wings due to the vertical component of the Earth’s magnetic field. Due to this, induced emf is produced across the wings of the aircraft. Therefore, the wings of the aircraft will not be at the same potential.

Question 5.
Assertion: In series LCR circuit resonance can take place.
Reason: Resonance takes place if inductance and capacitive reactances are equal and opposite.
Answer:
(a) If both assertion and reason are hue and the reason is the correct explanation of the assertion.
Solution:
At resonant frequency X_L = X_C
So, Impedance, Z = R (minimum)
Therefore, the current in the circuit is maximum.

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Short Answer Questions

Question 1.
Define magnetic flux (Φ_B).
The magnetic flux through an area A in a magnetic field is defined as the number of magnetic field lines passing through that area normally and is given by the equation,

Question 2.
Write down the drawbacks of Eddy currents.
Answer:
When eddy currents flow in the conductor, a large amount of energy is dissipated in the form of heat. The energy loss due to the flow of eddy current is inevitable but it can be reduced to a greater extent with suitable measures. The design of transformer core and electric motor armature is crucial in order to minimise the eddy current loss.

To reduce these losses, the core of the transformer is made up of thin laminas insulated from one another while for electric motor the winding is made up of a group of wires insulated from one another. The insulation used does not allow huge eddy currents to flow and hence losses are minimized.

Question 3.
Define the unit of self-inductance.
Answer:
The unit of self-inductance is henry. One henry is defined as the self-inductance of a coil in which a change in current of one ampere per second produces an opposing emf of one volt.

Question 4.
Define mutual inductance in terms of flux and current.
Answer:
The mutual inductance M₂₁ is defined as the flux linkage of the coil 2 when 1A current flows through coil 1.
M₂₁ = \(\frac{\mathrm{N}_{2} \mathrm{\phi}_{21}}{i_{1}}\)

Question 5.
Define mutual inductance in terms of emf and current.
Answer:
Mutual inductance M₂₁ is also defined as the opposing emf induced is the coil 2 when the rate of change of current through the coil 1 is 1 As^-1.
M₁₂ = \(\frac{-\varepsilon_{1}}{d i_{2} / d t}\)

Question 6.
List out the advantages of three phase alternator.
Answer:
Three-phase system has many advantages over single-phase system, which is as follows:
(i) For a given dimension of the generator, three-phase machine produces higher power output than a single-phase machine.
(ii) For the same capacity, three-phase alternator is smaller in size when compared to single phase alternator.
(iii) Three-phase transmission system is cheaper. A relatively thinner wire is sufficient for transmission of three-phase power.

Question 7.
Mentions the differences betw een a step up and step down transformer.
Answer:

Question 8.
Define efficiency of transformer.
Answer:
The efficiency p of a transformer is defined as the ratio of the useful output power to the input power. Thus

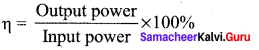
Transformers are highly efficient devices having their efficiency in the range of 96 – 99%. Various energy losses in a transformer will not allow them to be 100% efficient.

Question 9.
What is meant by sinusoidal alternating voltage?
Answer:
If the waveform of alternating voltage is a sine wave, then it is known as sinusoidal alternating voltage, which is given by the relation.
υ = V_m sin ωt

Question 10.
An inductor blocks AC but it allows DC. Why? and How?
Answer:
An inductor L is a closely wound helical coil. The steady DC current flowing through L produces uniform magnetic field around it and the magnetic flux linked remains constant. Therefore there is no self-induction and self-induced emf (back emf). Since inductor behaves like a resistor, DC flows through an inductor.

The AC flowing through L produces time-varying magnetic field which in turn induces self- induced emf (back emf). This back emf, according to Lenz’s law, opposes any change in the current. Since AC varies both in magnitude and direction, its flow is opposed in L. For an ideal inductor of zero ohmic resistance, the back emf is equal and opposite to the applied emf. Therefore L blocks AC.

Question 11.
A capacitor blocks DC but allows AC. Explain.
Answer:
Capacitive reactance, X_C = \(\frac { 1 }{ ωC }\) = \(\frac { 1 }{ 2πƒc }\)
where, ƒ = 0, X_C = ∞
where, ƒ is the frequency of the ac supply. In a dc circuit ƒ = 0. Hence the capacitive reactance has infinite value for dc and a finite value for ac. In other words, a capacitor serves as a block for dc and offers an easy path to ac.

Question 12.
Why dc ammeter cannot read ac?
Answer:
A dc ammeter cannot read ac because, the average value of ac is zero over a complete cycle.

Question 13.
Write down the applications of series RLC resonant circuit.
Answer:
RLC circuits have many applications like filter circuits, oscillators and voltage multipliers, etc. An important use of series RLC resonant circuits is in the tuning circuits of radio and TV systems. The signals from many broadcasting stations at different frequencies are available in the air. To receive the signal of a particular station, tuning is done.

Question 14.
What is meant by ‘Wattful current’?
Answer:
The component of current (I_rms cos Φ) which is in phase with the voltage is called active component. The power consumed by this current = V_rms I_rms cos Φ. So that it is also known as ‘Wattful’ current.

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Long Answer Questions

Question 1.
Derive an expression for Mutual Inductance between two long co-axial solenoids.
Answer:
Mutual inductance between two long co-axial solenoids:
Consider two long co-axial solenoids of same length 1. The length of these solenoids is large when compared to their radii so that the magnetic field produced inside the solenoids is uniform and the fringing effect at the ends may be ignored. Let A₁ and A₂ be the area of cross section of the solenoids with A₁ being greater than A₂. The turn density of these solenoids are n₁ and n₂ respectively.

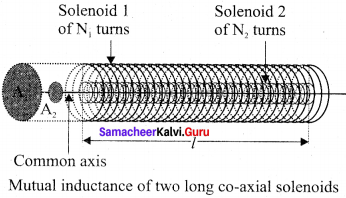
Let i₁ be the current flowing through solenoid 1, then the magnetic field produced inside it is
B₁ = μ₀n₁i₁.
As the field lines of \(\vec {{ B }_{1}} \) are passing through the area bounded by solenoid 2, the magnetic flux is linked with each turn of solenoid 2 due to solenoid 1 and is given by

since θ = 0°
The flux linkage of solenoid 2 with total turns N₂ is
N₂Φ₂₁ = (n₂l)(μ₀ n₁ i₁)
since N₂ = n₂l
N₂Φ₂₁ = (μ₀ n₁ n₂ A₂l)i₁ ….. (1)
From equation of mutual induction
N₂Φ₂₁ = M₂₁ i₁ …… (2)
Comparing the equations (1) and (2),
M₂₁ = μ₀ n₁ n₂ A₂l ….. (3)
This gives the expression for mutual inductance M₂₁ of the solenoid 2 with respect to solenoid 1. Similarly, we can find mutual inductance M₂₁ of solenoid 1 with respect to solenoid 2 as given below.
The magnetic field produced by the solenoid 2 when carrying a current i₂ is
B₂ = μ₀ n₂ i₂
This magnetic field B₂ is uniform inside the solenoid 2 but outside the solenoid 2, it is almost zero. Therefore for solenoid 1, the area A₂ is the effective area over which the magnetic field B₂ is present; not area A₂ Then the magnetic flux Φ₁₂ linked with each turn of solenoid 1 due to solenoid 2 is

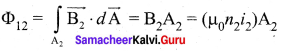
The flux linkage of solenoid 1 with total turns N₁ is
[Since N₁ = n₁l]
[Since N₁ Φ₁₂ = M₁₂i₂]
N₁ Φ₁₂ = (n₁l) (μ₀ n₂ i₂) A₂
N₁ Φ₁₂ = (μ₀ n₁ n₂ A₂l) i₂
M₁₂i₂ = (μ₀ n₁ n₂ A₂l) i₂
Therefore, we get
∴ M₁₂ = μ₀ n₁ n₂ A₂l ……. (4)
From equation (3) and (4), we can write
M₁₂ = M₂₁ = M ……. (5)
In general, the mutual inductance between two long co-axial solenoids is given by
M= μ₀ n₁ n₂ A₂l ……. (6)
If a dielectric medium of relative permeability’ pr is present inside the solenoids, then
M = μn₁ n₂ A₂l
or M = μ₀ μ_r n₁ n₂ A₂l

Question 2.
How will you define the unit of mutual-inductance?
Answer:
Unit of mutual inductance:
The unit of mutual inductance is also henry (H).
If i_A= 1 A and N₂ Φ₂₁ = 1 Wb turns, then M₂₁ = 1 H.
Therefore, the mutual inductance between two coils is said to be one henry if a current of 1A in coil 1 produces unit flux linkage in coil 2.
If \(\frac {{ di }_{1}}{ 2 }\) = 1 As^-1 and ε₂ = -1V, theen M₂₁ = 1H.
Therefore, the mutual inductance between two coils is one henry if a current changing at the rate of lAs-1 in coil 1 induces an opposing emf of IV in coil 2.

Question 3.
Find out the phase relationship between voltage and current in a pure resister circuit.
Answer:
AC circuit containing pure resistor:
Consider a circuit containing a pure resistor of resistance R connected across an alternating voltage source. The instantaneous value of the alternating voltage is given by

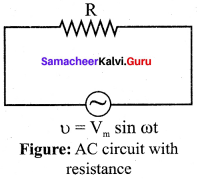
υ = V_m sin ωt ….. (1)
An alternating current i flowing in the circuit due to this voltage, develops a potential drop across R and is given by
V_R = iR ……. (2)
Kirchoff’s loop rule states that the algebraic sum of potential differences in a closed circuit is zero. For this resistive circuit,
υ – V_R = 0
From equation (1) and (2),
V_m sin ωt = iR
⇒ i = \(\frac {{ V }_{m}}{ R }\) sin ωt
i = I_m sin ωt …… (3)

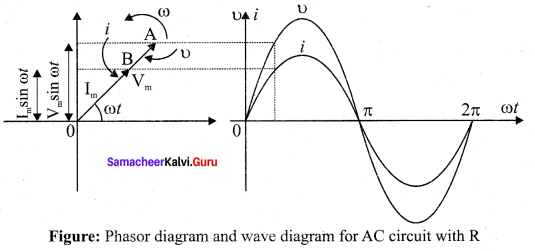
where V\(\frac {{ V }_{m}}{ R }\) = I_m the peak value of alternating current in the circuit. From equations (1) and and (3), it is clear that the applied voltage and the current are in phase with each other in a resistive circuit. It means that they reach their maxima and minima simultaneously. This is indicated in the phasor diagram. The wave diagram also depicts that current is in phase with the applied voltage.

Question 4.
Find out the phase relationship between voltage and current in a pure capacitor circuit.
Answer:
AC circuit containing only a capacitor:
Consider a circuit containing a capacitor of capacitance C connected across an alternating voltage source.
The alternating voltage is given by

V_m sin ωt …… (1)
Let q be the instantaneous charge on the capacitor. The emf across the capacitor at that instant is \(\frac { q }{ C }\). According to Kirchoff’s loop rule,.
υ = \(\frac { q }{ C }\) = 0
⇒ CV_m sin ωt
By the definition of current,
i = \(\frac { dq }{ dt }\) = \(\frac { d }{ dt }\) CV_m \(\frac { d }{ dt }\) (sin ωt)
= CV_m sin ωt
or i = \(\frac{\frac{\mathrm{V}_{m}}{1}}{\frac{\mathrm{l}}{\mathrm{C} \omega}}\) sin \(\left(\omega t+\frac{\pi}{2}\right)\)
i = I_m sin \(\left(\omega t+\frac{\pi}{2}\right)\) ….. (2)
where \(\frac{\frac{\mathrm{V}_{m}}{1}}{\frac{\mathrm{l}}{\mathrm{C} \omega}}\) = I_m, the peak value of the alternating current. From equation (1) and (2), it is clear that current leads the applied voltage by π/2 in a capacitive circuit. The wave diagram for a capacitive circuit also shows that the current leads the applied voltage by 90°.

Question 5.
What are LC oscillation? and explain the generation of LC oscillation.
Answer:
Whenever energy is given to a circuit containing a pure inductor of inductance L and a capacitor of capacitance C, the energy oscillates back and forth between the magnetic field of the inductor and the electric field of the capacitor. Thus the electrical oscillations of definite frequency are generated. These oscillations are called LC oscillations.

Generation of LC oscillations:
Let us assume that the capacitor is fully charged with maximum charge Q_m at the initial stage. So that the energy stored in the capacitor is maximum and is given by U_Em = \(\frac{\mathrm{Q}_{\mathrm{m}}^{2}}{2 \mathrm{C}}\) As there is no current in the inductor, the energy stored in it is zero i.e., UB = 0. Therefore, the total energy is wholly electrical.

The capacitor now begins to discharge through the inductor that establishes current i in clockwise direction. This current produces a magnetic field around the inductor and the energy stored in the inductor is given by U_B = \(\frac {{ Li }_{ 2 }}{ 2 }\). As the charge in the capacitor decreases, the energy stored in it also decreases and is given by U_E = \(\frac {{ q }_{ 2 }}{ 2C }\). Thus there is a transfer of some part of energy from the capacitor to the inductor. At that instant, the total energy is the sum of electrical and magnetic energies.

When the charges in the capacitor are exhausted, its energy becomes zero i.e., UE = 0. The energy is fully transferred to the magnetic field of the inductor and its energy is maximum. This maximum energy is given by UB = \(\frac{\mathrm{LI}_{\mathrm{m}}^{2}}{2}\) where I_m is the maximum current flowing in the circuit. The total energy is wholly magnetic.

Even though the charge in the capacitor is zero, the current will continue to flow in the same direction because the inductor will not allow it to stop immediately. The current is made to flow with decreasing magnitude by the collapsing magnetic field of the inductor. As a result of this, the capacitor begins to charge in the opposite direction. A part of the energy is transferred from the inductor back to the capacitor. The total energy is the sum of the electrical and magnetic energies.

When the current in the circuit reduces to zero, the capacitor becomes frilly charged in the opposite direction. The energy stored in the capacitor becomes maximum. Since the current is zero, the energy stored in the inductor is zero. The total energy is wholly electrical. The state of the circuit is similar to the initial state but the difference is that the capacitor is charged in opposite direction. The capacitor then starts to discharge through the inductor with anti-clockwise current. The total energy is the sum of the electrical and magnetic energies.

As already explained, the processes are repeated in opposite direction. Finally, the circuit returns to the initial state. Thus, when the circuit goes through these stages, an alternating current flows in the circuit. As this process is repeated again and again, the electrical oscillations of definite frequency are generated. These are known as LC oscillations. In the ideal LC circuit, there is no loss of energy. Therefore, the oscillations will continue indefinitely. Such oscillations are called undamped oscillations.

Samacheer Kalvi 12th Physics Electromagnetic Induction and Alternating Current Numerical Problems

Question 1.
A coil has 2000 turns and area 70 cm². The magnetic field perpendicular to the plane of the coil is 0.3 Wb/m². The coil takes 0.1 s to rotate through 180°. Then what is the value of induced emf?
Solution:
Magnitude of change in flux,
|∆Φ | = |NBA (cos 180° – cos 0°
= |NBA(-1 – 1)| = |-2 NBA| = |2 NBA|
Where,
N = 2000
B = 0.3 Wb/m²
A = 70 x 10^-4 m²
t = 0.1 sec
Induced emf, ε = \(\frac { \left| \Delta \phi \right| }{ \Delta t } \) = \(\frac { 2NBA }{ ∆t }\) = \(\frac {{ 2 × 2000 × 0.3 × 70 × 10 }^{-4}}{ 0.1 }\)
ε = 84 V

Question 2.
A rectangular loop of sides 8 cm and 2 cm is lying in a uniform magnetic field of magnitude 0.5 T with its plane normal to the field. The field is now gradually reduced at the rate of 0.02 T/s. If the resistance of the loop is 1.6 Ω, then find the power dissipated by the loop as heat.
Solution:
Induced emf, |ε| = \(\frac { dΦ }{ dt } \) = A \(\frac { dB }{ dt } \) = 8 × 2 × 10^-4 × 0.02
ε = 3.2 × 10^-5 V
Induced current, I = \(\frac { ε }{ R } \) = 2 × 10^-5 A
Power loss = I²R = 4 × 10^-10 × 1.6 = 6.4 × 10^-10 W

Question 3.
A current of 2 A flowing through a coil of 100 turns gives rise to a magnetic flux of 5 x 10^-5 Wb per turn. What is the magnetic energy associated with the coil?
Solution:
Self inductance of coil, L = \(\frac { NΦ }{ I } \) = \(\frac {{ 100 × 5 × 10 }^{-3}}{ 2 } \)
= 2.5 × 10^-3 H
Magnetic energy associated with inductance,
U = \(\frac { 1 }{ 2 }\) LI² = \(\frac { 1 }{ 2 }\) × 2.5 × 10^-3 × (2)²
= \(\frac { 1 }{ 2 }\) × 2.5 × 10^-3 × 4 = 5 × 10^-3 J

Question 4.
A transformer is used to light a 140 W, 24 V bulb from a 240 V AC mains. The current in the main cable is 0.7 A. Find the efficiency of the transformer.
Solution:

η = \(\frac { 140 }{ 240 × 0.7 }\) × 100 = 83.3%

Question 5.
In an ideal step up transformer the turns ratio is 1 : 10. A resistance of 200 ohm connected across the secondary is drawing a current of 0.5 A. What are the primary voltage and current?
Solution:

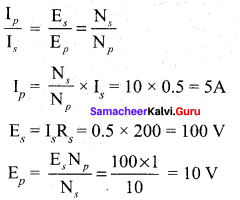
Primary current, I_p = 5 A
Promary voltage, E_p = 10 V

Question 6.
A capacitor of capacitance 2 μF is connected in a tank circuit oscillating with a frequency of 1 kHz. If the current flowing in the circuit is 2 mA, then find the voltage across the capacitor.
Solution:

Question 7.
An ideal inductor takes a current of 10 A when connected to a 125 V, 50 Hz AC supply. A pure resistor across the same source takes 12.5 A. If the two are connected in series across a 100 √2 V, 40 Hz supply, then calculate the current through the circuit.
Solution:

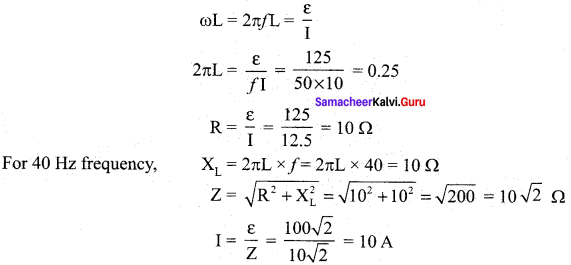
Question 8.
An LCR series circuit containing a resistance of 120 Ω. has angular resonance frequency 4 x 10⁵ rad s^-1. At resonance the voltages across resistance and inductance are 60 V and 40 V, respectively. Find the values of L and C.
Solution:

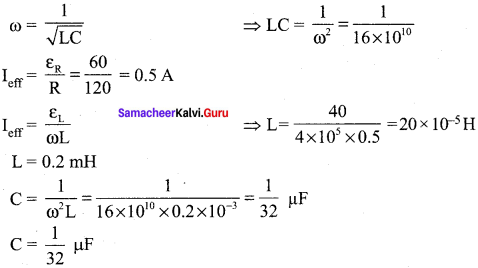
Question 9.
A coil of inductive reactance 31 Ω has a resistance of 8 Ω. It is placed in series with a capacitor of capacitance reactance 25 Ω. The combination is connected to an ac source of 110 volt. Find the power factor of the circuit.
Solution:

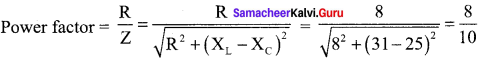
Power faactor = 0.8

Question 10.
The power factor of an RL circuit is \(\frac { 1 }{ √2 }\). If the frequency of AC is doubled, what will be the power factor?
Solution:

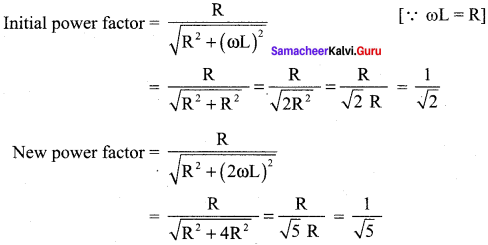
Question 11.
The instantaneous value of alternating current and voltage are given as i = \(\frac { 1 }{ √2 }\) sin (100 πt) A and e = \(\frac { 1 }{ √2 }\) sin(100 πt + \(\frac { π }{ 3 }\)) volt. Find the average power in watts consumed in the circuit.
Solution:

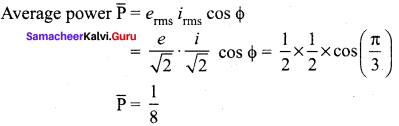
Common Errors and its Rectifications:

Common Errors:

1. Students sometimes may confuse the peak current and instantaneous value of current and emf.
2. They may confuse in the area of R, L and C with AC. The relation between current and induced emf.

Rectifications:

1. Instantaneous current, i = I₀ sin tot Peak current, I₀ = √2 I_rms Instantaneous emf, e = E₀ sin cor Peak emf, E₀ = √2 E_rms
2. In Inductor: current is \(\frac { π }{ 2 }\) rad less than that of emf.
   In Resistor: current and emf are same phase.
   In Capacitor: current is \(\frac { π }{ 2 }\) rad greater than that of emf.

We believe that the shared knowledge about Tamilnadu State Board Solutions for 12th Physics Chapter 4 Electromagnetic Induction and Alternating Current Questions and Answers learning resource will definitely guide you at the time of preparation. For more details visit Tamilnadu State Board Solutions for 12th Physics Solutions and for more information ask us in the below comments and we’ll revert back to you asap.

You can Download Samacheer Kalvi 9th Social Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Social Science History Solutions Chapter 6 The Middle Ages

The Middle Ages Textual Exercise

I. Choose the correct answer.

The Middle Ages Class 9 Question 1.
……………….. was the old religion of Japan.
(a) Shinto
(b) Confucianism
(c) Taoism
(d) Animism
Answer:
(a) Shinto

Europe In The Middle Ages 9th Standard Question 2.
…………. means great name/lord.
(a) Daimyo
(b) Shogun
(c) Fujiwara
(d) Tokugawa
Answer:
(a) Daimyo

Samacheer Kalvi Guru 9th Social Science Question 3.
The Arab General who conquered Spain was …………..
(a) Tariq
(b) Alaric
(c) Saladin
(d) Mohammad the Conqueror
Answer:
(a) Tariq

Samacheer Kalvi Guru 9th Social Question 4.
Harun-al-Rashid was the able emperor of ……………
(a) Abbasid dynasty
(b) Umayyad dynasty
(c) Sassanid dynasty
(d) Mongol dynasty
Answer:
(a) Abbasid dynasty

Class 9 History Chapter 6 Question 5.
Feudalism centred around ……………
(a) vassalage
(b) slavery
(c) serfdom
(d) land
Answer:
(a) vassalage

II. Find out the correct statement.

Question 1.
(i) Chengiz Khan was an intolerant person in religion
(ii) Mongols destroyed the city of Jerusalem
(iii) Crusades weakened the Ottoman Empire
(iv) Pope Gregory succeeded in making King Henry IV to abdicate the throne by means of Interdict
(a) (i) is correct
(b) (ii) is correct
(c) (ii) and (iii) are correct
(d) (iv) is correct
Answer:
(d) (iv) is correct

Question 2.
(i) Mangu Khan was the Governor of China.
(ii) Mongol court in China impressed Marco Polo.
(iii) The leader of Red Turbans was Hung Chao.
(iv) Mongols established their rule in China in the name of Yuan dynasty.
(a) (i) is correct
(b) (ii) is correct
(c) (ii) and (iv) are correct
(d) (iv) is correct
Answer:
(c) (ii) and (iv) are correct

Question 3.
(i) Boyang and Changon were built during Sung dynasty.
(ii) Peasant uprisings led to the collapse of Tang dynasty.
(iii) Seljuq Turks were a tribe of Tartars.
(iv) Mongols established their rule in China in the name of Yuan dynasty.
(a) (i) is correct
(b) (ii) is correct
(c) (iii) is correct
(d) (iv) is correct
Answer:
(iii) and (iv) are correct

Question 4.
Assertion (A): Buddhism went to China from India.
Reason (R): The earliest Indian inhabitants in China were the followers of Buddhism.
(a) A is correct; R is wrong
(b) Both A & R are wrong
(c) Both A &, R are correct
(d) A is wrong R is irrelevant to A
Answer:
(a) A is correct; R is wrong

Question 5.
Assertion (A): The fall of Jerusalem into the hands of Seljuk Turks led to the Crusades.
Reason (R): European Christian pilgrims were denied access to Jerusalem. .
(a) A is correct; R is not the correct explanation of A ‘
(b) A and R are correct
(c) A and R are wrong
(d) A is correct, R is the correct explanation of A
Answer:
(d) A is correct, R is the correct explanation of A

III. Fill in the blanks.

1. ……………. were the original inhabitants of Japan.
2. ……………. was the original name of Japan.
3. ………… was the original name of Medina. ,
4. ………….were the barbarians posing a threat to the Chinese in the north.
5. …………… established Ottoman supremacy in the Balkans.
Answer:
1. Ainus
2. Yamato
3. Yethrib
4. The Mongols
5. Mohammed II

IV. Match the following:

Answer:
1. (d)
2. (e)
3. (a)
4. (c)
5. (b)

V. Answer all questions given under each heading.

Question 1.
Shogunate in Japan.
(a) Name the two Daimyo families that fought for power in Japan.
Answer:
The Tara and Minamota

(b) Who emerged successful in the fight?
Answer:
Yoritomo emerged successful in the fight.

(c) What was the title given by the Emperor to the victorious?
Answer:
The high sounding title of Sei-i-tai Shogun (which means the Barbarian-Subduing-Great- General).

(d) Where was the capital of the first Shogunate established?
Answer:
The capital of the first Shogunate established at Kamakura,

Question 2.
Rule of Abbasids.
(a) Who were the Abbasids?
Answer:
The descendants of the Prophet Mohammad’s uncle Abbas and his followers were called Abbasids. ’ ,

(b) What was the title assumed by Abbasid Caliph?
Answer:
“The commander of the faithful” was the title assumed by Abbasid Caliph.

(c) Where did they have their new capital?
Answer:
Baghdad in Iraq

(d) In whose period was the Abbasid Empire at the height of its glory?
Answer:
The Abbasid Empire was at the height of its glory during the reign of Harun-al-Rashid.

VI. Answer the following briefly.

Question 1.
The Great Wall of China.
Answer:
Between 8th and 7th centuries B.C. (BCE), the warring states in China built defensive walls to protect themselves from enemies from the north. During Chin (Qin) Dynasty, the separate walls were connected and consequently the wall stretched from east to west for about 5000 kilometres. This wall, considered to be one of the wonders of the world, served to keep nomadic tribes out. The Wall was further extended and strengthened by the succeeding dynasties. Now ’ it is 6,700 kilometres in length.

Question 2.
Contribution of Arabs to Science and Technology.
Answer:
The Arabs had a scientific spirit of inquiry. In some subjects like medicine and mathematics they learnt much from India. Many Arab students went to Takshashila, which was still a great university for specialized medicine. Indian scholars and mathematicians came in large numbers to Baghdad. Sanskrit books on medicine and other subjects were translated into Arabic. In medicine and surgery, Arab physicians and surgeons earned a great reputation.

Question 3.
Impact of Crusades.
Answer:
Crusades ended the feudal relations. Many of the nobles who went to East to take part in the Crusades either stayed too long a period or did not return. The serfs took advantage of their absence to break away from their bondage to the soil. Increasing demand for products of the East led to expansion of trade. Venice, Genoa and Pisa emerged as important commercial centres in the Mediterranean region.

Constantinople ceased to be the middle man in the trade between the East and the West. The elimination of powerful nobles had its influence in strengthening the monarchy in France and England. One notable outcome of Crusades was the loss of prestige suffered by Pope and Papacy.

Question 4.
How was Feudalism organized in the Middle Ages?
Answer:

Question 5.
Write about the two instruments used by Medieval Pope to assert his authority.
Answer:
New elements were included in Christian theology. They were the theory of priesthood and the theory of sacraments. These two elements increased the power of the clergy. These two elements also helped the Church to extend its authority over all of its lay members. Excommunication and Interdict were the two instruments used against those who defied the Church.

VII. Answer the following in detail.

Question 1.
Discuss the emergence of Japan under the Shogunate.
Answer:
During the two-hundred-year rule of Fujiwaras, a new class of large landholders emerged. These landholders were also military men, called Daimyos (meaning great names-lords). The Daimyos became powerful with their retainers and armies. Involved in personal fights, they ignored the central government in Kyoto. Out of the fight between two chief families, the Tara and the Minamota, Yoritomo emerged successful. In AD (CE) 1192, the emperor gave him the high sounding title of Sei-i-tai-Shogun, which means the Barbarian-subduing-Great-General. The title carried full power to govern hereditarily. The Shogun became the real ruler. In this way began the rule of Shogunate.

Question 2.
Who were the Mongols? How did they rule China?
Answer:

1. Mongols were nomads. They came into Europe from the Steppes of Asiatic Russia.
2. They were herdsmen. ‘
3. The Mongols were experts in warfare and produced a remarkable chief, Chengiz Khan.
4. He was a great military genius.
5. His religion was Shamanism, a worship of the “Everlasting Blue Sky. Mongols’ hold over Russia for about 300 years made Russia technologically backward from the rest of Europe until the end of Middle Ages”.

Rule in China

1. The Mongols established their rule in the name of Yuan dynasty.
2. The Mongols, who overran Persia and the whole of Central Asia, did not spare China either.
3. Mangu Khan became the Great Khan in 1252 who appointed Kublai Khan the Governor of China.
4. The Mongol presence from one end of Eurasia to the other played a key role in spreading Chinese technological advances to the less developed societies in the west.
5. Though the Mongol court in Beijing impressed a foreigner like Marco Polo, the poverty of peasantry continued.
6. There were revolts of religious sects and secret societies.
7. Finally, the leader of “Red Turbans” Chu Yuan Chang took the Mongol capital Beijing and proclaimed himself emperor in 1369.
8. The Ming Empire, which replaced the Mongol empire, consciously discouraged industry and foreign trade in order to concentrate on agriculture.
9. This resulted in China lagging behind in the 16th century. ‘
10. Other parts of Eurasia, building on the techniques of the Chinese, began to march ahead.

Student Activities

Question 1.
In an outline map of Europe, the students are to sketch the extent of Ottoman Empire at the height of its glory
Answer:

Question 2.
Students are to be guided by teachers to look through Google the architectural splendours of Saracenic architecture.
Answer:
You can do this activity under the guidance of your teacher.

Assignment with Teacher’s guidance.

Question 1.
Sketching Ottoman family tree and attempting a biographical account of Saladin of Egypt and Suleiman the Magnificent of Ottoman Empire.
Answer:
The teacher can guide the students to google and find out. Narrate the entire Ottoman family tree.

Question 2.
Attempting an account of the Crusades led by Richard the Lion-Hearted of England and German Emperor Frederick Barbarossa.
Answer:
You can do this activity under the guidance of your teacher.

The Middle Ages Additional Questions

I. Choose the correct answer.

Question 1.
Historians call the period between ………………. and …………… as the Middle Ages.
(a) 470 A.D and 1400 A.D.-(C.E)
(b) 460 A.D (C.E) and 1450 A.D (C.E)
(c) 475 A.D (C.E) and 1453 A.D (C.E)
(d) 476 A.D (C.E) and 1453 A.D (C.E)
Answer:
(d) 476 A.D (C.E) and 1453 A.D (C.E)

Question 2.
The founders of Saracenic Civilization were …………….
(a) Arabs
(b) Jews
(c) Persians
(d) Syrians
Answer:
(a) Arabs

Question 3.
……………. dynasty undertook enormous public works.
(a) Sui
(b) Tang
(c) Sung
(d) Yuan
Answer:
(b) Tang

Question 4.
……………… excelled in Ceramics and Porcelain-making.
(a) Japan
(b) Korea
(c) China
(d) Europe
Answer:
(c) China

Question 5.
Japan’s name was given by a ………….. Emperor.
(a) Mongol
(b) Chinese
(c) Korean
(d) Russian
Answer:
(b) Chinese

Question 6.
…………… established Islam.
(a) Abu Bakr
(b) Abbas
(c) Prophet Mohammed
(d) None of the above
Answer:
(c) Prophet Mohammed

Question 7.
……………. is the holy city of the Christians.
(a) Jerusalem
(b) Baghdad
(c) Venice
(d) Pisa
Answer:
(a) Jerusalem

Question 8.
Chengiz Khan was the remarkable chief of ……………..
(a) Turks
(b) Arabs
(c) Mongols
(d) Chinese
Answer:
(c) Mongols

II. Find out the correct statement.

Question 1.
(i) Tang dynasty undertook enormous public works.
(ii) Land was divided into smdll peasant holdings.
(iii) Now the length of the Great Wall of China is 6,800 kilometres.
(iv) The agricultural surplus went to the Aristocrats as rents.
(a) (i) is correct
(b) (i) and (ii) are correct
(c) (iii) is correct
(d) (iv) is correct
Answer:
(b) (i) and (ii) are correct

Question 2.
(i) The message of equality and brotherhood had great appeal only for Arabs.
(ii) Mohammed and his followers stayed in their birth place.
(iii) The flight of Mohammad from Mecca in 622 A.D is called Hijrat. :
(iv) Mohammad died 20 years after the Hijrat.
(a) (i) is correct
(b) (ii) is correct
(c) (iii) is correct
(d) (iv) is correct
Answer:
(c) (iii) is correct

Question 3.
(i) Traders and artisans were brought under the feudal system.
(ii) The merchants and artisans formed guilds and groups.
(iii) In course of time they obeyed the nobles and kings. ,
(iv) This development continued the Feudal system. –
(a) (i) is correct
(b) (ii) is correct
(c) (iii) is correct
(d) (iv) is correct
Answer:
(b) (ii) is correct

Question 4.
Assertion: Seljuq Turks were a tribe of Tartars from Central Asia.
Reason: They established a powerful empire in Persia.
(a) A is correct R is wrong
(b) Both A and R are wrong
(c) Both A and R are correct
(d) A is correct R is irrelevant to A.
Answer:
(c) Both A and R are correct

Question 5.
Assertion: The Abbasid Empire was at the height of its glory during the reign of Harun-al- Rashid.
Reason: The Arab Empire flourished soon after the death of Harun-al-Rashid.
(a) A is correct; R is not the correct explanation of A
(b) A and R are correct
(c) A and R are wrong
(d) A is correct, R is the correct explanation of A .
Answer:
(a) A is correct; R is not the correct explanation of A

III. Fill in the blanks.

1. …………….. period was also a period of great prosperity to the landowning class, officials and rich merchants. .
2. The original religion of Japan, the Shinto was a mixture of nature and ……………..
3. The first great family that controlled the state was the ……………… family.
4. The first Shogunate is called the ……………. Shogunate.
5. …………… advocated simplicity and equality.
6. The capital of Umayyads was …………..
7. The other name of Baghdad was ……………..
8. …………….. ended the feudal relations.
9. The religion of Chengiz Khan was ……………..
10. …………… meant depriving a person of all the privileges of a Christian.
Answers:
1. Sung
2. ancestor worship
3. Soga
4. Kamakura
5. Islam
6. Damascus
7. the city of Arabian Nights
8. Crusades
9. Shamanism
10. Excommunication

IV. Match the following:

Answer:
1. (g)
2. (a)
3. (b)
4. (f)
5. (c)
6. (d)
7. (e)

V. Answer all questions given under each heading.

Question 1.
Yuan Dynasty
(a) Who overran Persia and China?
Answer:
The Mongols overran Persia and China.

(b) Who was appointed as the Governor of China?
Answer:
Kublai Khan

(c) Mention the foreigner who impressed the Beijing.
Answer:
Marco Polo

(d) Who was the leader of the “Red Turbans”?
Answer:
Chu Yuan Chang

Question 2.
Punic Wars
(a) Who were Carthaginians?
Answer:
The Carthaginians were the descendants of the Phoenicians who excelled in seafaring and trade.

(b) Write about the Third Punic War.
Answer:
After the defeat and destruction of the Carthage in the Third Punic War, Rome emerged as an unrivalled power in the western world.

(c) Who united to drive out the Greeks?
Answer:
Rome and Carthage united to drive out the Greeks.

(d) Who was Hannibal?
Answer:
Hannibal was a general who defeated the Roman army and made a great part of Italy a desert.

Question 3.
Silk Route
(a) What is meant by Silk route?
Answer:
The trade route from China to Asia Minor and India, known as the Silk Road or Silk Route.

(b) Which places were linked by this route?
Answer:
It linked China with the West. Goods and ideas between the two great civilizations of Rome and China were exchanged through this route.

(c) Name the good exchanged from East to West and West to East.
Answer:
Silk went westward, and wools, gold, and silver went east.

(d) Name the religion which reached China through this route.
Answer:
China received Buddhism from India via the Silk Road. .

Question 4.
Slave Trade in Rome
(a) Why was the new labour force produced by Rome?
Answer:
Rome produced a new labour force for the rich to exploit. Big landholders bought slaves cheaply and used them to cultivate their estates.

(b) What was the strength of the Slave population in the 1st century B.C.?
Answer:
The strength of the slave population in the 1st century B.C. was 3.25 million.

(c) What was the result of Slave trade?
Answer:
Slave trade led to the impoverishment of free labour. Many poor peasants had to abandon their children who also ended up in the slave markets.

(d) Which place became a great slave market?
Answer:
The island of Delos became a great slave market.

Question 5.
Arabs’ Scholarly Pursuits.
(a) What did the Abbasid Caliphs do?
Answer:
Abbasid Caliphs did not attempt to conquer new lands.

(b) What were their interest?
Answer:
They were more interested in scholarly pursuits.

(c) Name the subjects, they learnt from India.
Answer:
Medicine and Mathematics.

(d) In which field (Arabs) they earned a great reputation? .
Answer:
In medicine and surgery, Arab physicians and surgeons earned a great reputation.

VI. Answer the following briefly.

Question 1.
Write a short account of the public works undertaken by Tang dynasty.
Answer:

• Tang dynasty undertook enormous public works. Two capital cities, Boyang and Chang- on, were built.
• Scholar officials, trained in Confucius Philosophy, were appointed to counterbalance the landowning aristocratic class.
• Land was divided into small peasant holdings.
• As a result, the agricultural surplus went to the state as taxes, not to the aristocrats as rents. State monopoly of salt, and tea added to its- revenues.

Question 2.
What led to the collapse of Chin dynasty?
Answer:

• Shih Huang Ti crushed all local rulers and established a strong central government.
• However, uprisings of the peasantry, unlike in other cultures, occurred again and again in China.
• Such uprisings led to the collapse of Chin dynasty.

Question 3.
What do you know about Sung Dynasty?
Answer:

1. The rebellion of hard-pressed peasantry under the leadership of Hung Ch’ao dealt a death knell to the tottering Tang empire.
2. The empire split into five rival states, until it was reunited under a new dynasty, Sung.
3. Trade and industry flourished during the reign of Sung dynasty.
4. Iron and steel industries became highly organized.

Question 4.
Why did Oligarchy start in Greece?
Answer:

1. When the Greek City-States first emerged, they still carried the legacy of the past.
2. The rulers came from lines of traditional chieftains.
3. Those who grew rich from the expansion of trade, resented the privileges enjoyed by the old ruling families.
4. The outcome was the overthrow of the kings and the establishment of “oligarchies” in many city-states.

Question 5.
Name the Empire which replaced the Mongol Empire. What did they do?
Answer:
The Ming Empire, which replaced the Mongol empire, consciously discouraged industry and foreign trade in order to concentrate on agriculture. This resulted in China lagging behind in the 16th century. Other parts of Eurasia, building on the techniques of the Chinese, began to march ahead.

Question 6.
Write about the reign of Alexander, the Great.
Answer:

1. Under Alexander the Great, the Greeks were able to establish a kingdom in Macedonia.
2. This kingdom succeeded in annexing two historic empires of Egypt and the Middle East.
3. But the entire period of Alexander’s reign was spent on wars.
4. The Greek school of Science, Mathematics and Philosophy reached its peak in the Greek.

Question 7.
What was the message given by Islam?
Answer:
Islam gave a message of brotherhood. Mohammed laid stress on the equality of all those who were Muslims. This message of equality and brotherhood had great appeal not only for the Arabs, who were divided into warring tribes but also for people in other parts of the world.

Question 8.
What do you know about Excommunication and Interdict?
Answer:
Excommunication meant depriving a person of all the privileges of a Christian. He was denied the right to sacraments in Church. His or her body could not be buried in the consecrated ground. Interdict was to deny benefits of religion to a ruler’s subject, intended to kindle their resentment against him.

VII. Answer the following in detail.

Question 1.
Describe Feudalism in detail, with diagram.
Answer:
Despite the hold of powerful religions such as Christianity and Islam, the economic life of . people was governed by feudal relations.
In the prevailing anarchy and violence, the mighty living in strong castles seized whatever they could and the poor peasants and labourers suffered. The latter were not organized to defend their interests. There was no strong central government either to protect them. Out of this chaos and disorder evolved the feudal system.

The king, supposed to represent God on earth, was at the head of the feudal regime. Immediately after him were the great nobles, known as dukes, counts, earls. The relationship was one of a vassal. The nobles in turn had vassals of their own, dividing and distributing their fief to lesser nobles called viscounts or barons. Last in this order were the knights, whose fiefs could not be divided.

At the bottom were the villeins or serfs. In the feudal system which centered around vassalage, there was no idea of equality or freedom.
There were only rights and obligations. The Bishops, Abbots and Cardinals and the Church came under this socio-political structure. The nobility and the clergy did not do any physical work. So the burden of producing the food and other necessities of life fell on the peasants and. Feudalism artisans.

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.1

11th Maths Exercise 4.1 Question 1.

(i) A person went to a restaurant for dinner. In the menu card, the person saw 10 Indian and 7 Chinese food items. In how many ways the person can select either an Indian or a Chinese food?
Solution:
Selecting an Indian food item from the given 10 can be done in 10 ways. Selecting a Chinese food item from the given 7 can be done in 7 ways.
∴ Selecting an Indian or a Chinese food can be done in 10 + 7 = 17 ways.

(ii) There are 3 types of toy car and 2 types of toy train available in a shop. Find the number of ways a baby can buy a toy car and a toy train?
Solution:
Given, Number of toy cars = 3
Number of toy trains = 2
∴ A baby buying a toy car from 3 can be done in 3 ways
∴ A baby buying a toy train from 2 can be done in 2 ways
∴ Buying a toy car and a toy train together can be done in 3 × 2 = 6 ways

(iii) How many of two-digit numbers can be formed using 1, 2, 3, 4, 5 without repetition of digits?
Solution:
The given digits are 1, 2, 3, 4, 5
A two digit number has unit place and 10’s place. We are given 5 digits (1, 2, 3, 4, 5). The unit place can be filled (using the 5 digits) in 5 ways. After filling the unit place since repetition is not allowed one number (filled in the unit place) should be excluded. So the 10’s place can be filled (using the remaining 4 digits) in 4 ways
∴ Unit place and 10’s place together can be filled in 5 × 4 = 20 ways. So the number of two digit numbers = 20

(iv) Three persons enter in to a conference hall in which there are 10 seats. In how many ways they can take their places?
Solution:
Given, Number of the persons = 3 and Number of seats = 10
The first person can take his place (from 10 seats) in 10 ways
The second person can take his place (from the remaining 9 seats) in 9 ways
The third person can take his place (from the remaining 8 seats) in 8 ways
∴ The three persons together can take their places in 10 × 9 × 8 = 720 ways

(v) In how many ways 5 persons can be seated in a row?
Solution:
5 persons can be arranged among themselves in 5! ways
(i.e) 5 × 4 × 3 × 2 × 1 = 120 ways

11th Maths 4th Chapter Solutions Question 2.

(i) A mobile phone has a passcode of 6 distinct digits. What is the maximum number of attempts one makes to retrieve the passcode?
Solution:
Number of digits = 10
∴ Number of attempts made = 10 × 9 × 8 × 7 × 6 × 5 = 151200 ways

(ii) Given four flags of different colours, how many different signals can be generated if each signal requires the use three flags, One below the other?
Solution:
Number of flags given = 4
Number of flag needed (to show a signal) = 3
The first flag can be chosen in 4 ways (from the 4 flags)
The second flag can be chosen (from the remaining 3 flags) in 3 ways
The third flag can be chosen (from the remaining 2 flags) in 2 ways
So the first, second and the third flags together can be chosen in (to generate a signal) 4 × 3 × 2 = 24 ways
(i.e) 24 signals can be generated

11th Maths Exercise 4.1 In Tamil Question 3.
Four children are running a race.

(i) In how many ways can the first two places be filled?
Solution:
Number of children in the running race = 4
The first place can be filled in (from the 4 children) 4 ways
After filling in first place only 3 children are left out
So the second place can be filled in (from the remaining 3 children) 3 ways
So the first and the second places together can be filled in 4 × 3 = 12 ways

(ii) In how many different ways could they finish the race?
Solution:
The first and second places can be filled in 12 ways
The third place can be filled (from the remaining 2 children) in 2 ways and the fourth place can be filled in 1 way
So the race can be finished in 12 × 2 × 1 = 24 ways

11th Maths Exercise 4.1 Solutions Question 4.
Count the number of three-digit numbers which can be formed from the digits 2, 4, 6, 8? if.

(i) repetitions of digits is allowed
Solution:
Number of digit given = 4 (2,4, 6, 8)
So the unit place can be filled in 4 ways, 10’s place can be filled in 4 ways and 100’s place can be filled in 4 ways
∴ The unit place, 10’s place and 100’s place together can be filled (i.e) So the Number of 3 digit numbers = 4 × 4 × 4 = 64 ways

(ii) repetitions of digits is not allowed.
Solution:
The unit place can be filled (using the 4 digits) in 4 ways after filling the unit place since repetition of digits is not allowed that digit should be excluded.
So the 10’s place can be filled in (4 – 1) 3 ways and the 100’s place can be filled in (3 – 1) 2 ways
So the unit place, 10’s and 100’s places together can be filled in 4 × 3 × 2 = 24 ways
(i.e) The number of 3 digit numbers = 4 × 3 × 2 = 24 ways

11th Maths Exercise 4.1 Solution Question 5.
How many three-digit numbers are there with 3 in the unit place?

(i) with repetition
Solution:
with repetition
The unit place is filled (by 3) in 1 way
The 10’s place can be filled in 10 ways
The 100’s place can be filled in 9 ways (excluding 0)
So the number of 3 digit numbers with 3 unit – place = 9 × 10 × 1 = 90

(ii) without repetition
Solution:
The digits are 0, 1,2, 3, 4, 5, 6, 7, 8, 9
A three digit number has 3 digits l’s, 10’s and 100’s place.
The unit place is (filled by 3) filled in one way.
After filling the unit place since the digit ‘0’ is there, we have to fill the 100’s place. Now to fill the 100’s place we have 8 digits (excluding 0 and 3) So 100’s place can be filled in 8 ways.
Now to fill the 10’s place we have again 8 digits (excluding 3 and any one of the number) So 10’s place can be filled in 8 ways.
∴ Number of 3 digit numbers with ‘3’ in unit place = 8 × 8 × 1 = 64

Combinatorics And Mathematical Induction Question 6.
How many numbers are there between 100 and 500 with the digits 0, 1, 2, 3, 4, 5 if

(i) repetition of digits allowed
Solution:
repetition of digits allowed
The given digits are 0, 1, 2, 3, 4, 5
We have to find numbers between 100 and 500. So the 100’s place can be filled (by the numbers 1, 2, 3, 4) in 4 ways.
The 10’s place can be filled in (using 0, 1, 2, 3, 4, 5) 6 ways
and the unit-place can be filled in (using 0,1, 2, 3, 4, 5) 6 ways
But the number 100 should be excluded
So the number of numbers between 100 and 500 = 4 × 6 × 6 = 144

(ii) the repetition of digits is not allowed
Solution:
The 100’s place can be filled (by using 1, 2, 3, 4) 10’s in 4 ways
The 10’s place can be filled in (6 – 1) 5 ways and the unit place can be filled in (5 – 1) 4 ways
So the number of 3 digit number 4 × 5 × 4 = 80

10th Maths Exercise 4.1 11th Sum Question 7.
How many three-digit odd numbers can be formed by using the digits 0, 1, 2, 3, 4, 5 if

(i) The repetition of digits is not allowed
Solution:
The repetition of digits is not allowed
The given digits are 0, 1, 2, 3, 4, 5. Here the odd number are 1, 3, 5.
So the unit place can be filled in 3 ways (using the 3 odd number)
After filling the unit place since 0 is a given digit be fill the 100’s place which can be
filled in

Then the 10’s place can be filled in (6 – 2) 4 ways.
So the number of 3 digit odd numbers = 3 × 4 × 4 = 48

(ii) The repetition of digits is allowed
Solution:
The unit place can be filled in 3 ways. We are given 6 digits.
So 10’s place can be filled in 6 ways and the 100’s place can be filled in (6 – 1) (excluding zero) 5 ways
So the Number of 3 digit numbers = 3 × 6 × 5 = 90

11th Maths 4.1 Question 8.
Count the numbers between 999 and 10000 subject to the condition that there are

(i) no restriction
Solution:
no restriction
We have to find 4 digit numbers
The 1000’s place can be filled in 9 ways (excluding zero) and the 100’s, 10’s and unit places respectively can be filled in 10, 10, 10 ways (including zero)
So the number of numbers between 999 and 10000 = 9 × 10 × 10 × 10 = 9000

(ii) no digit is repeated
Solution:
Since 0 is given as a digit we have to start filling 1000’s place.
Now 1000’s place can be filled in 9 ways (excluding 0)
Then the 100’s place can be filled in 9 ways (excluding one digit and including 0)
10’s place can be filled in (9 – 1) 8 ways and unit place can be filled in (8 – 1) 7 ways So the number of 4 digit numbers are 9 × 9 × 8 × 7 = 4536 ways

(iii) at least one of the digits is repeated
Solution:
Required number of numbers = 9000 – 4536 = 4464 numbers

11th Maths Chapter 4 Exercise 4.1 Question 9.
How many three-digit numbers, which are divisible by 5, can be formed using the digits 0, 1, 2, 3, 4, 5 if

(i) The repetition of digits are not allowed?
Solution:
The repetition of digits are not allowed.
The given digits are 0, 1, 2, 3, 4, 5. A number will be divisible by 5 if the digit in the unit place is 0 or 5
So the unit place can be filled by 0 or 5

(a) When the unit place is 0 it is filled in 1 way
And so 10’s place can be filled in 5 ways (by using 1, 2, 3, 4, 5) and 100’s place can be filled in (5 – 1) 4 ways
So the number of 3 digit numbers with unit place 0 = 1 × 5 × 4 = 20

(b) When the unit place is 5 it is filled in 1 way
Since 0 is given as a digit to fill 100’s place 0 should be excluded
So 100’s place can be filled in (excluding 0 and 5) 4 ways and 10’s place can be filled in (excluding 5 and one digit and including 0) 4 ways So the number of 3 digit numbers with unit place 5 = 1 × 4 × 4 = 16
∴ Number of 3 digit numbers ÷ by 5 = 20 + 16 = 36

(ii) The repetition of digits are allowed.
Solution:
The digits are
0 1 2 3 4 5
To get a number divisible by 5 we should have the unit place as 5 or 0 So the unit place (using 0 or 5) can be filled in 2 ways.
The 10’s place can be filled (Using 0, 1, 2, 3, 4, 5) in 6 ways and the 100’s place (Using 1, 2, 3, 4, 5) can be filled in 5 ways.
So the number of 3 digit numbers ÷ by 5 (with repetition) = 2 × 6 × 5 = 60

Class 11 Maths Exercise 4.1 Solutions Question 10.
To travel from a place A to place B, there are two different bus routes B₁, B₂ two different train routes T₁, T₂ and one air route A₁. From place B to place C there is one bus route say B₁‘, two different train routes say T₁‘, T₂‘ and one air route A₁‘. Find the number of routes of commuting from place A to place C via place B without using similar mode of transportation.
Solution:

From the above diagram the number of routes from A to C
= (2 × 2 + 2 × 1) + [(2 × 1) + (2 × 1)] + [(1 × 1) + (1 × 2)]
= 4 + 2 + 2 + 2 + 1 + 2 = 13

Class 11 Maths Chapter 4 Exercise 4.1 Solution Question 11.
How many numbers are there between 1 and 1000 (both inclusive) which are divisible neither by 2 nor by 5?
Solution:
From 1 to 1000, the numbers ÷ by 2 = 500
the number ÷ by 5 = 200
and the numbers ÷ by 10 = 100(5 × 2 = 10)
So number ÷ by 2 or 5 = 500 + 200 – 100 = 600
Total numbers from 1 to 1000 = 1000
So the number of numbers which are ÷ neither by 2 nor by 5 = 1000 – 600 = 400

11th Maths Chapter 4 Question 12.
How many strings can be formed using the letters of the word LOTUS if the word

(i) either starts with L or ends with S?
Solution:
either starts with L or ends with S?
To find the number of words starting with L
Number of letters in LOTUS = 5 when the first letter is L it can be filled in 1 way only. So the remaining 4 letters can be arranged in 4! =24 ways = n(A). When the last letter is S it can be filled in the 1 way and the remaining 4 letters can be arranged is 4! = 24 ways = n(B)

(1) (1) 3! = 6 = n(A ∩ B)
Now n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 24 + 24 – 6 = 42
Now, neither words starts with L nor ends with S = 42

(ii) neither starts with L nor ends with S?
Solution:
Number of letters of the word LOTUS = 5.
They can be arranged in 5 ! = 120 ways
Number of words starting with L and ending with S = 42
So the number of words neither starts with L nor ends with S = 120 – 42 = 78

Ex 4.1 Class 11 Pdf Question 13.
(i) Count the total number of ways of answering 6 objective type questions, each question having 4 choices.
Solution:
Count the total number of ways of answering 6 objective type questions, each question having 4 choices.
One question can be answered in 4 ways
Two questions can be answered in 4 × 4 = 4² ways
∴ Six questions can be answered in 46 ways

(ii) In how many ways 10 pigeons can be placed in 3 different pigeon holes ?
Solution:
First pigeons can be placed in pigeon hole in 3 ways (selecting 1 from 3 holes)
Second pigeons can be placed in pigeon hole in 3 ways Tenth pigeons can be placed in pigeon hole in 3 ways
So total number of ways in which all the number 10 place can be sent = 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 = 310 ways

(iii) Find the number of ways of distributing 12 distinct prizes to 10 students?
Solution:
To give the first prize we have to select, from the 10 students which can be done in 10 ways.
To give the second prize we have to select one from the 10 students which can be done is 10 ways.
To give the 12th prize we have to select one from 10 students which can be done in 10 ways.
So all the 12 prizes can be given in (10 × 10 × 10 …. 12 times) = 1012 ways.

Samacheerkalvi.Guru 11th Maths Question 14.
Find the value of

(i) 6!
Solution:
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720

(ii) 4! + 5!
Solution:
4! + 5! = (4 × 3 × 2 × 1) + (5 × 4 × 3 × 2 × 1)
= 24 + 120 = 144

(iii) 3! – 2!
Solution:
3! – 2! = (3 × 2 × 1) – (2 × 1)
= 6 – 2 = 4

(iv) 3! × 4!
Solution:
3! × 4! = (3 × 2 × 1) × (4 × 3 × 2 × 1) = 6 × 24 = 144
12!

(v) \(\frac{12 !}{9 ! \times 3 !}\)
Solution:

(vi) \(\frac{(n+3) !}{(n+1) !}\)
Solution:

Exercise 4.1 Class 11 Question 15.
Evaluate \(\frac{n !}{r !(n-r) !}\) when

(i) n = 6,
r = 2
Solution:

(ii) n = 10,
r = 3
Solution:

(iii) For any n with r = 2
Solution:

Chapter 4 Maths Class 11 Question 16.
Find the value of n if

(i) (n + 1)! = 20(n – 1)!
Solution:

(ii) \(\frac{1}{8 !}+\frac{1}{9 !}=\frac{n}{10 !}\)
Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.1 Additional Questions Solved

Samacheer Kalvi 11th Maths Example Sums Question 1.
If the letter of the word ‘RACHIT’ are arranged in all possible ways as listed in dictionary, then what is the rank of the word ‘RACHIT’?
Solution:
The alphabetical order of RACHIT is A, C, H, I, R and T
Number of words beginning with A = 5!
Number of words beginning with C = 5!
Number of words beginning with H = 5!
Number of words beginning with 1 = 5!
and Number of words beginning with R (i.e) RACHIT = 1
∴ The rank of the word ’RACHIT’ in the dictionary = 5! + 5! + 5! + 5! + 1 = 4 × 5! + 1
= 4 × 5 . 4 . 3 . 2 . 1 + 1 = 4 × 120 + 1 = 480 + 1 = 481

Samacheer Kalvi Guru 11th Maths Question 2.
Find the number of positive integers greater than 6000 and less than 7000 which are divisible by 5, provided that no digit is to be repeated.
Solution:
Any number divisible by 5, its unit place must have 0 or 5. We have to find 4-digit number greater than 6000 and less than 7000.
So, the unit place can be filled with 2 ways (0 or 5) since, repetition is not allowed.
∴ Tens place can be filled with 7 ways and hundreds place can be filled with 8 ways.
But the required number is greater than 6000 and less than 7000. So, thousand place can be filled with 1 digits (i.e) 6.

So, the total number of integers =1 × 8 × 7 × 2 = 112
Hence, the required number of integers = 112

Ex 4.1 Class 11 Question 3.
Find the number of integers greater than 7000 that can be formed with the digits 3, 5, 7, 8 and 9 where no digits are repeated.
Solution:
Given that all the 5 digit numbers are greater than 7000.
So, the ways of forming 5-digit numbers = 5 × 4 × 3 × 2 × 1 = 120
Now, all the four digit number greater than 7000 can be formed as follows.
Thousand place can be filled with 3 ways
Hundred place can be filled with 4 ways
Tenths place can be filled with 3 ways
Units place can be filled with 2 ways
So, the total number of 4-digits numbers = 3 × 4 × 3 × 2 = 72
∴ Total number of integers = 120 + 72 = 192
Hence, the required number of integers = 192

Ch 4 Maths Class 11 Question 4.
How many words (with or without dictionary meaning) can be made from the letters of the word MONDAY, assuming that no letter is repeated, if

Solution:

(c) All letters are used but the first is a vowel = 2 × 5! = 2 × 120 = 240
Hence, the required matching is
(a) ↔ (iii), (b) ↔ (i), (c) ↔ (ii)

Chapter 4 Class 11 Maths Question 5.
Five boys and 5 girls form a line. Find the number of ways of making the seating arrangement under the following condition.

Solution:
(a) Total number of arrangement when boys and girls alternate : = (5!)² + (5!)²
(b) No two girls sit together = 5! 6!
(c) All the girls sit together = 2! 5! 5!
(d) All the girls sit never together = 10! – 5! 6!
Hence, the required matching is (a) ↔ (iii), (b) ↔ (i), (c) ↔ (iv), (d) ↔ (ii)

Class 11 Chapter 4 Maths Question 6.
How many automobile license plates can be made, if each plate contains two different letters followed by three different digits?
Solution:
We have 26 English alphabet and 10 digits (0 to 9)
Since, it is given that each plate contains 2 different letters followed by 3 different digits.
∴ Number of arrangement of 26 letter taken 2 at a time

Three digit number can be formed out of 10 digit = ¹⁰P₃

Total number of license plates = 650 × 720 = 468000
Hence, the required number of plates = 468000.