Prasanna

Students can Download Maths Chapter 2 Measurements Ex 2.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.4

Miscellaneous Practice Problems

Question 1.
Two gates are fitted at the entrance of a library. To open the gates easily, a wheel is fixed at 6 feet istance from the wall ito which the gate is fixed. If one of the gates is opened to 90°, find the distance moved by the wheel (π = 3.14).

Solution:
Let A be the position of the wall AC be the gate in initial position and AB be position when it is moved 90°.
Now the arc length BC gives the distance moved by the wheel.
Length of the arc
= \(\frac{\theta}{360^{\circ}}\) × 2πr units
= \(\frac{90^{\circ}}{360^{\circ}}\) × 2 × 3.14 × 6 feets
= 3.14 × 3 feets
= 9.42 feets
∴ Distance moved by the wheel = 9.42 feets.

Question 2.
With his usual speed, if a person covers a circular track of radius 150 ra in 9 minutes, find the distance that he covers in 3 minutes (π = 3.14).
Solution:
Radius of the circular track = 150m
Distance covers in 9 minutes = Perimeter of the circle = 2 × π × r units
Distance covered in 9 min = 2 × 3.14 × 150 m

Distance he covers in 3 min = 314 m

Question 3.
Find the area of the house drawing given in the figure.

Solution:
Area of the house = Area of a square of side 6 cm + Area of a rectangle with l = 8cm, h = 6 cm + Area of a ∆ with b = 6 cm and h = 4 cm + Area of a parallelogram with b = 8 cm, h = 4 cm
= (side × side) + (l × b) + (\(\frac{1}{2}\) × b × h) + 6h cm²
= (6 × 6) + (8 × 6) + (\(\frac{1}{2}\) × 6 × 4) + (8 × 4) cm²
= 36 + 48 + 12+ 32 cm²
Required Area = 128 cm²

Question 4.
Draw the top, front and side view of the following solid shapes.

Solution:

Question 5.
Draw the net for the cube of side 4 cm in a graph sheet.
Solution:

Challenging Problems

Question 6.
Guna has fixed a single door of 3 feet wide in his room whereas Nathan has fixed a double door, each 1 \(\frac{1}{2}\) feet wide in his room. From the closed state, if each of the single and double doors can open up to 120°, whose door requires a minimum area?

Solution:
(a) Width of the door that Guna fixed = 3 feet.
When the door is open the radius of the sector = 3 feet
Angle covered = 120°
∴ Area required to open the door = \(\frac{120^{\circ}}{360^{\circ}}\) × πr² = \(\frac{120^{\circ}}{360^{\circ}}\) × π × 3 × 3 = 37π feet²

(b) Width of the double doors that Nathan fixed = 1\(\frac{1}{2}\) feet.
Angle described to open = 120°
Area required to open = 2 × Area of the sector
= 2 × \(\frac{120^{\circ}}{360^{\circ}} \times \pi \times \frac{3}{2} \times \frac{3}{2} \text { feets }^{2}=\frac{3 \pi}{2}\) feet²
= \(\frac{1}{2}\) (3π) feet²
∴ The double door requires the minimum area.

Question 7.
In a rectangular field which measures 15 m × 8m, cows are tied with a rope of length 3m at four corners of the field and also at the centre. Find the area of the field where none of the cow can graze. (π = 3.14).
Solution:
Area of the field where none of the cow can graze = Area of the rectangle – [Area of 4 quadrant circles] – Area of a circle

Area of the rectangle = l × b units²
= 15 × 8 m² = 120 m²
Area of 4 quadrant circles = 4 × \(\frac{1}{4}\) πr² units
Radius of the circle = 3 m
Area of 4 quadrant circles = 4 × \(\frac{1}{4}\) × 3.14 × 3 × 3 = 28.26m²
Area of the circle at the middle = πr² units
= 3.14 × 3 × 3m² = 28.26m²
∴ Area where none of the cows can graze
= [120 – 28.26 – 28.26]m² = 120 – 56.52 m² = 63.48m²

Question 8.
Three identical coins, each of diameter 6 cm are placed as shown. Find the area of the shaded region between the coins, (π = 3.14) ( \(\sqrt{3}\) = 1.732)

Solution:
Given diameter of the coins = 6 cm
∴ Radius of the coins = \(\frac{6}{2}\) = 3 cm
Area of the shaded region = Area of equilateral triangle – Area of 3 sectors of angle 60°
Area of the equilateral triangle

∴ Area of the shaded region = 15.588 – 14.13 cm² = 1.458 cm²
Required area 1.458 cm² (approximately)

Question 9.
Using graph sheet, draw the net for the cuboid whose length is 5cm, breadth is 4cm and height is 3cm and also find its area.
Solution:
Net for the cuboid is:

One of the possible nets for a cuboid of length = 5 cm, breadth = 4 cm, height = 3 cm is given above
Area of the cuboid
= 20 cm² + 15 cm² + 20 cm² + 15 cm² + 12 cm² + 12 cm² = 94 cm²
Using formula,
Surface area of a cuboid
= 2 (lb + bh + lh) unit²
= 2(5 × 4 + 4 × 3 + 5 × 3) cm²
= 2(20 + 12 + 15) cm²
= 94 cm²

Question 10.
Using Euler’s formula, find the unknowns.

Solution:
Euler’s formula is given by F + V- E = 2
(i) V = 6, E = 14
By Euler’s formula
= F + 6 – 14 = 2
F = 2 + 14 – 6
F = 10

(ii) F = 8, E = 10
By Euler’s formula
= 8 + V – 10 = 2
V = 2 – 8 + 10
V = 4

(iii) F = 20, V = 10
By Euler’s formula
= 20 + 10 – E = 2
30 – E = 2
E = 30 – 2
E = 28
Tabulating the required unknowns

Students can Download Maths Chapter 2 Measurements Ex 2.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.3

Question 1.
Fill in the blanks:
(i) The three dimensions of a cuboid are _____.
(ii) The meeting point of more than two edges- is called as ______.
(iii) A cube has _____ faces.
(iv) The cross section of a solid cylinder is ______.
(v) If a net of a 3-D shape has six plane squares, then it is called ______.
Solution:
(i) length, breadth and height
(ii) vertex
(iii) six
(iv) circle
(v) cube

Question 2.
Match the following:

Solution:
(i) b
(ii) a
(iii) d
(iv) c

Question 3.
Which 3-D shapes do the following nets represent? Draw them.

Solution:
(i) The net represents cube, because it has 6 squares

(ii) The net represents cuboid

(iii) The net represents Triangular prism

(iv) The net represents square pyramid

(v) The net represents cylinder

Question 4.
For each solid, three views are given. Identify for each solid, the corresponding top, front and side (T, F & S) views.

Solution:

Question 5.
Verify Euler’s formula for the table given below

Solution:
Euler’s formula is given by F + V – E
(i) F = 4 ; V = 4; E = 6
F + V – E = 4 + 4 – 6 = 8 – 6
F + V – E = 2
∴ Euler’s formula is satisfied.

(ii) F = 10; V = 6; E = 12
F + V – E = 10 + 6 – 12
= 16 – 12 = 4 ≠ 2
∴ Euler’s formula is not satisfied.

(iii) F = 12 ; V = 20 ; E = 30
F + V – E = 12 + 20 – 30
= 32 – 30 = 2
∴ Euler’s formula is satisfied.

(iv) F = 20 ; V = 13 ; E = 30
F + V – E = 20 + 13 – 30
= 33 – 30 = 3 ≠ 2
∴ Euler’s formula is not satisfied.

(v) F = 32 ; V = 60 ; E = 90
F + V – E = 32 + 60 – 90
= 92 – 90 = 2
∴ Euler’s formula is satisfied.

Question 6.
Find the area of the given nets.

Solution:
(i) Area = Area of 6 squares of side 4 cm
= 6 × a² sq. units
= 6 × 4 × 4 cm²
= 96 cm²
(ii) Area = Area of 2 rectangles of
l = 10, b = 6 + Area of 2 rectangles of l = 6, b = 4 + Area of 2 rectangles of l= 10,b = 4
= (10 × 6) + (6 × 4)+ (10 × 4) cm²
= 60 + 24 + 40 cm²
= 124 cm²

Question 7.
Can a polyhedron have 12 faces, 22 edges and 17 vertices?
Solution:
By Euler’s formula F + V- E = 2 fora polyhedron.
Here F = 12, V = 17, E = 22
F + V – E = 12 + 17 – 22
= 29 – 22
= 7 ≠ 2
∴ The polyhedron cannot have 12 faces 22 edges and 17 vertices.

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.4

Question 1.
Find the value of x in the given figure.

Solution:
In the cyclic quadrilateral ABCD
∠ABC = 180° – 120° = 60°
∠BCA = 90°
∴ x = ∠BAC = 180°- (90° + 60°) = 30°

Question 2.
In the given figure, AC is the diameter of the circle with centre O. If ∠ADE = 30°; ∠DAC = 35° and ∠CAB = 40°.
Find
(i) ∠ACD
(ii) ∠ACB
(iii) ∠DAE

Solution:
(i) ∠ACD = 180°- (90° + 35°) = 180°- 125° = 55°
(ii) ∠ACB = 180°- (90°+ 40°)= 180° – 130° = 50°
(iii) ∠ADC = 90°
∠CAE = 180° – 120° = 60°
∴ ∠DAE = 60°- 35° = 25°

Question 3.
Find all the angles of the given cyclic quadrilateral ABCD in the


Solution:

Question 4.
In the given figure, ABCD is a cyclic quadrilateral where diagonals intersects at P such that ∠DBC = 40° and ∠BAC = 60° find
(i) ∠CAD
(ii) ∠BCD

Solution:

Question 5.
In the given figure, AB and CD are the parallel chords of a circle with centre O. Such that AB = 8 cm and CD = 6 cm. If OM ⊥ AB and OL ⊥ CD distance between LM is 7 cm. Find the radius of the circle?

Solution:
In the figure LM = 7 cm

Question 6.
The arch of a bridge has dimensions as shown, where the arch measure 2 m at its highest point and its width is 6 m. What is the radius of the circle that contains the arch?

Solution:

Question 7.
In figure ∠ABC = 120°, where A,B and C are points on the circle with centre O. Find ∠OAC ?

Solution:

Question 8.
A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6 m ground to nineth standard students for planting sapplings. Four students plant trees at the points A, B, C and D as shown in figure. Here AB = 8 m, CD = 10 m and AB ⊥ CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P.

Solution:

ONPM is a rectangle with all the angles 90° and with length \(\sqrt{20}\) cm, breadth \(\sqrt{11}\) cm.

We need to find OP which is the diagonal of the rectangle ONPM.

Question 9.
In the given figure, ∠POQ = 100° and ∠PQR = 30°, then find ∠RPO.
Solution:

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.3

Question 1.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre.
Solution:
The distance of the chord from the centre O

Question 2.
The chord of length 30 cm is drawn at the distance of 8cm from the centre of the circle. Find the radius of the circle.
Solution:

Question 3.
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius 4 \(\sqrt{2}\) cm and also find ∠OAC and ∠OCA.
Solution:
∆OAC is an isoceles triangle with one angle 90°
∴ ∠OAC + ∠OCA = 180° – 90°

2∠OAC = 90°
∠OAC = 45°
∴ ∠OCA = 45°

Question 4.
A chord is 12cm away from the centre of the circle of radius 15 cm. Find the length of the chord.
Solution:

Question 5.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?

Solution:
The distance between the two chord FE = OE + OF

∴ Distance between the chords is 14 cm

Question 6.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:

The length of the common chord AB = AD + BD = (3 + 3) cm = 6 cm

Question 7.
Find the value of x° in the following

Solution:

Question 8.
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB

Solution:

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 4 Geometry Additional Questions

Question 1.
From the given figure, name the parallel lines

Solution:
(i) Parallel Lines:
\(\overrightarrow{\mathrm{CD}}\) and \(\overrightarrow{\mathrm{EF}}\) ; \(\overrightarrow{\mathrm{CD}}\) and \(\overrightarrow{\mathrm{IJ}}\) ; \(\overrightarrow{\mathrm{EF}}\) and \(\overrightarrow{\mathrm{IJ}}\) are parallel lines.
(ii) Intersecting lines:
(a) \(\overrightarrow{\mathrm{AB}} \text { and } \overrightarrow{\mathrm{CD}}\)
(b) \(\overrightarrow{\mathrm{AB}} \text { and } \overrightarrow{\mathrm{EF}}\)
(c) \(\overrightarrow{\mathrm{AB}} \text { and } \overrightarrow{\mathrm{GH}}\)
(d) \(\overrightarrow{\mathrm{AB}} \text { and } \overrightarrow{\mathrm{IJ}}\)
(e) \(\overrightarrow{\mathrm{GH}} \text { and } \overrightarrow{\mathrm{IJ}}\)
(iii) Points of Intersection:
P, Q and R are the points of intersection.

Question 2.
(a) Name the line segments in the figure.
(b) Is Q, the endpoint of each line segment?

Solution:
(a) \(\overline{\mathrm{QP}} \text { and } \overline{\mathrm{QR}}\) are the line segments
(b) Yes, Q is the end point of each line segment

Question 3.
How many lines can pass through
(a) one given point
(b) two given points.
Solution:

(a) An infinite number of lines can pass through one given point.
(b) Exactly one and only one line can pass through two given points.

Question 4.
A line contains how many points?
(a) minimum?
(b) maximum?
Solution:
(a) A line contains a minimum of two points.
(b) A line contain a maximum of infinitely many points.

Question 5.
Write the (a) maximum and (b) the minimum number of point of intersection of three lines.
Solution:

Maximum – 3 points of intersection
Minimum – No point of intersection

Fill in the blanks.

Question 6.
Complementary angle of 20° is _____
Solution:
70°

Question 7.
The supplementary angle of 90° is _____
Solution:
90°

Question 8.
78°, 12°, ______
Solution:
Complementary angle

Answer the following question.

Question 9.
∠ABD =?

Solution:
On Sum of complementary angles = 90°
∠ABC = 90°
∠CBD = 30°
∠ABD = ∠ABC – ∠DBC = 90° – 30° = 60°
∠ABD = 60°
Complementary angle of 30° = 60°

Question 10.
In the following figure, name the angles.

Solution:
∠AOB, ∠BOZ, ∠AOZ

Question 11.
Write the alternate name of the angle ∠XYZ in the given figure.

Solution:
∠Y or ∠ZYX

Question 12.
Draw the diagram of two angles having only one common point.

Solution:
∠COD and ∠AOB have the point ‘O’ in common

Question 13.
What are the supplementary and complementary angles of 60°?
Solution:
Supplementary angle is 120°
Complementary angle is 30°

Question 14.
How many lines can you draw passing through three collinear points? Draw the figure also.
Solution:
Only one.

Question 15.
Write the maximum number of lines that can pass through a single point.
Solution:
Infinite.

Question 16.
Use a protractor to draw an angle 45°.
Solution:

Construction:
1. Drawn the base ray PQ.
2. Placed the centre of the protractor at the vertex P. Lined up the ray \(\overrightarrow{\mathrm{PQ}}\) with the 0° line. Then drawn and labelled a pointed (R) at the 45° mark on the inner scale (a) anticlockwise and (b) outer scale (clockwise)
3. Removed the protractor and drawn at \(\overrightarrow{\mathrm{PR}}\) to complete the angle
Now ∠P = ∠QPR = ∠RPQ = 45°.

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.2

Question 1.
The angles of a quadrilateral are in the ratio 2 : 4 : 5 : 7. Find all the angles.
Solution:
In a quadrilateral the angles add upto 360°.
Let’s call the angles 2x, 4x, 5x, 7x
2x + 4x + 5x + 7x = 360°
18x = 360°

A = 2x = 2 × 20° = 40°
B = 4x = 4 × 20° = 80°
C = 5x = 5 × 20° = 100°
D = 7x = 7 × 20° = 140°

Question 2.
In a quadrilateral ABCD, ∠A = 12° and ∠C is the supplementary of ∠A. The other two angles are 2x – 10 and x + 4. Find the value of x and the measure of all the angles.
Solution:
∠A = 72°
∠C = 180° – 72° (∵ Supplementary at ∠A) = 108°
The other two angles are 2x – 10 and x + 4.
2x – 10 + x + 4 + 108° + 12° = 360°

3x + 174° = 360°
3x = 360° – 174°

∴ ∠A = 72°
∠B = 2x – 10 = 2(62)- 10 = 124 – 10 = 114°
∠C = 108°
∠D = x + 4 = 62 + 4 = 66°

Question 3.
ABCD is a rectangle whose diagonals AC and BD intersect at O. If ∠OAB = 46°, find ∠OBC.
Solution:
∠ABC = 90°

∠OAB + ∠OBC = 90°
46° + ∠OAB = 90°
∠OBC = 90° – 46° = 44°

Question 4.
The lengths of the diagonals of a Rhombus are 12 cm and 16 cm. Find the side of the rhombus.
Solution:
Let ABCD be a rhombus with AC and BD as its diagonals.
We know that the diagonals of a rhombus bisect each other at right angles.
Let O be the intersecting point of both the diagonals
Let AC = 16 cm and BD = 12 cm


use Pythagoras theorem, we have
AB² = OA² + OB²
AB² = 100
∴ AB = 10 cm

Question 5.
Show that the bisectors of angles of a parallelogram form a rectangle.
Solution:
Given ABCD is a parallelogram. Draw the angular bisectors AP, BP, CR and DR of the angles ∠A, ∠B, ∠C and ∠D respectively.
Now to prove : PQRS is a rectangle.
Proof: A rectangle is a parallelogram with one angle 90°.
First we will prove PQRS is a parallelogram.
Now AB || CD and AD is transversal. [ ∴ Interior angles on the same side of transversal are supplementary]
[Opposite sides of a parallelogram are parallel]

Also lines AP and DR intersects
So ∠PSR = ∠DS A
∴ ∠PSR = 90° [∵ Vertically opposite angles]
Similarly we can prove that ∠SPQ = 90°, ∠PQR = 90° and ∠SRQ = 90°
∴ ∠PSR = ∠PQR and ∠SPQ = ∠SRQ
∴ Both pair of opposite angles of PQRS is a parallelogram.
Also ∠PSR = ∠PQR = ∠SPQ = ∠SRQ = 90°
∴ PQRS is a parallelogram with one angle 90°.
∴ PQRS is a rectangle. Hence proved.

Question 6.
If a triangle and a parallelogram lie on the same base and between the same parallels, then prove that the area of the triangle is equal to half of the area of parallelogram.
Solution:
Given: ∆ABE and parallelogram ABCD have the same base and are between the same parallel lines (i.e) l₁ || l₂.

Perpendicular distance between l₁ and l₂ = P (say).
Prove that: area of (∆ABE) = \(\frac{1}{2}\) × area of the parallelogram ABCD
Proof: Area of ∆ABE = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × AB × (Perpendicular distance between l₁
= \(\frac{1}{2}\) × AB × P ….(1)
Area of parallelogram ABCD = base × height.
∴ Area of parallelogram ABCD = AB × P …. (2)
From (1) and (2),
Area of ∆ABE = \(\frac{1}{2}\) × Area of parallelogram ABCD.
Hence proved.

Question 7.
Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in the figure. If a || b, c || d, e || f, find the marked angles between
(i) b and c
(ii) d and e
(iii) d and f
(iv) c and f.

Solution:
Since l, m are two parallel lines and PQ, RS, TU, VW are transversal.
Then ∠1 = ∠QOR [vertically opposite angles]
∠1 = 30° [∴ ∠QOR = 30°]
Also, PQ and TU are parallel and m and l are transversal.

Also ∠3 + ∠4 = 180°
⇒ 75° + ∠4 = 180°
∠4 = 180° – 75° = 105°
Hence,
(i) 30°
(ii) 105°
(iii) 75°
(iv) 105°

Question 8.
In the given figure ∠A = 64° , ∠ABC = 58°. If BO and CO are the bisectors of ∠ABC and ∠ACB respectively of ∆ABC, find x° and y°.
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180°
⇒ 64° + 58° + ∠C = 180°
⇒ 122°+ ∠C = 180°
⇒ ∠C = 180°- 122° = 58°

Also BO and CO are the bisectors of ∠ABC and ∠ACB respectively

Question 9.
In the given Fig. if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ACDF.

Solution:
Given: AB = 2,
BC = 6,
AE = 6,
BF = 8,
CE = 7 and
CF = 7
Consider ∆AEC and ∆BCF,
In ∆AEC,
AC = 8,
AE = 6,
CE = 7
In ∆BCF,
BF = 8,
BC = 6,
CF = 7
∴ ∆AEC ≅ ∆BCF
∴ Area of ∆AEC = Area of ∆BCF
Subtract.area of ∆BDC both sides, we get
Area of ∆AEC – Area of ∆BDC = Area of ∆BCF – Area of ∆BDC
⇒ Area of quadrilateral ABDE = Area of ∆CDF
∴ The required ratio is 1 : 1

Question 10.
In the figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to \(\overline{\mathbf{H E}}\) and \(\overline{\mathbf{F G}}\) ?

Solution:
Area of ABCD = length × breadth.
= DC × BC = 10 × 8 = 80.
Area of ∆AEH = Area of ∆CGF [since they are congruent by RHS rule]
Similarly, Area of ∆BEF = Area of ∆DGH
∴ Area of parallelogram = EFGH = Area of rectangle ABCD – 2(area of ∆AEH) – 2(area of ∆BEF)

Question 11.
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is \(\frac{9}{8}\) of the area of the parallelogram ABCD.

Solution:

Area of ∆QDP = Area of ∆QMA + Area of ∆MNO + Area of MNBS + Area of ∆MAB
= Area of ∆DCM + Area of ∆MNO + Area of MNBA + Area of ∆NDC
= 2Area of ∆OMN + Area of ∆MNO + 4 Area of ∆OMN + 2 Area of ∆OMN

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.1

Question 1.
In the figure, AB is parallel to CD, find x

Solution:
(i) From the figure
∠1 = 140° (∴ corresponding angles are equal)
∠2 = 40° (∴ ∠1 + ∠2= 180°)
∠3 = 30° (∵ ∠3 + 150= 180°)
∠4 = 110° (∵ ∠2 + ∠3 + ∠4 = 180°)
∴ ∠x = 70° (∵ ∠4 + ∠x = 180°)

(ii) From the figure
∠1 = 48°
∠3 = 108° (∠1 +24° + ∠3 = 180°)
∠4 = 108° (If two lines are intersect, then the vertically the opposite angles are equal)
∠5 = 72° (∵ ∠3 + ∠5 = 180°)
∴ ∠3 + ∠4 + ∠5 = 108° + 108° + 72°
x = 288°

(iii) From the figure
∠D = 53° ( ∵ ∠B and ∠D are alternate interior angles)
Sum of the three angles of a triangle is 180°
∠x° = 180°- (38°+ 53°)
= 180°- 91° = 89°

Question 2.
The angles of a triangle are in the ratio 1 : 2 : 3, find the measure of each angle of the triangle.
Solution:
Let the angles be x, 2x and 3x respectively.
Sum of the three angles of a triangle = 180°

The 3 angles of the triangle are 30°, 60°, 90°.

Question 3.
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent:

Solution:
(i) Consider ∆PQR and ∆ABC
Given, RQ = BC
PQ = AB
∆ABC is not congruent to ∆PQR
If PR = AC, then ∆ABC ≅ ∆PQR

(ii) Consider ∆ABD and ∆BCD for the triangles to be congruent.
Given, AB = DC
AD = BC and AB is common side.
∴ By SSS rule ∆ABD ≅ ∆BCD.

(iii) Consider ∆PXY and ∆PXz,
Given, XY = XZ
PY = PZ and PX is common
∴ By SSS rule ∆PXY ≅ ∆PXZ.

(iv) Consider ∆OAB and ∆ODC,
Given, OA = OC

∠ABO = ∠ODC and ∠AOB = ∠DOC (vertically opposite angles)
∴ By AAS rule, AOAB = AODC.

(v) Consider ∆AOB and ∆DOC,
Given, AO = OC
OB = OD


and ∠AOB = ∠DOC [vertically opposite angles]
∴ By SAS rule, ∆AOB = ∆DOC.

(vi) Consider ∆AMB and ∆AMC,
Given, AB = AC

∠AMB = ∠AMC = 90°
∴ AM is common.
∴ By RHS rule
∆AMB ≅ ∆AMC.

Question 4.
∆ABC and ∆DEF are two triangles in which AB = DF, ∠ACB = 70°, ∠ABC = 60°; ∠DEF = 70° and ∠EDF = 60°. Prove that the triangles are congruent.
Solution:

∴ By ASA rule ∆ABC ≅ ∆FDE

Question 5.
Find all the three angles of the ∆ABC

Solution:
Exterior angle = Sum of the two opposite interior angles.

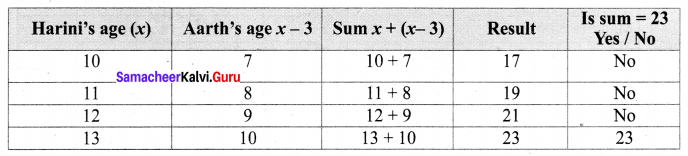
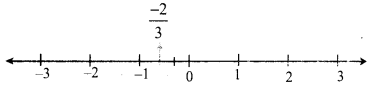
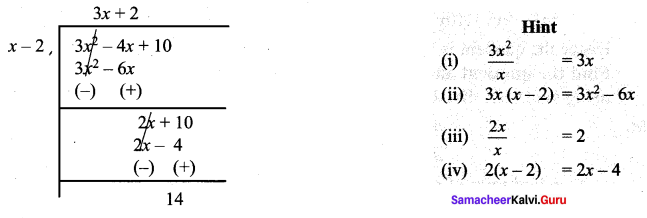
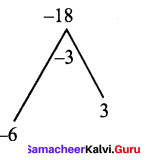
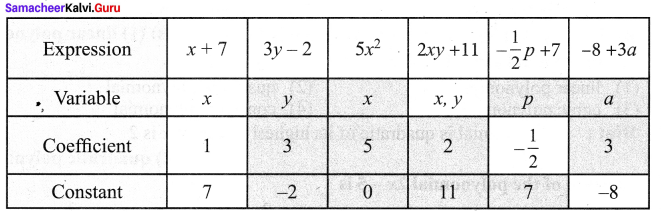
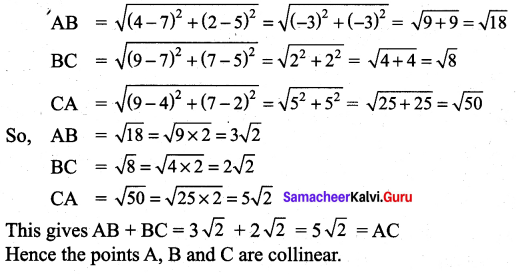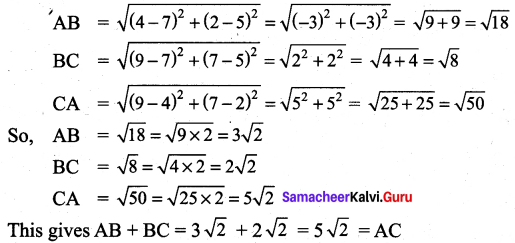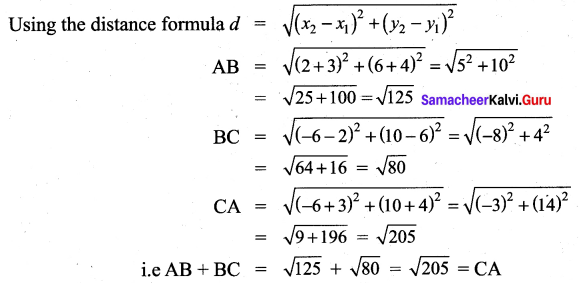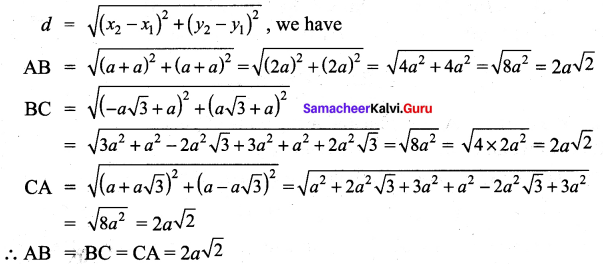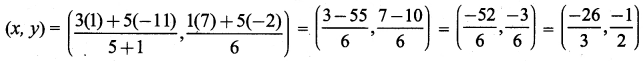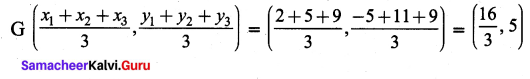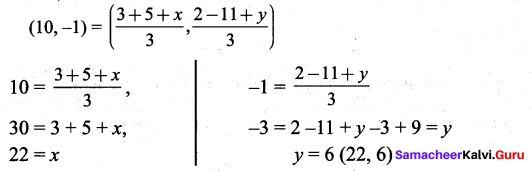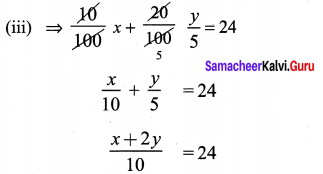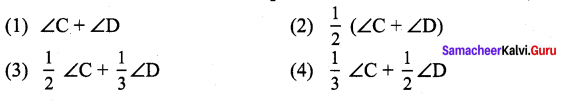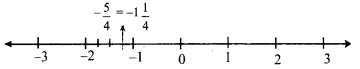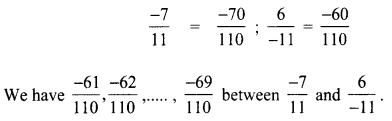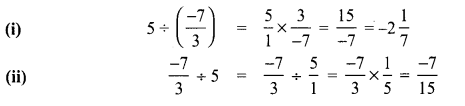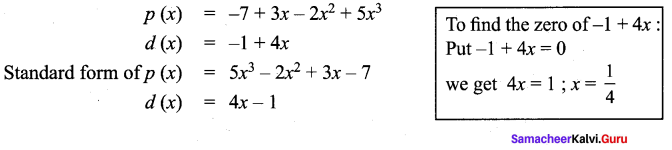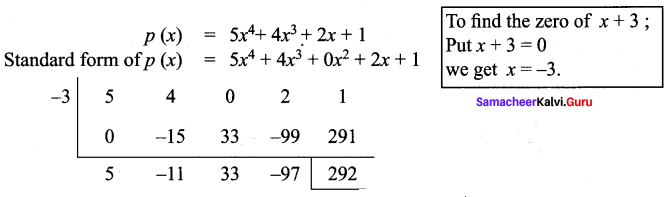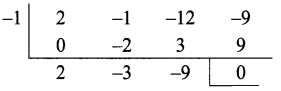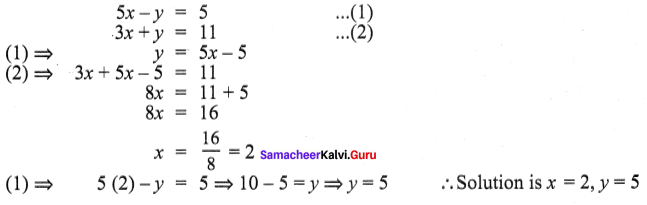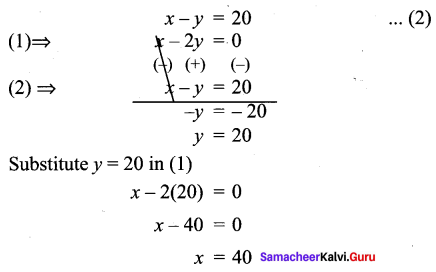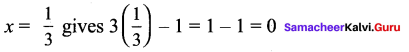You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.12

Question 1.
Solve by the method of elimination
(i) 2x – y = 3; 3x + y = 7
(ii) x – y = 5; 3x + 2y = 25
(iii) \(\frac{x}{10}+\frac{y}{5}\) = 14; \(\frac{x}{8}+\frac{y}{6}\) = 15
(iv) 3(2x + y) = 7xy; 3(x + 3y) = 11xy
(v) \(\frac{4}{x}\) + 5y = 7; \(\frac{3}{x}\) + 4y = 5
(vi) 13x + 11y = 70; 11x + 13y = 74
Solution:
(i) 2x – y = 3 ………….. (1)
3x + y = 7 ………… (2)

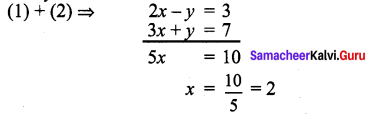
Substitute x = 2 in (1)
2(2) – y = 3
4 – y = 3
-y = 3 – 4
-y = -1
∴ Solution: x = 2; y = 1
Verification:
Substitute x = 2, y = 1 in (2)
3(2) + 1 = 7 = RHS
∴ Verified.

Substitute y = 2 in (1)
x – 2 = 5
x = 5 + 2
x = 7
∴ Solution: x = 7, y = 2
Verification:
Substitute x = 7, y = 2 in (2)
3(7) + 2(2) = 21 + 4 = 25 = RHS
∴ Verified.

Substitute y = 30 in (1)
x + 2 (30) = 140
x + 60 = 140
x = 140 – 60
x = 80
∴ Solution: x = 80; y = 30
Verification:
Substitute x = 80, y = 30 in (2)
3(80) + 4(30) = 240 + 120 = 360 = RHS
∴ Verified.

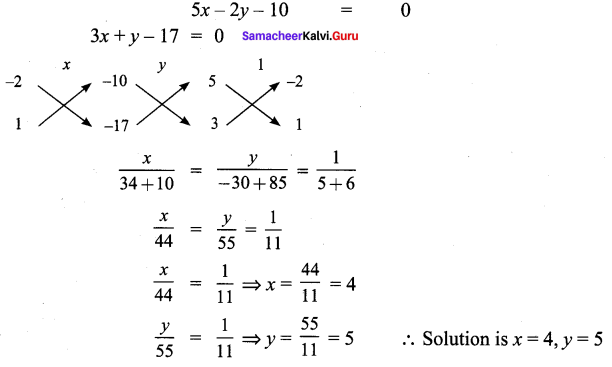
(iv) 3(2x +y) = 7xy ⇒ 6x + 3y = 7xy ………. (1)
3(x + 3y) = 11xy ⇒ 3x + 9y = 11xy ………….. (2)


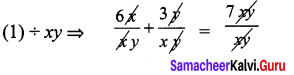
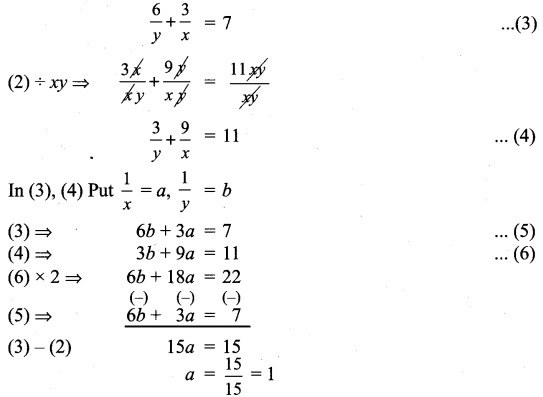
Substitute a = 1 in (5)
6b + 3(1) = 7
6b + 3 = 7
6b = 7 – 3
b = \(\frac{4}{6}=\frac{2}{3}\)
∴a = \(\frac{1}{x}\) = 1 ⇒ x = 1
b = \(\frac{1}{y}=\frac{2}{3}\) ⇒ y = \(\frac{3}{2}\)
∴ Solution: x = 1; y = \(\frac{3}{2}\)

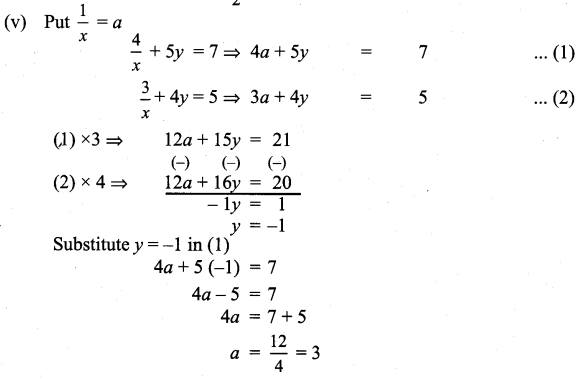
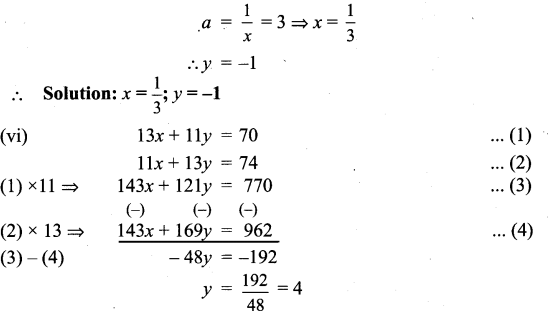
Substitute y = 4 in (1)
13x + 11 (4) = 70
13x + 44 = 70
13x = 70 – 44 = 26
x = \(\frac{26}{13}\) = 2
∴ Solution: x = 2; y = 4

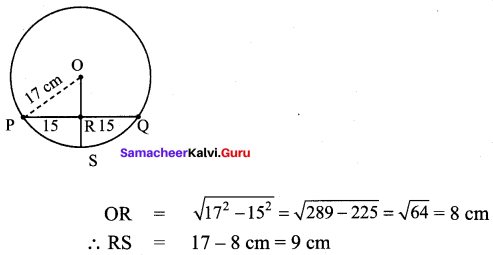
Question 2.
The monthly income of A and B are in the ratio 3:4 and their monthly expenditures are in the ratio 5 : 7. If each saves ₹ 5,000 per month, find the monthly income of each.
Solution:
Let the monthly income of A and B be 3x and 4x respectively.
Let the monthly expenditure of A and B be 5y and 7y respectively.
∴ 3x – 5y = 5000 ……… (1)
4x – 7y = 5000 ……….. (2)

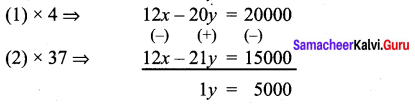
Substitute y = 5000 in (1)
3x – 5 (5000) = 5000
3x – 25000 = 5000
3x = 5000 + 25000
3x = 30000
x = 10000
∴ Monthly income of A is 3x = 3 × 10000 = ₹ 30000
Monthly income of B is 4x = 4 × 10000 = ₹ 40000

Question 3.
Five years ago, a man was seven times as old as his son, while five year hence, the man will be four times as old as his son. Find their present age.
Solution:
Let the man’s present age = x
Five years ago his age is = x – 5
Let his son’s age be = y
5 years ago his son’s age = y – 5
∴ x – 5 = 7(y – 5)
x – 5 = 7y – 35
x – 7y = -35 + 5
x – 7y = – 30 ……….. (1)
After 5 years, man’s age will be = x + 5
His son’s age will be = y + 5
∴ x + 5 = 4(y + 5)
x + 5 = 4y + 20
x – 4y = 20 – 5
⇒ x – 4y = 15 ………….. (2)

Substitute y = 15 in (1)
x – 7 (15) = -30
x – 105 – 30
x = – 30 + 105
x = 75
∴ Man’s Age = 75, His son’s Age =15

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Additional Questions

Exercise 5.1

Question 1.
State whether the following statements are true/false.
(i) (5, 7) is a point in the IV quadrant.
(ii) (-2, -7) is a point in the III quadrant.
(iii) (8, -7) lies below the x-axis.
(iv) (-2, 3) lies in the II quadrant.
(v) For any point on the x-axis its y-coordinate is zero.
Solution:
(i) False
(ii) True
(iii) True
(iv) True
(v) True

Question 2.
Locate the points
(i) (3, 5) and (5, 3)
(ii) (-2, -5) and (-5, -2) in the rectangular coordinate system.
Solution:

Question 3.
In which quadrant does the following points lie?
(i) (5, 2)
(ii) (-5, -8)
(iii) (-7, 1)
(iv) (8, -3)
Solution:
(i) I quadrant
(ii) III quadrant
(iii) II quadrant
(iv) IV quadrant.

Question 4.
Write down the ordinate of the following points.
(i) (7, 5)
(ii) (2, 9)
(iii) (-5, 8)
(iv) (7, -4)
Solution:
(i) 5
(ii) 9
(iii) 8
(iv) -4 (ordinate is the y-coordinate)

Exercise 5.2

Question 1.
Find the distance between the following pairs of points.
(i) (-4, 0) and (3, 0)
(ii) (-7, 2) and (5, 2)
Solution:
(i) The points (-4, 0) and (3, 0) lie on the x-axis. Hence,

(ii) The points (5,2) and (-7,2) lie on a line parallel to the x-axis. Hence the distance

Question 2.
Show that the three points (4, 2), (7, 5) and (9, 7) lie on a straight line.
Solution:
Let the points be A(4, 2), B(7, 5) and C(9, 7). By the distance formula.

Hence the points A, B and C are collinear.

Question 3.
Determine whether the points are vertices of a right triangle A(-3, -4), B(2, 6) and C (-6, 10).
Solution:

Hence ABC is a right angled triangle since the square of one side is equal to sum of the squares of the other two sides.

Question 4.
Show that the points (a, a), (-a, -a) and (\(-a \sqrt{3}, a \sqrt{3}\)) form an equilateral triangle.
Solution:
Let the points be represented by A (a, a), B(-a, -a) and C(\(-a \sqrt{3}, a \sqrt{3}\)) using the distance formula.

Since all the sides are equal the points form an equilateral triangle.

Question 5.
Prove that the points (-7, -3), (5, 10), (15, 8) and (3, -5) taken in order are the corners of a parallelogram.
Solution:
Let A, B, C and D represent the points (-7, -3), (5, 10), (15, 8) and (3, -5) respectively.

i.e. The opposite sides are equal. Hence ABCD is a parallelogram.

Question 6.
Show that the following points A (3, 1) B(6, 4) and C(8, 6) lies on a straight line.
Solution:
Using the distance formula, we have

Therefore the points lie on a straight line.

Question 7.
If the distance between the points (5, -2), (1, a) is 5 units. Find the value of a.

Solution:

Exercise 5.3

Question 1.
A, B and C are vertices of ∆ ABC. D, E and F are mid points of sides AB, BC and AC respectively. If the coordinates of A, D and F are (-3, 5), (5, 1) and (-5, -1) respectively. Find the coordinates of B, C and E.
Solution:

Question 2.
If A(10, 11) and B(2, 3) are the coordinates of end points of diameter of circle. Then find the centre of the circle.
Solution:

Question 3.
Find the coordinates of the point which divides the line segment joining the points (3, 1) and (5, 13) internally in the ratio 3 : 5.
Solution:

Exercise 5.4

Question 1.
Using section formula, show that the points A(7, -5), B(9, -3) and C(13, 1) are collinear.
Solution:

Question 2.
A car travels at an uniform speed. At 2pm it is at a distance of 5 km at 6 pm it is at a distance of 120 km. Using section formula, find at what distance it will reach 2 mid night.
Solution:

Question 3.
Find the coordinates of the point which divides the line segment joining the point A(3, 7) and B(-11, -2) in the ratio 5 : 1.
Solution:

Exercise 5.5

Question 1.
Find the centroid of the triangle whose vertices are (2, -5), (5, 11) and (9, 9)
Solution:

Question 2.
If the centroid of a triangle is at (10, -1) and two of its vertices are (3, 2) and (5, -11). Find the third vertex of the triangle.
Solution:

Exercise 5.6

Multiple Choice Questions :

Question 1.
The point (-2, 7) lies is the quadrant
(1) I
(2) II
(3) III
(4) IV
Hint:
(-, +) lies in II^nd quadrant
Solution:
(2) II

Question 2.
The point (x, 0) where x < 0 lies on
(1) OX
(2) OY
(3) OX’
(4) OY’
Hint:
(-, 0) lies on OX’
Solution:
(3) OX’

Question 3.
For a point A(a, b) lying in quadrant III.
(1) a > 0, b < 0
(2) a < 0, b < 0
(3) a > 0, b > 0
(4) a < 0, b > 0
Hint:
(-, -) lies in III^rd quadrant
Solution:
(2) a < 0, b < 0

Question 4.
The diagonal of a square formed by the points (1, 0) (0, 1) and (-1, 0) is
(1) 2
(2) 4
(3) \(\sqrt{2}\)
(4) 8
Hint:

Solution:
(1) 2

Question 5.
The triangle obtained by joining the points A(-5, 0) B(5, 0) and C(0, 6) is
(1) an isosceles triangle
(2) right triangle
(3) scalene triangle
(4) an equilateral triangle
Hint:
Triangles having two sides equal are called isosceles.
Solution:
(a) an isosceles triangle

Text Book Activities

Activity 1.
Plot the following points on a graph sheet by taking the scale as 1cm = 1 unit. Find how far the points are from each other? A (1, 0) and D (4, 0). Find AD and also DA. Is AD = DA? You plot another set of points and verify your result.

Solution:
AD = DA is correct.

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.11

Question 1.
Solve, using the method of substitution
(i) 2x – 3y = 7; 5x + y = 9
(ii) 1.5x + 0.1y = 6.2; 3x – 0.4y = 11.2
(iii) 10% of x + 20% of y = 24; 3x – y = 20
(iv) \(\sqrt{2} x-\sqrt{3} y=1 ; \sqrt{3} x-\sqrt{8} y=0\)
Solution:
(i) 2x – 3y = 7 ………….. (1)
5x + y = 9 ………….. (2)
Step (1)
From the equation (2)
5x+ y = 9
y = -5x + 9
Step (2)
substitute (3) in (1)
2x – 3(-5x + 9) = 7
2x + 15x – 27 = 7
17x = 7 + 27
17x = 34
x = \(\frac{34}{17}\) = 2; x = 2
Step (3)
substitute x = 2 in (3)
y = – 5(2) + 9 = -10 + 9 = -1
Solution: x = 2; y = -1

(ii) 1.5x + 0.1y = 6.2 …………. (1)
3x – 0.1y = 11.2 ………….. (2)
Multiply (1 ) x 10 15x + y = 62 ……….(1)
(2) × 10 ⇒ 30x – 4y = 112 …………. (4)
Step (1)
From equation (3)
15x + y = 62
y = -15x + 62 …………. (5)
Step (2)
substitute (5) in (4)
30x – 4 (-15x + 62) = 112
30x + 60x – 248 = 112
90x = 112 + 248
90x = 360
x = \(\frac{360}{90}\)
x = 4
Step (3)
substitute x = 4 in (5)
y = -15(4) + 62
= -60 + 62
y = 2
Solution: x = 4; y = 2

x + 2y = 240 ………. (1)
3 x – y =20 ……….. (2)
Step (1)
From equation (2)
3x – y = 20
-y = 20 – 3x
y = 3x – 20 — (3)
Step (2)
substitute (3) in (1)
x + 2(3x – 20) = 240
x + 6x – 40 = 240
7x = 240 + 40
x = \(\frac{280}{7}\)
x = 40
Step (3)
substitute x = 40 in (3)
y = 3 (40) – 20
= 120 – 20 = 100
Solution : x = 40 and y = 100

(iv) \(\sqrt{2} x-\sqrt{3} y\) = 1 ………… (1)
\(\sqrt{3} x-\sqrt{8} y\) = 0 ……….. (2)
Step (1)
From the equation (2)


Solution: x = \(\sqrt{8}\) and y = \(\sqrt{3}\)

Question 2.
Raman’s age is three times the sum of the ages of his two sons. After 5 years his age will be twice the sum of the ages of his two sons. Find the age of Raman.
Solution:
Let Raman’s age = x
Let the sum of his two sons age = y
now x = 3y ⇒ x – 3y = 0 ……… (1)
After 5 years,
Step (3)
x + 5 = 2(y + 10)
x + 5 = 2y + 20
x – 2y = 20 – 5
x – 2y = 15
Step (1)
From equation (1) x = 3y
Step (2)
Substitute x = 3y in (2)
3y – 2y = 15
y = 15
Step (3)
Substitute y = 15 in (1)
x = 3y = 3 × 15
x = 45
∴ Raman’s age is 45 years.

Question 3.
The middle digit of a number between 100 and 1000 is zero and the sum of the other digit is 13. If the digits are reversed, the number so formed exceeds the original number by 495. Find the number.
Solution:
Let the number be x0y
x + y = 13 …………….. (1)
If the digits are reversed the number so formed is y0x
x0y = 100x + 10 × 0 + 1 × y
y0x = 100y + 10 × 0 + 1 × x
100y + x – (100x + y) = 495
100y + x – 100x – y = 495
-99x + 99y = 495 ………….. (2)

Substitute x = 4 in (1)
4 + y = 13 = 13 – 4 = 9
The number is 409.