Laxmi

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Poster Making

Exercises
I. The Sports dub of your school is organizing a sports meet at Nehru Stadium. Design an attractive poster for the same.
Answer:

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Diary Writing

Exercises
Write a Diary Entry

1. Write a diary entry in 60-80 words describing your thoughts about Water Scarcity.
Answer:

Diary Entry About Water Scarcity

12-10-2018, Friday
9.30 p.m.

Dear diary,
People are suffering due to water scarcity everywhere. Do you know the reasons for water scarcity? It is mainly because of excess population growth and mismanagement of water resources. Inefficient use of water for agriculture is prevalent everywhere. ’ Traditional water recharging areas are reduced due to the rapid construction of residential and commercial buildings. Sewage and waste water drainage management is not properly implemented. These sewage-disposal lines are connected to water bodies. Chemicals and effluents are dumped into rivers, streams, and ponds. De-silting operations in large water bodies like dams, lakes, ponds are not being carried out at proper timings. Hence water storage capacity during monsoon is not enhanced. All these problems should be solved.

Rajan.

2. Write a diary entry in 60-80 words describing your thoughts about the Effect of an Earthquake.
Answer:

Diary Entry About The Effect Of Earthquake

29-09-2018, Saturday
9.30 p.m.

Dear diary,
Today an earthquake hit the Indonesian city of Palu. The Richter magnitude scale of the earthquake is 7.7 and 384 people had been killed and the death toll was expected to rise. Most deaths are caused by the collapse of structures and the construction practices also play a major part in the death toll of an earthquake. Other effects such as landslides, soil liquefaction, and tsunamis have also played an important role in destruction produced by earthquakes.

3. Write a diary entry in 60-80 words describing your thoughts about Union is Strength.
Answer:

Diary Entry About Union Is Strength

14-08-2018, Tuesday
9.30 p.m.

Dear diary,
The topic that I am going to talk about is “Union is Strength.” In a word, unity means oneness or togetherness. When there is oneness there is likely to be more strength in opinion, more strength in action and more strength in character. For example: if you take a stick, it could break easily. But when you take a bundle of sticks, it is hard to break. This is the unique power of unity. One very good example is this Elocution Contest. All the Rotarians are united in their stand. They work hard to make this elocution contest a success. Unity among the various races is vital for the progress of the nation as the saying goes; “United we Stand, Divided we Fall”.

Rajesh.

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Expressing Views on a Given Picture

Tips on Views on Pictures

1. Understand the picture
2. Identity the theme
3. Bring out the causes
4. Suggest a remedy
5. Write about ten sentences with coherence
6. Give a title

Exercises
Look, at the picture given below. Express your views on it in about five sentences :
1.

Answer:
1. In the picture depicts the wastage of water.
2. The tap is opened and the water is over flouring from a bucket.
3. At every place, people are suffering from water scarcity.
4. So, it is our duty to avoid wastage of water.
5. We should create awareness on saving water among others.

2.

Answer:
1. In the given picture, two persons are practicing Silambaattam.
2. It is a martial art form, practiced from the days of the Tamil kings.
3. It has metamorphosed into a non-violent form of folk dance, adding stepping styles into the dance to the measure of time.
4. This martial art form also teaches the performer the methods of self-defense.
5. Silambam was banned in Tamil Nadu during the British rule. Britishers viewed this martial art as a potential threat in the face of revolts.

3.

Answer:
Circus
1. It seems to be a circus.
2.1 want to visit the circus.
3.1 can see a ring of fire in the picture.
4.1 can see mickey mouse with balloons.
5. I’ll enjoy a lot if I go there.
6. Generally children will have a lot of fun there.

4.

Answer:
Railway Platform
1. This is a scene on a railway platform.
2. We see passengers alighting the train with their luggage.
3. More of them are waiting to board it.
4. The passengers are standing before a sleeper class compartment.
5. Yet boarding and alighting will be more convenient if the passengers queue up.

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Unknown Poem Paraphrase

Exercises
Read the poem given below and complete its paraphrase with suitable phrases in the given blanks :

1. I love to rise in a summer mom,
When the birds sing on every tree;
The distant huntsman winds his home,
And the sky-lark sings with me.
O! what sweet company!
But to go to school in a summer mom,
O!’ it drives all joy away;
Under a cruel eye outworn
The little ones spend the day,
In sighing and dismay.

– William Blake

Paraphrase:
I like to wake up on a …………..(i)………….. when the birds …………..(ii)………….. The distant …………..(iii)………….. has already gone on his hunting. The skylark sings happily. Everything is happy around me. The thought of going to …………..(iv)………….. drives all joy away. The children spend their time …………..(v)………….. in the classroom, supervises by an old teacher. They are dismayed at the instructions that do not give them joy.
Answer:
(i) summer morning
(ii) sing on every tree
(iii) huntsman
(iv) school in a summer morning
(v) in sighing and dismay

2. Little drops of water
Little grains of sand
Make the mighty ocean
And the pleasant land
Little deeds of kindness,
Little words of love,
Make the earth and Eden
Like the heaven above
And the little moments
Humble thoughts they be
Make the mighty ages
of eternity.

Paraphrase :
Little drops …………..(i)………….. make the might ocean …………..(ii)………….. of sand make the pleasant land. Little deeds of …………..(iii)………….. make the earth and even like (iv) The little moments and humble thoughts make the mighty …………..(v)…………..
Answer:
(i) of water
(ii) Little grains
(iii) Kindness and little words of love
(iv) the haven above
(v) ages of eternity

3. If you can’t be a banyan on
The top of the hill
Be a scrub in the plain but be
The best little scrub by the side of the hill;
Be a bush if you can’t be a tree.
If you can’t be a bush be a bit of the grass,
And some highway you will happier make;
If you can‘t be a lotus then just be a bass
But the liveliest bass in the lake!

Paraphrase:
The poet tells the readers not to …………..(i)………….. because of their positions in life. Though one can’t be a banyan tree on top of the hill, one can still be the best …………..(ii)………….. One can at least be a …………..(iii)………….. if not a tree. If one can’t be a …………..(iv)………….. one can be grass or a lotus. If one can’t even be a lotus, then one can just be a bass and be the …………..(v)………….. bass in the lake.
Answer:
(i) be worry
(ii) little scrub by the side of the hill
(iii) bush
(iv) tree
(v) liveliest

4. I took a piece of plastic clay
And idly fashioned it, one day,
And as my fingers pressed it, still
It moved and yielded to my will
I came again when days were passed
That bit of clay was hard at last
The form I gave it, still it bore,
And I could change that form no more.

Paraphrase :
The artist took a piece of …………..(i)………….. He pressed it with …………..(ii)………….. It moved and gave into …………..(iii)………….. Finally, he molded it into a statue and went away. He returned after many days. The clay was now …………..(iv)………….. It still bore the form he had given. But he …………..(v)………….. that form no more.
Answer:
(i) plastic clay
(ii) his fingers
(iii) his will
(iv) hard
(v) could change

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Completion of Dialogues (Fill in type)

Exercises
Complete the following dialogue appropriately :
1. Selvi : (i) _________?
Librarian : Yes, Come in. (ii) _________?
Selvi : I wish to become a member of the library.
Librarian You have to pay a membership fee.
Selvi : (iii) _________?
Librarian : An annual fee of two hundred rupees.
Selvi : (iv) _________?
Librarian : You can borrow four books at a time.
Selvi : (v) _________?
Librarian : You should return the books within fifteen days.
Answer:
(i) May I come in sir
(ii) What can I do for you?
(iii) How much should I pay?
(iv) How many books can I borrow at a time?
(v) When should I return the books?

2. Bookseller Hello Sir! (1) __________?
Customer Sir, would you allow me to exchange this book with another book?
Bookseller (ii) __________?
Customer A few pages are missing in this book.
Bookseller (iii) __________?
Customer I bought the book this morning.
Bookseller (iv) __________?
Customer : Here is the bill (v) __________?
Am:
(i) May I help you
(ii) Is something wrong with this book
(iii) When did you buy it
(iv) Do you have the biu
(v) and the book. Kindly exchange it

3. (Telephonic Conversation)
Rm : Hello (i) __________?
Rahim : Yes, may I know who is calling?
Ram : (ii) __________?
Rahim : Hi Ram, what can I do for you?
Ram : (iii) __________? Are you free after six this evening?
Rahim : Sorry. Ram (iv) __________? Will it be convenient for you to come tomorrow morning.
Ram : Ok (v) __________?
Answer:
(i) Is Mr. Rahim at home
(ii) It’s Ram. May I see you for five minutes
(iii) It’s an important personal matter
(iv) I have an urgent appointment with my boss
(v) See you tomorrow at 9 a.m.

4. TTR : Ticket please.
Traveller : Sorry sir, somehow I have lost my ticket.
TTR : (i) ________ ?
Traveller : (ii) ________?
TTR : Then (iii) ________?
Traveller : Just a minute sir (iv) ________?
TTR : Be quick.
Traveller : I got it. Here it is sir.
TTR : (v) ________?
Traveller : OK. Thank you sir.
Answer:
(i) Then you have to take a new ticket with penalty.
(ii) I don’t have enough money to take another ticket sir.
(iii) Then, what are you going to do?
(iv) Shall I check once again in my bags?
(v) 0k. Always keep your ticket at safe place. Don’t waste others time.

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Dialogue Writing

Exercises
1. Write a dialogue between a customer and a shop keeper.
Answer:
Customer : Good morning sir.
Shop Keeper : Good morning. What do you want?
Customer : I want an LED TV.
Shop Keeper : Which brand do you like, sir?
Customer : I want Philips TV.
Shop Keeper : What features do you want in it?
Customer : I want 40 inches along with 3D provision.
Shop Keeper : Here it is, sir. It costs Rs. 50,000/-.
Customer : Could I pay the money through debit card?
Shop Keeper : Yes sir. May I pack this for you?
Customer : Yes.

2. Write a dialogue with a minimum five utterances between a doctor and a patient who complains of stomachache.
Answer:
Patient : Good morning, doctor. I have stomach ache.
Doctor : Good morning. Since when?
Patient : From yesterday, doctor.
Doctor : Did you eat oily food from some platform stalls?
Patient : Yes doctor. I took non-veg items from a platform shop.
Doctor : The pain is due to bacterial infection. Take these tablets and tonic twice a day after food.
Patient : O.K. doctor. How much is the bill amount?
Doctor : It is Rs. 200. Take care of your health.
Patient : Thank you doctor.

3. Write a dialogue between you and your mother about the upcoming food carnival in your school.
Answer:
Daughter : Mummy, there will be a food carnival in our school.
Mother : Oh, It is very nice. When will it be organized?
Daugher : Coming weekend Mummy.
Mother : Do you know who are the participants?
Daughter : My teacher told that around 100 students of classes XI and XII would participate.
Mother : What type of food will they prepare? .
Daughter : They will prepare national and international delicacies that represent various states.
Mother : Will there be fast food stalls?
Daughter : Definitely such stalls will not be allowed. Only traditional food items will be prepared by them.
Mother : That is very good.
Daughter : My teacher instructed that each and every student should bring their parents to the carnival, Mummy.

4. WrIte a dialogue with at least 5 utterances between the manager of a restaurant and an angry customer who finds a fly in his soup.
Answer:
Waiter : Here’s your soup, Sir.
Customer : Thank you. (tastes the hot soup). What’s this? Eek! A fly in my soup. (shouts) Waiter! No, I’d better talk to the manager.
Manager : Is something wrong?
Customer : It is the soup that is wrong.
Manager : What happened, sir?
Customer : I ordered for a vegetarian soup but ¡ was served a non-veg soup.
Manager : A non-veg. soup? In this hotel?
Customer : Yes, certainly. See this.
Manager : Oh, I’m extremely sorry. Waiter, get him another bowl of soup.
Customer : Oh, no, thank you, not another non-veg. soup.

5. Write a dialogue with at least five utterances between a bank manager and a student who wants to open a bank account.
Answer:
Student : Good morning sir, I wish to open a Savings Bank account.
Banker : Good morning. Go through this application, please.
Student : Application seeks information about my address, occupation and income details.
Banker : Yes. Please fill it.
Student : How much should I deposit initially?
Banker : You should deposit at least 500/- If you need a cheque book, you have to maintain a minimum balance of 1000/-
Student : Should I produce any documents?
Banker : Yes, bring a xerox copy of your ration card and you need to give two passport size photos. An account holder of this bank should give a letter of introduction.
Student : Sure, Sir. Thank you.
Banker : Come with all the necessary papers and meet the clerk.
Student : 0k sir, Thank you!

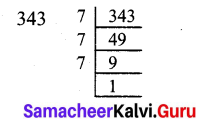
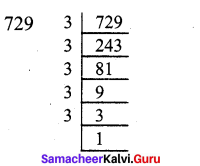
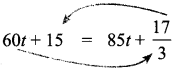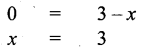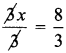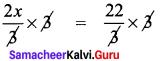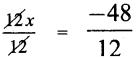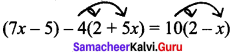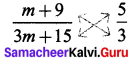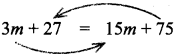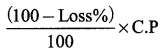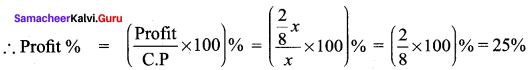Students can Download Maths Chapter 2 Algebra Ex 2.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 2 Algebra Ex 2.3

Question 1.
Fill in the blanks:

Question (i)
X – axis and Y – axis intersect at ……..
Answer:
Origin (0, 0)

Question (ii)
The coordinates of the point in third quadrant are always ……….
Answer:
negatives

Question (iii)
(0, -5) point lies on ………. axis.
Answer:
y – axis.

Question (iv)
The x coordinate is always ……… on the y – axis.
Answer:
Zero

Question (v)
Coordinates are the same for a line parallel to Y – axis.
Answer:
X.

Question 2.
Say True or False:

Question (i)
(-10, 20) lies in the second quadrant.
Answer:
True
Hint:
(-10, 20)
x = – 10,
y = 20
∴ (- 10, 20) lies in second quadrant – True

Question (ii)
(-9, 0) lies on the x – axis.
Answer:
True
Hint:
(-9, 0) on x – axis, Y – coordinate is always zero.
∴ (-9, 0) lies on x – axis – True

Question (iii)
The coordinates of the origin are (1, 1).
Answer:
False
Hint:
Coordinate of origin is (0, 0), not (1, 1). Hence – False

Question 3.
Find the quadrants without plotting the points on a graph sheet.
(3, -4), (5, 7), (2, 0), (- 3, – 5), (4, – 3), (- 7, 2), (- 8, 0), (0,10), (- 9, 50).
Solution:

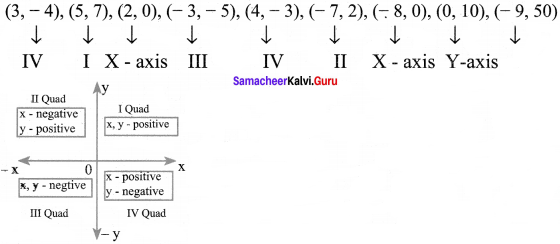
• If x & y coordinate are positive – I quad
• If x is positive, y is negative – IV quad
• If x is negative, y is positive – II quad
• If both are negative, then – III quad

Question 4.
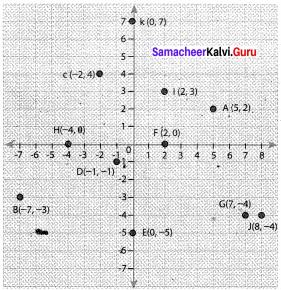
Plot the following points in a graph sheet.
A(5, 2), B(- 7, – 3), C(- 2, 4), D(- 1, – 1), E(0, – 5), F(2, 0), G(7, – 4), H(- 4, 0), 1(2,3), J(8, – 4) K (0, 7).
Solution:

Question 5.
Use the grid graph to determine the coordinates where each figure is located.

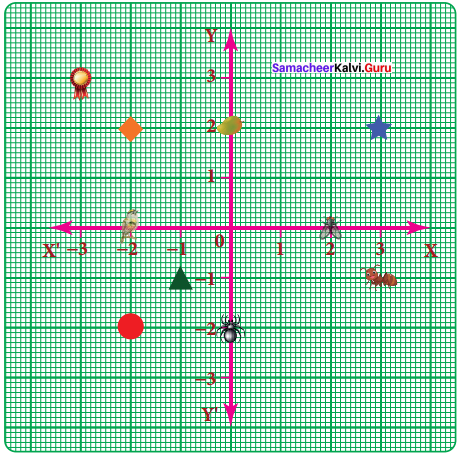
a) Star ……..
b) Bird ……..
c) Red Circle ……..
d) Diamond ……..
e) Triangle ……..
f) Ant ……..
g) Mango ……..
h) Housefly ……..
i) Medal ……..
j) Spider ……..
Solution:
a) Star (3, 2)
b) bird (-2, 0)
c) Red Circle (-2, -2)
d) Diamond (-2, 2)
e) Triangle (-1, -1)
f) Ant (3, -1)
g) Mango (0, 2)
h) Housefly (2, 0)
i) Medal (-3, 3)
j) Spider (0, -2)

Students can Download Maths Chapter 3 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Intext Questions

Exercise 3.1

Try These (Text book Page No. 44)

Question 1.
Observe and complete the following table. First one is done for you.

Solution:

Try These (Text book Page No. 46)

Question 1.
Simplify and write the following in exponential form.
1. 2³ × 2⁵
2. p² × P⁴
3. x⁶ × x⁴
4. 3¹ × 3⁵ × 3⁴
5. (-1)² × (-1)³ × (-1)⁵
Solution:
1. 2³ × 2⁵ = 2³⁺⁵ = 2⁸ [since a^m × aⁿ = a^m+n]

2. p² × p⁴ = p²⁺⁴ = p⁶ [since a^m × aⁿ = a^m+n]

3. x⁶ × x⁴ = x⁶ + 4 = x¹⁰ [since a^m × aⁿ = a^m+n]

4. 3¹ × 3⁵ × 3⁴ = 3¹⁺⁵ × 3⁴ [since a^m × aⁿ = a^m+n]
= 3⁶ × 3⁴ [since a^m × aⁿ = a^m+n]
= 3¹⁰

5. (-1)² × (-1)³ × (-1)⁵
= (-1)²⁺³ × (-1)⁵ [Since a^m × aⁿ = a^m+n]
= (-1)⁵ × (-1)⁵
= (-1)⁵⁺⁵ [Since a^m × aⁿ = a^m+n]
= (-1)¹⁰

Try These (Text book Page No. 48)

Question 1.
Simply the following.
1. 23⁵ ÷ 23²
2. 11⁶ ÷ 11³
3. (-5)³ ÷ (-5)²
4. 7³ ÷ 7³
5. 15⁴ ÷ 15
Solution:

Try These (Text book Page No. 48)

Question 1.
Simplify and write the following in exponent form.
1. (3²)³
2. [(-5)³]²
3. (20⁶)²
4. (10³)⁵
Solution:
1. (3²)³ = 3^2×3 = 3⁶ [since (a^m)ⁿ = a^m×n]
2. [(-5)]² = (-5)^3×2 = (-5)⁶ [since (a^m)ⁿ = a^m×n]
3. (20⁶)² = 20^6×2 = 20¹² [since (a^m)ⁿ = a^m×n]
4. (10³)⁵ = 10^3×5 = 10¹⁵ [since (a^m)ⁿ = a^m×n]

Question 2.
Express the following exponent numbers using a^m × b^m = (a × b)^m.
(i) 5² × 3²
(ii) x³ × y³
(iii) 7⁴ × 8⁴
Solution:
(i) 5² × 3² = (5 × 3)² = 15² [since a^m × b^m = (a × b)^m]
(ii) x³ × y³ = (x × y)³ = (x y)³
(iii) 7⁴ × 8⁴ = (7 × 8)⁴ = 56⁴

Question 3.
Simplify the following exponent numbers by using (\(\frac { a }{ b } \))^m = \(\frac{a^{m}}{b^{m}}\)
(i) 5³ ÷ 2³
(ii) (-2)⁴ ÷ 3⁴
(iii) 8⁶ ÷ 5⁶
(iv) 6³ ÷ (-7)³
Solution:
(i) 5³ ÷ 2³ = (\(\frac { 5 }{ 2 } \))³ – [Since \(\frac{a^{m}}{b^{m}}\) = (\(\frac { a }{ b } \))^m]
(ii) (-2)⁴ ÷ 3⁴ = (\(\frac { -2 }{ 3 } \))⁴
(iii) 8⁶ ÷ 5⁶ = (\(\frac { 8 }{ 6 } \))⁶
(iv) 6³ ÷ (-7)³ = (\(\frac { 6 }{ -7 } \))³

Exercise 3.2

Try These (Text book Page No. 54)

Question 1.
Find the unit digit of the following exponential numbers:
(i) 106²¹
(ii) 25⁸
(iii) 31¹⁸
(iv) 20¹⁰
Solution:
(i) 106²¹ Unit digit of base 106 is 6 and the power is 21 and is positive.
Thus the unit digit of 106²¹ is 6.

(ii) 25⁸ Unit digit of base 25 is 5 and the power is 8 and is positive.
Thus the unit digit of 25⁸ is 5.

(iii) 31¹⁸ Unit digit of base 31 is 1 and the power 18 and is positive.
Thus the unit digit of 31¹⁸ is 1.

(iv) 20¹⁰ Unit digit of base 20 is 0 and the power 10 and is positive.
Thus the unit digit of 20¹⁰ is 0.

Try These (Text book Page No. 55)

Question 1.
Find the unit digit of the following exponential numbers:
(i) 64¹¹
(ii) 29¹⁸
(iii) 79¹⁹
(iv) 104³²
Solution:
(i) 64¹¹ Unit digit of base 64 is 4 and the power is 11 (odd power).
∴ Unit digit of 64¹¹ is 4.

(ii) 29¹⁸ Unit digit of base 29 is 9 and the power is 18 (even power).
Therefore, unit digit of 29¹⁸ is 1.

(iii) 79¹⁹ Unit digit of base 79 is 9 and the power is 19 (odd power).
Therefore, unit digit of 7919 is 9.

(iv) 104³² Unit digit of base 104 is 4 and the power is 32 (even power).
Therefore, unit digit of 104³² is 6.

Exercise 3.3

Try These (Text book Page No. 35)

Question 1.
Complete the following table:

Solution:

Question 2.
Identify the like terms from the following:
(i) 2x²y, 2xy²,3xy²,14x²y, 7yx
(ii) 3x³y², y³x, y³x², – y³x, 3y³x
(iii) 11pq, -pq, 11pqr, -11pq,pq
Solution:
(i) 2x²y, 2xy², 3xy², 14x²y, 7yx
(a) 2x²y and 14x²y are like terms.
(b) 2xy² and 3xy² are like terms.

(ii) 3x³y², y³x, y³x², – y³x, 3y³x
(a) y³x, – y³x and 3y³x are like terms.

(iii) 11 pq, -pq, 11pqr , -11 pq, pq
(a) 11 pq, -pq, -pq and pq are like terms.

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Article Writing

An article is a piece of written work, the purpose of which is to propagate news, inform about results of research, analyze academic information, express opinions or persuade through suggestions.

Components of an article :
Title – it should be catchy enough to draw the reader’s attention
Byline – the name of the writer of the article Introduction – outlines the topic
Body – builds upon the topic; consists of two to four paragraphs
Conclusion – summarises and offers final opinions

Tips for writing articles :

• Be brief and concise.
• Cover the essential elements of who, what, when, where, how and why?
• Focus on the theme or topic of the article. Do not deviate from it.
• Use simple language.

Exercises
1. Write an article for your school magazine. Describing your experience about the Clean India Campaign.
Answer:

Clean India Campaign

– by Anitha

The ‘Clean India Campaign’ or ‘Swachh Bharat Abhiyan’ launched by our Prime Minister, Mr. Narendra Modi was implemented to fulfill the vision of a clean India. But it has not been as effective as it should have been opinion polls conducted in various cities of India suggested that nearly two-thirds of the residents surveyed felt there was no impact of the campaign on their city or surroundings. The fact remains that the government alone cannot bring about a change unless we the people take initiatives to keep our surroundings clean. It is all about changing our attitude which cannot be changed by imposing fines of punishments.

There is a significant percentage of our population who are totally unaware of and neglect basic cleanliness hygiene. These are people who don’t even think once before littering on the road or throwing garbage anywhere and everywhere. Their lack of awareness has led to the ineffectiveness of such cleanliness initiatives. It is important to sensitize people on the importance of hygiene and cleanliness through awareness programs in electronic, print and social media. Enlightened people need to work with not only individuals but also organizations to make those people aware of the importance of cleanliness.

2. Write an article for your school magazine. Describing your experience about River Pollution.
Answer:

River Pollution

– by Rama

It is indeed unfortunate that rivers, which are our largest source of water are victims of pollution. Countless tanneries, chemical plants, textile mills, slaughter houses, hospitals contribute to pollution of rivers by dumping untreated waste into it. People who do not have the proper living conditions in India, resort to carrying out all their daily activities like bathing, washing and defecation, on the bank of rivers, and thus pollute them. Discharge of sewage and other domestic waste into the rivers is yet another environmentally hazardous practice, that is polluting the rivers. Religious practices also demand that floral offerings be cast-off in rivers and the ashes, after cremating a person should also be poured into rivers.
Unfortunately one concludes despite laws dealing with the task of prevention and control of river pollution there is no end to the misery we humans inflict on our rivers.

3. Write an article for your school magazine. Describing your experience about Serve Mankind.
Answer:

Serve Mankind

– by Bala

Men represent society in a Microform. God made man to serve those who need the service. It may be in any field or in any form. But the best form is “Voluntary Community Work” which means that the work should be done not for an individual but for all. For example, I see that the village is full of garbage. Let us together dig pits far away from the village and bury these garbage there, which will turn to manure in a couple of years’ time.

At the same time, the removal of the garbage will give a better look to the village. The second community work for our village is to make drains. Let us control the dirty water and direct it to the pits where the garbage has been buried. But this is not the work done by one or two men. Let the people realise that the best service to God is to serve His creation.

4. Write an article for your school magazine. Describing your experience about school picnic.
Answer:

SCHOOL PICNIC TO MAMALLAPURAM

– by Srinivasan

School picnics are the most awaited ones. They are with great fun. The memories of school picnics are the one to be cherished for a lifetime. This year’s picnic was destined to be at Mamallapuram which is situated around 60 km from Chennai. On the day of the picnic, we reported to the school assembly hall at 5 a.m. Since it was the last week of December, the weather was very cold. The school bus departed at sharp 5.10 a.m. in the morning. Almost one and half hour travel to the heritage town felt like a matter of few minutes. We reported to the guest house at around 6.30 a.m., we were all provided welcome drinks. Then we left for the Shore Temple.

Sunrise at Shore Temple is an unforgettable sight. Five Rathas, Cave Temple, Tiger Cave, Elephant and other creatures carved in granite, Arjuna’s Penance, Lord Krishna’s Butter Ball (a huge stone almost spherical in shape) are the important sculptures to be seen there. It was the most exciting part of the picnic. Then we had lunch, followed by some fun activities. The time had passed so soon that we couldn’t even realize the day was over. This was indeed a day I will remember for a long time.

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Speech Writing (on a given

topic)

Exercises
1. How do you prepare a speech for the morning assembly, stressing on the importance of ‘Sound mind in a sound body?
Answer:

Sound Mind In A Sound Body

Respected teachers and students,
Warm greetings to all of you.
I am here to deliver a speech on “Sound mind in a sound body”.

‘A sound mind in a sound body’ is the adage. It is true and worthy. The mind when free from pain or physical stress thinks clearly and remains active. It has the ability to march towards its goal as there are no stress psychologically and physically due to fear and illness. Active exercises, fresh air, activities like cycling, swimming and walking refresh the mind and keep it cheerful and relaxed. To overcome our stress we should play our favorite game, be it chess, cricket or any other game and remain calm and relaxed. Hence sports are an essential part of life.

Thank you for listening to my speech.

2. Prepare a speech in about 80-100 words of the morning assembly on highlighting the importance of Saving Water.
Answer:

Saving Water

Water is used by us for various purposes. Water is used for drinking. The human body depends on water for survival. Water is used for cooking food too. The water that we need for consuming must be clean, potable water. If humans use dirty or contaminated water for these purposes they can fall sick and die from the diseases. Therefore, for good health we need clean drinking water to be available for our use. Water is also needed for farming. We also use water to maintain personal hygiene. We also need water to wash our clothes, as also to keep our homes and surroundings clean.

3. Prepare a speech in about 80-100 words of the morning assembly on highlighting the importance conservation of Nature.
Answer:

Conservation Of Nature

Nature fulfills our basic requirement to live by providing us air, water, land, sunlight and plants. These resources are further used to manufacture various things that make life more convenient and comfortable for human beings. As a result, many of these resources are depleting at a fast pace and if it continues this way then the survival of human beings, as well as other living beings on Earth, would become very difficult. Conservation of nature means the preservation of forests, land, water bodies and conservation of resources such as minerals, fuels, natural gases, etc. to ensure that all these continue to be available in abundance.

4. Prepare a speech in about 80 – 100 words of the morning assembly on highlighting the importance of Saving Trees.
Answer:

Saving Trees

Respected teachers and students,
Warm greetings to all of you.
I am here to deliver a speech on “Saving Trees”.

Trees play a significant role in our daily life. Trees provide oxygen. They absorb carbon dioxide, thereby reducing the global warming. They provide food for us and also for forest animals. Trees offer habitation to birds, insects, lichen and fungi. Their trunks provide the hollow cover needed by species such as bats, wood-boring beetles, owls and woodpeckers. They benefit the environment by the way of preventing soil erosion and flooding. They reduce the speed of the wind. They act as natural air conditioners by cooling the roadsides by their shade. They are helpful for children to play in and discover their sense of adventure. They also help in protecting us from the harmful effect of ultra-violet rays. So it is our responsibility to save trees.

Thank you for listening to my speech.

5. Prepare a speech in about 80-100 words on Peacock.
Answer:

Peacock

Peacock is one of the most beautiful birds on the earth. It is particularly known for its colourful feathers that are a sight to behold. It looks best when it dances merrily in » the rain. Peacock is the national bird of India. It finds several references in the Indian mythology and history. It is known for its metallic blue and green colour and spectacular feather. These feathers are also considered auspicious and are used to bring in good luck and prosperity. Peacock has inspired many notable artists in the past and continues to do so.

6. Prepare a speech in about 80-100 words of the morning assembly on highlighting the Importance of Saving Pets.
Answer:

Saving Pets

Respected teachers and students,
Warm greetings to all of you.
I am, here to deliver a speech on “Saving Pets”.

Saving the life of a pet animal like a dog or a cat is our moral responsibility. There are so many ways in which we can save pets. A person can adopt his pet and encourage his friends and family to adopt pet. Most people don’t realize that they are unknowingly supporting the puppy mill industry when they purchase animals from pet stores or buy a puppy online. A person may talk with the owners of pet stores and ask them to feature homeless pets for adoption instead. We can add an advocacy message in the signature line of our email to help educate people about the issue.

Instead of buying pet animals, we can adopt them. We can use our social networking skills to promote adoptable animals. Most rescue groups need volunteers who can help with a variety of professional services. So as a volunteer, we can save a lot of lives. There are lots of ways to provide assistance without giving a donation. However, donations allow shelters and rescue groups to increase adoptions, promote spay/neuter, create lifesaving programs, educate the public about animal welfare issues, and much more. A person can save lives by fostering homeless animals.

Thank you for listening to my speech.