Prasanna

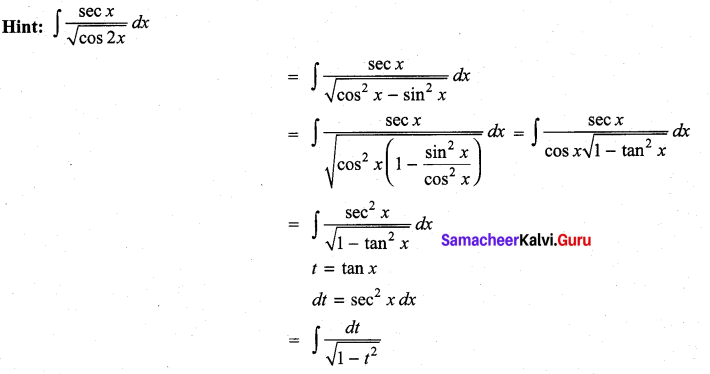
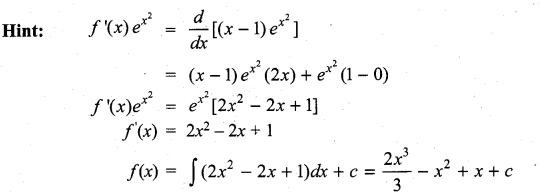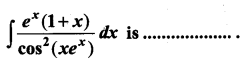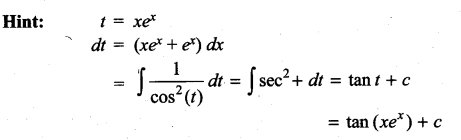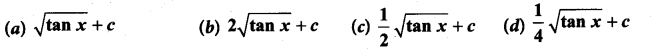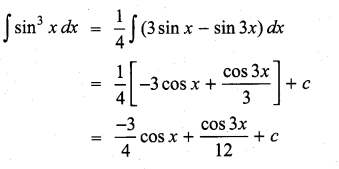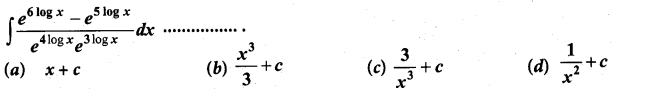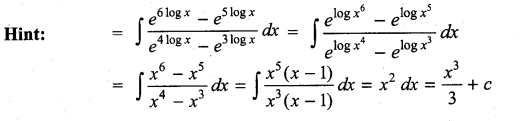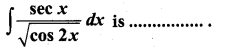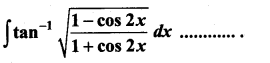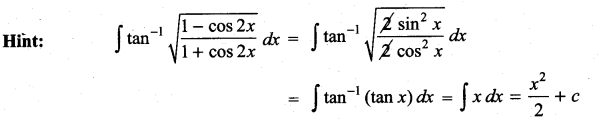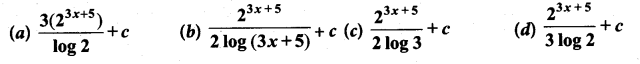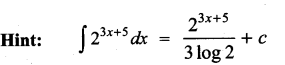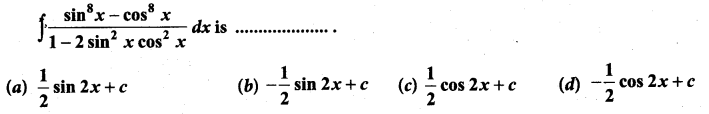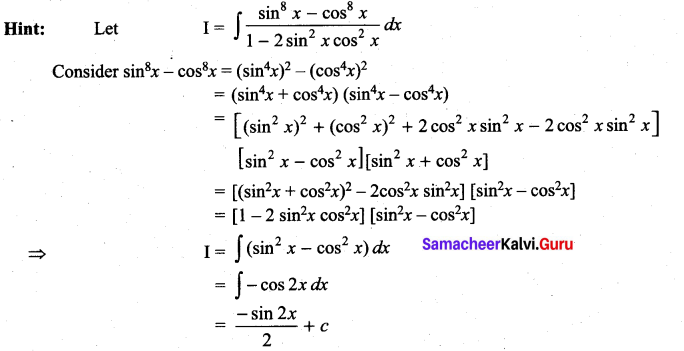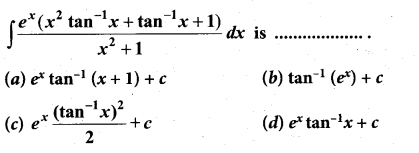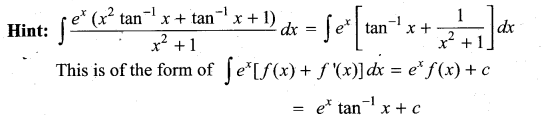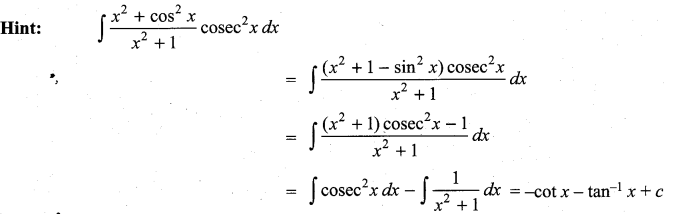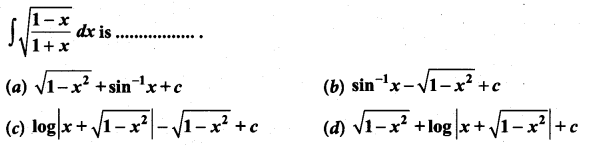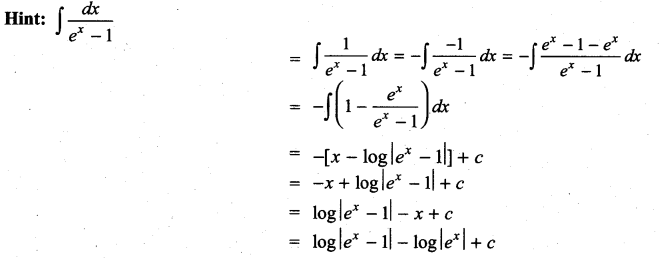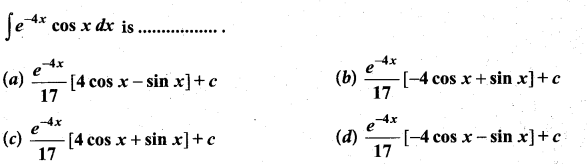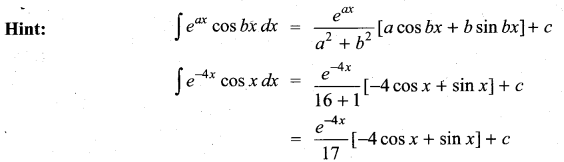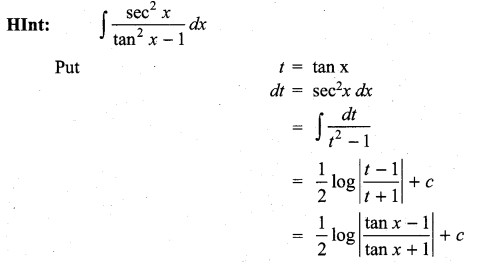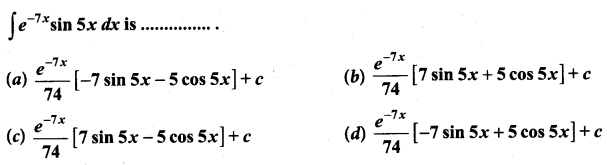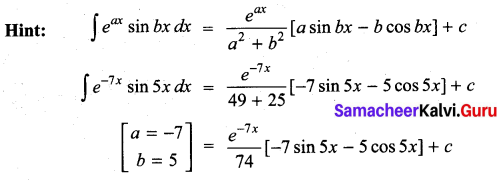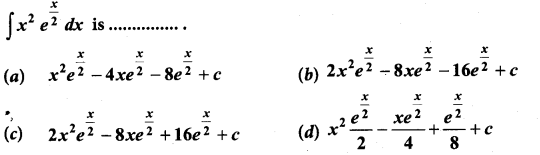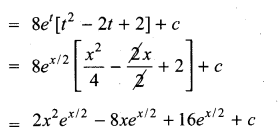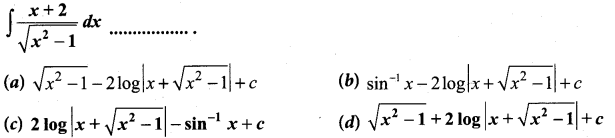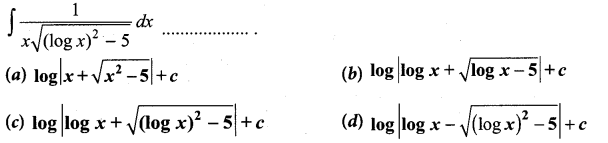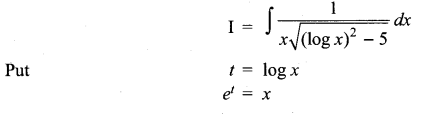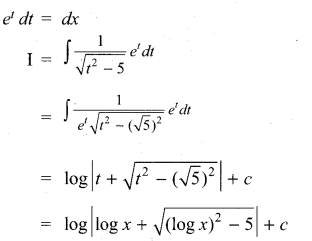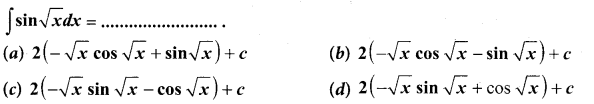Students can Download Computer Science Chapter 3 Scoping Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Computer Science Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 3 Scoping

Samacheer Kalvi 12th Computer Science Scoping Text Book Back Questions and Answers

PART – 1
I. Choose The Best Answer

Question 1.
Which of the following refers to the visibility of variables in one part of a program to another part of the same program?
(a) Scope
(b) Memory
(c) Address
(d) Accessibility
Answer:
(a) Scope

Question 2.
The process of binding a variable name with an object is called ………………………….
(a) Scope
(b) Mapping
(c) Late binding
(d) Early binding
Answer:
(b) Mapping

Question 3.
Which of the following is used in programming languages to map the variable and object?
(a) ::
(b) : =
(c) =
(d) = =
Answer:
(c) =

Question 4.
Containers for mapping names of variables to objects is called ………………………….
(a) Scope
(b) Mapping
(c) Binding
(d) Namespaces
Answer:
(d) Namespaces

Question 5.
Which scope refers to variables defined in current function?
(a) Local Scope
(b) Global scope
(c) Module scope
(d) Function Scope
Answer:
(a) Local Scope

Question 6.
The process of subdividing a computer program into separate sub – programs is called ………………………….
(a) Procedural Programming
(b) Modular programming
(c) Event Driven Programming
(d) Object oriented Programming
Answer:
(b) Modular programming

Question 7.
Which of the following security technique that regulates who canuse resources in a computing environment?
(a) Password
(b) Authentication
(c) Access control
(d) Certification
Answer:
(c) Access control

Question 8.
Which of the following members of a class can be handled only from within the class?
(a) Public members
(b) Protected members
(c) Secured members
(d) Private members
Answer:
(d) Private members

Question 9.
Which members are accessible from outside the class?
(a) Public members
(b) Protected members
(c) Secured members
(d) Private members
Answer:
(a) Public members

Question 10.
The members that are accessible from within the class and are also available to its subclasses is called ………………………….
(a) Public members
(b) Protected members
(c) Secured members
(d) Private members
Answer:
(b) Protected members

PART – II
II. Answer The Following Questions

Question 1.
What is a scope?
Answer:
Scope refers to the visibility of variables, parameters and functions in one part of a program to another part of the same program.

Question 2.
Why scope should be used for variable. State the reason?
Answer:
Essentially, variables are addresses (references, or pointers), to an object in memory. When you assign a variable with := to an instance (object), you’re binding (or mapping) the variable to that instance. Multiple variables can be mapped to the same instance.

Question 3.
What is Mapping?
Answer:
The process of binding a variable name with an object is called mapping. = (equal to sign) is used in programming languages to map the variable and object.

Question 4.
What do you mean by Namespaces?
Answer:
Programming languages keeps track of all these mappings with namespaces. Namespaces are containers for mapping names of variables to objects.

Question 5.
How Python represents the private and protected Access specifiers?
Answer:
Private members of a class are denied access from the outside of the class. They can be handled only within the class.
Protected members of a class are accessible from within the class and are also available to its sub-classes. No other process is permitted access to it.

PART – III
III. Answer The Following Questions

Question 1.
Define Local scope with an example?
Answer:
Local Scope:
Local scope refers to variables defined in current function. Always, a function will first look up for a variable name in its local scope. Only if it does not find it there, the outer scopes are checked.
Look at this example

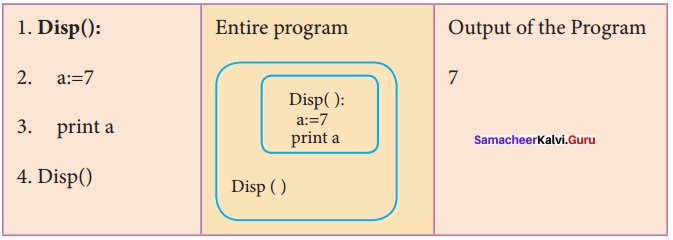
On execution of the above code the variable a displays the value 7, because it is defined and available in the local scope.

Question 2.
Define Global scope with an example?
Answer:
Global Scope:
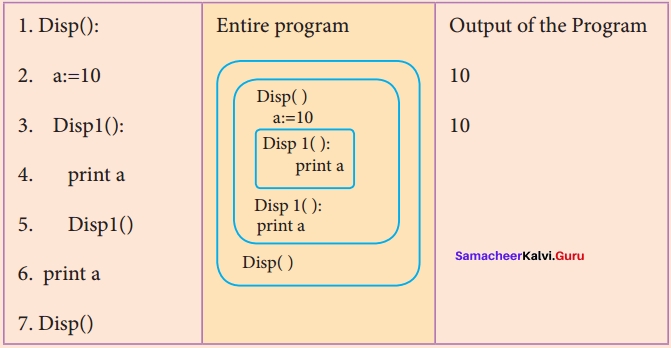
A variable which is declared outside of all the functions in a program is known as global variable. This means, global variable can be accessed inside or outside of all the functions in a program. Consider the following example

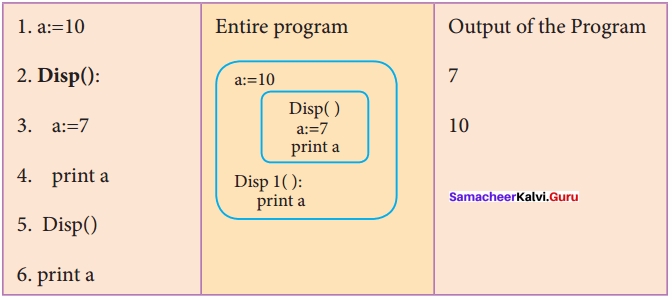
On execution of the above code the variable a which is defined inside the function displays the value 7 for the function call Disp( ) and then it displays 10, because a is defined in global scope.

Question 3.
Define Enclosed scope with an example?
Answer:
Enclosed Scope:
All programming languages permit functions to be nested. A function (method) with in another function is called nested function. A variable which is declared inside a function which contains another function definition with in it, the inner function can also access the variable of the outer function. This scope is called enclosed scope. When a compiler or interpreter search for a variable in a program, it fist search Local, and then search Enclosing scopes. Consider the following example

Question 4.
Why access control is required?
Answer:
Access control is a security technique that regulates who or what can view or use resources in a computing environment.
It is a fundamental concept in security that minimizes risk to the object. In other words access control is a selective restriction of access to data.
In Object oriented programming languages it is implemented through access modifies.
Classical object – oriented languages, such as C++ and Java, control the access to class members by public, private and protected keywords.

Question 5.
Identify the scope of the variables in the following pseudo code and write its output?
Answer:

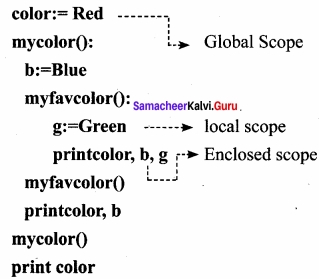
Output:
Red, blue, green
Red blue
Red

PART – IV
IV. Answer The Following Questions

Question 1.
Explain the types of scopes for variable or LEGB rule with example?
Answer:
LEGB rule
Scope also defines the order in which variables have to be mapped to the object in order to obtain the value. Let us take a simple example as shown below:

1. x: = ‘outer x variable’
2. display ( ):
3. x: = ‘inner x variable’
4. print x
5. display ( )

When the above statements are executed the statement (4) and (5) display the result as
Output
outer x variable
inner x variable
Above statements give different outputs because the same variable name x resides in different scopes, one inside the function display( ) and the other in the upper level. The value ‘outer x variable’ is printed when x is referenced outside the function definition. Whereas when display( ) gets executed, ‘inner x variable’ is printed which is the x value inside the function definition. From the above example, we can guess that there is a rule followed, in order to decide from which scope a variable has to be picked. The LEGB rule is used to decide the order in which the scopes are to be searched for scope resolution. The scopes are listed below in terms of hierarchy (highest to lowest).

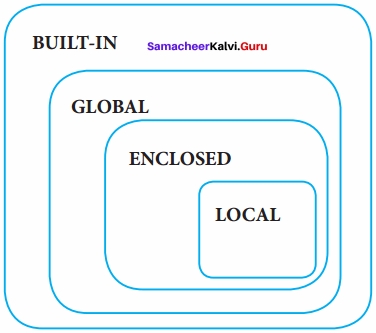
Types of Variable Scope:
There are 4 types of Variable Scope, let’s discuss them one by one:

Local Scope:
Local scope refers to variables defined in current function. Always, a function will first look up for a variable name in its local scope. Only if it does not find it there, the outer scopes are checked. Look at this example

On execution of the above code the variable a displays the value 7, because it is defined and available in the local scope.

Global Scope:
A variable which is declared outside of all the functions in a program is known as global variable. This means, global variable can be accessed inside or outside of all the functions in a program. Consider the following example

On execution of the above code the variable a which is defined inside the function displays the value 7 for the function call Disp( ) and then it displays 10, because a is defined in global scope.

Enclosed Scope:
All programming languages permit functions to be nested. A function (method) with in another function is called nested function. A variable which is declared inside a function which contains another function definition with in it, the inner function can also access the variable of the outer function. This scope is called enclosed scope. When a compiler or interpreter search for a variable in a program, it first search Local, and then search Enclosing scopes. Consider the following example

In the above example Disp1 ( ) is defined with in Disp ( ). The variable ‘a’ defined in Disp ( ) can be even used by Disp 1 ( ) because it is also a member of Disp

Built – in Scope:
Finally, we discuss about the widest scope. The built-in scope has all the names that are pre-loaded into the program scope when we start the compiler or interpreter. Any variable or module which is defined in the library functions of a programming language has Built-in or module scope. They are loaded as soon as the library files are imported to the program.

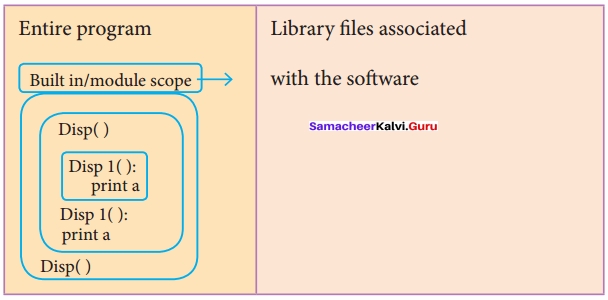
Normally only Functions or modules come along with the software, as packages. Therefore they will come under Built in scope.

Question 2.
Write any Five Characteristics of Modules?
Answer:
Characteristics of Modules:
The following are the desirable characteristics of a module.

1. Modules contain instructions, processing logic, and data.
2. Modules can be separately compiled and stored in a library.
3. Modules can be included in a program.
4. Module segments can be used by invoking a name and some parameters.
5. Module segments can be used by other modules.

Question 3.
Write any five benefits in using modular programming?
Answer:
The benefits of using modular programming include:

1. Less code to be written.
2. A single procedure can be developed for reuse, eliminating the need to retype the code many times.
3. Programs can be designed more easily because a small team deals with only a small part of the entire code.
4. Modular programming allows many programmers to collaborate on the same application.
5. The code is stored across multiple files.
6. Code is short, simple and easy to understand.
7. Errors can easily be identified, as they are localized to a subroutine or function.
8. The same code can be used in many applications.
9. The scoping of variables can easily be controlled.

Practice Programs

Question 1.
Observe the following diagram and Write the pseudo code for the following?
Answer:

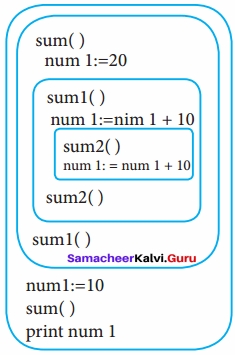
sum ( ):
num 1: = 20
sum 1 ( )
num1: = num1 + 10 sum2 ( )
num1: = num1 + 10
sum2 ( ) sum1 ( ) num1: = 10
sum ( )
Print num 1

Samacheer kalvi 12th Computer Science Scoping Additional Questions and Answers

PART -1
I. Choose The Best Answer

Question 1.
Names paces are compared with ……………………….
(a) Programs
(b) Dictionaries
(c) Books
(d) Notebooks
Answer:
(b) Dictionaries

Question 2.
Write the output (value stored in b)
1. a: = 5
2. b: = a
(a) 0
(b) 3
(c) 5
(d) 2
Answer:
(c) 5

Question 3.
Find the value of a.
1. a: = 5
2. b: = a
3. a: = 3
(a) 0
(b) 3
(c) 5
(d) 2
Answer:
(b) 3

Question 4.
The ………………………. of a variable is that part of the code where it is visible.
Answer:
Scope

Question 5.
The duration for which a variable is alive is called its ……………………………
(a) Scale
(b) Life time
(c) Static
(d) Function
Answer:
(b) Life time

Question 6.
…………………………… also defines the order in which variables have to be mapped to the object in order to obtain the value.
(a) Scope
(b) Local
(c) Event
(d) Object
Answer:
(a) Scope

Question 7.
The …………………………… rule is used to decide the order in which the scopes are to be searched for scope resolution.
Answer:
LEGB

Question 8.
How many types of variable scopes are there?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4

Question 9.
A function will first look up for a variable name in its …………………………… scope.
(a) Local
(b) Enclosed
(c) Global
(d) Built in
Answer:
(a) Local

Question 10.
A variable which is declared outside of all the functions in a program is known as …………………………… variable.
(a) L
(b) E
(c) G
(d) B
Answer:
(c) G

Question 11.
A …………………………… variable can be accessed inside or outside of all the functions in a program.
(a) Local
(b) Global
(c) Enclosed
(d) Built – in
Answer:
(b) Global

Question 12.
A function defined within another function is called …………………………… function
(a) Member
(b) Looping
(c) Nested
(d) Invariant
Answer:
(c) Nested

Question 13.
Functions are otherwise called as …………………………..
(a) Methods
(b) Attributes
(c) Class
(d) Structures
Answer:
(a) Methods

Question 14.
The scope of nested function is …………………………… scope
(a) Local
(b) Global
(c) Enclosed
(d) Built – in
Answer:
(c) Enclosed

Question 15.
When a compiler or interpreter search for a variable in a program, it first search and then search …………………………… scope
(a) L, E
(b) EG
(c) GB
(d) BL
Answer:
(a) L, E

Question 16.
Built – in scopes are called as …………………………… scope.
Answer:
Module

Question 17.
Any variable or module defined in the library functions has …………………………… scope.
Answer:
Built – in

Question 18.
Variables of built – in scopes are loaded as …………………………… files.
(a) Exe
(b) Linker
(c) Object
(d) Library
Answer:
(d) Library

Question 19.
Identify which is not a variable scope.
(a) Module
(b) Built – in
(c) Enclosed
(d) Pointer
Answer:
(d) Pointer

Question 20.
A single …………………………… can contain one or several statements closely related to each other.
Answer:
Module

Question 21.
A …………………………… is a part of a program.
(a) Code
(b) Module
(c) Flowchart
(d) System software
Answer:
(b) Module

Question 22.
Identify which is not a module?
(a) Algorithm
(b) Procedures
(c) Subroutines
(d) Functions
Answer:
(a) Algorithm

Question 23.
Find the wrong statement from the following
(a) Modules contains data and instructions
(b) Modules can be included in a program
(c) Modules cannot have processing logic
(d) Modules can be separately combined
Answer:
(c) Modules cannot have processing logic

Question 24.
Which is true about modular programming?
(a) Single procedure can be reused
(b) Single procedure cannot be reused
Answer:
(a) Single procedure can be reused

Question 25.
The arrangement of private instance variables and public methods ensures the principle of ……………………………
(a) Security
(b) Data encapsulation
(c) Inheritance
(d) Class
Answer:
(b) Data encapsulation

Question 26.
All members in a python class are by …………………………… default.
(a) Private
(b) Public
(c) Protected
(d) Local
Answer:
(b) Public

Question 27.
The members in C ++ and Java, by default are ……………………………
(a) Private
(b) Public
(c) Protected
(d) Local
Answer:
(a) Private

PART – II
II. Answer The Following Questions

Question 1.
Define life time?
Answer:
The duration for which a variable is alive is called its ‘life time’.

PART – III
III. Answer The Following Questions

Question 1.
Write the output for the pseudo code?
Answer:

1. x: = ‘outer x variable’
2. display( ):
3. x: = ‘inner x variable’
4. print x
5. display Q

Output:
outer x variable
inner x variable

Question 2.
List the scope in hierarchical order from highest to lowest?
Answer:

Question 3.
Write note on modules?
Answer:
A module is a part of a program. Programs are composed of one or more independently developed modules. A single module can contain one or several statements closely related each other. Modules work perfectly on individual level and can be integrated with other modules.

Question 4.
Write note on public members?
Answer:
Public members (generally methods declared in a class) are accessible from outside the class. The object of the same class is required to invoke a public method. This arrangement of private instance variables and public methods ensures the principle of data encapsulation.

Students can Download Computer Science Chapter 8 Strings and String Manipulations Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Computer Science Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 8 Strings and String Manipulations

Samacheer Kalvi 12th Computer Science Strings and String Manipulations Text Book Back Questions and Answers

PART – I
I. Choose The Best Answer

Question 1.
Which of the following is the output of the following python code?
Answer:
str1=”TamilNadu”
print (str1 [:: -1])
(a) Tamilnadu
(b) Tmlau
(c) UdanlimaT
(d) UdaNlimaT
Answer:
(c) UdanlimaT

Question 2.
What will be the output of the following code?
Answer:
str1= “Chennai Schools”
str1[7] = “_”
(a) Chennai – Schools
(b) Chenna – School
(c) Type error
(d) Chennai
Answer:
(c) Type error

Question 3.
Which of the following operator is used for concatenation?
(a) +
(b) &
(c) *
(d) =
Answer:
(a) +

Question 4.
Defining strings within triple quotes allows creating:
(a) Single line Strings
(b) Multiline Strings
(c) Double line Strings
(d) Multiple Strings
Answer:
(b) Multiline Strings

Question 5.
Strings in python:
(a) Changeable
(b) Mutable
(c) Immutable
(d) Flexible
Answer:
(c) Immutable

Question 6.
Which of the following is the slicing operator?
(a) { }
(b) [ ]
(c) <>
(d) ( )
Answer:
(b) [ ]

Question 7.
What is stride?
(a) Index value of slide operation
(b) First argument of slice operation
(c) Second argument of slice operation
(d) Third argument of slice operation
Answer:
(d) Third argument of slice operation

Question 8.
Which of the following formatting character is used to print exponential notation in upper case?
(a) % e
(b) % E
(c) % g
(d) % n
Answer:
(b) % E

Question 9.
Which of the following is used as placeholders or replacement fields which get replaced along with format ( ) function?
(a) { }
(b) <>
(c) ++
(d) ^^
Answer:
(a) { }

Question 10.
The subscript of a string may be:
(a) Positive
(b) Negative
(c) Both (a) and (b)
(d) Either (a) or (b)
Answer:
(d) Either (a) or (b)

PART – II
II. Answer The Following Questions

Question 1.
What is String?
Answer:
String is a data type in python, which is used to handle array of characters. String is a sequence of Unicode characters that may be a combination of letters, numbers, or special symbols enclosed within single, double or even triple quotes.
Example:
‘Welcome to learning Python’
“Welcome to learning Python”
“Welcome to learning Python”

Question 2.
Do you modify a string in Python?
Answer:
If you want to modify the string, a new string value can be assign to the existing string variable. To define a new string value to the existing string variable. Python completely overwrite new string on the existing string.
Example:
>>> str1=”How are you”
>>> print (str1)
How are you
>>> str1=”How about you”
>>> print (str1)
How about you

Question 3.
How will you delete a string in Python?
Answer:
Python will not allow deleting a particular character in a string. Whereas you can remove entire string variable using del command.
Example: Code lines to delete a string variable
>>> str1=”How about you”
>>> print (str1)
How about you
>>> del str1
>>> print (str1)
NameError: name ‘str1’ is not defined

Question 4.
What will be the output of the following python code?
Answer:
str1 = “School”
print (str1*3)
Output:
School School School

Question 5.
What is slicing?
Answer:
String slicing:
Slice is a substring of a main string. A substring can be taken from the original string by using [ ] operator and index or subscript values. Thus, [ ] is also known as slicing operator. Using slice operator, we can slice one or more substrings from a main string.

General format of slice operation:
str[start:end]
Where start is the beginning index and end is the last index value of a character in the string. Python takes the end value less than one from the actual index specified. For example, if you want to slice first 4 characters from a string, you have to specify it as 0 to 5. Because, python consider only the end value as n – 1.
Example: slice a single character from a string
>>> str1=”THIRUKKURAL”
>>> print (str1[0])
T

PART – III
III. Answer The Following Questions

Question 1.
Write a Python program to display the given pattern?
Answer:
C O M P U T E R
C O M P U T E
C O M P U T
C O M P U
C O M P
C O M
C O
C
Program:
str1 = “COMPUTER”
index = len (str1)
for i in str 1:
print (str 1[: index])
index – = 1

Question 2.
Write a short about the followings with suitable example?
Answer:

Question 3.
What will be the output of the given python program?
str1 = “welcome”
str2 = “to school”
str3 = str1[: 2] str2[len(str2)-2:]
print (str3)
output:
Answer:
weoo 1

Question 4.
What is the use of format( )? Give an example?
Answer:
The format( ) function used with strings is very versatile and powerful function used for formatting strings. The curly braces { } are used as placeholders or replacement fields which get replaced along with format( ) function.
Example:
num1 = int (input (“Number 1: “))
num2 = int (input (“Number 2: “))
print (“The sum of { } and { } is { }”.format (num1, num2,(num1 + num2)))
OutPut:
Number 1 : 34
Number 2 : 54
The sum of 34 and 54 is 88.

Question 5.
Write a note about count ( ) function in python?
Answer:

PART – IV
IV. Answer The Following Questions.

Question 1.
Explain about string operators in python with suitable example?
Answer:
String Operators:
Python provides the following operators for string operations. These operators are useful to manipulate string.

(i) Concatenation (+):
Joining of two or more strings is called as Concatenation. The plus (+) operator is used to concatenate strings in python.
Example:
>>> “welcome” + “Python”
‘welcomePython’

(ii) Append (+=):
Adding more strings at the end of an existing string is known as append. The operator += is used to append a new string with an existing string.
Example:
>>> str1 =”Welcome to ”
>>> str1+=”Leam Python”
>>> print (str1)
Welcome to Learn Python

(iii) Repeating (*):
The multiplication operator (*) is used to display a string in multiple number of times.
Example:
>>> str1 =”Welcome”
>>> print (str1*4)
Welcome Welcome Welcome Welcome

(iv) String slicing:
Slice is a substring of a main string. A substring can be taken from the original string by using [ ] operator and index or subscript values. Thus, [ ] is also known as slicing operator. Using slice operator, you have to slice one or more substrings from a main string.
General format of slice operation:
str[start: end]
Where start is the beginning index and end is the last index value of a character in the string. Python takes the end value less than one from the actual index specified. For example, if you want to slice first 4 characters from a string, you have to specify it as 0 to 5. Because, python consider only the end value as n – 1.
Example:
(i) slice a single character from a string
>>> str1=”THIRUKKURAL ”
>>> print (str1 [0])
T .

(v) Stride when slicing string
When the slicing operation, you can specify a third argument as the stride, which refers to the number of characters to move forward after the first character is retrieved from the string. The default value of stride is 1.
Example:
>>> str1= “Welcome to learn Python”
>>> print (str1 [10:16])
learn
Note: Remember that, python takes the last value as n – 1
You can also use negative value as stride (third argument). If you specify a negative value, it prints in reverse order.
Example:
>>> str1 = “Welcome to learn Python”
>>> print(str1 [::-2])
nhy re teoIW

Practice Programs

Question 1.
Write a python program to find the length of a string?
Answer:
str=input (“Enter a string: “)
print (len(str))
Output:
Enter a string: HELLO
5

Question 2.
Write a program to count the occurrences of each word in a given string?
Answer:
def word_count(str):
counts = dict ( )
words = str.split ( ) for word in words:
if word in counts:
counts[word] +=1
else:
counts[word]=1
return counts
print (word_count (‘the quick brown fox jumps over the lazy dog.’))
Ouput:
{‘the’: 2, ‘jumps’: 1, ‘brown’: 1, ‘lazy’: 1, ‘fox’: 1, ‘over’: 1, ‘quick’: 1, ‘dog’: 1}

Question 3.
Write a program to add a prefix text to all the lines in a string?
Answer:
import
text =
“‘Strings are immutable. Slice is a
substring of a main string. Stride
is a third argument in slicing operation'”
text_without_lndentation= textwrap.dedent (text)
wrapped = extwrap.fill (text_without_Indentation, width = 50)
print (textwrap.indent(wrapped, ‘*’)
print ()
Output:

• Strings are immutable. Slice is a
• substring of a main string. Stride
• is a third argument in slicing operation

Question 4.
Write a program to print integers with ‘*’ on the right of specified width?
Answer:
x = 1 2 3
print (“original number: “, x)
print (“formatted number(right padding, width 6): “+” {: * < 7 d}”.format(x));
Output:
original number : 1 2 3
formatted number (right padding, width 6): 1 2 3 ***

Question 5.
Write a program to create a mirror of the given string. For example, “wel” = “lew“?
Answer:
str1 = input (“Enter a string: “)
str2 = ‘ ‘
index= -1
for i in str1:
str2 += str1 [index]
index -= 1
print (“The given string = { } \n The Reversed string = { }”.format(str 1, str 2))
Output:
Enter a string: welcome
The given string = welcome
The Reversed string = emoclew

Question 6.
Write a program to removes all the occurrences of a given character in a string?
Answer:
def removechar(s,c):
# find total no of occurrence of a character
counts = s.count(c)
# convert into list of characters
s = list(s)
# keep looping until counts become 0
while counts:
# remove char, from list
s.remove(c)
counts -= 1
# join remaining characters s = ” .join(s)
print(s)
s = “python programming”‘
remove char(s, ‘p’)
Output:
ython rogramming

Question 7.
Write a program to append a string to another string without using + = operator?
Answer:
s1 = input (“Enter the first string: “)
s2 = input (“Enter the second string: “)
print (‘concatenated strings =’,” ” ,join ([s1, s2]))
Output:
Enter the first string: Tamil
Enter the second string: Nadu
concatenated strings = Tamil Nadu

Question 8.
Write a program to swap two strings?
Answer:
print (“Enter Y for exit.”)
string1 = input(“Enter first string: “)
if string1 = = ‘x’:
exit();
else:
string2 = input (“Enter second string : “)
print (” \n Both strings before swap : “)
print (“First string = “, string1)
print (” Second string = “, string2)
temp = string1
string1 = string2
string2 = temp
print (“\n Both strings after swap: “)
print (“First string = “, string1)
print (” Second string = “, string2)
Output:
Enter ‘x’ for exit
Enter first string: code
Enter second string: python
Both strings before swap:
First string = code
Second string = python
Both strings after swap:
First string = python
Second string = code

Question 9.
Write a program to replace a string with another string without using replace ( )?
Answer:
s1 = input (“Enter the string to be replaced: “)
s2 = input (“Enter the string to replace with “)
s1 = s2
print (“Replaced string is “, s1)
Output:
Enter the string to be replaced: Computer
Enter the string to replace with: repcomputer
Replaced string is repcomputer

Question 10.
Write a program to count the number of characters, words and lines in a given string?
Answer:
string = input (“Enter string:”)
char = 0
word = 0
line = 0
for i in string:
char = char + 1
if (i = = “):
word = word + 1
elif (i = = ‘ \n’):
line = line +1
print (“Number of words in the string: “)
print (word)
print (“Number of characters in the string: “)
print (char)
print (“Number of lines in the string: “)
print (line)
Output:
Enter string: welcome to learning python
Number of words in the string : 4
Number of characters in the string : 26
Number of lines in the string : 1

Samacheer kalvi 12th Computer Science Strings and String Manipulations Additional Questions and Answers

PART – 1
I. Choose The Correct Answer

Question 1.
Strings in python can be created using ………………………….. quotes
(a) Single
(b) Double
(c) Triple
(d) All the above
Answer:
(d) All the above

Question 2.
Strings which contains double quotes should be defined with …………………….. quotes
(a) Single
(b) Double
(c) Triple
(d) All the these
Answer:
(c) Triple

Question 3.
The positive subscript of the string starts from ………………………….. and ends with …………………………
Answer:
0, n – 1

Question 4.
In strings, the negative index assigned from the last character to the first character in reverse order begins with …………………………
(a) 0
(b) 1
(c) -1
(d) -2
Answer:
(c) -1

Question 5.
How will you modify the string?
(a) A new string value can be assigned to the existing string variable
(b) Updating the string character by character
Answer:
(a) A new string value can be assigned to the existing string variable

Question 6.
Which function is used to change all occurrences of a particular character in a string?
(a) Replace ( )
(b) Change ( )
(c) Edit ( )
(d) Append ( )
Answer:
(a) Replace ( )

Question 7.
Which command is used to remove the entire string variable?
(a) Remove
(b) Del
(c) Delete
(d) Strike
Answer:
(b) Del

Question 8.
Joining of two or more strings is called as …………………………..
(a) Append
(b) Repeating
(c) Concatenation
(d) Strike
Answer:
(c) Concatenation

Question 9.
Adding more strings at the end of an existing strings is ………………………….
(a) Append
(b) Concatenation
(c) Repeating
(d) Slicing
Answer:
(a) Append

Question 10.
Find the wrongly matched pair from the following.
(a) Append ⇒ + =
(b) Concate ⇒ +
(c) Repeat ⇒ /
(d) Slice ⇒ [ ]
Answer:
(c) Repeat ⇒ /

Question 11.
Which operator is used to append a new string with an existing string?
(a) +
(b) + =
(c) *
(d) * =
Answer:
(b) + =

Question 12.
The multiplication operator is also called as ………………………….
(a) Append
(b) Concatenate
(c) Repeat
(d) Slice
Answer:
(c) Repeat

Question 13.
Which is used to display a string multiple number of times?
(a) Repeating
(b) *
(c) Multiplication operator
(d) All the above
Answer:
(d) All the above

Question 14.
…………………………. is a substring of a main string.
Answer:
Slice

Question 15.
In python, end value is considered as ……………………….
(a) 0
(b) n
(c) n – 1
(d) 1
Answer:
(c) n – 1

Question 16.
Find the wrong statement from the following.
(I) Slice a single character from a string
(II) Slice a substring
(III) Slice a substring without specifying beginning index
(IV) Slice a substring without specifying end index

(a) (I), (II)
(b) (II), (III), (IV)
(c) All are wrong
(d) All are correct
Answer:
(d) All are correct

Question 17.
The default value of stride is …………………………
(a) 0
(b) 1
(c) n
(d) n – 1
Answer:
(b) 1

Question 18.
If the stride is negative, then it will prints
(a) Third character
(b) Third word
(c) Full string
(d) Reverse order
Answer:
(d) Reverse order

Question 19.
…………………………. is the formatting character for signed decimal integer.
(a) %d or %i
(b) %d and %i
(c) %d %u
(d) %i &u
Answer:
(a) %d or %i

Question 20.
…………………….. is the formatting character for short numbers in floating point or exponential notation.
Answer:
% g or % G

Question 21.
Escape sequences starts with a ………………………..
Answer:
Back Slash

Question 22.
Find the wrong match
(a) Backslash – \b
(b) Backslash – //
(c) Carriage return – \r
(d) Line feed – \n
Answer:
(b) Backslash – //

Question 23.
Which function returns the length of the string?
(a) str len( )
(b) len(str)
(c) length( )
(d) strlength( )
Answer:
(b) len(str)

Question 24.
The function isalnum( ) returns ………………………. when it contains special characters.
Answer:
False

Question 25.
How many membership operators are there?
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(a) 2

Question 26.
……………………. is the membership operator.
(a) is
(b) at
(c) to
(d) in
Answer:
(d) in

Question 27.
……………………. function is a powerful function used for formatting strings.
Answer:
Format ( )

Question 28.
The ……………………. and ………………………. operators can be used with strings to determine whether a string is present another string.
Answer:
In, Not in

PART – II
II. Answer The Following Questions

Question 1.
Fill the Table with appropriate values.
Answer:

Question 2.
Find the output?
Answer:
Program
str1 = ‘ * ‘
i=1
while i<=5: print (str1*i)
i+=1
Output
*
* *
* * *
* * * *
* * * * *

PART – III
III. Answer The Following Question

Question 1.
Write note on replace function?
Answer:
The replace function replaces all occurrences of char 1 with char 2.
Example
>>> str1 =”How are you”
>>> print (str1)
How are you
>>>print (str1.replace(“o”, “e”))
Hew are yeu

Question 2.
Write note on Append Operator?
Answer:
Append (+ =)
Adding more strings at the end of an existing string is known as append. The operator + = is used to append a new string with an existing string.
Example:
>>> str1=’Welcome to ”
>>> str1+=”Leam Python”
>>> print (str1)
Welcome to Learn Python

Question 3.
Give any 6 formatting characters with their usage?
Formatting characters
Answer:

Question 4.
Write any 6 escape sequences with their description?
Answer:

PART – IV
IV. Answer The Following Questions

Question 1.
Explain any 10 Built-in string functions?
Answer:
Built – in String functions
Python supports the following built – in functions to manipulate string.

Students can Download Computer Science Chapter 2 Data Abstraction Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Computer Science Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 2 Data Abstraction

Samacheer Kalvi 12th Computer Science Data Abstraction Text Book Back Questions and Answers

PART – I
I. Choose The Best Answer

Question 1.
Which of the following functions that build the abstract data type?
(a) Constructors
(b) Destructors
(c) Recursive
(d) Nested
Answer:
(a) Constructors

Question 2.
Which of the following functions that retrieve information from the data type?
(a) Constructors
(b) Selectors
(c) Recursive
(d) Nested
Answer:
(b) Selectors

Question 3.
The data structure which is a mutable ordered sequence of elements is called ………………………
(a) Built in
(b) List
(c) Tuple
(d) Derived data
Answer:
(b) List

Question 4.
A sequence of immutable objects is called ………………………
(a) Built in
(b) List
(c) Tuple
(d) Derived data
Answer:
(c) Tuple

Question 5.
The data type whose representation is known are called ………………………
(a) Built in data type
(b) Derived data type
(c) Concrete data type
(d) Abstract data type
Answer:
(c) Concrete data type

Question 6.
The data type whose representation is unknown are called ………………………
(a) Built in data type
(b) Derived data type
(c) Concrete data type
(d) Abstract datatype
Answer:
(d) Abstract datatype

Question 7.
Which of the following is a compound structure?
(a) Pair
(b) Triplet
(c) Single
(d) Quadrat
Answer:
(a) Pair

Question 8.
Bundling two values together into one can be considered as ………………………
(a) Pair
(b) Triplet
(c) Single
(d) Quadrant
Answer:
(a) Pair

Question 9.
Which of the following allow to name the various parts of a multi – item object?
(a) Tuples
(b) Lists
(c) Classes
(d) quadrats
Answer:
(c) Classes

Question 10.
Which of the following is constructed by placing expressions within square brackets?
(a) Tuples
(b) Lists
(c) Classes
(d) Quadrats
Answer:
(b) Lists

PART – II
II. Answer The Following Questions

Question 1.
What is abstract data type?
Answer:
Abstract Data type (ADT) is a type (or class) for objects whose behavior is defined by a set of value and a set of operations. The definition of ADT only mentions what operations are to be performed but not how these operations will be implemented.

Question 2.
Differentiate constructors and selectors?
Answer:
Constructors are functions that build the abstract data type. Selectors are functions that retrieve information from the data type.
To create a city object, you’d use a function like
city = makecity (name, lat, Ion)
To extract the information of a city object, you would use functions like
getname (city)

Question 3.
What is a Pair? Give an example?
Answer:
Pair is a compound structure which is made up of list or Tuple.
lst[(0, 10), (1, 20)] -where

Any way of bundling two values together into one can be considered as a pair. Lists are a common method to do so. Therefore List can be called as Pairs.

Question 4.
What is a List? Give an example?
Answer:
List is constructed by placing expressions within square brackets separated by commas. Example for List is [10, 20].

Question 5.
What is a Tuple? Give an example?
Answer:
A tuple is a comma-separated sequence of values surrounded with parentheses. Tuple is similar to a list. The difference between the two is that you cannot change the elements of a tuple once it is assigned whereas in a list, elements can be changed.
Example colour = (‘red’, ‘blue’, ‘Green’)

PART – III
III. Answer The Following Questions

Question 1.
Differentiate Concrete data type and abstract datatype?
Answer:
Concrete data type:

1. A concrete data type is a data type whose representation is known.
2. Concrete data types or structures (CDT’s) are direct implementations of a relatively simple concept.

Abstract data type:

1. Abstract data type the representation of a data type is unknown.
2. Abstract Data Types (ADT’s) offer a high level view (and use) of a concept independent of its implementation.

Question 2.
Which strategy is used for program designing? Define that Strategy?
Answer:
We are using here a powerful strategy for designing programs: ‘wishful thinking’.
Wishful Thinking is the formation of beliefs and making decisions according to what might be pleasing to imagine instead of by . appealing to reality.

Question 3.
Identify Which of the following are constructors and selectors?
Answer:
(a) N1 = number ( ) – constructors
(b) Accetnum (n1) – selectors
(c) Displaynum (n1) – selectors
(d) eval (a/b) – selectors
(e) x, y = makeslope(m), makeslope (n) – constructors
(f) display O – selectors

Question 4.
What are the different ways to access the elements of a list. Give example?
Answer:
List is constructed by placing expressions within square brackets separated by commas. Example for List is [10, 20].
The elements of a list can be accessed in two ways. The first way is via our familiar method of multiple assignment, which unpacks a list into its elements and binds each element to a different name.
1st: = [10, 20]
x, y: = 1st
In the above example x will become 10 and y will become 20.
A second method for accessing the elements in a list is by the element selection operator, also expressed using square brackets. Unlike a list literal, a square – brackets expression directly following another expression does not evaluate to a list value, but instead selects an element from the value of the preceding expression.
1st [0]
10
1st [1]
20

Question 5.
Identify Which of the following are List, Tuple and class?
(a) arr [1, 2, 34]
(b) arr (1, 2, 34)
(c) student [rno, name, mark]
(d) day = (‘sun’, ‘mon’, ‘tue’, ‘wed’)
(e) x= [2, 5, 6.5, [5,6], 8.2]
(f) employee [eno, ename, esal, eaddress]
Answer:
List: (a) arr [1, 2, 34]
(e) x= [2, 5, 6.5, [5,6], 8.2]
Tuple: (b) arr (1, 2, 34)
(d) day = (‘sun’, ‘mon’, ‘tue’, ‘wed’)
Class: (c) student [mo, name, mark]
(f) employee [eno, ename, esal, eaddress]

PART – IV
IV. Answer The Following Questions

Question 1.
How will you facilitate data abstraction. Explain it with suitable example?
Answer:
The definition of ADT only mentions what operations are to be performed but not how these operations will be implemented. It does not specify how data will be organized in memory and what algorithms will be used for implementing the operations. It is called “abstract” because it gives an implementation independent view. The process of providing only the essentials and hiding the details is known as abstraction.
To facilitate data abstraction, you will need to create two types of functions.

constructors and selectors:
Constructors are functions that build the abstract data type. Selectors are functions that retrieve information from the data type.
To create a city object, you’d use a function like city = makecity (name, lat, Ion)
To extract the information of a city object, you would use functions like

1. getname(city)
2. getlat(city)
3. getlon(city)

In the above pseudo code the function which creates the object of the city is the constructor, city = makecity (name, lat, Ion)
Here makecity (name, lat, Ion) is the constructor which creates the object city.

Selectors are nothing but the functions that retrieve information from the data type. Therefore in the above code

1. getname(city)
2. getlat(city)
3. getlon(city)

are the selectors because these functions extract the information of the city object.

Data abstraction is supported by defining an abstract data type (ADT), which is a collection of constructors and selectors. Constructors create an object, bundling together different pieces of information, while selectors extract individual pieces of information from the object.

Question 2.
What is a List? Why List can be called as Pairs. Explain with suitable example?
Answer:
List is constructed by placing expressions within square brackets separated by commas. Example for List is [10, 20],
The elements of a list can be accessed in two ways. The first way is via our familiar method of multiple assignment, which unpacks a list into its elements and binds each element to a different name.
1st: = [10, 20]
x, y: = 1st
In the above example x will become 10 and y will become 20.
A second method for accessing the elements in a list is by the element selection operator, also expressed using square brackets. Unlike a list literal, a square – brackets expression directly following another expression does not evaluate to a list value, but instead selects an element from the value of the preceding expression.
1st [0]
10
1st [1]
20
In both the example mentioned above mathematically we can represent list similar to a set.
1st [(0, 10), (1, 20)] – where

Any way of bundling two values together into one can be considered as a pair. Lists are a common method to do so. Therefore List can be called as Pairs.

Question 3.
How will you access the multi – item. Explain with example?
Answer:
List allow data abstraction in that you can give a name to a set of memory cells. For instance, in the game Mastermind, you must keep track of a list of four colors that the player guesses. Instead of using four separate variables (color 1, color2, color3, and color4) you can use a single variable ‘Predict’, e.g.,
Predict = [‘red’, ‘blue’, ‘green’, ’green’]
What lists do not allow us to do is name the various parts of a multi- item object. In the case of a Predict, you don’t really need to name the parts:
using an index to get to each color suffices.
But in the case of something more complex, like a person, we have a multi – item object where each ‘item’ is a named thing: the firstName, the last Name, the id, and the email. One could use a list to represent a person.

Person = [‘Padmashri’, ‘Baskar’, ‘994 – 222 – 1234’, ‘[email protected]’]
but such a representation doesn’t explicitly specify what each part represents.
For this problem instead of using a list, you can use the structure constmct (In OOP languages it’s called class construct) to represent multi-part objects where each part is named (given a name). Consider the following pseudo code:
class Person:
creation( )
firstName: = “”
lastName: = ” ”
id: = ” ”
email : = “”
The new data type Person is pictorially represented as

The class (structure) constmct defines the form for multi – part objects that represent a person. Its defintion adds a new data type, in this case a type named Person. Once defined, we can create new variables (instances) of the type. In this example Person is referred to as a class or a type, while p1 is referred to as an object or an instance. You can think of class Person as a cookie cutter, and p1 as a particular cookie. Using the cookie cutter you can make many cookies. Same way using class you can create many objects of that type.

Samacheer kalvi 12th Computer Science Data Abstraction Additional Questions and Answers

PART – 1
I. Choose The Best Answer

Question 1.
How many types of functions are needed to facilitate abstraction?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2

Question 2.
ADT stands for …………………………..
(a) Advanced Data Typing
(b) Application Developing Tool
(c) Abstract data types
(d) Advanced data types
Answer:
(c) Abstract data types

Question 3.
The Splitting of program into many modules are called as ……………………………
(a) Modularity
(b) Structures
(c) Classes
(d) List
Answer:
(a) Modularity

Question 4.
……………………………. are the representation for ADT.
(a) List
(b) Classes
(c) Int
(d) Float
Answer:
(b) Classes

Question 5.
Linked list are of …………………………..
(a) Single
(b) Double
(c) Multiple
(d) Both a and b
Answer:
(d) Both a and b

Question 6.
The process of providing only the essentials and hiding the details is known as …………………………..
(a) Modularity
(b) Structure
(c) Tuple
(d) Abstraction
Answer:
(d) Abstraction

Question 7.
Identify the constructor from the following
(a) City = makecity(name, lat, lon)
(b) getname(city)
(c) getlat(city)
(d) getlon(city)
Answer:
(a) City = makecity(name, lat, lon)

Question 8.
: = is called as …………………………..
(a) Assigned as
(b) Becomes
(c) Both a and b
(d) None of these
Answer:
(c) Both a and b

Question 9.
In list 1st [(0, 10), (1, 20)] – 0 and 1 represents …………………………..
(a) Value
(b) Index
(c) List identifier
(d) Tuple
Answer:
(b) Index

Question 10.
How many ways of representing pair data type are there?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2

Question 11.
nums [1] represent that you are accessing ………………………….. element.
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(b) 1

Question 12.
nums [1] indicate that we are accessing ………………………….. element.
(a) 0
(b) 1
(c) 2
(d) many
Answer:
(c) 2

Question 13.
How many objects can be created from a class?
(a) 0
(b) 1
(c) 2
(d) many
Answer:
(d) many

PART – II
II. Answer The Following Questions

Question 1.
What are the two parts of a program?
Answer:
The two parts of a program are, the part that operates on abstract data and the part that defines a concrete representation.

Question 2.
Give the pseudo code to represent a rational number as a pair of two integers?
Answer:
You can now represent a rational number as a pair of two integers in pseudo code: a numerator and a denominator.
rational (n, d):
return [n, d]
numer (x):
return x [0]
denom (x):
return x [1]

Question 3.
What are the two ways of representing the pair data type?
Answer:
Two ways of representing the pair data type. The first way is using List construct and the second way to implement pairs is with the tuple construct.

Question 4.
Differentiate tuple and list?
List:
In List square bracket is used.

Tuple:
In Tuple parenthesis is used.

Question 5.
Give an example for representation of Tuple as a pair?
Answer:
Representation of Tuple as a Pair
nums : = (1, 2)
nums [0]
1
nums [1]
2

Question 6.
Define class?
Answer:
A class as bundled data and the functions that work on that data.

PART – III
III. Answer The Following Questions

Question 1.
Give the pseudo code to compute the distance between two city objects?
Answer:
The following pseudo code will compute the distance between two city objects:
distance(city 1, city2):
1t1, 1g1: = getlat (city1), getlon (city1)
1t2, 1g2: = getlat (city2), getlon (city2)
return ((1t1 – 1t2) ** 2 + (1g1 – 1g2) ** 2)^1/2

Students can Download Computer Science Chapter 1 Function Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Computer Science Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Computer Science Solutions Chapter 1 Function

Samacheer Kalvi 12th Computer Science Function Text Book Back Questions and Answers

PART – 1
I. Choose The Best Answer

Question 1.
The small sections of code that are used to perform a particular task is called ……………………….
(a) Subroutines
(b) Files
(c) Pseudo code
(d) Modules
Answer:
(a) Subroutines

Question 2.
Which of the following is a unit of code that is often defined within a greater code structure?
(a) Subroutines
(b) Function
(c) Files
(d) Modules
Answer:
(b) Function

Question 3.
Which of the following is a distinct syntactic block?
(a) Subroutines
(b) Function
(c) Definition
(d) Modules
Answer:
(c) Definition

Question 4.
The variables in a function definition are called as ……………………….
(a) Subroutines
(b) Function
(c) Definition
(d) Parameters
Answer:
(d) Parameters

Question 5.
The values which are passed to a function definition are called ……………………….
(a) Arguments
(b) Subroutines
(c) Function
(d) Definition
Answer:
(a) Arguments

Question 6.
Which of the following are mandatory to write the type annotations in the function definition?
(a) Curly braces
(b) Parentheses
(c) Square brackets
(d) Indentations
Answer:
(b) Parentheses

Question 7.
Which of the following defines what an object can do?
(a) Operating System
(b) Compiler
(c) Interface
(d) Interpreter
Answer:
(c) Interface

Question 8.
Which of the following carries out the instructions defined in the interface?
(a) Operating System
(b) Compiler
(c) Implementation
(d) Interpreter
Answer:
(c) Implementation

Question 9.
The functions which will give exact result when same arguments are passed are called ……………………….
(a) Impure functions
(b) Partial Functions
(c) Dynamic Functions
(d) Pure functions
Answer:
(d) Pure functions

Question 10.
The functions which cause side effects to the arguments passed are called ……………………….
(a) Impure functions
(b) Partial Functions
(c) Dynamic Functions
(d) Pure functions
Answer:
(a) Impure functions

PART – II
II. Answer The Following Questions

Question 1.
What is a subroutine?
Answer:
Subroutines are the basic building blocks of computer programs. Subroutines are small sections of code that are used to perform a particular task that can be used repeatedly. In Programming languages these subroutines are called as Functions.

Question 2.
Define Function with respect to Programming language?
Answer:
A function is a unit of code that is often defined within a greater code structure. Specifically, a function contains a set of code that works on many kinds of inputs, like variants, expressions and produces a concrete output.

Question 3.
Write the inference you get from X: = (78)?
Answer:
Value 78 being bound to the name X.

Question 4.
Differentiate interface and implementation?
Answer:
Interface:
Interface just defines what an object can do, but won’t actually do it.

Implementation:
Implementation carries out the instructions defined in the interface.

Question 5.
Which of the following is a normal function definition and which is recursive function definition?
Answer:
(I) Let Recursive sum x y:
return x + y

(II) let disp:
print ‘welcome’

(III) let Recursive sum num:
if (num! = 0) then return num + sum (num – 1) else
return num

1. Recursive function
2. Normal function
3. Recursive function

PART – III
III. Answer The Following Questions

Question 1.
Mention the characteristics of Interface?
Answer:
Characteristics of interface:

1. The class template specifies the interfaces to enable an object to be created and operated properly.
2. An object’s attributes and behaviour is controlled by sending functions to the object.

Question 2.
Why strlen is called pure function?
Answer:
strlen (s) is called each time and strlen needs to iterate over the whole of ‘s’. If the compiler is smart enough to work out that strlen is a pure function and that ‘s’ is not updated in the lbop, then it can remove the redundant extra calls to strlen and make the loop to execute only one time. This function reads external memory but does not change it, and the value returned derives from the external memory accessed.

Question 3.
What is the side effect of impure function. Give example?
Answer:
Impure Function:

• The return value of the impure functions does not solely depend on its arguments passed. Hence, if you call the impure functions with the same set of arguments, you might get the different return values. For example, random( ), Date( ).
• They may modify the arguments which are passed to them.

Question 4.
Differentiate pure and impure function?
Answer:
Pure Function:

1. The return value of the pure functions solely depends on its arguments passed.
2. If you call the pure functions with the same set of arguments, you will always get the same return values.
3. They do not have any side effects.
4. They do not modify the arguments which are passed to them.

Impure Function:

1. The return value of the impure functions does not solely depend on its arguments passed.
2. If you call the impure functions with the same set of arguments, you might get the different return values. For example, random( ), Date( ).
3. They have side effects.
4. They may modify the arguments which are passed to them.

Question 5.
What happens if you modify a variable outside the function? Give an example?
Answer:
When a function depends on variables or functions outside of its definition block, you can never be sure that the function will behave the same every time it’s called.
For example let y: = 0
(int) inc (int) x
y: = y + x;
return (y)
In the above example the value of y get changed inside the function defintion due to which the result will change each time. The side effect of the inc ( ) function is it is changing the data ‘ of the external visible variable ‘y’.

PART – IV
IV. Answer The Following Questions

Question 1.
What are called Parameters and write a note on?
Answer:

1. Parameter without Type
2. Parameter with Type Parameters (and arguments)

Parameters are the variables in a function definition and arguments are the values which are passed to a function definition.

(I) Parameter without Type
Let us see an example of a function definition:
(requires: b> = 0)
(returns: a to the power of b)
let rec pow a b: =
if b = 0 then 1
else a * pow a (b – 1)
In the above function definition variable ‘b’ is the parameter and the value which is passed to the variable ‘b’ is the argument. The precondition (requires) and postcondition (returns) of the function is given. Note we have not mentioned any types: (data types). Some language compiler solves this type (data type) inference problem algorithmically, but some require the type to be mentioned.

In the above function definition if expression can return 1 in the then branch, by the typing rule the entire if expression has type int. Since the if expression has type ‘int ’, the function’s return type also be ‘inf. ‘b ’is compared to 0 with the equality operator, so ‘b ’is also a type of ‘int. Since a is multiplied with another expression using the * operator, ‘a’ must be an int.

(II) Parameter with Type
Now let us write the same function definition with types for some reason:
(requires: b > 0)
(returns: a to the power of b)
let rec pow (a: int) (b: int): int : =
if b = 0 then 1
else a * pow b (a – 1)
When we write the type annotations for ‘a ’ and ‘b ’ the parentheses are mandatory. Generally we can leave out these annotations, because it’s simpler to let the compiler infer them. There are times we may want to explicitly write down types. This is useful on times when you get a type error from the compiler that doesn’t make sense. Explicitly annotating the types can help with debugging such an error message.

The syntax to define functions is close to the mathematical usage: the definition is introduced by the keyword let, followed by the name of the function and its arguments; then the formula that computes the image of the argument is written after an = sign. If you want to define a recursive function: use “let rec ” instead of “let
Syntax: The syntax for function definitions:

let rec fnal a2 … an : = k
Here the fn is a variable indicating an identifier being used as a function name. The names ‘al ’ to ‘an ’ are variables indicating the identifiers used as parameters. The keyword ‘rec ’ is required if fn ’ is to be a recursive function; otherwise it may be omitted.
For example: let us see an example to check whether the entered number is even or odd.
(requires: x> = 0)
let rec even x : = x = 0 || odd (x – 1)
return ‘even’
(requires: x> = 0)
let odd x : =
x< >0 && even (x – 1)
return ‘odd’
The syntax for function types:
x → y
x₁ → x₂ → y
x₁ → … → x_n → y
The ‘x’ and ‘y’ are variables indicating types. The type x → y is the type of a function that gets an input of type ‘x’ and returns an output of type ‘y’. Whereas x₁ → x₂ → y is a type of a function that takes two inputs, the first input is of type ‘x1 ’ and the second input of type ‘x2’, and returns an output of type ‘y’. Likewise x1 → … → xn → y has type ‘x’ as input of n arguments and ‘y’ type as output.

Question 2.
Identify in the following program
Answer:
let rec gcd a b : =
if b < > 0 then gcd b (a mod b) else return a
(I) Name of the function
gcd

(II) Identify the statement which tells it is a recursive function
let rec

(III) Name of the argument variable
a, b

(IV) Statement which invoke the function recursively
gcd b(a mod b) [when b < > 0]

(V) Statement which terminates the recursion
return a (when b becomes 0).

Question 3.
Explain with example Pure and impure functions?
Answer:
Pure functions:
Pure functions are functions which will give exact result when the same arguments are passed. For example the mathematical function sin (0) always results 0. This means that every time you call the function with the same arguments, you will always get the same result. A function can be a pure function provided it should not have any external variable which will alter the behaviour of that variable.
Let us see an example
let square x
return: x * x
The above function square is a pure function because it will not give different results for same input. There are various theoretical advantages of having pure functions. One advantage is that if a function is pure, then if it is called several times with the same arguments, the compiler only needs to actually call the function once. Let’s see an example let i: = 0;
if i < strlen (s) then – Do something which doesn’t affect s ++ i If it is compiled, strlen (s) is called each time and strlen needs to iterate over the whole of ‘s’.

If the compiler is smart enough to work out that strlen is a pure function and that ‘s’ is not updated in the loop, then it can remove the redundant extra calls to strlen and make the #loop to execute only one time. From these what we can understand, strlen is a pure function because the function takes one variable as a parameter, and accesses it to find its length.

This function reads external memory but does not change it, and the value returned derives from the external memory accessed. Impure functions: The variables used inside the function may cause side effects through the functions which are not passed with any arguments.

In such cases the function is called impure function. When a function depends on variables or functions outside of its definition block, you can never be sure that the function will behave the same every time it’s called. For example the mathematical function random Q will give different outputs for the same function call, let Random number let a : = random( ) if a > 10 then
return: a
else
return: 10
Flere the function Random is impure as it is not sure what will be the result when we call the function.

Question 4.
Explain with an example interface and implementation?
Answer:
Interface Vs Implementation:
An interface is a set of action that an object can do. For example when you press a light switch, the light goes on, you may not have cared how it splashed the light. In Object Oriented Programming language, an Interface is a description of all functions that a class must have in order to be a new interface.

In our example, anything that “ACTSLIKE” a light, should have function defnitions like turn on ( ) and a turn off ( ). The purpose of interfaces is to allow the computer to enforce the properties of the class of TYPE T (whatever the interface is) must have functions called X, Y, Z, etc.

A class declaration combines the external interface (its local state) with an implementation of that interface (the code that carries out the behaviour). An object is an instance created from the class. The interface defines an object’s visibility to the outside world.

The difference between interface and implementation is:

Interface:
Interface just defines what an object can do, but won’t actually do it. Implementation carries out the instructions defined in the interface.

Implementation:
Implementation carries out the instructions defined in the interface.
In object oriented programs classes are the interface and how the object is processed and executed is the implementation.

Characteristics of interface

1. The class template specifies the interfaces to enable an object to be created and operated properly.
2. An object’s attributes and behaviour is controlled by sending functions to the object.

For example, let’s take the example of increasing a car’s speed.

The person who drives the car doesn’t care about the internal working. To increase the speed of the car he just presses the accelerator to get the desired behaviour. Here the accelerator is the interface between the driver (the calling / invoking object) and the engine (the called object). In this case, the function call would be Speed (70): This is the interface.

Internally, the engine of the car is doing all the things. It’s where fuel, air, pressure, and electricity come together to create the power to move the vehicle. All of these actions are separated from the driver, who just wants to go faster.

Let us see a simple example, consider the following implementation of a function that finds the minimum of its three arguments:
let min 3 x y z : =
if x < y then
if x < z then x else z
else
if y < z then y else z

Practice Programs
Question 1.
Write algorithmic function definition to find the minimum among 3 numbers?
Answer:
let min 3 x y z : =
if x < y then
if x < z then x else z
else
if y < z then y else z

Question 2.
Write algorithmic recursive function definition to find the sum of n natural numbers?
Answer:
let rec sum num:
if (num! = 0) then return num + sum (num – 1)
else
return num

Samacheer kalvi 12th Computer Science Function Additional Questions and Answers

PART – 1
I. Choose The Best Answer

Question 1.
……………………… are expressed using statements of a programming language.
(a) Algorithm
(b) Procedure
(c) Specification
(d) Abstraction
Answer:
(a) Algorithm

Question 2.
……………………… are the basic building blocks of a computer programs.
(a) Code
(b) Subroutines
(c) Modules
(d) Variables
Answer:
(b) Subroutines

Question 3.
In programming languages, subroutines are called as …………………………..
(a) Functions
(b) Task
(c) Modules
(d) Code
Answer:
(a) Functions

Question 4.
Find the correct statement from the following.
(a) a : = (24) has an expression
(b) (24) is an expression
Answer:
(a) a : = (24) has an expression

Question 5.
……………………… binds values to names.
(a) Algorithms
(b) Variables
(c) Interface
(d) Definitions
Answer:
(d) Definitions

Question 6.
Identify the statement which is wrong.
(a) Definitions are expressions
(b) Definitions are distinct syntactic blocks.
(c) Definitions can have expressions, nested inside them.
Answer:
(a) Definitions are expressions

Question 7.
The name of the function in let rec pow ab : = is …………………………
(a) Let
(b) Rec
(c) Pow
(d) a b
Answer:
(c) Pow

Question 8.
In function definition pre condition is given by ……………………….
(a) Needed
(b) Let
(c) Returns
(d) Requires
Answer:
(d) Requires

Question 9.
In function definition post condition is given by …………………………
(a) Needed
(b) Let
(c) Returns
(d) Requires
Answer:
(c) Returns

Question 10.
In b = 0, = is ……………………….. operator
(a) Assignment
(b) Equality
(c) Logical
(d) Not equal
Answer:
(b) Equality

Question 11.
The formula should be written after ……………………….. sign
(a) +
(b) –
(c) =
(d) ++
Answer:
(c) =

Question 12.
To define a recursive function, …………………………. is used.
(a) Let
(b) Let r
(c) Let rfn
(d) Let rec
Answer:
(d) Let rec

Question 13.
Find which is false.
(a) All function definitions are static
(b) All function definitions are dynamic
Answer:
(b) All function definitions are dynamic

Question 14.
A ……………………….. combines the external interface with an implementation of that interface.
Answer:
class declaration

Question 15.
An …………………………. is an instance created from the class.
(a) Object
(b) Functions
(c) Subroutines
(d) Definitions
Answer:
(a) Object

Question 16.
Find the statement which is not true.
(a) The interface defines an objects visibility to the outside world
(b) Interface defines what an object can do.
(c) In object oriented programs, objects are interfaces
Answer:
(c) In object oriented programs, objects are interfaces

Question 17.
An ………………………… attributes and behaviour is controlled by sending functions to the object.
Answer:
Objects

Question 18.
The class template specifies the ………………………. to enable an object to be created and operated properly.
Answer:
Interfaces

Question 19.
The accelerator is the …………………………… between the driver and the engine.
(a) Interface
(b) Object
(c) Instruction
(d) Code
Answer:
(a) Interface

Question 20.
sin (0) = 0 is an example for ………………………. function.
(a) Impure
(b) Pure
(c) Interface
(d) Instruction
Answer:
(b) Pure

Question 21.
Find the impure function from the following.
(a) Sin (0)
(b) Square x
(c) Strlen (s)
(d) None of these
Answer:
(d) None of these

Question 22.
The function random ( ) is an example for …………………….. functions.
Answer:
Impure

Question 23.
Why is the function random( ) is a impure function?
(a) It gives different outputs for same function call
(b) It gives different outputs when 0 is given
(c) It will not give different output
Answer:
(a) It gives different outputs for same function call

Question 24.
Which function definition, doesn’t modify the arguments passed to them?
(a) Pure function
(b) Impure function
(c) Object
(d) Interface
Answer:
(a) Pure function

Question 25.
How many parameters are defined in the function let rec gcd a b : =
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(c) 2

Question 26.
In the function definition, the keyword let is followed by …………………………
(a) Function name
(b) Arguments
(c) Parameters
(d) Implementations
Answer:
(a) Function name

Question 27.
Find the correct statement from the following function definitions. let rec p on a b : =
(a) data type of the parameters are given
(b) data type of the parameters are not mentioned
Answer:
(b) data type of the parameters are not mentioned

Question 28.
If a function is not a recursive one, then ……………………………. is used
(a) abc
(b) gcd
(c) let
(d) let rec
Answer:
(c) let

Question 29.
Find the name of the function,
let rec even x : =
(a) Let
(b) Rec
(c) Even
(d) x
Answer:
(c) Even

Question 30.
Match the following function definitions with their terms.
let rec odd xy : =

1. Keyword – (i) Xy
2. Recursion – (ii) Odd
3. Function name – (iii) Rec
4. Parameters – (iv) let

(a) 1 – (iv) 2 – (iii) 3 – (ii) 4 – (i)
(b) 1 – (i) 2 – (ii) 3 – (iii) 4 – (iv)
(c) 1 – (iv) 2 – (i) 3 – (ii) 4 – (iii)
(d) 1 – (i) 2 – (iv) 3 – (ii) 4 – (iii)
Answer:
(a) 1 – (iv) 2 – (iii) 3 – (ii) 4 – (i)

Question 31.
In object oriented programming language, an is a description of all functions that a class must have
(a) Object
(b) Class
(c) Interface
(d) Code
Answer:
(c) Interface

Question 32.
The ……………………… defines an object’s visibility to the outside world.
(a) Object
(b) Interface
(c) Pure function
(d) Impure function
Answer:
(b) Interface

Question 33.
Find the correct statement.
(i) Evaluation of pure function causes side effects to its output.
(ii) Evaluation of Impure function causes side effects to its output.
Answer:
(ii) Evaluation of Impure function causes side effects to its output.

PART – II
II. Answer The Following Questions

Question 1.
What are the two types of parameter passing?
Answer:

1. Parameter without type
2. Parameter with type

Question 2.
In the function definition
let rec pow a b : = Is it recursive function. If so Explain. Why?
Answer:
Yes it is a recursive function. It is given in the function definition as rec which indicates recursive function.

Question 3.
Write the syntax for the function definitions?
Answer:
let rec f_n a₁ a₂ … a_n : = k
f_n : Function name
a₁ … a_n – variable
rec: recursion

Question 4.
Define recursive functions: How will you define it?
Answer:
A function definition which calls itself is called recursive functions. It is given by let rec.

PART – III
III. Answer The Following Questions

Question 1.
Write note on Definitions?
Answer:
Definitions bind values to names, Definitions are not expressions, Definitions are distinct syntactic blocks. Definitions can have expressions nested inside them, and vice – versa.

Question 2.
Write the pre condition and post condition for the function?
Answer:
(requires: b > 0)
– (returns: a to the power of b) let rec pow(a : int) (b : int): int: =

1. Pre condition : b > 0
2. Post condition : a to the power of b.

Question 3.
Give function definition for the Chameleons of Chromeland problem?
Answer:
let rec monochromatize abc : =
if a > 0 then
a, b, c : = a – 1, b – 1, c + 2
else
a: = 0, b: = 0, c: = a + b + c
return c

Question 4.
Give the flow chart for Chameleons of Chromeland problem?
Answer:
The algorithm is depicted in the flowchart as below:

Question 5.
Give the example function definition for parameter with type?
Answer:
Parameter with Type:
Now let us write the same function definition with types for some reason:
(requires: b> 0)
(returns: a to the power of b ) let rec pow (a: int) (b: int): int : =
if b = 0 then 1
else a * pow b (a – 1)

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 11 Integral Calculus Ex 11.13

Choose the correct or most suitable answer from given four alternatives.
Question 1.
If \(\int f(x) d x\) = g(x) + c, then \(\int f(x) g^{\prime}(x) d x\)

Solution:
(a)

Question 2.
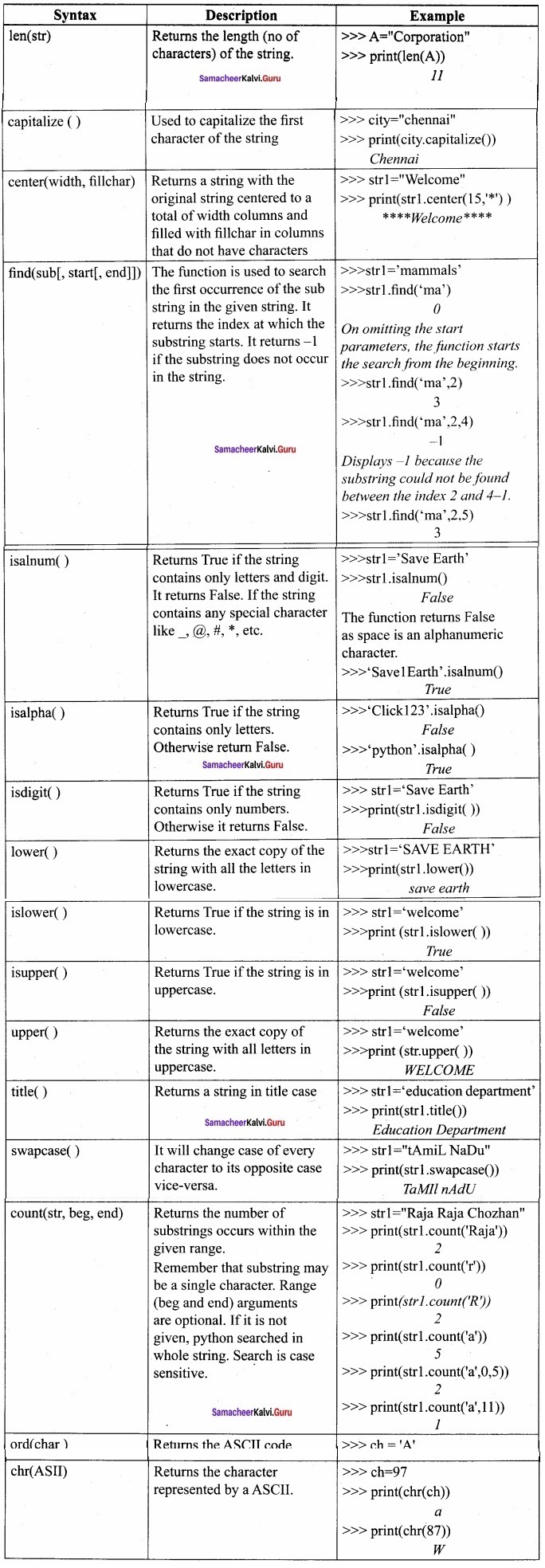
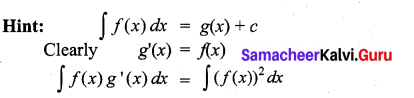
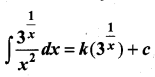If , then the value of k is ……………
(a) log 3
(b) -log 3
(c) \(-\frac{1}{\log ^{3}}\)
(d) \(\frac{1}{\log 3}\)
Solution:
(c)

Question 3.
If \(\int f^{\prime}(x) e^{x^{3}} d x\) = (x – 1)e^x2, then f(x) is …………………

Solution:
(d)

Question 4.
The gradient (slope) of a curve at any point (x, y) is \(\frac{x^{2}-4}{x^{2}}\). If the curve passes through the point(2, 7), then the equation of the curve is ………….
(a) y = x + \(\frac{4}{x}\) + 3
(b) y = x + \(\frac{4}{x}\) + 4
(c) y = x² + 3x + 4
(d) y = x² – 3x + 6
Solution:

Question 5.

(a) cot (xe^x) + c
(b) sec (xe^x) + c
(c) tan (xe^x) + c
(d) cos (xe^x) + c
Solution:
(c)

Question 6.
\(\int \frac{\sqrt{\tan x}}{\sin 2 x} d x\) is ……………..

Solution:
(a)

Question 7.
\(\int \sin ^{3} x d x\) is …………….

Solution:
(c)
Hint: sin³x = \(\frac{1}{4}\) (3 sin x – sin 3x)

Question 8.

Solution:
(b)

Question 9.

(a) tan^-1 (sin x) + c
(b) 2 sin^-1 (tan x) + c
(c) tan^-1 (cos x) + c
(d) sin^-1 (tan x) + c
Solution:
(d)

= sin^-1 (t) + c
= sin^-1 (tan x) + c

Question 10.

(a) x² + c
(b) 2x² + c
(c) \(\frac{x^{2}}{2}\) + c
(d) \(-\frac{x^{2}}{2}\) + c
Solution:
(c)

Question 11.
\(\int 2^{3 x+5} d x\) is ……………

Solution:
(d)

Question 12.

Solution:
(b)

Question 13.

Solution:
(d)

Question 14.
\(\int \frac{x^{2}+\cos ^{2} x}{x^{2}+1}\) cosec²xdx is …………….
(a) cot x + sin^-1 x + c
(b) -cot x + tan^-1 x + c
(c) -tan x + cot^-1 x + c
(d) -cot x – tan^-1 x + c
Solution:
(d)

Question 15.
\(\int x^{2} \cos x d x\) is ……………
(a) x² sin x + 2x cos x – 2 sin x + c
(b) x² sin x – 2x cos x – 2 sin x + c
(c) -x² sin x + 2x cos x + 2 sin x + c
(d) -x² sin x – 2x cos x + 2 sin x + c
Solution:
(a)
Hint: \(\int x^{2} \cos x d x\)
By Bernoullis formula dv = cosxdx
u = x² v = sinx
u’ = 2x v₁ = -cos x
u” = 2 v₂ = -sinx
= uv – u’v₁ + u”v₂
= x²sin x + 2x cos x – 2 sin x + c

Question 16.

Solution:
(b)

Question 17.
\(\int \frac{d x}{e^{x}-1}\) is …………….
(a) log |e^x| – log |e^x – 1| + c
(b) log |e^x| + log |e^x – 1| + c
(c) log |e^x – 1| – log |e^x| + c
(d) log |e^x + 1| – log |e^x| + c
Solution:
(c)

Question 18.

Solution:
(b)
We know that

Question 19.

Solution:
(d)

Question 20.

Solution:
(a)
We know that

Question 21.

Solution:
(c)
Hint:

By Bernoullis formula,

Question 22.

Solution:
(d)

Question 23.

Solution:
(c)

Question 24.

Solution:
(a)

Question 25.

Solution:
(d)
Hint: Let I = \(\int e^{\sqrt{x}} d x\)
t = \(\sqrt{x}\)

Must Follow:

ICICIBANK Pivot Point Calculator

Students can Download Maths Chapter 1 Numbers Ex 1.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Ex 1.2

Question 1.
Fill in the blanks:
(i) If a number has 5 or 6 digits in it then, its square root will have………digits.
(ii) The value of 180 lies between integers………and……….
(iii) \(\sqrt{10}\) × \(\sqrt{6}\) × \(\sqrt{15}\) =……………
(iv) \(\frac{\sqrt{300}{\sqrt{192}}\) =…………….
(v) \(\sqrt{65.61}\) =…………….
Solution:
(i) 3
(ii) 13, 14
(iii) 30
(iv) \(\frac{5}{4}\)
(v) 8.1

Question 2.
Estimate the value of the following square roots to the nearest whole number:
(i) \(\sqrt{440}\)
(ii) \(\sqrt{800}\)
(iii) \(\sqrt{1020}\)
Solution:
(i) We have 20² = 400
21² = 441
∴ \(\sqrt{440}\)  \(\widetilde { – } \) 21

(ii) We have 28² = 784
29² = 841
∴ \(\sqrt{800}\) \(\widetilde { – } \) 28

(iii) We have 31² = 961
32² = 1024
∴ \(\sqrt{1020}\) \(\widetilde { – } \) = 32

Question 3.
Find the least number that must be added to 1300 so as to get a perfect square. Also find the square root of the perfect square.
Solution:
We work out the process of finding square root by long division method.
The given number is 1300

So we have 36² < 1300 < 37²
Also 1300 is (469 – 400) = 69 less than 37². So if we add 69 to 1300 it will be perfect square. Hence the required, least number is 69 and the perfect square number is 1300 + 69 = 1369

∴ \(\sqrt{1369}\) = 37

Question 4.
Find the least number that must be subtracted to 6412 so as to get a perfect square. Also find the square root of the perfect square.
Solution:
Let us work out the process of finding the square root of 6412 by long division method.

The remainder in the last step is 12. Is if 12 be subtracted from the given number the remainder will be zero and the new number will be a perfect square.
∴ The required number is 12.
The square number is 6412 – 12 = 6400
Also \(\sqrt{6400}\) = 80

Question 5.
Find the square root by long division method.
(i) 17956
(ii) 11025
(iii) 6889
(iv) 1764
(v) 418609
Solution:

Question 6.
Find the square root of the following decimal numbers:
(i) 2.89
(ii) 1.96
(iii) 67.24
(iv) 31.36
(v) 2.0164
(vi) 13.9876
Solution:

Question 7.
Find the square root of each of the following fractions:
(i) \(\frac{144}{225}\)
(ii) 7\(\frac{18}{49}\)
(iii) 6\(\frac{1}{4}\)
(iv) 4\(\frac{25}{36}\)
Solution:

Question 8.
Say True or False:
(i) \(\frac{\sqrt{32}}{\sqrt{8}}=2\)
(ii) \(\sqrt{\frac{625}{1024}}=\frac{25}{32}\)
(iii) \(\sqrt{28}{7}=2\sqrt{7}\)
(iv) \(\sqrt{225}{64}=\sqrt{289}\)
(v) \(\sqrt{1 \frac{400}{441}}=1 \frac{20}{21}\)
Solution:
(i) true
(ii) true
(iii) false
(iv) false
(v) false

Objective Type Questions

Question 9.
\(\sqrt{48}\) is approximately equal to
(a) 5
(b) 6
(c) 7
(d) 8
Solution:
(c) 7
Hint:
\(\sqrt{49}\) = 7

Question 10.
\(\sqrt{128}\) – \(\sqrt{98}\) + \(\sqrt{18}\) =
(a) \(\sqrt{2}\)
(b) \(\sqrt{8}\)
(c) \(\sqrt{48}\)
(d) \(\sqrt{32}\)
Solution:
(d) \(\sqrt{32}\)
Hint:
\(\sqrt{128}-\sqrt{98}+\sqrt{18}=8 \sqrt{2}-7 \sqrt{2}+3 \sqrt{2}=4 \sqrt{2}=\sqrt{32}\)

Question 11.
\(\sqrt{22+\sqrt{7+\sqrt{4}}}=\)
(a) \(\sqrt{25}\)
(b) \(\sqrt{33}\)
(c) \(\sqrt{31}\)
(d) \(\sqrt{29}\)
Solution:
(a) \(\sqrt{25}\)
Hint:
\(\sqrt{22+\sqrt{7+\sqrt{4}}}=\sqrt{22+\sqrt{7+2}}=\sqrt{22+3}=\sqrt{25}\)

Question 12.
The number of digits in the square root of 123454321 is
(a) 4
(b) 5
(c) 6
(d) 7
Solution:
(b) 5
Hint:
\(=\frac{n+1}{2}=\frac{10}{2}=5\)

Students can Download Maths Chapter 1 Numbers Ex 1.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 1 Numbers Ex 1.1

Question 1.
Fill in the blanks:
i. The ones digit in the square of 77 is …………
ii. The number of non-square numbers between 24² and 25² is ……………….
iii. If a number ends with 5, its square ends with …………
iv. A square number will not end with numbers ………….
v. The number of perfect square numbers between 300 and 500 is …………
Solution:
i. 9
ii. 48
iii. 5
iv. 2, 3, 7, 8
v. 5

Question 2.
Say True or False:
i. When a square number ends in 6, its square root will have 6 in the unit’s place.
ii. A square number will not have odd number of zeros at the end.
iii. The number of zeros in the square of 961000 is 9.
iv. (7, 24, 25) is a Pythagorean triplet.
v. The square root of 221 is 21.
Solution:
i. True
ii. True
iii. False
iv. True
v. False

Question 3.
What will be the ones digit in the squares of the following numbers?
(i) 36
(ii) 252
(iii) 543
Solution:
(i) If a number ends with 6, its square ends with 6.
∴ Ones’ digit in the square of 36 is 6.

(ii) If a number ends with 2, its square ends with 4.
∴ Ones’ digit in the square of 252 is 4

(iii) If a number ends with 3, its square ends with 9.
∴ Ones’ digit in the square of 543 is 9.

Question 4.
Study the given numbers and justify why each of them obviously cannot be a perfect square.
(i) 1000
(ii) 34567
(iii) 408
Solution:
We know that the numbers end with odd number of zeros, 7 and 8 not perfect squares.
∴ 1000, 34567 and 408 cannot be perfect squares.

Question 5.
Find the sum without actually adding the following odd numbers:
(i) 1 + 3 + 5 + 7 +……..+ 35
(ii) The first 99 odd natural numbers.
Solution:
1 + 3 + 5 + 7 +……..+ 35.
Here there are 18 odd numbers from 1 to 35.
Sum of first n consecutive odd natural numbers = n²
∴ Sum of first 18 consecutive odd natural numbers = 18² = 18 × 18 = 324

(ii) The first 99 odd natural numbers.
Sum of first n consecutive natural numbers = n²
∴ Sum of 99 odd natural numbers = 99² = 99 × 99 = 9801

Question 6.
Express
(i) 15² and
(ii) 19²
as the sum of two consecutive positive integers.
Solution:

Question 7.
Write
(i) 10² and
(ii) 11²
as the sum of consecutive odd natural numbers.
Solution:
(i) 10²
10² = 100 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(ii) 11²
11² = 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21

Question 8.
Find a Pythagorean triplet whose
(i) largest member is 65
(ii) smallest member is 10
Solution:
(i) Largest number is 65
Given largest number is 65.
We know that 2m, m² – 1, m² + 1 form a Pythagorean triplet.
let m² + 1 = 65
m² = 65 – 1
m² = 64
m² = 8 × 8
m = 8
∴ 2m = 2 × 8 = 16
m² – 1 = 64 – 1 = 63
∴ The required Pythagorean triplet is (16, 63, 65)

(ii) Smallest number is 10
We know that (2m, m² – 1, m² + 1) form a Pythagorean triplet.
Given smallest number is 10
let 2m = 10
m = \(\frac{10}{2}\)
m = 5
m² + 1 = 5² + 1 = 25 + 1 = 26
m² – 1 = 5² – 1 = 25 – 1 = 24
∴ The required Pythagorean triplet is (10, 24, 26)

Question 9.
Find the square root of the following by repeated subtraction method.
(i) 144
(ii) 256
(iii) 784
Solution:
(i) 144
Step 1: 144 – 1 = 143
Step 2: 143 – 3 = 140
Step 3: 140 – 5 = 135
Step 4: 135 – 7 = 128
Step 5: 128 – 9 = 119
Step 6: 119 – 11 = 108
Step 7: 108 – 13 = 95
Step 8: 95 – 15 = 80
Step 9: 80 – 17 = 63
Step 10: 63 – 19 = 44
Step 11: 44 – 21 = 23
Step 12: 23 – 23 = 0.
We get 0 in the 12th step.
∴ 144 is a perfect square and ⇒ \(\sqrt{144}\) = 12.

(ii) 256
Step 1: 256 – 1 = 255
Step 2: 255 – 3 = 252
Step 3: 252 – 5 = 247
Step 4: 247 – 7 = 240
Step 5: 240 – 9 = 231
Step 6: 231 – 11 = 220
Step 7: 220 – 13 = 207
Step 8: 207 – 15 = 192
Step 9: 192 – 17 = 175
Step 10: 175 – 19 = 156
Step 11: 156 – 21 = 135
Step 12: 135 – 23 = 112
Step 13: 112 – 25 = 87
Step 14: 87 – 27 = 60
Step 15: 60 – 29 = 31
Step 16: 31 – 31 = 0
We have subtracted odd numbers starting from 1 repeatedly from 256. We get 0 in the 8th step.
∴ 256 is a perfect square and \(\sqrt{256}\) = 16

(iii) 784
Step 1: 784 – 1 = 783
Step 2: 783 – 3 = 780
Step 3: 780 – 5 = 775
Step 4: 775 – 7 = 768
Step 5: 768 – 9 = 759
Step 6: 759 – 11 = 748
Step 7: 748 – 13 = 735
Step 8: 735 – 15 = 720
Step 9: 720 – 17 = 703
Step 10: 703 – 19 = 684
Step 11: 684 – 21 = 663
Step 12: 663 – 23 = 640
Step 13: 640 – 25 = 615
Step 14: 615 – 27 = 588
Step 15: 588 – 29 = 559
Step 16: 559 – 31 = 528
Step 17: 528 – 33 = 495
Step 18: 495 – 35 = 460
Step 19: 460 – 37 = 423
Step 20: 423 – 39 = 384
Step 21: 384 – 41 = 343
Step 22: 343 – 43 300
Step 23: 300 – 45 = 255
Step 24: 255 – 47 = 208
Step 25: 208 – 49 = 159
Step 26: 159 – 51 = 108
Step 27: 108 – 53 = 55
Step 28: 55 – 55 = 0
We have subtracted odd numbers starting from 1 repeatedly from 784, we get zero in the 28th step.
∴ 784 is a perfect square. \(\sqrt{784}\) = 28

Question 10.
Find the square root by prime factorisation method.
(i) 1156
(ii) 4761
(iii) 9025
Solution:
(i) 1156

1156 = 2 × 2 × 17 × 17
1156 = 2² × 17²
1156 = (2 × 17)²
∴ \(\sqrt{1156}\) = \((\sqrt{2×17})^{2}\) = 2 × 17 = 34
∴ \(\sqrt{1156}\) = 34

(ii) 4761

4761 = 3 × 3 × 23 × 23
4761 = 3² × 23²
4761 = (3 × 23)²
\(\sqrt{4761}\) = \((\sqrt{3 × 23})^{2}\)
\(\sqrt{4761}\) = 3 × 23
\(\sqrt{4761}\) = 69

(iii) 9025

9025 = 5 × 5 × 19 × 19
9025 = 5² × 19²
9025 = (5 × 19)²
\(\sqrt{925}\) = \((\sqrt{5 × 19})^{2}\) = 5 × 19 = 95

Question 11.
Examine if each of the following is a perfect square:
(i) 725
(ii) 190
(iii) 841
(iv) 1089
Solution:
(i) 725

725 = 5 × 5 × 29 = 5² × 29
Here the second prime factor 29 does not have a pair.
Hence 725 is not a perfect square number.

(ii) 190

190 = 2 × 5 × 19
Here the factors 2, 5 and 9 does not have pairs.
Hence 190 is not a perfect square number.

(iii) 841
841 = 29 × 29
Hence 841 is a perfect square

(vi) 1089
1089 = 3 × 3 × 11 × 11 = 33 × 33

Hence 1089 is a perfect square

Question 12.
Find the least number by which 1800 should be multiplied so that it becomes a perfect square. Also, find the square root of the perfect square thus obtained.
Solution:

We find 1800 = 2 × 2 × 3 × 3 × 5 × 5 × 2
= 2² × 3² × 5² × 2
Here the last factor 2 has no pair. So if we multiply 1800 by 2, then the number becomes a perfect square.
∴ 1800 × 2 = 3600 is the required perfect square number.
∴ 3600 = 1800 × 2
3600 = 2² × 3² × 5² × 2 × 2
3600 = 2² × 3² × 5² × 2²
= (2 × 3 × 5 × 2)²
\(\sqrt{3600}\) = \((\sqrt{2 × 3 × 5 × 2})^{2}\) = 2 × 3 × 5 × 2 = 60
∴ \(\sqrt{3600}\) = 60.

Question 13.
Find the smallest number by which 10985 should be divided so that the quotient is a perfect square.
Solution:
We find 10985 = 5 × 13 × 13 × 13
= 5 × 13 × 13²
Here the prime factors 5 and 13 do not have pairs.
∴ We can divide 10985 by 65 (5 × 13) to get a perfect square
∴ When we divide 10985 by 65 we get quotient 169.
169 = 13 × 13
\(\sqrt{169}\) = 13

Question 14.
Is 2352 a perfect square? If not, find the smallest number by which 2352 must be multiplied so that the product is a perfect square. Find the square root of the new number.
Solution:

We find 2352 = 2 × 2 × 2 × 2 × 3 × 7 × 7
2352 = 2² × 2² × 3 × 7²
Here the factor 3 has no pair.
∴ 2352 is not a perfect square.
We have to multiply 2352 by 3 so that the product is a perfect square.
Img 13
∴ 2352 × 3 = 2² × 2² × 7² × 3 × 3
7056 = 2² × 2² × 7² × 3²
7056 = (2 × 2 × 7 × 3)²
∴ \(\sqrt{7056}\) = \((\sqrt{2 × 2 × 7 × 3})^{2}\)
= 2 × 2 × 7 × 3 = 84
\(\sqrt{7056}\) = 84

Question 15.
Find the least square number which is divisible by each of the numbers 8, 12 and 15.
Solution:
The least number divisible by each of the numbers 8, 12, 15 is their L.C.M

∴ LCM of 8, 12, 15 is (4 × 3 × 2 × 5) = 120
Resolving 120 into prime factors
We get 120 = 2 × 2 × 2 × 3 × 5
Grouping into pairs of equal factors

120 = (2 x 2) x 2 x 3 x 5
∴ The factors 2, 3 and 5 had no pairs.
Thus to make 120 a perfect square, we must multiply it by (2 x 3 x 5) = 30.
∴ The least square number divisible by 8,12 and 15 is 120 x 30 = 3600

Students can Download Maths Chapter 4 Statistics Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 4 Statistics Intext Questions

Exercise 4.1
Try These (Text book Page no. 77)

Question 1.
Arrange the given data in ascending and descending order:
9, 34, 4, 13, 42, 10, 25, 7, 31, 4, 40
Solution:
Ascending order: 4, 4, 7, 9, 10, 13, 25, 31, 34, 40, 42.
Descending order : 42, 40, 34, 31, 25, 13, 10, 9, 7, 4, 4

Question 2.
Find the range of the given data : 53, 42, 61, 9, 39, 63, 14, 20, 06, 26, 31, 4, 57
Solution:
Ascending order of the given data:
4, 6, 9, 14, 20, 26, 31, 39, 42, 53, 57, 61, 63
Here largest value = 63
Smallest value = 4
∴ Range = Largest value – smallest value = 63 – 4 = 59

Think (Text book Page no. 79)

How will you change the given series as continuous series
15 – 25
28 – 38
41 – 51
54 – 64
Solution:
Given series
15 – 25
28 – 38
41 – 51
54 – 64
Difference in the gap = 28 – 25 = 3
Here half of the gap = \(\frac{1}{2}\)(3) = 1.5
∴ 1.5 is the adjustment factor. So we subtract 1.5 from the lower limit and add 1.5 to the upper limit to make it as a continuous series.

Think (Text book Page no. 80)

If we want to represent the given data by 5 classes, then how shall we find the interval?
Solution:
We can find the class size by the formula
Number of class intervals = \(\frac{Range}{Class size}\)

Try These (Text book Page no. 82)

Question 1.
Prepare a frequency table for the data : 3, 4, 2, 4, 5, 6, 1, 3, 2, 1, 5, 3, 6, 2, 1, 3, 2, 4
Solution:
Ascending order of the given data.
1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 6, 6
The distribution table:

∴ Frequency Table:

Question 2.
Prepare a grouped frequency table for the data :
10, 9, 3, 29, 17, 34, 23, 20, 39, 42, 5, 12, 19, 47, 18, 19, 27, 7, 13, 40, 38, 24, 34, 15, 40
Largest value = 47
Smallest value = 3
Range = Largest value – Smallest value = 47 – 3 = 44
Suppose we take class size as 10, then Number of class intervals possible
= \(\frac{Range}{Class size}\) = \(\frac{44}{10}\) = 4.4
\(\tilde { – } \) 5

Exercise 4.2
Think (Text book Page no. 94)

When joining two adjacent midpoints w ithout using a ruler, can you get a polygon?
Solution:
No, because it may be curved lines and they are not considered as polygons.

Students can Download Maths Chapter 3 Geometry Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 3 Geometry Additional Questions

Question 1.
In ΔPQR, PS is a median. If QS = 7 cm find the length of QR?
Solution:
PS is the median ⇒ S is the midpoint of QR

Given
QS = 7 cm
∴ SR = 7 cm
QR = QS + SR
= 7 + 7 = 14cm

Question 2.
In ΔABC, G is the centroid. If AD = 6 cm, BC = 4 cm and BE = 9 cm find the perimeter of ΔBDG.
Solution:
In ΔABC, G is the centroid.

If AD = 6 cm
⇒ GD = \(\frac{1}{3}\) of AD = \(\frac{1}{3}\) (6)
BE = 9 cm
⇒ BG = \(\frac{2}{3}\) of BE = \(\frac{2}{3}\) (9) = 6cm
Also D is the midpoint of BC ⇒ BD
= \(\frac{1}{1}\) of BC = \(\frac{1}{2}\) (4) = 2cm
∴ Perimeter of ΔBDG = BD + GD + BG = 2 + 2 + 6 = 10 cm

Question 3.
Construct a rhombus FISH with FS = 8 cm and ∠F = 80°
Solution:
Given FS = 8 cm and ∠F = 80°

Steps :
(i) Drawn a line segment FS = 7 cm.
(ii) At F, made ∠SFX = ∠SFY = 40° on either side of FS.
(iii) At S, made ∠FSP = ∠FSQ = 40° on either side of FS
(iv) Let FX and SP cut at H and FY and SQ cut at I.
(v) FISH is the required rhombus

Calculation of Area:
Area of the rhombus FISH = \(\frac{1}{2}\) × d₁ × d₂ sq.units = \(\frac{1}{2}\) × 5.9 × 7 cm² = 20.65 cm²

Students can Download Maths Chapter 2 Life Mathematics Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 2 Life Mathematics Additional Questions

Question 1.
120 men had food for 200 days. After 5 days 30 men left the camp. How long will the remaining food last.
Solution:
Since 30 men left after 5 days, the remaining food is sufficient for 120 men for 195 days. Suppose the remaining food lasts for x days for the remaining 90 men.
We have

More men means less days the food lasts
∴ It is inverse proportion
120 : 90 = x : 195
Product of extremes = Product of means
120 × 195 = 90 × x
x = \(\frac{120×195}{90}\)
x = 90
x = 260.
∴ Remaining food last for 260 days.

Question 2.
15 men earn Rs 900 in 5 days, how much will 20 men earn in 7 days?
Solution:
In one day 15 men earn Rs 900
In one day 15 men earn \(\frac{900}{5}\) = Rs 180
In one day 1 men earn \(\frac{180}{5}\) = Rs 12
∴ 1 men earn in 7 days = 12 × 7 = Rs 84
∴ 20 men earn in 7 days = 84 × 20 = 1680

Question 3.
A and B together can do a piece of work in 10 days, B and C can do the same work together in 12 days, A and C can do together in 15 days. How long will it take to complete the work working three of them altogether?
Solution:
(A + B)’s 1 day’s work = \(\frac{1}{10}\)……….(1)
(B + C)’s 1 day’s work = \(\frac{1}{12}\)……….(2)
(A + C)’s 1 day’s work = \(\frac{1}{15}\)……….(3)
(l) + (2) + (3) ⇒
[A + B + B + C + A + C]’s 1 day work = \(\frac{1}{10}\) + \(\frac{1}{12}\) + \(\frac{1}{15}\)
(2A + 2B + 2C)’s 1 day work = \(\frac{6 + 5 + 4}{60}\)
2(A + B + C)’s 1 day work = \(\frac{15}{60}\)
(A + B + C)’s 1 day’s work = \(\frac{1}{4 × 2}\) = \(\frac{1}{8}\)
∴ A + B + C work together to finish the work in 8 days.