Prasanna

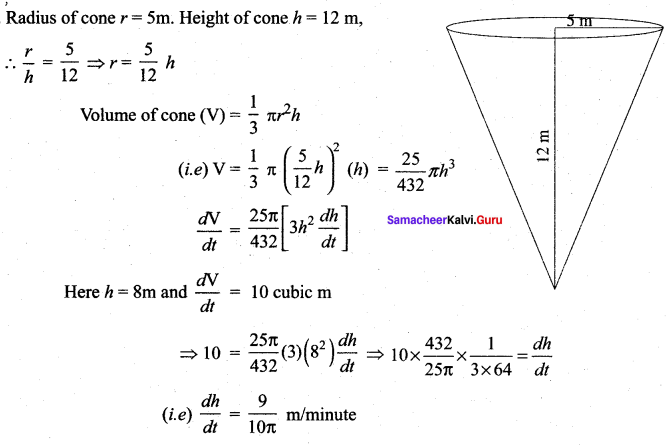
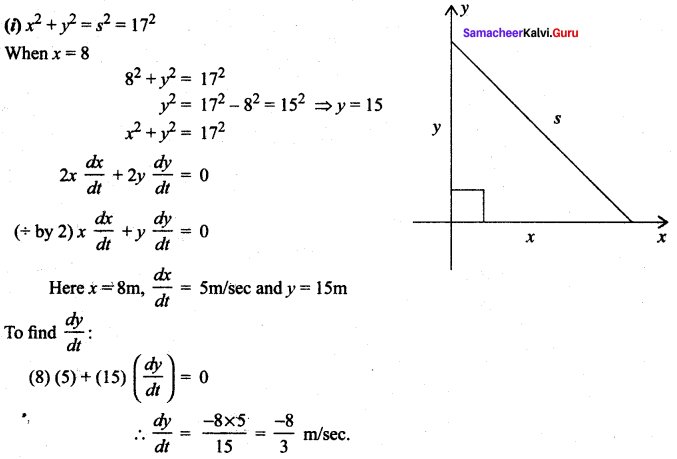
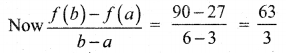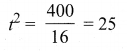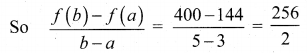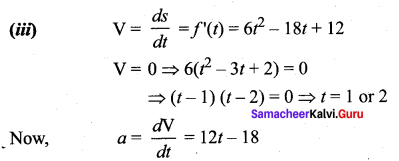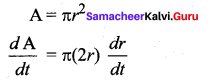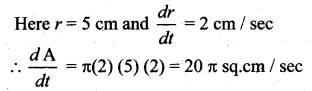For those looking for help on 11th Physics can use the Tamilnadu State Board Solutions for 11th Physics Chapter 5 Motion of System of Particles and Rigid Bodies prevailing for free of cost.

Download the Samacheer Kalvi 11th Physics Book Solutions Questions and Answers Notes Pdf, for all Chapter Wise through the direct links available and take your preparation to the next level. The Tamilnadu State Board Solutions for 11th Physics Chapter 5 Motion of System of Particles and Rigid Bodies Questions and Answers covers all the topics and subtopics within it. Practice using these Samacheer Kalvi 11th Physics Book Solutions Questions and Answers for Chapter 5 Motion of System of Particles and Rigid Bodies PDF and test your preparation level and bridge the knowledge gap accordingly.

Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 5 Motion of System of Particles and Rigid Bodies

If you have any queries take the help of the Tamilnadu State Board Solutions for 11th Physics Chapter 5 Motion of System of Particles and Rigid Bodies Questions and Answers learn all the topics in it effectively. We have everything covered and you can Practice them often to score better grades in your exam. By going through the Samacheer Kalvi 11th Physics Book Solutions Questions and Answers you can attempt the actual exam with utmost confidence.

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Textual Questions Solved

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Multiple Choice Questions

11th Physics Chapter 5 Book Back Answers Question 1.
The center of mass of a system of particles does not depend upon,
(a) position of particles
(b) relative distance between particles
(c) masses of particles
(d) force acting on particle
Answer:
(d) force acting on particle

11th Physics 5th Chapter Book Back Answers Question 2.
A couple produces, [AIPMT 1997, AIEEE 2004]
(a) pure rotation
(b) pure translation
(c) rotation and translation
(d) no motion [AIPMT 1997]
Answer:
(a) pure rotation

11th Physics Lesson 5 Book Back Answers Question 3.
A particle is moving with a constant velocity along a line parallel to positive X – axis. The magnitude of its angular momentum with respect to the origin is –
(a) zero
(b) increasing with x
(c) decreasing with x
(d) remaining constant [IIT 2002]
Answer:
(d) remaining constant

Samacheer Kalvi 11th Physics Question 4.
A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force 30 N?
(a) 0.25 rad s^-2
(b) 25 rad s^-2
(c) 5 m s^-2
(d) 25 m s^-2
[NEET 2017]
Answer:
(b) 25 rad s^-2

11th Physics Samacheer Kalvi Question 5.
A closed cylindrical container is partially filled with water. As the container rotates in a horizontal plane about a perpendicular bisector, its moment of inertia,
(a) increases
(b) decreases
(c) remains constant
(d) depends on direction of rotation. [IIT 1998]
Answer:
(a) increases

Samacheer Kalvi Guru 11th Physics Question 6.
A rigid body rotates with an angular momentum L. If its kinetic energy is halved, the angular momentum becomes,
(a) L
(b) L / 2
(c) 2 L
(d) L / 2 [AFMC 1998, AIPMT 2015]
Answer:
(d) L / 2

Samacheer Kalvi Physics 11th Question 7.
A particle undergoes uniform circular motion. The angular momentum of the particle remain conserved about –
(a) the center point of the circle.
(b) the point on the circumference of the circle
(c) any point inside the circle.
(d) any point outside the circle. [IIT 2003]
Answer:
(a) the center point of the circle.

Samacheer Kalvi 11th Physics Solution Book Question 8.
When a mass is rotating in a plane about a fixed point, its angular momentum is directed along –
(a) a line perpendicular to the plane of rotation
(b) the line making an angle of 45° to the plane of rotation
(c) the radius
(d) tangent to the path [AIPMT 2012]
Answer:
(a) a line perpendicular to the plane of rotation

Samacheerkalvi.Guru 11th Physics Question 9.
Two discs of same moment of inertia rotating about their regular axis passing through center and perpendicular to the plane of disc with angular velocities ω₁ and ω₁. They are brought in to contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is-
(a) \(\frac {1}{4}\) I(ω₁ – ω₂)ω²
(b) I(ω₁ – ω₂)ω₂
(c) \(\frac {1}{8}\) I(ω₁ – ω₂)ω²
(d) \(\frac {1}{2}\) I(ω₁ – ω₂)ω²
Answer:
(a) \(\frac {1}{4}\) I(ω₁ – ω₂)ω²

11 Physics Samacheer Solutions Question 10.
A disc of moment of inertia I_a is rotating in a horizontal plane about its symmetry axis with a constant angular speed to. Another disc initially at rest of moment of inertia I_b is dropped coaxially on to the rotating disc. Then, both the discs rotate with same constant angular speed. The loss of kinetic energy due to friction in this process is-

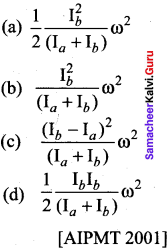
Answer:

Samacheer Kalvi Class 11 Physics Solutions Question 11.
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle 0 without slipping and slipping down the incline without rolling is –
(a) 5 : 7
(b) 2 : 3
(c) 2 : 5
(d) 7 : 5
[AIPMT 2014]
Answer:
(a) 5 : 7

Samacheer Kalvi Guru 11 Physics Question 12.
From a disc of radius R a mass M, a circular hole of diameter R, whose rim passes through the center is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis passing through it?
(a) 15MR²/32
(b) 13MR²/32
(c) 11MR²/32
(d) 9MR²/32 [NEET 2016]
Answer:
(b) 13MR²/32

Samacheer Kalvi 11 Physics Question 13.
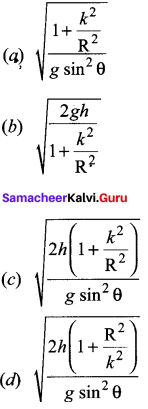
The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is,
(a) \(\sqrt{\frac{4}{3} g h}\)
(b) \(\sqrt{\frac{10}{7} g h}\)
(c) \(\sqrt{2gh}\)
(d) \(\sqrt{\frac{1}{2} g h}\)
Answer:
(a) \(\sqrt{\frac{4}{3} g h}\)

Physics Class 11 Samacheer Kalvi Question 14.
The speed of the center of a wheel rolling on a horizontal surface is vQ. A point on the rim in level with the center will be moving at a speed of speed of,
(a) zero
(b) v₀
(c) \(\sqrt{2}\)v₀
(d) 2 v₀
[PMT 1992, PMT 2003, IIT 2004]
Answer:
(c) \(\sqrt{2}\)v₀

Samacheer Kalvi 11th Physics Solution Question 15.
A round object of mass m and radius r rolls down without slipping along an inclined plane. The fractional force,
(a) dissipates kinetic energy as heat.
(b) decreases the rotational motion.
(c) decreases the rotational and transnational motion ,
(d) converts transnational energy into rotational energy [PMT 2005]
Answer:
(d) converts transnational energy into rotational energy

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Short Answer Questions

Samacheer Kalvi.Guru 11th Physics Question 1.
Define center of mass.
Answer:
The center of mass of a body is defined as a point where the entire mass of the body appears to be concentrated.

11th Physics Samacheer Kalvi Solution Question 2.
Find out the center of mass for the given geometrical structures.
(a) Equilateral triangle
(b) Cylinder
(c) Square
Answer:

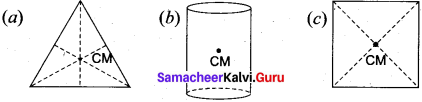
(a) For equilateral triangle, center of mass lies at its centro-id.
(b) For cylinder, center of mass lies at its geometrical center.
(c) For square, center of mass lies at the point where the diagonals meet.

11 Samacheer Physics Solutions Question 3.
Define torque and mention its unit.
Answer:
Torque is defined as the moment of the external applied force about a point or axis of rotation. The expression for torque is,
\(\vec{\tau}\) = \(\vec{r}\) x \(\vec{F}\)

11th Physics Samacheer Solutions Question 4.
What are the conditions in which force cannot produce torque?
Answer:
The forces intersect (or) passing through the axis of rotation cannot produce torque as the perpendicular distance between the forces is 0 i.e. r = 0.
∴ \(\vec{\tau}\) = \(\vec{r}\) x \(\vec{F}\) = 0

Question 5.
Give any two examples of torque in day – to – day life.
Answer:

• The opening and closing of a door about the hinges.
• Turning of a nut using a wrench.

Question 6.
What is the relation between torque and angular momentum?
Answer:
We have the expression for magnitude of angular momentum of a rigid body as, L = I ω. The expression for magnitude of torque on a rigid body is, τ = I α.
We can further write the expression for torque as,
τ = I\(\frac {dω}{dt}\) (∴ α = \(\frac {dω}{dt}\))
Where, ω is angular velocity and α is angular acceleration. We can also write equation,
τ = \(\frac {d(Iω)}{dt}\)
τ = \(\frac {dL}{dt}\)

Question 7.
What is equilibrium?
Answer:
A rigid body is said to be in mechanical equilibrium where both its linear momentum and angular momentum remain constant.

Question 8.
How do you distinguish between stable and unstable equilibrium?
Answer:
Stable Kquilibrium:

• The body tries to come back to equilibrium if slightly disturbed and released.
• The center of mass of the body shifts slightly higher if disturbed from equilibrium.
• Potential energy of the body is minimum and it increases if disturbed.

Unstable Equilibrium:

• The body cannot come back to equilibrium if slightly disturbed and released.
• The center of mass of the body shifts slightly lower if disturbed from equilibrium.
• Potential energy of the body is not minimum and it decreases if disturbed.

Question 9.
Define couple.
Answer:
A pair of forces which are equal in magnitude but opposite in direction and separated by a perpendicular distance so that their lines of action do not coincide that causes a turning effect is called a couple.

Question 10.
State principle of moments.
Answer:
Principle of moment states that when an object is in equilibrium the sum of the anticlockwise moments about a point is equal to the sum of the clockwise moments.

Question 11.
Define center of gravity.
Answer:
The center of gravity of a body is the point at which the entire weight of the body acts, irrespective of the position and orientation of the body.

Question 12.
Mention any two physical significance of moment of inertia
Answer:
Moment of inertia for point mass,
I = \(m_{i} r_{i}^{2}\)
Moment of inertia for bulk object,
I = ∑\(m_{i} r_{i}^{2}\)

Question 13.
What is radius of gyration?
Answer:
The radius of gyration of an object is the perpendicular distance from the axis of rotation to an equivalent point mass, which would have the same mass as well as the same moment of inertia of the object.

Question 14.
State conservation of angular momentum.
Answer:
The law of conservation of angular momentum states that when no external torque acts on the body the net angular momentum of a rotating rigid body remains constant.

Question 15.
What are the rotational equivalents for the physical quantities, (i) mass and (ii) force?
Answer:
The rotational equivalents for (i) mass and (ii) force are moment of inertia and torque respectively.

Question 16.
What is the condition for pure rolling?
Answer:
In pure rolling, there is no relative motion of the point of contact with the surface when the rolling object speeds up or shows down. It must accelerate or decelerate respectively.

Question 17.
What is the difference between sliding and slipping?
Sliding:

• Velocity of center of mass is greater than Rω i.e. V_CM > Rω.
• Velocity of transnational motion is greater than velocity of rotational motion.
• Resultant velocity acts in the forward direction.

Slipping:

• Velocity of center of mass is lesser than Rω. i.e. V_CM < Rω
• Velocity of translation motion is lesser than velocity of rotational motion.
• Resultant velocity acts in the backward direction.

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Long Answer Questions

Question 1.
Explain the types of equilibrium with suitable examples.
Answer:

• Transnational motion – A book resting on a table.
• Rotational equilibrium – A body moves in a circular path with constant velocity.
• Static equilibrium – A wall – hanging, hanging on the wall.
• Dynamic equilibrium – A ball decends down in a fluid with its terminal velocity.
• Stable equilibrium – A table on the floor
• Unstable equilibrium – A pencil standing on its tip.
• Neutral equilibrium – A dice rolling on a game board.

Question 2.
Explain the method to find the center of gravity of a irregularly shaped lamina.
Answer:
There is also another way to determine the center of gravity of an irregular lamina. If we suspend the lamina from different points like P, Q, R as shown in figure, the vertical lines I PP’, QQ’, RR’ all pass through the center of gravity. Here, reaction force acting at the point of suspension and the gravitational force acting at the center of gravity cancel each other and the torques caused by them also cancel each other.

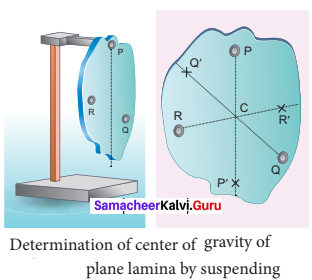
Determination of center of gravity of plane lamina by suspending

Question 3.
Explain why a cyclist bends while negotiating a curve road? Arrive at the expression for angle of bending for a given velocity.
Answer:
Let us consider a cyclist negotiating a circular level road (not banked) of radius r with a speed v. The cycle and the cyclist are considered as one system with mass m. The center gravity of the system is C and it goes in a circle of radius r with center at O. Let us choose the line OC as X – axis and the vertical line through O as Z – axis as shown in Figure.

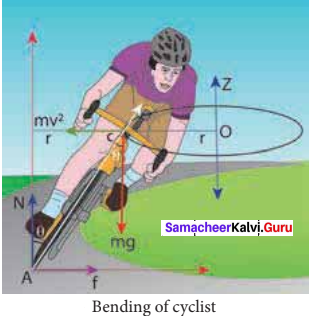
The system as a frame is rotating about Z – axis. The system is at rest in this rotating frame. To solve problems in rotating frame of reference, we have to apply a centrifugal force (pseudo force) on the system which will be \(\frac{m v^{2}}{r}\) This force will act through the center of gravity. The forces acting on the system are,

• gravitational force (mg)
• normal force (N)
• frictional force (f)
• centrifugal force (\(\frac{m v^{2}}{r}\)).

As the system is in equilibrium in the rotational frame of reference, the net external force and net external torque must be zero. Let us consider all torques about the point A in Figure.
For rotational equilibrium,
τ_net = 0
The torque due to the gravitational force about point A is (mg AB) which causes a clockwise turn that is taken as negative. The torque due to the centripetal force is I BC which causes an (\(\frac{m v^{2}}{r}\) BC) Which causes an anticlockwise turn that is taken as positive.


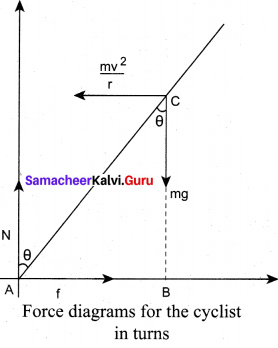
While negotiating a circular level road of radius r at velocity v, a cyclist has to bend by an angle 0 from vertical given by the above expression to stay in equilibrium (i.e. to avoid a fall).

Question 4.
Derive the expression for moment of inertia of a rod about its center and perpendicular to the rod.
Answer:
Let us consider a uniform rod of mass (M) and length (l) as shown in figure. Let us find an expression for moment of inertia of this rod about an axis that passes through the center of mass and perpendicular to the rod. First an origin is to be fixed for the coordinate system so that it coincides with the center of mass, which is also the geometric center of the rod. The rod is now along the x axis. We take an infinitesimally small mass (dm) at a distance (x) from the origin. The moment of inertia (dI) of this mass (dm) about the axis is, dI = (dm) x²

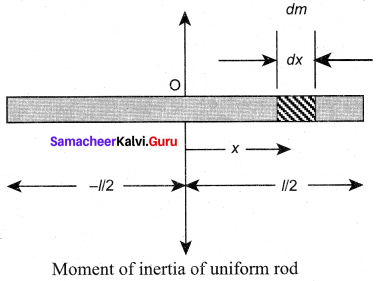
As the mass is uniformly distributed, the mass per unit length (λ) of the rod is, λ = \(\frac {M}{l}\)
The (dm) mass of the infinitesimally small length as, dm = λ dx = \(\frac {M}{l}\) dx
The moment of inertia (I) of the entire rod can be found by integrating dl,

As the mass is distributed on either side of the origin, the limits for integration are taken from to – l/2 to l/2.

Question 5.
Derive the expression for moment of inertia of a uniform ring about an axis passing through the center and perpendicular to the plane.
Answer:
Let us consider a uniform ring of mass M and radius R. To find the moment of inertia of the ring about an axis passing through its center and perpendicular to the plane, let us take an infinitesimally small mass (dm) of length (dx) of the ring. This (dm) is located at a distance R, which is the radius of the ring from the axis as shown in figure.
The moment of inertia (dl) of this small mass (dm) is,
dI = (dm)R²
The length of the ring is its circumference (2πR). As the mass is uniformly distributed, the mass per unit length (λ) is,
λ = \(\frac {mass}{lengh}\) = \(\frac {M}{2πR}\)
The mass (dm) of the infinitesimally small length is,
dm = λ dx = \(\frac {M}{2πR}\) dx
Now, the moment of inertia (I) of the entire ring is,
To cover the entire length of the ring, the limits of integration are taken from 0 to 2πR.

Question 6.
Derive the expression for moment of inertia of a uniform disc about an axis passing through the center and perpendicular to the plane.
Answer:
Consider a disc of mass M and radius R. This disc is made up of many infinitesimally small rings as shown in figure. Consider one such ring of mass (dm) and thickness (dr) and radius (r). The moment of inertia (dl) of this small ring is,
dI = (dm)R²
As the mass is uniformly distributed, the mass per unit area (σ) is σ = \(\frac {mass}{area}\) = \(\frac{M}{\pi R^{2}}\)
The mass of the infinitesimally small ring is,
dm = σ 2πr dr = \(\frac{\mathrm{M}}{\pi \mathrm{R}^{2}}\) 2πr dr
where, the term (2πr dr) is the area of this elemental ring (2πr is the length and dr is the thickness), dm = \(\frac{2 \mathrm{M}}{\mathrm{R}^{2}}\) r dr
dI = \(\frac{2 \mathrm{M}}{\mathrm{R}^{2}}\) r³ dr
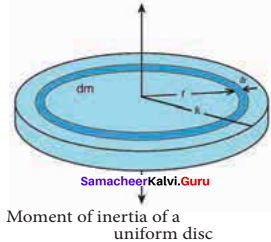The moment of inertia (I) of the entire disc is,

Question 7.
Discuss conservation of angular momentum with example.
Answer:
When no external torque acts on the body, the net angular momentum of a rotating rigid body remains constant. This is known as law of conservation of angular momentum.
τ = \(\frac {dL}{dt}\)
If τ = 0 then, L = constant.
As the angular momentum is L = Iω, the conservation of angular momentum could further be written for initial and final situations as,
I_iω_i = I_iω_i (or) Iω = constant
The above equations say that if I increases ω will decrease and vice – versa to keep the angular momentum constant.

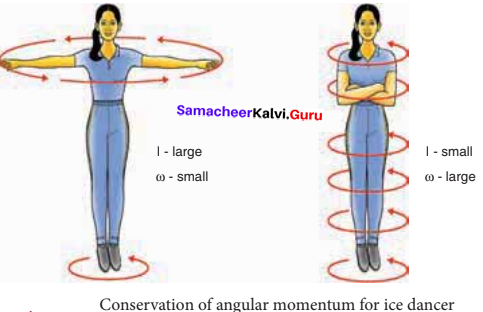
There are several situations where the principle of conservation of angular momentum is applicable. One striking example is an ice dancer as shown in Figure A. The dancer spins slowly when the hands are stretched out and spins faster when the hands are brought close to the body.

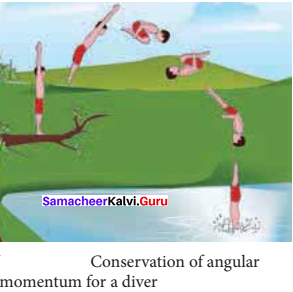
Stretching of hands away from body increases moment of inertia, thus the angular velocity decreases resulting in slower spin. When the hands are brought close to the body, the moment of inertia decreases, and thus the angular velocity increases resulting in faster spin. A diver while in air as in Figure B curls the body close to decrease the moment of inertia, which in turn helps to increase the number of somersaults in air.

Question 8.
State and prove parallel axis theorem.
Answer:
Parallel axis theorem:
Parallel axis theorem states that the moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of mass and the product of the mass of the body and the square of the perpendicular distance between the two axes.

If I_C is the moment of inertia of the body of mass M about an axis passing through the center of mass, then the moment of inertia I about a parallel axis at a distance d from it is – given by the relation,
I = I_C + M d²
Let us consider a rigid body as shown in figure. Its moment of inertia about an axis AB passing through the center of mass is I_C. DE is another axis parallel to AB at a perpendicular distance d from AB. The moment of inertia of the body about DE is I. We attempt to get an expression for I in terms of I_C. For this, let us consider a point mass m on the body at position x from its center of mass.

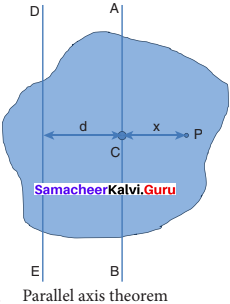
The moment of inertia of the point mass about the axis DE is, m (x + d)². The moment of inertia I of the whole body about DE is the summation of the above expression.
I = ∑ m (x + d)²
This equation could further be written as,
I = ∑ m(x² + d² + 2xd)
1= ∑ (mx² + md² + 2 dmx)
l = ∑ mx² + md² + 2d ∑ mx
Here, ∑ mx² is the moment of inertia of the body about the center of mass. Hence,I_C = ∑ mx²
The term, ∑ mx = 0 because, x can take positive and negative values with respect to the axis AB. The summation (∑ mx) will be zero.
Thus, I = I_C + ∑ m d² = I_C + (∑m) d²
Here, ∑ m is the entire mass M of the object (∑ m = M).
I = I_C + Md²

Question 9.
State and prove perpendicular axis theorem.
Answer:
Perpendicular axis theorem:
This perpendicular axis theorem holds good only for plane laminar objects. The theorem states that the moment of inertia of a plane laminar body about an axis perpendicular to its plane is equal to the sum of moments of inertia about two perpendicular axes lying in the plane of the body such that all the three axes are mutually perpendicular and have a common point.

Let the X and Y – axes lie in the plane and Z – axis perpendicular to the plane of the laminar object. If the moments of inertia of the body about X and Y-axes are I_X and I_Y respectively – and I_Z is the moment of inertia about Z-axis, then the perpendicular axis theorem could be expressed as,
I_Z = I_X + I_Y

To prove this theorem, let us consider a plane laminar object of negligible thickness on which lies the origin (O). The X and Y – axes lie on the plane and Z – axis is perpendicular to it as shown in figure. The lamina is considered to be made up of a large number of particles of mass m. Let us choose one such particle at a point P which has coordinates (x, y) at a distance r from O.

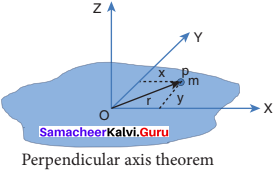
The moment of inertia of the particle about Z – axis is, mr².
The summation of the above expression gives the moment of inertia of the entire lamina about Z – axis as, I_Z = ∑ mr²
Here, r² = x² + y²
Then, I_Z = ∑ m (x² + y²)
I_Z = ∑ m x² + ∑ m y²
In the above expression, the term ∑ m x² is the moment of inertia of the body about the Y-axis and similarly the term ∑ m y²is the moment of inertia about X- axis. Thus,
I_X = ∑ m y² and I_Y = ∑ m x²
Substituting in the equation for Iz gives,
I_Z = I_X + I_Y
Thus, the perpendicular axis theorem is proved.

Question 10.
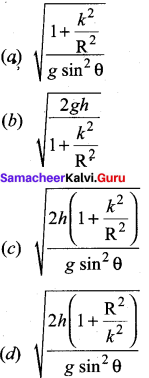
Discuss rolling on inclined plane and arrive at the expression for the acceleration.
Answer:
Let us assume a round object of mass m and radius R is rolling down an inclined plane without slipping as shown in figure. There are two forces acting on the object along the inclined plane. One is the component of gravitational force (mg sin θ) and the other is the static frictional force (f). The other component of gravitation force (mg cos θ) is cancelled by the normal force (N) exerted by the plane. As the motion is happening along the incline, we shall write the equation for motion from the free body diagram (FBP) of the object.

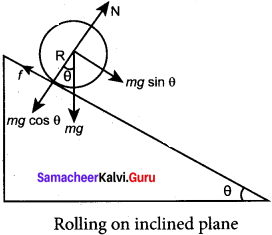
For transnational motion, mg sin θ is the supporting force and f is the opposing force, mg sin θ f = ma
For rotational motion, let us take the torque with respect to the center of the object. Then mg sin 0 cannot cause torque as it passes through it but the frictional force f can set torque of Rf = Iα
By using the relation, a = rα, and moment of inertia I = mK² we get,
Rf = mK² \(\frac {a}{R}\); f = ma \(\left(\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\right)\)
Now equation becomes,
mg sin θ – ma \(\left(\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\right)\) = ma
mg sin θ = ma + ma \(\left(\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\right)\)
a \(\left(1+\frac{\mathrm{K}^{2}}{\mathrm{R}^{2}}\right)\) = g sin θ
After rewriting it for acceleration, we get,
a = \(\frac{g \sin \theta}{\left(1+\frac{K^{2}}{R^{2}}\right)}\)
We can also find the expression for final velocity of the rolling object by using third equation of motion for the inclined plane.
v² = u² + 2as. If the body starts rolling from rest, u = 0. When h is the vertical height of the incline, the length of the incline s is, s = \(\frac {h}{sin θ}\)
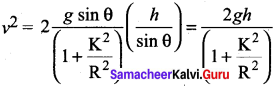By taking square root,

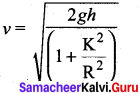
The time taken for rolling down the incline could also be written from first equation of motion as, v = u + at. For the object which starts rolling from rest, u = 0. Then,
t = \(\frac {v}{a}\)

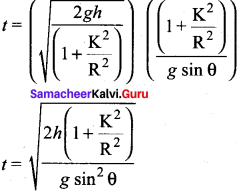
The equation suggests that for a given incline, the object with the least value of radius of gyration K will reach the bottom of the incline first.

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Conceptual Questions

Question 1.
When a tree is cut, the cut is made on the side facing the direction in which the tree is required to fall. Why?
Answer:
A cut on the tree is made on the side facing the direction in which the tree is required to fall because that side will no longer be supported by the normal force from the bottom, therefore the gravitational force tries to rotate it. So the torque given by the gravity to the tree makes the tree fall on the side as anticipated.

Question 2.
Why does a porter bend forward while carrying a sack of rice on his back?
Answer:
When a porter carries a sack of rice, the line of action of his center of gravity will go away from the body. It affects the balance, to avoid this he bends. By which center of gravity will realign within the body again. So balance is maintained.

Question 3.
Why is it much easier to balance a meter scale on your finger tip than balancing on a match stick?
Answer:
A meter scale is larger then a match stick. So the center of gravity for meter scale is higher than a matchstick when we keep it vertically. It is easier to balance the object whose center of gravity is higher than the object whose centro of gravity is lower. So, it is hard to balance a match stick than a meter scale.

Question 4.
Two identical water bottles one empty and the other filled with water are allowed to roll down an inclined plane. Which one of them reaches the bottom first? Explain your answer.
Answer:
Mass of the empty water bottle mostly concentrated on its surface. So moment of inertia of empty water bottle is more than the bottle filled with water. As we know, moment of inertia is inversely proportional to angular velocity. Therefore, the bottle filled with water whirls with greater speed and reaches the ground first.

Question 5.
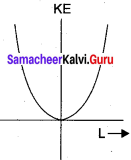
Write the relation between angular momentum and rotational kinetic energy. Draw a graph for the same. For two objects of same angular momentum, compare the moment of inertia using the graph.
Answer:
Let a rigid body of moment of inertia I rotate with angular velocity ω.
The angular momentum of a rigid body is, L = Iω
The rotational kinetic energy of the rigid body is, KE = \(\frac { 1 }{ 2 }\) Iω².
By multiplying the numerator and denominator of the above equation with I, we get a relation between L and KE as,

It resembles with y = Kx². If angular momentum is same for two objects, kinetic energy is inversely proportional to moment of inertia.
Moment of inertia of the object whose kinetic energy is lesser will have greater magnitude.

Question 6.
Three identical solid spheres move down through three inclined planes A, B and C all same dimensions. A is without friction, B is undergoing pure rolling and C is rolling with slipping. Compare the kinetic energies E_A, E_B and E_C at the bottom.
Answer:
Even though, the three identical solid spheres of same dimensions move down through three different inclined plane, according to the law of conservation of energy, the potential energy possessed by these three solid spheres will be converted into kinetic energies. So the kinetic energies E_A, E_B and E_C are equal at the bottom.

Question 7.
Give an example to show that the following statement is false. Any two forces acting on a body can be combined into single force that would have same effect.
Answer:
A single force i.e. resultant of two forces acting on a body depends upon the angle between them also. The simple example for this is if two forces 5 N and 5 N acting on the object in the opposite direction, the single resultant force acting on the body is zero. But, if two forces acting on the object along the same direction, then the resultant i.e. the single force is 5 + 5 = 10 N. Hence the given statement “any two forces acting on a body can be combined into single force that would leave same effect” is wrong.

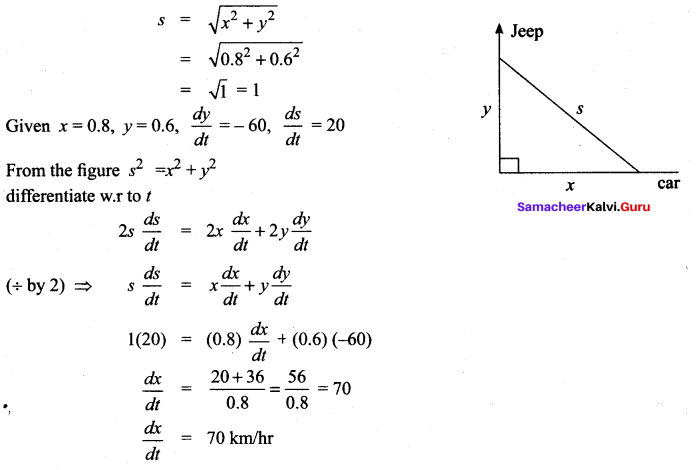
Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Numerical Problems

Question 1.
A uniform disc of mass 100 g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along a horizontal table with a velocity of 20 cm s^-2.
Answer:
Given,
Mass of the disc = 100 g = 100 x 10^-3 kg = \(\frac { 1 }{ 10 }\)kg
Velocity of disc = 20 cm s^-1 = 20 x 10^-2 ms^-1 = 0.2 ms^-1

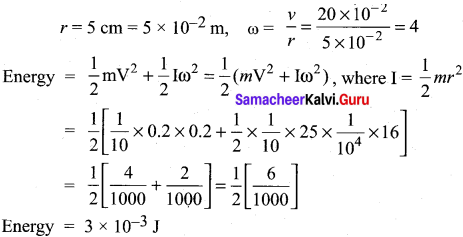
Question 2.
A particle of mass 5 units is moving with a uniform speed of v = \(3 \sqrt{2}\) units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum.
Answer:
Given,
Mass = 5 units
Speed = v = \(3 \sqrt{2}\) units
Y = X + 4
Angular momentum = L = m(\(\bar{r} \times \bar{v}\))
= m(x\(\hat{i}\) +y\(\hat{j}\))x(v\(\hat{i}\) + v\(\hat{j}\)) = m[xv\(\hat{k}\)-vy\(\hat{k}\)] = m[xv\(\hat{k}\)– v(x + 4)\(\hat{k}\)]
L = -mv\(\hat{k}\) = -4 x 5 x \(3 \sqrt{2}\)\(\hat{k}\) = – 60\(\sqrt{2}\)\(\hat{k}\)
L = 60\(\sqrt{2}\) units.

Question 3.
A fly wheel rotates with a uniform angular acceleration. If its angular velocity increases from 20π rad/s to 40π rad/s in 10 seconds, find the number of rotations in that period.
Answer:
Given,
Initial angular velocity ω₀ = 20 π rad/s
Final angular velocity ω = 40 π rad/s
Time t = 10 s
Solution:
Angular acceleration α = \(\frac{\omega-\omega_{0}}{t}\) = \(\frac {40π – 20π }{ 10 }\)
α = 2π rad/s²
According to equation of motion for rotational motion

The number of rotations = n = \(\frac {θ}{ 2π }\)
n = \(\frac {300π}{ 2π }\) = 150 rotations.

Question 4.
A uniform rod of mass m and length / makes a constant angle 0 with an axis of rotation which passes through one end of the rod. Find the moment of inertia about this gravity is.
Answer:
Moment of inertia of the rod about the axis which is passing through its center of gravity is


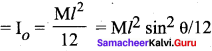
Moment of inertia of a uniform rod of mass m and length l about one axis which passes through one end of the rod

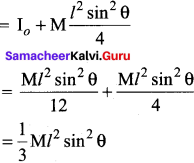
Question 5.
Two particles P and Q of mass 1 kg and 3 kg respectively start moving towards each other from rest under mutual attraction. What is the velocity of their center of mass?
Answer:
Given,
Mass of particle P = 1 kg Mass of particle Q = 3 kg
Solution:
Particles P and Q forms a system. Here no external force is acting on the system,

We know that M = \(\frac {d}{dt}\) (V_CM ) = f
It means that, C.M. of an isolated system remains at rest when no external force is acting and internal forces do not change its center of mass.

Question 6.
Find the moment of inertia of a hydrogen molecule about an axis passing through its center of mass and perpendicular to the inter-atomic axis.
Given: mass of hydrogen atom 1.7 x 10²⁷kg and inter atomic distance is equal to 4 x 10^-10m.
Answer:
Given,
Inter-atomic distance : 4 x 10^-10 m
Mass of H₂ atom : 1.7 x 10^-27 kg
Moment of inertia of H₂ =

Question 7.
On the edge of a wall, we build a brick tower that only holds because of the bricks’ own weight. Our goal is to build a stable tower whose overhang d is greater than the length l of a single brick. What is the minimum number of bricks you need?
(Hint: Find the center of mass for each brick and add.)
Answer:
Given:

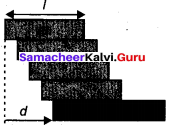
Length of the brick = l
Length of the overhang = d
The mono of bricks can be decided only by using the concept of position of center of gravity. The first brick is in contact with the ground and it will not fall over.
Let one end of brick 2 is coinciding with the center of brick 1 i.e. x = 0.
∴ The position of n brick is
x_n = (n – 1) \(\frac {L}{4}\)
The center of gravity is in the midway between the center of brick 2 and the center of brick n.
position of G =

brick tower will fall when G >\(\frac {L}{4}\) it shows that n > 4.

Question 8.
The 747 boing plane is landing at a speed of 70 m s^-1. Before touching the ground, the wheels are not rotating. How long a skid mark do the wing wheels leave (assume their mass is 100 kg which is distributed uniformly, radius is 0.7 m, and the coefficient of friction with the ground is 0.5)?
Answer:
The types of the plane will leave a skid mark if the speed of the types in contact with ground is lesser than the velocity of the plane. The condition for this is –
v > ω
(When the type attained an angular velocity of V/R)
The types will stop the skidding and starts the rolling.
The forces acting on the wheel after the plane touches down are,
N – P Normal force W – weight
The wheel is not accelerating means
N = ω
The torque about the center of the wheel is
τ = RF = µωR
The angular acceleration is

According to equation of motion, time taken to stop the skidding by the wheel is,

The six mark will have a length of
l = vt = 70 x 0.03 = 2.1 m
Note:
The 747 is resting on the runway, supported by 16 wheels under the wing, and 2 under the nose total length is 68.63 m. The normal force experienced by plane through its 16 wheels is ω = 232 KN.

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Additional Questions Solved

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Multiple Choice Questions

Question 1.
The changes produced by the deforming forces in a rigid body are –
(a) very large
(b) infinity
(c) negligibly small
(d) small
Answer:
(c) negligibly small

Question 2.
When a rigid body moves all particles that constitute the body follows-
(a) same path
(b) different paths
(c) either same or different path
(d) circular path
Answer:
(b) different path

Question 3.
For bodies of regular shape and uniform mass distribution, the center of mass is at –
(a) the comers
(b) inside the objects
(c) the point where the diagonals meet
(d) the geometric center
Answer:
(d) the geometric center

Question 4.
For square and rectangular objects center of mass lies at –
(a) the point where the diagonals meet
(b) at the comers
(c) on the center surface
(d) any point
Answer:
(a) the point where the diagonals meet

Question 5.
Center of mass may lie –
(a) within the body
(b) outside the body
(c) both (a) and (b)
(d) only at the center
Answer:
(c) both (a) and (b)

Question 6.
The dimension of point mass is –
(a) positive
(b) negative
(c) zero
(d) infinity
Answer:
(c) zero

Question 7.
The motion of center of mass of a system of two particles is unaffected by their internal forces –
(a) irrespective of the actual directions of the internal forces
(b) only if they are along the line joining the particles
(c) only if acts perpendicular to each other
(d) only if acting opposite
Answer:
(a) irrespective of the actual directions of the internal forces

Question 8.
A circular plate of diameter 10 cm is kept in contact with a square plate of side 10 cm. The density of the material and the thickness are same everywhere. The center of mass of the system will be
(a) inside the circular plate
(b) inside the square plate
(c) At the point of contact
(d) outside the system
Answer:
(6) inside the square plate

Question 9.
The center of mass of a system of particles does not depend on
(a) masses of particles
(b) position of the particles
(c) distribution of masses
(d) forces acting on the particles
Answer:
(d) forces acting on the particles

Question 10.
The center of mass of a solid cone along the line from the center of the base to the vertex is at –
(a) \(\frac { 1 }{ 2 }\) th of its height
(b) \(\frac { 1 }{ 3 }\) of its height
(c) \(\frac { 1 }{ 4 }\) th of its height
(d) \(\frac { 1 }{ 5 }\) th of its height
Answer:
(d) \(\frac { 1 }{ 5 }\) th of its height

Question 11.
All the particles of a body are situated at a distance of X from origin. The distance of the center of mass from the origin is –
(a) ≥ r
(b) ≤ r
(c) = r
(d) > r

Question
A free falling body breaks into three parts of unequal masses. The center of mass of the three parts taken together shifts horizontally towards –
(a) heavier piece
(b) lighter piece
(c) does not shift horizontally
(d) depends on vertical velocity
Answer:
(c) does not shift horizontally

Question 13.
The distance between the center of carbon and oxygen atoms in the gas molecule is 1.13 A. The center of mass of the molecule relative to oxygen atom is –
(a) 0.602 Å
(b) 0.527 Å
(c) 1.13 Å
(d) 0.565 Å
Answer:
(b) 0.527 Å
Given,
Inter atomic distance = 1.13 Å
Mass of carbon atom = 14
Mass of oxygen atom = 16
Let C.M. of molecule lies at a distance of X from oxygen atom-
i.e. m₁r₁ = m₂r₂
16 X = 14(1.13 – X)
30 X = 15.82
X = 0.527 Å

Question 14.
The unit of position vector of center of mass is-
(a) kg
(b) kg m²
(c) m
(d) m²
Answer:
(c) m

Question 15.
The sum of moments of masses of all the particles in a system about the center of mass is-
(a) minimum
(b) maximum
(c) zero
(d) infinity
Answer:
(c) zero

Question 16.
The motion of center of mass depends on-
(a) external forces acting on it
(b) internal forces acting within it
(c) both (a) and (b)
(d) neither (a) nor (b)
Answer:
(a) external forces acting on it

Question 17.
Two particles P and Q move towards with each other from rest with the velocities of 10 ms^-1 and 20 ms^-1 under the mutual force of attraction. The velocity of center of mass is-
(a) 15 ms^-1
(b) 20 ms^-1
(c) 30 ms^-1
(d) zero
Answer:
(d) zero

Question 18.
The reduced mass of the system of two particles of masses 2 m and 4 m will be –
(a) 2 m
(b) \(\frac {2 }{ 3 }\)y m
(c) \(\frac {3}{ 2 }\)y m
(d) \(\frac { 4 }{ 3 }\)m
Answer:
(d) \(\frac { 4 }{ 3 }\)m

Question 19.
The motion of the center of mass of a system consists of many particles describes its –
(a) rotational motion
(b) vibratory motion
(c) oscillatory motion
(d) translator y motion
Answer:
(c) oscillatory motion

Question 20.
The position of center of mass can be written in the vector form as –

Answer:

Question 21.
The positions of two masses m₁ and m₂ are x₁ and x₂. The position of center of mass is –

Answer:

Question 22.
In a two particle system, one particle lies at origin another one lies at a distance of X. Then the position of center of mass of these particles of equal mass is –

Answer:
(a) \(\frac {X}{2}\)

Question 23.
Principle of moments is –

Answer:

Question 24.
Infinitesimal quantity means –
(a) collective particles
(b) extremely small
(c) nothing
(d) extremely larger
Answer:
(b) extremely small

Question 25.
In the absence of external forces the center of mass will be in a state of –
(a) rest
(b) uniform motion
(c) may be at rest or in uniform motion
(d) vibration
Answer:
(c) may be at rest or in uniform motion

Question 26.
The activity of the force to produce rotational motion in a body is called as –
(a) angular momentum
(b) torque
(c) spinning
(d) drive force
Answer:
(b) torque

Question 27.
The moment of the external applied force about a point or axis of rotation is known as –
(a) angular momentum
(b) torque
(c) spinning
(d) drive force
Answer:
(b) torque

Question 28.
Torque is given as –
(a) \(\vec{r}\) . \(\vec{F}\)
(b) \(\vec{r}\) x \(\vec{F}\)
(c) \(\vec{F}\) x \(\vec{r}\)
(d) r F cos θ
Answer:
(b) \(\vec{r}\) x \(\vec{F}\)

Question 29.
The magnitude of torque is –
(a) rF sin θ
(b) rF cos θ
(c) rF tan θ
(d) rF
Answer:
(a) rF sin θ

Question 30.
The direction of torque ácts –
(a) along \(\vec{F}\)
(b) along \(\vec{r}\) & \(\vec{F}\)
(c) Perpendicular to \(\vec{r}\)
(d) Perpendicular to both \(\vec{r}\) & \(\vec{F}\)
Answer:
(d) Perpendicular to both \(\vec{r}\) & \(\vec{F}\)

Question 31.
The unit of torque is –
(a) is
(b) Nm^-2
(c) Nm
(d) Js^-1
Answer:
(c) Nm

Question 32.
The direction of torque is found using –
(a) left hand rule
(b) right hand rule
(c) palm rule
(d) screw rule
Answer:
(b) right hand rule

Question 33.
if the direction of torque is out of the paper then the rotation produced by the torque is –
(a) clockwise
(b) anticlockwise
(c) straight line
(d) random direction
Answer:
(a) clockwise

Question 34.
If the direction of the torque is inward the paper then the rotation is –
(a) clockwise
(b) anticlockwise
(c) straight line
(d) random direction
Answer:
(a) clockwise

Question 35.
if \(\vec{r}\) and \(\vec{F}\) are parallel or anti parallel, then the torque is –
(a) zero
(b) minimum
(c) maximum
(d) infinity
Answer:
(a) zero

Question 36.
The maximum possible value of torque is –
(a) zero
(b) infinity
(c) \(\vec{r}\) + \(\vec{F}\)
(d) rF
Answer:
(d) rF

Question 37.
The relation between torque and angular acceleration is –
(a) \(\vec{τ}\) = \(\frac{1}{\alpha}\)
(b) \(\vec{α}\) = \(\frac{\vec{\tau}}{\mathrm{I}}\)
(c) \(\vec{α}\) = I \(\vec{τ}\)
(d) \(\vec{τ}\) = \(\frac{\vec{\alpha}}{\mathrm{I}}\)
Answer:
(b) \(\vec{α}\) = \(\frac{\vec{\tau}}{\mathrm{I}}\)

Question 38.
Angular momentum is –
(a) \(\vec{P}\) x \(\vec{r}\)
(b) \(\vec{r}\) x \(\vec{P}\)
(c) \(\overrightarrow{\frac{r}{\vec{p}}}\)
(d) \(\vec{r}\) . \(\vec{P}\)
Answer:
(b) \(\vec{r}\) x \(\vec{P}\)

Question 39.
The magnitude of angular momentum is given by –
(a) rp
(b) rp sin θ
(c) rp cos θ
(d) rp tan θ
Answer:
(b) rp sin θ

Question 40.
Angular momentum is associated with –
(a) rotational motion
(b) linear motion
(c) both (a) and (b)
(d) circular motion only
Answer:
(c) both (a) and (b)

Question 41.
Angular momentum acts perpendicular to –
(a) \(\vec{r}\)
(b) \(\vec{P}\)
(c) both \(\vec{r}\) and \(\vec{P}\)
(d) plane of the paper
Answer:
(c) both \(\vec{r}\) and \(\vec{P}\)

Question 42.
Angular momentum is given by –
(a) \(\frac {I}{ω}\)
(b) τω
(c) Iω
(d) \(\frac {ωI}{2}\)
Answer:
(c) Iω

Question 43.
The rate of change of angular momentum is –
(a) Torque
(b) angular velocity
(c) centripetal force
(d) centrifugal force
Answer:
(a) Torque

Question 44.
The forces acting on a body when it is at rest –
(a) is gravitational force
(b) Normal force
(c) both gravitational as well as normal force
(d) No force is acting
Answer:
(c) both gravitational as well as normal force

Question 45.
The net force acting on a body when it is at rest is –
(a) gravitational force
(b) Normal force
(c) Sum of gravitational and normal force
(d) zero
Answer:
(d) zero

Question 46.
If net force acting on a body is zero, then the body is in –
(a) transnational equilibrium
(b) rotational equilibrium
(c) both (a) and (b)
(d) none
Answer:
(a) transnational equilibrium

Question 47.
If the net torque acting on the body is zero, then the body is in –
(a) transnational equilibrium
(b) rotational equilibrium
(c) mechanical equilibrium
(d) none
Answer:
(b) rotational equilibrium

Question 48.
when the net force and net torque acts on the body is zero then the body is in –
(a) transnational equilibrium
(b) rotational equilibrium
(c) mechanical equilibrium
(d) none
Answer:
(d) none

Question 49.
When the net force and net torque acts on the body is zero then the body is in –
(a) static equilibrium
(b) Dynamic equilibrium
(c) both (a) and (b)
(d) transnational equilibrium
Answer:
(c) both (a) and (b)

Question 50.
When two equal and opposite forces acting on the body at two different points, it may give –
(a) net force
(b) torque
(c) stable equilibrium
(d) none
Answer:
(b) torque

Question 51.
The torque in rotational motion is analogous to in transnational motion –
(a) linear momentum
(b) mass
(c) couple
(d) force
Answer:
(d) force

Question 52.
Which of the following example does not constitute a couple?
(a) steering a car
(b) turning a pen cap
(c) ball rolls on the floor
(d) closing the door
Answer:
(c) ball rolls on the floor

Questioner 53.
If the linear momentum and angular momentum are zero, then the object is said to be in –
(a) stable equilibrium
(b) unstable equilibrium
(c) neutral equilibrium
(d) all the above
Answer:
(d) all the above

Question 54.
When the body is disturbed, the potential energy remains same, then the body is in –
(a) stable equilibrium
(b) unstable equilibrium
(c) neutral equilibrium
(d) all the above
Answer:
(c) neutral equilibrium

Question 55
The point where the entire weight of the body acts is called as –
(a) center of mass
(b) center of gravity
(c) both (a) and (b)
(d) pivot
Answer:
(b) center of gravity

Question 56.
The forces acting on a cyclist negotiating a circular Level road is /are –
(a) gravitational force
(b) centrifugal force
(c) frictional force
(d) all the above
Answer:
(d) all the above

Question 57.
While negotiating a circular level road a cyclist has to bend by an angle θ from vertical to stay in an equilibrium is-
(a) \(\tan \theta=\frac{r g}{r^{2}}\)
(b) θ = \(\tan ^{-1}\left(\frac{v^{2}}{r g}\right)\)
(c) θ = \(\sin ^{-1}\left(\frac{r g}{r^{2}}\right)\)
(d) zero
Answer:
(b) θ = \(\tan ^{-1}\left(\frac{v^{2}}{r g}\right)\)

Question 58.
Moment of inertia for point masses –
(a) m²r
(b) rw²
(c) mr²
(d) zero
Answer:
(c) mr²

Question 59.
Moment of inertia for bulk object –
(a) rm²
(b) rw²
(c) \(m_{i} r_{i}^{2}\)
(d) \(\Sigma m_{i} r_{i}^{2}\)
Answer:
(d) \(\Sigma m_{i} r_{i}^{2}\)

Question 60.
For rotational motion, moment of inertia is a measure of –
(a) transnational inertia
(b) mass
(c) rotational inertia
(d) invariable quantity
Answer:
(c) rotational inertia

Question 61.
Unit of moment of inertia –
(a) kgm
(b) mkg^-2
(c) kgm²
(d) kgm^-1
Answer:
(c) kgm²

Question 62.
Dimensional formula for moment of inertia is –
(a) [ML^-2]
(b) [M²L^-1]
(c) [M^-2]
(d) [ML²]
Answer:
(d) [ML²]

Question 63.
Moment of inertia of a body is a –
(a) variable quantity
(b) invariable quantity
(c) constant quantity
(d) measure of torque
Answer:
(a) variable quantity

Question 64.
Moment of inertia of a thin uniform rod about an axis passing through the center of mass and perpendicular to the length is –
(a) \(\frac { 1 }{ 3 }\)Ml²
(b) \(\frac { 1 }{ 12 }\)Ml²
(c) \(\frac { 1 }{ 2 }\)M(l² + b² )
(d) Ml²
Answer:
(b) \(\frac { 1 }{ 12 }\)Ml²

Question 65.
Moment of inertia ofa thin uniform rod about an axis passing through one end and perpendicular to the length is-
(a) \(\frac { 1 }{ 3 }\)Ml²
(b) \(\frac { 1 }{ 12 }\)Ml²
(c) \(\frac { 1 }{ 2 }\)M(l² + b² )
(d) Ml²
Answer:
(a) \(\frac { 1 }{ 3 }\)Ml²

Question 66.
Moment of inertia of a thin uniform rectangular sheet about an axis passing through the center of mass and perpendicular to the plane of the sheet is-
(a) \(\frac { 1 }{ 3 }\)Ml²
(b) \(\frac { 1 }{ 12 }\)Ml²
(c) \(\frac { 1 }{ 2 }\)M(l² + b² )
(d) Ml²
Answer:
(c) \(\frac { 1 }{ 2 }\)M(l² + b² )

Question 67.
Moment of inertia of a thin uniform ring about an axis passing through the center of gravity and perpendicular to the plane is –
(a) MR²
(b) 2 MR²
(c) \(\frac { 1 }{ 2 }\)MR²
(d) \(\frac { 3 }{ 2 }\)MR²
Answer:
(a) MR²

Question 68.
Moment of inertia of a thin uniform ring about an axis passing through the center and lying on the plane (along diameter) is –
(a) MR²
(b) 2 MR²
(c) \(\frac { 1 }{ 2 }\) MR²
(d) \(\frac { 2 }{ 3 }\)MR²
Answer:
(c) \(\frac { 1 }{ 2 }\) MR²

Question 69.
Moment of inertia of a thin uniform disc about an axis passing through the center and perpendicular to the plane is –
(a) MR²
(b) 2 MR²
(c) \(\frac { 1 }{ 2 }\) MR²
(d) \(\frac { 2 }{ 3 }\)MR²
Answer:
(c) \(\frac { 1 }{ 2 }\) MR²

Question 70.
Moment of inertia of a thin uniform disc about an axis passing through the center lying on the plane (along diameter is)
(a) MR²
(b) \(\frac { 1 }{ 2 }\) MR²
(c) \(\frac { 3 }{ 2 }\) MR²
(d) \(\frac { 1 }{ 4 }\) MR²
Answer:
(d) \(\frac { 1 }{ 4 }\) MR²

Question 71.
Moment of inertia of a thin uniform hollow cylinder about an axis of the cylinder is –
(a) MR²
(b) \(\frac { 1 }{ 2 }\) MR²
(c) \(\frac { 3 }{ 2 }\) MR²
(d) \(\frac { 1 }{ 4 }\) MR²
Answer:
(a) MR²

Question 72.
Moment of inertia of a thin uniform hollow cylinder about an axis of the cylinder is –
(a) MR²
(b) M\(\left(\frac{\mathrm{R}^{2}}{2}+\frac{l^{2}}{12}\right)\)
(c) \(\frac { 1 }{ 2 }\) MR²
(d) M\(\left(\frac{\mathrm{R}^{2}}{4}+\frac{l^{2}}{12}\right)\)
Answer:
(b) M\(\left(\frac{\mathrm{R}^{2}}{2}+\frac{l^{2}}{12}\right)\)

Question 73.
Moment of inertia of a uniform solid cylinder about an axis passing through the center and along the axis of the cylinder is –
(a) MR²
(b) M\(\left(\frac{\mathrm{R}^{2}}{2}+\frac{l^{2}}{12}\right)\)
(c) \(\frac { 1 }{ 2 }\) MR²
(d) M\(\left(\frac{\mathrm{R}^{2}}{4}+\frac{l^{2}}{12}\right)\)
Answer:
(c) \(\frac { 1 }{ 2 }\) MR²

Question 74.
Moment of inertia of a uniform solid cylinder about as axis passing perpendicular to the length and passing through the center is –
(a) MR²
(b) M\(\left(\frac{\mathrm{R}^{2}}{2}+\frac{l^{2}}{12}\right)\)
(c) \(\frac { 1 }{ 2 }\) MR²
(d) M\(\left(\frac{\mathrm{R}^{2}}{4}+\frac{l^{2}}{12}\right)\)
Answer:
(d) M\(\left(\frac{\mathrm{R}^{2}}{4}+\frac{l^{2}}{12}\right)\)

Question 75.
Moment of inertia of a thin hollow sphere about an axis passing through the center along its diameter is
(a) \(\frac { 2 }{ 3 }\)MR²
(b) \(\frac { 5 }{ 3 }\)MR²
(c) \(\frac { 7 }{ 5 }\)MR²
(d) \(\frac { 2 }{ 5 }\)MR²
Answer:
(a) \(\frac { 2 }{ 3 }\)MR²

Question 76.
Moment of inertia of a thin hollow sphere about an axis passing through the edge along its tangent is –
(a) \(\frac { 2 }{ 3 }\)MR²
(b) \(\frac { 5 }{ 3 }\)MR²
(c) \(\frac { 7 }{ 5 }\)MR²
(d) \(\frac { 2 }{ 5 }\)MR²
Answer:
(b) \(\frac { 5 }{ 3 }\)MR²

Question 77.
torment of inertia of a uniform solid sphere about an axis passing through the center along its diameter is –
(a) \(\frac { 2 }{ 3 }\)MR²
(b) \(\frac { 5 }{ 3 }\)MR²
(c) \(\frac { 7 }{ 5 }\)MR²
(d) \(\frac { 2 }{ 5 }\)MR²
Answer:
(d) \(\frac { 2 }{ 5 }\)MR²

Question 78.
Moment of inertia of a uniform solid sphere about an axis passing through the edge along its tangent is –
(a) \(\frac { 2 }{ 3 }\)MR²
(b) \(\frac { 5 }{ 3 }\)MR²
(c) \(\frac { 7 }{ 5 }\)MR²
(d) \(\frac { 2 }{ 5 }\)MR²
Answer:
(c) \(\frac { 7 }{ 5 }\)MR²

Question 79.
The ratio of K²/R² of a thin uniform ring about an axis passing through the center and perpendicular to the plane is-
(a) 1
(b) 2
(c) \(\frac { 7 }{ 5 }\)
(d) \(\frac { 3 }{ 2 }\)
Answer:
(a) 1

Question 80.
The ratio of K²/ R² of a thin uniform disc about an axis passing through the center and perpendicular to the plane is –
(a) 1
(b) 2
(c) \(\frac {1}{ 2 }\)
(d) \(\frac { 3 }{ 2 }\)
Answer:
(c) \(\frac {1}{ 2 }\)

Question 81.
When no external torque acts on the body, the net angular momentum of a rotating body.
(a) increases
(b) decreases
(c) increases or decreases
(d) remains constant
Answer:
(d) remains constant

Question 82.
Moment of inertia of a body is proportional to –
(a) ω
(b) \(\frac { 1 }{ ω }\)
(c) ω²
(d) \(\frac{1}{\omega^{2}}\)
Answer:
(b) \(\frac { 1 }{ ω }\)

Question 83.
When the hands are brought closer to the body, the angular velocity of the ice dancer –
(a) decreases
(b) increases
(c) constant
(d) may decrease or increase
Answer:
(b) increases

Question 84.
When the hands are stretched out from the body, the moment of inertia of the ice dancer –
(a) decreases
(b) increases
(c) constant
(d) may decrease or increase
Answer:
(b) increases

Question 85.
The work done by the torque is –
(a) F. ds
(b) F. dθ
(c) τ dθ
(d) r.dθ
Answer:
(c) τ dθ

Question 86.
Rotational Kinetic energy of a body is –
(a) \(\frac { 1 }{ 2 }\)mr
(b) \(\frac { 1 }{ 2 }\) Iω²
(c) \(\frac { 1 }{ 2 }\)Iv²
(d) \(\frac { 1 }{ 2 }\)mω²
Answer:
(b) \(\frac { 1 }{ 2 }\) Iω²

Question 87.
Rotational kinetic energy is given by –
(a) \(\frac { 1 }{ 2 }\)mr
(b) \(\frac { 1 }{ 2 }\)Iv²
(c) \(\frac{\mathrm{L}^{2}}{2 \mathrm{I}}\)
(d) \(\frac{2 \mathrm{I}}{\mathrm{L}^{2}}\)
Answer:
(c) \(\frac{\mathrm{L}^{2}}{2 \mathrm{I}}\)

Question 88.
If E is a rotational kinetic energy then angular momentum is-
(a) \(\sqrt{2 \mathrm{IE}}\)
(b) \(\frac{\mathrm{E}^{2}}{2 \mathrm{I}}\)
(c) \(\frac{2 \mathrm{I}}{\mathrm{E}^{2}}\)
(d) \(\frac{E}{I^{2} \omega^{2}}\)
Answer:
(a) \(\sqrt{2 \mathrm{IE}}\)

Question 89.
The product of torque acting on a body and angular velocity is –
(a) Energy
(b) power
(c) work done
(d) kinetic energy
Answer:
(b) power

Question 90.
The work done per unit time in rotational motion is given by –
(a) \(\vec{F}\) .v
(b) \(\frac {dθ}{dt}\)
(c) τ ω
(d) I ω
Answer:
(c) τ ω

Question 91.
While rolling, the path of center of mass of an object is –
(a) straight line
(b) parabola
(c) hyperbola
(d) circle
Answer:
(a) straight line

Question 92.
In pure rolling, the velocity of the point of the rolling object which comes in contact with the surface is –
(a) maximum
(b) minimum
(c) zero
(d) 2 V_CM
Answer:
(c) zero

Question 93.
In pure rolling velocity of center of mass is equal to –
(a) zero
(b) Rω
(c) \(\frac { ω }{ R }\)
(d) \(\frac { R }{ ω }\)
Answer:
(b) Rω

Question 94.
In pure rolling, rotational velocity of points at its edges is equal to-
(a) Rω
(b) velocity of center of mass
(c) transnational velocity
(d) all the above
Answer:
(a) Rω

Question 95.
Sliding of the object occurs when –
(a) V_trans < V_rot
(b) V_trans = V_rot
(c) V_trans > V_rot
(d) V_trans = 0
Answer:
(c) V_trans > V_rot

Question 96.
Sliding of the object occurs while –
(a) V_trans = V_rot
(b) V_CM = Rω
(c) V_CM < Rω
(d) V_CM > Rω
Answer:
(d) V_CM > Rω

Question 97.
Slipping of the object occurs when –
(a) V_trans < V_rot
(b) V_trans = V_rot
(c) V_trans > V_rot
(d) V_trans = 0
Answer:
(a) V_trans < V_rot

Question 98.
Slipping of the object occurs when –
(a) V_trans = V_rot
(b) V_CM = Rω
(c) V_CM < Rω
(d) V_CM > Rω
Answer:
(c) V_CM < Rω

Question 99.
In sliding, the resultant velocity of a point of contact acts along –
(a) forward direction
(b) backward direction
(c) either (a) or (b)
(d) tangential direction
Answer:
(a) forward direction

Question 100.
In slipping, the resultant velocity of a point of contact acts along –
(a) forward direction
(b) backward direction
(c) either (a) or (b)
(d) tangential direction
Answer:
(b) backward direction

Question 101.
When a solid sphere is undergoing pure rolling, the ratio of transnational kinetic energy to rotational kinetic – energy is –
(a) 2 : 5
(b) 5 : 2
(c) 1 : 5
(d) 5 : 1
Answer:
(b) 5 : 2

Question 102.
Time taken by the rolling object in inclined plane to reach its bottom is –

Answer:

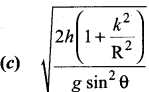
Question 103.
The velocity of the rolling object on inclined plane at the bottom of inclined plane is –

Answer:

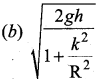
Question 104.
Moment of inertia of an annular disc about an axis passing through the centre and perpendicular to the plane of disc is –

Answer:

Question 105.
Moment of inertia of a cube about an axis passing through the center of mass and perpendicular to face is –
(a) \(\frac{\mathrm{Ma}^{2}}{6}\)
(b) \(\frac {1}{3}\) Ma²
(c) \(\frac {Ma}{6}\)
(d) \(\frac{\mathrm{Ma}^{2}}{12}\)
Answer:
(a) \(\frac{\mathrm{Ma}^{2}}{6}\)

Question 106.
Moment of inertia of a rectangular plane sheet about an axis passing through center of mass and perpendicular to side b in its plane is –
(a) \(\frac{\mathrm{Ml}^{2}}{12}\)
(b) \(\frac{\mathrm{Ma}^{2}}{12}\)
(c) \(\frac{\mathrm{Mb}^{2}}{12}\)
(d) \(\frac{\mathrm{Ml}^{2}}{6}\)
Answer:
(c) \(\frac{\mathrm{Mb}^{2}}{12}\)

Question 107.
Rotational kinetic energy can be calculated by using –
(a) \(\frac{1}{2}\) I ω²
(b) \(\frac{\mathrm{L}^{2}}{2I}\)
(c) \(\frac{1}{2}\) Lω
(d) all the above
Answer:
(b) \(\frac{\mathrm{L}^{2}}{2I}\) )

Question 108.
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of that axis from the center of the sphere is –
(a) \(\frac{2}{5}\)r
(b) \(\sqrt{\frac{2}{5}}\)r
(c) \(\sqrt{0.6r}\)
(d) \(\sqrt{\frac{5}{3}}\)
Answer:
(c) \(\sqrt{0.6r}\)
From parallel axis theorem
I = I_G + Md²
mr² = \(\frac{2}{5}\) mr² + md²
d = \(\sqrt{\frac{3}{5}}\)r = \(\sqrt{0.6r}\)

Question 109.
A wheel is rotating with angular velocity 2 rad/s. It is subjected to a uniform angular acceleration 2 rad/s² then the angular velocity after 10 s is
(a) 12 rad/s
(b) 20 rad/s
(c) 22 rad/s
(d) 120 rad/s
Answer:
(c) 22 rad/s
ω = ω₀ + αt
Here ω₀ = 2 rad/s,
α = 2 rad/s2
ω = 10 s
ω = 2 + 2 x 10 = 22 rad/s

Question 110.
Two rotating bodies A and B of masses m and 2m with moments of inertia I_A and I_B (I_b > I_A) have equal kinetic energy of rotation. If L_A and L_B be their angular momenta respectively,
then,
(a) L_B > L_A
(b) L_A > L_B
(c) L_A = \(\frac{L_{B}}{2}\)
(d) L_A = 2L_B
Answer:
(a) L_B > L_A

Question 111.
Three identical particles lie in x, y plane. The (x, y) coordinates of their positions are (3, 2), (1, 1), (5, 3) respectively. The (x, y) coordinates of the center of mass are –
(a) (a, b)
(b) (1, 2)
(c) (3, 2)
(d) (2, 1)
Answer:
(c) The X and Y coordinates of the center of mass are

Question 112.
A solid cylinder of mass 3 kg and radius 10 cm is rotating about its axis with a frequency of 20/π. The rotational kinetic energy of the cylinder
(a) 10 π J
(b) 12 J
(c) \(\frac{6 \times 10^{2}}{\pi}\) J
(d) 3 J
Answer:
(b) 12 J
Given,
M = 3 kg
R = 0.1 m
v = 20 / π
Angular frequency ω = 2πv = \(\frac{2π x 20}{π}\) = 40 rad/s^-1
Moment of inertia of the cylinder about its axis = I = \(\frac{1}{2}\) mR² = \(\frac{1}{2}\) x 3 x (0.1)² = 0.015 kg m²
K.E. = \(\frac{1}{2}\) Iω² = \(\frac{1}{2}\) x 0.015 x (40)² = 12 J

Question 113.
A circular disc is rolling down in an inclined plane without slipping. The percentage of rotational energy in its total energy is
(a) 66.61%
(b) 33.33%
(c) 22.22%
(d) 50%
Answer:
(b) 33.33%
Rotational K.E. = \(\frac{1}{2}\)Iω² \(\frac{1}{2}\)(\(\frac{1}{2}\)MR²)ω² = \(\frac{1}{4}\) MR²ω²
Transnational K.E. = \(\frac{1}{2}\)MV² = \(\frac{1}{2}\)M(Rω)² = \(\frac{1}{2}\) MR²ω²
Total kinetic energy = E_rot + E_trans = \(\frac{1}{4}\) MR²ω²\(\frac{1}{2}\)M(Rω)² = \(\frac{3}{4}\) MR²ω²
% of E_rot = \(\frac{E_{\text {rot }}}{E_{\text {Tot }}}\) x 100% = 33.33%

Question 114.
A sphere rolls down in an inclined plane without slipping. The percentage of transnational energy in its total energy is
(a) 29.6%
(b) 33.4%
(c) 71.4%
(d) 50%
Answer:
(c) 71.4%
Rotational K.e. E_rot =

Question 115.
Two blocks of masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block in the direction of the lighter block. The velocity of the center of mass is –
(a) 30 m/s
(b) 20 m/s
(c) 10 m/s
(d) 5 m/s
Answer:
(c) According to law of conservation of linear momentum
MV = (M + M) V_CM
V_CM = \(\frac{MV}{M + M}\) = \(\frac{10 × 10}{10 + 4}\) = 10 ms^-1

Question 116.
A mass is whirled in a circular path with constant angular velocity and its angular momentum is L. If the string is now halved keeping the angular velocity the same, the angular momentum is –
(a) \(\frac{L}{4}\)
(b) \(\frac{L}{2}\)
(c) L
(d) 2L
Answer:
(a) \(\frac{L}{4}\)
We know that
angular momentum L = Mr²
Here, m and co are constants L α r²
If r becomes \(\frac{r}{2}\) angular momentum becomes \(\frac{1}{4}\) th of its initial value.

Question 117.
The moment of inertia of a thin uniform ring of mass 1 kg and radius 20 cm rotating about the axis passing through the center and perpendicular to the plane of the ring is –
(a) 4 x 10^-2 kg m²
(b) 1 x 10^-2 kg m²
(c) 20 x 10^-2 kg m²
(d) 10 x 10^-2 kg m²
Answer:
(b) Moment of inertia I = MR² = 1 x (10 x 10^-2)² = 1 x 10^-2 kg m².

Question 118.
A solid sphere is rolling down in the inclined plane, from rest without slipping. The angle of inclination with horizontal is 30°. The linear acceleration of the sphere is –
(a) 28 ms^-2
(b) 3.9 ms^-2
(c) \(\frac{25}{7}\)ms^-2
(d) \(\frac{1}{20}\)ms^-2
Answer:
(c) \(\frac{25}{7}\)ms^-2
We know that,a =

Question 119.
An electron is revolving in an orbit of radius 2 A with a speed of 4 x 10⁵ m /s. The angular momentum of the electron is [Me = 9 x 10^-31 kg]
(a) 2 x 10^-35 kg m² s^-1
(b) 72 x 10^-36 kg m² s^-1
(c) 7.2 x 10^-34 kg m² s^-1
(d) 0.72 x 10^-37 kg m² s^-1
Answer:
(b) Angular momentum L = mV x r = 9 x 10^-31 x 4 x 10⁵ x 2 x 10^-10 = 72 x 10^-36kg m² s^-1

Question 120.
A raw egg and hard boiled egg are made to spin on a table with the same angular speed about the same axis. The ratio of the time taken by the eggs to stop is –
(a) =1
(b) < 1
(c) > 1
(d) none of these
Answer:
(d) When a raw egg spins, the fluid inside comes towards its side.
∴ “1” will increase in – turn it decreases ω. Therefore it takes lesser time than boiled egg.
∴\(\frac {time fìr raw egg}{time for boiled egg}\) < 1

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Short Answer Questions (1 Mark)

Question 1.
What is a rigid body?
Answer:
A rigid body is the one which maintains its definite and fixed shape even when an external force acts on it.

Question 2.
When an object will have procession? Give one example.
Answer:
The torque about the axis will rotate the object about it and the torque perpendicular to the axis will turn the axis of rotation when both exist simultaneously on a rigid body the body will have a procession.
Example:
The spinning top when it is about to come to rest.

Question 3.
Define angular momentum. Give an expression for it.
Answer:
The angular momentum of a point mass is defined as the moment of its linear momentum.
\(\vec{L}\) = \(\vec{r}\) x \(\vec{p}\) or L = rp sin θ

Question 4.
When an angular momentum of the object will be zero?
Answer:
If the straight path of the particle passes through the origin, then the angular momentum is zero, which is also a constant.

Question 5.
When an object be in-mechanical equilibrium?
Answer:
A rigid body is said to be in mechanical equilibrium when both its linear momentum and angular momentum remain constant.

Question 6.
Derive an expression for the power delivered by torque.
Answer:
Power delivered is the work done per unit time. IF we differentiate the expression for work done with respect to time, we get the instantaneous
power (P).
p = \(\frac{dw}{dt}\) = τ \(\frac{dθ}{dt}\)
p = τ dω

Question 7.
A boy sits near the edge of revolving circular disc

1. What will be the change in the motion of a disc?
2. If the boy starts moving from edge to the center of the disc, what will happen?

Answer:

1. As we know L = Iω = constant if the boy sits on the edge of revolving disc, its I will be increased in turn it reduces angular velocity.
2. If the boy starts moving towards the center of the disc, its I will decrease in turn that increases its angular velocity.

Question 8.
Are moment of inertia and radius of gyration of a body constant quantities?
Answer:
No, moment of inertia and radius of gyration depends on axis of rotation and also on the distribution of mass of the body about its axis..

Question 9.
A cat is able to land on its feet after a fall. Which principle of physics is being used? Explain.
Answer:
A cat is able to land on its feet after a fall. This is based on law of conservation of angular ~ momentum. When the cat is about to fall, it curls its body to decrease the moment of inertia and increase its angular velocity. When it lands it stretches out its limbs. By which it increases its moment of inertia and inturn it decreases its angular velocity. Hence, the cat lands safety.

Question 10.
About which axis a uniform cube will have minimum moment of inertia ?
Answer:
It will be about an axis passing through the center of the cube and connecting the opposite comers.

Question 11.
State the principle of moments of rotational equilibrium.
Answer:
∑ =\(\bar{\tau}\) = 0

Question 12.
Write down the moment of inertia of a disc of radius R and mass m about an axis in its plane at a distance R / 2 from its center.
Answer:
\(\frac { 1 }{ 2 }\) MR²

Question 13.
Can the couple acting on a rigid body produce translator motion ?
Answer:
No. It can produce only rotatory motion.

Question 14.
Which component of linear momentum does not contribute to angular momentum?
Answer:
Radial Component.

Question 15.
A system is in stable equilibrium. What can we say about its potential energy ?
Answer:
PE. is minimum.

Question 16.
Is radius of gyration a constant quantity ?
Answer:
No, it changes with the position of axis of rotation.

Question 17.
Two solid spheres of the same mass are made of metals of different densities. Which of them has a large moment of inertia about the diameter?
Answer:
Sphere of smaller density will have larger moment of inertia.

Question 18.
The moment of inertia of two rotating bodies A and B are I_A and I_B (I_A > I_B) and their angular momenta are equal. Which one has a greater kinetic energy ?
Answer:
K = \(\frac{\mathrm{L}^{2}}{2 \mathrm{I}}\) ⇒ K_A > K_A

Question 19.
A particle moves on a circular path with decreasing speed. What happens to its angular momentum?
Answer:
As \(\vec{L}\) = \(\vec{r}\) x m\(\vec{v}\) i.e., \(\vec{L}\) magnitude decreases but direction remains constant.

Question 20.
What is the value of instantaneous speed of the point of contact during pure rolling ?
Answer:
Zero.

Question 21.
Which physical quantity is conserved when a planet revolves around the sun ?
Answer:
Angular momentum of planet.

Question 22.
What is the value of torque on the planet due to the gravitational force of sun ?
Answer:
Zero.

Question 23.
If no external torque acts on a body, will its angular velocity be constant ?
Answer:
No.

Question 24.
Why there are two propellers in a helicopter ?
Answer:
Due to conservation of angular momentum.

Question 25.
A child sits stationary at one end of a long trolley moving uniformly with speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, then what is the effect of the speed of the centre of mass of the (trolley + child) system ?
Answer:
No change in speed of system as no external force is working.

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Short Answer Questions (2 Marks)

Question 26.
State the factors on which the moment of inertia of a body depends.
Answer:

• Mass of body
• Size and shape of body
• Mass distribution w.r.t. axis of rotation
• Position and orientation of rotational axis

Question 27.
On what factors does radius of gyration of body depend?
Answer:
Mass distribution.

Question 28.
Why the speed of whirl wind in a Tornado is alarmingly high?
Answer:
In this, air from nearly regions get concentrated in a small space, so I decreases considerably. Since Iω = constant so ω increases so high.

Question 29.
Can a body be in equilibrium while in motion? If yes, give an example.
Answer:
Yes, if body has no linear and angular acceleration then a body in uniform straight line of motion will be in equilibrium.

Question 30.
There is a stick half of which is wooden and half is of steel, (i) it is pivoted at the wooden end and a force is applied at the steel end at right angle to its length (ii) it is pivoted at the steel end and the same force is applied at the wooden end. In which case is the angular acceleration more and why?
Answer:
I (first case) > 1 (Second case)
∴ τ r = l α
⇒ α (first case) < α (second case)

Question 31.
If earth contracts to half of its present radius what would be the length of the day at equator?
Answer:

Question 32.
An internal force cannot change the state of motion of center of mass of a body. Flow does the internal force of the brakes bring a vehicle to rest?
Answer:
In this case the force which bring the vehicle to rest is friction, and it is an external force.

Question 33.
When does a rigid body said to be in equilibrium? State the necessary condition for a body to be in equilibrium.
Answer:
For translation equilibrium
∑ F_ext  = 0
For rotational equilibrium
∑ \(\overline{\mathrm{τ}}\)_ext  = 0

Question 34.
How will you distinguish between a hard boiled egg and a raw egg by spinning it on a table top’
Answer:
For same external torque, angular acceleration of raw egg will be small than that of Hard boiled egg.

Question 35.
Equal torques are applied on a cylinder and a sphere. Both have same mass and radius. Cylinder rotates about its axis and sphere rotates about one of its diameter. Which will acquire greater speed and why?
Answer:
τ = I α α = \(\frac { τ }{ I }\)
α in cylinder, α_C = \(\frac{\tau}{I_{C}}\)
α in sphere, α_S = \(\frac{\tau}{I_{S}}\)

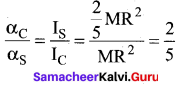
Question 36.
In which condition a body lying in gravitational field is in stable equilibrium?
Answer:
When vertical line through center of gravity passes through the base of the body.

Question 37.
Give the physical significance of moment of inertia. Explain the need of fly wheel in Engine.
Answer:
It plays the same role in rotatory motion as the mass does in translator y motion.

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Short Answer Questions (3 Marks)

Question 38.
Three mass point m₁, m₂, m₃ are located at the vertices of equilateral A of side ‘a’. What is the moment of inertia of system about an axis along the altitude of A passing through mi?
Answer:

Question 39.
A disc rotating about its axis with angular speed ω₀ is placed lightly (without any linear push) on a perfectly friction less table. The radius of the disc is R. What are the linear velocities of the points A, B and C on the disc shown in figure. Will the disc roll?
Answer:

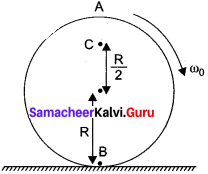
For A V_A = R ω₀ in forward direction
For B = V_B = R ω₀ in backward direction R
For C, V_C = \(\frac {R}{2}\) ω₀ in forward direction disc will not roll.

Question 40.
Find the torque of a force 7\(\hat{i}\) – 3\(\hat{j}\) – 5\(\hat{k}\) about the origin which acts on a particle whose position vector is \(\hat{j}\) +\(\hat{j}\) – \(\hat{j}\)
Answer:

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Numericals

Question 41.
Three masses 3 kg, 4 kg and 5 kg are located at the comers of an equilateral triangle of side 1 m. Locate the center of mass of the system.
Answer:
(x,y) = (0.54 m, 0.36 m)

Question 42.
Two particles mass 100 g and 300 g at a given time have velocities 10\(\hat{j}\) – 7\(\hat{j}\) – 3\(\hat{j}\) and 7\(\hat{i}\) – 9 \(\hat{j}\) + 6\(\hat{k}\) ms^-1 respectively. Determine velocity of center of mass.
Answer:
Velocity of center of mass = \(\frac{31 \hat{i}-34 \hat{j}+15 \hat{k}}{2}\) ms^-1

Question 43.
From a uniform disc of radius R, a circular disc of radius R / 2 is cut out. The center of the hole is at R / 2 from the center of original disc. Locate the center of gravity of the resultant flat body.
Answer:
Center of mass of resulting portion lies at R/6 from the center of the original disc in a direction opposite to the center of the cut out portion.

Question 44.
The angular speed of a motor wheel is increased from 1200 rpm to 3120 rpm in 16 seconds,

1. What is its angular acceleration (assume the acceleration to be uniform)
2. How many revolutions does the wheel make during this time ?

Answer:
a = 4π rad s^-2
n = 576

Question 45.
A meter stick is balanced on a knife edge at its center. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm, what is the mass of the meter stick?
Answer:
m = 66.0 gm.

Question 46.
A solid sphere is rolling op a friction less plane surface about its axis of symmetry. Find ratio of its rotational energy to its total energy.
Answer:

Question 47.
Calculate the ratio of radii of gyration of a circular ring and a disc of the same radius with respect to the axis passing through their centers and perpendicular to their planes.
Answer:
2 : 1

Question 48.
Two discs of moments of inertia I₁ and I₂ about their respective axes (normal to the disc and passing through the center), and rotating with angular speed col and ω₂ are brought into contact face to face with their axes of rotation coincident,

1. What is the angular speed of the two – disc system ?
2. Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy ? Take ω₁ ≠ ω₂.

Answer:

1. Let co be the angular speed of the two-disc system. Then by conservation of angular momentum
   
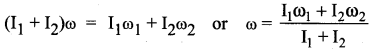
2. Initial K.E. of the two discs.
   

Hence there is a loss of rotational K.E. which appears as heat.
When the two discs are brought together, work is done against friction between the two discs.

Question 49.
In the HCL molecule, the separating between the nuclei of the two atoms is about 1.27 Å (1Å = 10^-10m). Find the approximate location of the CM of the molecule, given that the chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in all its nucleus.
Answer:
As shown in Fig. suppose the H nucleus is located at the origin. Then,
x₁ = 0, x₂ = 1.27 Å, m₁ = 1, m₂ = 35.5
The position of the CM of HCl molecule is


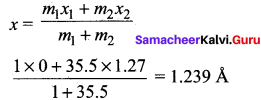
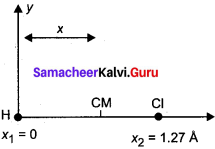
Thus the CM of HCl is located on the line joining H and Cl nuclei at a distance of 1.235 Å from the H nucleus.

Question 50.
A child stands at the center of turn table with his two arms out stretched. The turn table is set rotating with an angular speed of 40 rpm. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/3 times the initial value?

1. Assume that the turn table rotates without friction
2. Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation.

How do you account for this increase in kinetic energy ?
Answer:
Here ω = 40 rpm, I₂ = \(\frac { 1 }{ 2 }\) I₁
By the principle of conservation of angular momentum,
I₁ω₁ = I_2ω2 or I₁ x 4o = \(\frac {2}{5}\) I₁ ω₁ or ω₂ = 100 rpm
(ii) Initial kinetic energy of rotation –

new kinetic energy of rotation –

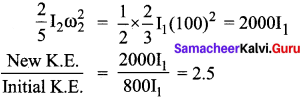
Thus the child’s new kinetic energy of rotation is 2.5 times its initial kinetic energy of rotation. This increase in kinetic energy is due to the internal energy of the child which he uses in folding his hands back from the out stretched position.

Question 51.
To maintain a rotor at a uniform angular speed of 200 rad s^-1 an engine needs to transmit a torque of 180 N m. What is the power required by the engine? Assume that the engine is 100% efficient.
Here ω = 200 rad s^-1, τ = 180 N m
Power, P = τω = 180 x 200 = 36,000 W = 36 kW.

Question 52.
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its center of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front and back wheel.
Answer:

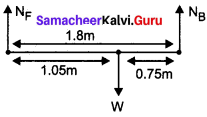
For transnational equilibrium of car
N_F + N_B = W = 1800 x 9.8 = 17640 N
For rotational equilibrium of car
1.05 N_F = 0.75 N_B
1.05 N_F = 0.75(17640 – N_F )
1.8 N_F = 13230
N_F = 13230 / 1.8 = 7350 N
N_B = 17640 – 7350 = 10290 N
Force on each front wheel = \(\frac {7350}{ 2 }\) = 3675 N
Force on each back wheel = \(\frac {10290}{ 2 }\) = 5145 N

Samacheer Kalvi 11th Physics Motion of System of Particles and Rigid Bodies Long Answer Questions (5 Marks)

Question 1.
Derive an expression for center of mass for distributed point masses.
Answer:
A point mass is a hypothetical point particle which has nonzero mass and no size or shape. To find the center of mass for a collection of n point masses, say,m₁ , m₂, m₃ ….. m_n  we have to first choose an origin and an appropriate coordinate system as shown in Figure. Let, x₁, x₂, x₃ …….. x_n be the X – coordinates of the positions of these point masses in the X direction from the origin.
The equation for the X coordinate of the center of mass is,

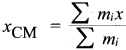
where, ∑ mi ¡s the total mass M of all the particles. ( ∑ mi = M).Hence,

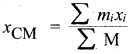
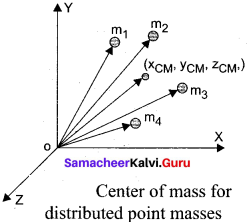
Similarly, we can also find y and z coordinates of the center of mass for these distributed point masses as indicated in figure.

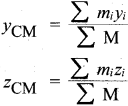
Hence, the position of center of mass of these point masses in a Cartesian coordinate system is (x_CM, y_CM z_CM). in general, the position of center of mass can be written in a vector form as,

where, is the position vector of the center of mass and \(\vec{r}_{i}\) = x_i \(\hat{j}\) + y_i\(\hat{j}\) + z_i\(\hat{k}\) is the position vector of the distributed point mass; where, \(\hat{i}\), \(\hat{j}\), and \(\hat{j}\) are the unit vectors along X, Y and Z-axis respectively.

Question 2.
Discuss the center of mass of two point masses with pictorial representation.
Answer:
With the equations for center of mass, let us find the center of mass of two point masses m₁ and m₂, which are at positions x₁ and x₂ respectively on the X – axis. For this case, we can express the position of center of mass in the following three ways based on the choice of the coordinate system.

(1) When the masses are on positive X-axis:
The origin is taken arbitrarily so that the masses m₁ and m₂ are at positions x₁ and x₂ on the positive X-axis as shown in figure (a). The center of mass will also be on the positive X- axis at x_CM as given by the equation,
\(x_{\mathrm{CM}}=\frac{m_{1} x_{1}+m_{2} x_{2}}{m_{1}+m_{2}}\)

(2) When the origin coincides with any one of the masses:
The calculation could be minimized if the origin of the coordinate system is made to coincide with any one of the masses as shown in figure (b). When the origin coincides with the point
mass m₁, its position x₁ is zero, (i.e. x₁ = 0). Then,
\(x_{\mathrm{CM}}=\frac{m_{1}(0)+m_{2} x_{2}}{m_{1}+m_{2}}\)
The equation further simplifies as,
x_CM = \(\frac{m_{2} x_{2}}{m_{1}+m_{2}}\)

(3) When the origin coincides with the center of mass itself:
If the origin of the coordinate system is made to coincide with the center of mass, then, x_CM = O and the mass rn1 is found to be on the negative X- axis as shown in figure (c). Hence, its position x1 is negative, (i.e. – x₁).

The equation given above is known as principle of moments.

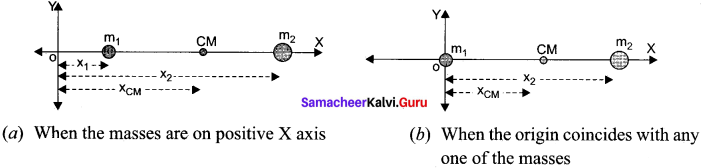
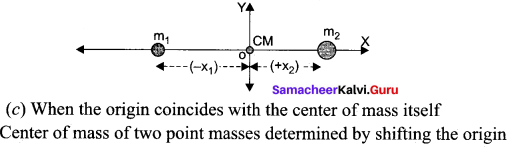
Question 3.
Derive an expression for kinetic energy in rotation and establish the relation between rotational kinetic energy and angular momentum.
Answer:
Let us consider a rigid body rotating with angular velocity ω about an axis as shown in figure. Every particle of the body will have the same angular velocity ω and different tangential velocities v based on its positions from the axis of rotation. Let us choose a particle of mass m_i situated at distance r_i from the axis of rotation. It has a tangential velocity v_i given by the relation, v_i = r_i ω. The kinetic energy KE_i. of the particle is,
KE_i = \(\frac{1}{2} m_{i} v_{i}^{2}\)
Writing the expression with the angular velocity,
KE = \(\frac{1}{2}\) m_i(r_iω)² = \(\frac{1}{2} m_{i} r_{i}^{2}\)ω²

For the kinetic energy of the whole body, which is made up of large number of such particles, the equation is written with summation as,
KE = \(\frac{1}{2}\left(\sum m_{i} r_{i}^{2}\right)\)ω²
where, the term ∑ m_ir_i^r is the moment of inertia I of the whole body. ∑ m_ir_i^r
Hence, the expression for KE of the rigid body in rotational motion is –
KE = \(\frac{1}{2}\) Iω²
This is analogous to the expression for kinetic energy in transnational motion.
KE = \(\frac{1}{2}\) Mv²

Relation between rotational kinetic energy and angular momentum
Let a rigid body of moment of inertia I rotate with angular velocity ω.
The angular momentum of a rigid body is, L = Iω
The rotational kinetic energy of the rigid body is, KE = \(\frac{1}{2}\) Iω²
By multiplying the numerator and denominator of the above equation with I, we get a relation between L and KE as,

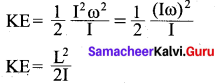
Question 4.
Discuss how the rolling is the combination of transnational and rotational and also be possibilities of velocity of different points in pure rolling.
Answer:
The rolling motion is the most commonly observed motion in daily life. The motion of wheel is an example of rolling motion. Round objects like ring, disc, sphere etc. are most suitable for rolling. Let us study the rolling of a disc on a horizontal surface. Consider a point P on the edge of the disc. While rolling, the point undergoes transnational motion along with its center of mass and rotational motion with respect to its center of mass.

Combination of Translation and Rotation:
We will now see how these transnational and rotational motions arc related in rolling. If the radius of the rolling object is R, in one full rotation, the center of mass is displaced by 2πR (its circumference). One would agree that not only the center of mass. but all the points Of l the disc are displaced by the same 2πR after one full rotation. The only difference is that the center of mass takes a straight path; but, all the other points undergo a path which has a combination of the transnational and rotational motion. Especially the point on the edge undergoes a path of a cyclonic as shown in the figure.

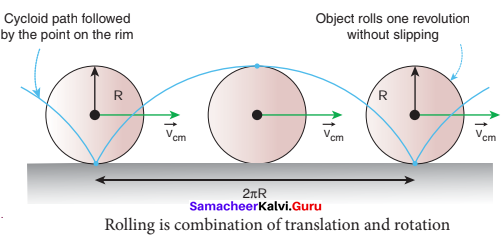
As the center of mass takes only a straight line path. its velocity v_CM is only transnational velocity v_TRANS (v_CM = v_TRANS). All the other points have two velocities. One is the transnational velocity v_TRANS (which is also the velocity of center of mass) and the other is the rotational velocity v_ROT (v_ROT = rω). Here, r ¡s the distance of the point from the center of mass and o is the angular velocity. The rotational velocity v_ROT is perpendicular to the instantaneous position vector from the center of mass as shown in figure (a). The resultant of these two velocities is v. This resultant velocity y is perpendicular to the position vector from the point of contact of the rolling object with the surface on which it is rolling as shown in figure (b).

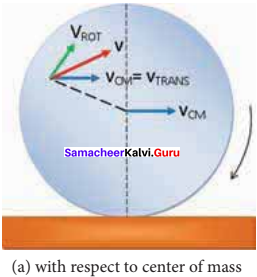
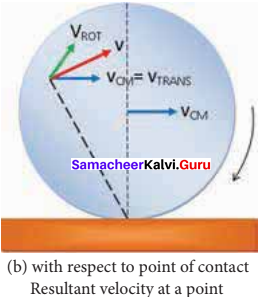
We shall now give importance to the point of contact. In pure rolling, the point of the rolling object which comes in contact with the surface is at momentary rest. This is the case with every point that is on the edge of the rolling object. As the rolling proceeds, all’the points on the edge, one by one come in contact with the surface; remain at momentary rest at the time of contact and then take the path of the cycloid as already mentioned.
Hence, we can consider the pure rolling in two different ways.
(i) The combination of transnational motion and rotational motion about the center of mass.
(or)
(ii) The momentary rotational motion about the point of contact.
As the point of contact is at momentary rest in pure rolling, its resultant velocity v is zero (v = o). For example, in figure, at the point of contact, v_TRANS is forward (to right) and v_ROT is backwards (to the left).

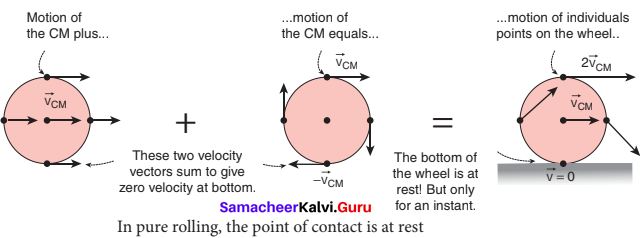
That implies that, v_TRANS and v_ROT are equal in magnitude and opposite in direction (v = v_TRANS – v_ROT = 0). Hence, we conclude that in pure rolling, for all the points on the edge, the magnitudes of v_TRANS and v_ROT are equal (v_TRANS = v_ROT) As v_TRANS = v_CM and v_ROT = Rω, in pure rolling we have,
v_CM = Rω

We should remember the special feature of the above equation. In rotational motion, as per the relation v = rω, the center point will not have any velocity as r is zero. But in rolling motion, it suggests that the center point has a velocity v_CM given by above equation v_CM – Rω. For the topmost point, the two velocities v_TRANS and v_ROT are equal in magnitude and in the same direction (to the right). Thus, the resultant velocity v is the sum of these two velocities, v = v_TRANS + v_ROT In other form, v = 2 v_CM as shown in figure below.

Question 5.
Derive an expression for kinetic energy in pure rolling.
Answer:
As pure is the combination of transnational and rotational motion, we can write the total kinetic energy (KE) as the sum of kinetic energy due to transnational motion (KE_TRANS) and kinetic energy due to rotational motion (KE_ROT).
KE = KE_TRANS + KE_ROT ………(i)
If the mass of the rolling object is M, the velocity of center of mass is v_CM, its moment of inertia about center of mass is I_CM and angular velocity is ω, then

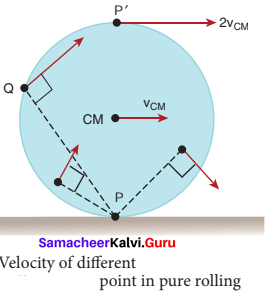
With center of mass as reference:
The moment of inertia (I_CM) of a rolling object about the center of mass is, I_CM = MK² and v_CM = Rω. Here, K is radius of gyration.

With point of contact as reference:
We can also arrive at the same expression by taking the momentary rotation happening with respect to the point of contact (another approach to rolling). If we take the point of contact as o, then,
KE = \(\frac {1}{2}\) I₀ω²

Here, I₀ is the moment of inertia of the object about the point of contact. By parallel axis
theorem, I₀ = I_CM + MK² Further we can write, I₀ MK² + MR². With v_CM = Rω or ω = \(\frac{v_{\mathrm{CM}}}{\mathrm{R}}\)

As the two equations (v) and (vi) are the same, it ¡s once again confirmed that the pure tolling problems could be solved by considering the motion as any one of the following two cases.
(i) The combination of transnational motion and rotational motion about the center of mass.
(or)
(ii) The momentary rotational motion about the point of contact.

Question 6.

1. Can a body in translator y motion have angular momentum? Explain.
2. Why is it more difficult to revolve a stone by tying it to a longer string than by tying it to a shorter string?

Answer:
(1) Yes, a body in translatory motion shall have angular momentum unless fixed point about which angular momentum is taken lies on the line of motion of body
\(|\overrightarrow{\mathrm{L}}|\) = rp sin θ
= 0 only when θ = O° or 180°

(2) MI of stone I = ml² (l – length of string) l is large, a is very small
τ = Iα
α = \(\frac {τ}{I}\) = \(\frac{\tau}{m l^{2}}\)
if l is large a is very small.
∴ more difficult to revolve.

We as a team believe the knowledge shared on our page regarding the Samacheer Kalvi 11th Physics Book Solutions Questions and Answers for Chapter 5 Motion of System of Particles and Rigid Bodies has cleared all your queries. For any other help don’t hesitate and leave us a comment so that we will get back to you at the soonest. Stay connected to our page to avail the latest updates regarding the Tamilnadu State Board Solutions for various subjects in a matter of seconds.

Students who are preparing for the Science exam can download this Tamilnadu State Board Solutions for Class 10th Science Chapter 20 from here for free of cost. These Tamilnadu State Board Textbook Solutions PDF cover all 10th Science Breeding and Biotechnology Book Back Questions and Answers.

All these concepts of Chapter 20 Breeding and Biotechnology are explained very conceptually by the subject teachers in Tamilnadu State Board Solutions PDF as per the prescribed Syllabus & guidelines. You can download Samacheer Kalvi 10th Science Book Solutions Chapter 20 Breeding and Biotechnology State Board Pdf for free from the available links. Go ahead and get Tamilnadu State Board Class 10th Science Solutions of Chapter 20 Breeding and Biotechnology.

Tamilnadu Samacheer Kalvi 10th Science Solutions Chapter 20 Breeding and Biotechnology

Kickstart your preparation by using this Tamilnadu State Board Solutions for Class 20th Science Chapter 20 Breeding and Biotechnology Questions and Answers and get the max score in the exams. You can cover all the topics of Chapter 20 easily after studying the Tamilnadu State Board Class 20th Science Textbook solutions pdf. Download the Tamilnadu State Board Science Chapter 20 Breeding and Biotechnology solutions of Class 20th by accessing the links provided here and ace up your preparation.

Samacheer Kalvi 10th Science Breeding and Biotechnology Textual Evaluation Solved

I. Choose the Correct Answer.

Breeding And Biotechnology Class 10 Question 1.
Which method of crop improvement can be practised by a farmer if he is inexperienced?
(a) clonal selection
(b) mass selection
(c) pure line selection
(d) hybridisation.
Answer:
(a) clonal selection

Breeding And Biotechnology In Tamil Question 2.
Pusa Komai is a disease resistant variety of:
(a) sugarcane
(b) rice
(c) cow pea
(d) maize
Answer:
(c) cow pea

Samacheerkalvi.Guru Science Question 3.
Himgiri developed by hybridisation and selection for disease resistance against rust pathogens is a variety of ______.
(a) chilli
(b) maize
(c) sugarcane
(d) wheat.
Answer:
(d) wheat.

Question 4.
The miracle rice which saved millions of lives and celebrated its 50th birthday is:
(a) IR 8
(b) IR 24
(c) Atomita 2
(d) Ponni
Answer:
(a) IR 8

Question 5.
Which of the following is used to produce products useful to humans by biotechnology techniques?
(a) enzyme from organism
(b) live organism
(c) vitamins
(d) both (a) and (b).
Answer:
(d) both (a) and (b).

Question 6.
We can cut the DNA with the help of:
(a) scissors
(b) restriction endonucleases
(c) knife
(d) RNAase
Answer:
(b) restriction endonucleases

Question 7.
rDNA is a ______.
(a) vector DNA
(b) circular DNA
(c) recombinant of vector DNA and desired DNA
(d) satellite DNA.
Answer:
(c) recombinant of vector DNA and desired DNA

Question 8.
DNA fingerprinting is based on the principle of identifying sequences of DNA:
(a) single-stranded
(b) mutated
(c) polymorphic
(d) repetitive
Answer:
(d) repetitive

Question 9.
Organisms with a modified endogenous gene or a foreign gene are also known as ______.
(a) transgenic organisms
(b) genetically modified
(c) mutated
(d) both (a) and (b).
Answer:
(a) transgenic organisms

Question 10.
In hexaploid wheat (2n = 6x = 42) the haploid (n) and the basic(x) number of chromosomes are:
(a) n = 7 and x = 21
(b) n = 21 and x = 21
(c) n = 1 and x = 1
(d) n = 21 and x = 7
Answer:
(d) n = 21 and x = 7

II Fill in the blanks.

Question 1.
Economically important crop plants with superior quality are raised by ______.
Answer:
Breeding.

Question 2.
A protein rich wheat variety is ______.
Answer:
Atlas 66.

Question 3.
_______ is the chemical used for doubling the chromosomes.
Answer:
Colchicine.

Question 4.
The scientific process which produces crop plants enriched with desirable nutrients is called ______.
Answer:
Biofortification.

Question 5.
Rice normally grows well in alluvial soil, but _____ is a rice variety produced by mutation breeding that grows well in saline soil.
Answer:
Atomita – 2 rice

Question 6.
_____ technique made it possible to genetically engineer living organism.
Answer:
Recombinant DNA.

Question 7.
Restriction endonucleases cut the DNA molecule at specific positions known as ______.
Answer:
Molecular scissors.

Question 8.
Similar DNA fingerprinting is obtained for ______.
Answer:
Identical twins.

Question 9.
______ cells are undifferentiated mass of cells.
Answer:
Pleuripotent.

Question 10.
In gene cloning, the DNA of interest is integrated in a ______.
Answer:
Vector [plasmid].

III. State whether true or false. If false, write the correct statement.

Question 1.
Raphano brassica is a man – made tetraploid produced by colchicine treatment.
Answer:
True.

Question 2.
The process of producing an organism with more than two sets of chromosome is called mutation.
Answer:
False.
Correct statement: The process of producing an organism with more than two sets of chromosome is called polyploidy.

Question 3.
A group of plants produced from a single plant through vegetative or asexual reproduction are called a pureline.
Answer:
False.
Correct statement: A group of plants produced from a single plant through vegetative or asexual reproduction are called clones.

Question 4.
Iron fortified rice variety determines the protein quality of the cultivated plant.
Answer:
False.
Correct statement: Iron fortified rice variety determines the iron quality of the cultivated plant.

Question 5.
Golden rice is a hybrid.
Answer:
False.
Correct statement: Golden rice is a genetically modified plant.

Question 6.
Bt gene from bacteria can kill insects.
Answer:
True.

Question 7.
In vitro fertilisation means the fertilisation done inside the body.
Answer:
False.
Correct statement: In vitro fertilisation means the fertilisation done outside the body.

Question 8.
DNA fingerprinting technique was developed by Alec Jeffrey.
Answer:
True.

Question 9.
Molecular scissors refers to DNA ligases.
Answer:
False.
Correct statement: Molecular scissors refers to Restriction Enzymes.

IV. Match the following:

Question 1.

Answer:

1. (c) Semi – dwarf wheat
2. (e) Semi – dwarf Rice
3. (b) Sugarcane
4. (a) Phaseolus mungo
5. (d) Groundnut
6. (h) the first hormone produced using rDNA technique
7. (f) Bacillus thuringienesis
8. (g) Beta carotene.

V. Understand the assertion statement, justify the reason given and choose the correct choice:

(a) The assertion is correct and the reason is wrong.
(b) Reason is correct and the assertion is wrong.
(c) Both assertion and reason are correct.
(d) Both assertion and reason are wrong.

Question 1.
Assertion: Hybrid is superior to either of its parents.
Reason: Hybrid vigour is lost upon inbreeding.
Answer:
(a) The assertion is correct and the reason is wrong.

Question 2.
Assertion: Colchicine reduces the chromosome number.
Reason: It promotes the movement of sister chromatids to the opposite poles.
Answer:
(d) Both assertion and reason are wrong.

Question 3.
Assertion: rDNA is superior over hybridisation techniques.
Reason: Desired genes are inserted without introducing the undesirable genes in target organisms.
Answer:
(c) Both assertion and reason are correct.

VI. Answer in a Sentence

Question 1.
Give the name of the wheat variety having higher dietary fibre and protein.
Answer:
Atlas 66, a protein-rich variety, having higher dietary fibre and protein.

Question 2.
Semi-dwarf varieties were introduced in rice. This was made possible by the presence of dwarfing gene in rice. Name this dwarfing gene.
Answer:
Dee-geo-woo-gen a dwarf variety from China.

Question 3.
Define genetic engineering.
Answer:
Genetic engineering is the manipulation and transfer of genes from one organism to another organism to create a new DNA called recombinant DNA (rDNA). Genetic engineering is also called recombinant DNA technology.

Question 4.
Name the types of stem cells.
Answer:
Embryonic stem cells and somatic stem cells are the types of stem cells.

Question 5.
What are transgenic organisms?
Answer:
Plants or animals expressing a modified endogenous gene or a foreign gene are called transgenic organisms.

Question 6.
State the importance of biofertiliser.
Answer:
Biofertilizer adds nutrients through the natural process of nitrogen fixation, stimulate the plant growth through the synthesis of growth-promoting substance.

VII. Short Answer Questions

Question 1.
Discuss the method of breeding for disease resistance.
Answer:
Plant diseases are caused by pathogens like viruses, bacteria and fungi. This affects crop yield. To develop disease-resistant varieties of crops, that would increase the yield and reduce the use of fungicides and bactericides are important. Some disease-resistant varieties are as follows:

Question 2.
Name three improved characteristics of wheat that helped India to achieve high productivity.
Answer:
Sonalika, kalyan and sona are the three improved characteristic of wheat that helped India to achieve high productivity.

Question 3.
Name two maize hybrids rich in amino acid lysine.
Answer:
Protina, Shakti and Rathna are lysine – rich maize hybrids, which are developed in India.

Question 4.
Distinguish between
(a) Somatic gene therapy and germline gene therapy.
(b) Undifferentiated cells and differentiated cells.
Answer:
(a) Somatic gene therapy and germline gene therapy.

(b) Undifferentiated cells and differentiated cells.

Question 5.
State the applications of DNA fingerprinting technique.
Answer:
Applications of DNA Fingerprinting:
(i) DNA fingerprinting technique is widely used in forensic applications like crime investigation such as identifying the culprit. It is also used for paternity testing in case of disputes.
(ii) It also helps in the study of genetic diversity of population, evolution and speciation.

Question 6.
How are stem cells useful in the regenerative process?
Answer:
Sometimes cells, tissues and organs in the body may be permanently damaged or lost due to genetic condition or disease or injury. In such situations, stem cells are used for the treatment of diseases, which is called stem – cell therapy. In treating neurodegenerative disorders like Parkinson’s disease and Alzheimer’s disease neuronal stem cells can be used to replace the damaged or lost neurons.

Question 7.
Differentiate between outbreeding and inbreeding.
Answer:
Inbreeding:
When breeding or mating takes place between animals of the same breed, for about 4 – 6 generations, then it is called inbreeding. Superior males and superior females of the same breed are identified and mated in pairs. It helps in the accumulation of superior genes and the elimination of undesirable genes. Inbreeding depression is the continued inbreeding, which reduces fertility and productivity. Inbreeding exposes harmful recessive genes that are eliminated by selection.

Outbreeding:
The breeding of unrelated animals is outbreeding. The offsprings formed are called hybrids. The hybrids are stronger and vigorous than their parents. Cross between two different species with desirable features of economic value is mated. Mule is superior to the horse in strength, intelligence, ability to work and resistance to diseases, but they are sterile.

VIII. Long Answer Questions

Question 1.
What are the effects of hybrid vigour in animals.
Answer:

1. Increased production of milk by cattle.
2. Increased production of egg by poultry.
3. High quality of meat is produced.
4. Increased growth rate in domesticated animals.

Question 2.
Describe mutation breeding with an example.
Answer:
The mutation is defined as the sudden heritable change in the nucleotide sequence of DNA in an organism. The genetic variations brings out changes in an organism. The organism which undergoes mutation is called a mutant.
The factors which induce mutations are known as mutagens or mutagenic agents. The mutagens are of two types:
(a) Physical mutagens: Radiations like X – rays, a, P and Y – rays, UV rays and temperature, etc, which induce, maturations are called physical mutagens.

(b) Chemical mutagens: Chemical substances that induce mutations are called chemical mutagens, eg. Mustard gas and nitrous acid. The utilization of induced mutation in crop improvement is called mutation inbreeding.
Achievements of mutation breeding:

• Sharbati Sonora wheat produced from Sonora – 64 by using gamma rays.
• Atomica – 2 rice with saline tolerance and pest resistance.
• Groundnuts with thick shells.

Question 3.
Biofortification may help in removing hidden hunger. How?
Answer:
Biofortification: Biofortification is the scientific process of developing crop plants enriched with high levels of desirable nutrients like vitamins, proteins and minerals. Some examples of crop varieties developed as a result of biofortification are given below:

1. Protina, Shakti and Rathna are lysine rich maize hybrids (developed in India).
2. Atlas 66, a protein rich wheat variety.
3. Iron rich fortified rice variety’.
4. Vitamin A enriched carrots, pumpkin and spinach.

Question 4.
With a neat labelled diagram explain the techniques involved in gene cloning.
Answer:
The carbon copy or more appropriately, a clone means to make a genetically exact copy of an organism. ‘Dolly’ is the cloned sheep.

In gene cloning, a gene or a piece of DNA fragment is inserted into a bacterial cell, where DNA will be multiplied (copied) as the cell divides.
The basic steps involved in gene cloning are:

• Isolation of desired DNA fragment by using restriction enzymes.
• Insertion of the DNA fragment into a suitable vector (plasmid) to make rDNA.
• Transfer of rDNA into the bacterial host cell (Transformation).
• Selection and multiplication of the recombinant host cell to get a clone.
• Expression of the cloned gene in the host cell.

Using this strategy several enzymes, hormones and vaccines can be produced.

Question 5.
Discuss the importance of biotechnology in the field of medicine.
Answer:
Using genetic engineering techniques medicinally important valuable proteins or polypeptides that form the potential pharmaceutical products for the treatment of various diseases have been developed on a commercial scale.
Pharmaceutical products developed by rDNA technique:

1. Insulin used in the treatment of diabetes.
2. Human growth hormone used for treating children with growth deficiencies.
3. Blood clotting factors are developed to treat haemophilia.
4. Tissue plasminogen activator is used to dissolve blood clots and prevent heart attack.
5. Development of vaccines against various diseases like Hepatitis B and rabies.

IX. Higher Order Thinking Skills (HOTS) Questions

Question 1.
A breeder wishes to incorporate desirable characters into the crop plants. Prepare a list of characters he will incorporate.
Answer:
The list of character he will incorporate are:

1. High yielding and better quantity
2. Disease resistance
3. Insects pest resistance
4. Improved nutritional quality
5. Short duration

Question 2.
Organic farming is better than Green Revolution. Give reasons.
Answer:

• Dwarfness is desired in cereals, so fewer nutrients are consumed by the crops.
• Fertilizer is responsive.
• Disease resistant varieties.
• Insect and pest resistant crop varieties.
• High levels of desirable nutrients like vitamins, proteins and minerals.

Question 3.
Polyploids are characterised by gigantism. Justify your answer.
Answer:
An organism having more than two set of chromosome is called polyploidy. It can be induced by physical agents such as heat or cold treatment, X-rays and chemical agents like colchicine. As organisms produced by polyploidy have more than two set of chromosomes they are gigantic.

Question 4.
‘P’ is a gene required for the synthesis of vitamin A. It is integrated with the genome of ‘Q’ to produce genetically modified plant ‘R’.
(i) What is P, Q and R?
(ii) State the importance of ‘R’ in India.
Answer:
(i)  The P, Q and R:

• P – Beta – carotene gene.
• Q – Prevent vitamin A deficiency.
• R – Golden rice.

(ii) Importance of rice in India:

• Rice is the most important staple food for millions of people in developing countries like India.
• Beta – carotene is produced in the endosperm of the grain. It could control the chronic health problems caused by vitamin A deficiency, especially among the poor in developing countries like India.

Samacheer Kalvi 10th Science Breeding and Biotechnology Additional Questions Solved

I. Fill in the blanks.

Question 1.
Plant ______ is the art of developing economically important plants.
Answer:
Breeding.

Question 2.
Plant diseases are caused by ______ like viruses, bacteria and fungi.
Answer:
Pathogen.

Question 3.
______ is the first man – made cereal hybrid.
Answer:
Triticale.

Question 4.
The superiority of the hybrid obtained by cross-breeding is called _____ or ______.
Answer:
Heterosis
or
Hybrid vigour.

Question 5.
The other name for genetic engineering is ______.
Answer:
Recombinant DNA technology.

Question 6.
The organism which undergoes mutation is called a ______ and the factors which induce mutations are ______.
Answer:
Mutant; mutagenic agents.

Question 7.
The replacement of the defective gene in a germ cell (egg or sperm) is called ______.
Answer:
Germline gene therapy.

Question 8.
Blood clotting factors are developed to treat ______.
Answer:
Haemophilia.

Question 9.
Stem cells, which are undifferentiated or unspecialised mass of cells can be used for the treatment is called ______.
Answer:
Stem cell therapy.

Question 10.
_______ is used in the treatment of diabetes.
Answer:
Insulin.

II. Match the following:

Question 1.

Answer:
1. (c) Bacterial blight
2. (f) Induce mutation
3. (e) Pusa Sawani
4. (a) Joining the DNA fragments
5. (d) Flat bean
6. (b) New breed of sheep.

III. Write “True or False” statements. Correct the false statements:

Question 1.
Modem Agricultural practices are activities carried out to improve the plants.
Answer:
True.

Question 2.
When breeding takes place between animals of the same breed, it is called outbreeding.
Answer:
False.
Correct statement: When breeding takes place between animals of the same breed, it is called inbreeding.

Question 3.
The process of introducing high yielding varieties of plants from one place to another is called a selection.
Answer:
False.
Correct statement: The process of introducing high yielding varieties of plants from one place to another is called Exotic species.

Question 4.
The mutation is a sudden inheritable change in the nucleus sequence of DNA in an organism.
Answer:
False.
Correct statement: Mutation is a sudden heritable change in the nucleotide sequence of DNA in an organism.

Question 5.
A breed is a group of animals of common origin within a species, which has certain characters, that are not found in other members of the same species.
Answer:
True.

IV. Choose the correct answer.

Question 1.
The high yielding rice variety from Indonesia and China are ______.
(a) Peta and DGWG
(b) IR-8 and Gold rice
(c) Hexaploid Triticale and Triticum durum
(d) Sonalika and Kalyan Sona.
Answer:
(a) Peta and DGWG

Question 2.
First artificially synthesized hormone is:
(a) Secretin
(b) Insulin
(c) Glucagon
(d) Renin
Answer:
(b) Insulin

Question 3.
The presence of this substance in bacteria can undergo replication independently along with chromosomal DNA ______.
(a) heritable
(b) colchicine
(c) mutation
(d) plasmid.
Answer:
(d) plasmid.

Question 4.
Bacillus thuringiensis (Bt) stains have been used for designing novel.
(a) Bio-metallogical techniques
(b) Bio-insecticidal plants
(c) Bio-mineralization
(d) Bio-fertilizer
Answer:
(b) Bio-insecticidal plants

Question 5.
A group of plants produced from a single plant through vegetative or asexual reproduction is called ______.
(a) Transgenic
(b) Hexaploid
(c) clones
(d) mutation.
Answer:
(b) Hexaploid

V. Answer the following briefly:

Question 1.
What is the green revolution? Who is the “Father of Green Revolution”?
Answer:
Green Revolution is the process of increasing food production through high yielding crop varieties and modem agricultural techniques in underdeveloped and developing nations. Dr Norman. E. Borlaug, an American agronomist is the “Father of Green Revolution”.

Question 2.
Write the role of polyploidy in crop improvement.
Answer:
The role of polyploidy in crop improvement are production of:

1. Seedless watermelons (3n) and bananas (3n).
2. TV-29 (triploid variety of tea) with larger shoots and drought tolerance.
3. Triticale (6n) is a hybrid of wheat and rye. To make this plant fertile polyploidy is induced. It has higher dietary fibre and protein.
4. Raphanobrassica is an allotetraploid by colchicine treatment.

Question 3.
What is Bio – fortification? Give any two examples.
Answer:
Bio – fortification is the scientific process of developing crop plants enriched with high levels of desirable nutrients like vitamins, proteins and minerals.
Examples of crop varieties developed as a result of bio – fortification are:

• Protina, Shakti and Rathna are lysine – rich maize hybrids.
• Atlas 66, A protein – rich wheat variety.

Question 4.
Give two examples of cross-breeding in animals.
Answer:
Cross breed of fowls: White Leghorn X Plymouth Rock
↓
Hybrid fowl – yield more eggs

Cross breed of cows : Developed by mating the bulls of exotic breeds and cows of indigenous breeds.
Brown Swiss X Sahiwal
↓
Karan Swiss – yield 2-3 times more milk than indigenous cows.

Question 5.
What is hybridization? Explain the hybridization experiment.
Answer:
The process of crossing two or more types of plants for bringing their desired characters together into one progeny hybrid is called hybridization. Hybridization is creating a genetic variation to get improved varieties.

Hybridization Experiment:
Triticale is the first man-made cereal hybrid. It is obtained by crossing wheat (Triticum durum, 2n = 28) and rye (Secale cereal, 2n = 14). The F, a hybrid is sterile (2n = 21). Then the chromosome number is doubled using colchicine and it becomes hexaploid triticale (2n = 42). The cycle of crop raising and selection continues until the plants with the desired characters are finally obtained.

Question 6.
Name the methods of plant breeding for crop improvement.
Answer:
The methods of plant breeding to develop high yielding varieties, for crop improvement, are as follows:

• Introduction of new varieties of plants
• Selection
• Polyploid breeding
• Mutation breeding
• Hybridization.

Question 7.
Explain briefly about gene therapy.
Answer:
The replacement of a defective gene by the direct transfer of functional genes into humans to treat genetic disease or disorder is referred to as gene therapy.
The recombinant DNA technology is used for gene therapy:

• Somatic gene therapy is the replacement of the defective gene in somatic cells.
• Gene line gene therapy is the replacement of the defective gene in the germ cell (egg or sperm).

Question 8.
What were the important discoveries that led to the stepping stones of recombinant DNA technology?
Answer:

1. Presence of plasmid in bacteria that can undergo replication independently along with chromosomal DNA.
2. Restriction enzymes cuts or break DNA at specific sites and are also called as molecular scissors.
3. DNA ligases are the enzymes which help in ligating (joining) the broken DNA fragments.

Question 9.
What does modern agriculture include?
Answer:
Modem agricultural practices are activities carried out to improve the cultivation of plants. It includes:

1. Preparation of soil
2. Sowing
3. Application of manures and fertilizers
4. Proper irrigation
5. Protection from weeds and pests
6. Harvesting and threshing
7. Storage

Question 10.
What is the aim of crop improvement?
Answer:
The aim of crop improvement is to develop improved crop varieties possessing higher yield, better quality, resistance to diseases and shorter duration.

Question 11.
(a) What are the two important properties of stem cells?
(b) Write a short note on two types of stem cells.
Answer:
(a) Properties of stem cells:
It’s the ability to divide and give rise to more stem cells by self-renewal.
It’s the ability to give rise to specialised cells with specific functions by the process of differentiation.

(b) Types of cells:

• Embryonic stem cells: Embryonic stem cells are derived from the inner cell mass of the blastocyst, which can be extracted from the early embryos. These cells can be developed into any cell in the body.
• Adult stem cell or somatic stem cell: These cells are found in the newborn and adults. They have the ability to divide and give rise to specific cell types. Sources of adult stem cells are amniotic fluid, umbilical cord and bone marrow.

Question 12.
What are bulk genomic DNA and satellite DNA?
Answer:
In human beings, 99 % of the DNA base sequences are the same and this is called a bulk genomic DNA. The remaining 1 % of the DNA sequence differs from one individual to another. This 1 % DNA sequence is present as a small stretch of repeated sequences, which is called satellite DNA.

VI. Answer the following in detail.

Question 1.
What are stem cells? Explain its types.
Answer:
Stem cells are undifferentiated or unspecialised mass of cells. The stem cells are the cells of variable potency. The two important properties of stem cells that differentiate them from other cells are:

1. Its ability to divide and give rise to more stem cells by self-renewal.
2. Its ability to give rise to specialised cells with specific functions by the process of differentiation.

Types of stem cells Embryonic stem cells can be extracted and cultured from the early embryos. These cells are derived from the inner cell mass of the blastocyst. These cells can be developed into air, cell in the body.

Adult stem cell or somatic stem cell are found in the neonatal (new bom) and adults. They have tne ability to divide and give rise to specific cell types. Sources of adult stem cells are amniotic fluid, umbilical cord and bone marrow.

Question 2.
Explain with examples the inbreeding and outbreeding of animal breeding.
Answer:
Animal breeding aims at the genotypes of domesticated animals to increase their yield and improve the desirable qualities to produce milk, egg and meat. When breeding takes place between animals of the same breed, it is called inbreeding.
The cross between different – breeds is called outbreeding.

1. Inbreeding:
Inbreeding refers to the mating of closely related animals within the same breed for about 4 – 6 generations. Superior males and superior females of the same breed are identified and mated in pairs. It helps in the accumulation of superior genes and elimination of genes, which are undesirable. Hissardale is a new breed of sheep developed in Punjab by crossing Bikaneri (Magra) ewes and Australian Marino rams.

2. Inbreeding depression:
Continued inbreeding reduces fertility and productivity. Inbreeding exposes harmful recessive genes that are eliminated by selection.

3. Outbreeding:
It is the breeding of unrelated animals. The offsprings formed are called hybrids. The hybrids are stronger and vigorous than their parents. Cross between two different species with desirable features of economic value are mated. Let’s see what cross produce a mule. Mule is superior to a horse in strength, intelligence, ability to work and resistance to diseases but they are sterile

Question 3.
Explain the DNA fingerprinting technology with an illustration.
Answer:
The DNA pattern of two individuals cannot be the same except for identical twins. Each persons DNA sequence is unique, due to the small difference in the base pairs. DNA fingerprinting is the easier and quicker method, to compare the genetic difference among the two individuals. This technique was developed by Alec Jeffrey.

Each individual’s unique DNA sequences provides distinct characteristics of an individual, which helps in identification. A variable number of tandem repeat sequences [VNTRs] serve as molecular markers for identification.

In human beings, 99 % of DNA base sequences are the same and this is called as bulk genomic DNA. The remaining 1 % DNA sequence differs from one individual to another. This 1 % DNA sequence is present as a small stretch of repeated sequences which is called as satellite DNA. The number of copies of the repeat sequence also called VNTRs differs from one individual to another and results in variation in the size of the DNA segment.

As shown in the illustration, the sequence AGCT is repeated six times in the first person, five times in the second person and seven times in the third person. Because of this, the DNA segment of the third person will be larger in size followed by a DNA segment of first – person and then the second person. Thus it is clear that satellite DNA brings about variation within the population. Variation in the DNA banding pattern reveals differences among the individuals.

Question 4.
Write a detailed account of stem cells, types of stem cells and stem cell therapy?
Answer:
Our body is composed of over 200 specialised cell types, that can carry out specific functions, eg. Neurons or nerve cell that can transmit signals or heart cells which contract to pump blood or pancreatic cells to secrete insulin. These specialised cells are called differentiated cells. These specialised cells are called as differentiated cells. In contrast to differentiated cells, stem cells are the undifferentiated or unspecialised mass of cells. The stem cells are the cells of variable potency.
The two important properties of stem cells are:

• its ability to divide and give rise to more stem cells by self-renewal,
• its ability to give rise to specialised cells with specific functions by the process of differentiation.

Types of stem cells:

1. Embryonic stem cells: These cells are extracted and cultured from the early embryos. These cells are derived from the inner cell mass of the blastocyst. These cells can be developed into any cell in the body.
2. Adult stem cell or somatic stem cell: They are found in the neonatal (newborn) and adults. They have the ability to divide and give rise to specific cell types. The sources of adult stem cells are amniotic fluid, umbilical cord and bone marrow.
3. Stem – cell therapy: Sometimes cells, tissues and organs in the body may be permanently damaged or lost due to genetic condition or disease or injury. In such situations, stem cells are used for the treatment of diseases, which is called stem cell therapy. In treating neurodegenerative disorders like Parkinson’s disease and Alzheimer’s disease neuronal stem cells can be used to replace the damaged or lost neurons.

Question 5.
(a) Explain genetically modified organisms |GMOs|.
(b) With the help of a tabular column tabulate the genetically modified plants and animals, with the objectives, gene inserted and achievement.
Answer:
(a) Genetic modification is the alteration or manipulation of genes in the organisms using rDNA techniques in order to produce the desired characteristics. The DNA fragment inserted is called transgene. Plants or animals expressing a modified endogenous gene or a foreign gene are also known as transgenic organisms.

The transgenic plants are much stable, with improved nutritional quality, resistant to diseases and tolerant to various environmental conditions. Similarly, transgenic animals are used to produce proteins of medicinal importance at low cost and improve livestock quality.

(b) Genetically modified plants and animals:
1. Genetically Modified Plants:

2. Genetically Modified Animals:

VII. Higher Order Thinking Skills (HOTS) Questions

Question 1.
Name the Indian scientist who is known for his leading role in India’s green revolution.
Answer:
Dr M. S. Swaminathan.

Question 2.
The application of biotechnology ‘A’ to treat a person born with a hereditary disease.
(a) What does ‘A’ mean?
(b) Mention its types.
Answer:
(a) Gene therapy refers to the replacement of defective gene.
(b) The two type of gene therapy are Somatic and Germline.

Question 3.
Write the crossbreeds of the following:
(a) Crossbreed of fowls
(b) Crossbreed of cows
Answer:
(a) A crossbreed of fowls:

• White Leghorn × Plymouth Rock
  ↓
  Hybrid fowl – yield more eggs

(b) A crossbreed of cows:

• Brown Swiss × Sahiwal
  ↓
  Karan Swiss [yield 2 – 3 times more milk than indigenous cows]

Believing that the Tamilnadu State Board Solutions for Class 20th Science Chapter 20 Breeding and Biotechnology Questions and Answers learning resource will definitely guide you at the time of preparation. For more details about Tamilnadu State Board Class 20th Science Chapter 20 textbook solutions, ask us in the below comments and we’ll revert back to you asap.

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.2

11th Maths Exercise 4.2 Question 1.
If ^{(n – 1)} P₃ : ⁿP₄, find n:
Solution:

Class 11 Maths Ex 4.2 Solutions Question 2.
If ¹⁰P_{r – 1} = 2 × ⁶P_r, find r.
Solution:

11th Maths Chapter 4 Exercise 4.2 Question 3.

(i) Suppose 8 people enter an event in a swimming meet. In how many ways could the gold, silver and bronze prizes be awarded?
Solution:
From 8 persons we have to select and arrange 3 which can be done in ⁸P₃ ways So the prizes can be awarded in ⁸P₃ = 8 × 7 × 6 = 336 ways

(ii) Three men have 4 coats, 5 waist coats and 6 caps. In how many ways can they wear them?
Solution:
Selecting and arranging 3 coats from 4 can be done in ⁴P₃ ways
Selecting and arranging 3 waist coats from 5 can be done in ⁵P₃ ways Selecting and arranging 3 caps from 6 can be done in ⁶P₃ ways
∴ Total number of ways = ⁴P₃ × ⁵P₃ × ⁶P₃ = 172800 ways

Combinatorics And Mathematical Induction Question 4.
Determine the number of permutations of the letters of the word SIMPLE if all are taken at a time?
Solution:
SIMPLE
Total Number of letters = 6
They can be arranged in 6! ways
∴ Number of words = 6!
= 6 × 5 × 4 × 3 × 2 × 1 = 720

Ex 4.2 Class 11 Maths Question 5.
A test consists of 10 multiple choice questions. In how many ways can the test be answered if

(i) Each question has four choices?
Solution:
Each question has 4 choices. So each questions can be answered in 4 ways.
Number of Questions = 10
So they can be answered in 410 ways

(ii) The first four questions have three choices and the remaining have five choices?
Solution:
The first four questions have 3 choices. So they can be answered in 3⁴ ways. Remaining 6 questions have 5 choices. So they can be answered in 5⁶ ways.
So all 10 questions can be answered in 3⁴ × 5⁶ ways.

(iii) Question number n has n + 1 choices?
Solution:
Given question n has n + 1 choices
question 1 has 1 + 1 = 2 choices
question 2 has 2 + 1 = 3 choices
question 3 has 3 + 1 = 4 choices
question 4 has 4 + 1 = 5 choices
question 5 has 5 + 1 = 6 choices
question 6 has 6 + 1 = 7 choices
question 7 has 7 + 1 = 8 choices
question 8 has 8 + 1 = 9 choices
question 9 has 9 + 1 = 10 choices
So the number of ways of answering all the 10 questions
= 2 × 3 × 4 ×…. × 11 = 11! ways

Exercise 4.2 Class 11 Question 6.
A student appears in an objective test which contain 5 multiple choice questions. Each question has four choices out of which one correct answer.

(i) What is the maximum number of different answers can the students give?
Solution:
Selecting a correct answer from the 4 answers can be done in 4 ways.
Total number of questions = 5 So they can be answered in 45 ways

(ii) How will the answer change if each question may have more than one correct answers?
Solution:
When each question has more than 1 correct answer. Selecting the correct choice from the 4 choice can be done is ⁴C₁ or ⁴C₂ or ⁴C₃ or ⁴C₄ ways.

Each question can be answered in 15 ways.
Number of questions = 5
∴ Total number of ways = 15⁵

Class 11 Maths Chapter 4 Exercise 4.2 Solution Question 7.
How many strings can be formed from the letters of the word ARTICLE, so that vowels occupy the even places?
Solution:
ARTICLE
Vowels A, I, E = 3
Total number of places = 7
1 2 3 4 5 6 7
Number of even places = 3
3 Vowels can occupy 3 places in 3! = 3 × 2 × 1 = 6 ways
Then the remaining 4 letters can be arranged in 4! ways
So total number of arrangement = 3! × 4! = 6 × 24 = 144 ways

Exercise 4.2 Maths Class 11 Solutions Question 8.
8 women and 6 men are standing in a line.

(i) How many arrangements are possible if any individual can stand in any position?
Solution:
Total number of persons = 8 + 6 = 14
They can be arranged in 14! ways

(ii) In how many arrangements will all 6 men be standing next to one another?
Solution:
There are 6 men and 8 women. To make all 6 men together treat them as 1 unit. Now there are 1 + 8 = 9 persons.
They can be arranged in 9! ways. After this arrangement the 6 men can be arranged in 6! ways. So total number of arrangement = 9! × 6!

(iii) In how many arrangements will no two men be standing next to one another?
Solution:
Since no two men be together they have to be placed between 8 women and before and after the women.
w | w | w | w | w | w | w | w
There are 9 places so the 6 men can be arranged in the 9 places in ⁹P₆ ways.
After this arrangement, the 8 women can be arranged in 8! ways.
∴ Total number of arrangements = (⁹P₆) × 8!

Ex 4.2 Class 11 Question 9.
Find the distinct permutations of the letters of the word MISSISSIPPI?
Solution:
MISSISSIPPI
Number of letters = 11
Here M – 1 time
I – 4 times
S – 4 times
P – 2 times

4.2 Maths Class 11 Question 10.
How many ways can the product a2b3c4 be expressed without exponents?
Solution:
a²b³c⁴ = aabbbcccc
Number of letters = 9
a = 2 times,
b = 3 times,
c = 4 times,

Class 11 Maths Chapter 4 Exercise 4.2 Question 11.
In how many ways 4 mathematics books, 3 physics books, 2 chemistry books and 1 biology book can be arranged on a shelf so that all books of the same subjects are together.
Solution:
Number of maths book = 4
Number of physics books = 3
Number of chemistry books = 2
Number of biology books = 1
Since we want books of the same subjects together, we have to treat all maths books as 1 unit, all physics books as 1 unit, all chemistry books as 1 unit and all biology books as 1 unit. Now total number of units = 4
They can be arranged in 4! ways. After this arrangement.
4 maths book can be arranged in 4! ways
3 physics book can be arranged in 3! ways
2 chemistry book can be arranged in 2! ways and 1 biology book can be arranged in 1! way
∴ Total Number of arrangements 4! 4! 3! 2! = 6912

11th Maths 4th Chapter Solutions Question 12.
In how many ways can the letters of the word SUCCESS be arranged so that all Ss are together?
Solution:
SUCCESS
Number of letters = 7
Number of ‘S’ = 3
Since we want all ‘S’ together treat all 3 S’s as 1 unit.
Now the remaining letters = 4
∴ Total number of unit = 5
They can be arranged in 5! ways of them C repeats two times.
So total number of arrangements = \(\frac{5 !}{2 !}\) = 60

Exercise 4.2 Class 11 Maths Question 13.
A coin is tossed 8 times,

(i) How many different sequences of heads and tails are possible?
Solution:
Number of coins tossed = 8
Number of out come for each toss = 2
Total number of out comes = 28

(ii) How many different sequences containing six heads and two tails are possible?
Solution:
Getting 6 heads and 2 tails can be done in ⁸P₆ or ⁸P₂ ways

10th Maths Exercise 4.2 11th Sum Question 14.
How many strings are there using the letters of the word INTERMEDIATE, if

(i) The vowels and consonants are alternative
Solution:
INTERMEDIATE

The number of ways in which vowels and consonants are alternative = \(\frac{6 ! 6 !}{3 ! 2 !}=\) 43200

(ii) All the vowels are together
Solution:
The number of arrangements:
Keeping all the vowels as a single unit. Now we have 6 + 1 = 7 units which can be arranged in 7! ways.
Now the 6 consonants can be arranged in \(\frac{6 !}{2 !}\) (T occurs twice) ways
in vowels I – repeats thrice
and E – repeats twice

(iii) Vowels are never together (and) (iv) No two vowels are together.
Solution:
Vowels should not be together = No. of all arrangements – No. of all vowels together

So number of ways in which No two vowels are together = 19958400 – Number of ways in which vowels are together = 19958400 – 151200 = 19807200

Tn Class 11 Maths Solutions Question 15.
Each of the digits 1,1, 2, 3, 3 and 4 is written on a separate card. The seven cards are then laid out in a row to form a 6-digit number.

(i) How many distinct 6-digit numbers are there?
Solution:
The given digits are 1, 1, 2, 3, 3, 4
The 6 digits can be arranged in 6! ways
In which 1 and 3 are repeated twice.

(ii) How many of these 6-digit numbers are even?
Solution:
To find the number even numbers
The digit in unit place is 2 or 4 which can be filled in 2 ways

(iii) How many of these 6-digit numbers are divisible by 4?
Solution:
To get a number -f- by 4 the last 2 digits should be -r- by 4 So the last two digits will be 12 or 24 or 32.
When the last 2 digits are 1 and 2.

When the last 2 digit are 3 and number of 6 digit numbers (remaining number 1, 1, 3, 4)
So there of 6 digit numbers ÷ by 4 = 12 + 6 + 12 = 30

Exercise 4.2 Class 11 Pdf Question 16.
If the letters of the word GARDEN are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, then find the ranks of the words
(i) GARDEN
(ii) DANGER.
Solution:
The given letters are GARDEN.
To find the rank of GARDEN:
The given letters in alphabetical order are A D E G N R

The rank of GARDEN is 379
To find the rank of DANGER

(ii) The No. of words starting with A = 5! =120

Samacheer Kalvi 11th Maths Answers Question 17.
Find the number of strings that can be made using all letters of the word THING. If these words are written as in a dictionary, what will be the 85^th string?
Solution:
(i) Number of words formed = 5! = 120
(ii) The given word is THING
Taking the letters in alphabetical order G H I N T
To find the 85^th word

Question 18.
If the letters of the word FUNNY are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, find the rank of the word FUNNY.
Solution:
The given word is FUNNY

Question 19.
Find the sum of all 4-digit numbers that can be formed using digits 1, 2, 3, 4, and 5 repetitions not allowed?
Solution:
The given digits are 1, 2, 3, 4, 5
The no. of 4 digit numbers

Sum of the digits = 1 + 2 + 3 + 4 + 5 = 15
Sum of number’s in each place = 24 × 15 = 360

Question 20.
Find the sum of all 4-digit numbers that can be formed using digits 0, 2, 5, 7, 8 without repetition?
Solution:
The given digits are 0, 2, 5, 7, 8
To get the number of 4 digit numbers
1000’s place can be filled in 4 ways (excluding 0)
100’s place can be filled in 4 ways (excluding one number and including 0)
10’s place can be filled in (4 – 1) = 3 ways
and unit place can be filled in (3 – 1) = 2 ways
So the number of 4 digit numbers = 4 × 4 × 3 × 2 = 96

To find the sum of 96 numbers:

In 1000’s place we have the digits 2, 5, 7, 8. So each number occurs \(\frac{96}{4}\) = 24 times.
Now in 100’s place 0 come 24 times. So the remaining digits 2, 5, 7, 8 occurs 96 – 24 = \(\frac{72}{4}\) = 18 times
Similarly in 10’s place and in unit place 0 occurs 24 times and the remaining digits 2, 5, 7, 8 occurs 18 times.
Now sum of the digits = 2 + 5 + 7 + 8 = 22
Sum in 1000’s place = 22 × 24 = 528
Sum in 100’s, 10’s and in unit place = 22 × 18 = 396
∴ Sum of the 4 digit numbers is

Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.2 Additional Questions

Question 1.

Solution:

Question 2.
How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7 if no digit is repeated?
Solution:
Here total number of digits = 6
The unit place can be filled with any one of the digits 2, 4, 6.

Question 3.
Find n if ^{n – 1}P₃ : ⁿP₄ = 1 : 9
Solution:

Question 4.
How many words can be formed by using the letters of the word ORIENTAL so that A and E always occupy the odd places?
Solution:
[Hint: There are 4 odd places in the word]

Now the remaining 6 places filled with remaining 6 letters

Hence the total number of permutations = 12 × 720 = 8640

Question 5.
Out of 18 points in a plane, no three are in the same line except five points which are collinear. Find the number of lines that can be formed joining the points.
Solution:
Total number of points = 18
Out of 18 numbers, 5 are collinear and we get a straight line by joining any two points.
∴ Total number of straight line formed by joining 2 points out of 18 points = ¹⁸C₂
Number of straight lines formed by joining 2 points out of 5 points = ⁵C₂
But 5 points are collinear and we get only one line when they are joined pairwise.
So, the required number of straight lines are

Hence, the total number of straight lines = 144

Question 6.
We wish to select 6 person from 8 but, if the person A is choosen, then B must be choosen. In how many ways can selections be made?
Solution:
Total number of persons = 8
Number of persons to be selected = 6
Condition is that if A is choosen, B must be choosen

Case I: When A is choosen, B must be choosen
Number of ways = ⁶C₄
[∴ A and B are set to be choosen]

Case II: When A is not choosen, then B may be choosen
∴ Number of ways = ⁷C₆

Hence, the required number of ways = 22

Question 7.
How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?
Solution:
For 3-digit even numbers, the unit’s place can be occupied by one of the 3 digits 2, 4 or 6. The remaining 5 digits can be arranged in the remaining 2 places in ⁵P₂ ways.

∴ By the multiplication rule, the required number of 3-digit even numbers is 3 × ⁵P₂ = 3 × 5 × 4 = 60.

Question 8.
Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?
Solution:
For 4 digit numbers, we have to arrange the given 5 digits in 4 vacant places. This can be done in ⁵P₄ = 5 × 4 × 3 × 2 = 120 ways.

For 4-digit even numbers, the unit’s place can be occupied by one of the 2 digits 2 or 4. The remaining 4 digits can be arranged in the remaining 3 places in ⁴P₃ ways.
∴ By the multiplication rule, the required number of 4-digit even numbers is 2 × ⁴P₃ = 2 × 4 × 3 × 2 = 48.

Question 9.
Find r if

(i) ⁵P_r = 2 ⁶P_{r – 1} 4
Solution:

(ii) ⁵P_r = ⁶P_{r – 1}

⇒ 42 – 13r + r² = 6 ⇒ r² – 13r + 36 = 0
⇒ (r – 4)(r – 9) = 0 ⇒ r = 4, 9
Now, we know that ⁿP_r is meaningful only when r ≤ n.
∴ ⁵P_r and ⁶P_{r – 1} are meaningless when r ≤ 9.
∴ Rejecting r = 9, we have r = 4

Question 10.
How many words, with or without meaning, can be made from the letters of the word MONDAY, assuming that no letter is repeated, if

(i) 4 letters are used at a time
(ii) all letters are used at a time
(iii) all letters are used but first letter is a vowel?
Solution:
The word MONDAY has 6 distinct letters.

(i) 4 letters out of 6 can be arranged in ⁶P₄ ways.
∴ The required number of words = ⁶P₄ = 6 × 5 × 4 × 3 = 360

(ii) 6 letters can be arranged among themselves in 6P6 ways.
∴ The required number of words = ⁶P₆ = 6!
= 1 × 2 × 3 × 4 × 5 × 6 = 720.

(iii) The first place can be filled by anyone Of the two vowels O or A in 2 ways. The remaining 5 letters can be arranged in the remaining 5 places II to VI in ⁵P₅ = 5! ways.
∴ By the multiplication rule, the required number of words = 2 × 5! = 2 × 1 × 2 × 3 × 4 × 5 = 240

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.9

10th Maths Exercise 3.9 Samacheer Kalvi Question 1.
Determine the quadratic equations, whose sum and product of roots are
(i) -9, 20
(ii) \(\frac{5}{3}\), 4
(iii) \(\frac{-3}{2}\), -1
(iv) -(2 – a)², (a + 5)²
Solution:
If the roots are given, general form of the quadratic equation is x² – (sum of the roots) x + product of the roots = 0.
(i) Sum of the roots = -9
Product of the roots = 20
The equation = x² – (-9x) + 20 = 0
⇒ x² + 9x + 20 = 0

(ii) Sum of the roots = \(\frac{5}{3}\)
Product of the roots = 4
Required equation = x² – (sum of the roots)x + product of the roots
= 0
⇒ x² – \(\frac{5}{3}\)x + 4 = 0
⇒ 3x² – 5x + 12 = 0

(iii) Sum of the roots = (\(\frac{-3}{2}\))
(α + β) = \(\frac{-3}{2}\)
Product of the roots (αβ) = (-1)
Required equation = x² – (α + β)x + αβ = 0
x² – (\(\frac{-3}{2}\))x – 1 = 0
2x² + 3x – 2 = 0

(iv) α + β = – (2 – a)²
αβ = (a + 5)²
Required equation = x² – (α + β)x – αβ = 0
⇒ x² – (-(2 – a)²)x + (a + 5)² = 0
⇒ x² + (2 – a)²x + (a + 5)² = 0

Exercise 3.9 Class 10 Samacheer Kalvi Question 2.
Find the sum and product of the roots for each of the following quadratic equations
(i) x² + 3x – 28 = 0
(ii) x² + 3x = 0
(iii) 3 + \(\frac{1}{a}=\frac{10}{a^{2}}\)
(iv) 3y² – y – 4 = 0

(i) x² + 3x – 28 = 0
Answer:
Sum of the roots (α + β) = -3
Product of the roots (α β) = -28

(ii) x² + 3x = 0
Answer:
Sum of the roots (α + β) = -3
Product of the roots (α β) = 0

(iii) 3 + \(\frac{1}{a}=\frac{10}{a^{2}}\)
3a² + a = 10
3a² + a – 10 = 0 comparing this with x² – (α + β)
x + αβ = 0

Students can Download Maths Chapter 2 Measurements Ex 2.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.2

8th Maths Exercise 2.2 Question 1.
Find the perimeter and area of the combined figures given below, (π = \(\frac{22}{7}\))

Solution:

∴ Perimeter = Sum of all lengths of sides that form the closed boundary
P = 11 + 10 + 7 + 10m
Perimeter = 38 m
Area = Area of the rectangle – Area of semicircle

= 50.75 m² (approx)
Area of the figure = 50.75m² approx.

(ii) Perimeter = sum of outside lengths

Samacheer Kalvi 8th Maths Book Question 2.
Find the area of the shaded part of the following figures. (π = 3.14 )

Solution:
Area of the shaded part = Area of 4 quadrant circles of radius \(\frac{10}{2}\) cm
= 4 × \(\frac{1}{4}\) × πr² = 3.14 × \(\frac{10}{2} \times \frac{10}{2}\) cm²
= \(\frac{314}{4}\) cm² = 78.5cm²
Area of the shaded part = 78.5 cm²
Area of the unshaded part = Area of the square – Area of shaded part
= a² – 78.5 cm² = (10 × 10) – 78.5 cm²
= 100 – 78.5 cm² = 21.5 cm²
Area of the unshaded part = 21.5 cm² (approximately)

(ii) Area of the shaded part = Area of semicircle – Area of the triangle

∴ Area of the shaded part = 27.93 cm² (approximately)

8th Standard Maths Measurement Question 3.
Find the area of the combined figure given which is got by joining of two parallelograms.

Solution:
Area of the figure = Area of 2 parallelograms with base 8 cm and height 3 cm
= 2 × (bh) sq. units
= 2 × 8 × 3 cm² = 48 cm²
∴ Area of the given figure = 48 cm²

8th Class Maths Exercise 2.2 Question 4.
Find the area of the combined figure given, formed by joining a semicircle of diameter 6 cm with a triangle of base 6 cm and height 9 cm. (π = 3.14 )

Solution:
Area of the figure = Area of the semicircle of radius 3 cm + 2 (Area of triangle with b = 9 cm and h = 3 cm)

= 14.13 + 27 cm² = 41.13 cm²
∴ Area of the figure = 41.13 cm² (approximately)
The door mat which is in a hexagonal shape

Samacheer Kalvi 8th Books Maths Question 5.
The door mat which is in a hexagonal shape has the following measures as given in the figure. Find its area.

Solution:
Area of the doormat = Area of 2 trapezium
Height of the trapezium h = \(\frac{70}{2}\) cm;
a = 90 cm; b = 70 cm
∴ Area of the trapezium
= \(\frac{1}{2}\)h (a + b) sq. units
Area of the door mat
= 2 × \(\frac{1}{2}\) × 35 (90 + 70) cm²
= 35 × 160 cm² = 5600 cm²
∴ Area of the door mat = 5600 cm²

Samacheer Kalvi 8th Maths Question 6.
Find the area of an invitation card which has two semicircles attached to a rectangle as in the figure given. (π = \(\frac{22}{7}\))

Solution:
Area of the card = Area of the rectangle + area of 2 semicircles
Length of the rectangle l = 30 cm
Breadth b = 21 cm
Radius of the semicircle = \(\frac{21}{27}\)
∴ Area of the card
= (l × b) + (2 × \(\frac{1}{2}\) πr²) sq. units
= 30 × 21 + \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\) cm² = 630 + 346.5
= 976.5 cm² (approximately)
∴ Area of the Invitation card = 976.5 cm²

8th Maths Book Samacheer Kalvi Question 7.
Find the area of the combined figure given, which has two triangles attached to a rectangle.

Solution:
Area of the combined shape = Area of the rectangle + Area of 2 triangles
Length of the rectangle l = 10 cm
Breadth b = 8 cm
Base of the triangle base = 8 cm
Height h = 6 cm
∴ Area of the shape = (l × b) + (2 × \(\frac{1}{2}\) × base × h) cm²
= (10 × 8) + (8 × 6) cm² = 80 + 48 cm² = 128 cm²
Area of the given shape = 128 cm²

Samacheer Kalvi 8th Standard Maths Question 8.
A rocket drawing has the measures as given in the figure. Find its area.

Solution:
Area = Area of a rectangle + Area of a triangle + Area of a trapezium
For rectangle length l = 120 – 20 – 20 cm = 80 cm
Breadth b = 30 cm
For the triangle base = 30 cm
Height = 20 cm
For the trapezium height h = 20 cm
Parallel sided a = 50 cm
b = 30 cm
∴ Area of the figure = (l × b) + (\(\frac{1}{2}\) × base × height) + \(\frac{1}{2}\) × h × (a + b) sq. units
= (80 × 30) + ( \(\frac{1}{2}\) × 30 × 20) + \(\frac{1}{2}\) × 20 × (50 + 30) cm²
= 2400 + 300 + 800 cm² = 3500 cm²
Area of the figure = 3500 cm²

Samacheer Kalvi 8 Maths Book Question 9.
Find the area of the glass painting which has a triangle on a square as given in the figure.

Solution:
Area of the glass painting = Area of the square + Area of the triangle
Side of the square a = 30 cm
Base of the triangle b = 30 cm
Height of the triangle h = 8 cm
∴ Area of the painting = (a)² + (\(\frac{1}{2}\) bh) sq. units
= (30 × 30) + (\(\frac{1}{2}\) × 30 × 8) cm² = 900 + 120 cm²
= 1020 cm²
Area of the glass painting = 1020 cm²

8th Standard Maths Samacheer Kalvi Question 10.
Find the area of the irregular polygon shaped fields given below.

Solution:
(i) Area of the irregular field = Area of ∆AHF + Area of trapezium FHIE + Area of triangle EID + Area of ∆JDC + Area of rectangle BGJC + Area of ∆AGB

(ii) Area of the field = Area of trapezium FBCH + Area of ∆DHC + Area of ∆EGD + Area of ∆EGA + Area of ∆BFA

You can Download Samacheer Kalvi 9th Social Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Social Science History Solutions Chapter 7 State and Society in Medieval India

State and Society in Medieval India Textual Exercise

I. Choose the correct answer.

State And Society In Medieval India Class 9 Question 1.
……………… was the second stronghold of Ala-ud-din Khalji’s expanding Kingdom.
(a) Dauladabad
(b) Delhi
(c) Madurai
(d) Bidar
Answer:
(a) Dauladabad

Samacheer Kalvi Guru 9th Social Science Question 2.
The Deccan Sultanates were conquered by ………………
(a) Ala-ud-din Khilji
(b) Ala-ud-din Bahman- shah
(c) Aurangzeb
(d) Malik Kaffir
Answer:
(c) Aurangzeb

State And Society In Medieval India Question 3.
The establishment of ……………… empire changed the administrative and institutional structures of South India.
(a) Bahmani
(b) Vijayanagar
(c) Mughal
(d) Nayak
Answer:
(b) Vijayanagar

Question 4.
Krishnadeva Raya was a contemporary of …………………
(a) Babur
(b) Humayun
(c) Akbar
(d) Aihole
Answer:
(d) Aihole

II. Find out the correct statement.

Question 1.
(i) The establishment of the Vijayanagar Kingdom witnessed the most momentous . development in the history of South India.
(ii) The Saluva dynasty ruled for a longer period.
(iii) The rulers of Vijayanagara had smooth relations with the Bahmani Sultanate.
(iv) Rajput kingdoms attracted migrants from Persia and Arabia.
Answer:
(i) and (iv) are correct

Question 2.
(i) The Nayak Kingdom came up in Senji.
(ii) The appointment of Telugu Nayaks resulted in the migration of Telugu-speaking people from Madurai.
(iii) Mughal Empire started declining from the time of Jahangir.
(iv) The Europeans came to India in search of slaves.
Answer:
(i) and (ii) are correct

Question 3.
(i) Mythical geneologies were collected by Col. Mackenzie.
(ii) Indigo was the most important beverage crop in India.
(iii) Mahmud Gawan was the minister in Alauddin Khalji’s kingdom.
(iv) The Portuguese built their first fort in Goa.
Answer:
(i) is correct

Question 4.
Assertion (A): India was an integral part of maritime trade, extending from China in the east to Africa in the west.
Reason (R): Geographical location of India in the middle of Indian Ocean.
(a) (i) A is correct; R explains about A
(b) (ii) A is wrong; R is correct
(c) (iii) A and R are wrong
(d) (iv) A is correct; R does not explains about A.
Answer:
(a) (i) A is correct; R explains about A

Question 5.
(i) Gold images of great beauty and artistry were made by Cholas.
(ii) The best example for Chola architecture is Siva asNataraja performing the cosmic dance.
(a) (i) is correct (ii) is wrong
(b) Both (i) and (ii) is correct
(c) Both (i) and (ii) are wrong
(d) (i) is wrong, (ii) is correct.
Answer:
(d) (i) is wrong, (ii) is correct.

III. Match the following:

Answer:
1. (d)
2. (c)
3. (a)
4. (e)
5. (b)

IV. Fill in the blanks.

1. ………………. were Europeans who arrived on the west coast of India.
2. The combined forces of the five Deccan Sultanates defeated Vijayanagar army in 1565 A.D. (C.E.) at the battle of ……………
3. Vijayanagara evolved as a ………………
4. The tempo of urbanization increased during ……………… period.
5. ……………… was the enterprising period in the history of Tamil Nadu.
Answers:
1. Portuguese
2. Talikota
3. Militaristic State
4. Vijayanagar
5. The Chola period

V. Answer all questions given under each heading.

Question 1.
The arrival of the Europeans
(a) Who controlled the spice trade from India?
Answer:
Muslims controlled the Spice trade from India.

(b) What enabled the Portuguese to have control over maritime trade over the entire region?
Answer:
The Naval superiority enabled the Portuguese to have control over the Maritime trade over the entire region.

(c) How were the trading activities of the Europeans carried on in India?
Answer:
The trading activities of the Europeans carried on through the respective East India Companies in India. ‘

(d) Mention the enclaves of the Dutch, the English, the French and the Danes in India.
Answer:
The Dutch were in Pulicat (and later Nagapatnam)
the English in Madras
the French in Pondicherry and
the Danes in Tarangampadi (Tranquebar).

Question 2.
Society, Religion and Culture.
(а) Which is the most distinctive aspect of Indian Society?
Answer:
Caste is the most distinctive aspect of Indian Society.

(b) What is a guild?
Answer:
The occupational caste groups are referred to as guilds.

(c) Mention some Saivite movements.
Answer:
Saiva Siddhanta in TamilNadu
Virasaivas in Karnataka
Varkarisampradaya in Maharashtra.

(d) Name the court musician of Akbar.
Answer:
Tansen was the court musician of Akbar.

VI. Answer the following briefly.

Question 1.
Write about the military expeditions of Malik Kafur.
Answer:
Alauddin Khalji’s slave and commander, Malik Kafur, was sent on military expeditions further south in the first decade of the 1300s A.D. (C.E.).

Question 2.
Who founded the Vijayanagar Kingdom? Mention the dynasties that ruled over the kingdom.
Answer:
Harihara and Bukka, two brothers founded the Vijayanagar Kingdom.
Sangama Dynasty, Saluva Dynasty and Tuluva Dynasties ruled over the Kingdom.

Question 3.
Mention the two natural advantages that India had in cotton weaving.
Answer:
India had two natural advantages in cotton weaving. The first was that cotton grew in almost all parts of India, so that the basic raw material was easily available. Second, the technology of producing a permanent colour on cotton using vegetable dyes was known from very early times in India.

Question 4.
What were the factors which facilitated urbanization?
Answer:

1. It has been observed that cities and towns fulfilled diverse and overlapping roles in the economy.
2. The large cities were centres of manufacturing and marketing, banking and financial services.
3. They were usually located at the intersection of an extensive network of roads which connected them to other parts of the country.
4. Smaller towns were marketing centres in local trade connecting the immediate rural hinterland.
5. Cities also served as political and administrative centres, both in the capital region (for instance, Agra and Delhi) and in the provinces.

Question 5.
What is sericulture?
Answer:

1. Silk production by breeding the mulberry silkworm is Sericulture.
2. Sericulture was introduced in the 14th and 15th centuries.
3. Bengal had become one of the largest silk-producing regions in the world.

VII. Answer the following in detail.

Question 1.
Discuss the political changes during 1526-1707 A.D.*(C.E.).
Answer:
(i) The Mughal empire was founded by Babur in 1526 A.D. (C.E.) after he defeated Ibrahim Lodi at Panipat.

(ii) The first six Mughal emperors are referred to as the ‘Great Mughals’. Aurangzeb was the last of the great Mughals.

(iii) Akbar consolidated the Mughal empire through conquests and through a policy of conciliation with the Religious based kingdoms of Rajasthan.

(iv) The Mughal empire through began to disintegrate after Aurangzeb, continued to exist nominally till 1857 A.D. (C.E.) when the British finally ended the virtually non-existent empire.

(v) A new power centre rose in Maharashtra in the seventeenth century, and the Marathas
under the leadership of Shivaji seriously undermined the authority of the Mughals in western India.

(vi) At its height, the empire stretched over most of the Indian sub-continent.

(vii) Only the south-western region of Kerala and southern Tamilnadu were not directly under Mughal rule.

Question 2.
Explain the commercial developments in Medieval India.
Answer:

• The large manufacturing sector essentially produced goods for exchange.
• India had an extensive network of trade for marketing the goods.
• At the next level the producer was de-linked from marketing, the trade was undertaken by merchant intermediaries.
• Big cities were usually major commercial centres with bazzars and shops.
• Major parts were the nodal points in international, maritime trade.
• Maritime trade across the Indian ocean, extending from China in the east to Africa in the West had flourished for many centuries.
• Merchants operated at different levels.
• Trade on a large scale could function only with the availability of financial and banking services.
• The European trading companies realized that they could not function in India without the services of the rich and influential merchants. They entered into contracts.
• The Indian merchants were under contract to the Europeans to supply textiles and other goods.
• Political disturbances disrupted the economic activity.

Question 3.
“Chola Period was a enterprising period in the history of Tamil Nadu” – Elucidate.
Answer:
(i) The CHOLA PERIOD was an enterprising period when trade and the economy expanded, accompanied by urbanization.

(ii) The administrative machinery was re-organised during Chola rule.

(iii) The basic unit of local administration was the village (ur), followed by the sub-region (nadu) and district (kottam). Tax-free villages granted to Brahmins were known as brahmadeya. Marketing centres and towns were known as nagaram.

(iv) The ur, nadu, brahmadeya and nagaram each had its own assembly.

(v) They were responsible for the maintenance and management of the water resources and land; the local temples; resolving local issues and disputes; and for collecting the taxes due to the government.

(vi) While the Chola state did not intervene in this fundamental system of local administration, they introduced innovations in revenue administration by creating new revenue divisions (mandalam and valanadu). Several new taxes on agriculture and commerce were also introduced.

(vii) The second notable feature was the great increase in the construction of temples. This had two dimensions: new temples were constructed, and existing temples became multi-functional social and economic institutions.

(viii) The construction of great temples also was a reflection of the growing prosperity in the kingdom, since the activity involved great expenditure.

Student Activities

Question 1.
On the outline map of India mark the important places of medieval India.
Answer:

Question 2.
Collect pictures of architectural importance of the Cholas.
Answer:
You can collect the pictures of architectural importance of the Cholas and paste it in the Album.

IX Assignment

Question 1.
Collect the pictures of Angkor Wat in Cambodia.
Answer:
You can collect the pictures of Angkor Wat in Cambodia. You can do this as Home Assignment.

Question 2.
Arrange a debate in the class on the advantages and disadvantages of urbanization.
Answer:
The teacher can arrange a debate on the advantages and disadvantages of Urbanization.

State and Society in Medieval India Additional Questions

I. Choose the correct answer.

Question 1.
Muslim rule was established in Delhi at the end of the 12th century by …………..
(a) Muhammad Ghori
(b) Alauddin Khalji
(c) Mahmud Gawan
(d) Aurangazeb
Answer:
(a) Muhammad Ghori

Question 2.
……………… was sent on military expeditions further south in the first decade of the 1300 AD.
(a) Muhammad-bin-Tughlaq
(b) Alauddin Bahman Shah
(c) Malik Kafur
(d) None of the above
Answer:
(c) Malik Kafur

Question 3.
Maritime trade with South East Asia and China expanded greatly during the ………….. period.
(a) Chera
(b) Chola
(c) Pandya
(d) Pallava
Answer:
(b) Chola

Question 4.
The last of the great Mughal was …………….
(a) Humayun
(b) Akbar
(c) Jahangir
(d) Aurangazeb
Answer:
(d) Aurangazeb

Question 5.
…………… period was an enterprising period.
(a) The Chola
(b) The Chera
(c) The Pandya
(d) The Pallava
Answer:
(a) The Chola

Question 6.
The most distinctive aspect of Indian society is ……………….
(a) Religion
(b) Caste
(c) Culture
(d) None of the above
Answer:
(b) Caste

Question 7.
…………….. is a pilgrimage centre.
(a) Mumbai
(b) Calcutta
(c) Varanasi
(d) Delhi
Answer:
(c) Varanasi

Question 8.
………….. was introduced in the 14th century.
(a) Sericulture
(b) Horticulture
(c) Agriculture
(d) None of the above
Answer:
(a) Sericulture

II. Find out the correct statement.

Question 1.
(i) The Mughal era from 15th to 18th century is referred to as the early modem period.
(ii) Muslim rule was established in Delhi at the end of the 12th century.
(iii) Arab Muslims had been trading in the ports of the west coast.
(iv) The impact of Muslim rule was felt during the reign of Malik Kafur.
Answer:
(ii) and (iii) are correct

Question 2.
(i) The Europeans were pre-occupied with trying a find a dirrect sea route to India.
(ii) The spice trade from India was controlled by Muslims.
(iii) The second notable feature was the great increase in the construction of temple.
(iv) The Chola period was an enterprising peirod.
Answer:
(iii) and (iv) are correct

Question 3.
(i) Textiles accounted for nearly 90% of the total exports from India.
(ii) Ainnurruvar had their headquarters in Aihole.
(iii) Coromandel merchants operated from Persian Gulf and Red sea.
(iv) The Indian merchants were under contract to the Europeans.
Answer:
(ii) is correct

Question 4.
Assertion (A): Sikhism was founded by Guru Nanak.
Reason (R): He lived during 15th and 16th century.
(a) A is correct R explains about A
(b) A is wrong R is correct
(c) A and R are wrong
(d) A is correct R does not explains about A
Answer:
(d) A is correct R does not explains about A

Question 5.
(i) India was predominantly an agricultural country.
(ii) A very large population lived in Rural area and depends on agriculture.
(a) (i) is correct (ii) is wrong
(b) Both (i) and (ii) are correct
(c) Both (i) and (ii) are wrong
(d) (i) is wrong (ii) is correct
Answer:
(b) Both (i) and (ii) are correct

III. Match the following:

Answer:
1. (g)
2. (e)
3. (a)
4. (b)
5. (f)
6. (c)
7. (d)

IV. Fill in the blanks.

1. The Mughal era from the 16th to 18th century is referred to as the …………….
2. The impact of Muslim rule was felt during the reign of ……………
3. Maritime trade with South-east Asia and China expanded greatly during the …………….
4. The last known Chola empiror was ………………
5. The Mughal empire was founded by ……………. in 1526 A.D.
6. In 1498 A.D Vasco da Gama landed on the …………… coast.
7. The …………….. empire transformed the economy and society of North India.
8. ……………. took roots when the Portuguese arrived in Kerala and set themselves up in Goa.
9. In ……………. India especially the Tamil region urbanization went hand in hand with temples.
10. …………… had become one of the largest silk-producing regions in the world.
Answers:
1. early modem period
2. Alauddin Khalji
3. Chola period
4. Rajendralll
5. Babur
6. Kerala
7. Mughal
8. Christianity
9. South
10. Bengal

V. Answer all questions given under each heading.

Question 1.
The Advent of Islam.
(a) When was Muslim rule established in Delhi? By whom?
Answer:
Muslim rule was established in Delhi at the end of the 12th century by Muhammad Ghori.

(b) Who were trading in the ports of the west coast?
Answer:
Arab Muslim merchants had been trading in the ports of the west coast especially Kerala.

(c) When was the impact of Muslim rule felt?
Answer:
The impact of Muslim rule was felt during the reign of Alauddin Khalji.

(d) What was his primary objective?
Answer:
His primary objective was to plunder the wealth, rather than to expand his territory.

Question 2.
The Chola empire in the south.
(a) Who began the territorial expansion?
Answer:
The territorial expansion of the Chola empire began under Rajaraj a I.

(b) What do you know about Rajendra I?
Answer:
The Chola empire expanded further under Rajendra I.
He had successfully taken his armies as far to the north east up to the river Ganges.

(c) In whose period Maritime trade expanded?
Answer:
Maritime trade expanded with South-east Asia and China greatly during the Chola period.

(d) Against whom did the Naval expeditions sent?
Answer:
The Naval expeditions had been sent against the Sailendra Kingdom of Sri Vijaya, Kadarand and Ceylon. .

(e) What did he earn from this war?
Answer:
This war earned him the title of “the Chola who had conquered the Ganga and Kadaram”.

Question 3.
Urbanization in South India.
(a) Comment on South Indian temples.
Answer:
In South India especially the Tamil region urbanization went hand in hand with temples.

(b) How were the temples?
Answer:
Temples were large economic enterprises requiring a variety of goods and services to function.

(c) In whose period did the pace of urbanization increase?
Answer:
The pace of urbanization increased during the Vijayanagar period.

(d) How were the Urban centres?
Answer:
Most Urban centres displayed rural characteristics.
For instance, it was not uncommon to find fields with crops within the city.

VI. Answer the following briefly.

Question 1.
How did the historian ‘Burton Stein describe the different periods of Indian History?
Answer:
The historian Burton Stein, uses the term ‘classical’ to describe the period up to the Gupta empire, and dates the ‘medieval’ period from the 7th century A.D.(CE) till the beginning of Mughal rule in the 16th century. The Mughal era, from the 16th to 18th century is referred to as the early modem peroid.

Question 2.
Who brought out the isolated southern parts into the orbit of the rulers of the North?
Answer:
The Tughlaq kings who came after Alauddin also sent their armies to the south. As a result, the generally more isolated southern part of the country came into the orbit of the rulers of the north. Governors were appointed in various provinces in the Deccan region, and a Sultanate was even established in Madurai.

Question 3.
Mention the five Sultanates who came up in Deccan in the 15th century.
Answer:
By the end of the fifteenth century, five sultanates came up in the Deccan: Bijapur, Golkonda, Ahftiednagar, Berar and Bidar. Bijapur and Golkonda were the largest of these sultanates and the region entered a phase of considerable economic growth and expansion of trade.

Question 4.
How did the Vijayanagar empire wither away?
Answer:

• The rulers of Vijayanagar were almost continuously at war with the Bahmani sultanate as well as with the religion-based kingdoms of Kondavidu and Orissa.
• Finally, the combined forces of the five Deccani Sultanates defeated Vijayanagar in 1565 A.D. (C.E.) at the Battle of Talikota.
• The Vijayanagar emperors then shifted their capital further south to Penugonda, and eventually to Chandragiri near Tirupati.
• The empire (or what remained of it) finally withered away in the middle of the seventeenth century.

Question 5.
What was the impact of Islamic rule on Indian society?
Answer:
The establishment of Islamic Rule in Delhi made a big impact on Indian society. Initially, Islam did not cause any social tension. Arab merchants, for instance, when they came and settled on Kerala coast, married local women and led a peaceful life. The situation changed when Islam became a state power. For a medieval ruler one way of asserting imperial authority was to demolish the place of worship of the enemies. Otherwise Islam as a monotheistic religion had its positive impact in Indian society. It played a decisive role in the evolution of a composite culture.

Question 6.
Why did the Europeans come to India?
Answer:
The Europeans came to India primarily in search of spices. But soon there was an explosion in the demand for Indian textiles in the European markets, often referred to as the ‘Indian craze’. This led to a significant expansion of textile production in India, which was accompanied by an expansion of the production of commercial crops like cotton and indigo and other dyes.

Question 7.
Give an account of genealogies collected by Colin Mackenzie.
Answer:
(i) Caste groups often petitioned the local ruler for permission to use various symbols of higher status, like the right to wear footw ear, the right to carry umbrellas, the right to use certain decorations at funerals and so on.

(ii) Each caste also created a mythical genealogy to establish its origins; this was used to justify the claim for the right to a higher status in the hierarchy.

(iii) These genealogies are found in many of the manuscripts collected by Colin Mackenzie.

Question 8.
Write a short note on the literary works of the Chola period.
Answer:

• The Chola period was an era of remarkable cultural activity. These were the centuries when major literary works were written.
• The best known classical poet, Kamban, wrote Ramayana in Tamil which was formally
  presented (Arangetram) in the temple at Srirangam. Sekkilar’s Periyapuranam, similarly was presented at the temple in Chidambaram.
• Among the other great works of the period is Kalingattup-parani and Muvarula.
• It was also a period when great religio-philosophical treatises like the Sankara-bhashyam and Sri-bhashyam were produced.

Question 9.
Explain the Art and Architecture of the Mughal period.
Answer:
The Mughals were well-known for their aesthetic values, and were great patrons of the arts. They left behind numerous monuments, in addition to constructing entire cities like Shahjahanabad (Delhi) and Fatehpur Sikri, gardens, mosques and forts. Decorative arts – especially jewellery set with precious and semi-precious gems for items of personal use – flourished under the patronage of the royal household and urban elites. The art of painting also flourished in the Mughal period. Primarily known as Mughal miniatures, they were generally intended as book illustrations or were single works to be kept in albums.

Question 10.
What happened in the business scenario in the beginning of the 18th century in India?
Answer:

• The Indian merchants benefitted from the business opportunities offered by the European companies. .
• But this scenario began to change from the beginning of the eighteenth century.
• The Indian merchants were under contract to the Europeans to supply textiles and other goods.
• But by then the local resources were not enough to produce the quantities required and political disturbances also disrupted all economic activity.
• This resulted in most merchants being bankrupted diminishing the economic vitality of the merchant community.

VII. Answer the following in detail.

Question 1.
Describe the major political changes.
Answer:
(i) The expansion of the Chola empire from the time of Rajaraja which eclipsed the Pandyan and Pallava kingdoms, extending north till Orissa.

(ii) From the twelfth century, the beginning of several centuries of Muslim rule in Delhi, extending throughout North India and the spread of Islam to different parts of the country.

(iii) By the end of the 13th century the eclipse of the great empire of the Cholas and the consequent rise of many religious kingdoms in South India. This ultimately culminated in the rise of the Vijayanagar empire which exercised authority over all of South India and came to be considered the bastion of religious rule in the south.

(iv) The consolidation of Muslim rule under the Mughals in the north, beginning in 1526 A.D. (C.E.) with the defeat of the Ibrahim Lodi by Babur. At its height, the Mughal empire stretched from Kabul to Gujarat to Bengal, from Kashmir to South India.

(v) The coming of the Europeans, beginning with the Portuguese who arrived on the west coast of India in 1498.

Question 2.
Explain the important feature of Indian agriculture.
Answer:
An important feature of Indian agriculture was the large number of crops that were cultivated. The peasant in India was more knowledgeable about many crops as compared to peasants in most of the world at the time. A variety of food grains like wheat, rice, and millets were grown apart from lentils and oilseeds. Many other commercial crops were also grown such as sugarcane, cotton and indigo. Other than the general food crops, south India had a regional specialization in pepper, cinnamon, spices and coconut.

In general, two different crops were grown in the different seasons, which protected the productivity of the soil. Maize and tobacco were two new crops which were introduced after the arrival of the Europeans. Many new varieties of fruit or horticultural crops like papaya, pineapple, guava and cashew nut were also introduced which came from the west, especially America. Potatoes, chillies and tomatoes also became an integral part of Indian food.

Guys who are planning to learn and understand the topics of 10th Social Science History can grab this Tamilnadu State board solutions for Chapter 9 Freedom Struggle in Tamil Nadu Questions and Answers from this page for free of cost. Make sure you use them as reference material at the time of preparation & score good grades in the final exams.

Students who feel tough to learn concepts can take help from this Samacheer Kalvi 10th Social Science Book Solutions Guide Pdf, all the Questions and Answers can easily refer in the exams. Go to the below sections and get 10th Social Science History Chapter 9 Freedom Struggle in Tamil Nadu Tamilnadu State Board Solutions PDF.

Tamilnadu Samacheer Kalvi 10th Social Science History Solutions Chapter 9 Freedom Struggle in Tamil Nadu

Do you feel scoring more marks in the 10th Social Science History Grammar sections and passage sections are so difficult? Then, you have the simplest way to understand the question from each concept & answer it in the examination. This can be only possible by reading the passages and topics involved in the 10th Social Science History Board solutions for Chapter 9 Freedom Struggle in Tamil Nadu Questions and Answers. All the Solutions are covered as per the latest syllabus guidelines. Check out the links available here and download 10th Social Science History Chapter 9 textbook solutions for Tamilnadu State Board.

Freedom Struggle in Tamil Nadu Textual Exercise

I. Choose the correct answer.

Freedom Struggle In Tamil Nadu Class 10 Question 1.
Who was the first President of the Madras Mahajana Sabha?
(a) T.M. Nair
(b) P. Rangaiah Naidu
(c) G. Subramaniam
(d) G.A. Natesan
Answer:
(b) P. Rangaiah Naidu

Freedom Struggle In Tamil Nadu Question 2.
Where was the third session of the Indian National Congress held?
(a) Marina
(b) Mylapore
(c) Fort St. George
(d) Thousand Lights
Answer:
(d) Thousand Lights

Question 3.
Who said “Better bullock carts and freedom than a train de luxe with subjection”?
(a) Annie Besant
(b) M. Veeraraghavachari
(c) B.P. Wadia
(d) G.S. Arundale
Answer:
(a) Annie Besant

Question 4.
Which among the following was SILF’s official organ in English?
(a) Dravidian
(b) Andhra Prakasika
(c) Justice
(d) New India
Answer:
(c) Justice

Question 5.
Who among the following were Swarajists?
(a) S. Satyamurti
(b) Kasturirangar
(c) P. Subbarayan
(d) Periyar EVR
Answer:
(a) S. Satyamurti

Question 6.
Who set up the satyagraha camp in Udyavanam near Madras?
(a) Kamaraj
(b) Rajaji
(c) K. Santhanam
(d) T. Prakasam
Answer:
(d) T. Prakasam

Question 7.
Where was the anti-Hindi Conference held?
(a) Erode
(b) Madras
(c) Salem
(d) Madurai
Answer:
(c) Salem

Question 8.
Where did the congress volunteers clash with the military during Quit India Movement?
(a) Erode
(b) Madras
(c) Salem
(d) Madurai
Answer:
(d) Madurai

II. Fill in the blanks.

1. …………… was appointed the first Indian Judge of the Madras High Court.
2. The economic exploitation of India was exposed by …………….., through his writings.
3. Nilakanta Brahmachari started the secret society name …………….
4. The starting of trade unions in Madras was pioneered by ……………..
5. The Dravidian Association Hostel for non-Brahmin students was established by ………………
6. ……………… formed the first Congress Ministry in Madras.
7. …………….. was the founder of the Madras branch of the Muslim League.
8. ……………. hoisted the national flag atop Fort St. George on 26 January 1932.
Answers:
1. T. Muthuswami
2. G. Subramaniam
3. Bharata Matha Society
4. B.P. Wadia
5. C. Natesanar
6. Rajaji
7. Yakub Hasan
8. Bhashyam

III. Choose the correct statement.

Question 1.
(i) Madras Native Association was founded in 1852.
(ii) Tamil nationalist periodical Swadesamitran was started in 1891.
(iii) The Madras Mahajana Sabha demanded conduct of civil services examinations only in India.
(iv) V.S. Srinivasanar was an extremist.
(a) (i) and (ii) are correct
(b) (iii) is correct
(c) (iv) is correct
(d) All are correct
Answer:
(a) (i) and (ii) are correct

Question 2.
(i) EVR did not participate in the Non – Cooperation Movement.
(ii) Rajaji worked closely with Yakub Hasan of the Muslim League.
(iii) Workers did not participate in the Non- Cooperation Movement.
(iv) Toddy shops were not picketed in Tamil Nadu.
(a) (i) and (ii) are correct
(b) (i) and (iii) are correct
(c) (ii) is correct
(d) (i) (iii) and (iv) are correct.
Answer:
(c) (ii) is correct

Question 3.
Assertion (A): The Justice Party opposed the Home Rule Movement.
Reason (R): The Justice Party feared that Home Rule would give the Brahmins more power.
(a) Both A and R are correct but R is not the correct explanation
(b) A is correct but R is wrong
(c) Both A and R are wrong
(d) Both A and R are correct and R is the correct explanation
Answer:
(d) Both A and R are correct and R is the correct explanation

Question 4.
Assertion (A): EVR raised the issue of representation for non-Brahmins in legislature.
Reason (R): During the first Congress Ministry, Rajaji abolished sales tax.
(a) Both A and R are correct but R is not the correct explanation
(b) A is correct but R is wrong
(c) Both A and R are wrong
(d) Both A and R are correct and R is the correct explanation
Answer:
(b) A is correct but R is wrong

IV. Match the following.

Answer:
1. (d)
2. (e)
3. (b)
4. (c)
5. (a)

V. Answer the questions briefly.

Question 1.
List out the contribution of the moderates.
Answer:
Contributions of the Moderates:

1. They exposed the liberal claims of the British and how the British exploited India.
2. They exposed British’s hypocrisy in following democratic principles in England and imposing an unrepresentative Government in the colonies.

Question 2.
Write a note on the Tirunelveli Uprising.
Answer:
The Tirunelveli uprising took place after the arrests of V.O. Chidambaram Pillai and Subramania Siva in 1908. They were charged with sedition. During the protests, a police station, a court building and municipal office were burnt down and four people died in police firing.

Question 3.
What is the contribution of Annie Besant to India’s freedom struggle?
Answer:

1. Annie Besant, an Irish lady and the leader of the Theosophical society started the Home Rule League on the modelof Irish Home Rule League in 1916.
2. She carried forward the demand for Home Rule all over India: She started the newspapers “New India, Commonweal” to carry forward her agenda.
3. Large number of students who joined the movement were trained in Home Rule classes.
4. They were formed into boy scouts and volunteer troops.
5. By forming trade unions with her member B.P Wadia improved the working conditions of’the workers and they made them part of the struggle for freedom.

Question 4.
Mention the various measures introduced by the Justice Ministry.
Answer:
Measures introduced by Justice Ministry:

• reservation for non-Brahmins in local bodies and education
• establishment of Staff Selection Board
• enactment of Hindu Religious, Endowment Act,
• abolition of devadasi system
• allotment of waste government land to the poor, and extension of primary education to depressed classes.

Question 5.
Write briefly on EVR’s contribution to the constructive programme.
Answer:

1. E.V.R played an important role in Tamil Nadu during the period of Non – Cooperation movement.
2. He campaigned vigorously for the promotion and sale of Khadi.
3. In his opposition to consumption of liquor he cut down on entire coconut grove owned by him.
4. He played a key role in Satyagraha for temple entry in vaikom, then under Travancore.
5. E.V.R went to Vaikom and galvanised the movement.
6. He was imprisoned and released after one-month.
7. He refused to leave vaikom and sentenced to six month rigorous imprisonment for making inspiring speeches.
8. Due to his undeterred effort, in 1925, the ban on the roads around the temple where the permission was not given to the depressed classes to enter was lifted.
9. He was hailed as “Vaikom Hero” for his contribution against caste discrimination and temple entry agitation.

Question 6.
What is Cheranmadevei Gurukuiam controversy?
Answer:
V.V.S. Iyer established a Gurukuiam in Cheranmadevi. It got funds from Congress, but students were discriminated on the basis of caste. E.V. Ramaswamy got to know about the practices in 1925 and he severely criticised it.

Question 7.
Why was anti-Hindi agitation popular?
Answer:

1. Congress Ministry under Rajaji introduced Hindi as a compulsory subject in schools.
2. This was considered as a form of Aryan and North. Indian imposition detrimental to Tamil language and culture, and therefore caused much public resentment.
3. E.V.R led a massive campaign against it.
4. He organised an anti-Hindi conference at Salem and formulated a definite programme of action.
5. A rally was organised from Trichirapalli to Madras.
6. More than 1200 protesters including E.V.R were arrested.
7. As a result after the resignation of Congress Ministry the then Governor of Madras removed Hindi as a compulsory subject in schools. Thus the anti-Hindi agitation became popular as it succeeds in its objective.

Question 8.
Outline the key incidents during the Quit India Movement in Tamil Nadu.
Answer:
All sections of the society in Tamil Nadu participated in the Quit India Movement. There were workers’ strikes and students also protested. There were many incidents of violence and disruption of rail traffic. Congress volunteers clashed with the military in Madurai. There were police firings at some places.

VI. Answer the questions given under each caption.

Question 1.
Early Nationalist Movement In Tamil Nadu

(a) What were the objectives of Madras Native Association?
Answer:

1. To promote the interests of its members.
2. Focused on reduction of taxation.

(b) What led to the emergence of nationalist press in Tamil Nadu?
Answer:
The entire press was owned by the Europeans. When the appointment of Indian T. Muthuswami as Judge was criticised they felt the need of nationalist press to express the Indian perspective.

(c) What were the demands of Madras Mahajana Sabha?
Answer:

1. Conduct of simultaneous civil services examinations in England and India.
2. Reduction of taxes and reduction of civil and military expenditure.

(d) Who were the early nationalist leaders in Tamil Nadu?
Answer:
The early nationalists leaders in Tamil Nadu were V.S. Srinivasa Sastri. RS.Sivasamy and G.A.Natesan, T.R.Venkatramanar, S.Subramaniar, V.krishnasamy.

Question 2.
Revolutionary Movement in Tamil Nadu
(a) List a few revolutionaries in Tamil Nadu. ‘
Answer:
Some revolutionaries in Tamil Nadu were M.P.T. Acharya, V.V.S. Iyer and T.S.S. Rajan.

(b) Why did Subramania Bharati moved to Pondicherry?
Answer:
Subramania Bharati went to Pondicherry to escape imprisonment after the Tirunelveli uprising in 1908. Pondicherry was under French rule.

(c) Name a few of the revolutionary literature?
Answer:
Some revolutionary literature includes India, Vijaya, and Suryodayam, which came out of Pondicherry.

(d) What did Vanchinathan do?
Answer:
Vanchinathan shot dead by Robert W.D’E. Ashe, the collector of Tirunelveli, at Maniyachi junction on 17th June 1911. He shot himself after that.

Question 3.
Non-Brahmin Movement

(a) Why was the South Indian Liberal Federation formed?
Answer:
South Indian Liberal Federation was formed to promote the interests of the Non – Brahmins.

(b) What is the Non-Brahmin Manifesto?
Answer:
Reservation of jobs for Non – Brahmins in Government service and seats in representative bodies.

(c) Why did EVR join the Non-Brahmin Movement?
Answer:
When EVR raised the issue of representation for Non – Brahmins in the legislature his efforts to achieve this since 1920 had met with.

(d) What do you know about anti-Hindi agitation?
Answer:
It Caused much resentment as it was considered to be a form of Aryan and North India imposition detrimental to Tamil language and culture.

VII. Answer the following in detail.

Question 1.
Discuss the response to Swadeshi Movement in Tamil Nadu.
Answer:
During the Swadeshi movement, public meetings were organized in various parts of Tamil Nadu, and they were attended by thousands of people. Tamil was used for the first time to mobilize people. Many journals came into existence to spread Swadeshi ideals. Students and youth participated widely in the movement. Some lectures were delivered by Bipin Chandra Pal, while Subramania Bharati’s patriotic songs stirred patriotic emotions in people.

Question 2.
Examine the origin and growth of Non- Brahmin Movement in Tamil Nadu.
Answer:
Origin of Non – Brahmin Movemet.

Cause: In the Madras presidency due to the rapid growth of education, there was an increase in the number of educated Non – Brahmins.

Reason: Intense political and social activities politicised the educated Non-Brahmins to raise the issue of caste discrimination and unequal opportunities in Government employment and representation in the elected bodies which were dominated by Brahmins.

Formation: The Non – Brahmins organised themselves into political organisations to protect their interests.

1. In 1912 the Madras Dravidian Association was founded with C.Natesanar as its secretary. Active role if C.Natesanar. for the.growth of Non – Brahmin movement.
2. In June 1916 he established the Dravidian Association Hostel for Non¬Brahmin students.
3. He bridged the gap between the two leading Non-Brahmin leaders of the time Dr. T.M.Nair and P.Thiyagarayar.
4. On 20th November 1916 a meeting was held for about thirty Non-Brahmins under the leadership of P.Thiyagarayar Dr. T.M.Nair and C.Natesanar at Victoria public hall (Chennai).

South Indian Liberal Federation (SILF):

South Indian Liberal Federation was founded to promote the interests of the Non-Brahmins.

News papers launching: They launched three newspapers Justice – in English, Dravidian – in Tamil and Andhra prakasika in Telugu.

1. SILF popularly known as ‘Justice party’ after its English Newspaper.
2. They held several meetings throughout the presidency to set up branches.

Objectives of Non- Brahmin Manifesto:

1. Reservation of jobs in Government services.
2. Seats in local bodies

Achievement: The act of 1919 provided reservation of seats to Non-Brahmins.

In the elections held in 1920 the Justice Party won the majority seats in the Legislative Council. A. Subburayalu of the Justice Party became the first Chief Minister.

Question 3.
Describe the role of Tamil Nadu in the Civil Disobedience Movement.
Answer:
Tamil Nadu was at the forefront of the Civil Disobedience Movement. Shops were picketed and foreign goods were boycotted in Madurai. C. Rajagopalachari led the Salt Satyagraha march to Vedaranyam and was arrested. The march took place in April 1930. Twelve volunteers broke the salt law by picking up the salt.

VIII. Activity

Question 1.
Students can be asked to write a sentence or two about the important places of freedom struggle in Tamil Nadu.
Answer:
Panchalankuruchi is a place 17 km from Tuticorin. This small village holds a lot of historic value in terms of India’s freedom struggle against English dominance. It is home to an 18th century chieftain Veerapandya Kattabomman who fought valiantly against the English, but was defeated and hanged.

Velunachiyar employed agents for gathering intelligence to find where the British had stored their ammunition. With military assistance from Gopala Nayakar and Hyder Ali she recaptured Sivagangai. She was the first female ruler or queen to resist the British colonial power in India.

A procession carrying national flags and singing patriotic songs was brutally beaten by the police in Tirupur. O.K.S.R. Kumaraswamy, popularly Tirupur Kumaran, fell dead holding the national flag aloft.

The Salt satyagraha under the leadership of T. Prakasam and K. Nageswara Rao set up a camp at Udayavanam near Madras. However, the police arrested them. In Madras, the Simon Boycott Propaganda Committee was set up with S. Satyamurti as the president. There was widespread campaign among the students, shopkeepers, lawyers and commuters in train to boycott.

Rowlatt Satyagraha: On 6 April 1919 hartal was organised to protest against the “Black Act”. Protest demonstrations were held at several parts of Tamil Nadu. Processions from many areas of the city converged in the Marina beach where there was a large gathering.

Annie Besant started the Home Rule League in 1916 and carried forward the demand for home rule all over India. G.S. Arundale, B.P. Wadia and C.P. Ramaswamy assisted her in this campaign.

Radical papers such as India, Vijaya and Suryodayam came out of Pondicherry. Such revolutionary papers and Bharati’s poems were banned as seditious literature. These activities in Pondicherry intensified with the arrival of Aurobindo Ghosh and V.V. Subramanianar in 1910.

Question 2.
Role Play: Students can be divided into groups and asked to debate the views of the Moderates, Extremists, Revolutionaries, Annie Besant’s supporters, Justice Party, and British Government.
Answer:
Do it yourself.

Freedom Struggle in Tamil Nadu Additional Questions

I. Choose the correct answer.

Question 1.
The first organization in the Madras presidency to agitate for the rights of people was the …………..
(a) Indian National Congress
(b) Madras Native Association
(c) Muslim league
Answer:
(b) Madras Native Association

Question 2.
…………………. played an active role as the secretary of Madras Mahajana Sabha.
(a) P.Anandacharlu
(b) Gazalu
(c) T.Muthuswami
(d) G.Subramaniam
Answer:
(a) P.Anandacharlu

Question 3.
The Headquarters of the Tamil Nadu Congress Committee is named as ……………
(a) Raj Bhavan
(b) Sathyamurthi Bhavan
(c) Rajaji Bhavan
Answer:
(b) Sathyamurthi Bhavan

Question 4.
…………………. purchased two ships for Swadeshi Indian Trade.
(a) Bipin Chandra Pal
(b) V.O.Chidambaranar
(c) T.S.S.Rajan
(d) V.V.Subramaninar
Answer:
(b) V.O.Chidambaranar

Question 5.
Who made Hindi a compulsory subject …………..
(a) Rajaji
(b) V.O.C
(c) Nehru
Answer:
(a) Rajaji

Question 6.
Annie Besant was the leader of …………………. society who propagated Home Rule Movement in Madras.
(a) Theosophical
(b) Madras Dravidian Association
(c) Madras Mahajana Sabha
(d) Madurai Labour Union
Answer:
(a) Theosophical

Question 7.
Who started the Tamil nationalist periodical Swadesamitram?
(a) T. Muthuswami
(b) G. Subramaniam
(c) M. Veeraraghavachari
(d) P. Anandacharlu
Answer:
(b) G. Subramaniam

Question 8.
In Tamil Nadu Khilafat day was observed on:
(a) 19th April 1920
(b) 15 th April 1920
(c) 21st April 1920
(d) 17th April 1920
Answer:
(d) 17th April 1920

Question 9.
What was Bharata Matha Society?
(a) A newspaper
(b) A periodical
(c) A secret society
(d) A political party
Answer:
(c) A secret society

Question 10.
…………………. was hailed as Vaikom Hero.
(a) Periyar
(b) P.Subbarayan
(c) Rajaji
(d) M.A.Ansari
Answer:
(a) Periyar

II. Fill in the blanks :

1. The third session of the Indian National Congress was held at …………., now known as the thousand lights.
2. ………….. provided a safe haven for the revolutionaries.
3. On 18th march 1919 Gandhi addressed a meeting on …………..
4. …………….. was the epicenter of Khilafat Agitaion.
5. A no-tax campaign took place in ……………
6. ………….. and ……………. was the first woman to pay penalty for violation of salt laws.
7. E.V.R organized an Anti-Hindi conference at …………..
8. In Madras, the Simon Boycott Propaganda Committee was set up with ……………… as the President.
9. The Government of India Act of 1935 introduced ……………….
10. ……………One of the controversial measures of Rajaji was the introduction of ………………. as a compulsory subject in school.
11. The Swarajists did not contest the 1930 elections leading to an easy victory for the ……………. party.
12. The Madras Native Association or MNA was the earliest organization to be founded in ……………. to articulate larger public rather than sectarian interests.
Answers:
1. Makkis Garden
2. Pondicherry
3. Marina beach
4. Vaniyambadi
5. Thanjavur
6. Rukmani Lakshmipathi
7. Salem
8. S. Satyamurthi
9. Provincial Autonomy
10. Hindi
11. Justice
12. South India

III. Choose the correct statement.

Question 1.
(i) The Non-Brahmin Manifesto opposed the Home Rule Movement as a movement of Brahmins and feared that Home Rule might give them more power.
(ii) However, it never criticized the Congress as the party of the Brahmins.
(iii) The Justice Party demanded communal representation in society.
(iv) The Madras government was supportive of the Justice Party. .
(a) (i) and (ii) are correct
(b) (ii) and (iii) are correct
(c) (i) (iii) and (iv) are correct
(d) (ii) and (iv) are correct
Answer:
(c) (i) (iii) and (iv) are correct

Question 2.
Assertion: E. V. R. was becoming increasingly dissatisfied with the Congress.
Reason: He felt it was promoting the interests of the Brahmins alone.
(a) Both A and R are correct but R is not the right explanation
(b) A is right but R is wrong
(c) Both A and R are wrong
(d) Both A and R are correct and R is the right explanation
Answer:
(d) Both A and R are correct and R is the right explanation

IV. Match the following.

Answer:
1. (c)
2. (a)
3. (d)
4. (e)
5. (b)

V. Answer briefly:

Question 1.
Who was appointed as High court Judge of Madras in 1877? How it was criticized?
Answer:
The appointment of T. Muthuswami as the First Indian Judge of Madras High court in 1877. The press entirely owned by Europeans criticized the appointment of an Indian as Judge.

Question 2.
Write a note on Subramaniya Siva.
Answer:

• Subramaniya Siva was bom in Vathalagundu in Dindigal district.
• He was a freedom fighter and a creative writer.
• He was arrested many times for his anti-imperialist activities.
• While in jail he was affected by leprosy and he was ordered to be shifted to Salem jail.
• But the British Government enacted a law for Siva stating that leprosy patient should not travel by rail. So he had to walk a long distance with sores on his body.
• He died of the disease on 23rd July 1925.

Question 3.
Name the states that was then a part of the Madras Presidency.
Answer:
Tamil Nadu was then a part of Madras Presidency which included larger parts of the present day states of Andhra Pradesh (Coastal districts and Royalaseema) Karnataka (Bengaluru, Bellary, South Canara) Kerala (Malabar) and even Odhisha (Ganjam).

Question 4.
Name the paper edited by Subramania Bharathiyar in 1907.
Answer:
Tamil weekly India and the English Newspaper ‘Bala Bharatham’ were edited by Subramania Bharathiyar in 1907.

Question 5.
Name the persons who assisted Annie Besant to carry the Home Rule Movement campaign.
Answer:
G.S.Arundale, B.P. Wadia and C.P.Ramaswamy were some of the personalities who assisted Annie Besant to carry the Home Rule movement campaign.

Question 6.
Who established the Madras Native Association? Why?
Answer:
It was established by Harley Lakshmi Narasu Chetty and Srinivasa Pillai in 1852.

Question 7.
Name the Newspapers launched by SILF.
Answer:
The Newspapers launched by SILF (South Indian Liberal Federation) were
Justice – in English
Dravidian – In Tamil – and
Andhra prakasika – in Telugu

Question 8.
When was the need for a newspaper keenly felt?
Answer:
The appointment of T. Muthuswami Iyer as the first South Indian Judge of the Madras High Court in 1878 created resentment in Madras Presidency. The entire press in Madras criticised the appointment of an Indian as a judge. This left a deep impact on the educated youth of India. For the first time they realized that the entire press was owned by Europeans. At this very moment the need for a newspaper to express the Indian perspective was keenly felt,

Question 9.
Name the persons who organised the “Black Act” protest, How?
Answer:
On 6^th April 1919 hartal was organised to protest against the ‘Black Act’ (Rowlatt Act).

1. Processions from many areas of the city converged at Marina Beach.
2. Rajaji, Kasturirangari S.Sathyamurthy, and George Joseph addressed the meeting.
3. Workers meeting was addressed by Thiru.V. Kalyanasundaranar, B.P. Wadia and V.O.C.. They devoted the whole day to fasting and prayers along with large number of people in the Marina Beach.

Question 10.
Why were the moderates disappointed with the Minto-Morley reforms?
Answer:
They were disappointed with the Minto-Morley reforms as it did not provide for responsible government. Despite this the Congress extended support to the British war effort in the hope of getting more reforms.

Question 11.
What resulted in India’s Independence?
Answer:
The Royal Navy Mutiny, the negotiations initiated by the newly formed • labour party Government in England resulting in India’s independence.

VI. Answer all the questions given under each caption:

Question 1.
Vanchinathan
(a) Whom did Vanchinathan kill?
Answer:
Collector Ashe.

(b) Where did he kill him?
Answer:
At Maniyachi Railway Station.

(c) Why did he kill him?
Answer:
To take revenge against the death of four extremists.

(d) What was the end of Vanchinathan?
Answer:
He committed suicide.

Question 2.
Salt March to Vedaranyam (second part)

(a) Who composed the marching song?
Answer:
A special song was composed for the salt march by Nammakkal Ramalinganar.

(b) How was the response from the people along their route?
Answer:
The marching Satyagraha’s were provided warm reception along the route.

(c) How many volunteers along with Rajaji picked up the salt ?
Answer:
Twelve volunteers under the leadership of Rajaji picked up the salt.

(d) Who were the other prominent leaders from Tamil Nadu participated?
Answer:
T.S.S.Rajan, Rukmani Lakshmipathi, Sardar Vedarathnam, C.Swaminathar and K.Santhanam were the prominent leaders who participated in Vedaranyam Salt march.

Question 3.
No Tax Campaign and Movement against Liquor
(a) Name the city where no-tax campaign took place. How did people respond to this campaign?
Answer:
Thanjavur. People boycotted councils, schools and courts. They also boycotted foreign goods.

(b) What was temperance movement? How was this movement made successful?
Answer:
Temperance Movement was a movement against liquor. This movement was made successful by picketing toddy shops.

(c) Why were Rajaji, Subramania Sastri and E. V. R. arrested?
Answer:
They were arrested because they were going to organise civil disobedience movement in Tamil Nadu.

(d) Why was the Non Co-operation Movement withdrawn?
Answer:
It was withdrawn after the Chauri Chaura incident in which 22 policemen were killed.

VII. Answer the following in detail.

Question 1.
What were the reforms brought forth by the first Congress Ministry led by C. Rajaji?
Answer:

1. C. Rajaji formed the first Congress Ministry in 1937.
2. He introduced prohibition on an experimental basis in salem.
3. To compensate the loss of revenue he introduced a sales tax.
4. He opened temples to the ‘untouchables’ (Harijans).
5. He appointed a committee to enquire into the condition of the tenants in the zamindari areas.
6. One of the controversial measures of Rajaji was the introduction of Hindi as a compulsory subject in schools [and Kula Kalvi Thittam in 1953].
7. After the resignation of Congress Ministry in 1939 the then, Governor of Madras Lord Erskine in Feb 1940 who took over the reigns of administration removed Hindi as compulsory subject.

Question 2.
Throw light on the Madras Native Association or MNA. When did it cease to exist?
Answer:
(i) The Madras Native Association was the earliest organization to be founded in South India.
It was started by Gazulu Lakshminarasu, Srinivasanar and their associates in 1852. It con¬sisted primarily of merchants.

(ii) The objective of MNA was to promote the interests of its members and their focus was on reduction in taxation. It also protested against the support of the government to Christian missionary activities.

(iii) It drew attention of the government to the condition and needs of the people. Its main contribution was its agitation against torture of the peasants by revenue officials.

(iv) The efforts of MNA led to the establishment of the Torture Commission and the eventual abolition of the Torture Act, which justified the forcible collection of land revenue through tortuous methods.

(v) The Madras Native Association ceased to exist by 1862.

Question 3.
Reason out why James Neill statue was moved to Madras Museum.
Answer:

1. James Neill of the Madras Fusilers (Infantry men with fire arms) was brutal in wrecking vengence at Kanpur. Women and children were massacred in 1857 Revolt.
2. A statue was erected for him at mount road, Madras.
3. Nationalist felt this as an insult to Indian sentiments.
4. They organised a series of demonstrations in Madras.
5. Protesters came from all over the Madras Presidency and were led by S.N.Somayajulu of Tirunelveli.
6. Many were arrested and sentenced to prison.
7. Gandhi who visited Madras during the same time gave his support to the agitation.
8. The statue was finally moved to Madras Museum when Congress Ministry, led by C.Rajaji formed the Government in 1917.

IMPORTANT EVENTS AND YEAR

We think the data given here clarify all your queries of Chapter 9 and make you feel confident to attempt all questions in the examination. So, practice more & more from Tamilnadu State Board solutions for 10th Social Science History Chapter 9 Freedom Struggle in Tamil Nadu Questions and Answers & score well. Need any information regarding this then ask us through comments & we’ll give the best possible answers very soon.

Students who are preparing for the Science exam can download this Tamilnadu State Board Solutions for Class 11th Science Chapter 11 from here for free of cost. These Tamilnadu State Board Textbook Solutions PDF cover all 11th Science Carbon and its Compounds Book Back Questions and Answers.

All these concepts of Chapter 11 Carbon and its Compounds are explained very conceptually by the subject teachers in Tamilnadu State Board Solutions PDF as per the prescribed Syllabus & guidelines. You can download Samacheer Kalvi 10th Science Book Solutions Chapter 11 Carbon and its Compounds State Board Pdf for free from the available links. Go ahead and get Tamilnadu State Board Class 11th Science Solutions of Chapter 11 Carbon and its Compounds.

Tamilnadu Samacheer Kalvi 10th Science Solutions Chapter 11 Carbon and its Compounds

Kickstart your preparation by using this Tamilnadu State Board Solutions for Class 11th Science Chapter 11 Carbon and its Compounds Questions and Answers and get the max score in the exams. You can cover all the topics of Chapter 11 easily after studying the Tamilnadu State Board Class 11th Science Textbook solutions pdf. Download the Tamilnadu State Board Science Chapter 11 Carbon and its Compounds solutions of Class 11th by accessing the links provided here and ace up your preparation.

Samacheer Kalvi 10th Science Carbon and its Compounds Textual Evaluation Solved

I. Choose the best answer.

Carbon And Its Compounds Class 10 Samacheer Question 1.
The molecular formula of an open – chain organic compound is C₃H₆. The class of the compound is ______.
(a) alkane
(b) alkene
(c) alkyne
(d) alcohol.
Answer:
(b) alkene
Hint:
As we know the general molecular formula of alkene is C_nH_2n.
n = 2, C₂H₄
n = 3, C₃H₆
n = 4, C₄H₈

Carbon And Its Compounds Samacheer Kalvi Question 2.
The IUPAC name of an organic compound is 3-Methyl butan-1-ol. What type of compound it is?
(a) Aldehyde
(b) Carboxylic acid
(c) Ketone
(d) Alcohol.
Answer:
(d) Alcohol
3-Methyl butan-1-ol

This compound contains -OH group, i.e. alcohol.

Carbon And Its Compounds Class 10 Hots Questions With Answers Question 3.
The secondary suffix used in IUPAC nomenclature of an aldehyde is ______.
(a) – ol
(b) – oic acid
(c) – al
(d) – one.
Answer:
(c) – al

Suffix ‘al’ is used to exhibit the aldehyde group.

Carbon And Its Compounds Class 10 Book Pdf Question 4.
Which of the following pairs can be the successive members of a homologous series?
(a) C₃H₈ and C₄H₁₀
(b) C₂H₂ and C₂H₄
(c) CH₄ and C₃H₆
(d) C₂H₅OH and C₄H₈OH
Answer:
(a) C₃H₈ and C₄H₁₀

Carbon And Its Compounds Class 10 In Tamil Question 5.
C₂H₅OH + 3O₂ → 2CO₂ + 3H₂O is a ______.
(a) Reduction of ethanol
(b) Combustion of ethanol
(c) Oxidation of ethanoic acid
(d) Oxidation of ethanol.
Answer:
(b) Combustion of ethanol
Hint: Above chemical reaction is an example of combustion reaction because it produces CO₂ and H₂O on the action of O₂.

Carbon And Its Compounds Class 10 Solutions Question 6.
Rectified spirit is an aqueous solution which contains about ………… of ethanol.
(a) 95.5%
(b) 15.5%
(c) 55.5%
(d) 45.5%
Answer:
(a) 95.5%

Class 10 Carbon And Its Compounds Solutions Question 7.
Which of the following are used as anaesthetics?
(a) Carboxylic acids
(b) Ethers
(c) Esters
(d) Aldehydes.
Answer:
(b) Ethers

Chapter Carbon And Its Compounds Class 10 Question 8.
TFM in soaps represents ………… content in soap.
(a) mineral
(b) vitamin
(c) fatty acid
(d) carbohydrate
Answer:
(c) fatty acid

Carbon And Its Compounds Pdf Question 9.
Which of the following statements is wrong about detergents?
(a) It is a sodium salt of long – chain fatty acids
(b) It is sodium salts of sulphonic acids
(c) The ionic part in a detergent is \(-\mathrm{SO}_{3}-\mathrm{Na}^{+}\)
(d) It is effective even in hard water.
Answer:
(a) It is a sodium salt of long-chain fatty acids
Hint: Detergents are not sodium salt of long – chain fatty acids. Actually soaps are sodium salts of long – chain fatty acids.

II. Fill in the blanks.

Carbon Compounds Question 1.
An atom or a group of atoms which is responsible for chemical characteristics of an organic compound is called ______.
Answer:
Functional group.

Class 10 Science Chapter 11 Extra Questions Question 2.
The general molecular formula of alkynes is ______.
Answer:
C_nH_2n-2.

Carbon And Its Compounds Worksheet With Answers Pdf Question 3.
In IUPAC name, the carbon skeleton of a compound is represented by ______ (root word / prefix / suffix)
Answer:
Root word.

Question 4.
______ compounds decolourize bromine water. (Saturated/Unsaturated)
Answer:
Unsaturated.

Question 5.
Dehydration of ethanol by concentrated Sulphuric acid forms ________ (ethene/ethane)
Answer:
Ethene.

Question 6.
100% pure ethanol is called ______.
Answer:
Absolute alcohol.

Question 7.
Ethanoic acid turns ________ litmus to ______.
Answer:
Blue, red.

Question 8.
The alkaline hydrolysis of fatty acids is termed as ______.
Answer:
Saponification.

Question 9.
Biodegradable detergents are made of ______ (branched / straight) chain hydrocarbons.
Answer:
Straight.

III. Match the following

Question 1.

Answer:
i – c, ii – d, iii – e, iv – b , iv – a.
Hint:
i. Alcohol (-OH) is a functional group.
ii. Furan is a heterocyclic compound because it contains an oxygen atom in the cyclic ring.
iii. Ethene contains a double bond, so it is unsaturated.
iv. Soap is potassium/sodium stearate.
v. Benzene is a six-membered carbon atom ring, so it is carbocyclic.

IV. Assertion and Reason.

Answer the following questions using the data given below:
(i) A and R are correct, R explains the A.
(ii) A is correct, R is wrong.
(iii) A is wrong, R is correct.
(iv) A and R are correct, R doesn’t explain A.

Question 1.
Assertion: Detergents are more effective cleansing agents than soaps in hard water.
Reason: Calcium and magnesium salts of detergents are water – soluble.
Answer:
(ii) A is correct, R is wrong.

Question 2.
Assertion: Alkanes are saturated hydrocarbons.
Reason: Hydrocarbons consist of covalent bonds.
Answer:
(iv) A and R are correct, R doesn’t explain A.
Alkanes are saturated hydrocarbons due to the presence of single bonds.

V. Short Answer Questions.

Question 1.
Name the simplest ketone and give its structural formula.
Answer:
Simplest ketone contains three carbon atom chain with the molecular formula C₃H₆O.

Question 2.
Classify the following compounds based on the pattern of the carbon chain and give their structural formula:

1. Propane
2. Benzene
3. Cyclobutane
4. Furan.

Answer:

1. Propane is an open chain or a cyclic compound because it contains an open chain.
   CH₃-CH₃-CH₃ [Propane].
2. Benzene is a carbocyclic compound because it contains carbon atoms cyclic ring of 6 atoms.
   
3. Cyclobutane is a carbocyclic compound.
   
4. Furan is a heterocyclic compound because in the cyclic chain one atom is oxygen atom. HC – CH
   

Question 3.
How is ethanoic acid prepared from ethanol? Give the chemical equation.
Answer:
Ethanoic acid can be prepared by oxidation of ethanol in the presence of alkaline potassium permanganate of acidified potassium dichromate.

Question 4.
How do detergents cause water pollution? Suggest remedial measures to prevent this pollution?
Answer:
(i) Some detergents having a branched hydrocarbon chain are not fully biodegradable by microorganism present in water and they cause water pollution.
(ii) Remedial Action: We have to use biodegradable detergents which have linear hydrocarbon chains.

Question 5.
Differentiate soaps and detergents.
Answer:

VI. Long Answer Questions.

Question 1.
What is called a homologous series? Give any three of its characteristics?
Answer:
A homologous series is a group or a class of organic compounds having same general formula and similar chemical properties in which the successive members differ by a -CH₂ group.
Characteristics of homologous series:

1. Each member of the series differs from the preceeding or succeeding member by one methylene group (-CH₂) and hence by a molecular mass of 14 amu.
2. All members of a homologous series contain the same elements and functional group.
3. They are represented by a general molecular formula. Eg: Alkanes, C₂H_2n+2.
4. The members in each homologous series show a regular gradation in their physical properties with respect to their increase in molecular mass.
5. Chemical properties of the members of a homologous series are similar.
6. All the members can be prepared by a common method.

Question 2.
Arrive at, systematically, the IUPAC name of the compound: CH₃ – CH₂ – CH₂ – OH.
Answer:

• Step 1: The parent chain consists of 4 carbon atoms. The root word is ‘but’.
• Step 2: All are single bonds between the carbon atoms of the chain. So the primary suffix is ‘ane’.
• Step 3: Since the compound contains the -OH group, it is an alcohol. The secondary suffix is ‘ol’.
  But + ane + ol = Butan-ol = Butanol.

Question 3.
How is ethanol manufactured from sugarcane?
Answer:
Fermentation method can be used to obtain ethanol from sugarcane. Actually, in industries, C₂H₅OH is prepared by the fermentation of molasses, which is a by – product obtained during the manufacture of sugar from sugarcane.
It is converted into ethanol by following steps:

• Dilution of molasses
• Addition of nitrogen source
• Addition of yeast
• Distillation of wash.

Chemical Reductions:

Question 4.
Give the balanced chemical equation of the follows ing reactions:
(i) Neutralization of NaOH with ethanoic acid.
(ii) Evolution of carbon dioxide by the action of ethanoic acid with NaHCO₃
(iii) Oxidation of ethanol by acidified potassium dichromate.
(iv) Combustion of ethanol.
Answer:

Question 5.
Explain the mechanism of cleansing action of soap.
Answer:
(i) A soap molecule contains two chemically distinct parts that interact differently with water. It has one polar end, which is a short head with a carboxylate group (-COONa) and one non-polar end having the long tail made of the hydrocarbon chain.

(ii) The polar end is hydrophilic (Water loving) in nature and this end is attracted towards water. The non-polar end is hydrophobic (Water hating) in nature and it is attracted towards dirt or oil on the cloth, but not attracted towards water. Thus, the hydrophobic part of the soap molecule traps the dirt and the hydrophilic part makes the entire molecule soluble in water.

(iii) When a soap or detergent is dissolved in water, the molecules join together as clusters called ‘micelles’. Their long hydrocarbon chains attach themselves to the oil and dirt. The dirt is thus surrounded by the non-polar end of the soap molecules. The charged carboxylate end of the soap molecules makes the micelles soluble in water. Thus, the dirt is washed away with the soap.

VII. HOT Questions.

Question 1.
The molecular formula of an alcohol is C₄H₁₀O. The locant number of its -OH group is 2.
(i) Draw its structural formula.
(ii) Give its IUPAC name.
(iii) Is it saturated or unsaturated?
Answer:

the group is placed in the secondary carbon atom.

(ii) Butan-2-ol

(iii) In butan-2-al all bonds are single bonds. So, this is a saturated compound.

Question 2.
An organic compound ‘A’ is widely used as a preservative and has the molecular formula C₂H₄O₂. This compound reacts with ethanol to form a sweet – smelling compound ‘B’.

1. Identify the compound ‘A’.
2. Write the chemical equation for its reaction with ethanol to form compound ‘B’.
3. Name the process.

Answer:

1. Acetic acid (CH₃COOH) is widely used as a preservative.
2. CH₃COOH reacts with ethanol to form fruity smell ester, this reaction is known as an esterification reaction.
   
3. Esterification process.

Samacheer Kalvi 10th Science Carbon and its Compounds Additional Questions

I. Choose the best answer.

Question 1.
Most of the organic compounds are insoluble in ______.
(a) Ether
(b) CCl₄
(c) Toluene
(d) Water.
Answer:
(d) Water.

Question 2.
Which is/are unsaturated compounds among the following?
(a) Methane
(b) Ethene
(c) Propyne
(d) Both (b) and (c)
Answer:
(d) Both (b) and (c)

Question 4.
Pick out the saturated compound form the following ______.
(a) propane
(b) propene
(c) propyne
(d) butene.
Answer:
(a) propane

Question 4.
The alkane with six carbon atoms is known as:
(a) Propane
(b) Pentane
(c) Hexene
(d) Hexane
Answer:
(d) Hexane

Question 5.
Which one of the following is an example for the carbocyclic compound?
(a) Benzene
(b) Toluene
(c) Propane
(d) Furan.
Answer:
(d) Furan.

Question 6.
Structure of cyclobutane is ______.

Answer:

Question 7.
The general formula for ketones is written as:
(a) R – OH
(b) R-COOR
(c) ROR
(d) RCOR
Answer:
(d) RCOR

Question 8.
General formula for alkane is ______.
(a) C_nH_2n
(b) C_nH_2n+2
(c) C_nH_2n-2
(d) C_nH_n
Answer:
(b) C_nH_2n+2

Question 9.
Which one of the following is a general formula for an alkene?
(a) C_nH_2n
(b) C_nH_2n+2
(c) C_nH_2n-2
(d) C_nH_n
Answer:
(a) C_nH_2n

Question 10.
Hand sanitizers contain:
(a) Ethanol
(b) Ethanal
(c) Ethanoic acid
(d) Ethane
Answer:
(a) Ethanol

Question 11.
Lower hydrocarbons are ______ state at room temperature.
(a) solid
(b) liquid
(c) gaseous
(d) viscous.
Answer:
(c) gaseous

Question 12.
Reagent which distinguishes alkane and alkene is ______.
(a) Br₂ / H₂O
(b) H₂O
(c) C₂H₅OH
(d) Ether.
Answer:
(a) Br₂ / H₂O

Question 13.
Pick out the functional group for alcohol ______.
(a) -CHO
(b) -COOH
(c) -OH
(d) -OR.
Answer:
(c) -OH

Question 14.
-COOH is a functional group of ______.
(a) carboxylic acid
(b) ester
(c) ether
(d) aldehyde.
Answer:
(a) carboxylic acid

Question 15.
Which one of the following is the correct sequence to get the IUPAC name of the cojnpound?
(a) Prefix + Root word + Suffix → IUPAC name
(b) Prefix + Suffix + Root word → IUPAC name
(c) Suffix + Root word + Prefix → IUPAC name
(d) Root word + Prefix + Suffix → IUPAC name.
Answer:
(a) Prefix + Root word + Suffix → IUPAC name

Question 16.
What is the root word, if the compound has nine number of carbon atoms?
(a) Meth-
(b) Oct-
(c) Non-
(d) Dec-.
Answer:
(c) Non-

Question 17.

(a) pentane
(b) 2-methyl pentane
(c) 4-methyl pentane
(d) 1, 1-dimethyl butane.
Answer:
(b) 2-methyl pentane

Question 18.
Dehydration of ethanol gives ______.
(a) Ethane
(b) Ethene
(c) Ethyne
(d) no reaction.
Answer:
(b) Ethene

Question 19.
Dehydration of ethanol gives ______.
(a) Ethanol
(b) Ethanoic acid
(c) Ethyne
(d) Ethene.
Answer:
(a) Ethanol

Question 20.
Power alcohol is a mixture of ______.
(a) Ethanol + Methane
(b) Ethanol + water
(c) Ethanol + Petrol
(d) Ethanol + Pyridine.
Answer:
(c) Ethanol + Petrol

Question 21.
Which one of the following has sour in taste?
(a) Ethanol
(b) Ethanoic acid
(c) Ethanal
(d) Ethyne.
Answer:
(b) Ethanoic acid

Question 22.
Decarboxylation of ethanoic acid is ______.
(a) Ethane
(b) Methane
(c) Propane
(d) Ethanol.
Answer:
(b) Methane

Question 23.
______ compounds hold the key to plant and animal life on the earth.
(a) Sulphur
(b) Carbon
(c) Nitrogen
(d) Boron.
Answer:
(b) Carbon

Question 24.
All living organisms are made of ______ atoms.
(a) phosphorous
(b) sodium
(c) carbon
(d) sulphur.
Answer:
(c) carbon

Question 25.
Which of the following is not the characteristic of carbon?
(a) carbon form allotropes
(b) carbon is a tetravalent atom
(c) carbon is a metal
(d) catenation is possible in carbon.
Answer:
(c) carbon is a metal

Question 26.
Which one is the characteristic of carbon compounds?
(a) Carbon compounds have high melting and boiling point.
(b) Carbon compounds show isomerism.
(c) Carbon compounds are electrovalent compounds.
(d) Carboncompoundsarenotcombustible.
Answer:
(b) Carbon compounds show isomerism.

Question 27.
The hydrocarbons containing at least one carbon to carbon double bond are called ______.
(a) paraffin
(b) alkyne
(c) alkene
(d) alkane.
Answer:
(c) alkene

Question 28.
Decolourisation of bromine takes place in ______.
(a) CH₂ = CH₂
(b) CH₄
(c) CH₃ – CH₃
(d) CH₃ – CH₂OH.
Answer:
(a) CH₂ = CH₂

Question 29.
The hydrocarbons containing carbon to carbon triple bond are called ______.
(a) Alkane
(b) Alkyne
(c) Paraffin
(d) Alkene.
Answer:
(b) Alkyne

Question 30.
The IUPAC name of \(\mathrm{H}_{3} \mathrm{C}-\mathrm{CH}_{2}-\mathrm{C} \equiv \mathrm{CH}\) is ______.
(a) 2-butyne
(b) But-2-ene
(c) 1-butyne
(d) But-1-ene.
Answer:
(c) 1-butyne

Question 31.
The common name of methanoic acid is ______.
(a) Acetic acid
(b) Formic acid
(c) Propionic acid
(d) Butyric acid.
Answer:
(b) Formic acid

Question 32.
Molasses contains ______.
(a) 50 % glucose
(b) 90 % sucrose
(c) 30 % sucrose
(d) 50 % fructose.
Answer:
(c) 30 % sucrose

Question 33.
______ acts as food for yeast during the fermentation of molasses?
(a) Ammonium sulphate
(b) Dilute H₂SO₄
(c) Ammonium nitrate
(d) Quick lime.
Answer:
(a) Ammonium sulphate

Question 34.
The rectified spirit contains ______.
(a) 100 % ethanol
(b) 50 % ethanol + 50 % water
(c) 95.5 % ethanol and 4.5 % water
(d) Ethanol + pyridine.
Answer:
(c) 95.5 % ethanol and 4.5 % water

Question 35.
The enzyme used in the conversion of glucose into ethanol is ______.
(a) invertase
(b) maltase
(c) diastase
(d) zymase.
Answer:
(d) zymase.

Question 36.
100% pure ethanol is known as ______.
(a) power alcohol
(b) rectified spirit
(c) absolute alcohol
(d) denatured spirit.
Answer:
(c) absolute alcohol

Question 37.
Denatured spirit is obtained by mixing ethanol with ______.
(a) pyridine
(b) petrol
(c) methanol
(d) quicklime.
Answer:
(a) pyridine

Question 38.
The reaction has taken place when ethanol is heated with Conc. H₂SO₄ of 443K is ______.
(a) oxidation
(b) reduction
(c) intermolecular dehydration
(d) intramolecular dehydration.
Answer:
(d) intramolecular dehydration.

Question 39.
The reaction took place when ethanol is heated with Conc. H₂SO₄ at 413K is ______.
(a) intermolecular dehydration
(b) hydrogenation
(c) oxidation
(d) intramolecular dehydration.
Answer:
(a) intermolecular dehydration

Question 40.
Which reagent is used to identify alcohol consumed persons?
(a) CH₃COOH
(b) CaO
(c) K₂Cr₂O₇
(d) H₂SO₄
Answer:
(c) K₂Cr₂O₇

Question 41.
The reaction of ethanol with ethanoic acid in the presence of Conc. H₂SO₄ is known as ______.
(a) etherification
(b) esterification
(c) dehydrogenation
(d) dehydration.
Answer:
(b) esterification

Question 42.
Which reagent is used to convert ethanol to acetaldehyde?
(a) Conc.H₂SO₄
(b) Acidified
(c) Alkaline KMnO₄
(d) Copper.
Answer:
(d) Copper.

Question 43.
Which compound is used as an anti-freeze in automobile radiators?
(a) Acetic acid
(b) Ethyl ethanoate
(c) Ethanol
(d) Acetaldehyde.
Answer:
(c) Ethanol

Question 44.
The organic compound used in cough syrups and in digestive syrups is ______.
(a) ethanoic acid
(b) ethyl ethanoate
(c) methanol
(d) ethanol.
Answer:
(d) ethanol.

Question 45.
The organic compound that depresses the central nervous system after consumption is ______.
(a) ethanol
(b) methanol
(c) acetic acid
(d) ethyl ethanoate.
Answer:
(b) methanol

Question 46.
The organic compound used for coagulating rubber from latex is ______.
(a) methanoic acid
(b) ethanoic acid
(c) ethanol
(d) methanol.
Answer:
(b) ethanoic acid

Question 47.
The alcohol that is poisonous in nature is ______.
(a) methanol
(b) ethanol
(c) benzyl alcohol
(d) phenol.
Answer:
(a) methanol

Question 48.
In a homologous series, the successive compounds differ by a ______ group.
(a) CH₂
(b) CH
(c) CH₃
(d) C₂H₅
Answer:
(a) CH₂

Question 49.
The fermented liquid wash contains ____ % alcohol.
(a) 90
(b) 8 – 25
(c) 15 – 18
(d) 40 – 60.
Answer:
(c) 15 – 18

Question 50.
Carbon has the ability to form ______ bonds.
(a) ionic
(b) covalent
(c) electrovalent
(d) dative.
Answer:
(b) covalent

Question 51.
Decarboxylation is removal of ______.
(a) CO
(b) CO₂
(c) H₂
(d) \(\mathrm{CO}_{3}^{-}\).
Answer:
(b) CO₂

Question 52.
The enzyme used in the conversion of molasses into glucose and fructose is ______.
(a) zymase
(b) diastase
(c) invertase
(d) maltase.
Answer:
(c) invertase

II. Fill in the blanks.

Question 1.
Organic compounds are _____ reactive.
Answer:
Less.

Question 2.
The reaction involving organic compounds proceed at ______ rates.
Answer:
Slower.

Question 3.
Organic compounds form ____ bonds in nature.
Answer:
Covalent.

Question 4.
If organic compounds contain carbon and other atoms like O, N, S etc., these compounds are called ______.
Answer:
Heterocyclic compounds.

Question 5.
The organic compounds that are composed of only carbon and hydrogen atoms are called ______.
Answer:
Hydrocarbons.

Question 6.
Alkynes are the most reactive due to the presence of the ______.
Answer:
Triple bond.

Question 7.
A series of compounds containing the same functional group is called ______.
Answer:
Class of organic compounds.

Question 8.
______ is used as an anti-freeze in automobile radiators.
Answer:
Ethanol.

Question 9.
Vanilla beans solution is made up of ______ and ______.
Answer:
Ethanol, water.

Question 10.
Soda – lime is a mixture of ______.
Answer:
3 parts of NaOH(s) + 1 part of CaO(s).

Question 11.
_____ is used as a flavouring agent and preservative.
Answer:
Ethanoic acid.

Question 12.
Formaldehyde is used as a ______.
Answer:
Disinfectant.

Question 13.
______ is a Anaesthetic agent.
Answer:
Ethers.

Question 14.
All the cooking oils and lipids contain ______.
Answer:
Esters.

Question 15.
The most commonly used alkali for preparation of soap is ______.
Answer:
Sodium hydroxide.

Question 16.
______ process helps to manufacture of soap.
Answer:
Kettle.

Question 17.
________ are salts of sulphonic acids.
Answer:
Detergents.

Question 18.
When soap or detergent is dissolved in water, the molecules join together as clusters called ______.
Answer:
Micelles.

Question 19.
A soap which has ______ TFM is a good bathing soap.
Answer:
Higher.

Question 20.
______ is present in many fruits.
Answer:
Acetic acid.

Question 21.
______ are sodium salts of long-chain carboxylic acids.
Answer:
Soap.

Question 22.
Unsaturated carbon compounds undergo _____ reactions whereas saturated carbon compounds undergo ______ reactions.
Answer:
Addition, substitution.

Question 23.
Each member of the homologous series differ from the succeeding member by a common difference of _____ and by a molecular mass of ______.
Answer:
CH₂, 14 amu.

Question 24.
Saturated hydrocarbons were earlier named as ______ and by IUPAC system they are named as ______.
Answer:
Paraffin, Alkanes.

Question 25.
Alkenes have the general formula ______ and they were previously called ______.
Answer:
C_nH_2n, olefins.

Question 26.
The slow chemical change that takes place in complex organic compounds by the action of _______ leading to the formation of simple molecules is called ______.
Answer:
Enzymes, fermentation.

Question 27.
A mixture contains 95.5% ethanol and 4.5% water is called ______ and 100% pure ethanol is called ______.
Answer:
Rectified spirit, absolute alcohol.

Question 28.
Ethanol when heated with Conc. H₂SO₄ at 443K gives ______ and at 413K gives ______ as products.
Answer:
Ethene, diethyl ether.

Question 29.
During the oxidation of ethanol with acidified K₂Cr₂O₇, the _____ colour changes to ______ colour.
Answer:
Orange, green.

Question 30.
The compound formed by the reaction of an alcohol with a carboxylic acid is known as ______ and the reaction is called ______.
Answer:
Ester, esterification.

Question 31.
______ is used as a preservative for biological specimens and ______ is used as a preventative in food and fruit juices.
Answer:
Ethanol, Ethanoic acid.

III. Match the following.

Question 1.

Answer:
1. (c), 2. (a), 3. (d), 4. (b).

Question 2.

1. CH3 – CH2OH	(a) Ethanal
2. CH3 – COOH	(b) Ethanol
3. CH3 – CHO	(c) Propanone
	(d) Ethanoic acid

Answer:
1. (b), 2. (d), 3. (a), 4. (c).

Question 3.

Answer:
1. (d), 2. (c), 3. (b), 4. (a).

Question 4.

Answer:

Question 5.

Answer:
1. (d), 2. (c), 3. (a), 4. (b).

Question 6.

Answer:
1. (c), 2. (d), 3. (a), 4. (b).

Question 7.

Answer:
1. (d), 2. (c), 3. (a), 4. (b).

Question 8.

Answer:
1. (c), 2 .(d), 3. (b), 4. (a).

Question 9.

Answer:
1. (b), 2. (a), 3. (d), 4. (c).

Question 10.

Answer:
1. (d), 2. (a), 3. (b), 4. (c).

IV. State True or False. If false give the correct statement.

Question 1.
Carbon circulates through air, plants, animals and soil by means of complex reactions is called the Kreb cycle.
Answer:
False.
Correct statement: Carbon circulates through air, plants, animals and soil by means of complex reactions is called the carbon cycle.

Question 2.
Carbon atoms form the building blocks of living organisms.
Answer:
True.

Question 3.
The characteristics of a carbon atom by virtue of which it forms four covalent bonds are referred to as catenation.
Answer:
False.
Correct statement: The characteristic of a carbon atom by virtue of which it forms four covalent bonds is referred to as tetravalency of carbon.

Question 4.
Carbon compounds show isomerism and possess the characteristic property catenation.
Answer:
True.

Question 5.
Carbon compounds have high melting and boiling points because of their electrovalent nature.
Answer:
False.
Correct statement: Carbon compounds have low melting and boiling points because of their covalent nature.

Question 6.
Alcohols react with sodium metal to liberate oxygen gas.
Answer:
False.
Correct statement: Alcohols react with sodium metal to liberate hydrogen gas.

Question 7.
All members of each homologous series contain different elements and different functional groups.
Answer:
False.
Correct statement: All members of each homologous series contain the same elements and same functional groups.

Question 8.
The chemical properties of the members of each homologous series are similar.
Answer:
True.

Question 9.
Decolourisation of bromine takes place in saturated compounds.
Answer:
False.
Correct statement: Decolourisation of bromine takes place in unsaturated compounds.

Question 10.
Molasses is a dark coloured syrupy liquid left after the crystallization of sugar from sugarcane juice.
Answer:
True.

Question 11.
Rectified spirit on heating with Cone. H₂SO₄ for about 5 to 6 hours and allowed to stand for 12 hours to get absolute alcohol.
Answer:
False.
Correct statement: Rectified spirit on heating with quicklime for about 5 to 6 hours and allowed to stand for 12 hours to get absolute alcohol.

Question 12.
Ethanol is a clear liquid with burning taste whereas ethanoic acid is a colourless liquid with a sour taste.
Answer:
True.

Question 13.
Ethanol affects the optic nerve causing blindness.
Answer:
False.
Correct statement: Methanol affects the optic nerve causing blindness.

Question 14.
Consumption of ethanol slows down the metabolism of our body and depresses the central nervous system.
Answer:
True.

Question 15.
On cooling, pure ethanol is frozen to form ice – like flakes.
Answer:
False.
Correct statement: On cooling, pure ethanoic acid is frozen to form ice – like flakes.

Question 16.
Methanol is oxidised to methanal in the liver and reacts with components of cells.
Answer:
True.

Question 17.
Removal of carbon dioxide is known as dehydrogenation.
Answer:
False.
Correct statement: Removal of carbon dioxide is known as decarboxylation.

Question 18.
Organic compounds have a high molecular weight and a simple structure.
Answer:
False.
Correct statement: Organic compounds have a high molecular weight and a complex structure.

Question 19.
The organic compound is less reactive than inorganic compounds.
Answer:
True.

Question 20.
Answer:
Organic compounds have high melting and boiling points.
Answer:
False.
Correct statement: Organic compounds have low melting and boiling points.

Question 21.
Furan is a carbocyclic compound.
Answer:
False.
Correct statement: Furan is a heterocyclic compound.

Question 22.
The boiling point of hydrocarbons increases with an increase in the number of carbon atoms.
Answer:
True.

Question 23.
Saturated compounds, decolourise the bromine water.
Answer:
False.
Correct statement:

• Unsaturated compounds, decolourise the bromine water.
• Saturated compounds do not decolourise bromine water.

Question 24.
Chemical properties of the members of a homologous series are similar.
Answer:
True.

Question 25.
IUPAC stands for International Union of Pure and Analytical Chemistry.
Answer:
False.
Correct statement: IUPAC stands for International Union of Pure and Applied Chemistry.

Question 26.
Hard soaps are used for cleaning the body.
False.
Correct statement: Soft soaps are used for cleaning the body.

Question 27.
Hard water limits the cleaning action of soap.
Answer:
True.

Question 28.
Soap forms a scum in hard water.
Answer:
True.

Question 29.
Soap has greater foaming capacity.
Answer:
False.
Correct statement: Soap has a poor foaming capacity.

Question 30.
Most of the detergents are biodegradable.
Answer:
False.
Correct statement: Most of the detergents are non-biodegradable.

V. Assertion and Reason.

Question 1.
Assertion (A): Carbon compounds hold the key to plant and animal life on the earth.
Reason (R): Carbon circulates through air, plants, animals and soil by means of complex reactions.
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are wrong
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct

Question 2.
Assertion (A): Carbon chemistry is called as living chemistry.
Reason (R): The carbon atoms form the building blocks of living organisms and carbon combined with other atoms decide life on earth.
(a) Both (A) and (R) are wrong
(b) Both (A) and (R) are correct
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct

Question 3.
Assertion(A): C⁴⁺ cation formation is easy.
Reason (R): Carbon can lose four electrons to form C⁴⁺ cation require less amount of energy.
(a) Both (A) and (R) are correct
(b) (A) is wrong but (R) is correct
(c) (A) is correct but (R) is wrong
(d) Both (A) and (R) are wrong.
Answer:
(d) Both (A) and (R) are wrong.

Question 4.
Assertion (A): Methane is formed when four electrons of carbon are shared with four hydrogen atoms.
Reason (R): This characteristic of a carbon atom by virtue of which it forms four covalent bonds is referred to as tetra valency of carbon.
(a) (A) is correct and (R) explains (A)
(b) Both (A) and (R) are wrong
(c) (A) is correct but (R) does not explain (A)
(d) (A) is wrong but (R) is correct.
Answer:
(a) (A) is correct and (R) explains (A)

Question 5.
Assertion (A): Diamond is a rigid substance and it is very hard.
Reason (R): In diamond, each carbon atom is bonded to three other carbon atoms in the same place giving hexagonal layers held together by weak van der Waals forces.
(a) Both (A) and (R) are correct
(b) (A) is correct but (R) does not explain (A)
(c) Both (A) and (R) are wrong
(d) (A) is wrong but (R) is correct.
Answer:
(b) (A) is correct but (R) does not explain (A)

Question 6.
Assertion (A): Graphite is a good conductor of electricity, unlike other non – metals.
Reason (R): Graphite has free electrons in it.
(a) Both (A) and (R) are correct
(b) (A) is correct but (R) does not explain (A)
(c) (A) is wrong but (R) is correct
(d) Both (A) and (R) are wrong.
Answer:
(a) Both (A) and (R) are correct

Question 7.
Assertion (A): Carbon combines with many other elements to form various stable compounds.
Reason (R): The stability of carbon compounds is due to the small size of carbon which enables the nucleus to hold on to the shared pair of electrons strongly.
(a) Both (A) and (R) are wrong
(b) Both (A) and (R) are correct
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct.

Question 8.
Assertion (A): Carbon compounds have low melting and boiling points and they are easily combustible.
Reason (R): Carbon compounds are electrovalent compounds.
(a) Both (A) and (R) are correct
(b) (A) is correct but (R) is wrong
(c) Both (A) and (R) are wrong
(d) (A) is wrong but (R) is correct.
Answer:
(b) (A) is correct but (R) is wrong

Question 9.
Assertion (A): Ethanol has a much higher boiling point than ethane.
Reason (R): Presence of hydrogen bond in a molecule increases the boiling point.
(a) Both (A) and (R) are correct, (R) explains (A)
(b) (A) is correct but (R) is wrong
(c) (A) is wrong but (R) is correct
(d) Both (A) and (R) are correct, but (R) doesn’t explain (A).
Answer:
(a) Both (A) and (R) are correct, (R) explains (A)

Question 10.
Assertion (A): Hard water limits the cleaning action of soap.
Reason (R): When combined with soap, hard water develops a thin layer.
(a) Both (A) and (R) are correct, (R) explains (A)
(b) (A) is correct but (R) is wrong
(c) (A) is wrong but (R) is correct
(d) Both (A) and (R) are correct, but (R) doesn’t explain (A).
Answer:
(a) Both (A) and (R) are correct, (R) explains (A)

VI. Short Answer Questions.

Question 1.
How will you test to identify saturated and unsaturated compounds?
Answer:
Test to identify saturated and unsaturated compounds:

• Take the given sample solution in a test tube.
• Add a few drops of bromine water and observe any characteristic change in colour.
• If the given compound is unsaturated, it will decolourise bromine water.
• Saturated compounds do not decolourise bromine.
  

Question 2.
What is a functional group?
Answer:
A functional group is an atom or group of atoms in a molecule, which gives its characteristic chemical properties.

Question 3.
What is a locant number?
Answer:
Number the carbon atoms of the parent chain, beginning at the closest end of the substituent or functional group. These are called locant numbers.

Question 4.
Obtain the IUPAC name of the following compounds systematically.
(i) CH₃ – CH₂ – CH₂ – CH₂ – CH₃

Answer:
(i) CH₃ – CH₂ – CH₂ – CH₂ – CH₃

• Step 1: It is a five-carbon chain and hence the root word is ‘Pent’. (Rule 1)
• Step 2: All the bonds between carbon atoms are single bonds, and thus the suffix is ‘ane’. So, its name is Pent + ane = Pentane

• Step 1: The longest chain contains five carbon atoms and hence the root word is ‘Pent’.
• Step 2: There is a substituent. So, the carbon chain is numbered from the left end, which is closest to the substituent. (Rule 2)
  
• Step 3: All are single bonds between the carbon atoms and thus the suffix is ‘ane’.
• Step 4: A substituent is a methyl group and it is located at a second carbon atom. So, its locant number is 2. Thus the prefix is ‘2-Methyl’.(Rule 6).
  The name of the compound is 2-Methyl + pent + ane = 2-Methylpentane

Question 5.
Mention the uses of ethanol?
Answer:

• Ethanol is used in medical wipes, as an antiseptic.
• Ethanol is used as an antifreeze in automobile radiators.
• Ethanol is used for effectively killing microorganisms like bacteria, fungi, etc., by including it in many hand sanitizers.
• Ethanol is used as an antiseptic to sterilize wounds in hospitals.
• Ethanol is used as a solvent for drugs, oils, fats, perfumes, dyes, etc.
• Ethanol is used in the preparation of methylated spirit (a mixture of 95 % of ethanol and 5 % of methanol) rectified spirit (a mixture of 95.5 % of ethanol and 4.5 % of water), power alcohol (a mixture of petrol and ethanol) and denatured spirit (ethanol mixed with pyridine).
• Ethanol is used to enhance the flavour of food extracts, for example, vanilla extract; a common food flavour, which is made by processing vanilla beans in a solution of ethanol and water.

Question 6.
What is a decarboxylation reaction?
Answer:
When a sodium salt of ethanoic acid is heated with soda lime (a solid mixture of 3 parts of NaOH and 1 part of CaO), methane gas is formed. During this reaction, the CO₂ molecule is eliminated. Therefore, this reaction is called a decarboxylation reaction.

Question 7.
What is soap?
Answer:
Soaps are sodium or potassium salts of some long-chain carboxylic acids, called fatty acids. Soap requires two major raw materials:

• fat
• alkali.

Question 8.
|What are the two types of soaps? Explain.
Answer:

1. Hard Soap : Soaps, which are prepared by the saponification of oils or fats with caustic soda (sodium hydroxide), are known as hard soaps. They are usually used for washing purposes.
2. Soft Soap : Soaps, which are prepared by the saponification of oils or fats with potassium salts, are known as soft soaps. They are used for cleansing the body.

Question 9.
What is soft soap?
Answer:
Soaps, which are prepared by the saponification of oils or fats with potassium salts, are known as soft soaps. They are used for cleansing the body.

Question 10.
What are the disadvantages of detergents?
Answer:

1. Some detergents having a branched hydrocarbon chain are not fully biodegradable by micro-organisms present in water. So, they cause water pollution.
2. They are relatively more expensive than soap.

Question 11.
What are biodegradable and non-biodegradable detergents?
Answer:

1. Biodegradable detergents: They have straight hydrocarbon chains, which can be easily degraded by bacteria.
2. Non – biodegradable detergents: They have highly branched hydrocarbon chains, which cannot be degraded by bacteria.

Question 12.
Mention the disadvantages of detergents.
Answer:

1. Some detergents having a branched hydrocarbon chain are not fully biodegradable by micro-organisms present in water. So, they cause water pollution.
2. They are relatively more expensive than soap.

Question 13.
What is catenation?
Answer:
Carbon has the ability to form covalent bonds with other atoms of carbon giving rise to a large number of molecules through self linking property. This property is called catenation.

Question 14.
Define isomerism. Give a suitable example.
Answer:
The phenomenon by which two or more compounds have the same molecular formula but different structural formula with the difference in properties is known as isomerism.
C₂H₆O. This molecular formula has two isomeric structures.

1. C₂H₅OH → Ethyl alcohol
2. CH₃ – O – CH₃ → Dimethyl ether

Question 15.
How will you differentiate saturated and unsaturated hydrocarbon compounds?
Answer:

Saturated hydrocarbon	Unsaturated hydrocarbon
Saturated hydrocarbon undergoes substitution reactions in the presence of sunlight.	Unsaturated hydrocarbon undergoes an addition reaction with hydrogen in the presence of nickel catalyst.
Saturated hydrocarbon does not decolourise bromine water.	Unsaturated hydrocarbon decolourise bromine water.

VII. Long Answer Questions

Question 1.
All living organisms are made of carbon atoms. This means that carbon atoms form the building blocks of living organisms. Justify this statement by giving physical nature of carbon and its compounds.
Answer:
Physical nature of carbon and its compounds.

1. Carbon has the ability to form covalent bonds with other atoms of carbon giving rise to a large number of molecules through self linking property which is called catenation.
2. Carbon combines with oxygen, hydrogen, nitrogen sulphur, chlorine and many other elements to form various stable compounds.
3. The stability of carbon compounds is due to the small size of carbon which enables the nucleus to hold on to the shared pair of electrons strongly.
4. Carbon compounds show isomerism, the phenomenon by which two or more compounds have the same molecular formula but different structural formula with the difference in properties.
5. Carbon compounds have low boiling points and low melting points because of their covalent nature.
6. Carbon compounds are easily combustible.

Question 2.
Explain the preparation of detergents with their ingredients.
Answer:
Detergents are prepared by adding sulphuric acid to the processed hydrocarbon obtained from petroleum. This chemical reaction result in the formation of molecules similar to the fatty acid in soap. Then, an alkali is added to the mixture to produce the ‘surfactant molecules’, which do not bond with the minerals present in the hard water, thus preventing the formation of their precipitates.

In addition to a ‘surfactant’, the modem detergent contains several other ingredients. They are listed as follows:

1. Sodium silicate, which prevents the corrosion and ensures that the detergent does not damage the washing machine.
2. Fluorescent whitening agents that give a glow to the clothes.
3. Oxygen bleaches, such as ‘sodium perborate’,enable the removal of certain stains from the cloth.
4. Sodium sulphate is added to prevent the caking of the detergent powder.
5. Enzymes are added to break down some stains caused by biological substances like blood and vegetable juice.
6. Certain chemicals that give out a pleasant smell are also added to make the clothes fragrant after they are washed with detergents.

Question 3.
Explain the classification of organic compounds.
Answer:

Question 4.
Discuss the characteristics of hydrocarbons.
Answer:
Characteristics of hydrocarbons:

1. Lower hydrocarbons are gases at room temperature E.g. methane, ethane is gassed.
2. They are colourless and odourless.
3. The boiling point of hydrocarbons increases with an increase in the number of carbon atoms.
4. They undergo combustion reaction with oxygen to form CO₂ and water.
5. Alkanes are least reactive when compared to other classes of hydrocarbons.
6. Alkynes are the most reactive due to the presence of the triple bond.
7. Alkanes are saturated whereas alkenes and alkynes are unsaturated.
8. They are insoluble in water.

Question 5.
Identify the compounds using the clues given below.
(a) This is a dark coloured syrupy liquid containing 30% of sucrose.
Answer:
Molasses.

(b) During manufacture of ethanoic acid this acts as an oxidising agent.
Answer:
Alkaline KMnO₄ or acidified K₂Cr₂O₇.

(c) This enzyme converts sucrose into glucose and fructose.
Answer:
Invertase

(d) Ethanol on dehydrogenation with Cu/573K gives this compound.
Answer:
Ethanal

(e) This compound is used as an antiseptic.
Answer:
Ethanol

VIII. HOT Questions

Question 1.
An organic compound (A) of molecular formula C₂H₆O reacts with sodium metal and liberates H₂ gas. (A) on reaction with alkaline KMnO₄ gives (B) of formula C₂H₆O₂. The sodium salt of (B) on reaction with soda lime gives (C) a first member of alkane homologous series. Identify A, B, and C.
Answer:
(i) (A) is Ethanol: CH₃ – CH₂OH.
Ethanol reacts with sodium metal and liberates H₂ gas.

(ii) Ethanol on reaction with alkaline KMnO₄, oxidation takes place and the product formed is Ethanoic acid, CH₃COOH. It is (B).

(iii) The sodium salt of ethanoic acid on reaction with soda lime (NaOH + CaO) undergo decarboxylation reaction to give methane CH₄ (C) the first member of alkane homologous series.

Question 2.
In what way yeast is important in the fermentation process?
Answer:
Yeasts are single-celled microorganisms, belonging to the class of fungi. The enzymes present in yeasts catalyse many complex organic reactions. Fermentation is the conversion of complex organic molecules into simpler molecules by the action of enzymes. E.g. Curdling of milk.

Question 3.
Write and explain the reaction that can be used for the identification of alcohols.
Answer:
Oxidation reaction: Ethanol is oxidized to ethanoic acid with alkaline KMnO₄ or acidified K₂Cr₂O₇

During this reaction, the orange colour of K₂Cr₂O₇ changes to green. Therefore, this reaction can be used for the identification of alcohols.

Question 4.
How dirt is washed away with the soap?
Answer:
When soap or detergent is dissolved in water, the molecules join together as clusters called micelles. Their long hydrocarbon chain attaches themselves to the oil and dirt. The dirt is thus surrounded by the non-polar end of the soap molecules. The charged carboxylate end to the soap molecules makes the micelles soluble in water. Thus the dirt is washed away with the soap.

Question 5.
Why ordinary soap is not suitable for use with hard water?
Answer:
Ordinary soaps when treated with hard water, precipitate as salts of calcium and magnesium. They appear at the surface of the cloth as sticky grey scum. Thus, the soaps cannot be used conveniently in hard water.

Test Yourself

Question 1.
Obtain the IUPAC name of the following compounds systematically.
(i) CH₃CHO
(ii) CH₃CH₂COCH₃
(iii) ClCH₂ – CH₂ – CH₂ – CH₃
Answer:
(i) CH₃CHO

• Step 1: The parent chain consists of 2 carbon atoms. The root word is “Eth”.
• Step 2: All are single bonds between the carbon atom of the chain. So the primary suffix is “ane”.
• Step 3: Since the compound contains the – CHO group, it is an aldehyde. The secondary suffix is “al”.
  The name of the compound is Eth + ane + al = Ethanal

(ii) CH₃CH₂COCH₃

• Step 1: The parent chain consists of 4 carbon atoms. The root word is “But”.
• Step 2: All are single bonds between the carbon atom of the chain. So the primary suffix is “ane”.
• Step 3: Since the compound contains the – CO – group, it is a ketone group. The secondary suffix is “one”.
  The name of the compound is But + ane + one = Butanone

(iii) ClCH₂ – CH₂ – CH₂ – CH₃

• Step 1: The parent chain consists of 4 carbon atoms. The root word is “But”.
• Step 2: All are single bonds between the carbon atom of the chain. So the suffix is “ane”.
• Step 3: Since the compound contains the – Cl substituent. The prefix is Chloro.
• Step 4: The locant number of – Cl is 1 and thus prefix is 1-Chloro.
  The name of the compound is 1-Chloro + Butane = 1-Chlorobutane.

Believing that the Tamilnadu State Board Solutions for Class 11th Science Chapter 11 Carbon and its Compounds Questions and Answers learning resource will definitely guide you at the time of preparation. For more details about Tamilnadu State Board Class 11th Science Chapter 11 textbook solutions, ask us in the below comments and we’ll revert back to you asap.

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.3

10th Samacheer Maths Exercise 2.3 Solutions Question 1.
Find the least positive value of x such that
(i) 71 ≡ x (mod 8)
(ii) 78 + x ≡ 3 (mod 5)
(iii) 89 ≡ (x + 3) (mod 4)
(iv) 96 = \(\frac{x}{7}\) (mod 5)
(v) 5x ≡ 4 (mod 6)
Solution:
To find the least value of x such that
(i) 71 ≡ x (mod 8)
71 ≡ 7 (mod 8)
∴ x = 7.[ ∵ 71 – 7 = 64 which is divisible by 8]

(ii) 78 + x ≡ 3 (mod 5)
⇒ 78 + x – 3 = 5n for some integer n.
75 + x = 5 n
75 + x is a multiple of 5.
75 + 5 = 80. 80 is a multiple of 5.
Therefore, the least value of x must be 5.

(iii) 89 ≡ (x + 3) (mod 4)
89 – (x + 3) = 4n for some integer n.
86 – x = 4 n
86 – x is a multiple of 4.
∴ The least value of x must be 2 then
86 – 2 = 84.
84 is a multiple of 4.
∴ x value must be 2.

(iv) 96 ≡ \(\frac{x}{7}\) (mod 5)
96 – \(\frac{x}{7}\) = 5n for some integer n.
\(\frac { 672-x }{ 7 } \) = 5n
672 – x = 35n.
672 – x is a multiple of 35.
∴ The least value of x must be 7 i.e. 665 is a multiple of 35.

(v) 5x ≡ 4 (mod 6)
5x – 4 = 6M for some integer n.
5x = 6n + 4
x = \(\frac { 6n+4 }{ 5 } \)
When we put 1, 6, 11, … as n values in x = \(\frac { 6n+4 }{ 5 } \) which is divisible by 5.
When n = 1, x = \(\frac { 10 }{ 5 } \) = 2
When n = 6, x = \(\frac { 36+4 }{ 5 } \) = \(\frac { 40 }{ 5 } \) = 8 and so on.
∴ The solutions are 2, 8, 14…..
∴ Least value is 2.

10th Maths Exercise 2.3 Samacheer Kalvi Question 2.
If x is congruent to 13 modulo 17 then 7x – 3 is congruent to which number modulo 17?
Answer:
Given x ≡ 13 (mod 17) ……(1)
7x – 3 ≡ a (mod 17) ……..(2)
From (1) we get
x- 13 = 17 n (n may be any integer)
x – 13 is a multiple of 17
∴ The least value of x = 30
From (2) we get
7(30) – 3 ≡ a(mod 17)
210 – 3 ≡ a(mod 17)
207 ≡ a (mod 17)
207 ≡ 3(mod 17)
∴ The value of a = 3

Ex 2.3 Class 10 Samacheer Question 3.
Solve 5x ≡ 4 (mod 6)
Solution:
5x ≡ 4 (mod 6)
5x – 4 = 6M for some integer n.
5x = 6n + 4
x = \(\frac{6 n+4}{5}\) where n = 1, 6, 11,…..
∴ x = 2, 8, 14,…

10th Maths Exercise 2.3 In Tamil Question 4.
Solve 3x – 2 ≡ 0 (mod 11)
Solution:
3x – 2 ≡ 0 (mod 11)
3x – 2 = 11 n for some integer n.
3x = 11n + 2

Samacheer Kalvi 10th Maths Question 5.
What is the time 100 hours after 7 a.m.?
Solution:
100 ≡ x (mod 12) (∵7 comes in every 12 hrs)
100 ≡ 4 (mod 12) (∵ Least value of x is 4)
∴ The time 100 hrs after 7 O’ clock is 7 + 4 = 11 O’ clock i.e. 11 a.m

10th Maths Exercise 2.3 Question 6.
What is time 15 hours before 11 p.m.?
Answer:
15 ≡ x (mod 12)
15 ≡ 3 (mod 12)
The value of x must be 3.

The time 15 hours before 11 o’clock is (11 – 3) 8 pm

10th Maths Samacheer Kalvi Question 7.
Today is Tuesday. My uncle will come after 45 days. In which day my uncle will be coming?
Solution:
No. of days in a week = 7 days.
45 ≡ x (mod 7)
45 – x = 7n
45 – x is a multiple of 7.
∴ Value of x must be 3.
∴ Three days after Tuesday is Friday. Uncle will come on Friday.

Exercise 2.3 Class 10 Maths Samacheer Question 8.
Prove that 2ⁿ + 6 × 9n is always divisible by 7 for any positive integer n.
Answer:
9 = 2 (mod 7)
9ⁿ = 2ⁿ (mod 7) and 2ⁿ = 2ⁿ (mod 7)
2ⁿ + 6 × 9ⁿ = 2ⁿ (mod 7) + 6 [2ⁿ (mod 7)]
= 2ⁿ (mod 7) + 6 × 2ⁿ (mod 7)
7 × 2ⁿ (mod 7)
It is always divisible for any positive integer n

10th Samacheer Kalvi Maths Question 9.
Find the remainder when 2⁸¹ is divided by 17.
Solution:
2⁸¹ ≡ x (mod 17)
2⁴⁰ × 2⁴⁰ × 2⁴¹ ≡ x (mod 17)
(2⁴)¹⁰ × (2⁴)¹⁰ × 2¹ ≡ x (mod 17)
(16)¹⁰ × (16)¹⁰ × 2 ≡ x(mod 17)
(16⁵)² × (16⁵)² × 2
(16⁵) ≡ 16 (mod 17)
(16⁵)² ≡ 16² (mod 17)
(16⁵)² ≡ 256 (mod 17)
≡ 1 (mod 17) [∵ 255 is divisible by 17]
(16⁵)² × (16⁵)² × 2 ≡ 1 × 1 × 2 (mod 17)
∴ 2⁸¹ ≡ 2(mod 17)
∴ x = 2

Maths Class 10 Samacheer Kalvi Question 10.
The duration of flight travel from Chennai to London through British Airlines is approximately 11 hours. The aeroplane begins its journey on Sunday at 23:30 hours. If the time at Chennai is four and a half hours ahead to that of London’s time, then find the time in London, when will the flight lands at London Airport.
Solution:
The duration of the flight from Chennai to London is 11 hours.
Starting time at Chennai is 23.30 hrs. = 11.30 p.m.
Travelling time = 11.00 hrs. = 22.30 hrs = 10.30 a.m.
Chennai is \(4 \frac{1}{2}\) hrs ahead to London.
= 10.30 – 4.30 = 6.00
∴ At 6 a.m. on Monday the flight will reach at London Airport.

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.1

12th Maths Exercise 7.1 Samacheer Kalvi Question 1.
A point moves along a straight line in such a way that after t seconds its distance from the origin is s = 2t² + 3t metres.
(i) Find the average velocity of the points between t = 3 and t = 6 seconds.
(ii) Find the instantaneous velocities at t = 3 and t = 6 seconds.
Solution:
(i) Given s = 2t² + 3t
(i.e.) f(t) = 2t² +3t
Now f(3) = 18 + 9 = 27 = f(a)
f(6) = 72 + 18 = 90 = f(b)

= 21m/s

(ii) f(t) = 2t² + 3t
f'(t) = 4t + 3
f'(3) = 4(3) + 3 = 15
f'(6) = 4(3) + 3 = 15

12th Maths Exercise 7.1 Question 2.
A camera is accidentally knocked off an edge of a cliff 400 ft high. The camera falls a distance of s = 16t² in t seconds.
(i) How long does the camera fall before it hits the ground?
(ii) What is the average velocity with which the camera falls during the last 2 seconds?
(iii) What is the instantaneous velocity of the camera when it hits the ground?
Solution:
(i) s = 16t²
16t² = 400

t = 5sec

(ii) Last 2 seconds means t = 3 to t = 5
f(t) = 16t²
f(3) = 16(9) = 144 = f(a)
f(5) = 16(25) = 400 = f(b)

= 128 ft/sec

(iii) f(t) = ²
f'(t) = 32t
f'(t) at t = 5 = 32(5)
= 160 ft/sec

12 Maths Samacheer Kalvi Solutions Question 3.
A particle moves along a line according to the law s(t) = 2t³ – 9t² + 12t – 4, where t ≥ 0.
(i) At what times the particle changes direction?
(ii) Find the total distance travelled by the particle in the first 4 seconds.
(iii) Find the particle’s acceleration each time the velocity is zero.
Solution:
(i) s = f(t) = 2t³ – 9t² + 12t – 4
V = f'(t) = 6t² – 18t + 12
V = 0 ⇒ 6(t² -3t – 2) = 0
(t – 1)(t – 2) = 0
t = 1, 2
When t < 1, (say t = 0.5)
V = 6(0.25 – 1.5 + 2) = +ve
When 1 < t < 2, (say t = 1.5) V = 6(2.25 – 4.5 + 2) = -ve When t > 2, (say t = 3)
V = 6(9 – 6 + 2) = +ve
So the particle changes its direction when t lies between 1 and 2 secs.

(ii) The distance travelled in the first 4 seconds is
|s(0) – s(1)| + |s(1) – s(2)| + |s(2) – s(3)| + |s(3) – s(4)|
Here, s(t) = 2t³ – 9t² + 12t – 4
s(0) = -4
s(1) = 1
s(2) = 0
s(3) = 5
and s(4) = 28
∴ Distance travelled in first 4 seconds
= |-4 – 1| + |1 – 0| + |0 – 5| + |5 – 28|
= 5 + 1 + 5 + 23 = 34 m

a (at V = 0) is ‘a’ at t = 1 and 2
Now a (at t = 1) = 12 – 18 = -6m / sec²
a (at t = 2) = 24 – 18 = +6m / sec²

Samacheer Kalvi Guru 12th Maths Question 4.
If the volume of a cube of side length x is V = x³. Find the rate of change of the volume with respect to x when x = 5 units.
Solution:

Std 12 Maths Solutions Samacheer Kalvi Question 5.
If the mass m(x) (in kilograms) of a thin rod of length x (in metres) is given by, m(x) = \(\sqrt{3 x}\) then what is the rate of change of mass with respect to the length when it is x = 3 and x = 21 metres.
Solution:

12th Maths 7th Chapter Question 6.
A stone is dropped into a pond causing ripples in the form of concentric circles. The radius r of the outer ripple is increasing at a constant rate at 2 cm per second. When the radius is 5 cm find the rate of changing of the total area of the disturbed water?
Solution:

12th Maths 7.1 Question 7.
A beacon makes one revolution every 10 seconds. It is located on a ship which is anchored 5 km from a straight shore line. How fast is the beam moving along the shore line when it makes an angle of 45° with the shore?
Solution:
Time for 1 rotation = 10 sec

12th Math 7.1 Question 8.
A conical water tank with vertex down of 12 metres height.has a radius of 5 metres at the top. If water flows into the tank at a rate 10 cubic m/min, how fast is the depth of the water increases when the water is 8 metres deep?
Solution:

Class 12th Maths Exercise 7.1 Question 9.
A ladder 17 metre long is leaning against the wall. The base of the ladder is pulled away from the Waif at a rate of 5 m/s. When the base of the ladder is 8 metres from the wall
(i) How fast is the top of the ladder moving down the wall?
(ii) At what rate, the area of the triangle formed by the ladder, wall, and the floor, is changing?
Solution:

So the top of the ladder is moving down the wall at \(\frac{-8}{3}\) m/sec

(ii)

Class 12 Maths Solutions Chapter 7 Question 10.
A police jeep, approaching an orthogonal intersection from the northern direction, is chasing a speeding car that has turned and moving straight east. When the jeep is 0.6 km north of the intersection and the car is 0.8 km to the east. The police determine with a radar that the distance between them and the car is increasing at 20 km/hr. If the jeep is moving at 60 km/hr at the instant of measurement, what is the speed of the car?
Solution:

Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.1 Additional Questions

Samacheer Kalvi 12th Maths Guide Question 1.
A water tank has the shape of an inverted circular cone with base radius 2 metres and height 4 metres. If water is being pumped into the tank at a rate of 2mt³/min, find the rate at which the water level is rising when the water is 3m deep.
Solution:
We first sketch the cone and label it as in diagram. Let V, r and h be respectively the volume of the water, the radius of the cone and the height at time t, where t is measured in minutes.
We are given that \(\frac{d \mathrm{V}}{d t}\) = 2m³/min and we are asked to find \(\frac{d h}{d t}\) when h is 3m.

The quantities V and h are related by the equation V = \(\frac{1}{3} \pi r^{2} h\). But it is very useful to express V as function of h alone.

Samacheer Kalvi 12 Maths Solutions Question 2.
A car A is travelling from west at 50 km/hr and car B is travelling towards north at 60 km/hr. Both are headed for the intersection of the two roads. At what rate are the cars approaching each other when car A is 0.3 kilometers and car B is 0.4 kilometers from the intersection?
Solution:
We draw diagram where C is the intersection of the two roads. At a given time t, let x be the distance from car A to C, let y be the distance from car B to C and let z be the distance between the cars A and B where x, y and z are measured in kilometers.
We are given that \(\frac{d x}{d t}\) = – 50 km/hr and \(\frac{d y}{d t}\) – = -60 km/hr.

Note that x andy are decreasing and hence the negative sign.
We are asked to find \(\frac{d z}{d t}\)
The equation that relate x, y and z is given by the pythagoras theorem z² = x² + y²
Differentiating each side with respect to t,

i.e., The cars approaching each other at a rate of 78 km/hr

12 Maths Solutions Samacheer Kalvi Question 3.
The distance x metres travelled by a vehicle in time t seconds after the brakes are applied is given by x = 20t – \(\frac{5}{3}\)t². Determine
(i) the speed of the vehicle (in km/hr) at the instant the brakes are applied and
(ii) the distance the car travelled before it stops.
Solution:

Samacheer Kalvi.Guru 12th Maths Question 4.
At noon, ship A is 100 km west of ship B. Ship A is sailing east at 35 km/hr and ship B is sailing north at 25 km/hr. How fast is the distance between the ships changing at 4.00 pm?
Solution:
Distance travelled by A in 4 hrs
(12 noon to 4.00 pm) = 4 × 35 = 140 km

∴ BA’= 40 km (140 – 100)
Distance travelled by B in 4 hrs = 4 × 25 = 100 km
Now in right angled ∆A’BB’, x² + y² = s²
Here, x = BA’ = 40 km
y = BB’= 100 km
⇒ s² = 40² + 100²
= 1600 + 10000
= 11600

Samacheer Kalvi 12 Maths Guide Question 5.
Gravel is being dumped from a conveyor belt at a rate of 30 ft³/min and its coarsened such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 10 ft high?
Solution:
Given:
Diameter = Height
= h ft (say)

So, the height is increasing at the rate of \(\frac{6}{5 \pi}\) ft/min