Prasanna

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Additional Questions

Exercise 4.1

Question 1.
Find the complement of each of the following angles
(i) 63°
(ii) 24°
(iii) 48°
Solution:
(i) The complement of 63° = 90° – 63° = 27°
(ii) The complement of 24° = 90° – 24° = 66°
(iii) The complement of 48° = 90° – 48° = 42°

Question 2.
Find the supplement of each of the following angles
(i) 58°
(ii) 148°
(iii) 120°
Solution:
(i) The supplement of 58° = 180° – 58° = 122°
(ii) The supplement of 148° = 180° – 148° = 32°
(iii) The supplement of 120° = 180° – 120° = 60°

Question 3.
Find the value of x

Solution:

Question 4.
Find the values of x, y in the following figures

Solution:

Question 5.
In the given figure at right, side BC of ∆ABC is produced to D. Find ∠A and ∠C.

Solution:
From the figure
Exterior angle = 120°
⇒ ∠C = 180° – 120° = 60° (linear pair)
∴ ∠A = 180° – (40° + 60°) = 80°

Exercise 4.2

Question 1.
If the measures of three angles of a quadrilateral are 100°, 84° and 76° then, find the measure of fourth angle.
Solution:
Let the measure of the fourth angle be x°.
The sum of the angles of a quadrilateral is 360°
So, 100° + 84° + 76° + x° = 360°
260° + x° = 360°
x = 360° – 260° = 100°
Hence, the measure of the fourth angle is 100°.

Question 2.
In the parallelogram ABCD if ∠A = 65°, find ∠B, ∠C and ∠D.
Solution:
Let ABCD be a parallelogram in which ∠A = 65°
Since AD || BC we can treat AB as a transversal. So
∠A+∠B = 180°

65° +∠B = 180°
∠B = 180°-65°
∠B = 115°
Since the opposite angles of a parallelogram are equal, we have
∠C = ∠A = 65° and ∠D = ∠B = 115°
Hence, ∠B = 115°, ∠C = 65° and ∠D = 115°

Question 3.
If ABCD is a rhombus and if ∠A = 76°, find ∠CDB.
Solution:
∠A = ∠C = 76° (Opposite angles of a rhombus)
Let ∠CDB = x°. In ∆CDB, CD = CB
∠CDB + ∠CBD + ∠DCB = 180° (Angles of a triangle)

2x° + 76° = 180° ⇒ 2x° = 104°
x° = 52°
∴ ∠CDB = 52°

Question 4.
In a parallelogram, opposite sides are equal
Solution:
Given ABCD is a parallelogram
To Prove ABCD and DA = BC
Construction Join AC
Proof
Since ABCD is a parallelogram

AD || BC and AC is the transversal
∠DAC = ∠BCA ➝ (1) (alternate angles are equal)
AB || DC and AC is the transversal
∠BAC = ∠DCA ➝ (2) (alternate angles are equal)
In ∆ADC and ∆CBA
∠DAC = ∠BCA from (1)
AC is common
∠DCA = ∠BAC from (2)
∆ADC ≅ ∆CBA (By ASA)
Hence AD = CB and DC = BA (Corresponding sides are equal)

Question 5.
The angles of a quadrilateral are ¡n the ratio 1 : 2 : 3 : 4. Find all the angles. Let each ratio be x.

Solution:
Then the angles are x°, 2x°, 3x°, 4x°
x° + 2x° + 3x° + 4x° = 360°

Exercise 4.3

Question 1.
The radius of a circle 15 cm and the length of one of its chord is 24 cm. Find the distance of the chord from the centre.
Solution:
Distance of the chord from the centre.

Question 2.
The chord of length 32 cm is drawn at the distance of 12 cm from the centre of the circle. Find the radius of the circle.
Solution:

Question 3.
In a circle, AB and CD are two parallel chords with centre O and radius 5 cm such that AB = 8 cm and CD = 6 cm determine the distance between the chords?
Solution:

Question 4.
Find the value of x°

Solution:

Question 5.
Find the value of x°

Solution:

Exercise 4.4

Question 1.
Find the value of x in the figure.
Solution:

In the cyclic quadrilateral ABCD
∠ABC – 180°- 140° = 40°
∠BCA = 90°
∴ x = ∠BAC = 180°- (90° + 40°) = 50°

Question 2.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.

Solution:

Question 3.
AB and CD are two parallel sides of a cyclic quadrilateral ABCD in the figure. such that AB = 12 cm, CD = 16 cm and the radius of the circle is 10cm. Find the shortest distance between the two sides AB and CD.
Solution:
In this figure,

The shortest distance between the two sides = 8 + 6 = 14 cm

Question 4.
In the given figure, AB and CD are the parallel chords of a circle with centre O, such that AB = 30 cm and CD = 40 cm. If OM ⊥ AB and OL ⊥ CD distance between LM is 35 cm. Find the radius of the circle?

Solution:

Exercise 4.5

Question 1.
Construct an equilateral triangle of sides 6 cm and locate its orthocentre.
Solution:

Construction:
(1) Draw the ∆ABC with the given measurements.
(2) Construct the altitudes from any two vertices (A and B) to their opposite sides BC and AC respectively.
(3) The point of intersection of the altitudes H is the orthocentre of the given ∆ABC.

Question 2.
Draw and locate the orthocentre of a right triangle PQR right angled at Q, with PQ = 4.5 cm and QR = 6 cm.
Solution:

Construction:
(1) Draw the ∆PQR with the given measurements.
(2) Construct altitudes from any two vertices (Q and R) to their opposite sides PR and PQ respectively.
(3) The point of intersection of the altitudes H is the orthocentre of the given ∆PQR.

Question 3.
Construct the circumcentre of the ∆ABC with AB = 5 cm, ∠A = 60° and ∠B = 80°, also draw two circumcircle and find the circum radius of the ∆ABC.
Solution:



Solution:
Step 1: Draw the ∆ABC with the given measurements.
Step 2 : Construct the perpendicular bisector of any two sides (AC and BC) and let them meet at S which is the circumcentre.
Step 3 : S as centre and SA = SB = SC as radius, draw the Circumcircle to passes through A,B and C. Circumradius = 3.9 cm.

Exercise 4.6

Question 1.
Draw the circumcircle for an equilateral triangle of side 6 cm.
Solution:

Construction:
(1) Draw the ∆ABC with the given measurements.
(2) Construct the perpendicular bisectors of AC and BC and let them meet at S which is the circumcentre.
(3) With S as centre and SA = SB = SC as radius, draw the circumcircle to pass through A, B and C.

Question 2.
Construct the centroid of ∆PQR such that PQ = 9 cm, PQ = 7cm, RP = 8 cm.
Solution:
In ∆PQR,
PQ = 5 cm,
PR = 6 cm
∠QPR = 60°

Construction :
Step 1 : Draw ∆PQR using the given measurements PQ = 9 cm, QR = 7 cm and RP = 8 cm and construct the perpendicular bisector of any two sides (PQ and QR) to find the mid-points M and N of PQ and QR respectively.
Step 2 : Draw the medians PN and RM and let them meet at G. The point G is the centroid of the given ∆PQR.

Question 3.
Draw and locate the centroid of the triangle ABC where right angle at A, AB = 8 cm and AC = 6 cm.
Solution:

Step 1 : Draw ∆ABC with the given measurements AB = 8 cm, ∠A = 90° and AC = 6 cm and construct the perpendicular bisector of any two sides (AB and AC) to find the mid points M and N of AB and BC respectively.
Step 2 : Draw the medians (C and BN and let them meet at G. The point G is the centroid of the given ∆ABC.

Question 4.
Construct the centroid of Ø PQR whose sides are PQ = 8 cm, QR = 6 cm, RP = 7 cm.

Solution:
Side = 6.5 cm

Construction:
Step 1 : Draw ∆ABC with AB = BC = CA = 6.5 cm
Step 2 : Construct angle bisectors of any two angles (A and B) and let them meet at 1.1 is the incentre of ∆ABC.
Step 3 : Draw perpendicular from I to any one of the side (AB) to meet AB at D.
Step 4 : With I as centre, ID as radius draw the circle. This circle touches all the sides of triangle internally.
Step 5 : Measure in radius. In radius = 1.9 cm.

Exercise 4.7

Multiple Choice Questions :

Question 1.
If an angle is equal to one third of its supplement, its measure is equal to
(1) 40°
(2) 50°
(3) 45°
(4) 55°
Hint:

Solution:
(3) 45°

Question 2.
In the given figure, OP bisect ∠BOC and OQ bisect ∠AOC. Then ∠POQ is equal to
(1) 90°
(2) 120°
(3) 60°
(4) 100°
Hint:


Solution:
(1) 90°

Question 3.
The complement of an angle exceeds the angle by 60°. Then the angle is equal to
(1) 25°
(2) 30°
(3) 15°
(4) 35°
Hint:

Solution:
(3) 15°

Question 4.
ABCD is a parallelogram, E is the mid-point of AB and CE bisects ∠BCD. Then ∠DEC is
(1) 60°
(2) 90°
(3) 100°
(4) 120°
Solution:
(2) 90°

Question 5.
If the length of a chord decreases, then its distance from the centre.
(1) increases
(2) decreases
(3) same
(4) cannot say
Solution:
(1) increases

Question 6.
In the figure, O is the centre of the circle and ∠ACB = 60° then ∠AOB =
(1) 60°
(2) 90°
(3) 120°
(4) 180°

Solution:
(3) 120°

Question 7.
The angle subtend by a semicircle at the centre is.
(1) 60°
(2) 90°
(3) 120°
(4) 180°
Solution:
(4) 180°

Question 8.
The angle subtend by a semicircle at the remaining part of the circumference is ___.
(1) 60°
(2) 90°
(3) 120°
(4) 180°

Text Book Activities

Activity – 3

Angle sum for a polygon.
Draw any quadrilateral ABCD.
Mark a point P in its interior. Join the segments PA, PB, PC and PD.
You have 4 triangles now.

How much is the sum of all the angles of the 4 triangles?
How much is the sum of the angles at their vertex, now P?
Can you now find the ‘angle sum’ of the quadrilateral ABCD?
Can you extend this idea to any polygon?
Solution:
Sum of the angles of the 4 triangle = 180° × 4 = 720°
Sum of the angles at their vertex, now p = 360°
Angle sum of the quadrilateral ABCD = 720°- 360° = 360°
Yes we can extend this idea to any polygon.

Activity – 4

Procedure.

1. Draw a circle with centre O and with suitable radius.
2. Make it a semi-circle through folding. Consider the point A, B on it.

3. Make crease along AB in the semi circles and open it.
4. We get one more crease line on the another part of semi circle, name it as CD (observe AB = CD)

5. Join the radius to get the ∆OAB and ∆OCD.

6. Using trace paper, take the replicas of triangle ∆OAB and ∆OCD.
7. Place these triangles ∆OAB and ∆OCD one on the other.

Activity – 6
Procedure:
1. Draw a circle of any radius with centre O.
2. Mark any four points A, B, C and D on the boundary. Make a cyclic quadrilateral ABCD and name the angles as in figure.

3. Figure Make a replica of the cyclic quadrilateral ABCD with the help of tracing paper.
4. Make the cutout of the angles A, B, C and D
5. Paste the angle cutout ∠1, ∠2, ∠3 and ∠4 adjacent to the angles opposite to A, B, C and D as in Figure.
6. Measure the angles ∠1 + ∠3, and ∠2 + ∠4.
Solution:
∠1 + ∠3 = 180°
∠2 + ∠4 = 180°

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 2 Introduction to Algebra Intext Questions

Try These (Text hook Page No. 41)

Question 1.
Observe the following patterns and complete them.
(i) 5, 8, 11, 14, ___, ____, ____
(ii) If 15873 × 7 = 111111 and 15873 × 14 = 222222 then, what is 15873 × 21 = ? and 15873 × 28 = ?
Solution:
(i) 17, 20, 23
Hint: 5 + 3 = 8, 8 + 3 = 11, 11+3 = 14
(ii) 15873 × 21 = 333333; 15873 × 28 = 444444
Hint: 15873 × 14 = 15873 × 7 × 2 = 111111 × 2 = 222222

Question 2.
Draw the next two patterns and complete the table.

Solution:
The next two patterns:

Question 3.
Create your own patterns of shapes and prepare a table.
Solution:
(i) Match stick pattern of triangles.

(ii) Pattern of squares and circles.

Try These (Text hook Page No. 46 to 48)

Question 4.

Solution:

Question 5.

Solution:

Question 6.
Find the unknown.
(i) 37 + 43 = 43 + ____
(ii) (22 + 10) + 15 = ____ + (10 + 15)
(iii) If 7 × 46 = 322, then 46 × 7 = _____
Solution:
(i) 37 + 43 = 43 + 37
(ii) (22 + 10) + 15 = 22 + (10 + 15)
(iii) If 7 × 46 = 322, then 46 × 7 = 322

Question 7.
Find the suitable value of ‘m’, to get a sum of 9?

Solution:

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.5

Question 1.
Find the centroid of the triangle whose vertices are
(i) (2, -4 ), (-3, -7) and (7, 2)
(ii) (-5, -5), (1, -4) and (-4, -2)
Solution:


Question 2.
If the centroid of a triangle is at (4,-2) and two of its vertices are (3, -2) and (5, 2) then find the third vertex of the triangle.
Solution:
Centroid G (x, y) = (4, -2)

Question 3.
Find the length of median through Aof a triangle whose vertices are A(-1, 3), B(1, -1) and C(5, 1).
Solution:

Question 4.
The vertices of a triangle are (1, 2), (h, -3) and (-4, k). If the centroid of the triangle is at the point (5, -1) then find the value of \(\sqrt{(h+k)^{2}+(h+3 k)^{2}}\)
Solution:

Question 5.
Orthocentre and centroid of a triangle are A(-3, 5) and B(3, 3) respectively. If C is the circumcentre and AC is the diameter of this circle, then find the radius of the circle.
Solution:

Question 6.
ABC is a triangle whose vertices are A(3, 4), B(-2, -1) and C(5, 3). If G is the centroid and BDCG is a parallelogram then find the coordinates of the vertex D.
Solution:

∴ The co-ordinates of the vertex D(x, y) = (1, 0)

Question 7.
If \(\) \(\) and \(\) are mid points of the sides of a triangle, then find the centroid of the triangle.
Solution:
“The centroid of the triangle obtained by joining the mid points of the sides of a triangle is the same as the centroid of the original triangle.”
∴ The mid points of the sides of the triangle are given as

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.4

Question 1.
Find the coordinates of the point which divides the line segment joining the points
A (4, -3) and B (9, 7) in the ratio 3 : 2.
Solution:

Question 2.
In what ratio does the point P (2, -5) divide the line segment joining A (-3, 5) and B (4, -9).
Solution:

Question 3.
Find the coordinates of a point P on the line segment joining A(1, 2) and B (6, 7) in such a way that AP = \(\frac{2}{5}\)AB.
Solution:

Question 4.
Find the coordinates of the points of trisection of the line segment joining the points A (-5, 6) and B (4, -3).
Solution:

Question 5.
The line segment joining A(6, 3) and B(-1, -4) is doubled in length by adding half of AB to each end. Find the coordinates of the new end points.
Solution:


Similarly by Mid point of DM = A(6, 3)

Question 6.
Using section formula, show that the points A(7, -5), B(9, -3) and C(13, 1) are collinear.
Solution:
∴ AB + BC = AC, Here B is the common Point. ∴ A, B, C are collinear

Question 7.
A line segment AB is increased along its length by 25% by producing it to C on the side of B. If A and B have the coordinates(-2, -3) and (2, 1) respectively, then find the coordinates of C.
Solution:

P is at 25% distance from B on its left and C is at 25% distance from B on its right.
∴ B is the mid point of PC

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.1

Question 1.
Plot the following points in the coordinate system and identify the quadrants P(-7, 6), Q(7, -2), R(-6, -7), S(3, 5) and T(3, 9)
Solution:

(i) P(-7, 6) = II Quadrant
(ii) Q(7, -2) = IV Quadrant
(iii) R(-6, -7) = III Quadrant
(iv) S(3, 5) = I Quadrant
(v) T(3, 9) = I Quadrant

Question 2.
Write down the abscissa and ordinate of the following
(i) P
(ii) Q
(iii) R
(iv) S

Solution:
(i) P(-4, 4)
Abscissa is -4
Ordinate is 4.

(ii) Q(3, 3)
Abscissa is 3
Ordinate is 3

(iii) R(4, -2)
Abscissa is 4
Ordinate is -2

(iv) S(-5, -3)
Abscissa is -5
Ordinate is -3

Question 3.
Plot the following points in the coordinate plane and join them. What is your conclusion about the resulting figure?
(i) (-5, 3) (-1, 3) (0, 3) (5, 3)
(ii) (0, -4) (0, -2) (0, 4) (0, 5)
Solution:
(i)

When we join the points, we see that they lie on a line which is parallel to x-axis.

(ii)

When we join the points, we see that they lie on a straight line which is y-axis.

Question 4.
Plot the following points in the coordinate plane. Join them in order. What type of geometrical shape is formed?
(i) (0, 0) (-4, 0) (-4, -4) (0, -4)
(ii) (-3, 3) (2, 3) (-6, -1) (5, -1)
Solution:
(i) (0, 0) (-4, 0) (-4, -4) (0, -4)

The type of geometrical shape is square.

(ii) (-3, 3) (2, 3) (-6, -1) (5, -1)

The type of geometrical shape is Trapezium.

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Additional Questions

Exercise 6.1

Question 1.
Find the six trigonometric ratios of the angle 6 using the diagram
Solution:

Question 2.
If 3 cot θ = 1, then find the value of \(\frac{3 \cos \theta-4 \sin \theta}{5 \sin \theta+4 \cos \theta}\)
Solution:

Question 3.

Solution:

Hence proved

Question 4.
If 3 (tan θ) + 4 (sec θ × sin θ) = 24. Then find all the trigonometric ratios of the angle θ.
Solution:

Question 5.
From the given figure, find all the trigonometric ratios of angle θ.
Solution:

Exercise 6.2

Question 1.
Find the value of sin 3x. sin 6x. sin 9x when x = 10°
Solution:

Question 2.
Find the value of cot 15°. cot 30°. cot 45°. cot 60°. cot 75°
Solution:
cot (90° – 75) cot (90° – 60°) cot 45° cot 60° cot 75°
= tan 75° tan 60° (1) cot 60° cot 75° = 1

Exercise 6.3

Question 3.
Find the value of cos 19° 59′ + tan 12° 12′ + sin 49° 20′.
Solution:
cos 19° 59′ + tan 12° 12′ + sin 49° 20′ = 0

Question 4.
Given that sin α = \(\frac{1}{\sqrt{2}}\) and tan β = \(\sqrt{3}\) . Find the value of α + β.
Solution:

Question 5.
Find the value of \(\frac{\cos 63^{\circ} 20^{\prime}}{\sin 26^{\circ} 40^{\prime}}\)
Solution:

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.5

Multiple Choice Questions :

Question 1.
If sin 30° = x and cos 60° = y, then x² + y² is
(1) \(\frac{1}{2}\)
(2) 0
(3) sin 90°
(4) cos 90°
Hint:

Solution:
(1) \(\frac{1}{2}\)

Question 2.
If tan θ = cot 37°, then the value of θ is
(1) 37°
(2) 53°
(3) 90°
(4) 1°
Hint:
tan θ = cot 37°
tan (90° – 37°) = cot 37°
θ = 90°- 37° = 53°
Solution:
(2) 53°

Question 3.
The value of tan 72° tan 18° is
(1) 0
(2) 1
(3) 18°
(4) 72°
Hint:

Solution:
(2) 1

Question 4.
The value of \(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}\) is equal to
(1) cos 60°
(2) sin 60°
(3) tan 60°
(4) sin 30°
Hint:

Solution:
(3) tan 60°

Question 5.
If 2 sin 2θ = \(\sqrt{3}\), then the value of θ is
(1) 90°
(2) 30°
(3) 45°
(4) 60°
Hint:

Solution:
(2) 30°

Question 6.
The value of 3 sin 70° sec 20° + 2 sin 49° sec 51° is
(1) 2
(2) 3
(3) 5
(4) 60°
Hint:

Solution:
(3) 5

Question 7.
The value of \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\) is
(1) 2
(2) 1
(3) 0
(4) \(\frac{1}{2}\)
Hint:

Solution:
(3) 0

Question 8.
The value of cosec (70° + θ) – sec(20° – θ) + tan (65° + θ) – cot(25° – θ) is
(1) 0
(2) 1
(3) 2
(4) 3
Hint: cosec (70° + θ) – sec (20° – θ) + tan (65° + θ) – cot (25° – θ)

Solution:
(1) 0

Question 9.
The value of tan 1°tan 2° tan 3° … tan 89° is
(1) 0
(2) 1
(3) 2
(4) \(\frac{\sqrt{3}}{2}\)
Hint: tan (90° – 89°) tan (90° – 88°) …tan (90° -46°) tan 45° tan 46°… tan 88 tan 89° = cot 89° cot 88°… cot 46° (1) tan 46°… tan 88° tan 89° = 1
Solution:
(2) 1

Question 10.
Given that sin α = \(\frac{1}{2}\) and cos β = \(\frac{1}{2}\) , then the value of α + β is
(1) 0°
(2) 90°
(3) 30°
(4) 60°
Hint:

Solution:
(2) 90°

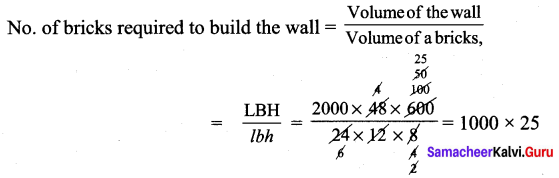
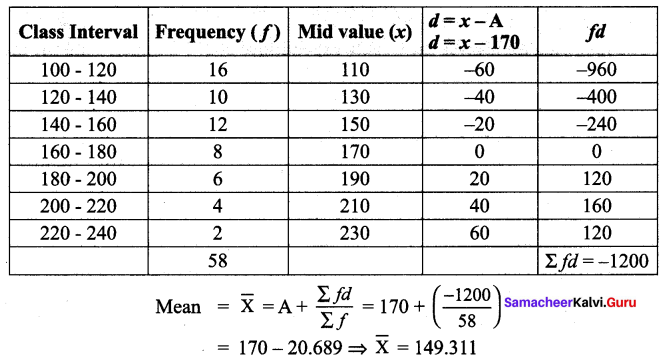
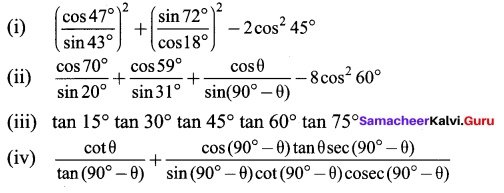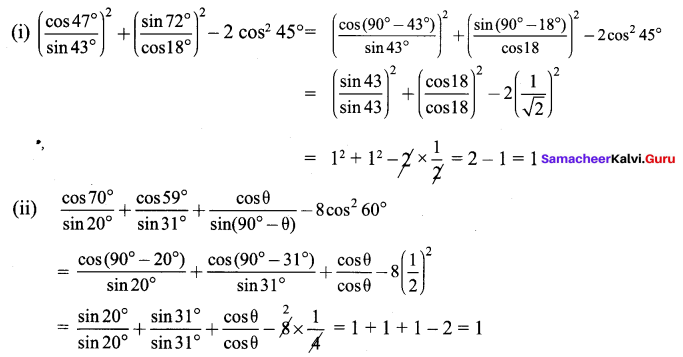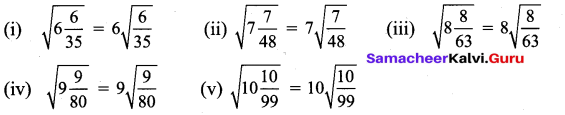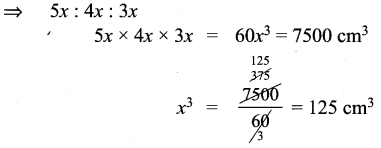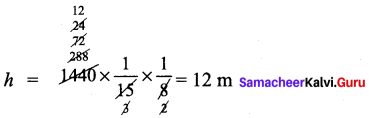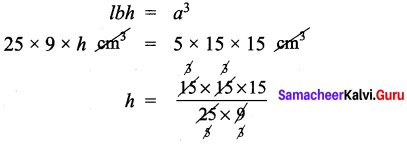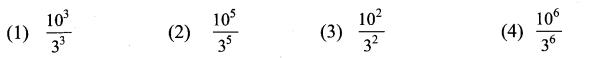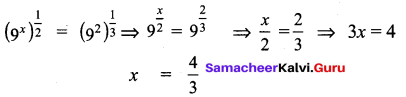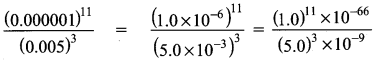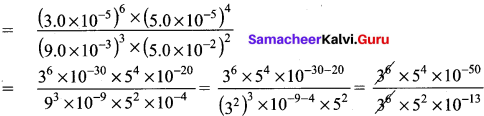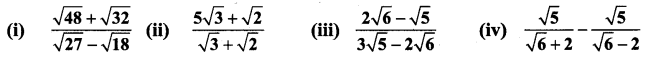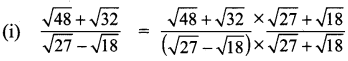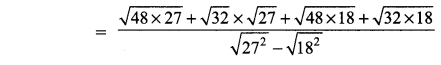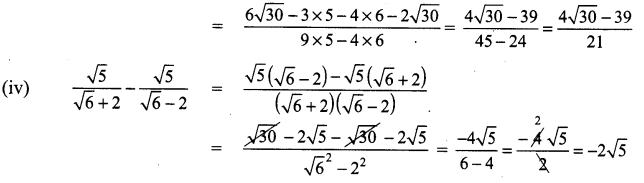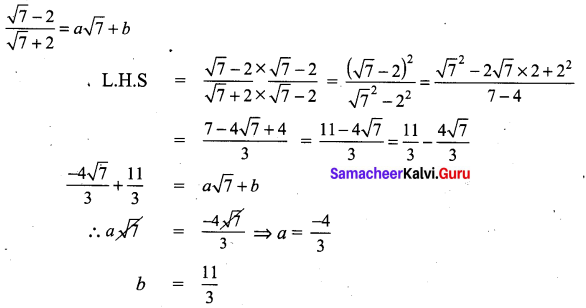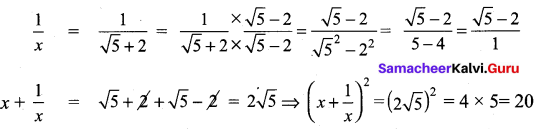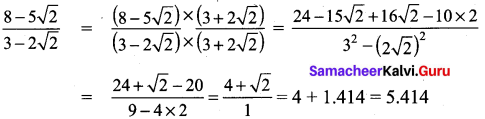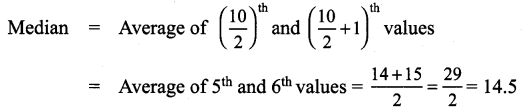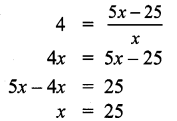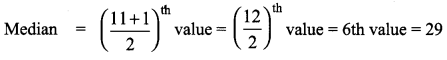You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.4

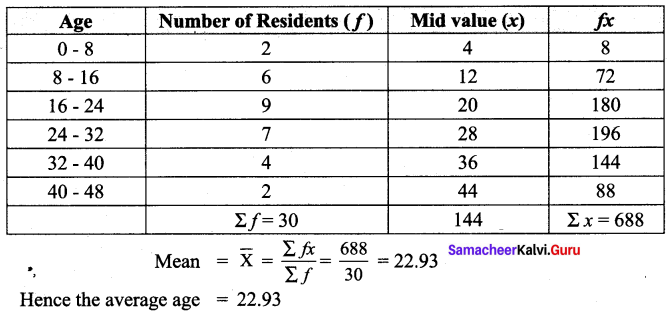
Question 1.
Find the value of the following :
(i) sin 49°
(ii) cos 74° 39′
(iii) tan 54° 26′
(iv) sin 21° 21′
(v) cos 33° 53′
(vi) tan 70° 17′
Solution:

Question 2.
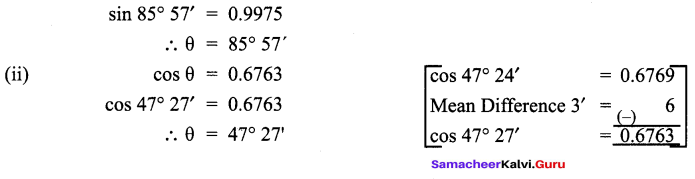
Find the value of θ if
(i) sin θ = 0.9975
(ii) cos θ = 0.6763
(iii) tan θ = 0.0720
(iv) cos θ = 0.0410
(v) tan θ = 7.5958
Solution:
(i) From the natural sines table

Question 3.
Find the value of the following :
(i) sin 65° 39′ + cos 24° 57′
(ii) tan 70° 58′ + cos 15° 26′ – sin 84° 59′
Solution:
(i) = 0.9111 + 0.9066 + 0.1793 = 1.9970
(ii) = 2.8982 + 0.9639 – 0.9962 = 3.8621 – 0.9962 = 2.8659

Question 4.
Find the area of a right triangle whose hypotenuse is 10cm and one of the acute angle is 24° 24′
Solution:

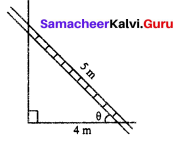
Question 5.
Find the angle made by a ladder of length 5m with the ground, if one of its end is
4m away from the wall and the other end is on the wall.
Solution:

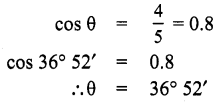
Question 6.
In the given figure, HT shows the height of a tree standing vertically. From a point P, the angle of elevation of the top of the tree (that is ∠P) measures 42° and the distance to the tree is 60 metres. Find the height of the tree.
Solution:

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.3

Question 1.
Find the value of the following:

Solution:

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.6

Multiple Choice Questions :

Question 1.
If the y-coordinate of a point is zero, then the point always lies
(1) in the I quadrant
(2) in the II quadrant
(3) on x-axis
(4) on y-axis
Solution:
(3) on x-axis

Question 2.
The points (-5, 2) and (2, -5) lie in the ___.
(1) same quadrant
(2) II and III quadrant respectively
(3) II and IV quadrant respectively
(4) IV and II quadrant respectively
Hint: (-, +) lies II^nd quadrant and (+, -) lies in IV^th quadrant
Solution:
(3) II and IV quadrant respectively

Question 3.
On plotting the points 0(0, 0), A(3, – 4), B(3, 4) and C(0, 4) and joining OA, AB, BC and CO, which of the following figure is obtained?
(1) Square
(2) Rectangle
(3) Trapezium
(4) Rhombus
Hint: In trapezium one pair of opposite side is parallel.
Solution:
(3) Trapezium

Question 4.
If P(-1, 1), Q(3, -4), R(1, -1), S(-2, -3) and T(-4, 4) are plotted on a graph paper, then the points in the fourth quadrant are ____.
(1) P and T
(2) Q and R
(3) only S
(4) P and Q
Hint: Points in IVth quadrant are (+, -)
Solution:
(2) Q and R

Question 5.
The point whose ordinate is 4 and which lies on they-axis is
(1) (4, 0)
(2) (0, 4)
(3) (1, 4)
(4) (4, 2)
Hint: Points in y-axis have abscissa a zero
Solution:
(2) (0, 4)

Question 6.
The distance between the two points (2, 3) and (1, 4) is ___ .
(1) 2
(2) \(\sqrt{56}\)
(3) \(\sqrt{10}\)
(4) \(\sqrt{2}\)
Hint: Distance = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Solution:
(4) \(\sqrt{2}\)

Question 7.
If the points A (2, 0), B (-6, 0), C (3, a – 3) lie on the x-axis then the value of a is ___.
(1) 0
(2) 2
(3) 3
(4) -6
Hint: Points in y-axis have ordinate zero. ∴ a – 3 = 0 ⇒ a = 3
Solution:
(3) 3

Question 8.
If ( x + 2, 4) = (5, y – 2), then the coordinates (x, y) are ___.
(1) (7, 12)
(2) (6, 3)
(3) (3, 6)
(4) (2, 1)
Hint: x + 2 = 5 ⇒ x = 3; y – 2 = 4 ⇒ y = 6
Solution:
(3) (3, 6)

Question 9.
If Q₁, Q₂, Q₃, Q₄ are the quadrants in a Cartesian plane then Q₂ ∩ Q₃ is
(1) Q₁ ∪ Q₂
(2) Q₂ ∪ Q₃
(3) Null set
(4) Negative x-axis
Hint: Quadrants do not contain the axis.
Solution:
(3) Null set

Question 10.
The distance between the point (5, -1) and the origin is
(1) \(\sqrt{24}\)
(2) \(\sqrt{37}\)
(3) \(\sqrt{26}\)
(4) \(\sqrt{17}\)
Hint:

Solution:
(3) \(\sqrt{26}\)

Question 11.
The coordinates of the point C dividing the line segment joining the points P(2, 4) and Q(5, 7) internally in the ratio 2 : 1 is
(1) \(\left(\frac{7}{2}, \frac{11}{2}\right)\)
(2) (3, 5)
(3) (4, 4)
(4) (4, 6)
Hint:

Question 12.
If P\(\left(\frac{a}{3}, \frac{b}{2}\right)\) is the mid-point of the line segment joining A(-4, 3) and B(-2, 4) then (a, b)
(1) (-9, 7)
(2) \(\left(-3, \frac{7}{2}\right)\)
(3) (9, -7)
(4) \(\left(3-\frac{7}{2}\right)\)
Hint:


Solution:
(1) (-9, 7)

Question 13.
In what ratio does the point Q(1, 6) divide the line segment joining the points P(2, 7) and R(-2, 3)
(1) 1 : 2
(2) 2 : 1
(3) 1 : 3
(4) 3 : 1.
Hint:

Question 14.
If the coordinates of one end of a diameter of a circle is (3, 4) and the coordinates of its center is (-3, 2), then the coordinate of the other end of the diameter is
(1) (0, -3)
(2) (0, 9)
(3) (3, 0)
(4) (-9, 0)

Solution:
(4) (-9, 0)

Question 15.
The ratio in which the x-axis divides the line segment joining the points A(a₁, b₁) and B(a₂, b₂) is
(1) b₁ : b₂
(2 ) -b₁ : b₂
(3 ) a₁ : a₂
(4 ) -a₁ : a₂
Hint:



Solution:
(2 ) -b₁ : b₂

Question 16.
The ratio in which the x-axis divides the line segment joining the points (6, 4) and (1, -7) is
(1) 2 : 3
(2) 3 : 4
(3) 4 : 7
(4) 4 : 3
Hint:

Solution:
(3) 4 : 7

Question 17.
If the coordinates of the mid-points of the sides AB, BC and CA of a triangle are (3, 4), (1, 1) and (2, -3) respectively, then the vertices A and B of the triangle are
(1) (3, 2), (2, 4)
(2) (4, 0), (2, 8)
(3) (3, 4), (2, 0)
(4) (4, 3), (2, 4)
Hint:


0 + y₂ = 8 ⇒ y₂ = 8
(x₁, y₁) = (4, 0) ; (x₂, y₂) = (2, 8)
Solution:
(2) (4, 0), (2, 8)

Question 18.
The mid-point of the line joining (-a, 2b) and (-3a, -4b) is
(1) (2a, 3b)
(2) (-2a, -b)
(3) (2a, b)
(4) (-2a, -3b)
Hint:

Solution:
(2) (-2a, -b)

Question 19.
In what ratio does the j-axis divides the line joining the points (-5, 1) and (2, 3) internally
(1) 1 : 3
(2) 2 : 5
(3) 3 : 1
(4) 5 : 2
Hint:

Solution:
(4) 5 : 2

Question 20.
If (1, -2), (3, 6), (x, 10) and (3, 2) are the vertices of the parallelogram taken in order, then the value of x is
(1) 6
(2) 5
(3) 4
(4) 3
Hint:
In parallelogram diagonals bisect each other.
Mid point of AC = Mid point of BD


Solution:
(2) 5