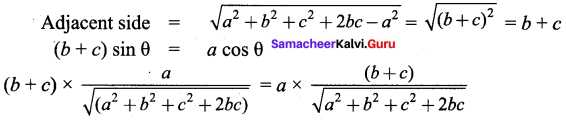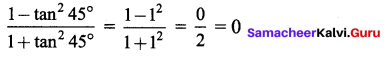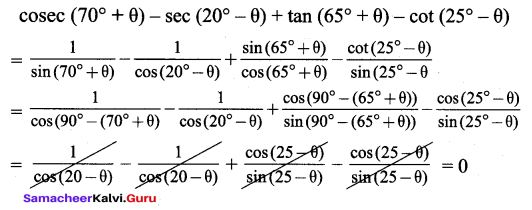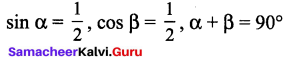You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.14
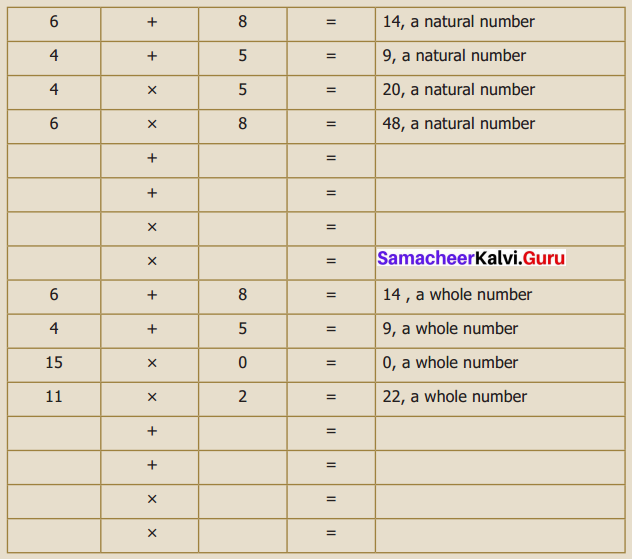
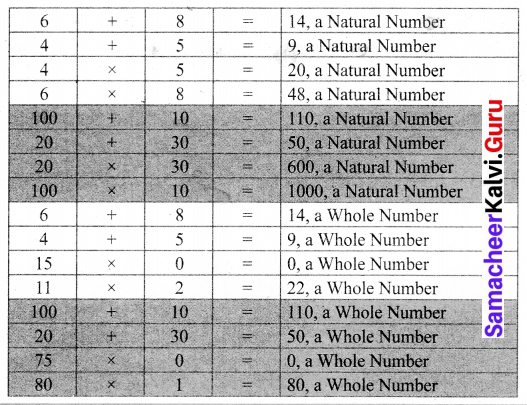
Solve by any one of the methods
Question 1.
The sum of a two digit number and the number formed by interchanging the digits is 110. If 10 is subtracted from the first number, the new number is 4 more than 5 times the sums of the digits of the first number. Find the first number.
Solution:
Let the two digit number be x y
Its place value = 10x + y
After interchanging the digits the number will be y x
Its place value = 10y + x
Their sum = 10x + y + 10y + x = 110
11x + 11y = 110
x + y = 10 ………….. (1)
If 10 is subtracted from the first number, the new number is 10x + y – 10
The sums of the digits of the first number is x + y
Its 4 more than 5 times is = 5(x + y) + 4
∴ 10x + y – 10 = 5x + 5y + 4
10x + y – 5x – 5y = 4 + 10
5x – 4y = 14 ………. (2)
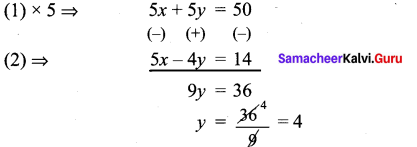
Substitute y = 4 in (1)
x + 4 = 10
x = 10 – 4
x = 6
The first number is 64
Question 2.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(\frac{1}{2}\). Find the fraction.
Solution:
Let the numerator be x
Denominator be y
x + y = 12 ………. (1)
\(\frac{x}{y+3}=\frac{1}{2}\)
2x = y + 3
2x – y = 3 …………. (2)
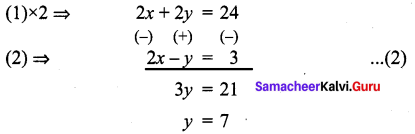
Substitute y = 7 in (1)
x + 7 = 12
x = 12 – 7
x = 5
∴ The fraction is \(\frac{x}{y}=\frac{5}{7}\)
Question 3.
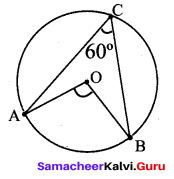
ABCD is a cyclic quadrilateral such that ∠A = (4y + 20)°, ∠B = (3y – 5)°, ∠C =(4x)° and ∠D = (7x + 5)°. Find the four angles.
Solution:
In a cyclic quadrilateral the sum of the four angles is 360° and
the sum of the opposite angles is 180°.
∠A + ∠C = 180°
4y + 20 + 4x = 180°
4x + 4y = 180 – 20
x + y = \(\frac{160}{4}\)
x + y = 40 ………….. (1)
∠B + ∠D = 180°
3y – 5 + 7x + 5 = 180
7x + 3y = 180 …………. (2)
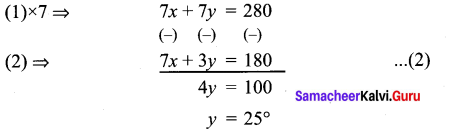
Substitute y = 25° in (1)
x + 25 = 40
x = 40 – 25
x = 15°
∠A = (4y + 20)° = (4 × 25 + 20) = 100 + 20 = 120°
∠B = (3y – 5)° = (3 × 25° – 5) = 75° – 5° = 70°
∠C = (4x)° = 4 × 15° = 60°
∠D = (7x + 5)° = (7 × 15 + 5) = 105° + 5° = 110°
∴ ∠A = 120°, ∠B = 70°, ∠C = 60°, ∠D = 110°
![]()
Question 4.
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains ₹ 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss, he gains ₹ 1500 on the transaction. Find the actual price of the T.V. and the fridge.
Solution:
Let the actual price of a T.V. = x
Let the actual price of a Fridge = y
\(\frac{5}{100}\)x + \(\frac{10}{100}\)y = 2000
\(\frac{5}{100}\) (x + 2y) = 2000
x + 2y = 2000 × \(\frac{100}{5}\)
x + 2y = 40000 ………. (1)
\(\frac{10}{100}\) x – \(\frac{5}{100}\)y = 1500
2x – y = 1500 × \(\frac{100}{5}\)
2x – y = 30000 ……….. (2)
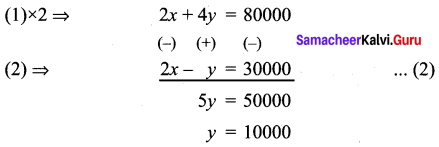
Substitute y = 10000 in (1)
x + 2(10000) = 40000
x + 20000 = 40000
x = 40000 – 20000
x = 20000
∴ Actual price of T.V. = ₹ 20000
Actual price of Fridge = ₹ 10000
Question 5.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers.
Solution:
Let the two numbers be x, y
\(\frac{x}{y}=\frac{5}{6}\)
⇒ 6x = 5y
6x – 5y = 0 ………… (1)
\(\frac{x-8}{y-8}=\frac{4}{5}\)
⇒ 5(x – 8) = 4(y – 8)
5x – 40 = 4y – 32
5x – 4y = 40 – 32
5x – 4y =8 ………….. (2)
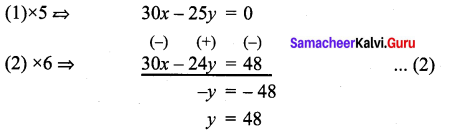
Substitute y = 48 in (1)
6x – 5(48) = 0
6x – 240 = 0
6x = 240
x = \(\frac{240}{6}\) = 40
\(\frac{x}{y}=\frac{40}{48}=\frac{5}{6}\)
∴ The numbers are in the ratio 5 : 6
Question 6.
4 Indians and 4 Chinese can do a piece of work in 3 days. While 2 Indians and 5 Chinese can finish it in 4 days. How long would it take for 1 Indian to do it? How long would it take for 1 Chinese to do it?
Solution:
Let for one Indian the rate of working be \(\frac{1}{x}\)
Let for one Chinese the rate of working be \(\frac{1}{y}\)

For cross multiplication method, we write the co-efficients as
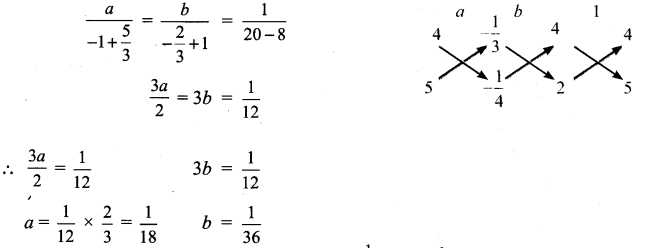
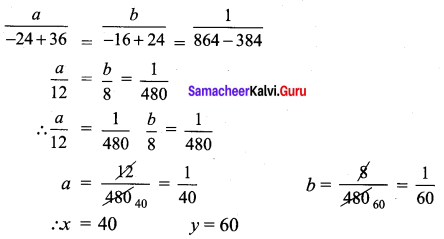
∴ 1 Chinese can do the same piece of work = \(\frac{1}{y}\) = b = \(\frac{1}{36}\) = 36 days
1 Indian can do the piece of work = \(\frac{1}{x}\) = a = \(\frac{1}{18}\) = 18 days
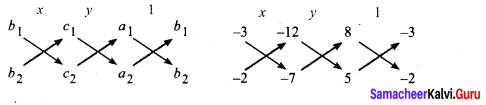
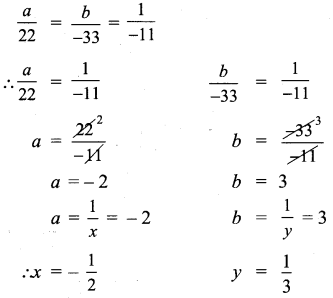
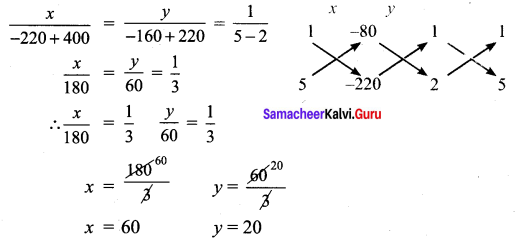
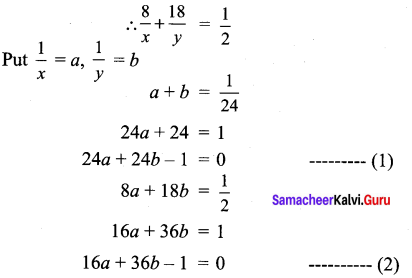
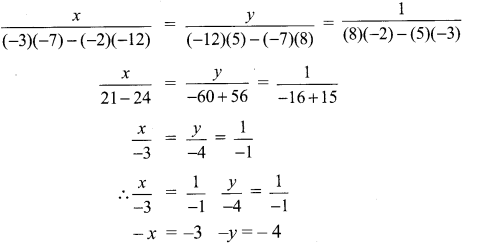

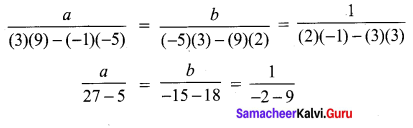










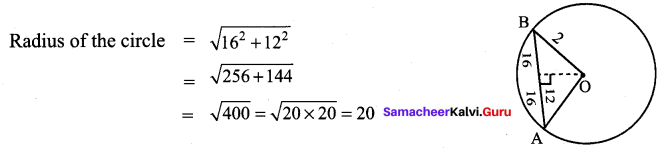

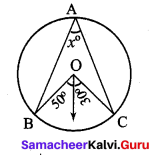
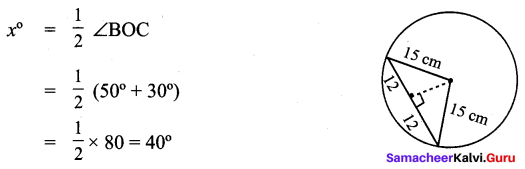
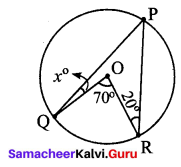
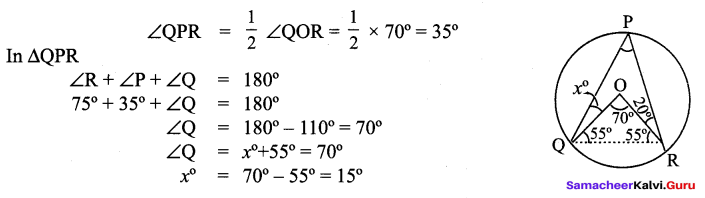
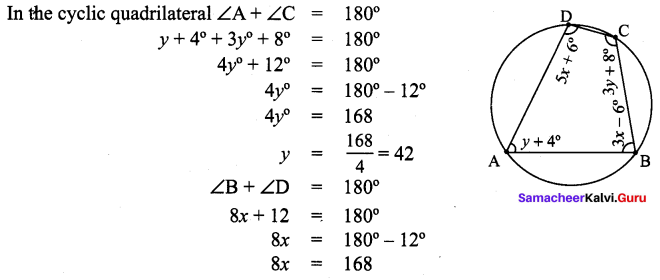

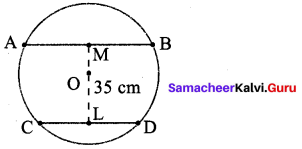

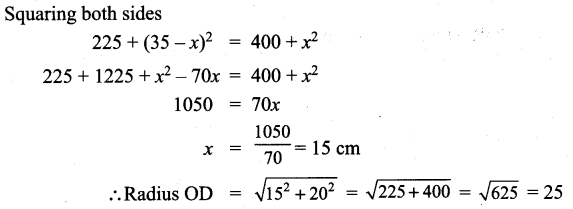
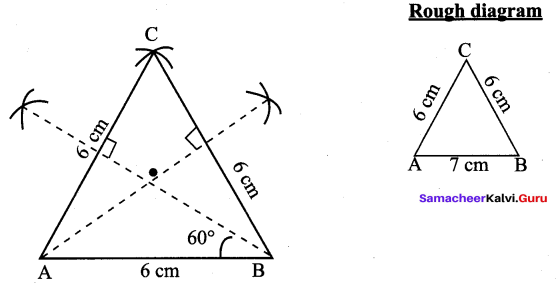
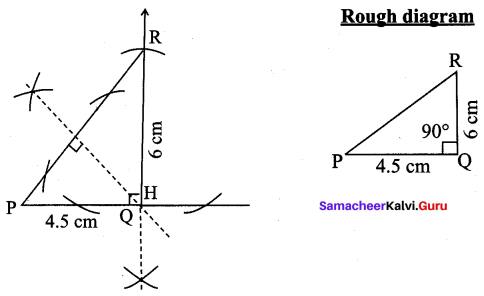




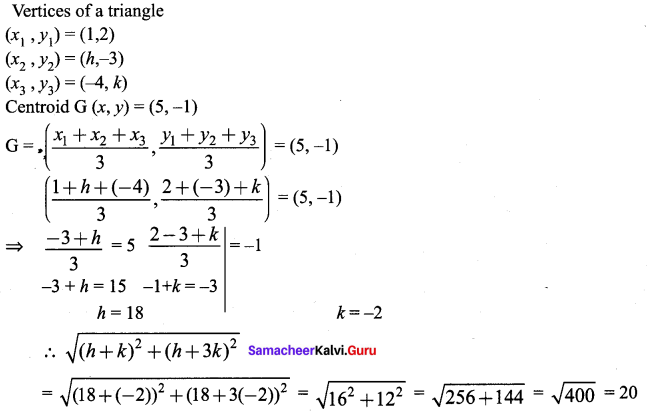
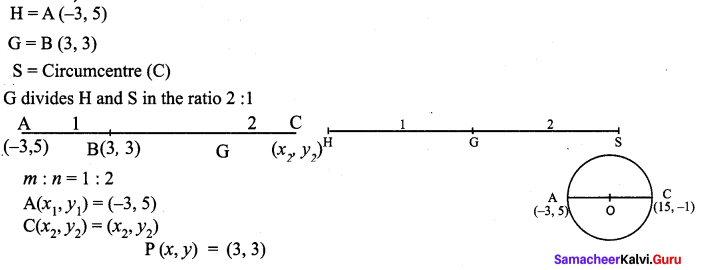


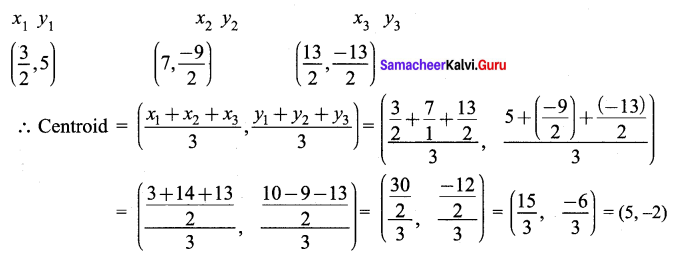
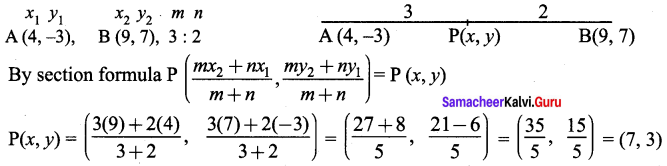


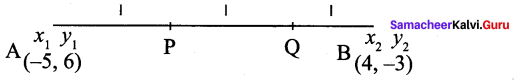
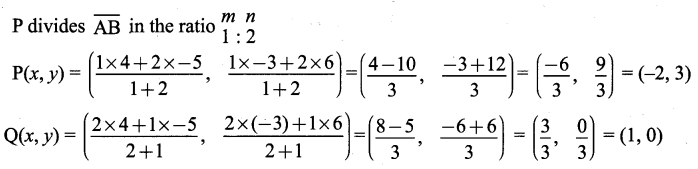


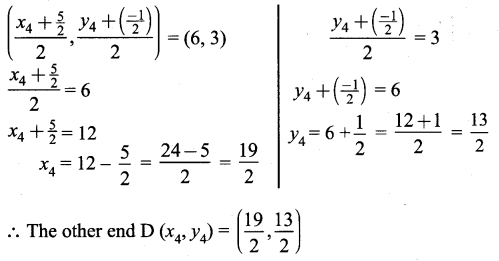
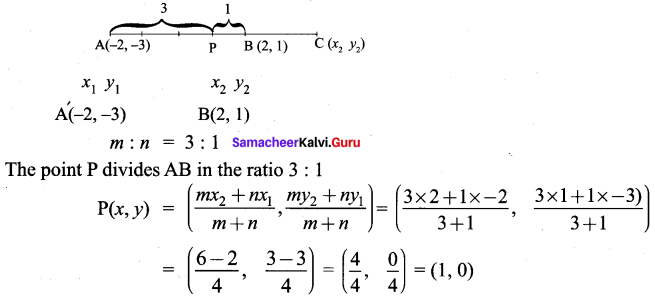
 ∴ AB + BC = AC, Here B is the common Point. ∴ A, B, C are collinear
∴ AB + BC = AC, Here B is the common Point. ∴ A, B, C are collinear