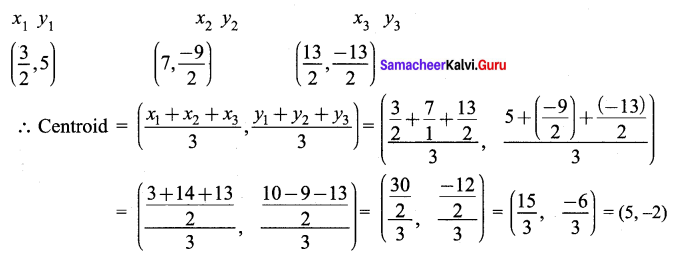You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.5
Question 1.
Find the centroid of the triangle whose vertices are
(i) (2, -4 ), (-3, -7) and (7, 2)
(ii) (-5, -5), (1, -4) and (-4, -2)
Solution:
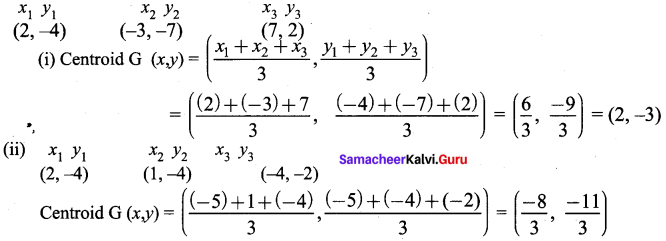
![]()
Question 2.
If the centroid of a triangle is at (4,-2) and two of its vertices are (3, -2) and (5, 2) then find the third vertex of the triangle.
Solution:
Centroid G (x, y) = (4, -2)

![]()
Question 3.
Find the length of median through Aof a triangle whose vertices are A(-1, 3), B(1, -1) and C(5, 1).
Solution:

Question 4.
The vertices of a triangle are (1, 2), (h, -3) and (-4, k). If the centroid of the triangle is at the point (5, -1) then find the value of \(\sqrt{(h+k)^{2}+(h+3 k)^{2}}\)
Solution:
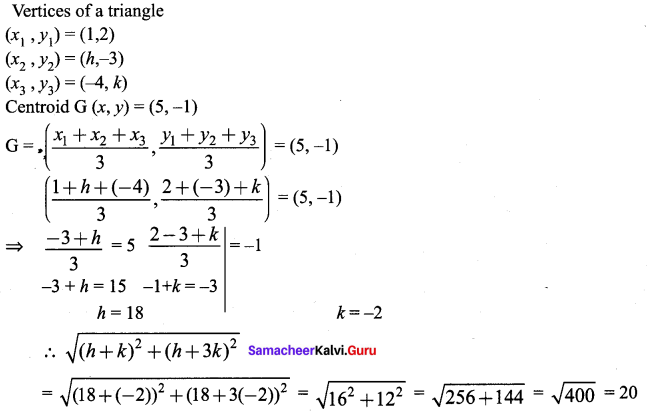
Question 5.
Orthocentre and centroid of a triangle are A(-3, 5) and B(3, 3) respectively. If C is the circumcentre and AC is the diameter of this circle, then find the radius of the circle.
Solution:
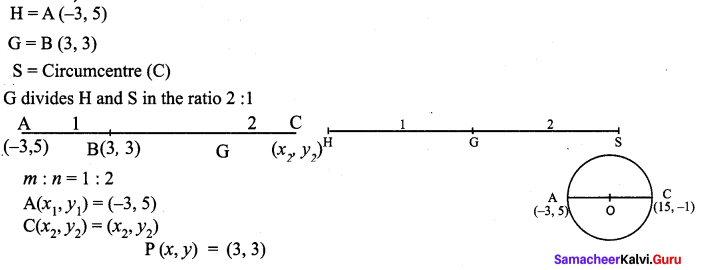

![]()
Question 6.
ABC is a triangle whose vertices are A(3, 4), B(-2, -1) and C(5, 3). If G is the centroid and BDCG is a parallelogram then find the coordinates of the vertex D.
Solution:

∴ The co-ordinates of the vertex D(x, y) = (1, 0)
Question 7.
If \(\) \(\) and \(\) are mid points of the sides of a triangle, then find the centroid of the triangle.
Solution:
“The centroid of the triangle obtained by joining the mid points of the sides of a triangle is the same as the centroid of the original triangle.”
∴ The mid points of the sides of the triangle are given as