You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Intext Questions
Try These (Textbook Page No. 2)
Question 1.
The Successor of 4576 is ____
Solution:
4577
Question 2.
The Predecessor of 8970 is ____
Solution:
8969
Question 3.
999 + 1 equals _____
Solution:
1000
![]()
Question 4.
10000 – 1 equals _____
Solution:
9999
Question 5.
The Predecessor of the smallest 5 digit number is ____
Solution:
Greatest 4 digit number 9999
Try These (Textbook Page No. 4)
Question 1.
Give 3 examples where the number of things counted by you would be a 5 digit number or more.
Solution:
- Number of stars in the sky.
- The number of people living in Tamilnadu.
- The number of accidents in India in the year 2017.
Question 2.
There are ten lakh people in a district. What would be the population of 10 such districts?
Solution:
Number of people in the district = 10,00,000
.’. Population of 10 such districts = 10,00,000 × 10 = 1,00,00,000
Total population of 10 districts would be one crore.
10 lakh = 10,000 Hundreds
Question 3.
The Government spends rupees 2 crores for education in a particular district every month. What would be its expenditure for over 10 months?
Solution:
Expenditure for one month = 2 crores,
Expenditure for ten months = 2,00,00,000 × 10 = 20,00,00,000
Expenditure for 10 months = twenty crores.
![]()
Try These (Textbook Page No. 5)
Question 1.
Complete the table:
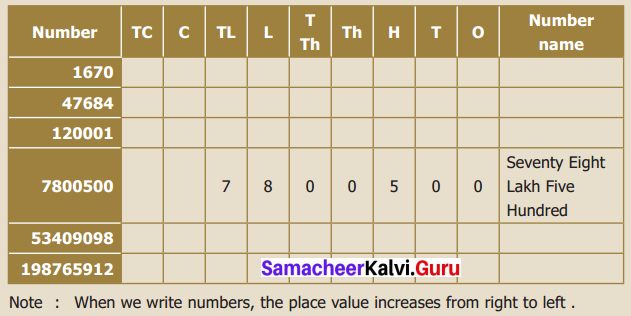
Solution:
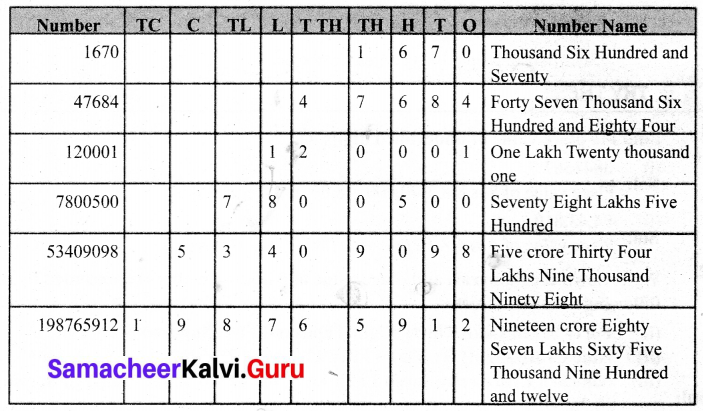
Try These (Textbook Page No. 6)
Question 1.
Read and expand the following numbers:
(i) 2304567
(ii) 4509888
(iii) 9553556
Solution:
(i) Number: 23,04,567
Expanded form: 2 × 1000000 + 3 × 100000 + 0 × 10000 + 4 × 1000 + 5 × 100 + 6 × 10 + 7 × 1
Read as: Twenty Three Lakh Four Thousand Five Hundred and Sixty Seven
(ii) Number: 45,09,888
Expanded form: 4 × 1000000 + 5 × 100000 + 0 × 10000 + 9 × 1000 + 8 × 100 + 8 × 10 + 8 × 1
Read as: Forty Five Lakh Nine Thousand Eight Hundred and Eighty Eight
(iii) Number: 95,53,556
Expanded form: 9 × 1000000 + 5 × 100000 + 5 × 10000 + 3 × 1000 + 5 × 100 + 5 × 10 + 6 × 1
Read as: Ninety Five Lakh Fifty Three Thousand Five Hundred and Fifty Six
![]()
Question 2.
How many hundreds are there in 10 lakh?
Solution:

There are four places to the left of a Hundred.
Question 3.
10 lakh candidates write the Public Exam this year. If each exam centre is allotted with 1000 candidates. How many exam centres would be needed?
Solution:
Candidate for one centre = 1000
For 10 lakh people
10,00,000
Ten lakh contains = \(\frac{10,00,000}{1000}\) = 1000 Thousands
For 10 lakh people 1000 centres are needed
Try These (Textbook Page No. 7)
Question 1.
Find the place value of underlined digits
(i) 3841567
(ii) 94,43,810
Solution:
(i) Place value of 8 is 8 × 1,00,000 = 8,00,000 (Eight Lakh)
(ii) Place value of 4 is 4 × 10,000 = 40,000 (Forty Thousand)
Question 2.
Write down the numerals and place value of 5 in the numbers represented by the following number names.
(i) Forty-Seven Lakh Thirty Fight Thousand Five Hundred Sixty One.
(ii) Nine Crore Eighty-Two lakh Fifty Thousand Two Hundred Forty-One
(iii) Nineteen Crore Fifty-Seven Lakh Sixty Thousand Three Hundred Seventy
Solution:
(i) 47,38,561
Place value of 5 is 5 × 100 = 500 (Five Hundred)
(iii) 9,82,50,241
Place value of 5 is 5 × 10000 = 50,000 (Fifty Thousand)
(iv) 19,57,60,370
Place value of 5 is 5 × 10,00,000 = 50,00,000 (Fifty Lakhs)
![]()
Try These (Textbook Page No. 9)
Question 1.
Identify the incorrect places of comma and rewrite correctly. Indian System: 56, 12, 34, 0, 1, 5 ; 9,90,03,2245
International System: 7,5613,4534; 30,30,304,040
Indian System: 56, 12, 34, 015; 99,00,32,245
Solution:
Indian System: 56,12,34,015; 99,00,32,245
International System: 756,134,534 ; 3,030,304,040
Try These (Textbook Page No. 13)
Question 1.
Write the numbers in ascending order: 688, 9, 23005, 50, 7500.
Solution:
Ascending order: 9, 50, 688,7500, 23005
9 < 50 < 688 < 7500 < 23005
Question 2.
Find the least and greatest among the numbers: 478, 98, 6348,3, 6007, 50935
Solution:
The lease number is 3.
The greatest number is 50935
Try These (Textbook Page No. 14)
Question 1.
Compare the two numbers and put <, > and = using a place value chart.
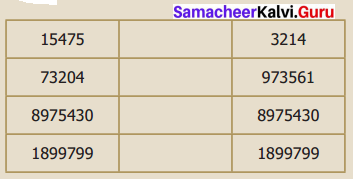
Solution:
(i) 15475, 3214
Comparing the place value using a place value chart.

comparing the place values from left we have 15475 > 3214
(ii) 73204, 973561
Place value chart

comparing the digits or two numbers 73204 < 973561
(iii) 8975430, 8975430

From the place value chart comparing tne digits trom left 8 = 8, 9 = 9, 7 = 7, 5 = 5, 4 = 4, 3 = 3, 0 = 0
8975430 = 8975430
(iv) 1899799, 1899799.

From the place value chart comparing the digits of the two numbers from the highest place value we have 1 = 1, 8 = 8, 9 = 9, 9 = 9, 7 = 7, 9 = 9, 9 = 9
1899799 = 1899799
![]()
Try These (Textbook Page No. 16)
Question 1.
The area in sq.km of 4 Indian states are given below:

List the areas of the above 4 Indian States in the ascending and the descending order.
Solution:
We can prepare place value chart
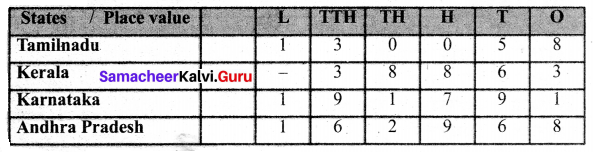
5 digit number 38,863 is the least value.
Comparing digits of other 6 digit numbers from left.
1 = 1 = 1, 3 < 6 < 9
Ascending order = 38,863 < 1,30,058 < 1,62,968 < 1,91,791
Kerala < Tamilnadu < Andhra Pradesh < Karnataka
Descending order = 1,91,791 > 1,62,968 > 1,30,058 > 38,863
Karnataka > Andhra Pradesh > Tamilnadu > Kerala
Try These (Textbook Page No. 17)
Question 1.
In the same way, try placing the digit 4 in thousandth place and get six different 4-digit numbers. Also, make different 4-digit numbers by fixing 8 and 5 in the thousandth place.
Solution:
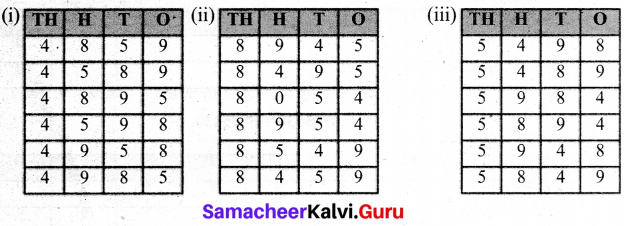
Question 2.
In the same way, make different 4 digit numbers by exchanging the digits and check every time whether the number made is small or big.
1432 < 4321 4321 > 3214
3214 > 2143
Solution:
Question 3.
Pedometer used in walking practice contains 5 digit number. What could be the largest measure?
Solution:
99,999
![]()
Try These (Textbook Page No. 25)
Question 1.
Round off the following numbers to the nearest ten
(i) 57
(ii) 189
(iii) 3,956
(iv) 57,312
Solution:
(i) 57
Given number = 57
Place value to be rounded off is ten.
Digit in tens place is 5.
Digit to’the right is 7 > 5
Adding 1 to 5 = 1 + 5 = 6
Changing the digits to the right of 6 to zero = 60
rounded off number is 60.
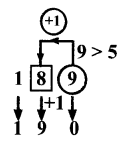
(ii) 189
Place value to be rounded off is ten
Digit is ten places is 8
Digit to the right is 9 > 5
Adding 1 to 8 = 1 + 8 = 9.
changing the digits to the right of 19 to zero = 190
Required rounded off number is 190
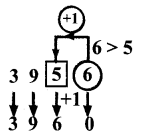
(iii) 3956
Place value to be rounded off is ten.
Digit in tens place is 5
Digit to the right is 6 > 5
Adding 1 to 5 = 1 + 5 = 6
Changing the right digits of 396 to zero = 3960
Required rounded off number is 3960.
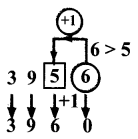
(iv) 57312
Place value to be rounded off is ten.
Digit in tens place is 1
Digit to the right is 2 < 5
Leaving the number 2 as it is changing the digits to the right of 5731 to zero = 57310.
The rounded number is 57310
Question 2.
Round off the following numbers to the nearest ten, hundred and thousand.
(i) 9,34,678
(ii) 73,43,489
(iii) 17,98,45,673
Solution:
(i) 9,34,678
Nearest Tens: 9,34,680
Nearest Hundreds: 9,34,700
Nearest Thousands: 9,35,000
(ii) 73,43,489
Nearest Tens: 73,43,490
Nearest Hundreds: 73,43,500
Nearest Thousands: 73,43,000
(iii) 17,98,45,673
Nearest Tens: 17,98,45,670
Nearest Hundreds: 17,98,45,700
Nearest Thousands: 17,98,46,000
Question 3.
The tallest mountain in the world Mount Everest, located in Nepal is 8,848 m high. Its height can be rounded off to the nearest thousands as ______
Solution:
9000 m
![]()
Try These (Textbook Page No. 27)
Question 1.
Estimate the sum and difference:
8457 and 4573
Solution:
(a) Sum
8457 ⇒ 8000
4573 ⇒ 5000
Sum = 13,000
(b) Difference
8457 ⇒ 8000
4573 ⇒ 5000
Difference = 3,000
Question 2.
Estimate the product 39 × 53
Solution:
39 ⇒ 40
53 ⇒ 50
Product 40 × 50 = 2000
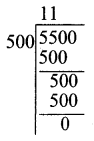
Question 3.
Estimate the quotient 5546 ÷ 524
Solution:
5546 ⇒ 5500
524 ⇒ 500
Quotient is 11
Try These (Textbook Page No. 29)
Question 1.
Find the value of 6 + 3 + 8 and 3 + 6 + 8
(i) Are the same?
(ii) Is there any other way of arranging these three numbers?
Solution:
6 + 3 + 8 = 3 + 6 + 8 = 17
(i) Yes, 6 + 3 + 8 = 3 + 6 + 8 = 17, Both are same
(ii) Yes, we can arrange these numbers as
3 + 8 + 6 = 8 + 6 + 3 = 8 + 3 + 6 = 6 + 8 + 3
Question 2.
Find the value of 5 × 2 × 6 and 2 × 5 × 6
(i) Are the same?
(ii) Is there any other way of arranging these three numbers?
Solution:
5 × 2 × 6 = 2 × 5 × 6 = 60
(i) Yes, they are the same
(ii) They can be arranged as
2 × 6 × 5 = 6 × 5 × 2 = 5 × 6 × 2 = 6 × 2 × 5.
Question 3.
Is 7 – 5 the same as 5 – 7? Why?
Solution:
7 – 5 ≠ 5 – 7.
Because subtraction is not commutative [∵ 7 – 5 = 2; 5 – 7 = -2]
Question 4.
What is the value of (15 – 8) – 6? Is it the same as 15 – (8 – 6)? Why?
Solution:
(15 – 8) – 6 = 7 – 6 = 1
(15 – 8) – 6 = 1
It is not same as 15 – (8 – 6).
15 – (8 – 6) = 15 – 2 = 13
(15 – 8) – 6 ≠ 15 – (8 – 6)
Question 5.
What is 15 ÷ 5? Is it the same as 5 ÷ 15? Why?
Solution:
(i) 15 ÷ 5 = 3
(ii) 15 ÷ 5 ≠ 5 ÷ 15
(iii) Division is not commutative for whole numbers.
Question 6.
What is the value of (100 ÷ 10) ÷ 5? Is it the same as 100 ÷ (10 ÷ 5)? Why?
Solution:
(i) (100 ÷ 10) ÷ 5 = 10 ÷ 5 = 2
(ii) 100 ÷ (10 ÷ 5) ≠ (100 ÷ 10) ÷ 5
(iii) Because division of whole numbers are not associative.
Also 100 ÷ (10 ÷ 5) = 100 ÷ 2 = 50
But (100 ÷ 10) ÷ 5 = 10 ÷ 5 = 2 = 50 ≠ 2
(i. e) (100 ÷ 10) ÷ 5 ≠ 100 ÷ (10 ÷ 5)
![]()
Try These (Textbook Page No. 30, 32, 33)
Question 1.
Use at least three different pairs of whole numbers to verify that subtraction is not commutative
Solution:
(a) 7 and 20
20 – 7 ≠ 7 – 20
(b) 300 and 100
300 – 100 ≠ 100 – 300
(c) 60 and 5
60 – 5 ≠ 5 – 60
Question 2.
Is 10 ÷ 5 the same as 5 ÷ 10? Justify it by taking two more combinations of numbers
Solution:
10 ÷ 5 ≠ 5 ÷ 10
Example:
(a) 20 ÷ 10 ≠ 10 ÷ 20 i.e. 2 ≠ \(\frac { 1 }{ 2 }\)
(b) 100 ÷ 50 ≠ 50 ÷ 100 i.e. 2 ≠ \(\frac { 1 }{ 2 }\)
Question 3.
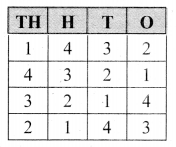
Complete the following tables.
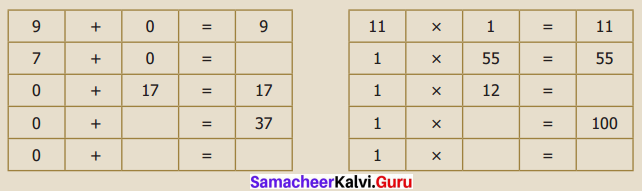
Solution:
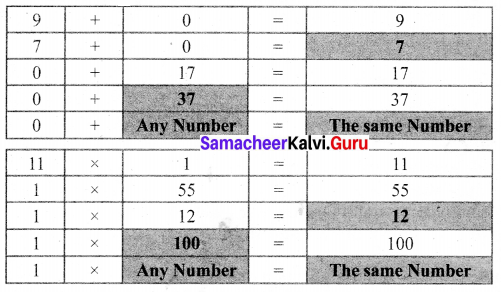
Question 4.
Complete the Table.
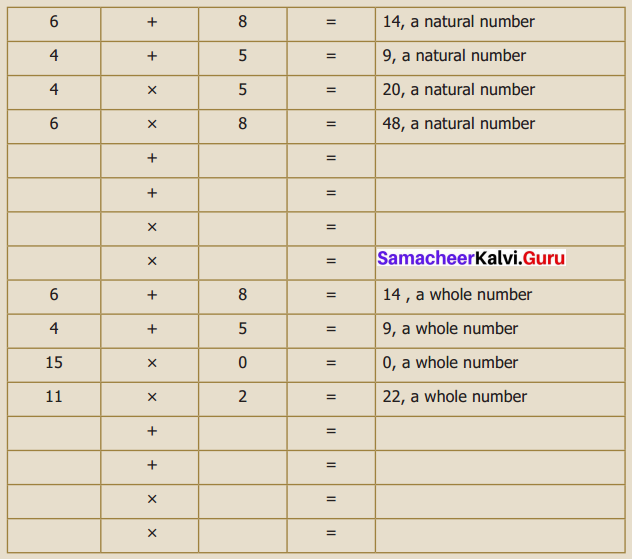
Solution:
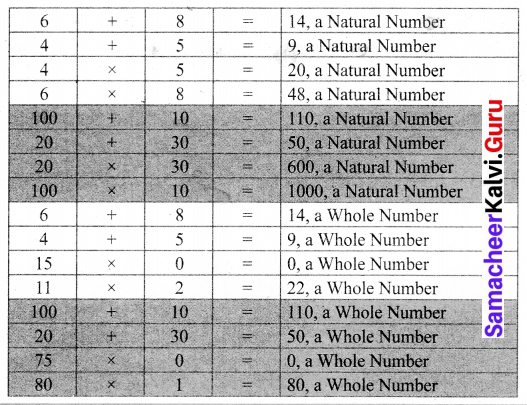
Question 5.
How will you read the large number given below?
731, 687, 303, 715, 884, 105, 727
Solution:
This is read as 731 quintillions, 687 quadrillions, 303 trillion, 715 billion, 884 million, 105 thousand, 727.
![]()