Prasanna

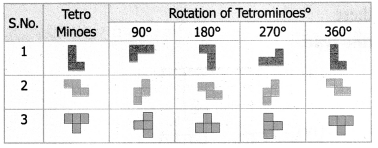
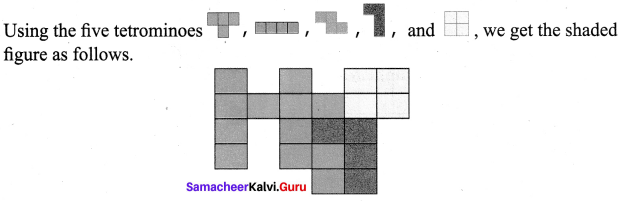
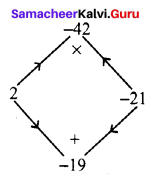
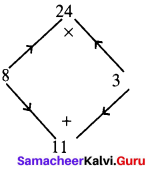
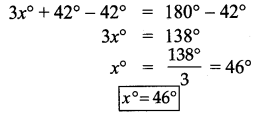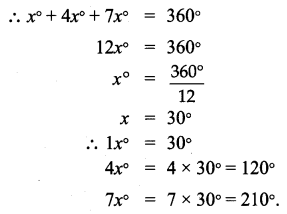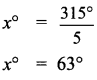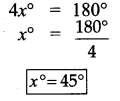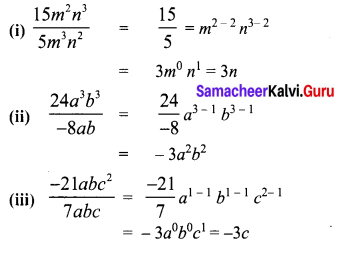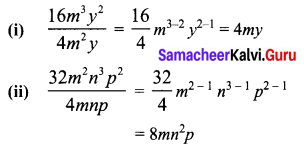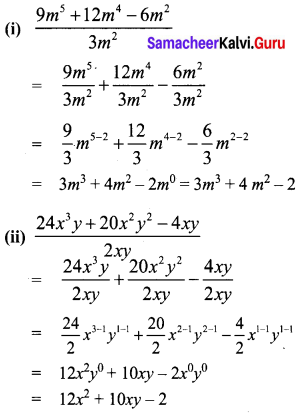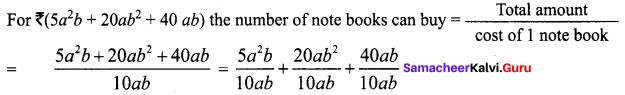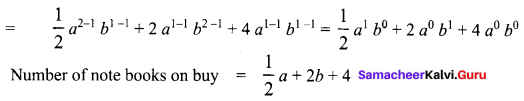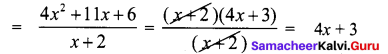Students can Download Maths Chapter 5 Geometry Ex 5.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.2

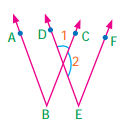
Question 1.
From the figures name pair of angles.

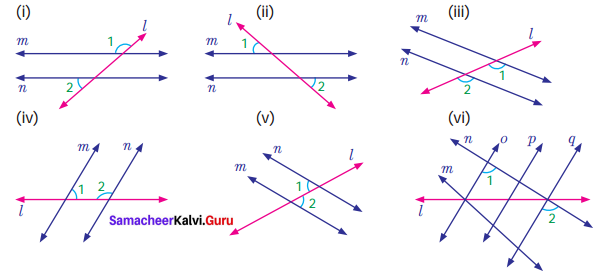
Solution:
(i) m and n are parallel lines and l is the transversal.
∴ ∠1 and ∠2 are exterior angles on the same side of the transversal.

(ii) m and n are parallel lines and l is the transversal
∠1 and ∠2 are alternate exterior angles.

(iii) m and n are parallel lines l is the transversal
∠1 and ∠2 are corresponding angles.

(iv) m and n are parallel lines l is the transversal.
∠1 and ∠2 are interior angles on the same side of the transversal.

(v) m and n are parallel lines and l is the transversal.
∠1 and ∠2 are alternate interior angles.

(vi) o and q are parallel lines and n is the transversal.
∠1 and ∠2 are corresponding angles.

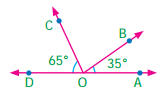
Question 2.
Find the measure of angle x in each of the following figures.

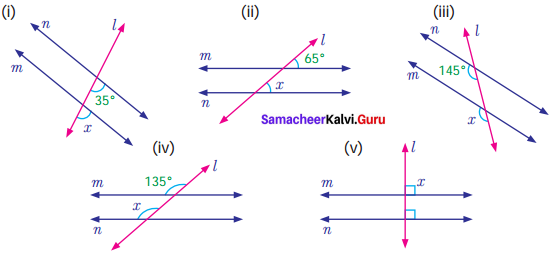
Solution:
(i) m and n are parallel lines and l is the transversal.
x° and 35° are corresponding angles and so they are equal.
∴ x = 35°

(ii) m and n are parallel lines and l is the transversal.
∴ x = 65°
[∴ corresponding angles are equal].

(iii) n and m are parallel lines and l is the transversal.
Corresponding angles are equal
∴ x = 145°

(iv) m and n are parallel lines and l is the transversal.
Corresponding angles are equal
∴ x = 135°

(v) m and n are parallel lines, l is the transversal perpendicular to both the lines
∴ x = 90°

Question 3.
Find the measure of angles in each of the following figures.

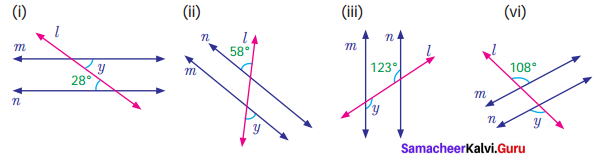
Solution:
(i) m and n are parallel lines. l is the transversal. Then alternate interior angles are equal
∴ y = 28°

(ii) m and n are parallel lines. l is the transversal. Alternate exterior angles are equal
∴ y = 58°

(iii) m and n are parallel lines. l is the transversal.
Alternate interior angles are equal
∴ y = 123°

(iv) m and n are parallel lines . l is the transversal
alternate exterior angles are equal.
∴ y = 108°

Question 4.
Find the measure of angle z in each of the following figures.

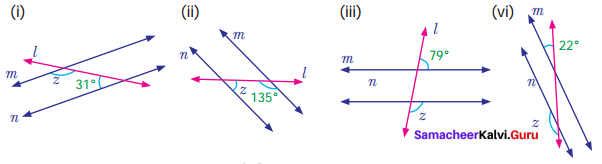
Solution:
(i) m and n are parallel lines l is the transversal
Then interior angles that lie on the same side of the transversal are supplementary
∴ z + 31° = 180°
z + 31° – 31° = 180° – 31°
z = 149°

(ii) m and n are parallel lines, l is the transversal
Interior angles that lie on the same side of the transversal are supplementary
∴ z + 135° = 180°
z + 135° – 135° = 180° – 135°
z = 45°

(iii) m and n are parallel lines l is the transversal exterior angles that lie on the same side of the transversal are supplementary.
∴ z + 79° = 80°
z + 79° – 79° = 180° – 79°
z = 101°

(iv) m and n are parallel lines and l is the transversal. Corresponding angles are equal
z + 22° = 180°
z + 22° – 22° = 180° – 22°
z = 158°

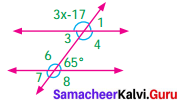
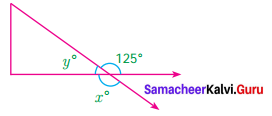
Question 5.
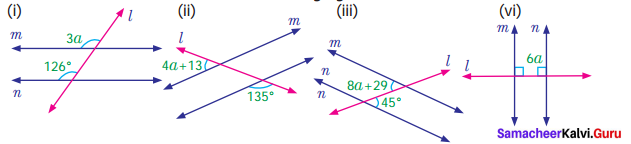
Find the value of angle ‘a’ in each of the following figures

Solution:
(i) m and n are parallel lines. l is the transversal
∴ Corresponding angles are equal

(ii) m and n are parallel lines l is the transversal
Exterior angles that lie on the same side of the transversal are supplementary
∴ (4a + 13) + 135° = 180°
4a + 13 + 135° = 180°
4a +148° = 180°
4a + 148° – 148° = 180° – 148°
4a = 32°

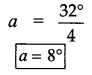
(iii) m and n are parallel lines l is the transversal
∴ Alternate interior angles are equal

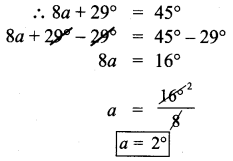
(iv) m and n are parallel lines l is the transversal which is perpendicular to m and n

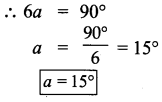
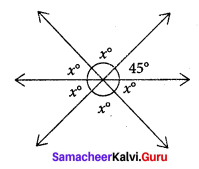
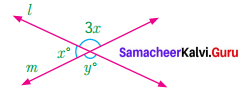
Question 6.
Find the value of the angle x in both the figures

Solution:
(i) m and n are parallel lines. l is the transversal
∴ Alternate interior angles are equal

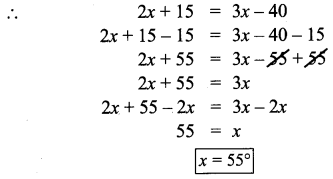
(ii) m and n are parallel lines. l is the transversal
Exterior angles on the same side of the transversal are supplementary

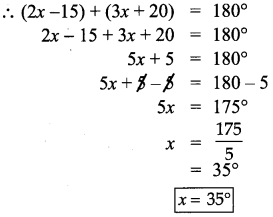
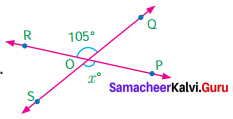
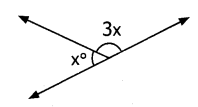
Question 7.
Anbu has marked the angles as shown below in (i) and (ii). Check whether both of them are correct. Give reasons

Solution:
(i) m and n are parallel lines. l is the transversal.
Interior angles on the same side of the transversal are supplementary. But here it is 75 + 75 ≠ 180°
105 + 105 ≠ 180°
∴ Angles marked are not correct

(ii) m and n are parallel lines. l is the transversal.
Corresponding angles must be equal. So here the marking is wrong.

Question 8.
Mention two real life situations where we use parallel lines.
Solution:
Two angles of a wall in a building Cross rods in a window.

Question 9.
Two parallel lines are intersected by a transversal. What is the minimum number of angles you need to know to find the remaining angles. Give reasons.
Solution:

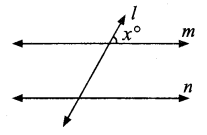
When two parallel lines are intersected by a transversal, we need a minimum of a single angle to find the remaining angle.
Using the concept of linear pair of angles, we can final one more angle.
By the concepts of corresponding angles, alternate interior angles and alternate , exterior angles we could find all other angles.

Objective Type Questions

Question 10.
A line which intersects two or more lines in different points is known as
(i) parallel lines
(ii) transversal
(iii) non-parallel lines
(iv) Intersecting lines
Solution:
(ii) Transversal

Question 11.
In the given figure angles a and b are
(i) alternate exterior angles
(ii) corresponding angles
(iii) Alternate interior angles
(iv) Vertically opposite angles
Solution:
(i) alternate exterior angles

Question 12.
Which of the following statement is ALWAYS TRUE when parallel lines are cut by a transversal
(i) corresponding angles supplementary
(ii) alternate interior angles supplementary
(iii) alternate exterior angles supplementary
(iv) interior angles on the same side of the transversal are supplementary
Solution:
(iv) Interior angles on the same side of the transversal are
supplementary.

Question 13.
In the diagram what is the value of angle x?
(i) 43°
(ii) 44°
(iii) 132°
(iv) 134°
Hint:

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 6 Information Processing Ex 6.2

Question 1.
In the following magic triangle, arrange the numbers from 1 to 6, so that you get the same sum on all its sides.

Solution:
Step 1: Complete the corners with smaller numbers 1, 2 and 3.

Step 2: The side having smallest numbers 1 & 2 are to be filled with the greatest number 6, the second smallest 1 & 3 side to be filled with the second largest 5 at the middle and so on.

The magic sum is 1 + 6 + 2 = 2 + 4 + 3 = 3 + 5 + 1 = 9. Some other ways are given below.

The magic sum = 1 + 6 + 3 = 3 + 2 + 5 = 5 + 4 + 1 = 10.

The magic sum 6 + 1 + 4 = 4 + 5 + 2 = 2 + 3 + 6 = 11.

The magic sum 4 + 3 + 5 = 5 + 1 + 6 = 6 + 2 + 4 = 12.

Question 2.
Using the numbers from 1 to 9
(i) Can you form a magic triangle?
(ii) How many magic triangles can be formed?
(iii) What are the sums of the sides of the magic triangle?

Solution:
(i) Yes, we can form
(ii) 5
(iii)


Sums are 17, 19, 20, 21 and 23.

Question 3.
Arrange the odd numbers from 1 to 17 without repetition to get a sum of 30 on each side of the magic triangle.

Solution:
The odd numbers between 1 to 17 are 1, 3, 5,7,9,11,13,15,17.
Step 1: Place the smaller numbers 1, 3, 5 on the comers.

Step 2: Arrange another set of smaller numbers 7, 9 and 11 on each side.

Step 3: Arrange the remaining numbers 13,15,17 to give the total 30.

Magic sum = 30.

Question 4.
Put the numbers 1, 2, 3, 4, 5, 6 and 7 in the circles so that each straight line of three numbers add up to the same total.

Solution:
Here there is even number of terms. Also we know that 1 + 6 = 7, 2 + 5 = 7, 3 + 4 = 7; so placing 7 at the centre, and the pairs (1, 6) (2, 5) and (3, 4) at. the opposite ends we get, the answer.

Question 5.
Place the number 1 to 12 in the 12 circles so that the sum of the numbers in each of the six lines of the star is 26. Use each number from 1 to 12 exactly once. Find more possible ways.

Solution:
The given star can be viewed as two magical triangular as.

Now the required arrangement is

Some other arrangements are

Students can Download Maths Chapter 1 Number System Ex 1.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 1 Number System Ex 1.5

Question 1.
One night in Kashmir, the temperature is -5°C. Next day the temperature is 9°C. What is the increase in temperature?
Solution:
Temperature in the first day = -5°C
Temperature in the next day = 9°C
∴ Increase in temperature = 9°C – (-5°C)
= 9°C + (+5°C) = 14°C

Question 2.
An atom can contain protons which have a positive charge (+) and electrons which have a negative charge (-). When an electron and a proton pair up, they become neutral (0) and cancel the charge at. Now determine the net charge:
(i) 5 electrons and 3 protons → -5 + 3 = -2 that is 2 electrons \(\ominus\ominus\)
(ii) 6 protons and 6 electrons →
(iii) 9 protons and 12 electrons →
(iv) 4 protons and 8 electrons →
(v) 7 protons and 6 electrons →
Solution:
(ii) 6 protons and 6 electrons → (+6) + (-6) = 0
(iii) 9 protons and 12 electrons → (+9) + (-12) = 9-12 = -3 ⇒ 3 electrons \(\ominus\ominus\ominus\)
(iv) 4 protons and 8 electrons → (+4) + (-8) = +4 – 8 = -4 ⇒ 4 electrons \(\ominus\ominus \ominus\ominus\)
(v) 7 protons and 6 electrons → (+7) + (-6) = +1 = 1 proton \(\oplus\)

Question 3.
Scientists use the Kelvin scale (K) as an alternative temperature scale to degrees Celsius (°C) by the relation T°C = (T + 273)K. Convert the following to Kelvin:
(i) -275°C
(ii) 45°C
(iii) -400°C
(iv) -273°C
Solution:
(i) -275°C = (-275 + 273)K = -2K
(ii) 45°C = (45 + 273)K = 318 K
(iii) -400°C = (-400 + 273)K = -127 K
(iv) -273°C = (-273 + 273) K = 0K

Question 4.
Find the amount that is left in the student’s bank account, if he has made the following transaction in a month. His initial balance is ₹ 690.
(i) Deposit (+) of ₹ 485
(ii) Withdrawal (-) of ₹ 500
(iii) Withdrawal (-) of ₹ 350
(iv) Deposit (+) of ₹ 89
(v) If another ₹ 300 was withdrawn, what would the balance be?
Solution:
(i) Initial balance of student’s account = ₹ 690
Deposited amount = ₹ 485 (+)
∴ Amount left in the account = ₹ 690 + ₹ 485 = ₹ 1175

(ii) Balance in the account = ₹ 1175
Amount withdrawn = ₹ 500 (-)
Amount left = ₹ 1175 – ₹ 500 = ₹ 675

(iii) Balance in the account = ₹ 675
Amount withdrawn = ₹ 350 (-)
Amount left = ₹ 675 – ₹ 350 = ₹ 325

(iv) Balance in the account = ₹ 325
Amount deposited = ₹ 89(+)
Amount left = ₹ 325 + ₹ 89 = ₹ 414

(v) Balance in the account = ₹ 414
Amount withdrawn = ₹ 300 (-)
Amount left = ₹ 414 – ₹ 300 = ₹ 114

Question 5.
A poet Tamizh Nambi lost 35 pages of his ‘lyrics’ when his file had got wet in the rain. Use integers, to determine the following.
(i) If Tamil Nambi wrote 5 pages per day, how many day’s work did he lose?
(ii) If four pages contained 1800 characters, (letters) how many characters were lost?
(iii) If Tamil Nambi is paid ₹ 250 for each page produced, how much money did he lose?
(iv) If Kavimaan helps Tamizh Nambi and they are able to produce 7 pages per day, how many days will it take to recreate the work lost?
(v) Tamizh Nambi pays Kavimann ₹ 100 per page for his help. How much money does Kavimaan receive?
Solution:
Total pages lost – 35
One day work = 5 page 35
35 pages = \(\frac{35}{5}\) = 7 days work
∴ 7 day’s work he lost.

(ii) Number of characters in four pages = 1800
Number of characters in one page = \(\frac{1800}{4}\) = 450
∴ Number of characters in 35 pages = 450 × 35 = 15,750 characters

(iii) Payment for one page = ₹ 250
∴ Payment for 35 pages = ₹ 250 × ₹ 35 = ₹ 8,750

(iv) Number of pages recreated a day = 7
∴ To recreate 35 pages day’s needed = \(\frac{35}{7}\) = 5 days

(v) Payment of Kavimaan = ₹ 100 per page
∴ for 35 pages payment = ₹ 100 × 35 = ₹ 3,500

Question 6.
Add 2 to me. Then multiply by 5 and subtract 10 and divide new by 4 and I will give you 15! Who am I?
Solution:
According to the problem {[(I + 2) × 5] – 10} ÷ 4 = 15
{[(I + 2) × 5] – 10} = 15 × 4 = 60
I + 2 = \(\frac{70}{5}\) = 14
(I + 2) × 5 = 60 + 10 = 70
I = 14 – 2 ; I = 12

Question 7.
Kamatchi, a fruit vendor sells 30 apples and 50 pomegranates. If she makes a profit of ? 8 per apple and loss ? 5 per pomegranate. What will be her overall profit or loss?
Solution:
Number of apples Kamatchi sold = 30
Profit per apple = ₹ 8(+)
∴ Profit for 30 apples = 30 × 8 = ₹ 240
Number of pomegranates sold 50
Loss per pomegranate = ₹ 5(-)
Loss on selling 50 pomegranates = 50 × (-5) = ₹ -250
Overall loss = -250 + 240 = ₹ -10
i.e. loss ₹ 10.

Question 8.
During a drought, the water level in a dam fell 3 inches per week for 6 consecutive weeks. What was the change in the water level in the dam at the end of this period?
Solution:
Water level fall per week = -3 inches
∴ Water level decrease for 6 weeks = 6 ₹ (-3) = 18 inches
∴ decrease of 18 inches of water level.

Question 9.
Buddha was born in 563 BC (BCE) and died in 483 BC (BCE). Was he alive in 500 BC (BCE)? and find his life time. (Source: Compton’s Encyclopedia)
Solution:
Years in BCC (BCE) are taken as negative integers.

Buddha was bom in -563
and died in -483
So he was alive in 500 BC (BCE)
Life time = -483 – (-563) = -483 + 563 = +80
Buddha’s life time = 80 years.

Students can Download Maths Chapter 5 Geometry Ex 5.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.1

Question 1.
Name the pairs of adjacent angles.
Solution:
(i) ∠ABG and ∠GBC are adjacent angles.
(ii) ∠BCF and ∠FCD are adjacent angles.
(iii) ∠BCF and ∠FCE are adjacent angles.
(iv) ∠FCE and ∠ECD are adjacent angles.

Question 2.
Find the angle ∠JIL from the given figure.
Solution:
∠LIK and ∠KIJ are adjacent angles.
∴ ∠JIL = ∠LIK + ∠KIJ
= 38° + 27°
= 65°
∴ ∠JIL = 65°

Question 3.
Find the angles ∠GEH from the given figure.
Solution:

∠HEF = ∠HEG + ∠GEF
120° = ∠HEG + 34°
120°- 34° = ∠GEH + 34° – 34°
∠GEH = 86°

Question 4.
Given that AB is a straight line. Calculate the value of x° in the following cases.

Solution:
(i) Since the angles are linear pair ∠AOC + ∠BOC = 180°
72° + x° = 180°
72° + x° – 12° = 180°- 72°
x° = 108°

(ii) Since the angles are linear pair
∠AOC + ∠BOC = 180°
3x + 42° = 180°

(iii) Since the angles are linear pair
∠AOC + ∠BOC = 180°
4x° + 2x° = 180°
6x° = 180°
x° = 180°

Question 5.
One angle of a linear pair is a right angle. What can you say about the other angle?
Solution:
If the angle are linear pair, then their sum is 180°.
Given one angle is right angle ie 90°.
∴ The other angle = 180° -90° = 90°
∴ The other angle also a right angle

Question 6.
If the three angles at a point are in the ratio 1 : 4 : 7, find the value of each angle?
Solution:
We know that the sum of angles at a point is 360°.
Given the three angles are in the ratio 1:4:7.
Let the three angles be 1x, 4x, 7x.

∴ The three angles are 30°, 120° and 210°.

Question 7.
Three are six angles at a point. One of them is 45° and the other five angles are all equal. What is the measure of all the five angles.
Solution:
We know that the sum of angles at a point is 360°.
One angle = 45°
Let the equal angles be x° each
∴ x° + x° + x° + x° + x° + 45° = 360°
5x° + 45° – 45° = 360° – 45°

5x° = 315°

∴ Measure of all 5 equal angles = 63°.

Question 8.
In the given figure, identify
(i) Any two pairs of adjacent angles.
(ii) Two pairs of vertically opposite angles.
Solution:
(i) (a) ∠PQT and ∠TOS are adjacent angles.
(b) ∠PQU and ∠UQR are adjacent angles.
(ii) (a) ∠PQT and ∠RQU are vertically opposite angles.
(b) ∠TQR and ∠PQU are vertically opposite angles.

Question 9.
The angles at a point are x°, 2x°, 3x°, 4x° and 5x°. Find the value of the largest angle?
Sum of angles at a point = 360°
∴ x° + 2x° + 3x° + 4x° + 5x° = 360°
15x° = 360°
x° = \(\frac{360^{\circ}}{15}\)
x° = 24°.
∴ The largest angle = 5x°
= 5 × 24° = 120°
The largest angle is 120°

Question 10.
From the given figure, find the missing angle.
Solution:
Lines \(\overleftrightarrow { RP }\) and \(\overleftrightarrow { SQ }\) are interesting at ‘O’

∴ Vertically opposite angles are equal.
∴ x = 105°
∴ Missing angle = 105°

Question 11.
Find the angles x° and y° in the figure shown.

Solution:
Consider the line m.
x° and 3x° are linear pair of angles
∴ x° + 3x° = 180°


x° = 45°
Also lines l and m intersects.
Vertically opposite angles are equal.
ie 3x° = y°
3 × 45° = y°
y = 135°
x° = 15° and
y° = 135°

Question 12.
Using the figure, answer the following questions.

(i) What is the measure of angle x°?
(ii) What is the measure of angle y°?
Solution:
From the figure x° and 125° are vertically opposite angles. So they are equal ie
ie x° = 125°
Also y° and 125° are linear pair of angles.
∴ y° + 125° = 180°
y° + 125° – 125° = 180°- 125°
y° = 55°
x° = 125°,
y° = 55°

Question 13.
Adjective angles have
(i) No common interior, no common arm, no common vertex.
(ii) One common vertex, one common arm, common interior
(iii) One common arm, one common vertex, no common interior.
(iv) One common arm, no common vertex, no common interior.
Solution:
(iii) one common arm, one common vertex, no common interior

Question 14.
In the given figure the angles ∠1 and ∠2 are
(i) Opposite angles
(ii) Adjacent angles
(iii) Linear angles
(iv) Supplementary angles

Solution:
(iii) Linear pair

Question 15.
Vertically opposite angles are
(i) not equal in measure
(ii) Complementary
(iii) supplementary
(iv) equal in measure
Solution:
(iv) equal in measure

Question 16.
The sum of all angles at a point is
(i) 360°
(ii) 180°
(iii) 90°
(iv) 0°
Solution:
(i) 360°

Question 17.
The measure of ∠BOC is
(i) 90°
(ii) 180°
(iii) 80°
(iv) 100°

Solution:
(iii) 80°

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 5 Statistics Intext Questions

Recap (Textbook Page No. 108)

Question 1.
Count the objects in the following figure and complete the table that follows :

From Fig 5.1 and the table, answer the following question.
(i) The total number of objects in the above picture is ______
(ii) The difference between the number of squares and the number of bats is ______
(iii) The ratio of the number of balls to the number of bats is _______
(iv) What are the objects equal in number?
(v) How many more balls are there than the number of bats?
Solution:
(i) 24
(ii) 0
(iii) \(\frac{8}{6}=\frac{4}{3}\)
(iv) Bat and Square
(v) 2 balls more

Students can Download Maths Chapter 6 Information Processing Ex 6.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 6 Information Processing Ex 6.1

Question 1.
A tetromino is a shape obtained by …… squares together.
Solution:
4

Question 2.
Draw a tetromino which passes symmetry ……..
Solution:

Question 3.
Complete the table.

Solution:

Question 4.
Shade the figure completely, by using five tetrominoes shapes only once.

Solution:

Question 5.

Solution:

More possible ways are the

Question 6.
Match the tetrominoes of same type.

Solution:

Question 7.
Using the given tetrominoes with numbers, compute the 4 × 4 magic square.

Solution:

(more possible ways are these)

Students can Download Maths Chapter 6 Information Processing Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 6 Information Processing Additional Questions

Question 1.
Form a 5 × 4 square shade the square completely by tetromino shapes.

Solution:

Question 2.
Shade the following figure using the five tetrominoes exactly once.

Solution:

Question 3.
Find the Shortest distance to reach the play ground from school.

Also find out all possible routes.
Solution:
Route 1: School ➝ Swimming pool ➝ canteen ➝ playground
Distance 9km + 2km + 10km = 21 km.
Route 2 : School ➝ canteen ➝ playground
Distance : 10 km + 10 km = 20 km.
Route 3 : School ➝ garden ➝ playground
Distance : 2 km + 20 km = 22 km.
Route 4 : School ➝ garden ➝ teashop ➝ playground
Distance : 2km + 17km + 2km = 21 km.
Route 5 : School ➝ Park ➝ teashop ➝ playground
Distance : 12 km + 12 km + 2 km = 24 km.
∴ Route 2 is the shortest distance.

Students can Download Maths Chapter 3 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Additional Questions

Additional Questions And Answers

Exercise 3.1

Very Short Answers [2 Marks]

Question 1.
Find the product of the following.
(i) (x, y)
(ii) (10x, 5y)
(iii) (2x², 5y²)
Solution:
(i) x × y = xy
(ii) 10x × 5y = (10 × 5) x × xy
= 50 xy
(iii) 2x² x 5y² = (2 x 5) x (x² + y²)
= 10x²y²

Short Answers [3 Marks]

Question 1.
Find the product of the following.
(i) 3ab² c³ by 5a³b²c
(ii) 4x²yz by \(\frac{3}{2}\) x²yz²
Solution:
(i) (3ab³c³) × (5a³b²c)
= (3 × 5)(a × a³ × b² × b² × c² × c)
= 15a¹⁺³.b²⁺².c³⁺¹ = 15a⁴b⁴c⁴

(ii) 4x²yz by \(\frac{3}{2}\) x²yz²
= (4 × \(\frac{3}{2}\)) × (x² × x² × y × y × z × z²)
= -6x²⁺² y¹⁺¹ x¹⁺² = -6x⁴y²z³

Long Answers [5 Marks]

Question 1.
Simplify (3x – 2) (x – 1) (3x + 5).
Solution:
(3x – 2) (x – 1) (3x + 5)
= {(3x – 2) (x – 1)} × (3x + 5) [∴Multiplication in associative]
= {3x (x – 1) – 2 x – 1)} × (3x + 5)
= (3x² – 3x – 2x + 2) × (3x + 5)
= (3x² – 5x + 2) (3x + 5)
= 3x² × (3x + 5) – 5x (3x + 5) + 2 (3x + 5)
= (9x³ + 15x²) + (-15x² – 25x) + (6x + 10)
= 9x³ + 15x² – 15x² – 25x + 6x + 10
= 9x³ – 19x + 10

Question 2.
Simplify (5 – x) (3 – 2x) (4 – 3x).
Solution:
(5 – x) (3 – 2x) (4 – 3x)
= {(5 – x)(3 – 2x)} × (4 – 3x) [∴ Multiplication in association]
= {5 (3 – 2x) -x (3 – 2x)} × (4 – 3x)
= (15 – 10x – 3x + 2x²) × (4 – 3x)
= (2x² – 13x + 15) (4 – 3x)
= 2x² × (4 – 3x) – 13x (4 – 3x) + 15 (4 – 3x)
= 8x³ – 6³ – 52x + 39x² + 60 – 45x
= -6x³ + 47x² – 97x + 60

Exercise 3.2

Very Short Answers [2 Marks]

Question 1.
Divide.
(i) 12x³y³ by 3x²y
(ii) -15a² bc³ by 3ab
(iii) 25x³y² by – 15x²y
Solution:

Short Answers [3 Marks]

Question 1.
Divide
(i) 15m²n³ by 5m²n²
(ii) 24a³b³ by -8ab
(iii) -21 abc² by 7 abc
Solution:

Question 2.
Divide
(i) 16m³y² by 4m²y
(ii) 32m² n³p² by 4mnp
Solution:

Long Answers [5 Marks]

Question 1.
Divide.
(i) 9m⁵ + 12m⁴ – 6m² by 3m²
(ii) 24x³y + 20x²y² – 4xy by 2xy
Solution:

Exercise 3.3

Question 1.
Evaluate:
(i) (2x + 3y)²
(ii) (2x – 3y)²
Solution:
(i) (2x + 3y)²
= (2x)² + 2 × (2x) × (3y) + (3y)²
[using (a + b)² = a² + 2ab + b²]
= 4x² + 12xy + 9y²

(ii) (2x – 3y)²
= (2x)² – 2(2x) (3y) + (3y)²
[∵ using (a – b)² = a² – 2ab + b²]
= 4x² – 12xy + 9y²

Short Answers [3 Marks]

Question 1.
Evaluate the following
(i) (2x – 3) (2x + 5)
(ii) (y – 7) (y + 3)
(iii) 107 × 103
Solution:
(i) (2x – 3) (2x + 5)
= (2x)² + (-3 + 5) (2x) + (-3) (5)
[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 2²x² + 2 × 2x + (-15)
= 4x² + 4x – 15

(ii) (y – 7) (y + 3)
= y² + (-7 + 3)y + (-7) (3)
[∵ (x + a)(x + b) = x² + (a + b)x + ab]
= y² – 4y + (-21) = y² – 4y – 21

(iii) 107 × 103
= (100 + 7) × (100+ 3)
= 100² + (7 + 3) × 100 +(7 × 3)
= 10000 + 10 × 100 + 21 = 10000 + 1000 + 21 = 11021

Long Answers [5 Marks]

Question 1.
If x + y = 12 and xy = 14 find x² + y².
Solution:
(x + y)² = x² + y² + 2xy
12² = x² + y² + 2 × 14
144 = x² + y² + 28
x² + y² = 144 – 28
x² + y² = 116

Question 2.
If 3x + 2y = 12 and xy = 6 find the value of 9x² + 4y².
Solution:
(3x + 2y)² = (3x)² + (2y)² + 2 (3x) (2y)
= 9x² + 4y² + 12xy
12² = 9x² + 4y² + 12 × 6
144 = 9x² + 4y² + 72
144 – 72 = 9x² + 4y²
∴ 9x² + 4y² = 72

Exercise 3.4

Question 1.
Factorize:
(i) 7(2x + 5) + 3 (2x + 5)
(ii) 12x³y⁴ + 16x²y⁵ – 4x⁵y²
Solution:
(i) 7(2x + 5) + 3 (2x + 5)
= (2x + 5) (7 + 3)
(ii) 12x³y⁴ + 16x²y⁵ – 4x⁵y²
= 4x²y² (3xy² + 4y³ – x³)

Short Answers [3 Marks]

1. Factorize
(i) 81a² – 121b²
(ii) x² + 8x + 16
Solution:
(i) 81a² – 121b²
= (9a)² – (11b)²
[∵ using a² – b² = (a + b)²]
= (9a + 11b) (9a – 11b)

(ii) x² + 8x + 16 = x² + 2 × x × 4 + 4²
[∵ using a² + 2ab + b² = (a + b)²]
= (x + 4)² = (x + 4)(x + 4)

Long Answers [5 Marks]

Question 1.
Factorize
(i) x² + 2xy + y² – a² + 2ab – b²
(ii) 9 – a⁶ + 2a³ – b⁶
Solution:
(i) x² + 2xy + y² – a² + 2ab – b².
= (x² + 2xy + y²) – (a² – 2ab + b²)
= (x + y)² – (a – b)²
= {(x + y) + (a – b)} {(x + y) – (a – b)}
= (x + y + a – b) (x + y – a + b)

(ii) a – a⁶ + 2a³b³ – b⁶
= 9 – (a⁶ – 2a³b³ + b⁶)
= 3² -{(a³)² – 2 × a³ × b³ + (b³)²}
= 3² – (a³ – 6³)²
= {3 + (a³ – b³)} {3 – (a³ – b³)}
= (3 + a³ – b³) (3 – a³ + b³)
= (a³ – b³ + 1){-a³ + b³ + 3)

Question 2.
Factorize
(i) 100 (x + y )² – 81 (a + b)²
(ii)(x + 1)² – (x – 2)²
Solution:
(i) 100 (x + y)² – 81 (a + b)²
= {10 (x + y)}² – {(a (a + b)}²
= {10 (x + y) + 9 (a + b)}
{10 (x + y) – 9(a + b)}
= (10x + 10y + 9a – 9b)}
(10x + 10y – 9a – 9b)

(ii) (x – 1)² – (x – 2)²
= {(x – 1 +(x – 2)}
{(x – 1) – (x – 2)}
= (2x – 3) – (x – 1 – x + 2)
= (2x – 3) × 1 = 2x – 3

Students can Download Maths Chapter 3 Algebra Ex 3.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.5

Miscellaneous Practice Problems

Question 1.
Subtract: -2(xy)² (y³ + 7x²y + 5) from 5y² (x²y³ – 2x⁴y + 10x²)
Solution:
5y² (x²y³ – 2x⁴y + 10x²) – [(-2)(xy)² (y³ + 7x²y + 5)]
= [5y² (x²y³) – 5y² (2x⁴y) + 5y² (10x²)] – [(-2)x²y² (y³ + 7x²y + 5)]
= (5y⁵5x² – 10x⁴y³ + 50x²y²)
= 5x²y⁵ – 10x⁴y³ + 50x²y² – [(-2x²y⁵) – 14x⁴y³ – 10x²y²]
= 5x²y⁵ – 10x⁴y³ + 50x²)y² + 2x² y⁵ + 14x⁴)y³ + 10x²)y²
= (5 + 2)x²y⁵ + (-10 + 14)x⁴y³ + (+50 + 10)x²y²
= 7x²y⁵ + 4x⁴y³ + 60x²y²

Question 2.
Multiply (4x² + 9) and (3x – 2).
Solution:
(4x² + 9) (3x – 2) = 4x²(3x – 2) + 9(3x – 2)
= (4x²)(3x) – (4x²)(2) + 9(3x) – 9(2) = (4 × 3 × x × x²) – (4 × 2 × x²) + (9 × 3 × x) – 18
= 12x³ – 8x² + 27x – 18 (4x³ + 9) (3x – 2) = 12x³ – 8x² + 27x – 18

Question 3.
Find the simple interest on Rs. 5a²b² for 4ab years at 7b% per annum.
Solution:

Question 4.
The cost of a note book is Rs. 10ab. If Babu has Rs. (5a²b + 20ab² + 40ab). Then how many note hooks can he buy?
Solution:
For ₹ 10 ab the number of note books can buy = 1.

Question 5.
Factorise : (7y² – 19y – 6)
Solution:
7y² – 19y – 6 is of the form ax² + bx + c where a = 7; b = -19; c = – 6

The product a × c = 7 × -6 = -42
sum b = – 19

The middle term – 19y can be written as – 21y + 2y
7y² – 19y – 6 = 7y² – 21y + 2y – 6
= 7y(y – 3) + 2(y – 3) = (y – 3)(7y + 2)
7y² – 19y – 6 = (y – 3)(7y + 2)

Challenging Problems

Question 6.
A contractor uses the expression 4x² + 11x + 6 to determine the amount of wire to order when wiring a house. If the expression comes from multiplying the number of rooms times the number of outlets and he knows the number of rooms to be (x + 2), find the number of outlets in terms of ‘x’ [Hint: factorise 4x² + 11x + 6]
Solution:
Given Number of rooms = x + 2
Number of rooms × Number of outlets = amount of wire.

Now factorising 4x² + 11x + 6 which is of the form ax² + bx + c with a = 4 b = 11 c = 6.
The product a × c = 4 × 6 = 24
sum b = 11


The middle term 11x can be written as 8x + 3x
∴ 4x² + 11x + 6 = 4x² + 8x + 3x + 6 = 4x (x + 2) + 3 (x + 2)
4x² + 11x + 6 = (x + 2) (4x + 3)
Now from (1) the number of outlets

∴ Number of outlets = 4x + 3

Question 7.
A mason uses the expression x² + 6x + 8 to represent the area of the floor of a room. If the decides that the length of the room will be represented by (x + 4), what will the width of the room be in terms of x ?
Solution:
Given length of the room = x + 4
Area of the room = x² + 6x + 8
Length × breadth = x² + 6x + 8

Question 8.
Find the missing term: y² + (-) x + 56 = (y + 7)(y + -)
Solution:
We have (x + a) (x + b) = x² + (a + b)x + ab
56 = 7 × 8 .
∴ y² + (7 + 8)x + 56 = (y + 7)(y + 8)

Question 9.
Factorise: 16p⁴ – 1
Solution:
16p⁴ – 1 = 2⁴p⁴ – 1 = (2²)²(p²)² – 1²
Comparing with a² – b² = (a + b)(a – b) where a = 2²p² and b = 1
∴ (2²p²)² – 1² = (2²p² + 1) (2²p² – 1) = (4p² + 1) (4p² – 1)
∴ 16p⁴ – 1 = (4p² + 1)(4p² – 1)(4p² + 1)(2²p² – 1²)
= (4p² + 1) [(2p)²– 1²] = (4p² + 1) (2p + 1)(2p – 1)
[∵ using a² – b² = (a + b) (a – b)]
∴ 16p⁴ – 1 = (4psup>2 + 1)(2p + 1)(2p – 1)

Question 10.
Factorise : x⁶ – 64y³
Solution:
x⁶ – 64y³ = (x²)³ – 4³y³ = (x²)³ – (4y)³
This is of the form a³ – b³ with a = x², b = 4y
a³ – b³ = (a – b)(a² + ab + b²)
(x²)³ – (4y)³ = (x² – 4y) [(x²)² + (x²)(4y) + (4y)²]
= (x² – 4y) [x⁴ + 4x²y + 16y²]
∴ x⁶ – 64y³ = (x² – 4y) [x⁴ + 4x²y + 16y²]

Students can Download Maths Chapter 1 Number System Ex 1.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 1 Number System Ex 1.3

Question 1.
Fill in the blanks.
(i) -80 × ____ = -80
(ii) (-10) × ____ = 20
(iii) 100 × ___ = -500
(iv) ____ × (-9) = -45
(v) ___ × 75 = 0
Solution:
(i) 1
(ii) -2
(iii) -5
(iv) 5
(v) 0

Question 2.
Say True or False:
(i) (-15) × 5 = 75
(ii) (-100) × 0 × 20 = 0
(iii) 8 × (-4) = 32
Solution:
(i) False
(ii) True
(iii) False

Question 3.
What will be the sign of the product of the following:
(i) 16 times of negative integers.
(ii) 29 times of negative integers.
Solution:
(i) 16 is an even interger.
If negative integers are multiplied even number of times, the product is a positive integer.
∴ 16 times a negative integer is a positive integer.

(ii) 29 times negative integer.
If negative integers are multiplied odd number of times, the product is a negative integer. 29 is odd.
∴ 29 times negative integers is a negative integer.

Question 4.
Find the product of
(i) (-35) × 22
(ii) (-10) × 12 × (-9)
(iii) (-9) × (-8) × (-7) × (-6)
(iv) (-25) × 0 × 45 × 90
(v) (-2) × (+50) × (-25) × 4
Solution:
(i) 35 × 22 = -770
(ii) (-10) × 12 × (-9) = (-120) × (-9) = +1080
(iii) (-9) × (-8) × (-7) × (-6) = (+72) × (-7) × (-6) = (-504) × (-6) = +3024
(iv) (-25) × 0 × 45 × 90 = 0 × 45 × 90 = 0 × 90 = 0
(v) (-2) × (+50) × (-25) × 4 = (-100) × -25 × 4 = 2500 × 4 = 10,000

Question 5.
Check the following for equality and if they are equal, mention the property.
(i) (8 – 13) × 7 and 8 – (13 × 7)
Solution:
Consider (8 – 13) × 7 = (-5) × 7 = -35
Now 8 – (13 × 7) = 8 – 91 = -83
∴ (8 – 13) × 7 ≠ 8 – (13 × 7)

(ii) [(-6) – (+8)] × (-4) and (-6) – [8 × (-4)]
Solution:
[(-6) – (+8)] × (-4) = [(-6) + (-8)] × (-4) = (-14) × (-4) = +56
Now (-6) – [8 × (-4)] = (-6) – (-32)
= (-6) + (+32) = +26
∴ [(-6) – (+8)] × (-4) ≠ (-6) – [8 × (-4)]

(iii) 3 × [(-4) + (-10)] and [3 × (-4) + 3 × (-10)]
Solution:
Consider 3 × [(-4) + (-10)] = 3 × -14 = -42
Now [3 × (-4) + 3 × (-10)] = (-12) + (-30) = -42
Here 3 × [(-4) + (-10)] = [3 × (-4) + 3 × (-10)]
It is the distributive property of multiplication over addition.

Question 6.
During summer, the level of the water in a pond decreases by 2 inches every week due to evaporation. What is the change in the level of the water over a period of 6 weeks?
Solution:
Level of water decreases a week = 2 inches.
Level of water decreases in 6 weeks = 6 × 2 = 12 inches

Question 7.
Find all possible pairs of integers that give a product of -50.
Solution:
Factor of 50 are 1, 2, 5, 10, 25, 50.
Possible pairs of integers that gives product -50:
(-1 × 50), (1 × (-50)), (-2 × 25), (2 × (-25)), (-5 × 10), (5 × (-10))

Objective Type Questions

Question 8.
Which of the following expressions is equal to -30.
(i) -20 – (-5 × 2)
(ii) (6 × 10) – (6× 5)
(iii) (2 × 5)+ (4 × 5)
(iv) (-6) × (+5)
Solution:
(iv) (-6) × (+5)
Hint:
(i) -20 + (10) = -10
(ii) 60 – 30 = 30
(iii) 10 + 20 = 30
(iv) (-6) × (+5) = – 30

Question 9.
Which property is illustrated by the equation: (5 × 2) + (5 × 5) = 5 × (2 + 5)
(i) commutative
(ii) closure
(iii) distributive
(iv) associative
Solution:
(iii) distributive

Question 10.
11 × (-1) = _____
(i) -1
(ii) 0
(iii) +1
(iv) -11
Solution:
(iv) -11

Question 11.
(-12) × (-9) =
(i) 108
(ii) -108
(iii) +1
(iv) -1
Solution:
(i) 108