Students can Download Maths Chapter 3 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Additional Questions
Additional Questions And Answers
Exercise 3.1
Very Short Answers [2 Marks]
Question 1.
Find the product of the following.
(i) (x, y)
(ii) (10x, 5y)
(iii) (2x2, 5y2)
Solution:
(i) x × y = xy
(ii) 10x × 5y = (10 × 5) x × xy
= 50 xy
(iii) 2x2 x 5y2 = (2 x 5) x (x2 + y2)
= 10x2y2
Short Answers [3 Marks]
Question 1.
Find the product of the following.
(i) 3ab2 c3 by 5a3b2c
(ii) 4x2yz by \(\frac{3}{2}\) x2yz2
Solution:
(i) (3ab3c3) × (5a3b2c)
= (3 × 5)(a × a3 × b2 × b2 × c2 × c)
= 15a1+3.b2+2.c3+1 = 15a4b4c4
(ii) 4x2yz by \(\frac{3}{2}\) x2yz2
= (4 × \(\frac{3}{2}\)) × (x2 × x2 × y × y × z × z2)
= -6x2+2 y1+1 x1+2 = -6x4y2z3
Long Answers [5 Marks]
Question 1.
Simplify (3x – 2) (x – 1) (3x + 5).
Solution:
(3x – 2) (x – 1) (3x + 5)
= {(3x – 2) (x – 1)} × (3x + 5) [∴Multiplication in associative]
= {3x (x – 1) – 2 x – 1)} × (3x + 5)
= (3x2 – 3x – 2x + 2) × (3x + 5)
= (3x2 – 5x + 2) (3x + 5)
= 3x2 × (3x + 5) – 5x (3x + 5) + 2 (3x + 5)
= (9x3 + 15x2) + (-15x2 – 25x) + (6x + 10)
= 9x3 + 15x2 – 15x2 – 25x + 6x + 10
= 9x3 – 19x + 10
![]()
Question 2.
Simplify (5 – x) (3 – 2x) (4 – 3x).
Solution:
(5 – x) (3 – 2x) (4 – 3x)
= {(5 – x)(3 – 2x)} × (4 – 3x) [∴ Multiplication in association]
= {5 (3 – 2x) -x (3 – 2x)} × (4 – 3x)
= (15 – 10x – 3x + 2x2) × (4 – 3x)
= (2x2 – 13x + 15) (4 – 3x)
= 2x2 × (4 – 3x) – 13x (4 – 3x) + 15 (4 – 3x)
= 8x3 – 63 – 52x + 39x2 + 60 – 45x
= -6x3 + 47x2 – 97x + 60
Exercise 3.2
Very Short Answers [2 Marks]
Question 1.
Divide.
(i) 12x3y3 by 3x2y
(ii) -15a2 bc3 by 3ab
(iii) 25x3y2 by – 15x2y
Solution:

Short Answers [3 Marks]
Question 1.
Divide
(i) 15m2n3 by 5m2n2
(ii) 24a3b3 by -8ab
(iii) -21 abc2 by 7 abc
Solution:
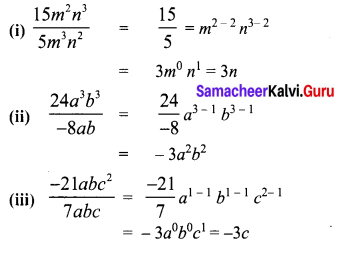
Question 2.
Divide
(i) 16m3y2 by 4m2y
(ii) 32m2 n3p2 by 4mnp
Solution:
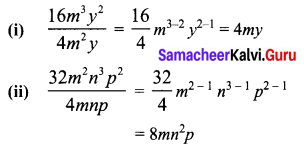
Long Answers [5 Marks]
Question 1.
Divide.
(i) 9m5 + 12m4 – 6m2 by 3m2
(ii) 24x3y + 20x2y2 – 4xy by 2xy
Solution:
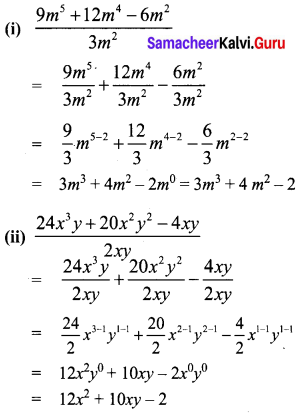
Exercise 3.3
Question 1.
Evaluate:
(i) (2x + 3y)2
(ii) (2x – 3y)2
Solution:
(i) (2x + 3y)2
= (2x)2 + 2 × (2x) × (3y) + (3y)2
[using (a + b)2 = a2 + 2ab + b2]
= 4x2 + 12xy + 9y2
(ii) (2x – 3y)2
= (2x)2 – 2(2x) (3y) + (3y)2
[∵ using (a – b)2 = a2 – 2ab + b2]
= 4x2 – 12xy + 9y2
Short Answers [3 Marks]
Question 1.
Evaluate the following
(i) (2x – 3) (2x + 5)
(ii) (y – 7) (y + 3)
(iii) 107 × 103
Solution:
(i) (2x – 3) (2x + 5)
= (2x)2 + (-3 + 5) (2x) + (-3) (5)
[∵ (x + a) (x + b) = x2 + (a + b)x + ab]
= 22x2 + 2 × 2x + (-15)
= 4x2 + 4x – 15
(ii) (y – 7) (y + 3)
= y2 + (-7 + 3)y + (-7) (3)
[∵ (x + a)(x + b) = x2 + (a + b)x + ab]
= y2 – 4y + (-21) = y2 – 4y – 21
(iii) 107 × 103
= (100 + 7) × (100+ 3)
= 1002 + (7 + 3) × 100 +(7 × 3)
= 10000 + 10 × 100 + 21 = 10000 + 1000 + 21 = 11021
![]()
Long Answers [5 Marks]
Question 1.
If x + y = 12 and xy = 14 find x2 + y2.
Solution:
(x + y)2 = x2 + y2 + 2xy
122 = x2 + y2 + 2 × 14
144 = x2 + y2 + 28
x2 + y2 = 144 – 28
x2 + y2 = 116
Question 2.
If 3x + 2y = 12 and xy = 6 find the value of 9x2 + 4y2.
Solution:
(3x + 2y)2 = (3x)2 + (2y)2 + 2 (3x) (2y)
= 9x2 + 4y2 + 12xy
122 = 9x2 + 4y2 + 12 × 6
144 = 9x2 + 4y2 + 72
144 – 72 = 9x2 + 4y2
∴ 9x2 + 4y2 = 72
Exercise 3.4
Question 1.
Factorize:
(i) 7(2x + 5) + 3 (2x + 5)
(ii) 12x3y4 + 16x2y5 – 4x5y2
Solution:
(i) 7(2x + 5) + 3 (2x + 5)
= (2x + 5) (7 + 3)
(ii) 12x3y4 + 16x2y5 – 4x5y2
= 4x2y2 (3xy2 + 4y3 – x3)
Short Answers [3 Marks]
1. Factorize
(i) 81a2 – 121b2
(ii) x2 + 8x + 16
Solution:
(i) 81a2 – 121b2
= (9a)2 – (11b)2
[∵ using a2 – b2 = (a + b)2]
= (9a + 11b) (9a – 11b)
(ii) x2 + 8x + 16 = x2 + 2 × x × 4 + 42
[∵ using a2 + 2ab + b2 = (a + b)2]
= (x + 4)2 = (x + 4)(x + 4)
Long Answers [5 Marks]
Question 1.
Factorize
(i) x2 + 2xy + y2 – a2 + 2ab – b2
(ii) 9 – a6 + 2a3 – b6
Solution:
(i) x2 + 2xy + y2 – a2 + 2ab – b2.
= (x2 + 2xy + y2) – (a2 – 2ab + b2)
= (x + y)2 – (a – b)2
= {(x + y) + (a – b)} {(x + y) – (a – b)}
= (x + y + a – b) (x + y – a + b)
(ii) a – a6 + 2a3b3 – b6
= 9 – (a6 – 2a3b3 + b6)
= 32 -{(a3)2 – 2 × a3 × b3 + (b3)2}
= 32 – (a3 – 63)2
= {3 + (a3 – b3)} {3 – (a3 – b3)}
= (3 + a3 – b3) (3 – a3 + b3)
= (a3 – b3 + 1){-a3 + b3 + 3)
Question 2.
Factorize
(i) 100 (x + y )2 – 81 (a + b)2
(ii)(x + 1)2 – (x – 2)2
Solution:
(i) 100 (x + y)2 – 81 (a + b)2
= {10 (x + y)}2 – {(a (a + b)}2
= {10 (x + y) + 9 (a + b)}
{10 (x + y) – 9(a + b)}
= (10x + 10y + 9a – 9b)}
(10x + 10y – 9a – 9b)
(ii) (x – 1)2 – (x – 2)2
= {(x – 1 +(x – 2)}
{(x – 1) – (x – 2)}
= (2x – 3) – (x – 1 – x + 2)
= (2x – 3) × 1 = 2x – 3