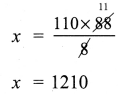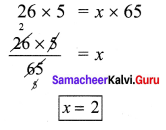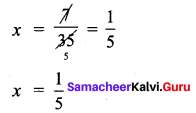Prasanna

Students can Download Maths Chapter 2 Measurements Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Additional Questions

Additional Questions and Answers

Exercise 2.1

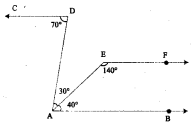
Question 1.
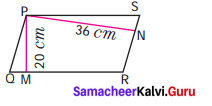
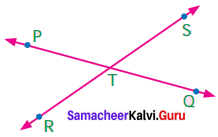
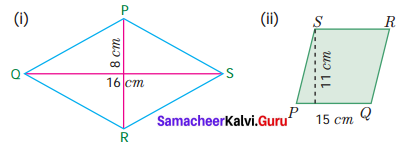
In the following figure, PQRS is a parallelogram find x and y.

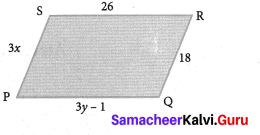
Solution:
We know that in a parallelogram opposite sides are equal.
∴ 3x = 18
x = \(\frac{18}{3}\)
x = 6 and
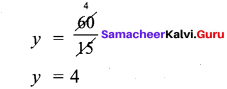
3y – 1 = 26
3y = 26 + 1 = 27
y = \(\frac{27}{9}\)
y = 9

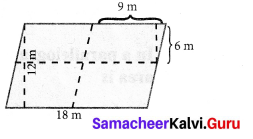
Question 2.
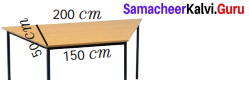
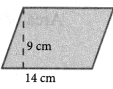
Two adjacent sides of a parallelogram are 5 cm and 7 cm respectively. Find its perimeter.
Solution:

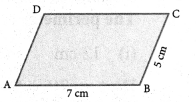
Perimeter = AB + BC + CD + AD [∵ AB = DC & AD = BC]
= 7 cm + 5 cm + 7 cm + 5 cm = 24 cm

Question 3.
The perimeter of a parallelogram is 150 cm. One of its sides is greater than the other by 25 cm. Find the length of the sides of the parallelogram.
Solution:

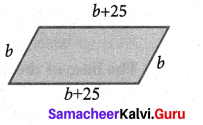
Given perimeter = 150 cm
Let one side of the parallelogram be ‘b’ cm
Then the other side = b + 25 cm
b + (b + 25) + b + (b + 25) = 150
b + b + 25 + b + b + 25 = 150
4h + 50 = 150 =4b = 100
b = \(\frac{100}{4}\) = 25
∴ One side b = 25 cm
Other side b + 25 = 50 cm

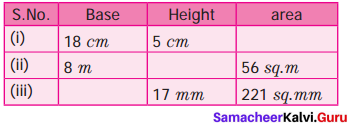
Exercise 2.2

Question 1.
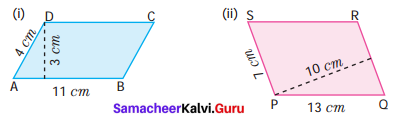
ABCD is a rhombus. Find x, y, and z.

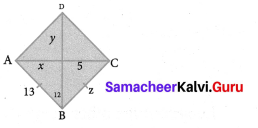
Solution:
We know that all sides of rhombus are equal and its diagonals bisect each other.
∴ x = 5, y = 12 and z = 13.

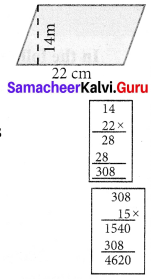
Question 2.
Find the altitude of the rhombus whose area is 315 cm² and its perimeter is 180 cm.
Solution:
Given perimeter of the rhombus = 180 cm
∴ One side of the rhombus = \(\frac{180}{4}\) = 45 cm
Given area of the rhombus = 315 cm²
b × h = 315
45 × h = 315 = \(\frac{315}{45}\)
h = 7 cm
Altitude of the rhombus = 7 cm

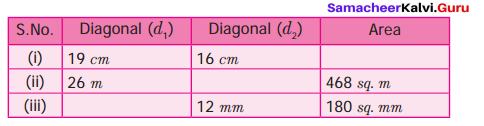
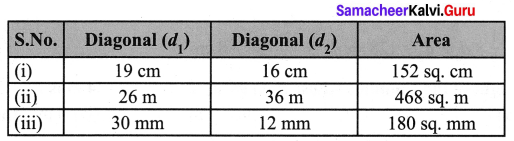
Question 3.
The floor of a building consists of 2000 titles which are rhombus shaped and each of its diagonals are 40 cm and 25 cm. Find the total cost of polishing the floor, if the cost per m² = ₹ 5.
Solution:
Area of each title = \(\frac{1}{2}\) × d₁ × d₂ sq. units
= \(\frac{1}{2}\) × 40 × 25 cm² = 500 cm²
∴ Area of 2000 titles = 500 × 20,000 = 10,000 cm² = 100 m²
Cost of polishing 1 m² = ₹ 5
∴ Cost of polishing 100 m² = 5 × 100 = ₹ 500

Students can Download Maths Chapter 4 Direct and Inverse Proportion Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 4 Direct and Inverse Proportion Intext Questions

Try These (Text Book Page No. 72)

Question 1.
Find the ratio of the number of circles to number of squares.

Solution:
Number of circles = 4 ;
Number of squares = 6
Number of circles : Number of squares = 4 : 6 = 2 : 3

Question 2.
Find the ratio (i) 555 g to 5 kg
(ii) 21 km to 175 m.
Solution:
(i) 1 kg = 1000 g
∴ 5 kg = 5000 g
∴ 555 g : 5 kg = 555 g : 5000 g = 111 : 1000

(ii) 21 km to 175m
1 km = 1000 m
21 km = 21 × 1000 = 21,000m
∴ 21 km : 175 m = 21000 : 175 = 120 : 1

Question 3.
Find the value of x in the following proportions :
(i) 110 8: 88
(ii) x : 26 :: 5: 65
Solution:
(i) Given 110 : x :: 8 : 88
Product of the means = Product of the extremes
x × 8 = 110 × 88

(ii) x : 26 :: 5 : 65
Product of the means = Product of the extremes

Try this (Text Book Page No. 74)

Question 1.
The number of chocolates to be distributed to the number of children. Is this statement in direct proportion?
Solution:
Let the number of students be x and the number of chocolates be y. As the valve of x increases also correspondingly increases.
ie \(\frac{x}{y}=k\)
∴ x and y are in direct proportion.

Try This (Text book Page No. 74)

Question 2.
Observe the following 5 squares of different sides given in the graph sheet.

The measures of the sides are recorded in the table given below. Find the corresponding perimeter and the ratios of each of these with the sides given and complete the table.

From the information so obtained state whether the side of a square is in direct proportion to the perimeter of the square.
Solution:
Perimeter of the square y = 4x, units where x is the side of a square

Completing the table

From the above table we find that as x increases y also increased in such a way that \(\frac{x}{y}=\frac{1}{4}\), constant.
∴ Side of a square is in direct proportion to the perimeter of the square.

Try this (Text book Page No. 75)

Question 3.
When a fixed amount is deposited for a fixed rate of interest, the simple interest changes proportionally with the number of years it is being deposited. Can you find any other examples of such kind.
Solution:
Some other examples of such kind are
(i) Cost of book and number of books
(ii) Distance and time to travel
(iii) Men workers and wages.

Exercise 4.2

Try this (Text book Page No. 78)

Question 1.
Think of an example in real life where two variable are inversely proportional.
Solution:
Example of inverse proportion are
(i) Men working and the amount of work.
(ii) Speed and time to travel

Try These (Text book Page No. 78)

Question 1.
Complete the table given below and find the type of proportion.

Solution:

Question 2.
Read the following examples and group them in two categories.

Solution:

Students can Download Maths Chapter 2 Measurements Ex 2.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.4

Miscellaneous Practice Problems

Question 1.
The base of the parallelogram is 16 cm and the height is 7 cm less than its base. Find the area of the parallelogram.
Solution:
In a parallelogram
Given base b = 16 cm; height h = base – 7 cm = 16 – 7 = 9 cm
Area of the parallelogram = (base × height) sq. units
= 16 × 9 cm² = 144 cm²
Area of the parallelogram = 144 cm²

Question 2.
An agricultural field is in the form of a parallelogram, whose area is 68.75 sq. hm. The distance between the parallel sides is 6.25 cm. Find the length of the base.
Solution:
Height of the parallelogram = 6.25 hm
Area of the parallelogram = 68.75 sq. hm
b × h = 68.75
b × 6.25 = 68.75
b = \(\frac{68.75}{6.25}=\frac{6875}{625}\) = 11 km
Length of the base = 11 km.

Question 3.
A square and a parallelogram have the same area. If the side of the square is 48m and the height of the parallelogram is 18 m. Find the length of the base of the parallelogram.
Solution:
Given side of the square is 48 m
Area of the square = (side × side) sq. unit = 48 × 48 m²
Height of the parallelogram = 18 m
Area of the parallelogram = ‘bh’ sq. units = b × 18 m²
Also area of the parallelogram = Area of the square
b × 18 = 48 × 48
b = \(\frac{{48} \times 48}{18 }\) = 8 × 16 = 128 m
Base of the parallelogram = 128 m

Question 4.
The height of the parallelogram is one fourth of its base. If the area of the parallelogram is 676 sq. cm, find the height and the base.
Solution:
Let the base of the parallelogram be ‘b’ cm
Given height = \(\frac{1}{4}\) × base ; Area of the parallelogram = 676 sq. cm
b × h = 676
b × \(\frac{1}{4}\)b = 676
b × b = 676 × 4
b × b = 13 × 13 × 4 × 4
b = 13 × 4 cm = 52 cm
Height = \(\frac{1}{4}\) × 52 cm = 13 cm
Height = 13 cm, Base 52 cm

Question 5.
The area of the rhombus is 576 sq. cm and the length of one of its diagonal is half of the length of the other diagonal then find the length of the diagonal.
Solution:
Let one diagonal of the rhombus = d₂ cm
The other diagonal d₂ = \(\frac{1}{2}\) × d₁ cm
Area of the rhombus = 576 sq. cm
\(\frac{1}{2}\) × (d₁ × d₂) = 576
\(\frac{1}{2}\) × (d₁ × \(\frac{1}{2}\) d₁) = 576
d₁ × d₁ = 576 × 2 × 2 = 6 × 6 × 4 × 4 × 2 × 2
d₁ × d₁ = 6 × 4 × 2 × 6 × 4 × 2
d₁ = 6 × 4 × 2
d₁ = 48 cm
d₂ = \(\frac{1}{2}\) × 48 = 24 cm
∴ Length of the diagonals d₁ = 48 cm and d₂ = 24 cm.

Question 6.
A ground is in the form of isoceles trapezium with parallel sides measuring 42 m and 36 m long. The distance between the parallel sides is 30 m. Find the cost of levelling it at the rate of ₹ 135 per sq. m.
Solution:
Parallel sides of the trapezium a = 42 m; b = 36 m
Also height h = 30 m
Area of the trapezium = \(\frac{1}{2}\) × h × (a + b) sq. unit
= \(\frac{1}{2}\) × 30 × (42 + 36) m²
= \(\frac{1}{2}\) × 30 × 78 m²
Area = 1,170 m²
Cost of levelling 1 m² = ₹ 135
∴ Cost of levelling 1170 m² = ₹ 1170 × 135 = ₹ 1,57,950
Cost of levelling the ground = ₹ 1,57,950

Challenge Problems

Question 7.
In a parallelogram PQRS (See the diagram) PM and PN are the heights corresponding to the sides QR and RS respectively. If the area of the parallelogram is 900 sq. cm and the length of PM and PN are 20 cm and 36 cm respectively, find the length of the sides QR and SR.

Solution:
Considering QR as base of the parallelogram height h₁ = 20 cm
Area of the parallelogram = 900 cm²
b₁ × h₁ = 900 ; b₁ × 20 = 900
b₁ = \(\frac{900}{20}\) = 45 cm
Again considering SR as base height = 36 cm ; Area = 900 cm²
b₂ × h₂ = 900 ; b₂ × 36 = 900
b₂ = \(\frac{900}{36}\)
b₂ = 25 cm
SR = 25 cm; QR = 45 cm ; SR = 25 cm

Question 8.
If the base and height of a parallelogram are in the ratio 7:3 and the height is 45 cm, then fixed the area of the parallelogram.
Solution:
Given base; height = 7 : 3
Let base = 7x cm
height = 3x cm
also given height = 45 cm
3x = 45 cm 45 .
x = \(\frac{45}{3}\) = 15
Now base = 7x cm = 7 × 15 cm = 105 cm
Area of the parallelogram = b × h sq. unit
= 105 × 45 = 4725 cm²
= 4725 cm²

Question 9.
Find the area of the parallelogram ABCD if AC is 24 cm and BE = DF = 8 cm.

Solution:
Area of the parallelogram ABCD Area of the triangle =Area of the triangle ABC + Area of the triangle ADC

Area of the parallelogram ABCD = 96 + 96 = 192 cm²

Question 10.
The area of the parallelogram ABCD is 1470 sq. cm. If AB = 49 cm and AD = 35 cm then, find the height, DF and BE.

Solution:
Area of the parallelogram = 1470 sq. cm
Considering AB = base = 49 cm
height = DF
Area = base × height
49 × DF = 1470
DF = \(\frac{1470}{49}\)
DF = 30 cm
Now considering AD as base
Base = AD = 35 cm ; height = BE
Base × Height = 1470
35 × BE = 1470 : BE = \(\frac{1470}{35}\)
BE = 42 cm ; DF = 30 cm ; BE = 42 cm

Question 11.
One of the diagonals of a rhombus is thrice as the other. If the sum of the length of the diagonals is 24 cm, then find the area of the rhombus.
Solution:
Let one of the diagonals of rhombus be ‘d₁’ cm and the other be d₂ cm.
Give d₁ = 3 × d₂
Also d₁ + d₂ = 24 cm
⇒ 3d₂ + d₂ = 24
4d₂ = 24
d₂ = \(\frac{24}{4}\)
d₂ = 6 cm
d₁ = 3 × d₂ = 3 × 6
d₁ = 18 cm
∴ Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq. units
= \(\frac{1}{2}\) × 18 × 6 cm² = 54 cm²
Area of the rhombus = 54 cm²

Question 12.
A man has to build a rhombus shaped swimming pool. One of the diagonal is 13 m and the other is twice the first one. Then find the area of the swimming pool and also find the cost of cementing the floor at the rate of ₹ 15 per sq. cm.
Solution:
Let the first diagonal d₁ = 13 m
d₂ = 2 × 13 m = 26 m
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq. units
= \(\frac{1}{2}\) × 13 × 26 m² = 169m²
Cost of cementing 1 m² = ₹ 15
Cost of cementing 169 m² = ₹ 169 × 15 = ₹ 2,535
Cost of cementing = ₹ 2,535

Question 13.
Find the height of the parallelogram whose base is four times the height and whose area is 576 sq. cm.
Solution:
Let the height be ‘A’ and base be ‘h’ units
Given b = 4 × h
Area of the parallelogram = 576 sq. cm
b × h = 576
4h × h = 576
h × h = \(\frac{576}{4}\) = 144
h × h = 12 × 12
h = 12 cm
Height = 12 cm; base = 4 × 12 = 48 cm

Question 14.
The table top is in the shape of a trapezium with measurements given in the figure. Find the cost of the glass used to cover the table at the rate of ₹ 6 per 10 sq. cm.

Solution:
Length of the parallel sides a = 200 cm
b = 150 cm
Height h = 50 cm
Area of the trapezium = \(\frac{1}{2}\) × h (a + b) sq. units
= \(\frac{1}{2}\) × 50 (200+ 150) cm²
= \(\frac{1}{2}\) × 50 × 350 cm² = 8750 cm²
Cost for 10 sq. cm glass = ₹ 68
∴ Cost of 8750 cm² glass = \(\frac{8750}{10}\) × 6 = ₹ 5250
Cost of glass used = ₹ 5,250

Question 15.
Arivu has a land ABCD with the measurements given in the figure. If a portion ABED is used for cultivation (where E is the midpoint of DC). D Find the cultivated area.

Solution:
From the figure given ABED is a trapazium with height h = 18 m
One of the parallel side a = 24 m
Since E is the midpoint of D.
Other parallel side b = \(\frac{24}{2}\) = 12 m
Area of the cultivated ADEB = \(\frac{1}{2}\) × h(a + b) m² = \(\frac{1}{2}\) × 18 (24 + 12)
= 9 × 36 m² = 324 m²
Area of cultivation = 324 m²

Students can Download Maths Chapter 6 Information Processing Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 6 Information Processing Intext Questions

Exercise 6.1

Try this (Text book Page No. 111)

Question 1.
Use the given five tetrominoes only once and create the shape given below.

Solution:
Using the given five tetrominoes in the proper places we can make the given shape as follows.

Try these (Text Book Page No. 113)

Question 1.
Complete the rectangle given below using five tetrominoes only once

Solution:
The given rectangle is halfly filled with the five tetrominoes.
Using the five tetrominoes only once we can fill the rectangles as follows:

Question 2.

Solution:

Exercise 6.2

Try these (Text Book Page No. 119)

Question 1.
Observe the pictures and answer the following.
(i) Find all the possible routes from house to school via fire station.
(ii) Find all the possible routes between central park and school with distance. Mention the shortest route?
(iii) Calculate the shortest distance between bank and school.
Solution:
(i) (a) House ➝ Fire station ➝ Library ➝ Central Park ➝ Hotel ➝ Fruit shop ➝ School.
(b) House ➝ Fire station ➝ Library ➝ Fruit shop ➝ School.
(c) House ➝ Fire station ➝ Library ➝ School.

(ii) Possible routes between Central park and school and their distances are
(a) School ➝ Fruit shop ➝ Hotel ➝ Central park.
Distance ➝ (150 + 300 + 100)m = 550 m

(b) School ➝ Fruit shop ➝ Library ➝ Central park Distance ➝(150 + 100 + 200)m
= 450 m

(c) School ➝ Library ➝ Central park
Distance = (20 + 200 m)
= 220 m

(d) School ➝ Library ➝ Fire station ➝ House ➝ central park Distance = (20 + 50 + 300 + 150) m
= 520 m

(e) School ➝ Emit shop ➝ Hotel ➝ Bank ➝ House ➝ Central park
Distance ➝ (150 + 300 + 150 + 200 + 150) m
= 950 m

(f) School ➝ fruit shop ➝ Hotel ➝ Bank ➝ House ➝ Fire station ➝ Library ➝ central park
Distance = (150 + 300 + 150 + 200 + 300 + 50 + 200)m = 1350 m
∴ Route (c) is the shortest path (i.e.,) School ➝ Library ➝ Central park

(iii) Shortest distance between school and Bank is calculated as follows Bank ➝ Hotel ➝ Central park ➝ Library ➝ school.
Distance = (150 + 100 + 200 + 20)m
= 470 m

Question 2.
A School has planned for a trip to Ooty. Using the route map, the school decides to visit the places such as Boat House Adam Fountain and Botanical Garden.

(i) How much distance you have to travel to Botanical Garden from Ooty Boat House?
(ii) Find the shortest route to Botanical from the Ooty main Bus stand.
(iii) Mention the direction of Botanical Garden from Adam Foundation.
(iv) In what direction, Ooty Boat House is situated from Ooty Main Bus Stand. Complete the following route map from Ooty Main Bus Stand to Botanical Garden.

Solution:
(i) (a) 700 m + 8.1 km = 700 m + (8 km + 100 m) = 8 km + 800 m = 8.8 km
(b) 700 m+ 1.7 km + 1.5 km = 700 m + (1 km, 700 m) + 1 km 500 m
= 2 km + 1900 m
= 2 km + 1 km + 900 m
= 3 km + 900 m
= 3.9 km
From the Ooty Boat House, the Botanical Garden is at a distance of 3.9 km(shortest)

(ii) The route from Botanical Garden from Ooty main Bus stand are
(a) Ooty main Bus stand ➝ Boat house ➝ Government Botanical garden Distance 1.5 km + 8.1 km + 700 m
= 1 km 500 m + 8 km 100 m + 700 m
= 9 km 1300 m
= 9 km + 1 km +300 m
= 10 km 300 m
= 10.3 km.

(b) Another route.
Ooty Main Bus stand ➝ Adam Fountain ➝ Botanical garden.
Distance = 1.7 + 700 m
= 1 Km 700 m + 700m
= 1 Km 1400 m
= 1 Km+ 1 Km 400 m
= 2 Km 400 m
= 2.4Km
∴ Shortest Route is Ooty main Bus stand ➝ Adams Foundation ➝ Botanical garden

iii. Botanical garden is north of Adam Foundation.

iv. Ooty Boat House is situated to the west of Ooty main bus bus stand.

v.

Students can Download Maths Chapter 3 Algebra Ex 3.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.2

Question 1.
Fill in the blanks
(i) The addition of – 7b and 2b is _______
(ii) The subtraction of 5m from -3m is ______
(iii) The additive inverse of -37xyz is _____
Solution:
(i) -5b
(ii) -8m
(iii) 37xyz

Question 2.
Say True or False
(i) The expressions 8x + 3y and 7x + 2y cannot be added
(ii) If x is a natural number, then x + 1 is its predecessor.
Hint: x – 1 is its predecessor.
(iii) Sum of a – b + c and -a + b – c is zero
Solution:
(i) False
(ii) False
(iii) True

Question 3.
Add: (i) 8x, 3x
(ii) 7mn, 5mn
(iii) -9y, 11y, 2y
Solution:
(i) 8x + 3x = (8 + 3) x = 11x
(ii) 7mn + 5mn = (7 + 5)mn = 12mn
(iii) -9y + 11y + 2y =(-9 + 11 + 2 )y = (2 + 2)y = 4y

Question 4.
Subtract:
(i) 4k from 12k
(ii) 15q from 25q
(iii) 7xyz from 17xyz
Solution:
(i) 4k from 12k
12k – 4k = (12 – 4) k = 8k
(ii) 15q from 25q
25q – 15q = (25 – 15)q = 10q
(iii) 7xyz from 17xyz
17xyz – 7xyz = (17 – 7)xyz = 10xyz

Question 5.
Find the sum of the following expressions
(i) 7p + 6q, 5p – q, q + 16p
Solution:
(7p + 6q) + (5p – q) + (q + 16p) = 7p + 6q + 5p – q + q + 16p
= (7p + 5p + 16p) + (6q – q + q)
= (7 + 5 + 16) p + (6 – 1 + 1) q
= (12 + 16) p + 6q = 28p + 6q

(ii) a + 5b + 7c, 2a + 106 + 9c
Solution:
(a + 5b + 7c) + (2a + 10b + 9c) = a + 5b + 7c + 2a + 10b + 9c
= a + 2a + 5b + 10b + 7c + 9c
= (1 + 2)a + (5 + 10)b + (7 + 9)c
= 3a + 15b + 16c

(iii) mn + t, 2mn – 2t, – 3t + 3mn
Solution:
(mn + t) + (2mn – 2t) + (-3t + 3mn)
= mn + t + 2mn – 2t + (-3t) + 3mn
= (mn + 2mn + 3mn) + (t – 2t – 3t)
= (1 + 2 + 3) mn + (1 – 2 – 3) t
= 6mn + (1 – 5)t
= 6mn + (- 4) t
= 6mn – 4t

(iv) u + v, u – v, 2u + 5v, 2u – 5v
Solution:
(u + v) + (u – v) + (2u + 5v) + (2u – 5v)
= u + v + u – v + 2u + 5v + 2u – 5v
= u + u + 2u + 2u + v – v + 5v – 5v
= (1 + 1 + 2 + 2) u +(1 – 1 + 5 – 5)v = 6u + 0v
= 6u

(v) 5xyz – 3xy, 3zxy – 5yx
Solution:
5xyz – 3xy + 3zxy – 5yx = 5xyz + 3xyz – 3xy – 5xy
= (5 + 3) xyz + [(-3) + (-5)] xy = 8xyz + (-8) xy
= 8xyz – 8xy

Question 6.
Subtract
(i) 13x + 12y – 5 from 27x + 5y – 43
Solution:
27x + 5y – 43 – (13x + 12y – 5) = 27z + 5y – 43 + (-13x – 12y + 5)
= 27x + 5y – 43 – 13x – 12y + 5
= (27 – 13) x + (5 – 12)y + (- 43) + 5
= 14x + (- 7) y + (- 38) = 14x – 7y – 38

(ii) 3p + 5 from p – 2q + 7
Solution:
p – 2q + 7 – (3p + 5) = p – 2q + 7 + (- 3p – 5)
= p – 2q + 7 – 3p – 5 = p – 3p – 2q + 7 – 5
= (1 – 3)p – 2q + 2 = -2p – 2q + 2

(iii) m + n from 3m – 7n
Solution:
3m – 7n – (m + n) = 3m – 7n + (-m – n)
= 3m – 7n – m – n = (3m – m) + (-7n – n)
= (3 – 1 )m + (-7 – 1) n = 2m + (-8) n
= 2m – 8n

(iv) 2y + z from 6z – 5y
Solution:
6z – 5y – (2y + z) = 6z – 5y + (-2y – z)
= 6z – 5y – 2y – z = 6z – z – 5y – 2y
= (6 – 1) z + (-5 -2) y = 5z + (-7) y
= 5z – 7y = -7y + 5z

Question 7.
Simplify
(i) (x + y – z) + (3x – 5y + 7z) – (14x + 7y – 6z)
Solution:
(x + y – z) + (3x – 5y + 7z) – (14x – 7y – 6z)
= (x + y – z) + (3x – 5y + 7z) + (-14x – 7y + 6z)
= (x + 3x – 14x) + (y – 5y – 7y) + (-z + 7z + 6z)
= (1 + 3 – 14) x + (1 – 5 – 7)y + (-1 + 7 + 6) z
= – 10x – 11y + 12z

(ii) p + p + 2 + p + 3 + p – 4 – p – 5 + p + 10
Solution:
p + p + 2 + 3 – p – 4 – p – 5 + p + 10 = (p + p + p – p – p + p) + (2 + 3 – 4 – 5 + 10)
= (1 + 1 + 1 – 1 – 1 + 1) p + 6 = 2p + 6

(iii) n + (m + 1) + (n + 2) + (m + 3) + (n + 4) + (m + 5)
Solution:
n + (m + 1) + (n + 2) + (m + 3) + (n + 4) + (m + 5)
= n + m + 1 + n + 2 + m + 3 + n + 4 + m + 5
= n + n + n + m + m + m + 1 + 2 + 3 + 4 + 5
= (1 + 1 + 1)n + (1 + 1 + 1)m + 15
= 3n + 3m + 15 = 3m + 3n + 15

Objective Type Questions

Question 8.
The addition of 3mn, -5mn, 8mn and – 4mn is
(i) mn
(ii) – mn
(iii) 2mn
(iv) 3mn
Solution:
(iii) 2mn
Hint: = 3 mn + 8mn – 5 mn – 4 mn = 11 mn – 9 mn = 2 mn

Question 9.
When we subtract ‘a’ from ‘-a’, we get ______
(i) a
(ii) 2a
(iii) -2a
(iv) -a
Solution:
(iii) -2a
Hint: – a – a = – 2a

Question 10.
In an expression, we can add or subtract only _____
(i) like terms
(ii) unlike terms
(iii) all terms
(iv) None of the above
Solution:
(i) like terms

Students can Download Maths Chapter 4 Direct and Inverse Proportion Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 4 Direct and Inverse Proportion Additional Questions

Exercise 4.1

Question 1.
The amount of extension in an elastic spring varies directly as the weight hung on it. If a weight of 150 gm produces an extension of 2.9 cm, then what weight would produce an extension of 17.4 cm?
Solution:
To produce 2.9 cm extension weight needed = 150 gm

Question 2.
Reeta types 540 words during half on hour. How many words would she type in 12 minutes?
Solution:
In \(\frac{1}{2}\) an hour number of words typed = 540
i.e., In 30 min No. of words typed = 540

= 18
In 12 minutes number of words typed = 18 × 12
= 216
216 words can be typed in 12 min

Question 3.
A call taxi charges ₹ 130 for 100 km. How much would one travel for ₹ 390?
Solution:

Exercise 4.2

Question 1.
In the following table find out x and y vary directly or inversely?

Solution:
From the table itself we observe that as x increases y decreases.
∴ x and y are inversely proportional
∴ xy = 8 × 32 = 16 × 16 = 32 × 8 = 256 × 1 = 256

Question 2.
If x and y vary inversely as each other and x = 10 when y = 6. Find y when x = 15.
Solution:
Since x and y vary inversely as each other
xy = constant
10 × 6 = 15 xy
60 = 15y

Question 3.
If x and y vary inversely and if y = 35 find x when constant of variation is 7.
Solution:
Given x andy are inversely proportional
xy = constant
when y = 35 and constant = 7 ; x × 35 = 7

Exercise 4.3

Question 1.
Sumathi sweeps 600 m long road in 2\(\frac{1}{2}\) hrs. Ramani sweeps \(\frac{2}{3}\) rd of same road in 1\(\frac{1}{2}\) hrs. Who sweeps more speedily?
Solution:

Question 2.
Suma weaves 25 baskets in 35 days. In how many days will she weave 110 baskets?
Solution:

Students can Download Maths Chapter 5 Geometry Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Intext Questions

Exercise 5.1

Recap
Try These (Text book Page No. 83)

Question 1.
Complete the following statements.
(i) A Line is a straight path that goes on endlessly in two directions.
(ii) A Line segment is a line with two end points.
(iii) A Ray is a straight path that begins at a point and goes on and extends endlessly the other direction.
(iv) The lines which intersect at right angles are Perpendicular lines.
(v) The lines which intersect each other at a point are called Intersecting lines.
(vi) The lines that never intersect are called Parallel lines.

Question 2.
Use a ruler or straightedge to draw each figure.

Question 3.
Look at the figure and answer the following questions.
(i) Which line is parallel to AB.
(ii) Name a line which intersect CD.
(iii) Name the lines which are perpendicular to GH
(iv) How many lines are parallel to IJ
(v) Will EF intersect AB? Explain.

Solution:
\(\overleftrightarrow { GH } \) is parallel to \(\overleftrightarrow { AB } \)
(ii) \(\overleftrightarrow { IJ } \) and \(\overleftrightarrow { KL } \) intersect \(\overleftrightarrow { CD } \)
(iii) \(\overleftrightarrow { IJ } \) and \(\overleftrightarrow { KL } \) are perpendicular to \(\overleftrightarrow { GH } \)
(iv) Only one line \(\overleftrightarrow { KL } \) is parallel to \(\overleftrightarrow { IJ } \)
(v) Yes, \(\overleftrightarrow { EF } \) will intersect \(\overleftrightarrow { AB } \) at some point.

Try These (Text Book Page No. 85)

Choose the correct answer

Question 1.
A straight angle measures
(a) 45°
(b) 90°
(c) 180°
(d) 100°
Solution:
(c) 180°
Solution:
No, they are not adjacent pairs.

Question 2.
An angle with measure 128° is called ___ angle.
(a) a straight
(b) an obtuse
(c) an acute
(d) Right
Solution:
(b) an obtuse

Question 3.
The corner of the A4 paper has
(a) An acute angle
(b) A right angle
(c) Straight
(d) An obtuse angle
Solution:
(b) a right angle

Question 4.
If a perpendicular line is bisecting the given line, you would have two
(a) right angles
(b) obtuse angles
(c) acute angles
(d) reflex angles
Solution:
(a) right angle

Question 5.
An angle that measure 0° is called
(a) right angle
(b) obtuse angle
(c) acute angle
(d) Zero angle.
Solution:
(d) Zero angle

Try this (Text Book Page No. 86)

Question 1.
In each of the following figures, observe the pair of angles that are marked as ∠1 and ∠2. Do you think that they are adjacent pairs? Justify your answer.

Solution:
No, they are not adjacent pairs.
In (i) and (ii) angles ∠1 and ∠2 have no common vertex.
In (iii) the interiors of ∠1 and ∠2 overlaps.
∴ they are not adjacent angles.

Try these (Text book Page No. 87)

Question 1.
Few real life examples depicting adjacent angles are shown below.

Can you give three more examples of adjacent angles seen in real life?
Solution:

(i) Angles between leaf veins. [ ∠1 and ∠2],
(ii) Angles between adjacent pages of a book, when it is open [ ∠1 and ∠2 ].
(iii) Adjacent angles of scissors [ ∠1 and ∠2 ]

Question 2.
Observe the six angles marked in the picture shown. Write any four pairs of adjacent angles and that are not.
Solution:
Four pairs of adjacent angles are
1. ∠A and ∠B
2. ∠B and ∠C
3. ∠C and ∠D
4. ∠D and ∠E

Four pairs of non adjacent angles are.
1. ∠A and ∠C
2. ∠C and ∠F
3. ∠E and ∠D
4. ∠A and ∠F

Question 3.
Identify the common arm, common vertex of the adjacent angles and shade the interior with two colours in each of the following figures.

Solution:

(ii)

Solution:

Question 4.
Name the adjacent angles in each of the following figure.

Solution:
(i) ∠BAC and ∠CAD are adjacent angles.
(ii) ∠XWY and ∠YWZ are adjacent angles.

Try These (Text Book Page No. 88)

Question 1.
Observe the following pictures and find the other angles of the linear pair.

Solution:
(i) Given one angle 84°
∴ Other angle of the linear pair is 180° – 84° = 96°

(ii) One angle is given as 86°
Other angle of linear pair is 180° – 86° = 94°

(iii) Given one angle = 159°
Other angle of the linear pair = 180° – 159° = 21°

Try this (Text book Page No. 88)

Question 1.
Observe the figure. There are two angles namely ∠PQR = 150° and ∠QPS = 30° Is all this pair of supplementary angles a linear pair? Discuss

Solution:
Given ∠PQR =150°
∠QPS = 30°
They are supplementary angles,
But they are not adjacent angles as they don’t have common vertex or common arm.
∴ They are not a linear pair.

Try this (Text book Page No. 90)

Question 1.
What would happen to the angles if we add 3 or 4 or 5 rays on a line as given below?

Solution:
New adjacent angles are formed.
The new angles become smaller in measure. But their sum is 180° as it is a linear angle.

Try this (Text book Page No. 90)

Question 1.
Can you justify the statement
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOF + ∠FOA = 360°?

Solution:
We know that the sum of angles at a point is 360°
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOF + ∠FOA = 360° as they are the sum of angles at the point ‘O’

Try These (Text book Page No. 91)

Question 1.
Four real life examples of vertically opposite angles are given below.

Solution:
(i) The four angles made in the scissors where the opposite angles are always equal.
(ii) The point where two roads intersect each other.
(iii) Rail road crossing signs.
(iv) An hourglass.

Question 2.
In the given figure two lines \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { CD } \) intersect at ‘O’. Observe the pair of angles and complete the following table. One is done for you.

Solution:

Question 3.
Name the two pairs of vertically opposite angles

Solution:
∠PTS and ∠QTR are vertically opposite angles.
∠PTR and ∠QTS are vertically opposite angles.

Question 4.
Find the value of x° in the figure given below.

Solution:
Lines l and m intersect at a point and making a pair of vertically opposite angles x° and 150°.
We know that vertically opposite angles are equal.
x = 150°

Exercise 5.2

Try this (Text book Page No. 93)

Question 1.
For a given set of lines, it is possible to draw more than one transversal.

Solution:
Yes, it is possible to draw more than one transversal for a given set of lines. l and m are given set of lines. n and p are transversal

Try these (Text Book Page No 94)

Question 1.
Draw as many possible transversals in the given figures.

Solution:

(i) a, b, c are transversal to l, m and n.
(ii) a, b, c are transversal to l, m, n and p. More transversals can be drawn.

Question 2.
Draw a line which is not the transversal to the above figures.
Solution:

Question 3.
How many transversals can you draw for the following two lines

Solution:
Infinite number of transversals can be drawn.

a, b, c, d, e, f, g are transversal to m and n.

Try these (Text book Page No. 96)

Question 1.
Four real life examples for transversal of parallel lines are given below.

Give four more examples for transversal of parallel lines seen in your surroundings.
Solution:
Some examples of parallel lines in our surroundings
(i) Zebra crossing on the road.
(ii) Railway tracks with sleepers.
(iii) Steps
(iv) Parallel bars in men’s gymnastics

Question 2.
Find the value of x.

Solution:
(i) We know that if two parallel lines are cut by a transversal, each pair of corresponding angles are equal.
∴ x = 125°

(ii) m and n are parallel lines and l is a transversal x° and 48° are corresponding angles.
∴ x = 48°

(iii) m and n are parallel lines and 7’ is the transversal.
∴ Corresponding angles are equal.
∴ x° = 138°

Try these (Text book Page No. 98)

Question 1.
Find the value of x°.

(i) m and n are parallel lines. ‘l’ is a transversal.
When two parallel lines are cut by a transversal each pair of alternate interior angles are equal.
∴ x° = 127°

(ii) m and n are parallel lines and l is the transversal.
When two parallel lines are cut by a transversal each pair of alternate exterior angles are equal.
∴ x° = 46°

Try These (Text Book Page No. 99)

Question 1.
Find the values of x.

Solution:
(i) m and n are parallel lines and l is the transversal.
When two parallel lines are cut by a transversal, each pair of interior angles that lie on the same side of the transversal are supplementary

(ii) m and n are parallel line and l is the transversal.
When two parallel lines are cut by a transversal, each pair of exterior angles that lie on the same side of the transversal are supplementary.
the same side of the transversal are supplementary.
∴ x° + 132° = 180°
x° = 180° – 132°
= 48°
∴ x = 48°

Exercise 5.3

Question 1.
What will happen If the radius of the arc is less than half of AB?
Solution:

If the radius of the arc is less than half of AB, then both the arcs will not cut at a point
and we can’t draw perpendicular bisector.

Students can Download Maths Chapter 2 Measurements Ex 2.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.2

Question 1.
Find the area of rhombus PQRS shown in the following figures.

Solution:
(i) Given the diagonals d₁ = 16 cm ; d₂ = 8 cm
Area of the rhombus = \(\frac{1}{2}\)(d₁ × d₂) sq. units
= \(\frac{1}{2}\) × 16 × 8 cm² = 64 cm²
Area of the rhombus = 64 cm²

(ii) Given base b = 15 cm ; Height h = 11 cm
Area of the rhombus = (base × height) sq. units
= 15 × 11 cm² = 165 cm²
Area of the rhombus = 165 cm²

Question 2.
Find the area of a rhombus whose base is 14 cm and height is 9 cm.
Solution:

Given base b = 14 cm ; Height h = 9 cm
Area of the rhombus = b × h sq. units
= 14 × 9 cm² = 126 cm²

Question 3.
Find the missing value.

Solution:
(i) Given diagonal d₁ = 19 cm ; d₂ = 16 cm
Area of the rhombus = \(\frac{1}{2}\)(d₁ × d₂) sq. units = \(\frac{1}{2}\) × 19 × 16
= 152 cm²

(ii) Given diagonal d₁ = 26 m ; Area of the rhombus = 468 sq. m
= \(\frac{1}{2}\)(d₁ × d₂) = 468 ; (26 × d₂) = 468 × 2
d₂ = \(\frac{468 \times 2}{26}\) = d₂ = 36 m

(iii) Given diagonal d₂ = 12 mm; Area of the rhombus = 180 sq. m
\(\frac{1}{2}\)(d₁ × d₂) = 180
\(\frac{1}{2}\)(d₁ × 12) = 180
d₁ × 12 = 180 × 2
d₁ = \(\frac{180 \times 2}{12}\)
d₁ = 30 mm
Diagonal d₁ = 30 mm
Tabulating the results we have

Question 4.
The area of a rhombus is 100 sq. cm and length of one of its diagonals is 8 cm. Find the length of the other diagonal.
Solution:
Given the length of one diagonal d₁ = 8 cm ; Area of the rhombus = 100 sq. cm
\(\frac{1}{2}\)(d₁ × d₂) = 100
\(\frac{1}{2}\) × 8 × d₂ = 100
8 × d₂ = 100 × 2
d₂ = \(\frac{100 \times 2}{8}\) = 25 cm
Length of the other diagonal d₂ = 25 cm

Question 5.
A sweet is in the shape of rhombus whose diagonals are given as 4 cm and 5 cm. The surface of the sweet should be covered by an aluminum foil. Find the cost of aluminum foil used for 400 such sweets at the rate of ₹ 7 per 100 sq. cm.
Solution:
Diagonals d₁ = 4 cm and d₂ = 5 cm
Area of one rhombus shaped sweet = \(\frac{1}{2}\)(d₁ × d₂) sq. units = \(\frac{1}{2}\) × 4× 5 cm² = 10 cm²
Aluminum foil used to cover 1 sweet = 10 cm²
∴ Aluminum foil used to cover 400 sweets = 400 × 10 = 4000 cm²
Cost of aluminum foil for 100 cm² = ₹ 7
∴ Cost of aluminum foil for 4000 cm² = \(\frac{4000}{100}\) × 7 = ₹ 280
∴ Cost of aluminum foil used = ₹ 280.

Objective Type Questions

Question 6.
The area of the rhombus with side 4 cm and height 3 cm is
(i) 7 sq. cm
(ii) 24 sq. cm
(iii) 12 sq. cm
(iv) 10 sq. cm
Solution:
(iii) 12 sq. cm
Hint:
Area = Base × Height = 4 × 3 = 12 cm²

Question 7.
The area of the rhombus when both diagonals measuring 8 cm is
(i) 64 sq. cm
(ii) 32 sq. cm
(iii) 30 sq. cm
(iv) 16 sq. cm
Solution:
(ii) 32 sq. cm
Hint:
Area = \(\frac{1}{2}\)(d₁ × d₂) = \(\frac{1}{2}\) × 8 × 8 = 32

Question 8.
The area of the rhombus is 128 sq. cm. and the length of one diagonal is 32 cm. The length of the other diagonal is
(i) 12 cm
(ii) 8 cm
(iii) 4 cm
(iv) 20 cm
Solution:
(ii) 8 cm
Hint:
\(\frac{1}{2}\) × d₁ × d₂ = 128 ⇒ d₂ = \(\frac{128 \times 2}{32}\) = 8cm

Question 9.
The height of the rhombus whose area 96 sq. m and side 24 m is
(i) 8 m
(ii) 10 m
(iii) 2 m
(iv) 4 m
Solution:
(iv) 4 m
Hint:
Area = Base × height = 96 ⇒ height = \(\frac{96}{24}\) = 4

Question 10.
The angle between the diagonals of a rhombus is
(i) 120°
(ii) 180°
(iii) 90°
(iv) 100°
Solution:
(iii) 90°
Hint:
Angles of a rhombus bisect at right angles.

Students can Download Maths Chapter 2 Measurements Ex 2.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.1

Question 1.
Find the area and perimeter of the following parallelograms.

Solution:
(i) Given base b = 11 cm ; height h = 3 cm
Area of the parallelogram = b × h sq. units = 11 × 3 cm²
= 33 cm²
Also perimeter of a parallelogram = Sum of 4 sides
= 11 cm + 4 cm + 11 cm + 4 cm = 30 cm
Area = 33 cm²; Perimeter = 30 cm.

(ii) Given base b = 7 cm
height h = 10 cm
Area of the parallelogram = b × h sq. units
= 7 × 10 cm² = 70 cm²
Perimeter = Sum of four sides
= 13 cm + 7 cm + 13 cm + 7 cm = 40 cm
Area = 70 cm², Perimeter = 40 cm

Question 2.
Find the missing values.

Solution:
(i) Given Base 6 = 18 cm ; Height h = 5 cm
Area of the parallelogram = b × h sq. units
= 18 × 5 cm²
= 90 cm²

(ii) Base b = 8m; Area of the parallelogram = 56 sq. m
b × h = 56
8 × A = 56
h = \(\frac{56}{8}\)
h = 7 m

(iii) Given Height h = 17 mm
Area of the parallelogram = 221 sq. mm
b × h = 221
b × 17 = 221
b = \(\frac{221}{17}\)
b = 13 m
Tabulating the results, we get

Question 3.
Suresh on a parallelogram shaped trophy in a state level chess tournament. He knows that the area of the trophy is 735 sq. cm and its base is 21 cm. What is the height of that trophy?

Solution:
Given base 6 = 21 cm
Area of parallelogram = 735 sq. cm
b × h = 735
21 × h = 735
h = \(\frac{735}{21}\)
h = 35 cm
∴ Height of the trophy = 35 cm

Question 4.
Janaki has a piece of fabric in the shape of a parallelogram. Its height is 12 m and its base is 18 m. She cuts the fabric into four equal parallelograms by cutting the parallel sides through its mid-points. Find the area of each new parallelogram.
Solution:

Area of a parallelogram = (base × height) sq. units
Base length = \(\frac{18}{2}\) = 9 m
Height = \(\frac{12}{2}\) = 6 m
Area = 9 × 6 = 54 m²
Area of each parallelogram = 54 m²

Question 5.
A ground is in the shape of parallelogram. The height of the parallelogram is 14 metres and the corresponding base is 8 metres longer than its height. Find the cost of levelling the ground at the rate of ₹ 15 per sq. m.
Solution:

Height of the parallelogram h = 14 m
Base = 8 m longer than height
= (14 + 8) m = 22 m
Area of the parallelogram = (base × height) sq. units
= (22 × 14)m² = 308 m²
Cost of levelling 1 m² = ₹ 15
Cost of levelling 308 m² = 308 × 15 = ₹ 4,620
Cost of levelling the ground = ₹ 4,620

Objective Type Questions

Question 6.
The perimeter of a parallelogram whose adjacent sides are 6 cm and 5 cm is
(i) 12 cm
(ii) 10 cm
(iii) 24 cm
(iv) 22 cm
Solution:
(iv) 22 cm
Hint:
= 2(6 + 5) = 2 × 11 = 22 cm

Question 7.
The area of parallelogram whose base 10 m and height 7 m is
(i) 70 sq.m
(ii) 35 sq.m
(iii) 7 sq.m
(iv) 10 sq.m
Solution:
(i) 70 sq. m
Hint: = base × height = 10m × 7m = 70 sq.m

Question 8.
The base of the parallelogram with area is 52 sq. cm and height 4 cm is
(i) 48 cm
(ii) 104 cm
(iii) 13 cm
(iv) 26 cm
Solution:
(iii) 13 cm
Hint:

Question 9.
What happens to the area of the parallelogram if the base is increased 2 times and the height is halved?
(i) Decreases to half
(ii) Remains the same
(iii) Increase by two times
(iv) None
Solution:
(ii) Remains the same
Hint:
Area = b × h sq. units
New base = 2 × old base
New height = \(\frac{1}{2}\) × old height
New Area = New base × New height = (2 × b)\(\frac{1}{2}\) × h = bh = old Area.

Question 10.
In a parallelogram the base is three times its height. If the height is 8 cm then the area is
(i) 64 sq. cm
(ii) 192 sq. cm
(iii) 32 sq. cm
(iv) 72 sq. cm
Solution:
(ii) 192 sq. cm
Hint: Given b = 3 × h; h = 8 cm
Area = b × h = 3h × 8 = 3 × 8 × 8 = 192 cm²

Students can Download Maths Chapter 5 Geometry Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Additional Questions

Exercise 5.1

Question 1.
Can two adjacent angles be supplementary?
Solution:
Yes, In the figure

∠AOB and ∠BOC are adjacent angles.
Also ∠AOB + ∠BOC = 180°
∴ ∠AOB and ∠BOC are supplementary

Question 2.
Can two obtuse angles form a linear pair?
Solution:
No, the sum of the measures of two obtuse angles is more than 180°.

Question 3.
Can two right angles form a linear pair?
Solution:
Yes, because the sum of two right angles is 180° and form a linear pair.

Question 4.
Find x, y and z from the figure.

Solution:
x = 55° vertically opposite angles
y + 55° = 180°
y = 180°- 55°
y = 125°

Execise 5.2

Question 1.
Can two lines intersect in more than one point ?
Solution:
No, two lines cannot intersect in more than one point.

Question 2.
In the figure EF parallel to GH
Solution:
∠EAB = 60° and ∠ACD = 105°
Determine (i) ∠CAF and
(ii) ∠BAC

Solution:
(i) Since EF || GH and AC is a transversal
⇒ ∠CAF + ∠ACH = 180°
⇒ ∠CAF + 105° = 180° .
= 75°
(ii) ∴ EF || GH and AC is transversal.
∴ ∠EAC = ∠ACH [ ∵ Alternate interior angles]
⇒ ∠BAC = 105°
⇒ ∠BAC + ∠BAB = 105°
⇒ ∠BAC + 60° = 105°
⇒ ∠BAC = 105° – 60°
= 45°
∴ ∠CAF = 75° and ∠BAC = 45°.

Question 3.
In the given figure, the arms of two angles are parallel. If ∠ABC = 70°, then find
(i) ∠DGC
(ii) ∠DEF

Solution:
We have AB||ED and BC || EF
(i) BC is transversal
∠DGC = ∠ABC [corresponding angles]
But ∠ABC = 70°
∠DGC = 70°

(ii) ED is a transversal to BC||EF
∴ ∠DEF = ∠DGC [corresponding]
∠DGC = 70°
∠DEF = 70°

Exercise 5.6

Question 1.
In the following figure, show that CD || EF
Solution:

∠BAD = ∠BAE + ∠EAD
= 40°+ 30° = 70°.
and ∠CDA = 70°
∠BAD = ∠CDA
But they form a pair of alternate angles
⇒ AB || CD
Also ∠BAE + ∠AEF = 40° + 140° = 180°
But they form a pair of interior opposite angles.
⇒ AB || EF
From (1) and (2), we get
AB || CD || EF
⇒ CD || EF

Question 2.
In the adjoining figure, the lines \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { CD } \) intersect at ‘O’. If ∠COB = 50°, find the measures of the other three angles.
Solution:
∠COB = 50°
∠AOD = 50° (vertically opposite angles)
Now ∠AOC and ∠COB form a linear pair,
Thus ∠AOC + ∠COB = 180°
⇒ ∠AOC + 50° = 180°.
∠AOC = 180° – 50° = 130°
Also ∠AOC and ∠BOD are vertically opposite angles.
∴ ∠BOD = ∠AOC = 130°
Thus the three angles are
∠AOD = 50°
∠AOC =130°
∠BOD = 130°