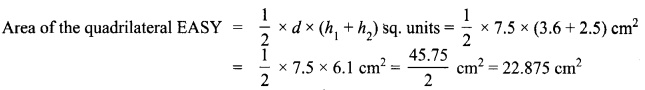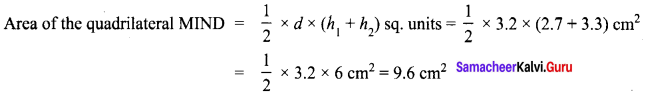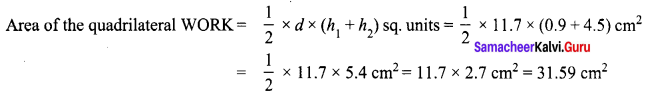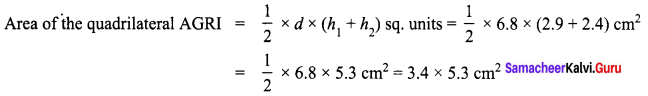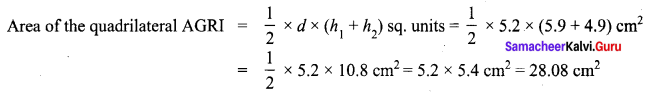Category: Class 8

Students can Download Maths Chapter 4 Geometry Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Intext Questions

Answer the following questions:

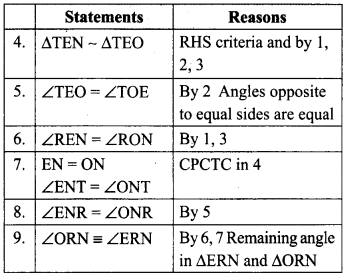
Question 1.
The sum of the three angles of a triangle is ______
Solution:
1800

Question 2.
The exterior angle of a triangle is equal to the sum of the _______ angles opposite to it.
Solution:
interior

Question 3.
In a triangle, the sum of any two sides is ____ than the third side.
Solution:
greater

Question 4.
The difference between any two sides of a triangle is _______ than the third side.
Solution:
Smaller

Question 5.
Angles opposite to equal sides are ______ and vice-versa.
Solution:
Equal

Question 6.
The angles of a triangle are in the ratio 4 : 5 : 6
(i) Is it an acute, right or obtuse triangle?
(ii) Is it scalene, isosceles or equilateral?
Solution:
(i) Given the angles of a triangle are in the ratio 4 : 5 : 6 Sum of three angles of a
triangle = 180°.
Let the three angles 4x, 5x and 6x
4x + 5x + 6x = 180°
15x = 180° [∵ Vertically opposite angles are equal]

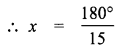
∴ x = 12°
∴ The angles are 4x ⇒ 4 × 12 = 48°
5x ⇒ 5 × 12 = 60°
6x ⇒ 6 × 12 = 72°
∴ The angle of the triangle are 48°, 60°, 72°
∴ It is an acute angles triangle.

(ii) We know that the sides opposite to equal angles are equal.
Here all the three angles are different.
∴ The sides also different.
∴ The triangle is a scalene triangle.

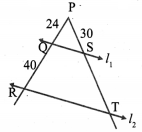
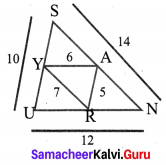
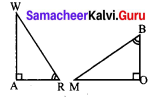
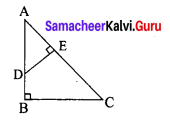
Question 7.
What is ∠A in the triangle ABC?

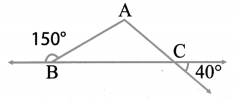
Solution:
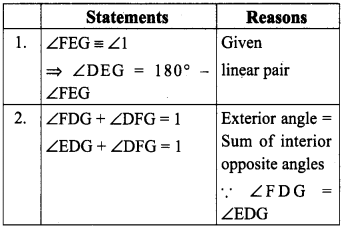
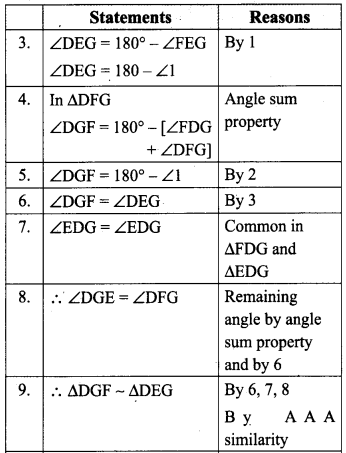
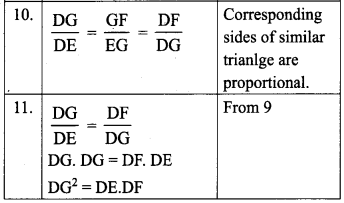
The exterior angle = sum of interior opposite angles.
∴ ∠A + ∠C = 150° in ∆ABC
But ∠C = 40° [∵ Vertically opposite angles are equal]

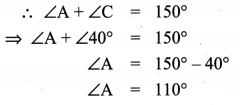
Question 8.
Can a triangle have two supplementary angles? Why?
Solution:
Sum of three angles of a triangle is 180°.
∴ Sum of any two angles in a triangle will be less than 180°.
∴ A triangle cannot have two supplimentary angles.

Question 9.
________ shapes have the same shapes but different sizes.
Solution:
Similar

Question 10.
shapes are exactly the same in shape and size.
Solution:
Congruent

Exercise 4.1

Try these Page No. 99

Identify the pairs of shapes which are similar and congruent.

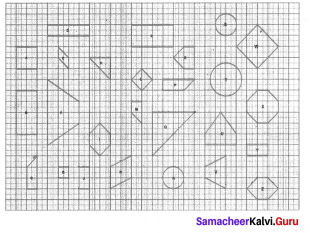
Similar shapes:
(i) W and L
(ii) B and J
(iii) A and G
(iv) B and J
(v) B and Y
Congruent shapes:
(i) Z and I
(ii) J and Y
(iii) C and P You can find more.
(iv) B and K
(v) R and S
(vi) I and Z

Try these Page No. 108

Question 1.
Match the following by their congruence

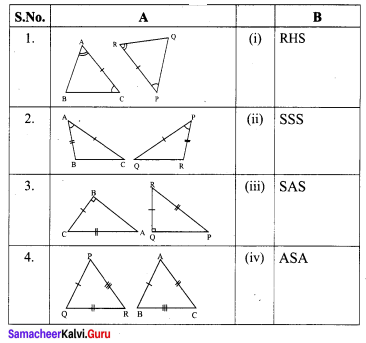
Solution:
1 – (iv)
2 – (iii)
3 – (i)
4 – (ii)

Try this Page No. 108

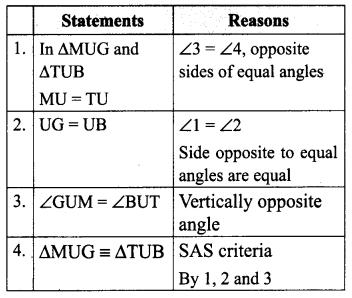
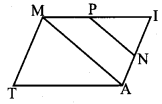
Question 1.
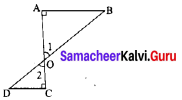
In the figure, DA = DC and BA = BC. Are the triangles DBA and DBC congruent? Why?
Solution:

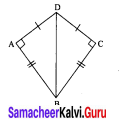
Here AD = CD
AB = CB
DB = DB (common)
∆DBA ≅ ∆DBC [∵ By SSS Congruency]
Also RHS rule also bind here to say their congruency.

Exercise 4.3

Try this Page No. 114

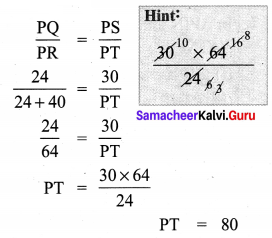
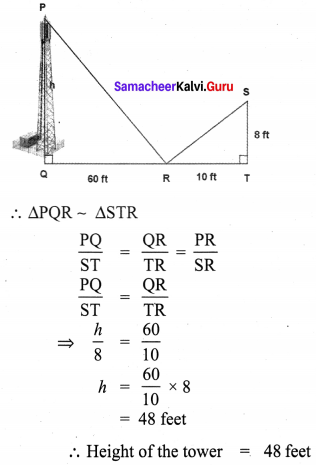
Question 1.
Is it possible to construct a quadrilateral PQRS with PQ = 5 cm, QR = 3 cm, RS = 6 cm, PS = 7 cm and PR = 10 cm. If not, why?
Solution:
The lower triangle cannot be constructed as the sum of two sides 5 + 3 = 8 < 10 cm. So this quadrilateral cannot be constructed.

Students can Download Maths Chapter 1 Rational Numbers Ex 1.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 1 Rational Numbers Ex 1.2

Question 1.
Fill in the blanks:
(i) The multiplicative inverse of \(2 \frac{3}{5}\) is _____.
(ii) If -3 × \(\frac{6}{-11}=\frac{6}{-11}\) × x, then x is _______.
(iii) If distributive property is true for \(\left(\frac{3}{5} \times \frac{-4}{9}\right)+\left(x \times \frac{15}{17}\right)=\frac{3}{5} \times(y+z)\), then x, y, z are _____, _____ and ____.
(iv) If x × \(\frac{-55}{63}=\frac{-55}{63}\) × x = 1, then x is called the _____ of \(\frac{55}{63}\).
(v) The multiplicative inverse of -1 is ______.
Solution:
(i) \(\frac{5}{13}\)
(ii) -3
(iii) \(\frac{3}{5}, \frac{-4}{9}\) and \(\frac{15}{13}\)
(iv) Mulitplicative inverse
(v) -1

Question 2.
Say True or False.
(i) \(\frac{-7}{8} \times \frac{-23}{27}=\frac{-23}{27} \times \frac{-7}{8}\) illustrates the closure property of rational number.
(ii) Associative property is not true for subtraction of rational numbers.
(iii) The additive inverse of \(\frac{-11}{-17}\) is \(\frac{11}{17}\).
(iv) The product of two negative rational numbers is a positive rational number.
(v) The multiplicative inverse exists for all rational numbers.
Solution:
(i) False
(ii) True
(iii) False
(iv) True
(v) False

Question 3.
Verify the closure property for addition and multiplication of the rational numbers \(\frac{-5}{7}\) and \(\frac{8}{9}\)
Solution:
Closure property for addition.
Let a = \(\frac{-5}{7}\) and b = \(\frac{8}{9}\) be the given rational numbers.

∴ Closure property is true for addition of rational numbers.
Closure property for multiplication

∴ Closure property is true for multiplication of rational numbers.

Question 4.
Verify the associative property for addition and multiplication of the rational numbers \(\frac{-10}{11}, \frac{5}{6}, \frac{-4}{3}\).
Solution:


a × (b × c) = \(\frac{100}{99}\)
From (1) and (2) a × (b × c) = (a × b) × c is true for rational numbers.
Thus associative property is true for addition and multiplication of rational numbers.

Question 5.
Check the commutative property for addition and multiplication of the rational numbers \(\frac{-10}{11}\) and \(\frac{-8}{33}\).
Solution:
Let a = \(\frac{-10}{11}\) and b = \(\frac{-8}{33}\) be the given rational numbers.

From (1) and (2)
a + b = b + a and hence addition is commutative for rational numbers.

From (3) and (4) a × b = b × a
Hence multiplication is commutative for rational numbers.

Question 6.
Verify the distributive property a × (b + c) = (a × b) + (a × c) for the rational numbers a = \(\frac{-1}{2}\) ,b = \(\frac{2}{3}\) and c = \(\frac{-5}{6}\).
Solution:
Given the rational number a = \(\frac{-1}{2}\) ,b = \(\frac{2}{3}\) and c = \(\frac{-5}{6}\).

From (1) and (2) we have a × (b + c) = (a × b) + (a × c) is true.
Hence multiplication is distributive over addition for rational numbers Q.

Question 7.
Evaluate:

Solution:

Question 8.
Evaluate using appropriate properties.

Solution:

Question 9.
Use commutative and distributive properties to simplify \(\frac{4}{5} \times \frac{-3}{8}-\frac{3}{8} \times \frac{1}{4}+\frac{19}{20}\)
Solution:
Since multiplication is commutative

Objective Type Questions

Question 10.
Mulitplicative inverse of 0 (is)
(A) 0
(B) 1
(C) -1
(D) does not exist
Solution:
(D) does not exist

Question 11.
Which of the following illustrates the inverse property for addition?

Solution:
(A) \(\frac{1}{8}-\frac{1}{8}\) = 0

Question 12.
Closure property is not true for division of rational numbers because of the number
(A) 1
(B) -1
(C) 0
(D) \(\frac{1}{2}\)
Solution:
(C) 0

Question 13.
\(\frac{1}{2}-\left(\frac{3}{4}-\frac{5}{6}\right) \neq\left(\frac{1}{2}-\frac{3}{4}\right)-\frac{5}{6}\) illustrates that subtraction does not satisfy the ____ law of rational numbers.
(A) commutative
(B) closure
(C) distributive
(D) associative
Solution:
(D) associative

Question 14.
\(\left(1-\frac{1}{2}\right) \times\left(\frac{1}{2}-\frac{1}{4}\right) \div\left(\frac{3}{4}-\frac{1}{2}\right)\) = ______________

Solution:
(A) \(\frac{1}{2}\)

Students can Download Maths Chapter 5 Information Processing Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 5 Information Processing Additional Questions

Additional Questions And Answers

Question 1.
A fast food restaurant has a meal special ?50 for a drink, sandwich, side item and dessert. The choices are Sandwich : Grilled chicken, All beef patty, Vegeburger and Fill filet.
Side : Regular fries, cheese fries, potato fries
Dessert: Chocolate chip cookie or Apple pie.
Drink: Fanta, Dr. Pepper, Coke, Diet coke and sprite.
How may meal combos are possible?
Solution:
There are 4 stages
1. Choosing a Sandwich
2. Choosing a side
3. Choosing a dessert
4. Choosing a drink
There are 4 different types of sandwich, 3 different types of side two different type of desserts and five different types of drink.
∴ The number of meal combos possible is = 4 × 3 × 2 × 5 = 120

Question 2.
A company puts a code on each different product they sell. The code is made up of 3 numbers and 2 letters. How many different codes are possible?
Solution:
There are 5 stages, Number – 1
Number – 2
Number – 3
Letter – 1
Letter – 2
There are 10 possible numbers 0 to 9
There are 26 possible letters A to Z.
We have 10 × 10 × 10 × 26 × 26 = 6,76, 000 possible codes.

Question 3.
Rani take a survey with five ‘yes’ or ‘No’ answers. How many different ways could she complete the survey?
Solution:
There are 5 stages
Question – 1
Question – 2
Question – 3
Question – 4
Question – 5
There are 2 choices for each question (Yes/No)
∴ Total number of possible ways to answer
= 2 × 2 × 2 × 2 × 2 = 32 ways.

Question 4.
There are 2 vegetarian entry options and 5 meat entry options on a dinner menu. What number of ways one can opt a dinner for any one of it?
Solution:
Number of veg options = 2
Number of meat option = 5
One can opt for any one dinner
∴ Total number of ways = 2 + 5 = 7 ways

Additional Questions And Answers

Question 1.
Colour the graph with minimum number of colours and no two adjacent vertices should have the same colour.
Solution:

Test Yourself

Question 1.
You have three dice, How many possible out comes are there on a toss?
Solution:
8

Question 2.
Your school offers tow English classes three maths classes and 3 history classes, you want to take one of each class. How many different ways are there to organize your schedule?
Solution:
18

Question 3.
A wedding caterer gives 3 choices for main dish, sin starters, five dessert. How many different meals (made up of starter, dinner and dessert and are there?
Solution:
90

Question 4.
In a company ID cards have 5 digit numbers.
(a) How many ID cards can he formed if repetition of the digits allowed?
(b) How many ID cards can be formed if repetition of digits is not allowed?
Solution:
(i) 10,000
(ii) 30,240

Question 5.
A student is shopping for a new computer. He is deciding among 3 desktop and 4 laptop computer. How many ways she can buy a computer?
Solution:
7

Question 6.
Colour the vertices bear the same colour using minimum number of colours.

Students can Download Maths Chapter 5 Information Processing Ex 5.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 5 Information Processing Ex 5.3

MISCELLANEOUS QUESTIONS

Question 1.
Shanthi has 5 chudithar sets and 4 Frocks. In how many possible ways, can she wear either a chudithar or a frock ?
Solution:
Shanthi his 5 chudidhar sets and 4 frocks.
She wear either chudidhar or a frock.
∴ Total possible ways = 5 + 4 = 9 ways

Question 2.
In a Higher Secondary School, the following types of groups are available in XI standard
I. Science Group:
(i) Physics, Chemistry, Biology and Mathematics
(ii) Physics, Chemistry, Mathematics and Computer Science
(iii) Physics, Chemistry, Biology and Home Science
II. Arts Group:
(i) 1. Accountancy, Commerce, Economics and Business Maths
(ii) 2. Accountancy, Commerce, Economics and Computer Science
(iii) 3. History, Geography, Economics and Commerce
III. Vocational Group:
(i) Nursing – Biology, Theory, Practical I and Practical II
(ii) Textiles and Dress Designing – Home Science, Theory, Practical I and Practical II
In how many possible ways, can a student choose the group?
Solution:
The student either select any one of science group in 3 ways or any of the arts group in 3 ways or any of the vocational group in 2 ways.
∴ Total possible ways = 3 + 3 + 2 = 8 ways

Question 3.
An examination paper has 3 sections, each with five instructed to answer one question from each section. In can the questions be answered?
Solution:
The tree diagram for this may be

∴ Number of possible ways to select one questions from each of 3 sections is 3 × 5 = 15 ways.

Question 4.
On a sports day, students must take also part in one of the one track events 100m Running and 4 × 100 m Relay. He must take part of any of the field events Long Jump, High Jump and Javelin Throw. In how many different ways can the student take part in the given events?
Solution:
Number of track events ⇒ (100m running, 4 × 100 m Relay) 2.
Number of field events ⇒ (Long jump, High jump, Javelin Throw) 3.
Students can take part in the given events in 2 × 3 = 6 ways.

Question 5.
The given spinner is spun twice and the two numbers got are used to form a 2 digit number. How many different 2 digits numbers are possible?

Solution:
On the first spin we get any of the five numbers to form ones place then insecond spin the number got will fill 10’s place.
∴ Number of ways = 5 × 5 = 25 ways.
Removing the repetitions (11, 22, 33, 44, 55) once we get 25 – 5 = 20 ways.
20 different two digit numbers are possbile

Question 6.
Colour the following pattern with as few colours as possible but make sure that no two adjacent sections are of the same colour.

Solution:

Students can Download Maths Chapter 5 Information Processing Ex 5.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 5 Information Processing Ex 5.2

Question 1.
Colour the following patterns with as few colours as possible but make sure that no two adjacent sections are of the same colour.
Solution:

Question 2.
Ramya wants to paint a pattern in her living room wall with a minimum budget. Help her to colour the pattern with 2 colours but make sure that no two adjacent boxes are the same colour. The pattern is shown in the picture.

Solution:

Question 3.
Colour the countries in the following maps with as few colours as possible but make
sure that no two adjacent countries are of the same colour.

Solution:

Students can Download Maths Chapter 3 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Additional Questions

Additional Questions And Answers

Exercise 3.1

Very Short Answers [2 Marks]

Question 1.
Find the product of the following.
(i) (x, y)
(ii) (10x, 5y)
(iii) (2x², 5y²)
Solution:
(i) x × y = xy
(ii) 10x × 5y = (10 × 5) x × xy
= 50 xy
(iii) 2x² x 5y² = (2 x 5) x (x² + y²)
= 10x²y²

Short Answers [3 Marks]

Question 1.
Find the product of the following.
(i) 3ab² c³ by 5a³b²c
(ii) 4x²yz by \(\frac{3}{2}\) x²yz²
Solution:
(i) (3ab³c³) × (5a³b²c)
= (3 × 5)(a × a³ × b² × b² × c² × c)
= 15a¹⁺³.b²⁺².c³⁺¹ = 15a⁴b⁴c⁴

(ii) 4x²yz by \(\frac{3}{2}\) x²yz²
= (4 × \(\frac{3}{2}\)) × (x² × x² × y × y × z × z²)
= -6x²⁺² y¹⁺¹ x¹⁺² = -6x⁴y²z³

Long Answers [5 Marks]

Question 1.
Simplify (3x – 2) (x – 1) (3x + 5).
Solution:
(3x – 2) (x – 1) (3x + 5)
= {(3x – 2) (x – 1)} × (3x + 5) [∴Multiplication in associative]
= {3x (x – 1) – 2 x – 1)} × (3x + 5)
= (3x² – 3x – 2x + 2) × (3x + 5)
= (3x² – 5x + 2) (3x + 5)
= 3x² × (3x + 5) – 5x (3x + 5) + 2 (3x + 5)
= (9x³ + 15x²) + (-15x² – 25x) + (6x + 10)
= 9x³ + 15x² – 15x² – 25x + 6x + 10
= 9x³ – 19x + 10

Question 2.
Simplify (5 – x) (3 – 2x) (4 – 3x).
Solution:
(5 – x) (3 – 2x) (4 – 3x)
= {(5 – x)(3 – 2x)} × (4 – 3x) [∴ Multiplication in association]
= {5 (3 – 2x) -x (3 – 2x)} × (4 – 3x)
= (15 – 10x – 3x + 2x²) × (4 – 3x)
= (2x² – 13x + 15) (4 – 3x)
= 2x² × (4 – 3x) – 13x (4 – 3x) + 15 (4 – 3x)
= 8x³ – 6³ – 52x + 39x² + 60 – 45x
= -6x³ + 47x² – 97x + 60

Exercise 3.2

Very Short Answers [2 Marks]

Question 1.
Divide.
(i) 12x³y³ by 3x²y
(ii) -15a² bc³ by 3ab
(iii) 25x³y² by – 15x²y
Solution:

Short Answers [3 Marks]

Question 1.
Divide
(i) 15m²n³ by 5m²n²
(ii) 24a³b³ by -8ab
(iii) -21 abc² by 7 abc
Solution:

Question 2.
Divide
(i) 16m³y² by 4m²y
(ii) 32m² n³p² by 4mnp
Solution:

Long Answers [5 Marks]

Question 1.
Divide.
(i) 9m⁵ + 12m⁴ – 6m² by 3m²
(ii) 24x³y + 20x²y² – 4xy by 2xy
Solution:

Exercise 3.3

Question 1.
Evaluate:
(i) (2x + 3y)²
(ii) (2x – 3y)²
Solution:
(i) (2x + 3y)²
= (2x)² + 2 × (2x) × (3y) + (3y)²
[using (a + b)² = a² + 2ab + b²]
= 4x² + 12xy + 9y²

(ii) (2x – 3y)²
= (2x)² – 2(2x) (3y) + (3y)²
[∵ using (a – b)² = a² – 2ab + b²]
= 4x² – 12xy + 9y²

Short Answers [3 Marks]

Question 1.
Evaluate the following
(i) (2x – 3) (2x + 5)
(ii) (y – 7) (y + 3)
(iii) 107 × 103
Solution:
(i) (2x – 3) (2x + 5)
= (2x)² + (-3 + 5) (2x) + (-3) (5)
[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 2²x² + 2 × 2x + (-15)
= 4x² + 4x – 15

(ii) (y – 7) (y + 3)
= y² + (-7 + 3)y + (-7) (3)
[∵ (x + a)(x + b) = x² + (a + b)x + ab]
= y² – 4y + (-21) = y² – 4y – 21

(iii) 107 × 103
= (100 + 7) × (100+ 3)
= 100² + (7 + 3) × 100 +(7 × 3)
= 10000 + 10 × 100 + 21 = 10000 + 1000 + 21 = 11021

Long Answers [5 Marks]

Question 1.
If x + y = 12 and xy = 14 find x² + y².
Solution:
(x + y)² = x² + y² + 2xy
12² = x² + y² + 2 × 14
144 = x² + y² + 28
x² + y² = 144 – 28
x² + y² = 116

Question 2.
If 3x + 2y = 12 and xy = 6 find the value of 9x² + 4y².
Solution:
(3x + 2y)² = (3x)² + (2y)² + 2 (3x) (2y)
= 9x² + 4y² + 12xy
12² = 9x² + 4y² + 12 × 6
144 = 9x² + 4y² + 72
144 – 72 = 9x² + 4y²
∴ 9x² + 4y² = 72

Exercise 3.4

Question 1.
Factorize:
(i) 7(2x + 5) + 3 (2x + 5)
(ii) 12x³y⁴ + 16x²y⁵ – 4x⁵y²
Solution:
(i) 7(2x + 5) + 3 (2x + 5)
= (2x + 5) (7 + 3)
(ii) 12x³y⁴ + 16x²y⁵ – 4x⁵y²
= 4x²y² (3xy² + 4y³ – x³)

Short Answers [3 Marks]

1. Factorize
(i) 81a² – 121b²
(ii) x² + 8x + 16
Solution:
(i) 81a² – 121b²
= (9a)² – (11b)²
[∵ using a² – b² = (a + b)²]
= (9a + 11b) (9a – 11b)

(ii) x² + 8x + 16 = x² + 2 × x × 4 + 4²
[∵ using a² + 2ab + b² = (a + b)²]
= (x + 4)² = (x + 4)(x + 4)

Long Answers [5 Marks]

Question 1.
Factorize
(i) x² + 2xy + y² – a² + 2ab – b²
(ii) 9 – a⁶ + 2a³ – b⁶
Solution:
(i) x² + 2xy + y² – a² + 2ab – b².
= (x² + 2xy + y²) – (a² – 2ab + b²)
= (x + y)² – (a – b)²
= {(x + y) + (a – b)} {(x + y) – (a – b)}
= (x + y + a – b) (x + y – a + b)

(ii) a – a⁶ + 2a³b³ – b⁶
= 9 – (a⁶ – 2a³b³ + b⁶)
= 3² -{(a³)² – 2 × a³ × b³ + (b³)²}
= 3² – (a³ – 6³)²
= {3 + (a³ – b³)} {3 – (a³ – b³)}
= (3 + a³ – b³) (3 – a³ + b³)
= (a³ – b³ + 1){-a³ + b³ + 3)

Question 2.
Factorize
(i) 100 (x + y )² – 81 (a + b)²
(ii)(x + 1)² – (x – 2)²
Solution:
(i) 100 (x + y)² – 81 (a + b)²
= {10 (x + y)}² – {(a (a + b)}²
= {10 (x + y) + 9 (a + b)}
{10 (x + y) – 9(a + b)}
= (10x + 10y + 9a – 9b)}
(10x + 10y – 9a – 9b)

(ii) (x – 1)² – (x – 2)²
= {(x – 1 +(x – 2)}
{(x – 1) – (x – 2)}
= (2x – 3) – (x – 1 – x + 2)
= (2x – 3) × 1 = 2x – 3

Students can Download Maths Chapter 3 Algebra Ex 3.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.5

Miscellaneous Practice Problems

Question 1.
Subtract: -2(xy)² (y³ + 7x²y + 5) from 5y² (x²y³ – 2x⁴y + 10x²)
Solution:
5y² (x²y³ – 2x⁴y + 10x²) – [(-2)(xy)² (y³ + 7x²y + 5)]
= [5y² (x²y³) – 5y² (2x⁴y) + 5y² (10x²)] – [(-2)x²y² (y³ + 7x²y + 5)]
= (5y⁵5x² – 10x⁴y³ + 50x²y²)
= 5x²y⁵ – 10x⁴y³ + 50x²y² – [(-2x²y⁵) – 14x⁴y³ – 10x²y²]
= 5x²y⁵ – 10x⁴y³ + 50x²)y² + 2x² y⁵ + 14x⁴)y³ + 10x²)y²
= (5 + 2)x²y⁵ + (-10 + 14)x⁴y³ + (+50 + 10)x²y²
= 7x²y⁵ + 4x⁴y³ + 60x²y²

Question 2.
Multiply (4x² + 9) and (3x – 2).
Solution:
(4x² + 9) (3x – 2) = 4x²(3x – 2) + 9(3x – 2)
= (4x²)(3x) – (4x²)(2) + 9(3x) – 9(2) = (4 × 3 × x × x²) – (4 × 2 × x²) + (9 × 3 × x) – 18
= 12x³ – 8x² + 27x – 18 (4x³ + 9) (3x – 2) = 12x³ – 8x² + 27x – 18

Question 3.
Find the simple interest on Rs. 5a²b² for 4ab years at 7b% per annum.
Solution:

Question 4.
The cost of a note book is Rs. 10ab. If Babu has Rs. (5a²b + 20ab² + 40ab). Then how many note hooks can he buy?
Solution:
For ₹ 10 ab the number of note books can buy = 1.

Question 5.
Factorise : (7y² – 19y – 6)
Solution:
7y² – 19y – 6 is of the form ax² + bx + c where a = 7; b = -19; c = – 6

The product a × c = 7 × -6 = -42
sum b = – 19

The middle term – 19y can be written as – 21y + 2y
7y² – 19y – 6 = 7y² – 21y + 2y – 6
= 7y(y – 3) + 2(y – 3) = (y – 3)(7y + 2)
7y² – 19y – 6 = (y – 3)(7y + 2)

Challenging Problems

Question 6.
A contractor uses the expression 4x² + 11x + 6 to determine the amount of wire to order when wiring a house. If the expression comes from multiplying the number of rooms times the number of outlets and he knows the number of rooms to be (x + 2), find the number of outlets in terms of ‘x’ [Hint: factorise 4x² + 11x + 6]
Solution:
Given Number of rooms = x + 2
Number of rooms × Number of outlets = amount of wire.

Now factorising 4x² + 11x + 6 which is of the form ax² + bx + c with a = 4 b = 11 c = 6.
The product a × c = 4 × 6 = 24
sum b = 11


The middle term 11x can be written as 8x + 3x
∴ 4x² + 11x + 6 = 4x² + 8x + 3x + 6 = 4x (x + 2) + 3 (x + 2)
4x² + 11x + 6 = (x + 2) (4x + 3)
Now from (1) the number of outlets

∴ Number of outlets = 4x + 3

Question 7.
A mason uses the expression x² + 6x + 8 to represent the area of the floor of a room. If the decides that the length of the room will be represented by (x + 4), what will the width of the room be in terms of x ?
Solution:
Given length of the room = x + 4
Area of the room = x² + 6x + 8
Length × breadth = x² + 6x + 8

Question 8.
Find the missing term: y² + (-) x + 56 = (y + 7)(y + -)
Solution:
We have (x + a) (x + b) = x² + (a + b)x + ab
56 = 7 × 8 .
∴ y² + (7 + 8)x + 56 = (y + 7)(y + 8)

Question 9.
Factorise: 16p⁴ – 1
Solution:
16p⁴ – 1 = 2⁴p⁴ – 1 = (2²)²(p²)² – 1²
Comparing with a² – b² = (a + b)(a – b) where a = 2²p² and b = 1
∴ (2²p²)² – 1² = (2²p² + 1) (2²p² – 1) = (4p² + 1) (4p² – 1)
∴ 16p⁴ – 1 = (4p² + 1)(4p² – 1)(4p² + 1)(2²p² – 1²)
= (4p² + 1) [(2p)²– 1²] = (4p² + 1) (2p + 1)(2p – 1)
[∵ using a² – b² = (a + b) (a – b)]
∴ 16p⁴ – 1 = (4psup>2 + 1)(2p + 1)(2p – 1)

Question 10.
Factorise : x⁶ – 64y³
Solution:
x⁶ – 64y³ = (x²)³ – 4³y³ = (x²)³ – (4y)³
This is of the form a³ – b³ with a = x², b = 4y
a³ – b³ = (a – b)(a² + ab + b²)
(x²)³ – (4y)³ = (x² – 4y) [(x²)² + (x²)(4y) + (4y)²]
= (x² – 4y) [x⁴ + 4x²y + 16y²]
∴ x⁶ – 64y³ = (x² – 4y) [x⁴ + 4x²y + 16y²]

Students can Download Maths Chapter 4 Geometry Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Additional Questions

Additional Questions And Answers

Very Short Answers [2 Marks]

Question 1.
In the given figure if ∠A = ∠C then prove that ∆AOB ~ ∆COD.

Solution:
In triangles ∆AOB and ∆COD
∠A = ∠C (Y given)
∠AOB = ∠COD [∵ Vertically opposite angles]
∠ABO = ∠CDO [Remaining angles of ∆AOB and ∆COD]
∴ ∆AOB ~ ∆COD [∵ AAA similarity]
∵ ∆AOB ~ ∆COD [∵ AAA similarity]

Question 2.
In the figure AB ⊥ BC and DE ⊥ AC prove that ∆ABC ~ ∆AED.

Solution:
In triangles ∆ABC and ∆AED
∠ABC = ∠AED = 90°
∠BAC = ∠EAD [Each equal to A]
∠ADE = ∠ACB [∵ Remaining angles]
∴ By AAA criteria of similarity ∆ABC ~ ∆AED

Short Answers [3 Marks]

Question 1.
In the figure with respect to ABEP and CPD prove that BP × PD = EP × PC.

Solution:
Proof:
In ∆EPB and ∆DPC
∠PEB = ∠PDC = 90° [given]
∠EPB = ∠DPC [Vertically opposite angles]
∠EPB = ∠PCD [∵ Remaining angles]
Thus,

Long Answers [5 Marks]

Question 1.
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm PB = 6cm, AQ = 5 cm and QC = 10 cm, show that BC = 3 PQ.
Solution:

AB = AP + PB
= 3 + 6 cm = 9 cm
AC = AQ + QC = 510 cm = 15

Students can Download Maths Chapter 4 Geometry Ex 4.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Additional Questions

Construct the quadrilaterals with the following measurements and also find their area.

Question 1.
ABCD, AB = 5 cm, BC 4.5 cm, CD = 3.8 cm, DA = 4.4 cm and AC = 6.2 cm.
Solution:
Given AB = 5 cm,
BC = 4.5 cm,
CD = 3.8 cm,
DA = 4.4 cm,
AC = 6.2 cm

Steps:
1. Draw a line segment AB = 5 cm
2. With A and B as centers drawn arcs of radii 6.2 cm and 4.5cm respectively and let them cut at C.
3. Joined AC and BC.
4. With A and C as centrers drawn arcs of radii 4.4cm and 3.8 cm respectively and let them at D.
5. Joined AD and CD.
6. ABCD is the required quadrilateral.
Calculation of Area:

Question 2.
KITE, KI = 5.4 cm, IT = 4.6 cm, TE= 4.5 cm, KE = 4.8 cm and IE = 6 cm.
Solution:
Given, KI = 5.4 cm,
IT = 4.6 cm,
TE= 4.5 cm,
KE = 4.8 cm,
IE = 6 cm.

Steps:
1. Draw a line segment KI = 5.4 cm
2. With K and I as centers drawn arcs of radii 4.8 cm and 6 cm respectively and let them cut at E.
3. Joined KE and IE.
4. With E and I as centers, drawn arcs of radius 4.5cm and 4.6 cm respectively and let them cut at T.
5. Joined ET and IT.
6. KITE is the required quadrilateral.
Calculation of Area:

Question 3.
PLAY, PL = 7 cm, LA = 6 cm, AY= 6 cm, PA = 8 cm and LY = 7 cm.
Solution:
Given PL = 7 cm,
LA = 6 cm,
AY= 6 cm,
PA = 8 cm,
LY = 7 cm

Steps:
1. Draw a line segment PL = 7 cm
2. With P and L as centers, drawn arcs of radii 8 cm and 6 cm respectively, let them cut at A.
3. Joined PA and LA.
4. With L and A as centers, drawn arcs of radii 7 cm and 6 cm respectively and let them cut at Y.
5. Joined LY, PY and AY.
6. PLAY is the required quadrilateral.
Calculation of Area:

Question 4.
LIKE, LI = 4.2 cm, IK = 7 cm, KE = 5 cm, LK = 6 cm and IE = 8 cm.
Solution:
LI = 4.2 cm,
IK = 7 cm,
KE = 5 cm,
LK = 6 cm,
IE = 8 cm

Steps:
1. Draw a line segment LI = 4.2 cm
2. With L and I as centers, drawn arcs of radii 6 cm and 7 cm respectively and let them cut at K.
3. Joined LK and IK.
4. With I and K as centers, drawn arcs of radius 8 cm and 5 cm respectively and let them cut at E.
5. Joined LE, IE and KE.
6. LIKE is the required quadrilateral.
Calculation of Area:

Question 5.
PQRS, PQ = QR = 3.5 cm, RS = 5.2 cm, SP = 5.3 cm and ∠Q =120° .
Solution:
PQ = QR = 3.5 cm,
RS = 5.2 cm,
SP = 5.3 cm ,
∠Q =120°

Steps:
1. Draw a line segment PQ = 3.5 cm
2. Made ∠Q = 120°. Drawn the ray QX.
3. With Q as centre drawn an arc of radius 3.5 cm. Let it cut the ray QX at R.
4. With R and P as centres drawn arcs of radii 5.2cm and 5.5 cm respectively and let them cut at S.
5. Joined PS and RS.
6. PQRS is the required quadrilateral.
Calculation of Area:
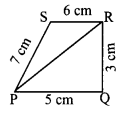
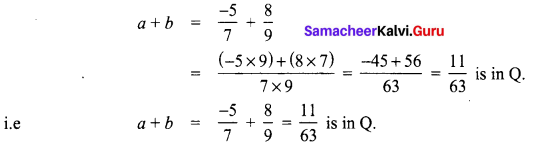
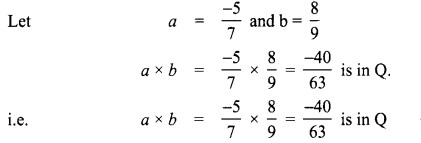
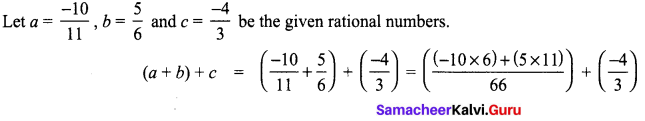
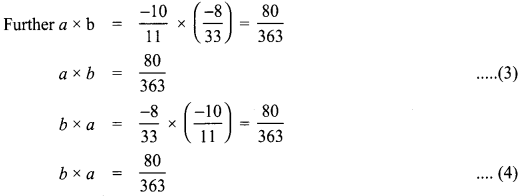
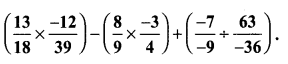
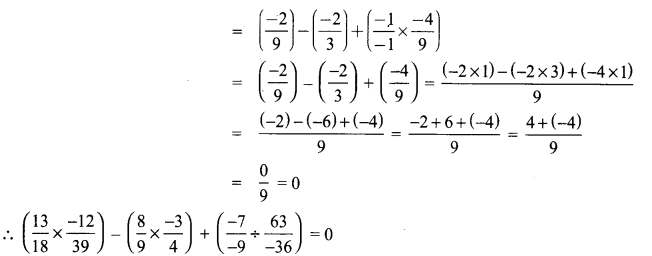
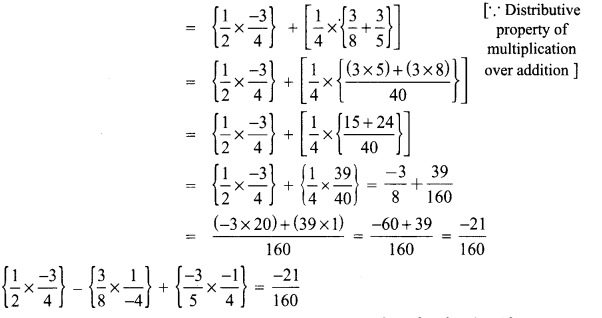
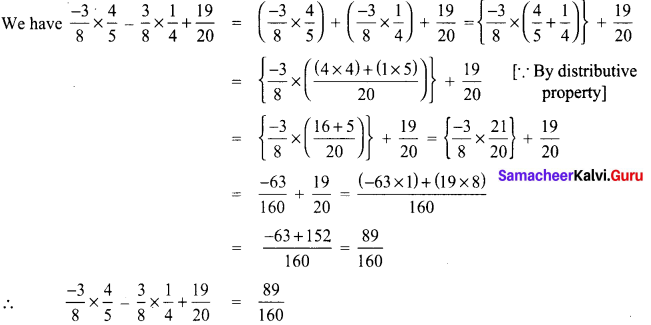
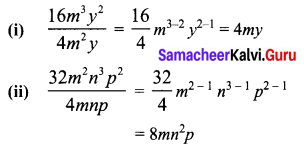
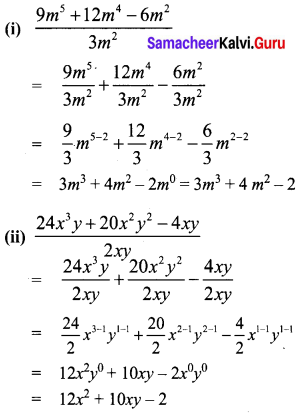
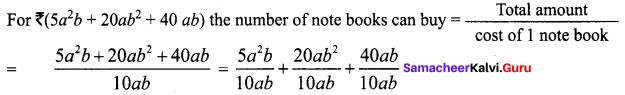
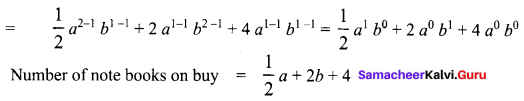
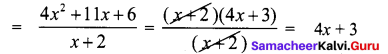
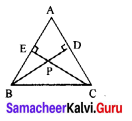
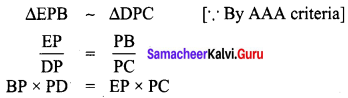
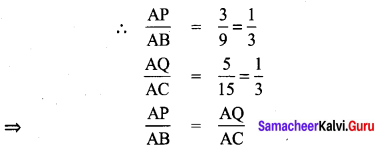
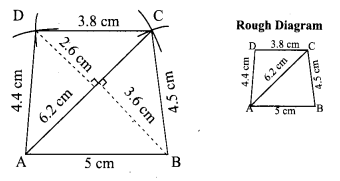
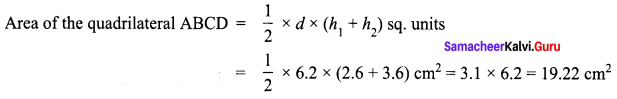
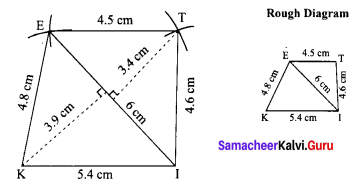
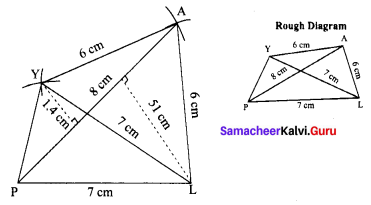
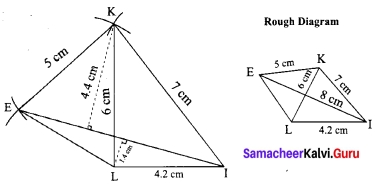
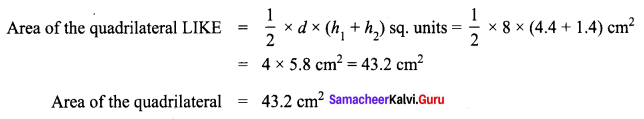
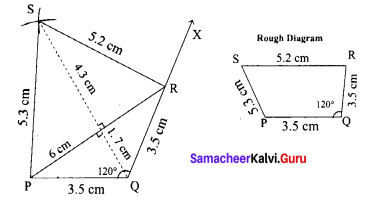
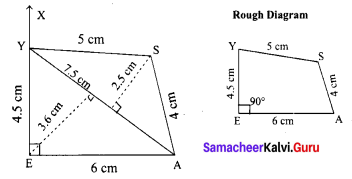
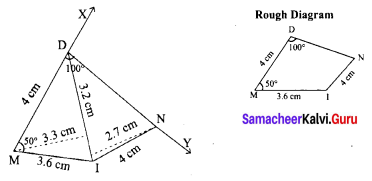
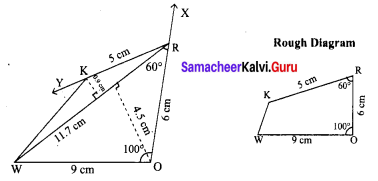
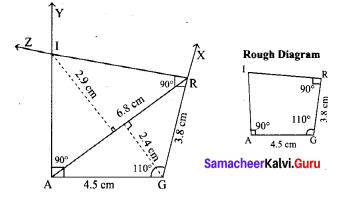
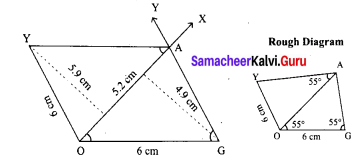
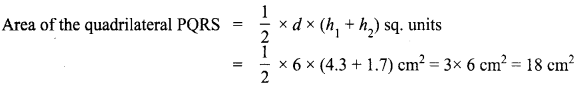Area of the quadrilateral PQRS = 18 cm²

Question 6.
EASY, EA = 6 cm, AS = 4 cm, SY = 5 cm, EY = 4.5 cm and ∠E = 90°.
Solution:
EA = 6 cm,
AS = 4 cm,
SY = 5 cm,
EY = 4.5 cm,
∠E = 90°

1. Drawn a line segment EA = 6 cm
2. Made ∠E = 90°. From E drawn the ray EX.
3. With E as center drawn an arc of 4.5 cm radius. Let of cut the ray EX at Y.
4. With A and Y as centres drawn arcs of radii 4 cm and 5 cm respectively and let them cut at S.
5. Joined AS and YS.
6. EASY is the required quadrilateral.
Calculation of Area:

∴ Area of the quadrilateral = 22.87 cm²

Question 7.
MIND, MI = 3.6 cm, ND = 4 cm, MD = 4 cm, ∠M = 50° and ∠D = 100°.
Solution:
MI = 3.6 cm,
ND = 4 cm,
MD= 4 cm,
∠M = 50°,
∠D = 100°

1. Draw a line segment MI = 3.6 cm
2. At M on MI made an angle ∠IMX = 50°
3. Drawn an arc with center M and radius 4 cm let it cut MX it D
4. At D on DM made an angle ∠MDY = 100°
5. With I as center drawn an arc of radius 4 cm, let it cut DY at N.
6. Joined DN and IN.
7. MIND is the required quadrilateral.
Calculation of Area:

Area of the quadrilateral = 9.6 cm²

Question 8.
WORK, WO = 9 cm, OR = 6 cm, RK = 5 cm, ∠O = 100° and ∠R = 60°.
Solution:
WO = 9 cm,
OR = 6 cm,
RK = 5 cm,
∠O = 100°,
∠R = 60°

Steps:
1. Drawn a line segment WO = 9 cm
2. At O on WO made an angle ∠WOR = 100° and drawn the ray OX.
3. Drawn an arc of radius 6 cm with center O. Let it intersect OX at R.
4. At R on OR, made ∠ORY = 60°, and drawn the ray RY.
5. With center R drawn an arc of radius 5 cm, let it intersect RY at K.
6. Joined WK.
7. WORK is the required quadrilateral.
Calculation of Area:

Area of the quadrilateral = 31.59 cm²

Question 9.
AGRI, AG = 4.5 cm, GR = 3.8 cm, ∠A = 90°, ∠G = 110° and ∠R = 90°.
Solution:
AG = 4.5 cm,
GR = 3.8 cm,
∠A = 90°,
∠G = 110°,
∠R = 90°

1. Draw a line segment AG = 4.5 cm
2. At G on AG made ∠AGX =110°
3. With G as centre drawn an arc of radius 3.8 cm let it cut GX at R.
4. At R on GR made ∠GRZ = 90°
5. At A on AG made ∠GAY = 90°
6. AY and RZ meet at I.
7. AGRI is the required quadrilateral.
Calculation of Area:

Question 10.
YOGA, YO = 6 cm, OG = 6 cm, ∠O = 55°, ∠G = 55° and ∠A = 55°.
Solution:
YO = 6 cm,
OG = 6 cm,
∠O = 55°,
∠G = 55°,
∠A = 55°

Steps:
1. Draw a line segment OG = 6 cm
2. At G on DG made an angle ∠OGY = 55°
3. AT G on GO made ∠GOX = 55°.
4. GY and OX meet cut A.
5. At A on OA made ∠OAZ = 55°
6. Drawn an arc of radius 6 cm with center O. It cut AZ at Y. Joined OY.
7. YOGA is the required quadrilateral.
Calculation of Area:

Area of the quadrilateral YOGA = 28.08 cm²

Students can Download Maths Chapter 4 Geometry Ex 4.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.2

Miscellaneous Practice Problems

Question 1.
In the given figure, find PT given that l₁ || l₂

Solution:
Given that l₁ || l₂
∴ In ∆PQS and ∆PRT
∠P is common
∠Q = ∠R [∵ PR is the transversal for l₁ and l₂ corresponding angles]
∠S = ∠T [∵ corresponding angles]
∴ ∆PQS ~ ∆PRT [∵ By AAA congruency]
In similar triangles, corresponding angles are proportional.

Question 2.
From the diagram, prove that ∆SUN ~ ∆RAY

Proof:
From the ∆SUN and ∆RAY
SU = 10;
UN = 12;
SN = 14;
RA = 5,
AY = 6;
RY = 7
We have

Question 3.
The height of a tower is measured by a mirror on the ground by which the top of the tower’s reflection is seen. Find the height of the tower.
Solution:
The image and its reflection make similar shapes

Question 4.
In the figure, given that ∠1 = ∠2 and ∠3 ≡ ∠4 Prove that ∆MUG ≡ ∆ TUB.

Proof:

Question 5.
If ∆WAR ≡ ∆MOB, name the additional pair of corresponding parts. Name the criterion used by you.
Solution:

Given ∆WAR ≡ ∆MOB
∠RWA ≡ ∠BMO [∵ sum of three angles of a triangle are 180°]
∴ Criteria used here is angle sum property of triangles.

Question 6.
In the figure, ∠TMA ≡ ∠IAM and ∠TAM ≡ ∠IMA. P is the midpoint of MI and N is the midpoint of AI. Prove that ∆ PIN ~ ∆ ATM.

Solution:

Question 7.
In the figure, if ∠FEG = ∠1 then, prove that DG² = DE.DF.

Proof:

Question 8.
In the figure, ∠TEN ≡ ∠TON = 90° and TO = TE. Prove that ∠ORN ≡ ∠ERN

Solution:

Question 9.
In the figure, PQ ≡ TS, Q is the midpoint of PR, S is the midpoint TR and ∠POU ≡ ∠TSU. Prove that QU ≡ SU.

Proof:

Question 10.
In the figure ∆TOP ≡ ∆ARM . Explain why?
Solution:
In ∆TOP and ∆ARM
OP = RM given
∠TOP = ∠ARM = 90°
given ∠OTP = ∠RAM
given ∠OPT = ∠RMA Remaining angle, by angle sum property.
∴ By ASA criteria we can say that ∆TOP ≡ ∆ARM