Category: Class 7

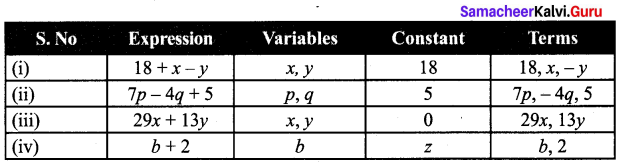
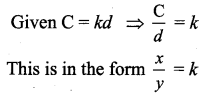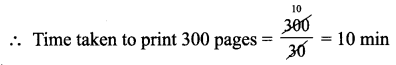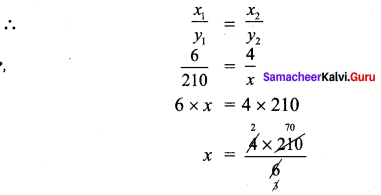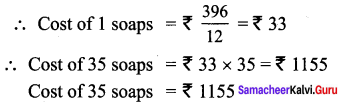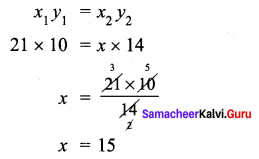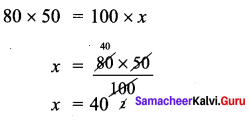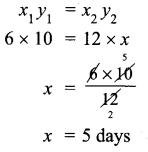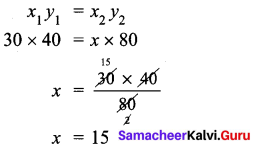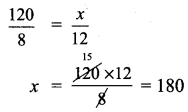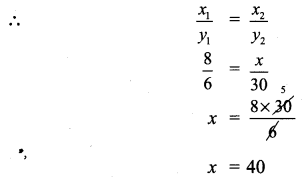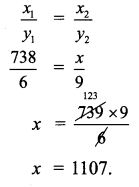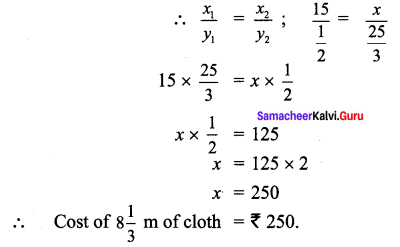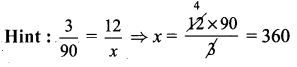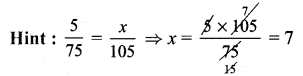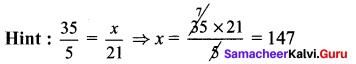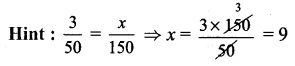Students can Download Maths Chapter 2 Measurements Ex 2.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.3

Question 1.
Find the area of a circular pathway whose outer radius is 32 cm and inner radius is 18 cm.
Solution:
Radius of the outer circle R = 32 cm
Radius of the inner circle r = 18 cm
Area of the circular pathway = π (R² – r²) sq. units = \(\frac { 22 }{ 7 } \) (32² – 18²) cm²
= \(\frac { 22 }{ 7 } \) × (32 + 18) × (32 – 18) cm²
= \(\frac { 22 }{ 7 } \) × 50 × 14 cm² = 2,200 cm²
Area of the circular pathway = 2,200 cm²

Question 2.
There is a circular lawn of radius 28 m. A path of 7 m width is laid around the lawn. What will be the area of the path?
Solution:
Radius of the circular lawn r = 28 m
Radius of the lawn with path = 28 + 7 m = 35 m
Area of the circular path = π (R² – r²) sq. units
Area of the path = \(\frac { 22 }{ 7 } \) (35² – 28²) m² = \(\frac { 22 }{ 7 } \) × (35 + 28) (35 – 28) m²
= \(\frac { 22 }{ 7 } \) × 63 × 7 m² = 1386 m²
Area of the path = 1386 m²

Question 3.
A circular carpet whose radius is 106 cm is laid on a circular hall of radius 120 cm. Find the area of the hall uncovered by the carpet.
Solution:
Radius of the circular hall R = 120 cm
Radius of the circular carpet r = 106 cm
Area of the hall uncovered = Area of the hall – Area of the carpet
= π (R² – r²) cm²
= \(\frac { 22 }{ 7 } \) × (120² – 106²) cm²
= \(\frac { 22 }{ 7 } \) × (120 + 106) × (120 – 106) cm²
= \(\frac { 22 }{ 7 } \) × 226 × 14 cm² = 9,944 cm²
Area of the hall uncovered = 9, 944 cm²

Question 4.
A school ground is in the shape of a circle with radius 103 m. Four tracks each of 3 m wide has to be constructed inside the ground for the purpose of track events. Find the cost of constructing the track at the rate of ₹ 50 per sq.m.

Solution:
Radius of the ground R = 103 m
Width of a track W = 3 m
Width of 4 tracks = 4 × 3 = 12 m
Radius of the ground without track
r = (103 – 12)m
r = 91 m
Area of 4 tracks = Area of the ground
– Area of the ground without crack
= πR² – πr² sq.units
= π(R² – r²) sq.units
= \(\frac { 22 }{ 7 } \) [103² – 91²]
= \(\frac { 22 }{ 7 } \) [103 + 91] [103 – 91]m²
= \(\frac { 22 }{ 7 } \) × 194 × 12 = \(\frac { 51216 }{ 7 } \) = 7316.57 m²
∴ Area of 4 tracks = 7316.57 m²
Cost of constructing 7316.57 m² = ₹ 50
∴ Cost of constructing 7316.57 m² = ₹ 50 × 7316.57 = ₹ 3,65,828,57
Cost of constructing the track ₹ 3,65,828,57

Question 5.
The figure shown is the aerial view of the pathway. Find the area of the pathway.

Solution:
Area of the rectangle = (Lenght × Breadth) sq. units
Area of the outer rectangle = (L × B) sq. units
Length of the outer rectangle L = 80 m
Breadth of the outer rectangle B = 50 m
Length of the inner rectangle l = 70 m
Breadth of the inner rectangle b = 40 m
Area of the outer rectangle = 80 × 50 m² = 4000 m²
Area of the inner rectangle = l × b sq. unit = 70 × 40 m² = 2800 m²
Area of the pathway = Area of the outer rectangle
– Area of the inner rectangle
= 4000 – 2800 m² = 1200 m²
Area of the pathway = 1200 m²

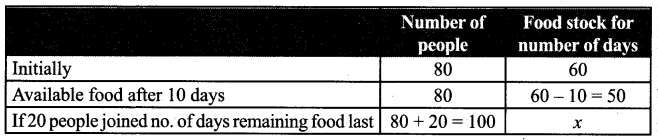
Question 6.
A rectangular garden has dimensions 11 m × 8 m. A path of 2 m wide has to be constructed along its sides. Find the area of the path.
Solution:
Area of the rectangular garden L × B = 11 m × 8 m = 88 m²
Length of the inner rectangle L = L – 2 W = 11 – 2(2) = 11 – 4 = 7 m
Breadth of the inner rectangle b = B – 2W = 8 – 2(2) = 8 – 4 = 4 m
Area of the inner rectangle = l × b sq. units = 7 × 4 m² = 28 m²
Area of the path = Area of the outer rectangular garden
– Area of the inner rectangle
= 88 m² – 28m² = 60 m²
Area of the path = 60 m²

Question 7.
A picture is painted on a ceiling of a marriage hall whose length and breadth are 18 m and 7 m respectively. There is a border of 10 cm along each of its sides. Find the area of the border.
Solution:
Length of the ceiling L = 18 m
Breadth of the ceiling B = 7 m
Area of the ceiling = L × B sq. units = 18 × 7 m² = 126 m²
Width of the boarder W = 10 cm = \(\frac { 10 }{ 100 } \) m = 0.1 m
Length of the ceiling without border = L – 2W = 18 – 2(0.1) m
= 18 – 0.2 m = 17.8 m
Breadth of the ceiling without border = B – 2W = 7 – 2 (0.1) m
= 7 – 0.2 m = 6.8 m
Area of the ceiling without border = l × b sq.units
= 17.8 × 6.8 m² = 121.04 m²
∴ Area of the border = Area of the ceiling
– Area of the ceiling without border
= 126 – 121.04 m² = 4.96 m²
Area of the border = 4.96 m²

Question 8.
A canal of width 1 m is constructed all along inside the field which is 24 m long and 15 m wide. Find (i) the area of the canal (ii) the cost of constructing the canal at the rate of ₹ 12 per sq.m.
Solution:
Length of the field L = 24 m
Width (Breadth) of the field B = 15 m
(i) Area of the field = L × B sq. units = 24 × 15 m² = 360 m²
(ii) Width of the canal (W) = 1 m
Length of the field without canal (l) = L – 2(W) = 24 – 2(1) m
= 24 – 2 m = 22 m
Width of the field without canal (b) = B – 2W = 15 – 2(1) m
= 15 – 2 m = 13 m
Area of the field without canal = l × b sq. units = 22 × 13 m² = 286 m²
Area of the canal = 360 – 286 = 74 m²
Cost of constructing 1 m² canal = ₹ 12
Cost of the constructing 74 m² canal = ₹ 12 × 74 = ₹ 888

Objective Type Question

Question 9.
The formula to find the area of the circular path is
(i) π(R² – r²) sq. units
(ii) πr² sq. units
(iii) 2πr² sq. units
(iv) πr² + 2r sq. units
Answer:
(i) π(R² – r2) sq. units

Question 10.
The formula used to find the area of the rectangular path is
(i) p(R² – r²) sq. units
(ii) (L × B) – (l × b) sq. units
(iii) LB sq. units
(iv) lb sq. units
Answer:
(ii) (L × B) – (l × b) sq. units

Question 11.
The formula to find the width of the circular path is
(i) (L – l) units
(ii) (B – b) units
(iii) (R – r) units
(iv) (r – R) units
Answer:
(iii) (R – r) units

Students can Download Maths Chapter 1 Number System Ex 1.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 1 Number System Ex 1.1

Question 1.
Write the decimal numbers for the following pictorial representation of numbers.

Solution:
(i) Tens 2 ones 2 tenths = 12.2
(ii) Tens 1 ones 3 tenths = 21.3

Question 2.
Express the following in cm using decimals.
(i) 5 mm
(ii) 9 mm
(iii) 42 mm
(iv) 8 cm 9 mm
(v) 375 mm
Solution:
(i) 5 mm
1 mm = \(\frac { 1 }{ 10 } \) cm = 0.1 cm
5 mm = \(\frac { 5 }{ 10 } \) = 0.5 cm

(ii) 9 mm
1 mm = \(\frac { 1 }{ 10 } \) cm = 0.1 cm
9 mm = \(\frac { 9 }{ 10 } \) cm = 0.9 cm

(iii) 42 mm
1 mm = \(\frac { 1 }{ 10 } \) cm = 0.1 cm
42 mm = \(\frac { 42 }{ 10 } \) cm = 4.2 cm

(iv) 8 cm 9 mm
1 mm = \(\frac { 1 }{ 10 } \) cm = 0.1 cm
8 cm 9 mm = 8 cm + \(\frac { 9 }{ 10 } \) cm = 8.9 cm

(v) 375 mm
1 mm = \(\frac { 1 }{ 10 } \) cm = 0.1 cm
375 mm = \(\frac { 375 }{ 10 } \) cm = 37.5 cm

Question 3.
Express the following in metres using decimals.
(i) 16 cm
(ii) 7 cm
(iii) 43 cm
(iv) 6 m 6 cm
(v) 2 m 54 cm
Solution:
(i) 16 cm
1 cm = \(\frac { 1 }{ 100 } \) cm = 0.01 m
16 cm = \(\frac { 16 }{ 100 } \) m = 0.16 m

(ii) 7 cm
1 cm = \(\frac { 1 }{ 100 } \) cm = 0.01 m
1 cm = \(\frac { 7 }{ 100 } \) m = 0.07 m

(iii) 43 cm
1 cm = \(\frac { 1 }{ 100 } \) cm = 0.01 m
43 cm = \(\frac { 43 }{ 100 } \) m = 0.43 m

(iv) 6 m 6 cm
1 cm = \(\frac { 1 }{ 10 } \) m = 0.01 m
6 m 6 cm = 6 m + \(\frac { 6 }{ 100 } \) m = 6 m + 0.06 m = 6.06 m

(v) 2 mm 54 cm
1 cm = \(\frac { 1 }{ 100 } \) cm = 0.01 m
2 m 54 cm = 2 m + \(\frac { 54 }{ 100 } \) m = 2 m + 0.54 m = 2.54 m

Question 4.
Expand the following decimal numbers.
(i) 37.3
(ii) 658.37
(iii) 237.6
(iv) 5678.358
Solution:
(i) 37.3 = 30 + 7 + \(\frac { 3 }{ 10 } \) = 3 × 10¹ + 7 × 10⁰ + 3 × 10^-1

(ii) 658.37 = 600 + 50 + 8 + \(\frac { 3 }{ 10 } \) + \(\frac { 7 }{ 100 } \)
= 6 × 10² + 5 × 10¹ + 8 × 100 + 3 × 10^-1 + 7 × 10^-2

(iii) 237.6 = 200 + 30 + 7 + \(\frac { 6 }{ 10 } \)
= 2 × 10² + 3 × 10¹ + 7 × 10⁰ + 6 × 10^-1

(iv) 5678.358 = 5000 + 600 + 70 + 8 + \(\frac { 3 }{ 10 } \) + \(\frac { 5 }{ 100 } \) + \(\frac { 8 }{ 1000 } \)
= 5 × 10³ + 6 × 10² + 7 × 10¹ + 8 × 10⁰ + 3 × 10^-1 + 5 × 10^-2 + 8 × 10^-3

Question 5.
Express the following decimal numbers in place value grid and write the place value of the underlined digit.
(i) 53.61
(ii) 263.271
(iii) 17.39
(iv) 9.657
(v) 4972.068
Solution:
(i) 53.61

(ii) 263.271

(iii) 17.39

(iv) 9.657

(v) 4972.068

Objective Type Questions

Question 6.
The place value of 3 in 85.073 is _____
(i) tenths
(ii) hundredths
(iii) thousands
(iv) thousandths
Answer:
(iv) thousandths
Hint: 1000 g = 1 kg; 1 g = \(\frac { 1 }{ 1000 } \) kg

Question 7.
To convert grams into kilograms, we have to divide it by
(i) 10000
(ii) 1000
(iii) 100
(iv) 10
Answer:
(ii) 1000
Hint: 85.073 = 8 × 10 + 5 × 1 + 0 × \(\frac { 1 }{ 10 } \) + 7 × \(\frac { 1 }{ 100 } \) + 3 × \(\frac { 1 }{ 1000 } \)

Question 8.
The decimal representation of 30 kg and 43 g is ____ kg.
(i) 30.43
(ii) 30.430
(iii) 30.043
(iv) 30.0043
Answer:
(iii) 30.043
Hint: 30 kg and 43 g = 30 kg + \(\frac { 43 }{ 1000 } \) kg = 30 + 0.043 = 30.043

Question 9.
A cricket pitch is about 264 cm wide. It is equal to _____ m.
(i) 26.4
(ii) 2.64
(iii) 0.264
(iv) 0.0264
Answer:
(ii) 2.64
Hint: 264 cm = \(\frac { 264 }{ 100 } \) m = 2.64 m

Students can Download Maths Chapter 3 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Additional Questions

Additional Questions and Answers

Exercise 3.1

Question 1.
Write any three expressions each having 4 terms:
Solution:
(i) 2x³ – 3x² + 3xy + 8
(ii) 7x³ + 9y² – 2xy² – 6
(iii) 9x² – 2x + 3xy – 1

Question 2.
Identify the co-efficients of the terms of the following expressions
(i) 2x – 2y
(ii) x + y +3
Solution:
(i) 2x – 2y
The co-efficient of x in 2x is 2
The co-efficient of y in – 2y is – 2

(ii) x + y + 3
The co-efficient of x is 1
The co-efficient ofy is 1
The constant term is 3

Question 3.
Group the like terms together from the following: 6x, 6, -5x, – 5, 1, x, 6y, y, 7y, 16x, 3
Solution:
We have 6x, -5x, x, 16x are like terms
6y, y, 7y, are like terms
6, – 5, 1, 3 are like terms

Question 4.
Give the algebraic expressions for the following cases:
(i) One half of the sum of a and b.
(ii) Numbers p and q both squared and added
Solution:
(i) \(\frac{1}{2}\) (a + b)
(ii) p² + q²

Exercise 3.2

Question 1.
If A = 2a² – 4b – 1 ; B = 5a² + 3b – 8 and C = 2a² – 9b + 3 then find the value of A – B + C.
Solution:
Given A = 2a² – 4b – 1 ; B = 5a² + 3b – 8 ; C = 2a² – 9b + 3
A – B + C = (2a² – 4b – 1) – (5a² + 3b – 8) + (2a² – 9b + 3)
= 2a² – 4b – 1 + (-5a² – 3b + 8) + 2a² – 9b + 3
= 2a² – 4b – 1 – 5a² – 3b + 8 + 2a² – 9b + 3
= 2a² – 5a² + 2a² – 4b – 3b – 9b – 1 + 8 + 3
= (2 – 5 + 2) a² + (-4 – 3 – 9) 6 + (-1 + 8 + 3)
= -a² – 16b + 10

Question 2.
How much 2x³ – 2x² + 3x + 5 is greater than 2x³ + 7x² – 2x + 7?
Solution:
The required expression can be obtained as follows.
= 2x³ – 2x² + 3x + 5 – (2x³ + 7x² – 2x + 7)
= 2x³ – 2x² + 3x + 5 + (-2x³ – 7x² + 2x – 7)
= 2x³– 2x² + 3x + 5 – 2x³ – 7x² + 2x – 7
= (2 – 2) x³ + (-2 – 7) x² + (3 + 2) x + (5 – 7)
= 0x³ + (-9x²) + 5x – 2 = -9x² + 5x – 2
∴ 2x³ – 2x² + 3x + 5 is greater than 2x³ + 7x² – 2x + 7 by -9x² + 5x – 2

Question 3.
What should be added to 2b² – a² to get b² – 2a²
Solution:
The required expression is obtained by subtracting 2b² – a² from b² – 2a²
b² – 2a² – (2b² – a²) = b² – 2a² + (-2b² + a²)
= b² – 2a² – 2b² + a²
= (1 – 2) b² + (-2 + 1) a² = -b² – a²
So -b² – a² must be added

Exercise 3.3

Question 1.
Length of one side of an equilateral triangle is 3x – 4 units. Find the perimeter.
Solution:
Equilateral triangle has three sides equal.
Perimeter = Sum of three sides
= (3x – 4) + (3x – 4) + (3x – 4) = 3x – 4 + 3x – 4 + 3x – 4
= (3 + 3 + 3)x + [(-4) + (-4) + (-4)] = 9x + (-12) = 9x – 12
∴ Perimeter = 9x – 12 units.

Question 2.
Find the perimeter of a square whose side is y – 2 units.
Solution:
Perimeter = (y – 2) + (y – 2) + (y – 2) + (y – 2)
= y – 2 + y – 2 + y – 2 + y – 2 = 4y – 8
Perimeter of the square = 4y – 8 units.

Question 3.
Simplify 3x – 5 – x + 9 if x = 3
Solution:
3x – 5 – x + 9 = 3(3) – 5 – 3 + 9
= 9 – 5 – 3 + 9 = 18 – 8 = 10

Students can Download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.4

Miscellaneous Practice Problems

Question 1.
Subtract – 3ab – 8 from 3ab – 8. Also subtract 3ab + 8 from -3ab – 8.
Solution:
Subtracting -3ab – 8 from 3ab + 8
= 3ab + 8 – (-3ab – 8) = 3ab + 8 + (3ab + 8)
= 3ab + 8 + 3ab + 8 = (3 + 3) ab + (8 + 8)
= 6ab + 16
Also subtracting 3 ab + 8 from – 3ab – 8
= – 3ab – 8 – (3ab + 8) = – 3ab – 8 + (-3ab – 8) = – 3ab – 8 – 3 ab – 8
= [(-3) + (- 3)] ab + [(-8) + (-8)] = – 6ab + (- 16)
= -6ab – 16

Question 2.
Find the perimeter of a triangle whose sides are x + 3y, 2x + y, x – y.
Solution:
Perimeter of a triangle = Sum of three sides
= (x + 3y) + (2x + y) + (x – y)
= x + 3y + 2x + y + x – y
= (1 + 2 + 1)x + (3 + 1 + (-1))y = 4x + 3y
∴ Perimeter of the triangle = 4x + 3y

Question 3.
Thrice a number when increased by 5 gives 44. Find the number.
Solution:
Let the required number be x.
Thrice the number = 3x.
Thrice the number increased by 4 = 3x + 5
Given 3x + 5 = 44
3x + 5 – 5 = 44 – 5
3x = 39
\(\frac{3 x}{3}=\frac{39}{3}\)
x = 13
∴ The required number = 13

Question 4.
How much smaller is 2ab + 4b – c than 5ab – 3b + 2c.
Solution:
To find the answer we have to find the difference.
Here greater number 5ab – 3ab + 2c.
∴ Difference = 5ab – 3b + 2c – (2ab + 4b – c) = 5ab – 3b + 2c + (- 2ab -4b + c)
= 5ab – 3b + 2c – 2ab – 4b + c
= (5 – 2) ab + (-3 – 4) b + (2 + 1) c = 3ab + (-7)b + 3c
= 3ab – 7b + 3c
It is 3ab – 7b + 3c smaller.

Question 5.
Six times a number subtracted from 40 gives – 8. Find the number.
Solution:
Let the required number be x. Six times the number = 6x.
Given 40 – 6x = – 8
-6x + 40 – 40 = -8 – 40
– 6x = – 48
\(\frac{-6 x}{-6}=\frac{-48}{-6}\)
x = 8
∴ The required number is 8.

Challenge Problems

Question 6.
From the sum of 5x + 7y -12 and 3x – 5y + 2, subtract the sum of 2x – 7y – 1 and – 6x + 3y + 9.
Solution:
Sum of 5x + 7y – 12 and 3x – 5y + 2 .
= 5x + 7y- 12 + 3x – 5y + 2 = (5 + 3) x + (7 – 5) y + ((- 12) + 2)
= 8x + 2y – 10.
Again Sum of 2x – 7y – 1 and – 6x + 3y + 9
= 2x – 7y – 1 + (- 6x + 3y + 9) = 2x – 7y – 1 – 6x + 3y + 9
= (2 – 6) x + (- 7 + 3) y + (- 1 + 9)
= – 4x – 4y + 8
Now 8x + 2y – 10 – (-4x – 4y + 8)
= 8x + 2y – 10 + (4x + 4y – 8)
= 8x + 2y – 10 + 4x + 4y – 8
= (8 + 4) x + (2 + 4) y + ((- 10) + (- 8))
= 12x + 6y – 18

Question 7.
Find the expression to be added with 5a – 3b – 2c to get a – 4b – 2c?
Solution:
To get the required expression we must subtract 5a – 3b + 2c from a – 4b – 2c.
∴ a – 4b – 2c – (5a – 3b + 2c) = a – 4b – 2c + (- 5a + 3b – 2c)
= a – 4b – 2c – 5a + 3b -2c
= (1 – 5) a + (- 4 + 3) b + (- 2 – 2) c
= – 4a – b – 4c.
∴ -4a – b – 4c must be added.

Question 8.
What should be subtracted from 2m + 8n + 10 to get – 3m + 7n + 16?
Solution:
To get the expression we have to subtract – 3m + 7n + 16 from 2m + 8n + 10.
(2m + 8n + 10) – (-3m + 7n + 16) = 2m + 8n + 10 + 3m – 7n – 16
= (2 + 3) m + (8 – 7) n + (10 – 16)
= 5m + n – 6

Question 9.
Give an algebraic equation for the following statement:
“The difference between the area and perimeter of a rectangle is 20”.
Solution:
Let the length of a rectangle = l and breadth = b then Area = lb; Perimeter = 2(1 + b)
Area – Perimeter = 20
∴ lb – 2(l + b)

Question 10.
Add : 2a + b + 3c and a + \(\frac{1}{3}\)b + \(\frac{2}{5}\)c
Solution:

Students can Download Maths Chapter 3 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Intext Questions

Exercise 3.1

Try These (Text Book Page No. 51)

Question 1.
Identify the variable and constants among the following terms.
a, 11 – 3x, xy, -89, -m, -n, 5, 5ab, -5 3y, 8pqr, 18, -9t, -1, -8
Solution:
Variable : a, -3x, xy, -m, -n, 5ab, 3y, -9t, 8pqr
Constants : 11, -89, 5, -5, 18, -1, -8

Question 2.
Complete the following table.

Solution:

Try this (Text book Page No. 53)

Question 1.
Can we use the operations multiplication and division to combine terms?
Solution:
No, We can use addition and subtraction to combine terms.
If we use multiplication or division to combine then it become a single term.
Eg : xy, \(\frac{x}{y}\) are monomials.

Try This (Text book Page No. 54)

Question 1.
Complete the following table by forming expressions using the terms given. One is done for you.

Solution:

Try this (Text book Page No. 56)

Question 1.
Identify the like terms among the following and group them.
7xy, 19x, 1, 5y, x, 3yx, 15, -13y, 6x, 12xy, -5, 16y, -9x, 15xy, 23, 45y, -8y, 23x, -y, 11
Solution:
7xy, 3yx, 12xy, 15xy, are like terms
19x, x, 6x,-9x, 23x, are like terms
5y, -13y, 16y, 45y, -8y, -y, are like terms
1, 15, -5, 23, 11, are like terms.

Try This (Text book Page No. 57)

Question 1.
Try to find the value of the following expressions if p = 5 and q = 6.
(i) p + q
(ii) q – p
(iii) 2p + 2 > q
(iv) pq – p – q
(v) 5pq – 1
Solution:
(i) Given p = 5; q = 6
p + q = 5 + 6 = 11
(ii) q – p = 6 – 5 = 1
(iii) 2p + 2 > q = 2(5) + 3(6) = 10 + 18 = 28
(iv) pq – p – q = (5) (6) – 5 – 6 = 30 – 5 – 6 = 25 – 6 = 19

Exercise 3.2

Try These (Text book Page No. 59)

Question 1.
Add the terms
(i) 3p, 14p
(ii) m, 12m, 21m
(iii) 11abc, 5abc
(iv) 12y, -y
(v) 4x, 2x, -7x.
Solution:
(i) 3p + 14p = 17p
(ii) m + 12m + 21m = (1 + 12 + 21 )m
= 34 m
(iii) 11abc + 5abc = (11 + 5) abc
= 16 abc
(iv) 12y + (-y) = (12 + (-1))y
= (12 – 1 )y
= 11y
(v) 4x + 2x + (-7x) = (4 + 2+(-7))x
= (6 + (-7))x
= -1x

Ty this (Text Book Page No. 60)

Question 1.
3x; + (y – x) = 3x + y – x, but 3x – (y – x) ≠ 3x – y – x. why ?
Solution:
In the first case
LHS = 3x + (y – x) = 3x + y – x = 3x – x + y = (3 – 1)x + y
= 2x + y
RHS = 3x + y – x = 2x + y
LHS = RHS ⇒ 3x + (y – x) = 3x + y – x
But in the second case
LHS = 3x – (y – x) = 3x – y + x
= (3 + 1)x – y = 4x – y
RHS = 3x – y – x = 3x – x – y
LHS ≠ RHS
∴ 3x – (y – x) ≠ 3x – y – x

Try this (Page No. 1)

Question 1.
What will you get if twice a number is subtracted from thrice the same number?
Solution:
Let the unknown number be x.
Twice the number = 2x.
Thrice the number = 3x.
Twice the number is subtracted from thrice the number = 3x – 2x = (3 – 2)x = x

Exercise 3.3

Try These (Text book Page No. 65)

Question 1.
Try to construct algebraic equations for the following verbal statements.

Question 1.
One third of a number plus 6 to 10.
Solution:
\(\frac{1}{3}\) + 6 = 10

Question 2.
The sum of five times of x and 3 is 28
Solution:
5 (x + 3) = 28

Question 3.
Taking away 8 from y gives 11
Solution:
y – 8 = 11

Question 4.
Perimeter of a square with side a is 16 cm.
Solution:
4 × a = 16

Question 5.
Venkat’s mother’s age is 7 years more than 3 times venkat’s age. His mother’s age is 43 years.
Solution:
3x + 7 = 43, where x is venkat’s age.

Try this (Text book Page No. 65)

Question 1.
Why should we subtract 5 and not some other number ? why don’t we add 5 on both sides? Discuss.
Solution:
Given x + 5 = 12
(i) Our aim is to find the value of x. Which means we have to eliminate the other values from LHS. Since 5 is given with x it should be subtracted.
(ii) If we add 5 on both sides we cannot eliminate the numbers from LHS and we get x + 10.

Try this (Text book Page No. 66)

Question 1.
If the dogs, cats and parrots represents unknown find them. Substitute each of the values so obtained in the equations and verify the answers.
Solution:
(i) 1 dog + 1 dog + 1 dog = 24
3 dog = 24

(ii) 1 dog + 1 cat + 1 cat = 14
1 dog + 2cat = 14
8 + 2cat = 14
2cat = 14 – 8
2 cat = 6
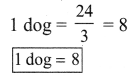
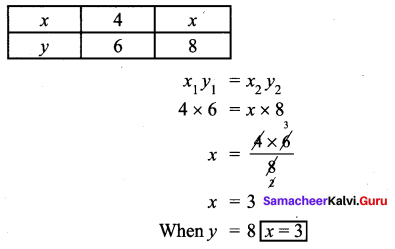
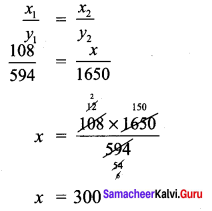
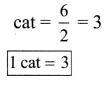ditional Questions 63″ width=”107″ height=”87″ />

(iii) 1 dog + 1 cat – 1 parrot = 9
8 + 3 – 1 parrot = 9
8 + 3 – 9 = 1 parrot
11 – 9 = 1 parrot
2 = 1 parrot
1 parrot = 2

(iv) 1 dog + 1 cat + 1 parrot = ?
8 + 3 + 2 = 13
Verification:
(i) 8 + 8 + 8 = 24
(ii) 8 + 3 + 3 = 14
(iii) 8+ 3 – 2 = 9
(iv) 8 + 3 + 2 = 13

Try These (Text book Page No. 68)

Question 1.
Kandhan and kaviya are friends. Both of them are having some pen. Kandhan: If you give me one pen then, we will have equal number of pens. Will you? Kaviya: But, if you give me one of your pens, then mine will become twice as yours. Will you?
Construct algebraic equations for this situation, can you guess and find the actual number of pens, they have?
Solution:
Let the number of pens initially Kandhan and Kaviya had be x and y respectively.

Students can Download Maths Chapter 3 Algebra Ex 3.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.3

Question 1.
Fill in the blanks.
(i) An expressions equated to another expression is called _______.
(ii) If a = 5, the value of 2a + 5 is _______.
(iii) The sum of twice and four times of the variable x is ______.
Solution:
(i) an equation
(ii) 15
(iii) 6x

Question 2:
Say True or False
(i) Every algebraic expression is an equation.
(ii) The expression 7x + 1 cannot be reduced without knowing the value of x.
(iii) To add two like terms, its coefficients can be added.
Solution:
(i) False
(ii) True
(iii) True

Question 3.
Solve (i) x + 5 = 8
(ii) p – 3 = 1
(iii) 2x = 30
(iv) \(\frac{m}{6}\) = 5
(v) 7x + 10 = 80
Solution:
(i) Given x + 5 = 8 ; Subtracting 5 on both the sides
x + 5 – 5 = 8 – 5
x = 3

(ii) Given p – 3 = 7 ; Adding 3 on both the sides,
p – 3 + 3 = 7 + 3
p = 10

(iii) Given 2x = 30 ; Dividing both the sides by 2,
\(\frac{2 x}{2}=\frac{30}{2}\)
x = 15

(iv) Given \(\frac{m}{6}\) = 5 ; Multiplying both the sides by 6,
\(\frac{m}{6}\) × 6 = 5 × 6
m = 30

(v) Given 7x + 10 = 80 ; Subtracting 10 from both the sides,
7x + 10 – 10 = 80 – 10
7x = 70
Dividing both sides by 7,
\(\frac{7 x}{7}=\frac{70}{7}\)
x = 10

Question 4.
What should be added to 3x + 6y to get 5x + 8y?
Solution:
To get the expression we should subtract 3x + 6y from 5x + 8y
5x + 8y – (3x + 6y) = 5x + 8y + (-3x – 6y)
= 5x + 8y – 3x – 6y = (5 – 3) x + (8 – 6) y
= 2x + 2y
So 2x + 2y should be added.

Question 5.
Nine added to thrice a whole number gives 45. Find the number
Solution:
Let the whole number required be x.
Thrice the whole number = 3x
Nine added to it = 3x + 9
Given 3x + 9 = 45
3x + 9 – 9 = 45 – 9 [Subtracting 9 on both sides]
3x = 36
\(\frac{3 x}{3}=\frac{36}{3}\)
x = 12
∴ The required whole number is 12

Question 6.
Find the two consecutive odd numbers whose sum is 200
Solution:
Let the two consecutive odd numbers be x and x + 2
∴ Their sum = 200
x + (x + 2) = 200
x + x + 2 = 200
2x + 2 = 200
2x + 2 – 2 = 200 – 2 [∵ Subtracting 2 from both sides]
2x = 198
\(\frac{2 x}{2}=\frac{198}{2}\) [Dividing both sides by 2]
x = 99
The numbers will be 99 and 99 + 2.
∴ The numbers will be 99 and 101.

Question 7.
The taxi charges in a city comprise of a fixed charge of ₹ 100 for 5 kms and ₹ 16 per km for ever additional km. If the amount paid at the end of the trip was ₹ 740, find the distance traveled.
Solution:
Let the distance travelled by taxi be ‘x’ km
For the first 5 km the charge = ₹ 100
For additional kms the charge = ₹ 16(x – 5)
∴ For x kms the charge = 100 + 16(x – 5)
Amount paid = ₹ 740
∴ 100 + 16 (x – 5) = 740
100 + 16 (x – 5) – 100 = 740- 100
16 (x – 5) = 640
\(\frac{16(x-5)}{16}=\frac{640}{16}\)
x – 5 = 40
x – 5 + 5 = 45 + 5
x = 45
x = 45 km
∴ Total distance travelled = 45 km

Objective Type Questions

Question 8.
The generalization of the number pattern 3, 6, 9, 12, …………. is
(i) n
(ii) 2n
(iii) 3n
(iv) 4n
Solution:
(iii) 3n

Question 9.
The solution of 3x + 5 = x + 9 is t
(i) 2
(ii) 3
(iii) 5
(iv)4
Solution:
(i) 2
Hint: 3x + 5 = x + 9 ⇒ 3x – x = 9 – 5 ⇒ 2x = 4 ⇒ x = 2

Question 10.
The equation y + 1 = 0 is true only when y is
(i) 0
(ii) -1
(iii) 1
(iv) – 2
Solution:
(ii) -1

Students can Download Maths Chapter 3 Algebra Ex 3.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.1

Question 1.
Fill in the blanks
(i) The variable in the expression 16x – 7 is _____
(ii) The constant term of the expression 2y – 6 is _____
(iii) In the expression 25m + 14M, the type of the terms are ______ terms
(iv) The number of terms in the expression 3ab + 4c – 9 is _____
Hint: Terms are 3ab, 4c – 9.
(v) The numerical co-efficient of the term -xy is ______
Hint: -x,y = (- 1 )xy.
Solution:
(i) x
(ii) -6
(iii) unlike
(iv) three
(v) -1

Question 2.
Say true or False
(i) x + (-x) = 0.
(ii) The co-efficient of ab in the term 15 abc is 15.
Hint: Coefficient of ab is 15c
(iii) 2pq and – 7qp are like terms.
(iv) When y = -1, the value of the expression 2y – 1 is 3.
Hint: 2(-1) – 1 = -2 – 1 = – 3
Solution:
(i) True
(ii) False
(iii) True
(iv) False

Question 3.
Fing the numerical co-efficient of each of the following terms: -3yx, 12k, y, 121bc, -x, 9pq, 2ab.
Solution:
(i) Numerical co-efficient of-3yx is – 3
(ii) Numerical co-efficient of 12k is 12
(iii) Numerical coefficient of y is 1
(iv) Numerical co-efficient of 1216c is 121
(v) Numerical co-efficient of – x is – 1
(vi) Numerical co-efficient of 9pq is 9
(vii) Numerical co-efficient of 2ab is 2

Question 4.
Write the variables, constants and terms of the following expressions,
(i) 18 + x – y
(ii) 7p – 4q + 5
(iii) 29x + 13y
(iv) b + 2
Solution:

Question 5.
Identify the like terms among the following 7x, 5y, -8x, 12y, 6z, z, -12x, -9y, 11 z
Solution:

Question 6.
If x = 2 andy = 3, then find the value of the following expressions,
(i) 2x – 3y
(ii) x + y
(iii) 4y – x
(iv) x + 1 – y
Solution:
Given x = 2; y = 3.
(i) 2x – 3y = 2 (2) – 3 (3) = 4 – 9
= 4 + (Additive inverse of 9)
= 4 +(-9) = -5
(ii) x + y = 2 + 3 = 5
(iii) 4y – x = 4 (3) – 2 = 12 – 2 = 10
(iv) x + 1 – y = 2 + 1 – 3 = 3 – 3 = 0

Objective Type Questions

Question 1.
An algebraic statement which is equivalent to the verbal statement “Three times the sum of ‘x’ and ‘y’ is
(i) 3 (x + y)
(ii) 3 + x + y
(iii) 3x + y
(iv) 3 + xy
Solution:
(i) 3 [(x + y)]

Question 2.
The numerical co-efficient of -7mn is
(i) 7
(ii) -7
(iii) p
(iv) -p
Solution:
(ii) -7

Question 3.
Choose the pair of like terms
(i) 7p, 7x
(ii) 7r, 7x
(iii) – 4x, 4
(iv) – 4x, 7x
Solution:
(iv) -4x, 7x

Question 4.
The value of 7a – 4b when a = 3, b = 2 is
(i) 21
(ii) 13
(iii) 8
(iv) 32
Solution:
(ii) 13
Hint: 7(3) – 4(2) = 21 – 8 = 13

Students can Download Maths Chapter 4 Direct and Inverse Proportion Ex 4.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 4 Direct and Inverse Proportion Ex 4.3

Miscellaneous Practice Problems

Question 1.
If the cost of 7 kg of onions is ₹ 84 find the following :
(i) Weight of the onions bought for ₹ 180
(ii) The cost of 3 kg of onions
Solution:
(i) For ₹ 84 weight of onion bought
for ₹ 1 weight of onion bought
∴ For ₹ 180 weight of onion bought w
∴ For ₹ 180 weight of onion bought

(ii) Cost of 7 kg of onions = 15 kg

Question 2.
If C = kd
(i) what is the relation between C and d ?
(ii) Find k when C = 30 and d = 6
(iii) Find C, when d = 10
Solution:

As C increases d also increases
∴ It is direct proportion

Question 3.
Every 3 months Tamilselvan deposits ₹ 5000 as savings in his bank account. In how many years he can save ₹ 1,50,000.
Solution:
Let the number of years required be x.

No. of years and deposit are direct proportion as they both increases simultaneously.

He can save ₹ 1,50,000 in \(7 \frac{1}{2}\) years.

Question 4.
A printer, prints a book of 300 pages at the rate of 30 pages per minute. Then, how long will it take to print the same book if the speed of the printer is 25 pages per minute?
Solution:
Let the required time taken to print be x
As the speed increases time taken to print decreases
∴ They are in inverse proportion
Time taken to print 30 pages = 1 min

Question 5.
If the cost of 6 cans of juice in ₹ 210, then what will be the cost of 4 cans of juice?
Solution:
Let the cost required be x

As number of cans increases cost also increases.
∴ They are in direct proportion

x = 140
Cost of 4 cans of juice = 140

Question 6.
x varies inversely as twice of y. Given that when y = 6, the value of x is 4. Find the value of x when y = 8.
Solution:
Given x varies inversely as twice of y.

Question 7.
A truck requires 108 litres of diesel for covering a distance of 594 km. How much diesel will be required to cover a distance of 1650 km?
Solution:
Let the required distance be x

As the distance increases fuel quantity also increases.
∴ They are direct proportion.

∴ The diesel required = 300 liters

Challenge Problems

Question 8.
If the cost of a dozen soaps is ₹ 396, what will be the cost of 35 such soaps?
Solution:
1 dozen = 12
Cost of 12 soaps = ₹ 396

Question 9.
In a school there is 7 periods a day each of 45 minutes duration. How long each period is if the school has 9 periods a day assuming the number of hours to be the same?
Solution:
Number of periods increases as duration decreases, since the number of hours is same.
Let the duration of each period be x.

Question 10.
Cost of 105 note books is ₹ 2415. How many notebooks can be bought for ₹ 1863?
Solution:
For 2415 number of notebooks bought = 105

Question 11.
10 farmers can plough a field in 21 days. Find the number of days reduced if 14 farmers ploughed the same field?
Solution:
Let the required number of days if 14 farmers ploughed = x

As number of farmers increases, number of days decreases.
∴ They are in inverse proportion

Initially the farmers worked for 21 days. Now they worked for 15 days.
∴ The number of days reduced = 21 – 15 = 6 days

Question 12.
A flood relief camp has food stock by which 80 people can be benefited for 60 days. After 10 days 20 more people have joined the camp. Calculate the number of days of food shortage due to the addition of 20 more people?
Solution:

As number of people increases food last for less number of days.

Remaining food is to be used for 50 days.
But it only last for 40 days.
No. of days shortage = 50 – 40 = 10 days.
∴ 10 days of food shortage due to the addition of 20 more people.

Question 13.
Six men can complete a work in 12 days. Two days later, 6 more men joined them. How many days will they take to complete the remaining work?
Solution:

As the number of men increases number of days increases.
∴ They are inversely proportional

x = 5 days
∴ Remaining work will be complete in 5 days

Students can Download Maths Chapter 4 Direct and Inverse Proportion Ex 4.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 4 Direct and Inverse Proportion Ex 4.2

Question 1.
Fill in the blanks
(i) 16 taps can fill a petrol tank in 18 minutes. The time taken for 9 taps to fill the same tank will be ___ minutes.
(ii) If 40 workers can do a project work in 8 days, then ____ workers can do it in 4 days.
Solutions:
(i) 32
(ii) 80

Question 2.
6 pumps are required to fill a water sump in 1 hr 30 minutes. What will be the time taken to fill the sump if one pump is switched off?
Solution:
Let x be the required time taken

Time taken in minutes 1 hr. 48m

Question 3.
A farmer has enough food for 144 ducks for 28 days. If he sells 32 ducks how long will the food last?
Solution:
Let the required number of days be x.

As the number of ducks decreases the food will last for more days.
∴ They are in inverse proportion. x₁y₁ = x₂y₂

The food lasts for 36 days

Question 4.
It takes 60 days for 10 machines to dig a hole. Assuming that all machines work at the same speed, how long will it take 30 machines to dig the same hole?
Solution:
Let the number of days required be x.

As the number of machines increases it takes less days to complete the work
∴ They are in inverse proportion, x₁y₁ = x₂y₂

It takes 20 days to dig the hole

Question 5.
Forty students stay in a hostel. They had food stock for 30 days. If the students are doubled then for how many days the stock will last?
Solution:
Let the required number of days be x.

As the number of students increases the food last for less number of days
∴ They are in inverse proportion.

The food stock lasts for 15 days

Question 6.
Meena had enough money to send 8 parcels each weighing 500 grams through a courier service. What would be the weight of each parcel, if she has to send 40 parcel for the same money?
Solution:
Let the required weight of the parcel be x grams.

As the number of parcels increases weight of a parcel decreases.
∴ They are in inverse proportion.

Weight of each parcel = 100 grams

Question 7.
It takes 120 minutes to weed a garden with 6 gardeners. If the same work is to be done in 30minutes, how many more gardeners are needed?
Solution:
Let the, number of gardeners needed be x.

As the number of gardeners increases the time decreases. They are in inverse proportion,
x₁y₁ = x₂y₂

∴ To complete the work in 30 min gardeners needed = 24
Already existing gardeners = 6
∴ More gardeners needed = 24 – 6 = 18
18 more gardeners are needed

Question 8.
Neelaveni goes by bicycle to her school every day. Her average speed is 12km/hr and she reaches school in 20 minutes. What is the increase in speed, If she reaches the school in 15 minutes?
Solution:
Let the speed to reach school in 15 min be x

∴ They are in inverse proportion x₁y₁ = x₂ y₂

If she reaches in 15 min the speed = 16 km/hr
Already running with 12 km / hr
∴ Increased speed = 16 – 12 = 4km / hr
Increase in speed = 4 km / hr

Question 9.
A toy company requires 36 machines to produce car toys in 54 days. How many machines would be required to produce the same number of car toys in 81 days?
Solution:
Let the required number of machines be x

As the number of machines increases number of days required decreases.

∴ 24 machines would be required

Objective Type Questions

Question 10.
12 cows can graze a field for 10 days. 20 cows can graze the same field for ____ days
(i) 15
(ii) 18
(iii) 6
(iv) 8
Solution:
(iii) 6
Hint:

Question 11.
4 typists are employed to complete a work in 12 days. If two more typists are added, they will finish the same work in days
(i) 7
(ii) 8
(iii) 9
(iv) 10
Solution:
(ii) 8

Students can Download Maths Chapter 4 Direct and Inverse Proportion Ex 4.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 4 Direct and Inverse Proportion Ex 4.1

Fill in the blanks.

(i) If the cost of 8 apples is 56 then the cost of 12 apples is ____.
(ii) If the weight of one fruit box is \(3 \frac{1}{2}\) kg, then the weight of 6 such boxes is ____.
(iii) A car travels 60 km with 3 liters of petrol. If the car has to cover the distance of
200 km, it requires ___ liters of the petrol.
(iv) If 7 m cloth costs ₹ 294, then the cost of 5m of cloth is ____.
(v) If a machine in a cool drinks factory fills 600 bottles in 5 hrs, then it will fill _____ bottles in 3 hours.
Solutions:
(i) 84
(ii) 21 kg
(iii) 10
(iv) ₹ 210
(v) 360

Question 2.
Say True or False
(i) Distance travelled by a bus and time taken are in direct proportion.
(ii) Expenditure of a family to number of members of the family are in direct proportion.
(iii) Number of students in a hostel and consumption of food are not in direct proportion.
(iv) If Mallika walks 1km in 20 minutes, then she can convert 3km in 1 hour.
(v) If 12 men can dig a pond in 8 days, then 18 men can dig it in 6 days.
Solutions:
(i) True
(ii) True
(iii) False
(iv) True
(v) False

Question 3.
A dozen bananas costs ₹ 20. What is the price of 48 bananas ?
Solution:
Let the required price be ₹ x. As the number of bananas increases price also increases
∴ Number of bananas and cost are in direct proportion.

Question 4.
A group of 21 students paid ₹ 840 as the entry fee for a magic show. How many students entered the magic show if the total amount paid was ₹ 1680?
Solution:
Let the required number of students be x.

As the number of students increases the entry fees also increases.
∴ They are in direct proportion .

∴ The number of students entered magic show = 42

Question 5.
A birthday party is arranged in third floor of a hotel. 120 people take 8 trips in a lift to go to the party hall. If 12 trips were made how many people would have attended the party?
Solution:
Let the number of people attended the party be x.

As the number of trips increases, number of people also increases.
∴ They are in direct proportion.


180 people attend the party in 12 trips

Question 6.
The shadow of a pole with height of 8m is 6m. If the shadow of another pole measured at the same time is 30m, find the height of the pole?
Solution:
Let the required height of the pole be ‘x’ m.

Height of the pole and its shadow are in direct proportion

∴ Height of the pole x = 40m.

Question 7.
A postman can sort out 738 letters in 6 hours. How many letters can be sorted in 9 hours?
Solution:
Let the required number of letters be x.

They are in direct proportion.

In 9 hours 1107 letters can be sorted.

Question 8.
If half a meter of cloth costs ₹ 15. Find the cost of \(8 \frac{1}{3}\) meters of the same cloth.
Solution:
Let the cost of cloth required be x.

Cost and length are in direct proportion.

Question 9.
The weight of 72 books is 9 kg. What is the weight of 40 such books (using unitary method)
Solution:
Weight of 72 books = 9 kg = 9000 g
∴ Weight of 1 book = \(\frac{9000}{72}\) = 125 g
∴ Weight of 40 books = 125 × 40 g = 5000 g = 5 kg.
Weight of 40 books = 5 kg

Question 10.
Thamarai pages ₹ 7500 as rent for 3 months. With the same rate how much does she have to pay for 1 year (using unitary method).
Solution:
Rent paid by Thamarai for 3 months = ₹ 7500
∴ Rent paid for 1 month = \(\frac{7500}{3}\) = 2500
Rent paid for 1 year or 12 moths = 2500 × 12 = ₹ 30,000
For 1 year rent to be paid = ₹ 30,000

Question 11.
If 30 men can reap a field in 15 days, then in how many days can 20 men reap the same field? (using unitary method).
Solution:

∴ 20 men can reap the field in 10 days.

Question 12.
Valli purchase 10 pens for ₹ 180 and Kamala boys 8 pens for ₹ 96. Can you say who bought the pen cheaper (using unitary method).
Solution:

∴ Kamala bought the pen cheaper.

Question 13.
A motorbike requires 2 liters of petrol to cover 100 kilometres. How many liters of petrol will be required to cover 250 kilometers? (using unitary method).
Solution:
To cover 100 km quantity of petrol required = 2 litres

5 litres of petrol required to cover 250 km

Objective Type Questions

Question 14.
If the cost of 3 books is ₹ 90, then find the cost of 12 books.
(i) ₹ 300
(ii) ₹ 320
(iii) ₹ 360
(iv) ₹ 400

Solution:
(iii) ₹ 360

Question 15.
If Mani buys 5 kg of potatoes for ₹ 75 then he can buy ₹ 105.
(i) 6
(ii) 7
(iii) 8
(iv) 5

Solution:
(ii) 7

Question 16.
35 cycles were produced in 5 days by a company then ___ cycles will be produced in 21 days.
(i) 150
(ii) 70
(iii) 100
(iv) 147

Solution:
(iv) 147

Question 17.
An aircraft can accommodate 280 people in 2 trips. It can take ______ trips to take 1400 people.
(i) 8
(ii) 10
(iii) 9
(iv) 12
Solution:
(ii) 10

Question 18.
Suppose 3 kg of sugar is used to prepare sweets for 50 members, then ___ kg of sugar is required for 150 members.
(i) 9
(ii) 10
(iii) 15
(iv) 6

Solution:
(i) 9