Category: Class 7

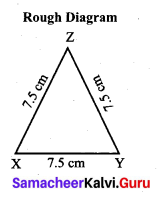
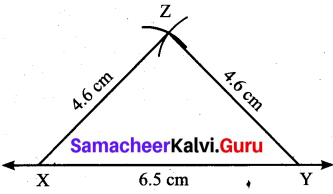
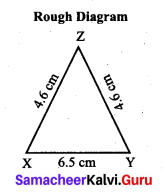
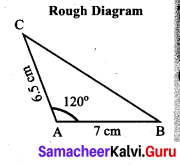
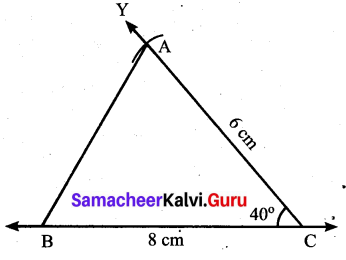
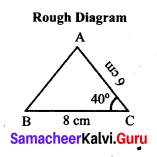
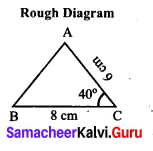
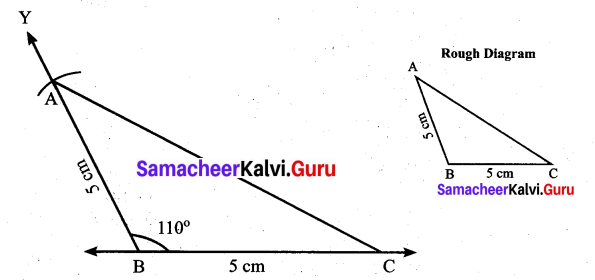
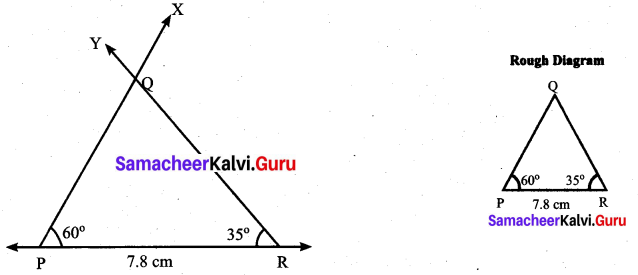
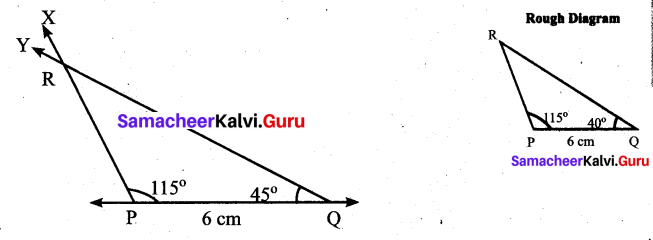
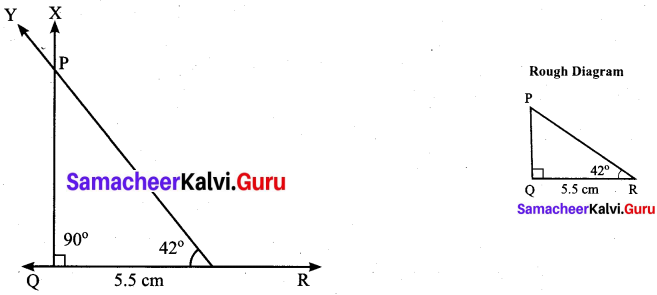
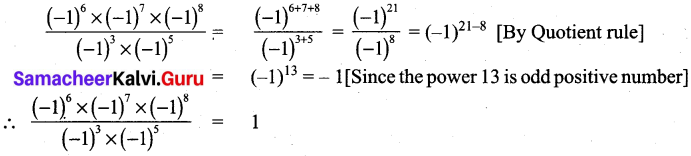Students can Download Maths Chapter 4 Geometry Ex 4.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.1

Question 1.
Can 30°, 60° and 90° be the angles of a triangle?
Solution:
Given angles 30°, 60° and 90°
Sum of the angles = 30° + 60° + 90° = 180°
∴ The given angles form a triangle.

Question 2.
Can you draw a triangle with 25°, 65° and 80° as angles?
Solution:
Given angle 25°, 65° and 80°.
Sum of the angles = 25° + 65° + 80° = 170° ≠ 180
∴ We cannot draw a triangle with these measures.

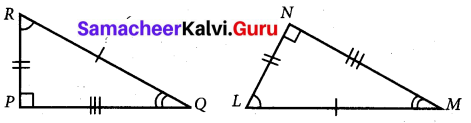
Question 3.
In each of the following triangles, find the value of x.

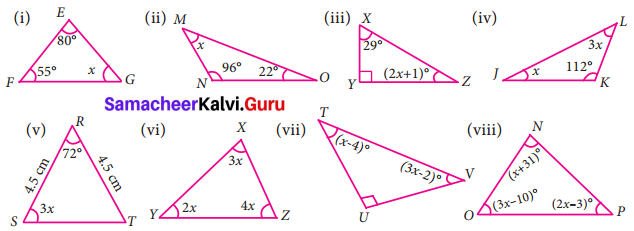
Solution:
(i) Let ∠G = x
By angle sum property we know that,
∠E + ∠F + ∠G = 180°
80° + 55° + x = 180°
135° + x = 180°
x = 45°

(ii) Let ∠M = x
By angle sum property of triangles we have
∠M + ∠M + ∠O = 180°
x + 96° + 22° = 180°
x + 118° = 180°
X = 180° – 118° = 620

(iii) Let ∠Z = (2x + 1)° and ∠Y = 90°
By the sum property of triangles we have
∠x + ∠y + ∠z = 180°
29° + 90° + (2x + 1)° = 180°
119° + (2x + 1)° = 180°
(2x + 1)° = 180° – 119°
2x + 1° = 61°
2x = 61° – 1°
2x = 60°
x = \(\frac{60^{\circ}}{2}\)
x = 30°

(iv) Let ∠J = x and ∠L – 3x.
By angle sum property of triangles we have
∠J + ∠K + ∠L = 180°
x + 112° + 3x = 180°
4x = 180° – 112°
x = 68°
x = \(\frac{68^{\circ}}{4}\)
x = 17°

(v) Let ∠S = 3x°
Given \(\overline{\mathrm{RS}}\) = Given \(\overline{\mathrm{RT}}\) = 4.5 cm
Given ∠S = ∠T = 3x° [∵ Angles opposite to equal sides are equal]
By angle sum property of a triangle we have,
∠R + ∠S + ∠T = 180°
72° + 3x + 3x = 180°
72° + 6x = 180°
x = \(\frac{108^{\circ}}{6}\)
x = 18°

(vi) Given ∠X = 3x; ∠Y = 2x; ∠Z = ∠4x
By angle sum property of a triangle we have
∠X + ∠Y + ∠Z = 180°
3x + 2x + 4x = 180°
∴ 9x = 180°
x = \(\frac{180^{\circ}}{9}\) = 20°

(vii) Given ∠T = (x – 4)°
∠U = 90°
∠V = (3x – 2)°
By angle sum property of a triang we have
∠T + ∠U + ∠V = 180°
(x – 4)° + 90° + (3x – 2)° = 180°
x – 4° + 90° + 3x – 2° = 180°
x + 3x + 90° – 4° – 2° = 180°
4x + 84° = 180°
4x = 180° – 84°
4x = 96°
x = \(\frac{96^{\circ}}{4}\) = 24°
x = 24°

(viii) Given ∠N = (x + 31)°
∠O = (3x – 10)°
∠P = (2x – 3)°
By angle sum property of a triangle we have
∠N + ∠O + ∠P = O
(x + 31)° + (3x – 10)° + (2x – 3)° = 180°
x + 31°+ 3x – 10° + 2x – 3° = 180°
x + 3x + 2x + 31° – 10° – 3° = 180°
6x + 18° = 180°
6x = 180° + 18°
6x = 162°
x = \(\frac{162^{\circ}}{6}\) = 27°
x = 27°

Question 4.
Two line segments \(\overline{A D}\) and \(\overline{B C}\) intersect at O. Joining \(\overline{A B}\) and \(\overline{D C}\) we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B.

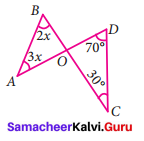
Solution:
In ∆AOB and ∆DOC,
∠AOB = ∠DOC [∵ Vertically opposite angles are equal]
Let ∠AOB = ∠DOC = y
By angle sum property of a triangle we have
∠A + ∠B + ∠AOB = ∠D + ∠C + ∠DOC = 180°
3x + 2x + y = 70° + 30° + y = 180°
5x + y = 100° + y = 180°
Here 5x + y = 100° + y
5x = 100° + y – y
5x = 100°
x = \(\frac{100^{\circ}}{5}\) = 20°
∠A = 3x = 3 × 20 = 60°
∠B = 2x = 2 × 20 = 40°
∠A = 60°
∠B = 40°

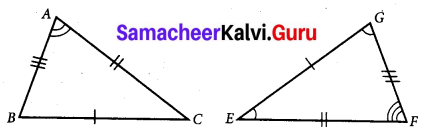
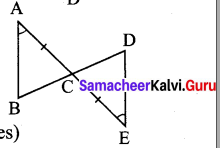
Question 5.
Observe the figure and find the value of
∠A + ∠N + ∠G + ∠L + ∠E + ∠S.

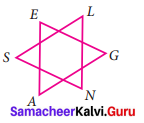
Solution:
In the figure we have two triangles namely ∆AGE and ∆NLS.
By angle sum property of triangles,
Sum of angles of ∆AGE = ∠A + ∠G + ∠E = 180° …(1)
Also sum of angles of ∆NLS = ∠N + ∠L + ∠S = 180° … (2)
(1) + (2) ∠A + ∠G + ∠E + ∠N + ∠L + ∠S = 180° + 180°
i.e., ∠A + ∠N + ∠G + ∠L + ∠E + ∠S = 360°

Question 6.
If the three angles of a triangle are in the ratio 3 : 5 : 4, then find them.
Solution:
Given three angles of the triangles are in the ratio 3 : 5 : 4.
Let the three angle be 3x, 5x and 4x.
By angle sum property of a triangle, we have
3x + 5x + 4x = 180°
12x = 180°
x = \(\frac{180^{\circ}}{12}\)
x = 15°
∴ The angle are 3x = 3 × 15° = 45°
5x = 5 × 15° = 75°
4x = 4 × 15° = 60°
Three angles of the triangle are 45°, 75°, 60°

Question 7.
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S , find the three angles of the triangle.
Solution:
In ∆RST. Let ∠R = x.
Then given S is ∠10° greater than ∠R
∴ ∠S = x + 10°
Also given ∠T is 5° less then ∠S.
So ∠T = ∠S – 5° = (x + 10)° – 5° = x + 10° – 5°
By angle sum property of triangles, sum of three angles = 180°.

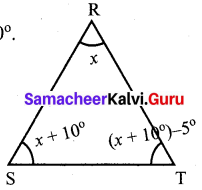
∠R + ∠S + ∠T = 180°
x + x + 10° + x + 5° = 180°
3x + 15° = 180°
3x = 180° – 15°
x = \(\frac{165^{\circ}}{3}\) = 55°
∠R = x = 55°
∠S = x + 10° = 55° + 10° = 65°
∠T = x + 5° = 55° + 5° = 60°
∴ ∠R = 55°
∠S = 65°
∠T = 60°

Question 8.
In ∆ABC , if ∠B is 3 times ∠A and ∠C is 2 times ∠A, then find the angles.
Solution:
In ABC, Let ∠A = x,
then ∠B = 3 times ∠A = 3x
∠C = 2 times ∠A = 2x
By angle sum property of a triangles,
Sum of three angles of ∆ABC =180°.
∠A + ∠B + ∠C = 180
x + 3x + 2x = 180°
x (1 + 3 + 2) = 180°
6x = 180°

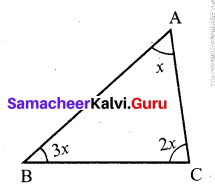
x = \(\frac{180^{\circ}}{6}\) = 30°
∠A = x = 30°
∠B = 3x = 3 × 30° = 90°
∠C = 2x = 2 × 30° = 60°
∴ ∠A = 30°
∠B = 90°
∠C = 60°

Question 9.
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z.
Solution:
Given in ∆XYZ, ∠X : ∠Z = 5 : 4
Let ∠X = 5x; and ∠Z = 4x given ∠Y = 72°
By the angle sum property of triangles sum of three angles of a triangles is 180°.
∠X + ∠Y + ∠Z = 180°
5x + 72 + 4x = 180°
5x + 4x = 180° – 72°
9x = 108°
x = \(\frac{108^{\circ}}{9}\) = 12°
∠X = 5x = 5 × 12° = 60°
∠Z = 4x = 4 × 12° = 48°
∴ ∠X = 60°
∠Z = 48°

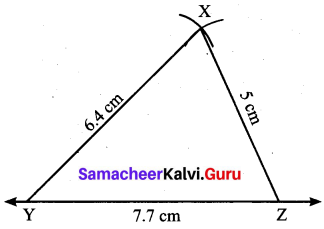
Question 10.
In a right angled triangle ABC, ∠B is right angle, ∠A is x + 1 and ∠C is 2x + 5. Find ∠A and ∠C.
Solution:
Given in ∆ABC ∠B = 90°
∠A = x + 1
∠B = 2x + 5

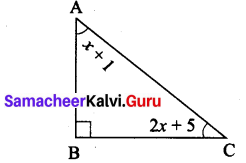
By angle sum property of triangles
Sum of three angles of ∆ABC = 180°
∠A + ∠B + ∠C = 180°
(x + 1) + 90° + (2x + 5) = 180°
x + 2x + 1° + 90° + 5° = 180°
3x + 96° = 180°
3x = 180° – 96° = 84°
x = \(\frac{84^{\circ}}{3}\) = 28°
∠A = x + 1 = 28 + 1 = 29
∠C = 2x + 5 = 2 (28) + 5 = 56 + 5 = 61
∴ ∠A = 29°
∠C = 61°

Question 11.
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO.
Solution:
Given ∠N = 90°
MO is extended to P, the exterior angle ∠NOP = 128°
Exterior angle is equal to the sum of interior opposite angles.

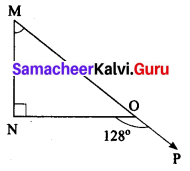
∴ ∠M + ∠N = 128°
∠M + 90° = 128°
∠M = 128° – 90°
∠M = 38°
By angle sum property of triangles,
∴ ∠M + ∠N + ∠O = 180°
38° + 90° + ∠O = 180°
∠O = 180° – 128°
∠O = 52°
∴ ∠M = 38° and ∠O = 52°

Question 12.
Find the value of x in each of the given triangles.

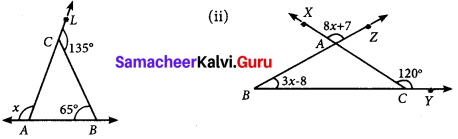
Solution:
(i) In ∆ABC, given B = 65°,
AC is extended to L, the exterior angle at C, ∠BCL = 135°
Exterior angle is equal to the sum of opposite interior angles.
∠A + ∠B = ∠BCL
∠A + 65° = 135°
∠A = 135° – 65°
∴ ∠A = 70°
x + ∠A = 180° [∵ linear pair]
x + 70° = 180° [∵ ∠A = 70°]
x = 180° – 70°
∴ x = 110°

(ii) In ∆ABC, given B = 3x – 8°
∠XAZ = ∠BAC [∵ vertically opposite angles]
8x + 7 + ∠BAC
i.e., In ∆ABC, ∠A = 8x + 7
Exterior angle ∠XCY = 120°
Exterior angle is equal to the sum of the interior opposite angles.
∠A + ∠B = 120°
8x + 7 + 3x – 8 = 120°
8x + 3x = 120° + 8 – 7
11x = 121°
x = \(\frac{121^{\circ}}{11}\) = 11°

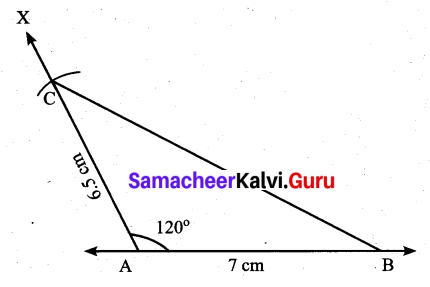
Question 13.
In ∆LMN, MN is extended to O. If ∠MLN = 100 – x, ∠LMN = 2x and ∠LNO = 6x – 5, find the value of x.
Solution:
Exterior angle is equal to the sum of the opposite interior angles.
∠LNO = ∠MLN + ∠LMN

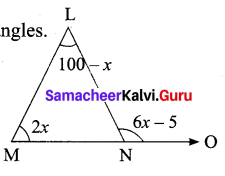
6x – 5 = 100° – x + 2x
6x – 5 + x – 2x = 100°
6x + x – 2x = 100° + 5°
5x = 105°
x = \(\frac{105^{\circ}}{5}\) = 21°
x = 21°

Question 14.
Using the given figure find the value of x.

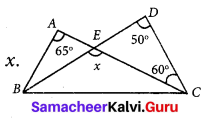
Solution:
In ∆EDC, side DE is extended to B, to form the exterior angle ∠CEB = x.
We know that the exterior angle is equal to the sum of the opposite interior angles
∠CEB = ∠CDE + ∠ECD
x = 50° + 60°
x = 110°

Question 15.
Using the diagram find the value of x.

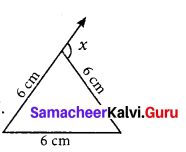
Solution:
Given triangle is an equilateral triangle as the three sides are equal. For an equilateral triangle all three angles are equal and is equal to 60° Also exterior angle is equal to sum of opposite interior angles.
x = 60° + 60°.
x = 120°

Objective Type Questions

Question 16.
The angles of a triangle are in the ratio 2:3:4. Then the angles are
(i) 20,30,40
(ii) 40, 60, 80
(iii) 80, 20, 80
(iv) 10, 15, 20
Answer:
(ii) 40, 60, 80

Question 17.
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
(i) 85°, 40°
(ii) 70°, 25°
(iii) 80°, 35°
(iv) 80° , 135°
Answer:
(iii) 80°,35°

Question 18.
In the given figure, AB is parallel to CD. Then the value of b is

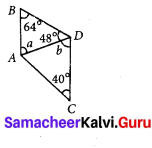
(i) 112°
(ii) 68°
(iii) 102°
(iv) 62° A
Answer:
(ii) 68°

Question 19.
In the given figure, which of the following statement is true?

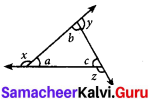
(i) x + y + z = 180°
(ii) x + y + z = a + b + c
(iii) x + y + z = 2(a + b + c)
(iv) x + y + z = 3(a + b + c)
Ans :
(iii) x + y + z = 2(a + b + c)]

Question 20.
An exterior angle of a triangle is 70° and two interior opposite angles are equal. Then measure of each of these angle will be
(i) 110°
(ii) 120°
(iii) 35°
(iv) 60°
Answer:
(iii) 35°

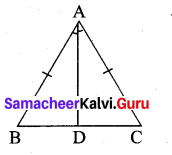
Question 21.
In a ∆ABC, AB = AC. The value of x is _____.

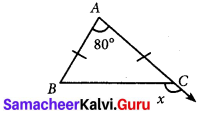
(i) 80°
(ii) 100°
(iii) 130°
(iv) 120°
Answer:
(iii) 130°

Question 22.
If an exterior angle of a triangle is 115° and one of the interior opposite angles is 35°, then the other two angles of the triangle are
(i) 45°, 60°
(ii) 65°, 80°
(iii) 65°, 70°
(iv) 115°, 60°
Answer:
(ii) 65°, 80°

Students can Download Maths Chapter 4 Geometry Ex 4.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.2

Question 1.
Given that ∆ABC = ∆DEF (i) List all the corresponding congruent sides
(ii) List all the corresponding congruent angles.
Solution:
Given ∆ABC ≅ DEF.

(i) Corresponding congruent sides.
\(\overline{A B}\) = \(\overline{D E}\); \(\overline{B C}\) = \(\overline{E F}\); \(\overline{A C}\) = \(\overline{D F}\)

(ii) Corresponding congruent angles.
∠ABC = ∠DEF; ∠BCA = ∠EFD ; ∠CAB = ∠FDE

Question 2.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles.
(i)
(ii)
Solution:
Given ∆PQR ≅ ∆LNM
(i) (a) Corresponding sides
\(\overline{P Q}\) = \(\overline{L N}\) ; \(\overline{P Q}\) = \(\overline{L M}\) ; \(\overline{R Q}\) = \(\overline{M N}\)
(b) Corresponding angles
∠RPQ = ∠NLM; ∠PQR = ∠LNM; ∠PRQ = ∠LMN

(ii) Given ∆PQR ≅ ∆NML
(a) Corresponding angles
\(\overline{Q R}\) = \(\overline{L M}\) ; \(\overline{R P}\) = \(\overline{L N}\); \(\overline{P Q}\) = \(\overline{M N}\)
(b) Corresponding angles
∠PQP = ∠NMN; ∠QRP = ∠MLN; ∠RPQ = ∠LNM

Question 3.
Find the unit digit of expanded form.

(i) ∠A and ∠G
(ii) ∠B and ∠E
(iii) ∠B and ∠G
(iv) \(\overline{A C}\) and \(\overline{G F}\)
(v) \(\overline{B A}\) and \(\overline{F G}\)
(vi) \(\overline{E F}\) and \(\overline{B C}\)
Solution:
Given ∆ABC ≅ ∆EFG. Also from given triangles.
\(\overline{A B}\) = \(\overline{F G}\) \(\overline{B C}\) = \(\overline{G F}\) \(\overline{A C}\) = \(\overline{E F}\)
Also ∠A = ∠F ∠B = ∠G ∠C = ∠E
Answer:
(i) ∠A and ∠G are not corresponding angles.
(ii) ∠B and ∠E are not corresponding angles.
(iii) ∠B and ∠G are corresponding angles.
(iv) \(\overline{A C}\) and \(\overline{G F}\) are not corresponding sides.
(v) \(\overline{B A}\) and \(\overline{F G}\) are corresponding sides.
(vi) \(\overline{E F}\) and \(\overline{B C}\) are not corresponding sides.

Question 4.
State whether the two triangles are congruent or not. Justify your answer.

Solution:
(i) Let the given triangle be ∆ABC. \(\overline{A D}\) divides ∆ABC into two parts giving ∆ABD and ∆ACD.
In ∆ABD and ∆ACD

\(\overline{A B}\) = \(\overline{A C}\) (given)
\(\overline{B D}\) = \(\overline{A D}\) (common side)
∠BAD = ∠CAD (included angles)
∴ By SAS criterion ∆ABD ≅ ∆ACD.

(ii) Let the given triangles in the figure be ∆ABC and ∆DCB.
In both the triangles

\(\overline{B C}\) = \(\overline{B C}\) (Common side)
\(\overline{A B}\) = \(\overline{D C}\)
\(\overline{A C}\) = \(\overline{B D}\)
∴ By SSS Criterion ∆ABC ≅ ∆DCB

(iii) Let the given triangles be ∆ABC and ∆CDE.

Here \(\overline{A C}\) = \(\overline{C E}\) (given)
∠BAC = ∠DEC (given)
∠ACB = ∠DCE (vertically opposite angles)
Two angles and the included side are equal.
Therefore by ASA criterion ∆ABC ≅ ∆CDE.

(iv) Let the two triangles be ∆XYZ and ∆XYW

Here ∠W = ∠Z = 90°
\(\overline{X Y}\) = \(\overline{X Y}\) (Common Hypothenure)
\(\overline{X W}\) = \(\overline{X Z}\) (given)
By RHS criterion ∆XYZ ≅ ∆XYW

(v) Let the two triangles be ∆ABC and ∆ADC

In both the triangles \(\overline{A C}\) = \(\overline{A C}\) (common sides)
\(\overline{A D}\) = \(\overline{B C}\) (given)
\(\overline{A B}\) = \(\overline{D C}\) (given)
By SSS criterion ∆ABC ≅ ∆ADC.

Question 5.
To conclude the congruency of triangles, mark the required information in the following figures with reference to the given congruency criterion.

Solution:
(i) In the given triangles one angle is equal and a side is common and so equal.

To satisfy ASA criterion one more angle should be equal such that the common side is the included side of both angles of a triangle.
The figure will be as follows.

(ii) In the two given triangles two sides of one triangle is equal to two sides of the other triangle.

To satisfy SSS criterion the third sides mut be equal.

(iii) The given triangles have one side in common. They are right angled tringles.

To satisfy RHS criterion their hypotenuse must be equal.

(iv) In the given triangles two angles of one triangle is equal to two angles of the other triangles?

To satisfy ASA criterion included side of two angles must be equal.

(v) In both the triangles one of their sides are equal.

One of their angles are equal or they are vertically opposite angles.
To satisfy SAS criterion, one more side is to be equal such that the angle is the included of the equal sides.

Question 6.
For each pair of triangles state the criterion that can be used to determine the congruency?

Solution:
(i) Given two pair of sides are equal and one side is common to both the triangles.
∴ SSS congruency criterion is used.

(ii) One of the sides and one of the angles are equal.
∴ One more angle is vertically opposite angle and so it is also equal.
ASA criterion is used.

(iii) From the figure hypotenuse and one side are equal in both the triangles.
RHS congruency criterion is used. (∵ Considering ∆ABC and ∆BAD)
∠A = ∠B = 90°
AD = BC
AB = AB (common)
∴ AC = BD (hypotenuse)

(iv) By ASA criterion both triangles are congruent.

(v) By ASA criterion both triangles are congruent. Since two angles in one triangle are equal to two corresponding angles of the other triangle. Again one side is common to both triangle and the side is the included side of the angles.

(vi) Two sides are equal. One angle is vertically opposite angles and one equal.
By SAS criterion both triangles are cogruent.

Question 7.
I. Construct a triangle XYZ with the given conditions.

(i) XY = 6.4 cm, ZY = 7.7 cm and XZ = 5 cm
Solution:


Construction:
Step 1: Draw a line. Marked Y and Z on the line such that YZ 7.7 cm.
Step 2: With Y as centre drawn an arc of radius 6.4 cm above the line YZ.
Step 3: With Z as centre, drwan an arc or radius 5 cm to intersect arc drawn in steps. Marked the point of intersection as X.
Step 3: Joined YX and ZX. Now XYZ is the required triangle.

(ii) An equilateral triangle of side 7.5 cm
Solution:

Construction:
Step 1: Drawn a line. Marked X and Y on the line such that XY = 7.5 cm.
Step 2: With X as centre, drawn an arc of radius 7,5 cm above the line XY.
Step 3: With Y as centre, drawn an arc of radius 7.5 cm to intersect arc drawn in steps. Marked the point of intersection as Z.
Step 4: Joined XZ and YZ. Now XYZ in the required triangle.

(iii) An isosceles triangle with equal sides 4.6 cm and third side 6.5 cm
Solution:

Construction: .
Step 1: Drawn a line. Marked X and Y on the line such that XY = 6.5 cm.
Step 2: With X as centre, drawn an arc of radius 4.6 cm above the line XY
Step 3: with Y as centre, drawn an arc of radius 4.6 cm to intersect arc drawn in steps. Marked the point of intersection as Z.
Step 4: Joined XZ and YZ. Now XYZ is the required triangle.

II. Construct a triangle ABC with given conditions.

(i) AB = 7 cm, AC = 6.5 cm and ∠A = 120°.
Solution:

Construction:
Step 1: Drawn a line. Marked A and B on the line such that AB = 7 cm.
Step 2: At A, drawn a ray AX making an angle of 120° with AB.
Step 3: With A as centre, drawn an arc of radius 6.5 cm to cut the ray AX. Marked the point of intersection as C.
Step 4: Joined BC.
ABC is the required triangle.

(ii) BC = 8 cm, AC = 6 cm and ∠C = 40°.
Solution:


Construction:
Step 1: Drawn a line. Marked B and C on the line such fhat BC = 8 Cm.
Step 2: At C, drawn a ray CY making an angle of 40° with BC.

Step 3: With C as centre, drawn an arc of radius 6 cm to cut the ray CY, marked the point of intersection as A.
Step 4: Joined AB.
AB is the required triangle.

(iii) An isosceles obtuse triangle with equal sides 5 cm
Solution:

Construction:
Step 1: Drawn a line. Marked B and C on the line such that BC = 5 cm.
Step 2: At B drawn a ray BY making on obtuse angle 110° with BC.
Step 3: With B as centre, drawn an arc of radius 5 cm to cut ray BY. Marked the point of intersection as C.
Step 4: Joined BC. ABC is the required triangle.

III. Construct a triangle PQR with given conditions.

(i) ∠P = 60°, ∠R = 35° and PR = 7.8 cm
Solution:

Construction:
Step 1: Drawn a line. Marked P and R on the line such that PR = 7.8 cm.
Step 2: At P, drawn a ray PX making an angle of 60° with PR.
Step 3: At R, drawn another ray RY making an angle of 35° with PR. Mark the point of intersection of the rays PX and RY as Q.
PQR is the required triangle.

(ii) ∠P = 115°, ∠Q = 40° and PQ = 6 cm
Solution:

Construction:
Step 1: Drawn a line. Marked P and Q on the line such that PQ = 6 cm.
Step 2: At P, drawn O ray PX making an angle of 115° with PQ.
Step 3: At Q, drawn another ray QY making an angle of 40° with PQ. Marked the point of intersection of the rays PX and Q Y as R.
PQR is the required triangle.

(iii) ∠Q = 90°, ∠R = 42° and QR = 5.5 cm
Solution:

Construction:
Step 1: Drawn a line. Marked Q and R on the line such that QR = 5.5 cm.
Step 2: At Q, drawn a ray QX making an angle of 90° with QR.
Step 3: At R, drawn another ray RY making an angle of 42° QR. Marked the point of intersection of the rays QX and RY as P.
PQR is the required triangle.

Objective Type Questions

Question 8.
If two plans figures are congruent then they have
(i) same size
(ii) same shape
(iii) same angle
(iv) same shape and same size
Answer:
(iv) same shape and same size

Question 9.
Which of the following methods are used to check the congruence of plane figures?
(i) translation method
(ii) superposition method
(iii) substitution method
(iv) transposition method
Answer:
(ii) superposition method

Question 10.
Which of the following rule is not sufficient to verify the congruency of two triangles.
(i) SSS rule
(ii) SAS rule
(iii) SSA rule
(iv) ASA rule
Answer:
(iii) SSA rule

Question 11.
Two students drew a line segment each. What is the condition for them to be congruent?
(i) They should be drawn with a scale.
(ii) They should be drawn on the same sheet of paper.
(iii) They should have different lengths.
(iv) They should have the same length.
Answer:
(iv) They should have the same length.

Question 12.
In the given figure, AD = CD and AB = CB. Identify the other three pairs that are equal.

(i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, BD = BD
(ii) AD = AB, DC = CB, BD = BD
(iii) AB = CD, AD = BC, BD = BD
(iv) ∠ADB = ∠CDB, ∠ABD = ∠CBD, ∠DAB = ∠DBC
Answer:
(i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, BD = BD

Question 13.
In ∆ABC and ∆PQR, ∠A = 50° = ∠P, PQ = AB, and PR = AC. By which property ∆ABC and ∆PQR are congruent?
(i) SSS property
(ii) SAS property
(iii) ASA property
(iv) RHS property
Answer:
(ii) SAS property

Students can Download Maths Chapter 3 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Additional Questions

Additional Questions and Answers

Exercise 3.1

Question 1.
Simplify the following and write the answer in Exponential form.
(i) 3² × 3⁴ × 3⁸
(ii) 6¹⁵ ÷ 6¹⁰
(iii) a³ × a²
(iv) 7^x × 7²
(v) (5²)³ ÷ 5³
Solution:
(i) 3² × 3⁴ × 3² = 3²⁺⁴⁺⁸ = 3¹⁴ [∵ a^m × aⁿ = a^m+n]
So 3² × 3⁴ × 3² = 3¹⁴
(ii) 6¹⁵ ÷ 6¹⁰ = 6^15-10 = 6⁵ [∵ a^m × aⁿ = a^m-n]
(iii) a³ × a² = a³⁺² = a⁵
(iv) 7^x × 7² = 7^x+2
(v) (5²)³ ÷ 5³ = 5^2×3 ÷ 5³ = 5⁶ ÷ 5³ [∵ (a^m)ⁿ = a^m×n]

Question 2.
Express the following as a product of factors only in exponential form
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
Solution:
(i) 108 × 192
108 = 2 × 2 × 3 × 3 × 3
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3

∴ 108 × 192 = (2 × 2 × 3 × 3 × 3) ×
(2 × 2 × 2 × 2 × 2 × 2 × 3)
= 2⁸ × 3⁴
Thus 108 × 192 = 2⁸ × 3⁴

(ii) 270
We have 270 = 2 × 3 × 3 × 3 × 5

= 2¹ × 3³ × 5¹
= 2 × 3³ × 5
So 270 = 2 × 3³ × 5

(iii) 729 × 64
729 = 3 × 3 × 3 × 3 × 3 × 3
64 = 2 × 2 × 2 × 2 × 2 × 2

729 × 64 = (3 × 3 × 3 × 3 × 3 × 3)
× (2 × 2 × 2 × 2 × 2 × 2)
= 3⁶ × 2⁶
∴ 729 × 64 = 3⁶ × 2⁶

(iv) 768
We have 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3

= 2⁸ × 3¹
= 2⁸ × 3
Thus 768 = 2⁸ × 3

Question 3.
Identify the greater number, wherever possible in each of the following.
(i) 5³ or 3⁵
(ii) 2⁸ or 8²
(iii) 100² or 2¹⁰⁰⁰
(iv) 2¹⁰ or 10²
Solution:
(i) 5³ or 3⁵ 5³ = 5 × 5 × 5 = 125
3⁵ = 3 × 3 × 3 × 3 × 3 = 243
243 > 125 ∴ 3⁵ > 5³

(ii) 2⁸ or 8² 2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
8² = 8 × 8 = 64
256 > 64 ∴ 2⁸ > 8²

(iii) 100² or 2¹⁰⁰⁰
We have 100² = 100 × 100 = 10000
2¹⁰⁰ = (2¹⁰)¹⁰ = (2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2)¹⁰
= (1024)¹⁰ = [(1024)²]⁵
= (1024 × 1024)⁵ = (1048576)⁵
Since 1048576 > 10000
(1048576)⁵ > 10000
i.e., (1048576) > 100²
(2¹⁰)¹⁰ > 100²
2¹⁰⁰ > 100²

(iv) 2¹⁰ or 10²
We have 2¹⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
10² = 10 × 10 = 100
Since1 1024 > 100
2¹⁰ > 10²

Exercise 3.2

Question 1.
Find the unit digit of the following exponential numbers.
(i) 255²²³
(ii) 8111¹⁰⁰⁰
(iii) 4866⁴³¹
Solution:
(i) 255²²³
Unit digit of base 255 is 5 and power is 223.
Thus the unit digit of 255²²³ is 5.

(ii) 8111¹⁰⁰⁰
Unit digit of base 8111 is 1 and power is 1000.
Thus the unit digit of 8111¹⁰⁰⁰ is 1.

(iii) 4866⁴³¹
Unit digit of base 4866 is 6 and power is 431.
Thus the unit digit of 4866⁴³¹ is 6.

Question 2.
Find the unit digit of the numbers
(i) 1844⁶⁷¹
(ii) 1564¹⁰⁰
Solution:
(i) 1844⁶⁷¹
Unit digit of base 1844 is 4 and the power is 671 (odd power)
Therefore unit digit of 1844⁶⁷¹ is 4

(ii) 1564¹⁰⁰
Unit digit of base 1564 is 4 and the power is 100 (even power)
Therefore unit digit of 1564¹⁰⁰ is 6.

Question 3.
Find the unit digit of the numbers
(i) 999²²²
(ii) 1549⁷⁷⁷
Solution:
(i) 999²²²
Unit digit of base 999 is 9 and the power is 222 (even power).
Therefore, unit digit of 999²²² is 1.

(ii) 1549⁷⁷⁷
Unit digit of base 1549 is 9 and the power is 777 (odd power).
Therefore, unit digit of 1549⁷⁷⁷ is 9.

Question 4.
Find the unit digit of 1549¹⁰¹ + 6541²⁰
Solution:
1549¹⁰¹ + 6541²⁰
In 1549¹⁰¹, the unit digit of base 1549 is 9 and power is 101 (odd power).
Therefore, unit digit of the 1549¹⁰¹ is 9.
In 6541²⁰, the unit digit of base 6541 is 1 and power is 20 (even power).
Therefore, unit digit of the 6541²⁰ is 1.
∴ Unit digit of 1549¹⁰¹ + 6541²⁰ is 9 + 1 = 10
∴ Unit digit of 1549¹⁰¹ + 6541²⁰ is 0.

Exercise 3.3

Question 1.
Find the degree of the following polynomials.
(i) x⁵ – x⁴ + 3
(ii) 2 – y⁵ – y³ + 2y⁸
(iii) 2
(iv) 5x³ + 4x² + 7x
(v) 4xy + 7x²y + 3xy³
Solution:
(i) x⁵ – x⁴ + 3
The terms of the given expression are x⁵, -x⁴, 3.
Degree of each of the terms : 5, 4, 0
Term with highest degree: x⁵
Therefore degree of the expression in 5.

(ii) 2 – y⁵ – y³ + 2y⁸
The terms of the given expression are 2, -y⁵ ,-y³, 2y⁸.
Degree of each of the terms : 0, 2, 3, 8.
Term with highest degree: 2y⁸
Therefore degree of the expression in 8.

(iii) 2
Degree of the constant term is 0.
∴ Degree of 2 is 0.

(iv) 5x³+ 4x² + 7x
The terms of the given expression are 5x³, 4x², 7x
Degree of each of the terms : 3, 2, 1
Term with highest degree: 5x³
Therefore degree of the expression in 3.

(v) 4xy + 7x²y + 3xy³
The terms of the given expression are 4xy , 7x²y, 3xy³
Degree of each of the terms : 2, 3, 4
Term with highest degree: 3xy³
Therefore degree of the expression in 4.

Question 2.
State whether a given pair of terms in like or unlike terms.
(i) 1,100
(ii) -7x,\(\frac { 5 }{ 2 } \)x
(iii) 4m²p, 4mp²
(iv) 12xz, 12x²z²
Solution:
(i) 1, 100 is a pair of like terms. [∵ 1 = x⁰ and 100 = 100 x⁰]
(ii) -7x, \(\frac { 5 }{ 2 } \)x is a pair of like terms.
(iii) 4m²p, Amp is a pair of unlike terms.
(iv) 12xz, 12x²z² is a pair of unlike terms.

Question 3.
Subtract 5a² – 7ab + 5b² from 3ab – 2a² – 2b² and find the degree of the expression
Solution:
(i) We have (3ab – 2a² – 2b²) – (5a² – 7ab + 5b²)
= 3ab – 2a² – 2b² – 5a² + 7ab – 5b²
= (3ab + 7ab) + (- 2 – 5)a² + (- 2 – 5)b²
= 10 ab + (-7)a² + (-7)b²
= 10ab – 7a² – 7b²
Degree of the expression is 2.

Question 4.
Add x² – y² -1,y² – 1 – x², 1 – x² – y² and find the degree of the expression.
Solution:
We have (x² – y² – 1) + (y² – 1 – x²) + (1 – x² – y²)
= x² – y² – 1 + y² – 1 – x² + 1 – x² – y²
= (x² – x² – x²) + (-y² + y² – y²) + (- 1 – 1 + 1)
= (1 – 1 – 1)x² + (- 1 + 1 – 1)y² + ( – 2 + 1)
= (- 1) x² + (- 1)y² + (-1) = – x² – y² – 1
Degree of the expression is 2.

Question 5.
Find the degree of the terms
(i) x²
(ii) 4xyz
(iii) \(\frac{7 x^{2} y^{4}}{x y}\)
(iv) \(\frac{x^{2} \times y^{2}}{x \times y^{2}}\)
Solution:
We have
(i) x²
The exponent in x² is 2. ∴ Degree of the term is 2.

(ii) 4xyz
In 4xyz the sum of the powers of x, y and z as 3.

(iii) \(\frac{7 x^{2} y^{4}}{x y}\)
We have \(\frac{7 x^{2} y^{4}}{x y}\) = 7x^2-1 y^4-1 = 7x¹y³ [Since \(\frac{a^{m}}{a^{n}}\) = am-n]
In 7 x¹ y³ the sum of the poweres of x and y is 4(1 + 3 = 4)
Thus degree of the expression is 4.

(iv) \(\frac{x^{2} \times y^{2}}{x \times y^{2}}\)
We have \(\frac{x^{2} \times y^{2}}{x \times y^{2}}\) = x^2-1 y^2-2 = x¹ y⁰ = x¹ [∵ y⁰ = 1]
The exponent of the expression is 1.

Students can Download Maths Chapter 3 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Intext Questions

Exercise 3.1

Try These (Text book Page No. 44)

Question 1.
Observe and complete the following table. First one is done for you.

Solution:

Try These (Text book Page No. 46)

Question 1.
Simplify and write the following in exponential form.
1. 2³ × 2⁵
2. p² × P⁴
3. x⁶ × x⁴
4. 3¹ × 3⁵ × 3⁴
5. (-1)² × (-1)³ × (-1)⁵
Solution:
1. 2³ × 2⁵ = 2³⁺⁵ = 2⁸ [since a^m × aⁿ = a^m+n]

2. p² × p⁴ = p²⁺⁴ = p⁶ [since a^m × aⁿ = a^m+n]

3. x⁶ × x⁴ = x⁶ + 4 = x¹⁰ [since a^m × aⁿ = a^m+n]

4. 3¹ × 3⁵ × 3⁴ = 3¹⁺⁵ × 3⁴ [since a^m × aⁿ = a^m+n]
= 3⁶ × 3⁴ [since a^m × aⁿ = a^m+n]
= 3¹⁰

5. (-1)² × (-1)³ × (-1)⁵
= (-1)²⁺³ × (-1)⁵ [Since a^m × aⁿ = a^m+n]
= (-1)⁵ × (-1)⁵
= (-1)⁵⁺⁵ [Since a^m × aⁿ = a^m+n]
= (-1)¹⁰

Try These (Text book Page No. 48)

Question 1.
Simply the following.
1. 23⁵ ÷ 23²
2. 11⁶ ÷ 11³
3. (-5)³ ÷ (-5)²
4. 7³ ÷ 7³
5. 15⁴ ÷ 15
Solution:

Try These (Text book Page No. 48)

Question 1.
Simplify and write the following in exponent form.
1. (3²)³
2. [(-5)³]²
3. (20⁶)²
4. (10³)⁵
Solution:
1. (3²)³ = 3^2×3 = 3⁶ [since (a^m)ⁿ = a^m×n]
2. [(-5)]² = (-5)^3×2 = (-5)⁶ [since (a^m)ⁿ = a^m×n]
3. (20⁶)² = 20^6×2 = 20¹² [since (a^m)ⁿ = a^m×n]
4. (10³)⁵ = 10^3×5 = 10¹⁵ [since (a^m)ⁿ = a^m×n]

Question 2.
Express the following exponent numbers using a^m × b^m = (a × b)^m.
(i) 5² × 3²
(ii) x³ × y³
(iii) 7⁴ × 8⁴
Solution:
(i) 5² × 3² = (5 × 3)² = 15² [since a^m × b^m = (a × b)^m]
(ii) x³ × y³ = (x × y)³ = (x y)³
(iii) 7⁴ × 8⁴ = (7 × 8)⁴ = 56⁴

Question 3.
Simplify the following exponent numbers by using (\(\frac { a }{ b } \))^m = \(\frac{a^{m}}{b^{m}}\)
(i) 5³ ÷ 2³
(ii) (-2)⁴ ÷ 3⁴
(iii) 8⁶ ÷ 5⁶
(iv) 6³ ÷ (-7)³
Solution:
(i) 5³ ÷ 2³ = (\(\frac { 5 }{ 2 } \))³ – [Since \(\frac{a^{m}}{b^{m}}\) = (\(\frac { a }{ b } \))^m]
(ii) (-2)⁴ ÷ 3⁴ = (\(\frac { -2 }{ 3 } \))⁴
(iii) 8⁶ ÷ 5⁶ = (\(\frac { 8 }{ 6 } \))⁶
(iv) 6³ ÷ (-7)³ = (\(\frac { 6 }{ -7 } \))³

Exercise 3.2

Try These (Text book Page No. 54)

Question 1.
Find the unit digit of the following exponential numbers:
(i) 106²¹
(ii) 25⁸
(iii) 31¹⁸
(iv) 20¹⁰
Solution:
(i) 106²¹ Unit digit of base 106 is 6 and the power is 21 and is positive.
Thus the unit digit of 106²¹ is 6.

(ii) 25⁸ Unit digit of base 25 is 5 and the power is 8 and is positive.
Thus the unit digit of 25⁸ is 5.

(iii) 31¹⁸ Unit digit of base 31 is 1 and the power 18 and is positive.
Thus the unit digit of 31¹⁸ is 1.

(iv) 20¹⁰ Unit digit of base 20 is 0 and the power 10 and is positive.
Thus the unit digit of 20¹⁰ is 0.

Try These (Text book Page No. 55)

Question 1.
Find the unit digit of the following exponential numbers:
(i) 64¹¹
(ii) 29¹⁸
(iii) 79¹⁹
(iv) 104³²
Solution:
(i) 64¹¹ Unit digit of base 64 is 4 and the power is 11 (odd power).
∴ Unit digit of 64¹¹ is 4.

(ii) 29¹⁸ Unit digit of base 29 is 9 and the power is 18 (even power).
Therefore, unit digit of 29¹⁸ is 1.

(iii) 79¹⁹ Unit digit of base 79 is 9 and the power is 19 (odd power).
Therefore, unit digit of 7919 is 9.

(iv) 104³² Unit digit of base 104 is 4 and the power is 32 (even power).
Therefore, unit digit of 104³² is 6.

Exercise 3.3

Try These (Text book Page No. 35)

Question 1.
Complete the following table:

Solution:

Question 2.
Identify the like terms from the following:
(i) 2x²y, 2xy²,3xy²,14x²y, 7yx
(ii) 3x³y², y³x, y³x², – y³x, 3y³x
(iii) 11pq, -pq, 11pqr, -11pq,pq
Solution:
(i) 2x²y, 2xy², 3xy², 14x²y, 7yx
(a) 2x²y and 14x²y are like terms.
(b) 2xy² and 3xy² are like terms.

(ii) 3x³y², y³x, y³x², – y³x, 3y³x
(a) y³x, – y³x and 3y³x are like terms.

(iii) 11 pq, -pq, 11pqr , -11 pq, pq
(a) 11 pq, -pq, -pq and pq are like terms.

Students can Download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Ex 3.4

Miscellaneous Practice Problems

Question 1.
6² × 6^m = 6⁵, find the value of ‘m’
Solution:
6² × 6^m = 6⁵
6^2+m = 6⁵ [Since a^m × aⁿ= a^m+n]
Equating the powers, we get
2 + m = 5
m = 5 – 2 = 3

Question 2.
Find the unit digit of 124¹²⁸ × 126¹²⁴
Solution:
In 124¹²⁸, the unit digit of base 124 is 4 and the power is 128 (even power).
Therefore, unit digit of 124¹²⁸ is 4.
Also in 126¹²⁴, the unit digit of base 126 is 6 and the. power is 124 (even power).
Therefore, unit digit of 126¹²⁴ is 6.
Product of the unit digits = 6 × 6 = 36
∴ Unit digit of the 124¹²⁸ × 126¹²⁴ is 6.

Question 3.
Find the unit digit of the numeric expression: 16²³ + 71⁴⁸ + 59⁶¹
Solution:
In 16²³, the unit digit of base 16 is 6 and the power is 23 (odd power).
Therefore, unit digit of 16²³ is 6.
In 71⁴⁸, the unit digit of base 71 is 1 and the power is 48 (even power).
Therefore, unit digit of 71⁴⁸ is 1.
Also in 59⁶¹, the unit digit of base 59 is 9 and the power is 61 (odd power).
Therefore, unit digit of 59⁶¹ is 9.
Sum of the unit digits = 6 + 1 + 9 = 16
∴ Unit digit of the given expression is 6.

Question 4.
Find the value of

Solution:

Question 5.
Identify the degree of the expression, 2a³be + 3a³b + 3a³c – 2a²b²c²
Solution:
The terms of the given expression are 2a³bc, 3a³b + 3a³c – 2a²b²c²
Degree of each of the terms: 5,4,4,6.
Terms with the highest degree: – 2a²b²c²
Therefore degree of the expression is 6.

Question 6.
If p = -2, q = 1 and r = 3, find the value of 3p²q²r.
Solution:
Given p = -2; q = 1; r = 3
∴ 3p²q²r = 3 × (-2)² × (1)² × (3)
= 3 × (-2 × 1)² × (3) [Since a^m × b^m = (a × b)^m]
= 3 × (-2)² × (3)
= 3 × (-1)² × 2² × 3
= 3¹⁺¹ × 1 × 4 [Since a^m × aⁿ = a^m+n]
= 3² × 4 = 9 × 4
∴ 3p²q²r = 36

Challenge Problems

Question 7.
LEADERS is a WhatsApp group with 256 members. Every one of its member is an admin for their own WhatsApp group with 256 distinct members. When a message is posted in LEADERS and everybody forwards the same to their own group, then how many members in total will receive that message?
Solution:
Members of the groups LEADERS = 256
Members is individual groups of the members of LEADERS = 256
Total members who receive the message

= 256 × 256 = 2⁸ × 2⁸
2⁸⁺⁸ = 2¹⁶
= 65536
Totally 65536 members receive the message.

Question 8.
Find x such that 3^x+2 = 3^x + 216.
Solution:
Given 3^x+2 = 3^x + 216 ; 3^x+2 = 3^x + 216
Dividing throught by 3^x, we get

Equating the powers of same base

Question 9.
If X = 5x² + 7x + 8 and Y = 4x² – 7x + 3, then find the degree of X + Y.
Solution:
Given x = 5x² + 7x + 8
X + Y = 5x² + 7x + 8 + (4x² – 7x + 3)
= (5x² + 4x²) + (7x – 7x) + (8 + 3)
= x² (5 + 4) + x(7 – 7) + (8 + 3) = 9x² + 11
Degree of the expression is 2.

Question 10.
Find the degree of (2a² + 3ab – b²) – (3a² -ab- 3b²)
Solution:
(2a² + 3ab – b²) – (3a² – ab – 3b²)
= (2a² + 3ab – b²) + (- 3a² + ab + 3b²)
= 2a² + 3ab – b² – 3a² + ab + 3b²
= 2a² – 3a² + 3ab + ab + 3b² – b²
= 2a² – 3a² + ab (3 + 1) + b²(3 – 1)
= – a² + 4 ab + 2b²
Hence degree of the expression is 2.

Question 11.
Find the value of w, given that x = 4, y = 4, z = – 2 and w = x² – y² + z² – xyz.
Solution:
Given x = 3; y = 4 and z = -2.
w = x² – y² + z² – xyz
w = 3² – 4² + (-2)² – (3)(3)(-2)
w = 9 – 16 + 4 + 24
w = 37 – 16
w = 21

Question 12.
Simplify and find the degree of 6x² + 1 – [8x – {3x² – 7 – (4x² – 2x + 5x + 9)}]
Solution:
6x² + 1 – [8x – (3x² – 7 – (4x² – 2x + 5x + 9)}]
= 6x² + 1 – [8x – {3x² – 7 – 4x² – 2x + 5x + 9}]
= 6x² + 1 – [8x – 3x² + 7 + 4x² – 2x + 5x + 9}]
= 6x² – 1 – [8x + 3x² – 7 – 4x² + 2x – 5x – 9]
= 6x² + 3x² – 4x² – 8x + 2x – 5x – 1 – 7 – 9]
= x²(6 + 3 – 4) + x(8 + 2 – 5) – 15
= 5x² – 11x – 15
Degree of the expression is 2.

Question 13.
The two adjacent sides of a rectangle are 2x² – 5xy + 3z² and 4xy – x² – z². Find the perimeter and the degree of the expression.
Solution:
Let the two adjacent sides of the rectangle as
l = 2x² – 5xy + 3z² and b = 4xy – x²y + 3z²

Perimeter of the rectangle
= 2(l + b) = 2(2x² – 5xy + 3z² + 4xy – x² – z²)
= 4x² – 10xy + 6z² + 8xy – 2x² – 2z²
= 4x² – 2x² – 10xy + 8xy + 6z² – 2z²
= x²(4 – 2) + xy (-10 + 8) + z² (6 – 2z²)
Perimeter = 2x² – 2xy + 4z²
Degree of the expression is 2.

Students can Download Maths Chapter 3 Algebra Ex 3.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Ex 3.3

Question 1.
Fill in the blanks.

(i) The degree of the term a³b²c⁴d² is _______
(ii) Degree of the constant term is _______
(iii) The coefficient of leading term of the expression 3z²y + 2x – 3 is _______
Answers:
(i) 11
(ii) 0
(iii) 3

Question 2.
Say True or False.

(i) The degree of m² n and mn² are equal.
(ii) 7a²b and -7ab² are like terms.
(iii) The degree of the expression -4x² yz is -4
(iv) Any integer can be the degree of the expression.
Answers:
(i) True
(ii) False
(iii) False
(iv) True

Question 3.
Find the degree of the following terms.
(i) 5x²
(ii) -7 ab
(iii) 12pq² r²
(iv) -125
(v) 3z
Solution:
(i) 5x²
In 5x², the exponent is 2. Thus the degree of the expression is 2.

(ii) -7ab
In -7ab, the sum of powers of a and b is 2. (That is 1 + 1 = 2).
Thus the degree of the expression is 2.

(iii) 12pq² r²
In 12pq² r², the sum of powers of p, q and r is 5. (That is 1 +2 + 2 = 5).
Thus the degree of the expression is 5.

(iv) -125
Here – 125 is the constant term. Degree of constant term is 0.
∴ Degree of -125 is 0.

(v) 3z
The exponent is 3z is 1.
Thus the degree of the expression is 1.

Question 4.
Find the degree of the following expressions.
(i) x³ – 1
(ii) 3x² + 2x + 1
(iii) 3t⁴ – 5st² + 7s²t²
(iv) 5 – 9y + 15y2 – 6y3
(v) u⁵ + u⁴v + u³v² + u₂v³ + uv⁴
Solution:
(i) x³ – 1
The terms of the given expression are x³, -1
Degree of each of the terms: 3,0
Terms with highest degree: x³.
Therefore, degree of the expression is 3.

(ii) 3x² + 2x + 1
The terms of the given expression are 3x², 2x, 1
Degree of each of the terms: 2, 1, 0
Terms with highest degree: 3x²
Therefore, degree of the expression is 2.

(iii) 3t⁴ – 5st² + 7s²t²
The terms of the given expression are 3t⁴, – 5st², 7s³t²
Degree of each of the terms: 4, 3, 5
Terms with highest degree: 7s²t²
Therefore, degree of the expression is 5.

(iv) 5 – 9y + 15y² – 6y³
The terms of the given expression are 5, – 9y , 15y², – 6y³
Degree of each of the terms: 0, 1, 2, 3
Terms with highest degree: – 6y³
Therefore, degree of the expression is 3.

(v) u⁵ + u⁴v + u³v² + u₂v³ + uv⁴
The terms of the given expression are u⁵, u⁴v , u³v², u²v³, uv⁴
Degree of each of the terms: 5, 5, 5, 5, 5
Terms with highest degree: u⁵, u⁴v , u³v², u²v³, uv⁴
Therefore, degree of the expression is 5.

Question 5.
Identify the like terms : 12x³y²z, – y³x²z, 4z³y²x, 6x³z²y, -5y³x²z
Solution:
-y³ x²z and -5y³x²z are like terms.

Question 6.
Add and find the degree of the following expressions.
(i) (9x + 3y) and (10x – 9y)
(ii) (k² – 25k + 46) and (23 – 2k² + 21 k)
(iii) (3m²n + 4pq²) and (5nm² – 2q²p)
Solution:
(i) (9x + 3y) and (10x – 9y)
This can be written as (9x + 3y) + (10x – 9y)
Grouping the like terms, we get
(9x + 10x) + (3y – 9y) = x(9 + 10) + y(3 – 0) = 19x + y(-6) = 19x – 6y
Thus degree of the expression is 1.

(ii) (k² – 25k + 46) and (23 – 2k² + 21k)
This can be written as (k² – 25k + 46) + (23 – 2k² + 21k)
Grouping the like terms, we get
(k² – 2k²) + (-25 k + 21 k) + (46 + 23)
= k² (1 – 2) + k(-25 + 21) + 69 = – 1k² – 4k + 69
Thus degree of the expression is 2.

(iii) (3m²n + 4pq²) and (5nm² – 2q²p)
This can be written as (3m²n + 4pq²) + (5nm² – 2q²p)
Grouping the like terms, we get
(3m²n + 5m²n) + (4pq² – 2pq²)
= m²n(3 + 5) + pq²(4 – 2) = 8m²n + 2pq²
Thus degree of the expression is 3.

Question 7.
Simplify and find the degree of the following expressions.
(i) 10x² – 3xy + 9y² – (3x² – 6xy – 3y²)
(ii) 9a⁴ – 6a³ – 6a⁴ – 3a² + 7a³ + 5a²
(iii) 4x² – 3x – [8x – (5x² – 8)]
Solution:
(i) 10x² – 3xy + 9y² – (3x² – 6xy – 3y²)
= 10x² – 3xy + 9y² + (-3x² + 6xy + 3y²)
= 10x² – 3xy + 9y² – 3x² + 6xy + 3y²
= (10x² – 3x²) + (- 3xy + 6xy) + (9y² + 3y²)
= x²(10 – 3) + xy(-3 + 6) + y²(9 + 3)
= x²(7) + xy(3) + y²(12)
Hence, the degree of the expression is 2.

(ii) 9a⁴ – 6a³ – 6a⁴ – 3a² + 7a³ + 5a²
= (9a⁴ – 6a⁴) + (- 6a³ + 7a³) + (- 3a² + 5a²)
= a⁴(9-6) + a³ (- 6 + 7) + a²(-3 + 5)
= 3a⁴ + a³ + 2a²
Hence, the degree of the expression is 4.

(iii) 4x² – 3x – [8x – (5x² – 8)]
= 4x² – 3x – [8x + -5x² + 8)]
= 4x² – 3x – [8x – 5x² – 8]
= 4x² – 3x – 8x + 5x² – 8
(4x² + 5x²) + (- 3x – 8x) – 8
= x²(4+ 5) + x(-3-8) – 8
= x²(9) + x(- 11) – 8
= 9x² – 11x – 8
Hence, the degree of the expression is 2.

Objective Type Question

Question 8.
3p² – 5pq + 2q² + 6pq – q² +pq is a
(i) Monomial
(ii) Binomial
(iii) Trinomial
(iv) Quadrinomial
Answer:
(iii) Trinomial

Question 9.
The degree of 6x⁷ – 7x³ + 4 is
(i) 7
(ii) 3
(iii) 6
(iv) 4
Answer:
(i) 7

Question 10.
If p(x) and q(x) are two expressions of degree 3, then the degree of p(x) + q(x) is
(i) 6
(ii) 0
(iii) 3
(iv) Undefined
Answer:
(iii) 3

Students can Download Maths Chapter 3 Algebra Ex 3.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 3 Algebra Ex 3.1

Question 1.
Fill in the blanks.

1. The exponential form 14⁹ should be read as ______
2. The expanded form of p³ q² is ______
3. When base is 12 and exponent is 17, its e×ponential form is _____
4. The value of (14 × 21)⁰ is _____

Answers:

1. 14 Power 9
2. p × p × p × q × q
3. 12¹⁷
4. 1

Question 2.
Say True or False.

1. 2³ × 3² = 65
2. 2⁹ × 3² = (2 × 3)^9×2
3. 3⁴ × 3⁷= 3¹¹
4. 2⁰ × 1000⁰
5. 2³ < 3²

Answers:

1. False
2. False
3. True
4. True
5. True

Question 3.
Find the value of the following.

1. 2⁶
2. 11²
3. 5⁴
4. 9³

Solution:

1. 2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64
2. 11² = 11 × 11 = 121
3. 5⁴ = 5 × 5 × 5 × 5 = 625
4. 9³ = 9 × 9 × 9 = 729

Question 4.
Express the following in e×ponential form.

1. 6 × 6 × 6 × 6
2. t × t
3. 5 × 5 × 7 × 7 × 7
4. 2 × 2 × a × a

Solution:

1. 6 × 6 × 6 × 6 = 6^1+1+1+1 = 64 [Since a^m × aⁿ = a^m+n]
2. t × t = t¹⁺¹ = t²
3. 5 × 5 × 7 × 7 × 7 = 5¹⁺¹ × 7¹⁺¹⁺¹ = 5² × 7³
4. 2 × 2 × a × a = 2¹⁺¹ × a¹⁺¹ = 2² × a² = (2a)²

Question 5.
E×press each of the following numbers using e×ponential form,
(i) 512
(ii) 343
(iii) 729
(iv) 3125
Solution:
(i) 512

512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2⁹ [Using product rule]

(ii) 343

343 = 7 × 7 × 7 = 7¹⁺¹⁺¹
= 7³ [Using product rule]

(iii) 729

729 = 3 × 3 × 3 × 3 × 3 × 3
= 3⁶ [Using product rule]

(iv) 3125

3125 = 5 × 5 × 5 × 5 × 5
= 5⁵ [Using product rule]

Question 6.
Identify the greater number in each of the following.
(i) 6³ or 3⁶
(ii) 5³ or 3⁵
(iii) 2⁸ or 8²
Solution:
(i) 6³ or 3⁶
6³ = 6 × 6 × 6 = 36 × 6 = 216
3⁶ = 3 × 3 × 3 × 3 × 3 × 3 = 729
729 > 216 gives 3⁶ > 6³
∴ 36 is greater.

(ii) 5³ or 3⁵
5³ = 5 × 5 × 5 = 125
3⁵ = 3 × 3 × 3 × 3 × 3 = 243
243 > 125 gives 3⁵ > 5³
∴ 3⁵ is greater.

(iii) 2⁸ or 8²
2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
8² = 8 × 8 = 64
256 > 64 gives 2⁸ > 8²
∴ 2⁸ is greater.

Question 7.
Simplify the following
(i) 7² × 3⁴
(ii) 3² × 2⁴
(iii) 5² × 10⁴
Solution:
(i) 7² × 3⁴ = (7 × 7) × (3 × 3 × 3 × 3)
= 49 × 81 = 3969

(ii) 3² × 2⁴ = (3 × 3) × (2 × 2 × 2 × 2)
= 9 × 16 = 144

(iii) 5² × 10⁴ = (5 × 5) × (10 × 10 × 10 × 10)
= 25 × 10000 = 2,50,000

Question 8.
Find the value of the following.
(i) (-4)²
(ii) (-3) × (-2)³
(iii) (-2)³ × (-10)³
Solution:
(i) (-4)² = (-1)² × (4)² [since a^m × b^m = (a × b)^m]
= 1 × 16 = 16 [since (-1)ⁿ = 1 if n is even]

(ii) (-3) × (-2)³ = (-1) × (-3) × (-1)³ × (-2)³
= (-1)⁴ × 24 [Grouping the terms of same base]
= 24

(iii) (-2)³ × (-10)³ = (-1)³ × (-2)³ × (-1)³ × (-10)³
= (-1)³⁺³ × 2³ × 10³ [Grouping the terms of same base]
= (-1)⁶ × (2 × 10)³
[∵ a^m × b^m = (a × b)^m]
= 1 × 20³ [since (-1)ⁿ = 1 if n is even]
= 8000

Question 9.
Simplify using laws of exponents.
(i) 3⁵ × 3⁸
(ii) a⁴ × a¹⁰
(iii) 7x × 7²
(iv) 2⁵ ÷ 2³
(v) 18⁸ ÷ 18⁴
(vi) (6⁴)³
(vii) (x^m)⁰
(viii) 9⁵ × 3⁵
(ix) 3^y × 12^y
(x) 25⁶ × 5⁶
Solution:

Question 10.
If a = 3 and b = 2, then find the value of the following.
(i) a^b + b^a
(ii) a^a – b^b
(iii) (a + b)^b
(iv) (a – b)^a
Solution:
(i) a^b + b^a
a = 3 and b = 2
we get 3² + 2³ = (3 × 3) + (2 × 2 × 2) = 9 + 8 = 17

(ii) (a^a – b^b)
Substituting a = 3 and b = 2
we get 3² – 2² = (3 × 3 × 3) – (2 × 2) = 27 – 4 = 23

(iii) (a + b)^b
Substituting a = 3 and b = 2
we get (3 + 2)² = 5² = 5 × 5 = 25

(iv) (a – b)^a
Substituting a = 3 and b = 2
we get (3 – 2)³ = 1³ = 1 × 1 × 1 = 1

Question 11.
Simplify and express each of the following in exponential form:
(i) 4⁵ × 4² × 4⁴
(ii) (3² × 3³)⁷
(iii) (5² × 5⁸) ÷ 5^s
(iv) 2⁰ × 3⁰ × 4⁰
(v) \(\frac{5^{5} \times a^{8} \times b^{3}}{4^{3} \times a^{5} \times b^{2}}\)
Solution:

Objective Type Questions

Question 12.
a × a × a × a × a equal to
(i) a⁵
(ii) 5 a
(iii) 5a
(iv) a + 5
Answer:
(i) a⁵

Question 13.
The exponential form of 72 is
(i) 72
(ii) 27
(iii) 2² × 3³
(iv) 2³ × 3²
Answer:
(iv) 2³ × 3²

Question 14.
The value of x in the equation a¹³ = x³ × a¹⁰ is
(i) a
(ii) 13
(iii) 3
(iv) 10
Answer:
(i) a

Question 15.
How many zeros are there in 100¹⁰ ?
(i) 2
(ii) 3
(iii) 100
(iv) 20
Answer:
(iv) 20

Question 16.
2⁴⁰ + 2⁴⁰ is equal to
(i) 4⁴⁰
(ii) 2⁸⁰
(iii) 2⁴¹
(iv) 4⁸⁰
Answer:
(iii) 2⁴¹

Students can Download Maths Chapter 2 Measurements Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 2 Measurements Additional Questions

Additional Questions and Answers

Exercise 2.1

Question 1.
A circular disc of radius 28 cm is divided into two equal parts. What is the perimeter of each semicircular shape disc? Also find the perimeter of the circular disc.
Answer:
Radius of the circular disc = 28 cm
∴ circumference of the circle = 2 π r units

= 2 × \(\frac { 22 }{ 7 } \) × 28 cm
= 2 × 22 × 4 = 44 × 4 = 176 cm
Perimeter of the circular disc = 176 cm
Now circumference of the semicircular disc = \(\frac { 1 }{ 2 } \) × (2 π r) = π r units
Perimeter of the semicircular disk = π r + r + r = \(\frac { 22 }{ 7 } \) × 28 + 28 + 28
= 22 × 4 + 28 + 28 = 88 + 28 + 28 = 144
Perimeter of each semicircular disc = 144 cm

Question 2.
A gardener wants to fence a circular garden of diameter 14m. Find the length of the rope he needs to purchase if he makes 3 rounds of fence. Also find the cost of the rope, if it costs ₹ 4 per metre.
Solution:
Diameter of the circular garden (d) = 14 m
Circumference = π d = \(\frac { 22 }{ 7 } \) × 14 = 44 m
Since the rope makes 3 rounds of fence,
length of the rope needed = 3 × circumference of the garden
= 3 × 44 m = 132 m
Cost of rope per meter = ₹ 4 × 132 = ₹ 528

Question 3.
Latha wants to put a lace on the edge of a circular table cover of diameter 3 m. Find the length of the lace required and also find the cost if one metre of the lace costs ₹ 30 (Take π = 3.15 )
Solution:
Diameter of the circular table cover = 3m
Circumference C = π d units = 3.15 × 3 m = 9.45 m
Length of the lace required = 9.45 m
Cost of lace per meter = ₹ 30
∴ Cost of 9.45m lace = ₹ 30 × 9.45 = ₹ 283.50

Exercise 2.2

Question 1.
The circumference of two circles are on the ratio 5 : 6. Find the ratio of their areas.
Solution:
Let the radii of the given circles be r₁ and r₂
Let their circumference be C₁ and C₂ respectively
C₁ = 2πr₁ and C₂ = 2πr₂

Now let the area of the given circles the A₁ and A₂

∴ The areas of two circles are in the ratio 25 : 36.

Question 2.
Find the area of the circle whose circumference is 88 cm.
Solution:
The circumference of the circle = 88 cm
2πr = 88 cm
2 × \(\frac { 22 }{ 7 } \) × r = 88 cm
r = \(\frac{88 \times 7}{2 \times 22}\) = 14 cm
r = 14 cm
Area of the circle A = πr²
= \(\frac { 22 }{ 7 } \) × 14 × 14 cm²
= 22 × 2 × 14 cm²
= 616 cm²

Question 3.
Find the cost of polishing a circular table top of diameter 16 dm if the rate of polishing is ₹ 15 per dm².
Solution:
Diameter of the circular table top = 16 dm
Radius (r) = \(\frac { 16 }{ 2 } \) = 8cm
Area of the circular table top
= πr² sq.units
= \(\frac { 22 }{ 7 } \) × 8 × 8 dm² = \(\frac { 1408 }{ 7 } \) dm²
= 201.14 dm²
Rate of the polishing per dm² = ₹ 15
∴ Rate of the polishing 201.14 dm²
= ₹ 15 × 201.14
= ₹ 3,017

Exercise 2.3

Question 1.
From a circular sheet of radius 5 cm a circle of radius 3 cm is removed. Find the area of the remaining sheet.
Solution:
Radius of the outer circle R = 5 cm
Radius of the inner circle r = 3 cm
Area of the remaining sheet = Area of the outer circle
– Area of the inner circle
= πR² – πr² sq. units = π(R² – r²) sq. units
= \(\frac { 22 }{ 7 } \) (5² – 3²) cm² = \(\frac { 22 }{ 7 } \) (5² – 3²) cm²
= \(\frac { 22 }{ 7 } \) × (5 + 3) (5 – 3) = \(\frac { 22 }{ 7 } \) × (8) (2)
= \(\frac { 352 }{ 7 } \) = 50.28 cm²

Question 2.
A picture is painted on a cardborad 8 cm long and 5 cm wide such that there is a margin of 1.5 cm along each of its sides. Find the total area of the margin.
Solution:
Length of the outer rectangle L = 8 cm
Breadth of the outer rectangle B = 5 cm
Area of the outer rectangle = L × B sq. units = 8 × 5 cm² = 40 cm²
Length of the inner rectangle l = L – 2W = 8 – 2(1.5)cm = 8 – 3cm
l = 5cm
Breadth of thqnner rectangle b = B – 2W = 5 – 2(1.5) cm
= 5 – 3cm = 2cm
∴ Area of the margin = Area of the outer rectangle
– Area of the inner rectangle
= (40 – 10) cm² = 30cm²

Question 3.
A circular piece of radius 2 cm is cut from a rectangle sheet of length 5 cm and breadth 3 cm. Find the area left in the sheet.
Solution:
Radius of the portion removed r = 2 cm
Area of the circular sheet = πr² sq.units
= \(\frac { 22 }{ 7 } \) × 2 × 2 cm² = \(\frac { 88 }{ 7 } \) cm² = 12.57 cm²
Length of the rectangular sheet L = 5 cm
Breadth of the rectangular sheet B = 3 cm
Area of the rectangle = L × B sq. units = 5 × 3 cm² = 15 cm²
Area of the sheet left over = Area of the rectangle – Area of the circle
= 15 cm² – 12.57 cm² = 2.43 cm²

Students can Download Maths Chapter 2 Measurements Ex 2.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.4

Miscellaneous Practice Problems

Question 1.
A wheel of a car covers a distance of 3520 cm in 20 rotations. Find the radius of the wheel?
Solutions:
Distance covered by circular wheel in 20 rotation = 3520 cm
∴ Distance covered ini rotation = \(\frac { 3520 }{ 20 } \) cm = 176 cm
∴ Circumference of the wheel = 176 cm
∴ 2πr = 176
2 × \(\frac { -2 }{ 6 } \) × r = 176
r = \(\frac{176 \times 7}{2 \times 22}\)
r = 28 cm
Radius of the wheel = 28 cm

Question 2.
The cost of fencing a circular race course at the rate of ₹ 8 per metre is ₹2112. Find the diameter of the race course.
Solution:
Cost of fencing the circumference = ₹ 2112
Cost of fencing one meter = ₹ 8
∴ Circumference of the circle = \(\frac { 2112 }{ 8 } \) = 264 m
πd = 264 m
\(\frac { 22 }{ 7 } \) × d = 264
d = \(\frac{264 \times 7}{22}\) = 12 × 7 m = 84 m
∴ Diameter of the race cource = 84 m

Question 3.
A path 2 m long and 1 m broad is constructed around a rectangular ground of dimensions 120 m and 90 m respectively. Find the area of the path.
Solution:
Length of the rectangular ground l = 120 m
Breadth b = 90 m
Length of the path W₁ = 2m
Length of the path W₂ = 1m
Length of the ground with path L = 1 + 2 (W₂) = 120 + 2(1) m
= 120 + 2 = 122 m
Breadth of the ground with path B = l + 2(W₁) units
= 90 + 2(2) m = 90 + 4 m = 94 m
∴ Area of the path = (L × B) – (1 × b) sq. units
= (122 × 94) – (122 × 94) m² = 668 m²
∴ Area of the path = 668 m²

Question 4.
The cost of decorating the circumference of a circular lawn of a house at the rate of ₹55 per metre is ₹16940. What is the radius of the lawn?
Solution:
Cost of decorating the circumference = ₹ 16,940
Cost of decorating per meter = ₹ 55
∴ Length of the circumference = \(\frac { 16940 }{ 55 } \) m = 308 m
Circumference of the circular lawn = 308 m
2 × πr = 308 m
2 × \(\frac { 22 }{ 7 } \) × r = 308 m
r = \(\frac{308 \times 7}{2 \times 22}\)
r = 49 m
Radius of the lawn = 49 m

Question 5.
Four circles are drawn side by side in a line and enclosed by a rectangle as shown below.
If the radius of each of the circles is 3 cm, then calculate:
(i) The area of the rectangle.
(ii) The area of each circle.
(iii) The shaded area inside the rectangle.

Solution:
Given radius of a circle r = 3 cm
Diameter of the circle = 2r = 2 × 3 = 6 cm
Breadth of the rectangle = Diamter of the circle
B = 6cm
Length of the rectangle L = 4 × diameter of a circle
L = 4 × 6
L = 24cm

(i) Area of the rectangle = L × B sq. units
= 24 × 6 cm²
Area of the rectangle = 144 cm²

(ii) Area of the circle = πr² sq. units
= \(\frac { 22 }{ 7 } \) × 3 × 3 cm²
= \(\frac { 198 }{ 7 } \) cm²
= 28.28 cm²

(iii) Area of the shaded area = Area of the rectangle – Area of the 4 circles
= 144 – (4 × \(\frac { 198 }{ 7 } \)) cm² = 144 – \(\frac { 792 }{ 7 } \) cm²
= 144 – 113.14 cm² = 30.85 cm²

Challenge Problems

Question 6.
A circular path has to be constructed around a circular lawn. If the outer and inner circumferences of the path are 88 cm and 44 cm respectively, find the width and area of the path.
Solution:
Outer circumference of the circular lawn = 88 cm
2πR = 88 cm
Inner circumference of the lawn 2πr = 44 cm
2πR – 2πr = 88 – 44
2 × \(\frac { 22 }{ 7 } \) (R – r) = 44
(R – r) = \(\frac{44 \times 7}{2 \times 22}\)
Outer radius – Inner radius = 7 cm
∴ Width of the lawn = 7 cm
Also 2πR + 2πr = 88 + 44
2π (R + r) = 132
π (R + r) = \(\frac { 132 }{ 2 } \) = 66 cm
Area of the path = πR² – πr² sq. units
= π (R + r) (R – r) = 66 × 7
Area of the path = 462cm²

Question 7.
A cow is tethered with a rope of length 35 m at the centre of the rectangular field of length 76 m and breadth 60 m. Find the area of the land that the cow cannot graze?
Solution:
Length of the field l = 76 m
Breadth of the field b = 60m
Area of the field A = l × b sq. units = 76 × 60 m²
Area of the field A = 4560 m²
Length of the rope = 35m
Radius of the land that the cow can graze = 35m
Area of the land tha the cow can graze = circle of radius 35 m = πr² sq.units
π × 35 × 35 m² = \(\frac { 22 }{ 7 } \) × 35 × 35 m²
= 3850 m²
Area of the land the cow cannot graze = Area of the field – Area that the cow can graze
= 4560 – 3860 m² = 710 m²
Area of the land that the cow cannot graze = 710 m²

Question 8.
A path 5 m wide runs along the inside of the rectangular field. The length of the rectangular field is three times the breadth.of the field. If the area of the path is 500 m² then find the length and breadth of the field.
Solution:
Let the length of the rectangular field = ‘L’ m
Breadth of the rectangular field = = ‘B’ m
Area of the rectangular field = (L × B) m²
Also given length = 3 × Breadth
L = 3B
Width of the path (W) = 5m
Lenth of the inner rectangle = L – 2W = l – 2(5)
= 3B – 10m
Breadth of the inner rectangle = B – 2W
= B – 2(5)
= B – 10 m
Area of the inner rectangle = (3B – 10) (B – 10)
= 3B² – 10B – 30B + 100
Area of the path = Area of outer rectangle
– Area of inner rectangle
= (L × B) – (3B² – 10B – 30B + 100)
3B × B – (3B² – 40B + 100)
= 3B² – 3B² + 40B – 100
Area of the path = 40B – 100
Given area of the path = 500 m²
40B – 100 = 500
40B = 500 + 100 = 600
B = \(\frac { 600 }{ 40 } \)
B = 15m
Length of the field = 45 m; Breadth of the field = 15 m

Question 9.
A circular path has to be constructed around a circular ground. 1f the areas of the outer and inner circles are 1386 m2 and 616 m2 respectively, find the width and area of the path.
Solution:
Area of the outer circle = 1386 m²
πR² = 1386m²
Area of the inner circle = 616 m²
πr² = 616m²
Area of the path = Area of outer circle – Area of the inner circle
1386 m² – 616 m²
Area of the path = 770m²
Also πR² = 1386
R² = \(\frac{1386 \times 7}{22}\)
R² = 63 × 7
R² = 9 × 7 × 7
R² = 32 × 72
R = 3 × 7
Outer Radius R = 21 m
Again πr² = 616
\(\frac { 22 }{ 7 } \) × r² = 616
r² = 28 × 7
r² = 4 × 7 × 7
r² = 22 × 72
r = 2 × 7
Inner radius r = 14m
Width of the path = Outer radius – Inner radius = 21 – 14
Width of the path = 7m

Question 10.
A goat is tethered with a rope of length 45 m at the centre of the circular grass land whose radius is 52 m. Find the area of the grass land that the goat cannot graze.
Solution:
Length of the rope = 45 m = Radius of the inner circle
∴ Area of the circular area that the goat graze = πr² sq. units
= \(\frac { 22 }{ 7 } \) × 45 × 45 m² = 6364.28 m²
Radius of the gross land = 52 m
Area of the grass land = \(\frac { 22 }{ 7 } \) × 52 × 52 = 8,498.28 m²
Area that the goat cannot graze
= Area of the outer circle – Area of the inner circle
= 8498.28 – 6364.28 = 2134 m²
Area of the goat cannot grass = 2134 m²

Question 11.
A strip of 4 cm wide is cut and removed from all the sides of the rectangular cardboard with dimensions 30 cm × 20 cm. Find the area of the removed portion and area of the remaining cardboard.
Solution:
Area of the outer rectangular cardboard
= L × B sq.units = 30 × 20 cm² = 600 cm²
Width of the stip = 4 cm
Length of the inner rectangle = L – 2W
l = 30 – 2(4) = 30 – 8
l = 22cm
Breadth of the inner rectangle B = 2W = 20 – 2(4) = 20 – 8
b = 12cm
Area of the inner rectangle = l × b sq.units = 22 × 12 cm² = 264 cm²
Area of the remaining cardboard = 264 cm²
Area of the removed portion = Area of outer rectangle
– Area of the inner rectangle
= 600 – 264 cm²
Area of the removed portion = 336 cm²

Question 12.
A rectangular field is of dimension 20 m × 15 m. Two paths run parallel to the sides of the rectangle through the centre of the field. The width of the longer path is 2m and that of the shorter path is 1 m. Find (i) the area of the paths (ii) the area of the remaining portion of the field (iii) the cost of constructing the roads at the rate of ₹ 10 per sq.m.
Solution:
Length of the rectangular field L = 20 m
Breadth B = 15m
Area = L × B
20 × 15 m²
Area of outer rectangle = 300 m²

Area of inner small rectangle = \(\frac { 19 }{ 2 } \) × \(\frac { 13 }{ 2 } \) = 61.75 cm²

(i) Area of the path = Area of the outer rectangle
– Area of 4 inner small rectangles
= 300 – 4(61.75) = 300 – 247 = 53 m²
Area of the paths = 53 m²

(ii) Area of the remaining portion of the field
= Area of the outer rectangle – Area of the paths
= 300 – 53 m² = 247 m²
Area of the remaining portion = 247 m²

(iii) Cost of constructing 1 m² road = ₹10
∴ Cost of constructing 53 m² road = ₹10 × 53 = ₹530
∴ Cost of constructing road = ₹530

Students can Download Maths Chapter 2 Measurements Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 2 Measurements Intext Questions

Exercise 2.1

Try These (Text book Page No. 23)

Question 1.
A few real life examples of circular shapes are given below.

Can you give three more examples.
Solution:

1. One and Two rupee coins
2. Bangles
3. Mouth of Bottle

Question 2.
Find the diameter of your bicycle wheel?
Solution:
Diameter of my bicycle wheel is 700 mm

Question 3.
If the diameter of the circle is 14cm, what will be it’s radius?
Solution:
diameter d = 14 cm
radius = \(\frac { d }{ 2 } \) = \(\frac { 14 }{ 2 } \) = 7cm

Question 4.
If the radius of a bangle is 2 inches then find the diameter.
Solution:
Given radius of the bangle = 2 inches
Diameter = 2 × radius = 2 × 2 = 4 inches

Exercise 2.2

Try These (Text book Page No. 33)

Question 1.
Draw circles of different radii on a graph paper. Find the area by counting the number of squares covered by the circle. Also find the area by using the formula.
(i) Find the area of the circle, if the radius is 4.2 cm.
(ii) Find the area of the circle if the diameter is 28 cm.
Solution:
(i) Radius of the circle r = 4.2 cm
Area of the circle A = π r² sq.units
= \(\frac { 22 }{ 7 } \) × 4.2 × 4.2 cm² = 5.44 cm²

(ii) Diameter of the circle d = 28 cm
radius r = \(\frac { d }{ 2 } \) = \(\frac { 28 }{ 2 } \) = 14 cm
Area of the circle A = π r² sq.units
= \(\frac { 22 }{ 7 } \) × 14 × 14 cm² = 616 cm²

Exercise 2.3

Try These (Text book Page No. 35)

Question 1.
If the outer radius and inner radius of the circles are respectively 9 cm and 6 cm, find the width of the circular pathway.
Solution:
Radius of the outer circle R = 9 cm
Radius of the inner circle r = 6 cm
Width of the circular pathway = Radius of the outer circle
– Radius of the inner circle
= (9 – 6) cm = 3 cm
Width of the circular pathway = 3 cm

Question 2.
If the area of the circular pathway is 352 sq.cm and the outer radius is 16 cm, find the inner radius.
Solution:
Given outer radius R = 16 cm
Area of the circular pathway = πR² = πr²
Area of the circular pathway = 352 sq. cm
πR² – πr² = 352 cm²
π(R² – r²) = 352
16² – r² = \(\frac{352 \times 7}{22}\)
16² – r² = 16 × 7
16² – r² = 112
16² – 112 = r²
r² = 256 – 112
r² = 144
r = 12 cm
Inner radius r = 12 cm

Question 3.
If the area of the inner rectangular region is 15 sq.cm and the area covered by the outer rectangular region is 48 sq.cm, find the area of the rectangular pathway. Area of the outer rectangle Area of the inner rectangle Area of the rectangular pathway
Solution:
Area of the outer rectangle = 48 sq.cm
Area of the inner rectangle = 15 sq.cm
Area of the rectangular pathway = Area of the outer rectangle
– Area of the inner rectangle
= 48 – 15 = 33 cm²