Category: Class 7

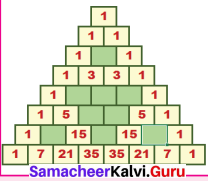
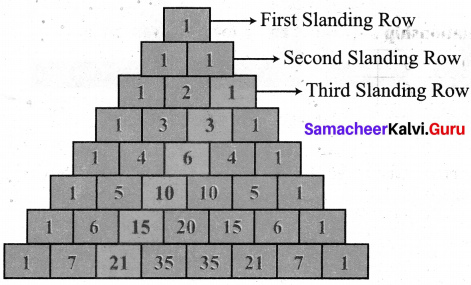
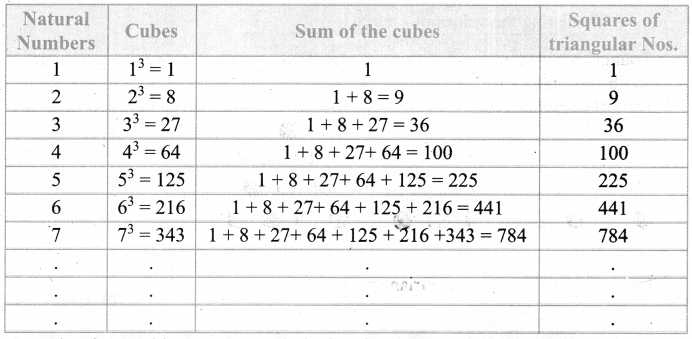
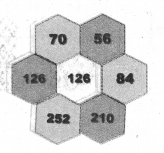
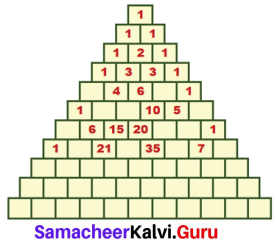
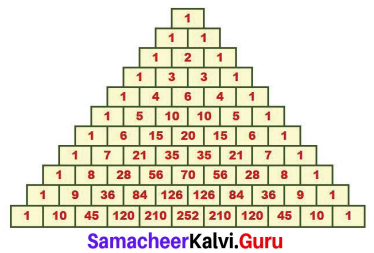
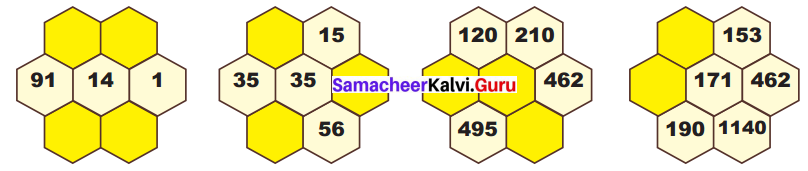
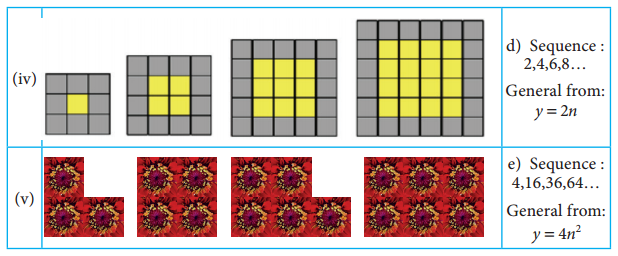
Students can Download Maths Chapter 1 Number System Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 1 Number System Additional Questions

Additional Questions and Answers

Exercise 1.1

Question 1.
Express as rupees using decimals.
(i) 4 paise
(ii) 4 rupees 4 paise
(iii) 44 rupees 44 paise
(iv) 50 paise
(v) 625 paise
Solution:
We know that 100 paise = ₹ 1
1 paise = ₹ \(\frac { 1 }{ 100 } \)
(i) 4 paise = ₹ 4 × \(\frac { 1 }{ 100 } \) = ₹ \(\frac { 4 }{ 100 } \) = ₹ 0.04
(ii) 4 rupees 4 paise = ₹ 4 + ₹ 0.04 = ₹ 4.04
(iii) 44 rupees 4 paise = ₹ 44 + 44 paise = ₹ 44 + ₹ \(\frac { 44 }{ 100 } \) = ₹ 44 + ₹ 0.44 = ₹ 44.44
(iv) 625 paise = 600 paise + 25 paise = ₹ 6 + ₹ \(\frac { 25 }{ 100 } \) = ₹ 6 + ₹ 0.25 = ₹ 6.25

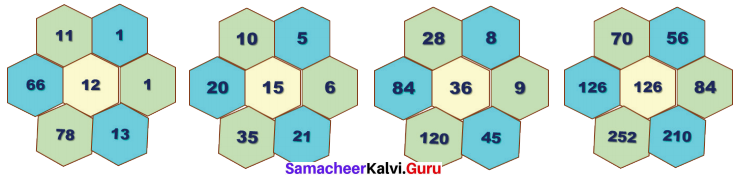
Question 2.
Express 7 cm in metre and kilometer.
Solution:
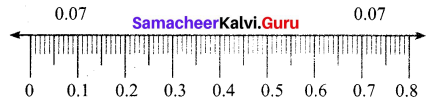
7 cm = \(\frac { 7 }{ 100 } \) m = 0.07 m
7 cm = \(\frac { 7 }{ 10000 } \) km = 0.00007 km

Question 3.
Write the following decimal numbers in the expanded form.
(i) 30.04
(ii) 3.04
(iii) 300.04
Solution:
(i) 30.04 = 3 × 10 + 0 × 1 + 0 × \(\frac { 1 }{ 10 } \) + 4 × \(\frac { 1 }{ 100 } \) = 3 × 10 + \(\frac { 4 }{ 100 } \)
(ii) 3.04 = 3 × 1 + 0 × \(\frac { 1 }{ 10 } \) + 4 × \(\frac { 1 }{ 100 } \) = 3 × 1 + \(\frac { 4 }{ 100 } \)
(iii) 300.04 = 3 × 100 + 0 × 10 + 0 × 1 + 0 × \(\frac { 1 }{ 10 } \) + 4 × \(\frac { 1 }{ 100 } \) = 3 × 100 + \(\frac { 4 }{ 100 } \) = 3 × 100 + \(\frac { 4 }{ 100 } \)

Question 4.
Write the place value of 2 in the following decimal numbers.
(i) 2.47
(ii) 26.89
(iii) 36.28
Solution:
(i) 2.47 Place value of 2 in 2.47 is ones.
(ii) 26.89 Place value of 2 in 26.89 is Tens.
(iii) 36.28 Place value of 2 in 36.28 is tenths

Exercise 1.2

Question 1.
Explain the following as fractions.
(i) Ajar containing 3.6 litres of milk.
(ii) A cup containing 9.63 mg of medicine.
Solution:
(i) 3.6 = 3 + \(\frac { 6 }{ 10 } \) = 3 + \(\frac { 3 }{ 5 } \) = 3 \(\frac { 3 }{ 5 } \) litre of milk
(ii) 9.63 = 9 + \(\frac { 6 }{ 10 } \) + \(\frac { 3 }{ 100 } \) = \(\frac { 900+60+3 }{ 100 } \) = \(\frac { 963 }{ 100 } \) mg of medicine

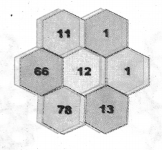
Question 2.
Convert into decimal.
(i) Three hundred three and nine hundredths.
(ii) Six and fifty five thousands
Solution:
(i) Three hundred three and nine hundredths
= 303 + \(\frac { 9 }{ 100 } \) = 303 + 0 × \(\frac { 1 }{ 10 } \) + 9 × \(\frac { 1 }{ 100 } \) = 303.09

(ii) Six and fifty five thousands
6 + \(\frac { 55 }{ 100 } \) = 6 + \(\frac { 5 }{ 100 } \) + \(\frac { 5 }{ 1000 } \) = 6 + \(\frac { 0 }{ 10 } \) + \(\frac { 5 }{ 100 } \) + \(\frac { 5 }{ 1000 } \) = 6.055

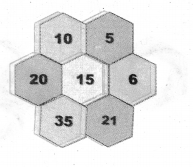
Question 3.
Find the decimal form of (i) 194 + 20 + 3 + \(\frac { 7 }{ 10 } \) + \(\frac { 2 }{ 100 } \)
(ii) 111 + 11 + 1 + \(\frac { 1 }{ 10 } \) + \(\frac { 1 }{ 1000 } \)
Solution:
(i) 194 + 20 + 3 + \(\frac { 7 }{ 10 } \) + \(\frac { 2 }{ 100 } \) = 217 + 7 × \(\frac { 1 }{ 10 } \) + 2 × \(\frac { 1 }{ 100 } \) = 217.72

(ii) 111 + 11 + 1 + \(\frac { 1 }{ 10 } \) + \(\frac { 1 }{ 1000 } \) = 123 + 1 × \(\frac { 1 }{ 10 } \) + 0 × \(\frac { 1 }{ 100 } \) + 1 × \(\frac { 1 }{ 1000 } \) = 123.101

Exercise 1.3

Question 1.
Maya bought 5 kg 300 g bananas and 3 kg 250 kg oranges. Diya bought 4 kg 800 g apples and 4 kg 150 g of mangoes. Who bought more fruits.
Solution:
Total fruits bought by Maya = 5 kg 300 g + 3 kg 250 g = 8 kg 550 g = 8.550 kg
Total fruits Diya bought = 4 kg 800 g + 4 kg 150 g = 8 kg 950 g = 8.950 kg
Comparing the whole number parts, they are equal.
Comparing thet tenths place we get 9 > 5.
∴ 8.950 kg > 8.550 kg
∴ Diya bought more fruits.

Question 2.
Which is greater 28 km or 42.6 km.
Solution:
Comparing the whole number part 42 > 28.
42.6 km is greater than 28 km.

Exercise 1.4

Question 1.
Show that the following numbers in a number line.
(i) 0.2
(ii) 1.8
(iii) 1.1
(iv) 2.6
Solution:

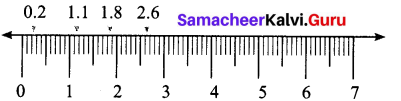
Question 2.
Write the decimal numbers represented by the points A, B, C, D, E and F.
Solution:

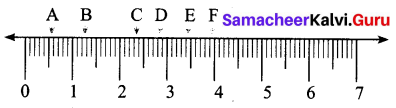
A (0.5); B (1.2); C (2.3); D (2.8); E (3.4); F (3.9)

Students can Download Maths Chapter 1 Number System Ex 1.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 1 Number System Ex 1.5

Question 1.
Write the following decimal numbers in the place value table.
(i) 247.36
(ii) 132.105
Solution:
(i) 247.36

(ii) 132.105

Question 2.
Write each of the following as decimal number.
(i) 300 + 5 + \(\frac { 7 }{ 10 } \) + \(\frac { 9 }{ 100 } \) + \(\frac { 2 }{ 100 } \)
(ii) 1000 + 400 + 30 + 2 + \(\frac { 6 }{ 10 } \) + \(\frac { 7 }{ 100 } \)
Solution:
(i) 300 + 5 + \(\frac { 7 }{ 10 } \) + \(\frac { 9 }{ 100 } \) + \(\frac { 2 }{ 100 } \) = 305.792
(ii) 1000 + 400 + 30 + 2 + \(\frac { 6 }{ 10 } \) + \(\frac { 7 }{ 100 } \) = 1432.67

Question 3.
Which is greater?
(i) 0.888 (or) 0.28
(ii) 23.914 (or) 23.915
Solution:
(i) 0.888 (or) 0.28
The whole number parts is equal for both the numbers.
Comparing the digits in the tenths place we get, 8 > 2.
0.888 > 0.28 ∴ 0.888 is greater.

(ii) 23.914 or 23.915
The whole number part is equal in both the numbers.
Also the tenth place and hundredths place are also equal.
∴ Comparing the thousandths place, we get 5 > 4.
23.915 > 23.914 ∴ 23.915 is greater.

Question 4.
In a 25 m swimming competition, the time taken by 5 swimmers A, B, C, D and E are 15.7 seconds, 15.68 seconds, 15.6 seconds, 15.74 seconds and 15.67 seconds respectively. Identify the winner.
Solution:
The winner is one who took less time for swimming 25 m.
Comparing the time taken by A, B, C, D, E the whole number part is equal for all participants.
Comparing digit in tenths place we get 6 < 7.
∴ Comparing 15.68, 15.6, 15.67, that is comparing the digits in hundredths place we get 15.60 < 15.67 < 15.68
One who took 15.6 seconds is the winner. ∴ C is the winner.

Question 5.
Convert the following decimal numbers into fractions
(i) 23.4
(ii) 46.301
Solution:
(i) 23.4 = \(\frac { 234 }{ 10 } \) = \(\frac{234 \div 2}{10 \div 2}\) = \(\frac { 117 }{ 5 } \)
(ii) 46.301 = \(\frac { 46301 }{ 1000 } \)

Question 6.
Express the following in kilometres using decimals,
(i) 256 m
(ii) 4567 m
Solution:
1 m = \(\frac { 1 }{ 1000 } \) km = 0.001 Km
(i) 256 m = \(\frac { 256 }{ 1000 } \) km = 0.256 km
(ii) 4567 m = \(\frac { 4567 }{ 1000 } \) km = 4.567 km

Question 7.
There are 26 boys and 24 girls in a class. Express the fractions of boys and girls as decimal numbers.
Solution:
Boys = 26; Girls = 24; Total = 50
Fraction of boys = \(\frac { 26 }{ 50 } \) = \(\frac{26 \times 2}{50 \times 2}\) = \(\frac { 52 }{ 100 } \) = 0.52
Fraction of girls = \(\frac { 24 }{ 50 } \) = \(\frac{24 \times 2}{50 \times 2}\) = \(\frac { 48 }{ 100 } \) = 0.48

Challenge Problems

Question 8.
Write the following amount using decimals.
(i) 809 rupees 99 paise
(ii) 147 rupees 70 paise
Solution:
100 paise = 1 rupee; 1 paise = \(\frac { 1 }{ 100 } \) rupee

(i) 809 rupees 99 paise = 809 rupees + \(\frac { 99 }{ 100 } \) rupees
= 809 + 0.99 rupees = ₹ 809.99

(ii) 147 rupees 70 paise = 147 rupees + \(\frac { 70 }{ 100 } \) rupees
= 147 rupees + 0.70 rupees = ₹ 147.70

Question 9.
Express the following in metres using decimals.
(i) 1328 cm
(ii) 419 cm
Solution:
100 cm = 1 m; 1 cm = \(\frac { 1 }{ 100 } \) m
(i) 1328 cm = \(\frac { 1328 }{ 100 } \) m = 13.28 m
(ii) 419 cm = \(\frac { 419 }{ 100 } \) m = 4.19 m

Question 10.
Express the following using decimal notation.
(i) 8 m 30 cm in metres
(ii) 24 km 200 m in kilometres
Solution:
(i) 8 m 30 cm in metres
8 m + \(\frac { 30 }{ 100 } \) m = 8 m + 0.30 m = 8.30 m

(ii) 24 km 200 m in kilometres
24 km + \(\frac { 200 }{ 1000 } \) km = 24 km + 0.200 km = 24.200 km

Question 11.
Write the following fractions as decimal numbers.
(i) \(\frac { 23 }{ 10000 } \)
(ii) \(\frac { 421 }{ 100 } \)
(iii) \(\frac { 37 }{ 10 } \)
Solution:
(i) \(\frac { 23 }{ 10000 } \) = 0.0023
(ii) \(\frac { 421 }{ 100 } \) = 4.21
(iii) \(\frac { 37 }{ 10 } \) = 3.7

Question 12.
Convert the following decimals into fractions and reduce them to the lowest form,
(i) 2.125
(ii) 0.0005
Solution:
(i) 2.125 = \(\frac { 2125 }{ 1000 } \) = \(\frac{2125 \div 25}{1000 \div 25}\) = \(\frac { 85 }{ 40 } \) = \(\frac{85 \div 5}{40 \div 5}\) = \(\frac { 17 }{ 8 } \)

(ii) 0.0005 = \(\frac { 5 }{ 1000 } \) = \(\frac{5 \div 5}{10000 \div 5}\) = \(\frac { 1 }{ 2000 } \)

Question 13.
Represent the decimal numbers 0.07 and 0.7 on a number line.
Solution:

0.07 lies between 0.0 and 0.1
The unit space between 0 and 0.1 is divided into 10 equal parts and 7th part is taken. Also 0.7 lies between 0 and 1.
The unit space between 0 and 1 is divided into 10 equal parts, and the 7th part is taken.

Question 14.
Write the following decimal numbers in words.
(i) 4.9
(ii) 220.0
(iii) 0.7
(iv) 86.3
Solution:
(i) 4.9 = Four and nine tenths
(ii) 220.0 = Two hundred and twenty
(iii) 0.7 = Seven tenths
(iv) 86.3 = Eighty six and three tenths.

Question 15.
Between which two whole numbers the given numbers lie?
(i) 0.2
(ii) 3.4
(iii) 3.9
(iv) 2.7
(v) 1.7
(vi) 1.3
Solution:
(i) 0.2 lies between 0 and 1.
(ii) 3.4 lies between 3 and 4.
(iii) 3.9 lies between 3 and 4.
(iv) 2.7 lies between 2 and 3.
(v) 1.7 lies between 1 and 2.
(vi) 1.3 lies between 1 and 2.

Question 16.
By how much is \(\frac { 9 }{ 10 } \) km less than 1 km. Express the same in decimal form.
Solution:
Given measures are 1 km and \(\frac { 9 }{ 10 } \) km. i.e., 1 km and 0.9 km.
Difference = 1.0 – 0.9 = 0.1 km.

Students can Download Maths Chapter 5 Information Processing Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 5 Information Processing Additional Questions

Additional Questions and Answers

Exercise 5.1

Question 1.
Find the relationship between x and y if

Solution:
The relationship between x and y is y = -5x

Question 2.
Find the relationship between x and y if

Solution:
The relationship between x andy is y = 3x + 2

Exercise 5.2

Question 1.
Find the sum of the elements of Pascal’s triangle and find the relationship between the numbers obtained.
Solution:
Pascal’s triangle with sum of elements is given by

The numbers formed are 1, 2, 4, 8, 16, 32, 64, …………..
They can be written as 2⁰, 2¹, 2², 2³, 2⁴, 2⁵, 2⁶, …………..
So they are the powers of base 2
The relationship is given by 2^x-1 if x represents the row.

Exercise 5.3

Question 1.
If the following numbers are taken from Pascal’s triangle find the missing numbers.

1. 9, 1, _____ = 45, 1, 11
2. 1, 6, _____ = 1, 4, 15
3. 21, 8, 1 = _____, 6, 28

Solutions:

1. 55
2. 10
3. 1

Students can Download Maths Chapter 5 Information Processing Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 5 Information Processing Intext Questions

Activity (Text book Page No. 91)

Question 1.
Observe the pattern given below. Continue the pattern for three more steps.

Let, ‘x’ be the number of steps and ‘y’ be the number of match sticks. Tabulate the values of ‘x’ and ‘y’ and verify the relationship y = 7x + 5.
Solution:
Three more patterns are

From the table y = 7x + 5 is verified.

Try These (Text book Page No. 92)

Question 1.
In the given figure, let Y denote the number of steps and y denote its area. Find the relationship between x and y by tabulation.

Solution:
Let x denote the number of steps and y denote the area.
In the first shape let x = 1 and the area be 1 cm²
when x = 2 : Area = 22 = 4 cm²
whenx = 3 : Area = 32 = 9 cm² and so on.
Tabulating the values of x and y

From the table:
x = 1 ⇒ y = 1²
x = 2 ⇒ y = 2²
x = 4 ⇒ y = 4²
x = 5 ⇒ y = 5²
Hence the relationship between x and y is y = x²

Question 2.
In the figure, let x denotes the number of steps and y denotes the number of matchsticks used. Find the relationship between Y and y by tabulation.

Solution:
Let x denote the number of steps and y denote the number of matchsticks used.
In step 1, x = 1 ⇒ y = number of mathsticks used is 1
In step 2, x = 2 ⇒ y = number of mathsticks used is 4
In step 3, x = 3 ⇒ y = number of mathsticks used is 7 and so on.
The values of v andy are tabulated as

x = 1 ⇒ y = 1 = 3(1) – 2
x = 2 ⇒ y = 4 = 3(2) – 2
x = 3 ⇒ y = 7 = 3(3) – 2
x = 4 ⇒ y = 10 = 3(4) – 2
From the table y = 3x – 2

Question 3.
Observe the table given below.

Find the relationship between x and y. What will be the value of y, when x = 8.
Solution:
Soil When x = – 2 y = 2 (-2) = -4
When x = -1 y = 2 (-1) = -2
When x = 0 y = 2 (0) = 0
When x =1 y = 2(1) = 2
When x = 2 y = 2 (2) = 4
When x = 8 y = 2 (8) = 16.
Also y = 2x is the relation between x and y.

Activity (Text book Page No. 93 & 94)

Question 1.
Complete the following Pascal’s Triangle by observing the number pattern.

Solution:
Pascal’s triangle is given by

Question 2.
Observe the above completed and r find the sequence that you see in it and complete them.

(i) 1,2, 3, 4, 5, 6, 7.
(ii) 1, 3, _____, _____, _____, _____.
(iii) 1, _____, _____, _____, _____,
(iv) _____, _____, _____, _____.
Solution:
(i) 1,2, 3, 4, 5, 6, 7.
(ii) 1,3,6,10,15,21.
(iii) 1,4,10,20,35.
(iv) 1,5,15,35.

Question 3.
Observe the sequence of numbers obtained in the 3rd and 4th slanting rows of Pascal’s Triangle and find the difference between the consecutive numbers and complete the table given below.

Solution:

Try These (Text book Page No. 96)

Question 1.
Observe the pattern of numbers given in the slanting rows earlier and complete the Pascal’s Triangle.

Solution:

Question 2.
Complete the given Pascal’s Triangle. Find the common property of the numbers filled by you. Can you relate this pattern with the pattern discussed in situation 2. Discuss.

Solution:

Common Properties:
The numbers filled by me are even numbers. Also they make triangular shape.
Yes, this pattern and the pattern given in situation 2 have the same properties.

Students can Download Maths Chapter 5 Information Processing Ex 5.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 5 Information Processing Ex 5.3

Miscellaneous Practice Problems

Question 1.
Choose the correct relationship between x and y for the given table.

(i) y = x + 4
(ii) y = x + 5
(iii) y = x + 6
(iv) y = x + 7
Answer:
(iii) y = x + 6

Question 2.
Find the triangular numbers from the Pascal’s Triangle and colour them.

Solution:
Triangular numbers are numbers the objects of which can be arranged in the form of equilateral triangle.
Example : 1, 3, 6, 10, 15,…
From Pascal’s Triangle, the triangular numbers are

Question 3.
Write the first five numbers in the third slanting row of the Pascal’s Triangle and find their squares. What do you infer?
Solution:

Numbers in the 3rd slanding row are 1, 3, 6, 10, 15, 21,….
The squares are 1², 3², 6², 10². 15², 21²,…. = 1, 9, 36, 100, 225, 441,…

From the above table we can conclude that the squares of the triangular numbers are the sum of cubes of natural numbers.

Challenge Problems

Question 4.
Tabulate and find the relationship between the variables (x and y) for the following patterns.

Solution:
(i) Let the number of steps be x and the number of shapes be y.
Tabulating the values of x and y

From the table
x = 1 ⇒ y = 1 = 12
x = 2 ⇒ y = 4 = 22
x = 3 ⇒ y = 9 = 32
x = 4 ⇒ y = 16 = 42
Hence the relationship between x and y is y = x2.

(ii) Let the number of steps be x and the number of shapes be y.
Tabulating the values of x and y

From the table x = 1 ⇒ y = 1 = 1
x = 2 ⇒ y = 2 + 1 = 3
x = 3 ⇒ y = 3 + 2 = 5
x = 4 ⇒ y = 4 + 3 = 7
x = 5 ⇒ y = 5 + 4 = 9
Hence the relationship between x and y is y = 2x-1.

Question 5.
Verify whether the following hexogonal shapes form a part of the Pascal’s Triangle.

Solution:
In Pascal’s Triangle product of the 3 alternate numbers given around the hexagon is equal to the product of remaining three numbers.

1 × 13 × 66 = 11 × 1 × 78 = 858
∴ It form a part of Pascal’s Triangle.

5 × 21 × 20 = 10 × 6 × 35 = 2100
∴ It form a part of Pascal’s Triangle

8 × 45 × 84 = 28 × 9 × 120 = 30240
∴ It form a part of Pascal’s Triangle

56 × 210 × 126 = 70 × 84 × 252 = 1481760
∴ It form a part of Pascal’s Triangle

Students can Download Maths Chapter 5 Information Processing Ex 5.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 5 Information Processing Ex 5.2

Question 1.
Complete the Pascal’s Triangle.

Solution:

Question 2.
The following hexagonal shapes are taken from Pascal’s Triangle. Fill in the missing numbers.

Solution:

Question 3.
Complete the Pascal’s Triangle by taking the numbers 1,2,6,20 as line of symmetry.

Solution:
Corresponding numbers are equal about the line of symmetry.

Objective Type Questions

Question 1.
The elements along the sixth row of the Pascal’s Triangle is
(i) 1,5,10,5,1
(ii) 1,5,5,1
(iii) 1,5,5,10,5,5,1
(iv) 1,5,10,10,5,1
Answer:
(iv) 1,5,10,10,5,1

Question 2.
The difference between the consecutive terms of the fifth slanting row containing four elements of a Pascal’s Triangle is
(i) 3,6,10,…
(ii) 4,10,20,…
(iii) 1,4,10,…
(iv) 1,3,6,…
Answer:
(ii) 4,10,20,…

Question 3.
What is the sum of the elements of ninth row in the Pascal’s Triangle?
(i) 128
(ii) 254
(iii) 256
(iv) 126
Answer:
(iii) 256

Students can Download Maths Chapter 5 Information Processing Ex 5.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 5 Information Processing Ex 5.1

Question 1.
Match the given patterns of shapes with the appropriate number pattern and its generalization.


Solution:
(i) (d)
(ii) (a)
(iii) (c)
(iv) (c)
(v) (b)

Objective Type Questions

Question 2.
Identify the correct relationship between x andy from the given table.

(i) y = 4x
(ii) y = x + 4
(iii) y = 4
(iv) y = 4 × 4
Answer:
(i) y = 4x

Question 3.
Identify the correct relationship between x and y from the given table.

(i) y = -2x
(ii) y = +2x
(iii) y = +3x
(iv) y = -3x
Answer:
(iv) y = -3x

Students can Download Maths Chapter 4 Geometry Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Additional Questions

Additional Questions and Answers

Exercise 4.1

Question 1.
“The sum of any two angles of a triangle is always greater than the third angle”. Is this statement true. Justify your answer.
Solution:
No, the sum of any two angles of a triangle is not always greater than the third angle. In an isosceles right angled triangles, the angle will be 90°, 45°, 45°.
Here sum of two angles 45° + 45° = 90°.

Question 2.
The three angles of a triangle are in the ratio 1:2:1. Find all the angles of the triangle. Classify the triangle in two different ways.
Solution:
Let the angles of the triangle be x, 2x, x.
Using the angle sum property, we have
x + 2x + x = 180°
4x = 180°
x = \(\frac{180^{\circ}}{4}\)
x = 45°
2x = 2 × 45° = 90°
Thus the three angles of the triangle are 45°, 90°, 45°.
Its two angles are equal. It is an isoscales triangle. Its one angle is 90°.
∴ It is a right angled triangle.

Question 3.
Find the values of the unknown x and y in the following figures

Solution:
(i) Since angles y and 120° form a linear pair.
y + 120° = 180°
y = 180° – 120°
y = 60°
Now using the angle sum property of a triangle, we have
x + y + 50° = 180°
x + 60° + 50° = 180°
x + 110° = 180°
x = 180° – 110°= 70°
x = 70°
y = 60

(ii) Using the angle sum property of triangle, we have
50° + 60° + y = 180°
110° + y = 180°
y = 180° – 110°
y = 70°
Again x and y form a linear pair
∴ x + y = 180°
x + 70° = 180°
x = 180° – 70°= 110°
∴ x = 110°; y = 70°

Question 4.
Two angles of a triangle are 30° and 80°. Find the third angle.
Solution:
Let the third angle be x.
Using the angle sum property of a triangle we have,
30° + 80° + x = 180°
x + 110° = 180°
x = 180° – 110° = 70°
Third angle = 70°.

Exercise 4.2

Question 1.
In an isoscleles ∆ABC, AB = AC. Show that angles opposite to the equal sides are equal.
Solution:

Given: ∆ABC in which \(\overline{A B}\) = \(\overline{A C}\).
To Prove: ∠B = ∠K.
Construction: Draw AD ⊥ BC.
Proof: In right ∆ADB and right ∆ADC.
we have side AD = side AD (common)
AB = AC (Hypoteneous) (given)
∆ADB = ADC (RHS criterion]
∴ Their corresponding parts are equal. ∠B = ∠C.

Question 2.
ABC is an isosceles triangle having side \(\overline{A B}\) = side \(\overline{A C}\). If AD is perpendicular to BC, prove that D is the mid-point of \(\overline{B C}\).
Solution:
In ∆ABD and ∆ACD, we have
∠ADB = ∠ADC [∵ AD ⊥ BC]
Side \(\overline{A D}\) = Side \(\overline{A D}\) [Common]
Side \(\overline{A B}\) = Side \(\overline{A C}\) [Common]
Using RHS congruency, we get
∆ABD ≅ ∆ACDc
Their corresponding parts are equal

∴ BD = CD
∴ O is the mid point of BC.

Question 3.
In the figure PL ⊥ OB and PM ⊥ OA such that PL = PM.
Prove that ∆PLO ≅ ∆PMO.
Solution:

In ∆PLO and ∆PMO, we have
∠PLO = ∠PMO = 90° [Given]
\(\overline{O P}\) = \(\overline{O P}\) [Hypotenuse]
PL = PM
Using RHS congruency, we get
∆PLO ≅ ∆PMO

Students can Download Maths Chapter 4 Geometry Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Intext Questions

Exercise 4.1

Try These (Text book Page No. 66)

Answer the following questions.

Question 1.
Triangle is formed by joining three ______ points.
Answer::
Non collinear

Question 2.
A triangle has ______ vertices and ______ sides.
Answer:
three, three

Question 3.
A point where two sides of a triangle meet is known as ______ of a triangle.
Answer:
vertese

Question 4.
Each angle of an equilateral triangle is of measure.
Answer:
same

Question 5.
A triangle has angle measurements of 29°, 65° and 86°. Then it is ______ triangle.
(i) an acute angled
(ii) a right angled
(iii) an obtuse angled
(iv) a scalene
Answer:
(i) an acute angled

Question 6.
A triangle has angle measurements of 30°, 30° and 120°. Then it is ______ triangle.
(i) an acute angled
(ii) scalene
(iii) obtuse angled
(iv) right angled
Answer:
obtuse angled

Question 7.
Which of the following can be the sides of a triangle?
(i) 5.9.14
(ii) 7,7,15
(iii) 1,2,4
(iv) 3, 6, 8
Answer:
(iv) 3, 6, 8
Solution:
(i) Here 5 + 9 = 14 = the measure of the third side.
In a triangle the sum of the measures of any two sides must be greater than the third side.
∴ 5, 9, 14 cannot be the sides of a triangle.

(ii) 7.7.15
Here sum of two sides 7 + 7 = 14 < the measures of the thrid side.
So 1,1, 15 cannot be the sides of a triangles.

(iii) 1,2,4
Here sum of two sides 1 + 2 = 3 < the measure of the third side.
∴ 1, 2, 4 cannot be the sides of a triangle.

(iv) 3, 6, 8
Sum of two sides 3 + 6 = 9 > the third side.
∴ 3, 6, 8 can be the sides of a triangle.

Question 8.
Ezhil wants to fence his triangular garden. If two of the sides measure 8 feet and 14 feet then the length of the third side is ______
(i) 11 ft
(ii) 6 ft
(iii) 5 ft
(iv) 22 ft
Answer:
(i) 11 ft

Question 9.
Can we have more than one right angle in a triangle?
Solution:
No, we cannot have more than one right angle in a triangle.
Because the sum of three angles of a triangle is 180°.
But if two angles are right angles then their sum itself become 180°.

Question 10.
How many obtuse angles are possible in a triangle?
Solution:
Only one.

Question 11.
In a right triangle, what will be the sum of other two angles?
Solution:
Sum of three angles of a triangle = 180°
If one angle is right angle (i.e. 90°) .
Sum of other two sides = 180° – 90° = 90°

Question 12.
Is it possible to form an isosceles right angled triangle? Explain.
Solution:
Yes, it is possible.
If one angle is right angle, then the other two angles will be 45° and 45°.

Exercise 4.2

Try These (Text book Page No. 76)

Question 1.
Measure and group the pair of congruent line segments.

Solution:
\(\overline{A B}\) = 3 cm
\(\overline{C D}\) = 4.8 cm
\(\overline{I J}\) = 4.8 cm
\(\overline{P Q}\) = 3 cm
\(\overline{R S}\) = 1.7 cm
\(\overline{X Y}\) = 1.7 cm
From the above measurement S, we can conclude that
(i) \(\overline{A B}\) ≅ \(\overline{P Q}\)
(ii) \(\overline{C D}\) ≅ \(\overline{I J}\)
(iii) \(\overline{R S}\) ≅ \(\overline{X Y}\)

Try These (Text book Page No. 77)

Question 1.
Find the pairs of congruent angles either by superposition method or by measuring them.

Solution:
From the given figures
∠ABC = 50°
∠EFG = 120°
∠HIJ = 120°
∠KLH = 90°
∠PON = 50°
∠RST = 90°
From the above measures, we can conclude that
(i) ∠ABC = ∠PON
(ii) ∠EFG = ∠HIJ
(iii) ∠KLH ≅ ∠RST

Try These (Text book Page No. 83)

Question 1.
If ∆ABC ≅ ∆XYZ then list the corresponding sides and corresponding angles.

Solution:
If ∆ABC ≅ ∆XYZ
\(\overline{A B}\) ≅ \(\overline{X Y}\) – \(\overline{B C}\) ≅ \(\overline{Y Z}\)
\(\overline{A C}\) ≅ \(\overline{X Z}\)
And also
∠A ≅ ∠X – ∠B ≅ ∠Y
∠C ≅ ∠Z

Question 2.
Given triangles are congruent. Identify the corresponding parts and write the congruent statement.

Solution:
Given the set of triangles are congruent. Also we observe from the triangles that the corresponding sides.
\(\overline{A B}\) = \(\overline{A C}\)
\(\overline{B C}\) = \(\overline{Y Z}\)
\(\overline{A C}\) = \(\overline{X Z}\)
Here three sides of ∆ABC are equal to the corresponding sides of ∆XYZ.
This criterion of congruency is side – side – side.

Question 3.
Mention the conditions needed to conclude the congruency of the triangles with reference to the above said criterions. Give reasons for your answer.

Solution:
(i) In ∆ABC and ∆XYZ
if \(\overline{A B}\) = \(\overline{X Y}\)
\(\overline{B C}\) = \(\overline{Y Z}\)
\(\overline{A C}\) = \(\overline{X Z}\)
then ∆ABC ≅ ∆XYZ. By the Side – Side -Side Congruency Criterion.

then ∆AB ≅ ∆XYZ.
By Side – Angle – Side Criterion.

then ∆ABC ≅ ∆XYZ.
By Angle – Side – Angle Congruency Critirion.

then by RHS criterion.
∆ABC ≅ ∆XYZ

Students can Download Maths Chapter 4 Geometry Ex 4.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.3

Miscellaneous Practice Problems

Question 1.
In an isoscales triangle one angle is 76°. If the other two angles are equal, find them.
Solution:
In an isoscales triangle, angle opposite to equal sides are equal. Let the equal angles be x° and x°.
In a triangle the sum of the three angles is 180°.
x° + x° + 76° = 180°
x° (1 + 1) = 180° – 76° = 104°
2x = 104°
x = \(\frac{104^{\circ}}{2}\) = 52°
x = 52°
∴ Other two angles are 52° and 52°.

Question 2.
If two angles of a triangle are 46° each, how can you classify the triangle?
Solution:
Given two angles of the triangle are same and is equal to 46°. If two angles are equal the sides opposite to equal angles are equal. Therefore it will be an isoscales triangle.

Question 3.
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle.
Solution:
Let ∠B is the greater angle then by the given condition ∠B = ∠A + ∠C.
Sum of three angle of a triangle = 180°.

∠A + ∠B + ∠C = 180°.
∠A + (∠A + ∠C) + ∠C) = 180°.
2∠A + 2∠C = 180°
2(∠A + ∠C) = 180°
∠A + ∠C = \(\frac{180^{\circ}}{2}\)
∠B = 90°
∴ One of the angle of the triangle = 90°
It will be a right angled triangle.

Question 4.
If the exterior angle of a triangle is 140° and its interior opposite angles are equal, find all the interior angles of the triangle.
Solution:
Given the exterior angle = 140°
Interior opposite angle are equal.

Let one of the interior opposite angle be x.
Then x + x = 140°.
[∵ Exterior angle = sum of interior opposite angles]
2x = 140°
x = \(\frac{140^{\circ}}{2}\) = 70°
x = 70°
Interior opposite angle = 70°, 70°.
Sum of the three angles of a triangle = 180°.
70° + 70° + Third angle = 180°
140° + Third angle = 180°
Third angle = 180° – 140° = 40°
∴ Interior angle are 40°, 70°, 70°.

Question 5.
In ∆JKL, if ∠J = 60° and ∠K = 40°, then find the value of exterior angle formed by extending the side KL.
Solution:
When extending the side KL, the exterior angle formed in equal
to the sum of the interior opposite angles.

∠JLX = ∠LJK + ∠LKJ
= 60°+ 40° =100°
Exterior angle formed = 100°

Question 6.
Find the value of ‘x’ in the given figure.

Solution:
Given ∠DCB = 1000 and ∠DBA = 128°
In the given figure
∠CBD + ∠DBA = 180°
∠CBD + 128° = 180°
∠CBD = 52°
Now exterior angle x = Sum of interior opposite angles.
x = ∠DCB + ∠CBD = 100° + 52° = 152°
x = 152°

Question 7.
If ∆MNO ≅ ∆DEF, ∠M = 60° and ∠E = 45° then find the value of ∠O.
Solution:
Given ∆MNO ≅ ∆DEF

∴ Corresponding parts of conqruent triangle are congruent.
∠M = ∠D = 60° [given ∠M = 60°]
∠N = ∠E = 45° [given ∠E = 45°]
∠O = ∠F
In triangle MNO, sum of the three angle – 180°.
∠M + ∠N + ∠O = 180°
60° + 45° + ∠O = 180°
105° + ∠O = 180°
∠O = 180° – 105° = 75°
Value of ∠O = 75°

Question 8.
In the given figure ray AZ bisects ∠BAD and ∠DCB, prove that
(i) ∆BAC ≅ ∆DAC
(ii) AB = AD

Solution:
(i) In ∆BAC and ∆DAC
∠BAC = ∠DAC [Given \(\overline{A Z}\) bisects ∠BAD]
∠BCA = ∠DCA[\(\overline{A Z}\) bisects ∠DCB]
AC = AC [∵ common side]
∴ Here AC is the included side of the angles. By ASA criterior, ∆BAC ≅ ∆DAC.

(ii) By (i) ∆BAC ≅ ∆DAC
BA = DA [By CPCTC]
i.e., AB = AD

Question 9.
In the given figure FG = FI and H is midpoint of GI, prove that ∆FGH ≅ ∆FHI
Solution:
In ∆FGH and ∆FHI
Given FG = HI
Also, GH = HI [∵ H is the midpoint of GI]

FH = FH [Common]
∴ By S.SS congruency criteria, ∆FGH ≅ ∆FIH. Hence proved.

Question 10.
Using the given figure, prove that the triangles are congruent. Can you conclude that AC is parallel to DE.
Solution:
In ∆ABC and ∆EBD,

AB = EB
BC = BD
∠ABC = ∠EBD [∵ Vertically opposite angles]
By SAS congruency criteria. ∆ABC ≅ ∆EBD.
We know that corresponding parts of congruent triangles are congruent.
∴ ∠BCA ≅ ∠BDE
and ∠BAC ≅ ∠BED
∠BCA ≅ ∠BDE means that alternate interior angles are equal if CD is the transversal to lines AC and DE.
Similarly, if AE is the transversal to AC and DE, we have ∠BAC ≅ ∠BED
Again interior opposite angles are equal.
We can conclude that AC is parallel to DE.

Challenge Problems

Question 11.
In given figure BD = BC, find the value of x.

Solution:
Given that BD = BC
∆BDC is on isoscales triangle.
In isoscales triangle, angles opposite to equal sides are equal.
∠BDC = ∠BCD ……(1)
Also ∠BCD + ∠BCX = 180° [∵ Liner Pair]
∠BCD + 115° = 180°
∠BCD = 180° – 115°
∠BCD = 65° [By (1)]
In ∆ADB
∠BAD + ∠ADB = ∠BDC
[∵ BDC is the exterior angle and ∠BAD and ∠ABD are interior opposite angles]
35° + x = 65°
x = 65° – 35°
x = 30°

Question 12.
In the given figure find the value of x.

Solution:
For ∆LNM, ∠LMK is the exterior angle at M.
Exterior angle = sum of opposite interior angles
∠LMK = ∠MLN + ∠LNM = 26° + 30° = 56°
∠JMK = 56° [∵ ∠LMK = ∠JMK]
x is the exterior angle at J for ∆JKM.
∴ x = ∠JKM + ∠KMJ [∵ Sum of interior opposite angles]
x = 58° + 56° [∵ ∠JMK = 56°]
x = 114°

Question 13.
In the given figure find the values of x and y.

Solution:
In ∆BCA, ∠BAX = 62° is the exterior angle at A.
Exterior angle = sum of interior opposite angles.
∠ABC + ∠ACB = ∠BAX
28°+ x = 62°
x = 62° – 28° = 34°
Also ∠BAC + ∠BAX = 180° [∵ Linear pair]
y + 62° = 180°
y = 180° – 62° = 118°
x = 34°
y = 118°

Question 14.
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD.

Solution:
Given ∠F = 48°
∠E = 68°
In ∆DEF,
∠D + ∠F + ∠E = 180° [By angle sum property]
∠D + 68° + 68° = 180°
∠D + 116° = 180°
∠D = 180° – 116° = 64°
Since DG is the angular bisector of ∠D.
∠FDG = ∠GDE
Also ∠FDG + ∠GDE = ∠D
2 ∠FDG = 64°
2 ∠FDG = 64°
∠FDG = \(\frac{64^{\circ}}{2}\) = 32°
∠FDG = 32°
In ∆FDG,
∠FDG + ∠GFD = 180° [By angle sum property of triangles]
32° + ∠FDG + 48° = 180°
∠FDG + 80° = 180°
∠FDG = 180° – 80°
∠FDG = 100°

Question 15.
In the figure find the value of x.

Solution:
Exterior angle is equal to the sum of opposite interior angles.
in ∆TSP ∠TSP + ∠SPT = ∠UTP
75° + ∠SPT = 105°
∠SPT = 105° – 75°
∠SPT = 30° ……(1)
∠SPT + ∠TPR + ∠RPQ = 180° [∵ Sum of angles at a point on a line is 180°]
30° + 90° + ∠RPQ = 180°
120° + ∠RPQ = 180°
∠RPQ = 180° – 120°
∠RPQ = 60° …… (2)
∠VRQ + ∠QRP = 180° [∵ linear pair]
145° + ∠QRP = 180°
∠QRP = 180° – 145°
∠QRP = 35°
Now in ∆ PQR
∠QRP + ∠RPQ = x [∵ x in the exterior angle]
35° + 60° = x
95° = x

Question 16.
From the given figure find the value of y.

Solution:
From the figure,
∠ACB = ∠XCY [Vertically opposite angles]
∠ACB = 48° …(1)
In ∆ABC, ∠CBD is the exterior angle at B.
Exterior angle = Sum of interior opposite angles.
∠CBD = ∠BAC + ∠ACB
∠CBE + ∠EBD = 57° + 48°
65° + ∠EBD = 105°
∠EBD = 105° + 65° = 40° ……… (2)
In ∆EBD, y is the exterior angle at D.
y = ∠EBD + ∠BED
[∵ Exterior angle = Sum of opposite interior angles]
y = 40° + 97° [∵ From (2)]
y = 137°