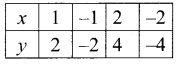
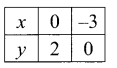
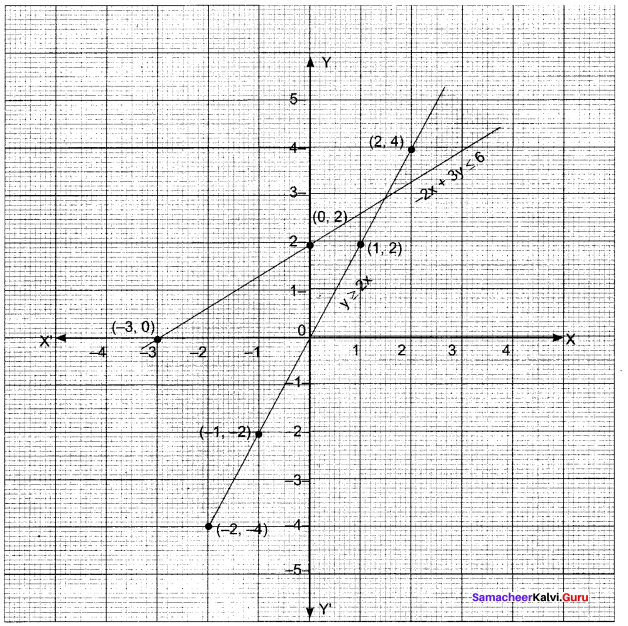
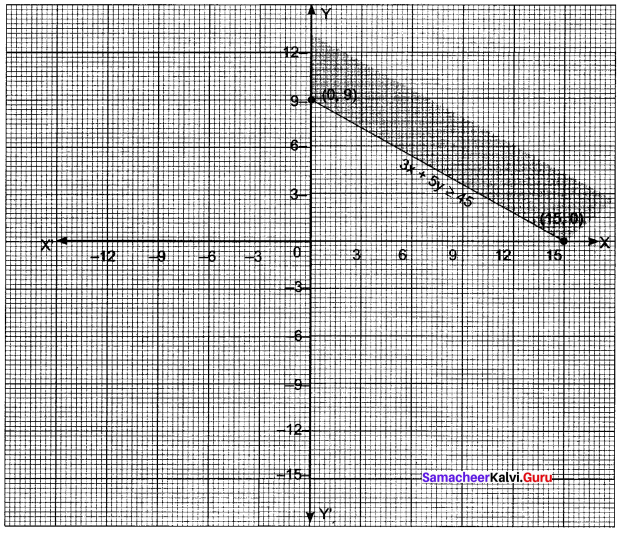
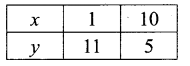
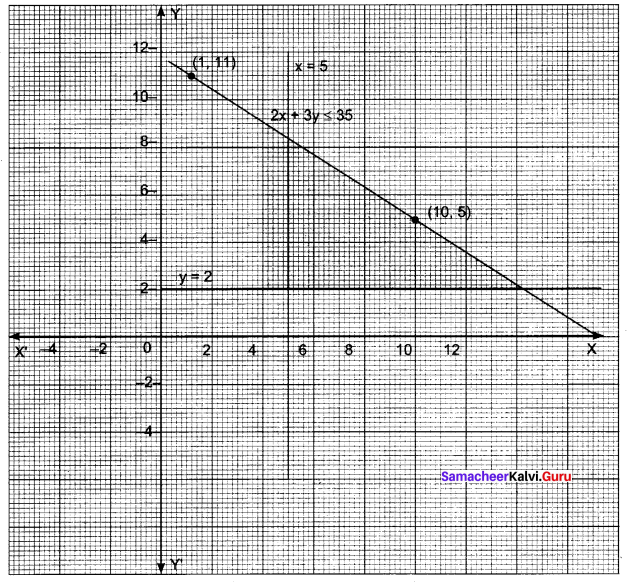
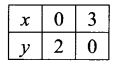
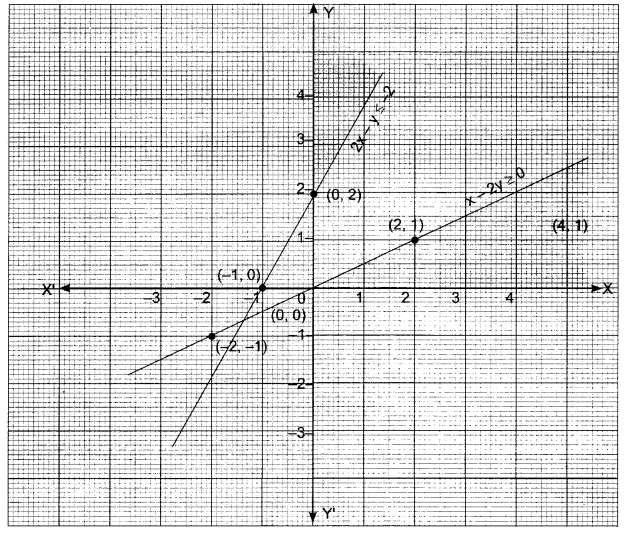
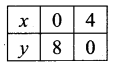
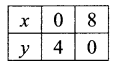
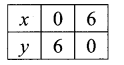
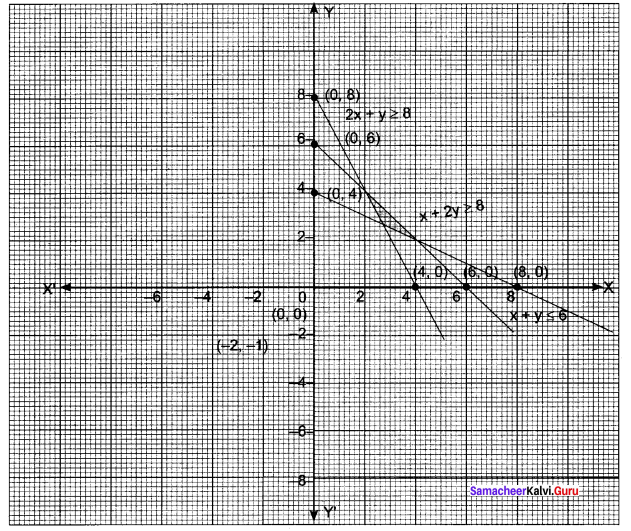
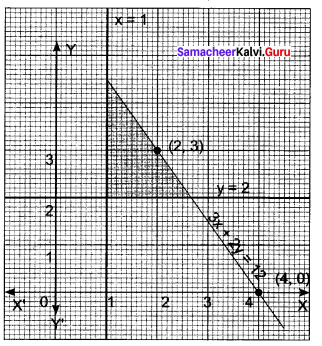
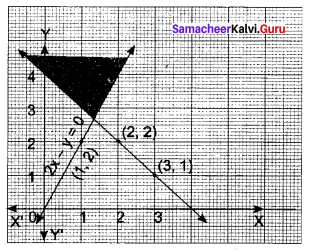
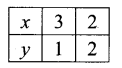
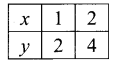
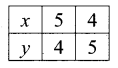
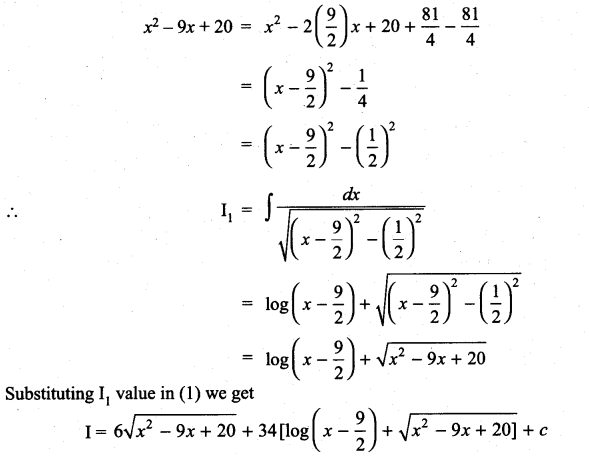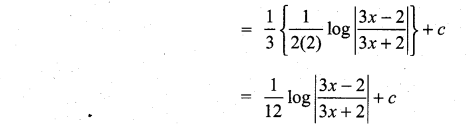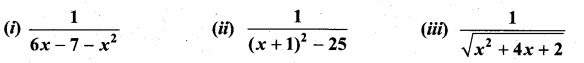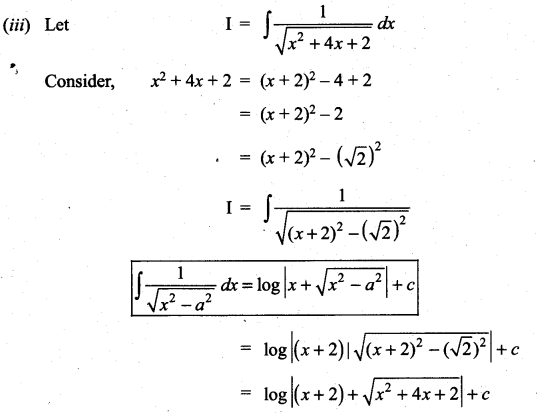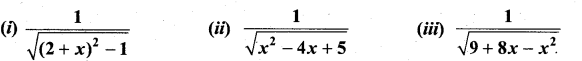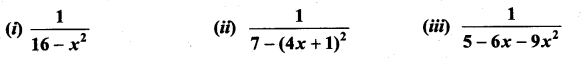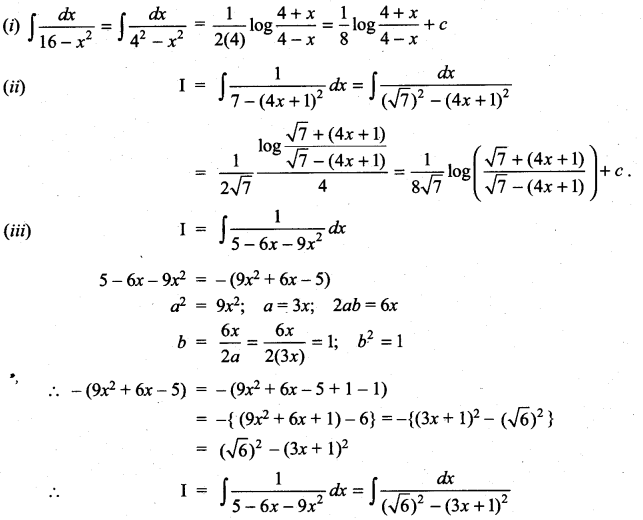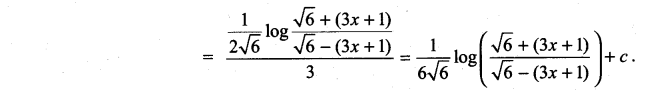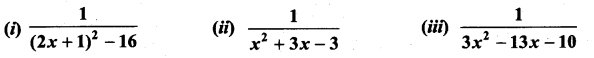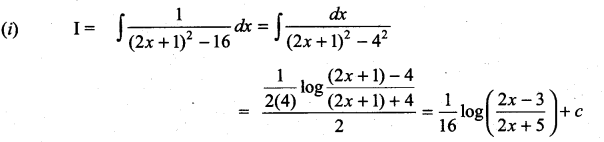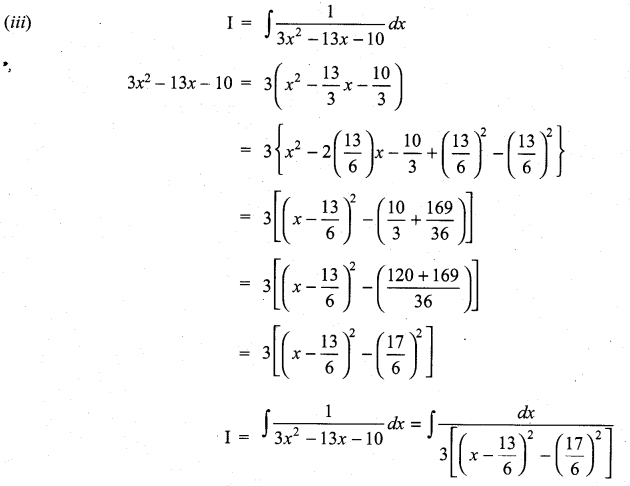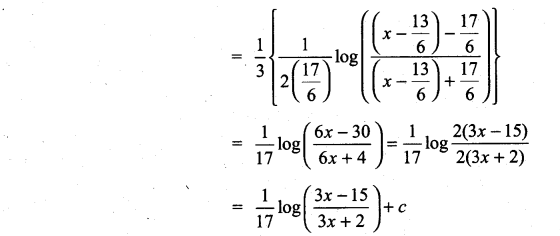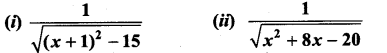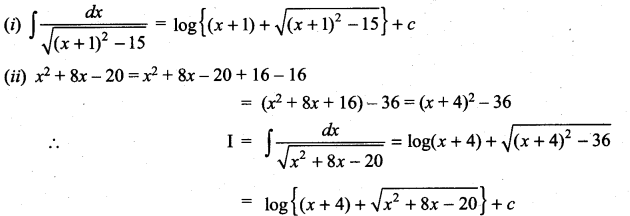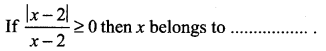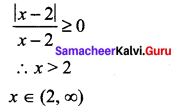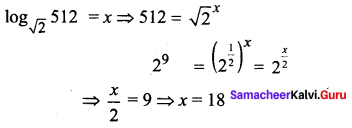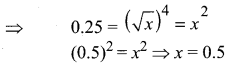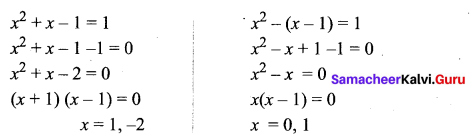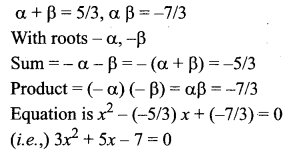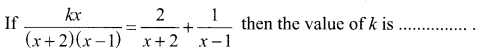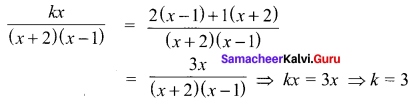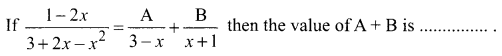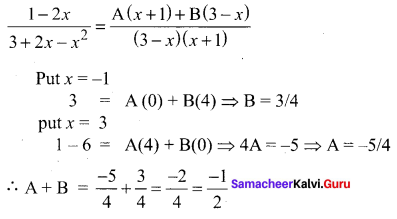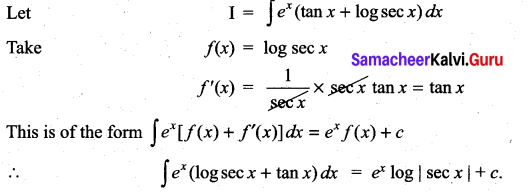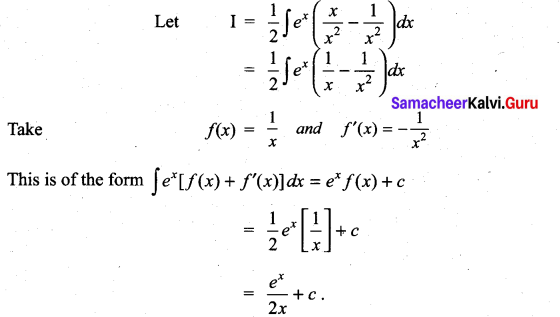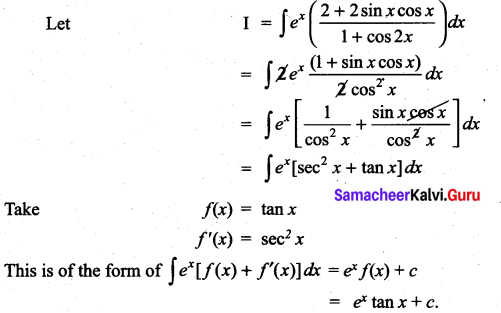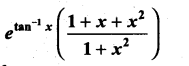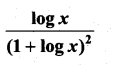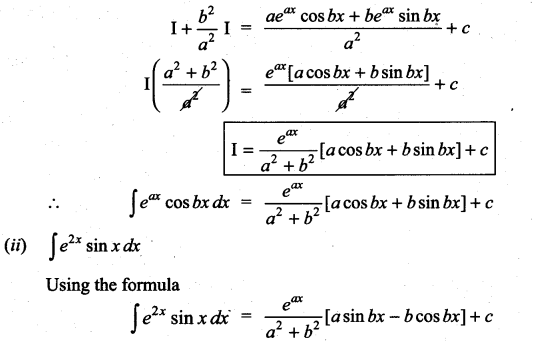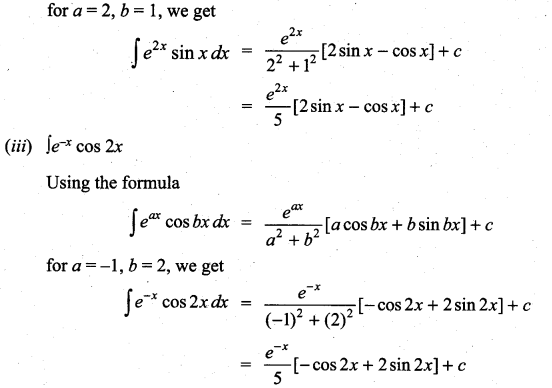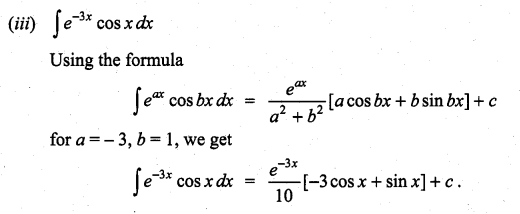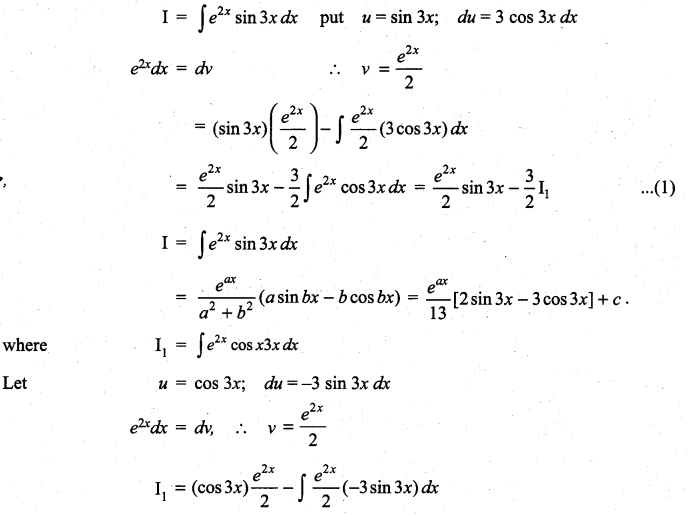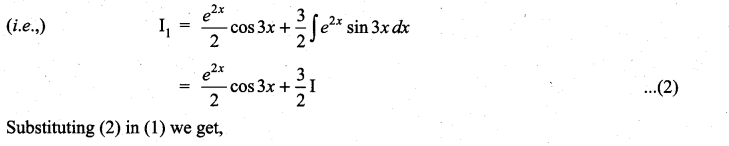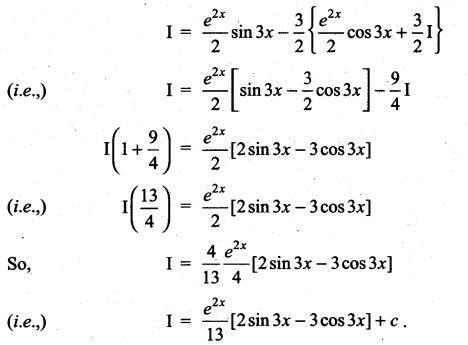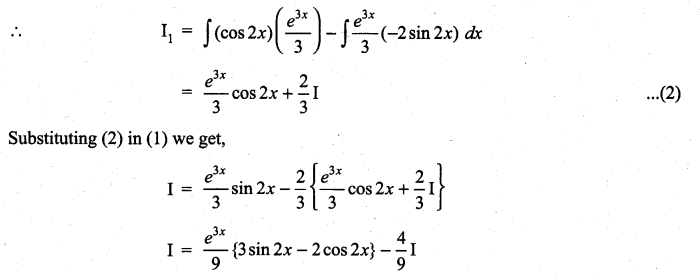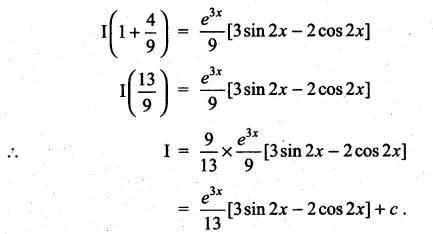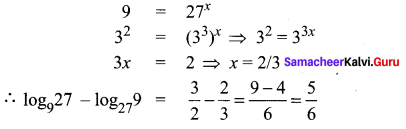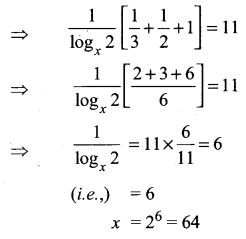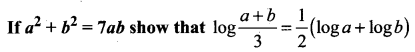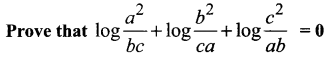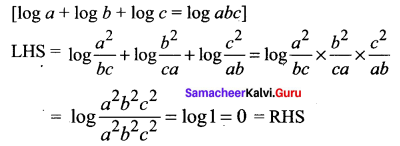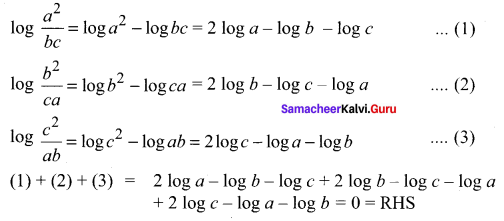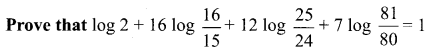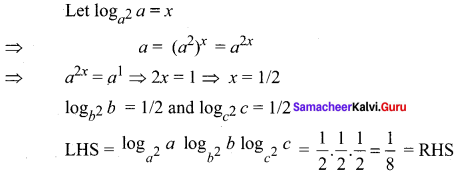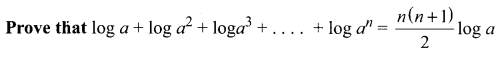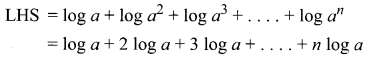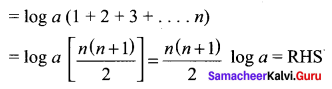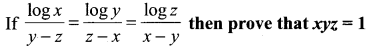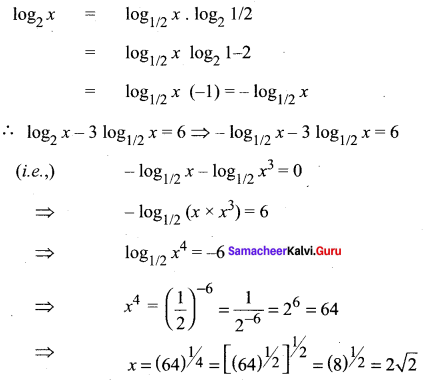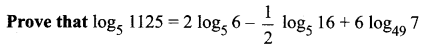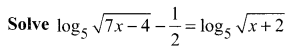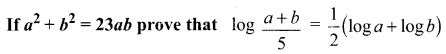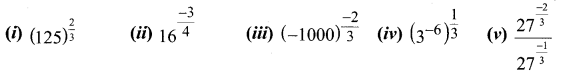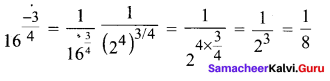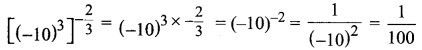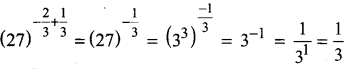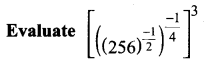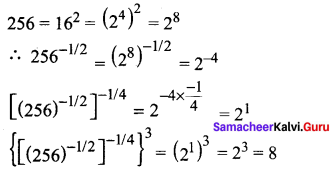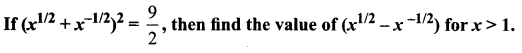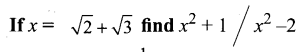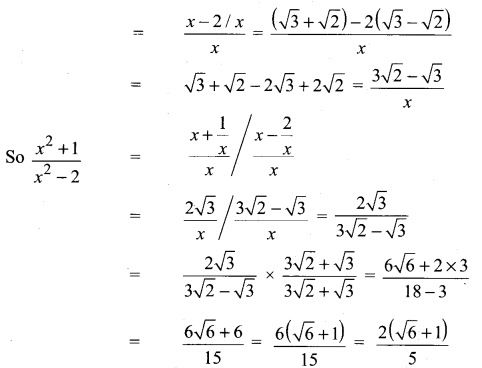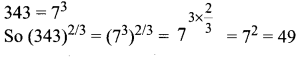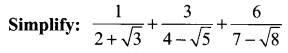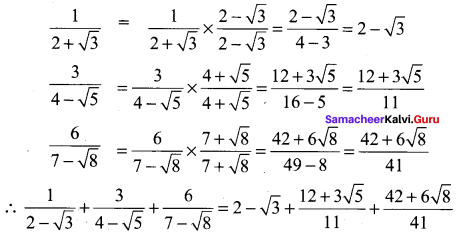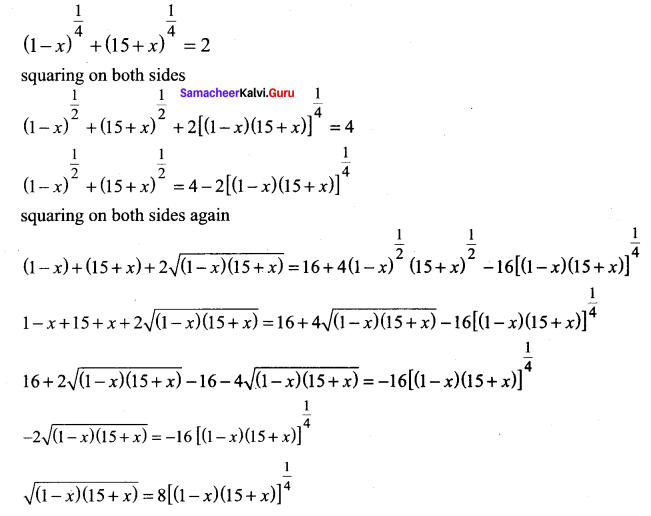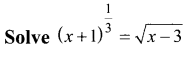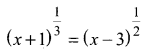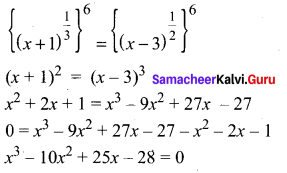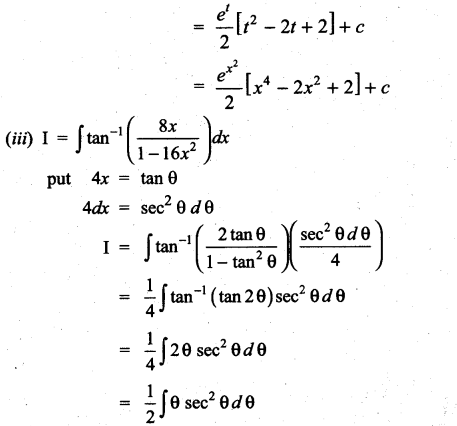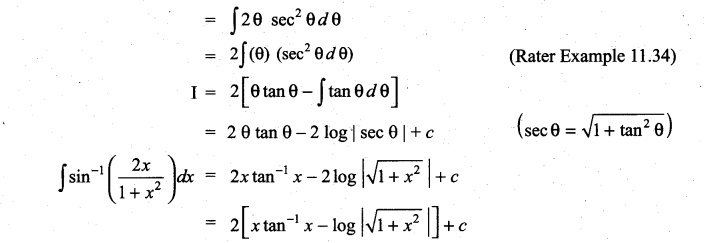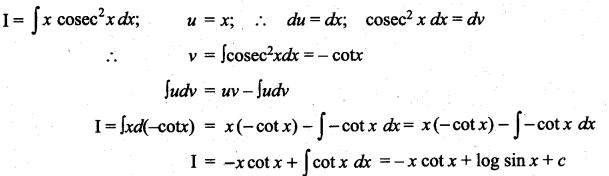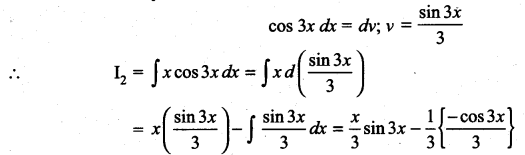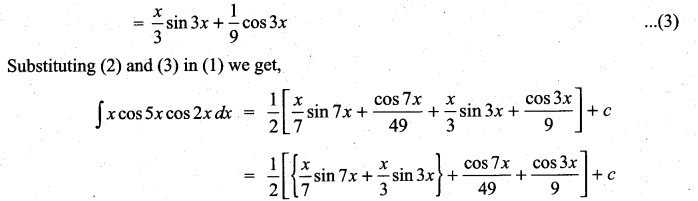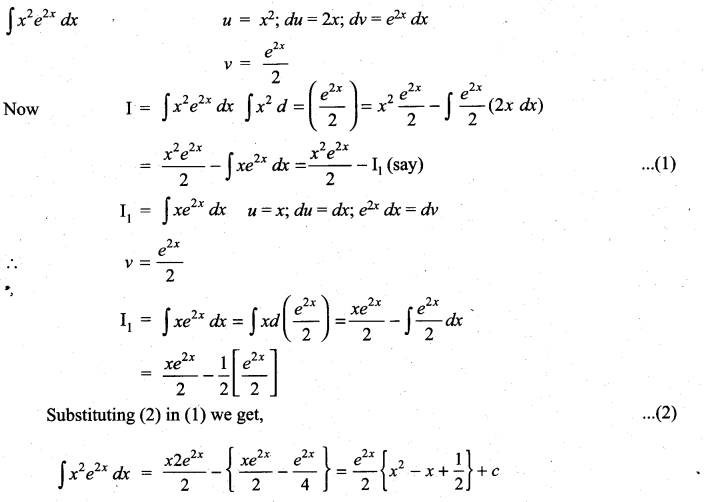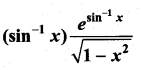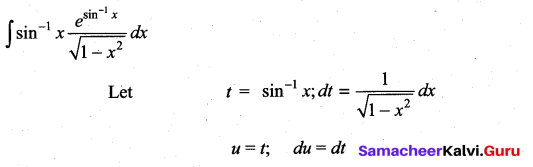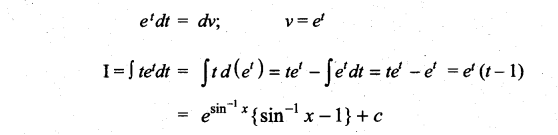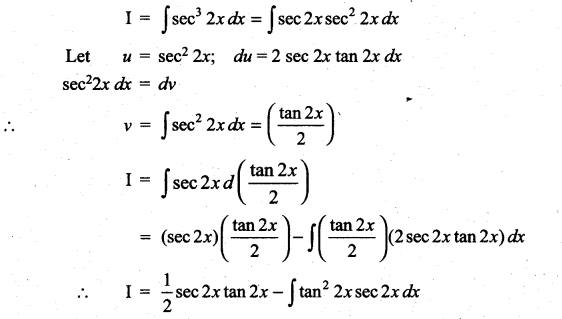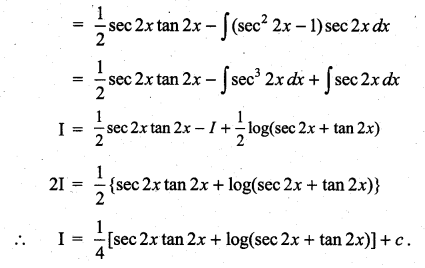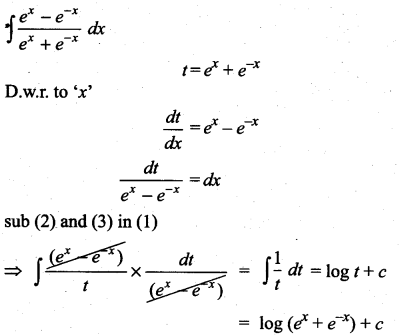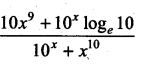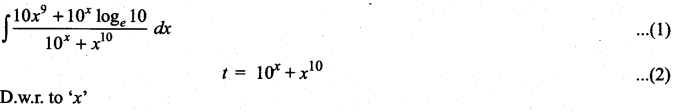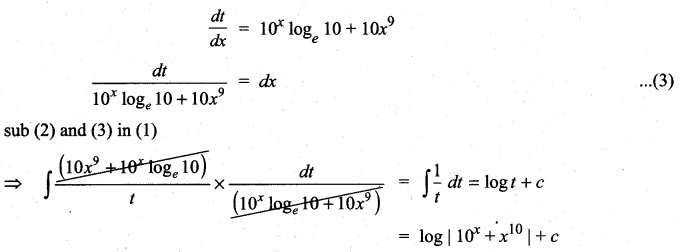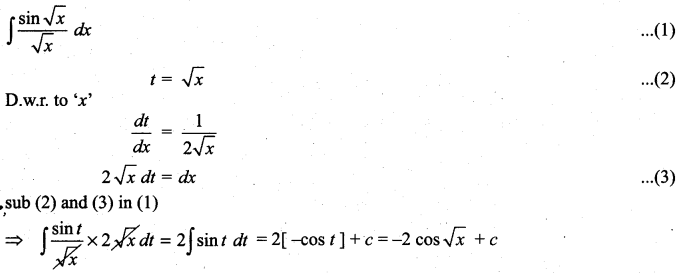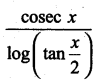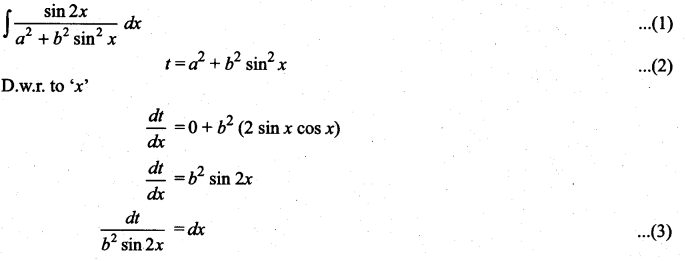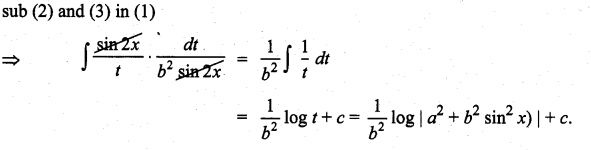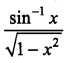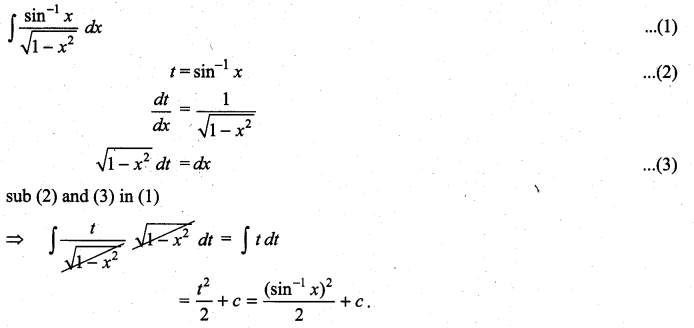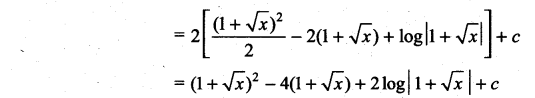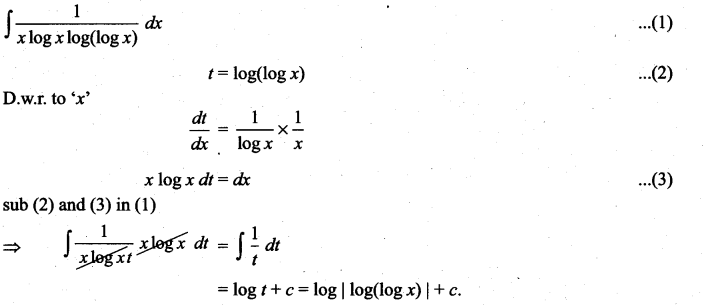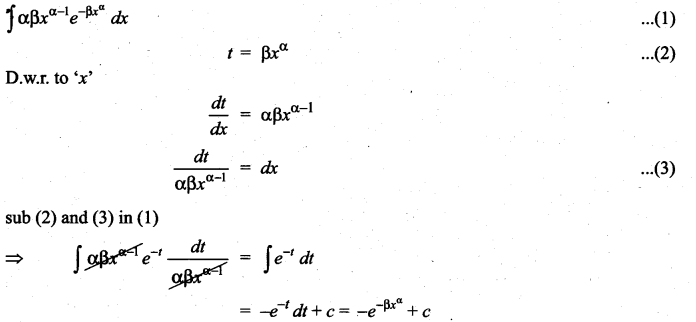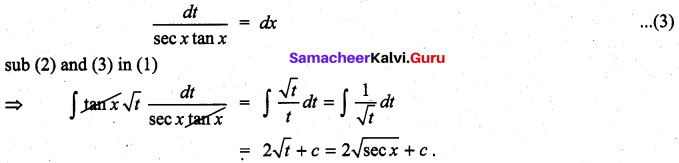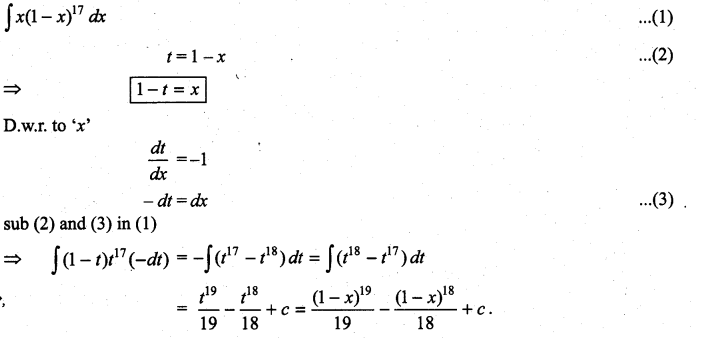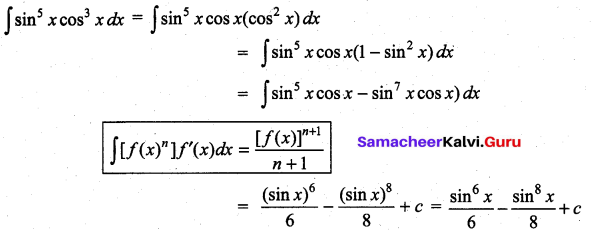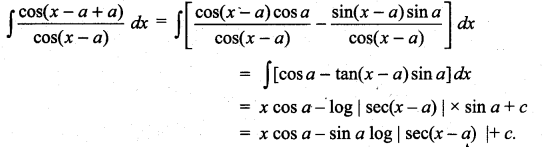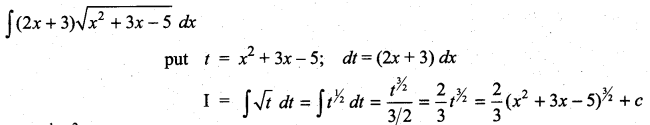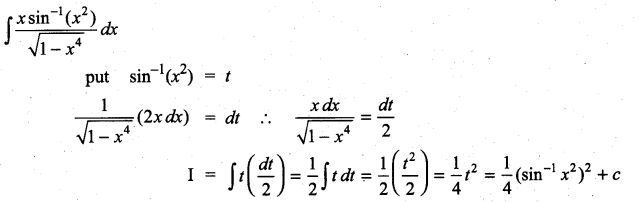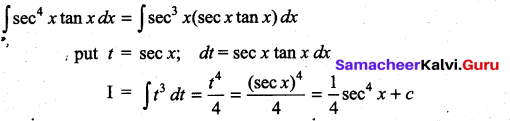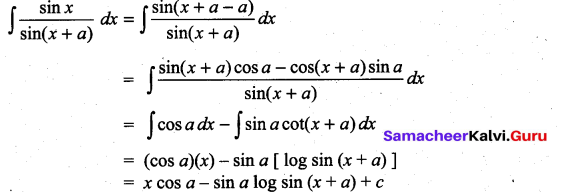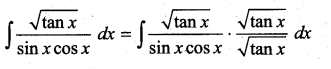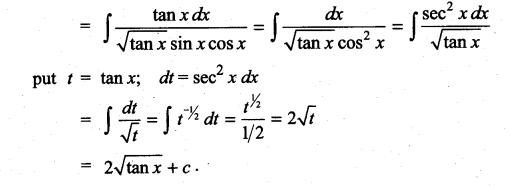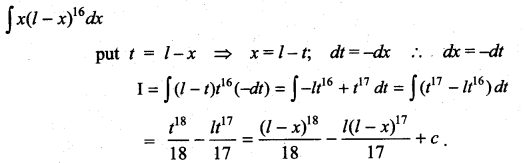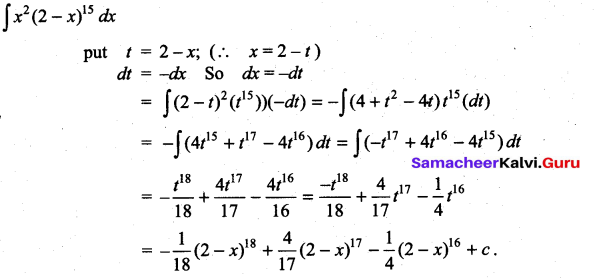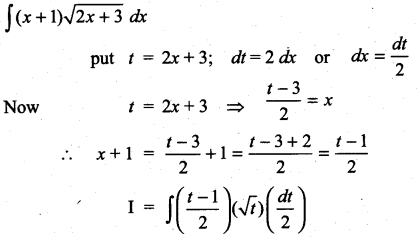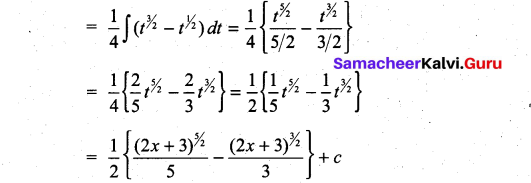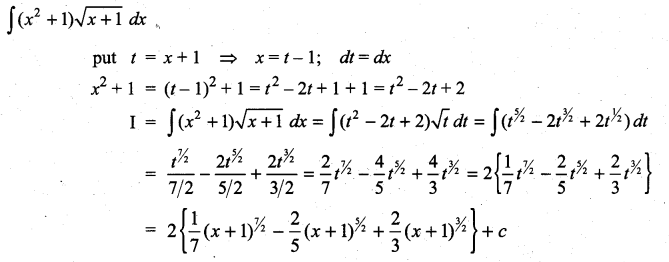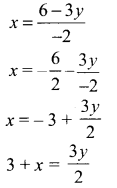You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 11 Integral Calculus Ex 11.11
Integrate the following with respect to x:
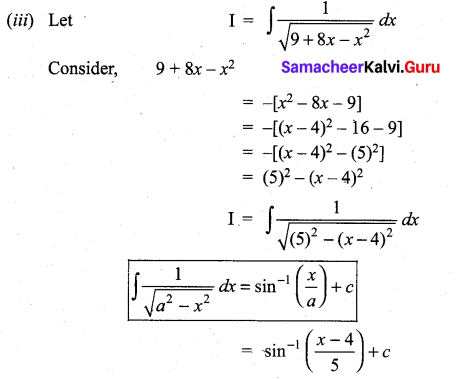
Question 1.
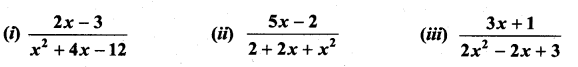
Solution:

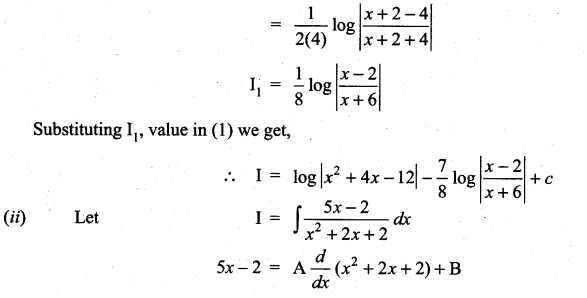

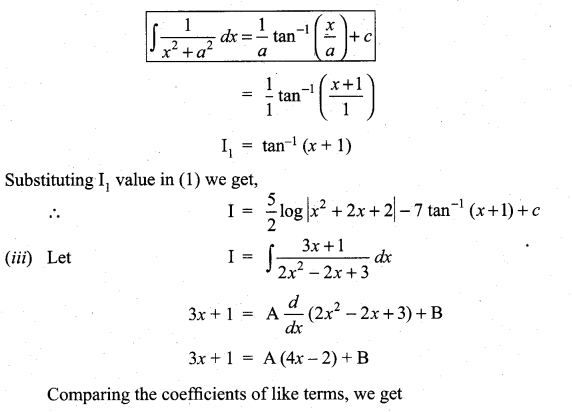
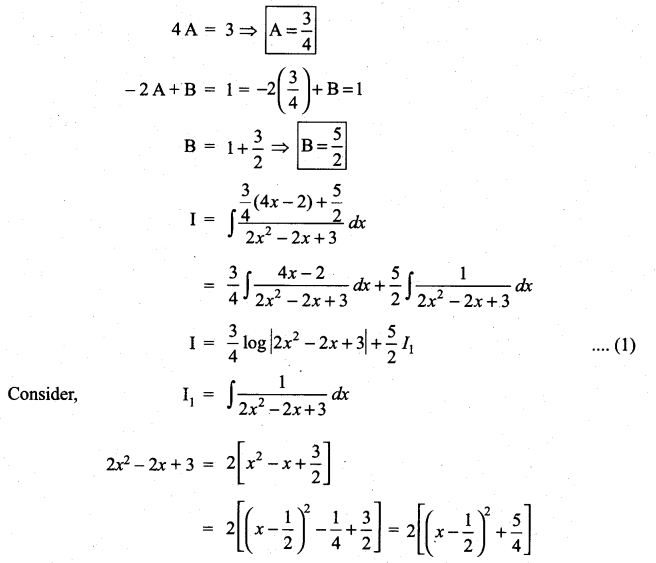
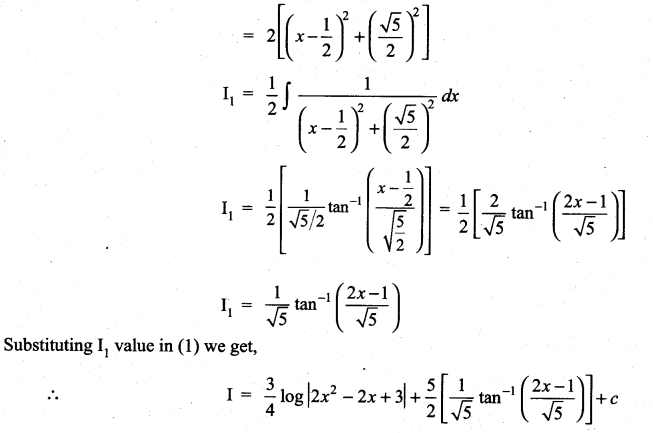
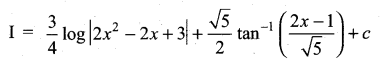
![]()
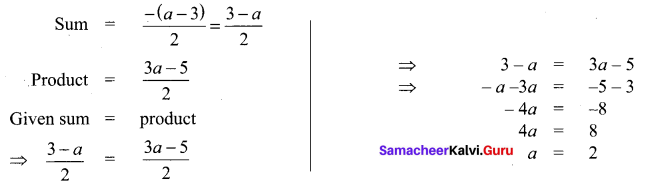
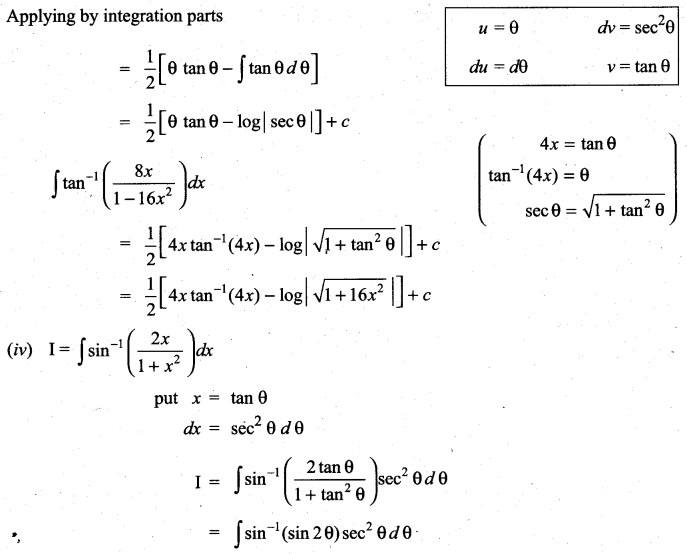
Question 2.
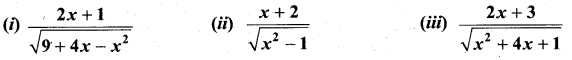
Solution:

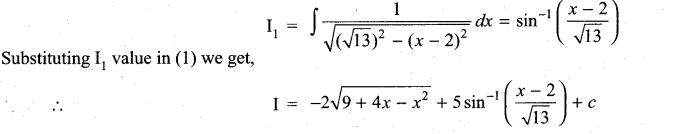


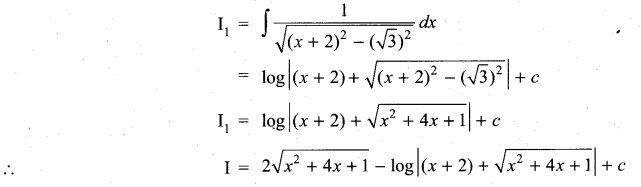
Samacheer Kalvi 11th Maths Solutions Chapter 11 Integral Calculus Ex 11.11 Additional Problems
Question 1.
\(\frac{2 x-1}{2 x^{2}+x+3}\)
Solution:

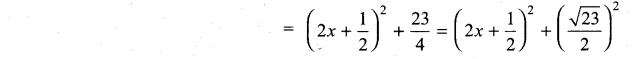
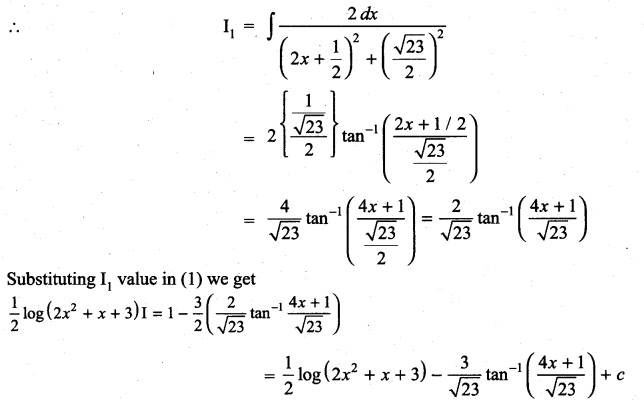
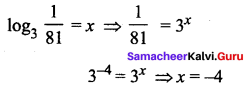
Question 2.
\(\frac{4 x+1}{x^{2}+3 x+1}\)
Solution:

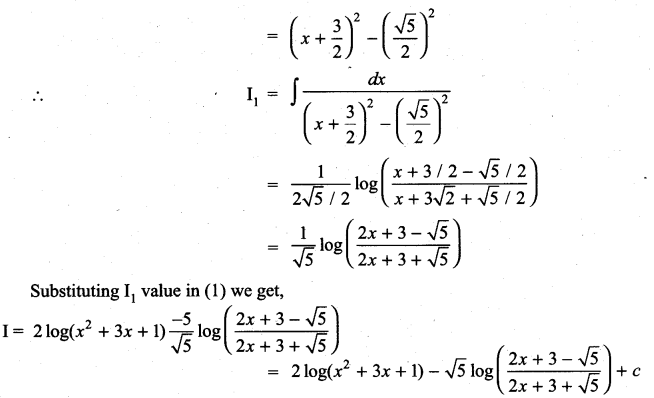
![]()
Question 3.
\(\frac{2 x-3}{\sqrt{10-7 x-x^{2}}}\)
Solution:

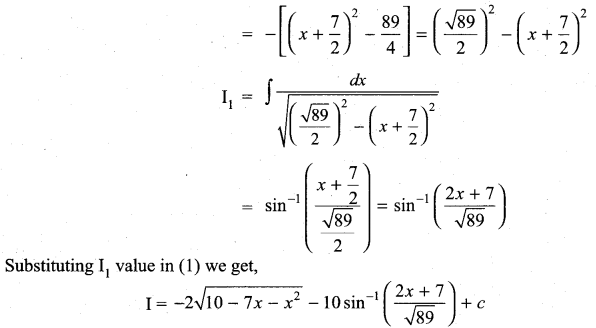
Question 4.
\(\frac{6 x+7}{\sqrt{(x-4)(x-5)}}\)
Solution: