Category: Class 11

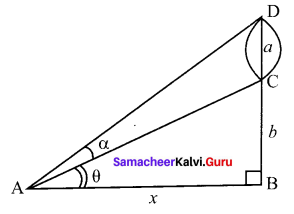
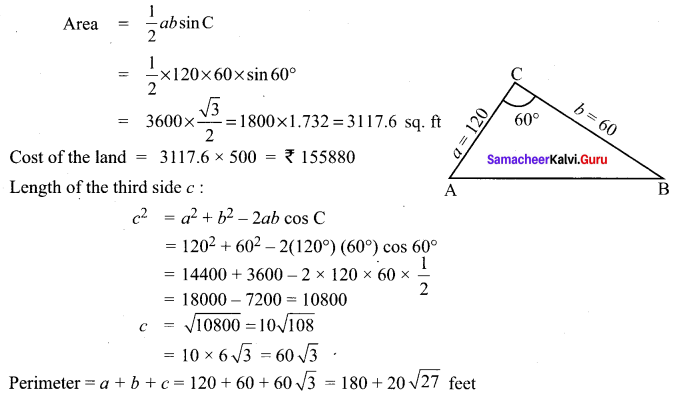
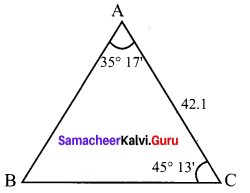
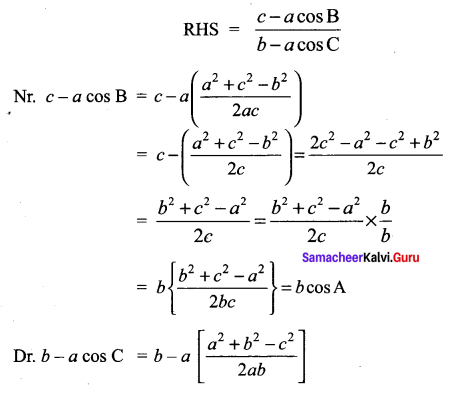
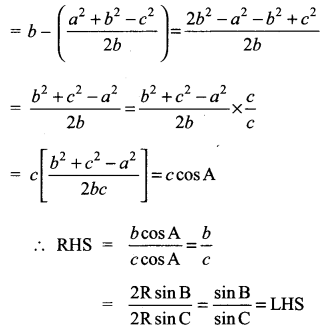
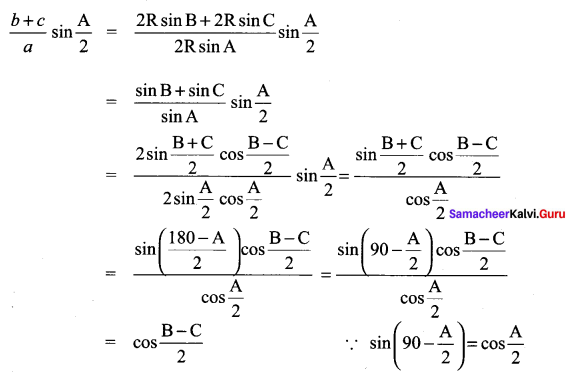
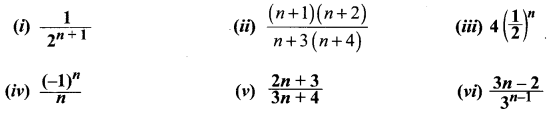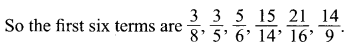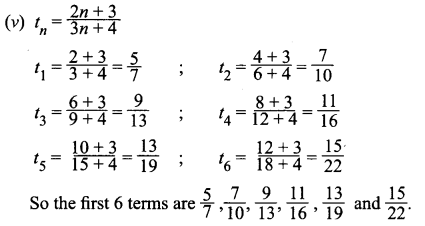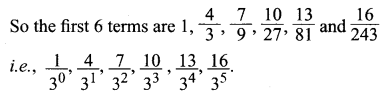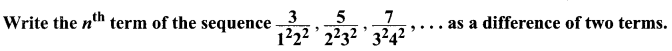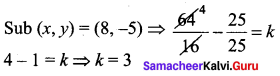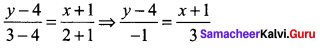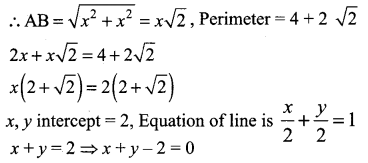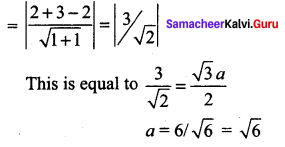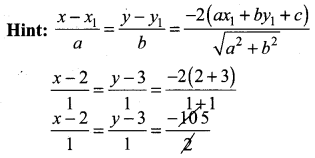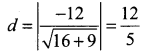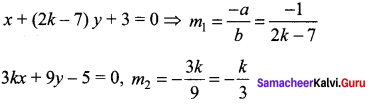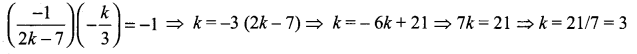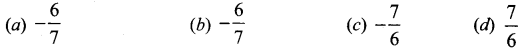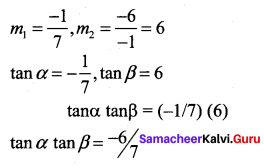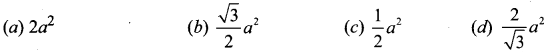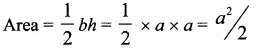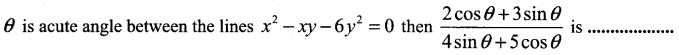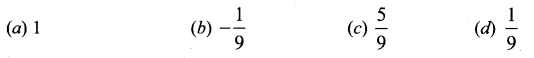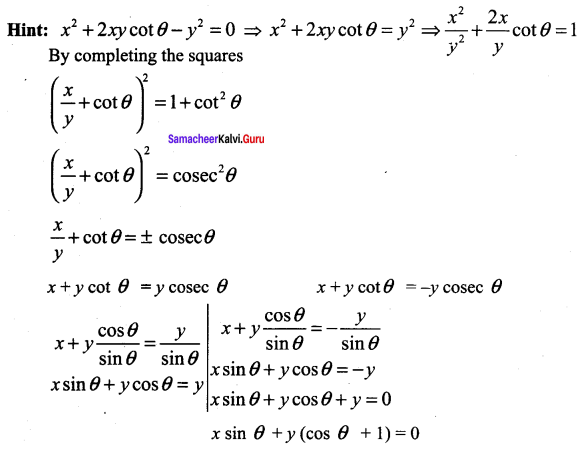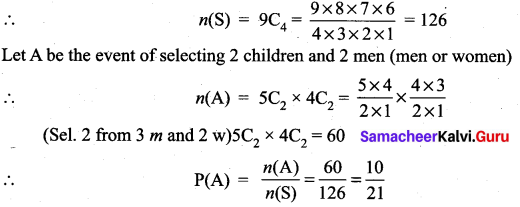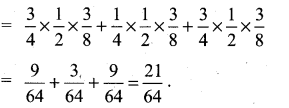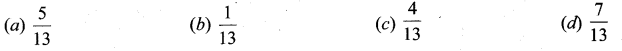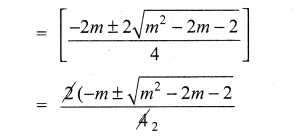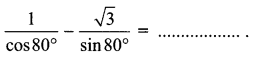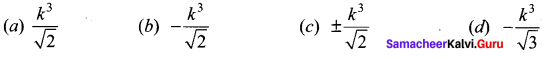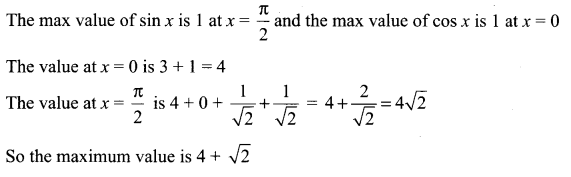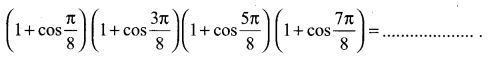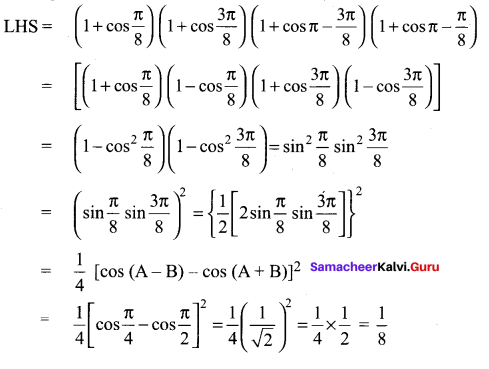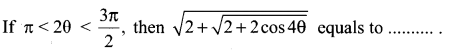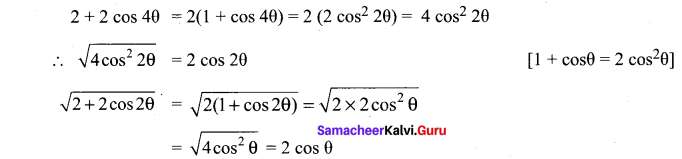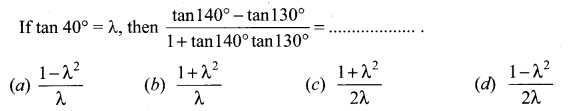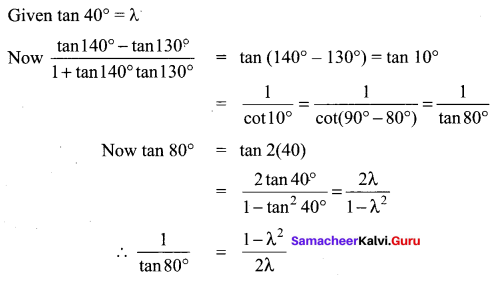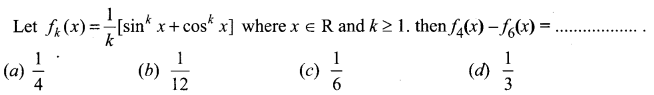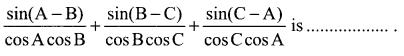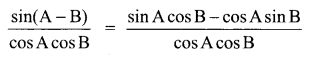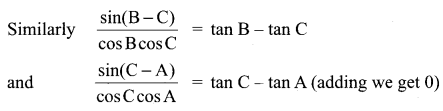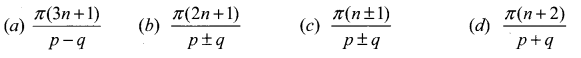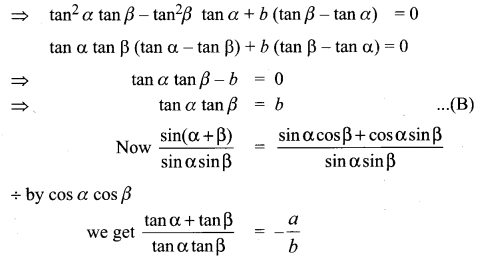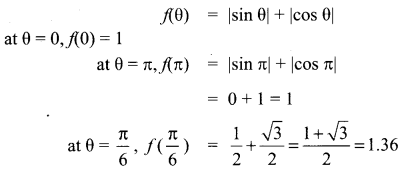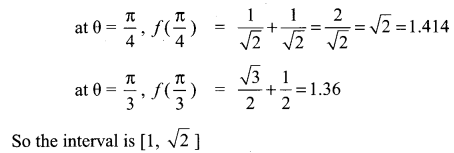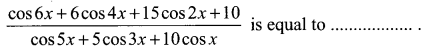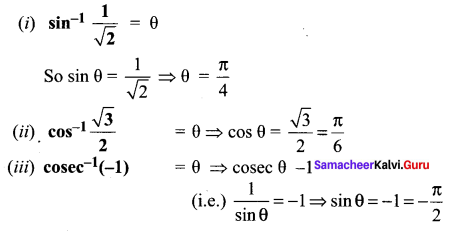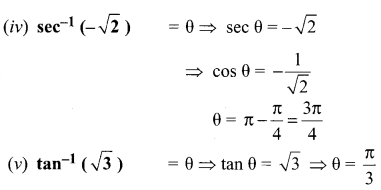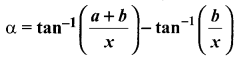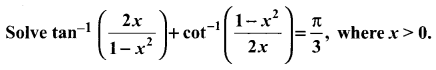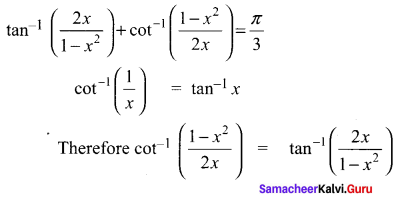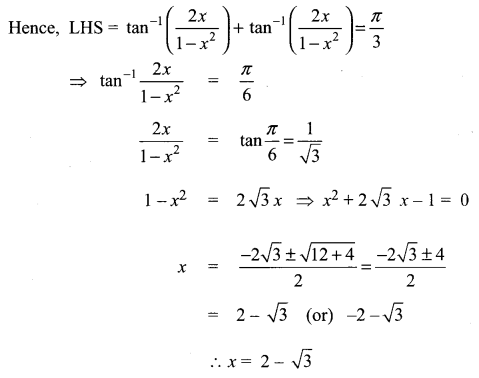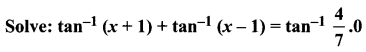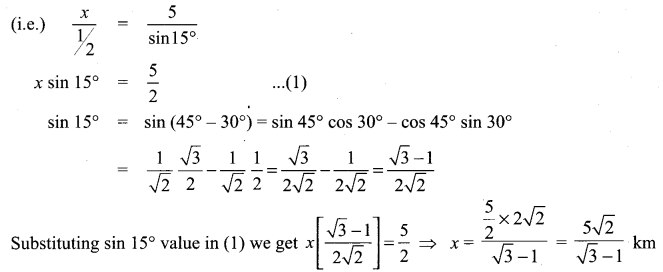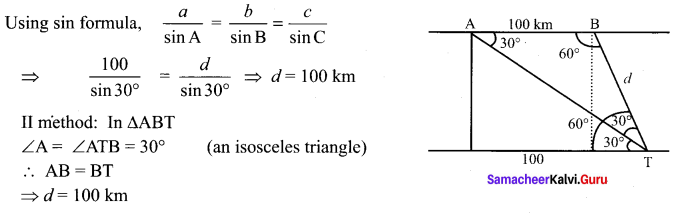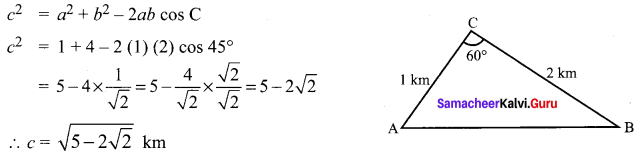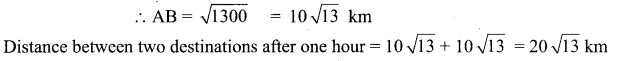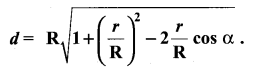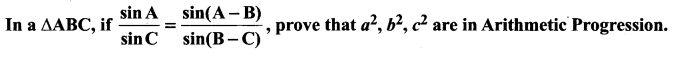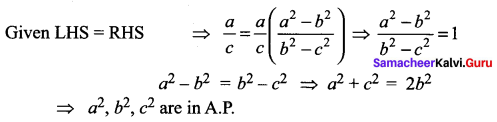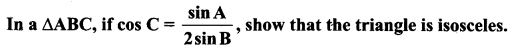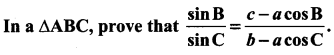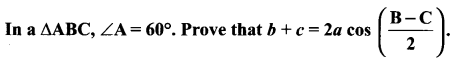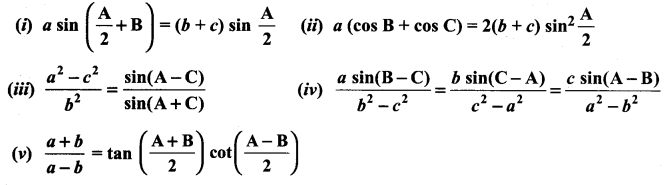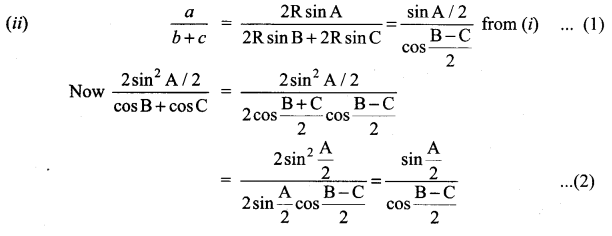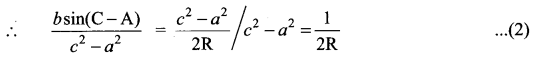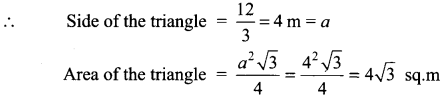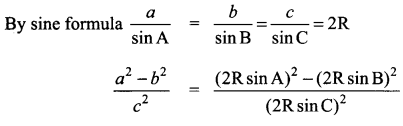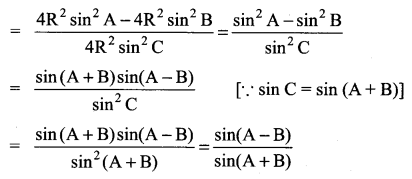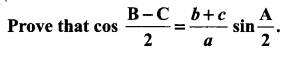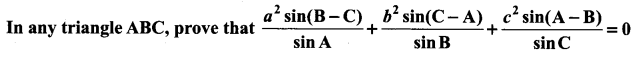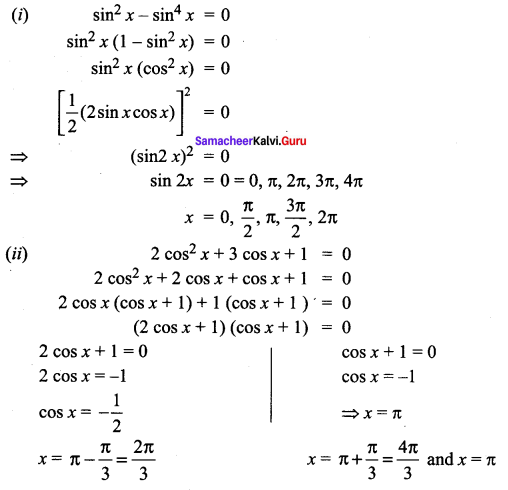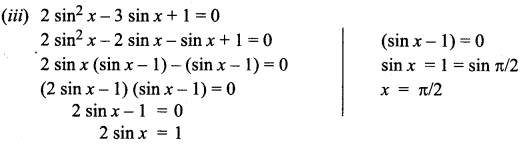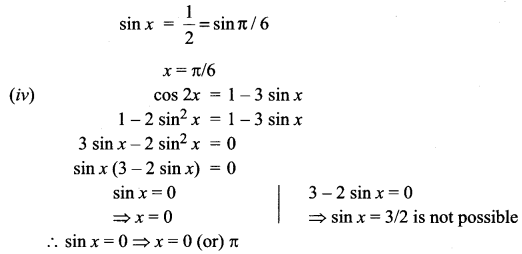You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 11 Integral Calculus Ex 11.13

Choose the correct or most suitable answer from given four alternatives.
Question 1.
If \(\int f(x) d x\) = g(x) + c, then \(\int f(x) g^{\prime}(x) d x\)

Solution:
(a)

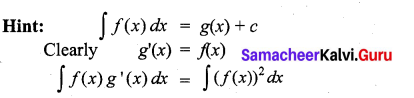
Question 2.
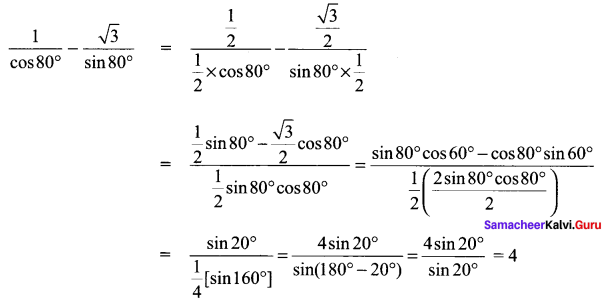
If 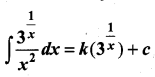, then the value of k is ……………
(a) log 3
(b) -log 3
(c) \(-\frac{1}{\log ^{3}}\)
(d) \(\frac{1}{\log 3}\)
Solution:
(c)

Question 3.
If \(\int f^{\prime}(x) e^{x^{3}} d x\) = (x – 1)e^x2, then f(x) is …………………

Solution:
(d)

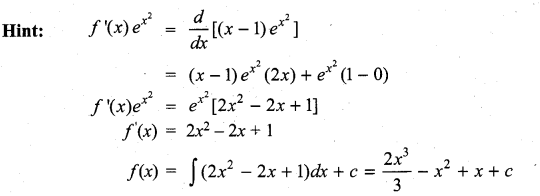
Question 4.
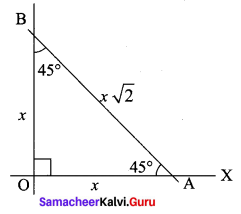
The gradient (slope) of a curve at any point (x, y) is \(\frac{x^{2}-4}{x^{2}}\). If the curve passes through the point(2, 7), then the equation of the curve is ………….
(a) y = x + \(\frac{4}{x}\) + 3
(b) y = x + \(\frac{4}{x}\) + 4
(c) y = x² + 3x + 4
(d) y = x² – 3x + 6
Solution:

Question 5.

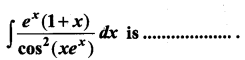
(a) cot (xe^x) + c
(b) sec (xe^x) + c
(c) tan (xe^x) + c
(d) cos (xe^x) + c
Solution:
(c)

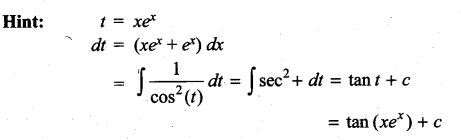
Question 6.
\(\int \frac{\sqrt{\tan x}}{\sin 2 x} d x\) is ……………..

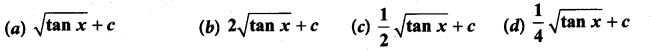
Solution:
(a)

Question 7.
\(\int \sin ^{3} x d x\) is …………….

Solution:
(c)
Hint: sin³x = \(\frac{1}{4}\) (3 sin x – sin 3x)

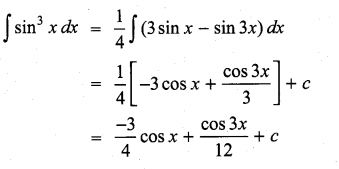
Question 8.

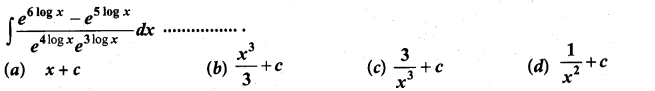
Solution:
(b)

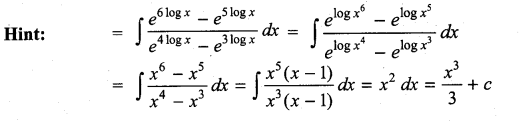
Question 9.

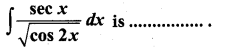
(a) tan^-1 (sin x) + c
(b) 2 sin^-1 (tan x) + c
(c) tan^-1 (cos x) + c
(d) sin^-1 (tan x) + c
Solution:
(d)

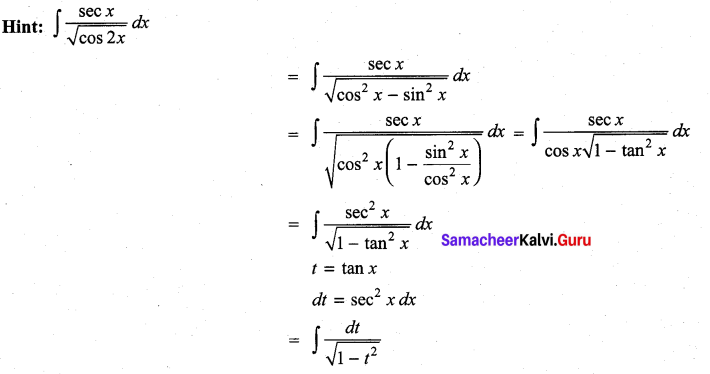
= sin^-1 (t) + c
= sin^-1 (tan x) + c

Question 10.

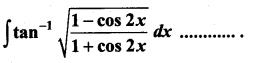
(a) x² + c
(b) 2x² + c
(c) \(\frac{x^{2}}{2}\) + c
(d) \(-\frac{x^{2}}{2}\) + c
Solution:
(c)

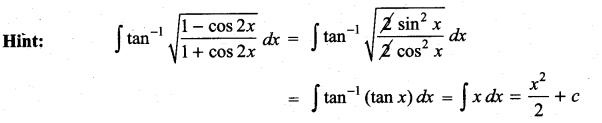
Question 11.
\(\int 2^{3 x+5} d x\) is ……………

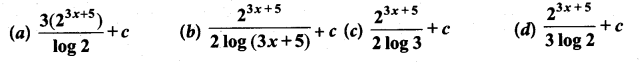
Solution:
(d)

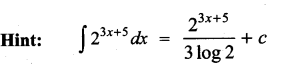
Question 12.

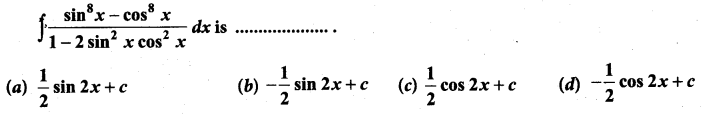
Solution:
(b)

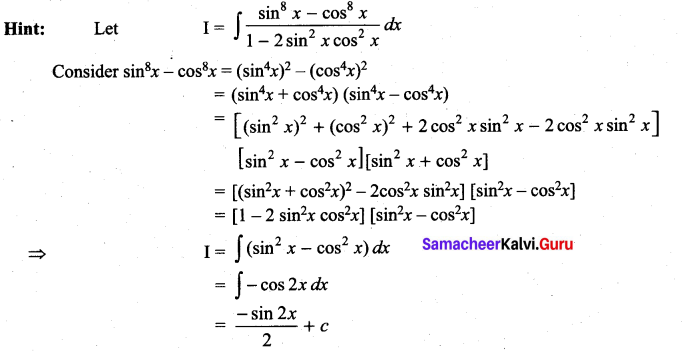
Question 13.

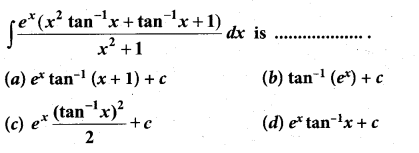
Solution:
(d)

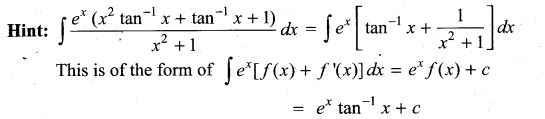
Question 14.
\(\int \frac{x^{2}+\cos ^{2} x}{x^{2}+1}\) cosec²xdx is …………….
(a) cot x + sin^-1 x + c
(b) -cot x + tan^-1 x + c
(c) -tan x + cot^-1 x + c
(d) -cot x – tan^-1 x + c
Solution:
(d)

Question 15.
\(\int x^{2} \cos x d x\) is ……………
(a) x² sin x + 2x cos x – 2 sin x + c
(b) x² sin x – 2x cos x – 2 sin x + c
(c) -x² sin x + 2x cos x + 2 sin x + c
(d) -x² sin x – 2x cos x + 2 sin x + c
Solution:
(a)
Hint: \(\int x^{2} \cos x d x\)
By Bernoullis formula dv = cosxdx
u = x² v = sinx
u’ = 2x v₁ = -cos x
u” = 2 v₂ = -sinx
= uv – u’v₁ + u”v₂
= x²sin x + 2x cos x – 2 sin x + c

Question 16.

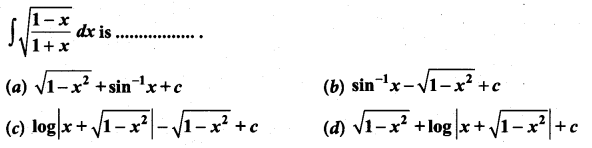
Solution:
(b)

Question 17.
\(\int \frac{d x}{e^{x}-1}\) is …………….
(a) log |e^x| – log |e^x – 1| + c
(b) log |e^x| + log |e^x – 1| + c
(c) log |e^x – 1| – log |e^x| + c
(d) log |e^x + 1| – log |e^x| + c
Solution:
(c)

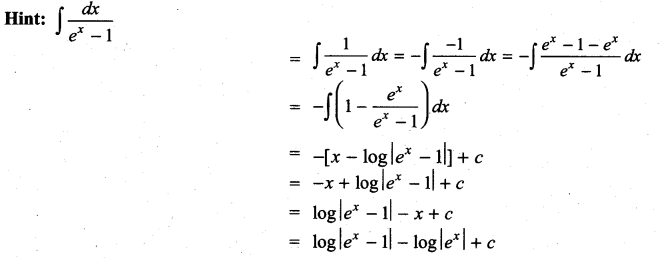
Question 18.

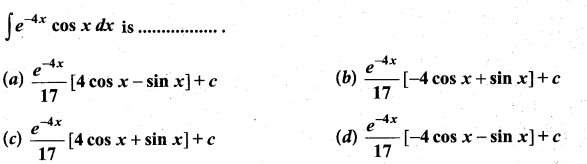
Solution:
(b)
We know that

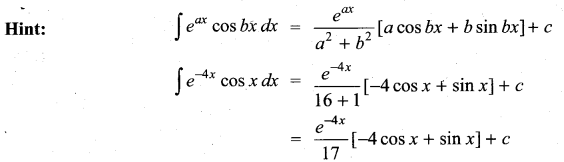
Question 19.

Solution:
(d)

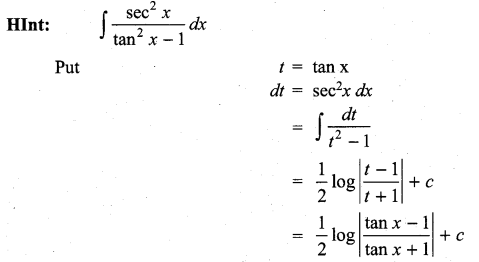
Question 20.

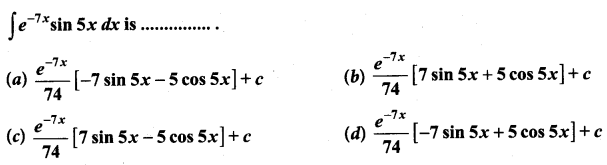
Solution:
(a)
We know that

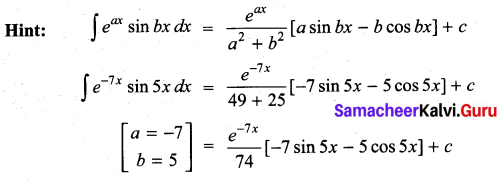
Question 21.

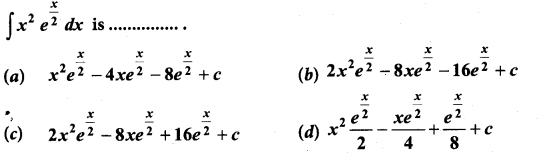
Solution:
(c)
Hint:

By Bernoullis formula,

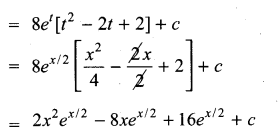
Question 22.

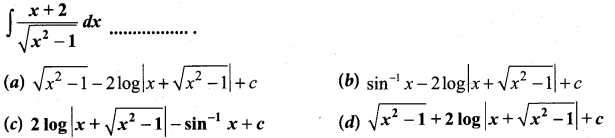
Solution:
(d)

Question 23.

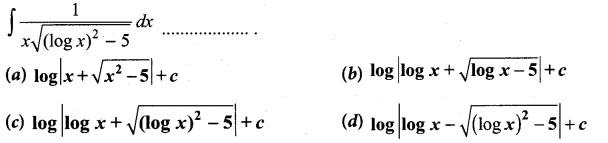
Solution:
(c)

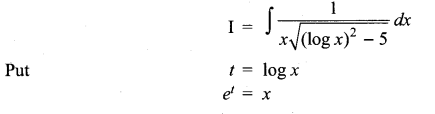
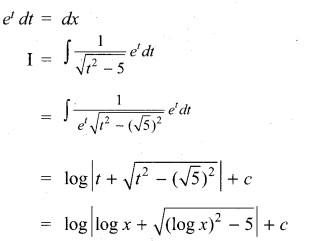
Question 24.

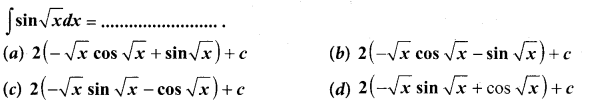
Solution:
(a)

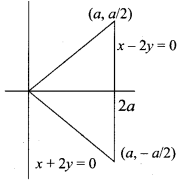
Question 25.

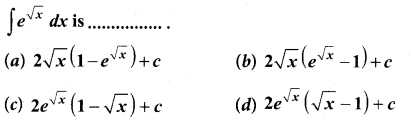
Solution:
(d)
Hint: Let I = \(\int e^{\sqrt{x}} d x\)
t = \(\sqrt{x}\)

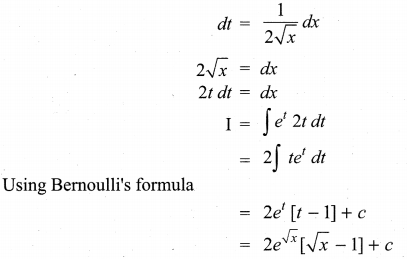
Must Follow:

ICICIBANK Pivot Point Calculator

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.4

Question 1.
Find the combined equation of the straight lines whose separate equations are x – 2y – 3 = 0 and x + y + 5 = 0.
Solution:
Separate equations are x – 2y – 3 = 0; x + y + 5 = 0
So the combined equation is (x – 2y – 3) (x + y + 5) = 0
x² + xy + 5x – 2y² – 2xy – 10y – 3x – 3y – 15 = 0
(i.e) x² – 2y² – xy + 2x – 13y – 15 = 0

Question 2.
Show that 4x² + 4xy + y² – 6x – 3y – 4 = 0 represents a pair of parallel lines.
Solution:
Comparing this equation with ax² + 2hxy + by² + 2gx + 2fy + c = 0
we get a = 4, h = \(\frac{4}{2}\) = 2 , b = 1, g = – 3, f = – 3/2, c = – 4
The condition for the lines to be parallel is h² – ab = 0
Now h² – ab = 2² – (4) (1) = 4 – 4 = 0
h² – ab = 0 ⇒ The given equation represents a pair of parallel lines.

Question 3.
Show that 2x² + 3xy – 2y² + 3x + y + 1 = 0 represents a pair of perpendicular lines.
Solution:
Comparing the given equation with the general form a = 2,h = 3/2, b = -2,g= 3/2, f = 1/2 and c = 1
Condition for two lines to be perpendicular is a + b = 0. Here a + b = 2 – 2 = 0
⇒ The given equation represents a pair of perpendicular lines.

Question 4.
Show that the equation 2x² – xy – 3y² – 6x + 19y – 20 = 0 represents a pair of intersecting lines. Show further that the angle between them is tan^-1(5).
Solution:

The given equation represents a pair of straight lines.

Question 5.
Prove that the equation to the straight lines through the origin, each of which makes an angle α with the straight line y = x is x² – 2xy sec 2α + y² = 0
Solution:
Slope of y = x is m = tan θ = 1
⇒ θ = 45°
The new lines slopes will be
m = tan(45 + α) and m = tan (45 – α)
∴ The equations of the lines passing through the origin is given by
y = tan(45 + α)x and y = tan(45 – α)x
(i.e) y = tan(45 + α)x = 0 and y = tan(45 – α)x = 0
The combined equation is [y – tan (45 + α)x] [y – tan (45 – α)x] = 0
y² + tan(45 + α)tan(45 – α)x² – xy[tan(45 – α) + tan(45 + α)] = 0


Let the equation of lines passes through the origin
So the equations are y = m₁x = 0 and y = m₂x = 0
So the combined equations is (y – m₁x) (y – m₂x) = 0
(i.e)y² – xy(m₁ + m₂) + m₁m₂x = 0
(i.e) y² – xy(2sec α) + x²(1) = 0
(i.e) y² – 2xy sec 2α + x² = 0

Question 6.
Find the equation of the pair of straight lines passing through the point (1, 3) and perpendicular to the lines 2x – 3y + 1 = 0 and 5x + y – 3 = 0
Solution:
Equation of a line perpendicular to 2x – 3y + 1 = 0 is of the form 3x + 2y + k = 0.
It passes through (1, 3) ⇒ 3 + 6 + k = 0 ⇒ k = – 9
So the line is 3x + 2y – 9 = 0
The equation of a line perpendicular to 5x + y – 3 = 0 will be of the form x – 5y + k = 0.
It passes through (1, 3) ⇒ 1 – 15 + k = 0 ⇒ k = 14
So the line is x – 5y + 14 = 0.
The equation of the lines is 3x + 2y – 9 = 0 and x – 5y + 14 = 0
Their combined equation is (3x + 2y – 9)(x – 5y + 14) = 0
(i.e) 3x² – 15xy + 42x + 2xy – 10y² + 28y – 9x + 45y – 126 = 0
(i.e) 3x² – 13xy – 10y² + 33x + 73y – 126 = 0

Question 7.
Find the separate equation of the following pair of straight lines
(i) 3x² + 2xy – y² = 0
(ii) 6 (x – 1)² + 5(x – 1)(y – 2) – 4(y – 2)² = 0
(iii) 2x² – xy – 3y² – 6x + 19y – 20 = 0
Solution:
(i) Factorising 3x² + 2xy – y² we get
3x² + 3xy – xy – y² = 3x (x + y) – y (x + y)
= (3 x – y)(x + y)
So 3x² + 2xy – y² = 0 ⇒ (3x – y) (x + y) = 0
⇒ 3x – y = 0 and x + y = 0

(ii) 6 (x – 1)² + 5 (x – 1)(y – 2) – 4(y – 2)² = 0
⇒ 6(x² – 2x +1) + 5(xy – 2x – y + 2) – 4( y² – 4y + 4) = 0
(i.e) 6x² – 12x + 6 + 5xy – 10x – 5y + 10 – 4y² + 16y – 16 = 0
(i.e) 6x² + 5xy – 4y² – 22x + 11y = 0
Factorising 6x² + 5xy – 4y² we get
6x² – 3xy + 8xy – 4y² = 3x (2x – y) + 4y (2x – y)
= (3x + 4y)(2x – y)
So, 6x² + 5xy – 4y² – 22x + 11y = (3x + 4y + l )(2x – y + m)
Equating coefficient of x ⇒ 3m + 21 = -22 …….. (1)
Equating coefficient of y ⇒ 4m – l = 11 ……. (2)
Solving (1) and (2) we get l = -11, m = 0
So the separate equations are 3x + 4y – 11 = 0 and 2x – y = 0

(iii) 2x² – xy – 3y² – 6x + 19y – 20 = 0
Factorising 2x² – xy – 3y² we get
2x² – xy – 3y² = 2x² + 2xy – 3xy – 3y²
= 2x(x + y) – 3y(x + y) = (2x – 3y) (x + y)
∴ 2x² – xy – 3y² – 6x + 19y – 20 = (2x – 3y + l)(x + y + m)
Equating coefficient of x 2m + l = -6 ……. (1)
Equating coefficient of y -3m + l = 19 …….. (2)
Constant term -20 = lm
Solving (1) and (2) we get l = 4 and m = – 5 where lm = – 20.
So the separate equations are 2x – 3y + 4 = 0 and x + y – 5 = 0

Question 8.
The slope of one of the straight lines ax² + 2hxy + by² = 0 is twice that of the other, show that 8h² = 9ab.
Solution:
ax² + 2 hxy + by² = 0
We are given that one slope is twice that of the other.
So let the slopes be m and 2m.
Now sum of the slopes = m + 2m

Question 9.
The slope of one of the straight lines ax² + 2hxy + by² = 0 is three times the other, show that 3h² = 4ab.
Solution:
Let the slopes be m and 3m.

Question 10.
A ∆OPQ is formed by the pair of straight lines x² – 4xy + y² = 0 and the line PQ. The equation of PQ is x + y – 2 = 0. Find the equation of the median of the triangle ∆OPQ drawn from the origin O.
Solution:
Equation of pair of straight lines is x² – 4xy + y² = 0 ….. (1)
Equation of the given line is x + y – 2 = 0 ⇒ y = 2 – x ……… (2)
On solving (1) and (2) we get x² – 4x (2 – x) + (2 – x)² = 0
(i.e) x² – 8x + 4x² + 4 + x² – 4x = 0
(i.e) 6x² – 12x + 4 = 0
(÷ by 2) 3x² – 6x + 2 = 0

Mid point of PQ is

Question 11.
Find p and q, ¡f the following equation represents a pair of perpendicular lines 6x² + 5xy – py² + 7x + qy – 50
Solution:
6x² + 5xy – py² + 7x + qy – 50
The given equation represents a pair of perpendicular lines
⇒ coefficient of x² + coefficient of y² = 0
(i.e) 6 – p = 0 ⇒ p = 6
Now comparing the given equation with the general form
ax² + 2hxy + by² + 2gx + 2fy + c = 0
we get a = 6, b = -6 and c = -5, f = q/2, g = 7/2 and h = 5/2
The condition for the general form to represent a pair of straight lines is abc + 2fgh – af² – bg² – ch² = 0

Question 12.
Find the value of k, if the following equation represents a pair of straight lines. Further, find whether these lines are parallel or intersecting, 12x² + 7xy – 12y² – x + 7y + k = 0.
Solution:
Comparing the given equation with the general form ax² + 2hxy + by² + 2gx + 2fy + c = 0
we get a = 12, b = -12, c = k, f = 7/2, g = – 1/2, h = 7/2
Here a + b = 0 ⇒ the given equation represents a pair of perpendicular lines
To find k: The condition for the given equation to represent a pair of straight lines is abc + 2fgh – af² – bg² – ch² = 0

Question 13.
For what value of k does the equation 12x² + 2kxy + 2y², + 11x – 5y + 2 = 0 represent two straight lines.
Solution:
12x² + 2 kxy + 2y² + 11x – 5y + 2 = 0
Comparing this equation with the general form we get

4k² + 55k + 175 = 0
4k² + 20k + 35k + 175 = 0
4k(k + 5) + 35(k + 5) = 0
(4k + 35) (k + 5) = 0
k = -5 or -35/4

Question 14.
Show that the equation 9x² – 24xy + 16y² – 12x + 16y – 12 = 0 represents a pair of parallel lines. Find the distance between them.
Solution:
Comparing the given equation with ax² + 2kxy + by² = 0 we get a = 9, h = -12, b = 16.
Now h² = (-12)² = 144, ab = (9) (16) = 144
h² = ab ⇒ The given equation represents a pair of parallel lines.
To find their separate equations:
9x² – 24xy + 16y² = (3x – 4y)²
So, 9x² – 24xy +16y² – 12x + 16y – 12 = (3x – 4y + l )(3x – 4y + m)
Here coefficient of x ⇒ 3m + 3l = -12 ⇒ m + l = -4
coefficient of y ⇒ -4m – 4l = 16 ⇒ m + l = -4
Constant term l m = -12
Now l + m = -4 and lm = -12 ⇒ l = -6 and m = 2
So the separate equations are 3x – 4y – 6 = 0 and 3x – 4y + 2 = 0

Question 15.
Show that the equation 4x² + 4xy + y² – 6x – 3y – 4 = 0 represents a pair of parallel lines. Find the distance between them.
Solution:
4x² + 4xy + y² – 6x – 3y – 4 = 0
a = 4,
b = 1,
h = 4/2 = 2
h² – ab = 2² – (4) (1) = 4 – 4 = 0
⇒ The given equation represents a pair of parallel lines.
To find the separate equations 4x² + 4xy + y² = (2x + y)²
So, 4x² + 4xy + y² – 6x – 3y – 4 = (2x + y + l )(2x + y + m)
Coefficient of x ⇒ 2m + 2l = -6 ⇒ l + m = – 3 ……. (1)
Coefficient of y ⇒ l + m = – 3 ……… (2)
Constant term ⇒ l m = – 4 ……… (3)
Now l + m = -3 and lm = -4 ⇒ l = -4, m = 1
So the separate equations are 2x + y + 1 = 0 and 2x + y – 4 = 0

Question 16.
Prove that one of the straight lines given by ax² + 2hxy + by² = 0 will bisect the angle between the co-ordinate axes if (a + b)² = 4h².
Solution:
Let the slopes be l and m
∵ One line bisects the angle between the coordinate axes ⇒ θ = 45°
So tan θ = 1
The slopes are l and m

Question 17.
If the pair of straight lines x² – 2kxy – y² = 0 bisect the angle between the pair of straight lines x² – 2lxy – y² = 0, show that the later pair also bisects the angle between the former.
Solution:
Given that x² – 2kxy – y² = 0 …….. (1)
Bisect the angle between the lines x² – 11xy – y² = 0 …… (2)

x² – 2kxy – y² = 0

Question 18.
Prove that the straight lines joining the origin to the points of intersection of 3x² + 5xy – 3y² + 2x + 3y = 0 and 3x – 2y – 1 = 0 are at right angles.
Solution:
Homogenizing the given equations 3x² + 5xy – 3y² + 2x + 3y = 0 and 3x – 2y – 1 = 0
(i.e) 3x – 2y = 1.
We get (3x² + 5xy – 3y²) + (2x + 3y)( 1) = 0
(i.e) (3x² + 5xy – 3y²) + (2x + 3y)(3x – 2y) = 0
3x² + 5xy – 3y² + bx² – 4xy + 9xy – 6y² = 0
9x² + 10xy – 9y² = 0
Coefficient of x² + coefficient of y² = 9 – 9 = 0
⇒ The pair of straight lines are at right angles.

Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.4 Additional Questions Solved

Question 1.
Find the angle between the pair of straight lines given by
(a² – 3b² )x² + 8ab xy + (b² – 3a²)y² =0 .
Solution:

Question 2.
Show that 9x² + 24xy + 16y² + 21x + 28y + 6 = 0 represents a pair of parallel straight lines and find the distance between them.
Solution:
9x² + 24xy + 16y² + 21x + 28y + 6 = 0
Here a = 9.6,
b = 16,
g = \(\frac{21}{2}\),
f = 14,
c = 6,
h = 12
h² – ab = (12)² – 9(16) = 144 – 144 = 0
∴ The lines are parallel.
9x² + 24xy + 16y² = (3x + 4y)(3x + 4y)
Let 9x² + 24xy + 16y² + 21x + 28y + 6 = (3x + 4y + l)(3x + 4y + m)
Equating the coefficients of x and constant term
3l + 3m = 21
lm = 6
Solving we get, l = 1 or 6
m = 6 or 1
∴ The separate equations are 3x + 4y + 1 = 0 and 3x + 4y + 6 = 0

Question 3.
If the equation 12x² – 10xy + 2y² + 14x – 5y + c = 0 represents a pair of straight lines, find the value of c. Find the separate equations of the straight lines and also the angle
between them.
Solution:
12x² – 10xy – 2y² + 14x – 5y + c = 0
ax² + 2hxy + by² +2gx + 2fy – c = 0
Here a = 12,
b = 2,
g = 7,
f = 5/2,
c = c,
h = -5
af² + bg² + ch² – 2fgh – abc = 0 is the condition

The equation is 12x² – 10y + 2y² + 14x – 5y + 2 = 0
12x² – 10xy + 2y = (3x – y)(4x – 2y)
Let 12x² – 10y + 2y² + 14x – 5y + 2(3x – y + l)(4x – 2y + m)
So that 4l + 3m = 14 , -2l – m = -5

Question 4.
For what value of k does 12x² + 7xy + ky² + 13x – y + 3 = 0 represents a pair of straight lines? Also write the separate equations.
Solution:
12x² + 7xy + ky² + 13x – y + 3 = 0
a = 12,
h = \(\frac{7}{2}\),
f = \(-\frac{1}{2}\) ,
c = 3
af² + bg² + ch² – abc – 2fgh = 0

⇒ 12 + 169k + 147 – 144k + 91 = 0
25k = – 250 ⇒ k = -10
The equation is 12x² + 7xy – 10y² + 13x – y + 3 = 0
To find separate equations: 12x² + 7xy – 10y² = (3x – 2y)(4x + 5y)
Let 12x² + 7xy – 10y² + 13x – y + 3 = 0(3x – 2y + l)(4x + 5y + m)
Equating the coefficient of x ⇒ 4l + 3m = 13 …… (1)
Equating the coefficient of y ⇒ 5l – 2m = -1 …… (2)
(1) × 2 ⇒ 8l + 6m = 26
(2) × 3 ⇒ 15l – 6m = -3
23l = 23 ⇒ l = 1
4 + 3 m = 13
3 m = 9 ⇒ m = 3
The separate equations are 3x – 2y + 1 = 0 and 4x + 5y + 3 = 0

Question 5.
Show that 3x² + 10xy + 8y² + 14x + 22y + 15 = 0 represents a pair of straight lines and the angle between them is tan^-1\(\left(\frac{2}{11}\right)\)
Solution:
3x² + 10xy + 8y² + 14x + 22y + 15 = 0
a = 3,
A = 5,
b = 8,
g = 7,
f = 11,
c = 15
The condition is af² + bg² + ch² – abc – 2fgh = 0
3(11)² + 8(7)² + 15 (5)² – (3)(8)(15) – 2(11)(7)(5) = 363 + 392 + 375 – 360 – 770 = 0
The angle between the pair of straight line is given by

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.2

Question 1.
Write the first 6 terms of the sequences whose n^th terms are given below and classify them as arithmetic progression, geometric progression, arithmetico-geometric progression, harmonic progression and none of them.

Solution:


It is not a G.P. or A.P. or H.P. or A.G.P.

It is not an A.P. or G.P. or H.P. or A.G.P

It is not an A.P. or G.P. or H.P. or A.G.P.


It is a A.G.P.

Question 2.
Write the first 6 terms of the sequences whose n^th term a_n is given below.

Solution:
a₁ = 1 + 1 = 2 ; a₂ = 2
a₃ = 3 + 1 = 4 ; a₄ = 4
a₅ = 5 + 1 = 6 ; a₆ = 6
So, the first 6 terms are 2, 2, 4, 4, 6, 6

Solution:
a₁ = 1 ; a₂ = 2, a₃ = 3
a₄ = a₃ + a₂ + a₁ = 3 + 2 + 1 = 6 ⇒ a₄ = 6
a₅ = a₄ + a₃ + a₂ = 6 + 3 + 2 = 11 ⇒ a₅ = 11
a₆ = a₅ + a₄ + a₃ = 11 + 6 + 3 = 20 ⇒ a₆ = 20
So the first 6 terms are 1, 2, 3, 5, 8, 13.

Solution:

Question 3.
Write the n_th term of the following sequences.
Solution:
(i) 2, 2, 4, 4, 6, 6……
Solution:

Solution:
Nr: 1, 2, 3, ……t_n = n
Dr: 2, 3, 4, …..t_n = n + 1


Solution:
Nr: 1, 3, 5, 7, . . .which is an A.P. a = 1, d = 3 – 1 = 2
t_n = a + (n – 1)d
t_n = 1 + (n – 1)2 = 1 + 2n – 2 = 2n – 1.
Dr : 2, 4, 6, 8, . . .
So the n^th term is 2 + (n – 1)2 = 2 + 2n – 2 = 2n.

(iv) 6, 10, 4, 12, 2, 14, 0, 16, -2,….
Solution:
t₁ = 6 ; t₂ = 10
t₃ = 4 ; t₄ = 12
t₅ = 2 ; t₆ = 14
t₇ = 0 ; t₈ = 16
When n is odd, the sequence is 6, 4, 2, 0,…
(i.e.) a = 6 and d = 4 – 6 = -2.
So, t_n = 6 + (n – 1)(-2) = 6 – 2n + 2 = 8 – 2n
When n is even, the sequence is 10, 12, 14, 16,…
Here a = 10 and d = 12 – 10 = 2
t_n = 10 + (n – 1)2 = 10 + 2n – 2 = 2n + 8 (i.e.) 8 + 2n

Question 4.
The product of three increasing numbers in GP is 5832. If we add 6 to the second number and 9 to the third number, then resulting numbers form an AP. Find the numbers in GP.
Solution:
The 3 numbers in a G.P. is taken as \(\frac{a}{r}\), a, ar
Their product is 5832.

6r² + 6 = 13
6r² – 13r + 6 = 0
(3r – 2)(2r – 3) = 0
r = 2/3 or 3/2

Question 5.

Solution:

Question 6.
If t_k is the k^th term of a G.P., then show that t_{n – k}, t_n, t_{n + k} also form a GP for any positive integer k.
Solution:
Let a be the first term and r be the common ratio.
We are given t_k = ar^{k – 1}
We have to Prove : t_{n – k}, t_n, t_{n + k} form a G.P.

Question 7.
If a, b, c are in geometric progression, and if \(a^{\frac{1}{x}}=b^{\frac{1}{y}}=c^{\frac{1}{z}}\), then prove that x, y, z are in arithmetic progression.
Solution:
Given a, b, c are in G.P.
⇒ b² = ac
⇒ log b² = log ac
(i.e.) 2log b = log a + log c …(1)

Substituting these values in equation (1) we get 2y = x + z ⇒ x, y z are in A.P.

Question 8.
The AM of two numbers exceeds their GM by 10 and HM by 16. Find the numbers.
Solution:
Let the two numbers be a and b.

So, (a + b – 20)² = 4ab
(i.e.) (a + b)² + 400 – 40(a + b) = 4ab
(a + b)² – 4ab = 40(a + b) – 400
from(3) (a + b)² – 4ab = 32(a + b)
⇒ 32(a + b) = 40(a + b) – 400
(÷ by 8) 4(a + b) = 5(a + b) – 50
4a + 4b = 5a + 5b – 50
a + b = 50
a = 50 – b
Substituting a = 50 – b in (3) we get
(50 – b – b)² = 32(50)
(50 – 2b)² = 32 × 50

When b = 5, a = 50 – 5 = 45
When b = 45, a = 50 – 45 = 5
So the two numbers are 5 and 45.

Question 9.
If the roots of the equation (q – r)x² + (r – p)x + p – q = 0 are equal, then show that p, q and r are in AP.
Solution:
The roots are equal ⇒ ∆ = 0
(i.e.) b² – 4ac = 0
Hence, a = q – r ; b = r – p ; c = p – q
b² – 4ac = 0
⇒ (r – p)² – 4(q – r)(p – q) = 0
r² + p² – 2pr – 4[qr – q² – pr + pq] = 0
r² + p² – 2pr – 4qr + 4q² + 4pr – 4pq = 0
(i.e.) p² + 4q² + r² – 4pq – 4qr + 2pr = 0
(i.e.) (p – 2q + r)² = 0
⇒ p – 2q + r = 0
⇒ p + r = 2q
⇒ p, q, r are in A.P.

Question 10.
If a, b, c are respectively the p^th, q^th and r^th terms of a G.P., show that (q – r) log a + (r – p) log b + (p – q) log c = 0.
Solution:
Let the G.P. be l, lk, lk²,…
We are given t_p = a, t_q = b, t_r = c

LHS = (q – r) log a + (r – p) log b + (p – q) log c

Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.2 Additional Questions Solved

Question 1.

Solution:
Here a₁ = 1
Substituting n = 2, we obtain a₂ = a₁ + 2 = 1 + 2 = 3
Substituting n = 3, 4 and 5, we obtain respectively
a₃ = a₂ + 2 = 3 + 2 = 5, a₄ = a₃ + 2 = 5 + 2 = 7
a₅ = a₄ + 2 = 7 + 2 = 9
Thus, the first five terms are 1, 3, 5, 7 and 9.

Question 2.
Find the 18^th and 25^th term of the sequence defined by

Solution:
When n = 18 (even)
a_n = n(n + 2) = 18(18 + 2) = 18(20) = 360
When n = 25(odd)

Question 3.
Write the first six terms of the sequences given by
(i) a₁ = a₂= 1 = a_{n – 1} + a_{n – 2} (n ≥ 3)
(ii) a₁ = 4, a_{n + 1} = 2na_n
Solution:
(i) Here a₁ = a₂= 1 = a_{n – 1} + a_{n – 2} (n ≥ 3)
Putting n = 3, a₃= a₂ + a₁ = 1 + 1 = 2
Putting n = 4, a₄ = a₃ + a₂ = 2 + 1 = 3
Putting n = 5, a₅ = a₄ + a₂ = 3 + 2 = 5
Putting n = 6, a₆ = a₅ + a₄ = 5 + 3 = 8
∴ First six terms of the sequence are 1, 1, 2, 3, 5, 8

(ii) Here a₁ = 4 and a_{n + 1} = 2na_n
Putting n = 1, a₂ = 2 × 1 × a₁ = 2 × 1 × 4 = 8
Putting n = 2, a₃ = 2 × 2 × a₂ = 4 × 8 = 32
Putting n = 3, a₄ = 8 × 192 = 1536
Putting n = 4, a₅ = 2 × 4 × a₄ = 8 × 192 = 1536
Putting n = 5, a₆ = 2 × 5 × a₅ = 10 × 1536 = 15360

Question 4.
An A.P. consists of 21 terms. The sum of the three terms in the middle is 129 and of the last three is 237. Find the series.
Solution:
Let a₁ be the first term and d, be the common difference. Here n = 21.
∴ The three middle terms are a₁₀,a₁₁, a₁₂
Now, a₁₀ + a₁₁ + a₁₂ = 129 [Given]
∴ (a₁ + 9d) + (a₁ + 10d) + (a₁ + 11d) = 129
⇒ 3a₁ + 30d = 129 ⇒ a₁ + 10d = 43 ……(i)
The last three terms are a₁₉, a₂₀, a₂₁
a₁₉, a₂₀, a₂₁ = 237 [Given]
∴ (a₁ + 18d)+(a₁ + 19d) + (a₁ + 20d) = 237
(i.e.,) 3a₁ + 57d = 237 ⇒ a₁ + 19d = 79 … (2)
Subtracting (i) from (ii), we get 9d = 36, ⇒ d = 4
∴ From (i), a₁ + 40 = 43 ⇒ a₁ = 3
Hence, the series is 3, 7, 11, 15 …….

Question 5.
Prove that the product of the 2^nd and 3^rd terms of an arithmetic progression exceeds the product of the first and fourth by twice the square of the difference between the 1^st and 2^nd.
Solution:
Let ‘a’ be the first term and ‘d’ be the common difference of A.P.
Then, a₁ = a, a₂ = a + (2 – 1)d = a + d
a₃ = a + (3 – 1)d = a + 2d, a₄ = a + (4 – 1)d = a + 3d
We have to show that a₂.a₃ – a₁.a₄ = 2(a₂ – a₁)²
LHS = a₂.a₃ – a₁.a₄ = (a + d)(a + 2d) – a(a + 3d)
= a₂ + 3ad + 2d₂ – a₂ – 3ad = 2d₂
RHS = 2(a₂ – a₁)² = 2d₂
Since LHS = RHS. Hence proved.

Question 6.
If the p^th, q^th and r^th terms of an A.P. are a, b, c respectively, prove that a(q – r) + b (r – p) + c(p – q) = 0.
Solution:
Let A be the first term and D be the common difference of A.P.
a_p = a, ∴ A + (p – 1)D = a ….. (1)
a_q = b, ∴ A + (q – 1)D = b ……. (2)
a_r = c, ∴ A + (r – 1)D = c …….. (3)
∴ a (q – r) + b (r – p) + c (p – q) = [A + (p – l) D] (q – r) + [A + (q – 1) D]
(r – p) + [A + (r – 1) D] (p – q) [Using (1), (2) and (3)]
= (q – r + r – p + p – q)A + [(p – l)(q – r) + (q – l)(r – p) + (r – l)(p – q)]D
= (0) A + (pq – pr – q + r + qr – pq – r + p + pr – p – qr + q)D
= (0)A + (0)D = 0.

Question 7.
If a, b, c are in A.P. and p is the A.M. between a and b and q is the A.M. between b and c, show that b is the A.M. between p and q.
Solution:
a, b, c are in A.P.
2b = a + c …… (1)
p is the A.M. between a and b

q is the A.M. between b and c


Hence, b is the A.M. between p and q

Question 8.
If x, y, z be respectively the p^th, q^th and r^th terms of a G.P. show that x^{q – r}, y^{r – p} ,z^{p – q} = 1
Solution:
Let A be the first term and R be the common ratio of G.P.
a_p = x ⇒ x = AR^{p – 1} ……… (1)
a_q = y ⇒ x = AR^{q – 1} ……… (2)
a_r = z ⇒ x = AR^{r – 1} ……… (3)
Raising (1), (2), (3) to the powers q – r, r – p, p – q respectively, we get

Multiplying (4), (5) and (6), we get

Hence, x^{q – r}, y^{r – p}, z^{p – q} = 1

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 6 Two Dimensional Analytical Geometry Ex 6.5

Choose the correct or more suitable answer

Question 1.
The equation of the locus of the point whose distance from y-axis is half the distance from origin is ……..
(a) x² + 3y² = 0
(b) x² – 3y² = 0
(c) 3x² + y² = 0
(d) 3x² – y² = 0
Solution:
(c) 3x² + y² = 0
Hint:
Given that PA = \([\frac{1}{2}/latex]OP
2PA = OP

4PA² = OP²
4(x)² = x² + y² ⇒ 3x² – y² = 0

Question 2.
Which of the following equation is the locus of (at², 2at) ……

Solution:
(d) y² = 4ax
Hint:
y² = 4ax ⇒ Equation that satisfies the given point (at², 2at)

Question 3.
Which of the following point lie on the locus of 3x² + 3y² – 8x – 12y + 17 = 0?
(a) (0, 0)
(b) (-2, 3)
(c) (1, 2)
(d) (0, -1)
Solution:
(c) (1, 2)
Hint:
The point that satisfies the given equations (0, 0) ⇒ 17 ≠ 0
(-2, 3) ⇒ 3 (4) + 3 (9) + 16 – 36 + 17 ≠ 0
(1, 2) ⇒ 3 + 3 (4) – 8 (1) – 12 (2) + 17
32 – 32 = 0, 0 = 0

Question 4.

(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(d) 3

Question 5.
Straight line joining the points (2, 3) and (-1, 4) passes through the point (α, β) if
(a) α + 2β = 7
(b) 3α + β = 9
(c) α + 3β = 11
(d) 3α + 3β = 11
Solution:
(c) α + 3β = 11
Hint:
Equation joining (2, 3), (-1, 4)

3y – 12 = – x -1 ⇒ x + 3y – 11 = 0, (α, β) lies on it ⇒ α + 3β – 11 = 0.

Question 6.
The slope of the line which makes an angle 45° with the line 3x – y = – 5 are
(a) 1, -1
(b) [latex]\frac{1}{2},-2\)
(c) \(1, \frac{1}{2}\)
(d) \(2,-\frac{1}{2}\)
Solution:
(c) \(1, \frac{1}{2}\)
Hint:
Equation of line 3x – y = -5, y = 3x + 5, m₁ = 3

Question 7.
Equation of the straight line that forms an isosceles triangle with coordinate axes in the I-quadrant with perimeter \(4+2 \sqrt{2}\) is
(a)x + y + 2 = 0
(b) x + y – 2 = 0
(c) x + y – \(\sqrt{2}\) = 0
(d) x + y + \(\sqrt{2}\) = 0
Solution:
(b) x + y – 2 = 0
Hint.
Let the sides be x, x

Question 8.
The coordinates of the four vertices of a quadrilateral are (-2, 4), (-1, 2), (1, 2) and (2, 4) taken in order. The equation of the line passing through the vertex (-1, 2) and dividing the quadrilateral in the equal areas is ………
(a) x + 1 = 0
(b) x + y = 1
(c) x + y + 3 = 0
(d) x – y + 3 = 0
Solution:
(b) x + y = 1
Hint:
This equation passes through (-1, 2)
-1 + 2 = 1 ⇒ 1 = 1

Question 9.
The intercepts of the perpendicular bisector of the line segment joining (1, 2) and (3, 4) with coordinate axes are ……….
(a) 5, -5
(b) 5, 5
(c) 5, 3
(d) 5, -4
Solution:
(b) 5, 5

Question 10.
The equation of the line with slope 2 and the length of the perpendicular from the origin equal to \(\sqrt{5}\) is ……
(a) x + 2y = \(\sqrt{5}\)
(b) 2x + y = \(\sqrt{5}\)
(c) 2x + y = 5
(d) x + 2y – 5 = 0
Solution:
(c) 2x + y = 5

The required line is y = 2x + 5 ⇒ 2x – y + 5 = 0

Question 11.
A line perpendicular to the line 5x – y = 0 forms a triangle with the coordinate axes. If the area of the triangle is 5 sq. units, then its equation is …….

Solution:
(a) x + 5y ± 5\(\sqrt{2}\) = 0
Hint:
Equation of a line perpendicular to 5x – y = 0 is

Question 12.
Equation of the straight line perpendicular to the line x – y + 5 = o, through the point of intersection the y-axis and the given line …….
(a) x – y – 5 = 0
(b) x + y – 5 = 0
(c) x + y + 5 = 0
(d) x + y + 10 = 0
Solution:
(b) x + y – 5 = 0
Hint:
x – y + 5 = 0 ⇒ put x = 0, y = 5
The point is (0, 5)
Equation of a line perpendicular to x – y + 5 = 0 is x + y + k = 0
This passes through (0, 5)
k = -5
x + 7 – 5 = 0

Question 13.
If the equation of the base opposite to the vertex (2, 3) of an equilateral triangle is x + y = 2, then the length of a side is ………

Solution:
\(\sqrt{6}\)
Hint:
In an equilateral ∆ the perpendicular will bisects the base in to two equal parts. Length of the perpendicular drawn from (2, 3) to the line x + 7 – 2 = 0

Question 14.
The line (p + 2q) x + (p – 3q)y = p – q for different values of p and q passes through the point ……

Solution:
(d) \(\left(\frac{2}{5}, \frac{3}{5}\right)\)
Hint:
(p + 2 q)x + (p – 3q)y = p – q
px + 2qx + py – 3qy = p – q
P(x + y) + q (2x – 3y) = p – q
The fourth option x = 2/5, y = 3/5

= p – q = RHS

Question 15.
The point on the line 2x – 3y = 5 is equidistance from (1, 2) and (3, 4) is …
(a) (7, 3)
(b) (4, 1)
(c) (1, -1)
(d) (-2, 3)
Solution:
(b) (4, 1)
Hint:
Let (a, b) be on 2x – 3y = 5 ⇒ 2a – 3b = 5
It is equidistance from (1, 2) and (3, 4)

(a – 1)² + (b – 2)² = (a – 3)² + (6 – 4)²
a² – 2a + 1 + b² – 4b + 4 = a² – 6a + 9 + b² – 8b + 16
4a + 4b = 20
2a+ 2b = 10
2a – 3b = 5
5b = 5
b = 1 ∴ a = 4
∴ The point is (4, 1)

Question 16.
The image of the point (2, 3) in the line y = – x is ………
(a) (-3, -2)
(b) (-3, 2)
(c) (-2, -3)
(d) (3, 2)
Solution:
(a) (-3, -2)

x – 2 = -5, y – 3 = -5
x = -3, y = -2
(-3,-2)

Question 17.
The length of ⊥ from the origin to the line \(\frac{x}{3}-\frac{y}{4}=1\) is ……

Solution:
(c) \(\frac{12}{5}\)
Hint:
4x – 3y = 12 ⇒ 4x – 3y – 12 = 0

Question 18.
The y-intercept of the straight line passing through (1, 3) and perpendicular to 2x – 3y + 1 = 0 is ……..

Solution:
(b) \(\frac{9}{2}\)
Hint:
Equation of a line perpendicular to 2x – 3y + 1 = 0 is 3x + 2y = k. It passes through (1, 3).
3 + 6 = k ⇒ k = 9, 3x + 2y = 9
To find y-intercept x = 0, 2y = 9, y = 9/2

Question 19.
If the two straight lines x + (2k – 7)y + 3 = 0 and 3kx + 9y – 5 = 0 are perpendicular then the value of k is ……

Solution:
(a) k = 3
Hint.

Since the lines are perpendicular m₁m₂ = – 1

Question 20.
If a vertex of a square is at the origin and its one side lies along the line 4x + 3y – 20 = 0, then the area of the square is ……..
(a) 20 sq. units
(b) 16 sq. units
(c) 25 sq. units
(d) 4 sq.units
Solution:
(b) 16 sq. units
Hint:
One side of a square = Length of the perpendicular from (0, 0) to the line.

Question 21.
If the lines represented by the equation 6x² + 41xy – 7y² = 0 make angles α and β with
x – axis, then tan α tan β =

Solution:
(a) \(-\frac{6}{7}\)
Hint.
6x² + 41xy – 7y² = 0 ⇒ 6x² – xy + 42xy – 7y² = 0 ⇒ x (6x – y) + 7y (6x – y) = 0
(x + 7y) (6x – y) = 0 ⇒ x + 7y = 0, 6x – y = 0

Question 22.
The area of the triangle formed by the lines x² – 4y² = 0 and x = a is …….

Solution:
(c) \(\frac{1}{2} a^{2}\)
Hint:
x² – 4y² = 0 , (x – 2y) (x + 2y) = 0 ⇒ x – 2y = 0, x + 2y = 0

Question 23.
If one of the lines given by 6x² – x + 4x² = 0 is 3x + 4y = 0, then c equals to ……
(a) -3
(b) -1
(c) 3
(d) 1
Solution:
(a) -3
Hint.
6x² – xy + 4cy² = 0, 3x + 4y = 0
The other line may be (2x + by)
(3x + 4y) (2x + by) = 6x² – xy + 4cy²
6x² + 3xby + 8xy + 4by² = 6x² – xy + 4cy²
6x² + xy (3b + 8) + 4by² = 6x² – xy + 4cy²
paring, 3b + 8 = -1
3b = -9 ⇒ b = -3
4b = 4c ⇒ 4(-3) = 4c
-12 = 4c ⇒ c = -3

Question 24.


Solution:
(c) \(\frac{5}{9}\)
Hint:

Question 25.
The equation of one the line represented by the equation x² + 2xy cot θ – y² = 0 is ………
(a) x – y cotθ = 0
(b) x + y tan θ = 0
(e) x cos θ + y(sin θ + 1) = 0
(d) x sin θ + y(cos θ + 1) = 0
Solution:
(d) x sin θ + y(cos θ + 1)=0

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 12 Introduction to Probability Theory Ex 12.5

Choose the correct or most suitable answer from the given four alternatives:
Question 1.
Four persons are selected at random from a group of 3 men, 2 women and 4 children. The probability that exactly two of them are children is
(a) \(\frac{3}{4}\)
(b) \(\frac{10}{23}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{10}{21}\)
Solution:
(d)
Hint:
Total no of person = 3 + 2 + 4 = 9
Selecting 4 from 9 can be done in 9 C₄ ways

Question 2.
A number is selected from the set {1, 2, 3, ….., 20}. The probability that the selected number is divisible by 3 or 4 is ……………
(a) \(\frac{2}{5}\)
(b) \(\frac{1}{8}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{2}{3}\)
Solution:
(c)
Hint:
n(S) = 20
A = {3, 6, 9, 12, 15, 18} ⇒ n(A) = 6
B = {4, 8, 12, 16, 20} ⇒ n(B) = 5
A ∩ B = {12} ⇒ n(A ∩ B) = 1
so P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{6}{20}+\frac{5}{20}-\frac{1}{20}=\frac{10}{20}=\frac{1}{2}\)

Question 3.
A, B and C try to hit a target simultaneously but independently. Their respective probabilities of hitting the target are \(\frac{3}{4}, \frac{1}{2}, \frac{5}{8}\). The probability that the target is hit by A or B but not by C

Solution:
(a)
Hint:
P(A) = \(\frac{3}{4}\) P(A’) = 1/4
P(B) = 1/2 P(B’) = 1/2
P(C) = 5/8 P(C’) = 3/8
Probability of hitting the target = 1

Question 4.
If A and B are any two events, then the probability that exactly one of them occur is …………
(a) P(A ∪ \(\overline{B}\)) + P(\(\overline{A}\) ∪ B)
(b) P(A ∩ \(\overline{B}\)) + P(\(\overline{A}\) ∩ B)
(c) P(A) + P(B) – P(A ∩ B)
(d) P(A) + P(B) + 2P(A ∩ B)
Solution:
(b)
Hint:

Question 5.
Let A and B be two events such that P(\(\overline{A \cup B}\)) = \(\frac{1}{6}\), P(A ∩ B) = \(\frac{1}{4}\) and P(\(\overline{A}\)) = \(\frac{1}{4}\).
Then the events A and B are …………………
(a) Equally likely but not independent
(b) Independent but not equally likely
(c) Independent and equally likely
(d) Mutually inclusive and dependent
Solution:
(b)
Hint:

So P(A). P(B) = \(\frac{3}{4} \times \frac{1}{3}=\frac{1}{4}\)
P(A ∩ B) = P(A). P(B)
⇒ A and B are independent and not equally likely

Question 6.
Two items are chosen from a lot containing twelve items of which four are defective, then the probability that at least one of the item is defective
when two items are chosen at random probability of atleast one of them is defective ………….

Solution:
(a)
Hint:
Total number = 12
Defective = 4
∴ good ones = 12 – 4 = 8
when two items are chosen at random probability of atleast one of them is defective
= P(one defective or 2 defectives) = P(GD or DD)
= P(G) P(D) + P(D) P(D)

Question 7.
A man has 3 fifty rupee notes, 4 hundred rupees notes and 6 five hundred rupees notes in his pocket. If 2 notes are taken at random, what are the odds in favour of both notes being of hundred rupee denomination?
(a) 1 : 12
(b) 12 : 1
(c) 13 : 1
(d) 1 : 13
Solution:
(d)
Hint:

The odds in favour done of P is P : 1 – P
(i.e.,) \(\frac{1}{13}: \frac{12}{13}\) = 1 : 12

Question 8.
A letter is taken at random from the letters of the word ‘ASSISTANT’ and another letter is taken at random from the letters of the word ‘STATISTICS’. The probability that the selected letters are the same is ………….

Solution:
(d)
Hint:

Question 9.
A matrix is chosen at random from a set of all matrices of order 2, with elements 0 or 1 only. The probability that the determinant of the matrix chosen is not zero will be

Solution:
(b)
Hint: Then given elements are 0 and So each term of a matrix can be filled (Using or 1) is 2 ways.
The No. of elements is a 2 × 2 matrix = 2 × 2 = 4. So the possible ways of filling the elements of a 2 × 2 matrix is 2⁴ = 16 (i.e.,) n(S) = 16
Let A be the event of getting a 2 × 2 matrix for which the determinant value is non zero.

Question 10.
A bag contains 5 white and 3 black balls. Five balls are drawn successively without replacement. The probability that they are alternately of different colours is …………..

Solution:
(c)
Hint:

Question 11.
If A and B are two events such that A ⊂ B and P(B) ≠ 0, then which of the following is correct?
(a) P(A/B) = \(\frac{\mathrm{P}(\mathrm{A})}{\mathrm{P}(\mathrm{B})}\)
(b) P(A/B) < P(A) (c) P(A/B) ≥ P(A) (d) P(A/B) > P(B)
Solution:
(c)
Hint:

Question 12.
A bag contains 6 green, 2 white, and 7 black balls. If two balls are drawn simultaneously then the probability that both are different colours is ………..

Solution:
(a)
Hint:

Question 13.
If X and Y be two events such that P(X/Y) = \(\frac{1}{2}\), P(Y/X) = \(\frac{1}{3}\) and P(X ∩ Y) = \(\frac{1}{6}\) then P(X ∪ Y) is …………
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{5}\)
(c) \(\frac{1}{6}\)
(d) \(\frac{2}{3}\)
Solution:
(d)
Hint:

Question 14.
An um contains 5 red and 5 black balls. A balls is drawn at random, its colour is noted and is returned to the um. Moreover, 2 additional balls of the colour drawn are put in the um and then a ball is drawn at random. The probability that the second ball drawn is red will be …………

Solution:
(b)
Hint:

Question 15.
A number x is chosen at random from the first 100 natural numbers. Let A be the event of numbers which satisfies \(\frac{(x-10)(x-50)}{x-30}\) ≥ 0, then P(A) is …………….
(a) 0.20
(b) 0.51
(c) 0.71
(d) 0.70
Solution:
(c)
Hint:

Question 16.
If two events A and B are independent such that P(A) = 0.35 and P(A ∪ B) = 0.6, then P(B) is …………..

Solution:
(a)
Hint:
Given A and B are independent
P(A ∩ B) = P(A) + P(B)
⇒ Now P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
(i.e.,) Now P(A ∪ B) = P(A) + P(B) – P(A).P(B)
0.6 = 0.35 + P(B) – (0.35) P(B)
⇒ P(B) = (1 – 0.35) = 0.6 – 0.35
0.65 P(B) = 0.25
∴ P(B) = \(\frac{0.25}{0.65}=\frac{25}{65}=\frac{5}{13}\)

Question 17.
If two event A and B are such that P(\(\overline{A}\)) and P(A ∩ \(\overline{B}\)) = 1/2, then P(A ∩ B) is ………….

Solution:
(d)
Hint:

Question 18.
If A and B are two events such that P(A) = 0.4, P(B) = 0.8 and P(B/A) = 0.6, then P(\(\overline{A}\) ∩ B) is …………..
(a) 0.96
(b) 0.24
(c) 0.56
(d) 0.66
Solution:
(c)
Hint:
P(B/A) = 0.6 ⇒ \(\frac{P(A \cap B)}{P(A)}\) = 0.6
⇒ P(B/A) = 0.6 × P(A) = 0.6 × 0.4 = 0.24
Now P(\(\overline{A}\) ∩ B) = P(B) – P(A ∩ B)
= 0.8 – 0.24 = 0.56

Question 19.
There are three events A, B, and C of which one and only one can happen. If the odds are 7 to 4 against A and 5 to 3 against B, then odds against C is ……………
(a) 23 : 65
(b) 65 : 23
(c) 23 : 88
(d) 88 : 23
Solution:
(b)
Hint: If the probability of an event is P then the odds against its occurrence are 1 – P to P.
Selecting 1 from the 4 number 1, 2, 3,4, can be done in 4 ways
Here for the event A we are given that = \(\frac{1-\mathrm{P}}{\mathrm{P}}=\frac{7}{4}\)
⇒ 4 – 4P = 7P
⇒ 11 P = 4 ⇒ P = \(\frac{4}{11}\) ⇒ P(A) = \(\frac{4}{11}\) for the event B we are given
\(\frac{1-\mathrm{P}}{\mathrm{P}}=\frac{5}{3}\) ⇒ 5P = 3 – 3P
⇒ 8P = 3 ⇒ P = 3/8
P(B) = \(\frac{3}{8}\)
Now we are given P(A) + P(B) + P(C) = 1
P(C) = 1 – P(A) – P(B)
P(C) = 1 – \(\frac{4}{11}-\frac{3}{8}\)

Question 20.
If a and b are chosen randomly from the set {1, 2, 3, 4} with replacement, then the probability of the real roots of the equation x² + ax + b = 0 is

Solution:
(c)
Hint:
x² + ax + b = 0 ⇒ x = \(\frac{-a \pm \sqrt{a^{2}-4 b}}{2}\)
Given that the roots are real ⇒ a² – 4b ≥ 0 or a² > 4b
When a = 1, b = 1 or 2 or 3 or 4 a² – 4b < 0
When a = 2, b = 1 a² – 4b = 0
When a = 3, b = 1 or 2 for which a² – 4b ≥ 0
When a = 4, b = 1 or 2, 3 or 4 for which a² – 4b ≥ 0
So, Selecting from the 4 number 4² = 16 ways.
(i.e.,) n(s) = 16
n(A) = (2 or 3 or 4) = 3
n(B) = (1 or 2 or 3 or 4) = 4
P(A) + P(B) = \(\frac{3}{16}+\frac{4}{16}=\frac{7}{16}\)

Question 21.
It is given that the events A and B are such that P(A) = \(\frac{1}{4}\), P(A/B) = \(\frac{1}{2}\) and P(B/ A) = \(\frac{2}{3}\) then P(B) is ……………

Solution:
(b)
Hint:

Question 22.
In a certain college 4% of the boys and 1% of the girls are taller than 1.8 meter. Further 60% of the students are girls. If a student is selected at random and is taller than 1.8 meters, then the probability that the students is a girls is ………….

Solution:
(b)
Hint:

Question 23.
Ten coins are tossed. The probability of getting at least 8 heads is …………….

Solution:
(d)
Hint:
When 10 coins are tossed, No. of element in sample space
n(S) = 2¹⁰ = 1024
Probability of getting atleast 8 heads

Question 24.
The probability of two events A and B are 0.3 and 0.6 respectively. The probability that both A and B occur simultaneously is 0.18. The probability that neither A nor B occurs is …………….
(a) 0.1
(b) 0.72
(c) 0.42
(d) 0.28
Solution:
(d)
Hint:
P(A) = 0.3, P(B) = 0.6
P(A ∩ B) = 0.18
So P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.3 + 0.6 – 0.18
= 0.9 – 0.18 = 0.72
P(A’ ∩ B’) = P[(A ∪ B)’] = 1 – P(A ∪B)
= 1 – 0.72 = 0.28

Question 25.
If m is a number such that m≤ 5, then the probability that quadratic equation 2x² + 2mx + m + 1 = 0 has real roots is ………….

Solution:
(c)
Hint:
2x² + 2mx + m + 1 = 0


roots are real ⇒ m² – 2m – 2 ≥ 0
Here m ≤ 5 ⇒ n(S) = 5
When m= 1,m² – 2m – 2
When m = 2, m² – 2m- 2
When m = 3, m² – 2m – 2
When m = 4, m² – 2n- 2
When m = 5, m² – 2m – 2
⇒ n{A) = 3 and so P(A) = \(\frac{3}{5}\)

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.12

Choose the correct answer or most suitable answer:

Question 1.

(a) \(\sqrt{2}\)
(b) \(\sqrt{3}\)
(c) 2
(d) 4
Solution:
(d) 4
Hint:

Question 2.
If cos 28° + sin 28° = k³, then cos 17° is equal to …….

Solution:
(a) \(\frac{k^{3}}{\sqrt{2}}\)
Hint:

Question 3.

(a) 4 + \(\sqrt{2}\)
(b) 3 + \(\sqrt{2}\)
(c) 9
(d) 4
Solution:
(a) 4 + \(\sqrt{2}\)
Hint:

Question 4.

Solution:
(a) \(\frac{1}{8}\)
Hint:

Question 5.

Solution:
(c) 2 cos θ
Hint:

Here θ is in II Quadrant

Question 6.

Solution:
(d) \(\text { (d) } \frac{1-\lambda^{2}}{2 \lambda}\)
Hint:

Question 7.
cos 1° + cos 2° + cos 3° + …. + cos 179° = …….
(a) 0
(b) 1
(c) -1
(d) 89
Solution:
(a) 0
Hint:
LHS = (cos 10 + cos 179°)+(cos 2° ÷ cos 178°)+ ….. +cos(89° + cos 91°)+cos 90°
cos 179° = cos (180° – 1) = – cos 1°
cos 178° = cos(180° – 2)= – cos 2°
So (cos 1°- cos 1°)+(cos 2° – cos 2°) + (cos 89° – cos 89°) + cos 90°
= 0 + 0 …. + 0 + 0 = 0.

Question 8.

Solution:
(b) \(\frac{1}{12}\)
Hint:

Question 9.
Which of the following is not true?

Solution:
(d) sec θ = \(\frac{1}{4}\)
Hint:
sec θ = \(\frac{1}{4}\) ⇒ cos θ = 4, which is not true.

Question 10.
cos 2θ cos 2ϕ+ sin² (θ – ϕ) – sin² (θ + ϕ) is equal to …….
(a) sin 2(θ + ϕ)
(b) cos 2(θ + ϕ)
(c) sin 2(θ – ϕ)
(d) cos 2(θ – ϕ)
Solution:
(b) cos 2(θ + ϕ)
Hint.
Given cos 2θ . cos 2ϕ + sin² (θ – ϕ) – sin² (θ + ϕ)
= cos 2θ cos 2ϕ + sin (θ – ϕ + θ + ϕ) sin (θ – ϕ – θ – ϕ)
= cos 2θ cos 2ϕ + sin 2θ sin(-2ϕ)
= cos 2θ cos 2ϕ – sin 2θ sin(2ϕ)
= cos (2θ + 2ϕ) = cos 2(θ + ϕ)

Question 11.

(a) sin A + sin B + sin C
(b) 1
(c) 0
(d) cos A + cos B + cos C
Solution:
(c) 0
Hint:

= tan A – tan B

Question 12.
cos pθ + cos qθ = 0 and if p ≠ q, then 0 is equal to (n is any integer) …….

Solution:
(b) \(\frac{\pi(2 n+1)}{p \pm q}\)
Hint:
cos pθ + cos qθ = 0

Question 13.
If tan α and tan β are the roots x² + ax + b = 0, then \(\frac{\sin (\alpha+\beta)}{\sin \alpha \sin \beta}\) is equal to …….
Solution:
(b) \(\frac{a}{b}\)
Hint:
tan² x + a tan x + b = 0
α and β are the roots of the equation
⇒ tan² α + a tan α + b = 0 ….. (1)
tan² β + a tan β + b = 0 …… (2)
(1) – (2) => tan² α – tan² β + a (tan α – tan β) = 0
(tan α – tan β) (tan α + tan β) + a (tan α – tan β) = 0
⇒ tan α + tan β = – a …. (A)
(1) × tan β – (2) × tan α

Question 14.
In a triangle ABC, sin² A + sin² B + sin² C = 2, then the triangle is …….
(a) equilateral triangle
(b) isosceles triangle
(c) right triangle
(d) scalene triangle
Solution:
(c) right triangle
Hint.
On simplifying we get
sin² A + sin² B + sin² C = 2 + 2 cos A cos B cos C
= 2 (given)
⇒ cos A cos B cos C = 0
cos A (or) cos B (or) cos C = 0
⇒ A (or) B (or) C = π/2
⇒ ABC (is a right angled triangle).

Question 15.
If f(θ) = |sin θ| + |cos θ|, θ ∈ R, then f(θ) is in the interval …….
(a) [0, 2]
(b) [1, \(\sqrt{2}\)]
(c) [1, 2]
(d) [0, 1]
Solution:
(b) [1, \(\sqrt{2}\)]
Hint:

Question 16.

Solution:
Nr: cos 6x + cos 4x + 5 cos 4x + 5 cos 2x + 10 cos 2x + 10
= 2 cos 5x cos x+5(2 cos 3x cos x)+ 10(2 cos²x)
= 2 cos x [cos 5x + 5 cos 3x + 10 cos x]

Question 17.
The triangle of maximum area with constant perimeter 12m
(a) is an equilateral triangle with side 4m
(b) is an isosceles triangle with sides 2m, 5m, 5m
(c) is a triangle with sides 3m, 4m, 5m
(d) does not exists
Solution:
(a) is an equilateral triangle with side 4m
Hint.
A triangle will have a max area (with a given perimeter) when it is an equilateral triangle.

Question 18.
A wheel is spinning at 2 radians/second. How many seconds will it take to make 10 complete rotations?
(a) 10π seconds
(b) 20π seconds
(c) 5π seconds
(d) 15π seconds
Solution:
(a) 10π seconds
Hint.
1 rotation makes 2π^c
Distance travelled in 1 second = 2 radians
So time taken to complete 10 rotations = 6 × 2π = 20 π^c
\(=\frac{20 \pi}{2}=10 \pi\) seconds

Question 19.
If sin α + cos α = b, then sin 2α is equal to ……..

Solution:
(b) b² – 1, if b > \(\sqrt{2}\)
Hint:
sin α + cos β = b
(sin α + cos β)² = b²
sin² α + cos² α + 2 sin α cos α = b²
sin² α = b² – 1

Question 20.

(a) Both (i) and (ii) are true
(b) Only (i) is true
(c) Only (ii) is true
(d) Neither (i) nor (ii) is true
Solution:
(a) Both (i) and (ii) are true
Hint.
When A + B + C = 180°

When A + B + C = 180° each angle will be lesser than 180°
So sin A, sin B, sin C > 0
⇒ sin A sin B sin C > 0
So both (i) and (ii) are true

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.11

Question 1.

Solution:

Question 2.
A man standing directly opposite to one side of a road of width x meter views a circular shaped traffic green signal of diameter a meter on the other side of the road. The bottom of the green signal is b meter height from the horizontal level of viewer’s eye. If a denotes the angle subtended by the diameter of the green signal at the viewer’s eye, then prove that

Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.11 Additional Questions

Question 1.

Solution:

Question 2.

Solution:

The negative value of x is rejected since it makes RHS negative
∴ x = \(\frac{1}{6}\)

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.10

Question 1.
Determine whether the following measurements produce one triangle, two triangles or no triangle:
∠B = 88°, a = 23, b = 2. Solve if solution exists.
Solution:
We are given a = 23,
b = 2, and
∠B = 88°.
So we can

Question 2.
If the sides of a ∆ABC are a = 4, b = 6 and c = 8, then show that 4 cos B + 3 cos C = 2.
Solution:
a = 4,
b = 6,
c = 8
To prove 4 cos B + 3 cos C = 2

Question 3.
In a ∆ABC, if a = \(\sqrt{3}\) – 1, b = \(\sqrt{3}\) + 1 and C = 60°, find the other side and other two angles.
Solution:

Question 4.

Solution:

Question 5.
In a ∆ABC, if a = 12 cm, b = 8 cm and C = 30°, then show that its area is 24 sq.cm.
Solution:
a = 12 cm,
b = 8 cm,
C = 30°

Question 6.
In a ∆ABC, if a = 18 cm, b = 24 cm and c = 30 cm, then show that its area is 216 sq.cm.
Solution:
a = 18 cm,
b = 24 cm,
c = 30 cm
The sides form a right angled triangle

Question 7.
Two soldiers A and B in two different underground bunkers on a straight road, spot an intruder at the top of a hill. The angle of elevation of the intruder from A and B to the ground level in the eastern direction are 30° and 45° respectively. If A and B stand 5 km apart, find the distance of the intruder from B.
Solution:
By using sine formula
\(\frac{x}{\sin 30^{\circ}}=\frac{5}{\sin 15^{\circ}}\)

Question 8.
A researcher wants to determine the width of a pond from east to west, which cannot be done by actual measurement. From a point P, he finds the distance to the eastern-most point of the pond to be 8 km, while the distance to the western most point from P to be 6 km. If the angle between the two lines of sight is 60°, find the width of the pond.
Solution:
p² = W² + E² – 2WE cos P
P² = 64 + 36 – 2 × 8 × 6 × Cos 60°

Question 9.
Two Navy helicopters A and B are flying over the Bay of Bengal at same altitude from the sea level to search a missing boat. Pilots of both the helicopters sight the boat at the same time while they are apart 10 km from each other. If the distance of the boat from A is 6 km and if the line segment AB subtends 60° at the boat, find the distance of the boat from B.
Solution:

Question 10.
A straight tunnel is to be made through a mountain. A surveyor observes the two extremities A and B of the tunnel to be built from a point P in front of the mountain. If AP = 3 km, BP = 5 km and ∠APB = 120°, then find the length of the tunnel to be built.
Solution:
p² = a² + b² – 2ab cos P
p² = 9 + 25 – 30 Cos 120°
p² = 9 + 25 – 30 (-1/2) = 34 + 15 = 49

⇒ p = \(\sqrt{49}\) = 7 km

Question 11.
A farmer wants to purchase a triangular shaped land with sides 120 feet and 60 feet and the angle included between these two sides is 60°. If the land costs ? 500 per sq.ft, find the amount he needed to purchase the land. Also find the perimeter of the land.
Solution:

Question 12.
A fighter jet has to hit a small target by flying a horizontal distance. When the target is sighted, the pilot measures the angle of depression to be 30°. If after 100 km, the target has an angle of depression of 60°, how far is the target from the fighter jet at that instant?
Solution:

Question 13.
A plane is 1 km from one landmark and 2 km from another. From the planes point of view the land between them subtends an angle of 60°. How far apart are the landmarks?
Solution:

Question 14.
A man starts his morning walk at a point A reaches two points B and C and finally back to A such that ∠A= 60° and ∠B = 45°, AC = 4 km in the ∆ABC. Find the total distance he covered during his morning walk.
Solution:

Question 15.
Two vehicles leave the same place P at the same time moving along two different roads. One vehicle moves at an average speed of 60 km/hr and the other vehicle moves at an average speed of 80 km/hr. After half an hour the vehicle reach the destinations A and B. If AB subtends 60° at the initial point P, then find AB.
Solution:

= 900+ 1600 – 1200 = 1300

Question 16.
Suppose that a satellite in space, an earth station and the centre of earth all lie in the same plane. Let r be the radius of earth and R be the distance from the centre of earth to the satellite. Let d be the distance from the earth station to the satellite. Let 30° be the angle of elevation from the earth station to the satellite. If the line segment connecting earth station and satellite subtends angle α at the centre of earth, then prove that

Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.10 Additional Questions Solved

Question 1.
Given a = 8, b = 9, c = 10, find all the angles.
Solution:

Question 2.
Given a = 31, b = 42, c = 57, find all the angles.
Solution:
Since the sides are larger quantities, use half angles formulae

Question 3.
In a triangle ABC, A = 35° 17′ ; C = 45° 13′ ; b = 42.1 Solve the triangle
Solution:
The unknown parts are B, a, c,
B = 180 – (A + C) = 180 – (35° 17′ + 45° 13′)
= 99° 30′
To find sides, use sine formula


log c = log 42.1 + log sin 45° 31 – log sin 99° 30′
= 1.6243 + 1.8511 – 1.9940
= 1.4754 – 1.9940
= 1.4754 – [-1 + 0.9940] = 1.4814
⇒ c = 30.3°
Thus B = 99° 30′ ; a = 24.65° ; c = 30.3°

Question 4.
Solve the triangle ABC if a = 5, b = 4 and C = 68°.
Solution:
To find c, use c² = a² + b² – 2ab cos C
c² = 25 + 16 – 2 × 5 × 4 cos 68°
= 41 – 40 × 0.3746 = 26.016
c = 5.1
To find the other two angles, use sine formula.

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.9

Question 1.

Solution:

Question 2.
The angles of a triangle ABC, are in Arithmetic Progression and if b : c = \(\sqrt{3}: \sqrt{2}\), find ∠A.
Solution:

Question 3.

Solution:

⇒ a² + b² – c² = a² ⇒ b² – c² = a² – a²
⇒ b² – c² = 0 ⇒ b = c
∴ ∆ ABC is isosceles

Question 4.

Solution:

Question 5.
In a ∆ABC, prove that a cos A + b cos B + c cos C = 2a sin B sin C.
Solution:
LHS = a cos A+ 6 cos B + c cos C
Using sine formula, we get k sin A cos A + k sin B cos B + k sin C cos C k
= \(\frac{k}{2}\) [2 sin A cos A + 2 sin B cos B + 2 sin C cos C]
= \(\frac{k}{2}\) [sin 2A + sin 2B + sin 2C]
= \(\frac{k}{2}\) [2 sin (A + B) . cos (A – B) + 2 sin C . cos C]
= \(\frac{k}{2}\) [2 sin (A – B) . cos (A – B) + 2 sin C . cos C]
= \(\frac{k}{2}\) [2 sin C . cos (A – B) + 2 sin C . cos C]
= k sin C [cos(A – B) + cos C]

= k sin C [cos (A – B) – cos (A + B)]
= k sin C . 2 sin A sin B
= 2k sin A . sin B sin C
= 2a sin B sin C = RHS

Question 6.

Solution:

Question 7.
In a ∆ ABC, prove the following.

Solution:

Question 8.
In a ∆ABC, prove that (a² – b² + c²) tan B = (a² + b² – c²)tan C
Solution:

Question 9.
An Engineer has to develop a triangular shaped park with a perimeter 120 m in a village. The park to be developed must be of maximum area. Find out the dimensions of the park.
Solution:
Given, the perimeter of triangular shaped park = 120 m

All sides of a triangular part would be 40 m.
i.e., a = 40 m,
b = 40 m,
c = 40 m.

Question 10.
A rope of length 12 m is given. Find the largest area of the triangle formed by this rope and find the dimensions of the triangle so formed.
Solution:
The largest triangle will be an equilateral triangle

Question 11.
Derive Projection formula from
(i) Law of sines,
(ii) Law of cosines.
Solution:
(i) To Prove a = b cos c + c cos B
Using sine formula
RHS = b cos C + c cos B
= 2R sin B cos C + 2R sin C cos B
= 2R [sin B cos C + cos B sin C]
= 2R sin (B + C) = 2R [sin π – A)
= 2R sin A = a = LHS

(ii) To prove a = b cos c + c cos B
Using cosine formula

Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.9 Additional Questions

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.8

Question 1.
Find the principal solution and general solutions of the following:

Solution:

Question 2.
Solve the following equations for which solutions lies in the interval 0° < θ < 360°
(i) sin⁴ = sin²x
(ii) 2 cos² x + 1 = – 3cos x
(iii) 2 sin² x + 1 = 3 sin x
(iv) cos 2x = 1 – 3 sin x – 3 sin x
Solution:

Question 3.
Solve the following equations:
(i) sin 5x – sin x = cos 3x
(ii) 2 cos² θ + 3 sin θ – 3 = 0
(iii) cos θ + cos 3θ = 2 cos 2θ
(iv) sin θ + sin 3θ + sin 5θ = 0
(v) sin 2θ – cos 2θ – sin θ + cos θ = 0
(vi) sin θ + cos θ = \(\sqrt{3}\)
(vii) sin θ + \(\sqrt{3}\) cos θ = 1
(viii) cot θ + cosec θ = \(\sqrt{3}\)

Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.8 Additional Questions

Question 1.
Solve: 2 cos² θ + 3 sin θ = 0
Solution:
2 cos² θ + 3 sin θ = 0
⇒ 2 (1 – sin² θ) + 3 sin θ = 0
⇒ 2 – 2 sin² θ + 3 sin θ = 0
⇒ -2 sin² θ + 3 sin θ + 2 = 0
⇒ 2 sin² θ – 3 sin θ – 2 = 0
⇒ (2 sin θ + 1)(sin θ – 2) = 0

Question 2.
Solve: 2 tan θ – cot θ = -1
Solution:
2 tan θ – cot θ = -1

Question 3.
Solve: tan² θ + (1 – \(\sqrt{3}\)) = 0
Solution:

Question 4.
Solve: \(\sqrt{3}\) x + cos x = 2
Solution:

Question 5.

Solution: