You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.2
Question 1.
Write the first 6 terms of the sequences whose nth terms are given below and classify them as arithmetic progression, geometric progression, arithmetico-geometric progression, harmonic progression and none of them.
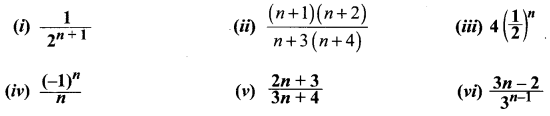
Solution:

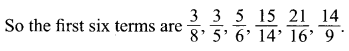
It is not a G.P. or A.P. or H.P. or A.G.P.

It is not an A.P. or G.P. or H.P. or A.G.P
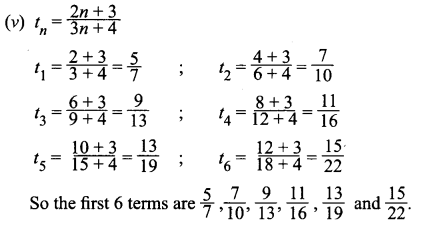
It is not an A.P. or G.P. or H.P. or A.G.P.

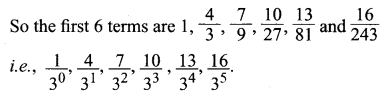
It is a A.G.P.
![]()
Question 2.
Write the first 6 terms of the sequences whose nth term an is given below.
![]()
Solution:
a1 = 1 + 1 = 2 ; a2 = 2
a3 = 3 + 1 = 4 ; a4 = 4
a5 = 5 + 1 = 6 ; a6 = 6
So, the first 6 terms are 2, 2, 4, 4, 6, 6
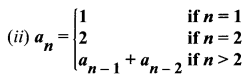
Solution:
a1 = 1 ; a2 = 2, a3 = 3
a4 = a3 + a2 + a1 = 3 + 2 + 1 = 6 ⇒ a4 = 6
a5 = a4 + a3 + a2 = 6 + 3 + 2 = 11 ⇒ a5 = 11
a6 = a5 + a4 + a3 = 11 + 6 + 3 = 20 ⇒ a6 = 20
So the first 6 terms are 1, 2, 3, 5, 8, 13.
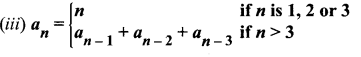
Solution:
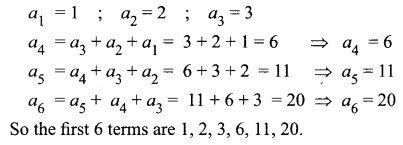
Question 3.
Write the nth term of the following sequences.
Solution:
(i) 2, 2, 4, 4, 6, 6……
Solution:
![]()
![]()
Solution:
Nr: 1, 2, 3, ……tn = n
Dr: 2, 3, 4, …..tn = n + 1
![]()
![]()
Solution:
Nr: 1, 3, 5, 7, . . .which is an A.P. a = 1, d = 3 – 1 = 2
tn = a + (n – 1)d
tn = 1 + (n – 1)2 = 1 + 2n – 2 = 2n – 1.
Dr : 2, 4, 6, 8, . . .
So the nth term is 2 + (n – 1)2 = 2 + 2n – 2 = 2n.
![]()
(iv) 6, 10, 4, 12, 2, 14, 0, 16, -2,….
Solution:
t1 = 6 ; t2 = 10
t3 = 4 ; t4 = 12
t5 = 2 ; t6 = 14
t7 = 0 ; t8 = 16
When n is odd, the sequence is 6, 4, 2, 0,…
(i.e.) a = 6 and d = 4 – 6 = -2.
So, tn = 6 + (n – 1)(-2) = 6 – 2n + 2 = 8 – 2n
When n is even, the sequence is 10, 12, 14, 16,…
Here a = 10 and d = 12 – 10 = 2
tn = 10 + (n – 1)2 = 10 + 2n – 2 = 2n + 8 (i.e.) 8 + 2n
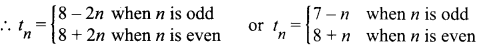
![]()
Question 4.
The product of three increasing numbers in GP is 5832. If we add 6 to the second number and 9 to the third number, then resulting numbers form an AP. Find the numbers in GP.
Solution:
The 3 numbers in a G.P. is taken as \(\frac{a}{r}\), a, ar
Their product is 5832.

6r2 + 6 = 13
6r2 – 13r + 6 = 0
(3r – 2)(2r – 3) = 0
r = 2/3 or 3/2

Question 5.
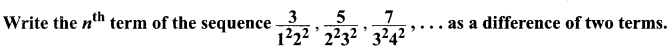
Solution:

Question 6.
If tk is the kth term of a G.P., then show that tn – k, tn, tn + k also form a GP for any positive integer k.
Solution:
Let a be the first term and r be the common ratio.
We are given tk = ark – 1
We have to Prove : tn – k, tn, tn + k form a G.P.

Question 7.
If a, b, c are in geometric progression, and if \(a^{\frac{1}{x}}=b^{\frac{1}{y}}=c^{\frac{1}{z}}\), then prove that x, y, z are in arithmetic progression.
Solution:
Given a, b, c are in G.P.
⇒ b2 = ac
⇒ log b2 = log ac
(i.e.) 2log b = log a + log c …(1)
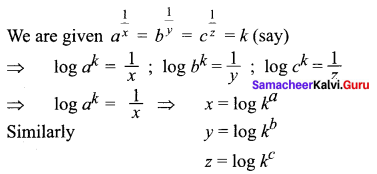
Substituting these values in equation (1) we get 2y = x + z ⇒ x, y z are in A.P.
![]()
Question 8.
The AM of two numbers exceeds their GM by 10 and HM by 16. Find the numbers.
Solution:
Let the two numbers be a and b.

So, (a + b – 20)2 = 4ab
(i.e.) (a + b)2 + 400 – 40(a + b) = 4ab
(a + b)2 – 4ab = 40(a + b) – 400
from(3) (a + b)2 – 4ab = 32(a + b)
⇒ 32(a + b) = 40(a + b) – 400
(÷ by 8) 4(a + b) = 5(a + b) – 50
4a + 4b = 5a + 5b – 50
a + b = 50
a = 50 – b
Substituting a = 50 – b in (3) we get
(50 – b – b)2 = 32(50)
(50 – 2b)2 = 32 × 50
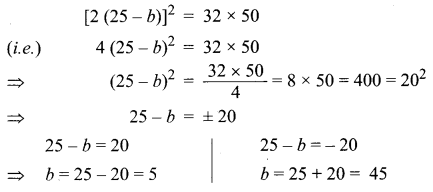
When b = 5, a = 50 – 5 = 45
When b = 45, a = 50 – 45 = 5
So the two numbers are 5 and 45.
Question 9.
If the roots of the equation (q – r)x2 + (r – p)x + p – q = 0 are equal, then show that p, q and r are in AP.
Solution:
The roots are equal ⇒ ∆ = 0
(i.e.) b2 – 4ac = 0
Hence, a = q – r ; b = r – p ; c = p – q
b2 – 4ac = 0
⇒ (r – p)2 – 4(q – r)(p – q) = 0
r2 + p2 – 2pr – 4[qr – q2 – pr + pq] = 0
r2 + p2 – 2pr – 4qr + 4q2 + 4pr – 4pq = 0
(i.e.) p2 + 4q2 + r2 – 4pq – 4qr + 2pr = 0
(i.e.) (p – 2q + r)2 = 0
⇒ p – 2q + r = 0
⇒ p + r = 2q
⇒ p, q, r are in A.P.
![]()
Question 10.
If a, b, c are respectively the pth, qth and rth terms of a G.P., show that (q – r) log a + (r – p) log b + (p – q) log c = 0.
Solution:
Let the G.P. be l, lk, lk2,…
We are given tp = a, tq = b, tr = c
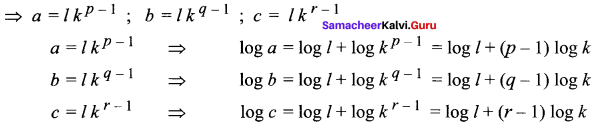
LHS = (q – r) log a + (r – p) log b + (p – q) log c
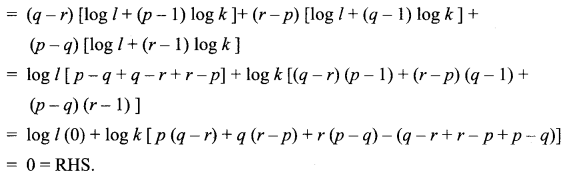
Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.2 Additional Questions Solved
Question 1.

Solution:
Here a1 = 1
Substituting n = 2, we obtain a2 = a1 + 2 = 1 + 2 = 3
Substituting n = 3, 4 and 5, we obtain respectively
a3 = a2 + 2 = 3 + 2 = 5, a4 = a3 + 2 = 5 + 2 = 7
a5 = a4 + 2 = 7 + 2 = 9
Thus, the first five terms are 1, 3, 5, 7 and 9.
Question 2.
Find the 18th and 25th term of the sequence defined by

Solution:
When n = 18 (even)
an = n(n + 2) = 18(18 + 2) = 18(20) = 360
When n = 25(odd)
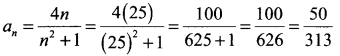
Question 3.
Write the first six terms of the sequences given by
(i) a1 = a2= 1 = an – 1 + an – 2 (n ≥ 3)
(ii) a1 = 4, an + 1 = 2nan
Solution:
(i) Here a1 = a2= 1 = an – 1 + an – 2 (n ≥ 3)
Putting n = 3, a3= a2 + a1 = 1 + 1 = 2
Putting n = 4, a4 = a3 + a2 = 2 + 1 = 3
Putting n = 5, a5 = a4 + a2 = 3 + 2 = 5
Putting n = 6, a6 = a5 + a4 = 5 + 3 = 8
∴ First six terms of the sequence are 1, 1, 2, 3, 5, 8
(ii) Here a1 = 4 and an + 1 = 2nan
Putting n = 1, a2 = 2 × 1 × a1 = 2 × 1 × 4 = 8
Putting n = 2, a3 = 2 × 2 × a2 = 4 × 8 = 32
Putting n = 3, a4 = 8 × 192 = 1536
Putting n = 4, a5 = 2 × 4 × a4 = 8 × 192 = 1536
Putting n = 5, a6 = 2 × 5 × a5 = 10 × 1536 = 15360
![]()
Question 4.
An A.P. consists of 21 terms. The sum of the three terms in the middle is 129 and of the last three is 237. Find the series.
Solution:
Let a1 be the first term and d, be the common difference. Here n = 21.
∴ The three middle terms are a10,a11, a12
Now, a10 + a11 + a12 = 129 [Given]
∴ (a1 + 9d) + (a1 + 10d) + (a1 + 11d) = 129
⇒ 3a1 + 30d = 129 ⇒ a1 + 10d = 43 ……(i)
The last three terms are a19, a20, a21
a19, a20, a21 = 237 [Given]
∴ (a1 + 18d)+(a1 + 19d) + (a1 + 20d) = 237
(i.e.,) 3a1 + 57d = 237 ⇒ a1 + 19d = 79 … (2)
Subtracting (i) from (ii), we get 9d = 36, ⇒ d = 4
∴ From (i), a1 + 40 = 43 ⇒ a1 = 3
Hence, the series is 3, 7, 11, 15 …….
Question 5.
Prove that the product of the 2nd and 3rd terms of an arithmetic progression exceeds the product of the first and fourth by twice the square of the difference between the 1st and 2nd.
Solution:
Let ‘a’ be the first term and ‘d’ be the common difference of A.P.
Then, a1 = a, a2 = a + (2 – 1)d = a + d
a3 = a + (3 – 1)d = a + 2d, a4 = a + (4 – 1)d = a + 3d
We have to show that a2.a3 – a1.a4 = 2(a2 – a1)2
LHS = a2.a3 – a1.a4 = (a + d)(a + 2d) – a(a + 3d)
= a2 + 3ad + 2d2 – a2 – 3ad = 2d2
RHS = 2(a2 – a1)2 = 2d2
Since LHS = RHS. Hence proved.
Question 6.
If the pth, qth and rth terms of an A.P. are a, b, c respectively, prove that a(q – r) + b (r – p) + c(p – q) = 0.
Solution:
Let A be the first term and D be the common difference of A.P.
ap = a, ∴ A + (p – 1)D = a ….. (1)
aq = b, ∴ A + (q – 1)D = b ……. (2)
ar = c, ∴ A + (r – 1)D = c …….. (3)
∴ a (q – r) + b (r – p) + c (p – q) = [A + (p – l) D] (q – r) + [A + (q – 1) D]
(r – p) + [A + (r – 1) D] (p – q) [Using (1), (2) and (3)]
= (q – r + r – p + p – q)A + [(p – l)(q – r) + (q – l)(r – p) + (r – l)(p – q)]D
= (0) A + (pq – pr – q + r + qr – pq – r + p + pr – p – qr + q)D
= (0)A + (0)D = 0.
Question 7.
If a, b, c are in A.P. and p is the A.M. between a and b and q is the A.M. between b and c, show that b is the A.M. between p and q.
Solution:
a, b, c are in A.P.
2b = a + c …… (1)
p is the A.M. between a and b
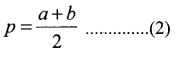
q is the A.M. between b and c
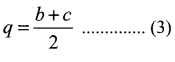
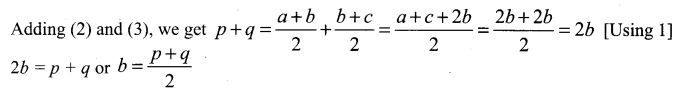
Hence, b is the A.M. between p and q
![]()
Question 8.
If x, y, z be respectively the pth, qth and rth terms of a G.P. show that xq – r, yr – p ,zp – q = 1
Solution:
Let A be the first term and R be the common ratio of G.P.
ap = x ⇒ x = ARp – 1 ……… (1)
aq = y ⇒ x = ARq – 1 ……… (2)
ar = z ⇒ x = ARr – 1 ……… (3)
Raising (1), (2), (3) to the powers q – r, r – p, p – q respectively, we get

Multiplying (4), (5) and (6), we get
![]()
Hence, xq – r, yr – p, zp – q = 1