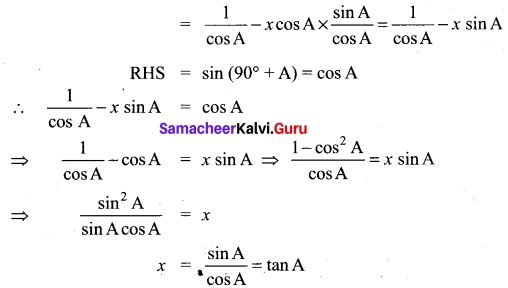
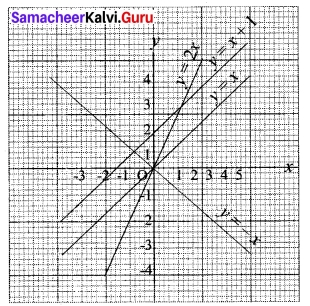
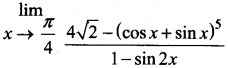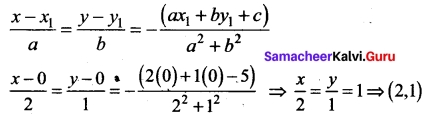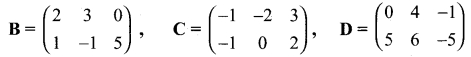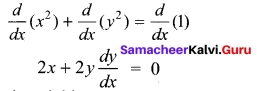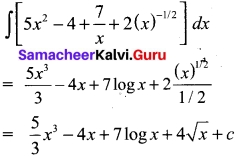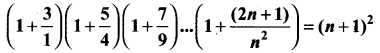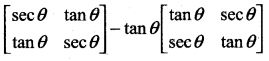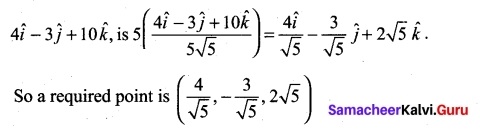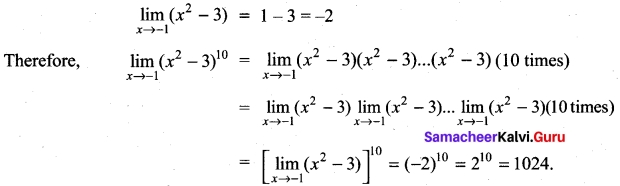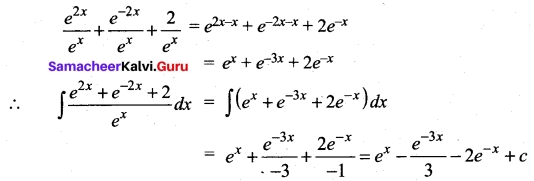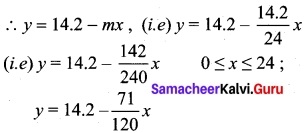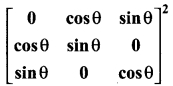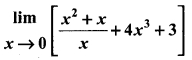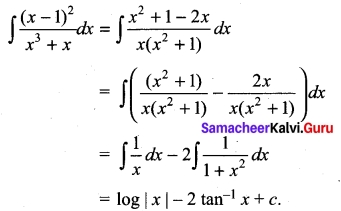Students can Download Tamil Nadu 11th English Previous Year Question Paper March 2019 Pdf, Tamil Nadu 11th English Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 11th English Previous Year Question Paper March 2019
Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- questions of Part I, II. III and IV are to be attempted separately
- Question numbers 1 to 20 in Part I are objective type questions of one -mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
- Question numbers 21 to 30 in Part II are two-marks questions. These are to be answered in about one or two sentences.
- Question numbers 31 to 40 in Parr III are three-marks questions, These are to be answered in about three to five short sentences.
- Question numbers 41 to 47 in Part IV are five-marks questions. These are to be answered) in detail. Draw diagrams wherever necessary.
Time: 3.00 Hours
Maximum Marks: 90
PART – I
I. Answer all the questions. [20 x 1 = 20]
Choose the correct synonym for the underlined words from the options given.
Question 1.
……….. and I do claim to represent him in all his ruggedness.
(a) toughness
(b) weakness
(c) brightness
(d) seriousness
Answer:
(a) toughness
Question 2.
The greatest disadvantage for me was my loss of appetite.
(a) hope
(b) memory
(c) alertness
(d) hunger
Answer:
(d) hunger
![]()
Question 3.
………..that we regard a man who does not possess it as eccentric.
(a) modem
(b) weary
(c) normal
(d) weird
Answer:
(d) weird
Choose the correct antonym for the underlined words from the options given.
Question 4.
Her happiest moments were with her sparrows whom she fed with frivolous rebukes,
(a) serious
(b) harmless
(c) funny
(d) decent
Answer:
(a) serious
Question 5.
“Don’t look so doleful, girls.”
(a) peaceful
(b) joyful
(c) doubtful
(d) powerful
Answer:
(b) joyful
Question 6.
There are, it must be admitted, some matters…………
(a) replied
(b) denied
(c) argued
(d) accepted
Answer:
(b) denied
Question 7.
Select the correct expansion of “HDTV”.
(a) High definition Television
(b) Heavy Dielectric Television
(c) Heavy Distributory Television
(d) Highly Decentralized Television
Answer:
(a) High definition Television
Question 8.
Choose the suitable option to pair it with the word “mantel” to form a compound word,
(a) cover
(b) cloth
(c) picture
(d) piece
Answer:
(d) piece
Question 9.
Form a derivative by adding the right suffix to the word ‘regular’.
(a) -ance
(b) -able
(c) -fill
(d) -ity
Answer:
(d) -ity
Question 10.
Choose the meaning of the foreign word in the sentence.
Nalini is a bonafide student of the Madras University.
(a) confident
(b) punctual
(c) brilliant
(d) genuine
Answer:
(d) genuine
Question 11.
Choose the right definition for the given term “Photophobia”.
(a) Fear of rain
(b) Fear of flight
(c) Fear of light
(d) Fear of pictures
Answer:
(c) Fear of light
![]()
Question 12.
Add a suitable question tag to the following sentence.
Many women candidates attended the interview, …………?
(a) haven’t they
(b) shouldn’t they
(c) don’t they
(d) didn’t they
Answer:
(d) didn’t they
Question 13.
Replace the underlined word with a phrasal verb.
I couldn’t understand what you meant.
(a) break out
(b) find out
(c) iron out
(d) figure out
Answer:
(d) figure out
Question 14.
Add a suitable prefix to the root word “Polite”.
(a) im-
(b) non-
(c) un-
(d) anti-
Answer:
(a) im-
Question 15.
One who studies the human mind and behaviour is called a ………..
(a) physicist
(b) psychologist
(c) pathologist
(d) physiologist
Answer:
(b) psychologist
Question 16.
Fill in the blank with the suitable preposition.
The angry champion broke the crystal cup ……….. million pieces.
(a) into
(b) with
(c) against
(d) upon
Answer:
(a) into
Question 17.
Choose the clipped form of the word “dormitory”.
(a) dormy
(b) dory
(c) dorm
(d) dormit
Answer:
(c) dorm
Question 18.
Substitute the underlined word with the appropriate polite alternative.
The gentleman in the black suit is a barber.
(a) hair clipper
(b) hair remover
(c) Mir splitter
(d) hair dresser
Answer:
(d) hair dresser
Question 19.
Substitute the phrasal verb in the sentence with a single word.
Never put off Until tomorrow what you can do today.
(a) continue
(b) finish
(c) halt
(d) postpone
Answer:
(d) postpone
Question 20.
Fill in the blank with a suitable relative pronoun.
The books………….are brought are often not read.
(а) that
(b) what
(c) who
(d) whose
Answer:
(а) that
![]()
PART – II
II. Answer any seven of the following: [7 x 2 = 14]
(i) Read the following sets of poetic lines and answer any four of the following. [4 × 2 = 8]
Question 21.
“Feel at home,” “come again.
They say………”
(a) Who are ‘they’?
(b) Do ‘they’ really mean it?
Answer:
(a) They are modem people.
(b) No they don’t mean it.
Question 22.
“And reassure myself anew
That you are not me and I’m not you.”
(a) Who does the poet refer to as “you”?
(b) What does the poet reassure?
Answer:
(a) The athletes who play games and sweat for fun and money are referred as ‘you’.
(b) The poet reassures himself that he is not one of the athletes and the athletes are not in his group either. So, he is safe.
Question 23.
“I heard a thousand blended notes While in a grove I sate reclined,”
(a) What is meant by “a thousand blended notes”?
(b) Where is the poet sitting?
Answer:
(a) The thousand blended notes mean the combined music of birds which cohabit in the grove.
(b) The poet is sitting in a grove.
Question 24.
“He sways his head from side to side,
with movements like a snake;”
(a) Who is ‘he’?
(b) Mention the figure of speech used here.
Answer:
(a) He is Macavity.
(b) Simile
Question 25.
“In dignity and pride no one need to be poor.”
(a) What are the two things mentioned here as our strength?
(b) Is the tone of the line positive or negative?
Answer:
(a) Dignity and pride are the two things mentioned as strength here.
(b) The tone of the line is positive.
Question 26.
“For you have but mistook me all this while…..”
(a) How is the speaker mistaken by the people?
(b) Write the words in alliteration.
Answer:
(a) People mistook the speaker to be a person endowed with divine right to rule them. He was after all like them with similar wants, likes, dislikes and grief. He too needs comfort of friends.
(b) Mistook and me alliterate.
(ii) Do as directed (any three) [3 x 2 = 6]
Question 27.
Report the following dialogue:
Conductor : Where do you want to go?
Passenger : I’m going to Coimbatore. Give me a ticket, please.
Answer:
The conductor asked the passenger where he was going. The passenger replied that he was going to Coimbatore and requested for a ticket.
Question 28.
Tom didn’t know Spanish. He didn’t get the job. (Combine using ‘if’).
Answer:
If Tom had known Spanish, he would have got the job.
(or)
If Tom didn’t know Spanish, he wouldn’t have got the job.
![]()
Question 29.
Rewrite the sentence making an inversion in the conditional clause.
If you were a King, you would know the difficulties.
Answer:
Were you a king you would know the difficulties.
Question 30.
The food was cheap. It was very tasty, (form a simple sentence using in spite of)
Answer:
In spite of the food being cheap it was also very tasty.
PART – III
III. Answer any seven of the following: [7 × 3 = 21]
(i) Explain any two of the following with Reference to the Context: [2 × 3 = 6]
Question 31.
“The birds around me hopp’d and play’d;
Their thoughts I cannot measure.”
Answer:
Reference: These lines are from the poem, “Lines Written in Early Spring” written by William Wordsworth.
Context: The poet was quite impressed with the beauty and peace that prevailed in the woodland. The birds were oblivious to the presence of the poet. They hopped and chirped around him in absolute bliss. The poet said these words while trying to fathom their thoughts.
Explanation: The poet was overwhelmed with delight in the company of birds, plant kingdom and the brook. He tried hard to understand the thoughts of the birds through the bird’s language. But he couldn’t succeed. He simply inferred that they were thrilled and enjoying the jocund company.
Question 32.
“How can you say to me, lam a king?”
Answer:
Reference: This lines is from the poem, “The Hollow Crown” by William Shakespeare. The ‘ poem is an excerpt from the play “Richard II”.
Context: King Richard II says these words to his loyal nobles when he talks about the power of death over monarchs.
Explanation: British subjects usually believe that a king is born with a divine right to rule. People respect his crown as a symbol of great power. After he is deposed from power, Henry II realizes the bitter truth that he is no way different from ordinary subjects. He also has wants, need for friends and the compulsion to taste grief. Nobody can escape death.
Question 33.
“I am just glad as glad can be
That I am not them, that they are not me…”
Answer:
Reference: The poet Ogden Nash says these words in the poem “Confession of a Bom Spectator’.
Context and Explanation: While discussing about the athletes he admires, the poet says these words. Right from his boyhood, he had seen boys aspire for sports championships. He had wondered at their ability to specialize in horse riding, to play hockey or basketball. He had seen young ones trying to play center in the football or be a tackle or offender in a game like kabaddi. But he has been absolutely glad that he is not them and they are not him.
(ii) Answer any two of the following questions briefly: [2 × 3 = 6]
Question 34.
How do the chemists make fortunes out of the medicines people forget to take?
Answer:
Similar to the author, many remember to forget medicine as soon as the appointed time arrives. The forgotten medicines tend to aggravate the illness. As a vicious cycle, again they are forced to buy costlier medicines. Thus people who forget to take medicines contribute to the fortunes of chemists.
Question 35.
Why did Mary Kom think that she should not return empty-handed?
Answer:
Mary Kom’s dad had given all he had for her trip to USA. Besides, her friends had raised funds through MPs. They had pinned their hopes on her. So, she thought she should not return empty handed.
![]()
Question 36.
What is the difference between a physical and mental tight corner?
Answer:
Physical tight comers are those situations which threaten the life of an individual. Mental tight comers are worries for which no solution is in sight. It upsets the individuals and confounds them.
(ii) Answer any three of the following questions briefly: [3 × 3 = 9]
Question 37.
Study the pie-chart and answer the questions that follow:
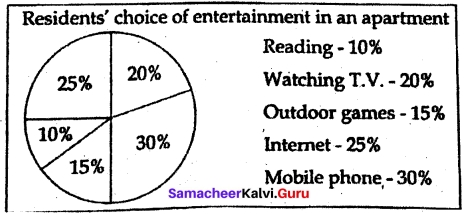
Questions:
(A) What is the most sought after entertainment activity in the apartment?
(B) Name the activity preferred by the least number of people.
(C) Which activity is chosen by half the number of people who use mobile phones?
Answer:
(A) Mobile phone is the most sought after entertainment activity in the apartment.
(B) Reading is preferred by the least number of people.
(C) Outdoor games is chosen by half the number of people who use mobile phones.
Question 38.
Build a dialogue of minimum three exchanges between a fruit vendor and a customer.
Answer:
Fruit Vendor : What fruits do you want to buy sir?
Customer : I would like to buy 1 Kg of Pineapple.
Fruit Vendor : Good choice sir. It is the right season. Anything else?
Customer : Yes. The fruits look so fresh. I would also like to buy some Kiwis and a dozen of bananas.
Fruit Vendor : Sure sir. Here is the bill.
Customer : Oh! It’s Rs. 250? No seasonal discount?
Fruit Vendor : This is the discounted price sir.
Customer : Okay. Thank you.
Question 39.
Describe the process of opening a bank account.
Answer:
- Go to the bank and get an application form from the counter.
- Fill in the details accurately in the mandatory fields.
- Affix your passport-size photograph on the form.
- Attach your address proof and the adhaar card photocopy.
- Obtain the signature of an introducer.
- Fill in the chalan and hand it over to the bank employee with initial amount.
- You will receive the bank passbook with the details of your newly created account details with the bank seal on the first page.
Question 40.
Complete the proverbs using the words given below.
(a) Waste not, ……… not. (fight, want, earn)
(b) ………….. waters run deep, (still, flowing, stagnant)
(c) One ……….. doesn’t make a garland, (pearl, bead, flower)
Answer:
(a) want
(b) Still
(c) flower
PART – IV
IV. Answer the following: [7 × 5 = 35]
Question 41.
What does Robert Lynd try to convey in his essay on ‘Forgetting’.
Answer:
Forgetting is deemed by many people leading prosaic lives as a mistake or an inefficiency of mind. But in reality, forgetfulness is freedom. Osho is right in his opinion of forgetfulness. In fact, it liberates painful memories and unpleasant things. We need to “let go” painful memories of the past and be free to aspire for better things in life. Robert Frost in his poem, “Let go” talks about mediocre person’s inability to let go things that hurt them. The capacity to. forget hurtful memories is a real blessing.
If human mind does not have the capacity to forget, life would be miserable for every one of us. Human mind is such a wonderful machine that it retains what is most important for personal or professional growth and allows the other things to slip away from the bank of memory. But young ones should remember to remember important assignments, deadlines for submission of homework, examination time-tables and hall tickets before leaving for examination. Td assist memory, we can have a checklist before leaving for the school. It is often said, “If you fail to plan, you plan to fail.” So students must love whatever work they do. The brain retains in memory whatever one does with great passion, love and involvement.
For a successful life, a strong memory is indispensable. So, one must cultivate a strong memory. However, one may forget failures, betrayals and hurts to grow into a happy and healthy person.
![]()
[OR]
How do Universities mould students apart from imparting academic education to them?
Answer:
Universities mould students by providing various opportunities to develop their soft skills and to develop values which would contribute to the process of nation building. They enable graduates to develop patience and perseverance. They help them develop faith in their own inherent ability to shoulder responsibilities. They are oriented to become citizens of democracy and repay to the society quality services which would reform the lives of the poor people.
They develop true spirit of democracy among young graduates. They enable appreciation of others point of view. The graduates are also provided opportunities to adjust with difference through amicable discussions. The universities, apart from imparting education mould the students’character and personality too.
Question 42.
Write an appreciation of the poem “The Hollow Crown”.
Answer:
Shakespeare portrays the fleeting nature of human glory. King Richard II, on the verge of surrender to his rebellious cousin Boling broke, talks about the nature of temporal power and death. He talks about graves, epitaphs and worms. He explains how even monarchs leave nothing behind as their own except a small patch of land in which they are buried. The dejected king talks on various ways kings get killed. Some are slain in the battle field, some poisoned to death by their own spouses.
The kings who believed their bodies to be impregnable brass are shattered by just a pinprick. In fact, death is in supreme command which waits for the king, and only allows the king to act as if he were ruling and in control of everything. He chides his loyal friends who still believe that he is a monarch and tells them that he is an ordinary mortal just like them. He is humbled as he is powerless before the impending death.
[OR]
How does Gabriel Okara criticise the modern life in his poem “Once Upon a Time”?
Answer:
The poet’s understanding of adult society is extremely negative. The poet distinctly portrays how people in modem times have become hypocrites and fake emotions to be socially accepted. The phrases of hospitality they use “feel at home” and “come again” are so fake that a third visit would be disallowed by the hosts. In modem times, people don’t value real emotions instead they value positions and possessions.
Even while shaking hands, they try to assess the material worth of a person. People don’t laugh with heart. Their ice-cold block eyes search the person they talk to. Most of them have acquired the skill of wearing a standard, deceitful, artificial smile on all occasions, i.e., “portrait smile”. Thus the poem is nothing but a criticism of modem life.
Question 43.
Write a paragraph (150 words) by developing the following hints.
Miss Meadows, a music teacher – gets a letter – feels upset – Fiance not interested,- reflects her gloom on students – changes the happy song to a sad one – Headmistress calls – delivers a telegram – Fiance agrees to wedding – Meadows happy – changes the song again to a cheerful one.
Answer:
Miss Meadow was heart-broken. The letter written by Basil had pierced her heart and she was bleeding. Her hatred and anger became a knife and she carried it with her. Her icy cold response to Science Mistress demonstrates it. She is least bothered about the tender feelings of young children who look at her face all time for a friendly nod or smile of approval.
Her favourite pupil Mary Beazley is baffled at her treatment of the chrysanthemum she had brought with so much love. The choice of the song “A lament” perfectly jells well with her worst mood. She is in fact in her heart lamenting over the loss of love, trust and future hopes. She is unnecessarily severe with young children forcing them to redo the singing which drives them to despair, pain and tears they manage to stifle.
After she receives the telegram from Basil apologizing for his insane letter, her mood changes to joy. She takes the chrysanthemum and keeps it close to her lips to conceal her blush. She goads the children to sing a song of joy congratulating someone for success. She persuades them to show warmth in their voices. Her warm and lively voice dominates the tremulous voices of the young ones. The young ones now realize that Miss Meadow who was in a wax earlier is now in her elements.
![]()
[OR]
Leacock goes to a studio – The photographer dislikes Leacock’s face – passes several comments – Leacock gets irritated the photo – taken – wants to see the proof – visits the studio again – The photo is edited – help of technology – Leacock upset over the changes – calls it worthless – leaves in anger.
Answer:
‘With the Photographer’ by Stephen Leacock is narrated in the first person. The narrator while sitting in the photographer’s studio begins to read some magazines and sees how other people look and the narrator begins to feel insecure about his appearance.
It is also noticeable that the photographer takes a dislike to his face judging it to be wrong. What should have been a simple process of taking a photograph becomes something of a nightmare for the narrator. How confident the narrator becomes is noticeable when he returns to the photographer’s studio the following Saturday.
He realises that the photograph that has been taken of him looks nothing like him. This angers the narrator as he was simply looking for a photograph that would show his likeness. He accepts that he may not be to everybody’s liking when it comes to his physical appearance but is angered by the changes made.
The photographer has retouched the photograph so much that the narrator does not recognise himself. The end of the story is also interesting as the reader realises that it is just a worthless bauble when he begins to cry. He has been judged solely by his appearance by the photographer whose job was to simply take a life like photograph.
Question 44.
Write a summary or Make notes of the following passage.
Answer:
The Chinese were the first to make gunpowder, invent the magnetic compass and gave to the world the art of making paper. About 2000 years ago the Chinese made gunpowder by mixing sulphur and saltpetre. The mixture exploded when set on fire. The Chinese were the first to find out the fact that a narrow magnet floating in a bowl of water would always point to the north. The discovery led to the invention of magnetic compass. This device helped the sailors to find out the direction when they were out of sight of land.
The Chinese also invented the art of making paper using vegetable pulp reached Arabia, Spain and Europe. In course of time paper factories came into existence. The fourth invention of the Chinese was the art of printing. Before this invention books were written by hand. The Chinese invented the art of printing with movable types. With this invention reading and learning became open to. ordinary people as they were able to print books in large numbers.
Summary:
No. of words given in the original passage: 171
No. of words to be written in the summary: 171/3 = 57 ± 5
Rough Draft
were the first to make gun powders, to invent the magnetic compass, paper \and printing. TheyTnadeJhegun powder by mixing sulphur with salt. The mixture exploded When set on fire. They foundlEaTa^naiiowmagnet floating in a bowl of water would always p|oint to die North. This led to the inventimToflnagaeticcompass. With this the sailors found tfteir direction. Explorers used this for their discoveries/TESyTeutid^the art of making paper using vegetable pulp. As a result factories came into existence. The inventron-oijnjnting led to tpe printing of books in large numbers.
Fair Draft:
The Great Inventions of China
The Chinese made gun powder mixing sulphur and saltpetre. They invented magnetic compass and paper. They enabled great explorers like Magellan, Vasco da Gama and Columbus discovered new lands by their invention the Mariner’s compass. They made papers from vegetable pulp and soon many factories started producing it. The greatest contribution of China to’he world is her invention of printing press which revolutionized printing of books. No. of words in the summary: 68
![]()
[OR]
Notes
Title: The Great Inventions of China
Answer:
1. Chinese Inventions – (a) gun powder, (b) magnetic compass, (c) paper, (d) printing
2. (a) Gun powder from sulphur and saltpeter – explosive.
(b) Magnetic powder – finding direction – great explorers used in discovery of lands.
(c) Paper from vegetable pulp – paper industry.
(d) Art of printing – books available to ordinary people.
Question 45.
Read the following advertisement and prepare a Bio-data considering yourself fulfilling the conditions mentioned.
(Write XXXX for name and YYYY for address.)
WANTED:
Qualified nurses for a multi-speciality hospital, Attractive salary, Flexible working hours, Age below 30
Apply to-
Post Box No : 3210,
The Times of India,
Chennai – 600 002.
Answer:
14th January, 2020
From
XXXX
YYYY
To
Post Box No : 3210
C/o. The Times of India
Chennai – 02.
Respected Sir/Madam,
Sub: Application for the post of a Senior Nurse.
With reference to your advertisement dated 12th December 2018,1 hereby wish to apply for the post of a senior nurse in your multi-speciality hospital. I have rich experience and can communicate well with a pleasing personality.
If given an opportunity, I will do my best in taking care of the patient needs.
Please find enclosed my resume for your kind perusal. Looking forward to a positive reply.
Yours sincerely,
XXXX
Address on the Envelope
To
Post Box No : 3210
C/o. The Times of India
Chennai – 02
Bio-data:
Name : XXXX
Date of Birth : 18th May, 1994
Marital Status : Married
Father’s Name : Mr. Rajan
Address For Communication : YYYY
Contact Number – Mobile : 9998777655
Residence : 22345576
Mother Tongue : Tamil
Language Known : Hindi, English and Tamil
Educational Background:
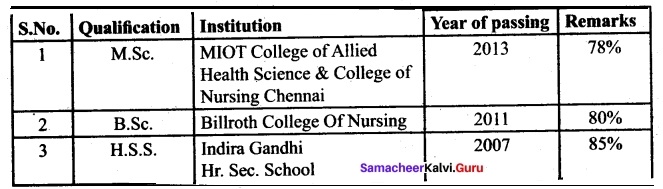
Professional Experience:

Hobbies : Reading, Music.
Expected Salary : 35,000/ per month
Salary Drawn : 28,000/ per month
Reference : 1. Dr. Ram (Dean, MIOT Hospital 9998887777
2. Dr. Yashodha (ICU in-charge) 9900000222
Declaration
I hereby declare that the above given information is true to my knowledge.
Station : YYY
Date : 14.01.2020
XXXX
Signature of the Applicant
![]()
[OR]
Write a paragraph of 150 words on “The Advantages and Disadvantages of Online Shopping”.
Answer:
The Advantages and Disadvantages of Online Shopping:
Due to rapid growth of technology, transformation in buying and selling has taken place. Sellers use internet as a main vehicle to conduct commercial transactions. But, like every coin has two sides, online shopping has got its own advantages and disadvantages.
Advantages:
- The biggest advantage is convenience. Online shops give us the opportunity to shop 24/7 without being held up in crowd or standing in queue for billing.
- As we receive products directly from the manufacturers the prices are lower.
- The choices are unlimited in almost all brands that one looks for.
- Out of stock products also can be booked which will be sent to us when available.
- Sending gifts to the persons we desire has become easier.
- One can analyse the consumer reviews before purchasing the products.
Disadvantages:
- Online shopping may lead one to spend too much time online. Also, one may end up buying unwanted things.
- Sometimes the products that you receive may not be the one you ordered or it can be of low quality. There is no guarantee that you are receiving the original product.
- Returning the product may be problematic.
- There’s a larger risk of: credit card scams, hacking, phishing, counterfeit products, identity theft, bogus websites, and other scams.
- Local retailers are affected which brings down the country’s economy.
Question 46.
(i) Read the following sentences, spot the errors and rewrite the sentence correctly.
(a) The colour of the curtains are very bright.
(b) I saw an uniformed soldier behind the wall.
(c) Nobody knows why was he killed.
(d) My older brother is living abroad.
(e) They are discussing about their picnic.
Answer:
(a) The colour of the curtains is very bright.
(b) I saw a uniformed soldier behind the wall.
(c) Nobody knows why he was killed.
id) My older brother lives abroad.
(e) They are discussing their picnic.
[OR]
(ii) Fill in the blanks suitably
(a) Have you ever…………such a beautiful ……… (scene/seen)
(b) How ………. you disobey my words? (use a quasi modal verb)
(c) What is done ………… not be undone, (use a modal verb)
(d) Take an umbrella with you ……….. you will get wet (use a suitable link word)
Answer:
(a) seen, scene
(b) dare
(c) can
(d) or else
Question 47.
Identify each of the following sentences with the given fields given below:
(a) In a democracy, we have the right to criticise anyone.
(ft) The price of the vegetable shot up suddenly.
(c) The passenger sat down to check his e-mails.
(d) It was a thrilling neck and neck finish.
(e) The programme will be telecast next week.
(Commerce, Sports, Literature, Computer, Politics, Media, Agriculture)
Answer:
(a) Politics
(b) Commerce
(c) Computer
(d) Sports
(e) Media
![]()
[OR]
Read the following passage and answer the questions that follow:
After the meal, the way we place our eating tools, our knives, forks, spoons or chopsticks is also culturally defined. In Australia, when we have finished eating the main course, we put the knife and fork across the middle of the plate parallel to each other with the handles facing towards us.
When we are resting during the meal, we place the knife and fork across each other in the middle of the plate. In China, the chopsticks go crossways across the top of the plate with the handles facing towards the right. In Indonesia, some people place the fork and spoon like the Australians do but not all. Indonesia is a multi-cultural society, so there may be a number of customs practised within the country.
Questions:
(a) Which table manners reveals one’s culture?
(b) Is table manners important? Why?
(c) What do you know about the table manners observed by the Australians?
(d) How do the Chinese practise their table manners?
(e) Explain the Indonesian culture.
Answer:
(a) After the meal, the way we place our eating tools, our knives, forks, spoons or chopsticks is culturally defined.
(b) Yes, because it ensures comfort of both the guests and hosts at the table.
(c) In Australia, when people have finished eating the main course, they put the knife and fork across the middle of the plate parallel to each other with the handles facing towards them. When they are resting during the meal, they place the knife and fork across each other in the middle of the plate.
(d) In China, the chopsticks go crossways across the top of the plate with the handles facing towards the right.
(e) Indonesia is a multi-cultural society, so there may be a number of customs practised within the country.







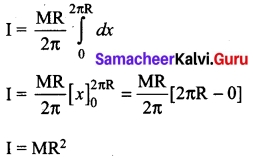

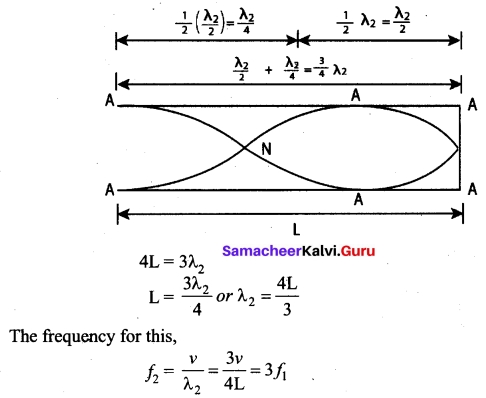
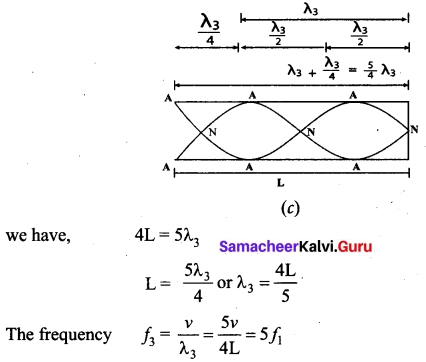
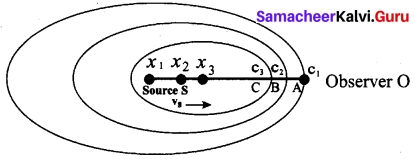
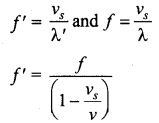
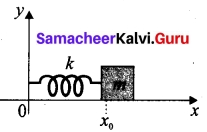
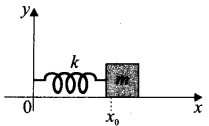
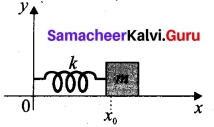


 is discontinuous at ………..
is discontinuous at ……….. + …..∞ then \(\frac{dx}{dy}\) =……..
+ …..∞ then \(\frac{dx}{dy}\) =……..














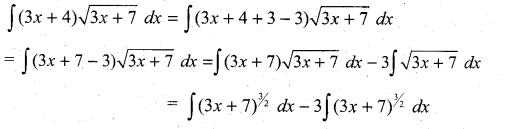
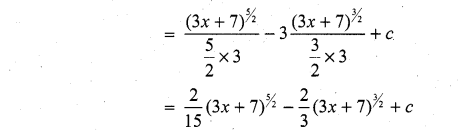
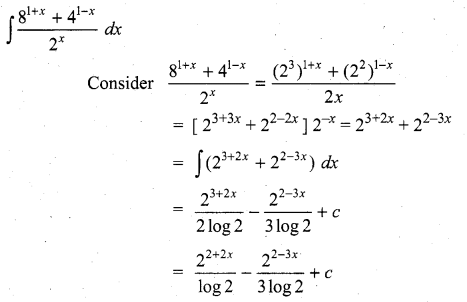

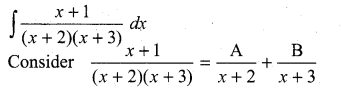
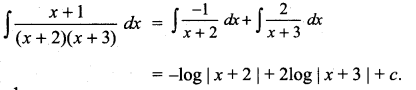


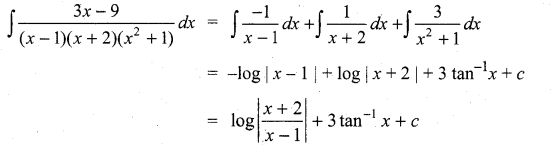
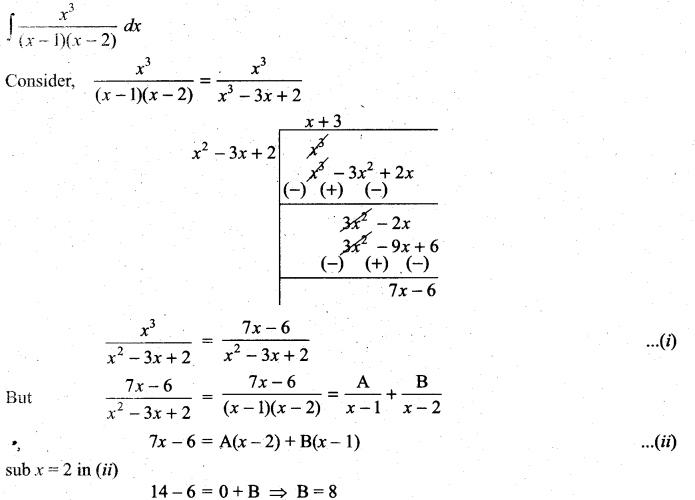
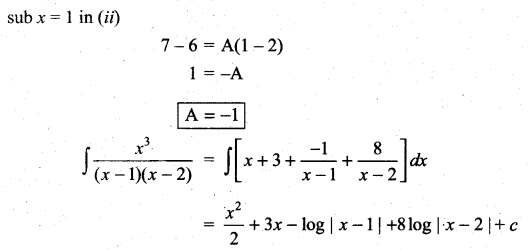


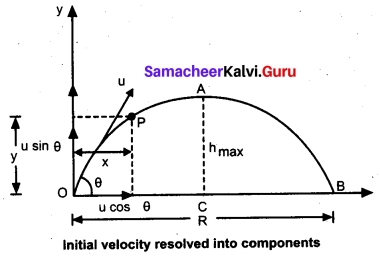
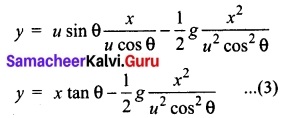
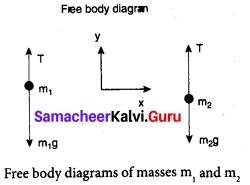
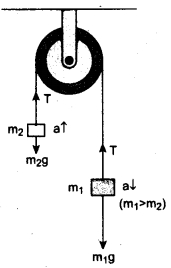




 is ……….
is ……….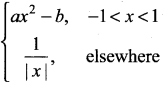 is differentiable at x = 1, then………
is differentiable at x = 1, then………