Students can Download Tamil Nadu 11th Physics Model Question Paper 2 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 11th Physics Model Question Paper 2 English Medium
![]()
Instructions:
- The question paper comprises of four parts
- You are to attempt all the parts. An internal choice of questions is provided wherever: applicable
- All questions of Part I, II, III, and IV are to be attempted separately
- Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
- Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
- Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
- Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Max Marks: 70
PART – I
Answer all the questions. [15 × 1 = 15]
Question 1.
The direction of the angular velocity vector is along…………
(a) the tangent to the circular path
(b) the inward radius
(c) the outward radius
(d) the axis of rotation
Answer:
(d) the axis of rotation
![]()
Question 2.
The angle between two vectors 2\(\hat{i}\) + 3\(\hat{j}\) + \(\hat{k}\) and -3\(\hat{j}\) + 6\(\hat{k}\) is………..
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Answer:
(d) 90°
Question 3.
The breaking stress of a wire depends on………….
(a) length of a wire
(b) nature of the wire
(c) diameter of the wire
(d) shape of the cross section
Answer:
(b) nature of the wire
Question 4.
The moment of inertia of a rigid body depends upon…………….
(a) distribution of mass from axis of rotation
(b) angular velocity of the body
(c) angular acceleration of the body
(d) mass of the body
Answer:
(a) distribution of mass from axis of rotation
Question 5.
The stress versus strain graphs for wires of two materials A and B are as shown in the graph.If YA and YB are the young’s moduli of the materials then……….
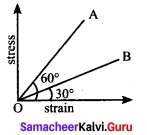
(a) YB = 2YA
(b) YA = YB
(c) YB = 3YA
(d) YA = 3YB
Answer:
(d) YA = 3YB
Hint:
Slope of stress strain curve gives the young’s modules YA = tan 60° = √3 ; YB = tan 30° \(\frac{1}{√3}\)
\(\frac{Y_A}{Y_B}\) = \(\frac{√3}{\frac{1}{√3}}\) = 3 ⇒ YA = 3YB
Question 6.
The ratio of the velocities of two particles as shown in figure is…………
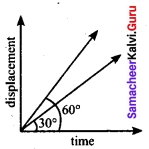
(a) 1 : √3
(b) √3 : 1
(c) 1 : 3
(d) 3 : 1
Answer:
(c) 1 : 3
Hint:
Velocity = Slope of the line formed in displacement v/s time graph = Tan θ
Va : Vb = Tan θA : Tan θB
= Tan 30° : Tan 60°
Va : Vb = 1 : 3
Question 7
The load-elongation graph of three wires of the same material are shown. Which of the following wire is the thickest?
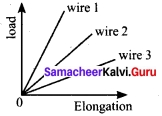
(a) wire 1
(b) wire 2
(c) wires
(d) all of them have same thickness
Answer:
(a) wire 1
Hint:
Wire 1 is the thickness compared to other wires. Because the elongation of the wire 1 is minimum.
Question 8.
The waves produced by a motor boat sailing in water.are………
(a) transverse
(b) longitudinal
(c) longitudinal and transverse
(d) stationary
Answer:
(c) longitudinal and transverse
Question 9.
A sound wave whose frequency is 5000 Hz travels in air and then hits the water surface. Theratio of its wavelengths in water surface. The ratio of its wavelengths in water and air is………….
(a) 4.30
(b) 0.23
(c) 5.30
(d) 1.23
Answer:
(a) 4.30
Hint:
f = 5000 Hz ; Va = 343 ms-1; Vb = 1480 ms-1
Ratio of wavelength \(\frac{λ_a}{λ_w}\) = \(\frac{V_w}{f}\) × \(\frac{f}{V_a}\) = \(\frac{1480}{343}\) = 4.31
Question 10.
The wavelength of two sine waves and λ1 = 1 m and λ2 = 6 m, the corresponding wave numbers are respectively…………
(a) 1.05 rad m-1 and 6.28 rad m-1
(b) 6.28 rad m-1 and 1.05 rad m-1
(c) 1 rad m-1 and 0.1666 rad m-1
(d) 0.166 rad m-1 and 1 rad m-1
Answer:
(b) 6.28 rad m-1 and 1.05 rad m-1
Hint:
Standard wave equation, Y = A sin (kx – ωt)
K1 = \(\frac{2π}{λ_1}\) = \(\frac{2π}{1}\) = 6.28 rad m-1
K2 = \(\frac{2π}{λ_2}\) = \(\frac{2π}{6}\) = 1.05 rad m-1
Question 11.
During an adiabatic process, the pressure of a gas is proportional to the cube of its absolute temperature. The value of \(\frac{C_p}{C_r}\) for that gas is ………..
(a) \(\frac{3}{5}\)
(b) \(\frac{4}{3}\)
(c) \(\frac{5}{3}\)
(d) \(\frac{3}{2}\)
Answer:
(b) \(\frac{4}{3}\)
Hint:
PT = \(\frac{γ}{1-γ}\) = constant …….(1)
PT-3 = constant ……….(2)
From equation (1) and (2) \(\frac{γ}{1-γ}\) = (-3)
∴ γ = \(\frac{3}{2}\)
![]()
Question 12.
If the rms speed of the molecules of a gas is 1000 ms-1 the average speed of the molecule is………..
(a) 1000 ms-1
(b) 922 ms-1
(c) 780 ms-1
(d) 849 ms-1
Answer:
(b) 922 ms-1
Hint:
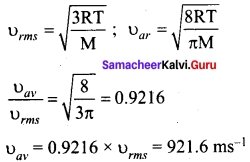
Question 13.
In a cyclic process, work done by the system will be ………….
(a) zero
(b) more than the heat given to the system
(c) equal to heat given to the system
(d) independent of heat given to system
Answer:
(c) equal to heat given to the system
Question 14.
A closed tube partly filled with water lies is a horizontal plane. If the tube is rotated about perpendicular bisector, the moment of inertia of the system…………
(a) increases
(b) decreases
(c) remains constant
(d) depends on sense of rotation
Answer:
(c) remains constant
Question 15.
Force acting on the particle moving with constant speed is…………..
(a) always zero
(b) need not be zero
(c) always non zero
(d) cannot be concluded
Answer:
(a) always zero
Hint:
In a straight line motion, velocity (speed) is constant, a = 0; F = ma = 0
PART – II
Answer any six questions in which Q. No 23 is compulsory. [6 × 2 = 12]
Question 16.
Write limitations of dimensional analysis with examples, (any 2 points only) Limitations of Dimensional analysis.
Answer:
- This method gives no information about the dimensionless constants in the formula like 1, 2, …..π, e, etc.
- This method is not suitable to derive relations involving trigonometric, exponential and logarithmic functions.
- It can only check on whether a physical relation is dimensionally correct but not the correctness of the relation. For example, using dimensional analysis, s = ut + \(\frac{1}{3}\) at² is dimensionally correct whereas the correct relation is s = ut +\(\frac{1}{2}\) at²
Question 17.
A particle of mass 2 kg experiences two forces \(\vec{F_1}\) =5\(\hat{i}\) + 8\(\hat{j}\) + 7\(\hat{k}\) and \(\vec{F_2}\) = 3\(\hat{i}\) – 4\(\hat{j}\) + 3\(\hat{k}\). What is the acceleration of the particle?
Answer:
We use Newton’s second law, \(\vec{F}_{net}\) = m\(\vec{a}\) where \(\vec{F}_{net}\) = \(\vec{F_1}\) + \(\vec{F_2}\). From the equations the acceleration is \(\vec{a}\) = \(\frac{\vec{F}_{net}}{m}\), where
\(\vec{F}_{net}\) = (5 + 3)\(\vec{i}\) + (8 – 4)\(\vec{j}\) + (7 + 3)\(\vec{k}\)
\(\vec{F}_{net}\) = 8\(\vec{i}\) + 4\(\vec{j}\) + 10\(\vec{k}\)
\(\vec{a}\) = (\(\frac{8}{2}\))\(\vec{i}\) + (\(\frac{4}{2}\))\(\vec{j}\) + (\(\frac{10}{2}\))\(\vec{k}\)
\(\vec{a}\) = 4\(\vec{j}\) + 2\(\vec{j}\) + 5\(\vec{k}\)
Question 18.
An electron and proton are detected in a cosmic ray experiment, the first with kinetic energy 10 KeV and the second with 100 KeV. Which is faster, the electron or the proton? Obtain the ratio of their speeds.
(electron mass : 9.11 × 10-31 kg : proton mass : 1.67 × 10-27 kg : lev = 1.6 × 10-19 J)
Answer:
Here Ke = 10 keV and Kp = 100 keV
me = 9.11 × 10-31 kg and mp = 1.67 × 10-27 kg
As K = \(\frac{1}{2}\) mv² or v = \(\sqrt {\frac{2K}{m}}\)
Hence
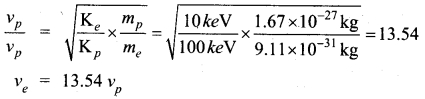
Question 19.
A bullet of mass 20 g strikes pendulum of mass 5 kg. The centre of mass of pendulum rises a vertical distance of 10 cm. If the bullet gets embedded into the pendulum, calculate its initial speed.
Answer:
Given data: m1 = 20 g = 20 × 10-3kg; m2 = 5 kg; s = 10 × 10-2m
Let the speed of the bullet be v. The common velocity of bullet and pendulum bob is V. According to law of conservation of linear momentum.
V = \(\frac{m_1v}{(m_1+m_2)}\) = \(\frac{20×10^{-3}v}{5+20×10^{-3}}\) = \(\frac{0.02}{5.02}\) v = 0.004 v
The bob with bullet go up with a deceleration of g= 9.8 ms-2. Bob and bullet come to rest at a height of 10 × 10-2 m.
from IIIrd equation of motion

![]()
Question 20.
Get the relation between rotational kinetic energy and angular momentum.
Answer:
Let a rigid body of moment of inertia I rotate with angular velocity ω
The angular momentum of a rigid body is, L = Iω
The rotational kinetic energy of the rigid body is, KE = \(\frac{1}{2}\)Iω²
By multiplying the numerator and denominator of the above equation with I, we get a relation between L and KE as,
KE= \(\frac{1}{2}\) \(\frac{I^2ω^2}{I}\) = \(\frac{1}{2}\) \(\frac{(Iω)^2}{I}\)
KE = \(\frac{L^2}{2I}\)
Question 21.
Why is there no lunar eclipse and solar eclipse every month?
Answer:
If the orbits of the Moon and Earth lie on the same plane, during full Moon of every month, we can observe lunar eclipse. If this is so during new oon we can observe solar eclipse. But Moon’s orbit is tilted 5° with respect to Earth’s orbit. Due to this 5° tilt, only during certain periods of the year, the Sun, Earth and Moon align in straight line leading to either lunar eclipse or solar eclipse depending on the alignment.
Question 22.
Calculate the change in internal energy of a block of copper of mass 200 g when it is heated from 25°C to 75°C. Specific heat of copper = 0.1 cal / g / °C and assume change in volume is negligible.
Answer:
dQ = cmΔT = 0.1 × 200 (75 – 25) = 100 calorie
dw = Pdv = 0
dU = dQ – dW = 100 – 0 = 100 calorie = 4200 J
Question 23.
The shortest distance travelled by a particle executing SHM from mean position in 2 seconds is equal to \(\frac{√3}{2}\) times of its amplitude. Determine its time period.
Answer:
Given data t = 2s ; y = \(\frac{√3}{2}\)A ; T = ?
displacement y = A sin ωt = A sin \(\frac{2π}{T}\) t
\(\frac{√3}{2}\)A = A sin \(\frac{2π×2}{T}\) ; sin \(\frac{4π}{T}\) = \(\frac{√3}{2}\) = sin \(\frac{π}{3}\)
∴ \(\frac{4π}{3}\) = \(\frac{π}{3}\) ; T = 12s
Question 24.
What are the differences from sliding and slipping?
Answer:
| Sliding | Slipping | |
| (i) | Velocity of centre of mass is greater than Rco i.e. VCM > Rco. | Velocity of centre of mass is lesser than Rco. i.e. VCM < Rco |
| (ii) | Velocity of translational motion is greater than velocity of rotational motion. | Velocity of translation motion is lesser than velocity of rotational motion. |
| (iii) | Resultant velocity acts in the forward direction. | Resultant velocity acts in the backward direction. |
PART – III
Answer any six questions in which Q.No. 29 is compulsory. [6 × 3 = 18]
Question 25.
You are given a thread and a metre scale. How will you estimate the diameter of the thread?
Answer:
The diameter of a thread is so small. Therefore we cannot measure it using metre scale. We wind a number of turns of the thread on the metre scale so that the turns are closely touching one another.
Measure the length (l) of the windings on the scale which contains number of turns.
∴ Diameter of thread = \(\frac{1}{n}\)
Question 26.
Consider two cylinders with same radius and same mass. Let one of the cylinders be solid and another one be hollow. When subjected to same torque, which one among them gets more angular acceleration than the other?
Answer:
Moment of inertia of a solid cylinder about its axis Is = \(\frac{π}{2}\)MR²
Moment of inertia of a hollow cylinder about its axis lh = MR³
Is = \(\frac{π}{2}\)Ih or Ih = 2Is
torque τ = lα ⇒ α = \(\frac{τ}{I}\)
αs = \(\frac{τ}{I_s}\) and ah = \(\frac{τ}{I_h}\)
αsIs = αhIh ⇒ αs = αh \(\frac{I_h}{I_s}\)
Ih > Ih ⇒ \(\frac{I_h}{I_s}\) > 1
∴ as > ah
Question 27.
The reading of pressure meter attached with a closed pipe is 5 × 105 Nm-2. On opening the valve of the pipe, the reading of the pressure meter is 4.5 × 105 Nm-2. Calculate the speed of the water flowing in the pipe.
Answer:
Using Bernoulli’s equation
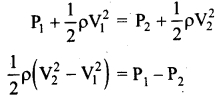
Here initial velocity V1 = 0 and density of water ρ = 1000 kg m 3

Question 28.
State and prove perpendicular axis theorem.
Answer:
Perpendicular axis theorem: This perpendicular axis theorem holds good only for plane laminar objects.
The theorem states that the moment of inertia of a plane laminar body about an axis perpendicular to its plane is equal to the sum of moments of inertia about two perpendicular axes lying in the plane of the body such that all the three axes are mutually perpendicular and have a common point.
![]()
Question 29.
State Stoke’s law and give some practical applications of Stoke’s law.
Answer:
The viscous force F acting on a spherical body of radius r depends directly on:
(i) radius (r) of the sphere
(ii) velocity (v) of the sphere and
(iii) coefficient of viscosity q of the liquid
Therefore F ∝ ηxryvz = F = k ηxryvz, where k is a dimensionless constant. Using dimensions, the above equation can be written as
[MLT-2] = k [ML-1T-1]z × [L]y × [LT-1]x
On solving, we get x = 1, y = 1 and z = 1. Therefore, F = kηrv
Experimentally, Stoke found that the value of k = 6π
F = 6πηrv
This relation is known as Stoke’s law.
Practical applications of Stoke’s law Since the raindrops are smaller in size and their terminal velocities are small, remain suspended in air in the form of clouds. As they grow up in size, their terminal velocities increase and they start falling in the form of rain.
This law explains the following:
- Floatation of clouds
- Larger raindrops hurt us more than the smaller ones
- A man coming down with the help of a parachute acquires constant terminal velocity.
Question 30.
Derive the ratio of two specific heat capacities of triatomic molecules.
(a) Linear molecule:
Answer:
Energy of one mole

(b) Non – Linear molecule:
Answer:
Energy of one mole

Note that according to kinetic theory model of gases the specific heat capacity at constant volume and constant pressure are independent of temperature. But in reality it is not sure. The specific heat capacity varies with the temperature.
Question 31.
If 5 L of water at 50°C is mixed with 4 L of of water at 30°C, what will be the final temperature of water? Take the specific heat capacity of water as 4184 J kg-1 k-1.
Answer:
We can use the equation Tf = \(\frac{m_{1} s_{1} \mathrm{T}_{1}+m_{2} s_{2} \mathrm{T}_{2}}{m_{1} s_{1}+m_{2} s_{2}}\)
m1 = 5L = 5 kg ancl m2 = 4 L = 4 kg, s1 = s2 and T1 = 50°C = 323K and T2 = 30°C = 303 K
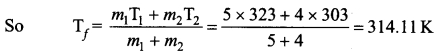
Tf = 314.11 K – 273 K ≈ 41°C.
Suppose if we mix equal amount of water (m1 = m2) with 50°C and 30°C, then the final temperature is average of two temperatures.
Tf = \(\frac{T_1+T_2}{2}\) = \(\frac{323+303}{2}\) = 313 K = 40°C
Suppose if both the water are at 30°C then the final temperature will also 30°C. It implies that they are at equilibrium and no heat exchange takes place between each other.
![]()
Question 32.
Smooth block is released at rest on a 45° incline and then slides a distance d. If the time taken of slide on rough incline is n times as large as that to slide than on a smooth incline. Show that co-efficient of friction µ = (1 – \(\frac{1}{n_2}\))
Answer:
When there is no friction, the block slides down the inclined plane with acceleration.
a – g sin θ
when there is friction, the downward acceleration of the block is
a’ = g (sin θ — µ cos θ)
As the block slides a distance d in each case so
d = \(\frac{1}{2}\) at² = \(\frac{1}{2}\) a’t’²
\(\frac{a}{a’}\) = \(\frac{t’^2}{t^2}\) = \(\frac{(nt)^2}{r^2}\) = n² or \(\frac{g sin θ}{g(sin θ – µ cos θ)}\) = n²
Solving, we get (Using θ = 45°)
µ = 1 – \(\frac{1}{n_2}\)
Question 33.
How do you distinguish between stable and unstable equilibrium?
Answer:
| Stable Equilibrium | Unstable Equilibrium | |
| (i) | The body tries to come back to equilibrium if slightly disturbed and released. | The body cannot come back to equilibrium if slightly disturbed and released. |
| (ii) | The center of mass of the body shifts slightly higher if disturbed from equilibrium. | The center of mass of the body shifts slightly lower if disturbed from equilibrium. |
| (iii) | Potential energy of the body is minimum and it increases if disturbed. | Potential energy of the body is not minimum and it decreases if disturbed. |
PART – IV
Answer all the questions. [5 × 5 = 25]
Question 34. (a).
What are the limitation of Dimensional formula? By assuming that the frequency y of a vibrating string may depend upon
(i) Tension
(ii) length (l)
(iii) mass per unit
length (m), prove that γ ∝ \(\frac{1}{l}\) \(\sqrt{\frac{T}{M}}\)
Answer:
(i) Limitations of Dimensional analysis:
- This method gives no information about the dimensionless constants in the formula like 1, 2, ……. π, e, etc.
- This method cannot decide whether the given quantity is a vector or a scalar.
- This method is not suitable to derive relations involving trigonometric, exponential and logarithmic functions.
- It cannot be applied to an equation involving more than three physical quantities.
- It can only check on whether a physical relation is dimensionally correct but not the correctness of the relation. For example, using dimensional analysis, s = ut + \(\frac{π}{2}\) at² is dimensionally correct whereas the correct relation is s = ut + \(\frac{π}{2}\) at².
(ii) n ∝ Ia Tbmc, [I] = [M0L1 T0]
[T] = [M1L1T-2] (force)
[M] = [M1L-1T0]
[M0L0T-1] = [M0L1T0]a [M1L1T-2]b [M0L-1T0]a
b + c = 0
a + b – c = 0
-2b = -1 ⇒ b = \(\frac{π}{2}\)
c = –\(\frac{π}{2}\)a = 1
γ ∝ \(\frac{1}{l}\) \(\sqrt{\frac{T}{M}}\)
![]()
[OR]
(b) Prove the law of conservation of linear momentum. Use it to find the recoil velocity of a gun when a bullet is fired from it.
Answer:
In nature, conservation laws play a very important role. The dynamics of motion of bodies can be analysed very effectively using conservation laws. There are three conservation laws in mechanics. Conservation of total energy, conservation of total linear momentum, and conservation of angular momentum. By combining Newton’s second and third laws, we can derive the law of conservation of total linear momentum.
When two particles interact with each other, they exert equal and opposite forces on each other. The particle 1 exerts force \(\frac{\vec{F}_{12}}{m}\) on particle 2 and particle 2 exerts an exactly equal and opposite force \(\frac{\vec{F}_{12}}{m}\) on particle 1 according to Newton’s third law.
\(\frac{\vec{F}_{21}}{m}\) = –\(\frac{\vec{F}_{21}}{m}\) ……….(1)
In terms of momentum of particles, the force on each particle (Newton’s second law) can be written as
\(\frac{\vec{F}_{12}}{m}\) = \(\frac{\vec{dp_1}}{dt}\) and \(\frac{\vec{F}_{21}}{m}\) = \(\frac{\vec{dp_2}}{dt}\) ………(2)
Here \(\vec{p}_1\) is the momentum of particle 1 which changes due to the force \(\vec{F}_{12}\) exerted by
particle 2. Further \(\vec{p}_2\) is the momentum of particle 2. This changes due to \(\vec{F}_{21}\) exerted by particle 1.
Substitute equation (2) in equation (1)

It implies that \(\vec{p_1}\) + \(\vec{p_2}\) constant vector (always).
\(\vec{p_1}\) + \(\vec{p_2}\) is the total linear momentum of the two particles (\(\vec{p_{tot}}\) = \(\vec{p_1}\) + \(\vec{p_2}\)).It is also called as total linear momentum of the system. Here, the two particles constitute the system. From this result, the law of conservation of linear momentum can be stated as follows.
If there are no external forces acting on the system, then the total linear momentum of the system (\(\vec{p}_{tot}\)) is always a constant vector. In other words, the total linear momentum of the system is conserved in time. Here the word ‘conserve’ means that \(\vec{p_1}\) and p\(\vec{p_2}\) can vary, in such a way that \(\vec{p_1}\) + \(\vec{p_2}\) is a constant vector.
The forces \(\vec{F_{12}}\) and \(\vec{F_{21}}\) are called the internal forces of the system, because they act only between the two particles. There is no external force acting on the two particles from outside. In such a case the total linear momentum of the system is a constant vector or is conserved.
To find the recoil velocity of a gun when a bullet is fired from it:
Consider the firing of a gun. Here the system is Gun+bullet. Initially the gun and bullet are at rest, hence the total linear momentum of the system is zero. Let \(\vec{p_1}\) be the momentum of the bullet and \(\vec{p_2}\) the momentum of the gun before firing. Since initially both are at rest,
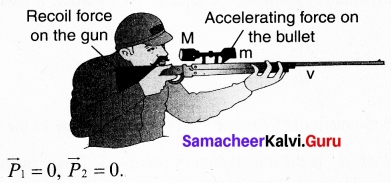
Total momentum before firing the gun is zero, \(\vec{p_1}\) + \(\vec{p_2}\) = 0
According to the law of conservation of linear momentum, total linear momemtum has to be zero after the firing also.
When the gun is fired, a force is exerted by the gun on the bullet in forward direction. Now the momentum of the bullet changes from \(\vec{p_1}\) + \(\vec{p_1}\). To conserve the total linear momentum of the system, the momentum of the gun must also change from \(\vec{p_2}\) to \(\vec{p_2}\) Due to the conservation of linear momentum, \(\vec{p_1}\)+ \(\vec{p_2}\)= 0. It implies that \(\vec{p_1}\) = – \(\vec{p_2}\), the momentum of the gun is exactly equal, but in the opposite direction to the momentum of the bullet. This is the reason after firing, the gun suddenly moves backward with the momentum (\(\vec{p_2}\)). It is called ‘recoil momentum’. Th is is an example of conservation of total linear momentum.
![]()
Question 35 (a).
Explain the variation of g with
(i) latitude
(ii) altitude.
Answer:
(i) Latitute: When an object is on the surface fo the Earth, it experiences a centrifugal force that depends on the latitude of the object on Earth. If the Earth were not spinning, the force on the object would have been mg. However, the object experiences an additional centrifugal force due to spinning of the Earth.
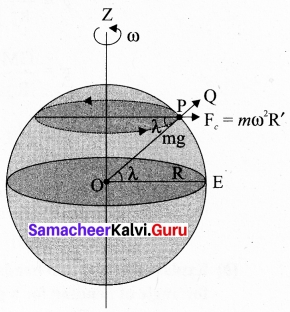
This centrifugal force is given by mω²R’.
OPz cos λ = \(\frac{PZ}{OP}\) = \(\frac{R’}{R}\)
R’ = R cos λ
where λ is the latitude. The component of centrifugal acceleration experienced by the object in the direction opposite to g is
NaPQ = ω²R cos λ = ω²R COS² λ
Since R’ = R cos λ
Therefore, g’ = g – ω²R cos² λ
From the above expression, we can infer that at equator, λ = 0, g’ = g ω²R. The acceleration due to gravity is minimum. At poles λ = 90; g’ = g, it is maximum. At the equator, g’ is minimum.
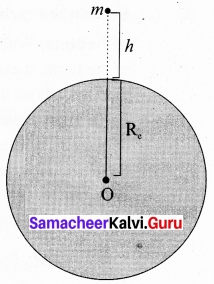
(ii) Altitude: Consider an object of mass m at a height h from the surface of the Earth. Acceleration experienced by the object due to Earth is
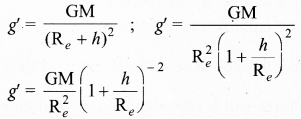
If h << Re: We can use Binomial expansion. Taking the terms up to first order
g’ =\( \frac{\mathrm{GM}}{\mathrm{R}_{e}^{2}}\left[1+\frac{h}{\mathrm{R}_{e}}\right]^{-2}\)
If h << R sub>e: We can use Binomial expansion. Taking the terms up to first order
(1 + x)ⁿ = 1 + nx

We find that g’ < g. This means that as altitude h increases the acceleration due to gravity g decreases.
[OR]
(b) Explain why a cyclist bends while negotiating a curve road? Arrive at the expression for angle of bending for a given velocity.
Answer:

Let us consider a cyclist negotiating a circular level road (not banked) of radius r with a speed v. The cycle and the cyclist are considered as one system with mass m. The center gravity of the system is C and it goes in a circle of radius r with center at O. Let us choose the line OC as X-axis and the vertical line through O as Z-axis as shown in Figure.
The system as a frame is rotating about Z-axis. The system is at rest in this rotating frame. To solve problems in rotating frame of reference, we have to apply a centrifugal force (pseudo force) on the system which will be \(\frac{mv^2}{r}\). this force will act through the center of gravity. the forces acting on the system are , (i) gravitational force (mg), (ii) Normal force (n), (iii) frictional force (f) and (iv) centrifugal force (\(\frac{mv^2}{r}\)). As the system is in equilibrium in the rotational frame of will be of reference, the net external force and net external torque must be zero. Let us consider all torques about the point A in Figure.
For rotational equilibrium,
\(\vec{τ}_{net}\) = 0
The torque due to the gravitational force about point A is (mg AB) which causes a clockwise turn that is taken as negative. The torque due to the centripetal force is (\(\frac{mv^2}{r}\) BC) which causes an anticlock wise turn that is taken as positive
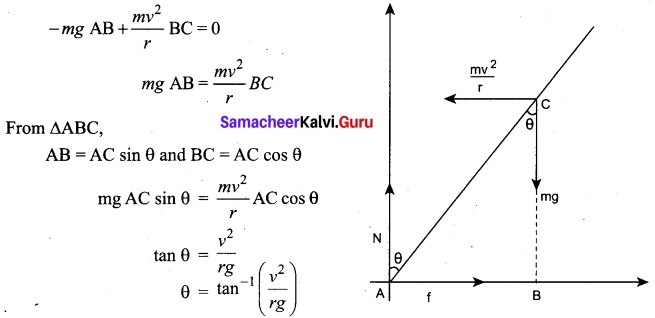
While negotiating a circular level road of radius Force diagrams for the cyclist r at velocity v, a cyclist has to bend by an angle in turns
0 from vertical given by the above expression to stay in equilibrium (i.e. to avoid a fall).
Question 36 (a).
Derive an expression for moment of inertia of a uniform ring and uniform disc.
Answer:
Let us consider a uniform ring of mass M and radius R. To find the moment of inertia of the ring about an axis passing through its center and perpendicular to the plane, let us take an infinitesimally small mass {dm) of length (dx) of the ring. This (dm) is located at a distance R, which is the radius of the ring from the axis as shown in figure.
The moment of inertia (dl) of this small mass (dm) is,
dl = (dm) R²
The length of the ring is its circumference (2πR). AS the mass is uniformly distributed, the mass per unit length (λ) is,
mass M
λ = \(\frac{mass}{length}\) = \(\frac{M}{2πR}\)
The mass (dm) of the infinitesimally small length is,
dm = λ dx = \(\frac{M}{2πR}\) dx
Now, the moment of inertia (I) of the entire ring is,
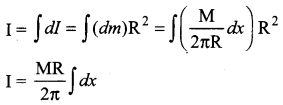
To cover the entire length of the ring, the limits of integration are taken from 0 to 2πR.
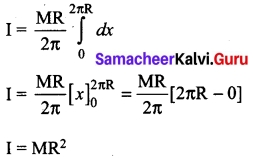
![]()
[OR]
(b) Explain how overtones are produced in a (i) closed organ pipe
Answer:
(i) Closed organ pipes: Look at the picture of a clarinet, shown in figure. It is a pipe with one end closed and the other end open. If one end of a pipe is closed, the wave reflected at this closed end is 180° out of phase with the incoming wave. Thus there is no displacement of the particles at the closed end. Therefore, nodes are formed at the closed end and anti¬nodes are formed at open end.

(a) No motion of particles which leads to nodes at closed end and antinodes at open and (fundamental mode) (N-node, A-antinode)
Let us consider the simplest mode of vibration of the air column called the fundamental mode. Anti-node is formed at the open end and node at closed end. From the figure, let L be the length of the tube and the wavelength of the wave produced. For the fundamental mode of vibration, we have,
L = \(\frac{λ_1}{4}\) or λ1 = 4L …(1)
The frequency of the note emitted is . v v
fp = \(\frac {v}{λ_1}\) = \(\frac{v}{4L}\) …….(2)
which is called the fundamental note.
The frequencies higher than fundamental frequency can be produced by blowing air strongly at open end. Such frequencies are called overtones.
The figure (b) shows the second mode of vibration having two nodes and two antinodes,
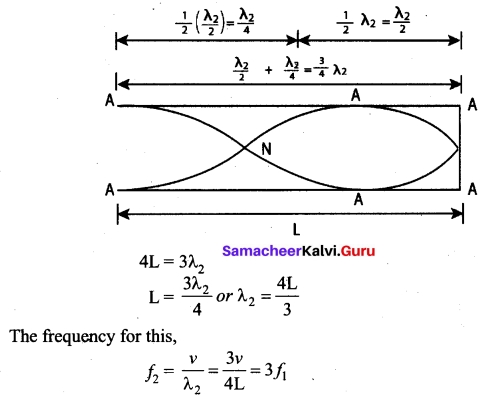
is called first over tone, since here, the frequency is three times the fundamental frequency it is called third harmonic.
The figure (c) shows third mode of vibration having three nodes and three anti-nodes.
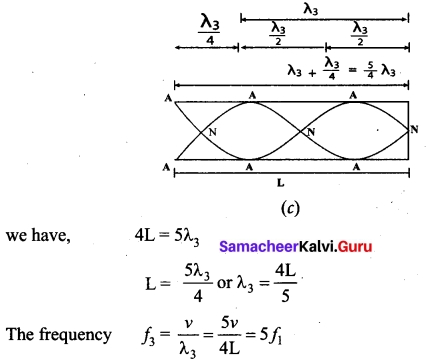
is called second over tone, and since n = 5 here, this is called fifth harmonic. Hence, the closed organ pipe has only odd harmonics and f1 : f2 : f3 : f4 : …… = 1 : 3 : 5 : 7 : …… ………(3)
Question 37 (a).
What is meant by Doppler effect? Discuss following cases.
(i) source moves towards stationary observer
(ii) source moves away from stationary observer
Answer:
When the source and the observer are in relative motion with respect to each other and to the medium in which sound propagates, the frequency of the sound wave observed is different from the frequency of the source. This phenomenon is called Doppler Effect.
(i) Source moves towards the observer: Suppose a source S moves to the right (as shown in figure) with a velocity vs and let the frequency of the sound waves produced by the source be fs. We assume the velocity of sound in a medium is v. The compression (sound wave front) produced by the source S at three successive instants of time are shown in the figure. When S is at position x1 the compression is at C1. When S is at position x2, the compression is at C2 and similarly for x3 and C3. Assume that if C1 reaches the observer’s position A then at that instant C2reaches the point B and C3 reaches the point C as shown in the figure. It is obvious to see that the distance between compressions C2 and C3 is shorter than distance between C3 and C2. This means the wavelength decreases when the source S moves towards the observer O (since sound travels longitudinally and wavelength is the distance between two consecutive compressions). But frequency is inversely related to wavelength and therefore, frequency increases.
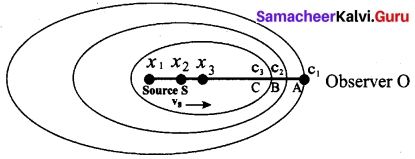
Let λ be the wavelength of the source S as measured by the observer when S is at position x1 and λ’ be wavelength of the source observed by the observer when S moves to position x2. Then the change in wavelength is Δλ = λ – λ’ = vst, where t is the time taken by the source to travel between x1 and x2. Therefore,
λ’ = λ – vst ………..(1)
But t = \(\frac{λ}{v}\) ………(2)
On substituting equation (2) in equation (3), we get
λ’ = λ\(\left(1-\frac{v_{s}}{v}\right)\)
Since frequency is inversely proportional to wavelength, we have
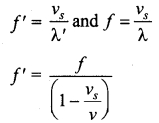
Since, \(\frac{v_s}{v}\) << 1, we use the binomial expansion and retaining only first order in \(\frac{v_s}{v}\) we get
f’ = f(1 + \(\frac{v_s}{v}\))v ………..(4)
(ii) Source moves away from the observer: Since the velocity here of the source is opposite in direction when compared to case (a), therefore, changing the sign of the velocity of the source in the above case i.e, by substituting (vs → -vs) in equation (1), we get
\(f^{\prime}=\frac{f}{\left(1+\frac{v_{s}}{v}\right)}\) ………(5)
Using binomial expansion again, we get,
\(f^{\prime}=f\left(1-\frac{v_{s}}{v}\right)\) ……….. (6)
![]()
[OR]
(b) (i) Define specific heat capacity of gas at constant volume
(ii) Define specific heat capacity of gas at constant pressure
(iii) Derive the relationship between Cp and Cv.
Answer:
(i) The amount of heat energy required to raise the temperature of one kg of a substance by 1 K or 1?C by keeping the volume constant is called specific heat capacity at constant volume.
(ii) The amount of heat required to rise the temperature of one mole of a substance by IK or 1°C at constant volume is called molar specific heat capacity at constant volume.
(iii) Application of law of equipartition energy in specific heat of a gas Meyer’s relation Cp – Cv = R connects the two specific heats for one mole of an ideal gas.
Equipartition law of energy is used to calculate the value of Cp – Cv and the ratio between them γ = \(\frac{C_p}{C_v}\) Here y is called adiabatic exponent.
Question 38 (a).
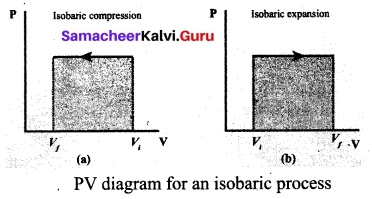
Explain Isobaric process and derive the work done in this process.
Answer:
Isobaric process: This is a thermodynamic process that occurs at constant pressure. Even though pressure is constant in this process, temperature, volume and internal energy are not constant. From the ideal gas equation, we have
V = (\(\frac{µR}{P}\))T ………(1)
Here \(\frac{µR}{P}\) = constant
In an isobaric process the temperature is directly proportional to volume.
V ∝ T (Isobaric process) …(2)
This implies that for a isobaric process, the V-T graph is a straight line passing through the origin.
If a gas goes from a state (Vi ,Ti) to (Vf, Tf) at constant pressure, then the system satisfies the following equation
\(\frac{T_f}{V_f}\) = \(\frac{T_i}{V_i}\) …(3)
Examples for Isobaric process:
(i) When the gas is heated and pushes the piston so that it exerts a force equivalent to atmospheric pressure plus the force due to gravity then this process is isobaric.
(ii) Most of the cooking processes in our kitchen are isobaric processes. When the food is cooked in an open vessel, the pressure above the food is always at atmospheric pressure.
The PV diagram for an isobaric process is a horizontal line parallel to volume axis. Figure (a) represents isobaric process where volume decreases figure (b) represents isobaric process where volume increases.
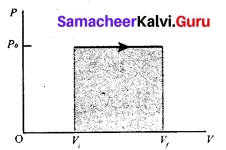
The work done in an isobaric process: Work done by the gas
\(\mathbf{W}=\int_{\mathbf{V}_{\mathbf{i}}}^{\mathbf{V}_{f}} \mathbf{P} d \mathbf{V}\) …….(4)
In an isobaric process, the pressure is constant, so P comes out of the integral,

Where ΔV denotes change in the volume. If ΔV is negative, W is also negative. This implies that the work is done on the gas. If ΔV is positive, W is also positive, implying that work is done by the gas.
The equation (6) can also be rewritten using the ideal gas equation.
From ideal gas equation
PV = µRT and V = \(\frac{µRT}{P}\)
Substituting this in equation (6) we get
W = µRTf (1 – \(\frac{T_i}{T_f}\)) …….(7)
In the PV diagram, area under the isobaric curve is equal to the work done in isobaric process.
The first law of thermodynamics for isobaric process is given by
ΔU = Q – PΔV ……..(8)
W = PΔY, ΔU = Q – µRTf [1 – \(\frac{T_i}{T_f}\)]
![]()
[OR]
(b) Explain how the interference of waves is formed.
Answer:
Consider two harmonic waves having identical frequencies, constant phase difference φ and same wave form (can be treated as coherent source), but having amplitudes A1 and A2, then
y1 = A1sin (kx – ωf), ……(1)
y2 = A2 sin (kx – ωt + φ) …..(2)
Suppose they move simultaneously in a particular direction, then interference occurs (i.e., overlap of these two waves). Mathematically
y = y1 + y2 …….(3)
Therefore, substituting equation (1) and equation (3) in equation (3), we get
y = A1 sin (kx – ωt) + A2 sin (kx – ωt + φ)
Using trigonometric identity sin (α + β) = (sin α cos β + cos α sin β ), we get
y= A1 sin (kx – ωt) + A2 [sin (kx – ωt) cos φ + cos (kx – ωt) sin φ]
y= sin (kx – ωt) (A1 + A2 cos φ) + A2 sin φ cos (kx – ωt) ……(4)
Let us re-define A cos θ = (A1 + A2 cos φ) …(5)
and A sin θ = A2 sin φ …(6)
then equation (4) can be rewritten as y = A sin (kx – ωt) cos θ + A cos (kx – ωt) sin θ
y = A (sin (kx – ωt) cos θ + sin θ cos (kx – ωt))
y = A sin (kx – ωt + θ) ……..(7)
By squaring and adding equation (5) and equation (6), we get
A2 =\mathrm{A}_{1}^{2}+\mathrm{A}_{2}^{2} + 2A1 A2 cos φ ……..(8)
Since, intensity is square of the amplitude (I = A2), we have
I = I1 + I2 + 2\(\sqrt{I_1I_2}\) COS φ ……..(9)
This means the resultant intensity at any point depends on the phase difference at that point.
(a) For constructive interference: When crests of one wave overlap with crests of another wave, their amplitudes will add up and we get constructive interference. The resultant wave has a larger amplitude than the individual waves as shown in figure (a). The constructive interference at a point occurs if there is maximum intensity at that point, which means that
cos φ = + 1 ⇒ φ = 0, 2π, 4π,… = 2πn,
where n = 0, 1, 2,…
This is the phase difference in which two waves overlap to give constructive interference. Therefore, for this resultant wave,

(b) For destructive interference: When the trough of one wave overlaps with the crest of another wave, their amplitudes “cancel” each other and we get destructive interference as shown in figure (b). The resultant amplitude is nearly zero. The destructive interference occurs if there is minimum intensity at that point, which means cos φ = – 1 ⇒ φ = π, 3π, 5π,… = (2 n – 1) π, where n = 0,1,2,…. i.e. This is the phase difference in which two waves overlap to give destructive interference. Therefore,
![]()
Hence, the resultant amplitude
A= |A1 – A2|
![]()