Students can Download Tamil Nadu 11th Physics Model Question Paper 4 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 11th Physics Model Question Paper 4 English Medium
![]()
Instructions:
- The question paper comprises of four parts
- You are to attempt all the parts. An internal choice of questions is provided wherever: applicable
- All questions of Part I, II, III, and IV are to be attempted separately
- Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
- Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
- Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
- Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Max Marks: 70
PART – I
Answer all the questions: [15 × 1 = 15]
Question 1.
A parallax of heavenly body measured from two points diametrically opposite on equator of Earth is 1.0 minute. If the radius of Earth is 6400 km the distance of the body is …………
(a) 8.8 × 1010m
(b) 4.4 × 1010m
(c) 0.29 × 10-10m
(d) 8.6 × 10-10m
Answer:
(b) 4.4 × 1010m
Hint:
θ = 1 min = \(\frac{1}{60}\) × \(\frac{π}{1800}\)rad
Diameter of earth, d = 2 × RE = 2 × 6400 × 10³m
Distance of the heavenly body from the centre of the earth, r = \(\frac{d}{θ}\) = \(\frac{2×6400×10^3}{\frac{π}{60×80}}\)
r = 4.4 × 1010m
Question 2.
A particle is thrown vertically upwards, its velocity at half of the height is 10 m/s then the maximum height attained by it is (g = 10 m/s²)
(a) 8 m
(b) 20 m
(c) 10 m
(d) 16 m
Answer:
(c) 10 m
Hint: From equation of motion, v² = u² – 2as
O = (10)² + 2(-10) s
∴S = 5 m
u = 10 ms-1
v = 0 ms-1
a = -10 ms-2
Total height = 2 × 5 = 10 m
Question 3.
If the velocity is \(\vec{v}\) = 2\(\vec{i}\) + t²\(\vec{j}\) – 9\(\vec{k}\), then the magnitude, of acceleration at t = 0.5 s is……….
(a) 1 ms-2
(b) 2 ms-2
(c) zero
(d) -1 ms-2
Answer:
(a) 1 ms-2
Hint:
a = \(\frac{dy}{dt}\) = \(\frac{d}{dt}\) (2\(\vec{i}\) + t²\(\vec{j}\) – 9\(\vec{k}\)) = 2t\(\vec{j}\)
at, t = 0.5 s ⇒ a = 2 (0.5).= 1 ms-2
![]()
Question 4.
A uniform force of (2\(\vec{i}\) + \(\vec{j}\))N acts on a particle of mass 1 kg. The particle displaces from position (3\(\vec{j}\) + \(\vec{k}\)) m to (5\(\vec{i}\) + 3\(\vec{j}\)) m. The work done by the force on the particle is……….
(a) 9 J
(b) 6 J
(c) 10 J
(d) 12 J
Answer:
(c) 10 J
Hint:
\(\vec{F}\) = (2\(\vec{i}\)+ \(\vec{j}\))N; Δ\(\vec{r}\) = \(\vec{j}_2\) – \(\vec{r}_2\) = (5\(\vec{i}\) + 3\(\vec{j}\)) – (3\(\vec{i}\) + \(\vec{k}\)); Δr = 5\(\vec{i}\) – \(\vec{k}\)
Workdone, \(\vec{W}\) = \(\vec{F}\). Δ\(\vec{r}\) = (2\(\vec{i}\) + \(\vec{j}\)) . (5\(\vec{i}\) – \(\vec{k}\))
\(\vec{W}\) = 10\(\vec{i}\) \(\vec{W}\) = 10Nm = 10J
Question 5.
A couple produces……….
(a) pure rotation
(b) pure translation
(c) rotation and translation
(d) no motion
Answer:
(a) pure rotation
Question 6.
What is the shape, when a non-wetting liquid is placed in a capillary tube?
(a) convex upwards
(b) concave upwards
(c) concave downwards
(d) convex downwards
Answer:
(a) convex upwards
Question 7.
An ideal gas heat engine operators in a carnot’s cycle between 227°C and 127°C. It absorbs 6 × 104J at high temperature. The amount of heat converted into work is………
(a) 2.4 × 104J
(b) 4.8 × 104J
(c) 1.2 × 104J
(d) 6 × 104J
Answer:
(c) 1.2 × 104J
Hint:
\(\frac{W}{Q}\) = 1 – \(\frac{T_2}{T_1}\)
W = (1 – \(\frac{273+127}{273+227}\)) × 104 = 1.2 × 104J
Question 8.
Four round objects namely a ring, a disc, a hollow sphere and a solid sphere with same radius R start to roll down an incline at the same time. Find out the order of objects reaching the bottom first?
(a) solid sphere, disc, hollow sphere, ring
(b) ring, disc, hollow sphere, solid sphere
(c) disc, ring, solid sphere, hollow sphere
(d) hollow sphere, disc, ring, solid sphere
Answer:
(a) solid sphere, disc, hollow sphere, ring
Question 9.
Two forces of magnitude F having a resultant of the same magnitude of F, the angle between the two forces is…………
(a) 45°
(b) 60°
(c) 120°
(d) 150°
Answer:
(c) 120°
Hint:
Magnitude of each force is F
∴ The resultant force, F = \(\sqrt{F^2+F^2+2F.Fcosθ}\)
F² = 2F² + 2F² cos θ ⇒ cos θ = –\(\frac{1}{2}\) ⇒ θ = 120°
![]()
Question 10.
If v0 and v denote the sound velocity and the rms velocity of the molecules in a gas, then……..
(a) v0 = v(\(\frac{3}{r}\))\(\frac{1}{2}\)
(b) v0 = 0
(c) v0 = v(\(\frac{r}{3}\))\(\frac{1}{2}\)
(d) v0 and v are not related
Answer:
(c) v0 = v(\(\frac{r}{3}\))\(\frac{1}{2}\)
Question 11.
The internal energy of an ideal gas depends on ………..
(a) pressure
(b) volume
(c) temperature
(d) size of molecules
Answer:
(c) temperature
Question 12.
The internal energy of an ideal gas increases during an isothermal process, when the gas is ……….
(a) expanded by adding more molecules to it
(b) expanded by adding more heat to it
(c) expanded against zero pressure
(d) compressed by doing work on it
Answer:
(a) expanded by adding more molecules to it
Question 13.
A particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4 cm/s. The frequency of its……….
(a) 3 Hz
(b) 2 Hz
(c) 4 Hz
(d) 1 Hz
Answer:
(d) 1 Hz
Hint:
A = 5 cm = 5 × 10-2m ; υmax = 31.4 cm/s = 31.4 × 10-2 m/s
Maximum speed Vmax = 2πη × A
∴ n = \(\frac{V_{max}}{2πA}\) = \(\frac{31.4×10^{-2}}{2π×5×10^{-2}}\) = \(\frac{31.4}{10×3.14}\); n = 1 Hz
Question 14.
A hollow sphere is filled with water. It is hung by a long thread. As the water flows out of a hole at the bottom, the period of oscillation will………
(a) first increase and then decrease
(b) first decrease and then increase
(c) increase continuously
(d) decrease continuously
Answer:
(a) first increase and then decrease
Question 15.
A wave travels in a medium according to the equation of displacement given by y(x, t) = 0.03 sin {π(2t – 0.01 x)} where y and x are in metres and t in seconds. The wave length of the wave is……….
(a) 200 m
(b) 100 m
(c) 20 m
(d) 10 m
Answer:
(a) 200 m
Hint:
λ = \(\frac{2π}{K}\) = \(\frac{π}{0.01π}\) = 200 m
PART – II
Answer any six questions in which Q. No 23 is compulsory. [6 × 2 = 12]
Question 16.
Distinguish scalar and vector.
Answer:
| Scalar | Vector | |
| (i) | Scalar can be described only by magnitude | Vector can be described by both magnitude and direction. |
| (ii) | Ex. mass, distance, speed | Ex. force, velocity, displacement |
![]()
Question 17.
Calculate the total number of degrees of freedom possessed by the molecular in one cm³ of H2 gas at NTP.
Answer:
22400 cm³ of every gas contains 6.02 × 1023 molecules
∴ Number of molecules in 1 cm² of H2 gas = \(\frac{6.02×10^{23}}{22400}\) = 0.26875 × 1020
Number of degrees of freedom of a H2 gas molecule = 5
∴ Total number of degrees of freedom of 0.26875 × 1020 molecules
= 0.26875 × 1020 × 5 = 1.34375 × 1020
Question 18.
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolution in 25 s, what is the magnitude and direction of acceleration of the stone?
Answer:
The acceleration will be directed towards the centre of the circular loop
angular velocity, ω = 2πf = 2 × 3.14 × \(\frac{14}{25}\); ω = \(\frac{88}{25}\) rad/s
Centripetal acceleration = rω² = \(\frac{0.8×(88)^2}{(25)^2}\); ac = 9.91 m/s²
Question 19.
There are two identical balls of same material, one being solid and the other being hollow. How will you distinguish them without weighting?
Answer:
Solid and hollow balls can be differentiated by different methods
(a) by spinning than using equal torques
(b) by determining their moment of inertia ie Ih > Is
(c) by rolling them down is an inclined plane
ie, when torques are equal angular acceleration of hollow must be smaller than that of solid. Similarly, on rolling, solid ball will reach the bottom before the hollow ball.
Question 20.
In a dark room would you be able to tell whether a given note had been produced by a Piano or a Violin?
Answer:
Yes, in a dark room we can easily identify a sound produced by a Piano or a Violin by using the knowledge of timber or quality of sound. The two sources even though having the same intensity and fundamental frequency will be associated with different number of overtones of different relative intensities. These overtones combine and produce different sounds which enables us to identify them.
Question 21.
Will water at the foot of the waterfall be at a different temperature from that at the top? If yes explain.
Answer:
When water reaches the ground, its gravitational potential energy is converted into kinetic energy which is further converted into heat energy. This raises the temperature of water. So, water at the foot of the water fall is at a higher temperature of water at the top of the waterfall.
Question 22.
Which one among a solid, liquid gas of same mass and at the same temperature has the greatest internal energy. Which one has least and why?
Answer:
A gas has greatest value of internal energy. Being a negative potential energy, potential energy of its molecules is smallest. Internal energy of solid is maximum because negative potential energy of its molecules is maximum.
Question 23.
Is it possible if work is done by the internal force. What will be the change in kinetic energy?
Answer:
Yes. this is possible. If work is done by the internal forces then kinetic energy will be increased. As an example, when a bomb explodes, the combined kinetic energy of all the fragments is greater than the initial energy.
![]()
Question 24.
What is red shift and blue shift in Doppler effect.
Answer:
If the spectral lines of the star are found to shift towards red end of the spectrum (called as red shift) then the star is receding away from the Earth. Similarly, if the spectral lines of the star are found to shift towards the blue end of the spectrum (called as blue shift) then the star is approaching Earth.
PART – III
Answer any six questions in which Q.No. 29 is compulsory. [6 × 3 = 18]
Question 25.
Give the difference between systematic errors and random errors.
Answer:
Systematic errors: Systematic errors are reproducible inaccuracies that are consistently in the same direction. These occur often due to a problem that persists throughout the experiment.
Random errors: Random errors may arise due to random and unpredictable variations in experimental conditions like pressure, temperature, voltage supply etc. Errors may also be due to personal errors by the observer who performs the experiment. Random errors are sometimes called “chance error”. When different readings are obtained by a person every time he repeats the experiment, personal error occurs.
Question 26.
Write down the kinematics equation for the object moving in a straight line with constant acceleration and also for free falling body.
Answer:
(a) the equation of motion of a moving object with constant acceleration is
- v – u + at
- s = ut+ \(\frac{1}{2}\) at²
- v² – u² = 2 as
(b) for free falling body u = 0 and a = g
- V = gt
- s = \(\frac{1}{2}\) gt2
- v² = 2 gs
Question 27.
A nucleus is at rest in the laboratory frame of reference show that if it disintegrates into two smaller nuclei. The products must be emitted in opposite directions.
Answer:
Let m1, m2 are be the masses of product nuclei and v1, v2 are the velocities of it.
∴ linear momentum after disintegration = m1v1 + m2v2
Before disintegration nucleus is at rest therefore its linear momentum before disintegration is zero. According to the principle of conservation of linear momentum
m1v1 + m2v2 = 0
v2 = –\(\frac{m_1v_1}{m_2}\)
![]()
Question 28.
How do you classify the physical quantities on the basis of dimension?
Answer:
- Dimensional variables: Physical quantities, which possess dimensions and have variable values are called dimensional variables. Examples are length, velocity, and acceleration etc.
- Dimensionless variables: Physical quantities which have no dimensions,. but have variable values are called dimensionless variables. Examples are specific gravity, strain, refractive index etc.
- Dimensional Constant: Physical quantities which possess dimensions and have constant values are called dimensional constants. Examples are Gravitational constant, Planck’s constant etc.
- Dimensionless Constant: Quantities which have constant values and also have no dimensions are called dimensionless constants. Examples are π, e, numbers etc.
Question 29.
Write short notes on the oscillations of liquid column in U-tube.
Answer:
Oscillations of liquid in U-tube.
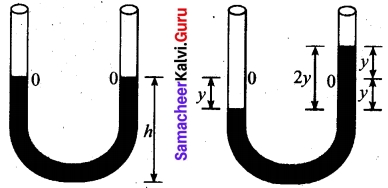
Consider a U-shaped glass tube which consists of two open arms with uniform cross sectional area A. Let us pour a non-viscous uniform incompressible liquid of density ρ in the U-shaped tube to a height h as shown in the figure. If the liquid and tube are not disturbed then the liquid surface will be in equilibrium position O. It means the pressure as measured at any point on the liquid is the same and also at the surface on the arm (edge of the tube on either side), which balances with the atmospheric pressure. Due to this the level of liquid in each arm will be the same. By blowing air one can provide sufficient force in one arm, and the liquid gets disturbed from equilibrium position O, which means, the pressure at blown arm is higher than the other arm. This creates difference in pressure which will cause the liquid to oscillate for a very short duration of time about the mean or equilibrium position and finally comes to rest, Time period of the oscillation is
T = 2π\(\sqrt{\frac{l}{2g}}\) second
Question 30.
What are the factors affecting the surface tension of a liquid.
Answer:
- The presence of any contamination or impurities.
- The presence of dissolved substances.
- Electrification
- Temperature
Question 31.
Write a note on Brownian motion.
Answer:
Brownian motion is due to the bombardment of suspended particles by molecules of the surrounding fluid. But during 19th century people did not accept that every matter is made up of small atoms or molecules. In the year 1905, Einstein gave systematic theory of Brownian motion based on kinetic theory and he deduced the average size of molecules.
According to kinetic theory, any particle suspended in a liquid or gas is continuously bombarded from all the directions so that the mean free path is almost negligible. This leads to the motion of the particles in a random and zig-zag manner. But when we put our hand in water it causes no random motion because the mass of our hand is so large that the momentum transferred by the molecular collision is not enough to move our hand.
Factors affecting Brownian Motion:
- Brownian motion increases with increasing temperature.
- Brownian motion decreases with bigger particle size, high viscosity and density of the liquid (or) gas.
![]()
Question 32.
What is the acceleration of the block and troller system as the figure. If the Co-efficient of kinetic friction between the trolley and the surface is 0.04? Also calculate friction in the string. Take G = 10 ms-2, mass of the string is negligible.
Answer:
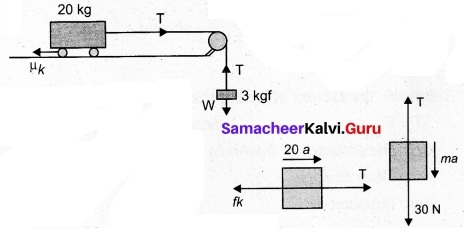
Free body diagram of the block
30 – T = 3a ……..(1)
Free body diagram of the trolley
T – fk = 20a ……(2)
where fk = = µk N = 0.04 × 20 × 10 = 8 N
Solving (1) & (2), a = 0.96 m/s² and T = 27.2 N
Question 33.
An increase in pressure of 100 kPa causes a certain volume of water to decrease by 0.005% of its original volume.
(a) Calculate the bulk modulus of water?
Answer:
Bulk modulus
B = v|\(\frac{Δp}{Δv}\)| = \(\frac{100×10^3}{0.005×10^{-2}}\)
B = 2000 MPa
(b) Compute the speed of sound (compressional waves) in water?
Answer:
v = \(\sqrt{\frac{B}{ρ}}\) = \(\sqrt{\frac{2000×10_6}{1000}}\)
v = 1414 ms-1
PART – IV
Answer all the questions. [5 × 5 = 25]
Question 34 (a).
Describe the vertical oscillations of a spring?
Answer:
Vertical oscillations of a spring: Let us consider a massless spring with stiffness constant or force constant k attached to a ceiling as shown in figure. Let the length of the spring before loading mass m be L.
If the block of mass m is attached to the other end of spring, then the spring elongates by a length. Let F, be the restoring force due to stretching of spring. Due to mass m, the gravitational force acts vertically downward. We can draw free-body diagram for this system as shown in figure. When the system is under equilibrium,
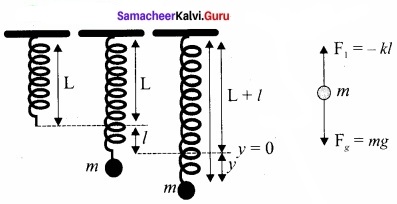
F1 + mg = 0 ……………… (1)
But the spring elongates by small displacement 1, therefore,
F1 ∝ l ⇒ F1 = -kl ……………….. (2)
Substituting equation (2) in equation (1) we get
-kl + mg = 0
mg = kl or
\(\frac{m}{k}\) = \(\frac{l}{g}\) ………………….. (3)
Suppose we apply a very small external force on the mass such that the mass further displaces downward by a displacement y, then it will oscillate up and down. Now, the restoring force due to this stretching of spring (total extension of spring is y + 1) is
F2 ∝ (y + l)
F2 = -k(y + l) = -ky – kl …………………… (4)
Since, the mass moves up and down with acceleration \(\frac{d^{2} y}{d t^{2}}\), by drawing the free body diagram for this case we get
-ky – kl + mg = m \(\frac{d^{2} y}{d t^{2}}\) ……………………. (5)
The net force acting on the mass due to this stretching is
F = F2 + mg
F = -ky – kl + mg …………………… (6)
The gravitational force opposes the restoring force. Substituting equation (3) in equation (6), we get
F = – ky- kl + kl = -ky
Applying Newton’s law we get
m \(\frac{d^{2} y}{d t^{2}}\) = -ky
\(\frac{d^{2} y}{d t^{2}}\) = –\(\frac{k}{m}\)y ………………… (7)
The above equation is in the form of simple harmonic differential equation. Therefore, we get the time period as
T = 2π\(\sqrt{m/k}\) second ……………………. (8)
The time period can be rewritten using equation (3)
T = 2π\(\sqrt{m/k}\) = 2πl\(\frac{1}{g}\) second ……………………. (9)
The accleration due to gravity g can be computed by the formula
g = 4π2\((\frac { 1 }{ T } )^{ 2 }\)ms-2 …………………….. (10)
![]()
[OR]
(b) Derive poiseuille’s formula for the volume of a liquid flowing per second through a pipe under streamlined flow?
Answer:
Consider a liquid flowing steadily through a horizontal capillary tube. Let v = (\(\frac{1}{g}\)) be the volume of the liquid flowing out per second through a capillary tube. It depends on (1) coefficient of viscosity (η) of the liquid, (2) radius of the tube (r), and (3) the pressure gradient (\(\frac{P}{l}\)) . Then,
v ∝ηarb(\(\frac{P}{l}\))c
v = kηarb(\(\frac{P}{l}\))c …………………….. (1)
where, k is a dimensionless constant.
Therefore, [v] = \(\frac { Volume }{ Time } \) = [L3T-1]; [ \(\frac{dP}{dX}\) ] = \(\frac { Pressure }{ Distance } \) = [ML-2T-2]
[η] = [Ml-1T-1] and [r] = [L]
Substituting in equation (1)
[L3T-1] = [ML-1T-1]a[L]b [ML-2T-2]c
M0L3T-1 = Ma+bL-a+b-2cT-a-2c = -1
So, equating the powers of M, L and T on both sides, we get
a + c = 0, – a + b – 2c = 3, and – a – 2c = – 1
We have three unknowns a, b and c. We have three equations, on solving, we get
a = – 1, b = 4 and c = 1
Therefore, equation (1) becomes,
v = kη-1r4(\(\frac{P}{l}\))1
Experimentally, the value of k is shown to be , we have \(\frac{π}{8}\), we have
v = \(\frac{\pi r^{4} \mathrm{P}}{8 \eta /}\)
The above equation is known as Poiseuille’s equation for the flow of liquid through a narrow tube or a capillary tube. This relation holds good for the fluids whose velocities are lesser than the critical velocity (vc).
![]()
Question 35 (a).
Describe briefly simple harmonic oscillation as a projection of uniform circular motion?
Answer:
Consider a particle of mass m moving with unifonn speed v along the circumference of a circle whose radius is r in anti-clockwise direction (as shown in figure). Let us assume that the origin of the coordinate system coincides with the center O of the circle.
If ω is the angular velocity of the particle and θ the angular displacement of the particle at any instant of time t, then θ = ωt. By projecting the uniform circular motion on its diameter gives a simple harmonic motion.
This means that we can associate a map (or a relationship) between uniform circular (or revolution) motion to vibratory motion. Conversely, any vibratory motion or revolution can be mapped to unifonn circular motion. In other words, these two motions are similar in nature.
Let us first project the position of a particle moving on a circle, on to its vertical diameter or on to a line parallel to vertical diameter as shown in figure. Similarly, we can do it for horizontal axis or a line parallel to horizontal axis.
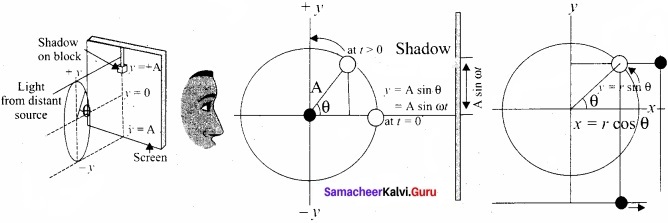
The projection of uniform circular motion on a diameter of SHM:
As a specific example, consider a spring mass system (or oscillation of pendulum). When the spring moves up and down (or pendulum moves to and fro), the motion of the mass or bob is mapped to points on the circular motion.
Thus, if a particle undergoes uniform circular motion then the projection of the particle on the diameter of the circle (or on a line parallel to the diameter) traces straight line motion which is simple harmonic in nature. The circle is known as reference circle of the simple harmonic motion. The simple harmonic motion can also be defined as the motion of the projection of a particle on any diameter of a circle of reference.
[OR]
(b) State and prove Bernoulli’s theorem for a flow of incompressible non viscous and stream lined flow of fluid?
Answer:
Bernoulli’s theorem:
According to Bernoulli’s theorem, the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains a constant. Mathematically,
\(\frac{P}{ρ}\) + \(\frac{1}{2}\)v2 + gh – constant
This is known as Bernoulli’s equation.
Proof:
Let us consider a flow of liquid through a pipe AB. Let V be the volume of the liquid when it enters A in a time t. Which is equal to the volume of the liquid leaving B in the same time. Let aA, vA and PA be the area of cross section of the tube, velocity of the liquid and pressure exerted by the liquid at A respectively.
Let the force exerted by the liquid at A is
FA = PAaA
Distance travelled by the liquid in time t is d = vAt
Therefore, the work done is W = FAd = PAaAvAt
But aAvAt = aAd = V, volume of the liquid entering at A.
Thus, the work done is the pressure energy (at A), W = FAd = PAV
Pressure energy per unit volume at
A = \($\frac{\text { Pressure energy }}{\text { Volume }}$\) = \(\frac { P_{ A }V }{ V } \) = PA
Pressure energy per unit mass at
A = \($\frac{\text { Pressure energy }}{\text { Mass }}$\) = \(\frac { P_{ A }V }{ m } \) = \(\frac { P_{ A } }{ \frac { m }{ V } } \) = \(\frac { P_{ A } }{ \rho } \)
Since m is the mass of the liquid entering at A in a given time, therefore, pressure energy of the liquid at A is
EPA = PAV = PAV × (\(\frac{m}{m}\)) = m\(\frac { P_{ A } }{ \rho } \)
Potential energy of the liquid at A,
PEA = mghA
Due to the flow of liquid, the kinetic energy of the liquid at A,
KEA = \(\frac{1}{2}\)mv2A
Therefore, the total energy due to the flow of liquid at A,
EA = EPA + KEA + PEA
EA = \(m \frac{P_{A}}{\rho}+\frac{1}{2} m v_{A}^{2}+m g h_{A}\)
Similarly, let aB, VB and PB be the area of cross section of the tube, velocity of the liquid and pressure exerted by the liquid at B. Calculating the total energy at FB, we get .
\(\mathrm{E}_{\mathrm{B}}=m \frac{\mathrm{P}_{\mathrm{B}}}{\rho}+\frac{1}{2} m v_{\mathrm{B}}^{2}+m g h_{\mathrm{B}}\)
From the law of conservation of energy.
EA = EB
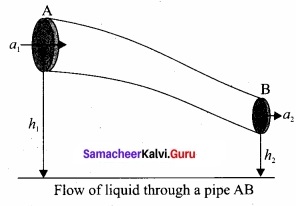
Thus, the above equation can be written as
\(\frac { P }{ \rho g } \) + \(\frac{1}{2}\) \(\frac { v^{ 2 } }{ g } \) + h = Constant
The above equation is the consequence of the conservation of energy which is true until there is no loss of energy due to friction. But in practice, some energy is lost due to friction. This arises due to the fact that in a fluid flow, the layers flowing with different velocities exert frictional forces on each other. This loss of energy is generally converted into heat energy. Therefore, Bernoulli’s relation is strictly valid for fluids with zero viscosity or non-viscous liquids. Notice that when the liquid flows through a horizontal pipe, then
h = 0 ⇒ \(\frac { P }{ \rho g } \) + \(\frac{1}{2}\) \(\frac { v^{ 2 } }{ g } \) = Constant
![]()
Question 36 (a).
Explain perfect inelastic collision and derive an expression for loss of kinetic energy in perfect inelastic collision?
Answer:
In a perfectly inelastic or completely inelastic collision, the objects stick together permanently after collision such that they move with common velocity. Let the two bodies with masses m1 and m2 move with initial velocities u1 and u2 respectively before collision. Aft er perfect inelastic collision both the objects move together with a common velocity v as shown in figure.
Since, the linear momentum is conserved during collisions,
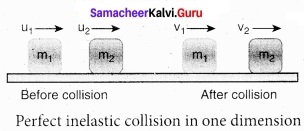
m1u1 + m2u2 = (m1 + m2) v
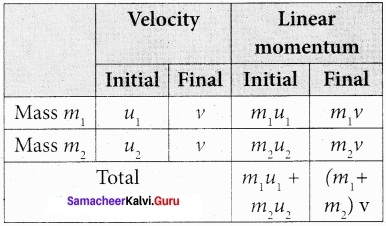
The common velocity can be computed by
v = \(\frac{m_{1} u_{1}+m_{2} u_{2}}{\left(m_{1}+m_{2}\right)}\) ………………….. (1)
Loss of kinetic energy in perfect inelastic collision;
In perfectly inelastic collision, the loss in kinetic energy during collision is transformed to another form of energy like sound, thermal, heat, light etc. Let KEi be the total kinetic energy before collision and KEf be the total kinetic energy after collision.
Total kinetic energy before collision,
KEe = \(\frac{1}{2} m_{1} u_{1}^{2}+\frac{1}{2} m_{2} u_{2}^{2}\) …………………… (2)
Total kinetic energy after collision,
KEf = \(\frac{1}{2}\left(m_{1}+m_{2}\right) v^{2}\) …………………….. (3)
Then the loss of kinetic energy is Loss of KE, ∆Q = KEf – KEi
= \(\frac{1}{2}\left(m_{1}+m_{2}\right) v^{2}-\frac{1}{2} m_{1} u_{1}^{2}-\frac{1}{2} m_{2} u_{2}^{2}\) ………………….. (4)
Substituting equation (1) in equation (4), and on simplifying (expand v by using the algebra (a + b)2 = a2 + b2 + 2ab), we get
Loss of KE, ∆Q = \(\frac{1}{2}\) \(\left(\frac{m_{1} m_{2}}{m_{1}+m_{2}}\right)\) (u1 – u2)2
[OR]
(b) Derive an expression for maximum height attained, time of flight, horizontal range for a projectile in oblique projection?
Answer:
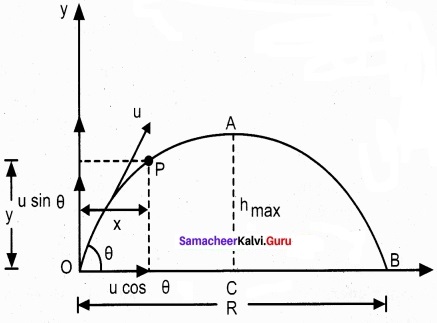
Maximum height (hmax):
The maximum vertical distance travelled by the projectile during the journey is called maximum height. This is determined as follows:
For the vertical part of the motion
\(v_{y}^{2}=u_{y}^{2}+2 a_{y} s\)
Here, uy= u sin θ, a = -g, s = hmax, and at the maximum height v = 0
Time of flight (Tf):
The total time taken by the projectile from the point of projection till it hits the horizontal plane is called time of flight. This time of flight is the time taken by the projectile to go from point O to B via point A as shown in figure.
We know that sy = uyt + \(\frac{1}{2}\)ayt2
Here, sy = y = 0 (net displacement in y-direction is zero), uy = u sin θ, ay = -g, t = Tf, Then
0 = u sin θ Tf – \(\frac{1}{2} g \mathrm{T}_{f}^{2}\)
Tf = 2u \(\frac{sin θ}{g}\) …………………….. (2)
Horizontal range (R):
The maximum horizontal distance between the point of projection and the point on the horizontal plane where the projectile hits the ground is called horizontal range (R). This is found easily since the horizontal component of initial velocity remains the same. We can write.
Range R = Horizontal component of velocity % time of flight = u cos θ × Tf = \(\frac{u^{2} \sin 2 \theta}{g}\)
The horizontal range directly depends on the initial speed (u) and the sine of angle of projection (θ). It inversely depends on acceleration due to gravity ‘g’.
For a given initial speed u, the maximum possible range is reached when sin 2θ is
maximum, sin 2θ = 1. This implies 2θ = π/2 or θ = π/4
This means that if the particle is projected at 45 degrees with respect to horizontal, it attains maximum range, given by
Rmax = \(\frac { u^{ 2 } }{ g } \).
![]()
Question 37 (a).
Explain the work-energy theorem in detail and also give three examples?
Answer:
- If the work done by the force on the body is positive then its kinetic energy increases.
- If the work done by the force on the body is negative then its kinetic energy decreases.
- If there is no work done by the force on the body then there is no change in its kinetic energy, which means that the body has moved at constant speed provided its mass remains constant.
- When a particle moves with constant speed in a circle, there is no change in the kinetic energy of the particle. So according to work energy principle, the work done by centripetal force is zero.
[OR]
(b) (i) Define molar specific heat capacity?
Answer:
Molar specific heat capacity is defined as heat energy required to increase the temperature of one mole of substance by IK or 1°C
(ii) Derive Mayer’s relation for an ideal gas?
Mayer’s relation: Consider p mole of an ideal gas in a container with volume V, pressure P and temperature T.
When the gas is heated at constant volume the temperature increases by dT. As no work is done by the gas, the heat that flows into the system will increase only the internal energy. Let the change in internal energy be dU.
If CV is the molar specific heat capacity at constant volume, from equation.
CV = \(\frac { 1 }{ \mu } \) \(\frac{dU}{dT}\) …………………… (1)
dU = µCV dT ………………… (2)
Suppose the gas is heated at constant pressure so that the temperature increases by dT. If ‘Q’ is the heat supplied in this process and ‘dV’ the change in volume of the gas.
Q = pCpdT ……………. (3)
If W is the workdone by the gas in this process, then
W = P dV ………………….. (4)
But from the first law of thermodynamics,
Q = dU + W ………………… (5)
Substituting equations (2), (3) and (4) in (5), we get,
For mole of ideal gas, the equation of state is given by
\(\mu \mathrm{C}_{\mathrm{p}} d \mathrm{T}=\mu \mathrm{C}_{\mathrm{v}} d \mathrm{T}+\mathrm{P} d \mathrm{V}\)
Since the pressure is constant, dP = 0
CpdT = CVdT + PdV
∴ Cp = CV + R (or) Cp – CV = R …………………… (6)
This relation is called Mayer’s relation It implies that the molar specific heat capacity of an ideal gas at constant pressure is greater than molar specific heat capacity at constant volume.
The relation shows that specific heat at constant pressure (sp) is always greater than specific heat at constant volume (sv).
![]()
Question 38 (a).
Derive an expression of pressure exerted by the gas on the walls of the container?
Answer:
Expression for pressure exerted by a gas : Consider a monoatomic gas of N molecules each having a mass m inside a cubical container of side l.
The molecules of the gas are in random motion. They collide with each other and also with the walls of the container. As the collisions are elastic in nature, there is no loss of energy, but a change in momentum occurs.
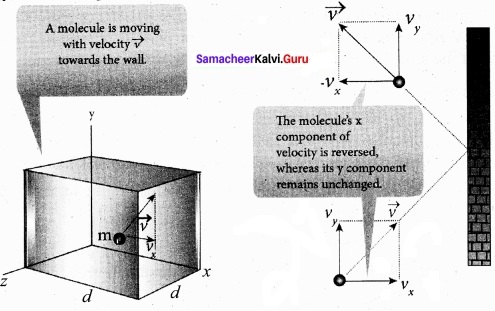
The molecules of the gas exert pressure on the walls of the container due to collision on it. During each collision, the molecules impart certain momentum to the wall. Due to transfer of momentum, the walls experience a continuous force. The force experienced per unit area of the walls of the container determines the pressure exerted by the gas. It is essential to determine the total momentum transferred by the molecules in a short interval of time.
A molecule of mass m moving with a velocity \(\vec { v } \) having components (vx, vy, vz) hits the right side wall. Since we have assumed that the collision is elastic, the particle rebounds with same speed and its x-component is reversed. This is shown in the figure. The components of velocity of the molecule after collision are (-vx, vy, vz).
The x-component of momentum of the molecule before collision = mvx
The x-component of momentum of the molecule after collision = – mvx
The change in momentum of the molecule in x direction
= Final momentum – initial momentum = – mvx – mvx = – 2mvx
According to law of conservation of linear momentum, the change in momentum of the wall = 2 mvx
The number of molecules hitting the right side wall in a small interval of time ∆t.
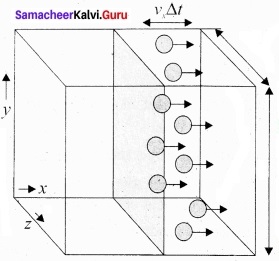
The molecules within the distance of vx∆t from the right side wall and moving towards the right will hit the wall in the time interval ∆t. The number of molecules that will hit the right side wall in a time interval ∆t is equal to the product of volume (Avx∆t) and number density of the molecules (n).
Here A is area of the wall and n is number of molecules per \(\frac{N}{V}\) unit volume. We have assumed that the number density is the same throughout the cube.
Not all the n molecules will move to the right, therefore on an average only half of the n molecules move to the right and the other half moves towards left side.
The number of molecules that hit the right side wall in a time interval ∆t
= \(\frac{n}{2}\) Avx∆t
In the same interval of time ∆t, the total momentum transferred by the molecules
\(\Delta \mathrm{P}=\frac{n}{2} \mathrm{A} v_{x} \Delta t \times 2 m v_{x}=\mathrm{A} v_{x}^{2} m n \Delta t\) ………………….. (2)
From Newton’s second law, the change in momentum in a small interval of time gives rise to force.
The force exerted by the molecules on the wall (in magnitude)
F = \(\frac{∆p}{∆t}\) = nmAv2x ……………………. (3)
Pressure, P = force divided by the area of the wall
P = \(\frac{F}{A}\) = nmAv2x ……………………….. (4)
p = \(nm\bar{v}_{x}^{2}\)
Since all the molecules are moving completely in random manner, they do not have same . speed. So we can replace the term vnmAv2x by the average \(\bar { v } \)2x in equation (4).
P = nm\(\bar { v } \)2x ……………………. (5)
Since the gas is assumed to move in random direction, it has no preferred direction of motion (the effect of gravity on the molecules is neglected). It implies that the molecule has same average speed in all the three direction. So, \(\bar{v}_{x}^{2}\) = \(\bar{v}_{y}^{2}\) = \(\bar{v}_{z}^{2}\). The mean square speed is written as
\(\bar{v}^{2}\) = \(\bar{v}_{x}^{2}\) + \(\bar{v}_{y}^{2}\) + \(\bar{v}_{z}^{2}\) = 3\(\bar{v}_{x}^{2}\)
\(\bar{v}_{x}^{2}\) = \(\frac{1}{3}\) \(\bar{v}^{2}\)
Using this in equation (5), we get
P = \(\frac{1}{3} n m \bar{v}^{2} \quad \text { or } P=\frac{1}{3} \frac{N}{V} m \bar{v}^{2}\) ………………….. (6)
[OR]
(b) Discuss the simple pendulum in detail?
Answer:
Simple pendulum

A pendulum is a mechanical system which exhibits periodic motion. It has a bob with mass m suspended by a long string (assumed to be massless and inextensible string) and the other end is fixed on a stand. At equilibrium, the pendulum does not oscillate and hangs vertically downward.
Such a position is known as mean position or equilibrium position. When a pendulum is displaced through a small displacement from its equilibrium position and released, the bob of the pendulum executes to and fro motion. Let l be the length of the pendulum which is taken as the distance between the point of suspension and the centre of gravity of the bob. Two forces act on the bob of the pendulum at any displaced position.
- The gravitational force acting on the body (\(\vec { F} \) = m\(\vec { g } \)) which acts vertically downwards.
- The tension in the string T which acts along the string to the point of suspension.
![]()
Resolving the gravitational force into its components:
- Normal component: The component along the string but in opposition to the direction of tension, Fas = mg cos θ.
- Tangential component: The component perpendicular to the string i.e., along tangential direction of arc of swing, Fps = mg sin θ.
Therefore, The normal component of the force is, along the string,
\(\mathrm{T}-\mathrm{W}_{a s}=m \frac{v^{2}}{l}\)
Here v is speed of bob
T -mg cos θ = m \(\frac{v^{2}}{l}\)
From the figure, we can observe that the tangential component Wps of the gravitational force always points towards the equilibrium position i.e., the direction in which it always points opposite to the direction of displacement of the bob from the mean position. Hence, in this case, the tangential force is nothing but the restoring force. Applying Newton’s second law along tangential direction, we have
\(m \frac{d^{2} s}{d t^{2}}+\mathrm{F}_{p s}=0 \Rightarrow m \frac{d^{2} s}{d t^{2}}=-\mathrm{F}_{p s}\)
\(m \frac{d^{2} s}{d t^{2}}=-m g \sin \theta\) …………………. (1)
where, s is the position of bob which is measured along the arc. Expressing arc length in terms of angular displacement i.e.,
s = lθ ………………… (2)
then its acceleration, \(\frac{d^{2} s}{d t^{2}}=l \frac{d^{2} \theta}{d t^{2}}\) …………………. (3)
Substituting equation (3) in equation (1), we get
\(\begin{aligned}
l \frac{d^{2} \theta}{d t^{2}} &=-g \sin \theta \\
\frac{d^{2} \theta}{d t^{2}} &=-\frac{g}{l} \sin \theta
\end{aligned}\) ………………….. (4)
Because of the presence of sin θ in the above differential equation, it is a non-linear differential equation (Here, homogeneous second order). Assume “the small oscillation approximation”, sin θ ~ 0, the above differential equation becomes linear differential equation.
\(\frac{d^{2} \theta}{d t^{2}}=-\frac{g}{l} \theta\) …………………… (5)
This is the well known oscillatory differential equation. Therefore, the angular frequency of this oscillator (natural frequency of this system) is
ω2 = \(\frac{g}{l}\) …………………… (6)
∴ ω = \(\sqrt{g/l}\) in rad s-1 ……………….. (7)
The frequency of oscillation is
f = \(f=\frac{1}{2 \pi} \sqrt{\frac{g}{l}} \text { in } \mathrm{Hz}\) ………………… (8)
and time period of sscillations is
T = 2π\(\sqrt{l/g}\) in second. ……………….. (9)