Prasanna

Students can Download Maths Chapter 6 Information Processing Ex 6.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 6 Information Processing Ex 6.2

Miscellaneous Practice Problems

Question 1.
Make a model of a fish using the given tetromino shapes

Complete the given rectangle using the given tetromino shapes.
Solution:

Question 2.
Complete the given rectangle using the given tetromino shapes.

Solution:

Question 3.
Shade the figure completely, by using five Tetromino shapes only once.

Solution:

Question 4.
Using the given tetrominoes with numbers on it complete the 4 × 4 magic square?

Solution:

Question 5.
Find the shortest route to Vivekanandar Memorial Hall from the Mandapam using the given map.

Solution:
Possible routes from Mandapam to Vivekandar Memorial are

route 1:
(a) Mandapam ➝ Pullivasal Island ➝ Krusadai Island ➝ Vivekanandar Memorial Hall.
Distance = 6 Km + 2 Km + 1.5 Km = 9.5 Km

route 2:
(b) Mandapam ➝ Krusadai Island ➝ Vivekanandar Memorial Hall.
Distance = 7 Km + 1.5 Km = 8.5 Km
8.5 km < 9.5 km
∴ Shortest route : Mandapam ➝ Krusadai Island ➝ Vivekanandar Memorial Hall.

Challenge Problems

Question 6.
Fill in 4 × 10 rectangle completely, using all the five tetrominoes twice.
Solution:

(more possible ways are there)

Question 7.
Fill in 8 × 5 rectangle completely, using all the five tetrominoes twice.
Solution:

(more possible way are there)

Question 8.
Observe the picture and answer the following.
(i) Find all the possible routes from A to D.
(ii) Find the shortest distance between E and C.
(iii) Find all the possible routes between B and F with distance. Mention the shortest route.

Solution:
(i) All possible routes from A to D are :
(a) A ➝ G ➝ F ➝ E ➝ D
(b) A ➝ G ➝ D
(c) A ➝ B ➝ C ➝ D
(d) A ➝ B ➝ D

(ii) Distance between E and C are
(a) Route 1: E ➝ D ➝ C
Distance: 120 m + 200 m = 320 m.
(b) Route 2: E ➝ D ➝ B ➝ C
Distance = 120 + 100 m + 120 m
= 340 m.
∴ Shortest distance is 320 m.

(iii) All possible routes between B and F are :
(a) Route 1: B ➝ A ➝ G ➝ F
Distance = 250 m + 100 m + 150 m = 600 m.

(b) Route 2: 2 ➝ D ➝ E ➝ F
Distance = 100 m + 120 m + 300 m
= 520 m.

(c) Route 3: B ➝ D ➝ G ➝ F
Distance = 100 m + 200 m + 150 m
= 450 m.

(d) Route 4: B ➝ C ➝ D ➝ E ➝ F
Distance = 120 m + 200 m + 120 m + 300 m
= 740 m.
We find that Route 3 is shortest.
ie B ➝ D ➝ G ➝ F is the shortest route.

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 5 Statistics Additional Questions

Question 1.
A _____ is a collection of numbers gathered to give some meaningful information.
Solution:
Data

Question 2.
The data can be arranged in a tabular form using ____ marks
Solution:
Tally

Question 3.
A observation occurring 8 times in a data is represented as _____ using tally marks.
Solution:

Question 4.
Tally marks  represents _____
Solution:
6

Question 5.
Following are the choice of sports for 20 students of class VI.

Arrange the names of sports in a table using tally marks.
Solution:

Question 6.
Mariana threw a die 40 times and noted the number appearing each time as shown below.

Make a table and enter the data using tally marks.
Find the number that appeared
(a) the minimum number of times
(b) the maximum number of times
(c) Find those numbers that appear an equal number of times.
Solution:
Table using Tally Marks

(a) The number ‘4’ appeared the minimum number of times
(b) The number ‘5’ appeared the maximum number of times
(c) Numbers ‘1’ and ‘6’ appeared the equal number of times.

Question 7.
What is the advantage of using pictograph?
Solution:
The data can be analyzed and interpreted. The pictures and symbols help us to understand better.

Question 8.
Total number of students of a school in different years is shown in the following table

(A) Prepare a pictograph of students using one symbol to represent 100 students and answer the following questions
(a) How many symbols represent the total number of students in the year 2000?
(b) How many symbols represent the total number of students in the year 1997?
Solution:
(A) The pictograph is given by

(a) 9 Full pictures and a half picture represent the number of students in the year 2000
(b) 5 symbols.

Question 9.
The number of bottles of honey sold by three different shops are given below.

(A) Draw a pictograph and answer the following questions (use the scale – 20 bottles)
(a) What is the total profit of shop A, if the profit gained on each bottle is ‘E’150?
(b) If the total number of bottles sold is 400 how many figures must be drawn to shops?
(c) Find the difference between the number of bottles sold by shop B and the number of bottles sold by shop ‘C’.
Solution:
(A) Pictograph of number of bottles sold

(a) Profit per bottle = ₹ 150
Shop A’s total profit = 80 × 150 = ₹ 12,000
(b) For 400 bottles, the figures to be drawn is \(\frac{400}{20}\) = 20 bottles for shop ‘C ’
(c) Difference = No. of bottles sold by shop ‘C’ – No. of bottles sold by shop ‘B’ = 180 – 140 = 40 bottles

Question 10.
The following data is the total savings of a group of 5 friends in a year.

Draw a pictograph to represent the data.
Solution:

Question 11.
The number of mathematics books sold by a shopkeeper on six consecutive days is shown below.

Draw a bar graph to represent the above information choosing the scale of your choice.
Solution:

Question 12.
The following bar graph shows the number of people visited Mahabalipuram over a period of 5 months.

Use the graph to answer the following questions
(a) How many people visited Mahabalipuram in April?
(b) How many more people visited Mahabalipuram in May than in January?
(c) In which month, were there as many visitors as in March?
(d) In which month was there 1500 more visitors than in January?
(e) How many visitors were there in 5 months?
Solution:
(a) 3500 people visited Mahabalipuram in April
(b) 500 more people
(c) January
(d) April
(e) 11,500 people

Students can Download Maths Chapter 4 Geometry Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Additional Questions

Additional Questions And Answers

Very Short Answers [2 Marks]

Question 1.
In the given figure if ∠A = ∠C then prove that ∆AOB ~ ∆COD.

Solution:
In triangles ∆AOB and ∆COD
∠A = ∠C (Y given)
∠AOB = ∠COD [∵ Vertically opposite angles]
∠ABO = ∠CDO [Remaining angles of ∆AOB and ∆COD]
∴ ∆AOB ~ ∆COD [∵ AAA similarity]
∵ ∆AOB ~ ∆COD [∵ AAA similarity]

Question 2.
In the figure AB ⊥ BC and DE ⊥ AC prove that ∆ABC ~ ∆AED.

Solution:
In triangles ∆ABC and ∆AED
∠ABC = ∠AED = 90°
∠BAC = ∠EAD [Each equal to A]
∠ADE = ∠ACB [∵ Remaining angles]
∴ By AAA criteria of similarity ∆ABC ~ ∆AED

Short Answers [3 Marks]

Question 1.
In the figure with respect to ABEP and CPD prove that BP × PD = EP × PC.

Solution:
Proof:
In ∆EPB and ∆DPC
∠PEB = ∠PDC = 90° [given]
∠EPB = ∠DPC [Vertically opposite angles]
∠EPB = ∠PCD [∵ Remaining angles]
Thus,

Long Answers [5 Marks]

Question 1.
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm PB = 6cm, AQ = 5 cm and QC = 10 cm, show that BC = 3 PQ.
Solution:

AB = AP + PB
= 3 + 6 cm = 9 cm
AC = AQ + QC = 510 cm = 15

Students can Download Maths Chapter 4 Geometry Ex 4.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Additional Questions

Construct the quadrilaterals with the following measurements and also find their area.

Question 1.
ABCD, AB = 5 cm, BC 4.5 cm, CD = 3.8 cm, DA = 4.4 cm and AC = 6.2 cm.
Solution:
Given AB = 5 cm,
BC = 4.5 cm,
CD = 3.8 cm,
DA = 4.4 cm,
AC = 6.2 cm

Steps:
1. Draw a line segment AB = 5 cm
2. With A and B as centers drawn arcs of radii 6.2 cm and 4.5cm respectively and let them cut at C.
3. Joined AC and BC.
4. With A and C as centrers drawn arcs of radii 4.4cm and 3.8 cm respectively and let them at D.
5. Joined AD and CD.
6. ABCD is the required quadrilateral.
Calculation of Area:

Question 2.
KITE, KI = 5.4 cm, IT = 4.6 cm, TE= 4.5 cm, KE = 4.8 cm and IE = 6 cm.
Solution:
Given, KI = 5.4 cm,
IT = 4.6 cm,
TE= 4.5 cm,
KE = 4.8 cm,
IE = 6 cm.

Steps:
1. Draw a line segment KI = 5.4 cm
2. With K and I as centers drawn arcs of radii 4.8 cm and 6 cm respectively and let them cut at E.
3. Joined KE and IE.
4. With E and I as centers, drawn arcs of radius 4.5cm and 4.6 cm respectively and let them cut at T.
5. Joined ET and IT.
6. KITE is the required quadrilateral.
Calculation of Area:

Question 3.
PLAY, PL = 7 cm, LA = 6 cm, AY= 6 cm, PA = 8 cm and LY = 7 cm.
Solution:
Given PL = 7 cm,
LA = 6 cm,
AY= 6 cm,
PA = 8 cm,
LY = 7 cm

Steps:
1. Draw a line segment PL = 7 cm
2. With P and L as centers, drawn arcs of radii 8 cm and 6 cm respectively, let them cut at A.
3. Joined PA and LA.
4. With L and A as centers, drawn arcs of radii 7 cm and 6 cm respectively and let them cut at Y.
5. Joined LY, PY and AY.
6. PLAY is the required quadrilateral.
Calculation of Area:

Question 4.
LIKE, LI = 4.2 cm, IK = 7 cm, KE = 5 cm, LK = 6 cm and IE = 8 cm.
Solution:
LI = 4.2 cm,
IK = 7 cm,
KE = 5 cm,
LK = 6 cm,
IE = 8 cm

Steps:
1. Draw a line segment LI = 4.2 cm
2. With L and I as centers, drawn arcs of radii 6 cm and 7 cm respectively and let them cut at K.
3. Joined LK and IK.
4. With I and K as centers, drawn arcs of radius 8 cm and 5 cm respectively and let them cut at E.
5. Joined LE, IE and KE.
6. LIKE is the required quadrilateral.
Calculation of Area:

Question 5.
PQRS, PQ = QR = 3.5 cm, RS = 5.2 cm, SP = 5.3 cm and ∠Q =120° .
Solution:
PQ = QR = 3.5 cm,
RS = 5.2 cm,
SP = 5.3 cm ,
∠Q =120°

Steps:
1. Draw a line segment PQ = 3.5 cm
2. Made ∠Q = 120°. Drawn the ray QX.
3. With Q as centre drawn an arc of radius 3.5 cm. Let it cut the ray QX at R.
4. With R and P as centres drawn arcs of radii 5.2cm and 5.5 cm respectively and let them cut at S.
5. Joined PS and RS.
6. PQRS is the required quadrilateral.
Calculation of Area:
Area of the quadrilateral PQRS = 18 cm²

Question 6.
EASY, EA = 6 cm, AS = 4 cm, SY = 5 cm, EY = 4.5 cm and ∠E = 90°.
Solution:
EA = 6 cm,
AS = 4 cm,
SY = 5 cm,
EY = 4.5 cm,
∠E = 90°

1. Drawn a line segment EA = 6 cm
2. Made ∠E = 90°. From E drawn the ray EX.
3. With E as center drawn an arc of 4.5 cm radius. Let of cut the ray EX at Y.
4. With A and Y as centres drawn arcs of radii 4 cm and 5 cm respectively and let them cut at S.
5. Joined AS and YS.
6. EASY is the required quadrilateral.
Calculation of Area:

∴ Area of the quadrilateral = 22.87 cm²

Question 7.
MIND, MI = 3.6 cm, ND = 4 cm, MD = 4 cm, ∠M = 50° and ∠D = 100°.
Solution:
MI = 3.6 cm,
ND = 4 cm,
MD= 4 cm,
∠M = 50°,
∠D = 100°

1. Draw a line segment MI = 3.6 cm
2. At M on MI made an angle ∠IMX = 50°
3. Drawn an arc with center M and radius 4 cm let it cut MX it D
4. At D on DM made an angle ∠MDY = 100°
5. With I as center drawn an arc of radius 4 cm, let it cut DY at N.
6. Joined DN and IN.
7. MIND is the required quadrilateral.
Calculation of Area:

Area of the quadrilateral = 9.6 cm²

Question 8.
WORK, WO = 9 cm, OR = 6 cm, RK = 5 cm, ∠O = 100° and ∠R = 60°.
Solution:
WO = 9 cm,
OR = 6 cm,
RK = 5 cm,
∠O = 100°,
∠R = 60°

Steps:
1. Drawn a line segment WO = 9 cm
2. At O on WO made an angle ∠WOR = 100° and drawn the ray OX.
3. Drawn an arc of radius 6 cm with center O. Let it intersect OX at R.
4. At R on OR, made ∠ORY = 60°, and drawn the ray RY.
5. With center R drawn an arc of radius 5 cm, let it intersect RY at K.
6. Joined WK.
7. WORK is the required quadrilateral.
Calculation of Area:

Area of the quadrilateral = 31.59 cm²

Question 9.
AGRI, AG = 4.5 cm, GR = 3.8 cm, ∠A = 90°, ∠G = 110° and ∠R = 90°.
Solution:
AG = 4.5 cm,
GR = 3.8 cm,
∠A = 90°,
∠G = 110°,
∠R = 90°

1. Draw a line segment AG = 4.5 cm
2. At G on AG made ∠AGX =110°
3. With G as centre drawn an arc of radius 3.8 cm let it cut GX at R.
4. At R on GR made ∠GRZ = 90°
5. At A on AG made ∠GAY = 90°
6. AY and RZ meet at I.
7. AGRI is the required quadrilateral.
Calculation of Area:

Question 10.
YOGA, YO = 6 cm, OG = 6 cm, ∠O = 55°, ∠G = 55° and ∠A = 55°.
Solution:
YO = 6 cm,
OG = 6 cm,
∠O = 55°,
∠G = 55°,
∠A = 55°

Steps:
1. Draw a line segment OG = 6 cm
2. At G on DG made an angle ∠OGY = 55°
3. AT G on GO made ∠GOX = 55°.
4. GY and OX meet cut A.
5. At A on OA made ∠OAZ = 55°
6. Drawn an arc of radius 6 cm with center O. It cut AZ at Y. Joined OY.
7. YOGA is the required quadrilateral.
Calculation of Area:

Area of the quadrilateral YOGA = 28.08 cm²

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Intext Questions

Recap (Textbook Page No. 55)

Question 1.
Which of the following fractions is not a proper fraction?
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{5}{10}\)
(d) \(\frac{10}{5}\)
Solution:
(d) \(\frac{10}{5}\)

Question 2.
The equivalent fraction of \(\frac{1}{7}\) is ____
(a) \(\frac{2}{15}\)
(b) \(\frac{1}{49}\)
(c) \(\frac{7}{49}\)
(d) \(\frac{100}{7}\)
Solution:
(c) \(\frac{7}{49}\)

Question 3.
Write >, < or = in the box.
(i) \(\frac{5}{8}\) ____ \(\frac{1}{10}\)
(ii) \(\frac{9}{12}\) _____ \(\frac{3}{4}\)
Solution:

Question 4.
Arrange these fractions from the least to the greatest: \(\frac{1}{2}, \frac{1}{4}, \frac{6}{8}, \frac{1}{8}\)
Solution:
\(\begin{array}{l}{\frac{1}{2}=\frac{1 \times 4}{2 \times 4}=\frac{4}{8}} \\ {\frac{1}{4}=\frac{1 \times 2}{4 \times 2}=\frac{2}{8}}\end{array}\)
Comparing \(\frac{4}{8}, \frac{2}{8}, \frac{6}{8} \text { and } \frac{1}{8}\). we have \(\frac{1}{8}<\frac{2}{8}<\frac{4}{8}<\frac{6}{8}\)
i.e, \(\frac{1}{8}<\frac{1}{4}<\frac{1}{2}<\frac{6}{8}\)

Question 5.
Annan says the \(\frac{2}{6}\) th of the group of triangles given below are blue. Is he correct?

Solution:
No, he is not correct because of the total of 6 triangles 4 are blue, i.e \(\frac{4}{6}^{\text {th }}\) triangles are blue.

Question 6.
Joseph has a flower garden. Draw a picture which shows that \(\frac{2}{10}\) th of the flowers are red and the rest of them are yellow.
Solution:

Question 7.
Malarkodi has 10 oranges. If she ate 4 oranges, what fraction of oranges she was not eaten by her?
Solution:
\(\frac{\text { Oranges not eaten }}{\text { Total oranges }}=\frac{10-4}{10}=\frac{6}{10}\)

Question 8.
After sowing seeds on day one, Muthu observes the growth of two plants and records it. In 10 days, if the first plant grew \(\frac{1}{4}\) th of an inch and the second plant grew \(\frac{3}{8}\) th of an inch, then which plant grew more?
Solution:
Comparing \(\frac{1}{4}\) th of an inch and \(\frac{3}{8}\) th of an inch.
\(\frac{1}{4}=\frac{2}{8}<\frac{3}{8}\)
Second plant grew more.

Try These (Textbook Page No. 57 to 60)

Question 1.
Write the ratio of red tiles to blue tiles and yellow tiles to red tiles.

Solution:
(i) Red tiles to blue tiles = 2 : 3
(ii) Yellow tiles to red tiles = 2 : 2

Question 2.
Write the ratio of blue tiles to that of red tiles and red tiles to that of total tiles.

Solution:
The ratio of blue tiles to red tiles = 3 : 5
The ratio of red tiles to total tiles = 5 : 8

Question 3.
Write the ratio of shaded portion to the unshaded portions in the following shapes.

Solution:
(i) Ratio = 1 : 2
(ii) Ratio = 5 : 4

Question 4.
If the given quantity is in the same unit, put ‘✓’ otherwise put ‘ ✗’ in the table below.

Solution:

Question 5.
Write the ratios in the simplest form and fill in the table.

Solution:

Try These (Textbook Page No. 64)

Question 1.
For the given ratios, find two equivalent ratios and complete the table.

Solution:

Question 2.
Write three equivalent ratios and fill in the boxes.

Solution:

Question 3.
Find the given ratios, find their simplest form and complete the table.

Solution:

Try These (Textbook Page No. 70)

Question 1.
Fill the box by using cross product rule of two ratios
Solution:

By cross product rule we have 1 × □ = 5 × 8
1 × 40 = 40
∴ \(\frac{1}{8}=\frac{5}{40}\)

Question 2.
Use the digits 1 to 9 only once and write as many ratios that are in proportion as possible (For example \(\frac{2}{4}=\frac{3}{6}\))
Solution:

Students can Download Maths Chapter 4 Geometry Ex 4.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.2

Miscellaneous Practice Problems

Question 1.
In the given figure, find PT given that l₁ || l₂

Solution:
Given that l₁ || l₂
∴ In ∆PQS and ∆PRT
∠P is common
∠Q = ∠R [∵ PR is the transversal for l₁ and l₂ corresponding angles]
∠S = ∠T [∵ corresponding angles]
∴ ∆PQS ~ ∆PRT [∵ By AAA congruency]
In similar triangles, corresponding angles are proportional.

Question 2.
From the diagram, prove that ∆SUN ~ ∆RAY

Proof:
From the ∆SUN and ∆RAY
SU = 10;
UN = 12;
SN = 14;
RA = 5,
AY = 6;
RY = 7
We have

Question 3.
The height of a tower is measured by a mirror on the ground by which the top of the tower’s reflection is seen. Find the height of the tower.
Solution:
The image and its reflection make similar shapes

Question 4.
In the figure, given that ∠1 = ∠2 and ∠3 ≡ ∠4 Prove that ∆MUG ≡ ∆ TUB.

Proof:

Question 5.
If ∆WAR ≡ ∆MOB, name the additional pair of corresponding parts. Name the criterion used by you.
Solution:

Given ∆WAR ≡ ∆MOB
∠RWA ≡ ∠BMO [∵ sum of three angles of a triangle are 180°]
∴ Criteria used here is angle sum property of triangles.

Question 6.
In the figure, ∠TMA ≡ ∠IAM and ∠TAM ≡ ∠IMA. P is the midpoint of MI and N is the midpoint of AI. Prove that ∆ PIN ~ ∆ ATM.

Solution:

Question 7.
In the figure, if ∠FEG = ∠1 then, prove that DG² = DE.DF.

Proof:

Question 8.
In the figure, ∠TEN ≡ ∠TON = 90° and TO = TE. Prove that ∠ORN ≡ ∠ERN

Solution:

Question 9.
In the figure, PQ ≡ TS, Q is the midpoint of PR, S is the midpoint TR and ∠POU ≡ ∠TSU. Prove that QU ≡ SU.

Proof:

Question 10.
In the figure ∆TOP ≡ ∆ARM . Explain why?
Solution:
In ∆TOP and ∆ARM
OP = RM given
∠TOP = ∠ARM = 90°
given ∠OTP = ∠RAM
given ∠OPT = ∠RMA Remaining angle, by angle sum property.
∴ By ASA criteria we can say that ∆TOP ≡ ∆ARM

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 4 Geometry Intext Questions

Try These (Textbook Page No. 80, 81)

Question 1.
Name all the line segments.

Solution:
\(\overline{\mathrm{AB}}, \overline{\mathrm{AE}}, \overline{\mathrm{EB}}, \overline{\mathrm{CD}}, \overline{\mathrm{CE}} \text { and } \overline{\mathrm{ED}}\)

Question 2.
If AB = 5 cm, say which of the following measures are correct in fig 4.9.

Solution:
Fig 4.9(i) and fig 4.9(ii) measures are correct.

Try These (Textbook Page No. 85)

Question 1.

1. Name the rays in the given figure.
2. What is the common point of all these rays?
Solution:
1. \(\overrightarrow{\mathrm{TA}}, \overrightarrow{\mathrm{TB}}, \overrightarrow{\mathrm{TC}} \text { and } \overrightarrow{\mathrm{TD}}\) are the rays given
2. Point T is the common point of all these rays.

Try These (Textbook Page No. 90, 95)

Question 1.
Which direction will you face if you start facing West and take three right turns clockwise?
Solution:
Will be facing South.

Question 2.
Which direction will you face if you start facing North and take two right turns anticlockwise?
Solution:
Will be facing South.

Question 3.
Adjust the hands of the clock for following time, note the angle made between the hour hand and the minute hand and write the type of angle.


Solution:

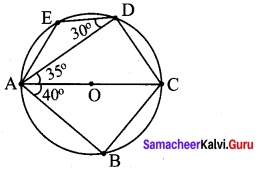
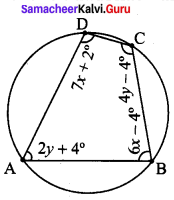
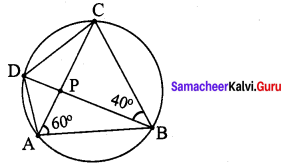
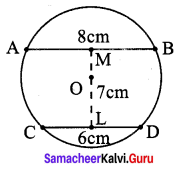
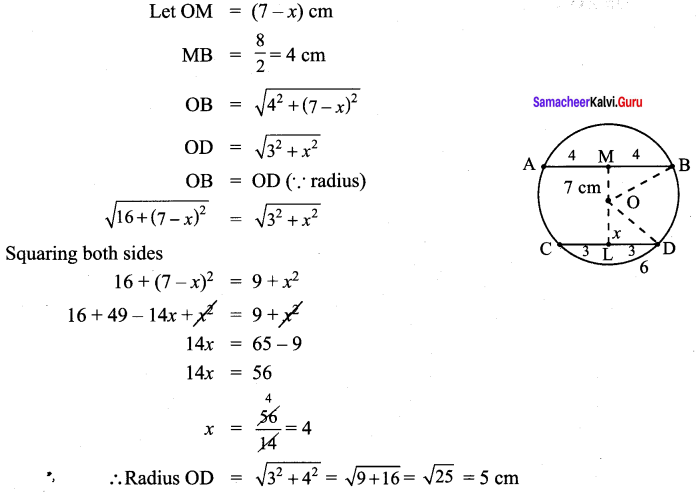
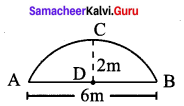
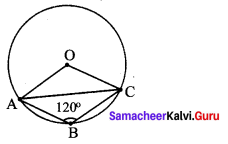
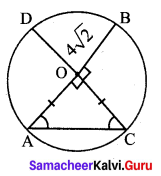
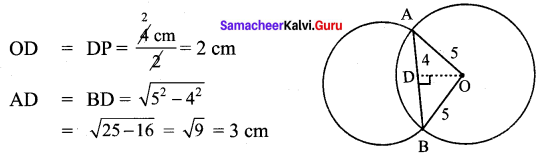
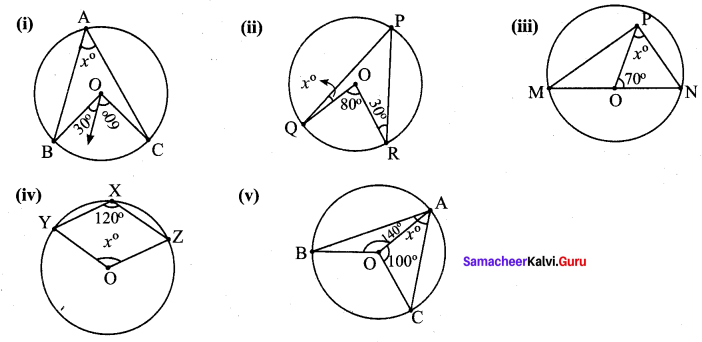
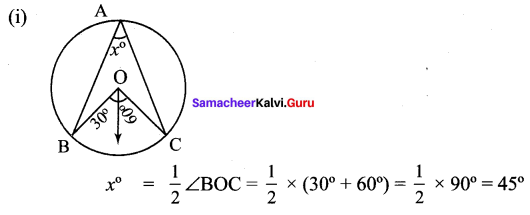
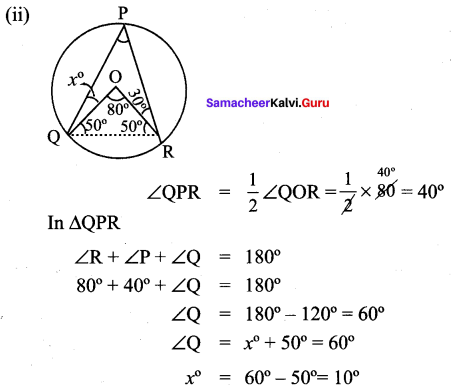
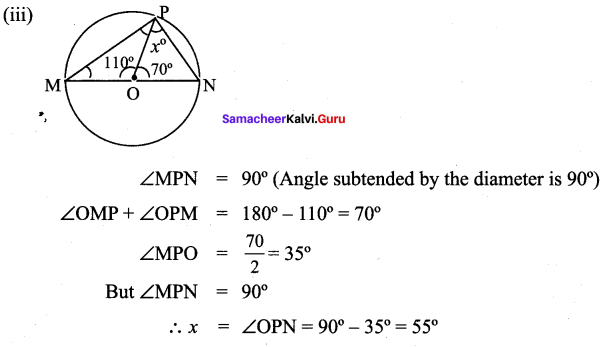
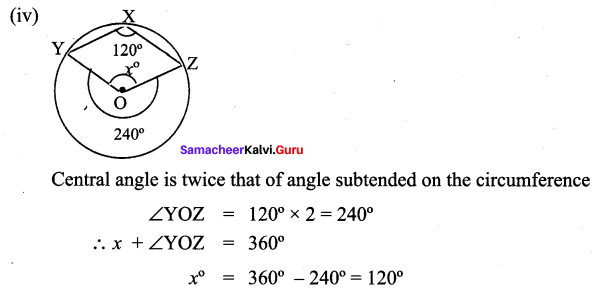
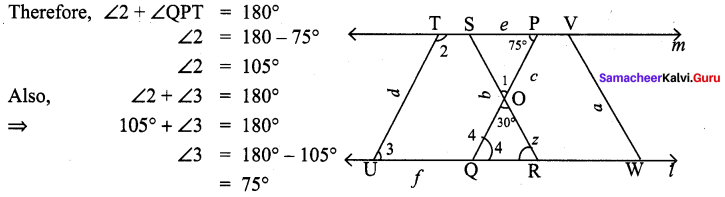
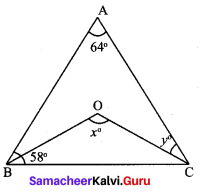
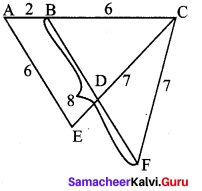
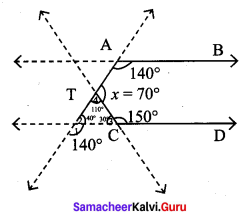
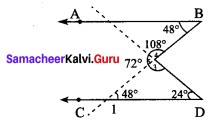
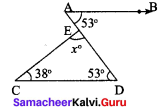
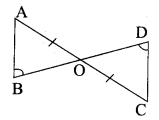
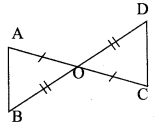
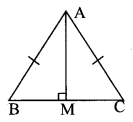
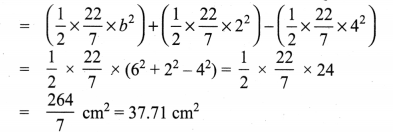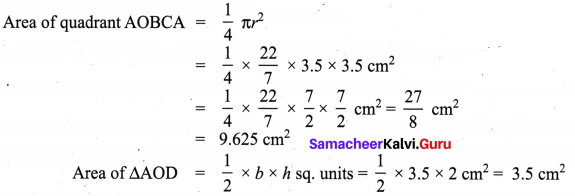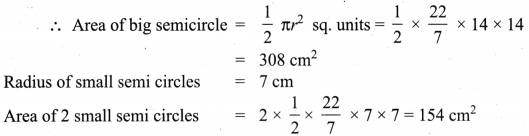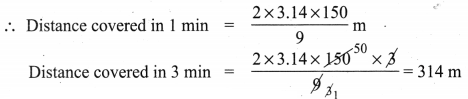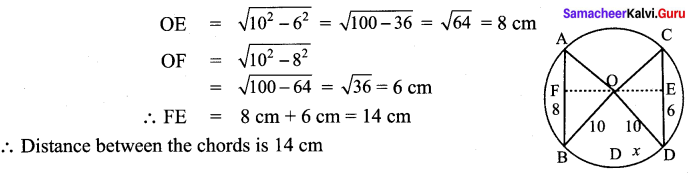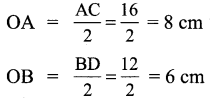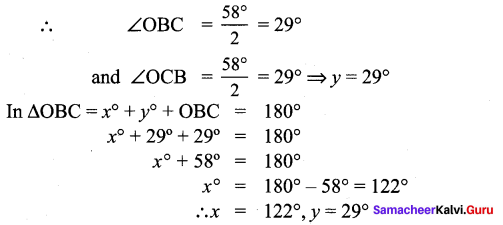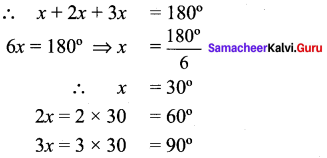Students can Download Maths Chapter 2 Measurements Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Intext Questions

Try this Page No. 35

Question 1.
\(\frac{22}{7}\) and 3.14 are rational numbers. Is ‘π’ a rational number? Why?
Solution:
\(\frac{22}{7}\) and 3.14 are rational numbers n has non-terminating and non -repeating decimal expansion. So it is not a rational number. It is an irrational number.

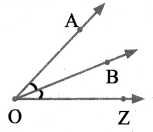
Try this Page No. 38

Question 1.
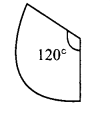
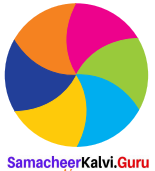
The given circular figure is divided into six equal parts. Can we call the parts as sectors? Why?

Solution:
No, the equal parts are not sectors. Because a sector is a plane surface that is enclosed between two radii and the circular arc of the circle.
Here the boundaries are not radii.

Try these Page No. 38

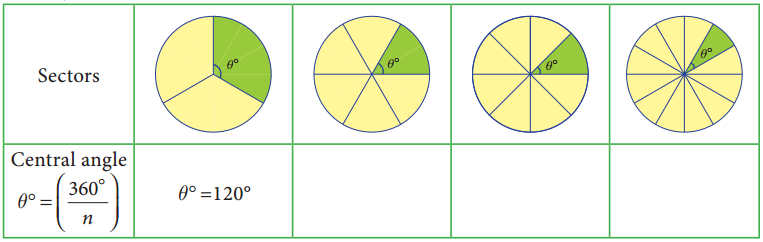
Question 1.
Fill the central angle of the shaded sector (each circle is divided into equal sectors)

Try this Page No. 44

Question 1.
If the radius of a circle is doubled, what will the area of the new circle so formed?
Solution:
If r = 2r₁ ⇒ Area of the circle = πr² = π(2r₁)² = π4r₁² = 4πr₁²
Area = 4 × old area.

Try this Page No. 49

Question 1.
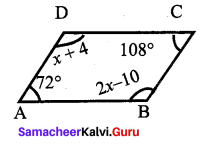
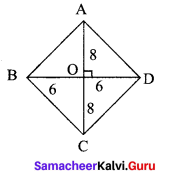
All the sides of a rhombus are equal. Is it a regular polygon?
Solution:
For a regular polygon all sides and all the angles must be equal. But in a rhombus all the
sides are equal. But all the angles are not equal
∴ It is not a regular polygon.

Try this Page No. 53

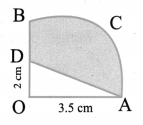
Question 1.
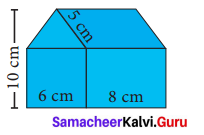
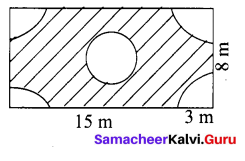
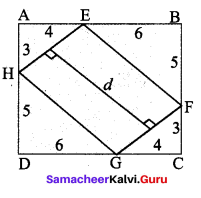
In the above example split the given mat as into two trapeziums and verify your answer.
Solution:
Area of the mat = Area of I trapezium + Area of II trapezium

∴ Cost per sq.feet = ₹ 20
Cost for 28 sq. feet = ₹ 20 × 28 = ₹ 560
∴ Total cost for the entire mat = ₹ 560
Both the answers are the same.

Try these Page No. 54

Question 1.
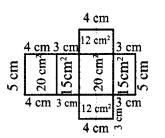
Show that the area of the unshaded regions in each of the squares of side ‘a’ units are the same in all the cases given below.

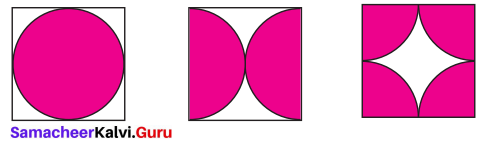
Solution:

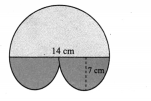
Question 2.
If π = \(\frac{22}{7}\), show that the area of the unshaded part of a square of side ‘a’ units is approximately \(\frac{3}{7}\) a² sq. units and that of the shaded part is approximately \(\frac{4}{7}\) a² sq. units for the given figure.

Solution:

Try this Page No. 57

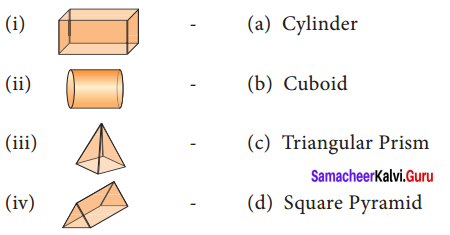
Question 1.
List out atleast three objects in each category which are in the shape of cube, cuboid,
cylinder, cone and sphere.
Solution:
(i) Cube – dice, building blocks, jewel box.
(ii) Cuboid – books, bricks, containers.
(iii) Cylinder – candles, electric tube, water pipe.
(iv) Cone – Funnel, cap, ice cream cone
(v) Sphere – ball, beads, lemon.

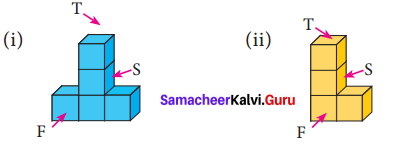
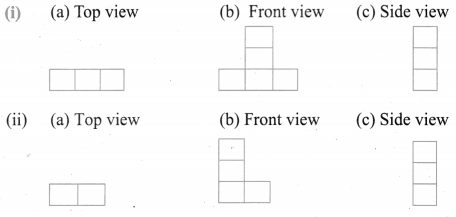
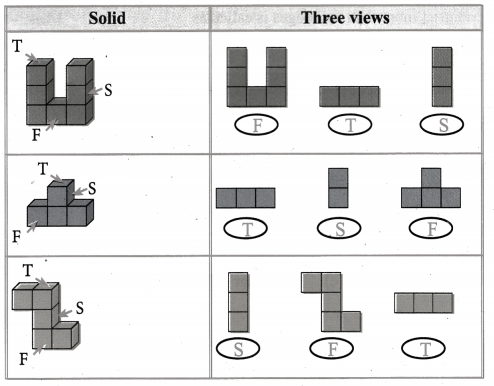
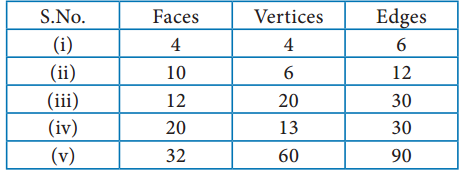
Try this Page No. 58

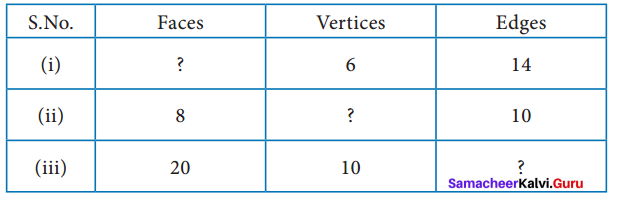
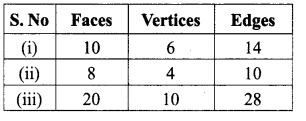
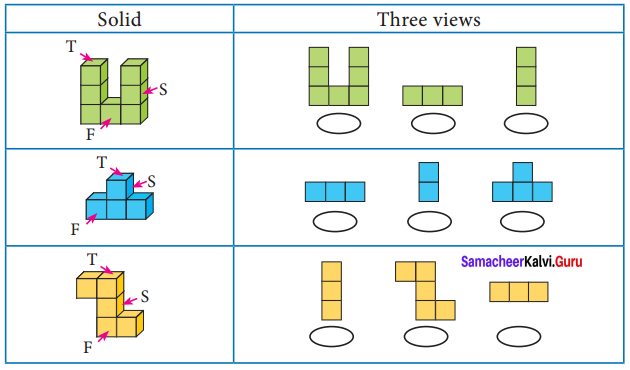
Question 1.
Tabulate the number of faces(F), vertices(V) and edges(E) for the following polyhedron. Also find F + V – E
Solution:

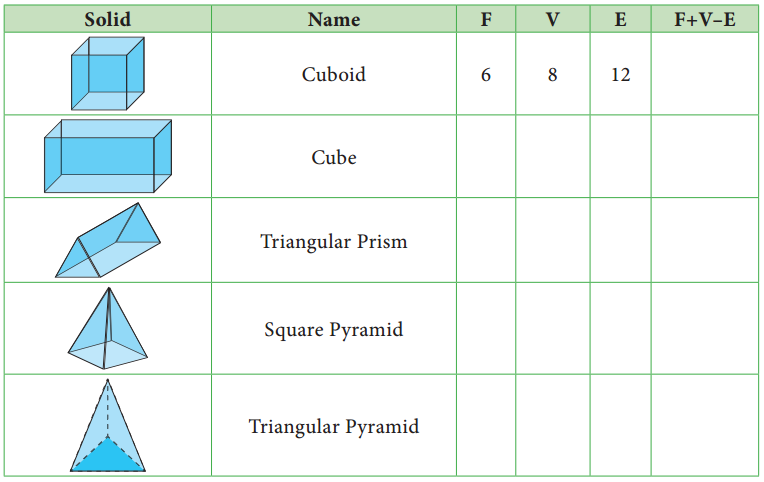
From the table F + V – E = 2 for all the solid shapes.

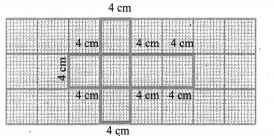
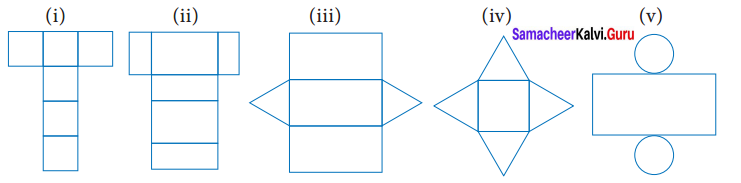
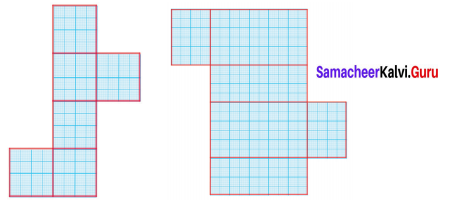
Try this Page No. 58

Question 1.
Find the area of the given nets.

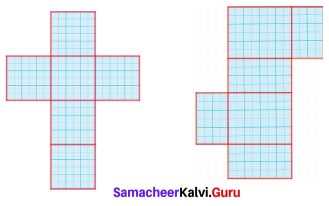
Solution:
Area = 6 × Area of a square of side 6 cm
= 6 × (6 × 6) cm²
= 216 cm²
(ii) Area = Area of 2 rectangles of side (8 × 6) cm² + Area of 2 rectangles of side (8 × 4) cm² + Area of 2 rectangles of side (6 × 4) cm²
= (8 × 6) + (8 × 4) + (6 × 4)cm²
= 48 + 32 + 24 cm²
= 104 cm²

Students can Download Maths Chapter 3 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Intext Questions

Exercise 3.1

Recap Page No. 66 and 67

Question 1.
Write the numbers of terms in the following expressions.
(i) x + y + z – xyz
Solution:
4 terms

(ii) m²n²c
Solution:
1 term

(iii) a²b²c – ab²c² + a²bc² + 3abc
Solution:
4 terms

(iv) 8x² – 4xy + 7xy²
Solution:
3 terms

Question 2.
Identify the numerical co-efficient of each term in the following expressions.
Question 1.
2x² – 5xy + 6y² + 7x – 10y + 9
Solution:
Numerical co efficient in 2x² is 2
Numerical co efficient in -5xy is -5
Numerical co efficient in 6y² is 6
Numerical co efficient in 7x is 7
Numerical co efficient in -10y is – 10
Numerical co-efficient in 9 is 9

Question 2.
\(\frac{x}{3}+\frac{2 y}{5}-x y+7\)
Solution:

Numerical co efficient in -xy is -1
Numerical co efficient in 7 is 7

Question 3.
Pick out the like terms from the following.

Solution:

Question 4.
Add : 2x, 6y, 9x – 2y
Solution:
2x + 6y + 9x – 2y = 2x + 9x + 6y – 2y = (2 + 9)x + (6 – 2)y = 11x + 4y

Question 5.
Simplify : (5x³ y³ – 3x² y² + xy + 7) + (2xy + x³y³ – 5 + 2x²y²)
Solution:
(5x³y³ – 3x²y² + xy + 7) + (2xy + x³y³ – 5 + 2x²y²)
= 5x³y³ + x³y³ – 3x²y² + 2x²y² + xy + 2xy + 7 – 5
= (5 + 1)x³y³ + (-3 + 2)x²y² +(1 +2)xy + 2
= 6x³y³ – x²y² + 3xy + 2

Question 6.
The sides of a triangle are 2x – 5y + 9, 3y + 6x – 7 and -4x + y +10 . Find perimeter of the triangle.
Solution:
Perimeter of the triangle = Sum of three sides
= (2x – 5y + 9) + (3y + 6x – 7) + (-4x + y + 10)
= 2x – 5y + 9 + 3y + 6x – 7 – 4x + y + 10
= 2x + 6x – 4x – 5y + 3y + y + 9 – 7 + 10
= (2 + 6 – 4)x + (-5 + 3 + 1)y + (9 – 7 + 10)
= 4x – y + 12
∴ Perimeter of the triangle = 4x – y + 12 units.

Question 7.
Subtract -2mn from 6mn.
Solution:
6 mn – (-2mn) = 6mn + (+2mn) = (6 + 2) mn = 8mn

Question 8.
Subtract 6a² – 5ab + 3b² from 4a² – 3ab + b².
Solution:
(4a² – 3ab+ b²) – (6a²– 5ab + 3b²)
= (4a² – 6a²) + (- 3ab -(-5 ab)] + (b²– 3b²)
= (4 – 6) a² + [-3ab + (+ 5ab)] + (1 – 3) b²
= [4 + (- 6)] a² + (-3 + 5) ab + [1+ (-3)]b²
= -2a² + 2ab – 2b²

Question 9.
The length of a log is 3a + 4b – 2 and a piece (2a – b) is remove from it. What is the length of the remaining log?
Solution:
Length of the log = 3a + 4b – 2

Length of the piece removed = 2a – b
Remaining length of the log = (3a + 4b – 2) – (2a – b)
= (3a – 2a) + [4b – (-b)] – 2
= (3 – 2)a + (4 + 1)b – 2
= a + 5b – 2

Question 10.
A tin had ‘x’ litre oil. Another tin had (3x² + 6x – 5) litre of oil. The shopkeeper added (x + 7) litre more to the second tin. Later he sold (x² + 6) litres of oil from the second tin. How much oil was left In the second tin?
Solution:
Quantity of oil in the second tin = 3x² + 6x – 5 litres.
Quantity of oil added = x + 7 litres
∴ Total quantity of oil in the second tin
= (3x² + 6x – 5) + (x + 7) litres
= 3x² + (6x + x) + (-5 + 7)
= 3x² + (6 + 1)x + 2
= 3x² + 7x + 2 litres
Quantity of oil sold = x + 6 litres
∴ Quantity of oil left in the second tin = (3x² + 7x + 2) – (x² + 6)(3x² – x² ) + 7x + (2 – 6)
= (3 – 1)x² + 7x + (-4) = 2x² + 7x – 4
Quantity of oil left = 2x² + 7x – 4 litres

Try this Page No. 70

Question 1.
Every algebraic expression is a polynomial. Is this statement true? Why?
Solution:
No, This statement is not true. Because Polynomials contain only whole numbers as the powers of their variables. But an algebraic expression may contains fractions and negative powers on their variables.
Eg. 2y² + 5y^-1 – 3 is a an algebraic expression. But not a polynomial.

Try this Page No. 71

Question 2.
-(5y² + 2y – 6) Is this correct? If not, correct the mistake.
Solution:
Taking -(5y² + 2y – 6) = 5y² + [(-)(+) 2y] + [(-) × (-)6]
= -5y² – 2y + 6
≠ -5y² – 2y + 6
∴ Correct answer is -5y² + 2y – 6 = -(5y² + 2y + 6)

Try this Page No 71

(i) 3ab², -2a²b³
(ii) 4xy, 5y²x, (-x²)
(iii) 2m, -5n, -3p
Solution:
(i) (3ab²) × (-2a²b²) = (+) × (-) × (3 × 2) × (a × a²) × (b² × b³) = -6a³ b⁵

(ii) (4xy) × (5y²x) × (-x²)
= (+) × (+) × (-) × (4 × 5 × 1) × (x × x × x²) × (y × y²)
= -20x⁴y³

(iii) (2m) × (-5n) × (-3p) = (+) × (-) × (-) × (2 × 5 × 3) × m × n × p
= + 30mnp = 30 mnp

Try this Page No. 71

Question 1.
Why 3 + (4x – 7y) ≠ 12x – 21y?
Solution:
Addition and multiplication are different
3 + (4x – 7y) = 3 + 4x – 7y
We can add only like terms.

Try this Page No. 72

Question 1.
Which is corrcet? (3a)² is equal to
(i) 3a²
(ii) 3²a
(iii) 6a²
(iv) 9a²
Solution:
(3a) =3²a² = 9a²
(iv) 9a² is the correct answer

Try These Page No.72

Question 1.
Multiply
(i) (5x² + 7x – 3) by 4x²
Solution:
(5x² + 7x – 3) × 4x²
= 4x²(5x² + 7x – 3) Multiplication is commutative
= 4x² (5x² + 4x² (7x) + 4x² (-3)
= (4 × 5)(x² × x²) + (4 × 7)(x² × x) + (4 × -3)(x²)
= 20x⁴ + 28x³ – 12x²

(ii) (10x – 7y + 5z) by 6xyz
Solution:
(10x – 7y + 5z) by 6xyz
(10x – 7y + 5z) × 6xyz = 6xyz (10x – 7y + 5z) [∵ Multiplication is commutative]
= 6xy (10x) + 6xyz (-7y) + 6xyz (5z)
= (6 × 10)(x × x × y × z) + (6 × -7) + (x × y × y × z) + (6 × 5)(x × y × z × z)
= 60x²yz + (-42xy²z) + 30xyz²
= 60x²yz – 42x²z + 30xyz²

(iii) (ab + 3bc – 5ca) by – 3abc
Solution:
(ab + 3bc – 5ca) × (- 3abc) = (-3abc) (ab + 3bc – 5ca)
[∵ Multiplication is commutativel
= (-3abc) (ab) + (-3abc) (3bc) + (-3abc) (5ca)
= (-3)(a × a × b × b × c) + (- 3 × 3) + (a × b × b × c × c)
= -3a²b²c – 9ab²c² – 30a²bc²

Try these Page No. 74

Question 1.
Multiply
(i) (a – 5) and (a + 4)
Solution:
(a – 5) (a + 4) = a(a + 4) – 5 (a + 4)
= (a × a) + (a × 4) + (-5 × a) + (-5 × 4)
= a² + 4a – 5a – 20 = a² – a – 20

(ii) (a + b) and (a – b)
Solution:
(a + b) (a – b) = a(a – b) + b (a – b)
= (a × a) + (a × -b)+(b × a) + b(-b)
= a² – ab + ab – b² = a² – b²

(iii) (m⁴ + n⁴) and (m – n)
Solution:
(m⁴ + n⁴)(m – n) = m⁴(m – n) + n⁴(m – n)
= (m⁴ × m) + (m⁴ × (-n)) + (n⁴ × m (n⁴ × (-n))
= m⁵ – m⁴n + mn⁴ – n⁵

(iv) (2x + 3)(x – 4)
Solution:
(2x + 3)(x – 4) = 2x(x – 4) + 3(x – 4)
= (2x² × x) – (2x × 4) + (3 × x) – (3 × 4)
= 2x² – 8x + 3x – 12 = 2x² – 5x – 12

(v) (x – 5)(3x + 7)
Solution:
(x – 5)(3x + 7) = x(3x + 7) – 5(3x + 7)
= (x × 3x) + (x × 7) + (-5 × 3x) + (-5 × 7)
= 3x² + 7x – 15x – 35
= 3x² – 8x – 35

(vi) (x – 2)(6x – 3)
Solution:
(x – 2)(6x – 3) × (6x – 3) – 2(6x – 3)
= (x × 6x)+(x × (-3) × (2 × 6x) – (2 × 3)
= 6x² – 3x – 12x + 6
= 6x² – 15x + 6

Try this Page No. 74

Question 2.
3x² (x⁴ – 7x³ + 2), what is the highest power in the expression.
Solution:
3x²(x⁴ – 7x³ + 2) = (3x²) (x⁴) + 3x² (-7x³)+ (3x²)²
= 3x⁶ – 21x⁵ + 6x²
Highest power is 6 in x⁶.

Exercise 3.2

Try this Page No. 77

Question 1.
Are the following correct?
(i) \(\frac{x^{3}}{x^{8}}=x^{8-3}=x^{5}\)
(ii) \(\frac{10 m^{4}}{10 m^{4}}=0\)
(iii) When a monomial is divided by itself, we will get I?
Solution:

Try this Page No. 77

Question 1.
Divide

Solution:

Try this Page No. 78

Question 1.
Are the following divisions correct ?

Solution:

Try this Page No. 78

Question 1.

Solution:

Exercise 3.3

Try these Page No. 81

Question 1.
1. (p + 2)² = …….
2. (3 – a)² = …….
3. (6² – x²) = ………
4. (a + b)² – (a – b)² = …….
= a² + 2ab + b² – a² – 2ab – b²
= (1 – 1)a² + (2 + 2)ab + (+1 – 1 )b² = 4ab
5. (a + b)² = (a + b) × (a + b)
6. (m + n)( m – n) = m² – n²
7. (m + 7)² = m² + 14m + 49
8. (k² – 36) ≡ k² – 6² = (k + 6)(k – 6)
9. m² – 6m + 9 = (m – 3)²
10. (m – 10)(m + 5) = m² + (-10 + 5)m + (-10)(5) = m² – 5m – 50
Solution:

Try these page No. 83

Question 1.
Expand using appropriate identities
Question 1.
(3p + 2q)²
Solution:
(3p + 2q)²
Comparing (3p + 2q)² with (a + b)², we get a = 3p and b = 2q.
(a + b)² = a² + 2ab + b²
(3p + 2q)² = (3p)²+ 2(3p) (2q) + (2q)²
= 9p² + 12pq + 4q²

Question 2.
(105)²
Solution:
(105)² = (100 + 5)²
Comparing (100 + 5)² with (a + b)², we get a = 100 and b = 5.
(a + b)² = a² + 2ab + b²
(100 + 5)² = (100)² + 2(100)(5) + 5² = 1oooo + 1000 + 25
105² = 11,025

Question 3.
( 2x – 5d)²
Solution:
(2x – 5d)²
Comparing with (a – b)², we get a = 2x b = 5d.
(a – b)² = a² – 2ab + b²
(2x – 5d)² = (2x)² – 2(2x)(5d) + (5d)²
= 2x² – 20 xd + 5²d² = 4x² – 20 xd + 25d²

Question 4.
(98)²
Solution:
(98)² = (100 – 2)²
Comparing (100 – 2)² with (a – b)² we get
a = 100, b = 2
(a – b)² = a² – 2ab + b²
(100 – 2)² = 100² – 2(100)(2) + 2²
= 10000 – 400 + 4 = 9600 + 4 = 9604

Question 5.
(y – 5)(y + 5)
Solution:
(y – 5)(y + 5)
Comparing (y – 5) (y + 5) with (a – b) (a + b) we get
a = y; b = 5
(a – b)(a + b) = a² – b²
(y – 5)(y + 5) = y² – 5² = y² – 25

Question 6.
(3x)² – 5²
Solution:
(3x)² – 5²
Comparing (3x)² – 5² with a² – b² we have
a = 3x; b = 5
(a² – b²) = (a + b)(a – b)
(3x)² – 5² = (3x + 5)(3x – 5) = 3x(3x – 5) + 5(3x – 5)
= (3x) (3x) – (3x)(5) + 5(3x) – 5(5)
= 9x² – 15x + 15x – 25 = 9x² – 25

Question 7.
(2m + n)(2m +p)
Solution:
(2m + n) (2m + p)
Comparing (2m + n) (2m + p) with (x + a) (x + b) we have
x = 2n; a = n ;b = p
(x – a)(x + b) = x² + (a + b)x + ab
(2m +n) (2m +p) = (2m²) + (n +p)(2m) + (n) (p)
= 2²m² + n(2m) + p(2m) + np
= 4m² + 2mn + 2mp + np

Question 8.
203 × 197
Solution:
203 × 197 = (200 + 3)(200 – 3)
Comparing (a + b) (a – b) we have
a = 200, b = 3
(a + b)(a – b) = a² – b²
(200 + 3)(200 – 3) = 200² – 3²
203 × 197 = 40000 – 9
203 × 197 = 39991

Question 9.
Find the area of the square whose side is (x – 2)
Solution:
Side of a square = x – 2
∴ Area = Side × Side
= (x – 2) (x – 2) = x(x – 2) – 2(x – 2)
= x(x) + (x)(-2) + (-2)(x) + (-2)(-2)
= x – 2x – 2x + 4x² – 4x + 4

Question 10.
Find the area of the rectangle whose length and breadth are (y + 4) and (y – 3).
Solution:
Length of the rectangle = y+ 4
breadth of the rectangle = y – 3
Area of the rectangle = length × breadth
= (y + 4)(y – 3) = y² + (4 +(-3))y + (4)(-3)
= y² + y – 12

Try these Page No. 88

Question 1.
Expand :
Question 1.
(x + 4)³
Solution:
Comparing (x + 4)³ with (a + b)³, we have a = x and b = 4.
(a + b)³ = a³ + 3a²b + 3ab² + b³
(x + 4)³ = x³ + 3x²(4) + 3(x)(4)² + 4³
= x³ + 12x² + 48x + 64

Question 2.
( y – 2)²
Solution:
Comparing (y – 2) with (a – b)³ we have a = y b = z
(a – b)³ = a³ – 3a²b + 3ab² – b³
(y – 2)² = y³ – 3y(2) + 3y(2)² + 2³
= y³ – 6y² + 12y + 8

Question 3.
(x + 1)(x + 3)(x + 5)
Solution:
Comparing (x + 1) (x + 3) (x + 5) with (x + a) (x + b) (x + c) we have
a = 1
b = 3
and c = 5

Exercise 3.4

Try These Page No.92

Question 1.
Factorize the following:
Question 1.
3y + 6
Solution:
3y + 6
3y + 6 = 3 × y + 2 × 3
Taking out the common factor 3 from each term we get 3 (y + 2)
∴ 3y + 6 = 3(y + 2)

Question 2.
10x² + 15y
Solution:
10x² + 15y²
10x² + 15y² = (2 × 5 × x × x) + (3 × 5 × y × y)
Taking out the common factor 5 we have
10x² + 15y² = 5(2x² + 3y²)

Question 3.
7m(m – 5) + 1(5 – m)
Solution:
7m(m – 5) + 1(5 – m)
7m(m – 5) + 1(5 – m) = 7m(m – 5) + (-1)(-5 + m)
= 7m(m – 5) – 1 (m – 5)
Taking out the common binomial factor (m – 5) = (m – 5)(7m – 1)

Question 4.
64 – x²
Solution:
64 – x²
64 – x² = 8² – x²
This is of the form a² – b²
Comparing with a² – b² we have a = 8, b = x
a² – b² = (a + b)(a – b)
64 – x² = (8 + x)(8 – x)

Students can Download Maths Chapter 2 Measurements Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Additional Questions

Additional Questions And Answers

Exercise 2.1

Very Short Answers [2 Marks]

Question 1.
Find the length of arc if the perimeter of sector is 45 cm and radius is 10 cm.
Solution:
Given Radius of the sector = 10 cm
Perimeter of the sector P = 45 cm
l + 2r = 45
l + 2(10) = 45
l + 20 = 45
l = 45 – 20
l = 25 cm
Length of the arc l = 25 cm

Question 2.
Find the radius of sector whose perimeter and length of arc are 30 cm and 16 cm respectively.
Solution:
Given length of the arc = 16 cm
Perimeter of the arc = 30 cm
l + 2r = 30
16 + 2 r = 30
2 r = 30 – 16
2 r = 14
r = \(\frac{14}{2}\)
r = 7 cm
Radius of the sector = 7 cm

Question 3.
Find the length of arc whose radius is 7 cm and central angle 90°.
Solution:
Here θ = 90°; radius r = 7cm
Length of the arc = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
= \(\frac{90^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × 7 = 11 cm
∴ Length of the arc = 11 cm

Short Answers [3 Marks]

Question 1.
Find the length arc whose radius is 42 cm and central angle is 60°.
Solution:
Length of the arc = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
Given central angle 0 = 60°
Radius of the sector r = 42 cm
l = \(\frac{60^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × 42 = 44 cm
∴ Length of the arc = 44 cm

Question 2.
Find the length of the arc whose radius is 10.5 cm and central angle is 36°.
Solution:

∴ Length of the arc = 6.6 cm

Long Answers [5 Marks]

Question 1.
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of its arc and area of the sector.
Solution:
Radius of the sector = 21 cm
Length of the arc

∴ Length of the arc = 55 cm
Area of the sector = 577.5 cm²

Question 2.
Find the perimeter of sector whose area is 324 sq. cm and radius is 27 cm.
Solution:
Radius of the sector = 27 cm
Area of the sector =324 cm²

Perimeter of the sector P = (l + 2r) units = 24 + 2(27) cm = (24 + 54) cm = 78 cm

Exercise 2.2

Question 1.
PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal semi-circles drawn on PQ and Question as diameters. Find the p perimeter and area of the shaded region.

Solution:
PS = Diameter of a circle of radius 6 cm = 12 cm
PQ = QR = RS = \(\frac{12}{3}\) = 4 cm Question = QR + RS = 4 + 4 = 8 cm
∴ Perimeter of the shaded part = Arc length of semi-circle of radius 6 cm + Arc length of semicircle of radius 4 cm + Arc length of semi-circle of radius 2 cm.
= (π × 6) + (π × 4) + (π × 2) cm
P = 12 π cm
Area required = Area of semicircle with PS as diameter + Area of semi circle with PQ as diameter – Area of semi-circle with Question as diameter.

Question 2.
In the figure AOBCA represents a quadrant of a circle of radius 3.5cm with center ‘O’ calculate the area of the shaded portion (π = \(\frac{22}{7}\))

Solution:

∴ Area of shaded region = Area of the quadrant – Area of triangle
= 9.625 – 3.5 cm² = 6.125 cm²

Question 3.
Find the area of the shaded region in the figure

Solution:
Radius of the big semicircle = 14 cm

∴ Required area = 308 + 154 cm² = 462 cm²

Exercise 2.3

Very Short Answers [2 Marks]

Question 1.
What is the least number of planes that can enclose a solid? What is the name of the solid?
Solution:
Least number of planes = 4, the solid is tetrahedron.

Question 2.
Can a polyhedron have for its faces = 12 edges = 16 and vertices = 6.
Solution:
Verifying Euler’s formula
F + V – E = 12 + 6 – 16 = 18 – 16 = 2
Yes, the polyhedron can have F = 12, E = 16 and V = 6

Short Answers [3 Marks]

Question 1.
Verify Euler’s formula for a pyramid.
Solution:
A pyramid has faces = 5, Vertices = 5, Edges = 8
By Euler’s formula F + V – E = 5 + 5 – 8 = 10 – 8 = 2

Question 2.
Verify Eulers formula for a triangular prism.
Solution:
For a triangular prism
Faces = 5, Edges = 9, Vertices = 6
By Euler’s formula F + V – E = 5 + 6 – 9 = 11 – 9 = 2

Long Answers [5 Marks]

Question 1.
(a) Dice are cubes where the numbers on the opposite faces must total 7. Is the following a die.

(b) The following shows a net with areas of faces. What can be the shape?

Solution:
(a) 2 + 5 = 6 + 1 = 3 + 4 = 7
∴ It can be a die.
(b) It is a cuboid