Laxmi

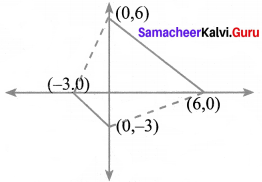
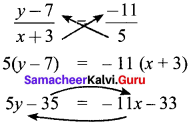
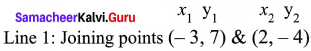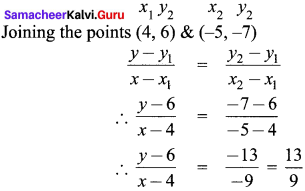You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Grammar Punctuation

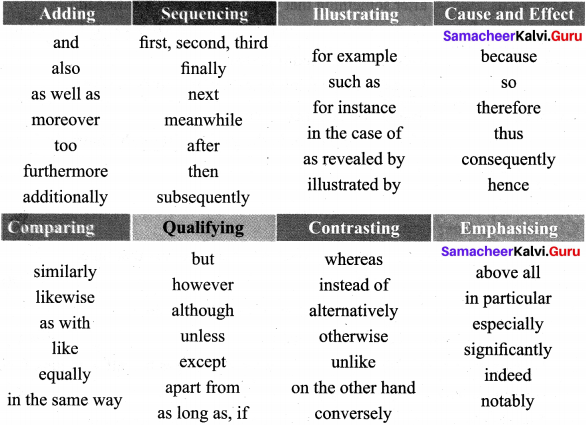
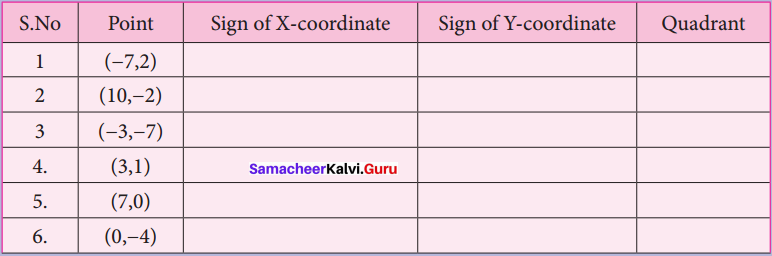
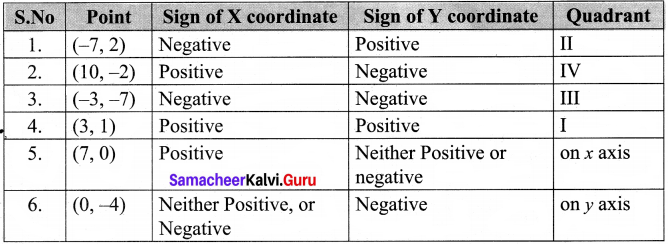
Punctuation refers to the specific markings, signs and symbols that are used in and around sentences to give them structure and to allow for correct understanding and comprehension.

• While writing prose or poetry, we use certain signs to mark the stages of reading. They are called punctuation marks.
• The main purpose of the Punctuation mark is to make the meaning of a sentence clear to the reader.
• Punctuation means the right use of different marks like Full–stop, Comma, Semicolon, Colon, Question Mark…in a written sentence.

Punctuation Marks

1. Full Stop

• Full stop is used to mark the end of a Statement or an Imperative sentence.
  Ex:
  Time is Gold. (Statement)
  Get me a glass of water. (Imperative)
• After an initial (first Letter of a person ‘s name)
  Ex:
  S. Raman
  M. Renu

2. COMMA

• To indicate a pause while reading.
  Ex:
  God willing, we will meet again.
• To separate words in a list. (The last two items are separated by and)
  Ex:
  Health, wealth and peace to together.
  He visited Kerala, Tamil Nadu, Gujarat and Kashmir.
• To separate the actual words spoken, from the rest of the sentences.
  Ex:
  Mala said, “I am writing a letter.”
• To mark off certain words like No, Yes prefixed to a sentence.
  Ex:
  Yes, I come. No, I don’t come.
• To break up group of numbers into tens, hundreds, thousands and lakhs.
  Ex:
  1,25,500
• After salutation in letters.
  Ex:
  Dear Sir, Dear Kannan,
• To separate the date and month from the year.
  Ex:
  1st January, 2005 22nd June, 1969

3. SEMICOLON

• The semicolon represents a pause greater than that indicated by the comma.
  Ex:
  Uma came quickly; she ate in a hurry she went out.
• The comma separates individual items. A semicolon separates groups of items.
  Ex:
  In the children’s room were toys, books, balls and colour pencils; in the kitchen were pots, pans, vegetables, and fruits; and the library had books, charts and maps.

4. COLON

• The colon shows a shorter pause than a full stop, but a longer pause than a semicolon.
  Ex:
  The three great books are: the Ramayana, the Mahabharata and the Gita.
  The days of the week are: Sunday, Monday, Tuesday, Wednesday, Thursday, Friday and Saturday.

5. APOSTROPHE

• To indicate the omission of a letter or letters when two words are joined.
  Ex:
  I’ve → I have I’m → I am Don’t → Do not won’t → will not
• Apostrophe is used with s– to give the meaning belongs to. (Possessiveness)
  Ex:
  Ramu’s book → The book belongs to Ramu.
• To indicate the plural of figures and letters.
  Ex:
  5’s Your 3’s and 8’s look alike.

6. QUESTION MARK

• To end the interrogative sentence.
  Ex:
  What is your name?
  How old are you?
  Are you interested in Maths?
• To mark off question tag.
  Ex:
  Pass the salt, will you?
  I am not angry, am I?

7. EXCLAMATION MARK

• After interjections.
  Ex:
  Ah! Hurrah! Alas! Oh! Hush!
• After exclamatory phrases.
  Ex:
  Well done! Miserable man!
• After exclamatory sentences.
  Ex:
  What a useful tree the coconut is!
  How cunning the fox is!

8. QUOTATION MARKS

• Single quotation marks or inverted commas are generally used in British English.
  Ex:
  ‘Help! I’m drowning!’
• In American English, double quotation marks are used.
  Ex:
  “Help! I’m drowning!”
• To mark the exact words of a speaker without any change.
  Ex:
  Rama said to Rahim, “Where are you going?”

9. CAPITAL LETTER

• To begin a sentence.
  Ex:
  They are playing cricket.
• To begin each line of poetry.
  Ex:
  If you can dream and not make dreams your master.
  If you can think and not make thoughts your aim.
• For all proper nouns and adjectives derived from them.
  Ex:
  India, Indian.
• To begin the names and surnames of persons, rivers, countries, cities, mountains, roads, buildings, days of the week, months, books, newspapers, magazines, communities, political parties.
  Ex:
  Raj, Cauvery, India, Trichy, Everest, Grand trunk road, The Hindu, Sunday…

10. HYPHEN

• It is used to join up words or syllables.
• To link pairs of words used as single words or group of words.
  Ex:
  home–work, father–in–law, co–operative, two–third.

Exercises
Punctuate the following :
1. On the drive, he would tell me dont waste your time playing insane games with these kids
Answer:
On the drive he would tell me, “Don’t waste your time playing insane games with these kids.

2. “Bow, wow, wow!” wagging his tail violently.
Answer:
“Bow, wow, wow!” wagging his tail violently.

3. Steady old pal weve been through bad things before and come out safely.
Answer:
Steady, old pal! We‘ve been through bad things before and come out safely.

4. do you want to buy it
Answer:
‘Do you want to buy it?’

5. only three years she smiled
Answer:
‘Only three years,’ she smiled.

6. I used to climb the jackfruit tree he said opening his eyes
Answer:
‘I used to climb the jackfruit tree,’ he said, opening his eyes.

7. She said where did you find it
Answer:
She said, “Where did you find it?”

8. A human how could a human be a teacher
Answer:
“A human? How could a human be a teacher?”

9. Oh Jim i’m scared
Answer:
Oh, Jim, I’m scared!

10. she is alive someone said
Answer:
“She is alive!” someone said.

11. Hey wait a minute, ’ pongo shouted.
Answer:
‘Hey! Wait a minute,’ Pongo shouted.

12. tom what on earth ails that cat
Answer:
‘Tom, what on earth ails that cat?’

13. Im a grizzly from alaska and Ive come to stay.
Answer:
“I’m a grizzly from Alaska and I‘ve come to stay.

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Grammar Framing Questions

The interrogative pronouns who, what, whom, whose, which and the interrogative Adverbs where, when, why and how are used to frame information questions. The structure ‘how + an adjective/adverb’ may also be used to frame questions.

Exercises
1. John is writing a letter.
Answer:
What is John’s writing?

2. She walks home from school.
Answer:
Who walks home from school?

3. The children are sitting in the garden.
Answer:
Where are the children sitting?

4. Peter runs with his dog on Sundays.
Answer:
When does Peter run with his dog?

5. My rabbit has a cage in the garden.
Answer:
What does your rabbit have in the garden?

6. They go to work by bus.
Answer:
How do they go to work?

7. David likes cats because they are nice.
Answer:
Why does David like cats?

8. Jenny isn’t sleeping late today.
Answer:
Who isn’t sleeping late today?

9. We are going to the cinema.
Answer:
Where are we going?

10. I’m leaving now.
Answer:
When are you leaving?

11. They went to Spain.
Answer:
Where did they go?

12. He writes novels.
Answer:
What does he write?

13. Lacy likes soccer
Answer:
Who likes soccer?

14. The girls watched a serial.
Answer:
What did the girls watch?

15. He discovered the truth.
Answer:
What did he discover?

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Grammar Connectors

Connectors

❖ We could go to the library or the park.
❖ He neither finished his homework nor studied for the test.
❖ I did not go out because the weather was hot.

In each of the above sentences, two different ideas are expressed in one sentence. To connect the ideas, some words like or, neither…nor, because are used. These words and phrases are called Connectors.

A connector may be used to indicate the relationship between the ideas expressed in a clause or a sentence.
The following connectors can be used for different purposes.

Look at the following sentences, how connectors are used.

• The man has much money. However, he isn’t happy at all.
• I like playing football. On the other hand, my brother likes playing basketball.
• His family made a lot of effort to make their son’s lessons better, conversely, he never made any effort.
• She spent four years studying for her law degree. Meanwhile, she continued to work at the bank.
• You are not allowed to use your phone here. Simi Early, you have to switch it off when you are in the library.

Exercises
(i) Choose the best connector.
1. you saved a lot, you wouldn’t be able to buy that bike. (So that, Even if, Therefore)
Answer:
Even if

2. your chances are small, you should try to do it. (Afterwards, Even though, Otherwise)
Answer:
Even though

3. He eats only healthy food his sister gorges herself with junk food. (therefore, because of, whereas)
Answer:
whereas

4. You should learn more, you might fail in your exams. (otherwise, although, because of)
Answer:
otherwise

5. Adhira wanted to play basket ball dance Bharathanatyam. (therefore, even though, as well as)
Answer:
As well as

6. _________ he was very tired, he worked very hard. (Afterwards, So that, Although)
Answer:
Although

7. Slice this meat and _________ you can boil it for thirty minutes. (after wards, although, because of)
Answer:
after wards

8. I cooked dinner _________ my friends wouldn’t have to eat out. (otherwise, unless, so that)
Ans :
so that

9. This street is slippery _________ the snow. (because of, even though, whereas)
Answer:
because of

10. I will pick you up. ________ you can get to the station on time. (Because of, So that, Afterwards)
Answer:
So that

11. Something must be wrong; _________Anu would go to school. (so that, because of, otherwise)
Answer:
otherwise

12. _________ he is very rich, he doesn’t help the poor. (Even if, Although, Therefore)
Answer:
Although

13. _________ the weather was windy, we went for a walk. (Therefore, Otherwise, Even though)
Answer:
Even though

14. She is always helpful and friendly to mc, 1 like her very much. (therefore, whereas, even though)
Answer:
therefore

15. He must be very clever; _________ he wouldn’t have passed such a hard exam. (whereas, otherwise, unless)
Answer:
otherwise

16. _________ I have a bike. I don’t often ride it. (Therefore, Although, Unless)
Answer:
Although

17. I like horror films ________ my friend prefers comedies. (unless, whereas, therefore)
Answer:
he was

18. _________ 1 learned so much, I didn’t manage to pass my exam. (Even though., So that, Because of)
Answer:
Een though

19. You’ll be sick _________ you stop eating so many sweets. (whereas, unless, otherwise)
Answer:
unless
20. _________ we are at the bus station by seven o’clock, we will miss our bus. (Whereas, Unless, Therefore)
Answer:
Unless

(ii) Complete the following with connectors.
1. After he seems quite intelligent _________ he often gets poor grades. (Nonetheless is used to connect two contrasting ideas.)
Answer:
nonetheless

2. This restaurant has some of the best chefs in the town. _________ their service is excellent.
Answer:
Moreover

3. I’ve never been to Kerala ________ having friends and relatives there.
Answer:
in spite of

4. Krishnan is a reckless driver _________ he hasn’t had any accidents.
Answer:
even so

5. My sister works ten hours a day _________ she doesn’t earn much money.
Answer:
however

6. We went out __________ the cold weather.
Answer:
despite

7. 1 tried to look happy _________ feeling ill.
Answer:
ln spite of

8. There is no more food left. _________ there is plenty of snacks.
Answer:
However

9. Wash the potatoes first, _________ you can boil them.
Answer:
After wards

10. I need to work hard _________ I can pass the exam.
Answer:
so that

11. __________ he was the best candidate, he didn’t win the elections.
Answer:
Although

12. _________ you come back from your trip, we’ll meet to discuss the problem.
Answer:
Then

13. They said that the movie was fantastic, _________ I watched it.
Answer:
so

14. _________ he was very ill, he didn’t take any medicine.
Answer:
Although

15. I don’t know ________ I can buy a pair of jeans.
Answer:
where

16. She went to the shops _________ couldn’t find anything that could fit her needs.
Answer:
but

17. Everybody likes him because he is nice _________ helpful.
Answer:
and

18. _________ he was angry with her, he didn’t utter a word.
Answer:
Since

19. Keep quiet _________ go out.
Answer:
or

20. She acted as __________ she is innocent.
Answer:
if

Students can Download Maths Chapter 4 Geometry Ex 4.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.1

Question 1.
Can 30°, 60° and 90° be the angles of a triangle?
Solution:
Given angles 30°, 60° and 90°
Sum of the angles = 30° + 60° + 90° = 180°
∴ The given angles form a triangle.

Question 2.
Can you draw a triangle with 25°, 65° and 80° as angles?
Solution:
Given angle 25°, 65° and 80°.
Sum of the angles = 25° + 65° + 80° = 170° ≠ 180
∴ We cannot draw a triangle with these measures.

Question 3.
In each of the following triangles, find the value of x.

Solution:
(i) Let ∠G = x
By angle sum property we know that,
∠E + ∠F + ∠G = 180°
80° + 55° + x = 180°
135° + x = 180°
x = 45°

(ii) Let ∠M = x
By angle sum property of triangles we have
∠M + ∠M + ∠O = 180°
x + 96° + 22° = 180°
x + 118° = 180°
X = 180° – 118° = 620

(iii) Let ∠Z = (2x + 1)° and ∠Y = 90°
By the sum property of triangles we have
∠x + ∠y + ∠z = 180°
29° + 90° + (2x + 1)° = 180°
119° + (2x + 1)° = 180°
(2x + 1)° = 180° – 119°
2x + 1° = 61°
2x = 61° – 1°
2x = 60°
x = \(\frac{60^{\circ}}{2}\)
x = 30°

(iv) Let ∠J = x and ∠L – 3x.
By angle sum property of triangles we have
∠J + ∠K + ∠L = 180°
x + 112° + 3x = 180°
4x = 180° – 112°
x = 68°
x = \(\frac{68^{\circ}}{4}\)
x = 17°

(v) Let ∠S = 3x°
Given \(\overline{\mathrm{RS}}\) = Given \(\overline{\mathrm{RT}}\) = 4.5 cm
Given ∠S = ∠T = 3x° [∵ Angles opposite to equal sides are equal]
By angle sum property of a triangle we have,
∠R + ∠S + ∠T = 180°
72° + 3x + 3x = 180°
72° + 6x = 180°
x = \(\frac{108^{\circ}}{6}\)
x = 18°

(vi) Given ∠X = 3x; ∠Y = 2x; ∠Z = ∠4x
By angle sum property of a triangle we have
∠X + ∠Y + ∠Z = 180°
3x + 2x + 4x = 180°
∴ 9x = 180°
x = \(\frac{180^{\circ}}{9}\) = 20°

(vii) Given ∠T = (x – 4)°
∠U = 90°
∠V = (3x – 2)°
By angle sum property of a triang we have
∠T + ∠U + ∠V = 180°
(x – 4)° + 90° + (3x – 2)° = 180°
x – 4° + 90° + 3x – 2° = 180°
x + 3x + 90° – 4° – 2° = 180°
4x + 84° = 180°
4x = 180° – 84°
4x = 96°
x = \(\frac{96^{\circ}}{4}\) = 24°
x = 24°

(viii) Given ∠N = (x + 31)°
∠O = (3x – 10)°
∠P = (2x – 3)°
By angle sum property of a triangle we have
∠N + ∠O + ∠P = O
(x + 31)° + (3x – 10)° + (2x – 3)° = 180°
x + 31°+ 3x – 10° + 2x – 3° = 180°
x + 3x + 2x + 31° – 10° – 3° = 180°
6x + 18° = 180°
6x = 180° + 18°
6x = 162°
x = \(\frac{162^{\circ}}{6}\) = 27°
x = 27°

Question 4.
Two line segments \(\overline{A D}\) and \(\overline{B C}\) intersect at O. Joining \(\overline{A B}\) and \(\overline{D C}\) we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B.

Solution:
In ∆AOB and ∆DOC,
∠AOB = ∠DOC [∵ Vertically opposite angles are equal]
Let ∠AOB = ∠DOC = y
By angle sum property of a triangle we have
∠A + ∠B + ∠AOB = ∠D + ∠C + ∠DOC = 180°
3x + 2x + y = 70° + 30° + y = 180°
5x + y = 100° + y = 180°
Here 5x + y = 100° + y
5x = 100° + y – y
5x = 100°
x = \(\frac{100^{\circ}}{5}\) = 20°
∠A = 3x = 3 × 20 = 60°
∠B = 2x = 2 × 20 = 40°
∠A = 60°
∠B = 40°

Question 5.
Observe the figure and find the value of
∠A + ∠N + ∠G + ∠L + ∠E + ∠S.

Solution:
In the figure we have two triangles namely ∆AGE and ∆NLS.
By angle sum property of triangles,
Sum of angles of ∆AGE = ∠A + ∠G + ∠E = 180° …(1)
Also sum of angles of ∆NLS = ∠N + ∠L + ∠S = 180° … (2)
(1) + (2) ∠A + ∠G + ∠E + ∠N + ∠L + ∠S = 180° + 180°
i.e., ∠A + ∠N + ∠G + ∠L + ∠E + ∠S = 360°

Question 6.
If the three angles of a triangle are in the ratio 3 : 5 : 4, then find them.
Solution:
Given three angles of the triangles are in the ratio 3 : 5 : 4.
Let the three angle be 3x, 5x and 4x.
By angle sum property of a triangle, we have
3x + 5x + 4x = 180°
12x = 180°
x = \(\frac{180^{\circ}}{12}\)
x = 15°
∴ The angle are 3x = 3 × 15° = 45°
5x = 5 × 15° = 75°
4x = 4 × 15° = 60°
Three angles of the triangle are 45°, 75°, 60°

Question 7.
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S , find the three angles of the triangle.
Solution:
In ∆RST. Let ∠R = x.
Then given S is ∠10° greater than ∠R
∴ ∠S = x + 10°
Also given ∠T is 5° less then ∠S.
So ∠T = ∠S – 5° = (x + 10)° – 5° = x + 10° – 5°
By angle sum property of triangles, sum of three angles = 180°.

∠R + ∠S + ∠T = 180°
x + x + 10° + x + 5° = 180°
3x + 15° = 180°
3x = 180° – 15°
x = \(\frac{165^{\circ}}{3}\) = 55°
∠R = x = 55°
∠S = x + 10° = 55° + 10° = 65°
∠T = x + 5° = 55° + 5° = 60°
∴ ∠R = 55°
∠S = 65°
∠T = 60°

Question 8.
In ∆ABC , if ∠B is 3 times ∠A and ∠C is 2 times ∠A, then find the angles.
Solution:
In ABC, Let ∠A = x,
then ∠B = 3 times ∠A = 3x
∠C = 2 times ∠A = 2x
By angle sum property of a triangles,
Sum of three angles of ∆ABC =180°.
∠A + ∠B + ∠C = 180
x + 3x + 2x = 180°
x (1 + 3 + 2) = 180°
6x = 180°

x = \(\frac{180^{\circ}}{6}\) = 30°
∠A = x = 30°
∠B = 3x = 3 × 30° = 90°
∠C = 2x = 2 × 30° = 60°
∴ ∠A = 30°
∠B = 90°
∠C = 60°

Question 9.
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z.
Solution:
Given in ∆XYZ, ∠X : ∠Z = 5 : 4
Let ∠X = 5x; and ∠Z = 4x given ∠Y = 72°
By the angle sum property of triangles sum of three angles of a triangles is 180°.
∠X + ∠Y + ∠Z = 180°
5x + 72 + 4x = 180°
5x + 4x = 180° – 72°
9x = 108°
x = \(\frac{108^{\circ}}{9}\) = 12°
∠X = 5x = 5 × 12° = 60°
∠Z = 4x = 4 × 12° = 48°
∴ ∠X = 60°
∠Z = 48°

Question 10.
In a right angled triangle ABC, ∠B is right angle, ∠A is x + 1 and ∠C is 2x + 5. Find ∠A and ∠C.
Solution:
Given in ∆ABC ∠B = 90°
∠A = x + 1
∠B = 2x + 5

By angle sum property of triangles
Sum of three angles of ∆ABC = 180°
∠A + ∠B + ∠C = 180°
(x + 1) + 90° + (2x + 5) = 180°
x + 2x + 1° + 90° + 5° = 180°
3x + 96° = 180°
3x = 180° – 96° = 84°
x = \(\frac{84^{\circ}}{3}\) = 28°
∠A = x + 1 = 28 + 1 = 29
∠C = 2x + 5 = 2 (28) + 5 = 56 + 5 = 61
∴ ∠A = 29°
∠C = 61°

Question 11.
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO.
Solution:
Given ∠N = 90°
MO is extended to P, the exterior angle ∠NOP = 128°
Exterior angle is equal to the sum of interior opposite angles.

∴ ∠M + ∠N = 128°
∠M + 90° = 128°
∠M = 128° – 90°
∠M = 38°
By angle sum property of triangles,
∴ ∠M + ∠N + ∠O = 180°
38° + 90° + ∠O = 180°
∠O = 180° – 128°
∠O = 52°
∴ ∠M = 38° and ∠O = 52°

Question 12.
Find the value of x in each of the given triangles.

Solution:
(i) In ∆ABC, given B = 65°,
AC is extended to L, the exterior angle at C, ∠BCL = 135°
Exterior angle is equal to the sum of opposite interior angles.
∠A + ∠B = ∠BCL
∠A + 65° = 135°
∠A = 135° – 65°
∴ ∠A = 70°
x + ∠A = 180° [∵ linear pair]
x + 70° = 180° [∵ ∠A = 70°]
x = 180° – 70°
∴ x = 110°

(ii) In ∆ABC, given B = 3x – 8°
∠XAZ = ∠BAC [∵ vertically opposite angles]
8x + 7 + ∠BAC
i.e., In ∆ABC, ∠A = 8x + 7
Exterior angle ∠XCY = 120°
Exterior angle is equal to the sum of the interior opposite angles.
∠A + ∠B = 120°
8x + 7 + 3x – 8 = 120°
8x + 3x = 120° + 8 – 7
11x = 121°
x = \(\frac{121^{\circ}}{11}\) = 11°

Question 13.
In ∆LMN, MN is extended to O. If ∠MLN = 100 – x, ∠LMN = 2x and ∠LNO = 6x – 5, find the value of x.
Solution:
Exterior angle is equal to the sum of the opposite interior angles.
∠LNO = ∠MLN + ∠LMN

6x – 5 = 100° – x + 2x
6x – 5 + x – 2x = 100°
6x + x – 2x = 100° + 5°
5x = 105°
x = \(\frac{105^{\circ}}{5}\) = 21°
x = 21°

Question 14.
Using the given figure find the value of x.

Solution:
In ∆EDC, side DE is extended to B, to form the exterior angle ∠CEB = x.
We know that the exterior angle is equal to the sum of the opposite interior angles
∠CEB = ∠CDE + ∠ECD
x = 50° + 60°
x = 110°

Question 15.
Using the diagram find the value of x.

Solution:
Given triangle is an equilateral triangle as the three sides are equal. For an equilateral triangle all three angles are equal and is equal to 60° Also exterior angle is equal to sum of opposite interior angles.
x = 60° + 60°.
x = 120°

Objective Type Questions

Question 16.
The angles of a triangle are in the ratio 2:3:4. Then the angles are
(i) 20,30,40
(ii) 40, 60, 80
(iii) 80, 20, 80
(iv) 10, 15, 20
Answer:
(ii) 40, 60, 80

Question 17.
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
(i) 85°, 40°
(ii) 70°, 25°
(iii) 80°, 35°
(iv) 80° , 135°
Answer:
(iii) 80°,35°

Question 18.
In the given figure, AB is parallel to CD. Then the value of b is

(i) 112°
(ii) 68°
(iii) 102°
(iv) 62° A
Answer:
(ii) 68°

Question 19.
In the given figure, which of the following statement is true?

(i) x + y + z = 180°
(ii) x + y + z = a + b + c
(iii) x + y + z = 2(a + b + c)
(iv) x + y + z = 3(a + b + c)
Ans :
(iii) x + y + z = 2(a + b + c)]

Question 20.
An exterior angle of a triangle is 70° and two interior opposite angles are equal. Then measure of each of these angle will be
(i) 110°
(ii) 120°
(iii) 35°
(iv) 60°
Answer:
(iii) 35°

Question 21.
In a ∆ABC, AB = AC. The value of x is _____.

(i) 80°
(ii) 100°
(iii) 130°
(iv) 120°
Answer:
(iii) 130°

Question 22.
If an exterior angle of a triangle is 115° and one of the interior opposite angles is 35°, then the other two angles of the triangle are
(i) 45°, 60°
(ii) 65°, 80°
(iii) 65°, 70°
(iv) 115°, 60°
Answer:
(ii) 65°, 80°

Students can Download Maths Chapter 4 Geometry Ex 4.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.2

Question 1.
Given that ∆ABC = ∆DEF (i) List all the corresponding congruent sides
(ii) List all the corresponding congruent angles.
Solution:
Given ∆ABC ≅ DEF.

(i) Corresponding congruent sides.
\(\overline{A B}\) = \(\overline{D E}\); \(\overline{B C}\) = \(\overline{E F}\); \(\overline{A C}\) = \(\overline{D F}\)

(ii) Corresponding congruent angles.
∠ABC = ∠DEF; ∠BCA = ∠EFD ; ∠CAB = ∠FDE

Question 2.
If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles.
(i)
(ii)
Solution:
Given ∆PQR ≅ ∆LNM
(i) (a) Corresponding sides
\(\overline{P Q}\) = \(\overline{L N}\) ; \(\overline{P Q}\) = \(\overline{L M}\) ; \(\overline{R Q}\) = \(\overline{M N}\)
(b) Corresponding angles
∠RPQ = ∠NLM; ∠PQR = ∠LNM; ∠PRQ = ∠LMN

(ii) Given ∆PQR ≅ ∆NML
(a) Corresponding angles
\(\overline{Q R}\) = \(\overline{L M}\) ; \(\overline{R P}\) = \(\overline{L N}\); \(\overline{P Q}\) = \(\overline{M N}\)
(b) Corresponding angles
∠PQP = ∠NMN; ∠QRP = ∠MLN; ∠RPQ = ∠LNM

Question 3.
Find the unit digit of expanded form.

(i) ∠A and ∠G
(ii) ∠B and ∠E
(iii) ∠B and ∠G
(iv) \(\overline{A C}\) and \(\overline{G F}\)
(v) \(\overline{B A}\) and \(\overline{F G}\)
(vi) \(\overline{E F}\) and \(\overline{B C}\)
Solution:
Given ∆ABC ≅ ∆EFG. Also from given triangles.
\(\overline{A B}\) = \(\overline{F G}\) \(\overline{B C}\) = \(\overline{G F}\) \(\overline{A C}\) = \(\overline{E F}\)
Also ∠A = ∠F ∠B = ∠G ∠C = ∠E
Answer:
(i) ∠A and ∠G are not corresponding angles.
(ii) ∠B and ∠E are not corresponding angles.
(iii) ∠B and ∠G are corresponding angles.
(iv) \(\overline{A C}\) and \(\overline{G F}\) are not corresponding sides.
(v) \(\overline{B A}\) and \(\overline{F G}\) are corresponding sides.
(vi) \(\overline{E F}\) and \(\overline{B C}\) are not corresponding sides.

Question 4.
State whether the two triangles are congruent or not. Justify your answer.

Solution:
(i) Let the given triangle be ∆ABC. \(\overline{A D}\) divides ∆ABC into two parts giving ∆ABD and ∆ACD.
In ∆ABD and ∆ACD

\(\overline{A B}\) = \(\overline{A C}\) (given)
\(\overline{B D}\) = \(\overline{A D}\) (common side)
∠BAD = ∠CAD (included angles)
∴ By SAS criterion ∆ABD ≅ ∆ACD.

(ii) Let the given triangles in the figure be ∆ABC and ∆DCB.
In both the triangles

\(\overline{B C}\) = \(\overline{B C}\) (Common side)
\(\overline{A B}\) = \(\overline{D C}\)
\(\overline{A C}\) = \(\overline{B D}\)
∴ By SSS Criterion ∆ABC ≅ ∆DCB

(iii) Let the given triangles be ∆ABC and ∆CDE.

Here \(\overline{A C}\) = \(\overline{C E}\) (given)
∠BAC = ∠DEC (given)
∠ACB = ∠DCE (vertically opposite angles)
Two angles and the included side are equal.
Therefore by ASA criterion ∆ABC ≅ ∆CDE.

(iv) Let the two triangles be ∆XYZ and ∆XYW

Here ∠W = ∠Z = 90°
\(\overline{X Y}\) = \(\overline{X Y}\) (Common Hypothenure)
\(\overline{X W}\) = \(\overline{X Z}\) (given)
By RHS criterion ∆XYZ ≅ ∆XYW

(v) Let the two triangles be ∆ABC and ∆ADC

In both the triangles \(\overline{A C}\) = \(\overline{A C}\) (common sides)
\(\overline{A D}\) = \(\overline{B C}\) (given)
\(\overline{A B}\) = \(\overline{D C}\) (given)
By SSS criterion ∆ABC ≅ ∆ADC.

Question 5.
To conclude the congruency of triangles, mark the required information in the following figures with reference to the given congruency criterion.

Solution:
(i) In the given triangles one angle is equal and a side is common and so equal.

To satisfy ASA criterion one more angle should be equal such that the common side is the included side of both angles of a triangle.
The figure will be as follows.

(ii) In the two given triangles two sides of one triangle is equal to two sides of the other triangle.

To satisfy SSS criterion the third sides mut be equal.

(iii) The given triangles have one side in common. They are right angled tringles.

To satisfy RHS criterion their hypotenuse must be equal.

(iv) In the given triangles two angles of one triangle is equal to two angles of the other triangles?

To satisfy ASA criterion included side of two angles must be equal.

(v) In both the triangles one of their sides are equal.

One of their angles are equal or they are vertically opposite angles.
To satisfy SAS criterion, one more side is to be equal such that the angle is the included of the equal sides.

Question 6.
For each pair of triangles state the criterion that can be used to determine the congruency?

Solution:
(i) Given two pair of sides are equal and one side is common to both the triangles.
∴ SSS congruency criterion is used.

(ii) One of the sides and one of the angles are equal.
∴ One more angle is vertically opposite angle and so it is also equal.
ASA criterion is used.

(iii) From the figure hypotenuse and one side are equal in both the triangles.
RHS congruency criterion is used. (∵ Considering ∆ABC and ∆BAD)
∠A = ∠B = 90°
AD = BC
AB = AB (common)
∴ AC = BD (hypotenuse)

(iv) By ASA criterion both triangles are congruent.

(v) By ASA criterion both triangles are congruent. Since two angles in one triangle are equal to two corresponding angles of the other triangle. Again one side is common to both triangle and the side is the included side of the angles.

(vi) Two sides are equal. One angle is vertically opposite angles and one equal.
By SAS criterion both triangles are cogruent.

Question 7.
I. Construct a triangle XYZ with the given conditions.

(i) XY = 6.4 cm, ZY = 7.7 cm and XZ = 5 cm
Solution:


Construction:
Step 1: Draw a line. Marked Y and Z on the line such that YZ 7.7 cm.
Step 2: With Y as centre drawn an arc of radius 6.4 cm above the line YZ.
Step 3: With Z as centre, drwan an arc or radius 5 cm to intersect arc drawn in steps. Marked the point of intersection as X.
Step 3: Joined YX and ZX. Now XYZ is the required triangle.

(ii) An equilateral triangle of side 7.5 cm
Solution:

Construction:
Step 1: Drawn a line. Marked X and Y on the line such that XY = 7.5 cm.
Step 2: With X as centre, drawn an arc of radius 7,5 cm above the line XY.
Step 3: With Y as centre, drawn an arc of radius 7.5 cm to intersect arc drawn in steps. Marked the point of intersection as Z.
Step 4: Joined XZ and YZ. Now XYZ in the required triangle.

(iii) An isosceles triangle with equal sides 4.6 cm and third side 6.5 cm
Solution:

Construction: .
Step 1: Drawn a line. Marked X and Y on the line such that XY = 6.5 cm.
Step 2: With X as centre, drawn an arc of radius 4.6 cm above the line XY
Step 3: with Y as centre, drawn an arc of radius 4.6 cm to intersect arc drawn in steps. Marked the point of intersection as Z.
Step 4: Joined XZ and YZ. Now XYZ is the required triangle.

II. Construct a triangle ABC with given conditions.

(i) AB = 7 cm, AC = 6.5 cm and ∠A = 120°.
Solution:

Construction:
Step 1: Drawn a line. Marked A and B on the line such that AB = 7 cm.
Step 2: At A, drawn a ray AX making an angle of 120° with AB.
Step 3: With A as centre, drawn an arc of radius 6.5 cm to cut the ray AX. Marked the point of intersection as C.
Step 4: Joined BC.
ABC is the required triangle.

(ii) BC = 8 cm, AC = 6 cm and ∠C = 40°.
Solution:


Construction:
Step 1: Drawn a line. Marked B and C on the line such fhat BC = 8 Cm.
Step 2: At C, drawn a ray CY making an angle of 40° with BC.

Step 3: With C as centre, drawn an arc of radius 6 cm to cut the ray CY, marked the point of intersection as A.
Step 4: Joined AB.
AB is the required triangle.

(iii) An isosceles obtuse triangle with equal sides 5 cm
Solution:

Construction:
Step 1: Drawn a line. Marked B and C on the line such that BC = 5 cm.
Step 2: At B drawn a ray BY making on obtuse angle 110° with BC.
Step 3: With B as centre, drawn an arc of radius 5 cm to cut ray BY. Marked the point of intersection as C.
Step 4: Joined BC. ABC is the required triangle.

III. Construct a triangle PQR with given conditions.

(i) ∠P = 60°, ∠R = 35° and PR = 7.8 cm
Solution:

Construction:
Step 1: Drawn a line. Marked P and R on the line such that PR = 7.8 cm.
Step 2: At P, drawn a ray PX making an angle of 60° with PR.
Step 3: At R, drawn another ray RY making an angle of 35° with PR. Mark the point of intersection of the rays PX and RY as Q.
PQR is the required triangle.

(ii) ∠P = 115°, ∠Q = 40° and PQ = 6 cm
Solution:

Construction:
Step 1: Drawn a line. Marked P and Q on the line such that PQ = 6 cm.
Step 2: At P, drawn O ray PX making an angle of 115° with PQ.
Step 3: At Q, drawn another ray QY making an angle of 40° with PQ. Marked the point of intersection of the rays PX and Q Y as R.
PQR is the required triangle.

(iii) ∠Q = 90°, ∠R = 42° and QR = 5.5 cm
Solution:

Construction:
Step 1: Drawn a line. Marked Q and R on the line such that QR = 5.5 cm.
Step 2: At Q, drawn a ray QX making an angle of 90° with QR.
Step 3: At R, drawn another ray RY making an angle of 42° QR. Marked the point of intersection of the rays QX and RY as P.
PQR is the required triangle.

Objective Type Questions

Question 8.
If two plans figures are congruent then they have
(i) same size
(ii) same shape
(iii) same angle
(iv) same shape and same size
Answer:
(iv) same shape and same size

Question 9.
Which of the following methods are used to check the congruence of plane figures?
(i) translation method
(ii) superposition method
(iii) substitution method
(iv) transposition method
Answer:
(ii) superposition method

Question 10.
Which of the following rule is not sufficient to verify the congruency of two triangles.
(i) SSS rule
(ii) SAS rule
(iii) SSA rule
(iv) ASA rule
Answer:
(iii) SSA rule

Question 11.
Two students drew a line segment each. What is the condition for them to be congruent?
(i) They should be drawn with a scale.
(ii) They should be drawn on the same sheet of paper.
(iii) They should have different lengths.
(iv) They should have the same length.
Answer:
(iv) They should have the same length.

Question 12.
In the given figure, AD = CD and AB = CB. Identify the other three pairs that are equal.

(i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, BD = BD
(ii) AD = AB, DC = CB, BD = BD
(iii) AB = CD, AD = BC, BD = BD
(iv) ∠ADB = ∠CDB, ∠ABD = ∠CBD, ∠DAB = ∠DBC
Answer:
(i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, BD = BD

Question 13.
In ∆ABC and ∆PQR, ∠A = 50° = ∠P, PQ = AB, and PR = AC. By which property ∆ABC and ∆PQR are congruent?
(i) SSS property
(ii) SAS property
(iii) ASA property
(iv) RHS property
Answer:
(ii) SAS property

Students can Download Maths Chapter 2 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 2 Algebra Intext Questions

Exercise 2.1
Try These (Text book page no. 32)

Question 1.
Identify which among the following are linear equations.

1. 2 + x = 19 – Linear as degree of the variable x is 1
2. 7x² – 5 = 3 – not linear as highest degree of x is 2
3. 4p³ = 12 – not linear as highest degree ofp is 3
4. 6m + 2 – Linear, but not an equation
5. n = 10 – Linear equation as degree of n is 1
6. 7k – 12= 0 – Linear equation as degree of Hs 1
7. \(\frac{6x}{8}\) + y = 1 – Linear equation as degree ofx & y is 1
8. 5 + y = 3x – Linear equation as degree ofy & x is 1
9. 10p + 2q = 3 – Linear equation a& degree ofp & q is 1
10. x² – 2x-4 – not linear equation as highest degree of x is 2

Think (Text book page no. 32)

Question 1.
Is t(t – 5)= =10 a linear equation? Why?
Solution:
t(t – 5) = 10
= t x t – 5 x t = 10
= t² – 5t = 10
This is not a linear equation as the highest degree of the variable ‘t’ is 2

Question 2.
Is x² = 2x, a linear equation? Why?
Solution:
x² = 2x
= x² – 2x = 0
This is not a linear equations as the highest degree of the variable ‘x’ is 2

Try These (Text book page no. 33)

Convert the following statements into linear equations:

Question 1.
On subtracting 8 from the product of 5 and a number, I get 32.
Solution:
Convert to linear equations:
Given that on subtracting 8 from product of 5 and a, we get 32
5 × x – 8 = 32
5x – 8 = 32

Question 2.
The sum of three consecutive integers is 78.
Solution:
Sum of 3 consecutive integers is 78
Let 1st integer be ‘x’
∴ x + (x + 1) + (x + 2) = 78
∴ x + x + 1 + x + 2 = 78
3x + 3 = 78

Question 3.
Peter had a Two hundred rupee note. After buying 7 copies of a book he was left with ₹ 60.
Solution:
Let cost of one book be ‘x’
∴ Given that 200 – 7 × x = 60
∴ 200 – 7x = 60

Question 4.
The base angles of an isosceles triangle are equal and the vertex angle measures 80°.
Solution:
Let base angles each be equal to x & vertex bottom angle is 80°. Applying triangle
property, sum of all angles is 180°
∴ x + x + 80 = 180°
2x + 80 = 180°

Question 5.
In a triangle ABC, ∠A is 10° more than ∠B. Also ∠C is three times ∠A. Express the equation in terms of angle B
Solution:
Let ∠B = b
Given ∠A = 10° + ∠B = 10 + b
Also given that ∠C = 3 x ∠A = 3 x (10 + 6) = 30 + 3b
Sum of the angles = 180°
∠A + ∠B + ∠C = 180°
10 + b + b + 30 + 3b = 180°
∴ 5b + 40 = 180°

Think (Text book page no. 34)

Question 1.
Can you get more than one solution for a linear equation?
Solution:
Yes, we can get. Consider the below line or equation
x + y = 5
here, when x = 1, y = 4
when x = 2, y = 2
x = 3, y = 2
x = 4, y = 1
Hence, we get multiple solutions for the same linear equation.

Think (Text book page no. 35)

Question 1.
“An equation is multiplied or divided by a non zero number on either side.” Will there be any change in the solution?
Solution:
Not be any change in the solution

Question 2.
“An equation is multiplied or divided by two different numbers on either side”. What will happen to the equation?
Solution:
When an equation is multiplied or divided by 2 different numbers on either side, there will be a change in the equation & accordingly, solution will also change.

Exercise 2.2
Think (Text book page no. 37)

Question 1.
Suppose we take the second piece to be x and the first piece to be (200 – x), how will the steps vary. Will the answer be different?
Solution:
Let 2nd piece be V & 1st piece is 200 – x
Given that 1st piece is 40 cm smaller than hence the other piece
∴ 200 – x = 2 × x – 40

200 + 40 = 2x + x
240 = 3x
∴ x = \(\frac{240}{3}\) = 80
∴ 1st piece = 200 – x = 200 – 80 = 120 cm
2nd piece = x = 80 cm
The answer will not change

Exercise 2.3
Think (Text book page no. 43)

Question 1.
If instead of (4, 3), we write (3, 4) and try to mark it, will it represent ‘M’ again?
Solution:
Let 3, 4 be M, when we mark, we find that it is a different point and not ‘M’

Try These (Text book page no. 45)

Question 1.
Complete the table given below.

Solution:

Question 2.
Write the coordinates of the points marked in the following figure

• A – (-3, 2)
• B – (5, 2)
• C – (5, -3)
• D – (-3, 3)
• E – (-1,4)
• F – (1, 2)
• G – (7, 4)
• H – (0, 2)
• i – (o, 3)
• J – (-3, 0)
• K – (5, 0)
• L – (-1, 0)
• M – (-2, 0)
• N – (-2, -1)
• O – (0, 0)
• P – (-1, -1)
• Q – (1, -1)
• R – (2, -1)
• S – (0, -3)
• T – (7, 0)
• U – (7, -2)

Exercise 2.4
Think (Text book page no. 49)

Question 1.
Which of the points (5, -10) (0, 5) (5, 20) lie on the straight line X = 5?
Solution:
All points on the line X = 5 will have X – coordinate as 5.
Therefore, any point with X – coordinate as 5 will lie on X = 5 line.
Hence the points (5, – 10) & (5,20) will lie on X = 5

Think (Text book page no. 54)

Question 1.
Why is it given that the speed is ‘constant’? If the speed is not constant, will the graph be the same? The graph is named as y = 80 x algebraically. Why?
Solution:

or in other words, the slope of a line in a distance – time graph. We observe that the slope of the graph is constant hence, speed is constant. If the speed is not constant, the graph will be different as slope of the line would change.

You can Download Samacheer Kalvi 9th Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Science Solutions Chapter 16 Applied Chemistry

Samacheer Kalvi 9th Science Applied Chemistry Textbook Exercises

I. Choose the correct answer.

Question 1.
One Nanometre is ………………
(a) 10^{– 7} metre
(b) 10^{– 8} metre
(c) 10^{– 6} metre
(d) 10^{– 9} metre
Answer:
(d) 10^{– 9} metre

Question 2.
The antibiotic Penicillin is obtained from …………………
(a) plant
(b) microorganism
(c) animal
(d) sunlight
Answer:
(b) microorganism

Question 3.
1 % solution of Iodoform is used as ……………..
(a) antipyretic
(b) antimalarial
(c) antiseptic
(d) antacid
Answer:
(c) antiseptic

Question 4.
The cathode of an electrochemical reaction involves …………….
(a) oxidation
(b) reduction
(c) neutralisation
(d) catenation
Answer:
(b) reduction

Question 5.
The age of a dead animal can be determined by using an isotope of ………………..
(a) carbon
(b) iodine
(c) phosphorous
(d) oxygen
Answer:
(a) carbon

Question 6.
Which of the following does not contain natural dyes?
(a) Potato
(b) Beetroot
(c) Carrot
(d) Turmeric
Answer:
(a) Potato

Question 7.
This type of food protect us from deficiency diseases.
(a) Carbohydrates
(b) Vitamins
(c) Proteins
(d) Fats
Answer:
(b) Vitamins

Question 8.
Radiochemistry deals with ……………….
(a) oxidants
(b) batteries
(c) isotopes
(d) nanoparticles
Answer:
(c) isotopes

Question 9.
The groups responsible for the colour of an organic compound is called ………………….
(a) isotopes
(b) auxochrome
(c) chromogen
(d) chromophore
Answer:
(d) chromophore

Question 10.
Chlorinated hydrocarbons are used as ……………..
(a) fertilizers
(b) pesticides
(c) food colourants
(d) preservatives
Answer:
(b) pesticides

II. Fill in the blanks.

1. ……………. is an electrochemical cell which converts electrical energy into chemical change (Reaction).
2. Painkiller drugs are called ……………..
3. Aspirin is an …………….
4. …………. , …………….. and …………… are macronutrients required for plant growth.
5. ……………. is a chemical used in fingerprint analysis.

Answer:

1. Electrolytic cell
2. Analgesic
3. Analgesics
4. Nitrogen, Phosphorous, Potassium
5. Ninhydrin

III. Match the following.

Answer:

1. (c) Fever
2. (e) Electroplating
3. (b) Iodine – 131
4. (a) Large surface area
5. (d) Cancer cell identification

IV. Answer in brief.

Question 1.
What is Chemotherapy?
Answer:
Treatment of certain diseases by destroying the invading organism without damaging the cells of the host, by the use of certain organic compounds is known as Chemotherapy.

Question 2.
What are called Anaesthetics? How are they classified?
Answer:
The drugs which cause loss of sensation are called Anaesthetics.
Types of Anaesthetics

General anaesthetics: They are the agents, which bring about loss of all modalities of sensation, particularly pain along with ‘reversible’ loss of consciousness.
Local anaesthetics: They prevent the pain sensation in localised areas without affecting the degree of consciousness.

Question 3.
What is the need for chemical fertilizers in crop fields?
Answer:
Chemical fertilizers provide the essential micro and macronutrients for crop growth that may not be sufficiently available in the soil.

Question 4.
What is Forensic chemistry related to?
Answer:
Forensic chemistry applies scientific principles, techniques, and methods to the investigation of crime.

V. Answer in detail.

Question 1.
Explain the types of dyes based on their method of application.
Answer:
Dyes are classified in two ways, one, based on the method of application and other on their parent structure.

Based on method of application:

• Acid dyes: These are acidic in nature and used for dyeing animal fibres and synthetic fibres. These can be used for protein fibre such as wool and silk. E.g. Picric acid, Naphthol yellow-s
• Basic dyes: These are basic dyes containing basic group (- NH₂,- NHR, – NR₂). They are used for dyeing animal fibres and plant fibres.
• Mordant dyes or Indirect dyes: These dyes have a poor affinity for cotton fabrics and hence do not dye directly. They require pretreatment of the fibre with a mordant. Mordant (latin: mordere = to bite) is a substance which can be fixed to the fibre and then can be combined with the dye to form an insoluble complex called lake. Aluminium, chromium, and iron salts are widely used as mordants. E.g. alizarin.
• Direct dyes: They have high affinity for cotton, rayon and other cellulose fibre. So they are applied directly as they fix firmly on the fabric. E.g. Congo red
• Vat dyes: It can be used only on cotton and, not on silk and wool. This dyeing is a continuous process and is carried out in a large vessel called vat. So it is called as vat dye. E.g. Indigo

Question 2.
Name various food additives and explain their functions.
Answer:

VI. HOTS

Question 1.
Batteries that are used in mobile phone can be recharged. Likewise, can you recharge the batteries used in watches? Justify your answer.
Answer:
A primary cell cannot be recharged. Watch batteries have a primary cell. In a primary cell, chemical energy is converted into electrical energy when current is drawn from it.

Whereas mobile phones use secondary cells. In secondary cells electrical energy is converted to chemical energy when current is passed through it and chemical energy is converted to electrical energy when current is drawn from it.

Question 2.
Sudha met with a fire accident. What kind of drug(s), she must take?
Answer:
Analgesics are to be administered to reduce the pain followed by antibiotics to prevent infection by microbes.

Question 3.
The soil pH of a cropland is 5. What kind of fertilizers should be used in that land?
Answer:
Organic fertilizer like compost can be used to maintain pH of soil at 6.5, which is ideal for soil and to moderate the acidity.

Samacheer Kalvi 9th Science Applied Chemistry Additional Questions

I. Answer briefly.

Question 1.
Explain the structure of an electrolytic cell.
Answer:

• It is an electrochemical cell which converts electrical energy into chemical energy i.e. in electrolytic cells, electricity is used to bring about chemical reactions.
• Here, both anode and cathode are in contact with Anode same electrolyte and thus the half-cells are not separated. As seen in galvanic cells, electrolytic cell also involves redox reaction. We get electricity from galvanic cells. But electrolytic cells use electricity.
• In electrolytic cells, when electricity is passed to the electrolyte, it dissociates into its constituent ions. These ions undergo redox reaction forming the respective elements. This phenomenon is called Electrolysis. So electrolysis is a process by which an electrolyte is decomposed into its constituent elements by passing electricity through its aqueous solution or fused (molten) state.

Question 2.
How does galvanic cell produce electricity?
Answer:
In a galvanic cell, at anode oxidation takes place which releases electrons. These electrons are attracted by cathode and hence the electrons flowing from anode to cathode are gained in reduction reaction. As long as the redox reaction proceeds, there is a flow of electrons and hence electricity.

Question 3.
What are drugs? What are their characteristics?
Answer:
The chemicals used for treating diseases are termed as drug.
Characteristics of drugs: A drug must possess the following;

1. It should not be toxic
2. It should not cause any side effects.
3. It should not affect the receptor tissue
4. It should not affect the normal physiological activities
5. It should be effective in its action.

Question 4.
Write the applications of Nanochemistry.
Answer:
Some applications of Nanochemistry are:

1. The metallic nanoparticles can be used as very active catalysts.
2. Chemical sensors from nanoparticles and nanowires enhance the sensitivity and sensor selectivity.
3. Nanocoatings and nanocomposites are found useful in making a variety of products such as sports equipment, bicycles and automobiles etc.
4. These are used as novel UV-blocking coatings on glass bottles which protect beverages from being damaged by sunlight.
5. Nanotechnology is being applied in the production of synthetic skin and implant surgery.
6. Nanomaterials that conduct electricity are being used in electronics as minute conductors to produce circuits for microchips.
7. Nanomaterials have extensive applications in the preparation of cosmetics, deodorants and sunscreen lotion and they are used to improve moisturizers without making them too oily.
8. Nanoparticle substances are incorporated in fabrics to prevent the growth of bacteria.
9. Biomedical devices like drug infusion pumps, microneedles and glucometer are made from nanomaterials.
10. Nanochemistry is used in making space, defence and aeronautical devices

Question 5.
What are the applications of Radiochemistry?
Answer:
Important applications of radioisotopes are as under –

• Radiocarbon dating – its a method by which the age of fossil wood or animal is determined using C-14 isotope.
• Study of chemical reactions – the nature of some chemical reactions can be studied by mixing a radioisotope with a non-radioactive isotope of the reactants. The radioisotope used for this purpose is radiotracer.
• Diagnosis – Radioisotope is found very useful to diagnose and understand many diseases.

Question 6.
Write a note on Natural dyes.
Answer:
Many natural dyes have been known from a long time. These are obtained from vegetable sources.

• Henna: It is a reddish-brown dye obtained from plant Lawsonia inermis (Tamil: Maruthondri). A paste of these leaves is used as a hair dye and also for colouring palms.
• Turmeric: It is the traditional natural cosmetic in India. It is obtained from the plant Curcuma. longa. It also acts as an antiseptic. Turmeric is mostly used in India for colouring food.

Question 7.
What is electroplating? Why is it done?
Answer:
The process of depositing a thin layer of one metal over another metal by the process of electrolysis is called electroplating.

It is done to protect the metal from corrosion. For example, metals like iron are electroplated with tin, nickel or chromium to protect from rusting.

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Vocabulary Idioms

An idiom is an expression in English with a special meaning of its own. Idioms do not give the literal meaning of the individual words used in them.

Here are a few sentences with idioms (meanings are given in brackets):

• Business is going from bad to worse, (deteriorate further)
• They always do things in a big way, (on a large scale)
• The government has taken a very hard line (not giving in) against illegal quarrying.
• Orders for the new product are coming in thick and fast, (in large numbers)
• How can any one make ends meet (manage with the money) with just ? 2000/- a month?
• Your son’s behavior is a matter of concern, (something to worry about)
• The name sounds familiar but I can’t call her face to mind, (recall something from memory; recognise)
• My uncle loves to tell us how to play cricket. He is an armchair expert.
  (one who gives advice in an area in which he was not actively involved)
• Ravi is our sincere employee. He has had a clean slate (a past record without discredit) for over twenty years.
• The policeman went near the damaged car to have a look at close quarters, (very near)
• Dr. Jacob is at the helm (in charge) of affairs in this hospital.
• No one can make a break even (make no profit or loss) in the first year of business.
• Because of the steep rice in prices, people living on pension feel the pinch, (feeling unpleasant change in one’s standard of living)
• Let us settle the bill for the damage fair and square, (in a fair way)
• I can hear you over phone loud and clear, (very clearly)
• By and by (as time goes by) he will realise that my going to Delhi was the right decision.

Idioms from the Textual Exercises
Idiom – Meaning
1. alarm bells ringing – a sign of something going wrong
2. back to the wall – in serious difficulty
3. below the belt – unfair or unsporting behavior
4. by the skin of one’s teeth – a narrow escape.
5. drive one up the wall – to annoy or irritate someone
6. asp / clutch at straws – try any method to overcome a crisis
7. hang out to dry – abandoning one who is in difficulty
8. have cold feet – feel nervousness and anxiety
9. hit the road – to begin one’s journey
10. in a nice pickle – in a troublesome or difficult situation
11. in our corner – on your side in an argument or dispute
12. in panic mode – in a frightening state
13. on the ropes – state of near collapse or defeat
14. right up to one’s alley – ideally suited to one’s interest
15. saved by the bell – help at the last moment rescuing one from a difficult situation
16. shot his bolt – to exhaust one’s effort
17. square off – prepare for a conflict
18. take (one) for a ride – to deceive someone
19. throw in the towel – to give up
20. tight corners – difficult situations

Some more idioms and meanings :

1	a bolt from the blue	unexpected event; complete surprise (usually unwelcome)
2	a drop in the ocean	a very small amount compared with what is needed or expected
3	a great deal	plenty of
4	a penny for your thoughts	a way of asking what someone is thinking.
5	a stone’s throw	a very short distance
6	a storm in a teacup	a big fuss about a small problem
7	a wild goose chase	a worthless hunt or chase
8	a yellow streak	cowardice in one’s character
9	above board	honest, not a secret
10	add insult to injury	to worsen an unfavorable situation
11	armchair expert	one who gives advice in an area in which he was not actively involved
12	at close quarters	very near
13	at hand	very near
14	at loggerheads	to disagree strongly
15	at snail’s pace	very slowly
16	at the drop of the hat	without any hesitation
17	at the eleventh hour	at the last moment
18	at the end of one’s tether	to have no power, patience or endurance left
19	at the helm	in charge
20	at the mercy of	under the control of
21	barking up the wrong tree	accusing the wrong person
22	be armed with	be equipped with
23	be fit for	suitable
24	be part of	belong to
25	beat around the bush	avoiding the main topic
26	bed of roses	comfortable position
27	best of both worlds	all the advantages
28	big way	on a large scale
29	bite the bullet	to get something over with because it is inevitable
30	blessing in disguise	something good that isn’t recognized at first.
31	bolt from the blue	something that happened without warning
32	break even	make no profit or loss
33	break the ice	make people feel more comfortable
34	break through	penetrate
35	bring forth	produce
36	burst into	enter suddenly
37	by and by	as time goes by
38	by nature	because of natural habits
39	call it a day	stop working on something
40	can’t judge a book by its cover	cannot judge something primarily on appearance.
41	clean slate	a past record without discredit
42	comparing apples to oranges	comparing two things that cannot be compared
43	costs an arm and a leg	very expensive
44	curiosity killed the cat	being inquisitive can lead you into an unpleasant situation.
45	devil’s advocate	to present a counter argument
46	draw a blank	unable to get information
47	every cloud has a silver lining	good-things come after bad things
48	eyesore	ugly sight
49	eyewash	something to deceive
50	fair and square	in a fair way
51	fall a prey to	become a victim
52	far cry from	very different from
53	far from	distant
54	feel the pinch	feeling unpleasant change in one’s standard of living
55	fit as a fiddle	in good health
56	fortune favours the bold	take risks
57	give (someone) a piece of one’s mind	to tell someone frankly what one thinks especially when one disapproves of the other’s behaviour
58	give someone the cold shoulder	ignore someone
59	go down in flames	fail spectacularly
60	go on a wild goose chase	to do something pointless
61	going from bad to worse	deteriorate further
62	good-for-nothing	worthless
63	hang around	someone strongly to loiter
64	hang in there	don’t give up
65	hard to come by	difficult to find
66	have a hand	to get involved
67	have no hand in	does not take part in an activity
68	head back	return
69	herculean task	difficult task
70	hit the nail on the head	do or say something exactly right
71	hit the sack	go to sleep
72	holds good	valid at the time of discussion
73 ,	honour bound (to do something)	required to do something as a moral duty but not by law
74	in a nutshell	briefly
75	in all walks of life	all social groups
76	in deep waters	in trouble
77	in hot pursuit	following closely
78	in short supply	Not enough / scarce
79	in the hands of	in the care of
80	in the service of	available for
81	it is a piece of cake	it is easy
82	it’s Taining cats and dogs	it’s raining hard
83	keep pace with	to move with same speed
84	keep something at bay	keep something away
85	kicked the bucket	passed away
86	leave no stone unturned	look everywhere
87	let the cat out of the bag	give away a secret
88	lion’s share	major share
89	look down upon	treat with contempt                        .
90	loud and clear	very clearly
91	make both ends meet	live within means
92	make fun of	ridicule
93	make up one’s mind	decide, determine
94	matter of concern	something to worry about
95	miss the boat	it’s too late
96	muffle up	to cover
97	not playing with a full deck	someone who lacks intelligence
98	note of hand	promissory note
99	null and void	invalid
100	on cloud nine	to be extremely happy
101	once and for all	completely and finally
102	once in a blue moon	vary rarely
103	one thing leads to another	series of events in which each event was caused by the previous one.
104	out of place	unsuitable
105	pink of health	extremely healthy, in perfect condition
106	play an important role	to have a significant position
107	pull yourself together	calm down
108	put on airs	behave in an unnatural way to impress others
109	shadow of one’s self	not having the strength, former self influence, etc., that one once had
110	side by side	along with
111	speak volumes	to express something very clearly and completely
112	spill the beans	give away a secret
113	take to one’s heels	to run away
114	taken a very hard line	not giving in
115	the ball is in your court	it’s your decision
116	the burning question	a crucial issue
117	the whys and wherefores	the reasons for something
118	thick and fast	in large numbers
119	tit for tat	revenge
120	told him flat	expressed opinion directly
121	tread on	walk with difficulty
122	trial and error	to try many times to succeed
123	tricks of the trade	the expertise of doing business
124	well-balanced	well adjusted
125	whole nine yards	everything, all of it
126	wouldn’t be caught dead	would never like to do something
127	with a bang	in a very exciting way

Exercises
(i) Choose the correct option to complete the given idioms.
1. A bolt from _________.
(a) the white (b) the sky (c) the green (d) the blue
Answer:
(d) the blue

2. A storm _________.
(a) at sea (b) in the ocean (c) in a coffee cup (d) in a tea cup
Answer:
(d) in a tea cup

3. Can’t judge a book, _________.
(a) by the colour (b) by its cover (c) by its pages (d) by its author
Answer:
(db) by its cover

4. Every cloud _________.
(a) is dark (b) hides the sun (c) has a silver lining (d) brings rain
Answer:
(c) has a silver lining

5. Casts an arm _________.
(a) and a face (b) and a finger (c) and a leg (d) and some money
Answer:
(c) and a leg

6. Add insult to _________.
(a) friend (b) enemy (c) neighbor (d) injury
Answer:
(d) injury

7. A penny for _________.
(a) a picture (b) honesty (c) hard work (d) your thoughts
Answer:
(d) your thoughts

8. Fortune favors
(a) the hardworking (b) the poor (c) the rich (d) the bold
Answer:
(d) the bold

9. Hit the nail _________.
(a) on the wall (b) on the door (c) in the bench (d) on the head
Answer:
(d) on the head

10. Once in a _________.
(a) blue moon (b) in a tea cup (c) new moon (d) full moon
Answer:
(a) blue moon

(ii) Give a suitable idiom for the given meanings.

1. Say something exactly right.
Answer:
To hit the nail on the head.

2. All social groups.
Answer:
All walks of life.

3. It’s raining hard.
Answer:
Its raining cats and dogs.

4. Passed away.
Answer:
Kicked the bucket.

5. Live within means.
Answer:
To make both ends meet.

6. Invalid.
Answer:
Null and void.

7. Extremely healthy.
Answer:
Pink of health.

8. Give away a secret.
Answer:
To let the cat out of the bag.

9. Revenge.
Answer:
Tit for that.

10. In trouble.
Answer:
In deep waters.

Students can Download Maths Chapter 2 Algebra Ex 2.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 2 Algebra Ex 2.4

Question 1.
Fill in the blanks:

Question (i)
y = px where p ∈ Z always passes through the ………
Answer:
Origin (0, 0)
Hint:
[When we substitute x = 0 in equation, y also becomes zero. (0,0) is a solution]

Question (ii)
The intersecting point of the line x = 4 and y = – 4 is ………
Answer:
4, -4
Hint:
x = 4 is a line parallel to the y – axis and
y = – 4 is a line parallel to the x – axis. The point of intersection is a point that lies on both lines & which should satisfy both the equations. Therefore, that point is (4, -4)

Question (iii)
Scale for the given graph, on the x – axis 1 cm = ……… units y – axis 1 cm = ………. units

Answer:
3 units, 25 units
Hint:
With reference to given graph,
On the x – axis, 1cm = 3 units
y axis, 1cm = 25 units

Question 2.
Say True or False:

Question (i)
The points (1, 1) (2, 2) (3, 3) lie on a straight line.
Answer:
True
Hint:
The points (1, 1), (2, 2), (3, 3) all satisfy the equation y = x
which is straight line. Hence, it is true

Question (ii)
y = – 9x not passes through the origin.
Answer:
False
Hint:
y = – 9x substituting forx as zero, we get y = – 9 x 0 = 0
∴ for x = 0, y = 0. Which means line passes through (0, 0), hence statement is false.

Question 3.
Will a line pass through (2, 2) if it intersects the axes at (2, 0) and (0, 2).
Solution:
Given a line intersects the axis at (2, 0) & (0, 2)
Let line intercept form be expressed as
ax + by = 1 Where a & b are the x & y intercept respectively.
Since the intercept points are (2, 0) & (0, 2)
a = 2, b = 2
∴ 2x + 2y = 1
When the point (2, 2) is considered & substituted in the equation
2x + 2y = 1 we get
2 x 2 + 2 x 2 = 4 ≠ 1
∴ The point (2, 2) does not satisfy the equation. Therefore the line does not pass through (2, 2)
Alternatively graphical method:
as we can see the line doesn’t pass through (2, 2)

Question 4.
A line passing through (4, – 2) and intersects the Y – axis at (0, 2). Find a point on the line in the second quadrant.
Solution:

Line passes through (4, – 2)
y – axis intercept point – (0, 2)
using 2 point formula,
\(\frac { y-y_{ 1 } }{ x-x_{ 1 } } \) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
\(\frac{y-2}{x-0}\) = \(\frac{1-2-2}{4-0}\)
∴ \(\frac{y-2}{x}\) = \(\frac{-4}{4}\) = – 1
y – 2 = – 1 × x

∴ x + y = 2 is the equation of the line.
Any point in II quadrant will have x as negative & y as positive.
So let us take x value as – 2
∴ – 2 + y = 2
y = 2 + 2 = 4
∴ Point in II Quadrant is (-2, 4)

Question 5.
If the points P (5, 3) Q(- 3, 3) R (- 3, – 4) and S form a rectangle then find the coordinate of S.
Solution:
Plotting the points on a graph (approximately)

Steps:

1. Plot P, Q, R approximately on a graph.
2. As it is a rectangle, RS should be parallel to PQ & QR should be parallel to PS
3. S should lie on the straight line from R parallel to x – axis & straight line from P parallel to y – axis
4. Therefore, we get S to be (5, -4)

[Note: We don’t need graph sheet for approximate plotting. This is just for graphical understanding]

Question 6.
A line passes through (6, 0) and (0, 6) and an another line passes through (- 3, 0) and (0, – 3). What are the points to be joined to get a trapezium?
Solution:
In a trapezium, there are 2 opposite sides that are parallel. The other opposite sides are non-parallel.
Now, let us approximately plot the points for our understanding [no need of graph sheet]

1. Plot the points (0, 6), (6, 0), (-3, 0) & (0, – 3)
2. Join (0, 6) & (6, 0)
3. Join (-3, 0) & (0, -3)
4. We find that the lines formed by joining the points are parallel lines.
5. So, for forming a trapezium, we should join (0, 6), (-3, 0) & (0, -3), (6, 0)

Question 7.
Find the point of intersection of the line joining points (- 3, 7) (2, – 4) and (4, 6) (- 5, 7). Also find the point of intersection of these lines and also their intersection with the axis.
Solution:

Equation of line joining 2 points by 2 point formula is given by
\(\frac { y-y_{ 1 } }{ x-x_{ 1 } } \) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
∴ \(\frac{y-7}{x-(-3)}\) = \(\frac{-4-7}{2-(-3)}\)
\(\frac{y-7}{x+3}\) = \(\frac{-11}{2+3}\)
∴ \(\frac{y-7}{x+3}\) = \(\frac{-11}{5}\)
Cross multiplying, we get

Transposing the variables, we get
11x + 5y = 35 – 33 = 2
11x + 5y = 2 – Line 1
Similarly, we should find out equation of second line

∴ 9y – 54 = 13x – 52
9y – 13x = 2 – Line 2
For finding point of intersection, we need to solve the 2 line equation to find a point that will satisfy both the line equations.
∴ Solving for x & y from line 1 & line 2 as below
11x + 5y = 2 ⇒ multiply both sides by 13,
11 x 13x + 5 x 13y = 26
Line 2:
9y – 13x = 2 ⇒ multiply both sides by 11
9 x 11y – 13 x 11x = 22

Substituting this value of y in line 1 we get
11x + 5y = 2
11x + 5 x \(\frac{12}{41}\) = 2
11x = 2 – \(\frac{60}{41}\) = \(\frac{82-60}{41}\) = \(\frac{22}{41}\)
x = \(\frac{2}{41}\)
∴ Point of intersection is (\(\frac{2}{41}\) \(\frac{12}{41}\))
To find point of intersection of the lines with the axis, we should substitute values & check
Line 1:
11x + 5y = 2
Point of intersection of line with x – axis, i.e y coordinate is ‘0’
∴ put y = 0 in above equation
∴ 11x – 5 x 0 = 2
11x + 0 = 2
x = \(\frac{2}{11}\)
∴ Point is (\(\frac{2}{11}\), 0)
Similarly, point of intersection of line with y – axis is when x – coordinate becomes ‘0’
∴ put x = 0 in above equation
∴ 11 x 0 + 5y = 2
∴ 0 + 5y = 2
y = \(\frac{2}{5}\)
∴ Point is (0, \(\frac{2}{5}\))
Similarly for line 2,
9y – 13x = 2
For finding x intercept, i.e point where line meets x axis, we know thaty coordinate becomes ‘0’
∴ Substituting y – 0 in above eqn. we get
9 x 0 – 13x = 2
∴ 0 – 13x = 2
x = \(\frac{-2}{13}\)
∴ Point is (\(\frac{-2}{13}\), 0)
Similarly for y – intercept, x – coordinate becomes ‘0’,
∴ Substituting for x = 0 in above equation, we get
9y – 13 x 0 = 2
9y – 0 = 2
9y = 2
y = \(\frac{2}{9}\)
Point is (0, \(\frac{2}{9}\))

Question 8.
Draw the graph of the following equations:

1. x = – 7
2. y = 6

Solution:

Question 9.
Draw the graph of

1. y = – 3x
2. y = x – 4

Solution:
To draw graph, we need to find out some points.
1. for y = – 3x, let us first substituting values & check
put x = 0
y = – 3 x 0 = 0 ∴ (0,0) is a point
put x = 1
y = – 3 x 1 = – 3 ∴ (1, – 3) is a point
If join these 2 points, we will get the line

2. for y = x – 4
put x = 0
y = 0 – 4 = -4 ∴ (0, – 4) is a point
x = 4
y = 4 – 4 = 0 ∴ (4, 0) is a point
Now let us plot the points & join them on graph

Question 10.
Find the values

Solution:
Let y = x + 3
(i) if x = 0
y = 0 + 3 = 3
∴ y = 3

(ii) y = 0
0 = x + 3
∴ x = – 3

(iii) x = – 2
y = – 2 + 3
∴ y = 1

(iv) y = -3
-3 = x + 3
∴ x = -6

Let 2x + 7 – 6 = 0
(i) x = 0
2 x 0 + y – 6 = 0
∴ 7 = 6

(ii) y = 0
2x + 0 – 6 = 0
2x = 6
x = 3

(iii) x = – 2
2 x (- 2) + y – 6 = 0
y – 10 = 0
y = 10

(iv) y = -3
2x – 3 – 6 = 0
2x = 9
x = \(\frac{9}{2}\)

Question 11.
The following is a table of , values connecting the radii of a few circles and their circumferences (Taking π = \(\frac{22}{7}\)) Illustrate the relation with a graph and find

1. The radius when the circumference is 242 units.
2. The circumference when the radius is 24.5 units.

Solution:

r = 24.5 Circumference?

Steps :

1. Draw the axis, x – axis = radius & y – axis = circumference
2. Mark the points by choosing scale of 1 cm = 7 units for x axis & 1 cm = 44 units for y – axis
3. Join the points to form a line.
4. Now for r value = 24.5 (mid value between 21 & 28), draw vertical line to touch the main line & from there drop line parallel to x axis and note where it meets y axis.

It meets between 132 & 176. Taking the mid value
i.e \(\frac{132+176}{2}\) = 154, we get circumference of 154 when r = 24.5.
Similarly, for circumference of 242, we get r value to be 38.5

Question 12.
An over-head tank is full with water. Water leaks out from it, at a constant rate of 10 litres per hour. Draw a “time-wastage” graph for this situation and find

1. The water wasted in 150 minutes
2. The time at which 75 litres of water is wasted.

Solution:
From over head tank, water leaks out at 10 l/hr.
∴ Let us see how much leakage happens with time
Time     Leakage
1 hr        10 ltrs.
2 hrs       20 ltrs.
3 hrs       30 ltrs.
4 hrs       40 ltrs.. and so on
150 min = 120 min + 30 min
= 2 hr 30 min = 2 \(\frac{1}{2}\) hrs
Now let us plot a graph between time & water leakage

Water wasted in 150 min (2\(\frac{1}{2}\) hrs) = 25 litres
Time at which 75 litre of water is wasted = 7\(\frac{1}{2}\) hrs = 450 minutes.

You can Download Samacheer Kalvi 9th English Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th English Grammar Phrasal Verbs

A phrasal verb is a verb that is made up of a main verb together with an adverb or a preposition or both, to create a completely new meaning.

Exercises