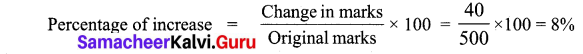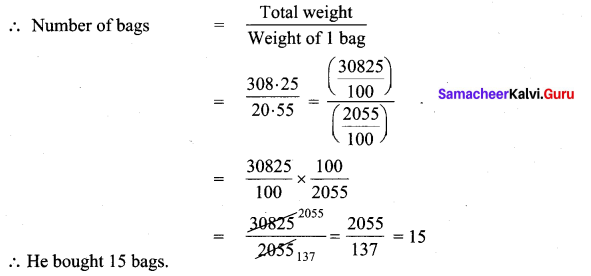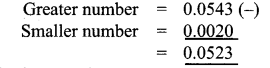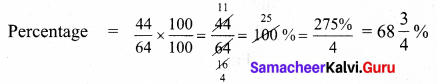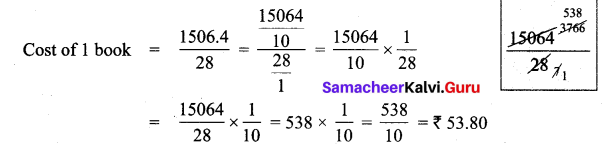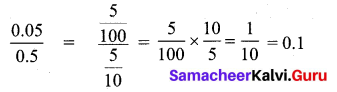Category: Class 7

Students can Download Maths Chapter 2 Percentage and Simple Interest Ex 2.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 2 Percentage and Simple Interest Ex 2.5

Miscellaneous Practice Problems

Question 1.
When Mathi was buying her flat she had to put down a deposit of \(\frac { 1 }{ 10 } \) of the value of the flat. What percentage was this?
Solution:
Percentage of \(\frac { 1 }{ 10 } \) = \(\frac { 1 }{ 10 } \) × 100 % = 10 %
Mathi has to put down a deposit of 10 % of the value of the flat.

Question 2.
Yazhini scored 15 out of 25 in a test. Express the marks scored by her in percentage.
Solution:
Yazhini’s score = 15 out of 25 = \(\frac { 15 }{ 25 } \)
Score in percentage = \(\frac { 15 }{ 25 } \) × 100% = 60%

Question 3.
Out of total 120 teachers of a school 70 were male. Express the number of male teachers as percentage.
Solution:
Total teachers of the school = 120
Number of male teachers = 70
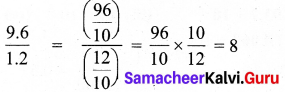
∴ Percentage of male teacher = \(\frac { 70 }{ 120 } \) × 100 % = \(\frac { 700 }{ 12 } \) %
Score in percentage = 58.33%
Percentage of male teachers = 58.33%

Question 4.
A cricket team won 70 matches during a year and lost 28 matches and no results for two matches. Find the percentage of matches they won.
Solution:
Number of Matches won = 70
Number of Matches lost = 28
“No result” Matches = 2
Total Matches = 70 + 28 + 2 = 100
Percentage of Matches won = \(\frac { 70 }{ 100 } \) × 100 % = 70 %
The won 70% of the matches

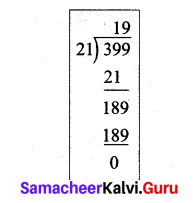
Question 5.
There are 500 students in a rural school. If 370 of them can swim, what percentage of them can swim and what percentage cannot?
Solution:
Total number of students = 500
Number of students who can swim = 370
Percentage of students who can swim = \(\frac { 370 }{ 500 } \) × 100 % = 74 %
Number of students who cannot swim = 500 – 370 = 130
Percentage of students who cannot swim = \(\frac { 130 }{ 500 } \) × 100 % = 26 %
i.e. 74% can swim and 26% cannot swim

Question 6.
The ratio of Saral’s income to her savings is 4 : 1. What is the percentage of money saved by her?
Solution:
Total parts of money = 4 + 1 = 5
Part of money saved = 1
∴ Percentage of money saved = \(\frac { 1 }{ 5 } \) × 100% = 20%
∴ 20% of money is saved by Saral

Question 7.
A salesman is on a commission rate of 5%. How much commission does he make on sales worth ₹ 1,500?
Solution:
Total amount on sale = ₹ 1,500
Commission rate = 5 %
Commission received = 5 % of ₹ 1,500 = \(\frac { 5 }{ 100 } \) × 1500 = ₹ 75
∴ Commission received = ₹ 75

Question 8.
In the year 2015 ticket to the world cup cricket match was ₹ 1,500. This year the price has been increased by 18%. What is the price of a ticket this year?
Solution.
Price of a ticket in 2015 = ₹ 1500
Increased price this year = 18% of price in 2015
= 18 % of ₹ 1500 = \(\frac { 18 }{ 100 } \) × 1500
= ₹ 270
Price of ticket this year = last year price + increased price
= ₹ 1500 + ₹ 270 = ₹ 1770
Price of ticket this year = ₹ 1770

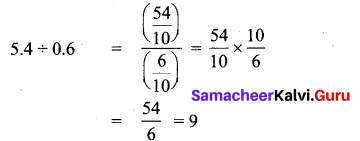
Question 9.
2 is what percentage of 50?
Solution:
Let the required percentage be x
x% of 50 = 2
\(\frac { x }{ 100 } \) × 50 = 2
x = \(\frac{2 \times 100}{50}\) = 4 %
∴ 4 % of 50 is 2

Question 10.
What percentage of 8 is 64?
Solution:
Let the required percentage be x
So x % of 8 = 64
\(\frac { x }{ 100 } \) × 8 = 64
x = \(\frac{64 \times 100}{8}\) = 800
∴ 800 % of 8 is 64

Question 11.
Stephen invested ₹ 10,000 in a savings bank account that earned 2% simple interest. Find the interest earned if the amount was kept in the bank for 4 years.
Solution:
Principal (P) = ₹ 10,000
Rate of interest (r) = 2%
Time (n) = 4 years
∴ Simple Interest I = \(\frac { pnr }{ 100 } \)
= \(\frac{10000 \times 4 \times 2}{100}\)
= ₹ 800
Stephen will earn ₹ 800

Question 12.
Riya bought ₹ 15,000 from a bank to buy a car at 10% simple interest. If she paid ₹ 9,000 as interest while clearing the loan, find the time for which the loan was given.
Solution:
Here Principal (P) = ₹ 15,000
Rate of interest (r) = 10 %
Simple Interest (I) = ₹ 9000
I = \(\frac { pnr }{ 100 } \)
9000 = \(\frac{15000 \times n \times 10}{100}\)
n = \(\frac{9000 \times 100}{15000 \times 10}\)
n = 6 years
∴ The loan was given for 6 years

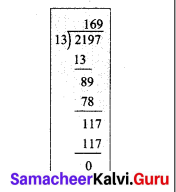
Question 13.
In how much time will the simple interest on ₹ 3,000 at the rate of 8% per annum be the same as simple interest on ?4,000 at 12% per annum for 4 years?
Solution:
Let the required number of years be x
Simple Interest I = \(\frac { pnr }{ 100 } \)
Principal P₁ = ₹ 3000
Rate of interest (r) = 8 %
Time (n₁) = n₁ years
Simple Interest I₁ = \(\frac{3000 \times 8 \times n_{1}}{100}\) = 240 n₁
Principal (P₂) = ₹ 4000
Rate of interest (r) = 12 %
Time n₂ = 4 years
Simple Interest I₂ = \(\frac{4000 \times 12 \times 4}{100}\)
I₂ = 1920
If I₁ = I₂
240 n₁ = 1920
n₁ = \(\frac { 1920 }{ 240 } \) = 8
∴ The required time = 8 years

Challenge Problems

Question 14.
A man travelled 80 km by car and 320 km by train to reach his destination. Find what percent of total journey did he travel by car and what per cent by train?
Solution:
Distance travelled by car = 80 km.
Distance travelled by train = 320 km
Total distance = 80 + 320 km = 400 km
Percentage of distance travelled by car = \(\frac { 80 }{ 400 } \) × 100 % = 20 %
Percentage of distance travelled by train = \(\frac { 320 }{ 800 } \) × 100 % = 40 %

Question 15.
Lalitha took a math test and got 35 correct and 10 incorrect answers. What was the percentage of correct answers?
Solution:
Number of correct answers = 35
Number of incorrect answers = 10
Total number of answers = 35 + 10 = 45
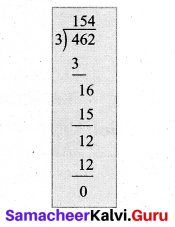
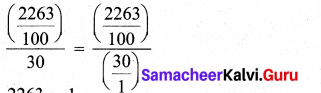
Percentage of correct answers = \(\frac { 35 }{ 45 } \) × 100 %
= 77.777 % = 77.78 %

Question 17.
The population of a village is 8000. Out of these, 80% are literate and of these literate people, 40% are women. Find the percentage of literate women to the total population?
Solution:
Population of the village = 8000 people
literate people = 80 % of population
= 80 % of 8000 = \(\frac { 80 }{ 100 } \) × 8000
literate people = 6400
Percentage of women = 40 %
Number of women = 40 % of literate people
= \(\frac { 40 }{ 100 } \) × 6400 = 2560
∴ literate women : Total population
= 8000 : 2560
= 25 : 8

Question 18.
A student earned a grade of 80% on a math test that had 20 problems. How many problems on this test did the student answer correctly?
Solution:
Total number of problems in the test = 20
Students score = 80 %
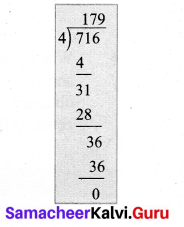
Number of problem answered = \(\frac { 80 }{ 100 } \) × 20 = 16

Question 19.
A metal bar weighs 8.5 kg. 85% of the bar is silver. How many kilograms of silver are in the bar?
Solution:
Total weight of the metal = 8.5 kg
Percentage of silver in the metal = 85%
Weight of silver in the metal = 85% of total weight
= \(\frac { 85 }{ 100 } \) × 8.5 kg
= 7.225 kg
7.225 kg of silver are in the bar.

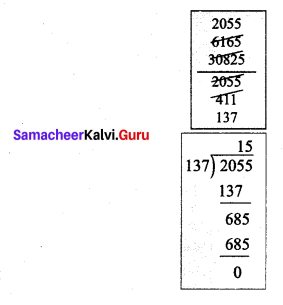
Question 20.
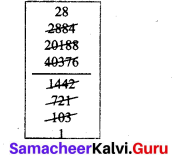
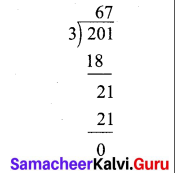
Concession card holders pay ₹ 120 for a train ticket. Full fare is ₹ 230. What is the percentage of discount for concession card holders?
Solution:
Train ticket fare = ₹ 230
Ticket fare on concession = ₹ 120
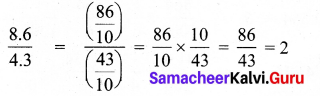
Discount = Ticket fare – concession fare = 230 – 120 = ₹ 110

Percentage of discount = 47.83%

Question 21.
A tank can hold 200 litres of water. At present, it is only 40% full. How many litres of water to fill in the tank, so that it is 75 % full?
Solution:
Capacity of the water tank = 200 litres
Percentage of water in the tank = 40%
Percentage of water to fill = Upto 75%
Difference in percentage = 75 % – 40 % = 35 %
∴ Volume of water to be filled = Percentage of difference × total capacity
= \(\frac { 35 }{ 100 } \) × 200 = 70 l
70 l of water to be filled

Question 22.
Which is greater 16 \(\frac { 2 }{ 3 } \) or \(\frac { 2 }{ 5 } \) or 0.17 ?
Solution:
16 \(\frac { 2 }{ 3 } \) = \(\frac { 50 }{ 30 } \)
= \(\frac { 50 }{ 30 } \) × 100 % = 1666.67 %
⇒ \(\frac { 2 }{ 5 } \)
= \(\frac { 2 }{ 5 } \) × 100 = 40 %
0.17 = \(\frac { 17 }{ 100 } \) = 17 %
∴ 1666.67 is greater
∴ 16 \(\frac { 2 }{ 3 } \) is greater

Question 23.
The value of a machine depreciates at 10% per year. If the present value is ₹ 1,62,000, what is the worth of the machine after two years.
Solution:
Present value of the machine = ₹ 1,67,000
Rate of depreciation = 10 % Per annum
Time (n) = 2 years
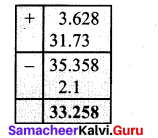
For 1 year depreciation amount = \(\frac{1,62,000 \times 1 \times 10}{100}\) = ₹ 16,200
Worth of the machine after one year = Worth of Machine – Depreciation
= 1,67,000 – 16,200 = 1,45,800
Depreciation of the machine for 2nd year = 145800 × 1 × \(\frac { 10 }{ 100 } \) = 14580
Worth of the machine after 2 years = 1,45,800 – 14,580 = 1,31,220
∴ Worth of the machine after 2 years = ₹ 1,31,220

Question 24.
In simple interest, a sum of money amounts to ₹ 6,200 in 2 years and ₹ 6,800 in 3 years. Find the principal and rate of interest.
Solution:
Let the principal P = ₹ 100
If A = 6200
⇒ Principal + Interest for 2 years = 6200
A = ₹ 7400
⇒ Principal + Interest for 3 years = 7400
∴ Difference gives the Interest for 1 year
∴ Interest for 1 year = 7400 – 6200
I = 1200
\(\frac { pnr }{ 100 } \) = 1200 ⇒ \(\frac{P \times 1 \times r}{100}\) = 1200
If the Principal = 10,000 then
\(\frac{10,000 \times 1 \times r}{100}\) = 1200 ⇒ r = 12 %
Rate of interest = 12 % Per month

Question 25.
A sum of ₹ 46,900 was lent out at simple interest and at the end of 2 years, the total amount was ₹ 53,466.Find the rate of interest per year.
Solution:
Here principal P = ₹ 46900
Time n = 2 years
Amount A = ₹ 53466
Let r n be the rate of interest per year p
Intrest I = \(\frac { pnr }{ 100 } \)
A = P + I
53466 = 46900 + \(\frac{46900 \times 2 \times r}{100}\)
53466 – 46900 = \(\frac{46900 \times 2 \times r}{100}\)
6566 = 469 × 2 × r
r = \(\frac{6566}{2 \times 469}\) % = 7 %
Rate of interest = 7 % Per Year

Question 26.
Arun lent ₹ 5,000 to Balaji for 2 years and ₹ 3,000 to Charles for 4 years on simple interest at the same rate of interest and received ₹ 2,200 in all from both of them as interest. Find the rate of interest per year.
Solution:
Principal lent to Balaji P₁ = ₹ 5000
Time n₁ = 2 years
Let r be the rate of interest per year
Simple interest got from Balaji = \(\frac { pnr }{ 100 } \) ⇒ I₁ = \(\frac{5000 \times 25 \times r}{100}\)
Again principal let to Charles P₂ = ₹ 3000
Time (n₂) = 4 years
Simple interest got from Charles (I₂) = \(\frac{3000 \times 4 \times r}{100}\)
Altogether Arun got ₹ 2200 as interest.
∴ I₁ + I₂ = 2200
\(\frac{5000 \times 2 \times r}{100}+\frac{3000 \times 4 \times r}{100}\) = 2200
100r + 120r = 2200
220r = 2200 = \(\frac { 2200 }{ 220 } \)
r = 10 %
Rate of interest per year = 10 %

Question 27.
If a principal is getting doubled after 4 years, then calculate the rate of interest. (Hint: Let P = ₹ 100)
Solution:
Let the principal P = ₹ 100
Given it is doubled after 4 years
i.e. Time n = 4 years
After 4 years A = ₹ 200
∴ A = P + I
A – P = I
200 – 100 = I
After 4 years interest I = 100
I = \(\frac { pnr }{ 100 } \) ⇒ 100 = \(\frac{100 \times 4 \times r}{100}\)
4r = 100 ⇒ r = 25 %
Rate of interest r = 25 %

Students can Download Maths Chapter 3 Algebra Ex 3.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 3 Algebra Ex 3.1

Question 1.
Fill in the blanks.
1. (p – q)² = _______
2. The product of (x + 5) and (x – 5) is _______
3. The factors of x² – 4x + 4 are _______
4. Express 24ab²c² as product of its factors is _______
Answers:
1. p² – 2pq + q²
2. x² – 25
3. (x – 2) and (x – 2)
4. 2 × 2 × 2 × 3 × a × b × b × c × c

Question 2.
Say whether the following statements are True or False.
(i) (7x + 3) (7x – 4) = 49 x² – 7x – 12
(ii) (a – 1)² = a² – 1.
(iii) (x² + y²)(y² + x²) = (x² + y²)²
(iv) 2p is the factor of 8pq.
Answers:
(i) True
(ii) False
(iii) True
(iv) True

Question 3.
Express the following as the product of its factors.
(i) 24ab²c²
(ii) 36 x³y²z
(iii) 56 mn²p²
Solution:
(i) 24ab²c² = 2 × 2 × 2 × 3 × a × b × b × c × c
(ii) 36 x³y²z = 2 × 2 × 3 × 3 × x × x × x × y × y × z
(iii) 56 mn²p² = 2 × 2 × 2 × 7 × m × n × n × p × p

Question 4.
Using the identity (x + a)(x + b) – x² + x(a + b) + ab, find the following product.
(i) (x + 3) (x + 7)
(ii) (6a + 9) (6a – 5)
(iii) (4x + 3y) (4x + 5y)
(iv) (8 + pq) (pq + 7)
Solution:
(i) (x + 3) (x + 7)
Let a = 3; b = 7, then
(x + 3) (x + 7) is of the form x² + x (a + b) + ab
(x + 3) (x + 7) = x² + x (3 + 7) + (3 × 7) = x² + 10x + 21

(ii) (6a + 9) (6a – 5)
Substituting x = 6a ; a = 9 and b = -5
In (x + a) (x + b) = x² + x (a + b) + ab, we get
(6a + 9)(6a – 5) = (6a)² + 6a (9 + (-5)) + (9 × (-5))
6² a² + 6a (4) + (-45) = 36a² + 24a – 45
(6a + 9) (6a – 5) = 36a² + 24a – 45

(iii) (4x + 3y) (4x + 5y)
Substituting x = 4x ; a = 3y and b = 5y in
(x + a) (x + b) = x² + x (a + b) + ab, we get
(4x + 3y) (4x – 5y) = (4x)² + 4x (3y + 5y) + (3y) (5y)
= 4² x² + 4x (8y) + 15y² = 16x² + 32xy + 15y²
(4x + 3y) (4x + 5y) = 16x² + 32xy + 15y²

(iv) (8 + pq) (pq + 7)
Substituting x = pq ; a = 8 and b = 7 in
(x + a) (x + b) = x² + x (a + b) + ab, we get
(pq + 8) (pq + 7) = (pq)² + pq (8 + 7) + (8) (7)
= p² q² + pq (15) + 56
(8 + pq) (pq + 7) = p² q² + 15pq + 56

Question 5.
Expand the following squares, using suitable identities.
(i) (2x + 5)²
(ii) (b – 7)²
(iii) (mn + 3p)²
(iv) (xyz – 1)²
Solution:
(i) (2x + 5)²
Comparing (2x + 5)² with (a + b)² we have a = 2x and b = 5
a = 2x and b = 5,
(a + b)² = a² + 2ab + b²
(2x + 5)² = (2x)² + 2(2x) (5) + 5² = 2² x² + 20x + 25
= 2² x² + 20x + 25
(2x + 5)² = 4x² + 20x + 25

(ii) (b – 7)²
Comparing (b – 7)² with (a – b)² we have a = b and b = 7
(a – b)² = a² – 2ab + b²
(b – 7)² = b² – 2(b) (7) + 7²
(b – 7)² = b² – 14b + 49

(iii) (mn + 3p)²
Comparing (mn + 3p)² with (a + b)² we have
(a + b)² = a² + 2ab + b²
(mn + 3p)² = (mn)² + 2(mn) (3p) + (3p)²
(mn + 3p)² = m² n² + 6mnp + 9p²

(iv) (xyz – 1)²
Comparing (xyz – 1)² with (a – b)² we have = a + xyz and b = 1
a = xyz and b = 1
(a – b)² = a² – 2ab + b²
(xyz – 1)² = (xyz)² – 2 (xyz) (1) + 1²
(xyz -1)² = x² y² z² – 2 xyz + 1

Question 6.
Using the identity (a + b)(a – b) = a² – b², find the following product.
(i) (p + 2) (p – 2)
(ii) (1 + 3b) (3b – 1)
(iii) (4 – mn) (mn + 4)
(iv) (6x + 7y) (6x – 7y)
Solution:
(i) (p + 2) (p – 2)
Substituting a = p ; b = 2 in the identity (a + b) (a – b) = a² – b², we get
(p + 2) (p – 2) = p² – 2²

(ii) (1 + 3b)(3b – 1)
(1 + 3b) (3b -1) can be written as (3b + 1) (3b – 1)
Substituting a = 36 and b = 1 in the identity
(a + b) (a – b) = a² – b², we get
(3b + 1)(3b – 1) = (3b)² – 1² = 3² × b² – 1²
(3b + 1) (3b – 1) = 9b² – 1²

(iii) (4 – mn) (mn + 4)
(4 – mn) (mn + 4) can be written as (4 – mn) (4 + mn) = (4 + mn) (4 – mn)
Substituting a = 4 and b = mn is
(a + b) (a – b) = a² – b², we get
(4 + mn) (4 – mn) = 4² – (mn)² = 16 – m² n²

(iv) (6x + 7y) (6x – 7y)
Substituting a = 6x and b = 7y in
(a + b) (a – b) = a² – b², We get
(6x + 7y) (6x – 7y) = (6x)² – (7y)² = 6²x² – 7²y²
(6x + 7y) (6x – 7y) = (6x)² – (7y)² = 6²x² – 7²y²
(6x + 7y) (6x – 7y) = 36x² – 49y²

Question 7.
Evaluate the following, using suitable identity.
(i) 51²
(ii) 103²
(iii) 998²
(iv) 47²
(v) 297 × 303
(vi) 990 × 1010
(vii) 51 × 52
Solution:
51²
= (50 + 1)²
Taking a = 50 and b = 1 we get
(a + b)² = a² + 2ab + b²
(50 + 1)² = 50² + 2 (50) (1) + 1² = 2500 + 100 + 1
51² = 2601

(ii) 103²
103² = (100 + 3)²
Taking a = 100 and b = 3
(a + b)² = a² + 2ab + b² becomes
(100 + 3)² = 100² + 2 (100) (3) + 3² = 10000 + 600 + 9
103² = 10609

(iii) 998²
998² = (1000 – 2)²
Taking a = 1000 and b = 2
(a – b)² = a² + 2ab + b² becomes
(1000 – 2)² = 1000² – 2 (1000) (2) + 2²
= 1000000 – 4000 + 4
998² = 10,04,004

(iv) 47²
47² = (50 – 3)²
Taking a = 50 and b = 3
(a – b)² = a² – 2ab + b² becomes
(50 – 3)² = 50² – 2 (50) (3) + 3²
= 2500 – 300 + 9 = 2200 + 9
47² = 2209

(v) 297 × 303
297 × 303 = (300 – 3) (300 + 3)
Taking a = 300 and b = 3, then
(a + b) (a – b) = a² – b² becomes
(300 + 3) (300 – 3) = 300² – 3²
303 × 297 = 90000 – 9
297 × 303 = 89,991

(vi) 990 × 1010
990 × 1010 = (1000 – 10) (1000 + 10)
Taking a = 1000 and b = 10, then
(a – b) (a + b) = a² – b² becomes
(1000 – 10) (1000 + 10) = 1000² – 10²
990 × 1010 = 1000000 – 100
990 × 1010 = 999900

(vii) 51 × 52
= (50 + 1) (50 + 1)
Taking x = 50, a = 1 and b = 2
then (x + a) (x + b) = x² + (a + b) x + ab becomes
(50 + 1) (50 + 2) = 50² + (1 + 2) 50 + (1 × 2)
2500 + (3) 50 + 2 = 2500 + 150 + 2
51 × 52 = 2652

Question 8.
Simplify: (a + b)² – 4ab
Solution:
(a + b)² – 4ab = a² + b² + 2ab – 4ab = a² + b² – 2ab = (a – b)²

Question 9.
Show that (m – n)² + (m + n)² = 2(m² + n²)
Solution:
Taking the LHS = (m – n)² + (m + n)²

Question 10.
If a + b = 10 , and ab = 18, find the value of a² + b².
Solution:
We have (a + b)² = a² + 2ab + b²
(a + b)² = a² + b² + 2ab
given a + b = 0 and ab = 18
10² = = a² + b² + 2(18)
100 = = a² + b² + 36
100 – 36 = a² + b²
a² + b² = 64

Question 11.
Factorise the following algebraic expressions by using the identity a² – b² = (a + b)(a – b).
(i) z² – 16
(ii) 9 – 4y²
(iii) 25a² – 49b²
(iv) x⁴ – y⁴
Solution:
(i) z² – 16
z² – 16 = z² – 4²
We have a² – b² = (a + b) (a – b)
let a = z and b = 4,
z² – 4² = (z + 4) (z – 4)

(ii) 9 – 4y²
9 – 4y² = 3² – 2² y² = 3² – (2y)²
let a = 3 and b = 2y, then
a² – b² = (a + b) (a – b)
∴ 3² – (2y)² = (3 + 2y) (3 – 2y)
9 – 4y² = (3 + 2y) (3 – 2y)

(iii) 25a² – 49b²
25a2 – 49b2 = 52 – a2 – 72 = (5a)2 – (7b)2
let A = 5a and B = 7b
A²  B²
(5a)² – (7b)² = (5a + 7b) (5a – 7b)

(iv) x⁴ – y⁴
Let x⁴ – y⁴ = (x²)² – (y²)²
We have a² – b² = (a + b) (a – b)
(x²)² – (y²)² = (x² + y²) (x² – y²)
x⁴ – y⁴ = (x² + y²) (x² – y²)
Again we have x² – y² = (x + y) (x – y)
∴ x⁴ – y⁴ = (x² + y²) (x + y) (x – y)

Question 12.
Factorise the following using suitable identity.
(i) x² – 8x + 16
(ii) y² + 20y + 100
(iii) 36m² + 60m + 25
(iv) 64x² – 112xy + 49y²
(v) a² + 6ab + 9b² – c²
Solution:
(i) x² – 8x + 16
x² – 8x + 16 = x² – (2 × 4 × x) + 4²
This expression is in the form of identity
a² – 2ab + b² = (a – b)²
x² – 2 × 4 × x + 4² = (x – 4)²
∴ x² – 8x + 16 = (x – 4) (x – 4)

(ii) y² + 20y + 100
y² + 20y + 100 = y² + (2 × (10)) y + (10 × 10)
= y² + (2 × 10 × y) + 10²
This is of the form of identity
a² + 2 ab + b² = (a + b)²
y² + (2 × 10 × y) + 10² = (y + 10)²
y² + 20y + 100 = (y + 10)²
y² + 20y + 100 = (y + 10) (y + 10)

(iii) 36m² + 60m + 25
36m² + 60m + 25 = 62 m² + 2 × 6m × 5 + 5²
This expression is of the form of identity
a² + 2ab + b² = {a + b)²
(6m)² + (2 × 6m × 5) + 5²
= (6m + 5)²
36m² + 60m + 25 = (6m + 5) (6m + 5)

(iv) 64x² – 112xy + 49y²
64x² – 112xy + 49y² = 82 x² – (2 × 8x × 7y) + 7²y²
This expression is of the form of identity
a² – 2ab + b² = (a- b)²
(8x)² – (2 × 8x × 7y) + (7y)² = (8x – 7y)²
64x² – 112xy + 49y² = (8x – 7y) (8x – 7y)

(v) a² + 6ab + 9b² – c²
a² + 6ab + 9b² – c² = a² + 2 × a × 3b + 3² b² – c²
= a² + (2 × a × 3b) + (3b)² – c²
This expression is of the form of identity
[a² + 2ab + b²] – c² = (a + b)² – c²
a² + (2 × a × 36) + (3b)² – c² = (a + 3b)² – c²
Again this RHS is of the form of identity
a² – b² = (a + b) (a – b)
(a + 3b)² – c² = [(a + 3b) + c] [(a + 3b) – c]
a² + 6ab + 9b² – c² = (a + 3b + c) (a + 3b – c)

Objective Type Questions

Question 1.
If a + b = 5 and a² + b² = 13, then ab = ?
(i) 12
(ii) 6
(iii) 5
(iv) 13
Answer:
(ii) 6
Hint: (a + b)² = 25
13 + 2ab = 25
2ab = 12
ab = 6

Question 2.
(5 + 20)(-20 – 5) = ?
(i) -425
(ii) 375
(iii) -625
(iv) 0
Answer:
(iii) -625
Hint: (50 + 20) (-20 – 5) = -(5 + 20)² = – (25)² = – 625

Question 3.
The factors of x² – 6x + 9 are
(i) (x – 3)(x – 3)
(ii) (x – 3)(x + 3)
(iii) (x + 3)(x + 3)
(iv) (x – 6)(x + 9)
Answer:
(i) (x – 3)(x – 3)
Hint: x² – 6x + 9 = x² – 2(x) (3) + 3²
a² – 2ab + b² – (a- b)² = (x – 3)² = (x – 3) (x – 3)

Question 4.
The common factors of the algebraic expression ax²y, bxy² and cxyz is
(i) x²y
(ii) xy²
(iii) xyz
(iv) x
Ans :
(iv) xy
Hint: ax²y = a × x × x × y
bxy² = b × x × y × y
cxyz = C × x × y × z
Common factor = xy

Students can Download Maths Chapter 1 Number System Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 1 Number System Additional Questions

Additional Questions and Answers

Exercise 1.1

Question 1.
Match the following:

Solution:
1 – (v)
2 – (iv)
3 – (i)
4 – (iii)
5 – (ii)

Question 2.
Round 89.357 to the nearest whole number.
Solution:
Underlining the digit to be rounded 89.357. Since the digit next to the underlined digit 3 which is less than 5, the underlined digit remains the same.
∴ The nearest whole number 89.357 rounds to 89.

Question 3.
Round 110.929 to the nearest tenths place.
Solution:
Underlining the digit to be rounded 110.929. Since the digit next to the underlined digit is 2 which is less than 5.
∴ The underlined digit 9 remains the same. Hence the rounded number is 110.9

Question 4.
Round 87.777 upto 2 places of decimal.
Solution:
Rounding 87.777 upto 2 places of decimal means round to the nearest hundredths place. Underlining the digit in the hundredth place of 87.777 gives 87.777. Since the digit after the hundredth place value is 7 which is more than 5, we add 1 to the underlined digit. So the rounded value of 87.777 upto 2 places of decimal is 87.78

Exercise 1.2

Question 1.
If Sheela bought 2.083 kg of grapes and 3.752 kg of orange. What is the total weight of fruits
Solution:

Weight of grapes = 2.083 Kg
Weight of orange = 2.752 Kg
Total weight = (2.083 + 2.752) Kg = 4.835 Kg

Question 2.
Kathir bought 8.72 kg of sugar, 7.302 kg of grains. His carry bag can contain only 15 kg of weight. What is the remaining weight of items bought?
Solution:

Question 3.
Use place value grid to add 7.357 and 13.92.
Solution:
Let as use place value grid.

Exercise 1.3

Question 1.
Cost of 1m cloth is ₹ 6.75. Find the cost of 14.75m correct to two places of decimal.
Solution:

Cost of 1 m cloth = ₹ 6.75
Cost of 14.75 m cloth = 14.75 × 6.75
= ₹ 99.5625
= ₹ 99.56

Question 2.
Length of a side of a square is 18.35 cm. Find its Area.
Solution:

Side of a square = 18.35 cm
Area of a square = (Side × Side) sq.units
= 18.35 × 18.35 cm²
= 336.7225 cm²

Exercise 1.4

Question 1.
A wire of length 363.987m is cut into 30 pieces. What is the length of each piece?
Solution:
Length of the wire = 363.987m
i.e Total length of 30 pieces = \(\frac { 363987 }{ 1000 } \) m

∴ Length of 1 piece
= 12132.9 × \(\frac { 1 }{ 1000 } \)
Length of 1 piece of wire = 12.1329 m

Question 2.
A cake of 50kg needs 23.4 kg sugar. Find the weight of cake made by 1 kg of sugar.
Solution:
Weight of cake made using 23.4 kg sugar = 50 kg
Weight of cake made using 1 kg sugar = \(\frac { 50 }{ 23.4 } \)
= \(\frac { 50 }{ 23.4 } \) x \(\frac { 10 }{ 10 } \) = \(\frac { 500 }{ 234 } \) = 2.1367 Kg
= 2.14 Kg
Weight of cake made using 1 kg sugar = 2.14 Kg

Question 3.
A pack of 20 pencils cost ₹ 94.4. What is the cost of each pencil?
Solution:
Cost of 20 pencils = ₹ 94.4

∴ Cost of 1 pencil = ₹ 4.72

Students can Download Maths Chapter 2 Percentage and Simple Interest Ex 2.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 2 Percentage and Simple Interest Ex 2.4

Question 1.
Find the simple interest on ₹ 35,000 at 9% per annum for 2 years?
Solution:

Principal P = ₹ 35,000
Rate of interest r = 9 % Per annum
Time (n) = 2 years
Simple Interest I = \(\frac { Pnr }{ 100 } \) = \(\frac{35000 \times 2 \times 9}{100}\) = ₹ 6300
Simple intrest I = ₹ 6300

Question 2.
Aravind borrowed a sum of ₹ 8,000 from Akash at 7% per annum. Find the interest and amount to be paid at the end of two years.
Solution:
Here Principal P = ₹ 8,000
Rate of interest r = 7% Per annum
Time (n) = 2 Years
Simple Interest (I) = \(\frac { Pnr }{ 100 } \) = \(\frac{8000 \times 2 \times 7}{100}\)
I = ₹ 1120
Amount = P + I
I = ₹ 8000 + 1120 = 9120
Interest to be paid = ₹ 1,120
Amount to be paid = ₹ 9,120

Question 3.
Sheela has paid simple interest on a certain sum for 4 years at 9.5% per annum is ₹ 21,280. Find the sum.
Solution:
Let the Principal be ₹ P
Rate of interest r = 9.5% per annum
Time (n) = 4 years
Simple Interest I = \(\frac { Pnr }{ 100 } \)
Given I = ₹ 21,280

∴ Sum of money Sheela bought = ₹ 56,000

Question 4.
Basha borrowed ₹ 8,500 from a bank at a particular rate of simple interest. After 3 years, he paid ₹ 11,050 to settle his debt. At what rate of interest he borrowed the money?
Solution:
Let the rate of interest be r% per annum
Here Principal P = ₹ 8,500
Time n = 3 years
Total amount paid = ₹ 11,050
A = P + 1 = ₹ 11,050
i.e. 8,500 + 1 = ₹ 11,050
I = ₹ 11,050 – ₹ 8,500 = ₹ 2,550

Question 5.
In What time will ₹ 16,500 amount to ₹ 22,935 at 13% per annum?
Solution:
Rate of interest r = 13% per annum
Here Amount A = ₹ 22,935
Principal P = ₹ 16,500
A = P + I
22935 = 16,500 + I
∴ Interest I = 22935 – 16,500 = ₹ 6,435
Simple Interest I = \(\frac { pnr }{ 100 } \)

6435 = \(\frac{16500 \times n \times 13}{100}\)
n =\(\frac{6435 \times 100}{16500 \times 13}\)
n = 3 years
Required time n = 3 years

Question 6.
In what time will ₹ 17800 amount to ₹ 19936 at 6% per annum?
Solution:
Let the require time be n years
Here Principal P = ₹ 17,800
Rate of interest r = 6% per annum
Amount A = ₹ 19,936
A = P + I
19936 = 17800 + 1
19936 – 17800 = I
2136 = I
Simple Interest (I) = \(\frac { pnr }{ 100 } \)
2136 = \(\frac{17800 \times n \times 6}{100}\)
n = \(\frac{2136 \times 100}{17800 \times 6}\)

n = 2 Years
Required time = 2 years

Question 7.
A sum of ₹ 48,000 was lent out at simple interest and at the end of 2 years and 3 months the total amount was ₹ 55,560. Find the rate of interest per year.
Solution:
Given Principal P = ₹ 48,000
Time n = 2 years 3 months
= 2 + \(\frac { 3 }{ 12 } \) years = 2 + \(\frac { 1 }{ 4 } \) years
= \(\frac { 8 }{ 4 } \) + \(\frac { 1 }{ 4 } \) years = \(\frac { 9 }{ 4 } \) years
Amount A = ₹ 55,660
A = p + 1
55660 = 48000 + I
I = 55660 – 48000 = ₹ 7660
∴ Interest for \(\frac { 9 }{ 4 } \) years = ₹ 7660
Simple intrest = \(\frac { pnr }{ 100 } \)
7660 = 48000 × \(\frac { 9 }{ 4 } \) × \(\frac { r }{ 100 } \)
r = \(\frac{7660 \times 4 \times 100}{9 \times 48000}\) = 7.09 % = 7 %
Rate of interest = 7 % Per annum

Question 8.
A principal becomes ₹ 17,000 at the rate of 12% in 3 years. Find the principal.
Solution:
Given the Principal becomes ₹ 17,000
Let the principle initially be P
Rate of Interest r Time = 12 % Per annum
Time n = 3 years
According to the problem given I = 17000 – P = \(\frac{P \times 3 \times 12}{100}\)
17000 = \(\frac { 36 }{ 100 } \) p + p
17000 = p(\(\frac { 36 }{ 100 } \) + 1)
17000 = p(\(\frac { 136 }{ 100 } \))
p = \(\frac{17000 \times 100}{136}\) = 12,500
∴ Principal P = ₹ 12,500

Objective Type Questions

Question 9.
The interest for a principle of? 4,500 which gives an amount of? 5,000 at end of certain period is
(i) ₹ 500
(ii) ₹ 200
(iii) 20%
(iv) 15%
Hint: Interest = Amount – Principle = ₹ 5000 – ₹ 4500 = ₹ 500
Answer:
(i) ₹ 500

Question 10.
Which among the following is the simple interest for the principle of ₹ 1,000 for one year at the rate of 10% interest per annum?
(i) ₹ 200
(ii) ₹ 10
(iii) ₹ 100
(iv) ₹ 1,000
Hint: Intrest = \(\frac { pnr }{ 100 } \) = \(\frac{1000 \times 1 \times 10}{100}\) = ₹ 100
Answer:
(iii) ₹ 100

Question 11.
Which among the following rate of interest yields an interest of ₹ 200 for the principle of ₹ 2,000 for one year.
(i) 10%
(ii) 20%
(iii) 5%
(iv) 15%
Hint: r = \(\frac{I \times 100}{P \times n}\) = \(\frac{200 \times 100}{2000 \times 1}\) = 10 %
Answer:
(i) 10%

Students can Download Maths Chapter 1 Number System Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 1 Number System Intext Questions

Exercise 1.1
Try These (Text book Page No. 1)

Question 1.
Represent the fraction \(\frac { 1 }{ 4 } \) in decimal form
Solution:
\(\frac { 1 }{ 4 } \) = \(\frac{1 \times 25}{4 \times 25}\) = \(\frac { 25 }{ 100 } \) = 0.25

Question 2.
What is the place value of 5 in 63.257.
Solution:
Place value of 5 in 63.257 is 5 hundredths (Hundreth place)

Question 3.
Identify the digit in the tenth place of 75.036.
Solution:
0

Question 4.
Express the decimal number 3.75 as a fraction.
Solution:
3.75 = \(\frac { 375 }{ 100 } \) = \(\frac { 15 }{ 4 } \)

Question 5.
Write the decimal number for the fraction 5 \(\frac { 1 }{ 5 } \)
Solution:
5 \(\frac { 1 }{ 5 } \) = \(\frac { 26 }{ 5 } \) = \(\frac{26 \times 2}{5 \times 2}\) = \(\frac { 52 }{ 10 } \) = 5.2

Question 6.
Identify the biggest number : 0.567 and 0.576.
Solution:
Comparing the digits of 0.567 and 0.576 from left to right, we have the tenths place same comparing the hundredths place 7 > 6.
⇒ 0.576 > 0.567

Question 7.
Compare 3.30 and 3.03 and identify the smaller number.
Solution:
The whole number is equal in both the numbers.
Now comparing the tenths place we have 3 > 0
⇒ 3.03 < 3.30 Smaller number is 3.03

Question 8.
Put the appropriate sign (<, >, =). 2.57 [ ] 2.570
Solution:
2.57 [=] 2.570

Question 9.
Arrange the following decimal numbers in ascending order.
5.14, 5.41, 1.54, 1.45, 4.15, 4.51.
Solution:
Comparing the numbers from left to right. Ascending order : 1.45, 1.54, 4.15, 4.51, 5.14, 5.41

Exercise 1.2
Try These (Text book Page No. 6)

Question 1.
Find the following using grid models:
(i) 0.83 + 0.04
(ii) 0.35 – 0.09
Solution:
(i) 0.83 + 0.04
0.83 = \(\frac { 83 }{ 100 } \) and 0.04 = \(\frac { 4 }{ 100 } \)

Shading the regions
0.83 and 0.04
The sum is the total shaded region.
S = 0.83 + 0.04 = 0.87

(ii) 0.35 – 0.09
0.35 = \(\frac { 35 }{ 100 } \) and 0.09 = \(\frac { 9 }{ 100 } \)

Shading the regions 0.35 by shading 35 boxes out of 100. Striking off 9 boxes out of 35 shaded boxes to subtract 0.09 from 0.35.
The left over shaded boxes represent the required value.
∴ 0.35 – 0.09 = 0.26

Try These (Text book Page No. 7)

Question 1.
Using the area models solve the following
(i) 1.2 + 3.5
(ii) 3.5 – 2.3
Solution:
(i) 1.2 + 3.5

Here 1.2 is represented in blue colour and 3.5 is represented in Green colour. Sum of 1.2 and 3.5 is 4.7.

(ii) 3.5 – 2.3

Representing 3.5 using 3 squares and 5 rectangular strips. Crossing out 2 squares from 3 squares and 3 rectangular strips from 5 to get the difference. So 3.5 – 2.3 = 1.2.

Try These (Text book Page No. 9)

Question 1.
Complete the magic square in such a way that rows, columns and diagonals give the same sum 1.5.

Solution:

Exercise 1.3
Think (Text book Page No. 13)

Question 1.
How are the products 2.1 × 3.2 and 21 × 32 alike? How are they different.
Solution:
2.1 × 3.2 = 6.72 and 21 × 32 = 672.
In both the cases the digits ambers are the same. But the place value differs.

Try These (Text book Page No. 13)

Question 1.
Shade the grid to multiply 0.3 × 0.6.

Solution:

3 rows of Yellow represent 0.3, 6 columns of Red colour represent 0.6 Double shaded 18 squares of orange colour represent.
∴ 0.3 × 0.6 = 0.18

Question 2.
Use the area model to multiply

Solution:

Here each row contains 1 whole and 2 tenths. Each column contains 2 wholes and 5 tenths. The entire area model represents 2 wholes 9 tenths and 10 hundredths ( = 1 tenths). So 1.2 × 2.5 = 3.

Try These (Text book Page No. 14)

Question 1.
Complete the following table

Solution:

Try These (Text book Page No. 15)

Question 1.
Find:

1. 9.13 × 10
2. 9.13 × 100
3. 9.13 × 1000

Solution:

1. 9.13 × 10 = 91.3
2. 9.13 × 100 = 913
3. 9.13 × 1000 = 9130

Try These (Text book Page No. 16)

Question 1.
Complete the following table

Solution:

Exercise 1.4
Try These (Text book Page No. 19)

Question.

Solution:

Try These (Text book Page No. 19)

Question 1.
Divide the following
(i) 17.237 ÷ 10
(ii) 17.237 ÷ 100
(iii) 17.237 ÷ 1000
Solution:
(i) 17.237 ÷ 10
= \(\frac { 17237 }{ 1000 } \) × \(\frac { 1 }{ 10 } \)
= \(\frac { 17237 }{ 1000 } \)
= 1.7237

(ii) 17.237 ÷ 100
= \(\frac { 17237 }{ 1000 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 17237 }{ 100000 } \)
= 0.17237

(iii) 17.237 ÷ 1000
= \(\frac { 17237 }{ 1000 } \) × \(\frac { 1 }{ 1000 } \)
= \(\frac { 17237 }{ 1000000 } \)
= 0.017237

Try These (Text book Page No. 21)

Question 1.
Find the value of the following:
(i) 46.2 ÷ 3 = ?
(ii) 71.6 ÷ 4 = ?
(iii) 23.24 ÷ 2 = ?
(iv) 127.35 ÷ 9 = ?
(v) 47.201 ÷ 7 = ?
Solution:
(i) 46.2 ÷ 3
= \(\frac { 462 }{ 10 } \) × \(\frac { 1 }{ 3 } \)
= \(\frac { 1 }{ 10 } \) × \(\frac { 462 }{ 3 } \)
= \(\frac { 1 }{ 10 } \) × 15.4
= \(\frac { 154 }{ 10 } \)
= 15.4

(ii) 71.6 ÷ 4
= \(\frac { 716 }{ 10 } \) × \(\frac { 1 }{ 4 } \)
= \(\frac { 1 }{ 10 } \) × \(\frac { 716 }{ 4 } \)
= \(\frac { 1 }{ 10 } \) × 179
= 17.9

(iii) 23.24 ÷ 2
= \(\frac { 2324 }{ 100 } \) × \(\frac { 1 }{ 2 } \)
= \(\frac { 2324 }{ 2 } \) × \(\frac { 1 }{ 100 } \)
= 1162 × \(\frac { 1 }{ 100 } \)
= \(\frac { 1162 }{ 100 } \)
= 11.62

(iv) 127.35 ÷ 9
= \(\frac { 12735 }{ 100 } \) × \(\frac { 1 }{ 9 } \)
= \(\frac { 12735 }{ 9 } \) × \(\frac { 1 }{ 100 } \)
= 1415 × \(\frac { 1 }{ 100 } \)
= \(\frac { 1415 }{ 100 } \)
= 14.15

(v) 47.201 ÷ 7
= \(\frac { 47201 }{ 1000 } \) × \(\frac { 1 }{ 7 } \)
= \(\frac { 47201 }{ 7 } \) × \(\frac { 1 }{ 1000 } \)
= 6743 × \(\frac { 1 }{ 1000 } \)
= \(\frac { 6743 }{ 1000 } \)
= 6.743

Try These (Text book Page No. 22)

Question 1.
Divide the following
(i) \(\frac { 9.25 }{ 0.25 } \)
(ii) \(\frac { 8.6 }{ 4.3 } \)
(iii) \(\frac { 44.1 }{ 0.21 } \)
(iv) \(\frac { 9.6 }{ 1.2 } \)
Solution:
(i) \(\frac { 9.25 }{ 0.25 } \)

(ii) \(\frac { 8.6 }{ 4.3 } \)

(iii) \(\frac { 44.1 }{ 0.21 } \)

(iv) \(\frac { 9.6 }{ 1.2 } \)

Think (Text book Page No. 22)

Question 1.
The price of a tablet strip containing 30 tablets is 22.63 Then how will you find the price of each tablet?
Solution:
Price of 30 tablets = ₹ 22.63 = ₹ \(\frac { 2263 }{ 100 } \)
∴ Price of 1 tablet

= \(\frac { 2263 }{ 100 } \) × \(\frac { 1 }{ 30 } \)
= \(\frac { 2263 }{ 30 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 2263 }{ 3 } \) × \(\frac { 1 }{ 1000 } \)
= 754.33 × \(\frac { 1 }{ 1000 } \)
= \(\frac { 754.33 }{ 1000 } \)
= 0.75433
Price of each tablet is ₹ 0.7543

Students can Download Maths Chapter 2 Percentage and Simple Interest Ex 2.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 2 Percentage and Simple Interest Ex 2.3

Question 1.
14 out of the 70 magazines at the bookstore are comedy magazines. What percentage of the magazines at the bookstore are comedy magazines?
Solution:
Total number of magazines in the bookstore = 100 m
Number of comedy magazines = 14
Percentage of comedy magzines = \(\frac { 14 }{ 70 } \) × 100% = 20%
20% of the magazines are comedy magazines.

Question 2.
A tank can hold 50 litres of water. At present, it is only 30% full. How many litres of water will fill the tank, so that it is 50% full?
Solution:
Capacity of the tank = 50 litres
Amount of water filled = 30% of 50 litres = \(\frac { 30 }{ 100 } \) × 50 = 15 litres
Amount of water to be filled = 50 – 15 = 35 litres

Question 3.
Karun bought a pair of shoes at a sale of 25%. If the amount he paid was ₹ 1000, then find the marked price.
Solution:
Let the marked price of the raincoat be ₹ P
Amount he paid at a discount of 25% = ₹ 1000
(Marked Price) – (25% of P) = 1000
P – (\(\frac { 25 }{ 100 } \) × P) = 1000
P – \(\frac { 1 }{ 4 } \) × P = 1000
P (1 – \(\frac { 1 }{ 4 } \)) = 1000
\(\frac { 3 }{ 4 } \) P = 1000
P = 1000 × \(\frac { 4 }{ 3 } \)
= \(\frac { 4000 }{ 3 } \)
P = 1333.33
∴ Marked price of the shoes = ₹ 1333

Question 4.
An agent of an insurance company gets a commission of 5% on the basic premium he collects. What will be the commission earned by him if he collects ₹ 4800?
Solution:
Premium collected = ₹ 4800
Commission earned = 5% of basic premium
Commission earned for ₹ 4800 = 5% of 4800
= \(\frac { 5 }{ 100 } \) × 4800
= ₹ 240
Commission earned = ₹ 240

Question 5.
A biology class examined some flowers in a local Grass land. Out of the 40 flowers they saw, 30 were perennials. What percentage of the flowers were perennials?
Solution:
Number of flowers examined = 40
Number of perennials = 30
Percentage = \(\frac { 30 }{ 40 } \) × 100%
= 75%
75% of the flowers were perennials.

Question 6.
Ismail ordered a collection of beads. He received 50 beads in all. Out of that 15 beads were brown. Find the percentage of brown beads?
Solution:
Number of beads received = 50
Number of brown beads = 5
Percentage of brown beads = \(\frac { 15 }{ 50 } \) × 100 %
= 10 %
10% of the beads was brown

Question 7.
Ramu scored 20 out of 25 marks in English, 30 out of 40 marks in Science and 68 out of 80 marks in mathematics. In which subject his percentage of marks is best?
Solution:
Ramu’s score in English = 20 out of 25
Percentage scored in English = \(\frac { 20 }{ 25 } \) × 100 % = 80 %
Ramu’s Score in Science = 30 out of 40
Percentage scored in Science = \(\frac { 30 }{ 40 } \) × 100 % = 75%
Ramu’s score in Mathematics = 68 out of 80
Percentage scored in Maths = \(\frac { 68 }{ 80 } \) × 100 % = 85 %
85% > 80% > 75%.
∴ In Mathematics his percentage of marks is the best.

Question 8.
Peter requires 50% to pass. If he gets 280 marks and falls short by 20 marks, what would have been the maximum marks of the exam?
Solution:
Peters score = 280 marks
Marks needed for a pass = 20
∴ Total marks required to get a pass = 280 + 20 = 300
i.e. 50% of total marks = 300
\(\frac { 50 }{ 100 } \) × Total marks = 300
\(\frac { 1 }{ 2 } \) × Total Marks = 300
Total Marks = 300 × 2 = 600
Total marks of the exam = 600

Question 9.
Kayal scored 225 marks out of 500 in revision test 1 and 265 out of 500 marks in revision test 2. Find the percentage of increase in her score.
Solution:
Marks scored in revision I = 225
Marks scored in revision II = 265
Change in marks = 265 – 225 = 40

Percentage of increase in marks = 8%

Question 10.
Roja earned ₹ 18,000 per month. She utilized her salary in the ratio 2 : 1 : 3 for education, savings and other expenses respectively. Express her usage of income in percentage.
Solution:
Amount of Salary = ₹ 18,000
(i) Total number of parts of salary = 2 + 1 + 3 = 6
Salary is divided into 3 portions as \(\frac { 2 }{ 6 } \),\(\frac { 1 }{ 6 } \) and \(\frac { 3 }{ 6 } \)
Portion of salary used for education = \(\frac { 2 }{ 6 } \)
Salary used for education = \(\frac { 2 }{ 6 } \) × 18,000 = ₹ 6,000
Percentage for Education = \(\frac { 6000 }{ 18000 } \) × 100 = 33.33%

(ii) Usage of salary for savings = \(\frac { 1 }{ 6 } \) × 18,000 = ₹ 3,000
Percentage for savings = \(\frac { 3000 }{ 18000 } \) × 100 = 16.67 %

(iii) Usage of salary for other expenses = \(\frac { 3 }{ 6 } \) × 18,000 = ₹ 9,000
Percentage for other expenses = \(\frac { 9000 }{ 18000 } \) × 100 = 50 %

Students can Download Maths Chapter 2 Percentage and Simple Interest Ex 2.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 2 Percentage and Simple Interest Ex 2.2

Question 1.
Write each of the following percentage as decimal.
(i) 21 %
(ii) 93.1 %
(iii) 151 %
(iv) 65 %
(v) 0.64 %
Solution:
(i) 21 %
= \(\frac { 21 }{ 100 } \) = 0.21

(ii) 93.1 %
= \(\frac { 93.1 }{ 100 } \) = 0.931

(iii) 151 %
= \(\frac { 151 }{ 100 } \) = 1.51

(iv) 65 %
= \(\frac { 65 }{ 100 } \) = 0.65

(v) 0.64 %
= \(\frac { 0.64 }{ 100 } \) = 0.0064

Question 2.
Convert each of the following decimal as percentage
(i) 0.282
(ii) 1.51
(iii) 1.09
(iv) 0.71
(v) 0.858
Solution:
(i) 0.282
= 0.282 × 100% = \(\frac { 282 }{ 1000 } \) × 100 %
= 28.2 %

(ii) 1.51
= \(\frac { 151 }{ 100 } \) × 100 %
= 151 %

(iii) 1.09
= \(\frac { 109 }{ 100 } \) × 100 %
= 109 %

(iv) 0.71
= \(\frac { 71 }{ 100 } \) × 100 %
= 71 %

(v) 0.858
= \(\frac { 858 }{ 1000 } \) × 100 %
= 85.8 %

Question 3.
In an examination a student scored 75% of marks. Represent the given the percentage in decimal form?
Solution:
Student’s Score = 75% = \(\frac { 75 }{ 100 } \) = 0.75

Question 4.
In a village 70.5% people are literate. Express it as a decimal.
Solution:
Percentage of literate people = 70.5%
= \(\frac { 70.5 }{ 100 } \)
= 0.705

Question 5.
Scoring rate of a batsman is 86%. Write his strike rate as decimal.
Solution:
Scoring rate of the batsman = 86%
= \(\frac { 86 }{ 100 } \)
= 0.86

Question 6.
The height of a flag pole in school is 6.75m. Write it as percentage.
Solution:
Height of flag pole = 6.75m
= \(\frac { 675 }{ 100 } \)
= 6.75%

Question 7.
The weights of two chemical substances are 20.34 g and 18.78 g. Write the difference in percentage?
Solution:
Weight of substance 1 = 20.34g
Percentage of substance 1 = \(\frac { 2034 }{ 100 } \) = 2034 %
Weight of substance 2 = 18.78g
Percentage of substance 2 = \(\frac { 1878 }{ 100 } \) = 1878 %
Their difference = 2034 – 1878 = 156%

Question 8.
Find the percentage of shaded region in the following figure.

Solution:
Total region = 4 parts
Shaded region = 1 part
Fraction of shaded region = \(\frac { 1 }{ 4 } \)
Percentage of shaded region = \(\frac { 1 }{ 4 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 1 }{ 4 } \) × 100 %
= 25 %

Objective Type Questions

Question 1.
Decimal value of 142.5% is
(i) 1.425
(ii) 0.1425
(iii) 142.5
(iv) 14.25
Hint:
142.5 % = \(\frac { 1425 }{ 10 } \) %
= \(\frac { 1425 }{ 10 } \) × \(\frac { 1 }{ 100 } \)
= 1.425
Answer:
(i) 1.425

Question 2.
The percentage of 0.005 is
(i) 0.005 %
(ii) 5 %
(iii) 0.5 %
(iv) 0.05 %
Hint:
0.005 = \(\frac { 5 }{ 1000 } \)
= \(\frac { 5 }{ 1000 } \) × \(\frac { 100 }{ 100 } \)
= 0.5 %
Answer:
(iii) 0.5 %

Question 3.
The percentage of 4.7 is
(i) 0.47 %
(ii) 4.7 %
(iii) 47 %
(iv) 470 %
Hint:
4.7 = \(\frac { 47 }{ 10 } \)
= \(\frac { 47 }{ 10 } \) × \(\frac { 100 }{ 100 } \)
= 470 %
Answer:
(iv) 470 %

Students can Download Maths Chapter 1 Number System Ex 1.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 1 Number System Ex 1.5

Miscellaneous Practice problems

Question 1.
Malini bought three ribbon of lengths 13.92 m, 11.5 m and 10.64 m. Find the total length of the ribbons?
Solution:
Length of ribbon 1 = 13.92 m
Length of ribbon 2 = 11.50 m
Length of ribbon 3 = 10.64 m

Total Length of the ribbons = 13.92 m + 11.5 m + 10.64 m = 36.06 m
Totla length of the ribbons = 36.06 m

Question 2.
Chitra has bought 10 kg 35 g of ghee for preparing sweets. She used 8 kg 59 g of ghee. How much ghee will be left?
Solution:
Total weight of ghee bought = 10 kg 35 g
Weight of ghee used = 8 kg 59 g
Weight of ghee left = 10.35 kg – 8.59 kg = 1.76 kg

∴ Weight of ghee left= 1 kg 76 g = 1.76 kg

Question 3.
If the capacity of a milk can is 2.53 l, then how much milk is required to fill 8 such cans?
Solution:
Capacity of 1 milk can= 2.53 l
∴ Capacity of 8 milk cans= 2.53 l × 8 = 20.24 l

To fill 8 cans 20.24 l of milk is required.

Question 4.
A basket of orange weighs 22.5 kg. If each family requires 2.5 kg of orange, families can share?
Solution:
Total weight of orange = 22.5 kg
Weight of orange required for 1 family = 2.5 kg
∴ Number of families sharing orange = 22.5 kg ÷ 2.5 kg
= \(\frac { 22.5 }{ 2.5 } \) = \(\frac { 22.5 }{ 2.5 } \) × \(\frac { 10 }{ 10 } \) = \(\frac { 225 }{ 25 } \) = 9
∴ 9 families can share the oranges.

Question 5.
A baker uses 3.924 kg of sugar to bake 10 cakes of equal size. How much sugar is used in each cake?
Solution:
For 10 cakes sugar required = 3.924 kg
For 1 cake sugar required = 3.924 ÷ 10 = \(\frac { 3.924 }{ 10 } \) = 0.3924 kg
For 1 cake sugar required = 0.3924 kg.

Question 6.
Evaluate:
(i) 26.13 × 4.6
(ii) 3.628 + 31.73 – 2.1
Solution:
(i) 26.13 × 4.6
26.13 × 4.6 = 120.198

(ii) 3.628 + 31.73 – 2.1 = 33.258

Question 7.
Murugan bought some bags of vegetables. Each bag weighs 20.55 kg. If the total weight of all the bags is 308.25 kg, how many bags did he buy?
Solution:
Total weight of all bags = 308.25 kg
Weight of 1 bag = 20.55 kg

Question 8.
A man walks around a circular park of distance 23.761 m. How much distance will he cover in 100 rounds?
Solution:
In 1 round distance covered = 23.761 m
∴ In 100 rounds distance = 23.761 × 100
= 2376.1 m
∴ In 100 round he covers 2376.1 m.

Question 9.
How much 0.0543 is greater than 0.002?
Solution:

∴ Required answer is 0.0523

Question 10.
A printer can print 15 pages per minute. How many pages can it print in 4.6 minutes?
Solution.
In 1 minute the pages printed = 15
In 4.6 minutes the pages printed = 15 × 4.6
= 69

The printer prints 69 pages.

Challenge Problems

Question 1.
The distance travelled by Prabhu from home to Yoga centre is 102 m and from Yoga centre to school is 165 m. What is the total distance travelled by him in kilometres (in decimal form)?
Solution:

∴ 267 metres = \(\frac { 267 }{ 1000 } \) km = 0.267 km
∴ Total distance travelled = 0.267 km

Question 2.
Anbu and Mala travelled from A to C in two different routes. Anbu travelled from place A to place B and from there to place C. A is 8.3 km from B and B is 15.6 km from C. Mala travelled from place A to place D and from there to place C. D is 7.5 km from A and C is 16.9 km from D. Who travelled more and by how much distance?
Solution:
Distance travelled by Anbu:

From place A to place B = 8.3 km
Distance from place B to place C = 15.6 km
∴ Total distance travelled by Anbu = 8.3 + 15.6
= 23.9 km

Distance travlled by Mala:

Distance travelled place A to D = 7.5 km
Distance from place D to place C = 16.9 km
Total distance travelled by mala = (7.5 + 16.9) km = 24.4 km
24.4 > 23.9
∴ Mala travelled more distance. She travelled (24.4 – 23.9) km more i.e she travelled 0.5 km more

Question 3.
Ramesh paid ₹ 97.75 per hour for a taxi and he used 35 hours in a week. How much he has to pay totally as taxi fare for a week?
Solution:
Payment for the taxi for an hour = ₹ 97.75
Total hours the taxi was used = 35 hrs
∴ Total payment for the taxi for the week

= 97.75 × 35
= 3421.25
Total payment for a week = ₹ 3421.25

Question 4.
An Aeroplane travelled 2781.20 kms in 6 hours. Find the average speed of the aeroplane in Km/hr.
Solution:
In 6 hours the distance travelled = 2781.20 km
In 1 hour the distance travelled = \(\frac { 2781.20 }{ 6 } \) km

Average speed of the aroplane = 463.53 km/hr.

Question 5.
Kumar’s car gives 12.6 km mileage per litre. If his fuel tank holds 25.8 litres then how far can he travel?
Solution.
Distance travelled with 1 litre fuel = 12.6 km
∴ with 25.8 litres distance travelled = 12.6 × 25.8
= 325.08 km

The car can travel 325.08 km

Students can Download Maths Chapter 2 Percentage and Simple Interest Ex 2.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 2 Percentage and Simple Interest Ex 2.1

Question 1.
In each of the following grid, find the numbers of coloured squares and express it as a fraction, decimal and percentage.

Solution:
Number of coloured square = 58
Total number of squares = 100
∴ Fraction : \(\frac { 58 }{ 100 } \)
Decimal : 0.58
Percentage : 58%

(ii) Number of coloured square = 53
Total number of squares = 100
∴ Fraction : \(\frac { 53 }{ 100 } \)
Decimal : 0.53
Percentage : 53%

(iii) Number of coloured square = 25
Total number of squares = 50
∴ Fraction : \(\frac { 25 }{ 50 } \)

Decimal : \(\frac { 25 }{ 50 } \) × \(\frac { 2 }{ 2 } \)
= \(\frac { 50 }{ 100 } \)
= 0.50

Percentage : \(\frac { 25 }{ 50 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 25 }{ 50 } \) × 100% = 50%

(iv) Number of coloured square = 17
Total number of squares = 25
∴ Fraction : \(\frac { 17 }{ 25 } \)
Decimal : \(\frac { 17 }{ 25 } \) × \(\frac { 4 }{ 4 } \)
= \(\frac { 68 }{ 100 } \) = 0.68
Percentage : \(\frac { 17 }{ 25 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 17 }{ 25 } \) × 100%
= 68%

(v) Number of coloured square = 15
Total number of squares = 30
∴ Fraction : \(\frac { 15 }{ 30 } \)
Decimal : \(\frac { 15 }{ 30 } \)
= \(\frac { 1 }{ 2 } \) × \(\frac { 50 }{ 50 } \)
= \(\frac { 50 }{ 100 } \) = 0.50
Percentage : \(\frac { 15 }{ 30 } \)
= \(\frac { 15 }{ 30 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 15 }{ 30 } \) × 100%
= 50 %

Question 2.
A picture of chess board is given.
(i) Find the percentage of the white coloured squares
(ii) Find the percentage of gray coloured squares
(iii) Find the percentage of the squares that have the pieces and
(iv) The squares that do not have the pieces.

Solution:
(i) Total number of squares in the chess board = 64
Number of white coloured squares = 32
Percentage = \(\frac { 32 }{ 64 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 32 }{ 64 } \) × 100 %
= 50%

(ii) Grey coloured squares = 64
Percentage = \(\frac { 32 }{ 64 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 32 }{ 64 } \) } [/latex] × 100 %
= 50 %

(iii) Number of squares having pieces = 20
Total number of squares = 64

(iv) Number of squares do not have pieces = 44

Question 3.
A picture of dart board is given. Find the percentage of white coloured portion and black coloured portion.

Solution:
Total sector = 20
White coloured sector = 10
Black coloured sector = 10
Percentage of white : \(\frac { 10 }{ 20 } \) × \(\frac { 100 }{ 100 } \)
Decimal : \(\frac { 10 }{ 20 } \) × 100 %
= 50 %
Percentage of black colour : \(\frac { 10 }{ 20 } \) × \(\frac { 100 }{ 100 } \)
Decimal : \(\frac { 10 }{ 20 } \) × 100 %
= 50 %

Question 4.
Write each of the following fraction as percentage.
(i) \(\frac { 36 }{ 50 } \)
(ii) \(\frac { 81 }{ 30 } \)
(iii) \(\frac { 42 }{ 56 } \)
(iv) 2 \(\frac { 1 }{ 4 } \)
(v) 1 \(\frac { 3 }{ 5 } \)
Solution:
(i) \(\frac { 36 }{ 50 } \)
= \(\frac { 36 }{ 50 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 36 }{ 50 } \) × 100 %
= 72 %

(ii) \(\frac { 81 }{ 30 } \)
= \(\frac { 81 }{ 30 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 81 }{ 30 } \) × 100 %
= 270 %

(iii) \(\frac { 42 }{ 56 } \)
= \(\frac { 42 }{ 56 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 42 }{ 56 } \) × 100 %
= \(\frac { 21 }{ 28 } \) × 100 %
= 75 %

(iv) 2 \(\frac { 1 }{ 4 } \)
= \(\frac { 9 }{ 4 } \)
= \(\frac { 9 }{ 4 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 9 }{ 4 } \) × 100 %
= 225 %

(v) 1 \(\frac { 3 }{ 5 } \)
= \(\frac { 8 }{ 5 } \)
= \(\frac { 8 }{ 5 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 8 }{ 5 } \) × 100 %
= 160 %

Question 5.
Anbu scored 436 marks out of 500 in his exams. What was the percentage he scored?
Answer:
Total marks = 500
Anbu’s Score = 436
Percentage = \(\frac { 436 }{ 500 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 436 }{ 500 } \) × 100 %
= 87.2 %
Anbu’s Score = 87.2 %

Question 6.
Write each of the following percentage as fraction,
(i) 21%
(ii) 93.1 %
(iii) 151 %
(iv) 65 %
(v) 0.64 %
Solution:
(i) 21%
= \(\frac { 21 }{ 100 } \)

(ii) 93.1 %
= \(\frac { 93.1 }{ 100 } \)
= \(\frac{93.1 \times 10}{100 \times 10}\)
= \(\frac { 931 }{ 1000 } \)

(iii) 151 %
= \(\frac { 151 }{ 100 } \)

(iv) 65 %
= \(\frac { 65 }{ 100 } \)
= \(\frac { 13 }{ 20 } \)

(v) 0.64 %
= \(\frac { 0.64 }{ 100 } \)
= \(\frac{0.64 \times 100}{100 \times 100}\)
= \(\frac { 64 }{ 10000 } \)
= \(\frac { 4 }{ 625 } \)

Question 7.
Iniyan bought 5 dozen eggs. Out of that 5 dozen eggs, 10 eggs are rotten. Express the number of good eggs as percentage.
Solution:
1 dozen eggs = 12
5 dozen = 5 × 12
Total eggs = 60 eggs
Rotten eggs = 10 Good
eggs = 60 – 10 = 50
Fraction of good eggs = \(\frac { 50 }{ 60 } \)
Percentage of good eggs = \(\frac { 50 }{ 60 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 50 }{ 60 } \) × 100 %
= \(\frac { 5 }{ 6 } \) × 100 %
= 83.33 %
Percentage of good eggs = 83.33 %

Question 8.
In an election, Candidate X secured 48% of votes. What fraction will represent his votes?
Solution:
Percentage of votes x secured = 48% = \(\frac { 48 }{ 100 } \)
Fraction of votes x secured = \(\frac { 12 }{ 25 } \)

Question 9.
Ranjith total income was ₹ 7,500. He saved 25% of his total income. Find the amount saved by him.
Solution:
Total income of Ranjith = ₹ 7500
His savings = 25 % of 7500
= \(\frac { 25 }{ 100 } \) of 7500
= \(\frac { 25 }{ 100 } \) × 7500
= ₹ 1,875
∴ Amount saved by Ranjith = ₹ 1,875

Objective Type Questions

Question 1.
Thendral saved one fourth of her salary. Her savings percentage is
(i) \(\frac { 3 }{ 4 } \)
(ii) \(\frac { 1 }{ 4 } \) %
(iii) 25 %
(iv) 1 %
Hint: \(\frac { 1 }{ 4 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 1 }{ 4 } \) × 100 %
= 25 %
Answer:
(iii) 25 %

Question 2.
Kavin scored 15 out of 25 in a test. The percentage of his marks is
(i) 60%
(ii) 15%
(iii) 25%
(iv) 15/25
Hint: \(\frac { 15 }{ 25 } \) × \(\frac { 100 }{ 100 } \)
= \(\frac { 15 }{ 25 } \) × 100 %
= 60 %
Answer:
(i) 60%

Question 3.
0.07% is
(i) \(\frac { 7 }{ 10 } \)
(ii) \(\frac { 7 }{ 100 } \)
(iii) \(\frac { 7 }{ 1000 } \)
(iv) \(\frac { 7 }{ 10,000 } \)
Hint: 0.07 %
= 0.07%
= \(\frac { 0.07 }{ 100 } \)
= \(\frac{7}{\frac{100}{100}}\)
= \(\frac{7}{100 \times 100}\)
= \(\frac { 7 }{ 10,000 } \)
Answer:
(iv) \(\frac { 7 }{ 10,000 } \)

Students can Download Maths Chapter 1 Number System Ex 1.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 1 Number System Ex 1.4

Question 1.
Simplify the following
(i) 0.6 ÷ 3
(ii) 0.90 ÷ 5
(iii) 4.08 ÷ 4
(iv) 21.56 ÷ 7
(v) 0.564 ÷ 6
(vi) 41.36 ÷ 4
(vii) 298.2 ÷ 3
Solution:
(i) 0.6 ÷ 3
= \(\frac { 6 }{ 10 } \) × \(\frac { 1 }{ 3 } \)
= \(\frac { 6 }{ 3 } \) × \(\frac { 1 }{ 10 } \)
= 2 × \(\frac { 1 }{ 10 } \)
= \(\frac { 2 }{ 10 } \)
= 0.2

(ii) 0.90 ÷ 5
= \(\frac { 90 }{ 100 } \) × \(\frac { 1 }{ 5 } \)
= \(\frac { 90 }{ 5 } \) × \(\frac { 1 }{ 100 } \)
= 18 × \(\frac { 1 }{ 100 } \) = \(\frac { 18 }{ 100 } \)
= 0.18

(iii) 4.08 ÷ 4
= \(\frac { 408 }{ 100 } \) × \(\frac { 1 }{ 4 } \)
= \(\frac { 408 }{ 4 } \) x \(\frac { 1 }{ 100 } \)
= 102 × \(\frac { 1 }{ 100 } \)
= \(\frac { 102 }{ 100 } \)
= 1.02

(iv) 21.56 ÷ 7
= \(\frac { 2156 }{ 100 } \) × \(\frac { 1 }{ 7 } \)
= \(\frac { 2156 }{ 7 } \) × \(\frac { 1 }{ 100 } \)
= 308 × \(\frac { 1 }{ 100 } \)
= \(\frac { 308 }{ 100 } \)
= 3.08

(v) 0.564 ÷ 6
= \(\frac { 564 }{ 1000 } \) × \(\frac { 1 }{ 6 } \)
= \(\frac { 564 }{ 6 } \) × \(\frac { 1 }{ 1000 } \)
= \(\frac { 94 }{ 1000 } \)
= 0.094

(vi) 41.36 ÷ 4
= \(\frac { 4136 }{ 100 } \) × \(\frac { 1 }{ 4 } \)
= \(\frac { 4136 }{ 4 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 1034 }{ 100 } \)
= 10.34

(vii) 298.2 ÷ 3
= \(\frac { 2982 }{ 10 } \) × \(\frac { 1 }{ 3 } \)
= \(\frac { 2982 }{ 3 } \) × \(\frac { 1 }{ 10 } \)
= \(\frac { 994 }{ 10 } \)
= 99.4

Question 2.
Simplify the following.
(i) 5.7 ÷ 10
(ii) 93.7 ÷ 10
(iii) 0.9 ÷ 10
(iv) 301.301 ÷ 10
(v) 0.83 ÷ 10
(vi) 0.062 ÷ 10
Solution:
(i) 5.7 ÷ 10
= \(\frac { 57 }{ 10 } \) × \(\frac { 1 }{ 10 } \)
= \(\frac { 57 }{ 100 } \)
= 0.57

(ii) 93.7 ÷ 10
= \(\frac { 937 }{ 10 } \) × \(\frac { 1 }{ 10 } \)
= \(\frac { 937 }{ 100 } \)
= 9.37

(iii) 0.9 ÷ 10
= \(\frac { 9 }{ 10 } \) × \(\frac { 1 }{ 10 } \)
= \(\frac { 9 }{ 100 } \)
= 0.09

(iv) 301.301 ÷ 10
= \(\frac { 301301 }{ 1000 } \) × \(\frac { 1 }{ 10 } \)
= \(\frac { 301301 }{ 10000 } \)
= 30.1301

(v) 0.83 ÷ 10
= \(\frac { 83 }{ 100 } \) × \(\frac { 1 }{ 10 } \)
= \(\frac { 83 }{ 1000 } \)
= 0.083

(vi) 0.062 ÷ 10
= \(\frac { 62 }{ 1000 } \) × \(\frac { 1 }{ 10 } \)
= \(\frac { 62 }{ 1000 } \)
= 0.0062

Question 3.
Simplify the following.
(i) 0.7 ÷ 100
(ii) 3.8 ÷ 100
(iii) 49.3 ÷ 100
(iv) 463.85 ÷ 100
(v) 0.3 ÷ 100
(vi) 27.4 ÷ 100
Solution:
(i) 0.7 ÷ 100
= \(\frac { 7 }{ 10 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 7 }{ 1000 } \)
= 0.007

(ii) 3.8 ÷ 100
= \(\frac { 38 }{ 10 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 38 }{ 1000 } \)
= 0.038

(iii) 49.3 ÷ 100
= \(\frac { 493 }{ 10 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 493 }{ 1000 } \)
= 0.493

(iv) 463.85 ÷ 100
= \(\frac { 46385 }{ 100 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 46385 }{ 1000 } \)
= 4.6385

(v) 0.3 ÷ 100
= \(\frac { 3 }{ 10 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 3 }{ 1000 } \)
= 4.6385

(vi) 27.4 ÷ 100
= \(\frac { 274 }{ 10 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 274 }{ 1000 } \)
= 0.274

Question 4.
Simplify the following.
(i) 18.9 ÷ 1000
(ii) 0.87 ÷ 1000
(iii) 49.3 ÷ 1000
(iv) 0.3 ÷ 1000
(v) 382.4 ÷ 1000
(vi) 93.8 ÷ 1000
Solution:
(i) 18.9 ÷ 1000
= \(\frac { 189 }{ 10 } \) × \(\frac { 1 }{ 1000 } \)
= \(\frac { 189 }{ 10000 } \)
= 0.0189

(ii) 0.87 ÷ 1000
= \(\frac { 87 }{ 100 } \) × \(\frac { 1 }{ 1000 } \)
= \(\frac { 87 }{ 100000 } \)
= 0.00087

(iii) 49.3 ÷ 1000
= \(\frac { 493 }{ 10 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 493 }{ 1000 } \)
= 0.493

(iv) 0.3 ÷ 1000
= \(\frac { 3 }{ 10 } \) × \(\frac { 1 }{ 1000 } \)
= \(\frac { 3 }{ 10000 } \)
= 0.0003

(v) 382.4 ÷ 1000
= \(\frac { 3824 }{ 10 } \) × \(\frac { 1 }{ 1000 } \)
= \(\frac { 3824 }{ 10000 } \)
= 0.3824

(vi) 93.8 ÷ 1000
= \(\frac { 938 }{ 10 } \) × \(\frac { 1 }{ 1000 } \)
= \(\frac { 938 }{ 10000 } \)
= 0.0938

Question 5.
Simplify the following.
(i) 19.2 ÷ 2.4
(ii) 4.95 ÷ 0.5
(iii) 19.11 ÷ 1.3
(iv) 0.399 ÷ 2.1
(v) 5.4 ÷ 0.6
(vi) 2.197 ÷ 1.3
Solution:
(i) 19.2 ÷ 2.4

(ii) 4.95 ÷ 0.5

(iii) 19.11 ÷ 1.3

(iv) 0.399 ÷ 2.1

(v) 5.4 ÷ 0.6

(vi) 2.197 ÷ 1.3

Question 6.
Divide 9.55 kg of sweet among 5 children. How much will each child get?
Solution:
Weight of the sweet = 9.55 Kg
Weight of sweet for 5 children = \(\frac { 955 }{ 100 } \) Kg
Weight of sweet for 1 child = \(\frac{\left(\frac{955}{100}\right)}{5}\) = \(\frac { 955 }{ 100 } \) × \(\frac { 1 }{ 5 } \) = \(\frac { 955 }{ 5 } \) × \(\frac { 1 }{ 100 } \)
= \(\frac { 191 }{ 100 } \) = 1.91
Each child will get 1.91 kg sweet.

Question 7.
A vehicle covers a distance of 76.8 km for 1.2 litre of petrol. How much distance will it cover for one litre of petrol?
Solution:
For 1.2 litre of petrol the distance covered = 76.8 Km = \(\frac { 768 }{ 10 } \) Km

For 1 litre of petrol distance covered = 64 Km

Question 8.
Cost of levelling a land at the rate of ₹ 15.50 sq. ft is ₹ 10,075. Find the area of the land.
Solution:
Cost of levelling the entire land = ₹ 10,075
Cost of levelling 1 sq. ft = ₹ 15.50

∴ Area of the land = 650 sq.ft.

Question 9.
The cost of 28 books are ₹ 1506.4. Find the cost of one book.
Solution:
Cost of 28 books = ₹ 1506.4

Cost of 1 book = ₹ 53.80

Question 10.
The product of two numbers is 40.376. One number is 14.42. Find the other number.
Product of two numbers = 40.376
One number = 14.42

Objective Type Questions

Question 1.
5.6 ÷ 0.5 = ?
(i) 11.4
(ii) 10.4
(iii) 0.14
(iv) 11.2
Answer:
(iv) 11.2
Hint:
\(\frac { 5.6 }{ 0.5 } \) = \(\frac { 56 }{ 5 } \)
= 11.2

Question 2.
2.01 ÷ 0.03 = ?
(i) 6.7
(ii) 67.0
(iii) 0.67
(iv) 0.067
Answer:
(ii) 67.0
Hint: \(\frac { 2.01 }{ 0.03 } \) = \(\frac { 201 }{ 3 } \)
= 67

Question 3.
0.05 ÷ 0.5 = ?
(i) 0.01
(ii) 0.1
(iii) 0.10
(iv) 1.0
Answer:
(ii) 0.1
Hint: