Category: Uncategorized

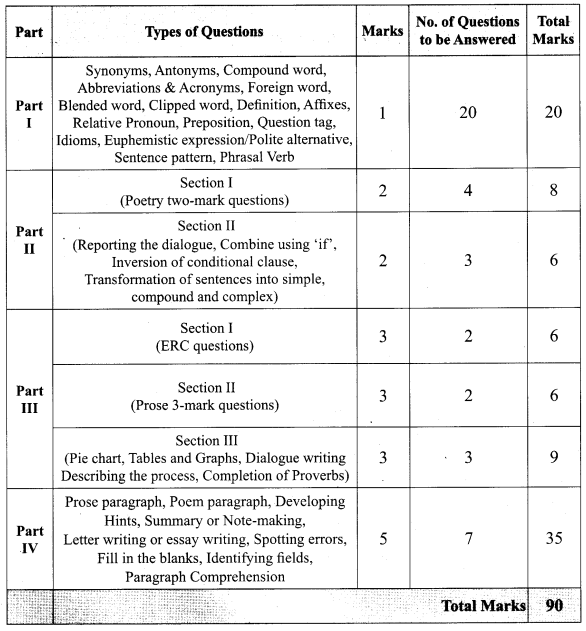
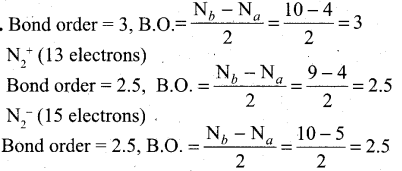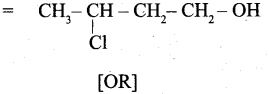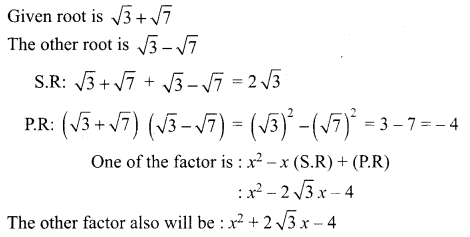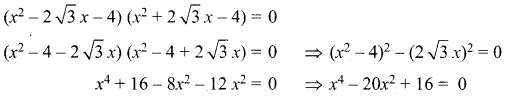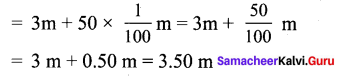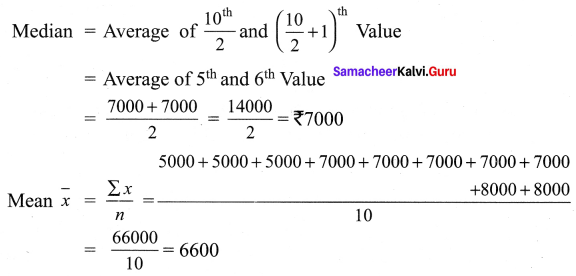Students can Download Tamil Chapter 1.4 ஆழ்கடலின் அடியில் Questions and Answers, Summary, Notes Pdf, Samacheer Kalvi 7th Tamil Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Tamil Solutions Term 2 Chapter 1.4 ஆழ்கடலின் அடியில்

மதிப்பீடு

Question 1.
ஆழ்கடலில் அடியில்’ கதையைச் சுருக்கி எழுதுக.
Answer:
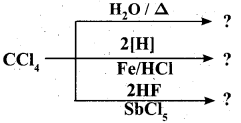
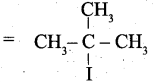
1886 ஆம் ஆண்டு கடலில் செல்லும் பெரிய கப்பல்களை, உலோகத்தால் ஆன உடலைக் கொண்ட ஒரு விந்தையான விலங்கு தாக்குவதாகச் செய்தி வெளியானது. அதனைக் கண்டறிய நியூயார்க் நகரிலிருந்து போர்க்கப்பல் ஒன்று புறப்பட்டது. அதில் விலங்கியல் பேராசிரியரான பியரி , அக்கப்பலின் தலைவர் ஃபராகட், திமிங்கலங்களை வேட்டையாடும் நெட் என்ற வீரர் மற்றும் பியரியின் உதவியாளர் கான்சீல் ஆகியோர் சென்றனர்.

மூன்று மாதங்கள் அவர்கள், அமெரிக்காவுக்கும், ஜப்பானுக்கும் உள்ள பெருங்கடல் பரப்பில் தேடினார்கள். அவ்விலங்கு கண்ணில் படவில்லை. அதனால் அவர்கள் தங்கள் நகரத்திற்குத் திரும்ப எண்ணினர். அப்போது பளபளப்பான உடலைக் கொண்ட விலங்கு கப்பலை நோக்கி வந்தது. நெட் வலிமை வாய்ந்த ஈட்டிகளை எய்தார். அவ்விலங்கு வேகமாக மோதியதில் அவர்கள் கப்பலில் இருந்து தூக்கி வீசப்பட்டனர். மயக்கமடைந்த பியரி கண் விழித்த போது, பியரி, நெட், கான்சீல் ஆகியோர் அவ்விலங்கின் மீது அமர்ந்திருந்தனர். நெட், “இது விலங்கு இல்லை ; ஒரு நீர்மூழ்கிக்கப்பல்” என்று கூறினார்.

மூவரும் அக்கப்பலின் உள்ளிருப்பவர்களை உதவிக்கு அழைத்தனர். கதவு திறக்கப்பட்டது. கப்பலின் உள்ளிருந்து வந்தவர்கள் மூவரையும் சிறைப்பிடித்தனர். நெமோ என்று ஒருவர் இம்மூவரிடம் பேசினார். “நாட்டிலஸ் என்னும் இந்த நீர்மூழ்கிக் கப்பலை ஒரு விந்தையான விலங்கு என்று நம்ப வைத்திருக்கிறோம். இவ்வுண்மை தெரிந்த உங்களை விடமாட்டேன்” என்று கூறினார்.

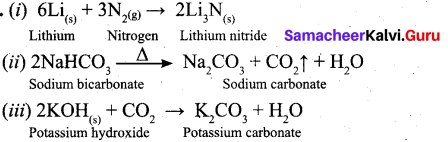
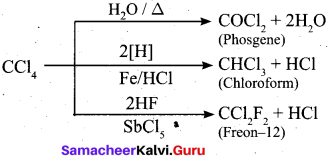
கப்பலினுள் எல்லா இடங்களுக்கும் சென்றனர். அதில் நூலகம் மற்றும் அருங்காட்சியகம் ஆகிய அரிய அறிவுக் கருவூலங்கள் யாருக்கும் பயன்படாமல் இருந்தன. கப்பலின் இயங்குமுறைகளைப் பற்றி நெமோவிடம் கேட்டறிந்தனர். கப்பலில் உள்ளோர் மூச்சு விடுவதற்கான காற்று எவ்வாறு கிடைக்கிறது என்பது பற்றியெல்லாம் கூறினார் நெமோ. ஒருநாள் கப்பல் கடலுக்குள் இருக்கும் மணல் திட்டில் சிக்கிக் கொண்டது.

நாட்டிலஸின் மேல்தளத்தில் நின்றபோது பக்கத்தில் ஒரு தீவு தெரிந்தது. இம்மூவரும் நெமோவிடம் அனுமதி பெற்று படகில் சென்று அத்தீவில் காய்கறிகளை வாங்கிக் கொண்டு படகில் ஏற்றினர். அத்தீவைச் சார்ந்த, மனிதர்களைக் கொன்று தின்னும் வழக்கமுடையவர்கள் துரத்தினார்கள். மூவரும் தப்பித்துக் கப்பலுக்குள் வந்துவிட்டனர். ஆனால் அம்மனிதர்கள் பல படகுகளில் வந்து கப்பலைச் சூழ்ந்து கொண்டனர். ஏழு நாட்களுக்குப் பிறகு மேல் மூடியைத் திறந்தார். அந்த மனிதர்கள் ஏணியில் ஏற முயன்றனர். நெமோ அதில் மின்சாரத்தைப் பாய்ச்சி இருந்ததால் ஓடிவிட்டனர்.

பல நாட்களுக்குப் பிறகு இந்தியாவுக்கும் இலங்கைக்கும் அருகில் நாட்டிலஸ் சென்று கொண்டிருந்தது. முத்துச் சிப்பிகளைச் சேகரிக்க நெமோவும் பியரியும் கடலுக்குள் சென்றனர். அப்போது முத்துக் குளிப்பதற்காக ஓர் இந்தியர் கடலுக்குள் இறங்கியதைப் பார்த்தனர். அவரைச் சுறாமீனிடமிருந்து காப்பாற்றினர்.

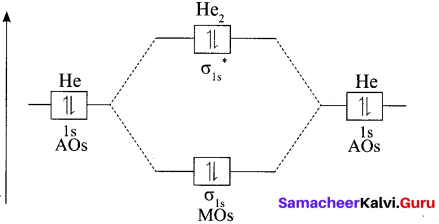
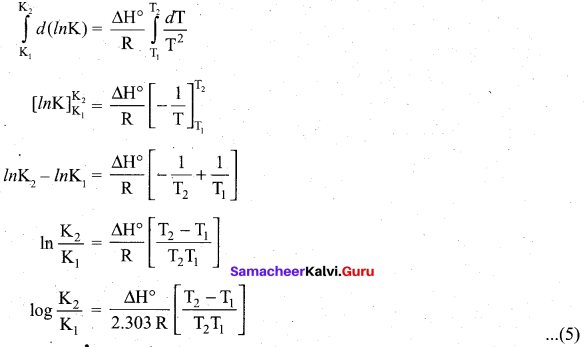
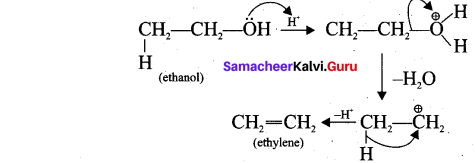
வழியில் போரின்போது கடலில் மூழ்கடிக்கப்பட்ட கப்பலைப் பார்த்தனர். அதில் 5 இருந்த தங்கம், வெள்ளி, வைரம் போன்றவற்றை எடுத்துக் கொண்டனர். கடலினுள் உள்ள எரிமலை, கடலுக்குள் மூழ்கிய அட்லாண்டிஸ் நகர இடிபாடுகளைக் கண்டனர். பூமியின் தென் துருவத்தில் பென்குவின், கடல் சிங்கம் போன்ற அரிய பறவைகளையும் விலங்குகளையும் கண்டனர். ஆக்டோபஸ் ஒன்றைக் கொன்றனர்.

மூவரும் தப்பிக்க முயன்றனர். அதனால் கப்பலுடன் இணைக்கப்பட்ட படகில் ஏறினர். அப்போது நாட்டிலஸ் கடல் சுழலுக்குள் சிக்கிக் கொண்டது. இம்மூவரும் கடலுக்குள் வீசப்பட்டனர். மயக்கம் தெளிந்த போது நார்வே நாட்டில் ஒரு மீனவரின் குடிசையில் இருந்தனர். நெமோ பற்றியும் நாட்டிலஸ் பற்றியும் யாருக்கும் எந்தச் செய்தியும் கிடைக்கவில்லை

கற்பவை கற்றபின்

Question 1.
ஆழ்கடல் காட்சியொன்றைக் கற்பனையாகப் படம் வரைந்து வண்ணம் தீட்டுக.
Answer:
மாணவர்கள் தாங்களாகவே செய்ய வேண்டியவை.

Question 2.
நீர்மூழ்கிக் கப்பல் இயங்கும் முறை பற்றிய செய்திகளைத் திரட்டித் தொகுத்து எழுதுக.
Answer:
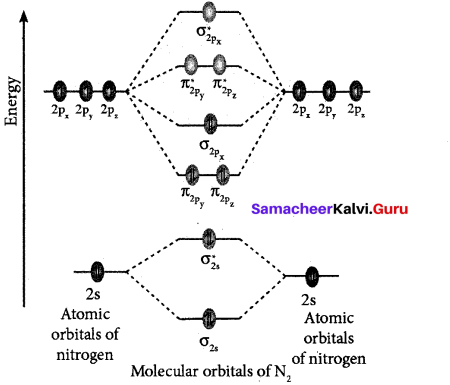
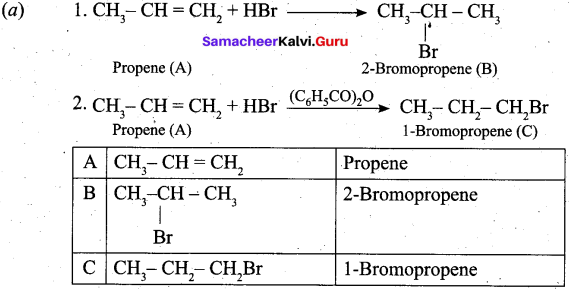
கடலுக்குள்ளே செல்லும் நீர்மூழ்கிக் கப்பலைப் பற்றிக் கேள்விப்பட்டிருப்போம். உள்ளே சென்று பார்ப்பதற்கு வாய்ப்பில்லை. இந்த நீர்மூழ்கிக் கப்பலின் பயன் என்ன? அது எப்படிச் செயல்படுகிறது? கடலில் நடைபெறும் போர்களில் ஒற்றர்களைப் போல செயல்படுபவையே நீர்மூழ்கிக் கப்பல்கள். கடலின் உள்ளே நீண்ட தூரம் வரை செல்லக்கூடியவை. புஷ்வெல் என்பவர் நீர்மூழ்கிக் கப்பலைக் கண்டுபிடித்தார். சில வருடங்களுக்கு முன்னால் சிறிய அளவில் செய்யப்பட்டன. தற்போது 400 அடி நீளம் வரை உள்ளன. நீர்மூழ்கிக் கப்பலில் இரண்டு என்ஜின்கள் உள்ளன. நீர்மட்டத்திற்கு மேலே ஒரு என்ஜின் உள்ளது.

இது கப்பல் செல்லும் போது நீராவியால் இயக்கப்படும். இன்னொன்று கப்பல் நீரில் மூழ்கிச் செல்லும்போது மின்சாரத்தால் இயக்கப்படும். தற்போதுள்ள புதிய கப்பல்கள் 12,000 மைல் தூரம் வரை நிற்காமல் செல்லக்கூடியவை. 60 மணிநேரம் மின்சார ஆற்றலும் செயல்படுத்தக்கூடிய வகையில் அமைக்கப்பட்டுள்ளன. காற்று வாங்க மேடை ஒன்று இருக்கும். மேலே பீரங்கி இருக்கும். கடலின் உள்ளே செல்லும்போது பீரங்கியை உள்ளே இழுத்துக் கொள்ளும் வசதி உள்ளது.

மேடையின் மீது ஒரு சிறிய கோபுரம் அமைந்திருக்கும். கோபுர உச்சியில் பெரிஸ்கோப் இரட்டைக் கண்ணாடி 2 அல்லது 3 பொருத்தப்பட்டிருக்கும். ஒன்று சரியாகத் தெரியாவிட்டாலும் திருப்பிப் பார்க்கும் வசதியும் உள்ளது. எனவே, நீரினுள் இருக்கும் போது கண்ணாடியின் உதவியால் மாலுமி மேலே நடைபெறும் செயல்களைப் பார்த்துத் தெரிந்து கொள்ளலாம். பெரிஸ்கோப் செயல்படவில்லையெனில் கப்பலுக்கு வழி தெரியாது. எனவே, நீர்மூழ்கிக் கப்பலின் கண்கள் என்றே இதனை அழைக்கலாம்.’

கப்பலின் ஓரங்களில் வெடிகுண்டு வைக்கும் அறை இருக்கும். நீரினுள் மூழ்கும் முன்பு அனைத்துக் கதவுகளும் அடைக்கப்பட்டு கோபுர வாசலும் மூடப்படும். பின்னர் நீர்த்தொட்டி திறக்கப்படும். கடல் நீர் தொட்டிகளுக்குள் வந்து நிறைந்ததும் கப்பலின் எடை மிகுந்து கீழே செல்லும். இதற்குச் சிறகுகளும் உறுதுணையாகச் செயல்படும். கப்பல் கடலுக்குள் மூழ்கும் போது, முன்புறம் தாழ்ந்தும் பின்புறம் உயர்ந்தும் மீன் போல நீந்திச் செல்வதுபோல் இருக்கும்.

எவ்வளவு ஆழம் செல்ல வேண்டுமோ அதற்கேற்ப தொட்டிகளில் தண்ணீர் நிரப்பப்பட வேண்டும். கப்பல் மேலே வரும்போது, காற்றுக் குழாய்கள் திறக்கப்படும். காற்றானது நீர்த்தொட்டிகளுக்குள் சென்று அங்கிருக்கும் நீரை வெளியேற்றும். இதனால் கப்பலின் எடை குறைந்து மேலே நீர்மட்டத்திற்கு வரும். கப்பலின் உள்ளே எடை ஒரே அளவில் இருக்க வேண்டும். கொஞ்சம் கவனிக்கத் தவறினாலும் ஆபத்து ஏற்பட வாய்ப்புள்ளது. கப்பலின் எடை குறையும் போதெல்லாம் அந்த அளவுக்குச் சரியான நீரைத் தொட்டிகளில் நிரப்ப வேண்டும். கப்பலின் இருமுனைகளிலும் உள்ள எடை தராசுத் தட்டுகள் போல் சமமாக இருக்க வேண்டும்.

நீராவிக் கருவிகள் கப்பலை நீர்மட்டத்திற்கு இழுத்துச் செல்வதுடன், வேண்டும் போது காற்றுக்குழாய்களை நிரப்பவும் மின்னாற்றலைப் புதுப்பிக்கவும் உதவுகின்றன. திடீரென ஏற்படும் ஆபத்திலிருந்து தப்பிக்க காற்று உடைகள் இருக்கும். இவை மூச்சுவிடவும், கரைசேரவும் உறுதுணை செய்யும்.

Students can Download Tamil Chapter 3.6 திருக்குறள் Questions and Answers, Summary, Notes Pdf, Samacheer Kalvi 7th Tamil Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Tamil Solutions Term 2 Chapter 3.6 திருக்குறள்

மதிப்பீடு

சரியான விடையைத் தேர்ந்தெடுத்து எழுதுக.

Question 1.
………….. தீமை உண்டாகும்.
அ) செய்யத்தகுந்த செயல்களைச் செய்வதால்
ஆ) செய்யத்தகாத செயல்களைச் செய்யாமல் இருப்பதால்
இ) செய்யத்தகுந்த செயல்களைச் செய்யாமல் இருப்பதால்
ஈ) எதுவும் செய்யாமல் இருப்பதால்
Answer:
இ) செய்யத்தகுந்த செயல்களைச் செய்யாமல் இருப்பதால்

Question 2.
தன்குடியைச் சிறந்த குடியாகச் செய்ய விரும்புவரிடம் ………. இருக்கக் கூடாது.
அ) சோம்பல்
ஆ) சுறுசுறுப்பு
இ) ஏழ்மை
ஈ) செல்வம்
Answer:
அ) சோம்பல்

Question 3.
‘எழுத்தென்ப என்னும் சொல்லைப் பிரித்து எழுதக் கிடைப்பது …………………….
அ) எழுத்து + தென்ப
ஆ) எழுத்து + என்ப
இ) எழுத்து + இன்ப
ஈ) எழுத் + தென்
Answer:
ஆ) எழுத்து + என்ப

Question 4.
‘கரைந்துண்ணும்’ என்னும் சொல்லைப் பிரித்து எழுதக் கிடைப்பது …
அ) கரைந்து + இன்னும்
ஆ) கரை – துண்ணும்
இ) கரைந்து + உண்ணும்
ஈ) கரை + உண்ணும்
Answer:
இ) கரைந்து + உண்ணும்)

Question 5.
கற்றனைத்து + ஊறும் என்பதனைச் சேர்த்தெழுதக் கிடைக்கும் சொல் ………..
அ) கற்றனைத்தூறும்
ஆ) கற்றனைதூறும்
இ) கற்றனைத்தீறும்
ஈ) கற்றனைத் தோறும்
Answer:
அ) கற்றனைத்தூறும்

பொருத்துக

1. கற்கும் முறை – செயல்
2. உயிர்க்குக் கண்கள் – காகம்
3. விழுச்செல்வம் – பிழையில்லாமல் கற்றல்
4. எண்ணித் துணிக – எண்ணும் எழுத்தும்
5. கரவா கரைந்துண்ணும் – கல்வி
Answer:
1. கற்கும் முறை – பிழையில்லாமல் கற்றல்
உயிர்க்குக் கண்கள் – எண்ணும் எழுத்தும்
3. விழுச் செல்வம் – கல்வி
4. எண்ணித்துணிக – செயல்
5. கரவா கரைந்துண்ணும் – காகம்

குறுவினா

Question 1.
நன்மை செய்வதிலும் தீமை உண்டாகும் எப்போது?
Answer:
நாம் ஒருவருடைய பண்பை அறிந்து நன்மை செய்ய வேண்டும் இல்லையென்றால்
நன்மை செய்வதிலும் தீமை உண்டாகும்.

Question 2.
தீமை உண்டாக்கும் இரண்டு செயல்களை எழுதுக.
Answer:
தீமை உண்டாக்கும் இரண்டு செயல்கள் செய்யத்தகாத செயல்களைச் செய்தல்
செய்யத்தக்க செயல்களைச் செய்யாமல் விடுதல்.

Question 3.
துன்பத்திற்குத் துன்பம் உண்டாக்குபவர் யார்?
Answer:
துன்பம் வரும் போது வருந்திக் கலங்காதவர். அந்தத் துன்பத்திற்குத் துன்பம் உண்டாக்குபவர் ஆவர்.

பாடப்பகுதியிலிருந்து படங்களுக்குப் பொருத்தமான திருக்குறளை எழுதுக


Answer:

Students can Download Tamil Chapter 2.5 அணி இலக்கணம் Questions and Answers, Summary, Notes Pdf, Samacheer Kalvi 7th Tamil Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Tamil Solutions Term 3 Chapter 2.5 அணி இலக்கணம்

மதிப்பீடு

குறுவினா

Question 1.
உருவக அணியை விளக்குக.
Answer:
உவமை வேறு உவமிக்கப்படும் பொருள் வேறு என்று இல்லாமல் இரண்டும் ஒன்றே என்பது தோன்றும்படி கூறுவது உருவக அணி ஆகும்.
எ.கா.
வையம் தகளியா வார்கடலே நெய்யாக
வெய்ய கதிரோன் விளக்காகச் – செய்ய
சுடர் ஆழியான் அடிக்கே சூட்டினேன் சொல்மாலை
இடர் ஆழி நீங்குகவே என்று

விளக்கம் : இப்பாடலில் பூமி அகல்விளக்காகவும், கடல் நெய்யாகவும், கதிரவன் சுடராகவும் உருவகப்படுத்தப்பட்டுள்ளன. எனவே, இப்பாடல் உருவக அணிக்குச் சான்றாயிற்று.

Question 2.
உருவக அணிக்கும் ஏகதேச உருவக அணிக்கும் உள்ள வேறுபாடு யாது?
Answer:

கற்பவை கற்றபின்

உவமைத் தொடர்களை எழுதி அவற்றை உருவகங்களாக மாற்றுக.
Answer:
(எ.கா.) மலர் போன்ற முகம் – முகமலர்

கூடுதல் வினாக்கள்

நிரப்புக.

1. உவமைவேறு உவமிக்கப்படும் பொருள் வேறு என்று இல்லாமல் இரண்டும் ஒன்றே என்பது தோன்றும்படிக் கூறுவது உருவக அணி ஆகும்.
2. கூறப்படும் இரு பொருள்களில் ஒன்றை மட்டும் உருவகப்படுத்தி மற்றொன்றை உருவகப்படுத்தாமல் விடுவது ஏகதேச உருவக அணி ஆகும்.

குறுவினா :

Question 1.
உருவக அணி என்றால் என்ன?
Answer:
உவமை வேறு உவமிக்கப்படும் பொருள் வேறு என்று இல்லாமல் இரண்டும் ஒன்றே என்பது தோன்றும்படிக் கூறுவது உருவக அணி ஆகும். எ.கா. தமிழ்த்தேன், துன்பக்கடல்.

Question 2.
ஏகதேச உருவக அணி என்றால் என்ன?
Answer:
கூறப்படும் இரு பொருள்களில் ஒன்றை மட்டும் உருவகப்படுத்தி, மற்றொன்றை உருவகப்படுத்தாமல் விடுவது ஏகதேச உருவக அணி ஆகும்.
எ.கா. பெருமைக்கும் ஏனைச் சிறுமைக்கும் தத்தம் கருமமே கட்டளைக் கல்.

மொழியை ஆள்வோம்

கேட்க. நீதிக்கதைகளைக் கேட்டு மகிழ்க.
மாணவர்கள் தாங்களாகவே நீதிக்கதைகளைக் கேட்டு மகிழ வேண்டும்.

பேசுக. நீதிக்கதை ஒன்றை அறிந்து வந்து வகுப்பறையில் கூறுக.
மாணவர்கள் தாங்களாகவே நீதிக்கதை ஒன்றை அறிந்து வந்து வகுப்பறையில் கூற வேண்டும்.

சொல்லக் கேட்டு எழுதுக

1. பொய்கையாழ்வார் திருவெஃகா என்னும் ஊரில் பிறந்தார்.
2. இனிய சொல்லையே விளைநிலமாகக் கொள்ள வேண்டும்.
3. வாழ்க்கை குறிக்கோள் உடையது.
4. செல்வத்துப் பயன் ஒப்புரவு வாழ்க்கை
5. உவமையும் உவமேயமும் ஒன்றாக அமைவது உருவக அணி.

அறிந்து பயன்படுத்துவோம்

ஏதேனும் ஒன்றை அறிந்து கொள்வதற்காக வினவப்படுவது வினாவாகும். வினா கேட்கப் பயன்படுத்தும் சொற்கள் வினாச்சொற்கள் எனப்படும்.
‘எது, என், எங்கு, எப்படி, எத்தனை, எப்பொழுது, எவற்றை , எதற்கு, ஏன், யார், யாது, யாவை’ போன்றன வினாச்சொற்கள் ஆகும்.

சரியான வினாச்சொல்லை இட்டு நிரப்புக.

Question 1.
நெல்லையப்பர் கோவில்…………….. உள்ளது?
Answer:
எங்கு

Question 2.
முதல் ஆழ்வார்கள் ……………. பேர்?
Answer:
எத்தனை

Question 3.
…….. சொற்களைப் பேச வேண்டும்?
Answer:
எந்தச்

Question 4.
அறநெறிச்சாரம் பாடலை எழுதியவர்………….?
Answer:
யார்

Question 5.
அறநெறிச்சாரம் என்பதன் பொருள் …………..?
Answer:
யாது

பின்வரும் தொடரைப் படித்து வினாக்கள் எழுதுக.

பூங்கொடி தன் தோழியுடன் திங்கட்கிழமை காலையில் பேருந்தில் ஏறிப் பள்ளிக்குச் சென்றாள்.
(எ.கா) பூங்கொடி பள்ளிக்கு எப்படிச் சென்றாள்?
1. ……………………………………………………………………………………………………………
2. ……………………………………………………………………………………………………………
3. ……………………………………………………………………………………………………………

Answer:

1. பூங்கொடி யாருடன் பள்ளிக்குச் சென்றாள்?
2. பூங்கொடி எப்போது பள்ளிக்குச் சென்றாள்?
3. பூங்கொடி தன் தோழியுடன் திங்கட்கிழமை காலையில் எங்குச் சென்றாள்?

தலைப்புச் செய்திகளை முழு சொற்றொடர்களாக எழுதுக.

(எ.கா) தலைப்புச் செய்தி : தமிழகத்தில் வடகிழக்குப் பருவமழை தொடக்கம் – வானிலை மையம் அறிவிப்பு.
தமிழகத்தில் வடகிழக்குப் பருவமழை தொடங்கி உள்ளது என்று வானிலை மையம் அறிவித்துள்ளது.

Question 1.
சாலையில் கிடந்த பணத்தை உரியவரிடம் ஒப்படைத்த மாணவன் – மாவட்ட ஆட்சியர் பாராட்டு.
Answer:
சாலையில் கிடந்த பணத்தை உரியவரிடம் ஒப்படைத்த மாணவனை மாவட்ட ஆட்சியர் பாராட்டினார்.

Question 2.
தமுக்கம் மைதானத்தில் புத்தகக் கண்காட்சி தொடக்கம் – மக்கள் ஆர்வத்துடன் வருகை
Answer:
தமுக்கம் மைதானத்தில் புத்தகக் கண்காட்சி தொடங்கியதால் மக்கள் ஆர்வத்துடன் வருகை தந்தனர்.

Question 3.
தேசிய அளவிலான கைப்பந்துப் போட்டி – தமிழக அணி வெற்றி
Answer:
தேசிய அளவிலான கைப்பந்துப் போட்டியில் தமிழக அணி வெற்றி பெற்றது.

Question 4.
மாவட்ட அளவிலான அறிவியல் கண்காட்சி – ஏழாம் வகுப்பு மாணவி முதலிடம்.
Answer:
மாவட்ட அளவிலான அறிவியல் கண்காட்சியில் ஏழாம் வகுப்பு மாணவி முதலிடம் பெற்றாள்.

Question 5.
மாநில அளவிலான பேச்சுப்போட்டி – சென்னையில் இன்று தொடக்கம்
Answer:
மாநில அளவிலான பேச்சுப்போட்டி சென்னையில் இன்று தொடங்குகிறது.

கட்டுரை எழுதுக.

ஒற்றுமையே உயர்வு

முன்னுரை :

ஒன்றுபட்டால் உண்டு வாழ்வே, நம்மில் ஒற்றுமை நீங்கில் அனைவர்க்கும் தாழ்வே’ என்று பாரதியார் பாடியுள்ளார். அப்படிப்பட்ட ஒற்றுமையைப் பற்றி இக்கட்டுரையில் காண்போம்.

வள்ளுவர் கூறும் ஒற்றுமை :
ஒற்றுமையின் பலத்தை அறிந்த வள்ளுவர் ஒப்புரவு அறிதல் என்ற அதிகாரத்தின் மூலம் அதனை விளக்கியுள்ளார்.

“புத்தே ளுலகத்தும் ஈண்டும் பெறலரிதே
ஒப்புரவின் நல்ல பிற”

என்ற குறளின் பொருள் ஒற்றுமையைப் போல் வேறொன்றைத் தேவருலகம் சென்றாலும் 6 பெற இயலாது என்பதாகும்.

இயற்கை காட்டும் ஒற்றுமை :
பல மரங்களும் செடிகளும் இணைந்தால்தான் இயற்கை உயிர்பெறுகிறது. மரங்களின் ஒற்றுமையால் சுற்றுச்சூழல் தூய்மை பெறும். கொஞ்சம் கொஞ்சமாக வரும் மழையினால் நீர்நிலை நிரம்புகிறது. பல மரங்களின் வேர்களின் ஒற்றுமை மண் அரிப்பைத் தடுத்து நிறுத்துகின்றது.

முடிவுரை :
கூடி வாழ்ந்தால் கோடி நன்மை – பலர் ஒன்று கூடி வாழ்ந்தால் நிறைய நன்மைகள் உண்டு. மகாகவி பாரதியார் வந்தே மாதரம்’ என்ற தம் கவிதையில், ஒன்று பட்டால் உண்டு வாழ்வே – நம்மில் ஒற்றுமை நீங்கிடில் அனைவர்க்கும் தாழ்வே’ என்ற பாடல் வரிகளுக்கு ஏற்றார்போல் ஒற்றுமையுடன் நாம் வாழ்ந்தால்தான் நம் நாடும் நாமும் முன்னேறலாம்.

மொழியோடு விளையாடு

கீழ்க்காணும் படங்கள் சார்ந்த சொற்களை எழுதுக.


Answer:

கீழ்க்காணும் சொற்களைப் பெயர்ச்சொல்லாகவும் வினைச்சொல்லாகவும் பயன்படுத்தித் தொடர்கள் உருவாக்குக. (விதை, கட்டு, படி, நிலவு, நாடு, ஆடு)


Answer:

நிற்க அதற்குத் தக

என் பொறுப்புகள்

1. எந்தச் சூழ்நிலையிலும் இனிய சொற்களையே பேசுவேன்.
2. அனைவரிடமும் மரியாதையுடன் நடந்து கொள்வேன்.
3. என் வாழ்வில் எளிமையைக் கடைப்பிடிப்பேன்.
4. திருக்குறள் கூறும் ஒப்புரவு நெறியைப் பின்பற்றி நடப்பேன்.

கலைச்சொல் அறிவோம்

இணையத்தில் காண்க

அறக்கருத்துகளைக் கூறும் நூல்களின் பெயர்களை இணையத்தில் தேடித் தொகுக்க.
அறக்கருத்துகளைக் கூறும் நூல்களின் பெயர்கள் :

Further Read:

HDFCLIFE Pivot Point Calculator

Students can Download Tamil Nadu 11th Chemistry Model Question Paper 1 English Medium Pdf, Tamil Nadu 11th Chemistry Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Chemistry Model Question Paper 3 English Medium

Time: 2½ Hours
Total Score: 90 Marks

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I. II, III and IV are to be attempted separately.
4. Question numbers 1 to 15 in Part I are Multiple Choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer.
5. Question numbers 16 to 24 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 25 to 33 in Part III are three-mark questions. These are to be answered in about three to five short sentences.
7. Question numbers 34 to 38 in Part IV are five-mark questions. These are to be answered in detail. Draw diagrams wherever necessary.

PART -1

Answer all the Questions.
Choose the most suitable answer from the given four alternatives.

Question 1.
The equivalent mass of a trivalent metal element is 9 g eq^-1 the molar mass of its anhydrous oxide is ………………………… .
(a) 102 g
(b) 27 g
(c) 270 g
(d) 78 g
Answer:
(a) 102 g

Let the trivalent metal be M³⁺
Equivalent mass = mass of the metal / valance factor
9 g eq-1 = mass of the metal/3 eq
Mass of the metal = 27g Oxide formed M₂O₃;
Mass of the oxide = (2 x 27) + (3 x 16) = 102g

Question 2.
Based on equation E = – 2,178 x 10^-18 J \(\left(\frac{z^{2}}{n^{2}}\right)\) certain conclusions are written.
Which of them is not correct? [NEET]
(а) Equation can be used to calculate the change in energy when the electron changes orbit
(b) For n = 1, the electron has a more negative energy than it does for n = 6 which means that the electron is more loosely bound in the smallest allowed orbit.
(c) The negative sign in equation simply means that the energy of electron bound to the nucleus is lower than it would be if the electrons Were at the infinite distance from the nucleus.
(d) Larger the value of n, the larger is the orbit radius.
Answer:
(b) For n = 1, the electron has a more negative energy than it does for n = 6 which means that the electron is more loosely bound in the smallest allowed orbit.

Correct statement: For n = 1, the electron has more negative energy than it does for n = 6 which means that the electron is strongly bound in the smallest allowed orbit.
Answer:

Question 3.
Match the following.
List-I – List-II
A. Jewels – 1. Sodium chloride
B. Bolts and cot – 2. Copper
C. Table salt – 3. Gold
D. Utensils – 4. Iron
Code: A B C D
(a) 3 4 1 2
(b) 4 1 3 2
(c) 1 4 2 3
(d) 2 3 4 1
Answer:
(a) 3 4 1 2

Question 4.
The reaction H₃PO₂ + D₂O → H₂DPO₂ + HDO indicates that hypo-phosphorus acid is …………… .
(a) tribasic acid
(b) dibasic acid
(c) mono basic acid
(d) none of these
Answer:
(c) mono basic acid

Hypophosphorous acid on reaction with D₂O, only one hydrogen is replaced by deuterium and hence it is mono basic.

Question 5.
RbO₂ is …………….. .

(a) superoxide and paramagnetic
(b) peroxide and diamagnetic
(c) superoxide and diamagnetic
(d) peroxide and paramagnetic
Answer:
(a) superoxide and paramagnetic

Question 6.
At identical temperature and pressure, the rate of diffusion of hydrogen gas is 3 \(\sqrt{3}\) times that of a hydrocarbon having molecular formula C_n H_2n-2. What is the value of n?
(a) 8
(b) 4
(c) n3
(d) 1
Answer:
(b) 4

Squaring on both sides and rearranging
27 x 2 = m_CnH2n-2
54 = n(12) + (2n-2) (1)
54 = 12n + 2n – 2 = 14n – 2
n = (54 + 2)/14 = 56/14 = 4

Question 7.
Statement-I: All living things are open systems.
Statement-II: Because they continuously exchange matter and energy with the surroundings,
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I.
(b) Statement-I and II are correct but Statement-II is not the correct explanation of Statement-I.
(c) Statement-I is correct and Statement-II is wrong.
(d) Statement-I is wrong but Statement-II is correct.
Answer:
(a) Statement-I and II are correct and Statement-II is the correct explanation of Statement-I.

Question 8.
The values of K_p1 and K_p2 for the reactions: \(\mathrm{X} \rightleftharpoons \mathrm{Y}+\mathrm{Z} \text { and } \mathrm{A} \rightleftharpoons 2 \mathrm{B}\) are in the ratio 9 : 1 if degree of dissociation and initial concentration of X and Abe equal then total pressure at equilibrium P₁ and P₂ are in the ratio ………………………… .
(a) 36: 1
(b) 1: 1
(c) 3: 1
(d) 1: 9
Answer:
(a) 36: 1

Question 9.
Which of the following is not an non-ideal solution showing negative deviation?
(a) Phenol and aniline
(b) Ethanol and water
(c) Acetone + Chloroform
(d) n-Heptane and n-Hexane
Answer:
(d) n-Heptane and n-Hexane

Question 10.
In C1F₃, NF₃ and BF₃ molecules the chlorine, nitrogen and boron atoms are …………………. .
(a) sp³ hybridised
(b) sp³, sp³ and sp² respectively
(c) sp2 hybridised
(d) sp³d, sp³ and sp² hybridised respectively
Answer:
(d) sp³d, sp³ and sp² hybridised respectively

Solution: C1F₃ – sp³d hybridisation ; NF₃ – sp³ hybridisation ; BF₃ – sp² hybridisation

Question 11.
The number of stereoisomers of 1, 2-dihydroxy cyclopentane is
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(c) 3

Question 12.
Consider the following statement.
(i) Covalent bonds .are break into two different ways.
(ii) They are Homolytic and Heterolytic cleavage.
(iii) During the fission of a covalent bond, organic compounds form a new organic molecules. Which of the above statement is/are not correct?
(a) (i) only
(b) (i) and (ii)
(c) (iii) only
(d) (ii) and (iii)
Answer:
(c) (iii) only

Question 13.
Major product of the below mentioned reaction is ………………….. .
\(\left(\mathrm{CH}_{3}\right)_{2} \mathrm{C}=\mathrm{CH}_{2} \stackrel{\mathrm{ICl}}{\longrightarrow}\)
(a) 2-chloro -1- iodo – 2 – methylpropane
(b) l-chloro-2-iodo-2-methylpropane
(c) 1,2 – dichloro – 2 – methylpropane
(d) 1,2- diiodo – 2 – methylpropane
Answer:
(a) 2-chloro -1- iodo – 2 – methylpropane

Question 14.
The formula of Chloropicrin is
(a) CHC1₃
(b) CCl₃CHO
(C) CH₂C1₂
(d) CC1₃NO₂
Answer:
(d) CC1₃NO₂

Question 15.
Which of the following is carcinogenic and causes irritation in eyes and mucous membranes?
(a) PAH
(b) THF
(c) CO
(d) PAN
Answer:
(a) PAH

Part-II

Answer any six questions in which question No. 17 is compulsory. [6 x 2 = 12]

Question 16.
Which is considered as to be Earth’s protective umbrella? Why?
Answer:

1. At high altitudes in the atmosphere consists of a layer of ozone (O₃) which acts as an umbrella for harmful UV radiations. Ozone is considered to be earth’s protective umbrella.
2. It protects us from harmful effects of UV-radiations of the sun such as skin cancer.
3. Ozone layer prevent the UV radiations to reach the earth surface. So it acts as an umbrella for the Earth.

Question 17.
Complete the following:
\(\text { (i) } 2 \text { – butyne } \frac{\mathrm{Pd}-\mathrm{CaCO}_{3}}{\rightarrow} \text { ? (ii) } \mathrm{CaC}_{2} \stackrel{\mathrm{H}_{2} \mathrm{O}}{\longrightarrow} ?\)
Answer:

Question 18.
How will you test sulfur present in organic compounds?
Answer:
To a portion of the Lassaigne’s extract, freshly prepared sodium nitroprusside solution is added. If deep violet or purple colour is formed, the presence of sulfur is confirmed.

Question 19.
Which one of the following has highest bond order? []\mathbf{N}_{2}, \mathbf{N}_{2}^{+} \text {or } \mathbf{N}_{2}^{-}[/latex]
Answer:

So N₂ has the highest bond order.

Question 20.
Define the term isotonic solution.
Answer:

1. Two solutions having same osmotic pressure at a given temperature are called isotonic solutions.
2. When such solutions are separated by a semipermeable membrane, solvent flow between one to the other on either direction is same, i.e., the net solvent flow between two isotonic solutions is zero.

Question 21.
A sample of gas has a volume of 8.5 dm³ at an unknown temperature. When the sample is submerged in ice water at 0°C, its volume gets reduced to 6.37 dm³. What is its initial temperature?
Answer:

Question 22.
Mention the uses of washing soda (or) sodium carbonate.
Answer:

1. Sodium carbonate is highly used in laundering.
2. It is an important laboratory reagent used in the qualitative analysis and in volumetric analysis.
3. It is also used in water treatment to convert the hard water to soft water.
4. It is used in the manufacture of glass, paper and paint.

Question 23.
What is water – gas shift reaction?
Answer:
The carbon monoxide of water gas can be converted to carbon dioxide by mixing the gas mixture with more steam at 400°C and passed over a shift converter containing iron/copper catalysts. This reaction is called water-gas shift reaction.
CO + H₂O → CO₂ + H₂↑

Question 24.
What are Ψ and Ψ²?
Answer:

1. Ψ itself has no physical meaning but it represents an atomic orbital.
2. Ψ² is related to the probability of finding the electrons within a given volume of space.

Part-III

Answer any six questions in which question No. 29 is compulsory. [16 x 3 = 18]

Question 25.
Distinguish between oxidation and reduction.
Answer:

Question 26.
Why there is a need for classification of elements?
Answer:

1. Classification is a fundamental and essential process in our day-to-day life for the effective utilization of resources, daily events and materials.
2. In such a way, for the effective utilization of discovered elements becomes fundamentally essential process.
3. The periodic classification of the elements is one of the outstanding contributions to the progress of chemistry.

Question 27.
Write the balanced equation for following reaction.
(i) Li metal with N₂ gas
(ii) Heating solid sodium bicarbonate
(iii) Solid potassium hydroxide with CO₂
Answer:

Question 28.
Discuss briefly the similarities between Be and Al.
Answer:

• Beryllium and aluminium have same electronegativity values.
• Their changes per unit area is closer.
• BeCl₂ and AlCl₃ forms dimeric structure. Both are soluble in organic solvents and are strong Lewis acids.
• Be(OH)₂ and Al(OH)₃ dissolves in excess alkali to give beryllate ion [Be(OH)₄]^3- and aluminate
• Be and A1 ions have strong tendency to form complexes, e.g. \(\mathrm{BeF}_{4}^{2}\) and \(\mathrm{AlF}_{6}^{3-}\).
• Both Be(OH)₂ and Al(OH)₃ are amphoteric in nature.
• Carbide of Be – beryllium carbide (Be₂C) and A1 – aluminium carbide (Al₄C₃) give methane on hydrolysis.
• Both beryllium and aluminium are rendered passive by nitric acid.

Question 29.
A tank contains a mixture of 52.5 g of oxygen and 65.1 g of CO₂ at 300 K the total pressure in the tank is 9.21 atm. Calculate the partial pressure (in atm) of each gas in the mixture?
Answer:

Question 30.
Why He₂ molecule does not exist?
Answer:
Diatomic Helium molecule, He₂ (Hypothetical). The electron configuration of Helium (Z = 2) in the ground state is Is². As each Helium atom contains two electrons, there will be 4 electrons in He₂ molecule. Keeping in view the Aufbau principle and Pauli’s exclusion principle its electron configuration would be as follows.
He₂ : (σ_ls)² (σ_ls)².
The molecular orbital energy level diagram of He₂:

Here, N_b = 2 and N_a = 2
Bond order = \(\frac{N_{b}-N_{a}}{2}=\frac{2-2}{2}=0\)
As the bond order for He₂ comes out to be zero, this molecule does not exist.

Question 31.
Write all the possible isomers of molecular formula C₄H₁₀O and identify the isomerisms found in them.
Answer:

Question 32.
Explain how oxygen deficiency is caused by carbon monoxide in our blood? Give its effect.
Answer:

1. Carbon monoxide binds with haemoglobin and form carboxy the haemoglobin which impairs normal oxygen transport by blood and hence the oxygen carrying capacity of blood is reduced.
2. This oxygen deficiency results in headache, dizziness, tension, loss of consciousness, blurring of eyesight and cardiac arrest.

Question 33.
Complete the reaction:

Answer:

Part – IV

Answer all the questions. [5 x 5 = 25]

Question 34.
(a) (i) How many orbitals are possible for n = 4? (2)
(ii) What are the limitations of Bohr’s model of an atom? (3)

[OR]

(b) (i) LiClO₄ is more soluble than NaClO₄. Why? (2)
(ii) Explain – IE₁ of alkaline earth metals are higher than that of alkali metals. (3)
Answer:
(a) (i) If n = 4, the possible number of orbitals are calculated as follows.
n = 4 – main shell = N
If n = 4 – l values are 0, 1, 2, 3
If l = 0 – 4s orbital = 1 orbital
If l = 1 – m = -l, 0, + 1 = 3 orbitals
If l = 2 – m = -2, -1, 0, + 1, + 2 = 5 orbitals
If l = 3 – m = -3, -2, -1, 0, +1, +2 , +3 = 7 orbit
∴ Total number of orbitals =16 orbitals

(ii) Limitations of Bohr’s atom model:
1. The Bohr’s atom model is applicable only to species having one electron such as hydrogen, Li²⁺ etc and not applicable to multi-electron atoms.
2. It was unable to explain the splitting of spectral lines in the presence of magnetic field (Zeeman effect) or an electric field (Stark effect).
3. Bohr’s theory was unable to explain why the electron is restricted to revolve around the nucleus in a fixed orbit in which the angular momentum of the electron is equal to nh/2π.

[OR]

(b) (i) The small size of the Li+ ion means that it has a very high enthalpy of hydration and so lithium salts are much more soluble than the salts of other group 1. E.g. LiClO₄ is upto 12 times more soluble than NaCIO₄.

(ii)

• IE₁ of alkaline earth metals > IE₁ of alkali metals.
• IE₂ of alkaline earth metals < IE₂ of alkali metals.
• This occurs because in alkali metals the second electron is to be removed from a cation, which has already acquired a noble gas configuration.
• In the case of alkaline earth metals, the second electron is to be removed from a monovalent cation, which still has one electron in the outermost shell.
• Thus, the second electron can be removed more easily in the case of group 2 elements than in group 1 elements.

Question 35.
(a)-(i) Can a Vanderwaal’s gas with a = 0 be liquefied? Explain. (2)
(ii) Deep sea divers ascend slowly and breath continuously by time they reach the surface. Give reason. (3)

[OR]

(b) (i) What are spontaneous reactions? (2)
(ii) Prove that for an ideal gas, C_p is greater than C_v (3)
Answer:
(a) (i)

1. a = 0 for a Van der Waals gas i. e. for a real gas. Van der Waals constant a = 0. It cannot be liquefied.
2. If a = 0, there is a very less interaction between the molecules of gas.
3. ‘a’ is the measure of strength of Van der Waals force of attraction between the molecules of the gas. ,
4. If a is equal to zero, the Van der Waals force of attraction is very less and the gas cannot be liquefied.

(ii)

1. For every 10 m of depth, a diver experiences an additional 1 atm of pressure due to the weight of water surrounding him.
2. At 20 m, the diver experiences a total pressure of 3 atm. So the most important rule in diving is never hold breath.
3. Divers must ascend slowly and breath continuously allowing the regulator to bring the air pressure in their lungs to 1 atm by the time they reach the surface.

[OR]

(b) (i) A reaction that does occur under the given set of conditions is called a spontaneous reaction. The expansion of a gas into a evacuated bulb is a spontaneous process, the reverse process that is gathering of all molecules into one bulb is not spontaneous. This example shows that processes that occur spontaneously in one direction cannot take place in opposite direction spontaneously.

Increase in randomness favours a spontaneous change. If enthalpy change of a process is negative, then the process is exothermic and occurs spontaneously. Therefore ΔH should be negative. If entropy change of a process is positive, then the process occurs spontaneously, therefore ΔS should be positive. If free energy of a process is negative, then the process occurs spontaneously, therefore AG should be negative.

For a spontaneous, irreversible process, ΔH < 0, ΔS > 0. ΔG < 0. i. e., ΔH = -ve, ΔS = +ve and ΔG = -ve.

(ii)

• It is clear that two heat capacities are not equal and C_p is greater than C_v by a factor which is related to the work done.
• At a constant pressure, a part of heat absorbed by the system is used up in increasing the internal energy of the system and the other for doing work by the system.
• At constant volume, the whole of heat absorbed is utilized in increasing the temperature of the system as there is no work done by the system.
  Thus C_p is greater than C_v.
• By definition, H= U+ PV for I mole of an ideal gas.
  H = U + RT

By differentiating this equation with respect to temperature T, we get, \(\frac{d H}{d T}=\frac{d U}{d T}+R\)
C_p = C_v + R; C_p – C_v = R

Thus for an ideal gas, C_p is greater than C_v by the gas constant R.

Question 36.
(a) (i) State law of mass action. (2)
(ii) Deduce the Vant IÌoff equation. (3)

[OR]

(b) (i) What is a π – bond? (2)
(ii) Discuss the formation of N₂ molecule using MO theory. (3)
Answer:
(a) (i) The law states that “At any instant, the rate of chemical reaction at a given temperature is directly proportional to the product of the active masses of the reactants at that instant.”
(ii) Vant hoff equation: This equation gives the quantitative temperature dependance of equilibrium constant K.

The relation between standard free energy change G° and equilibrium constant is
ΔG° = -RTlnK ……………………………… (1)
We know that, ΔG° = ΔH° — TΔS° ……………………………… (2)
Substituting (1) in equation (2)
– RTlnK = ΔH° – TΔS°
Rearranging, InK = \(\frac{-\Delta \mathrm{H}^{\circ}}{\mathrm{RT}}+\frac{\Delta \mathrm{S}^{\circ}}{\mathrm{R}}\) ……………………………… (3)
Differentiating equation (3) with respect to temperature
\(\frac{d(\ln \mathrm{K})}{d \mathrm{T}}=\frac{\Delta \mathrm{H}^{\circ}}{\mathrm{RT}^{2}}\) ……………………………… (4)

Equation (4) is known as differential form of van’t Hoff equation. On integrating the equation 4, between T₁ and T₂ with their respective equilibrium constants K₁ and K₂,

Equation (5) is knowi as integrated fónn of van’t Hoff equation.

(b) (i) Pi-bond: When two atomic orbitals overlap sideways, the resultant covalent bond is called a pi (π) bond.
(ii) Formation of N, molecule using MO theory:

1. Electronic configuration of N atom ls² 2s² 2p³.
2. Electronic configuration of N2 molecule is: \(\sigma 1 s^{2} \sigma^{*} 1 s^{2} \sigma 2 s^{2} \sigma^{*} 2 s^{2} \pi 2 p_{y}^{2} \pi 2 p_{z}^{2} \sigma 2 p_{x}^{2}\)
3. Bond order = \(\frac{N_{b}-N_{a}}{2} \frac{10-4}{2}=3\)
4. Molecule has no unpaired electrons hence, it is diamagnetic’.

Question 37.
(a) (i) Explain – Column chromatography. (3)
(ii) Give the structure for the following compound. (2)
(a) Tertiary butyl iodide
(b) 3 – Chlorobutanol

[OR]

(b)
(i) Explain – electromeric effect. (3)
(ii) Give the examples for β – elimination. (2)
Answer:
(a) (i) Column chromatography:

1. The principle behind chromatography is selective distribution of mixture of organic substances between two phases a stationary phase and a moving phase. The stationary phase can be a solid or liquid, while the moving phase is a liquid or a gas. When the stationary phase.is a solid, the moving phase is a liquid or gas.
2. If the stationary phase is solid, the basis is adsorption, and when it is a liquid, the basis is partition.
3. Chromatography is defined as a technique for the separation of a mixture brought about by differential movement of the individual component through porous medium under the influence of moving solvent.
4. In column chromatography, the above principle is carried out in a long glass, column.

(ii) (a) Tertiary butyl iodide =

(b) 3 – Chlorobutanol =

[OR]

(b) (i) Electromeric effect.
1. The electromeric effect refers to the polarity produced in a multiple bonded compound when it is attacked by a reagent when a double or a triple bond is exposed to an attack by an electrophile the two n electrons which from the n bond are completely transferred to one atom or the other.

2. When a nucleophile approaches the carbonyl compound, the π -electrons between C and O is instantaneously shifted to the more electronegative oxygen. This make the carbon electron deficient and thus facilitating the formation of a new bond between the incoming nucleophile and the carbonyl carbon atom.

3. When an electrophile such as H+ approaches an alkene molecule the n electrons are instantaneously shifted to the electrophile and a new bond is formed between carbon and hydrogen. This makes the other carbon electron deficient and hence it acquires a positive charge.

4. This effect denotes as E-effect.
(ii) β-elimination: Elimination reactions involve the cleavage of a π bond and formation of a n bond. A nucleophilic pair of electrons heads into a new n bond as a leaving group departs. This process is called β-elimination because the bond P to the nucleophilic pair of electrons breaks.

Example:
1. n-propyl bromide on reaction with alcoholic KOH give propene. In this reaction hydrogen and Br are eliminated.

2. Acid-catalysed dehydration of alcohols

Question 38.
(a) An organic compound A of a molecular formula C₃H₆, reacts with HBr to give B which is the major product for this reaction. A again reacts with HBr in presence of benzoyl peroxide to give C. Identify A, B and C. Explain the reactions. (5)

[OR]

(b) (i) Explain -The Bhopal Tragedy. (3)
(ii) What are the particulate that cause the pollutions in troposphere? (2)
Answer:

[OR]

(b) (i) On 3rd Decembers, 1984 at Bhopal city in India, by the early morning, an explosion at Union Carbide pesticide plant released a cloud of toxic gas (Methyl isocyanate) CH₃NCO into the air. Since the gas is twice as heavy as air, it did not drift away but formed a blanket over the surrounding area. It attacked people’s lungs and affect their breathing staying there or in the nearby areas. Thousands of people died and lives of many were ruined. The lungs, brain, eyes, muscles, as well as the gastrointestinal, neurological and immune systems of those people who survived, were severely affected.

(ii)
1. Viable particulates : The viable particulates are the same size, living organisms such as bacteria, fungi, moles, algae, etc. which are dispersed in air. Some of the fungi cause allergy in human beings and disease in plants.
2. Non-Viable particulates : The Non-viable particulates are small particles and liquid droplets suspended in air. They help in the transporting of particulates in the atmosphere.

They are classified according to

• smoke
• dust
• mists
• fumes.

Expert Teachers at SamacheerKalvi.Guru has created Samacheer Kalvi Tamil Nadu State Board Syllabus New Paper Pattern 12th English Model Question Papers 2020-2021 with Answers Pdf Free Download of TN 12th Standard English Public Exam Question Papers Answer Key, New Paper Pattern of HSC 12th Class English Previous Year Question Papers, Plus Two +2 English Model Sample Papers are part of Tamil Nadu 12th Model Question Papers.

Here we have given the Government of Tamil Nadu State Board 12th English Model Question Papers with Answers 2020-21 Pdf. Students can view or download the Class 12th English New Model Question Papers 2021 Tamil Nadu for their upcoming Tamil Nadu HSC Board Exams. Students can also read Tamilnadu Samacheer Kalvi 12th English Guide.

TN State Board 12th English Model Question Papers 2020 2021

12th English Model Question Papers 2020-2021 Tamil Nadu 

• Tamil Nadu 12th English Model Question Paper 1
• Tamil Nadu 12th English Model Question Paper 2
• Tamil Nadu 12th English Model Question Paper 3
• Tamil Nadu 12th English Model Question Paper 4
• Tamil Nadu 12th English Model Question Paper 5 (Board Model Paper)

12th English Model Question Paper Design 2020-2021 Tamil Nadu

It is necessary that students will understand the new pattern and style of TN 12th Standard English Model Question Papers 2021 Tamilnadu State Board Syllabus according to the latest exam pattern. These Tamil Nadu Plus Two 12th English Model Question Papers are useful to understand the pattern of questions asked in the board exam. Know about the important concepts to be prepared for TN HSLC Board Exams and Score More marks.

We hope the given Samacheer Kalvi Tamil Nadu State Board Syllabus New Paper Pattern Class 12th English Model Question Papers 2020 2021 with Answers Pdf Free Download will help you.

If you have any queries regarding the Government of Tamil Nadu State Board 12th English Model Question Papers with Answers 2020 21, TN 12th Std English Public Exam Question Papers with Answer Key, New Paper Pattern of HSC Class 12th English Previous Year Question Papers, Plus Two +2 English Model Sample Papers, drop a comment below and we will get back to you at the earliest.

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.2

Question 1.
If k is real, discuss the nature of the roots of the polynomial equation 2x² + kx + k = 0, in terms of k.
Solution:
The given quadratic equation is 2x² + kx + k = 0
a = 2, b = k, c = k
∆ = b² – 4ac = k² – 4(2) k = k² – 8k
(i) If the roots are equal
k² – 8k = 0
⇒ k(k – 8) = 0
⇒ k = 0, k = 8
(ii) If the roots are real
k² – 8k > 0
k(k – 8) > 0
k ∈ (-∞, 0) ∪ (8, ∞)
(iii) If this roots are imaginary
k² – 8k < 0
⇒ k ∈ (0, 8)

Question 2.
Find a polynomial equation of minimum degree with rational coefficients, having 2 + √3 i as a root.
Solution:
Given roots is (2 + √3 i)
The other root is (2 – √3 i), since the imaginary roots with real co-efficient occur as conjugate pairs.
x² – x(S.O.R) + P.O.R = 0
⇒ x² – x(4) + (4 + 3) = 0
⇒ x² – 4x + 7 = 0

Question 3.
Find a polynomial equation of minimum degree with rational coefficients, having 2i + 3 as a root.
Solution:
Given roots is (3 + 2i), the other root is (3 – 2i);
Since imaginary roots occur in with real co-efficient occurring conjugate pairs.
x² – x(S.O.R) + P.O.R = 0
⇒ x² – x(6) + (9 + 4) = 0
⇒ x² – 6x + 13 = 0

Question 4.
Find a polynomial equation of minimum degree with rational coefficients, having √5 – √3 as a root.
Solution:
The given one roots of the polynomial equation are (√5 – √3)
The other roots are (√5 + √3), (-√5 + √3) and (-√5 – √3).
The quadratic factor with roots (√5 – √3) and (√5 + √3) is
= x² – x(S.O.R) + P.O.R
= x² – x(2√5) + (√5 – √3) (√5 + √3)
= x² – 2√5 x + 2
The other quadratic factors with roots (-√5 + √3) (-√5 – √3) is
= x² – x (S.O.R) + P.O.R
= x² – x (-2√5 ) + (5 – 3)
= x² + 2√5x + 2
To rationalize the co-efficients with minimum degree
(x² – 2√5 x + 2) (x² + 2√5 x + 2) = 0
⇒ (x² + 2)² – (2√5 x)² = 0
⇒ x⁴ + 4 + 4x² – 20x² = 0
⇒ x⁴ – 16x² + 4 = 0

Question 5.
Prove that a straight line and parabola cannot intersect at more than two points.
Solution:
Let the standard equation of parabola y² = 4ax …..(1)
Equation of line be y = mx + c …(2)
Solving (1) & (2)
(mx + c)² = 4ax
⇒ mx² + 2mcx + c² – 4ax = 0
⇒ mx² + 2x(mc – 2a) + c² = 0
This equation can not have more than two solutions and hence a line and parabola cannot intersect at more than two points.

Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.2 Additional Problems

Question 1.
Find a polynomial equation of minimum degree with rational co-efficients having 1 – i as a root.
Solution:
Given root is 1 – i
The other root is 1 + i
Sum of the roots: 1 – i + 1 + i = 2
product of the roots: (1 – i) (1 + i) = (1)² + (1)² ⇒ 1 + 1 = 2
∴ The required polynomial equation of minimum degree with rational coefficients is
x² – x (S.R.) + (P.R.) = 0
x² – 2x + 2 = 0

Question 2.
Find a polynomial equation of minimum degree with rational co-efficients having \(\sqrt{3}+\sqrt{7}\) as a root.
Solution:

The required polynomial equation of minimum degree

Question 3.
If the roots of the equation x³ + px² + qx + r = 0 are in A.P then show that 2p³ – 9pq + 27 r = 0.
Solution:
Let the roots of the given equation is a – d, a, a + d

Question 4.
Solve 27x³ + 42x² – 28x -8 = 0 given that its roots are in geometric progressive.
Solution:

Question 5.
Solve the equation 15x³ – 23x² + 9x – 1 = 0. Where roots are in H.P.
Solution:

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 3 Perimeter and Area Additional Questions

Question 1.
The length of a rectangular field is twice its breadth. Ramu runs around it four times and covered a distance of 6 km. What is the length of the field.
Solution:
Breadth of rectangular field = b m
Length of the field = 2b m
Distance covered in one round = perimeter
Distance covered in 4 rounds = 4 × perimeter

Length of the field = 2 × 250 = 500 m

Question 2.
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are 70 cm and 36 cm?
Solution:
Given length of the rectangular region = 70 cm

Question 3.
A room is 4m long and 3m 50cm wide, How many square metres of carpet is needed to cover the floor of the room?
Solution:
Given length of the room = 4 m
Breadth = 3 m 50 cm = 3 m + 50 cm

Carpet needed = Area of the floor = length × breadth
= 4 × 3.5 m = 14 sq. m

Question 4.
Find the area of the square Whose side is 14 cm.
Solution:
Side of the square = 14 cm
Area of the square = side × side = (14 × 14) cm² = 196 sq cm.

Question 5.
Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side.
Solution:
Given two sides of a triangle = 12 cm and 14 cm
∴ Perimeter = 36 cm
12 cm + 14 cm + third side = 36 cm
Third side = 36 – 26 = 10 cm
∴ Length of the third side

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 8 Statistics Ex 8.3

Question 1.
The monthly salary of 10 employees in a factory are given below : ₹ 5000, ₹ 7000, ₹ 5000, ₹ 7000, ₹ 8000, ₹ 7000, 17000, ₹ 8000, ₹ 7000, ₹ 5000 Find the mean, median and mode.
Solution:
The monthly salary of 10 employees are ₹ 5000, ₹ 7000, ₹ 5000, ₹ 7000, ₹ 8000, ₹ 7000, ₹ 7000, ₹ 8000, ₹ 7000, ₹ 5000.
Writing in ascending order ₹ 5000, ₹ 5000, ₹ 5000, ₹ 7000, ₹ 7000, ₹ 7000, ₹ 8000, ₹ 8000
Number of values =10 which is an even number.

In this given data ₹ 7000 occurs maximum number of 5 times
∴ Mode = ₹ 7000/-
∴ Mean = ₹ 6600/-
Mode = ₹ 7000/-

Question 2.
Find the mode of the given data : 3.1, 3.2, 3.3, 2.1,1.3, 3.3, 3.1
Solution:
3.1, 3.2, 3.3, 2.1, 1.3, 3.3, 3.1
In this given data 3.1, 3.3 occurs twice
₹ Mode = 3.1 and 3.3 (bimodal)

Question 3.
For the data 11, 15, 17, x + 1, 19, x – 2, 3 if the mean is 14 , find the value of x. Also find the mode of the data.
Solution:
The data given is 11, 15, 17, x + 1, 19, x – 2, 3

The data 11, 15, 17, 17 + 1, 19, 17 – 2, 3 = 11, 15, 17, 18, 19, 15, 3
In this given data 15 occurs twice. Hence the mode is 15.

Question 4.
The demand of track suit of different sizes as obtained by a survey is given below:

Which size is in greater demand ?
Solution:

∴ Size 40 has maximum frequency 37.
∴ 40 is the mode.

Question 5.
Find the mode of the following data:

Solution:

Question 6.
Find the mode of the following distribution:

Solution:

Tamilnadu State Board New Syllabus Samacheer Kalvi 5th Maths Guide Pdf Term 3 Chapter 6 பின்னங்கள் InText Questions Textbook Questions and Answers, Notes.

TN Board 5th Maths Solutions Term 3 Chapter 6 பின்னங்கள் InText Questions

பக்க. எண்: 47

முயற்சி செய்

i. அடிக்கப்பட்ட சதுரத்தை பின்னமாகக் குறிப்பிடுக.

விடை:
\(\frac{2}{5}\)

ii. வட்டத்திற்கு வெளியே இருக்கும் வடிவங்களை பின்னமாக குறிப்பிடுக.

விடை:
\(\frac{2}{5}\)

பக்க. எண்: 48

முயற்சி செய்

i. \(\frac{3}{7}\) இல் __________ என்பது தொகுதி __________ என்பது பகுதி,
விடை:
\(\frac{3}{7}\) இல்   3   என்பது தொகுதி   7   என்பது பகுதி,

ii. \(\frac{6}{10}\) இல் தொகுதி __________ மற்றும் பகுதி __________ ஆகும்.
விடை:
\(\frac{6}{10}\) இல் தொகுதி    6   மற்றும் பகுதி   10    ஆகும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 5th Maths Guide Pdf Term 3 Chapter 2 எண்கள் InText Questions Textbook Questions and Answers, Notes.

TN Board 5th Maths Solutions Term 3 Chapter 2 எண்கள் InText Questions

பக்க. எண்: 11

சூழ்நிலை 1:

கேள்வி 1.
இரண்டு திராட்சைக் கொத்துகள் உள்ளன. A மற்றும் B என்ற இரண்டு திராட்சைக் கொத்துகளிலும் உள்ள திராட்சைகளின் எண்ணிக்கையை உத்தேசமாகக் காண்க.

கொத்து A இல் உள்ள திராட்சைகளின் எண்ணிக்கை ___________
விடை :
110

கொத்து B இல் உள்ள திராட்சைகளின் எண்ணிக்கை ____________
விடை :
60

திராட்சைகளின் எண்ணிக்கையைச் சரியாக எண்ணி எழுதுக கொத்து Aஇல் உள்ள திராட்சைகளின் சரியான எண்ணிக்கை ________
விடை :
118

கொத்து B இல் உள்ள திராட்சைகளின் சரியான எண்ணிக்கை __________
விடை :
64

பக்க. எண்: 12

செயல்பாடு 1:

கேள்வி 1.
கட்டங்களைப் பூர்த்தி செய்து மகிழ்க (தனித்தனியாக)

விடை :

பக்க. எண்: 16

கேள்வி 1.
இதனை முயல்க கொடுக்கப்பட்டுள்ள எண்களின் உத்தேச மதிப்புகளை எழுதி வகுத்த பிறகு, அவற்றின் உத்தேச மதிப்பிற்கும் உண்மையான மதிப்பிற்கும் இடையேயுள்ள வித்தியாசம் காண்க

விடை :

பக்க. எண்: 19

செயல்பாடு : 2

A. பின்வரும் குறிப்புகளைப் பயன்படுத்தி எண் வரிசைகளுக்கு வண்ணமிடுக.

கேள்வி 1.

1. பகா எண்கள் வரிசைக்கு ஆரஞ்சு நிறத்தில் வண்ணமிடுக.
2. ஒற்றை எண்கள் வரிசைக்கு வண்ணம் தீட்டுக.
3. உயர்ந்த எண்கள் வரிசைக்கு ஆரஞ்சு நிற வண்ணமிடுக.
4. இரட்டை எண்கள் வரிசைக்கு வண்ணமிடுக.
5. நீல நிறத்தில் வண்ண மிடுக.
6. 8 இன் மடங்கள் வரிசைக்கு நீலநிற வண்ண மிடுக எண் சக்கரத்தை நிரப்புவோம்.

விடை :

B. எண் சக்கரத்தில் நிரப்புவோம்.

கேள்வி 1.

விடை :

C. கொடுக்கப்பட்ட நான்கு அடிப்படைச் செயல்களைப் பயன்படுத்தி எண் 20 கிடைக்குமாறு வட்டங்களை நிரப்புக.

கேள்வி 1.

விடை :

D. கோடிட்ட இடங்களை நிரப்புக.

கேள்வி 1.
5, 10, 15, ___ , 25.
விடை :
20

கேள்வி 2.
30, 24, ___ , 12, 6
விடை :
18

கேள்வி 3.
7, 9, 11, ___ , 15, ___, 17
விடை :
13, 15

கேள்வி 4.
1, 4, 9, ___ , 25
விடை :
16

கேள்வி 5.
1, 4, 7, ___ , 13, ___, 19
விடை :
11, 17

E. பின்வருவனற்றிற்கு விடையளி:

கேள்வி 1.
BOOK என்பது 43 எனில் PEN என்பது ____________
விடை :
16 + 5 + 14 = 35

கேள்வி 2.
SCHOOL என்பது 1938151512 எனில், CLASS என்பது ____________
விடை :
31211919

கேள்வி 3.
BAG என்பது 10 எனில், BOOK என்பது ____________
விடை :
2 + 15 + 15 + 11 = 43

கேள்வி 4.
LION என்பது 50 எனில், TIGER என்பது ____________
விடை :
20 + 9 + 7 + 5 + 18 = 59

கேள்வி 5.
HEN என்பது 8514 எனில், COCK என்பது ____________
விடை :
315311