Category: Class 8

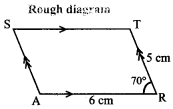
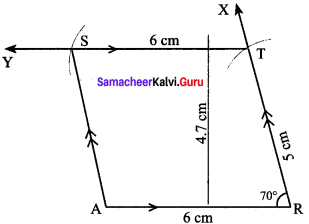
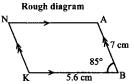
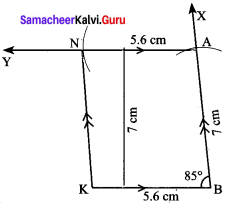
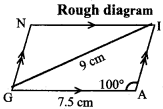
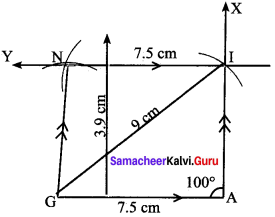
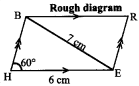
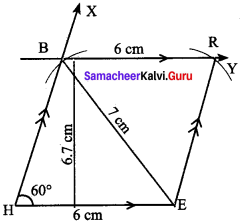
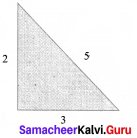
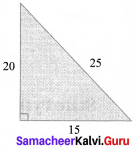
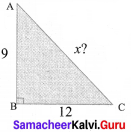
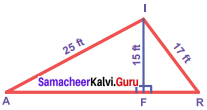
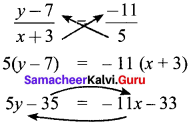
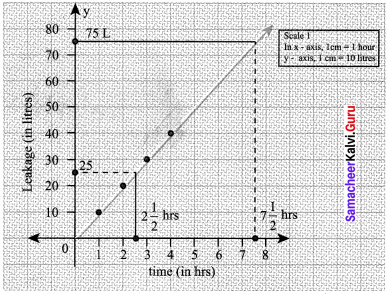
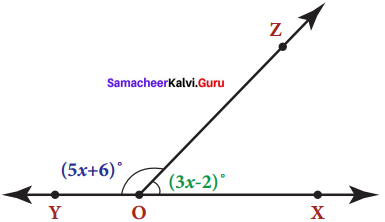
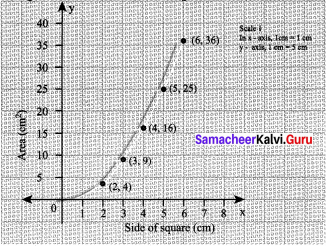
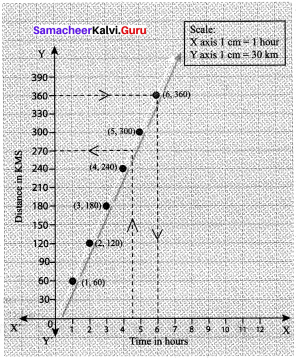
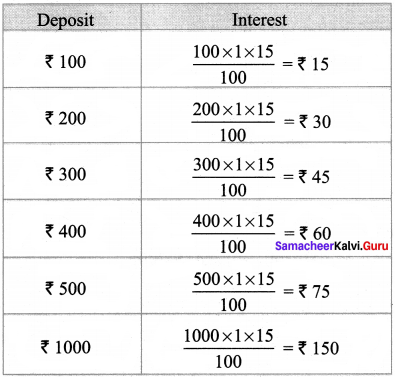
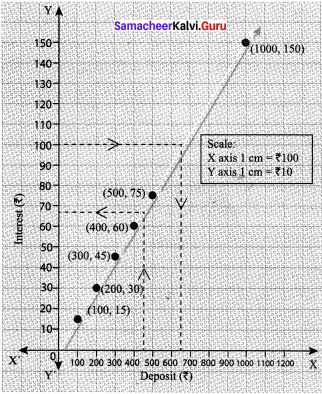
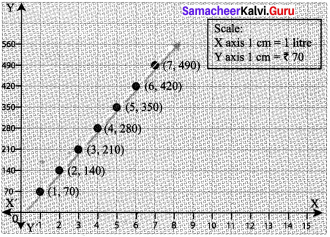
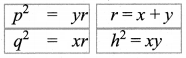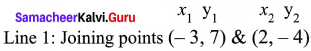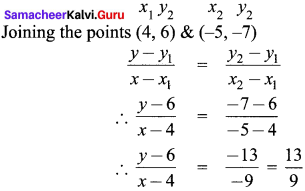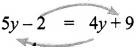Students can Download Maths Chapter 4 Information Processing Ex 4.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 4 Information Processing Ex 4.1

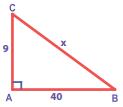
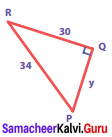
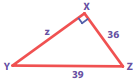
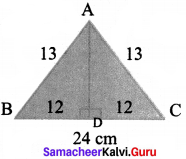
Question 1.
Choose the correct answer:

Question (i)
What is the eleventh Fibonacci number?
(a) 55
(b) 77
(c) 89
(d) 144
Answer:
(c) 89
Hint:

∴ 11th Fibonacci number is 89

Question (ii)
If F(n) is a Fibonacci number and n = 8, which of the following is true?
(a) F(8) = F(9) + F(10)
(b) F(8) = F(7) + F(6)
(c) F(8) = F(10) x F(9)
(d) F(8) = F(7) – F(6)
Answer:
(b) F(8) = F(7) + F(6)
Hint:
Given F(n) is a Fibonacci number & n = 8
F(8) = F(7) + F (6) as any term in Fibonacci series is the sum of preceding 2 terms

Question (iii)
Every 3^rd number of the Fibonacci sequence is a multiple of ………..
(a) 2
(b) 3
(c) 5
(d) 8
Answer:
(a) 2
Hint:
Every 3rd number in Fibonacci sequence is a multiple,of 2

Question (iv)
Every ……….. number of the Fibonacci sequence is a multiple of 8
(a) 2^nd
(b) 4^th
(c) 6^th
(d) 8^th
Answer:
(c) 6^th

Question (v)
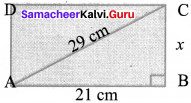
The difference between the 18th and 17th Fibonacci number is
(a) 233
(b) 377
(c) 610
(d) 987
Answer:
(d) 987
Hint:
F(18) = F(17) + F (16)
F(18) – F(17) = F(16) = F(15) + F(14) = 610-377 = 987

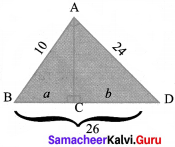
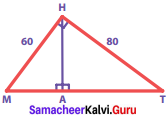
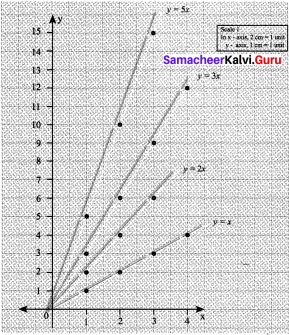
Question 2.
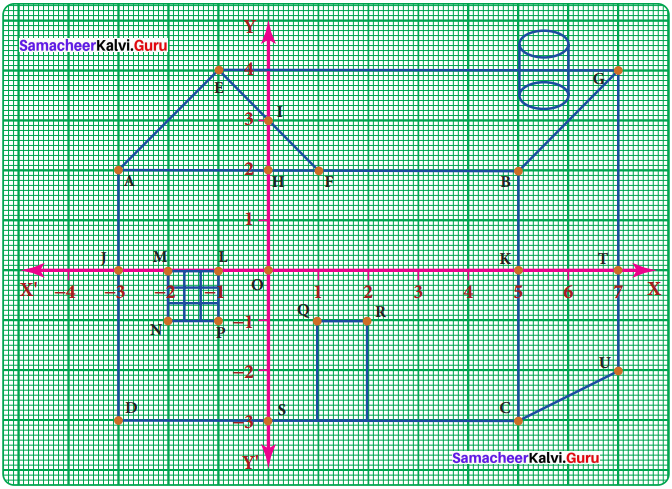
In the given graph sheet draw and colour how the Fibonacci number pattern makes a spiral in the Golden Rectangle.

Steps:
As per the instruction given, draw squares of side equal to each term of Fibonacci number – starting with 1 x 1 square, 2 x 2 square, 3 x 3 square and so on.
For spiral:
Starting from 1st square, join opposite diagonal points in a curve in all the squares to form a spiral.

Students can Download Maths Chapter 3 Geometry Ex 3.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Ex 3.4

Question I.
Construct the following parallelograms with the given measurements and find their area.

Question 1.
ARTS, AR = 6 cm, RT = 5 cm and ∠ART = 70°.
Solution:

Given:
In the Parallelogram ARTS,
AR = 6 cm
RT = 5 cm and ∠ART = 70°

Construction:
Steps:

1. Draw a line segment AR = 6 cm.
2. Make an angle ∠ART = 70° at R on AR
3. With R as centre, draw an arc of radius 5 cm cutting RX at T
4. Draw a line TY parallel to AR through T.
5. With T as centre, draw an arc of radius 6 cm cutting TY at S. Join AS
6. ARTS is the required parallelogram.

Calculation of area:
Area of the parallelogram ARTS = b x h sq. units
= 6 x 4.7 = 28.2 sq. cm

Question 2.
BANK, BA = 7 cm, BK = 5.6 cm and ∠KBA = 85°.
Solution:

Given:
In the parallelogram BANK, BA =7 cm, BK = 5.6 cm, and ∠KBA = 85°

Construction:
Steps:

1. Draw a line segment KB = 5.6 cm.
2. Make an angle ∠KBA = 85° at B
3. Draw an arc of radius 7 cm with B as centre on BX.
4. Draw a line AY parallel to KB.
5. With A as centre, draw an arc of radius 5.6 cm cutting AY at N. Join KN
6. BANK is the required parallelogram.

Calculation of area:
Area of the Parallelogram BANK = b x h sq. units
= 5.6 x 7 = 39.2 sq. cm

Question 3.
CAMP, CA = 6 cm, AP = 8 cm and CP = 5.5 cm.
Solution:

Given:
In the parallelogram CAMP,
CA = 6 cm
AP = 8 cm, and CP = 5.5cm

Construction:
Steps:

1. Draw a line segment CA = 6 cm.
2. With C as centre, draw an arc of length 5.5 cm
3. With A as centre, draw an arc of length 8 cm
4. Mark the intersecting point of these two arcs as P
5. Draw a line PX parallel to CA
6. With P as centre draw an arc of radius 6 cm cutting PX at M. Join AM
7. CAMP is the required parallelogram.

Calculation of area:
Area of the Parallelogram CAMP = b x h sq. units
= 6 x 5.5 = 33 sq. cm

Question 4.
DRUM, DR = 7 cm, RU = 5.5 cm and DU = 8 cm.
Solution:

Given:
In the parallelogram DRUM,
DR = 7 cm,
RU = 5.5 cm, and DU = 8 cm

Construction:
Steps:

1. Draw a line segment DR = 7 cm.
2. With D and R as centres, draw arcs of radii 8 cm and 5.5 cm.
3. Mark the intersecting point of these arcs as U. Join DU and RU
4. Draw a line UX parallel to DR through U.
5. With U as centre draw an arc of radius 7 cm cutting UX at M. Join DM
6. DRUM is the required parallelogram.

Calculation of area:
Area of the Parallelogram DRUM = b x h sq. units
= 7 x 5.4 = 37.8 sq. cm

Question 5.
EARN, ER = 10 cm, AN = 7 cm and ∠EOA 110° where \(\overline { ER } \) and \(\overline { AN } \) intersect at O.
Solution:

Given:
In the parallelogram EARN,
ER= 10 cm
AN = 7 cm, and ∠EOA = 110°

Construction:
Steps:

1. Draw a line segment PX. Mark a {Joint O on PX
2. Make an angle ∠EOA = 110° on PX at O
3. Draw arcs of radius 3.5 cm with O as centre on either side of PX. Cutting YZ on A and N
4. With A as centre, draw an arc of radius 10 cm, cutting PX at E. Join AE
5. Draw a line parallel to AE at N cutting PX at R. Join EN and AR
6. EARN is the required parallelogram

Calculation of area:
Area of the Parallelogram EARN = b x h sq. units
= 10 x 5.5 = 55 sq. cm

Question 6.
FAIR, FI = 8 cm, AR = 6 cm and ∠IOR = 80° where \(\overline { FI } \) and \(\overline { AR } \) intersect at O.
Solution:

Given:
In the parallelogram FAIR,
FI = 8cm
AR = 6 cm and ∠IOR = 80°, where \(\overline { FI } \) and \(\overline { AR } \) intersect at O

Construction:
Steps:

1. Draw a line segment \(\overline { FI } \) = 8 cm
2. Mark O the midpoint of \(\overline { FI } \)
3. Draw a line \(\overline { XY } \) through O which makes ∠IOX = 80°
4. With O as centre and 3 cm as radius draw two arcs on XY on either sides of \(\overline { FI } \). Let the arcs cut \(\overline { OX } \) at R and \(\overline { OY } \) at A
5. Join \(\overline { IR } \), \(\overline { FR } \), \(\overline { FA } \) and \(\overline { AI } \)
6. FAIR is the required parallelogram

Calculation of area:
Area of the Parallelogram FAIR = b x h sq. units
= 5.4 x 4.3 = 23.22 sq. cm

Question 7.
GAIN, GA = 7.5 cm, GI = 9 cm and ∠GAI – 100°
Solution:

Given:
In the parallelogram GAIN,
GA = 7.5 cm
GI = 9 cm and ∠GAI= 100°

Construction:
Steps:

1. Draw a line segment GA = 7.5 cm.
2. Make an angle GAI = 100° at A.
3. With G as centre, draw an arc of radius 9 cm cutting AX at I. Join GI.
4. Draw a line IY parallel to GA through I.
5. With I as centre, draw an arc of radius T.5 cm on IY cutting at N. Join GN
6. GAIN is the required parallelogram.

Calculation of area:
Area of Parallelogram GAIN = b x h sq.units
= 7.5 x 3.9 = 29.25 sq. cm

Question 8.
HERB, HE = 6 cm, ∠EHB = 60° and EB = 7 cm.
Solution:

Given:
In the parallelogram HERB,
HE = 6 cm, ∠EHB = 60° and
EB = 7 cm

Construction:
Steps:

1. Draw a line segment HE = 6 cm.
2. Make an angle ∠BHE = 60° at H.
3. With E as centre, draw an arc of radius 7 cm cutting HX at B.
4. Draw a line BY parallel to HE through B.
5. Draw an arc of radius 6 cm with B as centre, cutting BY at R. Join ER.
6. HERB is the required parallelogram.

Calculation of area:
Area of the Parallelogram HERB = b x h sq. units
= 6 x 6.7 = 40.2 sq. cm

Students can Download Maths Chapter 3 Geometry Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Intext Questions

Exercise 3.1
Try This (Text book Page No. 60)

Question 1.
How will you prove ∆ ABC ~ AD AC?
Proof:
In ∆ ABC & ∆ DAC, ∠C is common and ∠BAC = ∠ADC = 90°
Therefore ∆ ABC ~ AD AC (AA similarity)

Try This (Text book Page No. 61)

Question 1.
Check whether the following are Pythagorean triplets

1. 57, 176, 185
2. 264, 265, 23
3. 8, 41, 40

Solution:
1. For Pythagorean triplet, the sum of the squares of 2 sides is equivalent to square of 3rd side (hypotenuse)
Let us check of
57² + 176² whether = 185² or not
57² = 3249
176² = 30976
185² = 34225
57² + 176² = 3249 + 30976 = 34225 = 185²
∴ 57, 176 & 185 are Pythagorean triplet.

2. 23, 264, 265
23² = 529
264² = 69696
23² + 264² = 70225
265² = 70225
∴ 23² + 264² = 265²
∴ Pythagorean triplet

3. 8, 41, 40
8² = 64
40² = 1600
8² + 40² = 1664
41² = 1681
8² + 40² ≠ 41² = 1
∴ They are not Pythagorean triplet

Activity – 1 (Text book Page No. 62)

We can construct sets of Pythagorean triplets as follows. Let m and n be any two positive integers (m > n):
(a, b, c) is a Pythagorean triple if a = m² – n², b = 2mn and c = m² + n² (Think, why?) Complete the table.

Solution:

Activity – 2 (Text book Page No. 65)

Question 1.
Find all integer-sided right angled triangles with hypotenuse 85
Solution:
(x + y)² – 2xy = 85²

Pythagorean triplets with hypotenuse 85.

Exercise 3.3
Try These (Text book Page No. 68)

Question 1.
The area of the trepezium is ……..
Answer:
\(\frac{1}{2}\) x h x (a + b) sq. units!

Question 2.
The distance between the parallel sides of a trapezium is called as ………
Answer:
its height

Question 3.
If the height and parallel sides of a trapezium are 5 cm, 7 cm and 5 cm respectively, then its area is ……..
Answer:
30 sq cm
Hint:
= \(\frac{1}{2}\) x h x (a + b) sq. units
= \(\frac{1}{2}\) x 5 x (7 + 5)
= \(\frac{1}{2}\) x 5 x 12 = 30 sq.cm

Question 4.
In an isosceles trapezium, the non-parallel sides are ……….. in length.
Answer:
Equal.

Question 5.
To construct a trapezium, ………… measurements are enough.
Answer:
Four.

Question 6.
If the area and sum of the parallel sides are 60 cm2 and 12 cm, its height is ………..
Answer:
10 cm
Hint:
Area of the trapezium = \(\frac{1}{2}\) x h (a + b)
60 = \(\frac{1}{2}\) x h x (12)
h = \(\frac{60×2}{12}\) = 10 cm

Exercise 3.4
Think (Text book Page No. 74)

Question 1.
Can a rhombus, a square or a rectangle be called as a parallelogram? Justify your answer.
Solution:
Yes, a rhombus, a square or a rectangle can be called as parallelogram as the opposite sides are equal and parallel and diagonals bisect each other in this figures.

Try These (Text book Page No. 74)

Question 1.
In a parallelogram, the opposite sides are …….. and ……….
Answer:
equal, parallel

Question 2.
If ∠A of a parallelogram ABCD is 100° then, find ∠B, ∠C and ∠D .
Answer:

∠B = 80°
∠C = 100°
∠D = 80°

Question 3.
Diagonals of a parallelogram each other.
Answer:
Bisect

Question 4.
If the base and height of the parallelogram are 20 cm and 5 cm then, its area is ………
Answer:
100 sq.cm

Question 5.
Find the unknown values in the given parallelograms and write the property Used to find them.

Solution:

Students can Download Maths Chapter 3 Geometry Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Additional Questions

Question 1.
State Pythagoras theorem.
Solution:
In a right angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.

Question 2.
Write two uses of Pythagoras theorem in our daily life.
Solution:
The Pythagoras theorem is useful in finding the distance and the heights of objects.

Question 3.
Prove Pythagoras theorem.
Solution:
Proof of the Pythagoras theorem using similarity of triangles.

Given: ∠BAC = 90°
To Prove BC² = AB² + AC²
Construction: Draw AD ⊥ BC
Proof:

In ∆ ABC and ∆ DBA
∠B is common and ∠BAC = ∠ADB = 90°
Therefore, ∆ ABC ~ ∆ DBA, (AA similarity)
Hence, the ratio of corresponding sides are equal.
⇒ \(\frac{AB}{DB}\) = \(\frac{BC}{BA}\)
⇒ AB² = BC x DB
Similarity, ∆ ABC ~ ∆ DAC,
⇒ \(\frac{AC}{DC}\) = \(\frac{BC}{AC}\)
⇒ AC² = BC x DB
Adding (1) and (2), we get
AB² + AC² = BC x DB + BC x DC
= BC x (DB + DC) = BC x BC
⇒ AB² + AC² = BC² and hence the proof of the theorem

Question 4.
State the converse of Pythagoras theorem.
Solution:
If in a triangle, the square on the greatest side is equal to the sum of squares on the other two sides, then the triangle is right angled triangle.

Question 5.
Give 2 examples for Pythagorean triplet.
Solution:
(21, 28, 35), (24, 32, 40)

Question 6.
Check whether (2, 3, 5) is Pythagorean triplet.
Solution:

2² + 3² = 4 + 9 = 13
5² = 25
13 ≠ 25
∴ It is not a Pythagorean triplet.

Question 7.
Can the sides that measure 15 cm, 20 cm and 25 cm make a right triangle?
Solution:

20² + 15² = 400 + 225 = 625
25² = 625
20² + 15² = 25²
∴ It is Pythagorean triplet.
∴ The given sides make a right angled triangle.

Question 8.
In the figure, find the value of x.

Solution:
In ABC
12² + 9² = 144 + 81 =225 = 15²
∴ x = 15

Question 9.
In the figure find the value of a and b and verify ∆ ABD is a right angled triangle.
Solution:
Now by altitude – on – hypotenuse theorem,
AB² = BC x BD gives
10² = a x 26
a = \(\frac{100}{26}\) = \(\frac{50}{13}\)

and AD² = CD x BD
24² = b x 26
b = \(\frac{576}{26}\) = \(\frac{288}{13}\)
and in ∆ ABD;
AB² + AD² = BD²
10² + 24² = 576 = 26²
BD = 26
Therefore ∆ ABD is a right angled triangle.

Question 9.
State the altitude-on-Hypotenuse theorem.
Solution:
If an altitude is drawn to the hypotenuse of an right angled triangle then (i) the two triangles are similar to the given triangle and also to each other.

That is ∆ PRQ ~ ∆ PSR ~ ∆ RSQ

1. h² = xy
2. p² = yr and
3. q² = xr, where r = x + y

Students can Download Maths Chapter 3 Geometry Ex 3.2 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Ex 3.2

Miscellaneous Practice Problems

Question 1.
The sides of a triangle are 1.2 cm, 3.5 cm and 3.7cm. Is this triangle a right triangle? If so, which side is the hypotenuse?
Solution:
The sides of a triangle are a = 1.2 cm; b = 3.5 cm; c = 3.7 cm
By Pythagoras theorem,
c² = a² + b²
a² + b² = 1.2² + 3
5² – 1.44 +12.25 = 13.69
c² = 3.7² = 13.69
(1) = (2)
Yes, it is a right angled triangle. The hypotenuse c = 3.7 cm.

Question 2.
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Why?
Solution:

Take the sides of a right angled triangle ∆ ABC as
a = 7 inches
b = 25 inches
c = ?
By Pythagoras theorem,
b² = a² + c²
25 = 7² + c²
c² = 25² – 7² = 625 – 49 = 576
∴ c² = 24²
⇒ c = 24 inches
∴ Width of TV cabinet is 20 inches which is lesser than the width of the screen ie.24 inches. The TV will not fit into the cabinet.

Question 3.
Find the length of the support cable required to support the tower with the floor.

Solution:
From the figure, by Pythagoras theorem,
x² = 20² + 15² = 400 + 225 = 625
x² = 25² ⇒ x = 25ft.
∴ The length of the support cable required to support the tower with the floor is 25 ft.

Question 4.
A ramp is constructed in a hospital as shown. Find the length of the ramp.

Solution:
Take a = 7 ft ; b = 24 ft.
By Pythagoras theorem,
l² = c² + b²
= 7² + 24² = 49 + 576
l = 25ft

Question 5.
In the figure, find MT and AH

Solution:
By Pythagoras theorem,
MT² = MH² + HT²
= 60² + 80² = 3600 + 6400
= 10000 = 100²
∴ MT = 100
By the altitude – on – hypotenuse theorem,
MH² = MA x MT
60² = MA x 100
MA = \(\frac{3600}{100}\) = 36
∴ In ∆ MAH, by Pythagoras theorem,
AH² = MH² – MA²
= 60² – 36² = 3600 – 1296 = 2304 = 48²
∴ AH = 48
∴ Ans MT = 100
AH = 48

Challenging Problems

Question 6.
Mayan travelled 28 km due north and then 21 km due east. What is the least distance that he could have travelled from his starting point?
Solution:
From the figure AC is to be found.

By using Pythagoras theorem,
AC² = AB² + BC²
= 28² + 21² = 784 + 441 = 1225 = 352
∴ AC = 35 km
This is the least distance that he could have travelled from his starting point.

Question 7.
If ∆ APK is an isosceles right angled triangle, right angled at K. Prove that AP² = 2AK².
Solution:
From the figure, ∆ APK is a right triangle.

By using Pythagoras theorem,
AP² = AK² + PK²
= AK² + AK² (since it is an isosceles A)
= 2AK²
Hence it is proved.

Question 8.
The diagonals of the rhombus is 12 cm and 16 cm. Find its perimeter. (Hint: the diagonals of rhombus bisect each other at right angles).
Solution:

Here AO = CO = 8 cm
BO = DO = 6 cm
(∴ the diagonals of rhombus bisect each other at right angles)
∴ In ∆ AOB,
AB² = AO² + OB² = 8² + 6² = 64 + 36
= 100 = 10²
∴ AB = 10
Since it is a rhombus, all the four sides are equal.
AB = BC = CD = DA
∴ Its Perimeter = 10 + 10 + 10 + 10 = 40 cm

Question 9.
In the figure, find AR.

Solution:
∆ AFI, ∆ FRI are right triangles.
By Pythagoras theorem,
AF² = AT² – FT² = 25² – 15²
= 625 – 225 = 400 = 20²
∴ AF = 20 ft ….(1)
FR² = RI² – FI² = 17² – 15² = 289 – 225 = 64 = 8²
FR = 8 ft.
∴ AR = AF + FR = 20 + 8 = 28 ft.

Question 10.
∆ ABC is a right angled triangle in which ∠A = 90° and AM ⊥ BC. Prove that AM = \(\frac{ABxAC}{BC}\). Also if AB = 30 cm and AC = 40 cm, find AM.

Solution:
Given: ∆ ABC is a right angled triangle.
∠A = 90, AM ⊥ BC
To Prove: AM = \(\frac{ABxAC}{BC}\)
Proof:
In the given figure, Area of the triangle A ABC [taking AB as base and AC as height]
= \(\frac{1}{2}\) x AB x AC ….(1)
And also, Area of the triangle ∆ ABC [taking BC as base and AM as height]
= \(\frac{1}{2}\) x BC x AM ……(2)
Since (1) & (2) are the same, we can equate (2) and (1)
i.e. \(\frac{1}{2}\) x BC x AM = \(\frac{1}{2}\) x AB x AC
AM = \(\frac{ABxAC}{BC}\)
Hence proved. If AB = 30 cm, AC = 40 cm
By Pythagoras theorem, BC² = AB² + AC² = 30² + 40² = 900 + 1600 = 2500 = 50²
∴ BC = 50
Using the altitude – on – hypotenuse theorem

Here AC² = MC x BC
40² = MC x 50
∴ BM = BC – MC = 50 – 32 = 18 cm
AM² = BM x MC = 18 x 32 = 576 = 24²
∴ AM = 24 cm

Students can Download Maths Chapter 3 Geometry Ex 3.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 3 Geometry Ex 3.1

Question 1.
Fill in the blanks:

Question (i)
If in a ∆ PQR, PR² = PQ² + QR², then the right angle of ∆ PQR is at the vertex ………
Answer:
Q
Hint:

We have also given Lines and Angles concepts and problems for free of cost on our website.

Question:
(ii) If ‘l’ and ‘m’ are the legs and is the hypotenuse of a right angled triangle then, l² = ……….
Answer:
n² – m²
Hint:

Question (iii)
If the sides of a triangle are in the ratio 5:12:13 then, it is ………
Answer:
a right angled triangle.
13² = 169
5² = 25
12² = 144
169 = 25 + 144
132 = 5² + 12²
By Pythagoras theorem, In a right triangle, square of the hypotenuse is equal to the sum of the squares of other two sides.

Question (iv)
If a perpendicular is drawn to the hypotenuse of a right angled triangle, then each of the three pairs of triangles formed are …………
Answer:
Similar.

Question (v)
In the figure BE² = TE x ………

Answer:
EN

Question 2.
Say True or False.

Question (i)
8, 15, 17 is a Pythagorean triplet.
Answer:
True
Hint:
17² = 289
15² = 225
8² = 64
64 + 225 = 289 ⇒ 17² = 15² + 8²

Question (ii)
In a right angled triangle, the hypotenuse is the greatest side.
Answer:
False
Hint:

Question (iii)
One of the legs of a right angled triangle PQR having ∠R = 90° is PQ.
Answer:
False
Hint:

In ∆ PQR, QR and RP are legs and PQ is the hypotenuse

Question (iv)
The hypotenuse of a right angled triangle whose sides are 9 and 40 is 49.
Answer:
False
Hint:

49² = 2401
9² = 81
40² = 1600
40² + 9² = 1600 + 81 + 1681
49² = 2401
2401 ≠ 1681

Question (v)
Pythagoras theorem is true for all types of triangles.
Answer:
False
Hint:
Pyhtagoras theorem is true for only right angled triangles.

Question 3.
Check whether given sides are the sides of right – angled triangles, using Pythagoras theorem,

1. 8, 15, 17
2. 12, 13, 15
3. 30, 40, 50
4. 9, 40, 41
5. 24, 45, 51

Solution:
1. 8, 15, 17
Take a = 8,
b = 15 and
c = 17
Now a² + b² = 8² + 15² = 64 + 225 = 289
17² = 289 = c²
∴ a² + b² = c²
By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.
Answer:
yes.

2. 12, 13, 15
Take a = 12
b = 13 and
c = 15
Now a² + b² = 12² + 13² = 144 + 169 = 313
15² = 225 ≠ 313
By the converse of Pythagoras theorem, the triangle with given measures is not a right angled triangle.
Answer:
No.

3. 30, 40, 50
Take a = 30
b = 40 and
c = 50
Now a² + b² = 30² + 40² = 900 + 1600 = 2500
c² = 50² = 2500
∴ a² + b² = c²
By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.
Answer:
yes.

4. 9, 40, 41
Take a = 9
b = 40 and
c = 41
Now a² + b² = 9² + 40² = 81 + 1600= 1681
c² = 41² = 1681
∴ a² + b² = c²
By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.
Answer:
Yes.

5. 24, 45, 51
Take a = 24
b = 45 and
c = 51 Now
a² + b² = 24² + 45² = 576 + 2025 = 2601
c² = 51² = 2601
a² + b² = c²
By the converse of Pyhtagoreas theorem, the triangle with given measure is a right angled triangle.
Answer:
Yes.

Question 4.
Find the unknown side in the following triangles.

Solution:
(i) From ∆ ABC, by Pythagoras theorem

BC² = AB² + AC²
Take AB² + AC² = 9² + 40² = 81 + 1600 = 1681
BC² = AB² + AC² = 1681 = 41²
BC² = 41² ⇒ BC = 41
∴ x = 41

(ii) From ∆ PQR, by Pythagoras theorem,

PR² = PQ² + QR²
34² = y² + 30²
⇒ y² = 34² – 30²
= 1156 – 900
= 256 = 16²
y² = 16² ⇒ y = 16

(iii) From ∆ XYZ, by Pythagoras theorem,

YZ² = XY² + XZ²
⇒ XY² = YZ² – XZ²
Z² = 39² – 36²
= 1521 – 1296 = 225 = 15²
Z² = 15²
⇒ Z = 15

Question 5.
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height.
Solution:
In an isosceles triangle the altitude dives its base into two equal parts. Now in the figure, ∆ ABC is an isosceles triangle with AD as its height.

In the figure, AD is the altitude and Δ ABD is a right triangle.
By Pythagoras theorem,
AB² = AD² + BD²
⇒ AD² = AB² – BD²
= 13² – 12² = 169 – 144 = 25
AD² = 25 = ²
Height: AD = 5 cm

Question 6.
In the figure, find PR and QR.

Solution:
In the figure ∆ PQR is a right triangle.
By Pythagoras theorem,
PR² = PQ² + QR²
(x + 1)² = 7² + x²
x² +2 × x × 1 + 1² = 49+ x²
2x + 1 = 49
2x = 49 – 1 = 48
x = \(\frac{48}{2}\) = 24
∴ PR = x + 1 = 24 + 1 = 25
QR = x = 24

Question 7.
The length and breadth of the screen of an LED – TV are 24 inches and 18 inches. Find the length of its diagonal.

Solution:
The length and breadth of a LED TV form a right angled triangle with its diagonal.
Therefore by Pythagoras theorem,
AC² = AB² + BC²
= 24² + 18² = 576 + 324 = 900 = 30²
∴ AC = 30 ⇒ The length of the diagonal is 30 inches.

Question 8.
Find the distance between the helicopter and the ship.

Solution:
From the figure AS is the distance between the helicopter and the ship.
∆ APS is a right angled triangle, by Pythagoras theorem,
AS² = AP² + PS²
= 80² + 150²
= 6400 + 22500 = 28900 = 170²
∴ The distance between the helicopter and the ship is 170 m

Question 9.
From the figure, 1. If TA = 3 cm and OT = 6 cm, find TG.

Solution:
1. From the figure, if, TA = 3 cm, OT = 6 cm

By Pythagoras theorem,
OA² = OT² – TA² = 6² – 3²
i.e. h² = 36 – 9 = 27 cm.
Now, by altitude – on – hypotenuse theorem
h² = xy
27 = x × 3
x = \(\frac{27}{3}\) = 9 cm
TG = x + 3 = 9 + 3 = 12 cm

Question 10.
If RQ = 15 cm and RP = 20 cm, find PQ, PS and SQ.

Solution:

RQ = 15cm
RP = 20 cm and ∆ PQR is a right angled triangle
By Pythagoras theorem, p 20 cm
PQ² = PR² + RQ² = 20² + 15²
= 400 + 225 = 625 = 25²
∴ PQ = 25 cm
Now by altitude – on – hypotenuse theorem,
RQ² = q x r
15² = q x 25
q = \(\frac{225}{25}\) = 9 cm ⇒ SQ = 9 cm
PR² = P x r
20² = P x 25
P = \(\frac{400}{25}\) = 16 cm ⇒ PS = 16 cm
Answer:

1. PQ = 25 cm
2. PS = 16 cm
3. SQ = 9 cm

Objective Type Questions

Question 11.
If ∆ GUT is isosceles and right angled, then ∠TUG is …………

(a) 30°
(b) 40°
(c) 45°
(d) 55°
Answer:
(c) 45°
Hint:
∠U ∠T = 45° (∆ GUT is an isosceles given)
∴ ∠TUG = 45°

Question 12.
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is ……….
(a) 28 cm
(b)20cm
(c) 24 cm
(d)21cm
Answer:
(b) 20 cm
Hint:
Side take a = 12 cm
b = 16 cm
The hypotenuse c² = a² + b² = 12² + 16^2
2 = 400 ⇒ c = 20 cm

Question 13.
The area of a rectangle of length 21 cm and diagonal 29 cm is ………. cm²
(a) 609
(b) 580
(c) 420
(d) 210
Answer:
(c) 420
Hint:

Length = 21 cm
Diagonal = 29 cm
By the converse of Pythagoras theorem,
AB² + BC² = AC²
21² + x² = 29²
x² = 841 – 441 = 400 = 20²
x = 20 cm
Now area of the rectangle = length x breadth.
i.e. AB x BC = 21 cm x 20 cm = 420 cm²

Question 14.
if the square of the hypotenuse of an isosceles right triangle is 50 cm2, the length of each side is ………..
(c) 10 cm
(a) 25 cm
(b) 5 cm
(c) 10 cm
(d) 20 cm
Answer:
(b) 5 cm
Hint:
By Pythagoras theorem
c² = a² + b²
In an isosceles triangle, a = b
c² = a² + a² = 2a²
⇒ 2a² = 50
a² = 25 ⇒ a = 5cm
∴ The length of each sides a = 5cm, b = 5 cm.

Question 15.
The sides of a right angled triangle are in the ratio 5 : 12 : 13 and its perimeter is 120 units then, the sides are .
(a) 25, 36, 59
(b) 10, 24, 26
(c) 36, 39, 45
(d) 20, 48, 52
Answer:
(d) 20, 48, 52
Hint:
The sides of a right angled triangle are in the ratio 5 : 12 : 13
Take the three sides as 5a, 12a, 13a
Its perimeter is 5a + 12a + 13a = 30a
It is given that 30a = 120 units
a = 4 units
∴ The sides 5a = 5 x 4 = 20 units
12a = 12 x 4 = 48 units
13a = 13 x 4 = 52 units

Students can Download Maths Chapter 2 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 2 Algebra Intext Questions

Exercise 2.1
Try These (Text book page no. 32)

Question 1.
Identify which among the following are linear equations.

1. 2 + x = 19 – Linear as degree of the variable x is 1
2. 7x² – 5 = 3 – not linear as highest degree of x is 2
3. 4p³ = 12 – not linear as highest degree ofp is 3
4. 6m + 2 – Linear, but not an equation
5. n = 10 – Linear equation as degree of n is 1
6. 7k – 12= 0 – Linear equation as degree of Hs 1
7. \(\frac{6x}{8}\) + y = 1 – Linear equation as degree ofx & y is 1
8. 5 + y = 3x – Linear equation as degree ofy & x is 1
9. 10p + 2q = 3 – Linear equation a& degree ofp & q is 1
10. x² – 2x-4 – not linear equation as highest degree of x is 2

Think (Text book page no. 32)

Question 1.
Is t(t – 5)= =10 a linear equation? Why?
Solution:
t(t – 5) = 10
= t x t – 5 x t = 10
= t² – 5t = 10
This is not a linear equation as the highest degree of the variable ‘t’ is 2

Question 2.
Is x² = 2x, a linear equation? Why?
Solution:
x² = 2x
= x² – 2x = 0
This is not a linear equations as the highest degree of the variable ‘x’ is 2

Try These (Text book page no. 33)

Convert the following statements into linear equations:

Question 1.
On subtracting 8 from the product of 5 and a number, I get 32.
Solution:
Convert to linear equations:
Given that on subtracting 8 from product of 5 and a, we get 32
5 × x – 8 = 32
5x – 8 = 32

Question 2.
The sum of three consecutive integers is 78.
Solution:
Sum of 3 consecutive integers is 78
Let 1st integer be ‘x’
∴ x + (x + 1) + (x + 2) = 78
∴ x + x + 1 + x + 2 = 78
3x + 3 = 78

Question 3.
Peter had a Two hundred rupee note. After buying 7 copies of a book he was left with ₹ 60.
Solution:
Let cost of one book be ‘x’
∴ Given that 200 – 7 × x = 60
∴ 200 – 7x = 60

Question 4.
The base angles of an isosceles triangle are equal and the vertex angle measures 80°.
Solution:
Let base angles each be equal to x & vertex bottom angle is 80°. Applying triangle
property, sum of all angles is 180°
∴ x + x + 80 = 180°
2x + 80 = 180°

Question 5.
In a triangle ABC, ∠A is 10° more than ∠B. Also ∠C is three times ∠A. Express the equation in terms of angle B
Solution:
Let ∠B = b
Given ∠A = 10° + ∠B = 10 + b
Also given that ∠C = 3 x ∠A = 3 x (10 + 6) = 30 + 3b
Sum of the angles = 180°
∠A + ∠B + ∠C = 180°
10 + b + b + 30 + 3b = 180°
∴ 5b + 40 = 180°

Think (Text book page no. 34)

Question 1.
Can you get more than one solution for a linear equation?
Solution:
Yes, we can get. Consider the below line or equation
x + y = 5
here, when x = 1, y = 4
when x = 2, y = 2
x = 3, y = 2
x = 4, y = 1
Hence, we get multiple solutions for the same linear equation.

Think (Text book page no. 35)

Question 1.
“An equation is multiplied or divided by a non zero number on either side.” Will there be any change in the solution?
Solution:
Not be any change in the solution

Question 2.
“An equation is multiplied or divided by two different numbers on either side”. What will happen to the equation?
Solution:
When an equation is multiplied or divided by 2 different numbers on either side, there will be a change in the equation & accordingly, solution will also change.

Exercise 2.2
Think (Text book page no. 37)

Question 1.
Suppose we take the second piece to be x and the first piece to be (200 – x), how will the steps vary. Will the answer be different?
Solution:
Let 2nd piece be V & 1st piece is 200 – x
Given that 1st piece is 40 cm smaller than hence the other piece
∴ 200 – x = 2 × x – 40

200 + 40 = 2x + x
240 = 3x
∴ x = \(\frac{240}{3}\) = 80
∴ 1st piece = 200 – x = 200 – 80 = 120 cm
2nd piece = x = 80 cm
The answer will not change

Exercise 2.3
Think (Text book page no. 43)

Question 1.
If instead of (4, 3), we write (3, 4) and try to mark it, will it represent ‘M’ again?
Solution:
Let 3, 4 be M, when we mark, we find that it is a different point and not ‘M’

Try These (Text book page no. 45)

Question 1.
Complete the table given below.

Solution:

Question 2.
Write the coordinates of the points marked in the following figure

• A – (-3, 2)
• B – (5, 2)
• C – (5, -3)
• D – (-3, 3)
• E – (-1,4)
• F – (1, 2)
• G – (7, 4)
• H – (0, 2)
• i – (o, 3)
• J – (-3, 0)
• K – (5, 0)
• L – (-1, 0)
• M – (-2, 0)
• N – (-2, -1)
• O – (0, 0)
• P – (-1, -1)
• Q – (1, -1)
• R – (2, -1)
• S – (0, -3)
• T – (7, 0)
• U – (7, -2)

Exercise 2.4
Think (Text book page no. 49)

Question 1.
Which of the points (5, -10) (0, 5) (5, 20) lie on the straight line X = 5?
Solution:
All points on the line X = 5 will have X – coordinate as 5.
Therefore, any point with X – coordinate as 5 will lie on X = 5 line.
Hence the points (5, – 10) & (5,20) will lie on X = 5

Think (Text book page no. 54)

Question 1.
Why is it given that the speed is ‘constant’? If the speed is not constant, will the graph be the same? The graph is named as y = 80 x algebraically. Why?
Solution:

or in other words, the slope of a line in a distance – time graph. We observe that the slope of the graph is constant hence, speed is constant. If the speed is not constant, the graph will be different as slope of the line would change.

Students can Download Maths Chapter 2 Algebra Ex 2.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 2 Algebra Ex 2.4

Question 1.
Fill in the blanks:

Question (i)
y = px where p ∈ Z always passes through the ………
Answer:
Origin (0, 0)
Hint:
[When we substitute x = 0 in equation, y also becomes zero. (0,0) is a solution]

Question (ii)
The intersecting point of the line x = 4 and y = – 4 is ………
Answer:
4, -4
Hint:
x = 4 is a line parallel to the y – axis and
y = – 4 is a line parallel to the x – axis. The point of intersection is a point that lies on both lines & which should satisfy both the equations. Therefore, that point is (4, -4)

Question (iii)
Scale for the given graph, on the x – axis 1 cm = ……… units y – axis 1 cm = ………. units

Answer:
3 units, 25 units
Hint:
With reference to given graph,
On the x – axis, 1cm = 3 units
y axis, 1cm = 25 units

Question 2.
Say True or False:

Question (i)
The points (1, 1) (2, 2) (3, 3) lie on a straight line.
Answer:
True
Hint:
The points (1, 1), (2, 2), (3, 3) all satisfy the equation y = x
which is straight line. Hence, it is true

Question (ii)
y = – 9x not passes through the origin.
Answer:
False
Hint:
y = – 9x substituting forx as zero, we get y = – 9 x 0 = 0
∴ for x = 0, y = 0. Which means line passes through (0, 0), hence statement is false.

Question 3.
Will a line pass through (2, 2) if it intersects the axes at (2, 0) and (0, 2).
Solution:
Given a line intersects the axis at (2, 0) & (0, 2)
Let line intercept form be expressed as
ax + by = 1 Where a & b are the x & y intercept respectively.
Since the intercept points are (2, 0) & (0, 2)
a = 2, b = 2
∴ 2x + 2y = 1
When the point (2, 2) is considered & substituted in the equation
2x + 2y = 1 we get
2 x 2 + 2 x 2 = 4 ≠ 1
∴ The point (2, 2) does not satisfy the equation. Therefore the line does not pass through (2, 2)
Alternatively graphical method:
as we can see the line doesn’t pass through (2, 2)

Question 4.
A line passing through (4, – 2) and intersects the Y – axis at (0, 2). Find a point on the line in the second quadrant.
Solution:

Line passes through (4, – 2)
y – axis intercept point – (0, 2)
using 2 point formula,
\(\frac { y-y_{ 1 } }{ x-x_{ 1 } } \) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
\(\frac{y-2}{x-0}\) = \(\frac{1-2-2}{4-0}\)
∴ \(\frac{y-2}{x}\) = \(\frac{-4}{4}\) = – 1
y – 2 = – 1 × x

∴ x + y = 2 is the equation of the line.
Any point in II quadrant will have x as negative & y as positive.
So let us take x value as – 2
∴ – 2 + y = 2
y = 2 + 2 = 4
∴ Point in II Quadrant is (-2, 4)

Question 5.
If the points P (5, 3) Q(- 3, 3) R (- 3, – 4) and S form a rectangle then find the coordinate of S.
Solution:
Plotting the points on a graph (approximately)

Steps:

1. Plot P, Q, R approximately on a graph.
2. As it is a rectangle, RS should be parallel to PQ & QR should be parallel to PS
3. S should lie on the straight line from R parallel to x – axis & straight line from P parallel to y – axis
4. Therefore, we get S to be (5, -4)

[Note: We don’t need graph sheet for approximate plotting. This is just for graphical understanding]

Question 6.
A line passes through (6, 0) and (0, 6) and an another line passes through (- 3, 0) and (0, – 3). What are the points to be joined to get a trapezium?
Solution:
In a trapezium, there are 2 opposite sides that are parallel. The other opposite sides are non-parallel.
Now, let us approximately plot the points for our understanding [no need of graph sheet]

1. Plot the points (0, 6), (6, 0), (-3, 0) & (0, – 3)
2. Join (0, 6) & (6, 0)
3. Join (-3, 0) & (0, -3)
4. We find that the lines formed by joining the points are parallel lines.
5. So, for forming a trapezium, we should join (0, 6), (-3, 0) & (0, -3), (6, 0)

Question 7.
Find the point of intersection of the line joining points (- 3, 7) (2, – 4) and (4, 6) (- 5, 7). Also find the point of intersection of these lines and also their intersection with the axis.
Solution:

Equation of line joining 2 points by 2 point formula is given by
\(\frac { y-y_{ 1 } }{ x-x_{ 1 } } \) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
∴ \(\frac{y-7}{x-(-3)}\) = \(\frac{-4-7}{2-(-3)}\)
\(\frac{y-7}{x+3}\) = \(\frac{-11}{2+3}\)
∴ \(\frac{y-7}{x+3}\) = \(\frac{-11}{5}\)
Cross multiplying, we get

Transposing the variables, we get
11x + 5y = 35 – 33 = 2
11x + 5y = 2 – Line 1
Similarly, we should find out equation of second line

∴ 9y – 54 = 13x – 52
9y – 13x = 2 – Line 2
For finding point of intersection, we need to solve the 2 line equation to find a point that will satisfy both the line equations.
∴ Solving for x & y from line 1 & line 2 as below
11x + 5y = 2 ⇒ multiply both sides by 13,
11 x 13x + 5 x 13y = 26
Line 2:
9y – 13x = 2 ⇒ multiply both sides by 11
9 x 11y – 13 x 11x = 22

Substituting this value of y in line 1 we get
11x + 5y = 2
11x + 5 x \(\frac{12}{41}\) = 2
11x = 2 – \(\frac{60}{41}\) = \(\frac{82-60}{41}\) = \(\frac{22}{41}\)
x = \(\frac{2}{41}\)
∴ Point of intersection is (\(\frac{2}{41}\) \(\frac{12}{41}\))
To find point of intersection of the lines with the axis, we should substitute values & check
Line 1:
11x + 5y = 2
Point of intersection of line with x – axis, i.e y coordinate is ‘0’
∴ put y = 0 in above equation
∴ 11x – 5 x 0 = 2
11x + 0 = 2
x = \(\frac{2}{11}\)
∴ Point is (\(\frac{2}{11}\), 0)
Similarly, point of intersection of line with y – axis is when x – coordinate becomes ‘0’
∴ put x = 0 in above equation
∴ 11 x 0 + 5y = 2
∴ 0 + 5y = 2
y = \(\frac{2}{5}\)
∴ Point is (0, \(\frac{2}{5}\))
Similarly for line 2,
9y – 13x = 2
For finding x intercept, i.e point where line meets x axis, we know thaty coordinate becomes ‘0’
∴ Substituting y – 0 in above eqn. we get
9 x 0 – 13x = 2
∴ 0 – 13x = 2
x = \(\frac{-2}{13}\)
∴ Point is (\(\frac{-2}{13}\), 0)
Similarly for y – intercept, x – coordinate becomes ‘0’,
∴ Substituting for x = 0 in above equation, we get
9y – 13 x 0 = 2
9y – 0 = 2
9y = 2
y = \(\frac{2}{9}\)
Point is (0, \(\frac{2}{9}\))

Question 8.
Draw the graph of the following equations:

1. x = – 7
2. y = 6

Solution:

Question 9.
Draw the graph of

1. y = – 3x
2. y = x – 4

Solution:
To draw graph, we need to find out some points.
1. for y = – 3x, let us first substituting values & check
put x = 0
y = – 3 x 0 = 0 ∴ (0,0) is a point
put x = 1
y = – 3 x 1 = – 3 ∴ (1, – 3) is a point
If join these 2 points, we will get the line

2. for y = x – 4
put x = 0
y = 0 – 4 = -4 ∴ (0, – 4) is a point
x = 4
y = 4 – 4 = 0 ∴ (4, 0) is a point
Now let us plot the points & join them on graph

Question 10.
Find the values

Solution:
Let y = x + 3
(i) if x = 0
y = 0 + 3 = 3
∴ y = 3

(ii) y = 0
0 = x + 3
∴ x = – 3

(iii) x = – 2
y = – 2 + 3
∴ y = 1

(iv) y = -3
-3 = x + 3
∴ x = -6

Let 2x + 7 – 6 = 0
(i) x = 0
2 x 0 + y – 6 = 0
∴ 7 = 6

(ii) y = 0
2x + 0 – 6 = 0
2x = 6
x = 3

(iii) x = – 2
2 x (- 2) + y – 6 = 0
y – 10 = 0
y = 10

(iv) y = -3
2x – 3 – 6 = 0
2x = 9
x = \(\frac{9}{2}\)

Question 11.
The following is a table of , values connecting the radii of a few circles and their circumferences (Taking π = \(\frac{22}{7}\)) Illustrate the relation with a graph and find

1. The radius when the circumference is 242 units.
2. The circumference when the radius is 24.5 units.

Solution:

r = 24.5 Circumference?

Steps :

1. Draw the axis, x – axis = radius & y – axis = circumference
2. Mark the points by choosing scale of 1 cm = 7 units for x axis & 1 cm = 44 units for y – axis
3. Join the points to form a line.
4. Now for r value = 24.5 (mid value between 21 & 28), draw vertical line to touch the main line & from there drop line parallel to x axis and note where it meets y axis.

It meets between 132 & 176. Taking the mid value
i.e \(\frac{132+176}{2}\) = 154, we get circumference of 154 when r = 24.5.
Similarly, for circumference of 242, we get r value to be 38.5

Question 12.
An over-head tank is full with water. Water leaks out from it, at a constant rate of 10 litres per hour. Draw a “time-wastage” graph for this situation and find

1. The water wasted in 150 minutes
2. The time at which 75 litres of water is wasted.

Solution:
From over head tank, water leaks out at 10 l/hr.
∴ Let us see how much leakage happens with time
Time     Leakage
1 hr        10 ltrs.
2 hrs       20 ltrs.
3 hrs       30 ltrs.
4 hrs       40 ltrs.. and so on
150 min = 120 min + 30 min
= 2 hr 30 min = 2 \(\frac{1}{2}\) hrs
Now let us plot a graph between time & water leakage

Water wasted in 150 min (2\(\frac{1}{2}\) hrs) = 25 litres
Time at which 75 litre of water is wasted = 7\(\frac{1}{2}\) hrs = 450 minutes.

Students can Download Maths Chapter 2 Algebra Ex 2.5 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 2 Algebra Ex 2.5

Miscellaneous Practice Problems

Question 1.
The sum of three numbers is 58. The second numberis three times of two-fifth of the first number and the third number is 6 less than the first number. Find the three numbers.
Solution:
Here what we know
a + b + c = 58 (sum of three numbers is 58)
Let the first number be ‘x’
b = a + 3 (the second number is three times of \(\frac{1}{2}\) of the first number)
b = 3 x \(\frac{2}{5}\)x = \(\frac{6}{5}\)x
Third number = x – 6
Sum of the numbers is given as 58.
∴ x + \(\frac{6}{5}\)x + (x – 6) = 58
Multiplying by 5 throughout, we get
5 × x + 6x + 5 × (x – 6) = 58 x 5
5x + 6x + 5x – 30 = 290
∴ 16x = 290 + 30
∴ 16x = 320
∴ x = \(\frac{320}{16}\)x = 20
Answer:
1st number =20
2nd number = 3 x \(\frac{2}{5}\) x 20 = 24
3rd number = 24 – 6 = 14

Question 2.
In triangle ABC, the measure of ∠B is two third the measure of ∠A. The measure of ∠C is 20° more than the measure of ∠A. Find the measures of the three angles.
Solution:
Let angle ∠A be a°
Given that ∠B = \(\frac{2}{3}\) x ∠A = \(\frac{2}{3}\)a
& given ∠C = ∠A + 20 = a + 20
Since A, B & C are angles of a triangle, they add up to 180° (∆ property)
∠A + ∠B + ∠C = 180°
a + \(\frac{2}{3}\) a + a + 20 = 180°
\(\frac{3a+2a+3a}{3}\) + 20 = 180°
\(\frac{8a}{3}\) = 180 – 20 = 160°

∠C = 80°

Question 3.
Two equal sides of an isosceles triangle are 5y – 2 and 4y + 9 units. The third side is 2y + 5 units. Find y and the perimeter of the triangle.
Solution:
Given that 5y – 2 & 4y + 9 are the equal sides of an isosceles triangle.
The 2 sides are equal

∴ 5y – 4y = 9 + 2 (by transposing)
∴ y = 11
∴ 1st side = 5y – 2 = 5 x 11-2 = 55 – 2 = 53
2nd side = 53
3rd side = 2y + 5 = 2 x 11 + 5 = 22 + 5 = 27
Perimeter is the sum of all 3 sides
∴ P = 53 + 53 + 27 = 133 units

Question 4.
In the given figure, angle XOZ and angle ZOY form a linear pair. Find the value of x.

Solution:
Since ∠XOZ & ∠ZOY form a linear pair,
by property, we have their sum to be 180°
∴ ∠XOZ + ∠ZOY = 180°
3x – 2 + 5x + 6 = 180°
8x + 4 = 180 = 8x = 180 – 4
∴ 8x = 176 ⇒ x = \(\frac{176}{8}\) ⇒ x = 22°
XOZ = 3x – 2 = 3 x 22 – 2 = 66 – 2 = 64°
YOZ = 5x + 6 = 5 x 22 + 6
= 110 + 6 = 116

Question 5.
Draw a graph for the following data:

Does the graph represent a linear relation?
Solution:
Graph between side of square & area

When we plot the graph, we observe that it is not a linear relation.

Challenging Problems

Question 6.
Three consecutive integers, when taken in increasing order and multiplied by 2, 3 and 4 respectively, total up to 74. Find the three numbers.
Solution:
Let the 3 consecutive integers be ‘x’, ’x + 1 & ‘x + 2’
Given that when multiplied by 2, 3 & 4 respectively & added up, we get 74

Simplifying the equation, we get
2x + 3x + 3 + 4x + 8 = 74
9x + 11 = 74
9x = 63 ⇒ x = \(\frac{63}{9}\) = 7
First number = 7
Second numbers = x + 1
Third numbers = x + 2
∴ The numbers are 7, 8 & 9

Question 7.
331 students went on a field trip. Six buses were filled to capacity and 7 students had to travel in a van. How many students were there in each bus?
Solution:
Let the number of students in each bus be ‘x’
number of students in 6 buses = 6 × x = 6x
Apart from 6 buses, 7 students went in van
A total number of students is 331
∴ 6x + 7 = 331
∴ 6x = 331 – 7 = 324
∴ x = \(\frac{324}{6}\) = 54
∴ There are 54 students in each bus.

Question 8.
A mobile vendor has 22 items, some which are pencils and others are ball pens. On a particular day, he is able to sell the pencils and ball pens. Pencils are sold for ₹ 15 each and ball pens are sold at ₹ 20 each. If the total sale amount with the vendor is ₹ 380, how many pencils did he sell?
Solution:
Let vendor have ‘p’ number of pencils & ‘b’ number of ball pens
Given that total number of items is 22
∴ p + b = 22
Pencils are sold for ₹ 15 each & ball pens for ₹ 20 each
total sale amount = 15 x p + 20 x b
= 15p + 20b which is given to be 380.
∴ 15p + 20b = 380
Dividing by 5 throughout,
\(\frac{15p}{5}\) + \(\frac{20b}{5}\) = \(\frac{380}{5}\)
⇒ 3p + 4b = 76
Multiplying equation (1) by 3 we get
3 x 7 + 3 x b = 22 x 3
⇒ 3p + 3b = 66
Equation (2) – (3) gives

∴ b = 10
∴ p = 12
He sold 12 pencils

Question 9.
Draw the graph of the lines y = x, y = 2x, y = 3x and y = 5x on the same graph sheet. Is there anything special that you find in these graphs?
Solution:

1. y = x
2. y = 2x
3. y = 3x
4. y = 5x

1. y = x
When x = 1, y = 1
x = 2, y = 2
x = 3, y = 2

2. y = 2x
When x = 1, y = 2
X = 2, y = 4
X = 3, y = 6

3. y = 3x
when x = 1, y = 3
x = 2, y = 6
x = 3, y = 9

4. y = 5x
When x = 1, y = 5
x = 2, y = 10
x = 3, y = 15

When we plot the alijpve points & join the points to form line, we notice that the lines become progressively steeper. In other words, the slope keeps increasing.

Question 10.
Consider the number of angles of a convex polygon and the number of sides of that polygon. Tabulate as follows:

Use this draw a graph illustrating the relations hip between the number of angles and the number of sides of a polygon.
Solution:
Angles:

Students can Download Maths Chapter 2 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 2 Chapter 2 Algebra Additional Questions

Question 1.
A bus runs constantly at a speed of 60 km/hr. Draw a time-distance graph for the situation. Also find the

1. Time taken to cover 360 km.
2. Distance covered in 4\(\frac{1}{2}\) hours.

Solution:
Given the bus runs constantly at a speed of 60 km/hr.
i.e. for 1 hour = 60 km
2 hours = 2 x 60 = 120 km
3 hours = 3 x 60 = 180 km
We can tabulate as below,

Take a suitable scale:

1. Mark the number of hours on the x – axis
2. Mark the distance in km on the y – axis
3. Plot the points (1, 60), (2,120), (3, 180), (4, 240) and (5, 300)
4. Join the points and get a straight line from the graph.
   • Time taken to cover 360 km is 6 hours.
   • Distance covered in 4\(\frac{1}{2}\) hours is

Question 2.
A company dealing with finance gives 15% simple interest on deposits made by senior citizens. Illustrate by a graph the relation between the deposit and the interest gained. Use the graph to complete the following.

1. The annual interest obtainable for investment of ₹ 450
2. The amount a senior citizen has to invest to get an annual simple interest of ₹ 100.

Solution:
Using the formula for calculating the simple interest, the following table of values is prepared.


These are the points to be plotted in the graph sheet, let us take the deposits along x – axis and annual simple interest along y – axis.
We choose the scale as follows.
Then we plot the points and draw the straight line.
From the graph we find.

1. Corresponding to ₹ 450 on the x – axis, we get the interest as ₹ 67.5 on the y – axis.
2. Corresponding to ₹ 100 on the y – axis we get the deposit as ₹ 666 on the x – axis.

Question 3.
The following table gives the quantity of petrol and its cost

Plot the graph.
Solution:

1. Take a suitable scale on both the axes. Here we take on the x – axis
   1 cm = 1 litre, on the y axis 1 cm = 70 rupees.
2. Mark number of litres of petrol along the x – axis
3. Mark the cost of petrol along the y – axis.
4. Plot the points (1, 70), (2, 140), (3, 210), (4, 280), (5, 350), (6, 420) and (7,490)
5. Join the points.

The graph can help us to estimate few more things also.