Tamil Nadu 12th Maths Model Question Paper 3 English Medium

Students can Download Tamil Nadu 12th Maths Model Question Paper 3 English Medium Pdf, Tamil Nadu 12th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 12th Maths Model Question Paper 3 English Medium

Instructions:

1.  The question paper comprises of four parts.
2.  You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. questions of Part I, II. III and IV are to be attempted separately
4. Question numbers 1 to 20 in Part I are objective type questions of one -mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-marks questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Parr III are three-marks questions, These are to be answered in about three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-marks questions. These are to be answered) in detail. Draw diagrams wherever necessary.

Time: 3 Hours
Maximum Marks: 90

Part – I

I. Choose the correct answer. Answer all the questions.  [20 × 1 = 20]

Question 1.
If (QAB)^-1 = \(\left[\begin{array}{cc}
12 & -17 \\
-19 & 27
\end{array}\right]\) and A^-1 = \(\left[\begin{array}{cc}
1 & -1 \\
-2 & 3
\end{array}\right]\) then B^-1 = ……………

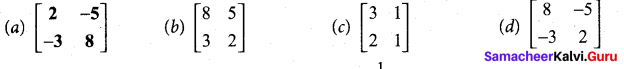
Answer:
(a) \(\left[\begin{array}{cc}
2 & -5 \\
-3 & 8
\end{array}\right]\)

Question 2.
If z is a complex number such that z ∈ C\R and \(z+\frac{1}{z}\) ∈ R, then |z| is ……………
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(b) 1

Question 3.
Let A = \(\left[\begin{array}{ccc}
2 & -1 & 1 \\
-1 & 2 & -1 \\
1 & -1 & 2
\end{array}\right]\) and 4B = \(\left[\begin{array}{ccc}
3 & 1 & -1 \\
1 & 3 & x \\
-1 & 1 & 3
\end{array}\right]\). If B is the inverse of A, then the value of x is ……………
(a) 2
(b) 4
(c) 3
(d) 1
Answer:
(d) 1

Question 4.
If sin^-1x + sin^-1y = \(\frac{2 \pi}{3}\) then cos^-1x + cos^-1y is equal to ……………
(a) \(\frac{2 \pi}{3}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{6}\)
(d) π
Answer:
(b) \(\frac{\pi}{3}\)

Question 5.
The eccentricity of the ellipse (x – 3)² + (y – 4)² = \(\frac{y^{2}}{9}\) is ……………
(a) √3/2
(b) 1/3
(c) 3√2
(d) 1/√3
Answer:
(b) 1/3

Question 6.
The directrix of the parabola y² = 4x is ……………
(a) y = -1
(b) x = -1
(c) y = 1
(d) x = 1
Answer:
(b) x = -1

Question 7.
The angle between the line \(\vec{r}=(\hat{i}+2 \hat{j}-3 \hat{k})+t(2 \hat{i}+\hat{j}-2 \hat{k})\) and the plane \(\vec{r} \cdot(\hat{i}+\hat{j})+4=0\) is ……………
(a) 0°
(b) 30°
(c) 45°
(d) 90°
Answer:
(c) 45°

Question 8.
The d.c.s. of a vector whose direction ratios are 2, 3, -6 are

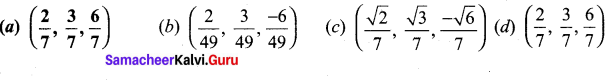
Answer:
(a) \(\left(\frac{2}{7}, \frac{3}{7}, \frac{6}{7}\right)\)

Question 9.
A balloon rises straight up at 10 m/s. An observer is 40 m away from the spot where the balloon left the ground. Find the rate of change of the balloon’s angle of elevation in radian per second when the balloon is 30 metres above the ground.
(a) 1/25 radians/sec
(b) 4/25 radians/sec
(c) 1/5 radians/sec
(d) 1/3 radians/sec
Answer:
(b) 4/25 radians/sec

Question 10.
The asymptote to the curve y²(2 +x) = x² (6 – x) is
(a) x = 2
(b) x = -2
(c) x = 6
(d) x = -6
Answer:
(b) x = -2

Question 11.
The change in the surface area S = 6x² of a cube when the edge length varies from x₀ to x₀ + dx is
(a) 12x₀ + dx
(b) 12x₀dx
(c) 6x₀dx
(d) 6x₀ + dx
Answer:
(b) 12x₀dx

Question 12.
The differential of y if y = sin 2x is
(a) 2 cos 2x
(b) 2 cos 2x.dx
(c) -2 cos lx.dx
(d) cos2x.dx
Answer:
(b) 2 cos 2x.dx

Question 13.
The value of \(\int_{-4}^{4}\left[\tan ^{-1}\left(\frac{x^{2}}{x^{4}+1}\right)+\tan ^{-1}\left(\frac{x^{4}+1}{x^{2}}\right)\right] d x\) is
(a) π
(b) 2π
(c) 3π
(d) 4π
Answer:
(d) 4π

Question 14.
\(\begin{aligned}
&\int^{b} f(x) d x=\\
&a
\end{aligned}\) ………

Answer:
(b) \(-\int_{b}^{a} f(x) d x\)

Question 15.
The integrating factor of the differential equation \(\frac{d y}{d x}+y=\frac{1+y}{x}\) is
(a) \(\frac{x}{e^{\lambda}}\)
(b) \(\frac{e^{x}}{x}\)
(c) λe^x
(d) e^x

Question 16.
The differential equation representing the family of curves y = A cos (x + B), where A and B are parameters, is

Answer:
(b)\(\frac{d^{2} y}{d x^{2}}+y=0\)

Question 17.
A rod of length 21 is broken into two pieces at random. The probability density function of
the shorter of the two pieces is \(f(x)=\left\{\begin{array}{ll}
\frac{1}{l}, & 0< x, \mathrm{x}=0, & l \leq x<2 l
\end{array}\right.\)
The mean and variance of the shorter of the two pieces are respectively ,

Answer:

Question 18.
A computer salesperson knows from his past experience that he sells computers to one in every twenty customers who enter the showroom. What is the probability that he will sell a computer to exactly two of the next three customer?

Answer:
(a) \(\frac{57}{20^{3}}\)

Question 19.
The operation * defined by a * b = \(\frac{a b}{7}\) is not a binary operation on
(a) Q⁺
(b) Z
(c) R
(d) C

Question 20.
If X is a discrete random variable then P(X >a) =
(a) P(X < a)
(b) 1 – P(X < a)
(c) 1 – P(X < a)
(D) = 0

Part – II

II. Answer any seven questions. Question No. 30 is compulsory.[7 x 2 = 14]

Question 21.
State the reason for \(\cos ^{-1}\left[\cos \left(-\frac{\pi}{6}\right)\right] \neq-\frac{\pi}{6}\)
Answer:
We know cos(-θ) = cos θ

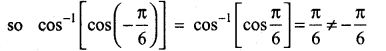
Question 22.
Find the equations of the tangent and normal to the circle x² + y² = 25 at P(-3, 4).
Answer:
Equation of tangent to the circle at P (x₁, y₁) is xx₁ +yy₁ = a².
That is, x(-3) + y(4) = 25
-3x + 4y = 25
Equation of normal is xy₁ – yx₁ = 0
That is, 4x + 3y = 0.

Question 23.
Determine whether the three vectors \(2 \hat{i}+3 \hat{j}+\hat{k}, \hat{i}-2 \hat{j}+2 \hat{k}\) and \(3 \hat{i}+\hat{j}+3 \hat{k}\) are coplanar.
Answer:

Question 24.
Find the intervals of monotonicities and hence find the local extremum for the following
functions f(x) = \(\frac{x}{x-5}\)
Answer:
f(x) = \(\frac{x}{x-5}\)


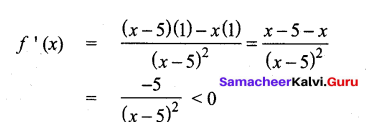
(when x ≠ 5)
f(x) is strictly decreasing on (-∞, 5) and (5, ∞)
And there is no local extremum

Question 25.
Find the linear approximation for f(x) = [altex]\sqrt{1+x}[/latex] , x ≥ -1, at x₀ = 3. Use the linear approximation to estimate f(3.2).
Answer:
We know from that L(x) = f(x₀) + f'(x₀)(x – x₀). We have x₀ = 3, ∆x = 0.2 and hence

Actually, if we use a calculator to calculate we get \(\sqrt{4.2}=2.04939\)

Question 26.
Evaluate \(\int_{0}^{2 \pi} \sin ^{4} x \cos ^{3} d x\)
Answer:
f(x) = sin⁴x cos³x
f(2π – x) = sin⁴(2π – x) cos³ (2π- x)
= sin⁴x cos³x = f(x)
\(2\int_{0}^{\pi} \sin ^{4} x \cos ^{3} d x\)
Again f(x) = sin⁴x cos³x
f(π – x) = sin⁴(π – x) cos³ (π – x)
f(π – x) = – sin⁴(π -x) cos³(π -x) = -f(x) = 0.

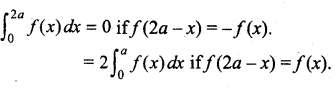
Question 27.
Solve the differential equation \(\frac{d y}{d x}=\sqrt{\frac{1-y^{2}}{1-x^{2}}}\)
Answer:

Question 28.
Suppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function
\(f(x)=\left\{\begin{array}{lr}
k & 200 \leq x \leq 600 \\
0 & \text { otherwise }
\end{array}\right.\)
Find the value of k.
Answer:

Question 29.
Let * be defined on R by (a*b) = a + b + ab – 7. Is * binary on R ? If so, find \(3*\left(\frac{-7}{15}\right)\)
Answer:
a*b = a + b + ab – 7
Now when a, b ∈ R, then ab ∈ R also a + b ∈ R.
So, a + b + ab ∈ R.
We know – 7 ∈ R.
So, a + b + ab – 7 ∈ R.
(i.e.) a * b ∈ R

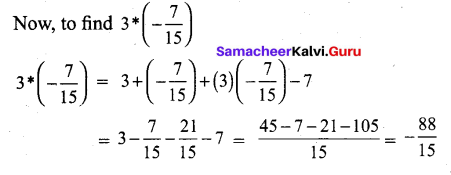
Question 30.
Examine for the rational roots of x⁸ – 3x + 1 = 0.
Answer:
x⁸ – 3x + 1 = 0……..(1)
Here a_n = – 1, a₀ = 1
If p/q is a rational root of (1)
Then q is a factor a_n, p is a factor of aQ
The possible values of p and q are ±1. Among the possible values 1,-1, [(p,q) = 1]
None of them satisfy the equation (1)
.’. The above equation has no rational roots.

Part – III

III. Answer any seven questions. Question No. 40 is compulsory. [7 x 3 = 21]

Question 31.
Solve the following system of linear equations by matrix inversion method:
2x + 5y = -2, x + 2y = -3
Answer:

Question 32.
If (x₁ + iy₁)(x₂ + iy₂)(x₃ + iy₃)…………(x_n +iy_n) = a + ib , show that
(i) (x₁² + y₁²)(x₂² + y₂²)(x₃² + y₃²)…….(x_n² + y_n²) = a² + b²
(ii)

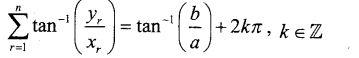
Answer:

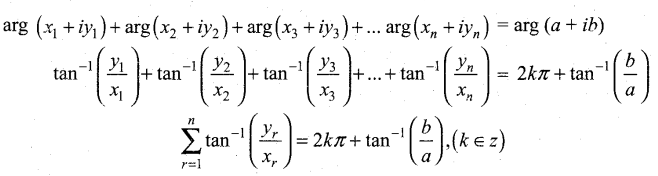
Question 33.
Find the sum of squares of roots of the equation 2x⁴ – 5x³ + 6x² – 3 = 0.
Answer:
The given equation is 2x⁴ – 8x³ + 6x² – 3 = 0.

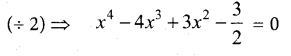
Let the roots be α β γ δ
α + β + γ + δ = -b = 4
α β + βγ + γδ + aδ + aγ + βδ ) = c = 3
α βγ + βγδ + γαδ = -d = 0
αβγδ? = -3/2
To Find α² + β² + γ² + δ ² = ( α + β + γ + δ)² – 2 (αβ + βγ + γδ + αδ + αγ +βδ)
= (4)² – 2(3) = 16 – 6 = 10

Question 34.
Find the non-parametric form of vector equation, and Cartesian equation of the plane
passing through the point (0, 1, -5) and parallel to the straight lines .
\(\vec{r}=(\hat{i}+2 \hat{j}-4 \hat{k})+s(2 \hat{i}+3 \hat{j}+6 \hat{k})\) and \(\hat{r}=(\hat{i}-3 \hat{j}+5 \hat{k})+t(\hat{i}+\hat{j}-\hat{k})\)
Answer:
We observe that the required plane is parallel to the vectors \(\vec{b}=2 \hat{i}+3 \hat{j}+6 \hat{k}, \vec{c}=\hat{i}+\hat{j}-\hat{k}\) and passing through the point (0, 1, —5) with position vector \(\vec{a}\). We observe that \(\vec{b}\) is not parallel to \(\vec{c}\)
Then the vector equation of the plane in non-parametric form is given by

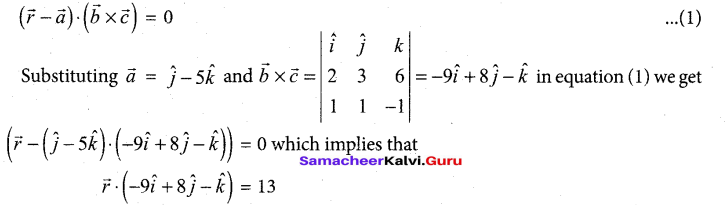
If \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) is the position vector of an arbitrary point on the plane, then from the above equation, we get the Cartesian equation of the plane as -9x + 8y – z = 13 or 9x – 8y + z +13 = 0.

Question 35.
Find ‘C’ of Lagrange’s mean value theorem for the function f(x) = x³ – 5x² – 3x in [1,3]
Answer:
f(x) = x³ – 5x² – 3x
a = 1, b = 3
f(a) = f(1)= 1 – 5 – 3 = -7
f(b) = f (3) = 21 – 5(9) – 3(3)
= 27 – 45 – 9 = -27

f(x) = x³ – 5x²– 3x
f(x) = 3² – 10x – 3
f'(c) = 3c² – 10c – 3 ………(2)
From (1) and (2),
3c² – 10c – 3
3c² – 10c – 3 + 10 = 0
3c² – 10c + 7 =0
3c² – 3c – 7c + 7 = 0

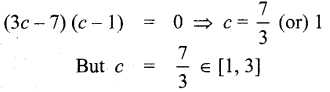
So, Lagrange’s mean value theorem is true with c = 7/3

Question 36.
Using differentials, find the approximate value of each of the following upto 3 places of decimal. (255)^1/4
Answer:

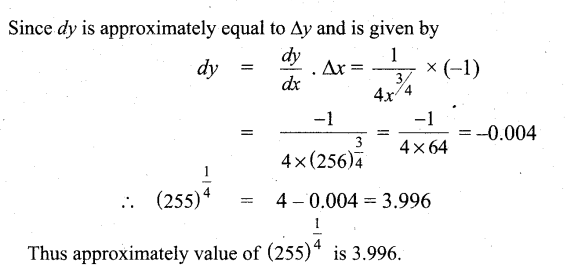
Question 37.
Find the area of the region bounded by the line 6x + 5y = 30, x – axis and the lines x = – 1 and x = 3.
Answer:
The region is sketched in Fig. It lies above the x – axis.
Hence, the required area is given by

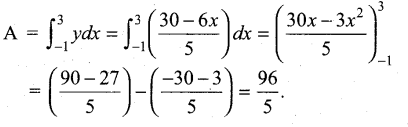
Question 38.
A six sided die is marked ‘2’ on one face, ‘3’ on two of its faces, and ‘4’ on remaining three faces. The die is thrown twice. If X denotes the total score in two throws, find the values of the random variable and number of points in its inverse images.
Answer:
Six sided die marked ‘2’ on one face, ‘3’ on two faces and ‘4’ on three faces.
When it is thrown twice, we get 36 sample points.
‘X’ denotes sum of the face numbers and the possible values of ‘X’ are 4, 5, 6, 7 and 8
For X = 4, the sample point is (2, 2)
For X = 5, the sample points are (2, 3), (3, 2)
For X = 6, the sample points are (3, 3), (2, 4), (4, 2)
For X = 7, the sample points are (3, 4), (4, 3)
For X = 8, the sample point is (4, 4)

Question 39.
Check whether the statement p —>• (q —► p) is a tautology or a contradiction without using the truth table.
Answer:

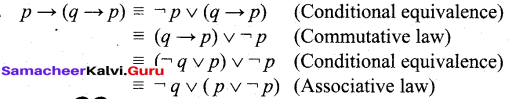
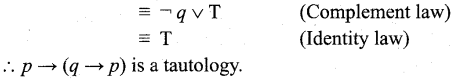
Question 40.
Solve: \(\left(1-x^{2}\right) \frac{d y}{d x}+2 x y=x \sqrt{1-x^{2}}\)
Answer:

Part – IV

IV. Answer all the questions. [7 x 5 = 35]

Question 41.
(a) Solve the following system of homogeneous equation.
3x + 2y + 7z – 0, 4x – 3y – 2z – 0, 5x + 9y + 23z = 0,
Answer:
The matrix form of the above equations is

The above matrix is in echelon form. Here ρ(A, B) = ρ( A) < number of unknowns.
⇒ The system is consistent with infinite number of solutions. To find the solutions.
Writing the equivalent equations.
We get 3x + 2y + 7z = 0
-17y – 34z = 0
Taking z = t in (2) we get -17y – 34t = 0

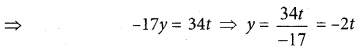
Taking z = t; y = -2t in (1) we get
3x + 2 (-2t) + 7t= 0
3x – 4f + 7f = 0 ⇒ 3x = -3f ⇒ x = -t
So the solution is x = -t; y = -2t; and z=t, t∈R [OR]

(b) Two cards are drawn with replacement from a well shuffled deck of 52 cards. Find the mean and variance for the number of aces.
Answer:
n (S) = 52
Number of aces = n (A) = 4

Let X denotes number of aces when two cards are drawn.

a) Show thatis purely imaginary.

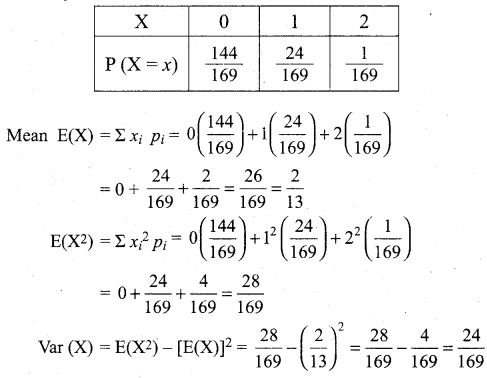
Question 42.
(a) Show that \(\left(\frac{19+9 i}{5-3 i}\right)^{15}-\left(\frac{8+i}{1+2 i}\right)^{15}\) is purely imaginary.
Answer:

[OR]

(b) (i) Define an operation * on Q as follows: a*b = \(\left(\frac{a+b}{2}\right) \) a,b ∈ Q . Examine the closure, commutative, and associative properties satisfied by * on Q
(ii) Define an operation * on Q as follows: a*b = \(\left(\frac{a+b}{2}\right) \) a,b ∈ Q
existence of identity and the existence of inverse for the operation * on Q
Answer:
(i) 1. Closure property:
Let a, b ∈ Q.
a*b = \(\left(\frac{a+b}{2}\right) \) ∈ Q (∵ a, b, 2 ∈ Q)
So, closure property is satisfied.

2. Commutative property:
Let a,b ∈ Q.
a*b = \(\left(\frac{a+b}{2}\right) \) …..(1)
b*a = \(\left(\frac{a+b}{2}\right) \) ……(2)
(1) = (2) ⇒ Now a * b = b * a
⇒ Commutative property is satisfied.

3. Associative property:
Let a, b,c ∈ Q.
To prove associative property we have to prove that a * (b * c) = (a * b) * c

So, associative property is not satisfied.

(ii) a* b = \(\left(\frac{a+b}{2}\right) \)
Let e ∈ Q be the identity element. Then a * e = a
To find e : a * e = a
(i.e.) \(\left(\frac{a+b}{2}\right) \) = a ⇒a + e = 2a ⇒ e = 2a- a
(i.e.) the identity element e = a which is not possible.
So, the identity element does not exist and so inverse does not exist.

Question 43.
(a) Solve (v – 3) (x – 6) (x – 1) (x + 2) + 54 = 0.
Answer:
(x – 3) (x – 1) (x – 6) (x + 2) + 54 = 0
(x²– 4x + 3) (x² – 4x – 12) + 54 = 0
Put x² – 4x = y
(y + 3)(y – 12) + 54 = 0
y²– 9y – 36 + 54 = 0
y² – 9y + 18 = 0
(y – 3) (y – 6) = 0
(y – 3) = 0
x² – 4x – 3 = 0


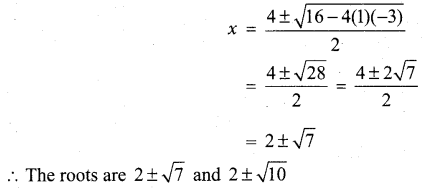
[OR]

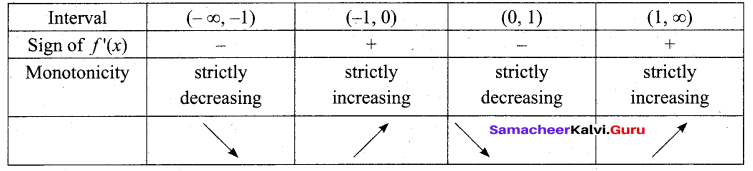
(b) Find the local extrema of the function f(x) = 4x⁶ – 6x⁴
Answer:
Differentiating with respect to x, we get
f (x) = 24x⁵ – 24x³
= 24x³ (x² – 1)
= 24x³ (x + 1) (x – 1)
f’ (x) = 0 ⇒ x = -1, 0, 1. Hence the critical
numbers are x = -1, 0, 1
Now, f'”(x) = 120x⁴ – 72x² = 24x² (5x² – 3)
⇒ f” (-1)= 48, f” (0) = 0, f”(1) = 48.
As f” (-1) and f”(1) are positive by the second derivative test, the function f(x) has local minimum. But at x = 0, f ” (0) = 0. That is the second derivative test does not give any information about local extrema at x = 0 . Therefore, we need to go back to the first derivative test. The intervals of monotonicity is tabulated in the table.

Question 44.
(a) Prove that \(\tan ^{-1} \frac{2}{11}+\tan ^{-1} \frac{7}{24}=\tan ^{-1} \frac{1}{2}\)
Answer:

(b) If v(x, y) = \(\log \left(\frac{x^{2}+y^{2}}{x+y}\right)\), prove that \(x \frac{\partial v}{\partial x}+y \frac{\partial v}{\partial y}=1\)
Answer:

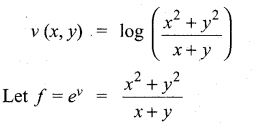
‘ f ‘ is a homogeneous function of degree 1. By Euler’s theorem, we have

Question 45.
(a) Find the equations of the two tangents that can be drawn from (5, 2) to the ellipse 2x² + 7y² = 14 .
Answer:
2x² + 7y² = 14

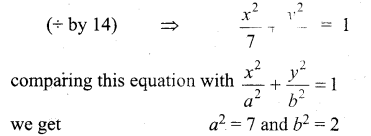
The equation of tangent to the above ellipse will be of the form

Here the tangents are drawn from the point (5, 2)

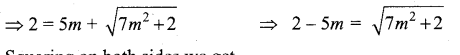
Squaring on both sides we get
(2 – 5m)² = 7m² + 2
25m² + 4 – 20m – 7m² – 2 = 0
18m² – 20m + 2 = 0
(= by 2) => 9m² – 10m + 1 = 0
(9m – 1) (m – 1) = 0
m = 1 (or) m = 1/9
When m = 1, the equation of tangent is
y = x + 3 or x-y + 3 = 0
When m = 1/9 the equation of tangent is 9

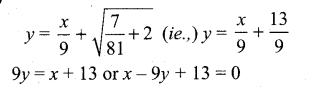
[OR]

(b) Find the coordinates of the foot of the perpendicular and length of the perpendicular from the point (4, 3, 2) to the plane x + 2y + 3z = 2.
Answer:

Direction of the normal plane (1, 2, 3) JP(4, 3,2)
d.c.s of the PQ is\(\frac{x_{1}-4}{1}=\frac{y_{1}-3}{2}=\frac{z_{1}-2}{3}=k\)
x₁k + 4, y₁ = 2k + 3, z₁ = 3k + 2
This passes through the plane x + 2y + 3z = 2
k + 4 + 2(2 k + 3) + 3(3 k + 2) = 2
k+ 4 + 4k + 6 + 9k + 6 = 2
14k = 2 – 16
14k = -14
k = -1
∴ The coordinate of the foot of the perpendicular is (3, 1, -1)
∴ Length of the perpendicular to the plane is

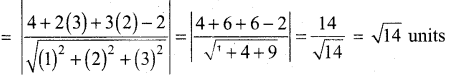
Question 46.
(a) Solve (x + y)²\(\frac{d y}{d x}\) = a² dx
Answer:
Put x+y = z. Differentiating with respect to x we get

(b) A police jeep, approaching an orthogonal intersection from the northern direction, is chasing a speeding car that has turned and moving straight east. When the jeep is 0.6 km north of the intersection and the car is 0.8 km to the east. The police determine with a radar that the distance between them and the car is increasing at 20 km/hr. If the jeep is moving at 60 km/hr at the instant of measurement, what is the speed of the car?
Answer:

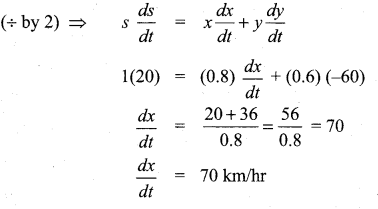
Question 47.
(a) Let w(x, y’ z) = \(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}(x, y, z)\) ≠ (0, 0, 0). Show that \(\frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}}+\frac{\partial^{2} w}{\partial z^{2}}=0\)
Answer:

(b) Evaluate \(\int_{0}^{\frac{\pi}{2}} \frac{e^{-\tan x}}{\cos ^{6} \pi x} d x\)
Answer: