Students can Download Tamil Nadu 12th Maths Model Question Paper 5 English Medium Pdf, Tamil Nadu 12th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 12th Maths Model Question Paper 5 English Medium
Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- questions of Part I, II. III and IV are to be attempted separately
- Question numbers 1 to 20 in Part I are objective type questions of one -mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
- Question numbers 21 to 30 in Part II are two-marks questions. These are to be answered in about one or two sentences.
- Question numbers 31 to 40 in Parr III are three-marks questions, These are to be answered in about three to five short sentences.
- Question numbers 41 to 47 in Part IV are five-marks questions. These are to be answered) in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Maximum Marks: 90
Part – I
I. Choose the correct answer. Answer all the questions. [20 × 1 = 20]
Question 1.
If A = \(\left[\begin{array}{ll}
2 & 0 \\
1 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
1 & 4 \\
2 & 0
\end{array}\right]\)
then adj (AB)| = ……….
(a) – 40
(b) -80
(c) -60
(b) -20
Answer:
(b) -80
Question 2.
in + 1n+1 + in + 2 + in +3 is ……….
(a) 0
(b) 1
(c)- 1
(d) i
Answer:
(a) 0
![]()
Question 3.
If ω = \(\text { cis } \frac{2 \pi}{3}\) , then the number of distinct roots of
\(\left|\begin{array}{ccc}
z+1 & \omega & \omega^{2} \\
\omega & z+\omega^{2} & 1 \\
\omega^{2} & 1 & z+\omega
\end{array}\right|=0\)
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(a) 1
Question 4.
sin-1(cos x) = \(\frac{\pi}{2}-x\) is valid for ……….
(a) -π ≤ x ≤0
(b) 0 ≤ x ≤ π
(c) \(-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}\)
(d) \(-\frac{\pi}{4} \leq x \leq \frac{3 \pi}{4}\)
Answer:
(b) 0 ≤ x ≤ π
Question 5.
tan-1 x + cot-1 = …….
(a) 1
(b) -π
(c) π/2
(d) π
Answer:
(c) π/2
Question 6.
The equation of the normal to the circle x2 + y2 – 2x – 2y + 1 = 0 which is parallel to the line 2x + 4y = 3 is …………..
(a) x + 2y = 3.
(b) x + 2y + 3 = 3
(c) 2x + 4y + 3 = 0
(d) x – 2y + 3 = 0
Answer:
(a) x + 2y = 3.
Question 7.
The axis of the parabola x2 = 20y is ……….
(a) y = 5
(b) x = 5
(c) x = 0
(d) y = 0
Answer:
(c) x = 0
![]()
Question 8.
If \(\vec{a} \times(\vec{b} \times \vec{c})=(\vec{a} \times \vec{b}) \times \vec{c}\) for non-coplanar vectors \(\vec{a}, \vec{b}, \vec{c}\) then…….
(a) \(\vec{a}\) parallel to \(\vec{b}\)
(b) \(\vec{b}\) parallel to \(\vec{c}\)
(c) \(\vec{c}\) parallel to \(\vec{a}\)
(d) \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\)
Question 9.
The vector equation of a plane whose distance from the origin is p and perpendicular to a unit vector n̂ is ….
(a) \(\vec{r} \cdot \vec{n}=p\)
(b) \(\begin{aligned}
&-n\\
&r \cdot n=q
\end{aligned}\)
(c) \(\vec{r} \times \vec{n}=p\)
(d) \(\vec{r} \cdot \hat{n}=p\)
Question 10.
The point of inflection of the curve y=(x – 1)3 is …………..
(a) (0,0)
(b) (0,1)
(c) (1,0)
(d) (1,1)
Answer:
(c) (1,0)
Question 11.
The asymptote to the curve y2(1 + x) = x2 (1 – x) is …………..
(a) x = 1
(b) y = 1
(c) y = -1
(d) x = -1
Answer:
(d) x = -1
Question 12.
The solution of a linear differential equation ax + Px = Q where P and Q are function of y, is ……….
(a) y (I.F) = ∫(I.F) Q dx + c
(b) y (I.F) = ∫(1.F) Q dy + c
(c) y (I.F) = ∫(1.F) Q dy + c .
(d) x (I.F) = ∫(1.F) Q dx + c
Question 13.
A circular template has a radius of 10 cm. The measurement of radius has an approximate error of 0.02 cm. Then the percentage error in calculating area of this template is ……..
(a) 0.2%
(b) 0.4%
(c) 0.04%
(d) 0.08%
Answer:
(b) 0.4%
Question 14.
For any value of n∈z, \(\int_{0}^{\pi} e^{\cos ^{2} x} \cos ^{3}[(2 n+1) x] d x \) is……….
(a) π/2
(b) π
(c) 0
(d) 2
Answer:
(c) 0
Question 15.
If n is odd then \(\int_{0}^{\pi / 2} \sin ^{n} x d x\) is …. ….

Answer:
(d) \(\frac{n-1}{n} \cdot \frac{n-3}{n-2} \cdot \frac{n-5}{n-4} \dots \frac{2}{3} \cdot 1\)
Question 16.
The solution of \(\frac{d y}{d x}=2^{y-x}\)is ……….
(a) 2x + 2y = c
(b) 2x – 2y = c
(c) \(\frac{1}{2^{x}}-\frac{1}{2^{y}}=c\)
(d) x + y = c
Answer:
(c) \(\frac{1}{2^{x}}-\frac{1}{2^{y}}=c\)
Question 17.
If p and q are the order and degree of the differential equation \(y \frac{d y}{d x}+x^{3}\left(\frac{d^{2} y}{d x^{2}}\right)+x y=\cos x\) when…..
(a) p < q
(b) p = q
(c) p > q
(d) p exists and q does not exist
Answer:
(c) p > q
Question 18.
A pair of dice numbered 1, 2, 3, 4, 5, 6 of a six-sided die and 1, 2, 3, 4 of a four-sided die is rolled and the sum is determined. Let the random variable X denote this sum. Then the number of elements in the inverse image of 7 is ……….
(a) 1
(6) 2
(c) 3
(d) 4
Answer:
(d) 4
![]()
Question 19.
If in 6 trials, X is a binomial variate which follows the relation 9P(X = 4) = P(X = 2),
then the probability of success is …….
(a) 0.125 .
(b) 0.25
(c) 0.375
(d) 0.75
Answer:
(b) 0.25
Question 20.
Which one of the following statements has truth value F ?
(a) Chennai is in India or √2 is an integer
(b) Chennai is in India or √2 is an irrational number
(c) Chennai is in China or √2 is an integer
(d) Chennai is in China or √2 is an irrational number
Answer:
(c) Chennai is in China or √2 is an integer
Part – II
II. Answer any seven questions. Question No. 30 is compulsory. [7 x 2 = 14)
Question 21.
If A = \(\left[\begin{array}{rr}
8 & -4 \\
-5 & 3
\end{array}\right]\), verify that A(adj A) = (adj A)A = |A|I2,

Question 22.
Find the value of \(\sum_{k=1}^{8}\left(\cos \frac{2 k \pi}{9}+i \sin \frac{2 k \pi}{9}\right)\)
Answer:
We know that the 9th roots of unity are 1, 6, 62, …, 08 Sum of the roots:
1 + ω + ω2 + … + ω8 = 0
⇒ ω + ω2 + … + ω8 = -1

Question 23.
Solve the equation 😡4 – 14x2 + 45 = 0.
Answer:
The given equation is x4 – 14x2 + 45 = 0
Let x2 = y
y2 – 14y + 45 = 0 ⇒ (y – 9)(y – 5) = 0
y = 9,5
∴ x2 = 9, x2= 5
x = ±3, x = ±√5
∴ The roots are ±3, ±√5
Question 24.
Find the principal value of sin \(\sin ^{-1}\left(-\frac{1}{2}\right)\) (in radians and degrees).
Answer:

Question 25.
Show that the points (2,3,4),(-1,4,5) and (8,1,2) are collinear.
Answer:
Given points are (2, 3, 4), (-1,4,5) and (8,1,2). Equation of the line joining of the first and
second point is
\(\frac{x-2}{-3}=\frac{y-3}{1}=\frac{z-4}{1}=m(\text { say })\)
(-3m + 2, m + 3, m + 4)
On putting m = -2, we get the third point is (8, 1, 2)
∴ Given points are collinear.
![]()
Question 26.
Evaluate: \(\int_{0}^{2 \pi} \frac{\cos x}{\sqrt{4+3 \sin x}} d x\)
Answer:
I = \(\int_{0}^{2 \pi} \frac{\cos x}{\sqrt{4+3 \sin x}} d x\)
Put 4 + 3 sin x = t, so that 3 cos x dx = dt = cosx dx = \(\frac{1}{3} dt\) When x = 0, t = 4 + 3(0) = 4 and when x = 2π, t = 4+ 3(0) = 4
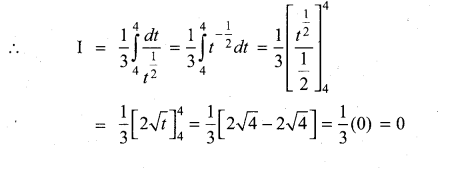
Question 27.
Find the order and degre of the diferential equation center equation \(\frac{d^{2} y}{d x^{2}}-y+\left(\frac{d y}{d x}+\frac{d^{3} y}{d x^{3}}\right)^{\frac{3}{2}}=0\)
Answer:

Question 28.
Suppose the amount of milk sold daily at a milk booth is distributed with a minimum
of 200 litres and a maximum of 600 litres with probability density function
\(f(x)=\left\{\begin{array}{lr}
k & 200 \leq x \leq 600 \\
0 & \text { otherwise }
\end{array}\right.\) Find the probability that daily sales will fall between 300 otherwise litres and 500 litres?
Answer:
The probability that daily sales will fall between 300 litres and 500 litres is
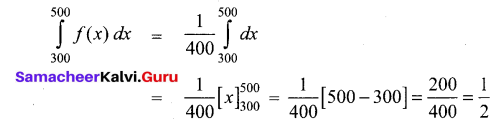
Question 29.
Let A = \(\left(\begin{array}{llll}
1 & 0 & 1 & 0 \\
0 & 1 & 0 & 1 \\
1 & 0 & 0 & 1
\end{array}\right)\) ,B = \(\left(\begin{array}{llll}
0 & 1 & 0 & 1 \\
1 & 0 & 1 & 0 \\
1 & 0 & 0 & 1
\end{array}\right)\) , C = \(\left(\begin{array}{llll}
1 & 1 & 0 & 1 \\
0 & 1 & 1 & 0 \\
1 & 1 & 1 & 1
\end{array}\right)\) be any three boolean matrices of the same type. Find A V B
Answer:
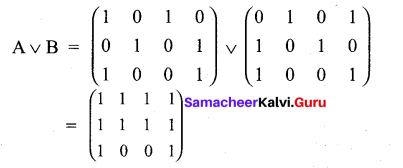
Question 30.
Find the general equation of a circle with centre (-3,- 4) and radius 3 units.
Answer:
Equation of the circle in standard form is (x – h)2 + (y – k)2 = p2
(x-(-3))2 + (y-(-4))2 = 32 .
(x + 3)2 + (y + 4)2 = 32
x2 + y2 + 6x + 8y + 16 = 0.
Part – III
III. Answer any seven questions. Question No. 40 is compulsory. [7 x 3 = 21]
Question 31.
If A = \(-\left[\begin{array}{lll}
8 & 1 & 4 \\
4 & 4 & 7 \\
1 & 8 & 4
\end{array}\right]\) prove that A-1 = AT.
Answer:

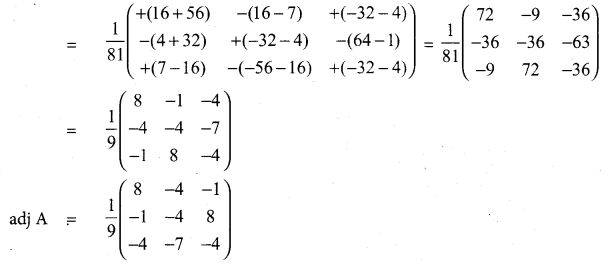
Question 32.
If z1 = 2 + 5i, z2 = -3 – 4i, and z3 = 1 + i, find the additive and multiplicative inverse of z1, z2, and z3.
Answer:

Question 33.
Solve the equation 3x3 – 26x2 + 52x – 24 = 0 if its roots form a geometric progression
Answer:
The given equation is 3x3 – 26x2 + 52x – 24 = 0
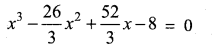
Given that the root are GP
∴ The roots are \(\frac{\alpha}{r}\) , α, αr
\(\frac{\alpha}{r}\) x α x αr = (-8)
α3 = 8
α = 2

Question 34.
Find the value of \(\cot \left(\sin ^{-1} \frac{3}{5}+\sin ^{-1} \frac{4}{5}\right)\)
Answer:

Question 35.
If the normal at the point“ t1‘ on the parabola y2 = 4ax meets the parabola again at the point ‘t2’, then prove that \(t_{2}=-\left(t_{1}+\frac{2}{t_{1}}\right)\)
Answer:
Equation of normal to y2 = 4ax at ‘t’ is y + xt = 2at + at3.
So equation of normal at ‘t1,’ is y + xt1, = 2at1 + at13 ……….(1)
The normal meets the parabola y2 = 4ax at “t2‘ (ie.,) at (at22, 2at2)

Question 36.
Find the coordinates of the foot of the perpendicular drawn from the point (-1, 2, 3) to the straight line \(\vec{r}=(\hat{i}-4 \hat{j}+3 \hat{k})+t(2 \hat{i}+3 \hat{j}+\hat{k})\). Also, find the shortest distance from the given point to the straight line.
Answer:
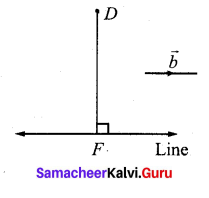
Comparing the given equation \(\vec{r}=(\hat{i}-4 \hat{j}+3 \hat{k})+t(2 \hat{i}+3 \hat{j}+\hat{k})\) with \(\vec{r}=\vec{a}+t \vec{b}\) we get \(\vec{a}=\hat{i}-4 \hat{j}+3 \hat{k} \hat{k}\) and \(\vec{b}=2 \hat{i}+3 \hat{j}+\hat{k}\). We denote the given point (-1,2,3) by D, and the point (1,-4,3) on the straight line by A . If F is the foot of the perpendicular from D to the straight line, then F is of the form (2t+1, 3t – 4, t + 3) and \(\overrightarrow{\mathrm{DF}}=\overrightarrow{\mathrm{OF}}-\overrightarrow{\mathrm{OD}}=(2 t+2) \hat{i}+(3 t-6) \hat{j}+t \hat{k}\) .
Since \(\vec{b}\) is perpendicular to \(\overrightarrow{\mathrm{DF}}\), we have
Line \(\vec{b} \cdot \overrightarrow{\mathrm{DF}}\) = 0 = 2(2t + 2) + 3(3-6) +1(t) = 0 = t=1
Therefore, the coordinate of F is (3,-1, 4).
Now, the perpendicular distance from the given point to the given line is
\(\mathrm{DF}=|\overrightarrow{\mathrm{DF}}|=\sqrt{4^{2}+(-3)^{2}+1^{2}}=\sqrt{26}\) units.
![]()
Question 37.
Find the asymptotes of the curve f(x) = \(\frac{x^{2}+6 x-4}{3 x-6}\)
Answer:
Since the numerator is of highest degree than the denominator. We have a slant
asymptote to find it we have to divide the numerator by the denominator.

So the equation of asymptote is \(y=\frac{x}{3}+\frac{8}{3}\) and 3x – 6 = 0
x = 2
Question 38.
Evaluate: \(\int_{0}^{1} x(1-x)^{n} d x\)
Answer:

Question 39.
For the distribution function given by \(\mathbf{F}(x)=\left\{\begin{array}{ll}
0 & x<0 \\ x^{2} & 0 \leq x \leq 1 \\ 1 & x>1
\end{array}\right.\), find the density function. Also evaluate
(i) P(0.5<x<0.75), (ii) P(X ≤ 50.5) (iii) P(x > 0.75)
Answer:

Question 40.
Let w (x, y) = \(x y+\frac{e^{y}}{y^{2}+1}\) for all (x, y) ∈ R2. Calculate \(\frac{\partial^{2} w}{\partial y \partial x}\) and \(\frac{\partial^{2} w}{\partial x \partial y}\)
Answer:

Part – IV
IV. Answer all the questions. [7 x 5 = 35]
Question 41.
(a) An amount of ₹ 65,000 is invested in three bonds at the rates of 6%, 8% and 10% per annum respectively. The total annual income is ₹ 5,000. The income from the third bond is ₹ 800 more than that from the second bond. Determine the price of each bond. (Use Gaussian elimination method.)
Answer:
Let the amount invested in 6% bond be ₹ x
and the amount invested in 8% bond be ₹y
and the amount invested in 10% bond be ₹z
Now x + y + z = 65000
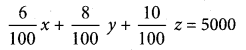
(i.e) 6x + 8y + 10z = 500000
(÷by 2) 3x + 4y + 5z = 250000
Also given that
\frac{10}{100} z-\frac{8}{100} y = 800 (i.e) -8y + 10z = 80000
(÷ by 2) -4y + 5z = 40000

(i.e,) x + y + z = 65000…..(1)
y + 2z = 55000…..(2)
13z = 260000 …..(3)
Form (3) z = \(\frac{260000}{13}\)
Substituting z = ₹ 20000 in (2) we get
y + 40000 = 55000 = y ⇒ 55000 – 40000 = ₹ 15000
Substituting z = ₹ 20000, y = ₹ 15000 in (1) we get
x + 15000 + 20000 = 65000
x = 65000 – 35000 = ₹ 30000
So the amount invested in
6% bond x = ₹ 30000
8% bond y = ₹ 15000
and 10% bond z = ₹ 20000
[OR]
(b) Find the equation of the curve whose slope is \(\frac{y-1}{x^{2}+x}\) and which passes through the point (1, 0).
Answer:

Question 42.
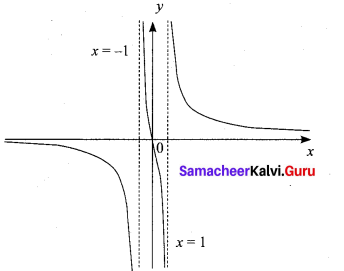
(a) If arg (z – 1) = \(\frac{\pi}{6}\) and arg (z + 1) = 2\(\frac{\pi}{3}\) , then prove that |z| = 1.
Answer:
Given arg (z-1) = \(\frac{\pi}{6}\) = 30° and arg (z + 1) = \(\frac{2 \pi}{3}\) = 120°
So, arg (z + 1) – arg (z – 1) = 120° – 30° = 90°
ie, ang \(\frac{z+1}{z-1}=90^{\circ}=\frac{\pi}{2}\)
\(\operatorname{Re} \frac{z+1}{z-1}=0\) [∴arg = \(\tan \theta=\frac{I P}{R P}\)
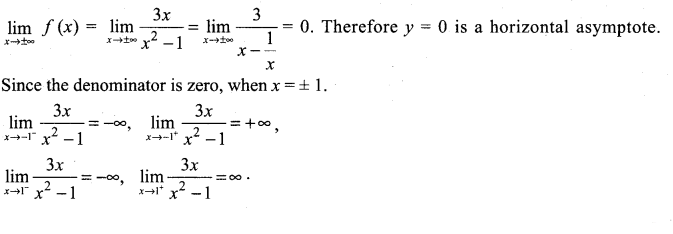
Therefore x= -1 and x=1 are vertical asymptotes.
The rough sketch of the curve is shown on the right side.
![]()
Question 43.
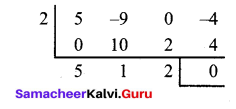
(a) Solve the equation x3 – 9x2 + 14x + 24 = 0 if it is given that two of its roots are in the ratio 3:2.
Answer:
The given equation is x3 – 9x2 +14x + 24 = 0…
Since, the two roots are in the ratio 3:2.
The roots are α , 3λ, 2λ
α + 3λ + 2λ = -b = 9
= a + 5λ = 9 (a) ….. (1)
α (3λ) (2λ) = -24
6λ2a = -24 => λ2α = -4 …….(2)
α = 9 – 5λ
λ2 (9 – 52) = -4
9λ2 – 5λ3 + 4 = 0
5λ3 – 9λ2 – 4 = 0
(λ – 2) (5λ2 + λ + 2) = 0
λ = 2,5λ2 + λ+ 2 = 0 has only Imaginary roots ∆ < 0
∴ when λ = 2, α = 9-5 (2) = 9 – 10 = -1
∴ The roots are α, 3λ, 2λ i.e., -1, 6, 4
[OR]
(b) Show that the lines \(\frac{x+3}{-3}=\frac{y-1}{1}=\frac{z-5}{5}\) and \(\frac{x+1}{-1}=\frac{y-2}{2}=\frac{z-5}{5}\)
are coplanar. Also -3 .. 1 5 -1 2 find the equation of the plane containing these two lines.
Answer:
From the lines we have,
(x1, y1, z1) = (-3, 1, 5); (b1, b2, b3) = (-3, 1, 5)
(x2, y2, z2) = (-1, 2, 5); (d1, d2, d3) = (-1, 2,5)
Conditions for coplanar
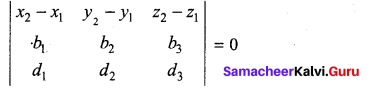
\(\left|\begin{array}{ccc}
2 & 1 & 0 \\
-3 & 1 & 5 \\
-1 & 2 & 5
\end{array}\right|\) = 2(5 – 10) – 1(-15 + 5) + ((-6 + 1) = -10 + 10 = 0
Given two lines are coplanar

(x + 3)(5 – 10) – (y – 1)[-15 + 5) + (2 – 5)(-6 + 1] = 0
5(x + 3) + 10(y – 1) – 5(z – 5) = 0
(÷ by -5) ⇒ (x + 3) – 2 (y – 1) + (z – 5) = 0
x + 3 – 2y + 2 + 2 – 5 = 0 .
or x – 2y + z = 0

(x + 1)(5 – 10) – (y – 2)(-15 + 5) + (z – 5)(-6 + 1) = 0
-5(x + 1) + 10(y – 2) – 5(2 – 5) = 0
(x + 1) – 2(y – 2) + (2 – 5) = 0
x + 1 – 2y + 4 + 2 – 5 = 0
x – 2y + z = 0
Question 44.
(a) Find the area of the region bounded by the parabola y2 = x and the line y = x -2.
Answer:
To find the points of intersection solve the two equations y2 = x and y=x-2
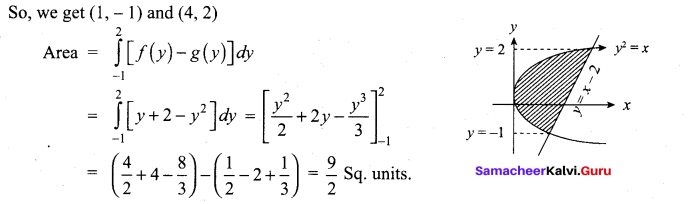
(b) Solve \(\frac{d y}{d x}+\frac{y}{x \log x}=\frac{\sin 2 x}{\log x}\)
Answer:

Question 45.
(a) Solve \(\cos \left(\sin ^{-1}\left(\frac{x}{\sqrt{1+x^{2}}}\right)\right)=\sin \left\{\cot ^{-1}\left(\frac{3}{4}\right)\right\}\)
Answer:
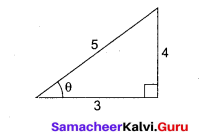

(b) Find the mean and variance of a random variable X, whose probability density x for x 20 function is \(f(x)=\left\{\begin{array}{cc}
\lambda e^{-\lambda x} & \text { for } x \geq 0 \\
0 & \text { otherwise }
\end{array}\right.\)
Answer:
Observe that the given distribution is continuous

Question 46.
(a) Show that the equation of the normal to the curve x= a cos3θ, y = a sin3 θ at ‘θ’ is
x cos θ – y sin θ= a cos 2 θ.
Answer:
x = a cos3θ
\(\frac{d x}{d \theta}\) = a[ 3cos2θ](-sin θ) = -3acos2θ sin θ
y= a sin3θ
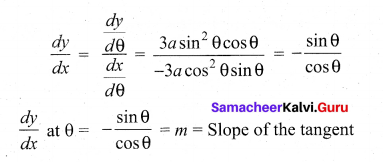
Slope of the normal = \(\frac{-1}{m}=\frac{\cos \theta}{\sin \theta}\)Point = (x1, yy) = (a cos3 θ , a sin3 θ ) sin θ
So, equation of the normal is
Y-a sin3 θ = \(\frac{\cos \theta}{\sin \theta}\)(x- a cos3 θ)
i.e. y sin θ – a sin4 θ = x cos θ – a cos4 θ
x cos θ – sin θ = a cos4 θ – a sin4 θ
i.e x cos θ – y sin θ = a [cos2θ+ sin2θ] [cos2θ – sin2θ]
= a [cos 2 θ]
So, the equation of the normal is x cos θ – y sin θ = a cos 2θ
[OR]
(b) Verify (i) closure property (ii) commutative property (iii) associative property (iv) existence of identity and (v) existence of inverse for the operation +5 on Z5 using table corresponding to addition modulo 5.
Answer:
It is known that Z5 = {[O], [1], [2], [3], [4]} . The table corresponding to addition modulo 5 is as follows: We take reminders {0,1,2,3,4} to represent the classes {[0],[1],[2],[3],[4]}.
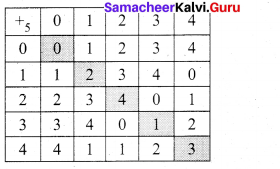
(i) Since each box in the table is filled by exactly one element of Z5, the output a +5b is unique
and hence +5 is a binary operation.
(ii) The entries are symmetrically placed with respect to the main diagonal. So +5 has commutative
property.
(iii) The table cannot be used directly for the verification of the associative property. So it is to be verified as usual.
For instance, (2 +53) +5 4 = 0 +5 4 = 4 (mod 5)
and 2 +5 (3 +5 4) = 2 +5 2 = 4 (mod 5). Hence (2 +53) +5 4 = 2 +5 (3 +54).
Proceeding like this one can verify this for all possible triples and ultimately it can be shown that +5 is associative.
(iv) The row headed by 0 and the column headed by 0 are identical. Hence the identity element is 0.
(v) The existence of inverse is guaranteed provided the identity O exists in each row and each column. From Table-A, it is clear that this property is true in this case. The method of finding the inverse of any one of the elements of Z5 , say 2 is outlined below.
First find the position of the identity element 0 in the III row headed by 2. Move horizonta along the III row and after reaching 0, move vertically above 0 in the IV column, because 0 is in the III row and IV column. The element reached at the topmost position of IV column is 3. This element 3 is nothing but the inverse of 2, because, 2 +5 3 = 0 (mod 5). In this way, the inverse of each and every element of Z5 can be obtained. Note that the inverse of 0 is 0, that of 1 is 4, that of 2 is 3, that of 3 is 2 , and that of 4 is 1.
Question 47.
(a) Identify the type of conic and find centre, foci, vertices, and directrices the following:
18x2 + 12y2 – 144x + 48y + 120 = 0
Answer:
18x2 + 12y2 – 144x + 48y + 120 = 0
(18x2 – 144x) + (12y2 + 48y) = -120
18(x2 – 8x) + 12 ( 12 + 4y) = -120
18(x2 – 8x + 16 – 16) + 12 (12+ 4y + 4 – 4) = -120
18(x – 4)2 – 288 + 12(y + 2)2 – 48 = -120
18(x – 4)2 + 12(y + 2)2 = -120 + 288 + 48 = 216


[OR]
(b) Prove that g(x, y) = x log \(\left(\frac{y}{x}\right)\) is homogeneous; what is the degree? Verify Euler’s Theorem for g.
Answer:
g (x, y) = x log(y/x)
8 (tx, ty) = (tx) log \(\left(\frac{t y}{t x}\right)\)
= txlog \(\left(\frac{y}{x}\right)\)
g(tx, ty) = t g(x, y)
∴ ‘g’is a homogeneous function of degree 1. By Euler’s theorem, we have

∴ Euler’s theorem verified.